Characterizing Chromophoric Dissolved Organic Matter Spatio-Temporal Variability in North Andean Patagonian Lakes Using Remote Sensing Information and Environmental Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area, Lakes, and Region Characteristics
2.2. Water Collection and Processing
2.3. Satellite Imagery Processing
2.4. Model Calibration
2.5. Model Validation
2.6. CDOM Time Series
2.7. Meteorological Variables and Lake Hydrogeomorphic and Watershed Characteristics
2.8. Gradient Boosting Regression
2.9. Statistical Processing
3. Results
3.1. In Situ CDOM Absorption and Water Quality Measurements
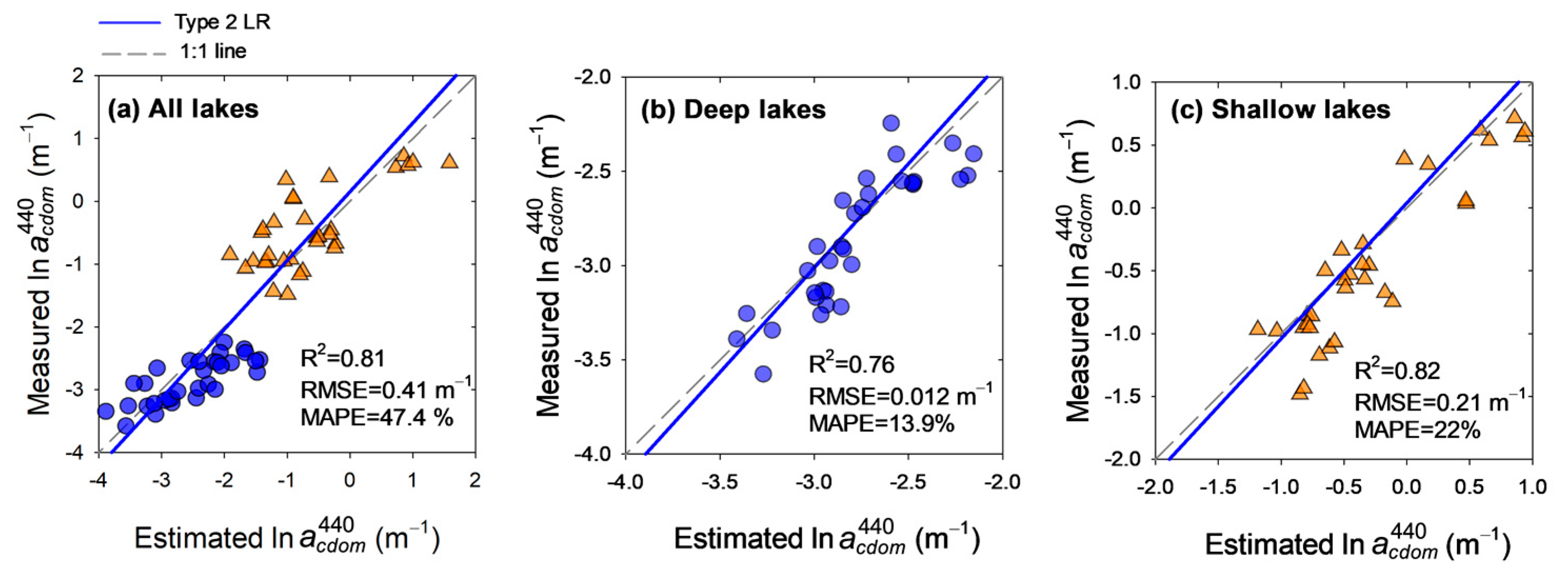
3.2. CDOM Absorption Retrieval Algorithms
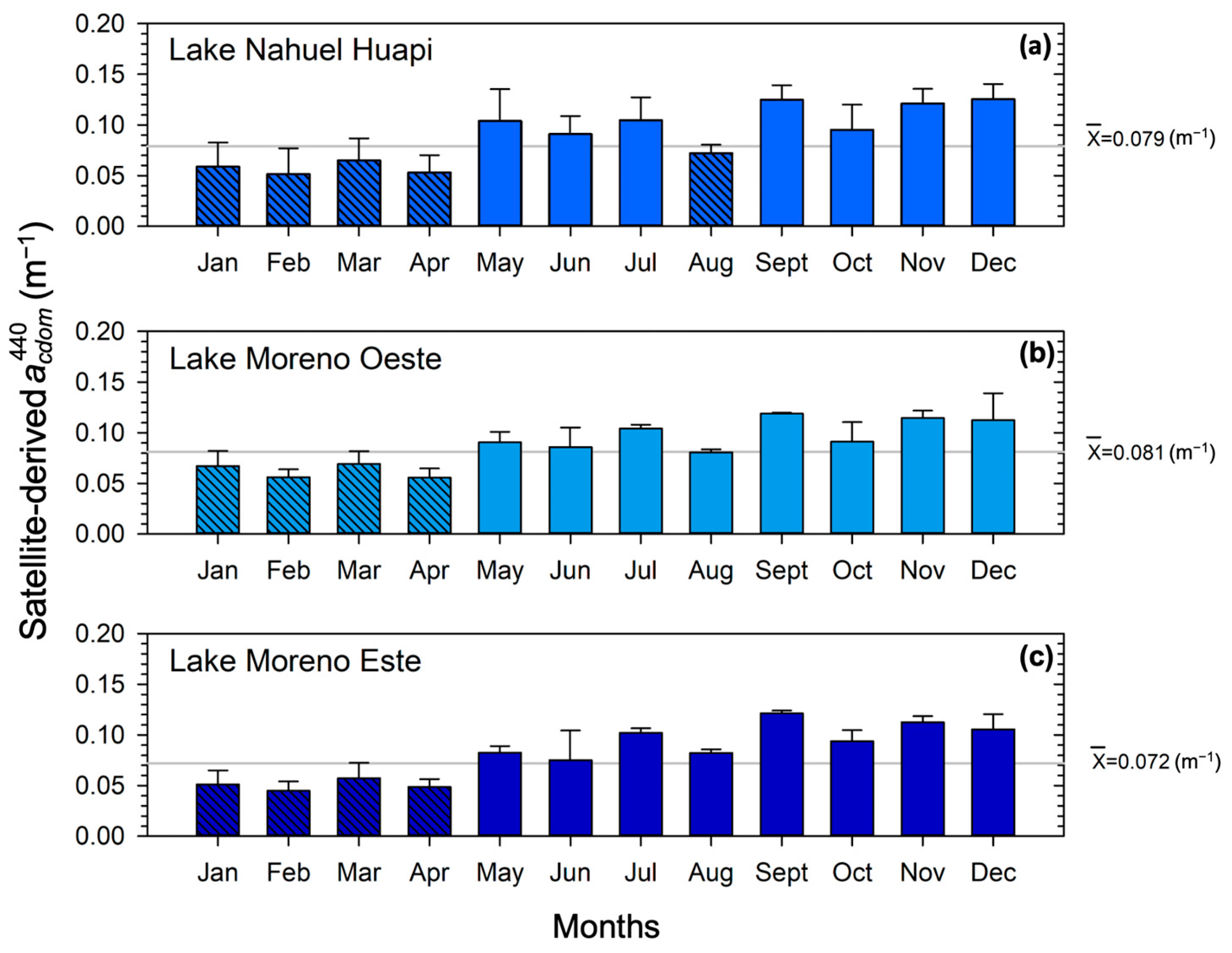
3.3. Spatio-Temporal Variability of CDOM in Study North Andean Patagonian Lakes
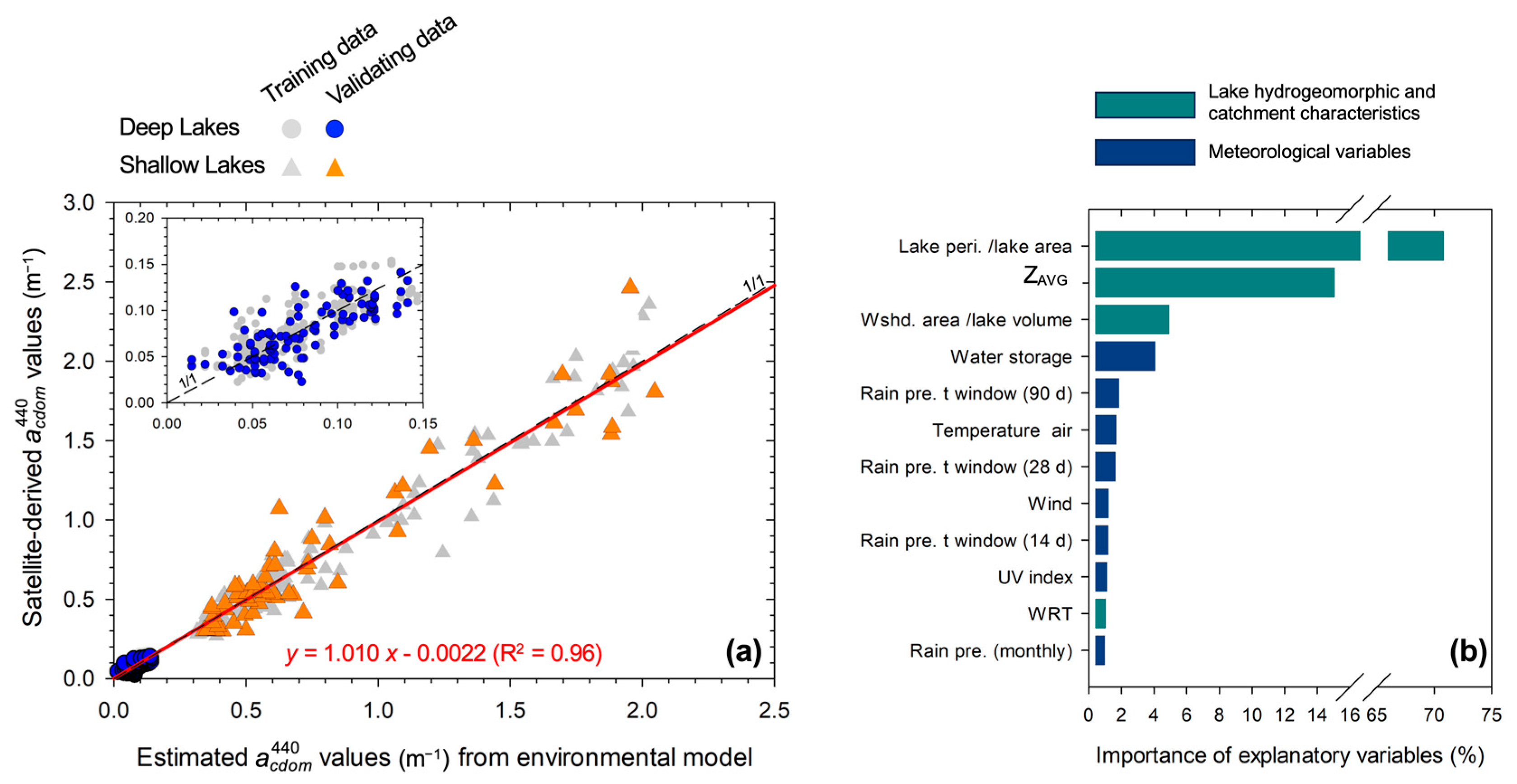
3.4. Relationships Between Environmental Variables and CDOM Dynamics in North Andean Patagonian Lakes
3.4.1. Meteorological Features and Water Storage
3.4.2. Lake Hydrogeomorphic and Watershed Features
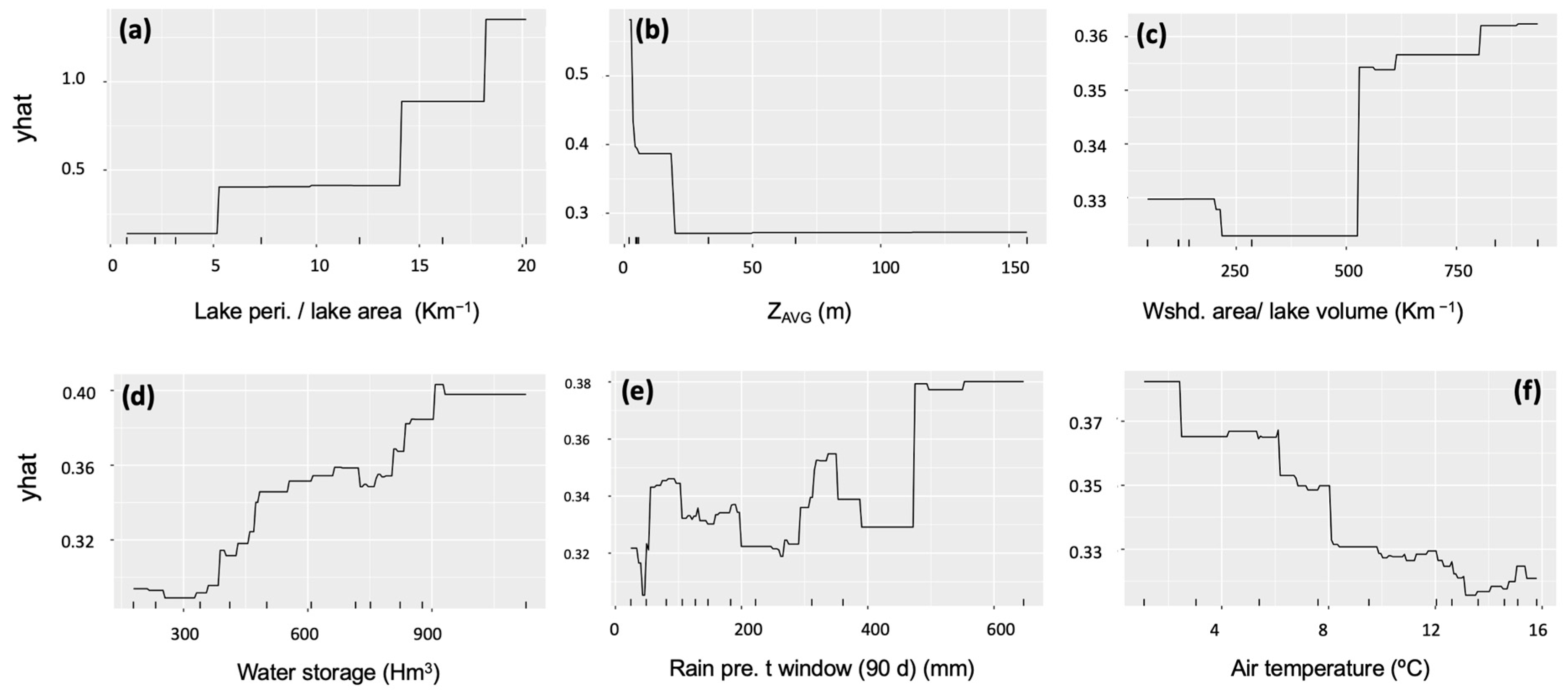
3.4.3. Drivers of CDOM Spatio-Temporal Variability
4. Discussion
4.1. Remote Sensing of CDOM in Inland Waters: From Clear to Brown Lakes
4.2. Spatio-Temporal Variability of CDOM in North Andean Patagonian Lakes and Its Main Driving Forces
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cole, J.J.; Prairie, Y.T.; Caraco, N.F.; McDowell, W.H.; Tranvik, L.J.; Striegl, R.G.; Duarte, C.M.; Kortelainen, P.; Downing, J.A.; Middelburg, J.J.; et al. Plumbing the Global Carbon Cycle: Integrating Inland Waters into the Terrestrial Carbon Budget. Ecosystems 2007, 10, 172–185. [Google Scholar] [CrossRef]
- Battin, T.J.; Luyssaert, S.; Kaplan, L.A.; Aufdenkampe, A.K.; Richter, A.; Tranvik, L.J. The Boundless Carbon Cycle. Nat. Geosci. 2009, 2, 598–600. [Google Scholar] [CrossRef]
- Tranvik, L.J.; Cole, J.J.; Prairie, Y.T. The Study of Carbon in Inland Waters—From Isolated Ecosystems to Players in the Global Carbon Cycle. Limnol. Ocean. Lett. 2018, 3, 41–48. [Google Scholar] [CrossRef]
- Regnier, P.; Resplandy, L.; Najjar, R.G.; Ciais, P. The Land-to-Ocean Loops of the Global Carbon Cycle. Nature 2022, 603, 401–410. [Google Scholar] [CrossRef] [PubMed]
- Mehner, T. Encyclopedia of Inland Waters; Academic Press: Cambridge, MA, USA, 2009; ISBN 0123706262. [Google Scholar]
- Ho, L.T.; Goethals, P.L.M. Opportunities and Challenges for the Sustainability of Lakes and Reservoirs in Relation to the Sustainable Development Goals (SDGs). Water 2019, 11, 1462. [Google Scholar] [CrossRef]
- Aung, H.H. Preserving the cultural heritage a study of the Silversmith in Inlay lake, Myanmar. J. Myanmar Acad. Arts Sci. XVI 2018, 8, 131–158. [Google Scholar]
- Reid, A.J.; Carlson, A.K.; Creed, I.F.; Eliason, E.J.; Gell, P.A.; Johnson, P.T.J.; Kidd, K.A.; MacCormack, T.J.; Olden, J.D.; Ormerod, S.J.; et al. Emerging Threats and Persistent Conservation Challenges for Freshwater Biodiversity. Biol. Rev. 2019, 94, 849–873. [Google Scholar] [CrossRef]
- Dudgeon, D.; Arthington, A.H.; Gessner, M.O.; Kawabata, Z.-I.; Knowler, D.J.; Lévêque, C.; Naiman, R.J.; Prieur-Richard, A.-H.; Soto, D.; Stiassny, M.L.J.; et al. Freshwater Biodiversity: Importance, Threats, Status and Conservation Challenges. Biol. Rev. Camb. Philos. Soc. 2006, 81, 163–182. [Google Scholar] [CrossRef]
- Williamson, C.E.; Brentrup, J.A.; Zhang, J.; Renwick, W.H.; Hargreaves, B.R.; Knoll, L.B.; Overholt, E.P.; Rose, K.C. Lakes as Sensors in the Landscape: Optical Metrics as Scalable Sentinel Responses to Climate Change. Limnol. Oceanogr. 2014, 59, 840–850. [Google Scholar] [CrossRef]
- Williamson, C.E.; Dodds, W.; Kratz, T.K.; Palmer, M.A. Lakes and Streams as Sentinels of Environmental Change in Terrestrial and Atmospheric Processes. Front. Ecol. Environ. 2008, 6, 247–254. [Google Scholar] [CrossRef]
- Adrian, R.; O’Reilly, C.M.; Zagarese, H.; Baines, S.B.; Hessen, D.O.; Keller, W.; Livingstone, D.M.; Sommaruga, R.; Straile, D.; Van Donk, E.; et al. Lakes as Sentinels of Climate Change. Limnol. Oceanogr. 2009, 54, 2283–2297. [Google Scholar] [CrossRef] [PubMed]
- Woolway, R.I.; Kraemer, B.M.; Lenters, J.D.; Merchant, C.J.; O’Reilly, C.M.; Sharma, S. Global Lake Responses to Climate Change. Nat. Rev. Earth Environ. 2020, 1, 388–403. [Google Scholar] [CrossRef]
- Williamson, C.E.; Saros, J.E.; Vincent, W.F.; Smol, J.P. Lakes and Reservoirs as Sentinels, Integrators, and Regulators of Climate Change. Limnol. Oceanogr. 2009, 54, 2273–2282. [Google Scholar] [CrossRef]
- Yang, H.; Kong, J.; Hu, H.; Du, Y.; Gao, M.; Chen, F. A Review of Remote Sensing for Water Quality Retrieval: Progress and Challenges. Remote Sens. 2022, 14, 1770. [Google Scholar] [CrossRef]
- Kirk, J.T.O. Light and Photosynthesis in Aquatic Ecosystems, 3rd ed.; Cambridge University Press: Cambridge, UK, 2011; ISBN 978-0-521-15175-7. [Google Scholar]
- Wetzel, R.G. Limnology Lake and Reservoir Ecosystems, 3rd ed.; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Häder, D.-P.; Kumar, H.D.; Smith, R.C.; Worrest, R.C. Effects of Solar UV Radiation on Aquatic Ecosystems and Interactions with Climate Change. Photochem. Photobiol. Sci. 2007, 6, 267–285. [Google Scholar] [CrossRef]
- Perdue, E.M. Chemical Composition, Structure, and Metal Binding Properties BT—Aquatic Humic Substances: Ecology and Biogeochemistry; Hessen, D.O., Tranvik, L.J., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; ISBN 978-3-662-03736-2. [Google Scholar]
- Anderson, L.E.; Krkošek, W.H.; Stoddart, A.K.; Trueman, B.F.; Gagnon, G.A. Lake Recovery Through Reduced Sulfate Deposition: A New Paradigm for Drinking Water Treatment. Environ. Sci. Technol. 2017, 51, 1414–1422. [Google Scholar] [CrossRef]
- Osburn, C.L.; Stedmon, C.A. Linking the Chemical and Optical Properties of Dissolved Organic Matter in the Baltic—North Sea Transition Zone to Differentiate Three Allochthonous Inputs. Mar. Chem. 2011, 126, 281–294. [Google Scholar] [CrossRef]
- Spencer, R.G.M.; Butler, K.D.; Aiken, G.R. Dissolved Organic Carbon and Chromophoric Dissolved Organic Matter Properties of Rivers in the USA. J. Geophys. Res. Biogeosci. 2012, 117. [Google Scholar] [CrossRef]
- Dekker, A.G.; Pinnel, N.; Gege, P.; Briottet, X.; Cour, A. Feasibility Study for an Aquatic Ecosystem Earth Observing System Version 1.2. In Feasibility Study for an Aquatic Ecosystem Earth Observing System; CEOS: Córdoba, Argentina, 2018. [Google Scholar]
- Brezonik, P.L.; Olmanson, L.G.; Finlay, J.C.; Bauer, M.E. Factors Affecting the Measurement of CDOM by Remote Sensing of Optically Complex Inland Waters. Remote Sens. Environ. 2015, 157, 199–215. [Google Scholar] [CrossRef]
- Zhu, W.; Yu, Q.; Tian, Y.Q.; Becker, B.L.; Zheng, T.; Carrick, H.J. An Assessment of Remote Sensing Algorithms for Colored Dissolved Organic Matter in Complex Freshwater Environments. Remote Sens. Environ. 2014, 140, 766–778. [Google Scholar] [CrossRef]
- Matthews, M.; William Matthews, M. A Current Review of Empirical Procedures of Remote Sensing in Inland and Near-Coastal Transitional Waters. Int. J. Remote Sens. 2010, 32, 6855–6899. [Google Scholar] [CrossRef]
- Li, J.; Yu, Q.; Tian, Y.Q.; Becker, B.L.; Siqueira, P.; Torbick, N. Spatio-Temporal Variations of CDOM in Shallow Inland Waters from a Semi-Analytical Inversion of Landsat-8. Remote Sens. Environ. 2018, 218, 189–200. [Google Scholar] [CrossRef]
- Toming, K.; Kutser, T.; Laas, A.; Sepp, M.; Paavel, B.; Nõges, T. First Experiences in Mapping Lakewater Quality Parameters with Sentinel-2 MSI Imagery. Remote Sens. 2016, 8, 640. [Google Scholar] [CrossRef]
- Olmanson, L.G.; Brezonik, P.L.; Finlay, J.C.; Bauer, M.E. Comparison of Landsat 8 and Landsat 7 for Regional Measurements of CDOM and Water Clarity in Lakes. Remote Sens. Environ. 2016, 185, 119–128. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, W.N.; Tian, Y.Q.; Yu, Q. Estimation of Colored Dissolved Organic Matter from Landsat-8 Imagery for Complex Inland Water: Case Study of Lake Huron. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2201–2212. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, W.; Tian, Y.Q.; Yu, Q.; Zheng, Y.; Huang, L. Remote Estimation of Colored Dissolved Organic Matter and Chlorophyll-a in Lake Huron Using Sentinel-2 Measurements. J. Appl. Remote Sens. 2017, 11, 1. [Google Scholar] [CrossRef]
- Al-Kharusi, E.S.; Tenenbaum, D.E.; Abdi, A.M.; Kutser, T.; Karlsson, J.; Bergström, A.-K.; Berggren, M. Large-Scale Retrieval of Coloured Dissolved Organic Matter in Northern Lakes Using Sentinel-2 Data. Remote Sens. 2020, 12, 157. [Google Scholar] [CrossRef]
- Topp, S.N.; Pavelsky, T.M.; Jensen, D.; Simard, M.; Ross, M.R.V. Research Trends in the Use of Remote Sensing for Inland Water Quality Science: Moving towards Multidisciplinary Applications. Water 2020, 12, 169. [Google Scholar] [CrossRef]
- Sagan, V.; Peterson, K.T.; Maimaitijiang, M.; Sidike, P.; Sloan, J.; Greeling, B.A.; Maalouf, S.; Adams, C. Monitoring Inland Water Quality Using Remote Sensing: Potential and Limitations of Spectral Indices, Bio-Optical Simulations, Machine Learning, and Cloud Computing. Earth Sci. Rev. 2020, 205, 103187. [Google Scholar] [CrossRef]
- Kutser, T.; Casal, G.; Barbosa, C.; Paavel, B.; Renato, F.; Carvalho, L.; Toming, K. Mapping Inland Water Carbon Content with Landsat 8 Data. Int. J. Remote Sens. 2016, 37, 2950–2961. [Google Scholar] [CrossRef]
- Kallio, K.; Attila, J.; Härmä, P.; Koponen, S.; Pulliainen, J.; Hyytiäinen, U.-M.; Pyhälahti, T. Landsat ETM+ Images in the Estimation of Seasonal Lake Water Quality in Boreal River Basins. Environ. Manag. 2008, 42, 511–522. [Google Scholar] [CrossRef] [PubMed]
- Olmanson, L.G.; Page, B.P.; Finlay, J.C.; Brezonik, P.L.; Bauer, M.E.; Griffin, C.G.; Hozalski, R.M. Regional Measurements and Spatial/Temporal Analysis of CDOM in 10,000+ Optically Variable Minnesota Lakes Using Landsat 8 Imagery. Sci. Total Environ. 2020, 724, 138141. [Google Scholar] [CrossRef] [PubMed]
- Koll-Egyed, T.; Cardille, J.A.; Deutsch, E. Multiple Images Improve Lake CDOM Estimation: Building Better Landsat 8 Empirical Algorithms across Southern Canada. Remote Sens. 2021, 13, 3615. [Google Scholar] [CrossRef]
- Kutser, T.; Pierson, D.C.; Kallio, K.Y.; Reinart, A.; Sobek, S. Mapping Lake CDOM by Satellite Remote Sensing. Remote Sens. Environ. 2005, 94, 535–540. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, W.; Pang, S.; Cheng, Q. Applicability Evaluation of Landsat-8 for Estimating Low Concentration Colored Dissolved Organic Matter in Inland Water. Geocarto Int. 2019, 37, 1–15. [Google Scholar] [CrossRef]
- Garcia, R.D.; Diéguez, M.d.C.; Gerea, M.; Garcia, P.E.; Reissig, M. Characterisation and Reactivity Continuum of Dissolved Organic Matter in Forested Headwater Catchments of Andean Patagonia. Freshw. Biol. 2018, 63, 1049–1062. [Google Scholar] [CrossRef]
- Queimaliños, C.; Reissig, M.; Pérez, G.L.; Soto Cárdenas, C.; Gerea, M.; Garcia, P.E.; García, D.; Diéguez, M.C. Linking Landscape Heterogeneity with Lake Dissolved Organic Matter Properties Assessed through Absorbance and Fluorescence Spectroscopy: Spatial and Seasonal Patterns in Temperate Lakes of Southern Andes (Patagonia, Argentina). Sci. Total Environ. 2019, 686, 223–235. [Google Scholar] [CrossRef]
- De Stefano, L.G.; Valdivia, A.S.; Gianello, D.; Gerea, M.; Reissig, M.; García, P.E.; García, R.D.; Soto Cárdenas, C.; Diéguez, M.C.; Queimaliños, C.P.; et al. Using CDOM Spectral Shape Information to Improve the Estimation of DOC Concentration in Inland Waters: A Case Study of Andean Patagonian Lakes. Sci. Total Environ. 2022, 824, 153752. [Google Scholar] [CrossRef]
- Iriondo, M. Quaternary Lakes of Argentina. Palaeogeogr. Palaeoclim. Palaeoecol. 1989, 70, 81–88. [Google Scholar] [CrossRef]
- Zagarese, H.E.; Diaz, M.; Pedrozo, F.; Úbeda, C. Mountain Lakes in Northwestern Patagonia. SIL Proceed. 1922–2010 2000, 27, 533–538. [Google Scholar] [CrossRef]
- Diaz, M.; Pedrozo, F.; Reynolds, C.; Temporetti, P. Chemical Composition and the Nitrogen-Regulated Trophic State of Patagonian Lakes. Limnologica 2007, 37, 17–27. [Google Scholar] [CrossRef]
- Pedrozo, F.; Chillrud, S.; Temporetti, P.; Diaz, M. Chemical Composition and Nutrient Limitation in Rivers and Lakes of Northern Patagonian Andes (39.5°-42° S; 71° W) (Rep. Argentina). SIL Proceed. 1922–2010 1993, 25, 207–214. [Google Scholar] [CrossRef]
- Pérez, G.L. Optical Characterization of Argentinean Lakes, from Deep Andean Lakes to Shallow Pampean Ones. Adv. Limnol. 2014, 65, 409–430. [Google Scholar] [CrossRef]
- Morris, D.P.; Zagarese, H.; Williamson, C.E.; Balseiro, E.G.; Hargreaves, B.R.; Modenutti, B.; Moeller, R.; Queimalinos, C. The Attenuation of Solar UV Radiation in Lakes and the Role of Dissolved Organic Carbon. Limnol. Oceanogr. 1995, 40, 1381–1391. [Google Scholar] [CrossRef]
- Pérez, G.L.; Queimaliños, C.; Modenutti, B.E. Light Climate and Plankton in the Deep Chlorophyll Maxima in North Patagonian Andean Lakes. J. Plankton Res. 2002, 24, 591–599. [Google Scholar] [CrossRef]
- Barros, V.R.; Boninsegna, J.A.; Camilloni, I.A.; Chidiak, M.; Magrín, G.O.; Rusticucci, M. Climate Change in Argentina: Trends, Projections, Impacts and Adaptation. WIREs Clim. Change 2015, 6, 151–169. [Google Scholar] [CrossRef]
- Bianchi, E.; Villalba, R.; Viale, M.; Couvreux, F.; Marticorena, R. New Precipitation and Temperature Grids for Northern Patagonia: Advances in Relation to Global Climate Grids. J. Meteorol. Res. 2016, 30, 38–52. [Google Scholar] [CrossRef]
- Paruelo, J.M.; Beltran, A.; Jobbagy, E.; Sala, O.E.; Golluscio, R.A. The Climate of Patagonia: General Patterns and Controls on Biotic Processes. Ecol. Austral 1998, 8, 85–101. [Google Scholar]
- Garcia, P.E.; Dieguez, M.C.; Queimali??os, C. Landscape Integration of North Patagonian Mountain Lakes: A First Approach Using Characterization of Dissolved Organic Matter. Lakes Reserv. 2015, 20, 19–32. [Google Scholar] [CrossRef]
- Gerea, M.; Pérez, G.L.; Unrein, F.; Soto Cárdenas, C.; Morris, D.; Queimaliños, C. CDOM and the Underwater Light Climate in Two Shallow North Patagonian Lakes: Evaluating the Effects on Nano and Microphytoplankton Community Structure. Aquat. Sci. 2017, 79, 231–248. [Google Scholar] [CrossRef]
- Soto Cárdenas, C.; Gerea, M.; Garcia, P.E.; Pérez, G.L.; Diéguez, M.C.; Rapacioli, R.; Reissig, M.; Queimaliños, C. Interplay between Climate and Hydrogeomorphic Features and Their Effect on the Seasonal Variation of Dissolved Organic Matter in Shallow Temperate Lakes of the Southern Andes (Patagonia, Argentina): A Field Study Based on Optical Properties. Ecohydrology 2017, 10, e1872. [Google Scholar] [CrossRef]
- Green, S.A.; Blough, N.V. Optical Absorption and Fluorescence Properties of Chromophoric Dissolved Organic Matter in Natural Waters. Limnol. Oceanogr. 1994, 39, 1903–1916. [Google Scholar] [CrossRef]
- Helms, J.R.; Stubbins, A.; Ritchie, J.D.; Minor, E.C.; Kieber, D.J.; Mopper, K. Absorption Spectral Slopes and Slope Ratios as Indicators of Molecular Weight, Source, and Photobleaching of Chromophoric Dissolved Organic Matter. Limnol. Oceanogr. 2008, 53, 955–969. [Google Scholar] [CrossRef]
- Mitchell, B.G.; Kahru, M.; Wieland, J.D.; Stramska, M. Determination of Spectral Absorption Coefficients of Particles, Dissolved Material and Phytoplankton for Discrete Water Samples. In Ocean Optics Protocols for Satellite Ocean Color Sensor Validation, Revision 3; Mueller, J.L., Fargion, G.S., Eds.; National Aeronautics and Space Administration, Goddard Space Flight Center: Greenbelt, MD, USA, 2002; Volume 2. [Google Scholar]
- Kishino, M.; Takahashi, M.; Okami, N.; Ichimura, S. Estimation of the Spectral Absorption Coefficients of Phytoplankton in the Sea. Bull. Marine Sci. 1985, 37, 634–642. [Google Scholar]
- Greg Mitchell, B.; Kiefer, D.A. Chlorophyll α Specific Absorption and Fluorescence Excitation Spectra for Light-Limited Phytoplankton. Deep. Sea Res. Part. A Oceanogr. Res. Pap. 1988, 35, 639–663. [Google Scholar] [CrossRef]
- Bricaud, A.; Stramski, D. Spectral Absorption Coefficients of Living Phytoplankton and Nonalgal Biogenous Matter: A Comparison between the Peru Upwelling Areaand the Sargasso Sea. Limnol. Oceanogr. 1990, 35, 562–582. [Google Scholar] [CrossRef]
- Pope, R.M.; Fry, E.S. Pure Water. II. Integrating Cavity Measurements. Appl. Opt. 1997, 36. [Google Scholar] [CrossRef]
- Kutser, T. The Possibility of Using the Landsat Image Archive for Monitoring Long Time Trends in Coloured Dissolved Organic Matter Concentration in Lake Waters. Remote Sens. Environ. 2012, 123, 334–338. [Google Scholar] [CrossRef]
- Chavez, P.S. An Improved Dark-Object Subtraction Technique for Atmospheric Scattering Correction of Multispectral Data. Remote Sens. Environ. 1988, 24, 459–479. [Google Scholar] [CrossRef]
- Congedo, L. Semi-Automatic Classification Plugin: A Python Tool for the Download and Processing of Remote Sensing Images in QGIS. J. Open Source Softw. 2021, 6, 3172. [Google Scholar] [CrossRef]
- QGIS. QGIS Geographic Information System. Open Source Geospatial Foundation Project. 2023. Available online: http://qgis.org (accessed on 20 September 2023).
- Bernstein, L.S. Quick Atmospheric Correction Code: Algorithm Description and Recent Upgrades. Opt. Eng. 2012, 51, 111719. [Google Scholar] [CrossRef]
- Franz, B.A.; Bailey, S.W.; Kuring, N.; Werdell, P.J. Ocean Color Measurements with the Operational Land Imager on Landsat-8: Implementation and Evaluation in SeaDAS. J. Appl. Remote Sens. 2015, 9, 096070. [Google Scholar] [CrossRef]
- Kuhn, C.; Matos, A.D.; Ward, N.; Loken, L.; Oliveira, H.; Kampel, M.; Richey, J.; Stadler, P.; Crawford, J.; Striegl, R.; et al. Remote Sensing of Environment Performance of Landsat-8 and Sentinel-2 Surface Reflectance Products for River Remote Sensing Retrievals of Chlorophyll- a and Turbidity. Remote Sens. Environ. 2019, 224, 104–118. [Google Scholar] [CrossRef]
- Wang, D.; Ma, R.; Xue, K.; Loiselle, S.A. The Assessment of Landsat-8 OLI Atmospheric Correction Algorithms for Inland Waters. Remote Sens. 2019, 11, 169. [Google Scholar] [CrossRef]
- Aboelnaga, A.H.; Abbas Afify, H.; Sharaf El Din, E.H. Evaluation of Different Atmospheric Correction Methods Prior to the Estimation of Total Dissolved Solids Concentrations from Satellite Imagery. J. Eng. Res. 2023, 7, 1–6. [Google Scholar] [CrossRef]
- Gayol, M.P.; Dogliotti, A.I.; Lagomarsino, L.; Zagarese, H.E. Temporal and Spatial Variability of Turbidity in a Highly Productive and Turbid Shallow Lake (Chascomús, Argentina) Using a Long Time-Series of Landsat and Sentinel-2 Data. Hydrobiologia 2024, 851, 4177–4199. [Google Scholar] [CrossRef]
- Dogliotti, A.I.; Piegari, E.; Rubinstein, L.; Perna, P.; Ruddick, K.G. Using the Automated HYPERNETS Hyperspectral System for Multi-Mission Satellite Ocean Colour Validation in the Río de La Plata, Accounting for Different Spatial Resolutions. Front. Remote Sens. 2024, 5, 1354662. [Google Scholar] [CrossRef]
- Khuri, A.I. Introduction to Linear Regression Analysis, Fifth Edition by Douglas C. Montgomery, Elizabeth A. Peck, G. Geoffrey Vining. Int. Stat. Rev. 2013, 81, 318–319. [Google Scholar] [CrossRef]
- Craven, P.; Wahba, G. Smoothing Noisy Data with Spline Functions—Estimating the Correct Degree of Smoothing by the Method of Generalized Cross-Validation. Numer. Math. 1978, 31, 377–403. [Google Scholar] [CrossRef]
- Cawley, G.C.; Talbot, N.L.C. Fast Exact Leave-One-out Cross-Validation of Sparse Least-Squares Support Vector Machines. Neural Netw. 2004, 17, 1467–1475. [Google Scholar] [CrossRef]
- IGN (Instituto Geografico Nacional). Available online: https://www.ign.gob.ar (accessed on 4 February 2022).
- Gianello, D.; Reissig, M.; Pérez, G.L.; Rechencq, M.; De Stefano, L.G.; Queimaliños, C. Effects of Water Level Fluctuations on the Trophic State of a Connected Lacustrine System (Southern Andes, Patagonia, Argentina): Applicability of the CDOM Method as a Tool for Monitoring of Eutrophication. Aquat. Sci. 2024, 86, 50. [Google Scholar] [CrossRef]
- Quiros, R.; Delfino, R.; Cuch, S.; Merello, R. Parte I: Ambientes Lénticos. In Diccionario Geográfico de Ambientes Acuáticos Continentales de la República Argentina; INIDEP Instituto Nacional de Investigación y Desarrollo Pesquero: Mar del Plata, Argentina, 1983. [Google Scholar]
- Soto Cárdenas, C.; Diéguez, M.C.; Ribeiro Guevara, S.; Marvin-DiPasquale, M.; Queimaliños, C.P. Incorporation of Inorganic Mercury (Hg2+) in Pelagic Food Webs of Ultraoligotrophic and Oligotrophic Lakes: The Role of Different Plankton Size Fractions and Species Assemblages. Sci. Total Environ. 2014, 494–495, 65–73. [Google Scholar] [CrossRef] [PubMed]
- Mansilla, C.; Patricia, F.; Mariana, E.G.; María, R. Bioclimatic Influence on Water Chemistry and Dissolved Organic Matter in Shallow Temperate Lakes of Andean Patagonia: A Gradient Approach. Freshwater Biol. 2024, 69, 724–738. [Google Scholar] [CrossRef]
- Queimaliños, C.; Reissig, M.; Diéguez, M.D.C.; Arcagni, M.; Ribeiro Guevara, S.; Campbell, L.; Cárdenas, C.S.; Rapacioli, R.; Arribére, M. Influence of Precipitation, Landscape and Hydrogeomorphic Lake Features on Pelagic Allochthonous Indicators in Two Connected Ultraoligotrophic Lakes of North Patagonia. Sci. Total Environ. 2012, 427–428, 219–228. [Google Scholar] [CrossRef] [PubMed]
- Quirós, R.; Drago, E. Relaciones Entre Variables Físicas, Morfométricas y Climáticas En Lagos Patagónicos. Rev. De La Asoc. De Cienc. Nat. Del Litoral 1985, 16, 181–199. [Google Scholar] [CrossRef]
- Rapacioli, R.A. De La Reserva Natural Urbana Lago Morenito—Laguna Ezquerra. Report 2011, 1–38. [Google Scholar]
- Rapacioli, R.A. Caracterización Hidrológica del lago el Trébol. Personal Comunicación, 2012. [Google Scholar]
- Messager, M.L.; Lehner, B.; Grill, G.; Nedeva, I.; Schmitt, O. Estimating the Volume and Age of Water Stored in Global Lakes Using a Geo-Statistical Approach. Nat. Commun. 2016, 7, 13603. [Google Scholar] [CrossRef]
- Autoridad Interjurisdiccional de Cuencas. Informes Hidrome-Teorológicos 2018–2020; Autoridad Interjurisdiccional de Cuencas: Río Negro, Argentina, 2020. [Google Scholar]
- Dvornikov, Y.; Leibman, M.; Heim, B.; Bartsch, A.; Herzschuh, U.; Skorospekhova, T.; Fedorova, I.; Khomutov, A.; Widhalm, B.; Gubarkov, A.; et al. Terrestrial CDOM in Lakes of Yamal Peninsula: Connection to Lake and Lake Catchment Properties. Remote Sens. 2018, 10, 167. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A Working Guide to Boosted Regression Trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Fernandes, P.M.; Davies, G.M.; Ascoli, D.; Fernández, C.; Moreira, F.; Rigolot, E.; Stoof, C.R.; Vega, J.A.; Molina, D. Prescribed Burning in Southern Europe: Developing Fire Management in a Dynamic Landscape. Front. Ecol. Environ. 2013, 11, e4–e14. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2. [Google Scholar]
- Athey, S.; Imbens, G. Recursive Partitioning for Heterogeneous Causal Effects. Proc. Natl. Acad. Sci. USA 2016, 113, 7353–7360. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. A Language and Environment for Statistical, Foundation for Statistical Computing, Vienna, Austria. 2023. Available online: https://www.R-project.org/ (accessed on 20 January 2024).
- Alcântara, E.; Bernardo, N.; Watanabe, F.; Rodrigues, T.; Rotta, L.; Carmo, A.; Shimabukuro, M.; Gonçalves, S.; Imai, N. Estimating the CDOM Absorption Coefficient in Tropical Inland Waters Using OLI/Landsat-8 Images. Remote Sens. Lett. 2016, 7, 661–670. [Google Scholar] [CrossRef]
- Butman, D.; Stackpoole, S.; Stets, E.; McDonald, C.P.; Clow, D.W.; Striegl, R.G. Aquatic Carbon Cycling in the Conterminous United States and Implications for Terrestrial Carbon Accounting. Proc. Natl. Acad. Sci. USA 2016, 113, 58–63. [Google Scholar] [CrossRef]
- Maciel, D.A.; Pahlevan, N.; Barbosa, C.C.F.; Martins, V.S.; Smith, B.; O’Shea, R.E.; Balasubramanian, S.V.; Saranathan, A.M.; Novo, E.M.L.M. Towards Global Long-Term Water Transparency Products from the Landsat Archive. Remote Sens. Environ. 2023, 299, 113889. [Google Scholar] [CrossRef]
- Park, J.; Khanal, S.; Zhao, K.; Byun, K. Remote Sensing of Chlorophyll-a and Water Quality over Inland Lakes: How to Alleviate Geo-Location Error and Temporal Discrepancy in Model Training. Remote Sens. 2024, 16, 2761. [Google Scholar] [CrossRef]
- Adjovu, G.E.; Stephen, H.; James, D.; Ahmad, S. Overview of the Application of Remote Sensing in Effective Monitoring of Water Quality Parameters. Remote Sens. 2023, 15, 1938. [Google Scholar] [CrossRef]
- Zhao, Z.; Shi, K.; Peng, Y.; Wang, W.; Lai, L.; Zhang, Y.; Zhou, Y.; Zhang, Y.; Qin, B. Widespread Decrease in Chromophoric Dissolved Organic Matter in Chinese Lakes Derived from Satellite Observations. Remote Sens. Environ. 2023, 298, 113848. [Google Scholar] [CrossRef]
- Brezonik, P.; Menken, K.D.; Bauer, M. Landsat-Based Remote Sensing of Lake Water Quality Characteristics, Including Chlorophyll and Colored Dissolved OrganiC Matter (CDOM). Lake Reserv. Manag. 2005, 21, 373–382. [Google Scholar] [CrossRef]
- Kutser, T.; Pierson, D.C.; Tranvik, L.; Reinart, A.; Sobek, S.; Reinart, A.; Kallio, K. Using Satellite Remote Sensing to Estimate the Clolored Dissolved Organic Matter Absorption Coeffecients in Lakes. Ecosystems 2005, 8, 709–720. [Google Scholar] [CrossRef]
- Griffin, C.G.; Frey, K.E.; Rogan, J.; Holmes, R.M. Spatial and Interannual Variability of Dissolved Organic Matter in the Kolyma River, East Siberia, Observed Using Satellite Imagery. J. Geophys. Res. Biogeosci. 2011, 116. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, W.; Chen, J.; Cheng, Q. Remotely Observed Variations of Reservoir Low Concentration Chromophoric Dissolved Organic Matter and Its Response to Upstream Hydrological and Meteorological Conditions Using Sentinel-2 Imagery and Gradient Boosting Regression Tree. Water Sci. Technol. Water Supply 2021, 21, 668–682. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, Y.; Zhang, Y.; Shi, K.; Zhou, Y.; Li, N. Machine Learning Algorithms for Chromophoric Dissolved Organic Matter (Cdom) Estimation Based on Landsat 8 Images. Remote Sens. 2021, 13, 3560. [Google Scholar] [CrossRef]
- Harkort, L.; Duan, Z. Estimation of Dissolved Organic Carbon from Inland Waters at a Large Scale Using Satellite Data and Machine Learning Methods. Water Res. 2023, 229, 119478. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Yan, X.; Kang, X. Applicability Study of Four Atmospheric Correction Methods in the Remote Sensing of Lake Water Color. Geocarto. Int. 2023, 38, 2240282. [Google Scholar] [CrossRef]
- Huang, Y.; Pan, J.; Devlin, A.T. Enhanced Estimate of Chromophoric Dissolved Organic Matter Using Machine Learning Algorithms from Landsat-8 OLI Data in the Pearl River Estuary. Remote Sens. 2023, 15, 1963. [Google Scholar] [CrossRef]
- Lehmann, M.K.; Gurlin, D.; Pahlevan, N.; Alikas, K.; Anstee, J.; Balasubramanian, S.V.; Barbosa, C.C.F.; Binding, C.; Bracher, A.; Bresciani, M.; et al. GLORIA—A Globally Representative Hyperspectral in Situ Dataset for Optical Sensing of Water Quality. Sci. Data 2023, 10, 100. [Google Scholar] [CrossRef]
- Spyrakos, E.; O’Donnell, R.; Hunter, P.D.; Miller, C.; Scott, M.; Simis, S.G.H.; Neil, C.; Barbosa, C.C.F.; Binding, C.E.; Bradt, S.; et al. Optical Types of Inland and Coastal Waters. Limnol. Oceanogr. 2018, 63, 846–870. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, L.; Zhou, Y.; Zhang, L.; Yao, X.; Shi, K.; Jeppesen, E.; Yu, Q.; Zhu, W. Chromophoric Dissolved Organic Matter in Inland Waters: Present Knowledge and Future Challenges. Sci. Total Environ. 2021, 759, 143550. [Google Scholar] [CrossRef]
- Zagarese, H.E.; Ferraro, M.; Queimaliños, C.; Diéguez, M.D.C.; Suárez, D.A.; Llames, M.E. Patterns of Dissolved Organic Matter across the Patagonian Landscape: A Broad-Scale Survey of Chilean and Argentine Lakes. Mar. Freshw. Res. 2017, 68, 2355–2365. [Google Scholar] [CrossRef]
- Pérez, G.L.; Torremorell, A.; Bustingorry, J.; Escaray, R.; Pérez, P.; Diéguez, M.; Zagarese, H. Optical Characteristics of Shallow Lakes from the Pampa and Patagonia Regions of Argentina. Limnol. Ecol. Manag. Inland Waters 2010, 40, 30–39. [Google Scholar] [CrossRef]
- Cardille, J.A.; Leguet, J.B.; del Giorgio, P. Remote Sensing of Lake CDOM Using Noncontemporaneous Field Data. Can. J. Remote Sens. 2013, 39, 118–126. [Google Scholar] [CrossRef]
- Shang, Y.; Liu, G.; Wen, Z.; Jacinthe, P.A.; Song, K.; Zhang, B.; Lyu, L.; Li, S.; Wang, X.; Yu, X. Remote Estimates of CDOM Using Sentinel-2 Remote Sensing Data in Reservoirs with Different Trophic States across China. J. Environ. Manag. 2021, 286, 112275. [Google Scholar] [CrossRef] [PubMed]
- Menken, K.D.; Brezonik, P.L.; Bauer, M.E. Influence of Chlorophyll and Colored Dissolved Organic Matter (CDOM) on Lake Reflectance Spectra: Implications for Measuring Lake Properties by Remote Sensing. Lake Reserv. Manag. 2006, 22, 179–190. [Google Scholar] [CrossRef]
- Xu, J.; Fang, C.; Gao, D.; Zhang, H.; Gao, C.; Xu, Z.; Wang, Y. Optical Models for Remote Sensing of Chromophoric Dissolved Organic Matter (CDOM) Absorption in Poyang Lake. ISPRS J. Photogramm. Remote Sens. 2018, 142, 124–136. [Google Scholar] [CrossRef]
- Yan, N.; Sun, Z.; Huang, W.; Jun, Z.; Sun, S. Assessing Landsat-8 Atmospheric Correction Schemes in Low to Moderate Turbidity Waters from a Global Perspective. Int. J. Digit. Earth 2023, 16, 66–92. [Google Scholar] [CrossRef]
- Ilori, C.O.; Pahlevan, N.; Knudby, A. Analyzing Performances of Different Atmospheric Correction Techniques for Landsat 8: Application for Coastal Remote Sensing. Remote Sens. 2019, 11, 469. [Google Scholar] [CrossRef]
- Raymond, P.A.; Hartmann, J.; Lauerwald, R.; Sobek, S.; McDonald, C.; Hoover, M.; Butman, D.; Striegl, R.; Mayorga, E.; Humborg, C.; et al. Global Carbon Dioxide Emissions from Inland Waters. Nature 2013, 503, 355–359. [Google Scholar] [CrossRef]
- Sobek, S.; Zurbrügg, R.; Ostrovsky, I. The Burial Efficiency of Organic Carbon in the Sediments of Lake Kinneret. Aquat. Sci. 2011, 73, 355–364. [Google Scholar] [CrossRef]
- Xia, F.; Zhou, Y.; Zhou, L.; Zhang, Y.; Jeppesen, E. Recalcitrant Dissolved Organic Matter in Lakes: A Critical but Neglected Carbon Sink. Carbon Res. 2024, 3, 47. [Google Scholar] [CrossRef]
- Macarthur, R.H.; Levin, S.A.; Macarthur, S.A.L.; Recipient, A. The Problem of Pattern and Scale in Ecology: The Robert H. MacArthur Award Lecture. Ecology 1992, 73, 1943–1967. [Google Scholar] [CrossRef]
- Wilkinson, G.M.; Pace, M.L.; Cole, J.J. Terrestrial Dominance of Organic Matter in North Temperate Lakes. Glob. Biogeochem Cycles 2013, 27, 43–51. [Google Scholar] [CrossRef]
- Roiha, T.; Peura, S.; Cusson, M.; Rautio, M. Allochthonous Carbon Is a Major Regulator to Bacterial Growth and Community Composition in Subarctic Freshwaters. Sci. Rep. 2016, 6, 34456. [Google Scholar] [CrossRef] [PubMed]
- Tranvik, L.J.; Downing, J.A.; Cotner, J.B.; Loiselle, S.A.; Striegl, R.G.; Ballatore, T.J.; Dillon, P.; Finlay, K.; Fortino, K.; Knoll, L.B.; et al. Lakes and Reservoirs as Regulators of Carbon Cycling and Climate. Limnol. Oceanogr. 2009, 54, 2298–2314. [Google Scholar] [CrossRef]
- Al-kharusi, E.S.; Hensgens, G.; Abdi, A.M.; Kutser, T.; Karlsson, J.; Tenenbaum, D.E.; Berggren, M. Drought Offsets the Controls on Colored Dissolved Organic Matter in Lakes. Remote Sens. 2024, 16, 1345. [Google Scholar] [CrossRef]
- Schindler, D.W.; Curtis, P.J.; Bayley, S.E.; Parker, B.R.; Beaty, K.G.; Stainton, M.P. Climate-Induced Changes in the Dissolved Organic Carbon Budgets of Boreal Lakes. Biogeochemistry 1997, 36, 9–28. [Google Scholar] [CrossRef]
- Tiwari, T.; Sponseller, R.A.; Laudon, H. The Emerging Role of Drought as a Regulator of Dissolved Organic Carbon in Boreal Landscapes. Nat. Commun. 2022, 13, 5125. [Google Scholar] [CrossRef]
- Pace, M.L.; Cole, J.J. Synchronous Variation of Dissolved Organic Carbon and Color in Lakes. Limnol. Oceanogr. 2002, 47, 333–342. [Google Scholar] [CrossRef]
- Strock, K.E.; Saros, J.E.; Nelson, S.J.; Birkel, S.D.; Kahl, J.S.; McDowell, W.H. Extreme Weather Years Drive Episodic Changes in Lake Chemistry: Implications for Recovery from Sulfate Deposition and Long-Term Trends in Dissolved Organic Carbon. Biogeochemistry 2016, 127, 353–365. [Google Scholar] [CrossRef]
- Weyhenmeyer, G.A.; Willén, E.; Sonesten, L. Effects of an Extreme Precipitation Event on Water Chemistry and Phytoplankton in the Swedish Lake Mälaren. Boreal Environ. Res. 2004, 9, 409–420. [Google Scholar]
- Winterdahl, M.; Erlandsson, M.; Futter, M.N.; Weyhenmeyer, G.A.; Bishop, K. Intra-Annual Variability of Organic Carbon Concentrations in Running Waters: Drivers along a Climatic Gradient. Glob. Biogeochem. Cycles 2014, 28, 451–464. [Google Scholar] [CrossRef]
- Du, Y.X.; Chen, F.Z.; Xiao, K.; Song, C.Q.; He, H.; Zhang, Q.Y.; Zhou, Y.Q.; Jang, K.S.; Zhang, Y.B.; Xing, P.; et al. Water Residence Time and Temperature Drive the Dynamics of Dissolved Organic Matter in Alpine Lakes in the Tibetan Plateau. Glob. Biogeochem. Cycles 2021, 35, e2020GB006908. [Google Scholar] [CrossRef]
- Reche, I.; Pace, M.L. Linking Dynamics of Dissolved Organic Carbon in a Forested Lake with Environmental Factors. Biogeochemistry 2002, 61, 21–36. [Google Scholar] [CrossRef]
- Müller, R.A.; Kothawala, D.N.; Podgrajsek, E.; Sahlée, E.; Tranvik, L.J.; Weyhenmeyer, G.A. Hourly, Daily, and Seasonal Variability in the Absorption Spectra of Chromophoric Dissolved Organic Matter in a Eutrophic, Humic Lake. J. Geophys. Res. Biogeosci. 2014, 119, 661–675. [Google Scholar] [CrossRef]
- Weyhenmeyer, G.A.; Karlsson, J. Nonlinear Response of Dissolved Organic Carbon Concentrations in Boreal Lakes to Increasing Temperatures. Limnol. Oceanogr. 2009, 54, 2513–2519. [Google Scholar] [CrossRef]
- Sobek, S.; Tranvik, L.J.; Prairie, Y.T.; Kortelainen, P.; Cole, J.J. Patterns and Regulation of Dissolved Organic Carbon: An Analysis of 7500 Widely Distributed Lakes. Limnol. Oceanogr. 2007, 52, 1208–1219. [Google Scholar] [CrossRef]
- Toming, K.; Kotta, J.; Uuemaa, E.; Sobek, S.; Kutser, T.; Tranvik, L. Predicting Lake Dissolved Organic Carbon at a Global Scale. Sci. Rep. 2020, 10, 8471. [Google Scholar] [CrossRef]
- Xenopoulos, M.A.; Schindler, D.W. Differential Responses to UVR by Bacterioplankton and Phytoplankton from the Surface and the Base of the Mixed Layer. Freshw. Biol. 2003, 48, 108–122. [Google Scholar] [CrossRef]
- Warner, K.A.; Saros, J.E. Variable Responses of Dissolved Organic Carbon to Precipitation Events in Boreal Drinking Water Lakes. Water Res. 2019, 156, 315–326. [Google Scholar] [CrossRef]
- Zhang, G.; Chen, W.; Xie, H. Tibetan Plateau’s Lake Level and Volume Changes From NASA’s ICESat/ICESat-2 and Landsat Missions. Geophys. Res. Lett. 2019, 46, 13107–13118. [Google Scholar] [CrossRef]
- Liu, C.; Hu, R.; Wang, Y.; Lin, H.; Zeng, H.; Wu, D.; Liu, Z.; Dai, Y.; Song, X.; Shao, C. Monitoring Water Level and Volume Changes of Lakes and Reservoirs in the Yellow River Basin Using ICESat-2 Laser Altimetry and Google Earth Engine. J. Hydro-Environ. Res. 2022, 44, 53–64. [Google Scholar] [CrossRef]
- Garcia, R.D.; Reissig, M.; Queimaliños, C.P.; Garcia, P.E.; Dieguez, M.C. Climate-Driven Terrestrial Inputs in Ultraoligotrophic Mountain Streams of Andean Patagonia Revealed through Chromophoric and Fluorescent Dissolved Organic Matter. Sci. Total Environ. 2015, 521–522, 280–292. [Google Scholar] [CrossRef] [PubMed]
- Soto Cárdenas, C.; Garcia, R.D.; Garcia, P.E. Allochthonous Dissolved Organic Matter Sources: Effect of Photodegradation on Leaf Leachates of Invasive and Native Species from an Andean Patagonia Catchment. Hydrobiologia 2024, 851, 4107–4121. [Google Scholar] [CrossRef]
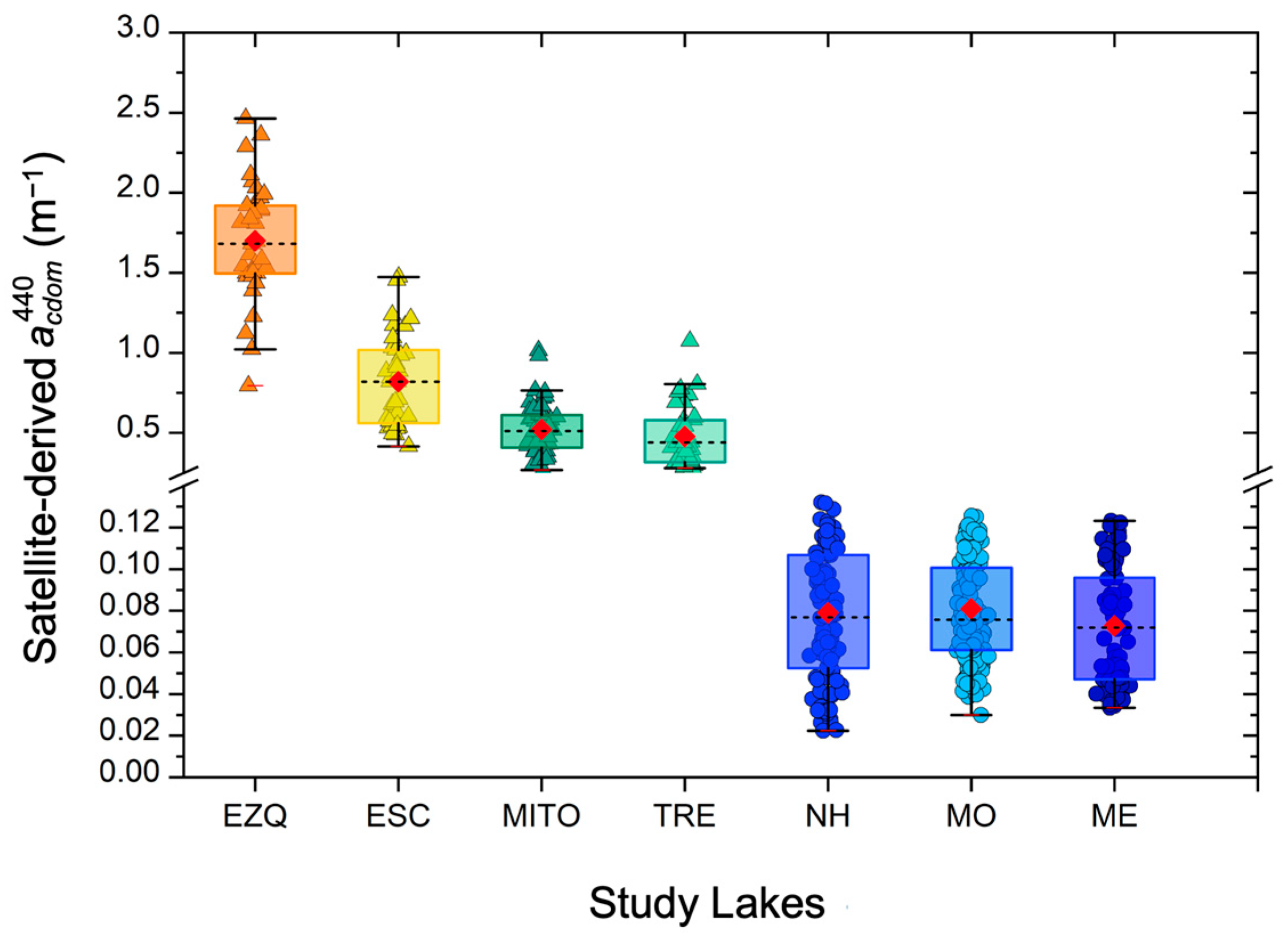
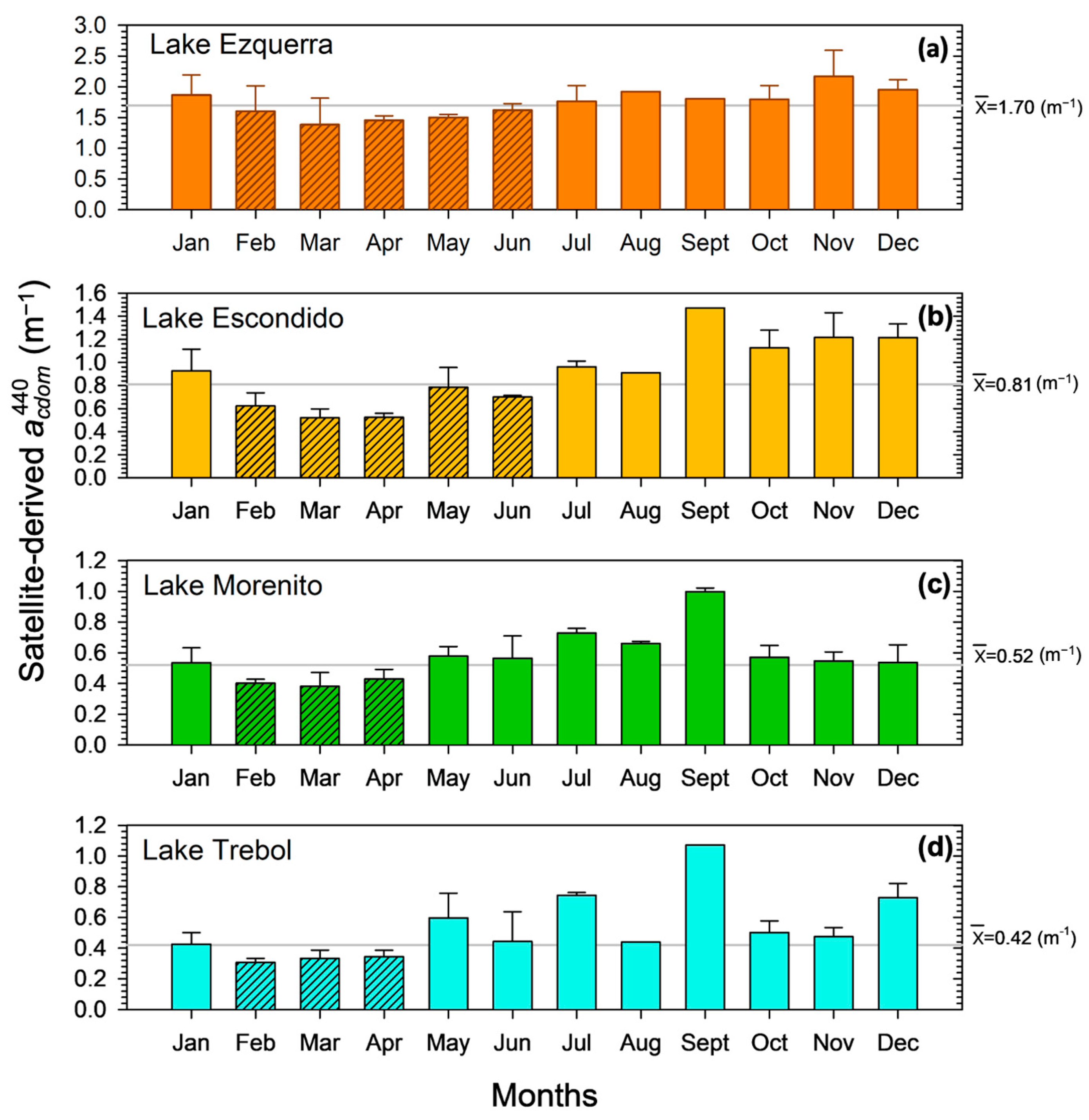
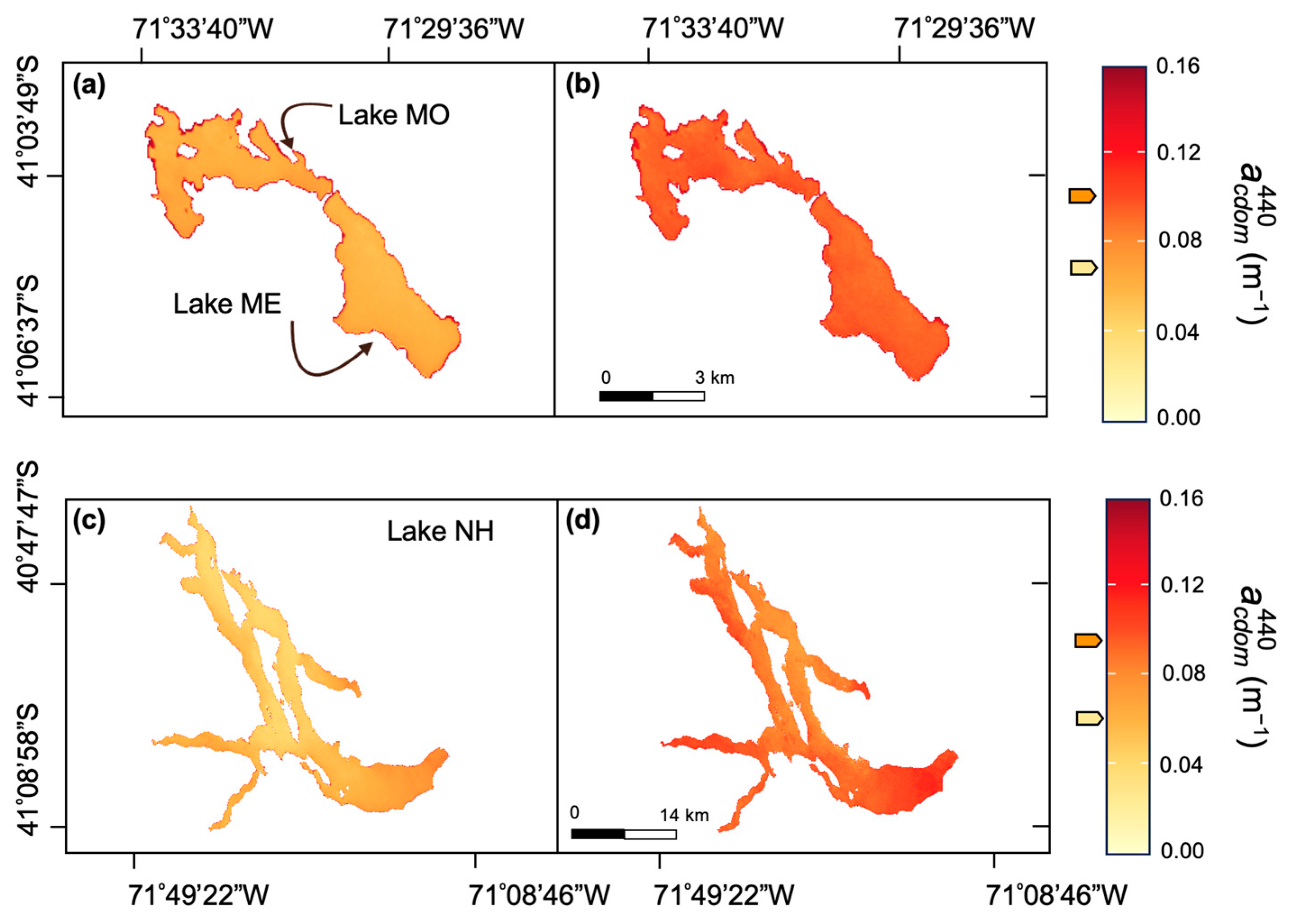
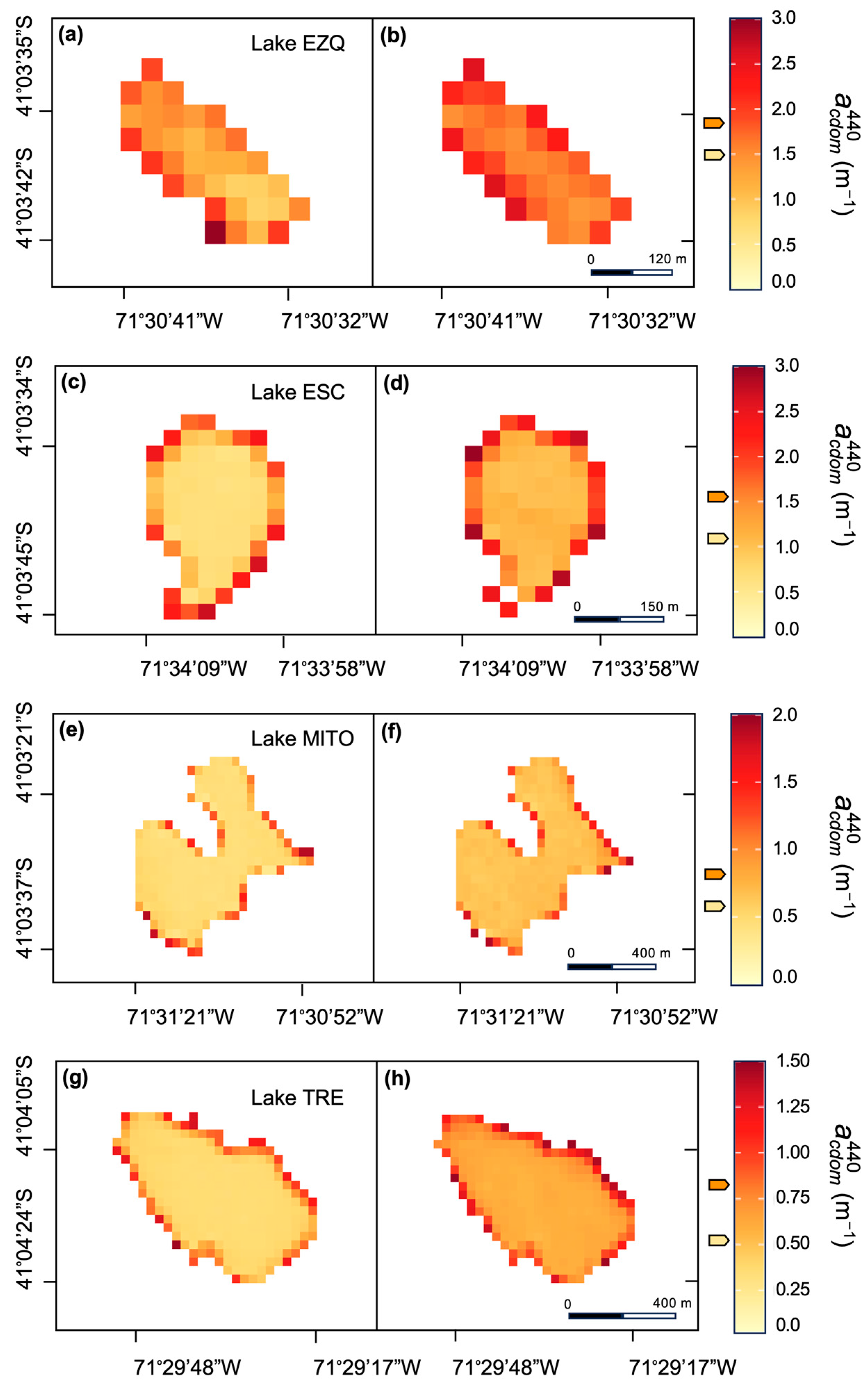

| Lakes | Geographic Location | ZMAX [m] | [m−1] | N | |||
|---|---|---|---|---|---|---|---|
| Average ± 1SD | Min | Max | |||||
| Lake Ezquerra | EZQ | 41°03′S; 71°30′W | 3.6 | 1.83 ± 0.17 | 1.52 | 2.08 | 9 |
| Lake Escondido | ESC | 41°03′S; 71°34′W | 8.0 | 1.05 ± 0.41 | 0.61 | 1.79 | 11 |
| Lake Morenito | MITO | 41°03′S; 71°31′W | 12.0 | 0.47 ± 0.12 | 0.34 | 0.75 | 23 |
| Lake Trébol | TRE | 41°04′S; 71°29′W | 12.0 | 0.30 ± 0.05 | 0.20 | 0.35 | 8 |
| Lake Moreno Oeste | MO | 41°04′S; 71°31′W | 90.0 | 0.063 ± 0.018 | 0.033 | 0.098 | 27 |
| Lake Moreno Este | ME | 41°05′S; 71°29′W | 106.0 | 0.053 ± 0.019 | 0.027 | 0.095 | 21 |
| Lake Nahuel Huapi | NH | 41°02′S; 71°27′W | 454.0 | 0.060 ± 0.034 | 0.033 | 0.106 | 8 |
| Data Levels | Independent Variables [x1, x2] # | Equation Coefficients | R2 | RMSE [m−1] | p Value | ||
|---|---|---|---|---|---|---|---|
| = b0 + b1.x1 +b2.x2 | |||||||
| b0 | b1 | b2 | |||||
| All lakes [N = 63] | |||||||
| TOA | B3/B4, B1/B2 | −35.62 | −11.03 | 40.60 | 0.79 | 0.34 | <0.001 |
| DOS 1 | B2/B4, B3/B1 | 10.67 | −6.35 | −3.74 | 0.84 | 0.40 | <0.001 |
| QUAC | Ln (B2/B4), Ln (B1/B2) | 0.63 | −2.80 | 3.96 | 0.83 | 0.36 | <0.001 |
| L2gen | B2/B4, B1/B2 | −3.11 | −1.71 | 5.40 | 0.74 | 0.38 | <0.001 |
| Deep lakes [N = 32] | |||||||
| TOA | B3/B4 | 5.03 | −4.30 | 0.57 | 0.012 | <0.001 | |
| DOS 1 | B2/B4, B2 | −0.823 | −2.57 | 104.72 | 0.67 | 0.012 | <0.001 |
| QUAC | B2/B4, B2/B5 | −1.67 | −0.18 | −0.18 | 0.81 | 0.010 | <0.001 |
| L2gen | B4 | −3.53 | 97.36 | 0.43 | 0.014 | <0.001 | |
| Shallow lakes [N = 32] | |||||||
| TOA | B4/B3, B1/B2 | −46.86 | 20.12 | 26.17 | 0.83 | 0.23 | <0.001 |
| DOS 1 | Ln (B3/B4), Ln B5 | 2.77 | −4.96 | 0.61 | 0.82 | 0.24 | <0.001 |
| QUAC | Ln (B3/B4), Ln (B4/B5) | 0.15 | −1.8 | −0.48 | 0.85 | 0.22 | <0.001 |
| L2gen | B4/B3, B2/B4 | −7.63 | 8.91 | 0.88 | 0.76 | 0.26 | <0.001 |
| Data Levels | R2 | RMSE [m−1] | MAPE [m−1] | Bias [m−1] | Slope |
|---|---|---|---|---|---|
| All lakes [N = 64] | |||||
| TOA | 0.77 | 0.39 | 61.8 | −0.003 | 1.11 |
| DOS 1 | 0.79 | 0.59 | 47.6 | 0.005 | 1.10 |
| QUAC | 0.81 | 0.41 | 47.4 | −0.005 | 1.09 |
| L2gen | 0.71 | 0.39 | 63.8 | −0.106 | 1.15 |
| Deep lakes [N = 32] | |||||
| TOA | 0.51 | 0.013 | 19.5 | −0.0011 | 1.29 |
| DOS 1 | 0.57 | 0.014 | 17.9 | −0.0008 | 1.19 |
| QUAC | 0.76 | 0.012 | 13.9 | −0.0006 | 1.10 |
| L2gen | 0.36 | 0.015 | 24.3 | −0.0016 | 1.51 |
| Shallow lakes [N = 32] | |||||
| TOA | 0.80 | 0.27 | 23.0 | −0.005 | 1.07 |
| DOS 1 | 0.78 | 0.32 | 25.5 | −0.004 | 1.07 |
| QUAC | 0.82 | 0.21 | 22.0 | −0.018 | 1.08 |
| L2gen | 0.71 | 0.29 | 25.5 | −0.055 | 1.15 |
| Hydrogeomorphic and Catchment Characteristics | Lake Escondido | Lake Trébol | Lake Ezquerra | Lake Morenito | Lake Moreno E. | Lake Moreno O. | Lake Nahuel Huapi |
|---|---|---|---|---|---|---|---|
| Lake perimeter [Km] | 1.46 [54] | 2.27 [76] | 0.88 [77] | 3.98 [54] | 13.30 [81] | 19.30 [81] | 357.40 [78] |
| Lake area [Km2] | 0.09 [54] | 0.31 [76] | 0.42 × 10−1 [77] | 0.33 [54] | 6.14 [81] | 6.10 [81] | 557.00 [78] |
| Lake peri./lake area [Km−1] | 16.13 | 7.32 | 20.70 | 12.09 | 2.16 | 3.16 | 0.64 |
| Lake volume [Km3] | 0.50 × 10−3 [54] | 0.14 × 10−2 [85] | 0.79 × 10−4 [77] | 1.55 × 10−3 [54] | 0.41 [81] | 0.20 [81] | 87.46 [82] |
| ZMAX [m] | 8.05 [54] | 12.00 [79] | 3.60 [77] | 12.00 [79] | 106.00 [81] | 90.00 [81] | 454.00 [78] |
| ZAVG [m] | 5.10 [54] | 6.20 [85] | 1.84 [77] | 5.10 [54] | 67.00 [81] | 33.50 [81] | 156.10 [85] |
| WRT [years] | 0.56 [54] | 1.23 [84] | 0.09 [77,83] | 0.50 [54] | 2.29 [81] | 0.98 [81] | 16.56 [85] |
| Watershed area [Km2] | 0.42 [54] | 1.85 [80] | 0.06 [83] | 1.49 [54] | 116.93 [81] | 23.77 [81] | 4260.00 [78] |
| Wshd. area/lake volume [Km−1] | 838.00 | 1321.43 | 769.62 | 961.29 | 285.19 | 118.85 | 48.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez Valdivia, A.; De Stefano, L.G.; Ferraro, G.; Gianello, D.; Ferral, A.; Dogliotti, A.I.; Reissig, M.; Gerea, M.; Queimaliños, C.; Pérez, G.L. Characterizing Chromophoric Dissolved Organic Matter Spatio-Temporal Variability in North Andean Patagonian Lakes Using Remote Sensing Information and Environmental Analysis. Remote Sens. 2024, 16, 4063. https://doi.org/10.3390/rs16214063
Sánchez Valdivia A, De Stefano LG, Ferraro G, Gianello D, Ferral A, Dogliotti AI, Reissig M, Gerea M, Queimaliños C, Pérez GL. Characterizing Chromophoric Dissolved Organic Matter Spatio-Temporal Variability in North Andean Patagonian Lakes Using Remote Sensing Information and Environmental Analysis. Remote Sensing. 2024; 16(21):4063. https://doi.org/10.3390/rs16214063
Chicago/Turabian StyleSánchez Valdivia, Ayelén, Lucia G. De Stefano, Gisela Ferraro, Diamela Gianello, Anabella Ferral, Ana I. Dogliotti, Mariana Reissig, Marina Gerea, Claudia Queimaliños, and Gonzalo L. Pérez. 2024. "Characterizing Chromophoric Dissolved Organic Matter Spatio-Temporal Variability in North Andean Patagonian Lakes Using Remote Sensing Information and Environmental Analysis" Remote Sensing 16, no. 21: 4063. https://doi.org/10.3390/rs16214063
APA StyleSánchez Valdivia, A., De Stefano, L. G., Ferraro, G., Gianello, D., Ferral, A., Dogliotti, A. I., Reissig, M., Gerea, M., Queimaliños, C., & Pérez, G. L. (2024). Characterizing Chromophoric Dissolved Organic Matter Spatio-Temporal Variability in North Andean Patagonian Lakes Using Remote Sensing Information and Environmental Analysis. Remote Sensing, 16(21), 4063. https://doi.org/10.3390/rs16214063







