Next Article in Journal
Center-Highlighted Multiscale CNN for Classification of Hyperspectral Images
Previous Article in Journal
Intelligent Monitoring Applications of Landslide Disaster Knowledge Graphs Based on ChatGLM2
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 16
Issue 21
10.3390/rs16214057
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Co-Seismic and Post-Seismic Slip Properties Associated with the 2024 M 7.5 Noto Peninsula, Japan Earthquake Determined by GNSS Observations

by
Yunfei Xiang
1,2,*,
Ming Qin
1,
Yuanyuan Chen
1,
Yin Xing
3 and
Yankai Bian
4
1
Department of Geomatics Engineering, Nanjing Forestry University, Nanjing 210037, China
2
College of Oceanography, Hohai University, Nanjing 210024, China
3
School of Geography Science and Geomatics Engineering, Suzhou University of Science and Technology, Suzhou 215009, China
4
School of Geomatics, Zhejiang University of Water Resources and Electric Power, Hangzhou 310018, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2024, 16(21), 4057; https://doi.org/10.3390/rs16214057
Submission received: 26 August 2024 / Revised: 27 October 2024 / Accepted: 29 October 2024 / Published: 31 October 2024
Browse Figures
Versions Notes

Abstract

:
Based on GNSS observations, the co-seismic and post-seismic slip of the 2024 Noto Peninsula earthquake and the spatio-temporal pattern of afterslip are investigated in this paper. The co-seismic slip is mainly distributed in the depth range of 2 to 15 km with the maximum value of 5.94 m. Compared with the co-seismic rupture pattern, a shallow afterslip can be observed after the earthquake, and the afterslip patch is formed northeast of the epicenter. The maximum value of afterslip during the post-seismic 180 days is 1.13 m, which is situated at the longitude of 137.53°, latitude of 37.75°, and epth of 5.43 km. The spatio-temporal evolution of afterslip indicates that the fault activity has continued throughout the post-seismic 180 days, and the coverage and magnitude of afterslip have gradually increased. As time goes on, the fault activity tends to weaken, as evidenced by a decrease in slip rate. The daily images of afterslip demonstrate that the fault activity is particularly strong in the early time period following the earthquake. The maximum value of afterslip in the first week accounts for about 18% of that in the post-seismic 180 days, and the maximum slip rate reaches 0.043 m/day. In addition, the Coulomb stress analysis indicates that afterslip and most aftershocks appear in the positive Coulomb stress region, suggesting that co-seismic Coulomb stress changes may be the driving mechanism of afterslip and aftershocks.

1. Introduction

A powerful M 7.5 earthquake struck off the west coast of Honshu, Japan at 07:10:09 (UTC) on 1 January 2024 according to the United States Geological Survey (USGS). The epicenter of the earthquake was situated in Ishikawa Prefecture, Noto Peninsula (37.49°N, 137.27°E) with a focal depth of 10.0 km, making it a shallow-source earthquake [1,2]. Compared with medium- and deep-source earthquakes, the energy generated by shallow-source earthquakes is released closer to the surface, producing greater damage and impact [3]. The offshore earthquake caused strong shaking on land and triggered a tsunami that killed 241 people in Ishikawa Prefecture [4,5,6]. Focal mechanism solutions of the earthquake suggest that the fault occurs on a moderately dipping reverse fault that strikes southwest or northeast. Japan is a seismically active region due to the subduction of the Pacific Plate, and most earthquakes occur off the east coast [7,8]. The west coast is less seismically active than the major subduction zones in the east coast (Figure 1). Nevertheless, since 1900, 30 earthquakes of M 6 and higher have occurred within 250 km of the 2024 Noto Peninsula earthquake, three of which occurred near the Noto Peninsula. On 16 June 1964, a magnitude 7.6 earthquake erupted 205 km northeast of this earthquake, killing 36 people. On 5 May 2023, a magnitude 6.2 earthquake struck the Noto Peninsula in Japan, killing one person and damaging hundreds of buildings [9,10,11].
Until now, few studies have revealed the fault activity properties in the co-seismic and post-seismic phases of this earthquake. Fujii et al. [12] inverted the co-seismic slip pattern of this earthquake based on constructed fault models using tsunami and GNSS observations, respectively. Then, a joint inversion of co-seismic slip pattern was performed by combining the two data sets. Ma et al. [13] obtained the detailed co-seismic rupture distribution of the 2024 Noto Peninsula earthquake using InSAR, GNSS, and seismological observations. Yang et al. [14] rapidly determined the early afterslip of this earthquake using 19-day post-seismic GNSS observations. The result indicated that the 19-day afterslip was distributed within co-seismic slip asperity and northward of the rupture region. Previously, most studies focused on slow slip transient deformations and seismic swarm activities in the Noto Peninsula. Nakajima [15] revealed the three-dimensional (3D) seismic velocity structure of the Noto Peninsula, Japan based on seismic tomography imaging and found that seismic swarm activity began in December 2020. Amezawa et al. [16] investigated the spatio-temporal properties of seismic swarm activity using relocated epicenters in order to understand the driving factors of the long-lasting seismic swarm activity in the Noto Peninsula. The result indicated that the seismic swarms in the Noto Peninsula consisted of four components. The intermittent fluid supply from the southern swarm to the other swarms and the relatively low permeability environment are the key factors of the seismic swarm activity. Nishimura et al. [17] modeled the episodic transient deformations in the Noto Peninsula using GNSS observations, and the spatial distribution of total displacements showed that there was horizontal inflation and uplift of ~70 mm around the swarm. This result suggested that the upwelling spread through the existing shallow-dipping permeable fault zone at a depth of about 16 km, triggering a persistent sub-meter fault slip at the seismogenic depth and further exacerbating the strong seismic swarm activity at the up-dip. The seismic swarm activity in the Noto Peninsula region began in 2020, which was initially confined to a small area thought to be associated with upwelling fluid. After the 2023 M 6.2 earthquake, the seismic swarm activity extended further, but still did not extend to offshore active faults. Toda and Stein [18] even suggested that this earthquake might be the end of the seismic swarm activity in this region. The seismic swarm activity in the Noto Peninsula has been well studied, and this earthquake provides a precious chance to explore fault activity properties in the co-seismic and post-seismic phases.
In this paper, the co-seismic and post-seismic slip properties of this earthquake are investigated based on GNSS observations. Firstly, the co-seismic rupture pattern of the earthquake is inverted using the GNSS co-seismic deformations. Secondly, the post-seismic signals included in the GNSS coordinate time series are modeled, and the spatial pattern of afterslip is estimated using the post-seismic deformations. Meanwhile, afterslip distributions of different time periods are determined to reveal its spatio-temporal evolution process, and then investigate the fault mechanism evolution after the earthquake. Finally, the co-seismic-rupture-generated Coulomb stress changes are estimated. The relationship between Coulomb stress changes and post-seismic activity is explored according to the comparison of the spatial distributions of afterslip and aftershocks.

2. Data and Methods

2.1. GNSS Observations

For the earthquake, the near-field high-density GNSS stations successfully record the crustal deformations in the co-seismic and post-seismic phases, which provides abundant data sets for investigating the fault activity properties in the co-seismic and post-seismic phases (Figure 2). The GNSS stations are derived from Japan’s GNSS Earth Observation Network System (GEONET). After the earthquake, the co-seismic deformations are rapidly estimated by the Nevada Geodetic Laboratory, University of Nevada, Reno (NGL/UNR) using the 5-min coordinate time series of GNSS stations. The co-seismic offset is typically determined by daily GNSS coordinate time series, which may include very early post-seismic deformation [19,20]. Thus, it is more reasonable to determine the co-seismic offset using sub-daily GNSS observations [21,22,23,24]. Considering this problem, the co-seismic rupture pattern is estimated using the GNSS co-seismic deformations provided by the NGL in this paper. Meanwhile, in order to explore the post-seismic fault activity properties, the post-seismic relaxation signals are determined by the daily coordinate time series of 42 near-field GNSS stations, which are also provided by the NGL (http://geodesy.unr.edu/gps_timeseries/, accessed on 15 August 2024).
For the NGL Data Analysis Center, the GIPSY-OASIS-II (6.1.1) software is adopted to carry out GNSS data processing. Among them, tropospheric delay is corrected using Global Mapping Function (GMF), and the influence of tidal loading is eliminated by the FES 2004 model. The effect of first-order ionospheric is eliminated by the LC-PC combination, and the effect of second-order ionospheric is modeled and corrected by IONEX data [25,26]. The effect of solid earth tide and pole tide is corrected using the IERS 2010 Conventions, while surface mass loading effect (e.g., atmospheric, non-tidal ocean, and hydrological loading) is not considered [27,28]. Subsequently, daily GNSS solutions are transformed into IGS 14 or other coordinate frames [29]. In this paper, the daily GNSS coordinate time series in the IGS 14 coordinate frame are utilized.

2.2. Post-Seismic Signal Modeling

The post-seismic GNSS coordinate time series consist of different geophysical signals and noise (e.g., trend signal, post-seismic relaxation signal, seasonal signal, white and colored noise) [30,31]. Among them, the nonlinear trend signal is generated by the long-term tectonic motions. The seasonal signal is generated by the non-tectonic effects generated by geophysical factors (e.g., surface mass loading). The post-seismic relaxation signal is primarily generated by afterslip, viscoelastic relaxation, and poroelastic rebound, which decays in logarithmic or exponential form. Thus, the influence of other geophysical signals and noise should be considered for the post-seismic relaxation signal modeling [32,33].
Considering the influence of tectonic motions, the GNSS observations of several years before the earthquake are appropriately selected in this paper. Then, the GNSS coordinate time series before and after the earthquake are modeled to extract the post-seismic signal. The specific process is listed as follows: (1) The outliers contained in the GNSS coordinate time series are removed through the iterative processing of interquartile range (IQR) and 3 δ ; (2) The range of relaxation time constants is estimated by seeking the local optimal solution using the simplex method, and then the optimal relaxation time constant is estimated by the trial-and-error method; (3) Based on the optimal relaxation time constant, the least-squares estimation (LSE) is adopted to simultaneously characterize different parameters of GNSS coordinate time series and extract the post-seismic relaxation signal.
According to the post-seismic signal modeling scheme, the post-seismic signals captured by the near-field GNSS stations are modeled. Figure 3 displays the modeled signals of the total coordinate time series for stations J052 and J972, and Figure 4 shows the modeled post-seismic signals of six GNSS stations in the three components.

2.3. Fault Slip Modeling

The Okada elastic dislocation theory is a method to establish the relationship of fault dislocation and surface displacement in a homogeneous Earth model [34]. However, there are large errors in the fault slip modeling in a homogeneous Earth model due to the inhomogeneity of the Earth’s medium. Considering this problem, Wang et al. [35] proposed the steepest descent method (SDM) to conduct fault slip modeling in the layered Earth model. The SDM-based fault slip modeling can be expressed by the following equations:
f ( s ) = y − M s 2 + β 2 H s
H s = ∂ 2 ∂ x 2 τ ( s ) + ∂ 2 ∂ y 2 τ ( s ) 2
where y is the surface displacement, s is the fault dislocation, M is the Green’s function, β is the smoothing factor, and τ ( s ) is the stress drop. y − M s 2 is the data misfit and β 2 H s is the model roughness. The optimal solution of fault slip modeling can be obtained by minimizing both the model roughness and data misfit [36]. The smoothing factor mainly controls the weight ratio of model roughness and data misfit. A larger value of β can obtain a smoother fault slip distribution, while the fitting performance is poor. A smaller value of β can obtain a better fitting performance, while the fault slip distribution is not smooth enough.
The USGS rapidly inverts the co-seismic rupture pattern using 38 teleseismic broadband P-waves, 28 broadband SH-waves, 70 long-period surface waves, and regional observations following this earthquake [37]. The strike and dip of the seismogenic fault are categorized as 213° and 50°, respectively. According to the USGS-provided fault model, a fault model along strike and dip of 175 and 45 km is constructed, and the fault plane is divided into 306 sub-faults with a dimension of 5 × 5 km. Based on the fault model and co-seismic deformations, the fault slip modeling is performed by the SDM code, and the Green’s function of fault dislocation is calculated by the EDGRN code [38]. The parameters of the USGS-provided layered Earth model utilized in this paper are shown in Table 1. For the afterslip inversion, the fault model of co-seismic slip modeling is slightly extended to the depth and sides. The constructed fault model is also divided into sub-faults with a dimension of 5 × 5 km and the number of sub-faults is 360.

3. Results

3.1. Co-Seismic Slip Pattern

For the co-seismic deformations, the NGL-provided results estimated from the 5-min GNSS coordinate time series are adopted. In the horizontal components, all GNSS stations produce co-seismic displacements moving northwestward and converging toward the epicenter. Among them, station J053 produces the largest co-seismic horizontal displacement in comparison with other stations, reaching −0.213 and −1.231 m in the north and east components, respectively. Most GNSS stations experience uplifts of different magnitudes in the vertical component, while several stations show a slight subsidence. Similarly, the uplift of station J053 is the largest, reaching 1.048 m. This is followed by stations J253 and G040, with uplifts of only 0.272 and 0.131 m, respectively.
Subsequently, the co-seismic slip pattern is determined according to the fault model and co-seismic deformations. The trade-off value of data misfit and model roughness is chosen as the optimal smoothing factor. The large area of shallow slip along the fault plane can be observed, and the peak slip region is located southwest of the epicenter (Figure 5). The co-seismic slip is primarily focused in the shallow region, which is distributed in the depth range of 2 to 15 km. The maximum co-seismic slip reaches 5.94 m, which is situated at a longitude of 136.78°, latitude of 37.27°, and depth of 5.43 km. For the fault slip modeling, the SDM code also estimates the moment magnitude according to the seismic moment released by fault slip. The moment magnitude estimated by co-seismic slip inversion is about Mw 7.51, which is close to the magnitude released by the USGS. The correlation coefficient between the SDM-simulated and GNSS-observed co-seismic deformations reaches 0.86. Meanwhile, our inversion result is in good agreement with the slip model provided by the USGS, indicating that the result of co-seismic slip modeling is relatively robust.

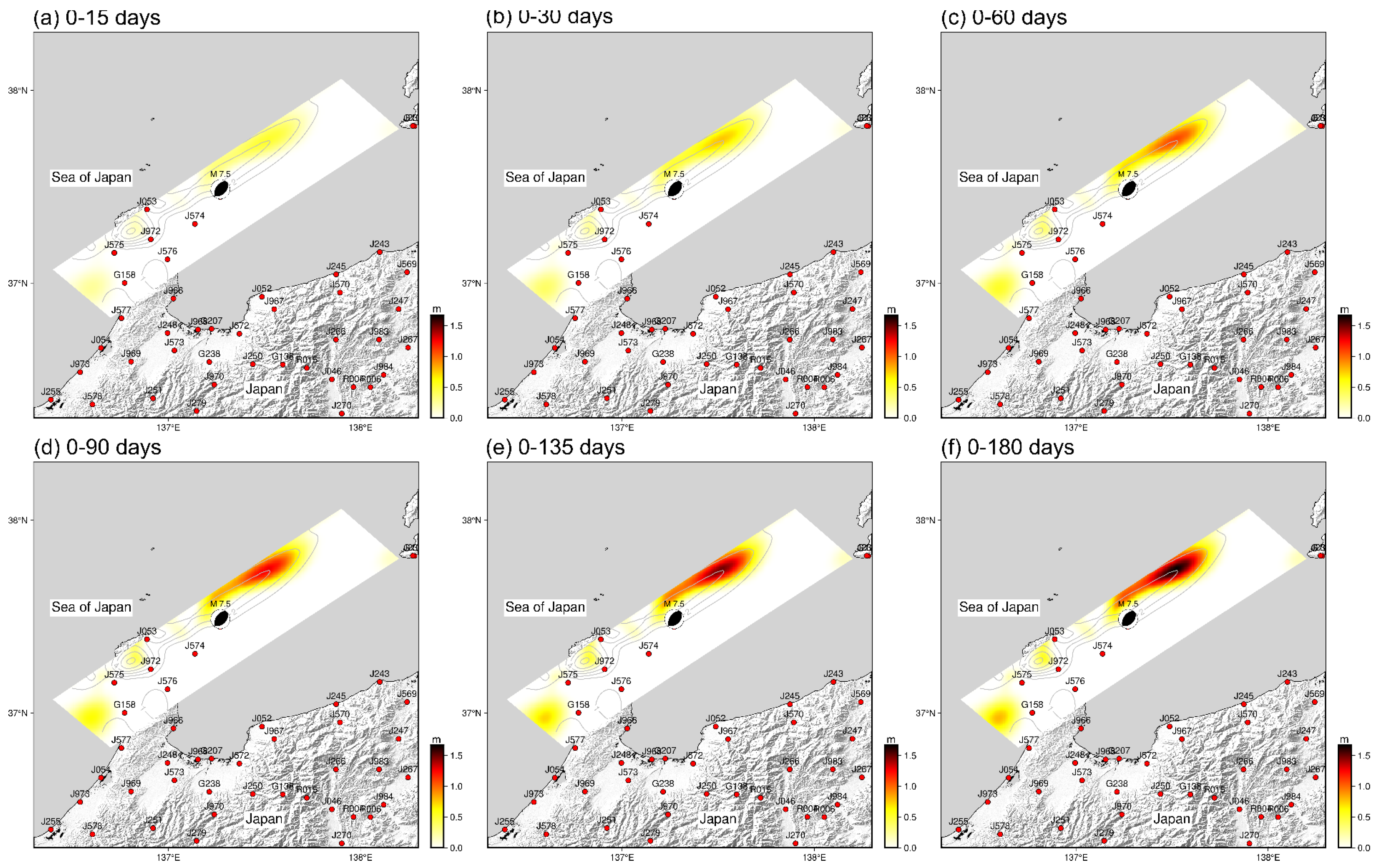
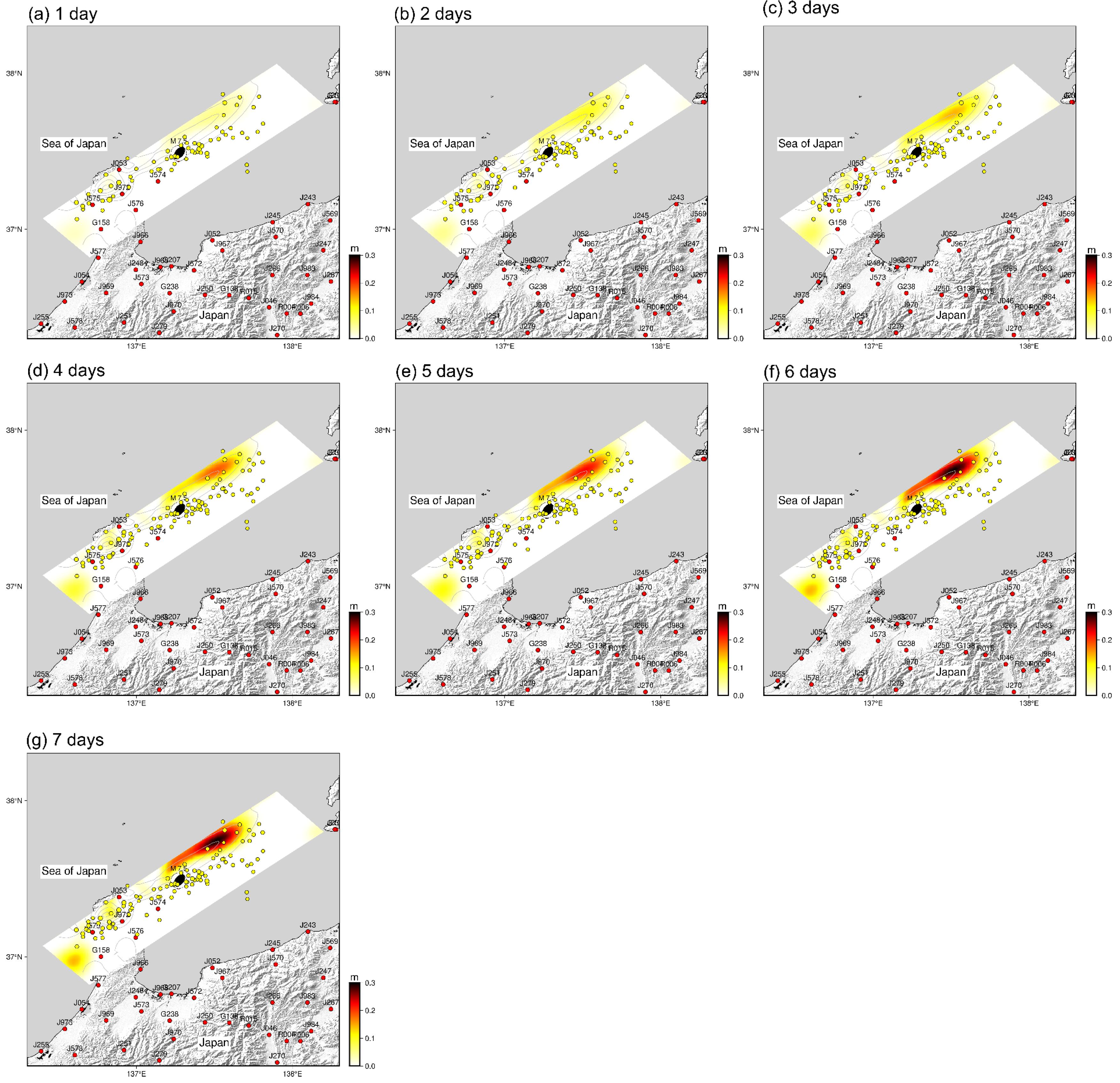
3.2. Spatial Pattern of Afterslip

Considering that the post-seismic GNSS coordinate time series decay in logarithmic form, the logarithmic model is utilized to model the post-seismic relaxation signals. Based on the post-seismic signals, the cumulative deformations of 42 GNSS stations in the post-seismic 180 days are calculated (Table 2). In the horizontal components, most GNSS stations are still moving to the northwest and converging toward the epicenter after the earthquake. However, the magnitude of post-seismic deformations at the near-field GNSS stations is significantly smaller than co-seismic deformations. Among them, station J253 produces the largest post-seismic displacement, reaching 30.6 and −26.9 mm in the north and east components, respectively. This is followed by station J052, whose post-seismic displacements in the north and east directions reach 23.5 and −24.6 mm, respectively. Some GNSS stations experience significant subsidence in the vertical component, and the largest subsidence (i.e., −59 mm) is observed at station J053.
Similarly, the spatial pattern of afterslip is determined according to the fault model and post-seismic deformations. A shallow afterslip can be observed after the earthquake, in comparison with co-seismic slips, which are mainly distributed in the depth range of 2 to 10 km (Figure 6). The afterslip patch is formed in the northeast of the epicenter, which is situated in the northeast margin of the co-seismic rupture region. In addition, a small area of afterslip also appears southwest of the epicenter, indicating that the slight slip also occurs in the deep region. The maximum value of afterslip reaches 1.13 m, which is situated at a longitude of 137.53°, latitude of 37.75°, and depth of 5.43 km. The seismic moment released by the afterslip during the post-seismic 180 days is equivalent to a moment magnitude 6.8 earthquake. The SDM code also computes the simulated co-seismic deformations using the estimated fault slip. Then, the correlation coefficient between GNSS-derived and SDM-simulated co-seismic deformations can be calculated. The correlation coefficient between the SDM-simulated and GNSS-observed post-seismic deformations of afterslip inversion is 0.83, suggesting that the result of afterslip inversion is also reliable. Yang et al. [14] used co-seismic and 19-day post-seismic GNSS observations to reveal the co-seismic and post-seismic slip of this earthquake, and found that afterslip occurred northeast of the co-seismic rupture region. Thus, in terms of the spatial pattern of afterslip, our result is consistent with the conclusion of Yang et al. [14].

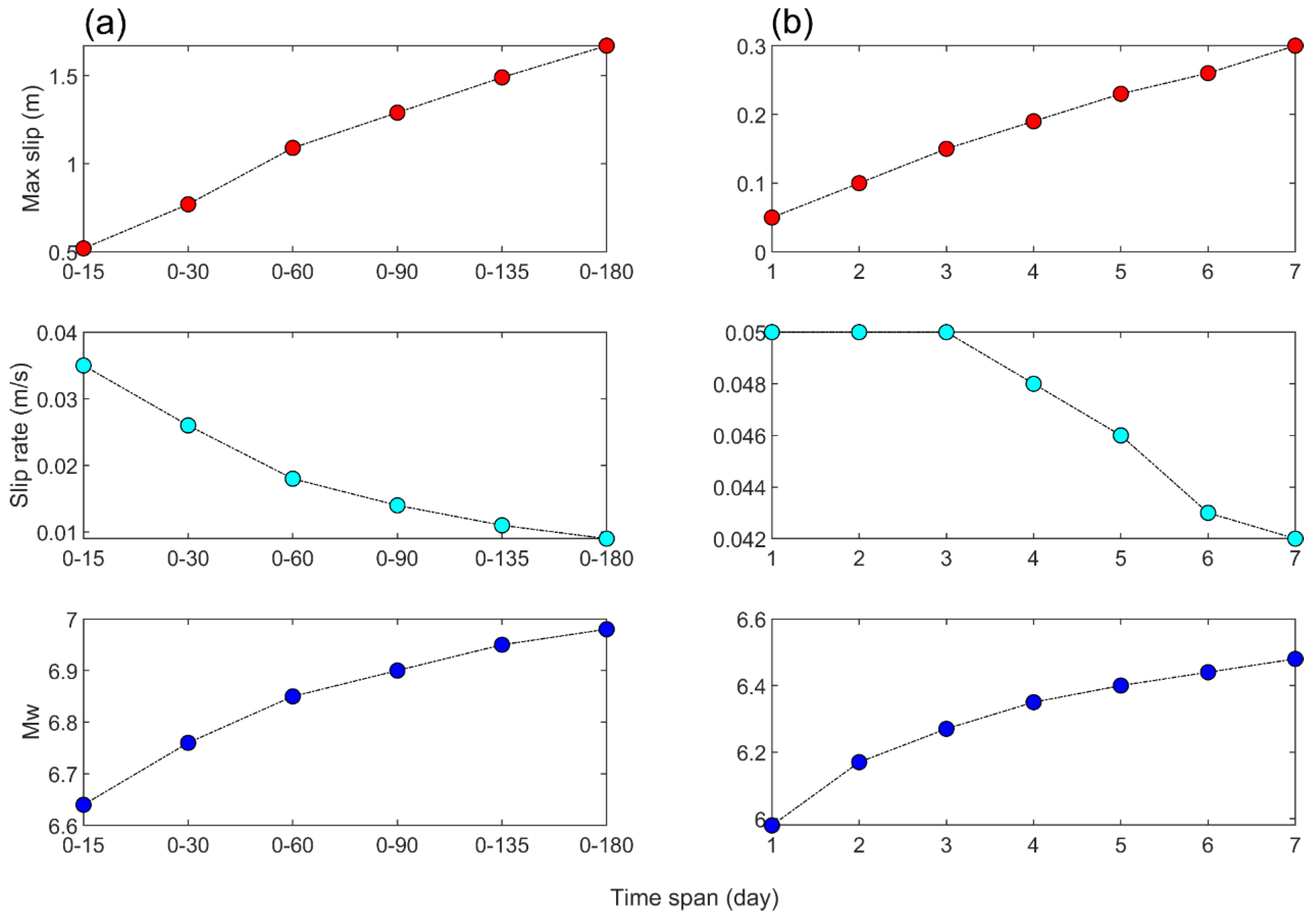
3.3. Spatio-Temporal Pattern Evolution of Afterslip

In order to determine the spatio-temporal pattern of afterslip, the 180 days after the earthquake are divided into six time periods (i.e., 0–15, 0–30, 0–60, 0–90, 0–135, and 0–180 days), and the cumulative deformations are calculated for each time period using the post-seismic signals. Considering the strong fault activity in the early phase, we divide the early post-seismic period into shorter intervals, and the intervals of next time periods are gradually extended. Then, the afterslip distribution of each time period is estimated based on the fault model and post-seismic deformations. As shown in Figure 7, afterslip patch is immediately formed in the northeast of the epicenter after the earthquake, demonstrating that a shallow afterslip is generated on the seismogenic fault following the earthquake. For the time period of 0–15 days, the maximum value of afterslip reaches 0.52 m and it accounts for about 31% of that in the post-seismic 180 days. The maximum value of afterslip in the time period of 0–15 days accounts for 67.5% and 47.7% of that in the time periods of 0–30 and 0–60 days, respectively. It implies strong fault activity in the early post-seismic period, which makes a significant contribution to the afterslip throughout the post-seismic phase. The afterslip-released seismic moment within the 15 days after the earthquake is about equivalent to a moment magnitude 6.64 earthquake. As time goes on, afterslip activity is continued along the formed patch, and the coverage and magnitude of afterslip gradually increase. The spatial pattern of afterslip changes significantly for the six time periods, especially for the first four time periods.
Subsequently, the slip rates are calculated to quantitatively characterize the fault activity after the earthquake (Table 3). Similarly, the maximum slip rate in the first time period (i.e., 0–15 days) is the largest, reaching 0.035 m/day, which suggests that the fault activity is relatively strong in the early time period following the earthquake. It is followed by the time periods of 0–30 and 0–60 days with maximum slip rates of 0.026 and 0.018 m/day, respectively. Our previous study also investigated the fault slip rates after the 2021 M 8.2 Chignik, Alaska earthquake [33]. The slip rates during the time periods of 0–7 and 0–60 days are 0.054 and 0.022 m/day, respectively. The slip rates during the two time periods are lower than those of the 2021 Chignik earthquake, which may be attributed to the relatively low magnitude of this earthquake. As time goes on, the maximum slip rate gradually decays, although the spatial distribution of afterslip is continuously changing. For the entire time period (i.e., 0–180 days), the maximum slip rate is only 0.009 m/day, suggesting that the fault activity is gradually weakening. The results indicate that afterslip continuously remains in the shallow region throughout the post-seismic 180 days, and the spatial pattern of afterslip changes significantly, especially in the early time period following the earthquake. In contrast, the slip rate decays as time goes on, indicating that the fault activity is gradually weakening in comparison with the early time period following the earthquake.
Considering the strong fault activity in the early time period, the spatio-temporal pattern properties of afterslip are further revealed according to daily images of afterslip distributions in the post-seismic seven days (Figure 8). The maximum value of afterslip reaches 0.3 m in the post-seismic seven days, which accounts for about 18% of that in the post-seismic 180 days. Meanwhile, the spatial pattern and magnitude of afterslip vary significantly in the first week after the earthquake. The maximum slip rate reaches 0.043 m/day in the first week after the earthquake, and the maximum slip rate is maintained at 0.05 m/day in the first three days, which is higher than that of other time periods. Meanwhile, the distribution of aftershocks in the longitude range of 136° to 138.5°, latitude range of 36.5° to 38.5°, and depth range of 0 to 60 km is also displayed. The number of aftershocks within the post-seismic seven days reaches 101, while the number of aftershocks on the first day reaches 65, suggesting that aftershock activity is strong on the first day after the earthquake. Aftershock activity is mainly distributed in the margin and surrounding areas of co-seismic rupture. In terms of spatial pattern, the distribution of aftershocks is not in good agreement with afterslip patch, demonstrating that afterslip may not be the driving factor of early aftershocks, and the aftershocks may be triggered by the co-seismic Coulomb stress changes.

4. Discussion

4.1. Coulomb Stress Changes

Generally, post-seismic activities (e.g., aftershock or afterslip) in the near field can be related to the Coulomb stress changes generated by co-seismic rupture [39,40]. Thus, the co-seismic-rupture-generated Coulomb stress changes are revealed to investigate the driving mechanism of post-seismic activities and carry out post-seismic disaster risk assessment. Based on the Coulomb stress criterion, the Coulomb stress changes generated by co-seismic rupture can be estimated. In this paper, the co-seismic Coulomb stress changes are determined by Coulomb 3.4 software [41,42,43]. Until now, previous studies have discussed the friction coefficient of Coulomb stress estimation. Jiang et al. [32] discussed the effect of different friction coefficients on Coulomb stress estimation, and an empirical friction coefficient of 0.4 was adopted. Thus, an empirical value (i.e., 0.4) is also regarded as the equivalent friction coefficient in this paper.
For the co-seismic Coulomb stress analysis, the spatial pattern of Coulomb stress changes along the fault plane is first estimated. As depicted in Figure 9, the co-seismic rupture region is covered by negative Coulomb stress, while the areas around the co-seismic rupture region are dominated by positive Coulomb stress. It implies that there may be seismic hazard risk in the northeast and southwest extension directions of the rupture zone. The thick black line represents the contour of afterslip. It can be seen that afterslip occurs in the region of positive Coulomb stress, implying that the co-seismic Coulomb stress changes may be a possible triggering factor for the generation of afterslip. Meanwhile, the distribution of aftershocks in the longitude range of 136° to 138.5° and latitude range of 36.5° to 38.5° is compared with the Coulomb stress changes along the fault plane. Most aftershocks are situated in the positive Coulomb stress region, and only a few aftershocks are situated in the negative Coulomb stress region. It suggests that the Coulomb stress changes generated by co-seismic rupture may have contributed to the occurrence of most aftershocks.
Moreover, considering the depth range of fault slip distribution, the Coulomb stress changes generated by co-seismic rupture at depths of 5, 8, and 10 km are also estimated. At the depth of 5 km, the co-seismic rupture region is covered by extensive negative Coulomb stress, while the north side of the co-seismic rupture region is covered by positive Coulomb stresses. The significant increase in Coulomb stress may contribute to the occurrence of earthquakes in the shallow region for the northeast extension direction of rupture zone. Afterslip is also distributed in the north side of the co-seismic rupture region, indicating that the co-seismic Coulomb stress changes may play a certain role in driving the afterslip process. This is also consistent with the conclusion of the Coulomb stress analysis along the fault plane. At the depth of 8 km, the coverage of negative Coulomb stress in the co-seismic rupture region is accordingly reduced due to the reduction of co-seismic slip coverage. Meanwhile, the magnitude of positive Coulomb stress on the north side of the co-seismic rupture region is also decreased to some extent. Similarly, at the depth of 10 km, the coverage of negative Coulomb stress in the co-seismic rupture region further decreases with the occurrence of a small amount of positive Coulomb stress, which is related to the further reduction of co-seismic slip coverage. The spatial pattern of co-seismic Coulomb stress changes at different depths is consistent with the properties of co-seismic and post-seismic slip distribution along the depth. In addition, at the depths of 8 and 10 km, the positive Coulomb stress is mainly distributed in the southwest of the rupture zone. Thus, there is still a certain seismic hazard risk in the deep region for the southwest of rupture zone.

4.2. Post-Seismic Fault Activity Properties

The Noto Peninsula is a seismically active region and is frequently hit by earthquakes. On 25 March 2007, a M 6.7 earthquake struck the Noto Peninsula, which is located southwest of the 2024 M 7.5 earthquake. The 21 cm southwestward displacement and 7 cm upheaval can be observed at the GNSS site near the hypocenter [44]. Toda [45] suggested that the stress changes induced by 2007 event were found to be negligible on the major faults south of the Noto Peninsula. Compared with the 2007 event, the co-seismic displacements induced by the 2024 event are significantly larger. Meanwhile, significant post-seismic deformation can be observed at near-field GNSS stations.
Currently, many studies have demonstrated that post-seismic deformation mechanisms primarily include afterslip, viscoelastic relaxation, and poroelastic rebound [46,47,48,49]. On the time scale, the poroelastic rebound effect is concentrated in the early time period following the earthquake, whereas the viscoelastic relaxation effect is concentrated in the medium and long time periods after the earthquake. On the spatial scale, the poroelastic rebound effect is mainly confined to the near-field region, whereas the viscoelastic relaxation effect is focused in the mid- and far-field regions. Among them, afterslip and viscoelastic relaxation are the two dominant factors causing post-seismic deformation [50,51]. Considering that we primarily pay attention to the fault activity properties within several months after the earthquake in this paper, the post-seismic deformation generated by poroelastic rebound effect is ignored. Meanwhile, the PSGRN/PSCMP code is adopted to quantitatively simulate the post-deformation deformation generated by the viscoelastic relaxation effect based on the co-seismic rupture model [52]. Then, the post-deformation deformation generated by the viscoelastic relaxation effect is removed from the GNSS coordinate time series in the post-seismic phase.
After removing the viscoelastic relaxation effect, the spatio-temporal pattern of afterslip during the post-seismic 180 days is determined, and then the properties of post-seismic fault activity on different time scales are explored. Compared with the co-seismic rupture pattern, a shallow afterslip can be observed following this earthquake, and afterslip patch is formed in the northeast of the epicenter with the maximum value of 1.13 m. For the spatial pattern of afterslip, afterslip distribution changes significantly within the post-seismic 180 days, and afterslip continues along the formed afterslip patch with a gradual increase in the coverage and magnitude. It indicates that afterslip activity continuously remains in the shallow region in the post-seismic 180 days. In contrast, although the fault activity has continued following the earthquake, the fault activity is gradually weakening with a gradual decrease in the slip rate (Figure 10). The maximum slip rate decreases from 0.035 m/day in the time period of 0–15 days to 0.01 m/day in the latest time period. Meanwhile, the spatio-temporal pattern of afterslip in the post-seismic seven days indicates that the fault activity is notably strong in the early time period following the earthquake. The maximum slip rate during the first week after the earthquake is 0.043 m/day, and the maximum slip rate during the first three days is around 0.05 m/day. The maximum value of afterslip in the first week reaches 0.3 m, which accounts for about 18% of that in the 180 days after the earthquake. The above results indicate that the shallow fault activity has persisted within the 180 days after the earthquake, which is notably strong in the early time period. As time goes on, the fault activity is gradually weakening, as evidenced by a decrease of slip rate.

5. Conclusions

In this paper, the fault slip in the co-seismic and post-seismic phases of the 2024 Noto Peninsula earthquake is explored using GNSS observations. Firstly, the co-seismic rupture pattern is determined according to GNSS co-seismic offsets and fault model. The co-seismic slip is mainly concentrated between 2 and 15 km in depth, with the maximum value of 5.94 m. Then, the post-seismic signals of 42 GNSS stations in the near-field are modeled, and the spatial pattern of afterslip in the post-seismic 180 days is inverted. For this earthquake, afterslip mainly occurs in the shallow region, which is situated in the northeast of the co-seismic rupture region. Moreover, the 180 days after the earthquake are divided into six time periods, and the spatio-temporal pattern of afterslip is revealed through the afterslip distribution changes of different time periods. To further reveal the properties of early post-seismic fault activity, the daily images of afterslip distributions in the post-seismic seven days are utilized to characterize the afterslip distribution changes on a finer time scale. Meanwhile, aftershock distributions within the first week following the earthquake are compared with the daily images of afterslip distributions to explore their relationship. Finally, the co-seismic Coulomb stress changes along the fault plane and at different depths are estimated. Meanwhile, the spatial pattern of afterslip and aftershocks is compared with Coulomb stress changes to further investigate the triggering relationship of co-seismic Coulomb stress on afterslip and aftershock activities.

Author Contributions

Conceptualization, Y.X. (Yunfei Xiang) and Y.X. (Yin Xing); methodology, M.Q., Y.C. and Y.B.; formal analysis, Y.X. (Yin Xing) and Y.B.; data curation, M.Q. and Y.C.; writing—original draft preparation, Y.X. (Yunfei Xiang); writing—review and editing, M.Q., Y.C. and Y.X. (Yin Xing); supervision, Y.X. (Yunfei Xiang); funding acquisition, Y.X. (Yunfei Xiang). All authors have read and agreed to the published version of the manuscript.

Funding

This study is funded by the National Natural Science Foundation of China (Grant No. 42304016, Funder: Yunfei Xiang) and Basic Science (Natural Science) Research Project for Colleges and Universities of Jiangsu Province (Grant No. 22KJB420002, Funder: Yunfei Xiang).

Data Availability Statement

The relevant information associated with the 2024 M 7.5 Noto Peninsula earthquake can be acquired from https://earthquake.usgs.gov/earthquakes/eventpage/us6000m0xl/ (accessed on 15 August 2024). The daily GNSS position time series derived from the NGL/NUR is available at http://geodesy.unr.edu/gps_timeseries/tenv/ (accessed on 15 August 2024). The aftershock catalog provided by the USGS can be obtained from https://earthquake.usgs.gov/earthquakes/search/ (accessed on 15 August 2024).

Acknowledgments

We are very grateful to the Geospatial Information Authority of Japan (GSI) and Nevada Geodetic Laboratory, University of Nevada, Reno (NGL/UNR) for providing GNSS observations. We are also very grateful to the United States Geological Survey (USGS) for providing the early aftershock catalog after the 2024 M 7.5 Noto Peninsula earthquake.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ishikawa, Y.; Bai, L. The 2024 Mj 7.6 Noto Peninsula, Japan earthquake caused by the fluid flow in the crust. Earthq. Res. Adv. 2024, 4, 100292. [Google Scholar] [CrossRef]
  2. Liu, Y.; Wu, Z.; Zhang, Y.; Yin, X. Tracing the pace of an approaching ‘seismic dragon king’: Additional evidence for the Noto earthquake swarm and the 2024 Mw 7.5 Noto earthquake. Earthq. Res. Adv. 2024, 4, 100290. [Google Scholar] [CrossRef]
  3. Mizuno, C.; Wang, X.; Dang, J. A Fast Survey Report About Bridge Damages by the 2024 Noto Peninsula Earthquake. Earthq. Res. Adv. 2024, 100312, accepted. [Google Scholar] [CrossRef]
  4. Kutschera, F.; Jia, Z.; Oryan, B.; Wing Ching Wong, J.; Fan, W.; Gabriel, A.A. Rapid earthquake-tsunami modeling: The multi-event, multi-segment complexity of the 2024 Mw 7.5 Noto Peninsula Earthquake governs tsunami generation. EarthArXiv 2024. [Google Scholar] [CrossRef]
  5. Mizutani, A.; Adriano, B.; Mas, E.; Koshimura, S. Fault model of the 2024 Noto Peninsula earthquake based on aftershock, tsunami, and GNSS data. Research Square 2024. [Google Scholar] [CrossRef]
  6. Pakoksung, K.; Suppasri, A.; Imamura, F. Preliminary modeling and analysis of the Tsunami generated by the 2024 Noto Peninsula earthquake on 1 January: Wave characteristics in the Sea of Japan. Ocean. Eng. 2024, 307, 118172. [Google Scholar] [CrossRef]
  7. Taira, A. Tectonic evolution of the Japanese island arc system. Annu. Rev. Earth Planet. Sci. 2001, 29, 109–134. [Google Scholar] [CrossRef]
  8. Hubbard, J.; Bradley, K. Tectonics of the January 1, 2024 M7.5 Earthquake in Japan: Exploring Earthquakes on Japan’s Western Coast. Earthquake Insights 2024. Available online: https://earthquakeinsights.substack.com/p/tectonics-of-the-january-1-2024-m75 (accessed on 15 August 2024).
  9. Yoshida, K.; Uchida, N.; Matsumoto, Y.; Orimo, M.; Okada, T.; Hirahara, S.; Kimura, S.; Hino, R. Updip fluid flow in the crust of the northeastern Noto Peninsula, Japan, triggered the 2023 Mw 6.2 Suzu earthquake during swarm activity. Geophys. Res. Lett. 2023, 50, e2023GL106023. [Google Scholar] [CrossRef]
  10. Shelly, D.R. Examining the connections between earthquake swarms, crustal fluids, and large earthquakes in the context of the 2020-2024 Noto Peninsula, Japan, earthquake sequence. Geophys. Res. Lett. 2024, 51, e2023GL107897. [Google Scholar] [CrossRef]
  11. Kato, A. Implications of fault-valve behavior from immediate aftershocks following the 2023 Mj 6.5 earthquake beneath the Noto Peninsula, central Japan. Geophys. Res. Lett. 2024, 51, e2023GL106444. [Google Scholar] [CrossRef]
  12. Fujii, Y.; Satake, K. Slip distribution of the 2024 Noto Peninsula earthquake (MJMA 7.6) estimated from tsunami waveforms and GNSS data. Earth Planets Space 2024, 76, 44. [Google Scholar] [CrossRef]
  13. Ma, Z.; Zeng, H.; Luo, H.; Liu, Z.; Jiang, Y.; Aoki, Y.; Wang, W.; Itoh, Y.; Lyu, M.; Cui, Y.; et al. Slow rupture in a fluid-rich fault zone initiated the 2024 M w 7.5 Noto earthquake. Science 2024, 385, 866–871. [Google Scholar] [CrossRef]
  14. Yang, S.; Sang, C.; Hu, Y.; Wang, K. Coseismic and early postseismic deformation of the 2024 Mw 7.45 Noto Peninsula earthquake. Geophys. Res. Lett. 2024, 51, e2024GL108843. [Google Scholar] [CrossRef]
  15. Nakajima, J. Crustal structure beneath earthquake swarm in the Noto peninsula, Japan. Earth Planets Space 2022, 74, 160. [Google Scholar] [CrossRef]
  16. Amezawa, Y.; Hiramatsu, Y.; Miyakawa, A.; Imanishi, K.; Otsubo, M. Long-living earthquake swarm and intermittent seismicity in the northeastern tip of the Noto Peninsula, Japan. Geophys. Res. Lett. 2023, 50, e2022GL102670. [Google Scholar] [CrossRef]
  17. Nishimura, T.; Hiramatsu, Y.; Ohta, Y. Episodic transient deformation revealed by the analysis of multiple GNSS networks in the Noto Peninsula, central Japan. Sci. Rep. 2023, 13, 8381. [Google Scholar] [CrossRef]
  18. Toda, S.; Stein, R.S. Intense seismic swarm punctuated by a magnitude 7.5 Japan shock. Temblor 2024. [Google Scholar] [CrossRef]
  19. Golriz, D.; Bock, Y.; Xu, X. Defining the coseismic phase of the crustal deformation cycle with seismogeodesy. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022002. [Google Scholar] [CrossRef]
  20. Golriz, D.; Hirshorn, B.; Bock, Y.; Weinstein, S.; Weiss, J.R. Real-time seismogeodetic earthquake magnitude estimates for local tsunami warnings. J. Geophys. Res. Solid Earth 2023, 128, e2022JB025555. [Google Scholar] [CrossRef]
  21. Liu, K.; Geng, J.; Wen, Y.; Ortega-Culaciati, F.; Comte, D. Very early postseismic deformation following the 2015 Mw 8.3 Illapel earthquake, Chile revealed from kinematic GPS. Geophys. Res. Lett. 2022, 49, e2022GL098526. [Google Scholar] [CrossRef]
  22. Twardzik, C.; Vergnolle, M.; Sladen, A.; Avallone, A. Unravelling the contribution of early postseismic deformation using sub-daily GNSS positioning. Sci. Rep. 2019, 9, 1175. [Google Scholar] [CrossRef] [PubMed]
  23. Tsang, L.L.; Vergnolle, M.; Twardzik, C.; Sladen, A.; Nocquet, J.-M.; Rolandone, F.; Agurto-Detzel, H.; Cavalié, O.; Jarrin, P.; Mothes, P. Imaging rapid early afterslip of the 2016 Pedernales earthquake, Ecuador. Earth Planet. Sci. Lett. 2019, 524, 115724. [Google Scholar] [CrossRef]
  24. Xiang, Y.; Bian, Y.; Liu, J.; Xing, Y. Insights into very early afterslip associated with the 2021 M 8.2 Chignik, Alaska earthquake using subdaily GNSS solutions. Remote Sens. 2023, 15, 5469. [Google Scholar] [CrossRef]
  25. Zhao, B.; Du, R.; Zhang, R.; Tan, K.; Qiao, X.; Huang, Y.; Zhang, C. Co-seismic displacements associated with the 2015 Nepal Mw7.9 earthquake and Mw7.3 aftershock constrained by global positioning system measurements. Chin. Sci. Bull. 2015, 60, 2758–2764. (In Chinese) [Google Scholar]
  26. Zhao, B.; Yong, H.; Zhang, C.; Wei, W.; Kai, T.; Du, R. Crustal deformation on the Chinese mainland during 1998–2004 based on GPS data. Geod. Geodyn. 2015, 6, 7–15. [Google Scholar] [CrossRef]
  27. Wei, H.H.; Yu, T.N.; Tu, J.S.; Ke, F.Y. Detection and Evaluation of Flood Inundation Using CYGNSS Data during Extreme Precipitation in 2022 in Guangdong Province, China. Remote Sens. 2023, 15, 297. [Google Scholar] [CrossRef]
  28. Wei, H.H.; He, X.F.; Feng, Y.M.; Jin, S.G.; Shen, F. Snow depth estimation on slopes using GPS-Interferometirc reflectometry. Sensors 2019, 19, 4994. [Google Scholar] [CrossRef]
  29. Wei, H.; Yang, X.; Pan, Y.; Shen, F. GNSS-IR Soil Moisture Inversion Derived from Multi-GNSS and Multi-Frequency Data Accounting for Vegetation Effects. Remote Sens. 2023, 15, 5381. [Google Scholar] [CrossRef]
  30. Jiang, Z.S.; Yuan, L.; Huang, D.; Yang, Z.; Chen, W. Postseismic deformation associated with the 2008 Mw 7.9 Wenchuan earthquake, China: Constraining fault geometry and investigating a detailed spatial distribution of afterslip. J. Geodyn. 2017, 112, 12–21. [Google Scholar] [CrossRef]
  31. Jiang, Z.S.; Yuan, L.; Huang, D.; Yang, Z.; Hassan, A. Postseismic deformation associated with the 2015 Mw7.8 Gorkha earthquake, Nepal: Investigating ongoing afterslip and constraining crustal rheology. J. Asian Earth Sci. 2018, 156, 1–10. [Google Scholar] [CrossRef]
  32. Jiang, Z.S.; Huang, D.; Yuan, L.; Hassan, A.; Zhang, L.; Yang, Z. Coseismic and postseismic deformation associated with the 2016 Mw 7.8 Kaikoura earthquake, New Zealand: Fault movement investigation and seismic hazard analysis. Earth Planets Space 2018, 70, 62. [Google Scholar] [CrossRef]
  33. Xiang, Y.; Yue, J.; Wang, H.; Chen, Y. GNSS imaging coseismic and postseismic slip associated with the 2021 M 8.2 Chignik, Alaska earthquake. Tectonophysics 2024, 876, 230273. [Google Scholar] [CrossRef]
  34. Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar] [CrossRef]
  35. Wang, R.; Diao, F.; Hoechner, A. SDM—A geodetic inversion code incorporating with layered crust structure and curved fault geometry. Proc. EGU Gen. Assem. 2013, 15, EGU2013–2411–1. [Google Scholar]
  36. Diao, F.; Xiong, X.; Wang, R.; Zheng, Y.; Walter, T.R.; Weng, H.; Li, J. Overlapping post-seismic deformation processes: Afterslip and viscoelastic relaxation following the 2011 Mw 9.0 Tohoku (Japan) earthquake. Geophys. J. Int. 2014, 196, 218–229. [Google Scholar] [CrossRef]
  37. Ji, C.; Wald, D.J.; Helmberger, D.V. Source description of the 1999 Hector Mine, California, earthquake, part I: Wavelet domain inversion theory and resolution analysis. Bull. Seismol. Soc. Am. 2002, 92, 1192–1207. [Google Scholar] [CrossRef]
  38. Wang, R.; Martín, F.L.; Roth, F. Computation of deformation induced by earthquakes in a multi-layered elastic crust—FORTRAN programs EDGRN/ EDCMP. Comput. Geosci. 2003, 29, 195–207. [Google Scholar] [CrossRef]
  39. Steacy, S. Introduction to special section: Stress transfer, earthquake triggering, and time-dependent seismic hazard. J. Geophys. Res. Solid Earth 2005, 110, B05S01. [Google Scholar] [CrossRef]
  40. Freed, A.M. Earthquake triggering by static, dynamic, and postseismic stress transfer. Annu. Rev. Earth Planet. Sci. 2005, 33, 335–367. [Google Scholar] [CrossRef]
  41. Stein, R.S. The role of stress transfer in earthquake occurrence. Nature 1999, 402, 605–609. [Google Scholar] [CrossRef]
  42. Lin, J.; Stein, R.S. Stress triggering in thrust and subduction earthquakes, and stress interaction between the southern San Andreas and nearby thrust and strikeslip faults. J. Geophys. Res. Solid Earth 2004, 109, B02303. [Google Scholar] [CrossRef]
  43. Toda, S.; Stein, R.S.; Richards-Dinger, K.; Bozkurt, S.B. Forecasting the evolution of seismicity in southern California: Animations built on earthquake stress transfer. J. Geophys. Res. Solid Earth 2005, 110, B03415. [Google Scholar] [CrossRef]
  44. Ozawa, S.; Yarai, H.; Tobita, M.; Une, H.; Nishimura, T. Crustal deformation associated with the Noto Hanto Earthquake in 2007 in Japan. Earth Planets Space 2008, 60, 95–98. [Google Scholar] [CrossRef]
  45. Toda, S. Coulomb stresses imparted by the 25 March 2007 M w = 6.6 Noto-Hanto, Japan, earthquake explain its ‘butterfly’distribution of aftershocks and suggest a heightened seismic hazard. Earth Planets Space 2008, 60, 1041–1046. [Google Scholar] [CrossRef]
  46. Feigl, K.L.; Thatcher, W. Geodetic observations of post-seismic transients in the context of the earthquake deformation cycle. C. R. Geosci. 2006, 338, 1012–1028. [Google Scholar] [CrossRef]
  47. Ozawa, S.; Nishimura, T.; Munekane, H.; Suito, H.; Kobayashi, T.; Tobita, M.; Imakiire, T. Preceding, coseismic, and postseismic slips of the 2011 Tohoku earthquake, Japan. J. Geophys. Res. Solid Earth 2012, 117, B07404. [Google Scholar] [CrossRef]
  48. Bedford, J.; Moreno, M.; Baez, J.C.; Lange, D.; Tilmann, F.; Rosenau, M.; Vigny, C. A high-resolution, time-variable afterslip model for the 2010 Maule Mw= 8.8, Chile megathrust earthquake. Earth Planet. Sci. Lett. 2013, 383, 26–36. [Google Scholar] [CrossRef]
  49. Perfettini, H.; Avouac, J.P. The seismic cycle in the area of the 2011 Mw 9.0 Tohoku-Oki earthquake. J. Geophys. Res. Solid Earth 2014, 119, 4469–4515. [Google Scholar] [CrossRef]
  50. Hsu, Y.J.; Simons, M.; Avouac, J.P.; Galetzka, J.; Sieh, K.; Chlieh, M.; Bock, Y. Frictional afterslip following the 2005 Nias-Simeulue earthquake, Sumatra. Science 2006, 312, 1921–1926. [Google Scholar] [CrossRef]
  51. Freed, A.M. Afterslip (and only afterslip) following the 2004 Parkfield, California earthquake. Geophys. Res. Lett. 2007, 34, L06312. [Google Scholar] [CrossRef]
  52. Wang, R.; Lorenzo-Martín, F.; Roth, F. PSGRN/PSCMP—A new code for calculating co-and post-seismic deformation, geoid and gravity changes based on the viscoelastic-gravitational dislocation theory. Comput. Geosci. 2006, 32, 527–541. [Google Scholar] [CrossRef]
Remotesensing 16 04057 g001
Figure 1. Regional seismic tectonic map of Japan. Beach balls represent the focal mechanisms of the earthquakes. For the east coast of Japan, the focal mechanism of M 7+ earthquakes are displayed.
Figure 1. Regional seismic tectonic map of Japan. Beach balls represent the focal mechanisms of the earthquakes. For the east coast of Japan, the focal mechanism of M 7+ earthquakes are displayed.
Remotesensing 16 04057 g001
Remotesensing 16 04057 g002
Figure 2. Regional tectonic setting and spatial distribution of GNSS stations. Beach balls represent the focal mechanisms. Red circles represent GNSS stations.
Figure 2. Regional tectonic setting and spatial distribution of GNSS stations. Beach balls represent the focal mechanisms. Red circles represent GNSS stations.
Remotesensing 16 04057 g002
Remotesensing 16 04057 g003
Figure 3. Modeled signals of the total coordinate time series for stations J052 (a) and J972 (b) in the three components. Red lines indicate the modeled signals.
Figure 3. Modeled signals of the total coordinate time series for stations J052 (a) and J972 (b) in the three components. Red lines indicate the modeled signals.
Remotesensing 16 04057 g003
Remotesensing 16 04057 g004
Figure 4. Modeled post-seismic signals of six GNSS stations (i.e., G158 (a), J052 (b), J241 (c), J247 (d), J570 (e), and J972 (f)) in the three components. Red lines indicate the modeled signals.
Figure 4. Modeled post-seismic signals of six GNSS stations (i.e., G158 (a), J052 (b), J241 (c), J247 (d), J570 (e), and J972 (f)) in the three components. Red lines indicate the modeled signals.
Remotesensing 16 04057 g004
Remotesensing 16 04057 g005
Figure 5. Co-seismic slip pattern and GNSS-derived co-seismic deformations. (a) Co-seismic slip pattern of the earthquake. (b) GNSS-derived co-seismic deformations in the horizontal components. (c) GNSS-derived co-seismic deformations in the vertical component.
Figure 5. Co-seismic slip pattern and GNSS-derived co-seismic deformations. (a) Co-seismic slip pattern of the earthquake. (b) GNSS-derived co-seismic deformations in the horizontal components. (c) GNSS-derived co-seismic deformations in the vertical component.
Remotesensing 16 04057 g005
Remotesensing 16 04057 g006
Figure 6. Cumulative afterslip in the post-seismic 180 days and GNSS-derived post-seismic deformations. (a) Spatial pattern of afterslip in the post-seismic 180 days. (b) GNSS-derived post-seismic deformations in the horizontal components. (c) GNSS-derived post-seismic deformations in the vertical component.
Figure 6. Cumulative afterslip in the post-seismic 180 days and GNSS-derived post-seismic deformations. (a) Spatial pattern of afterslip in the post-seismic 180 days. (b) GNSS-derived post-seismic deformations in the horizontal components. (c) GNSS-derived post-seismic deformations in the vertical component.
Remotesensing 16 04057 g006
Remotesensing 16 04057 g007
Figure 7. Snapshots of spatio-temporal pattern of afterslip in the post-seismic 180 days.
Figure 7. Snapshots of spatio-temporal pattern of afterslip in the post-seismic 180 days.
Remotesensing 16 04057 g007
Remotesensing 16 04057 g008
Figure 8. Snapshots of spatio-temporal pattern of afterslip and aftershocks in the post-seismic seven days.
Figure 8. Snapshots of spatio-temporal pattern of afterslip and aftershocks in the post-seismic seven days.
Remotesensing 16 04057 g008
Remotesensing 16 04057 g009
Figure 9. Co-seismic-generated Coulomb stress changes analysis. (a) Spatial pattern of Coulomb stress and aftershocks along the fault plane. (b) Coulomb stress changes at 5 km depth. (c) Coulomb stress changes at 8 km depth. (d) Coulomb stress changes at 10 km depth.
Figure 9. Co-seismic-generated Coulomb stress changes analysis. (a) Spatial pattern of Coulomb stress and aftershocks along the fault plane. (b) Coulomb stress changes at 5 km depth. (c) Coulomb stress changes at 8 km depth. (d) Coulomb stress changes at 10 km depth.
Remotesensing 16 04057 g009
Remotesensing 16 04057 g010
Figure 10. Result of spatio-temporal pattern evolution of afterslip on different time scales. (a) Variations of maximum slip, maximum slip rate, and equivalent moment magnitude for six time periods. (b) Variations of maximum slip, maximum slip rate, and equivalent moment magnitude for post-seismic seven days.
Figure 10. Result of spatio-temporal pattern evolution of afterslip on different time scales. (a) Variations of maximum slip, maximum slip rate, and equivalent moment magnitude for six time periods. (b) Variations of maximum slip, maximum slip rate, and equivalent moment magnitude for post-seismic seven days.
Remotesensing 16 04057 g010
Table 1. The depth-variable parameters of the layered Earth model utilized in this paper.
Table 1. The depth-variable parameters of the layered Earth model utilized in this paper.
Depth
(km)		P_vel
(km/s)		S_vel
(km/s)		Dens.
(g/cm3)		QpQs
0.0002.760.691.841200.0600.0
0.3766.183.592.681200.0600.0
9.7456.733.682.751200.0600.0
20.2916.963.832.811200.0600.0
33.5728.084.473.381200.0600.0
229.5728.594.663.45360.0140.0
Table 2. GNSS-derived post-seismic deformations in the north, east, and up component.
Table 2. GNSS-derived post-seismic deformations in the north, east, and up component.
SiteLon.Lat.Post-Seismic
Deformations (mm)		SiteLon.Lat.Post-Seismic
Deformations (mm)
NorthEastUpNorthEastUp
G109138.2837.8110.83−12.982.91J266137.8736.7010.42−5.210.76
G110138.5037.3510.15−14.399.65J267138.2436.6610.27−9.519.12
G158136.7737.006.12−15.42−16.31J448132.9932.990.232.504.85
G207137.2236.7613.22−15.668.65J567138.5137.3410.30−14.1613.19
I002140.1736.261.82−3.97−1.79J569138.2437.058.42−19.963.97
I028139.4635.522.91−1.32−1.26J570137.8936.9517.63−20.7212.92
I064138.9735.6212.27−0.17−0.38J572137.3636.7315.31−14.169.48
J050138.9837.892.91−8.064.09J573137.0336.647.33−10.92−0.26
J051138.5737.399.71−11.7410.92J574137.1337.3019.90−30.29−28.85
J052137.4836.9223.52−24.6122.43J575136.7137.153.47−6.00−12.07
J053136.8837.384.82−3.03−59.12J576136.9937.1214.16−16.43−29.44
J235138.2737.8110.30−11.240.61J807138.7737.496.15−13.3911.13
J241138.3337.2313.45−17.2813.42J962138.6337.217.95−14.4215.22
J243138.1037.1621.67−19.3419.10J964138.4537.1011.60−15.5415.75
J244138.6037.077.24−14.517.59J966137.0236.9115.39−18.78−3.56
J245137.8737.0422.87−21.2017.87J967137.5536.8619.87−21.527.80
J247138.1936.8613.36−19.374.85J968137.1536.7513.27−15.66−2.79
J248136.9936.7410.54−12.95−4.26J970137.2336.478.03−6.68−6.24
J250137.4336.5712.57−6.898.21J972136.9037.2210.60−24.05−36.36
J253137.2737.4430.59−26.97−67.75R006138.0536.4510.18−3.3512.07
J265138.4336.809.01−11.687.74R015137.7236.5512.42−11.309.62
Table 3. Afterslip inversion results for different time periods.
Table 3. Afterslip inversion results for different time periods.
Time Period
(days)		Mean
Slip (m)		Mean Stress Drop (MPa)Maximum SlipMaximum Slip Rate (m/day)Mw
Value (m)Depth (km)
0–150.040.460.525.430.0356.64
0–300.060.690.775.430.0266.72
0–600.090.991.095.430.0186.76
0–900.111.161.295.430.0146.90
0–1350.121.341.495.430.0116.95
0–1800.141.501.675.430.0096.98
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Xiang, Y.; Qin, M.; Chen, Y.; Xing, Y.; Bian, Y. Co-Seismic and Post-Seismic Slip Properties Associated with the 2024 M 7.5 Noto Peninsula, Japan Earthquake Determined by GNSS Observations. Remote Sens. 2024, 16, 4057. https://doi.org/10.3390/rs16214057

AMA Style

Xiang Y, Qin M, Chen Y, Xing Y, Bian Y. Co-Seismic and Post-Seismic Slip Properties Associated with the 2024 M 7.5 Noto Peninsula, Japan Earthquake Determined by GNSS Observations. Remote Sensing. 2024; 16(21):4057. https://doi.org/10.3390/rs16214057

Chicago/Turabian Style

Xiang, Yunfei, Ming Qin, Yuanyuan Chen, Yin Xing, and Yankai Bian. 2024. "Co-Seismic and Post-Seismic Slip Properties Associated with the 2024 M 7.5 Noto Peninsula, Japan Earthquake Determined by GNSS Observations" Remote Sensing 16, no. 21: 4057. https://doi.org/10.3390/rs16214057

APA Style

Xiang, Y., Qin, M., Chen, Y., Xing, Y., & Bian, Y. (2024). Co-Seismic and Post-Seismic Slip Properties Associated with the 2024 M 7.5 Noto Peninsula, Japan Earthquake Determined by GNSS Observations. Remote Sensing, 16(21), 4057. https://doi.org/10.3390/rs16214057

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop