Abstract
In this paper, we propose a 3D Digital Surface Model (DSM) reconstruction method from uncalibrated Multi-view Satellite Stereo (MVSS) images, where Rational Polynomial Coefficient (RPC) sensor parameters are not available. While recent investigations have introduced several techniques to reconstruct high-precision and high-density DSMs from MVSS images, they inherently depend on the use of geo-corrected RPC sensor parameters. However, RPC parameters from satellite sensors are subject to being erroneous due to inaccurate sensor data. In addition, due to the increasing data availability from the internet, uncalibrated satellite images can be easily obtained without RPC parameters. This study proposes a novel method to reconstruct a 3D DSM from uncalibrated MVSS images by estimating and integrating RPC parameters. To do this, we first employ a structure from motion (SfM) and 3D homography-based geo-referencing method to reconstruct an initial DSM. Second, we sample 3D points from the initial DSM as references and reproject them to the 2D image space to determine 3D–2D correspondences. Using the correspondences, we directly calculate all RPC parameters. To overcome the memory shortage problem while running the large size of satellite images, we also propose an RPC integration method. Image space is partitioned to multiple tiles, and RPC estimation is performed independently in each tile. Then, all tiles’ RPCs are integrated into the final RPC to represent the geometry of the whole image space. Finally, the integrated RPC is used to run a true MVSS pipeline to obtain the 3D DSM. The experimental results show that the proposed method can achieve 1.455 m Mean Absolute Error (MAE) in the height map reconstruction from multi-view satellite benchmark datasets. We also show that the proposed method can be used to reconstruct a geo-referenced 3D DSM from uncalibrated and freely available Google Earth imagery.
1. Introduction
High-resolution satellite imagery has various application areas: remote extraction and analysis of a variety of information, such as changes in precipitation or vegetation; identification of differences before and after disasters; and analysis of land-use changes. In particular, in the field of photogrammetry, a large number of investigations have been conducted in obtaining a high-precision, high-density Digital Surface Model (DSM) using many vision techniques [1,2,3,4,5]. A DSM represents geometrical information of the Earth’s surface and has a wide range of applications. Thus, obtaining an accurate DSM from satellite imagery is one of the interests in both photogrammetry and remote sensing.
The reconstruction of a 3D surface model using camera images has progressed greatly in the field of photogrammetry. The external pose and perspective projection equations of a vision camera are generally modelled using the pin-hole lens model. Then, image pixels are matched by stereo matching methods, such as SGM [6], MGM [7], Plane-Sweep-Stereo [8], Patch-Match-Stereo [9], GA-Net [10], etc., to obtain the 3D coordinates of the triangulated point of the matching pixels. However, most satellite imagery used for photogrammetry is generated by following the pushbroom camera model. Thus, in the remote sensing field, many investigations of DSM reconstruction have been conducted using the pushbroom camera model for satellite imagery [11].
The Rational Polynomial Coefficient (RPC) is a common mathematical representation of the pushbroom camera model, and it has been widely used in satellite stereo image matching [5,12,13]. As far as two-view satellite stereo images are concerned, satellite images can be rectified using RPC parameters. Then, stereo matching methods find pixel correspondences between the images. Stereo matching can be performed by using conventional methods such as S2P [13,14] or deep learning methods by transforming RPC parameters into tensor forms [15].
In the case of the true Multi-view Satellite Stereo (MVSS) problem, which addresses the simultaneous pixel matching across all satellite images, it is impossible to rectify all satellite images because of the nonlinear epipolar geometry of the RPC camera model. Thus, almost all recent investigations on true MVSS employ the pin-hole camera model instead of RPC for the DSM reconstruction [16,17,18]. However, employing the pin-hole camera model for the MVSS problem lacks accurate mapping between the 3D metric and 2D pixel space due to the much smaller number of pose parameters of the actual pushbroom camera. Gao et al. [15] show that the 3D surface reconstruction error increases with larger image sizes compared to the original RPC parameters.
To solve the true MVSS problem, it is necessary to obtain accurate RPC parameters. However, the raw RPC parameters recorded at the time of satellite image capture are usually erroneous due to the inaccuracy of the satellite sensor data. For this reason, a large number of investigations have addressed the correction or refinement of the raw RPC data to accurately define geometric formation between 3D and 2D space [19,20].
This paper addresses a novel approach of 3D DSM reconstruction from multi-view satellite images without using RPC sensor data. Instead of using any RPC sensor data, we propose to estimate the RPC parameters of all satellite images through a two-step algorithm. In the first step, we employ a Structure from Motion (SfM) method with the pin-hole camera model to initially reconstruct a geo-referenced 3D DSM [17]. And in the second step, the RPC parameters of all satellite images are estimated by using the direct least square error minimization of all correspondences between the 3D metric space and 2D pixel space [21]. After all RPC parameters are estimated, the final dense DSM is reconstructed. To overcome the computational memory shortage problem while processing the large size of satellite images, we also propose partitioning the satellite image into multiple image tiles. In each image tile, RPC estimation is performed independently, and all tiles’ RPCs are integrated into the final RPC of the whole image space.
Overview of the Proposed Method
Before describing the overview of the proposed method, we define all notations used in all of the following sections as below:
- : 3D point;
- : 2D pixel;
- : 3D sample point with index j in the RP space;
- : 2D point in the i-th satellite image;
- : 2D point in the i-th satellite image projected from ;
- : 2D point at the j-th tile in the i-th satellite image;
- : 2D sample point k in the i-th satellite image with height element;
- : Pin-hole camera parameters of the i-th satellite camera;
- : 3D homography transformation matrix to transform the initial DSM from distorted projective space to a geometric reference space (in this paper, we use the WGS84 coordinate system);
- : The forward RPC parameter and function from the geo-reference coordinate system to the i-th satellite image;
- : The inverse RPC parameter and function from the i-th satellite image to the geo-reference coordinate system;
- : The forward RPC parameter and function from the geo-reference coordinate system to the j-th tile in the i-th satellite image;
- : The inverse RPC parameter and function from the j-th tile in the i-th satellite image to the geo-reference coordinate system;
- : An RPC parameter in RPC sub-functions with index ;
- : Satellite image of the i-th camera;
- : Total number of satellite images;
- : Total number of tiles in a satellite image;
- : Total number of 3D sample points in the RP space or 2D samples in an image.
The motivation of the proposed method is to reconstruct a 3D DSM by using any freely available multi-view satellite images from the internet, even without using RPC sensor data. Due to the increase in image and open datasets, satellite imagery can also be obtained freely from the internet. For example, multi-date and multi-view satellite imagery can be obtained from the Google Earth (GE) Pro Ver. 7.3.6.9796 desktop software but without RPC data. The open satellite imagery datasets could provide raw RPC sensor data; however, the data are generally erroneous due the inherent sensor inaccuracy.
The proposed DSM reconstruction method can be used even without using RPC data. In this regard, this study mainly utilizes multi-view satellite imagery obtained from the GE desktop software [22]. GE provides satellite images of most parts of the earth, and the timeline function provides multi-date satellite images. Satellite images of one place on the earth’s surface obtained at different times can be used as multi-view stereo images due to the satellite pose difference at the time of image capture.
The proposed approach mainly consists of two steps. The first step is based on GEMVS [17]. In this step, we consider the cameras to follow the pin-hole model and find all camera poses by performing SfM [23,24] with the MVSS image obtained from GE. GEMVS uses these pin-hole camera parameters to generate the initial geo-referenced DSM. The second step is based on our previous study of virtual RPC estimation [21]. From the results of the first step, we find the 3D–2D correspondences between the geo-referenced (WGS84) coordinate system and the 2D pixel coordinate system to directly obtain the RPC parameters of each satellite image. The 3D reference points are uniformly sampled from the initial DSM, and the corresponding 2D pixel points are determined by two consecutive transformations from 3D to 2D space [21]. Finally, the estimated RPC and the satellite images are used again to address the true MVSS problem to reconstruct the final DSM. MS2P [25] is used to reconstruct the final DSM by using the estimated RPC parameters.
Because the proposed method is a true MVSS approach, which uses all satellite images simultaneously to find the best optimal DSM solution, it needs a large memory space, and this weakness causes failure when using multi-view and very large-sized images. To overcome this computational problem, we also propose an RPC integration method. Each high-resolution satellite image is divided into tiles, and RPC estimation is performed in each tile. Then, all RPCs are integrated into the final RPC, which represents the projective geometry of the whole image.
Figure 1 shows a pipeline of the proposed method. In this figure, an input image is cropped to tiles as an example. Each single tile consists of multiple satellite images with the same tile size. In the first step of the proposed method, multi-view images of a single tile enter into the grey box, and GEMVS performs to reconstruct the initial DSM in a geo-referenced space. In this paper, we use the WGS84 coordinate system as the reference. Using the initial DSM and multi-view images in the tile, is estimated using the correspondences between the 3D DSM and 2D pixels, where is the index of the image and is the index of the tile.
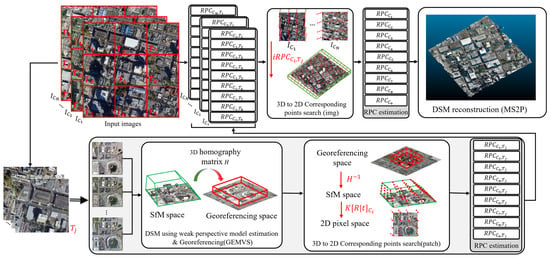
Figure 1.
Pipeline of the proposed method. (Reference: GEMVS [14], 3D to 2D correspondence search [17], MS2P [25]).
After the RPC parameters of all image tiles are estimated, the final RPC of the whole image space is estimated. To find , the final RPC of , the i-th satellite image, 3D–2D correspondences are searched again between the geo-referenced 3D space and the image space of . Then, using the proposed RPC integration method, is estimated. Finally, using all estimated RPCs from the multi-view images, MS2P is performed to generate the final DSM. In the experimental section, we will show that the proposed RPC estimation method can accurately generate the DSM using not only GE satellite images but also general satellite images.
2. Background and Related Work
2.1. Pin-Hole and Pushbroom Camera Models
In the computer vision field, the pin-hole model is most commonly used because of its linear representation of the perspective projective geometry [26,27,28]. In addition, recent investigations on multi-view satellite stereo images show that the pin-hole model can be effectively used for the approximation of 3D-to-2D relationships in high-resolution satellite images [16,17]. Assuming a pin-hole camera, the process of the perspective projection from a 3D point in the world space onto a 2D image plane is expressed by Equations (1) and (2) [26]. is transformed into the camera coordinates system through extrinsic rotation and translation parameters and then projected onto the pixel coordinate through intrinsic parameters such that
Here, is an element of the rotation matrix, is an element of the translation vector, and are the focal length in the x and y directions, and and are principal points of the camera, respectively.
In remote sensing, however, the pushbroom camera model is more commonly used in the processing of satellite imagery. The pushbroom camera model differs from the pin-hole model in terms of projective geometry due to different ways of image acquisition. The 3D-to-2D projection relationship of the pushbroom camera is represented by the RPC parameters, which are expressed as follows:
where
Here, s and l are sample and line coordinates, respectively. Sample and line are normalized pixel coordinates of a satellite image, and X, Y, and Z are similarly normalized latitude, longitude, and height. Therefore, sample, line, latitude, longitude, and height have offset and scale information for normalization.
2.2. DSM Reconstruction Using the Pin-Hole Model
Recently, many investigations in the fields of photogrammetry and remote sensing have addressed the MVSS problem using the pin-hole camera model, as applying the RPC model directly to the MVSS problem is highly complex [16,17,18]. Zhang et al. [16] introduce a method for reparameterization of the RPC model to the weak perspective model. They use the RPC parameters to set up the area of interest (AOI) to reconstruct a DSM and then generate a 3D bounding cube. Then, it is uniformly discretized into a finite grid, with each axis evenly divided into sample locations. These sampled points (latitude, longitude, altitude) are projected to the pixel coordinate by the RPC parameters of each satellite image. Using the 3D-to-2D correspondences, a perspective projection matrix is calculated. Then, a Multi-view Stereo (MVS) method such as COLMAP [23,24] and a Plane-Sweep-Stereo (PSS) are performed using the pin-hole parameters.
In contrast to Zhang et al.’s method, which converts RPC parameters to pin-hole camera parameters, Park et al. [17] propose a 3D DSM reconstruction method when there is no RPC parameter in multi-view satellite images. In their method, SfM is applied to multi-view satellite images to estimate the pin-hole camera parameters, which are then used as input for EnSoft3D [29]. Because the satellite images are actually obtained by a pushbroom camera, not a pin-hole model, the reconstructed DSM is distorted in a projective space. Park et al. propose a solution to this problem by using a 3D homography transformation of a DSM from the distorted space into a geo-referenced coordinate space.
2.3. DSM Reconstruction Using the Pushbroom Model
Because conventional satellite images are obtained with the pushbroom camera model, using RPC parameters to handle the MVSS problem yields an accurate DSM reconstruction compared to those using the pin-hole model.
Facciolo et al. [14] generate rectified images using the RPCs of the satellite images for two-view stereo matching. They create multiple two-view-based DSMs from MVSS images of a single scene and generate the final DSM result by taking the median height value. Seo et al. [25] generate inverse RPCs based on the RPCs from the satellite images. These inverse RPCs derive the latitude and longitude from the pixel coordinates and height value. By using forward and inverse RPCs, they modify the camera model of EnSoft3D to the pushbroom model. The method proposed by Gao et al. [20] defines the RPC of a single image as a set of four 4 × 4 × 4 tensors. This approach is the first investigation to include an RPC warping module in a deep learning-based framework, achieving better accuracy than pin-hole-based DSM reconstruction.
However, in studies using RPCs from MVSS images, the RPC correction process is essential. Typically, RPC parameters are obtained along with the acquisition of satellite images. Since the RPC parameters in their raw format have inherent errors, a correction process is necessary. Generally, to correct the RPC, a bundle adjustment is performed to minimize the reprojection error using corresponding points found through SIFT [19,30]. RPCs can also be corrected or newly generated using known ground control points (GCPs) within the image [19].
3. Proposed Method
3.1. Initial DSM Reconstruction
As mentioned earlier, the proposed method consists of two main steps: the first is the initial DSM reconstruction, and the second is the estimation and integration of RPC and the final DSM reconstruction as shown in Figure 1. In the first step, the proposed method starts with GEMVS to reconstruct an initial DSM from MVSS images. Suppose we have N multi-view satellite images and a geometric reference space as the input of GEMVS, we obtain the following camera pose parameters and 3D DSM information:
- : Estimated pin-hole camera parameters of the multi-view satellite images;
- : 3D homography matrix transforming an initial DSM from distorted SfM space to a geometric reference space (in this paper, we use the WGS84 coordinate system);
- : Vertex coordinates of the Rectangular Parallelepiped (RP) enclosing the initial DSM.
3.2. RPC Estimation
Equation (5) indicates that at least forty corresponding points are necessary to estimate the RPC between the WGS84 coordinate system and the pixel coordinate system. To define the correspondences between two spaces, first, we uniformly sample the RP space using the RP vertex information obtained after performing GEMVS as shown in Figure 2. Along each axis of the RP space, we sample points, and thus, total 3D points are sampled in the RP space, where , and stand for longitude, latitude, and height, respectively. Then, all 3D points are projected onto by the following equations, including the homography matrix and pin-hole camera parameters :
In Equation (8), a 3D point is transformed to the projective SfM space through . Then, it is projected again onto by using i-th camera parameters, . Total number of corresponding points and are then used to estimate . Singular value decomposition (SVD) [31] is used to directly find the solution of the RPC as shown in Equation (10).
In Equation (10), SVD runs after normalizing all components of and . The offset and scale parameters of each component for normalization are determined based on the geo-referenced RP space and the size of the satellite image.
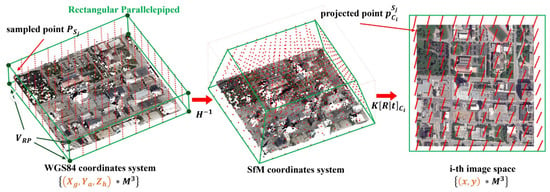
Figure 2.
3D-to-2D projection process for finding correspondence.
3.3. RPC Integration
Solving the true MVSS problem for DSM reconstruction often needs a lot of memory space because the size of the satellite imagery is generally very large and multiple satellite images need to be processed simultaneously. Due to this reason, a shortage of computational memory space often becomes a practical problem in MVSS.
To address the computational complexity due to the large size of the satellite images, this study also proposes an RPC integration method using the following steps. First, the whole image area of is divided into image tiles. Second, in each image tile, the RPC is estimated as described in Section 3.2. In each image tile, we also have N multi-view satellite images; thus, we can apply the same algorithm described in Section 3.2 to each image tile. Third, after all RPCs in image tiles are estimated, the RPC of the whole image space is computed as follows. Let be a 2D sample and height-augmented point in such that
Here, i is the camera index, and k is the sample index. We sample the image space points as the same number when RP space is sampled. However, the number of 2D samples in the RPC integration step can be different. Sample point is then reprojected to the 3D geo-reference system by using the inverse RPC function at each tile in . This inverse RPC function is already known after the initial DSM reconstruction step. Each 2D sample point is reprojected into 3D space using the RPCs of all tiles, resulting in a total of T (in this study, T = 9) 3D points, where = = 3 for each image, as follows:
After obtaining all 3D points projected from , the weighted average of is then computed by using the distance from to the center of each tile as shown in Figure 3. The weight average of is computed as
where is the distance from to the center of tile and is the summation of the distance to all tiles. Using the above equation, we decide as the 3D correspondence of . Using the processes mentioned above, all correspondences are determined, and the final is then computed by directly using SVD. SVD is one of the commonly used linear least square solvers, and it provides accurate RPC parameters for our overdetermined linear system.
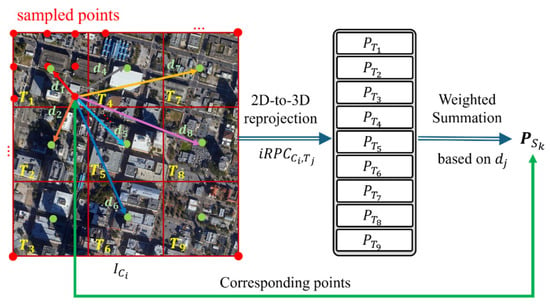
Figure 3.
2D-to-3D correspondence search process. For example, an image space is divided into tiles. Red-color points are uniform samples in image . A sampled point is reprojected to geo-referencing space by each tile’s inverse RPCs to obtain . Then, all are weighted averaged by the distance of the point to each tile center to obtain the final correspondence .
3.4. 3D DSM Reconstruction Using a True MVSS Method
The final step of the proposed method is to reconstruct the 3D DSM from the MVSS images and the estimated RPCs. Using the estimated RPC parameters of all input satellite images, we run a true MVSS method, MS2P [25], for accurate and dense DSM reconstruction. The baseline of MS2P is EnSoft3D, which addresses a true multi-view stereo problem in the field of photogrammetry [29]. As shown in the diagram of MS2P in Figure 4, the original EnSoft3D algorithm is modified to adapt the pushbroom camera geometry and the estimated RPC parameters. The modifications to EnSoft3D are summarized as follows. The first modification is that the 3D-to-2D projection model of EnSoft3D was changed from the pin-hole camera, based on intrinsic and extrinsic parameters, to the pushbroom camera, based on the forward and inverse RPC parameters. The second modification is that the height selection method in the raw cost volume was changed from the Winner Takes All (WTA) to a probability-based one.
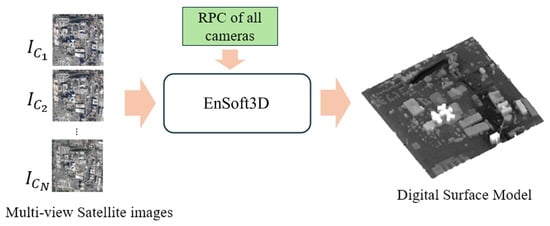
Figure 4.
A simplified flow diagram of MS2P. The baseline algorithm for MVS is EnSoft3D [29], and it is modified to use the estimated RPC parameters.
4. Experiments and Error Analysis
The motivation of the proposed method is to reconstruct a 3D DSM from multi-view satellite images with unknown RPC information. Thus, the proposed method can reconstruct a DSM using open satellite images, such as those from the GE desktop software. In the experiments of this study, we mainly use satellite imagery obtained from the GE desktop software. However, to analyze the DSM reconstruction accuracy, we need to compare the reconstructed DSM with the Ground Truth (GT) height maps in the area of reconstruction. For the error analysis, we use the GT height maps in the DFC19 [32] dataset, which has been obtained from LiDAR sensors.
The DFC19 dataset provides MVSS images and GT height maps of a couple of US cities, including Omaha (OMA) and Jacksonville (JAX). We use the OMA and JAX datasets and their GTs for the error analysis. Errors are measured based on the elevation of the DSM by two criteria, Mean Absolute Error (MAE) and Root Mean Squared Error (RMSE). In every experiment, we obtained satellite images corresponding to the DFC19 dataset from GE by screen capturing. A total of ten multi-view satellite images are used as the input for the proposed method, and the image size is resized to 1600 × 1600 pixels.
4.1. Qualitative Analysis and Comparison with the Pin-Hole Camera Model
As the first qualitative analysis, we used ten multi-view GE images for the 3D reconstructions of two landmarks: one is Sigiriya, Sri Lanka (7°57′22″N 80°45′32″E) and the other is Sydney, Australia (33°51′25″S 151°12′42″E). The 3D DSM and height map results are shown in Figure 5. As shown in the figure, the proposed method provides reasonably accurate RPC parameters for the 3D reconstruction of complex terrain and building areas.

Figure 5.
Results of the proposed method on GE imagery. The area of the first row is Sigiriya, Sri-Lanka (7°57′22″N 80°45′32″E), and second row is Sydney, Australia (33°51′25″S 151°12′42″E).
As the second experiment, we compare the height maps from two different methods: one is a 3D reconstruction by using the pin-hole model, and the other is a 3D reconstruction by using the estimated RPC model. For the pin-hole model reconstruction, we use GEMVS. Figure 6 shows the qualitative comparison between the pin-hole model and RPC model reconstructions. In Figure 6, we use two city areas for the experiment: Daegu, South Korea and Omaha, US. The satellite images of the Omaha city are obtained from the GE software, not from the DFC19 dataset. We obtain test images from GE in the same areas of OMA_284 and OMA_248 tiles of the DFC19 dataset.

Figure 6.
Comparison of the height map results from uncalibrated satellite images using the pin-hole camera model with GEMVS [17] and the RPC model with MS2P [25].
The proposed method shows better reconstruction performance because of the camera model difference. In the height maps from the pin-hole model, there are many noisy and blurred pixels. Especially in the red-box areas in Figure 6, containing high building areas in three test images, the proposed method shows more accurate and clear building structures than the pin-hole camera model.
The difference becomes even more noticeable in the 3D DSM reconstruction. Figure 7 compares the DSM reconstruction from COLMAP, GEMVS, and the proposed method. COLMAP is known as one of the best-performance softwares in SfM, and it is still popularly used in pose estimation and DSM reconstruction [16,33,34]. However, in the Figure 7 comparison, we find that the proposed method can reconstruct much denser and distortion-free structures of the city buildings than COLMAP. The DSM reconstruction result using the estimated RPC shows better structures of building edges and roofs. In contrast, the DSM using the pin-hole camera model shows that most building structures are collapsed or distorted.

Figure 7.
Comparison of the DSM reconstruction of two camera models, COLMAP and GEMVS, with the pin-hole model and MS2P with the estimated RPC model.
4.2. Quantitative Error Analysis
In this section, we show the error analysis of the DSM reconstruction using the GT height maps from DFC19. Five image areas of DFC19 are used: JAX_068, JAX_165, JAX_248, JAX_251, and JAX_284. In addition, images from Daegu are also used. In this error analysis, we use the GE imagery in the same areas of five DFC19 tiles instead of using the original images from DFC19. The exact same image areas of the five tiles are obtained from the GE imagery, and the resulting DSM is compared with the GT height maps from DFC19.
Figure 8 shows the error analysis results of the six test areas. In each test, one of the input satellite images, 3D DSM, and MAE and RMSE error analysis are presented. The Daegu dataset does not provide a GT height map; thus, only the DSM result is shown. In this analysis, the average MAE is 1.366 m, and the RMSE is 3.128 m. Among the results, OMA_284 shows the largest error. Except for the OMA_284 tile, the MAE is approximately 1.0~1.5 m. The large error in the OMA_284 tile is caused by new buildings in the GE images. In this test image, we find that there are a couple of new buildings; however, there is no height information in the GP map. This means that the new buildings have been built after the GT generation. An analysis of this issue is discussed more in Section Discussion about the Error of the OMA_284 Tile.
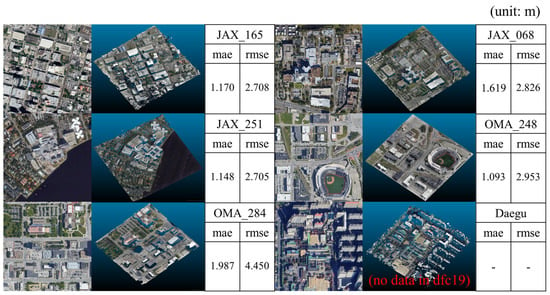
Figure 8.
MAE and RMSE error of the height map compared with the GT DSM from the DFC19 dataset.
In this quantitative analysis, we also compare our results with the other results reconstructed by using true RPC. The true RPC are provided from DFC19. In the test of using true RPC, the S2P and MS2P methods are used. For the comparison with the proposed method, the original EnSoft3D with the pin-hole model is also analyzed.
Table 1 shows the MAE and RMSE of four methods. MS2P with true RPC yields the best performance because it is a true MVSS method and uses correct RPC parameters. The error of the other methods can be relatively compared with MS2P. In the MAE measurement, the proposed method yields better performance than EnSoft3D, whether using RPC integration or not. When using RPC integration, the proposed method yields better performance than the other two methods. However, the RMSE error from the RPC integration is similar or a little better than the other two methods.

Table 1.
MAE and RMSE comparison of using true RPC and estimated RPC in three tiles from the DFC19 dataset.
Discussion about the Error of the OMA_284 Tile
In the previous section, we find that the height error of the OMA_284 tile is larger compared with the other tiles. The error is approximately 60 percent higher in both MAE and RMSE compared with the other tiles. The reason for this high error in the OMA_284 tile can be explained from the error map of the reconstructed DSM. Figure 9 shows, from the left, the digital surface model, GT model, and the error map of OMA_284. In the error map, compared to the true GT elevation values, the blue-color pixels represent a lower elevation, and the red-color pixels represent a higher elevation.

Figure 9.
Error analysis of the OMA_284 tile. From the left, reconstructed DSM, GT model, and error map.
Figure 9 shows that most red-color areas (yellow circles) in the error map are caused by some buildings that have been built after the GT map was constructed. The red-color buildings in the error map cannot be observed in the GT height map. This means that the GT height map of the OMA_284 tile was generated before the generation of the GE images we used. Thus, the high error of the OMA_284 tile is mainly caused by the capture time difference between the DFC19 height map and GE imagery.
4.3. Error Analysis Using DFC19 Multi-View Images
As the last experiment, we use the original multi-view satellite images from the DFC19 dataset and apply the proposed method to estimate the RPC and reconstruct the DSM. Because the image quality of the DFC19 dataset is much higher than that from GE imagery, the DSM reconstruction accuracy using the DFC19 dataset is better than that using GE imagery.
Among the DFC19 dataset, we have used the OMA_284 tile for comparison. In the last two rows in Table 2, the MAE and RMSE errors of the height maps reconstructed from the estimated RPC and the true RPC are presented. Using the estimated RPC, we have also compared the MS2P result with that from S2P. As shown in the table, the height map obtained by the original DFC19 images with the true RPC is the best among all four cases. The next best case is MS2P with the estimated RPC. S2P is a two-view stereo method; thus, a simple comparison with the other MVSS is not fair. Thus, to obtain the height map using S2P as best as possible, stereo image pairs of file indices 1–4 and 1–36 are mainly used, and the other pairs 20–22, 31–36, and 4–8 are combined. In each image tile, the best map from those five pairs is obtained.

Table 2.
Error analysis of DSM reconstruction using the original satellite images from the DFC19 dataset (OMA_284). The second row shows that the proposed method yields very similar performance with the result using true RPC as in the third row (Unit: m).
Compared with the S2P, the proposed RPC and MS2P provide better height map results in terms of both the MAE and RMSE. However, the S2P results using the estimated RPC also provide reasonably good accuracy. This means that the estimated RPC is accurate enough to be used in other two-view stereo satellite images. In addition, the proposed method provides similar results with those from the GT RPC. This analysis also shows that the proposed method can estimate the RPC parameters of all multi-view images almost similar to the true RPC data.
5. Conclusions
In this paper, we propose a novel method of DSM reconstruction from uncalibrated multi-view satellite stereo images. Without using any pose sensor data from the satellite images, the proposed method computes the RPC parameters using 3D-to-2D correspondences between geo-referenced metric space and image space.
To find 3D-to-2D correspondences, we first use an SfM method with the pin-hole camera model to reconstruct an initial DSM and transform the map to a geo-referenced space. The 3D sample points from the geo-referenced space are reprojected to the 2D image space to determine the correspondences. Using an adequate number of correspondences, we directly solve the RPC of all satellite images.
To estimate accurate RPC parameters of large-size satellite images, we propose an RPC integration method and reconstruct a 3D DSM. Using the RPC integration, the proposed method can estimate the RPC parameters close to the true RPC values. In consequence, the proposed method can estimate very accurate RPC parameters and reconstruct a dense and accurate 3D DSM through a MVSS method. The experimental results show that the proposed RPC estimation method can be used in any GE imagery or other dataset to reconstruct an accurate DSM.
The proposed method can directly use multi-view satellite images without any sensor calibration or RPC correction processes. In addition, open satellite image datasets, such as GE imagery, can be used for the 3D DSM reconstruction without RPC data. The 3D DSM reconstruction results can be used for many practical applications. One example is to synthesize road-view images from the top-view images for an autonomous vehicle study. Another application can be a 3D graphic model generation for Digital Twin of complex building areas or urban planning. Geographic information in either urban or rural areas can be obtained from the 3D DSM reconstruction. The proposed RPC estimation method is also used to correct the erroneous sensor data of satellite images.
In the future, we will improve the simple pixel distance-based weight of Equation (3) for more accurate RPC estimation. The proposed method currently requires a huge memory space for simultaneous multi-view image processing. Thus, in the future, we need to study an algorithm optimization to solve the memory problem.
Limitations
There are some limitations to the proposed pipeline. First, the 3D points in the WGS84 coordinate system used for geo-referencing in GEMVS are manually obtained from Google Earth, as RPC information is unavailable. This manual process can impact the accuracy of the results. Another limitation is that freely accessible high-resolution satellite images, such as those from Google Earth, are often orthorectified images. The challenges of 3D reconstruction using orthorectified images are demonstrated in Figure 9 and Table 2. In the reconstructed results from the proposed method, the satellite images from DFC19 show a curved terrain, whereas the images from Google Earth show a flat terrain. Therefore, images that were excessively distorted by GCP were excluded from the experiment.
Author Contributions
Conceptualization, S.-Y.P.; methodology, S.-Y.P. and D.-U.S.; software, D.-U.S.; validation, D.-U.S. and S.-Y.P.; resources, D.-U.S. and S.-Y.P.; writing—original draft preparation, D.-U.S.; writing—review and editing, D.-U.S. and S.-Y.P.; visualization, D.-U.S.; supervision, S.-Y.P.; project administration, S.-Y.P.; funding acquisition, S.-Y.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education (No. 2021R1A6A1A03043144).
Data Availability Statement
The original contributions presented in this study are included in the article; further inquiries can be directed to the corresponding author/s.
Acknowledgments
This article is a revised and expanded version of a paper entitled “3D Reconstruction from Multi-view Google Earth Satellite Stereo Images by Generating Virtual RPC based on 3D Homography-based Georeferencing”, which was presented at ISPRS Geospatial Week 2023, Egypt.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- De Franchis, C.; Meinhardt-Llopis, E.; Michel, J.; Morel, J.-M.; Facciolo, G. On Stereo-Rectification of Pushbroom Images. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 5447–5451. [Google Scholar]
- He, S.; Li, S.; Jiang, S.; Jiang, W. HMSM-Net: Hierarchical Multi-Scale Matching Network for Disparity Estimation of High-Resolution Satellite Stereo Images. ISPRS J. Photogramm. Remote Sens. 2022, 188, 314–330. [Google Scholar] [CrossRef]
- Liu, J.; Ji, S. A Novel Recurrent Encoder-Decoder Structure for Large-Scale Multi-View Stereo Reconstruction from an Open Aerial Dataset. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 6050–6059. [Google Scholar]
- Zhou, X.; Wang, Y.; Lin, D.; Cao, Z.; Li, B.; Liu, J. SatelliteRF: Accelerating 3D Reconstruction in Multi-View Satellite Images with Efficient Neural Radiance Fields. Appl. Sci. 2024, 14, 2729. [Google Scholar] [CrossRef]
- Gómez, A.; Randall, G.; Facciolo, G.; von Gioi, R.G. An Experimental Comparison of Multi-View Stereo Approaches on Satellite Images. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2022; pp. 844–853. [Google Scholar]
- Hirschmuller, H. Stereo Processing by Semiglobal Matching and Mutual Information. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 30, 328–341. [Google Scholar] [CrossRef]
- Facciolo, G.; De Franchis, C.; Meinhardt, E. MGM: A Significantly More Global Matching for Stereovision. In Proceedings of the BMVC 2015, Swansea, UK, 7–10 September 2015. [Google Scholar]
- Collins, R.T. A Space-Sweep Approach to True Multi-Image Matching. In Proceedings of the CVPR IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 18–20 June 1996; pp. 358–363. [Google Scholar]
- Bleyer, M.; Rhemann, C.; Rother, C. Patchmatch Stereo-Stereo Matching with Slanted Support Windows. In Proceedings of the BMVC, Dundee, UK, 29 August–2 September 2011; Volume 11, pp. 1–11. [Google Scholar]
- Zhang, F.; Prisacariu, V.; Yang, R.; Torr, P.H.S. Ga-Net: Guided Aggregation Net for End-to-End Stereo Matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 185–194. [Google Scholar]
- Li, Z.; Haiyan, W.Y.Z.; Song, M. A Review of 3D Reconstruction from High-Resolution Urban Satellite Images. Int. J. Remote Sens. 2023, 44, 713–748. [Google Scholar] [CrossRef]
- Tao, C.V. 3D Reconstruction Methods Based on the Rational Function Model. PERS 2002, 68, 705–714. [Google Scholar]
- Franchis, C.; Meinhardt-Llopis, E.; Michel, J.; Morel, J.-M.; Facciolo, G. An automatic and modular stereo pipeline for pushbroom images. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, II-3, 49–56. [Google Scholar] [CrossRef]
- Facciolo, G.; De Franchis, C.; Meinhardt-Llopis, E. Automatic 3D Reconstruction from Multi-Date Satellite Images. In Proceedings of the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 57–66. [Google Scholar]
- Gao, J.; Liu, J.; Ji, S. Rational Polynomial Camera Model Warping for Deep Learning Based Satellite Multi-View Stereo Matching. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 6148–6157. [Google Scholar]
- Zhang, K.; Snavely, N.; Sun, J. Leveraging Vision Reconstruction Pipelines for Satellite Imagery. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Long Beach, CA, USA, 15–20 June 2019; pp. 2139–2148. [Google Scholar]
- Park, S.-Y.; Seo, D.; Lee, M.-J. GEMVS: A Novel Approach for Automatic 3D Reconstruction from Uncalibrated Multi-View Google Earth Images Using Multi-View Stereo and Projective to Metric 3D Homography Transformation. Int. J. Remote Sens. 2023, 44, 3005–3030. [Google Scholar] [CrossRef]
- Bullinger, S.; Bodensteiner, C.; Arens, M. 3D Surface Reconstruction From Multi-Date Satellite Images. arXiv 2021, arXiv:2102.02502. [Google Scholar] [CrossRef]
- Marí, R.; Facciolo, G.; Ehret, T. Sat-Nerf: Learning Multi-View Satellite Photogrammetry with Transient Objects and Shadow Modeling Using RPC Cameras. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 1311–1321. [Google Scholar]
- Long, T.; Jiao, W.; He, G. RPC Estimation via ℓ1-Norm-Regularized Least Squares (L1ls). IEEE Trans. Geosci. Remote Sens. 2015, 53, 4554–4567. [Google Scholar] [CrossRef]
- Seo, D.U.; Park, S.Y. 3D Reconstruction from Multi-View Google Earth Satellite Stereo Images by Generating Virtual RPC Based on 3D Homography-Based Georeferencing. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, 48, 1075–1080. [Google Scholar] [CrossRef]
- Google Inc Google Earth Pro. Available online: https://www.google.com/earth/about/versions/#download-pro (accessed on 21 February 2024).
- Schonberger, J.L.; Frahm, J.-M. Structure-from-Motion Revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
- Schönberger, J.L.; Zheng, E.; Frahm, J.-M.; Pollefeys, M. Pixelwise View Selection for Unstructured Multi-View Stereo. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part III 14. pp. 501–518. [Google Scholar]
- Seo, D.; Lee, H.S.; Park, S.-Y. MS2P: A True Multi-View Satellite Stereo Pipeline without Rectification of Push Broom Images. In Proceedings of the IGARSS 2023–2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; pp. 5603–5606. [Google Scholar]
- Sturm, P. Pinhole Camera Model. In Computer Vision: A Reference Guide; Springer: Berlin/Heidelberg, Germany, 2021; pp. 983–986. [Google Scholar]
- Feng, S.; Zuo, C.; Zhang, L.; Tao, T.; Hu, Y.; Yin, W.; Qian, J.; Chen, Q. Calibration of Fringe Projection Profilometry: A Comparative Review. Opt. Lasers Eng. 2021, 143, 106622. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge Books Online; Cambridge University Press: Cambridge, UK, 2003; ISBN 9780521540513. [Google Scholar]
- Lee, M.-J.; Um, G.-M.; Yun, J.; Cheong, W.-S.; Park, S.-Y. Enhanced Soft 3D Reconstruction Method with an Iterative Matching Cost Update Using Object Surface Consensus. Sensors 2021, 21, 6680. [Google Scholar] [CrossRef]
- Marí, R.; de Franchis, C.; Meinhardt-Llopis, E.; Anger, J.; Facciolo, G. A Generic Bundle Adjustment Methodology for Indirect RPC Model Refinement of Satellite Imagery. Image Process. Line 2021, 11, 344–373. [Google Scholar] [CrossRef]
- Golub, G.H.; Reinsch, C. Singular Value Decomposition and Least Squares Solutions. In Handbook for Automatic Computation: Volume II: Linear Algebra; Springer: Berlin/Heidelberg, Germany, 1971; pp. 134–151. [Google Scholar]
- Le Saux, B.; Yokoya, N.; Hänsch, R.; Brown, M. 2019 Ieee Grss Data Fusion Contest: Large-Scale Semantic 3d Reconstruction. IEEE Geosci. Remote Sens. Mag. (GRSM) 2019, 7, 33–36. [Google Scholar] [CrossRef]
- Jiang, S.; Ma, Y.; Jiang, W.; Li, Q. Efficient Structure from Motion for UAV Images via Anchor-Free Parallel Merging. ISPRS J. Photogramm. Remote Sens. 2024, 211, 156–170. [Google Scholar] [CrossRef]
- Hermann, M.; Weinmann, M.; Nex, F.; Stathopoulou, E.K.; Remondino, F.; Jutzi, B.; Ruf, B. Depth Estimation and 3D Reconstruction from UAV-Borne Imagery: Evaluation on the UseGeo Dataset. ISPRS Open J. Photogramm. Remote Sens. 2024, 13, 100065. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).






