Multi-Scale Expression of Coastal Landform in Remote Sensing Images Considering Texture Features
Abstract
1. Introduction
- (1)
- Although commonly used image filtering and image pyramids can be used for boundary smoothing and image simplification in multi-scale research, these methods often lose image details, especially in retaining edge information [15].
- (2)
- For images with complex textures or rich colors, traditional image filtering and image pyramids may not be effective in preserving important texture information during the simplification process [16].
2. Previous Related Work
2.1. Areal Element Aggregation Method
2.2. Areal Element Simplification Method
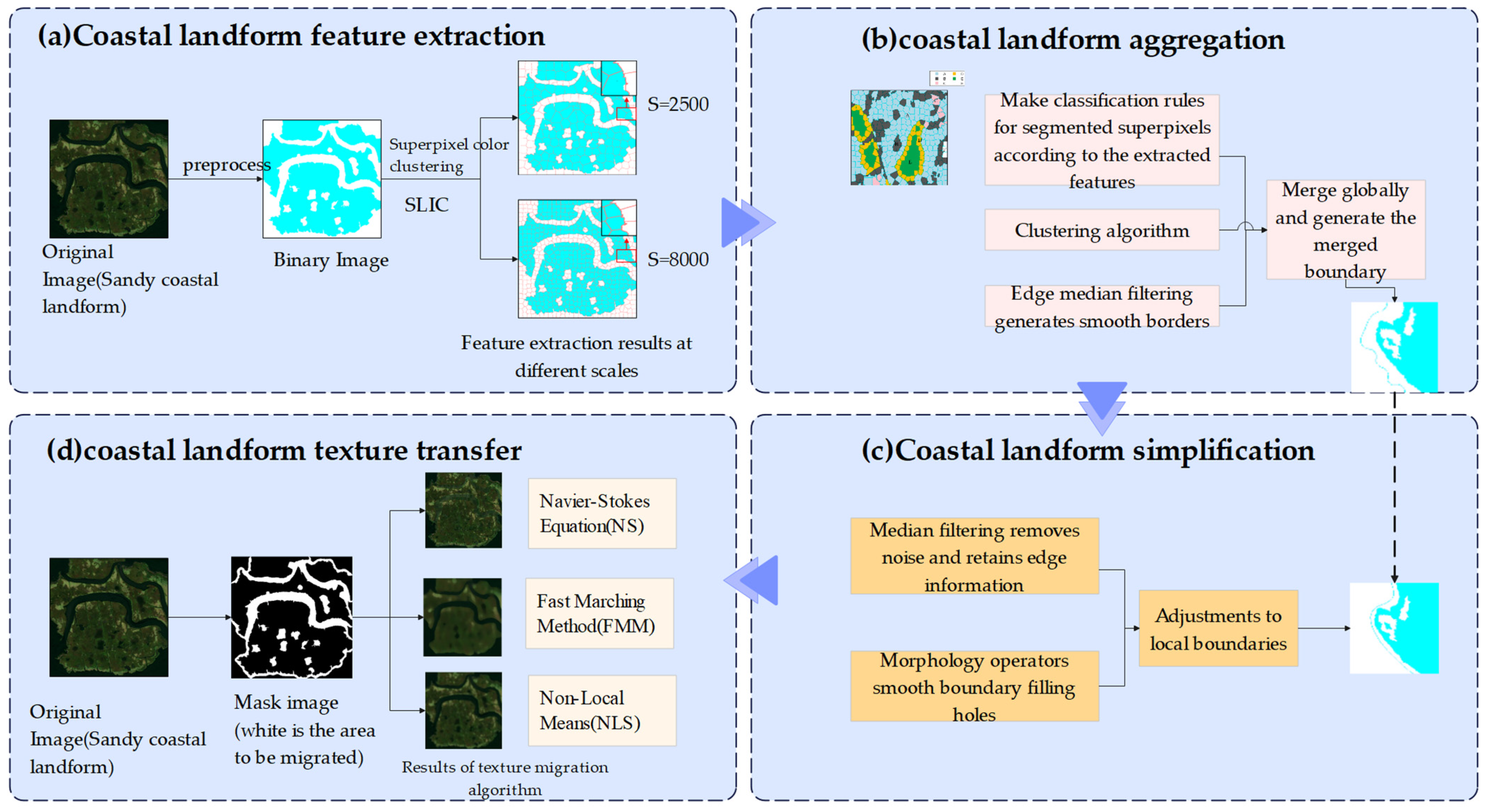
3. Method
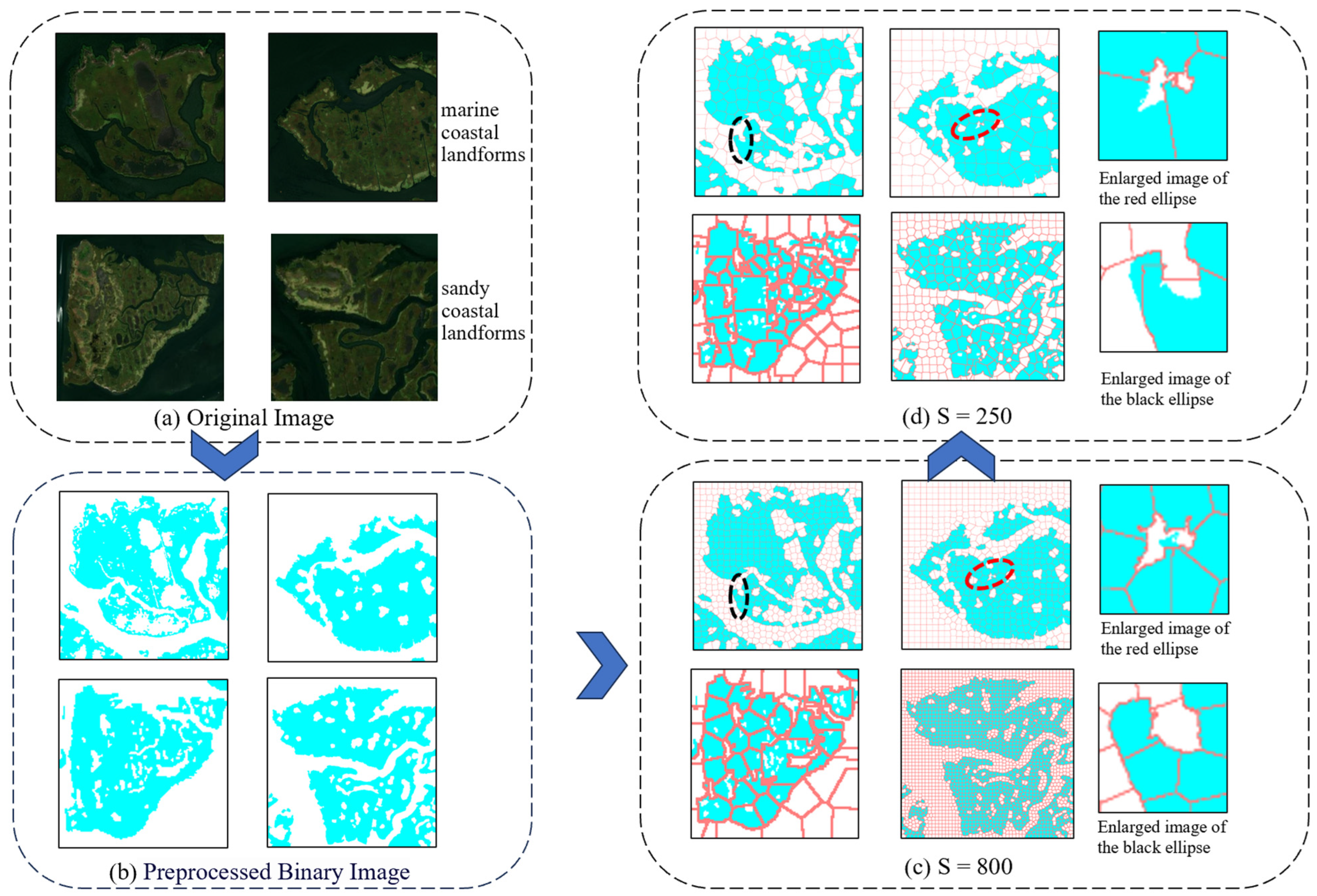
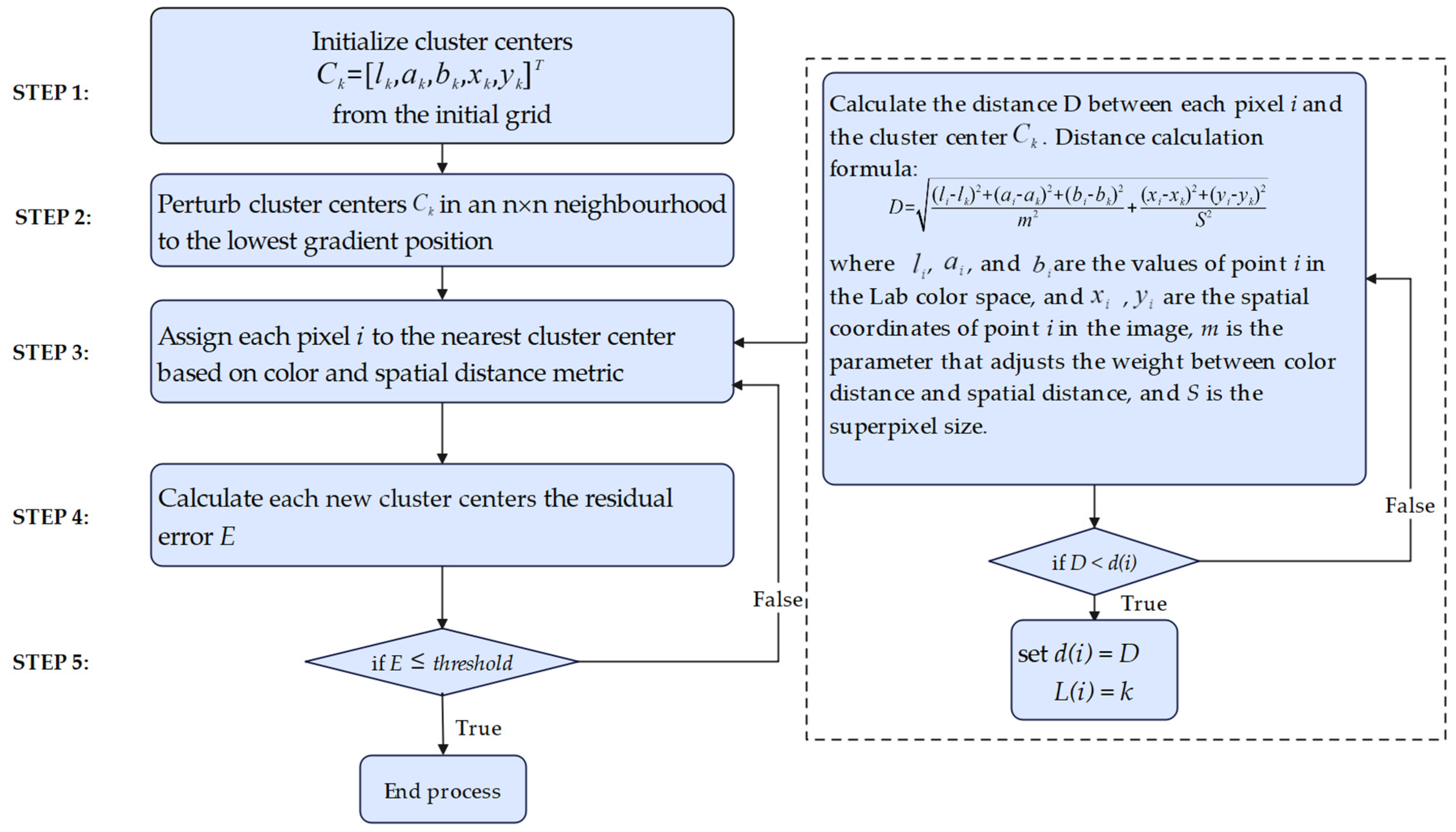
3.1. Extraction of Original Coastal Landform Features
3.2. Coastal Landform Simplification and Global Aggregation
3.3. Texture Transfer of the Merged Coastal Landform
4. Experiment—A Case Study of Coastal Landform Aggregation
4.1. Experimental Data
4.2. Experimental Process
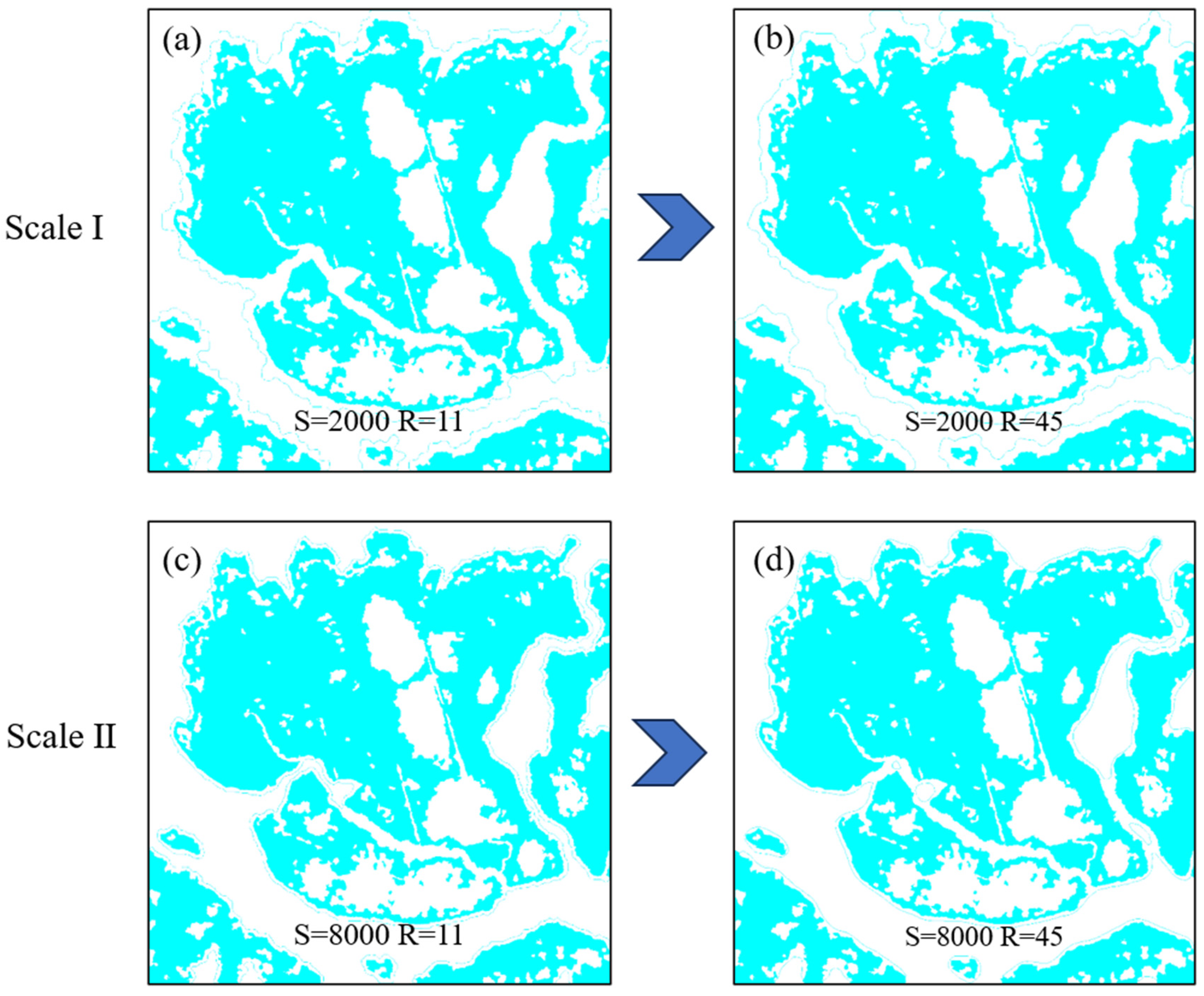
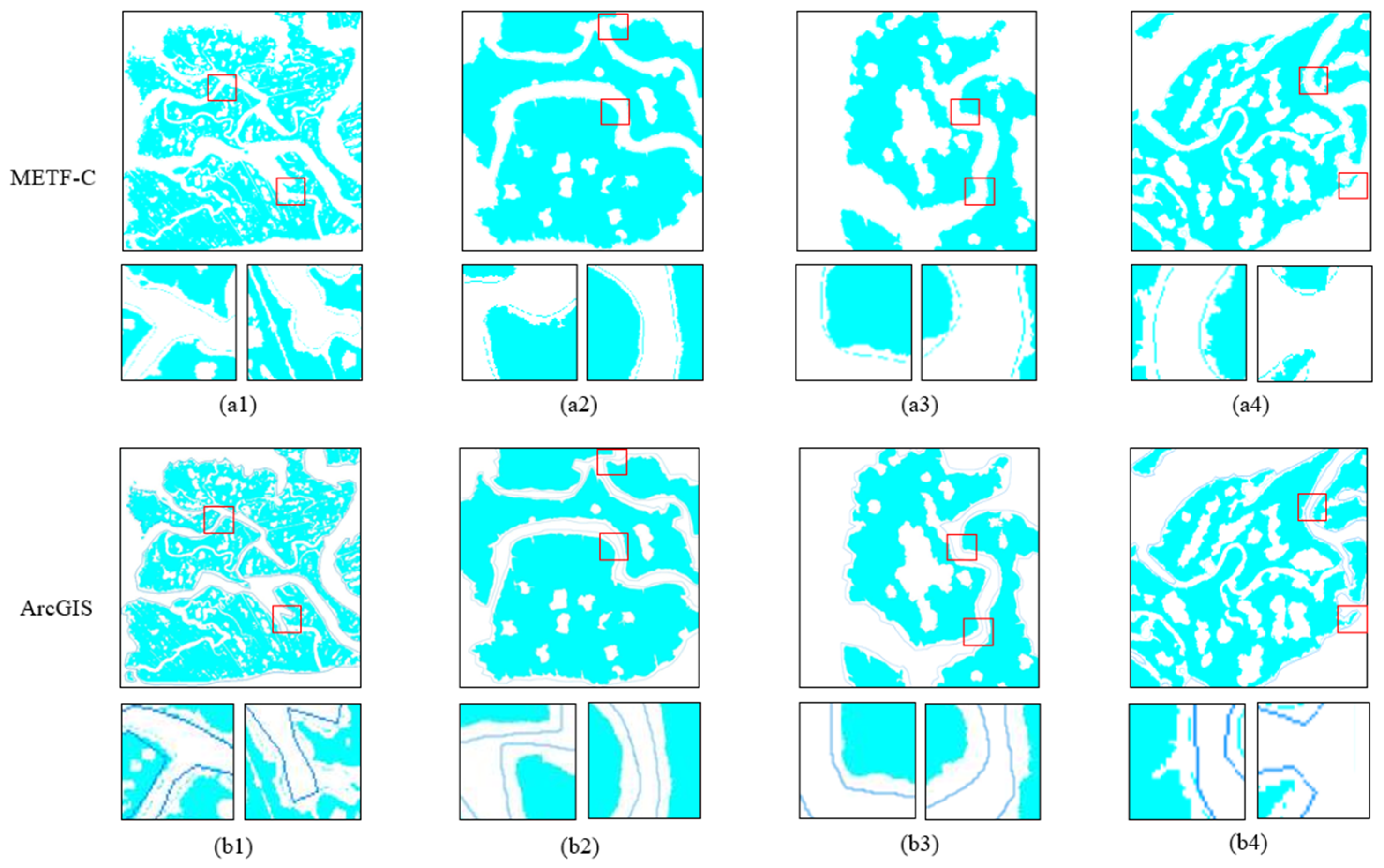
4.3. Comparison and Analysis of Experimental Results
5. Conclusions
- (1)
- The METF-C method uses superpixel segmentation technology to achieve fine segmentation of geomorphic elements, thereby improving the resolution and accuracy of the image and making the combined image clearer and more accurate;
- (2)
- The traditional method has limitations in processing complex texture features and colorful images [53], while the METF-C method effectively maintains the texture features of the original landform through texture transfer technology, making the combined image more realistic and accurate in texture;
- (3)
- The traditional method cannot effectively maintain the global features of images at the multi-scale level [54], while the METF-C method combines the technology of superpixel segmentation and rule selection, which can realize the combination of landform images with multiple scales and levels and effectively retain the global features of images.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dollár, P.; Appel, R.; Belongie, S.; Perona, P. Fast Feature Pyramids for Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1532–1545. [Google Scholar] [CrossRef]
- Hay, G.J.; Blaschke, T.; Marceau, D.J.; Bouchard, A. A Comparison of Three Image-Object Methods for the Multiscale Analysis of Landscape Structure. ISPRS J. Photogramm. Remote Sens. 2003, 57, 327–345. [Google Scholar] [CrossRef]
- Zou, Z.; Chen, K.; Shi, Z.; Guo, Y.; Ye, J. Object Detection in 20 Years: A Survey. Proc. IEEE 2023, 111, 257–276. [Google Scholar] [CrossRef]
- Sedaghat, A.; Mokhtarzade, M.; Ebadi, H. Uniform Robust Scale-Invariant Feature Matching for Optical Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4516–4527. [Google Scholar] [CrossRef]
- Irons, J.R.; Petersen, G.W. Texture Transforms of Remote Sensing Data. Remote Sens. Environ. 1981, 11, 359–370. [Google Scholar] [CrossRef]
- Fernandez-Beltran, R.; Haut, J.M.; Paoletti, M.E.; Plaza, J.; Plaza, A.; Pla, F. Remote Sensing Image Fusion Using Hierarchical Multimodal Probabilistic Latent Semantic Analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4982–4993. [Google Scholar] [CrossRef]
- Ben Hamza, A.; He, Y.; Krim, H.; Willsky, A. A Multiscale Approach to Pixel-Level Image Fusion. Integr. Comput.-Aided Eng. 2005, 12, 135–146. [Google Scholar] [CrossRef]
- Teodoro, A.C.; Pais-Barbosa, J.; Veloso-Gomes, F.; Taveira-Pinto, F. Evaluation of Beach Hydromorphological Behaviour and Classification Using Image Classification Techniques. J. Coast. Res. 2009, II, 1607–1611. [Google Scholar] [CrossRef]
- Wu, D.; Shen, Y.; Fang, R. Morphological Change Characteristics of Tidal Gullies in Central Jiangsu Coast. Acta Geograph. Sin. 2013, 68, 955–965. [Google Scholar]
- Tang, K.; Astola, J.; Neuvo, Y. Nonlinear Multivariate Image Filtering Techniques. IEEE Trans. Image Process. 1995, 4, 788–798. [Google Scholar] [CrossRef]
- Gluckman, J. Scale Variant Image Pyramids. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), New York, NY, USA, 17–22 June 2006; pp. 1069–1075. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing; Prentice Hall: Upper Saddle River, NJ, USA, 2008; pp. 165–170. [Google Scholar]
- Wei, G.; Yang, J.; Zhang, H. Comparative Study of Commonly Used Nonlinear Filtering Methods. Electro-Optics Control 2009, 16, 48–52. [Google Scholar]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A Tutorial on Particle Filters for Online Nonlinear/Non-Gaussian Bayesian Tracking. IEEE Trans. Signal Process. 2002, 50, 174–188. [Google Scholar] [CrossRef]
- Smith, S.M.; Brady, J.M. SUSAN—A New Approach to Low Level Image Processing. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 21, 443–456. [Google Scholar] [CrossRef]
- Burt, P.; Adelson, E. The Laplacian Pyramid as a Compact Image Code. IEEE Trans. Commun. 1983, 31, 532–540. [Google Scholar] [CrossRef]
- Usui, H. Automatic Measurement of Building Setbacks and Streetscape Widths and Their Spatial Variability Along Streets and in Plots: Integration of Streetscape Skeletons and Plot Geometry. Int. J. Geogr. Inf. Sci. 2023, 37, 810–838. [Google Scholar] [CrossRef]
- Shen, Y.; Ai, T.; Li, W.; Wu, L. A Polygon Aggregation Method with Global Feature Preservation Using Superpixel Segmentation. Comput. Environ. Urban Syst. 2019, 75, 117–131. [Google Scholar] [CrossRef]
- Hermosilla, T.; Ruiz, L.A.; Recio, J.A.; Estornell, J. Assessing Contextual Descriptive Features for Plot-Based Classification of Urban Areas. Landsc. Urban Plan. 2012, 106, 124–137. [Google Scholar] [CrossRef]
- Burger, P.R. Exploring Geographic Information Systems (Book Review). Geogr. Bull. 1998, 40, 59. [Google Scholar]
- Fairclough, H.; Gilbert, M. Layout Optimization of Simplified Trusses Using Mixed Integer Linear Programming with Runtime Generation of Constraints. Struct. Multidiscip. Optim. 2020, 61, 1977–1999. [Google Scholar] [CrossRef]
- Peng, D.; Wolff, A.; Haunert, J.H. Finding Optimal Sequences for Area Aggregation—A* vs. Integer Linear Programming. ACM Trans. Spat. Algorithms Syst. (TSAS) 2020, 7, 1–40. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Y.; Zhang, H. Coastal Line Simplification Based on Fuzzy Logic. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5015–5027. [Google Scholar] [CrossRef]
- Li, X.; Zhao, Q. Multi-Scale Analysis of Coastal Landforms Using Feature Extraction Techniques. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1698–1710. [Google Scholar] [CrossRef]
- Chen, L.; Xu, J.; Wang, Y. Automatic Coastal Landform Merging Using Convolutional Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5307–5318. [Google Scholar] [CrossRef]
- McMaster, R.B. A Conceptual Model of the Interaction between Simplification and Smoothing. Cartogr. J. 1986, 23, 27–34. [Google Scholar]
- Buchin, K.; van Kreveld, M.; Löffler, M.; Luo, J.; Silveira, R.I.; Wolff, A. Simplifying a Polygonal Subdivision While Keeping It Simple. Comput. Geom. 2011, 44, 435–446. [Google Scholar] [CrossRef][Green Version]
- Tong, X.; Shi, W. A Scale-Adaptive Model for the Simplification of Areal Features. Int. J. Geogr. Inf. Sci. 2002, 16, 323–343. [Google Scholar] [CrossRef]
- Gong, J.; Zhao, S.; Liu, Y.; Li, M. Multi-Resolution Terrain Simplification and Visualization Based on Triangulated Irregular Networks. Remote Sens. 2013, 5, 5447–5463. [Google Scholar] [CrossRef]
- French, J.; Payo, A.; Murray, B.; Orford, J.; Eliot, M.; Cowell, P. Appropriate Complexity for the Prediction of Coastal and Estuarine Geomorphic Behaviour at Decadal to Centennial Scales. Geomorphology 2016, 256, 3–16. [Google Scholar] [CrossRef]
- Liu, Y.J.; Yu, C.C.; Yu, M.J.; Su, D. Manifold SLIC: A Fast Method to Compute Content-Sensitive Superpixels. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 651–659. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef]
- Villar, S.A.; Torcida, S.; Acosta, G.G. Median Filtering: A New Insight. J. Math. Imaging Vis. 2017, 58, 130–146. [Google Scholar] [CrossRef]
- Raid, A.M.; Khedr, W.; El-Dosuky, M.; El-Bassiouny, A. Image Restoration Based on Morphological Operations. Int. J. Comput. Sci. Eng. Inf. Technol. 2014, 4, 9–21. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, L.; Chen, H.; Lu, S. Texture Reformer: Towards Fast and Universal Interactive Texture Transfer. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 22 February–1 March 2022; pp. 2624–2632. [Google Scholar] [CrossRef]
- McGill, J.T. Map of Coastal Landforms of the World. Geogr. Rev. 1958, 48, 402–405. [Google Scholar] [CrossRef]
- Tobler, W. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Harsimran, S.; Santosh, K.; Rakesh, K. Overview of Corrosion and Its Control: A Critical Review. Proc. Eng. Sci. 2021, 3, 13–24. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, L.; Wang, H. Sobel Edge Detection Based on Weighted Nuclear Norm Minimization Image Denoising. Appl. Sci. 2023, 12, 120–130. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Z.; Lin, Z.; Qi, H.; Wang, L.; Yang, Y. Image Super-Resolution by Neural Texture Transfer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 7982–7991. [Google Scholar]
- Wang, Z.; Wang, Q.; Moran, B.; Xia, Y.; Ha, L. Optimal Submarine Cable Path Planning and Trunk-and-Branch Tree Network Topology Design. IEEE/ACM Trans. Netw. 2020, 28, 1562–1572. [Google Scholar] [CrossRef]
- Radhakrishnan, R. A Survey of Multiscale Modeling: Foundations, Historical Milestones, Current Status, and Future Prospects. AIChE J. 2021, 67, e17026. [Google Scholar] [CrossRef]
- Zhang, X. Two-Step Non-Local Means Method for Image Denoising. Multidimens. Syst. Signal Process. 2022, 33, 341–366. [Google Scholar] [CrossRef]
- Liu, Y.L.; Wang, J.; Chen, X.; Li, W.; Xu, M. A Robust and Fast Non-Local Means Algorithm for Image Denoising. J. Comput. Sci. Technol. 2008, 23, 270–279. [Google Scholar] [CrossRef]
- Köksoy, O. Multiresponse Robust Design: Mean Square Error (MSE) Criterion. Appl. Math. Comput. 2006, 175, 1716–1729. [Google Scholar] [CrossRef]
- Hore, A.; Ziou, D. Image Quality Metrics: PSNR vs. SSIM. In Proceedings of the 2010 20th International Conference on Pattern Recognition (ICPR), Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar]
- Esri, Inc. ArcGIS Desktop: Release 10; Environmental Systems Research Institute: Redlands, CA, USA, 2011. [Google Scholar]
- Estévez, P.A.; Tesmer, M.; Pérez, C.A.; Nascimento, J.C. Normalized Mutual Information Feature Selection. IEEE Trans. Neural Netw. 2009, 20, 189–201. [Google Scholar] [CrossRef]
- Chen, B.; Liang, J.; Zheng, N.; Príncipe, J.C. Kernel least mean square with adaptive kernel size. Neurocomputing. 2016, 191, 95–106. [Google Scholar] [CrossRef]
- Weber, M.; Neri, F.; Tirronen, V. A study on scale factor in distributed differential evolution. Inf. Sci. 2011, 181, 2488–2511. [Google Scholar] [CrossRef]
- Cotton, F.; Archuleta, R.; Causse, M. What is sigma of the stress drop? Seismol. Res. Lett. 2013, 84, 42–48. [Google Scholar] [CrossRef]
- Yoo, D.; Park, S.; Lee, J.Y.; Paek, A.; Kweon, I.S. Multi-scale pyramid pooling for deep convolutional representation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Boston, MA, USA, 7–12 June 2015; pp. 71–80. [Google Scholar]
- Zhang, L.; Li, Q. Multi-scale and multi-level image processing for feature preservation. Comput. Vis. Image Underst. 2020, 200, 102–115. [Google Scholar]
- Gong, H.; Li, Y.; Liu, Y. Texture synthesis and transfer with deep learning: A review. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 2365–2380. [Google Scholar]





| Method | MSE | PSNR | NMI | SSIM |
|---|---|---|---|---|
| NS | 17.989 | 35.581 | 0.258 | 0.961 |
| FMM | 19.650 | 35.197 | 0.261 | 0.910 |
| NL-Means | 28.676 | 33.556 | 0.255 | 0.816 |
| Level | Method | Number of the Superpixels (S) | Radius of Filtering Kernel (R) | Aggregation Distance |
|---|---|---|---|---|
| I | METF-C | 2500 | 45 | - |
| ArcGIS | - | - | 100 m | |
| II | METF-C | 12,500 | 11 | - |
| ArcGIS | - | - | 150 m |
| Level | Method | Number of Superpixels (S) | Kernel Size | Scale Factor | Sigma |
|---|---|---|---|---|---|
| I | METF-C | 2500 | 45 | - | - |
| Median filtering | - | 5 | - | - | |
| Image pyramid | - | - | 2 | - | |
| Gaussian filtering | - | 3 | - | 1 | |
| II | METF-C | 12,500 | 11 | - | - |
| Median filtering | - | 7 | - | - | |
| Image pyramid | - | - | 4 | - | |
| Gaussian filtering | - | 5 | - | 2 |
| Level | Method | Edge Preservation Index | Texture Clarity Score | Information Retention Rate |
|---|---|---|---|---|
| I | METF-C | 0.988 | 39.086 | 2.175 |
| Median filtering | 0.978 | 0.542 | 1.947 | |
| Image pyramid | 0.861 | 45.107 | 2.084 | |
| Gaussian filtering | 0.93 | 5.92 | 2.104 | |
| II | METF-C | 0.983 | 1.387 | 2.087 |
| Median filtering | 0.967 | 1.092 | 2.330 | |
| Image pyramid | 0.982 | 1.431 | 2.027 | |
| Gaussian filtering | 0.92 | 1.52 | 2.075 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Shen, Y. Multi-Scale Expression of Coastal Landform in Remote Sensing Images Considering Texture Features. Remote Sens. 2024, 16, 3862. https://doi.org/10.3390/rs16203862
Zhang R, Shen Y. Multi-Scale Expression of Coastal Landform in Remote Sensing Images Considering Texture Features. Remote Sensing. 2024; 16(20):3862. https://doi.org/10.3390/rs16203862
Chicago/Turabian StyleZhang, Ruojie, and Yilang Shen. 2024. "Multi-Scale Expression of Coastal Landform in Remote Sensing Images Considering Texture Features" Remote Sensing 16, no. 20: 3862. https://doi.org/10.3390/rs16203862
APA StyleZhang, R., & Shen, Y. (2024). Multi-Scale Expression of Coastal Landform in Remote Sensing Images Considering Texture Features. Remote Sensing, 16(20), 3862. https://doi.org/10.3390/rs16203862






