Infrared and Visible Image Fusion via Sparse Representation and Guided Filtering in Laplacian Pyramid Domain

Abstract

The fusion of infrared and visible images together can fully leverage the respective advantages of each, providing a more comprehensive and richer set of information. This is applicable in various fields such as military surveillance, night navigation, environmental monitoring, etc. In this paper, a novel infrared and visible image fusion method based on sparse representation and guided filtering in Laplacian pyramid (LP) domain is introduced. The source images are decomposed into low- and high-frequency bands by the LP, respectively. Sparse representation has achieved significant effectiveness in image fusion, and it is used to process the low-frequency band; the guided filtering has excellent edge-preserving effects and can effectively maintain the spatial continuity of the high-frequency band. Therefore, guided filtering combined with the weighted sum of eight-neighborhood-based modified Laplacian (WSEML) is used to process high-frequency bands. Finally, the inverse LP transform is used to reconstruct the fused image. We conducted simulation experiments on the publicly available TNO dataset to validate the superiority of our proposed algorithm in fusing infrared and visible images. Our algorithm preserves both the thermal radiation characteristics of the infrared image and the detailed features of the visible image.

1. Introduction

Infrared and visible image fusion is a process that integrates the complementary information from infrared (IR) and visible light images to produce a single image that is more informative and suitable for human perception or automated analysis tasks [1]. This technique leverages the distinct advantages of both imaging modalities to enhance the visibility of features that are not apparent in either image alone [2,3].

Unlike visible light images, infrared images capture the thermal radiation emitted by objects. This allows for the detection of living beings, machinery, and other heat sources, even in total darkness or through obstructions like smoke and fog. IR imaging is invaluable for applications requiring visibility in low-light conditions, such as night-time surveillance, search and rescue operations, and wildlife observation [4].

Visible light images provide high-resolution details and color information, which are crucial for human interpretation and understanding of a scene. From photography to video surveillance, visible light imaging is the most common form of imaging, offering a straightforward depiction of the environment as perceived by the human eye. The fusion process integrates the thermal information from infrared images with the detail and color information from visible images [5,6,7,8]. This results in images that highlight both the thermal signatures and the detailed scene information. By combining these two types of images, the fused image enhances the ability to detect and recognize subjects and objects in various conditions, including complete darkness, smoke, fog, and camouflage situations.

Various algorithms and techniques, including multi-resolution analysis, image decomposition, and feature-based methods, have been developed to fuse the images. A major challenge in image fusion is to maintain and highlight the essential details from both source images in the combined image, while avoiding artifacts and ensuring that no crucial information is lost [9,10,11,12,13,14,15,16,17]. For some applications, such as surveillance and automotive safety, the ability to process and fuse images in real time is crucial. This creates difficulties in terms of processing efficiency and the fine-tuning of algorithms.

During the fusion process, some information may be lost or confused, especially in areas with strong contrast or rich details, where the fusion algorithm might not fully retain the information from each image. Additionally, noise or artifacts may be introduced during the fusion process, affecting the quality of the final image. To enhance the performance of the fused image in terms of both thermal radiation characteristics and detail clarity, a fusion method utilizing sparse representation and guided filtering in the Laplacian pyramid domain is constructed. Sparse representation has demonstrated excellent results in image fusion; it is used to process the low-frequency sub-bands, and guided filtering combined with the weighted sum of eight-neighborhood-based modified Laplacian (WSEML) is utilized to process the high-frequency sub-bands. Through experiments and validation on the publicly available TNO dataset, our algorithm has achieved significant fusion effects, incorporating both infrared characteristics and scene details. This is advantageous for subsequent target detection and recognition tasks.

The paper is structured as follows: Section 2 reviews related research. Section 3 introduces the Laplacian pyramid transform. Section 4 details the proposed fusion approach. Section 5 shows the experimental results and discussion. Finally, Section 6 concludes the paper. This structure ensures a clear progression through the background research, foundational concepts, algorithmic details, empirical findings, and concluding remarks, thereby comprehensively addressing the topic of image fusion in the Laplacian pyramid domain.

2. Related Works

2.1. Deep Learning on Image Fusion

Deep learning has achieved significant results in the field of image processing, with popular algorithms including CNNs [18], GANs [19], swin transformer [20,21], vision transformer [22], and mamba [23]. Deep learning has significantly advanced the field of image fusion by introducing models that can learn complex representations and fusion rules from data, leading to superior fusion performance compared with traditional techniques. Deep-learning models can automatically extract and merge the most pertinent features from both infrared and visible images. This process produces fused images that effectively combine the thermal information from infrared images with the detailed texture and color from visible images [24,25,26].

CNNs are widely employed as deep-learning models for image fusion. They excel at capturing spatial hierarchies in images through their deep architecture, making them ideal for tasks that involve spatial data, like images. In the context of image fusion, CNNs can be trained to identify and merge the salient features from both infrared and visible images, ensuring that the fused image retains critical information from both sources [27]. Liu et al. [28] introduced the fusion of infrared and visible images using CNNs. Their experimental findings showcase that this approach attains cutting-edge outcomes in both visual quality and objective metrics. Similarly, Yang et al. [29] devised a method for image fusion leveraging multi-scale convolutional neural networks alongside saliency weight maps.

GANs have also been applied to image fusion with promising results [30,31]. A GAN consists of two networks: a generator that creates images and a discriminator that evaluates them. For image fusion, the generator can be trained to produce fused images from input images, while the discriminator ensures that the fused images are indistinguishable from real images in terms of quality and information content. This approach can result in high-quality fused images that effectively blend the characteristics of both modalities. Change et al. [32] presented a GAN model incorporating dual fusion paths and a U-type discriminator. Experimental findings illustrate that this approach outperforms other methods.

Deep learning offers a powerful framework for image fusion, with the potential to significantly enhance the quality and usefulness of fused images across a wide range of applications. Ongoing research in this field focuses on developing more efficient, adaptable, and interpretable models that can provide even better fusion results.

2.2. Traditional Methods of Image Fusion

Traditional methods for image fusion focus on combining the complementary information from source images to enhance the visibility of features and improve the overall quality of the resulting image. These techniques are generally categorized via the domain in which the fusion takes place: transform- and spatial-domain methods [33,34,35,36,37].

In transform-domain methods, Chen et al. [38] introduced a spatial-frequency collaborative fusion framework for image fusion; this algorithm utilizes the properties of nonsubsampled shearlet transform for decomposition and reconstruction. Chen et al. [39] introduced a fusion approach tailored for image fusion, emphasizing edge consistency and correlation-driven integration. Through nonsubsampled shearlet transform decomposition, detail layers are acquired housing image details and textures alongside a base layer containing primary features. Li et al. [40] introduced the method for fusing infrared and visible images, leveraging low-pass filtering and sparse representation. Chen et al. [41] introduced the multi-focus image fusion with complex sparse representation (CSR); this model leverages the properties of hypercomplex signals to obtain directional information from real-valued signals by extending them to complex form. It then decomposes these directional components into sparse coefficients using specific directional dictionaries. Unlike traditional SR models, this approach excels at capturing geometric structures in images. This is because CSR coefficients offer accurate measurements of detailed information along particular directions.

In spatial domain methods, Li et al. [42] introduced a neural-network-based approach to assess focus properties using measures like spatial frequency, visibility, and edge features within the source image blocks.

3. Laplacian Pyramid Transform

The Laplacian pyramid of an image can be obtained by computing the difference between every two consecutive layers of the Gaussian pyramid [43,44,45]. Suppose $G_0$ represents a matrix of an image, and $G_k$ represents the $k\mathrm{th}$ layer of the Gaussian pyramid decomposition of the image. Similarly, the $k-1\mathrm{th}$ layer of the Gaussian pyramid is $G_{k-1}$, where the 0th layer is the image itself. The definition of $G_k$ is as follows [44]:

$$\begin{array}{l}\hfill G_k\left(i,j\right)={\displaystyle \sum _{m=-2}^2 {\displaystyle \sum _{n=-2}^{2}w\left(m,n\right)}}{G}_{k-1}\left(2i+m, 2j+n\right)\hfill \\ \hfill \left(1\le k\le N, 0\le i\le R_k, 0\le j\le C_k\right)\hfill \end{array}$$

(1)

where $N$ is the maximum number of layers in the Gaussian pyramid decomposition; $R_k$ and $C_k$ represent the number of rows and columns of the $k\mathrm{th}$ layer image of the Gaussian pyramid, respectively. $w\left(m,n\right)$ is a low-pass window function of size $5\times 5$ [44,45]:

$$w={\displaystyle \frac{1}{256}}\left(\begin{array}{l}1 4 6 4 1\\ 4 16 24 16 4\\ 6 24 36 24 6\\ 4 16 24 16 4\\ 1 4 6 4 1\end{array}\right)$$

(2)

To compute the difference between the $k\mathrm{th}$ layer image $G_k$ and the $(k-1)\mathrm{th}$ layer image $G_{k-1}$ in the Gaussian pyramid, it is necessary to upsample the low-resolution image $G_k$ to match the size of the high-resolution image $G_{k-1}$. Opposite to the process of image downsampling (Reduce), the operation defined for image upsampling is called Expand:

$$G_k^{\ast }=\mathrm{Expand}\left(G_k\right)$$

(3)

where $G_k^{\ast }$ and $G_{k-1}$ have the same dimensions. The specific operation is achieved by interpolating and enlarging the $k\mathrm{th}$ layer image, $G_k$, as defined in Equation (3):

$$\begin{array}{l}\hfill G_k^{\ast }\left(i,j\right)=4{\displaystyle \sum _{m=-2}^2 {\displaystyle \sum _{n=-2}^{2}w\left(m,n\right)}}{G}_k^{\prime }\left({\displaystyle \frac{i-m}{2}},{\displaystyle \frac{j-n}{2}}\right)\hfill \\ \hfill \left(1\le k\le N, 0\le i\le R_{k-1}, 0\le j\le C_{k-1}\right)\hfill \end{array}$$

(4)

where

$$G_k^{\prime }\left({\displaystyle \frac{i-m}{2}},{\displaystyle \frac{j-n}{2}}\right)=\left\{\begin{array}{l}{G}_k\left({\displaystyle \frac{i-m}{2}},{\displaystyle \frac{j-n}{2}}\right), \mathrm{when}{\displaystyle \frac{i-m}{2}},{\displaystyle \frac{j-n}{2}}\mathrm{are} \mathrm{integers}\\ 0, \mathrm{else}\end{array}\right.$$

(5)

From Equation (4), it can be inferred that the newly interpolated pixels between the original pixels are determined by the weighted average of the original pixel intensities.

At this point, the difference between the expanded $k\mathrm{th}$ image $G_k^{\ast }$ and the $\left(k-1\right)\mathrm{th}$ layer image $G_{k-1}$ in the pyramid can be obtained from the following equation:

$${\mathrm{LP}}_{k-1}=G_{k-1}-G_k^{\ast }=G_{k-1}-\mathrm{Expand}\left(G_k\right)$$

(6)

The above expression generates the $\left(k-1\right)\mathrm{th}$ level of the Laplacian pyramid. Since $G_k$ is obtained from $G_{k-1}$ through low-pass filtering and downsampling, the details in $G_k$ are significantly fewer than those in $G_{k-1}$, so the detail information contained in the interpolated $G_k^{\ast }$ of $G_k$ will still be less than $G_{k-1}$. ${\mathrm{LP}}_{k-1}$, as the difference between $G_k^{\ast }$ and $G_{k-1}$, also reflects the information difference between the two layers of images in the Gaussian pyramid $G_k$ and $G_{k-1}$. It contains the high-frequency detail information lost when $G_k$ is obtained through the blurring and downsampling of $G_{k-1}$.

The complete definition of the Laplacian pyramid is as follows:

$$\left\{\begin{array}{l}{\mathrm{LP}}_k=G_k-\mathrm{Expand}\left(G_{k+1}\right), 0\le k\le N\\ {\mathrm{LP}}_N=G_N, k=N\end{array}\right.$$

(7)

Thus, ${\mathrm{LP}}_0,{ \mathrm{LP}}_1, \cdots {, \mathrm{LP}}_N$ can form the Laplacian pyramid of the image, where each layer is the difference between the corresponding layers of the Gaussian pyramid and its upsampled version. This process is akin to bandpass filtering; therefore, the Laplacian pyramid can also be referred to as bandpass tower decomposition.

The decomposition process of the Laplacian pyramid can be summarized into four steps: low-pass filtering, downsampling, interpolation, and bandpass filtering. Figure 1 shows the decomposition and reconstruction process of the Laplacian pyramid transform. A series of pyramid images obtained through Laplacian decomposition can be reconstructed into the original image through an inverse transformation process. Below, we derive the reconstruction method based on Equation (7):

$$\begin{array}{c}{G}_0={\mathrm{LP}}_0+\mathrm{Expand}\left(G_1\right)\\ G_1={\mathrm{LP}}_1+\mathrm{Expand}\left(G_2\right)\\ G_{N-1}={\mathrm{LP}}_{N-1}+\mathrm{Expand}\left(G_N\right)\\ G_N={\mathrm{LP}}_N\end{array}$$

(8)

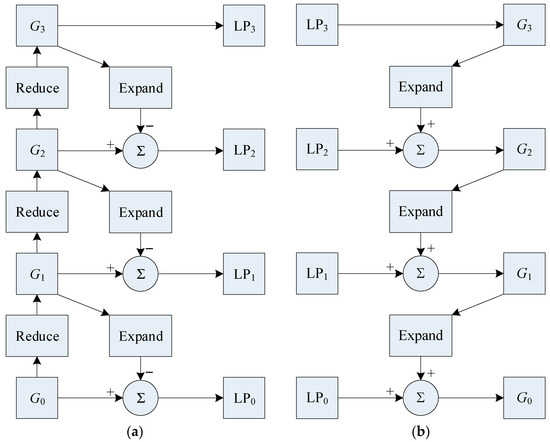
Figure 1. Laplacian pyramid. (a) Three-level Laplacian pyramid decomposition diagram; (b) Three-level Laplacian reconstruction diagram.

In summary, the reconstruction formula for the Laplacian pyramid can be expressed as

$$\left\{\begin{array}{l}{G}_N={\mathrm{LP}}_N, k=N\\ G_k={\mathrm{LP}}_k+\mathrm{Expand}\left(G_{k+1}\right), 0\le k<N\end{array}\right.$$

(9)

4. Proposed Fusion Method

In this section, we present a technique for fusing infrared and visible images using sparse representation and guided filtering within the Laplacian pyramid framework. The method involves four main stages: image decomposition, low-frequency fusion, high-frequency fusion, and image reconstruction. The structure of the proposed method is shown in Figure 2.

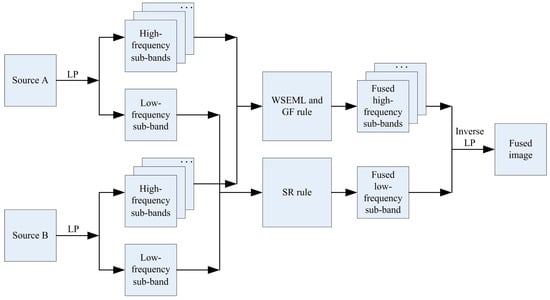
Figure 2. The structure of the proposed method.

4.1. Image Decomposition

The original image undergoes decomposition into a Laplacian pyramid (LP), yielding a low-frequency band $L{P}_N$ and a series of high-frequency bands. This LP transform is applied separately to the source images A and B, resulting in $L{A}_k$ and $L{B}_k$, which represent the $k\mathrm{th}$ layer of the source images. When $k=N$, $L{A}_N$ and $L{B}_N$ are the decomposed top-level images (i.e., low-frequency information).

4.2. Low-Frequency Fusion

The low-frequency band effectively encapsulates the general structure and energy of the image. Sparse representation [1] has demonstrated efficacy in image fusion tasks; hence, it is employed to process the low-frequency band.

The sliding window technique is used to partition $L{A}_N$ and $L{B}_N$ into image patches with the size $\sqrt{n}\times \sqrt{n}$, from upper left to lower right, with the step length of $s$ pixels. Let us denote that there are $T$ patches represented as ${\left\{p_A^i\right\}}_{i=1}^T$ and ${\left\{p_B^i\right\}}_{i=1}^T$ in $L{A}_N$ and $L{B}_N$, respectively.

For each position $i$, rearrange $\left\{p_A^i,p_B^i\right\}$ into column vectors $\left\{v_A^i,v_B^i\right\}$, and then normalize each vector’s mean value to zero to generate $\left\{{\widehat{V}}_A^i,{\widehat{V}}_B^i\right\}$ using the following equations [1]:

$${\widehat{V}}_A^i=V_A^i-{\overline{v}}_A^i\cdot 1$$

(10)

$${\widehat{V}}_B^i=V_B^i-{\overline{v}}_B^i\cdot 1$$

(11)

where 1 depicts an all-one valued $n\times 1$ vector, and ${\widehat{v}}_A^i$ and ${\widehat{v}}_B^i$ are the mean values of all the elements in $V_A^i$ and $V_B^i$, respectively.

To compute the sparse coefficient vectors $\left\{{\alpha }_A^i,{\alpha }_B^i\right\}$ of $\left\{{\widehat{V}}_A^i,{\widehat{V}}_B^i\right\}$, we employ the orthogonal matching pursuit (OMP) technique, applying the following formulas:

$${\alpha }_A^i=\arg \underset{\alpha }{\min }{‖\alpha ‖}_0 s.t. {‖{\widehat{V}}_A^i-D\alpha ‖}_2<\epsilon$$

(12)

$${\alpha }_B^i=\arg \underset{\alpha }{\min }{‖\alpha ‖}_0 s.t. {‖{\widehat{V}}_B^i-D\alpha ‖}_2<\epsilon$$

(13)

Here, $D$ represents the learned dictionary obtained through the K-singular value decomposition (K-SVD) approach.

Next, ${\alpha }_A^i$ and ${\alpha }_B^i$ are combined using the “max-L1” rule to produce the fused sparse vector:

$${\alpha }_F^i=\left\{\begin{array}{l}{\alpha }_A^i if {‖{\alpha }_A^i‖}_1>{‖{\alpha }_B^i‖}_1\\ {\alpha }_B^i else\end{array}\right.$$

(14)

The fused results of $V_A^i$ and $V_B^i$ can be calculated using the following method:

$$V_F^i=D{\alpha }_F^i+{\widehat{v}}_F^i\cdot 1$$

(15)

where the merged mean value ${\overline{v}}_F^i$ can be computed as follows:

$${\overline{v}}_F^i=\left\{\begin{array}{l}{\overline{v}}_A^i if {\alpha }_F^i={\alpha }_A^i\\ {\overline{v}}_B^i else\end{array}\right.$$

(16)

The above process is iterated for all the source image patches in ${\left\{p_A^i\right\}}_{i=1}^T$ and ${\left\{p_B^i\right\}}_{i=1}^T$ to generate all fused vectors ${\left\{V_F^i\right\}}_{i=1}^T$. Let $L{F}_N$ denotes the low-pass fused result. For each $V_F^i$, reshape it into a patch $p_F^i$, and then plug $p_F^i$ into its original position in $L{F}_N$. As the patches are overlapped, each pixel’s value in $L{F}_N$ is averaged over its accumulation times.

4.3. High-Frequency Fusion

The high-frequency bands contain detailed information. The activity level measure, named WSEML, is defined as follows [46]:

$$\begin{array}{l}\hfill {\mathrm{WSEML}}_S\left(i,j\right)={\displaystyle \sum _{m=-r}^r {\displaystyle \sum _{n=-r}^{r}W\left(m+r+1, n+r+1\right)}}\\ \hfill \times {\mathrm{EML}}_S\left(i+m, j+n\right)\end{array}$$

(17)

where $S\in \left\{L{A}_k, L{B}_k\right\}$, the $3\times 3$ normalized model of $W$, is defined as follows:

$$W={\displaystyle \frac{1}{16}}\left[\begin{array}{l}1 2 1\\ 2 4 2\\ 1 2 1\end{array}\right]$$

(18)

and the $EM{L}_S$ is computed by

$$\begin{array}{l}{\mathrm{EML}}_S\left(i,j\right)\\ =\left|2S\left(i,j\right)-S\left(i-1,j\right)-S\left(i+1,j\right)\right|\\ +\left|2S\left(i,j\right)-S\left(i,j-1\right)-S\left(i,j+1\right)\right|\\ +{\displaystyle \frac{1}{\sqrt{2}}}\left|2S\left(i,j\right)-S\left(i-1,j-1\right)-S\left(i+1,j+1\right)\right|\\ +{\displaystyle \frac{1}{\sqrt{2}}}\left|2S\left(i,j\right)-S\left(i-1,j+1\right)-S\left(i+1,j-1\right)\right|\end{array}$$

(19)

The two zero-value matrixes mapA and mapB are initialized, and the matrixes are computed by

$$mapA\left(i,j\right)=\left\{\begin{array}{l}1,{ \mathrm{if} \mathrm{WSEML}}_{L{A}_k}\left(i,j\right)\ge {\mathrm{WSEML}}_{L{B}_k}\left(i,j\right)\\ 0, \mathrm{else} \end{array}\right. 0\le k<N$$

(20)

$$mapB\left(i,j\right)=1-mapA\left(i,j\right)$$

(21)

Guided filtering, denoted as $G_{r,\epsilon }\left(p,I\right)$, is a linear filtering technique [47,48]. Here, the parameters that control the size of the filter kernel and the extent of blur are represented by $r$ and $\epsilon$, respectively. $p$ and $I$ depict the input image and guidance image, respectively. To enhance the spatial continuity of the high-pass bands in the context of using guided filtering on mapA and mapB, we utilize the corresponding high-pass bands $L{A}_k$ and $L{B}_k$ as the guidance images.

$$mapA=G_{r,\epsilon }\left(mapA,L{A}_l\right)$$

(22)

$$mapB=G_{r,\epsilon }\left(mapB,L{B}_l\right)$$

(23)

where mapA and mapB should be normalized, and the fused high-pass bands $L{F}_k\left(i,j\right)$ are calculated by

$$L{F}_k\left(i,j\right)=mapA\times L{A}_k+mapB\times L{B}_k, 0\le k<N$$

(24)

4.4. Image Reconstruction

Perform the corresponding inverse LP to reconstruct the final fused image.

5. Experimental Results and Discussion

5.1. Experimental Setup

In this section, we conducted simulation experiments using the TNO public dataset [49] and compared them through qualitative and quantitative evaluations. Figure 3 shows the examples from the TNO dataset. We compared our algorithm with eight other image fusion algorithms, namely, ICA [50], ADKLT [51], MFSD [52], MDLatLRR [53], PMGI [54], RFNNest [55], EgeFusion [56], and LEDIF [57]. For quantitative evaluation, we adopted 10 commonly used evaluation metrics to assess the effectiveness of the algorithm, namely, the edge-based similarity measurement $Q_{AB/F}$ [58,59,60,61,62,63], the human-perception-inspired metric $Q_{CB}$ [64,65], the structural-similarity-based metric $Q_E$ [64], the feature mutual information metric $Q_{FMI}$ [66], the gradient-based metric $Q_G$ [64], the mutual information metric $Q_{MI}$ [58,67], the nonlinear correlation information entropy $Q_{NCIE}$ [64], the normalized mutual information $Q_{NMI}$ [64], the phase-congruency-based metric $Q_P$ [64], and the structural-similarity-based metric introduced by Yang et al. $Q_Y$ [64,68,69]. $Q_{AB/F}$ computes and measures the amount of edge information transferred from the source images to the fused images using a Sobel edge detector. $Q_{CB}$ is a perceptual-fusion metric based on human visual system (HVS) models. $Q_E$ takes the original images and the edge images into consideration at the same time. $Q_{FMI}$ calculates the regional mutual information between corresponding windows in the fused image and the two source images. $Q_G$ is obtained from the weighted average of the edge information preservation values. $Q_{MI}$ computes how much information from the source images is transferred to the fused image. $Q_{NCIE}$ is an information-theory-based metric.$Q_{NMI}$ is a quantitative measure of the mutual dependence of two variables. $Q_P$ provides an absolute measure of image features. $Q_Y$ is a fusion metric based on SSIM. A higher index value indicates the algorithm’s superiority.

Figure 3. Examples from the TNO dataset.

The parameters for the compared algorithms correspond to the default parameters in the respective articles. For our method, the parameters are as follows: $r=3$, $\epsilon ={10}^{-6}$; the dictionary size is 256, with K-SVD iterated 180 times. Patch size is 6 × 6, step length is 1, and error tolerance is 0.1 [1].

5.2. Analysis of LP Decomposition Levels

Figure 4 shows the fusion results of LP with different decomposition levels. From the figure, it can be observed that the fusion effects in Figure 4a–c are poor, with severe artifacts. The fusion results in Figure 4d–f are relatively similar. Table 1 provides evaluation metrics for 42 image pairs under different LP decomposition levels. Since the fusion results are poor for decomposition levels 1–3, we first exclude these settings. Comparing the average metric values for decomposition levels 4–6, we see that at level 4, five metrics are optimal. Therefore, we set the LP decomposition level to 4.

Figure 4. Fusion results of different decomposition levels in LP. (a) 1 level; (b) 2 level; (c) 3 level; (d) 4 level; (e) 5 level; (f) 6 level.

Table 1. The average objective evaluation of different LP decomposition levels on 42 pairs of data from the TNO dataset.

Levels	${\mathit{Q}}_{\mathit{A}\mathit{B}/\mathit{F}}$	${\mathit{Q}}_{\mathit{C}\mathit{B}}$	${\mathit{Q}}_{\mathit{E}}$	${\mathit{Q}}_{\mathit{F}\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{G}}$	${\mathit{Q}}_{\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{N}\mathit{C}\mathit{I}\mathit{E}}$	${\mathit{Q}}_{\mathit{N}\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{P}}$	${\mathit{Q}}_{\mathit{Y}}$
1	0.5686	0.5392	0.6205	0.9068	0.5592	3.8195	0.8155	0.5440	0.3016	0.8307
2	0.5669	0.5467	0.6655	0.9124	0.5565	3.1350	0.8099	0.4438	0.3402	0.8317
3	0.5727	0.5394	0.6764	0.9138	0.5619	2.6628	0.8075	0.3760	0.3644	0.8301
4	0.5768	0.5306	0.6699	0.9140	0.5654	2.4378	0.8065	0.3460	0.3716	0.8233
5	0.5765	0.5131	0.6521	0.9138	0.5655	2.3160	0.8060	0.3321	0.3832	0.8079
6	0.5775	0.5113	0.6292	0.9133	0.5662	2.4575	0.8064	0.3540	0.3871	0.7980

5.3. Qualitative and Quantitative Analysis

Figure 5 illustrates the fusion outcomes of various methods applied to Data 1 alongside the corresponding metric data in Table 2. The ICA, ADKLT, PMGI, and RFNNest methods are observed to produce fused images that appear blurred, failing to maintain the thermal radiation characteristics and details present in the source images. Both MFSD and LEDIF methods yield similar fusion results, preserving human thermal radiation characteristics but suffering from noticeable loss of brightness information in specific areas. Conversely, the MDLatLRR and EgeFusion algorithms demonstrate over-sharpening effects, leading to artifacts and significant distortion in the fused images. Our algorithm enables comprehensive complementarity between the infrared and visible images while fully preserving the thermal infrared characteristics.

Figure 5. Results on Data 1. (a) ICA; (b) ADKLT; (c) MFSD; (d) MDLatLRR; (e) PMGI; (f) RFNNest; (g) EgeFusion; (h) LEDIF; (i) Proposed.

Table 2. The objective evaluation of different methods on Data 1.

	${\mathit{Q}}_{\mathit{A}\mathit{B}/\mathit{F}}$	${\mathit{Q}}_{\mathit{C}\mathit{B}}$	${\mathit{Q}}_{\mathit{E}}$	${\mathit{Q}}_{\mathit{F}\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{G}}$	${\mathit{Q}}_{\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{N}\mathit{C}\mathit{I}\mathit{E}}$	${\mathit{Q}}_{\mathit{N}\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{P}}$	${\mathit{Q}}_{\mathit{Y}}$
ICA	0.4017	0.4461	0.5300	0.9139	0.3956	1.8567	0.8038	0.2775	0.2654	0.7064
ADKLT	0.4026	0.5404	0.4651	0.8778	0.3976	1.5936	0.8034	0.2382	0.1851	0.7098
MFSD	0.4247	0.5756	0.5898	0.9017	0.4203	1.3551	0.8031	0.1983	0.2056	0.7252
MDLatLRR	0.3248	0.4957	0.4136	0.8874	0.3184	1.0944	0.8028	0.1556	0.2958	0.6882
PMGI	0.3880	0.5035	0.4399	0.9024	0.3803	1.8901	0.8041	0.2747	0.2028	0.7361
RFNNest	0.3372	0.4939	0.3991	0.9031	0.3300	1.7239	0.8036	0.2546	0.2155	0.6856
EgeFusion	0.1968	0.4298	0.3371	0.8688	0.1901	1.1886	0.8029	0.1665	0.2154	0.4970
LEDIF	0.5058	0.5702	0.6512	0.9087	0.5001	1.2948	0.8030	0.1929	0.2572	0.8143
Proposed	0.5860	0.6029	0.7047	0.9248	0.5838	2.7156	0.8067	0.3908	0.3280	0.8802

From Table 2, it can be observed that our algorithm achieves optimal objective metrics on Data 1, with a $Q_{AB/F}$ value of 0.5860, $Q_{CB}$ value of 0.6029, $Q_E$ value of 0.7047, $Q_{FMI}$ value of 0.9248, $Q_G$ value of 0.5838, $Q_{MI}$ value of 2.7156, $Q_{NCIE}$ value of 0.8067, $Q_{NMI}$ value of 0.3908, $Q_P$ value of 0.3280, and $Q_Y$ value of 0.8802.

Figure 6 displays the fusion results of various methods applied to Data 2, along with the corresponding metric data shown in Table 3. Observing the fusion results, it is evident that the ICA, ADKLT, and PMGI algorithms produced fused images that are blurred and exhibit low brightness. The MFSD, RFNNest, and LEDIF methods suffered from some loss of thermal radiation information. In contrast, the MDLatLRR and EgeFusion algorithms resulted in sharpened images, enhancing the human subjects but potentially causing distortion in other areas due to the sharpening effect. Our algorithm achieved the best fusion result.

Figure 6. Results on Data 2. (a) ICA; (b) ADKLT; (c) MFSD; (d) MDLatLRR; (e) PMGI; (f) RFNNest; (g) EgeFusion; (h) LEDIF; (i) Proposed.

Table 3. The objective evaluation of different methods on Data 2.

	${\mathit{Q}}_{\mathit{A}\mathit{B}/\mathit{F}}$	${\mathit{Q}}_{\mathit{C}\mathit{B}}$	${\mathit{Q}}_{\mathit{E}}$	${\mathit{Q}}_{\mathit{F}\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{G}}$	${\mathit{Q}}_{\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{N}\mathit{C}\mathit{I}\mathit{E}}$	${\mathit{Q}}_{\mathit{N}\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{P}}$	${\mathit{Q}}_{\mathit{Y}}$
ICA	0.4002	0.4417	0.4899	0.9569	0.3987	2.3254	0.8051	0.3427	0.2676	0.7434
ADKLT	0.4043	0.5699	0.4124	0.9249	0.3993	1.8767	0.8041	0.2756	0.1595	0.7093
MFSD	0.4175	0.6009	0.6229	0.9539	0.4128	1.7852	0.8039	0.2594	0.1677	0.6909
MDLatLRR	0.3382	0.4503	0.5120	0.9142	0.3370	1.2513	0.8030	0.1769	0.2772	0.7223
PMGI	0.4605	0.5269	0.5454	0.9516	0.4610	2.1395	0.8043	0.3089	0.1939	0.7885
RFNNest	0.4098	0.5803	0.4507	0.9460	0.4066	2.1851	0.8048	0.3098	0.1841	0.7168
EgeFusion	0.2011	0.3987	0.3715	0.8835	0.1971	1.1956	0.8029	0.1666	0.2133	0.5511
LEDIF	0.5870	0.5920	0.6801	0.9538	0.5845	1.5422	0.8034	0.2297	0.2578	0.8901
Proposed	0.6880	0.6771	0.7431	0.9623	0.6860	3.6399	0.8112	0.5043	0.2976	0.9458

From Table 3, it is apparent that our algorithm achieved superior objective metrics on Data 2, with a $Q_{AB/F}$ value of 0.6880, $Q_{CB}$ value of 0.6771, $Q_E$ value of 0.7431, $Q_{FMI}$ value of 0.9623, $Q_G$ value of 0.6860, $Q_{MI}$ value of 3.6399, $Q_{NCIE}$ value of 0.8112, $Q_{NMI}$ value of 0.5043, $Q_P$ value of 0.2976, and $Q_Y$ value of 0.9458.

Figure 7 depicts the fusion results of various methods applied to Data 3, accompanied by the corresponding metric data shown in Table 4. Analyzing the fusion outcomes, it is evident that the ICA and ADKLT algorithms produced blurry fused images with significant loss of information. The MFSD method introduced artifacts in certain regions. While the MDLatLRR and EgeFusion algorithms increased the overall brightness, they also introduced artifacts. The PMGI and RFNNest algorithms resulted in distorted fused images. The LEDIF algorithm achieved commendable fusion results, albeit with some artifacts present. Our algorithm yielded the best fusion result, achieving moderate brightness and preserving the thermal radiation characteristics.

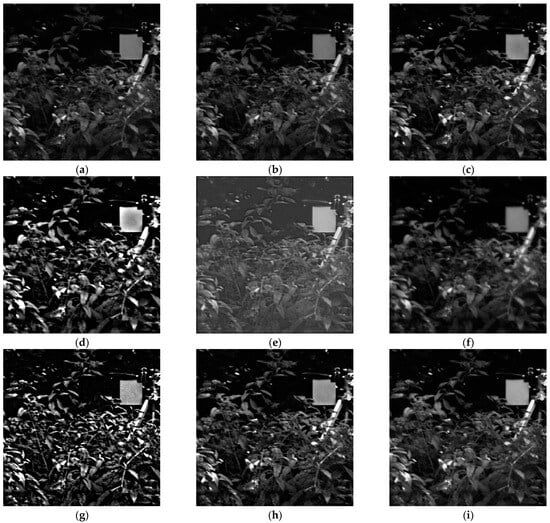
Figure 7. Results on Data 3. (a) ICA; (b) ADKLT; (c) MFSD; (d) MDLatLRR; (e) PMGI; (f) RFNNest; (g) EgeFusion; (h) LEDIF; (i) Proposed.

Table 4. The objective evaluation of different methods on Data 3.

	${\mathit{Q}}_{\mathit{A}\mathit{B}/\mathit{F}}$	${\mathit{Q}}_{\mathit{C}\mathit{B}}$	${\mathit{Q}}_{\mathit{E}}$	${\mathit{Q}}_{\mathit{F}\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{G}}$	${\mathit{Q}}_{\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{N}\mathit{C}\mathit{I}\mathit{E}}$	${\mathit{Q}}_{\mathit{N}\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{P}}$	${\mathit{Q}}_{\mathit{Y}}$
ICA	0.6748	0.6689	0.7446	0.8854	0.6642	4.1877	0.8113	0.6531	0.7358	0.8365
ADKLT	0.5891	0.6599	0.6499	0.8739	0.5764	3.7880	0.8098	0.5907	0.6140	0.7521
MFSD	0.6183	0.6423	0.7634	0.8751	0.6071	3.5683	0.8091	0.5492	0.6331	0.7636
MDLatLRR	0.3124	0.4782	0.4074	0.8460	0.3083	2.4512	0.8060	0.4063	0.5687	0.5580
PMGI	0.5529	0.2891	0.5425	0.8676	0.5400	3.2741	0.8082	0.5181	0.5801	0.5961
RFNNest	0.5053	0.6186	0.5145	0.8723	0.4964	3.6997	0.8095	0.5728	0.6163	0.7138
EgeFusion	0.2452	0.4732	0.3511	0.8070	0.2414	2.1513	0.8053	0.3561	0.4598	0.5115
LEDIF	0.6390	0.6455	0.7146	0.8829	0.6314	3.4861	0.8088	0.5387	0.7371	0.8444
Proposed	0.7252	0.6830	0.8105	0.8887	0.7182	4.4156	0.8131	0.6674	0.8141	0.9395

From Table 4, it is apparent that our algorithm attained optimal objective metrics on Data 3, with a $Q_{AB/F}$ value of 0.7252, $Q_{CB}$ value of 0.6830, $Q_E$ value of 0.8105, $Q_{FMI}$ value of 0.8887, $Q_G$ value of 0.7182, $Q_{MI}$ value of 4.4156, $Q_{NCIE}$ value of 0.8131, $Q_{NMI}$ value of 0.6674, $Q_P$ value of 0.8141, and $Q_Y$ value of 0.9395.

Figure 8 displays the fusion results of various methods applied to Data 4, alongside the corresponding metric data shown in Table 5. Upon reviewing the fusion outcomes, it is evident that the fusion images produced by the ICA, ADKLT, MFSD, PMGI, and LEDIF algorithms exhibit some loss of brightness information. The MDLatLRR and EgeFusion algorithms sharpened the fused image, while the RFNNest method resulted in a darker fused image with some information loss. In contrast, our algorithm produced a fused image with complementary information.

Figure 8. Results on Data 4. (a) ICA; (b) ADKLT; (c) MFSD; (d) MDLatLRR; (e) PMGI; (f) RFNNest; (g) EgeFusion; (h) LEDIF; (i) Proposed.

Table 5. The objective evaluation of different methods on Data 4.

	${\mathit{Q}}_{\mathit{A}\mathit{B}/\mathit{F}}$	${\mathit{Q}}_{\mathit{C}\mathit{B}}$	${\mathit{Q}}_{\mathit{E}}$	${\mathit{Q}}_{\mathit{F}\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{G}}$	${\mathit{Q}}_{\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{N}\mathit{C}\mathit{I}\mathit{E}}$	${\mathit{Q}}_{\mathit{N}\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{P}}$	${\mathit{Q}}_{\mathit{Y}}$
ICA	0.4523	0.3979	0.5932	0.9004	0.4478	2.1008	0.8045	0.3153	0.4024	0.7236
ADKLT	0.3585	0.4032	0.3922	0.8670	0.3529	1.7737	0.8038	0.2697	0.2615	0.6098
MFSD	0.4416	0.4786	0.6176	0.8861	0.4388	1.4931	0.8033	0.2229	0.3066	0.6666
MDLatLRR	0.3157	0.4746	0.3772	0.8874	0.3131	1.2763	0.8029	0.1830	0.4091	0.6339
PMGI	0.3799	0.3587	0.4497	0.8783	0.3764	1.7162	0.8035	0.2594	0.3257	0.7108
RFNNest	0.2971	0.4159	0.3138	0.8920	0.2961	2.0997	0.8046	0.3137	0.3343	0.6153
EgeFusion	0.2123	0.4800	0.3351	0.8582	0.2101	1.2046	0.8029	0.1720	0.2723	0.4726
LEDIF	0.5120	0.4597	0.6724	0.8911	0.5081	1.5419	0.8033	0.2354	0.3847	0.7865
Proposed	0.5947	0.5076	0.6975	0.9059	0.5915	2.5337	0.8062	0.3571	0.5059	0.8553

From Table 5, it is notable that our algorithm achieved optimal objective metrics on Data 4, with a $Q_{AB/F}$ value of 0.5947, $Q_{CB}$ value of 0.5076, $Q_E$ value of 0.6975, $Q_{FMI}$ value of 0.9059, $Q_G$ value of 0.5915, $Q_{MI}$ value of 2.5337, $Q_{NCIE}$ value of 0.8062, $Q_{NMI}$ value of 0.3571, $Q_P$ value of 0.5059, and $Q_Y$ value of 0.8553.

Figure 9 provides detailed insights into the objective performance of the various fusion methods across 42 pairs of data from the TNO dataset. The horizontal axis represents the number of data pairs used in our experiments, while the vertical axis represents the metric values. Each method’s scores across different source images are plotted as curves, with the average score indicated in the legend. Figure 9 illustrates that most methods show consistent trends across the metrics examined, and nearly all fusion methods demonstrate stable performance across all test images, with few exceptions. Therefore, comparisons based on average values in Table 6 hold significant value.

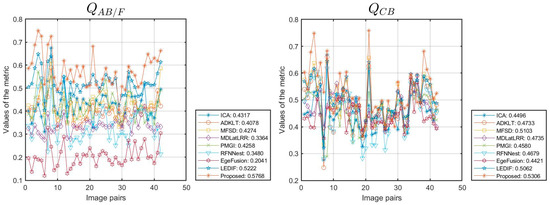
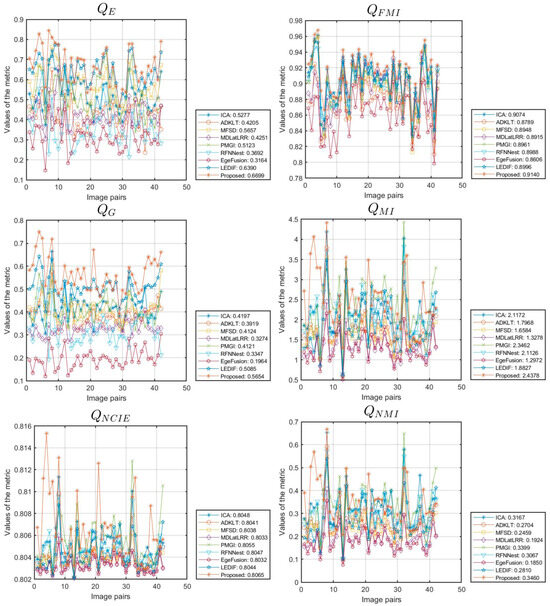
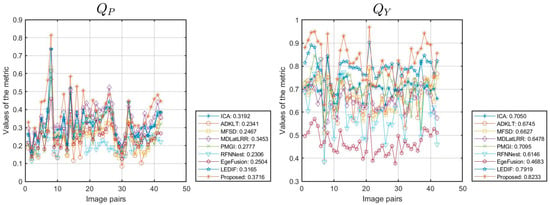
Figure 9. Objective performance of different methods on the TNO dataset.

Table 6. The average objective evaluation of the different methods on 42 pairs of data from the TNO dataset.

	${\mathit{Q}}_{\mathit{A}\mathit{B}/\mathit{F}}$	${\mathit{Q}}_{\mathit{C}\mathit{B}}$	${\mathit{Q}}_{\mathit{E}}$	${\mathit{Q}}_{\mathit{F}\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{G}}$	${\mathit{Q}}_{\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{N}\mathit{C}\mathit{I}\mathit{E}}$	${\mathit{Q}}_{\mathit{N}\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{P}}$	${\mathit{Q}}_{\mathit{Y}}$
ICA	0.4317	0.4496	0.5277	0.9074	0.4197	2.1172	0.8048	0.3167	0.3192	0.7050
ADKLT	0.4078	0.4733	0.4205	0.8789	0.3919	1.7968	0.8041	0.2704	0.2341	0.6745
MFSD	0.4274	0.5103	0.5657	0.8948	0.4124	1.6584	0.8038	0.2459	0.2467	0.6627
MDLatLRR	0.3364	0.4735	0.4251	0.8915	0.3274	1.3278	0.8033	0.1924	0.3453	0.6478
PMGI	0.4258	0.4580	0.5123	0.8961	0.4121	2.3462	0.8055	0.3399	0.2777	0.7095
RFNNest	0.3480	0.4679	0.3692	0.8988	0.3347	2.1126	0.8047	0.3067	0.2306	0.6146
EgeFusion	0.2041	0.4421	0.3164	0.8606	0.1964	1.2972	0.8032	0.1850	0.2504	0.4683
LEDIF	0.5222	0.5062	0.6390	0.8996	0.5085	1.8827	0.8044	0.2810	0.3165	0.7919
Proposed	0.5768	0.5306	0.6699	0.9140	0.5654	2.4378	0.8065	0.3460	0.3716	0.8233

5.4. Experimental Expansion

We expanded our proposed algorithm to include the fusion of multi-focus images from the Lytro [70] and MFI-WHU datasets [71], selecting 20 and 30 groups of data for testing, respectively. The simulation results for one of the data groups are shown in Figure 10. This extension involved a comparative evaluation against eight methods: ICA [50], FusionDN [72], PMGI [54], U2Fusion [73], LEGFF [74], ZMFF [75], EgeFusion [56], and LEDIF [57]. The assessment utilized both subjective visual inspection and objective metrics. Figure 11 and Figure 12 provide detailed insights into the objective performance of various fusion methods on the Lytro and MFI-WHU datasets, with the corresponding average metric values shown in Table 7 and Table 8. From the results in Figure 10, it is evident that the ICA and PMGI algorithms tended to produce fused images with noticeable blurriness, impacting the clarity of detailed information within the fused images. The fused images produced by the FusionDN and U2Fusion algorithms exhibited dark regions in specific areas, such as hair regions in portraits, which detracted from overall visual quality. The fusion results of the LEGFF, ZMFF, and LEDIF algorithms are quite similar, all achieving fully focused fusion effects. The fused image generated by the EgeFusion algorithm showed distortions that made it challenging to discern detailed parts of the image. Our algorithm demonstrated promising results both visually and quantitatively when compared with the other algorithms. Subjective visual assessment indicated that our method effectively enhanced the presentation of complementary information in the fused images, preserving clarity and detail across different focus levels.

Figure 10. Results on Lytro-01. (a) Near focus; (b) Far focus; (c) ICA; (d) FusionDN; (e) PMGI; (f) U2Fusion; (g) LEGFF; (h) ZMFF; (i) EgeFusion; (j) LEDIF; (k) Proposed.

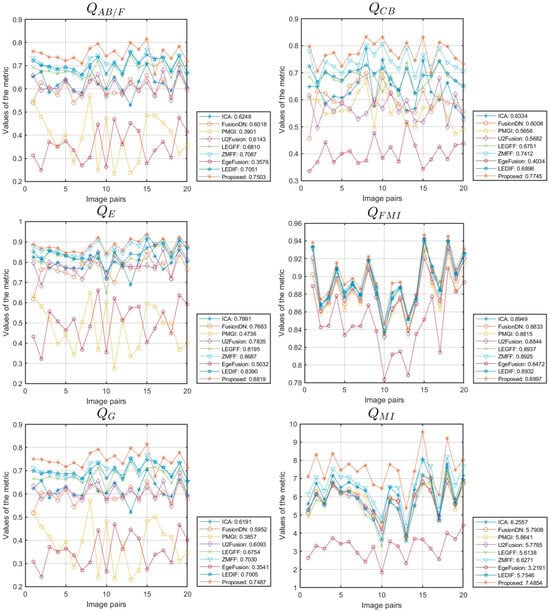
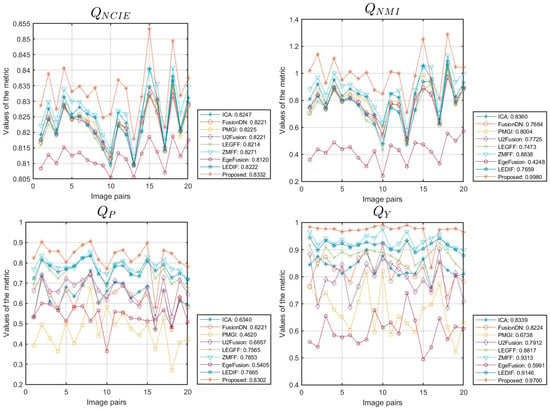
Figure 11. Objective performance of different methods on the Lytro dataset.

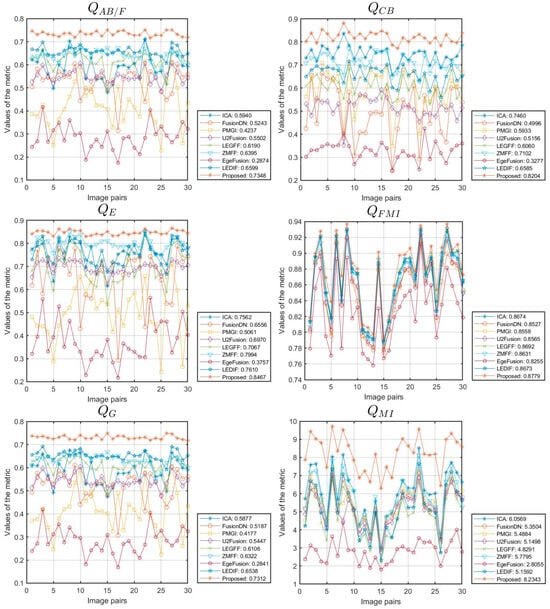
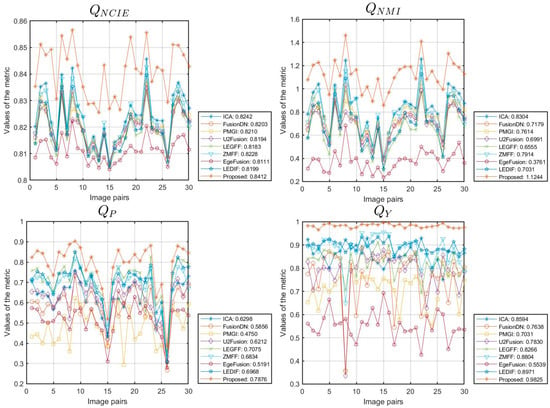
Figure 12. Objective performance of different methods on the MFI-WHU dataset.

Table 7. The average objective evaluation of different methods on 20 pairs of data from the Lytro dataset.

	${\mathit{Q}}_{\mathit{A}\mathit{B}/\mathit{F}}$	${\mathit{Q}}_{\mathit{C}\mathit{B}}$	${\mathit{Q}}_{\mathit{E}}$	${\mathit{Q}}_{\mathit{F}\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{G}}$	${\mathit{Q}}_{\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{N}\mathit{C}\mathit{I}\mathit{E}}$	${\mathit{Q}}_{\mathit{N}\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{P}}$	${\mathit{Q}}_{\mathit{Y}}$
ICA	0.6248	0.6334	0.7991	0.8949	0.6191	6.2557	0.8247	0.8360	0.6340	0.8339
FusionDN	0.6018	0.6008	0.7663	0.8833	0.5952	5.7908	0.8221	0.7684	0.6221	0.8224
PMGI	0.3901	0.5656	0.4736	0.8815	0.3857	5.8641	0.8225	0.8004	0.4620	0.6738
U2Fusion	0.6143	0.5682	0.7835	0.8844	0.6093	5.7765	0.8221	0.7725	0.6657	0.7912
LEGFF	0.6810	0.6751	0.8195	0.8937	0.6754	5.6138	0.8214	0.7473	0.7565	0.8817
ZMFF	0.7087	0.7412	0.8687	0.8925	0.7030	6.6271	0.8271	0.8838	0.7853	0.9313
EgeFusion	0.3576	0.4034	0.5032	0.8472	0.3541	3.2191	0.8120	0.4248	0.5405	0.5991
LEDIF	0.7051	0.6898	0.8390	0.8932	0.7005	5.7546	0.8222	0.7659	0.7665	0.9146
Proposed	0.7503	0.7745	0.8819	0.8997	0.7487	7.4854	0.8332	0.9980	0.8302	0.9700

Table 8. The average objective evaluation of different methods on 30 pairs of data from the MFI-WHU dataset.

	${\mathit{Q}}_{\mathit{A}\mathit{B}/\mathit{F}}$	${\mathit{Q}}_{\mathit{C}\mathit{B}}$	${\mathit{Q}}_{\mathit{E}}$	${\mathit{Q}}_{\mathit{F}\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{G}}$	${\mathit{Q}}_{\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{N}\mathit{C}\mathit{I}\mathit{E}}$	${\mathit{Q}}_{\mathit{N}\mathit{M}\mathit{I}}$	${\mathit{Q}}_{\mathit{P}}$	${\mathit{Q}}_{\mathit{Y}}$
ICA	0.5940	0.7460	0.7562	0.8674	0.5877	6.0569	0.8242	0.8304	0.6298	0.8594
FusionDN	0.5243	0.4996	0.6556	0.8527	0.5187	5.3504	0.8203	0.7179	0.5856	0.7638
PMGI	0.4237	0.5933	0.5061	0.8558	0.4177	5.4884	0.8210	0.7614	0.4750	0.7031
U2Fusion	0.5502	0.5156	0.6970	0.8565	0.5447	5.1498	0.8194	0.6991	0.6212	0.7830
LEGFF	0.6190	0.6060	0.7067	0.8692	0.6106	4.8291	0.8183	0.6555	0.7075	0.8266
ZMFF	0.6395	0.7102	0.7994	0.8631	0.6322	5.7795	0.8228	0.7914	0.6834	0.8804
EgeFusion	0.2874	0.3277	0.3757	0.8255	0.2841	2.8055	0.8111	0.3761	0.5191	0.5539
LEDIF	0.6599	0.6585	0.7610	0.8673	0.6538	5.1592	0.8199	0.7031	0.6968	0.8971
Proposed	0.7348	0.8204	0.8467	0.8779	0.7312	8.2343	0.8412	1.1244	0.7876	0.9825

6. Conclusions

To enhance the clarity and thermal radiation fidelity of infrared and visible image fusion, a fusion method based on sparse representation and guided filtering in the Laplacian pyramid domain is introduced. The Laplacian pyramid serves as an efficient multi-scale transform that decomposes the original image into distinct low- and high-frequency components. Low-frequency bands, crucial for capturing overall scene structure and thermal characteristics, are processed using the sparse representation technique. Sparse representation ensures that key features are preserved while reducing noise and maintaining thermal radiation attributes. High-frequency bands, which encompass fine details and textures vital for visual clarity, are enhanced using guided filtering integrated with WSEML. This approach successfully combines the contextual details from the source images, ensuring that the fused output maintains sharpness and fidelity across different scales. We carried out thorough simulation tests using the well-known TNO dataset to assess the performance of our algorithm. The results demonstrate that our method successfully preserves thermal radiation characteristics while enhancing scene details in the fused images. By continuing to innovate within the framework of sparse representation and guided filtering in the Laplacian pyramid domain, we aim to contribute significantly to the advancement of image fusion techniques, particularly in scenarios where preserving thermal characteristics and enhancing visual clarity are paramount. Moreover, we extended our approach to conducting fusion experiments on multi-focus images, achieving satisfactory results in capturing diverse focal points within a single fused output.

In our future research, we plan to further refine and expand our algorithm’s capabilities. Specifically, we aim to explore enhancements tailored for the fusion of synthetic aperture radar (SAR) and optical images [76]. By integrating SAR data, which provide unique insights into surface properties and structures, with optical imagery, which offers high-resolution contextual information, we anticipate developing a robust fusion framework capable of addressing diverse application scenarios effectively. Additionally, research on change detection based on fusion models is also one of our future research directions [77,78,79,80].