Figure 1.
Three instances of remote sensing data that are missing: (a) displays a MODIS instrument failure on the Aqua satellite, which caused about 70% of the data in Aqua MODIS band 6 to be lost; (b) displays a Landsat-7 satellite digital product, where the image had pixel failure due to a malfunctioning Landsat-7 ETM+ on-board scanning line corrector; and (c) displays a Landsat-8 OLI_TIRS satellite digital product that is useless for direct use due to its 87.3% cloud coverage.
Figure 1.
Three instances of remote sensing data that are missing: (a) displays a MODIS instrument failure on the Aqua satellite, which caused about 70% of the data in Aqua MODIS band 6 to be lost; (b) displays a Landsat-7 satellite digital product, where the image had pixel failure due to a malfunctioning Landsat-7 ETM+ on-board scanning line corrector; and (c) displays a Landsat-8 OLI_TIRS satellite digital product that is useless for direct use due to its 87.3% cloud coverage.
Figure 2.
Examples of Landsat-8 and Sentinel-2 satellite time series. There are two time series examples for Landsat-8 (a) and Sentinel-2 (b), respectively, with a linear stretch of 2% and a true color synthesis.
Figure 2.
Examples of Landsat-8 and Sentinel-2 satellite time series. There are two time series examples for Landsat-8 (a) and Sentinel-2 (b), respectively, with a linear stretch of 2% and a true color synthesis.
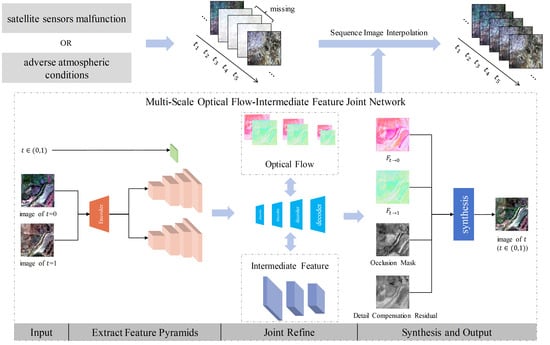
Figure 3.
The architecture of the Multi-scale Optical Flow-Intermediate Feature joint Network. The network begins with the encoder , which extracts the four-scale features from the two time-phase images, and . Subsequently, the intermediate optical flows and features are collectively refined by four decoders in an ascending order of scale. The time phase T is input into the decoder . The decoder outputs the bidirectional optical flows, a multi-channel occlusion information mask, and multi-channel detail compensation information residuals, all of which are equal in size to the original image. Finally, these outputs are synthesized with the images from the preceding and subsequent time phases to generate the image at the intermediate time phase T.
Figure 3.
The architecture of the Multi-scale Optical Flow-Intermediate Feature joint Network. The network begins with the encoder , which extracts the four-scale features from the two time-phase images, and . Subsequently, the intermediate optical flows and features are collectively refined by four decoders in an ascending order of scale. The time phase T is input into the decoder . The decoder outputs the bidirectional optical flows, a multi-channel occlusion information mask, and multi-channel detail compensation information residuals, all of which are equal in size to the original image. Finally, these outputs are synthesized with the images from the preceding and subsequent time phases to generate the image at the intermediate time phase T.
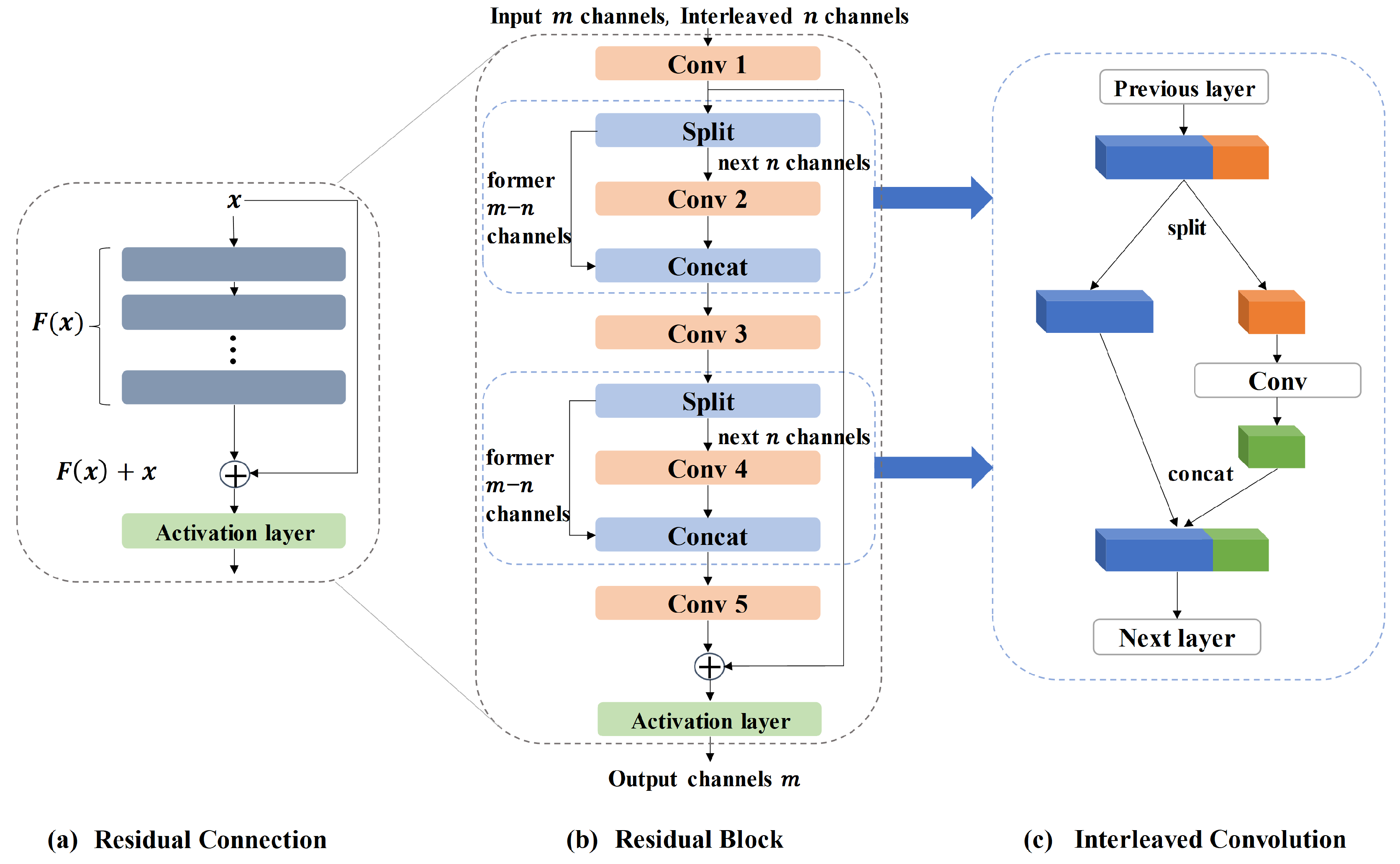
Figure 4.
Detailed structure of the residual block used by each sub-decoder. The residual block (b) uses a residual connection (a) as a whole. There are five convolution layers within the residual block, which uses an interleaved convolution (c) at convolution layer 2 and convolution layer 4.
Figure 4.
Detailed structure of the residual block used by each sub-decoder. The residual block (b) uses a residual connection (a) as a whole. There are five convolution layers within the residual block, which uses an interleaved convolution (c) at convolution layer 2 and convolution layer 4.
Figure 5.
Distribution of training, testing, and validation samples in our experiment: (a) Landsat-8 and (b) Sentinel-2 images; areas inside blue and red boxes and the remainder of the images show the distribution of testing, validation, and training samples, and training set:validation set:test set = 8:1:1.
Figure 5.
Distribution of training, testing, and validation samples in our experiment: (a) Landsat-8 and (b) Sentinel-2 images; areas inside blue and red boxes and the remainder of the images show the distribution of testing, validation, and training samples, and training set:validation set:test set = 8:1:1.
Figure 6.
Pixel error map for Experiment 2 of multi-temporal sequence image interpolation for the Landsat-8 satellite dataset. (a,b) are the results of two time series from Experiment 2 of the Landsat-8 satellite dataset. Time phase 1, 2 and 3 represent the experimental results for the middle three time phases t = 0.25, 0.50, and 0.75. , , and represent the real image, the interpolation result, and the pixel error between the two. In the pixel error map, grey, green, and blue represent the absolute value of the pixel difference in the ranges 0–10, 10–80, and 80–255, with larger values representing larger errors.
Figure 6.
Pixel error map for Experiment 2 of multi-temporal sequence image interpolation for the Landsat-8 satellite dataset. (a,b) are the results of two time series from Experiment 2 of the Landsat-8 satellite dataset. Time phase 1, 2 and 3 represent the experimental results for the middle three time phases t = 0.25, 0.50, and 0.75. , , and represent the real image, the interpolation result, and the pixel error between the two. In the pixel error map, grey, green, and blue represent the absolute value of the pixel difference in the ranges 0–10, 10–80, and 80–255, with larger values representing larger errors.
Figure 7.
Pixel error map for Experiment 2 of multi-temporal sequence image interpolation for the Sentinel-2 satellite dataset. Time phases 1, 2, and 3 represent the experimental results for the middle three time phases t = 0.25, 0.50, and 0.75. , , and represent the real image, the interpolation result, and the pixel error between the two. In the pixel error map, grey, green, and blue represent the absolute value of the pixel difference in the ranges 0–10, 10–80, and 80–255, with larger values representing larger errors.
Figure 7.
Pixel error map for Experiment 2 of multi-temporal sequence image interpolation for the Sentinel-2 satellite dataset. Time phases 1, 2, and 3 represent the experimental results for the middle three time phases t = 0.25, 0.50, and 0.75. , , and represent the real image, the interpolation result, and the pixel error between the two. In the pixel error map, grey, green, and blue represent the absolute value of the pixel difference in the ranges 0–10, 10–80, and 80–255, with larger values representing larger errors.
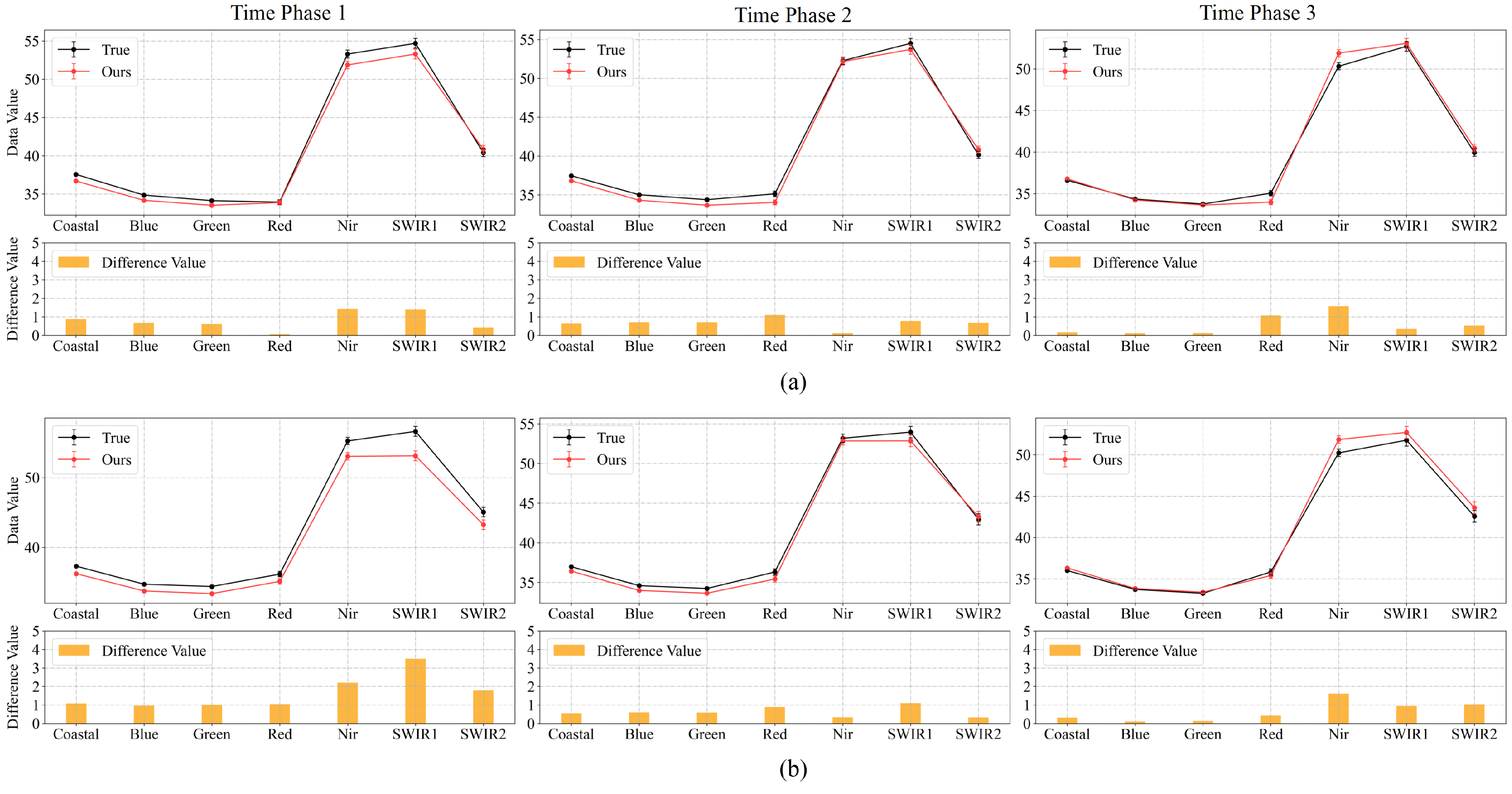
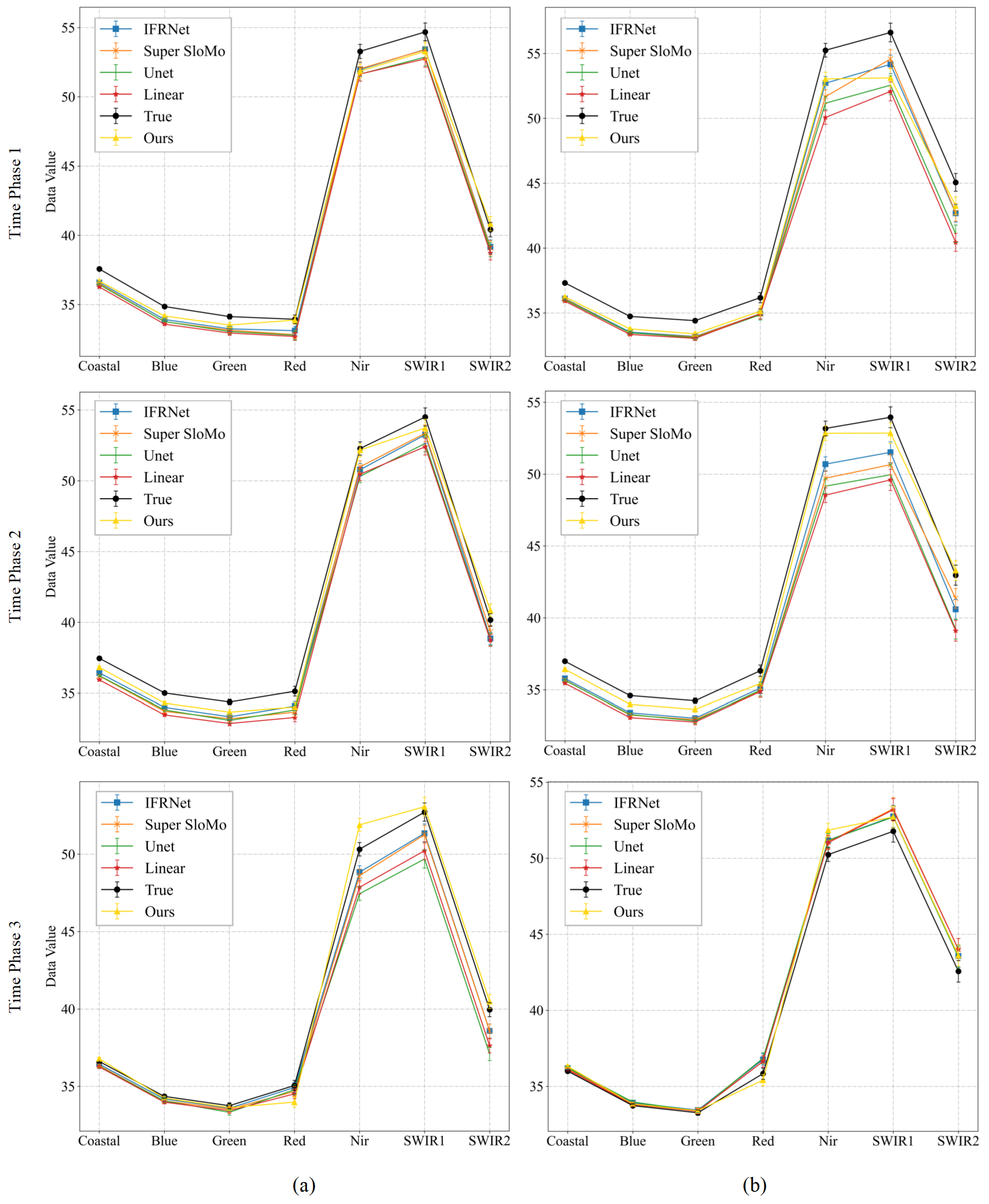
Figure 8.
Spectral curves map at 100 random points for Experiment 2 of multi-temporal sequence image interpolation for the Landsat-8 satellite dataset. (a,b) are the results of two time series from Experiment 2 of the Landsat-8 satellite dataset. Time phases 1, 2, and 3 represent the experimental results for the middle three time phases t = 0.25, 0.50, and 0.75. For each time phase image, we plotted the average of the spectra of the real image and the interpolated result at 100 random points (True and Ours), and the absolute value of the difference between the two spectra.
Figure 8.
Spectral curves map at 100 random points for Experiment 2 of multi-temporal sequence image interpolation for the Landsat-8 satellite dataset. (a,b) are the results of two time series from Experiment 2 of the Landsat-8 satellite dataset. Time phases 1, 2, and 3 represent the experimental results for the middle three time phases t = 0.25, 0.50, and 0.75. For each time phase image, we plotted the average of the spectra of the real image and the interpolated result at 100 random points (True and Ours), and the absolute value of the difference between the two spectra.
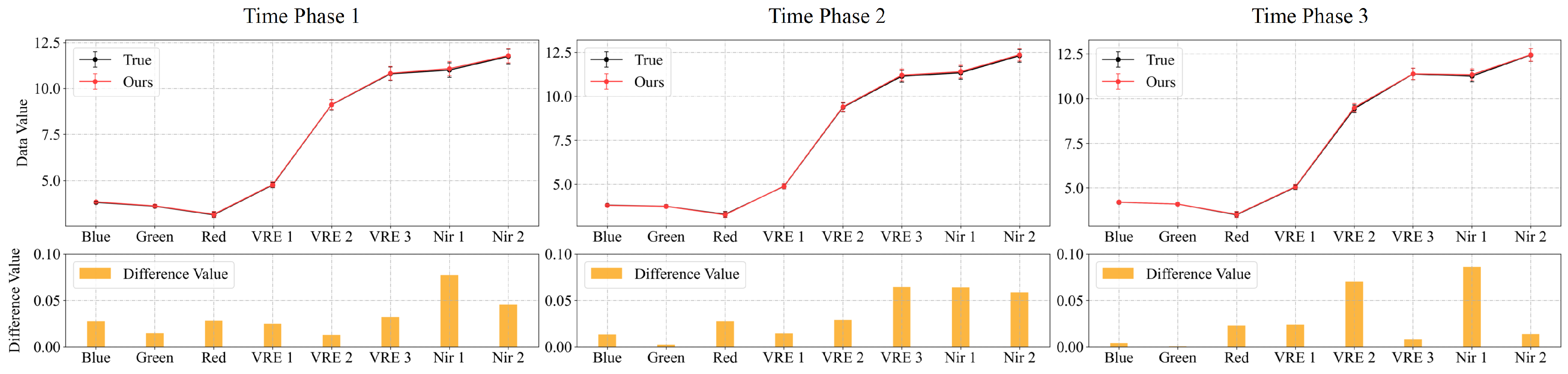
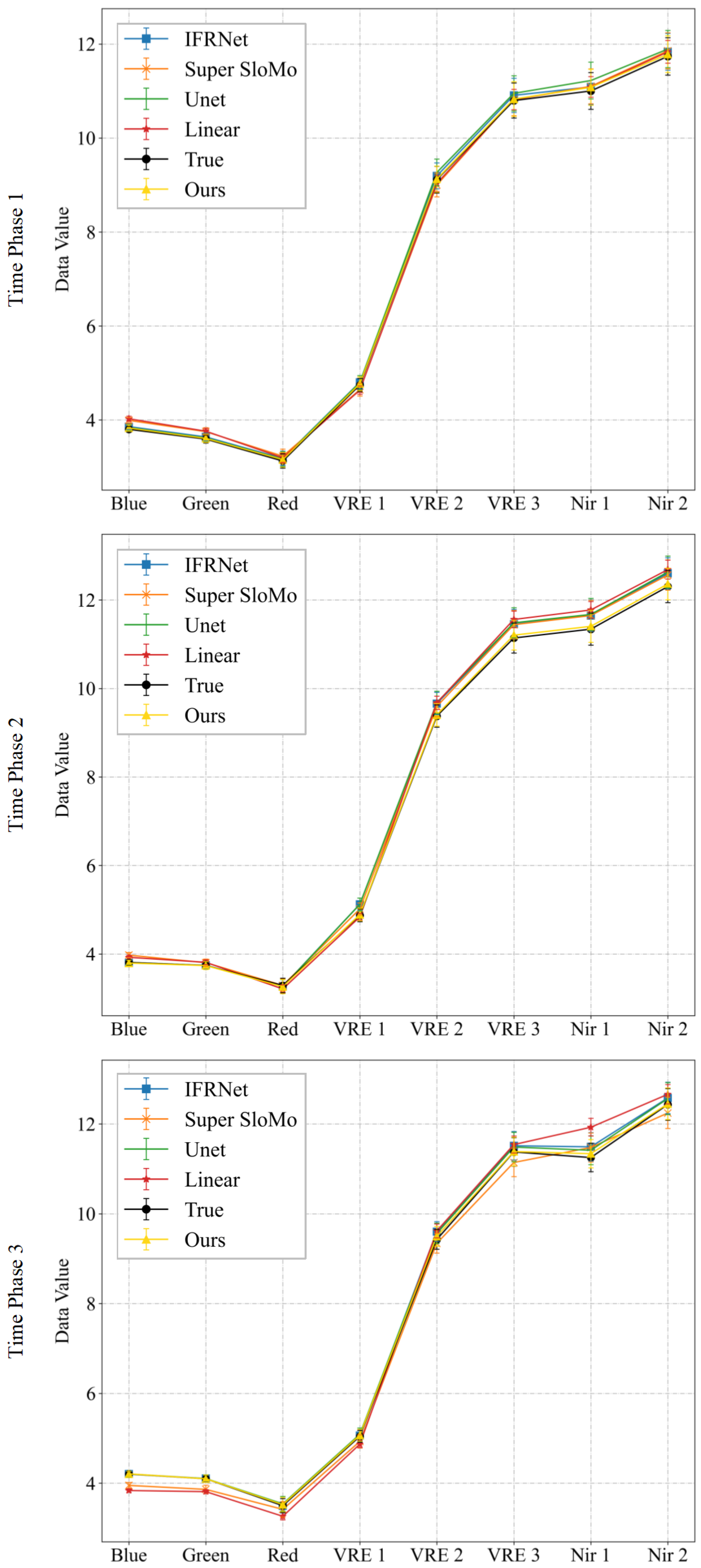
Figure 9.
Spectral curves map at 100 random points for Experiment 2 of multi-temporal sequence image interpolation for the Sentinel-2 satellite dataset. Time phases 1, 2, and 3 represent the experimental results for the middle three time phases t = 0.25, 0.50, and 0.75. For each time phase image, we plotted the average of the spectra of the real image and the interpolated result at 100 random points (True and Ours), and the absolute value of the difference between the two spectra.
Figure 9.
Spectral curves map at 100 random points for Experiment 2 of multi-temporal sequence image interpolation for the Sentinel-2 satellite dataset. Time phases 1, 2, and 3 represent the experimental results for the middle three time phases t = 0.25, 0.50, and 0.75. For each time phase image, we plotted the average of the spectra of the real image and the interpolated result at 100 random points (True and Ours), and the absolute value of the difference between the two spectra.
Figure 10.
Pixel error map for comparative experiments of Experiment 2 for multi-temporal sequence image interpolation on the Landsat-8 satellite dataset. (A,B) are the results of two time series from Experiment 2 of the Landsat-8 satellite dataset. Time phases 1, 2, and 3 represent the experimental results for the middle three time phases t = 0.25, 0.50, and 0.75. In the pixel error map, grey, green, and blue represent the absolute value of the pixel difference in the ranges 0–10, 10–80, and 80–255, with larger values representing larger errors.
Figure 10.
Pixel error map for comparative experiments of Experiment 2 for multi-temporal sequence image interpolation on the Landsat-8 satellite dataset. (A,B) are the results of two time series from Experiment 2 of the Landsat-8 satellite dataset. Time phases 1, 2, and 3 represent the experimental results for the middle three time phases t = 0.25, 0.50, and 0.75. In the pixel error map, grey, green, and blue represent the absolute value of the pixel difference in the ranges 0–10, 10–80, and 80–255, with larger values representing larger errors.
Figure 11.
Pixel error map for comparative experiments of Experiment 2 for multi-temporal sequence image interpolation on the Sentinel-2 satellite dataset. Time phases 1, 2, and 3 represent the experimental results for the middle three time phases t = 0.25, 0.50, and 0.75. In the pixel error map, grey, green, and blue represent the absolute value of the pixel difference in the ranges 0–10, 10–80, and 80–255, with larger values representing larger errors.
Figure 11.
Pixel error map for comparative experiments of Experiment 2 for multi-temporal sequence image interpolation on the Sentinel-2 satellite dataset. Time phases 1, 2, and 3 represent the experimental results for the middle three time phases t = 0.25, 0.50, and 0.75. In the pixel error map, grey, green, and blue represent the absolute value of the pixel difference in the ranges 0–10, 10–80, and 80–255, with larger values representing larger errors.
Figure 12.
Spectral curves map at 100 random points for comparative experiments of Experiment 2 for multi-temporal sequence image interpolation on the Landsat-8 satellite dataset. (a,b) are the results of two time series from Experiment 2 of the Landsat-8 satellite dataset. For each time phase image, we plotted the average of the spectra of the real image and the interpolated results of the five methods at 100 random points.
Figure 12.
Spectral curves map at 100 random points for comparative experiments of Experiment 2 for multi-temporal sequence image interpolation on the Landsat-8 satellite dataset. (a,b) are the results of two time series from Experiment 2 of the Landsat-8 satellite dataset. For each time phase image, we plotted the average of the spectra of the real image and the interpolated results of the five methods at 100 random points.
Figure 13.
Spectral curves map at 100 random points for comparative experiments of Experiment 2 for multi-temporal sequence image interpolation on the Sentinel-2 satellite dataset. For each time phase image, we plotted the average of the spectra of the real image and the interpolated results of the five methods at 100 random points.
Figure 13.
Spectral curves map at 100 random points for comparative experiments of Experiment 2 for multi-temporal sequence image interpolation on the Sentinel-2 satellite dataset. For each time phase image, we plotted the average of the spectra of the real image and the interpolated results of the five methods at 100 random points.
Figure 14.
Interpolation results and optical flow visualization of a Landsat-8 image block. The first row displays the images of the previous time phase and the next time phase; the second to third rows are the results of the three intermediate time phases of the images of the previous time phase and the next time phase.
Figure 14.
Interpolation results and optical flow visualization of a Landsat-8 image block. The first row displays the images of the previous time phase and the next time phase; the second to third rows are the results of the three intermediate time phases of the images of the previous time phase and the next time phase.
Figure 15.
Interpolation results and optical flow visualization of a Sentinel-2 image block. The first row displays the images of the previous time phase and the next time phase; the second to third rows are the results of the three intermediate time phases of the images of the previous time phase and the next time phase.
Figure 15.
Interpolation results and optical flow visualization of a Sentinel-2 image block. The first row displays the images of the previous time phase and the next time phase; the second to third rows are the results of the three intermediate time phases of the images of the previous time phase and the next time phase.
Table 1.
The details of the Landsat-8 satellite dataset. This table contains the path and row, the acquisition date, the latitude and longitude of the image center point, and the number of phases included for each Landsat-8 satellite time series.
Table 1.
The details of the Landsat-8 satellite dataset. This table contains the path and row, the acquisition date, the latitude and longitude of the image center point, and the number of phases included for each Landsat-8 satellite time series.
| Path,Row | Date | Center Latitude | Center Longitude | Phase Number |
|---|
| 91,78 | 21 June 2022 | 25°5942S | 150°3235E | 5 |
| | 7 July 2022 | | | |
| | 23 July 2022 | | | |
| 91,79 | 8 August 2022 | 27°262S | 150°112E | 5 |
| | 24 August 2022 | | | |
| 91,84 | 20 January 2019 | 34°3650S | 148°1634E | 5 |
| | 5 February 2019 | | | |
| | 21 February 2019 | | | |
| | 9 March 2019 | | | |
| | 24 March 2019 | | | |
| 92,85 | 20 January 2022 | 36°246S | 147°5158E | 5 |
| | 5 February 2022 | | | |
| | 21 February 2022 | | | |
| | 9 March 2022 | | | |
| | 24 March 2022 | | | |
| 99,73 | 31 March 2018 | 18°4724S | 139°5338E | 10 |
| | 16 April 2018 | | | |
| | 2 May 2018 | | | |
| | 18 May 2018 | | | |
| | 3 June 2018 | | | |
| 99,74 | 7 September 2018 | 20°1355S | 139°3340E | 10 |
| | 23 September 2018 | | | |
| | 9 October 2018 | | | |
| | 25 October 2018 | | | |
| | 1 November 2018 | | | |
Table 2.
The details of the Sentinel-2 satellite dataset. This table contains the tile ID, the acquisition date, the latitude and longitude of the image center point, and the number of phases included of each Landsat-8 satellite time series.
Table 2.
The details of the Sentinel-2 satellite dataset. This table contains the tile ID, the acquisition date, the latitude and longitude of the image center point, and the number of phases included of each Landsat-8 satellite time series.
| Tile ID | Date | Center Latitude | Center Longitude | Phase Number |
|---|
| 18STF | 11 January 2019 | 36°3112N | 77°4414W | 5 |
| | 16 January 2019 | | | |
| | 21 January 2019 | | | |
| | 26 January 2019 | | | |
| | 31 January 2019 | | | |
| 31TDN | 26 March 2020 | 47°2129N | 2°248E | 5 |
| | 31 March 2020 | | | |
| | 5 April 2020 | | | |
| | 10 April 2020 | | | |
| | 15 April 2020 | | | |
| 30TXT | 7 July 2020 | 47°2028N | 0°5657W | 5 |
| | 12 July 2020 | | | |
| | 17 July 2020 | | | |
| | 22 July 2020 | | | |
| | 27 July 2020 | | | |
| 35TNM | 28 September 2018 | 46°2726N | 27°4252E | 5 |
| | 3 October 2018 | | | |
| | 8 October 2018 | | | |
| | 23 October 2018 | | | |
| | 18 October 2018 | | | |
Table 3.
Setup of multi-temporal image interpolation experiments. We set up four sets of experiments using the Landsat-8 satellite dataset, and in each set of experiments the inputs are Input Image 1 and Input Image 2, as well as the intermediate time phase t (Input Time Phase). The interpolated results are compared with the Reference Image (the real image).
Table 3.
Setup of multi-temporal image interpolation experiments. We set up four sets of experiments using the Landsat-8 satellite dataset, and in each set of experiments the inputs are Input Image 1 and Input Image 2, as well as the intermediate time phase t (Input Time Phase). The interpolated results are compared with the Reference Image (the real image).
| Experiment ID | Path,Row | Input Image 1 | Input Image 2 | Reference Image | Input Time Phase |
|---|
| 1 | 91,84 | 20 January 2019 | 24 March 2019 | 5 February 2019 | 0.25 |
| 21 February 2019 | 0.5 |
| 9 March 2019 | 0.75 |
| 92,85 | 20 January 2022 | 24 March 2022 | 5 February 2022 | 0.25 |
| 21 February 2022 | 0.5 |
| 9 March 2022 | 0.75 |
| 2 | 99,73 | 31 March 2018 | 3 June 2018 | 16 April 2018 | 0.25 |
| 2 May 2018 | 0.5 |
| 18 May 2018 | 0.75 |
| 99,74 | 31 March 2018 | 3 June 2018 | 16 April 2018 | 0.25 |
| 2 May 2018 | 0.5 |
| 18 May 2018 | 0.75 |
| 3 | 91,78 | 21 June 2022 | 24 August 2022 | 7 July 2022 | 0.25 |
| 23 July 2022 | 0.5 |
| 8 August 2022 | 0.75 |
| 91,79 | 21 June 2022 | 24 August 2022 | 7 July 2022 | 0.25 |
| 23 July 2022 | 0.5 |
| 8 August 2022 | 0.75 |
| 4 | 99,73 | 7 September 2018 | 1 November 2018 | 23 September 2018 | 0.25 |
| 9 October 2018 | 0.5 |
| 25 October 2018 | 0.75 |
| 99,74 | 7 September 2018 | 1 November 2018 | 23 September 2018 | 0.25 |
| 9 October 2018 | 0.5 |
| 25 October 2018 | 0.75 |
Table 4.
Setup of multi-temporal image interpolation experiments. We set up four sets of experiments using the Sentinel-2 satellite dataset, and in each set of experiments the inputs are Input Image 1 and Input Image 2, as well as the intermediate time phase t (Input Time Phase). The interpolated results are compared with the Reference Image (the real image).
Table 4.
Setup of multi-temporal image interpolation experiments. We set up four sets of experiments using the Sentinel-2 satellite dataset, and in each set of experiments the inputs are Input Image 1 and Input Image 2, as well as the intermediate time phase t (Input Time Phase). The interpolated results are compared with the Reference Image (the real image).
| Experiment ID | Tile ID | Input Image 1 | Input Image 2 | Reference Image | Input Time Phase |
|---|
| 1 | 18STF | 11 January 2019 | 31 January 2019 | 16 January 2019 | 0.25 |
| 21 January 2019 | 0.5 |
| 26 January 2019 | 0.75 |
| 2 | 31TDN | 26 March 2020 | 15 April 2020 | 31 March 2020 | 0.25 |
| 5 April 2020 | 0.5 |
| 10 April 2020 | 0.75 |
| 3 | 30TXT | 7 July 2020 | 27 July 2020 | 12 July 2020 | 0.25 |
| 17 July 2020 | 0.5 |
| 22 July 2020 | 0.75 |
| 4 | 35TNM | 28 September 2018 | 18 October 2018 | 3 October 2018 | 0.25 |
| 8 October 2018 | 0.5 |
| 13 October 2018 | 0.75 |
Table 5.
Quantitative comparison of multi-temporal sequential image interpolation results on the Landsat-8 dataset. For each indicator, the results in bold are the best results and those marked with * are the second best results. Time phases 1, 2, and 3 represent the experimental results for the middle three time phases t = 0.25, 0.50, and 0.75. Arrows ↓ and ↑ stand for smaller is better and bigger is better.
Table 5.
Quantitative comparison of multi-temporal sequential image interpolation results on the Landsat-8 dataset. For each indicator, the results in bold are the best results and those marked with * are the second best results. Time phases 1, 2, and 3 represent the experimental results for the middle three time phases t = 0.25, 0.50, and 0.75. Arrows ↓ and ↑ stand for smaller is better and bigger is better.
| Experiment | Method | Time Phase 1 | Time Phase 2 | Time Phase 3 |
|---|
|
ID
|
RMSE↓
|
PSNR↑
|
SSIM↑
|
RMSE↓
|
PSNR↑
|
SSIM↑
|
RMSE↓
|
PSNR↑
|
SSIM↑
|
|---|
| 1 | Linear | 9.357 | 29.154 | 0.957 | 9.225 | 29.330 | 0.958 | 9.106 | 29.513 | 0.959 |
| Unet [31] | 10.997 | 27.980 | 0.942 | 10.074 | 28.769 | 0.949 | 9.823 | 29.028 | 0.955 |
| Super SloMo [30] | 8.996 | 29.550 | 0.961 | 8.813 | 29.766 | 0.963 | 8.584 | 30.102 | 0.966 |
| IFRNet [32] | 8.140 * | 30.197 * | 0.971 * | 7.892 * | 30.367 * | 0.977 | 7.642 * | 30.734 * | 0.975 * |
| Ours | 7.860 | 30.383 | 0.972 | 7.216 | 31.359 | 0.972 * | 7.069 | 31.736 | 0.978 |
| 2 | Linear | 8.448 | 30.091 | 0.967 | 8.395 | 30.224 | 0.972 | 6.528 | 32.299 | 0.979 |
| Unet [31] | 10.763 | 28.091 | 0.947 | 9.830 | 28.948 | 0.954 | 9.579 | 29.070 | 0.957 |
| Super SloMo [30] | 8.178 | 30.329 | 0.971 | 8.372 | 30.168 | 0.969 | 6.216 | 32.703 | 0.980 * |
| IFRNet [32] | 7.384 * | 31.173 * | 0.977 * | 6.900 * | 31.912 * | 0.979 * | 5.696 * | 33.434 * | 0.984 |
| Ours | 6.770 | 31.940 | 0.980 | 6.275 | 32.732 | 0.981 | 5.532 | 33.752 | 0.984 |
| 3 | Linear | 8.588 | 30.038 | 0.965 | 8.734 | 29.804 | 0.963 | 7.192 | 31.500 | 0.977 |
| Unet [31] | 9.304 | 29.228 | 0.958 | 9.254 | 29.298 | 0.958 | 8.862 | 29.740 | 0.961 |
| Super SloMo [30] | 7.841 | 30.401 | 0.974 | 7.800 | 30.446 | 0.975 | 6.928 | 31.738 | 0.979 |
| IFRNet [32] | 6.884 * | 31.931 * | 0.979 * | 7.077 * | 31.655 * | 0.978 * | 6.196 * | 33.150 * | 0.982 * |
| Ours | 6.154 | 33.375 | 0.983 | 6.268 | 33.112 | 0.981 | 5.648 | 33.453 | 0.984 |
| 4 | Linear | 8.618 | 29.858 | 0.964 | 8.976 | 29.674 | 0.961 | 8.509 | 30.163 | 0.967 |
| Unet [31] | 9.276 | 29.229 | 0.958 | 9.344 | 29.192 | 0.957 | 9.179 | 29.458 | 0.959 |
| Super SloMo [30] | 7.130 * | 30.981 | 0.976 | 7.396 | 31.111 | 0.976 * | 7.998 | 30.279 | 0.971 |
| IFRNet [32] | 7.130 * | 31.545 * | 0.978 * | 6.910 * | 31.910 * | 0.979 | 7.127 * | 31.615 * | 0.978 * |
| Ours | 6.377 | 32.436 | 0.980 | 6.889 | 31.917 | 0.979 | 6.210 | 33.119 | 0.980 |
Table 6.
Quantitative comparison of multi-temporal sequential image interpolation results on the Sentinel-2 dataset. For each indicator, the results in bold are the best results and those marked with * are the second best results. Time phases 1, 2, and 3 represent the experimental results for the middle three time phases t = 0.25, 0.50, and 0.75. Arrows ↓ and ↑ stand for smaller is better and bigger is better.
Table 6.
Quantitative comparison of multi-temporal sequential image interpolation results on the Sentinel-2 dataset. For each indicator, the results in bold are the best results and those marked with * are the second best results. Time phases 1, 2, and 3 represent the experimental results for the middle three time phases t = 0.25, 0.50, and 0.75. Arrows ↓ and ↑ stand for smaller is better and bigger is better.
| Experiment | Method | Time Phase 1 | Time Phase 2 | Time Phase 3 |
|---|
|
ID
|
RMSE↓
|
PSNR↑
|
SSIM↑
|
RMSE↓
|
PSNR↑
|
SSIM↑
|
RMSE↓
|
PSNR↑
|
SSIM↑
|
|---|
| 1 | Linear | 11.029 | 28.083 | 0.959 | 12.031 | 27.389 | 0.942 | 11.501 | 27.633 | 0.944 |
| Unet [31] | 9.211 | 29.751 | 0.963 | 9.308 | 29.745 | 0.962 | 10.167 | 28.557 | 0.961 * |
| Super SloMo [30] | 10.898 | 28.234 | 0.960 | 11.109 | 27.998 | 0.959 | 10.485 | 28.524 | 0.961 * |
| IFRNet [32] | 8.368 * | 30.754 * | 0.970 * | 9.969 | 28.949 | 0.961 * | 9.472 * | 29.709 * | 0.961 * |
| Ours | 7.486 | 31.411 | 0.975 | 9.821 * | 29.558 * | 0.960 | 9.140 | 29.820 | 0.965 |
| 2 | Linear | 11.961 | 27.458 | 0.943 | 12.924 | 26.499 | 0.940 | 11.135 | 27.765 | 0.959 |
| Unet [31] | 9.575 | 29.948 * | 0.959 | 9.124 | 29.854 | 0.966 * | 7.888 * | 31.104 * | 0.973 * |
| Super SloMo [30] | 11.276 | 27.996 | 0.948 | 10.157 | 28.816 | 0.960 | 10.313 | 28.536 | 0.961 |
| IFRNet [32] | 9.412 * | 29.733 | 0.962 * | 9.028 * | 29.980 * | 0.966 * | 8.821 | 29.858 | 0.970 |
| Ours | 8.597 | 30.856 | 0.967 | 8.471 | 30.664 | 0.970 | 7.237 | 31.873 | 0.978 |
| 3 | Linear | 11.295 | 27.914 | 0.948 | 11.822 | 27.466 | 0.943 | 14.500 | 25.598 | 0.932 |
| Unet [31] | 10.126 | 29.110 | 0.960 | 10.160 | 28.653 | 0.960 * | 12.852 | 26.000 | 0.940 * |
| Super SloMo [30] | 10.868 | 28.241 | 0.960 | 10.826 | 28.323 | 0.960 * | 13.053 | 26.403 | 0.936 |
| IFRNet [32] | 9.230 * | 29.747 * | 0.963 * | 9.670 * | 29.707 * | 0.959 | 11.911 * | 27.460 * | 0.943 |
| Ours | 8.962 | 30.123 | 0.967 | 9.194 | 29.787 | 0.964 | 11.809 | 27.501 | 0.943 |
| 4 | Linear | 11.440 | 27.687 | 0.946 | 13.121 | 26.249 | 0.936 | 11.392 | 27.835 | 0.947 |
| Unet [31] | 9.417 | 29.721 * | 0.962 | 11.158 | 28.170 * | 0.960 * | 8.352 | 30.531 | 0.968 |
| Super SloMo [30] | 10.111 | 29.207 | 0.960 | 12.191 | 26.936 | 0.941 | 9.771 | 29.690 | 0.959 |
| IFRNet [32] | 9.348 * | 29.679 | 0.963 * | 10.933 * | 28.149 | 0.960 * | 8.282 * | 30.791 * | 0.971 |
| Ours | 8.010 | 30.901 | 0.970 | 9.126 | 29.853 | 0.966 | 7.999 | 30.903 | 0.970 * |