Predicting Future Lake Water Storage Changes on the Tibetan Plateau under Different Climate Change Scenarios
Abstract
1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data
2.2.1. CMFD Data
2.2.2. CMIP6 Data
2.2.3. Landsat Images and SRTM Data
3. Methods
3.1. Estimation of Lake Water Storage Changes
3.2. Methodology for Correction of Precipitation Data Deviations
- Cumulative distribution function (CDF). The observed and simulated precipitation data from 1986~2014 were sorted in ascending order and, using the precipitation series of the modeling time period with the following Formula (3), the cumulative probability density values of the simulated and observed values were calculated separately.
- 2.
- Non-parametric transformation QUANT: makes the empirical cumulative probability distribution function of the original output data as close as possible to the observations over the historical period:
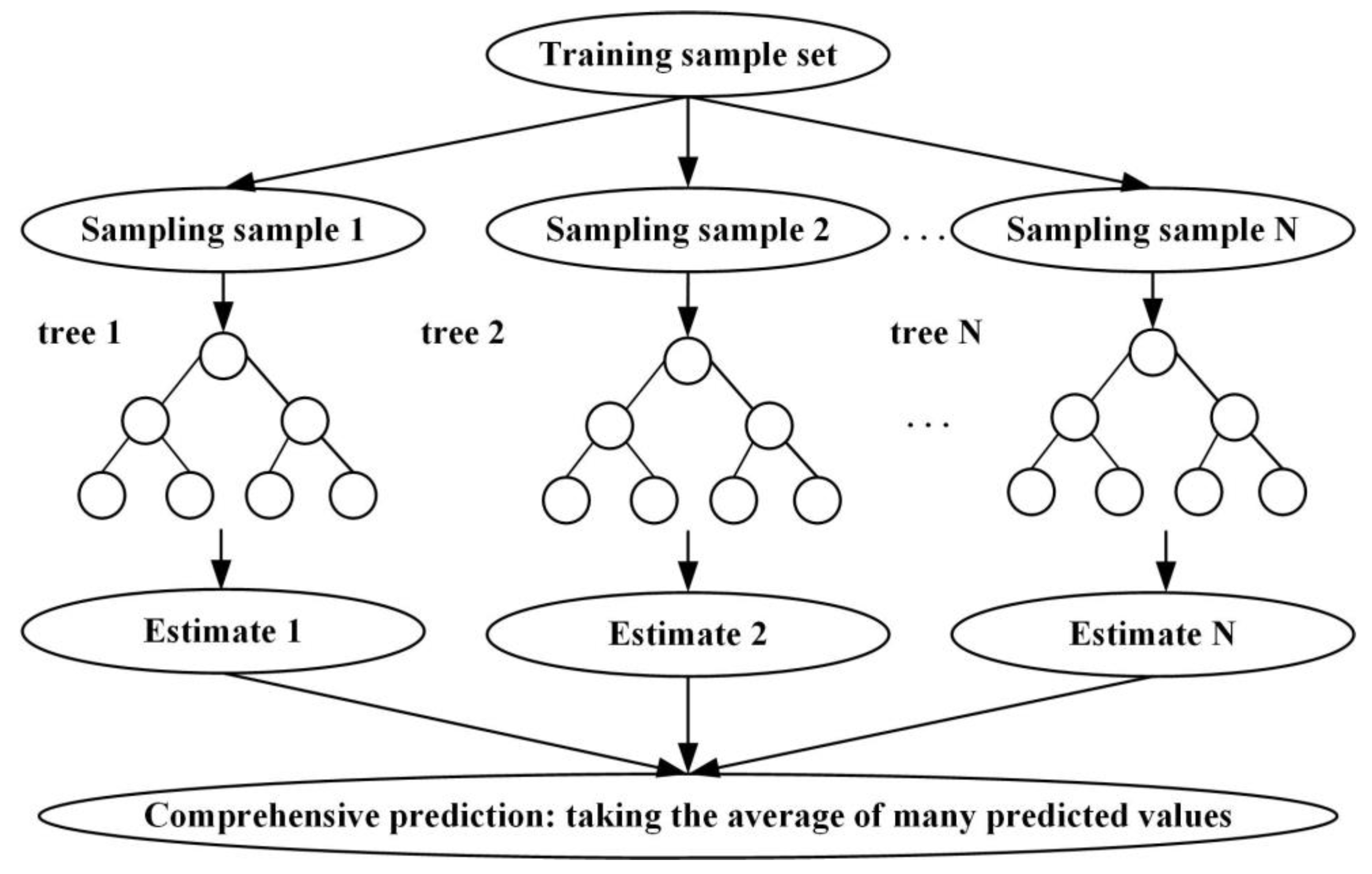
3.3. Random Forest Algorithm
3.4. Prediction Model
3.5. Accuracy Assessment
3.5.1. Model Accuracy
3.5.2. Computational Uncertainty
4. Results
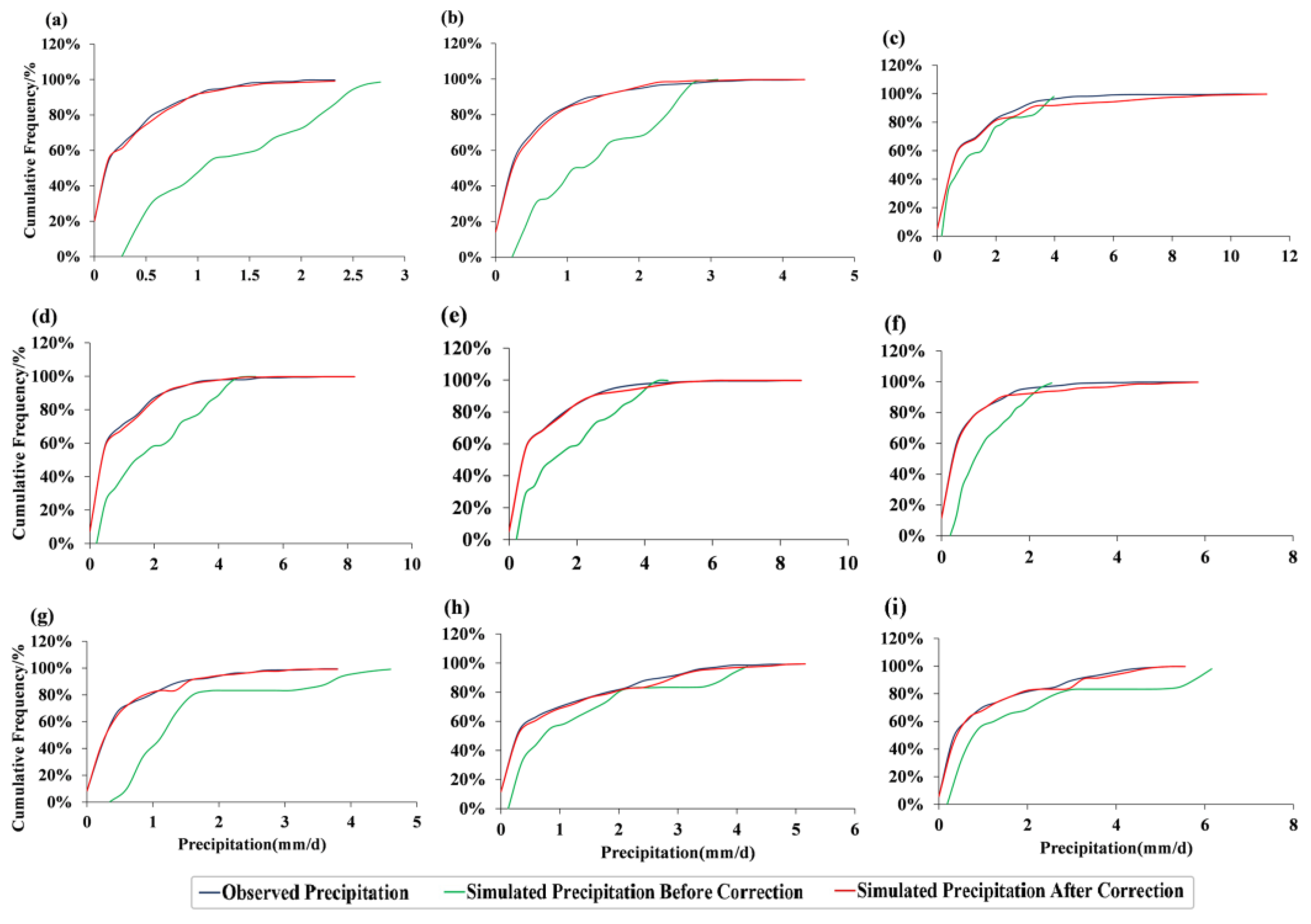
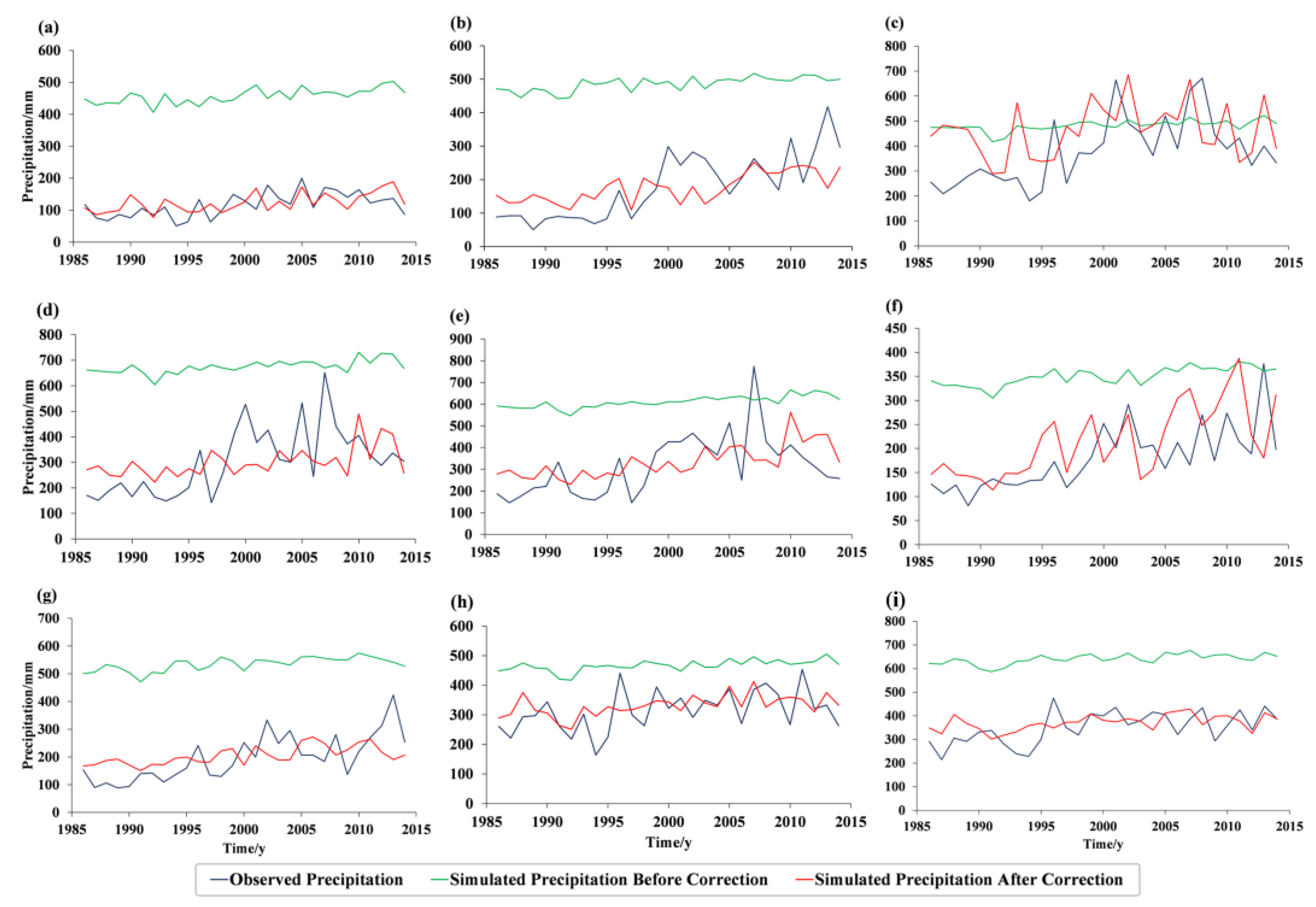
4.1. Deviation Correction Results of Precipitation Data
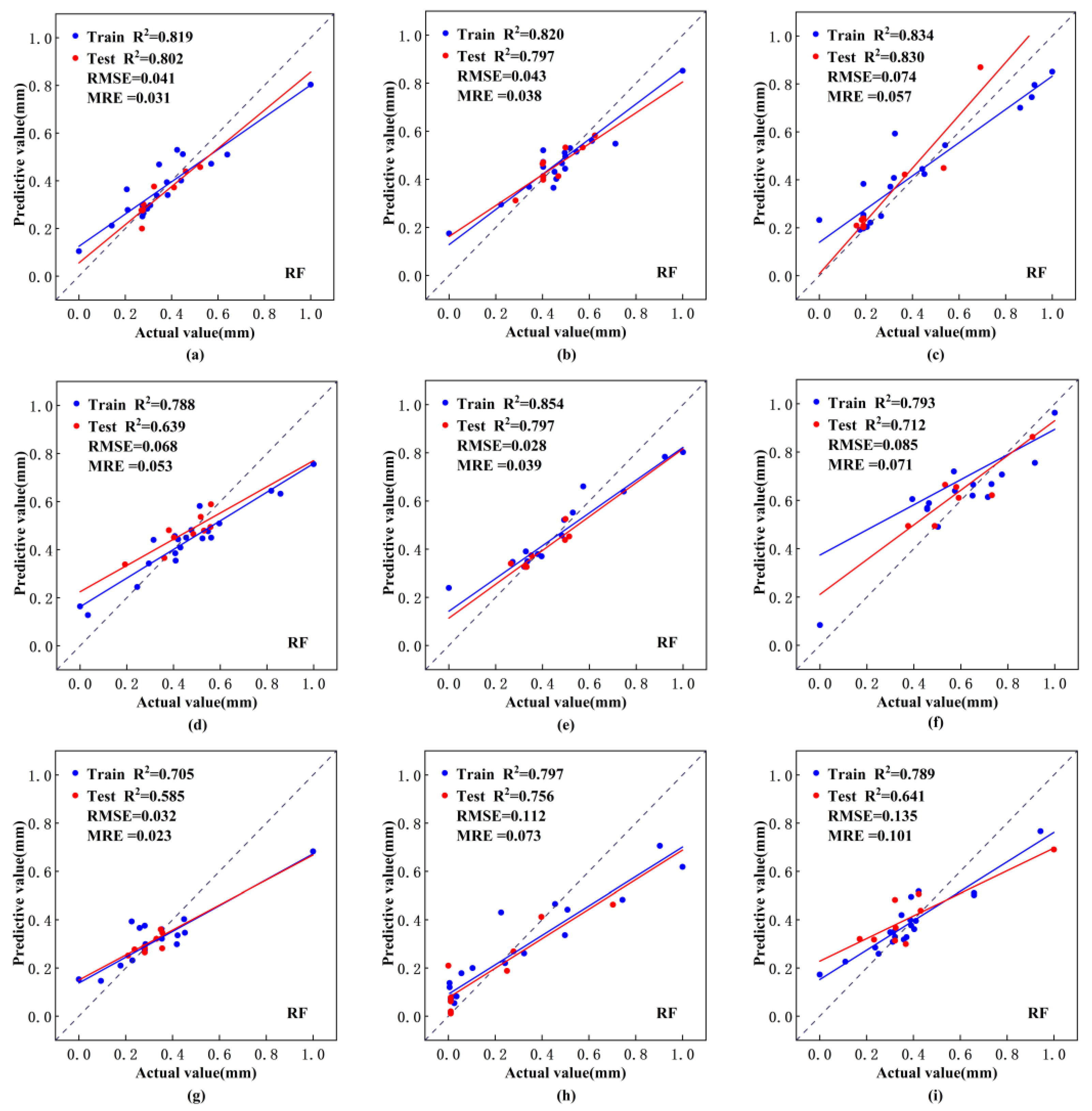
4.2. Model Accuracy Assessment
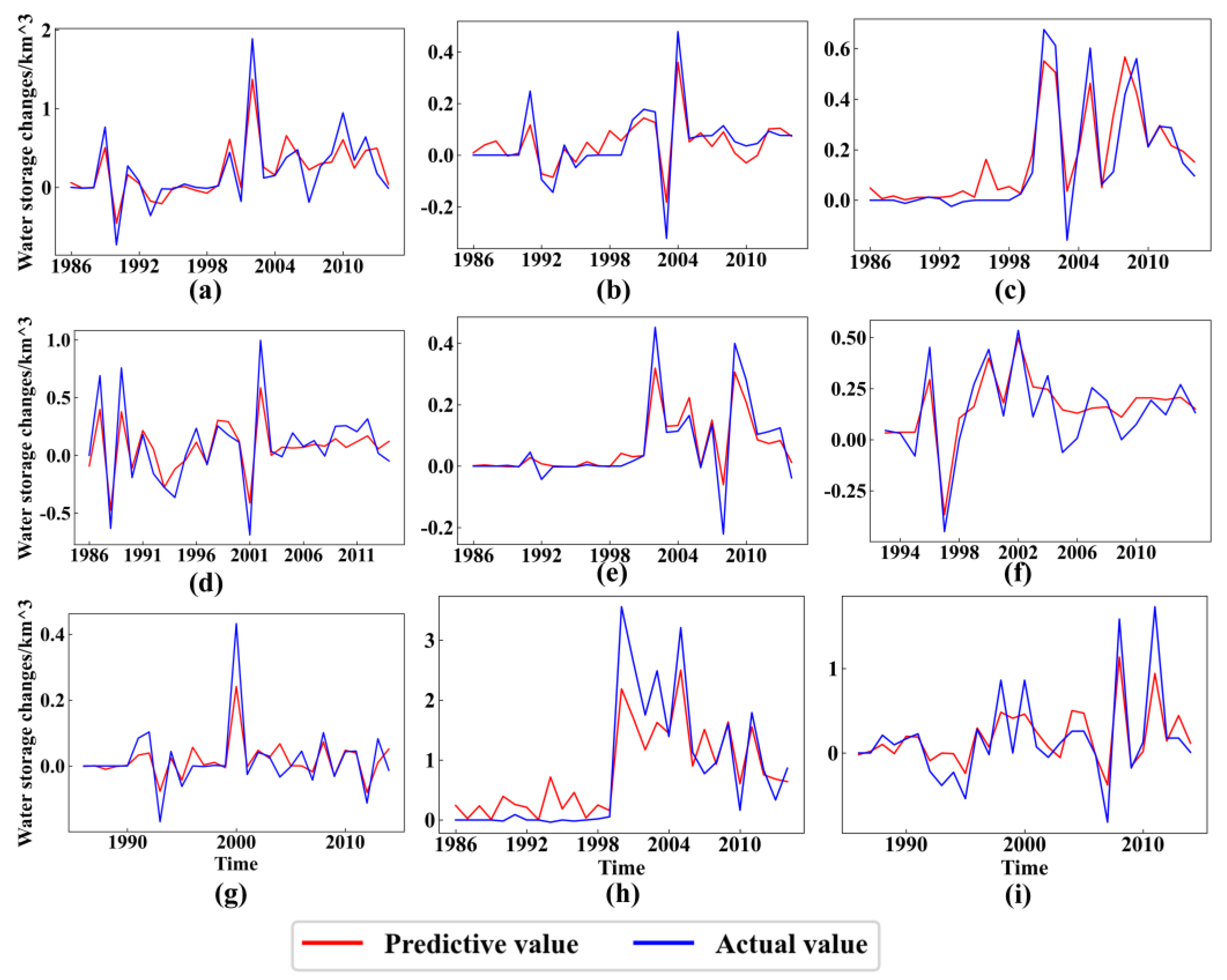
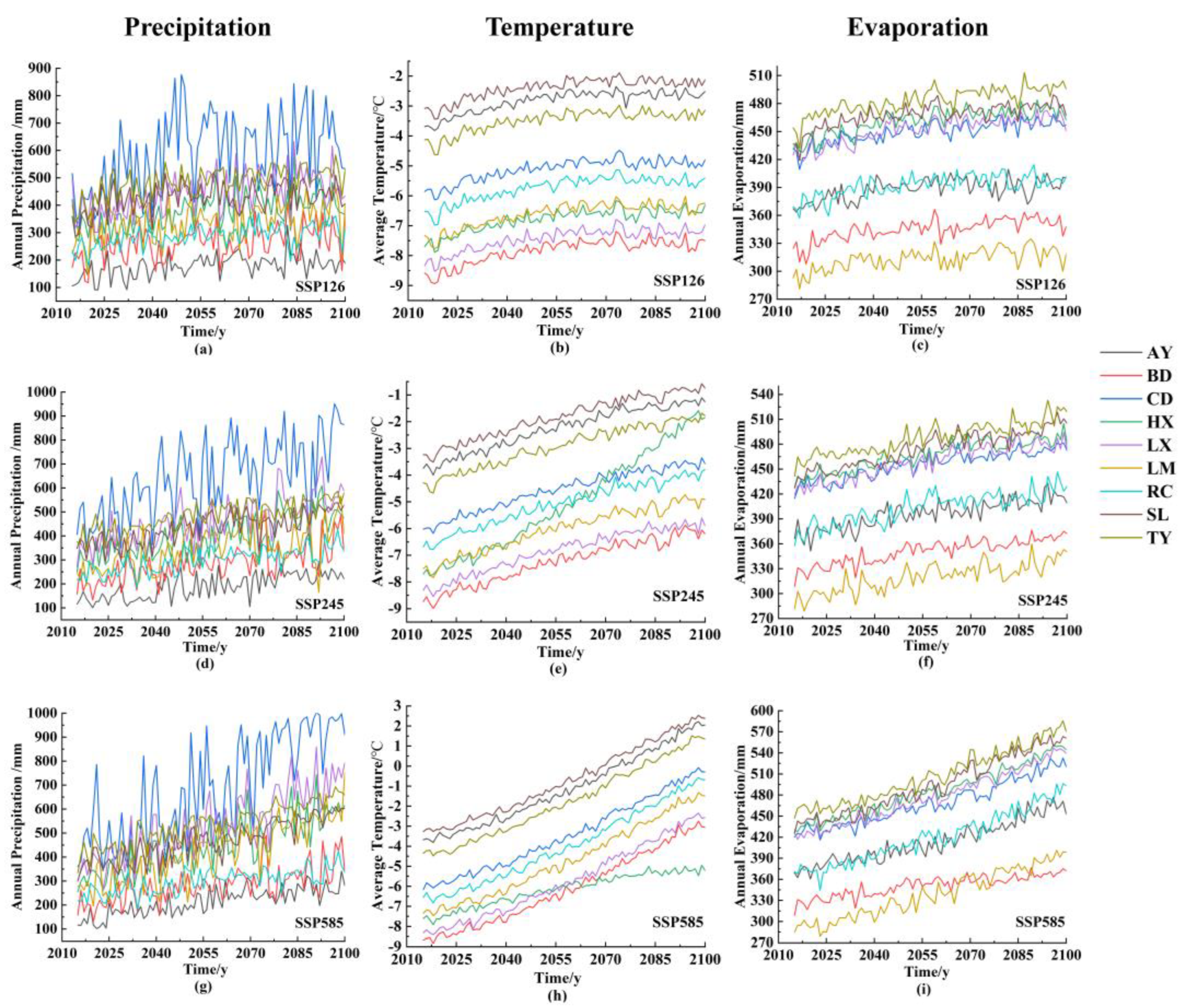
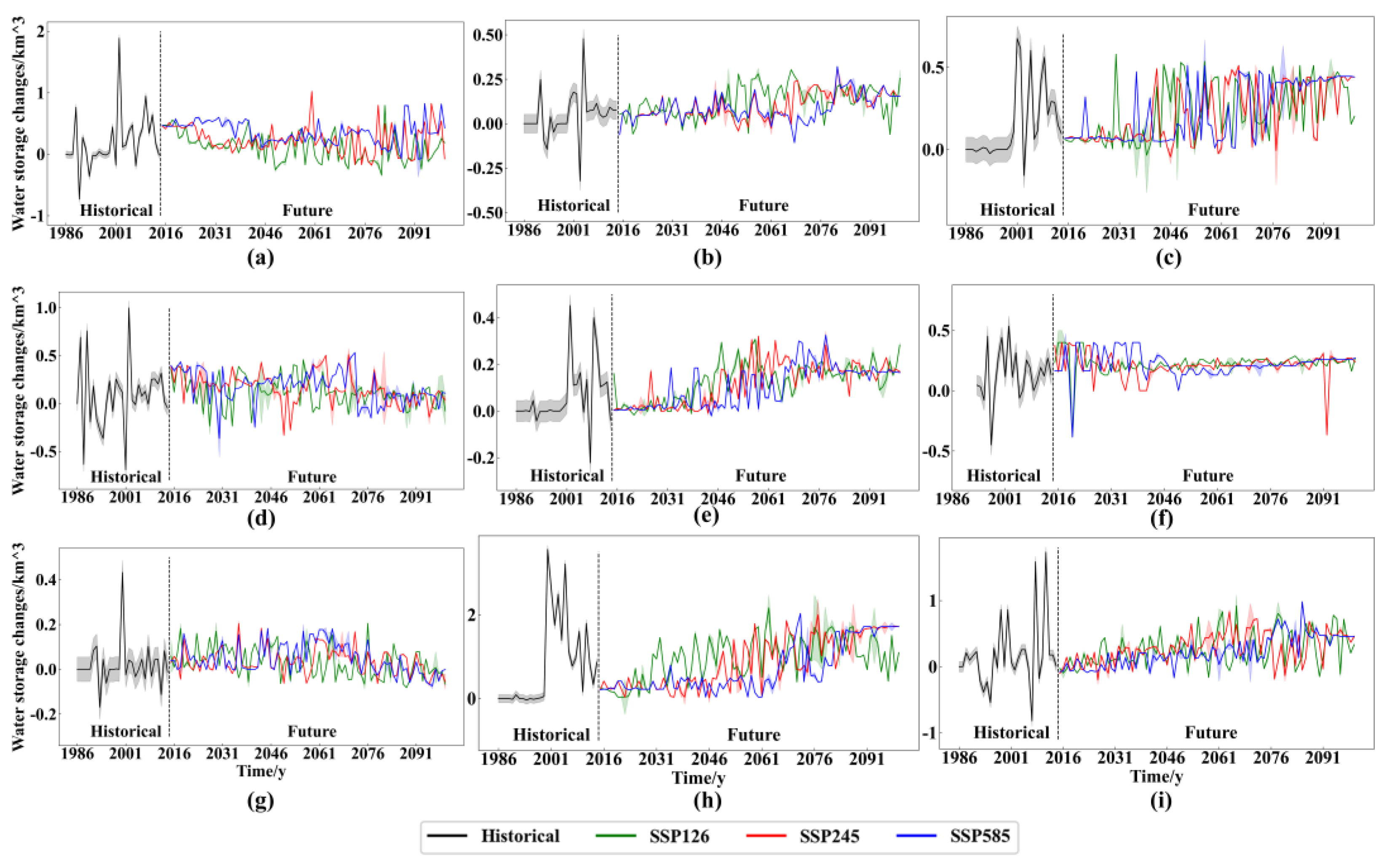
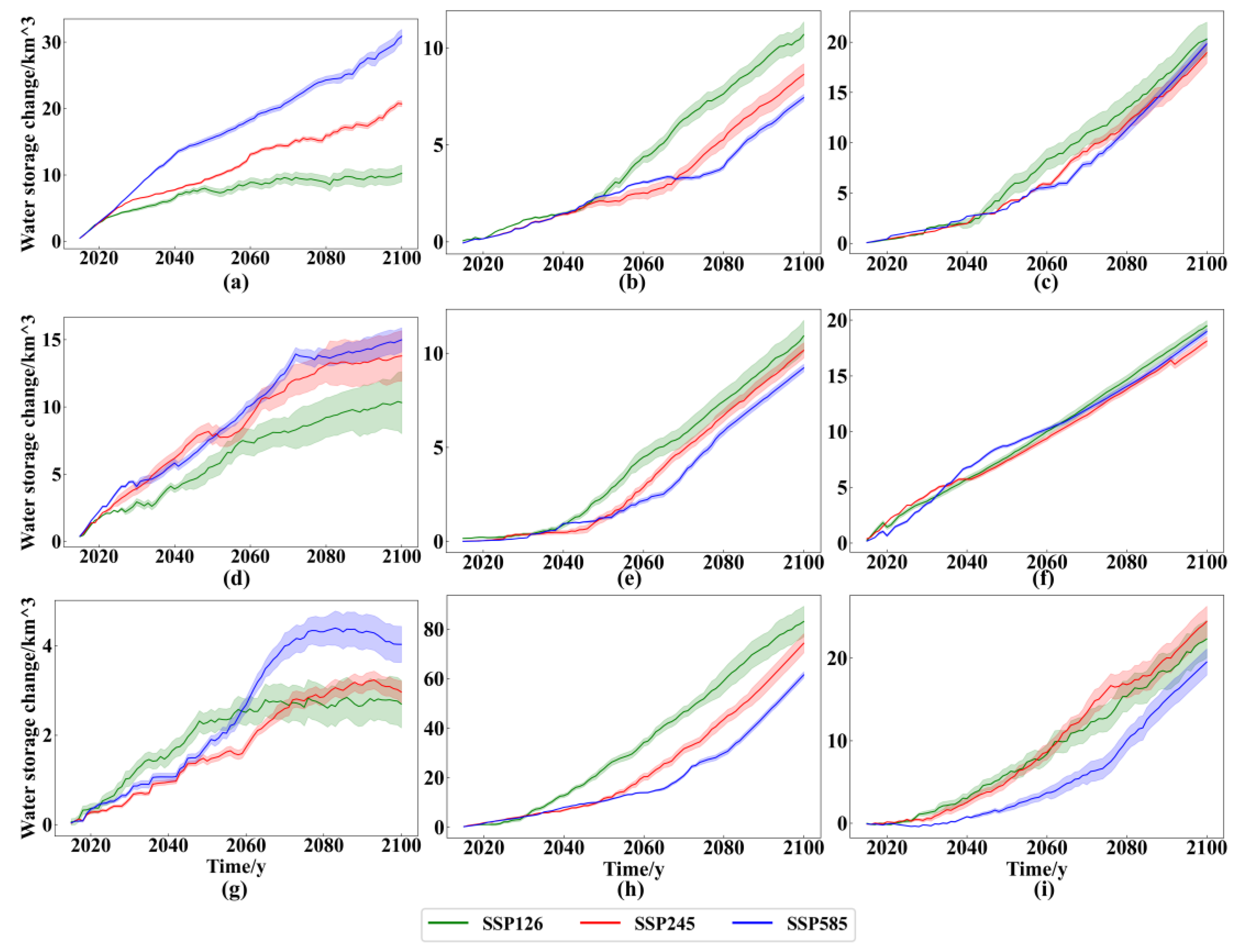
4.3. Prediction of Lake Water Storage Changes under Different SSP Scenarios
4.4. Future Changes of Lake Water Storage
5. Discussion
6. Conclusions
- (1)
- The correlation coefficients between CMFD and models derived from 20 CMIP6 temperature datasets in the historical period are more than 0.9, and the correlation coefficients for precipitation are 0.7. We used the QM method to correct precipitation data, resulting in a close match between corrected CMIP6 precipitation data and CMFD precipitation data in terms of frequency.
- (2)
- The RF model exhibited a strong performance in predicting historical water storage changes. The R2 values for the training and the testing sets of the nine lakes are greater than 0.7 and 0.6, and the MAE for most lakes was less than 0.1 km3. This indicates that the model accurately captured the relationship between historical water storage changes and climate factors.
- (3)
- Under the three future SSP scenarios, the temperature, precipitation, and evaporation of the nine lakes are projected to increase, leading to an expansion in lake water storage. For AY, HX, and RC, there is an initial rapid increase followed by a gradual decrease or stabilization; BD, CD, LX, SL, and TY exhibit an initial slow increase followed by a rapid increase; LM maintains a steady increase, and the rate of increase is consistent across the three scenarios.
- (4)
- The increasing rate under SSP585 in AY and HX is greater than in other scenarios, but the increasing rate under SSP126 in BD, LX, and SL is the largest among those scenarios. The increasing rates of CD and LM are consistent across the three scenarios.
- (5)
- SL is projected to experience the largest expansion, with an annual increase of 1.268 ± 0.065 km3/y during 2051~2100, followed by TY with 0.357 ± 0.002 km3/y. RC is projected to show little or no increase after 2050. The total water storage of the nine lakes will increase by 189.676 ± 16.266 km3, 191.762 ± 10.683 km3, and 186.212 ± 6.441 km3 until 2100 under the SSP126, SSP245, and SSP585 scenarios, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Montanari, A.; Young, G.; Savenije, H.H.G.; Hughes, D.; Wagener, T.; Ren, L.L.; Koutsoyiannis, D.; Cudennec, C.; Toth, E.; Grimaldi, S.; et al. “Panta Rhei—Everything flows”: Change in hydrology and society—The IAHS scientific decade 2013–2022. Hydrol. Sci. J. 2013, 58, 1256–1275. [Google Scholar] [CrossRef]
- Berghuijs, W.R.; Woods, R.A.; Hrachowitz, M. A precipitation shift from snow towards rain leads to a decrease in streamflow. Nat. Clim. Change 2014, 4, 583–586. [Google Scholar] [CrossRef]
- Climate Change 2013: The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014.
- Climate Change 2021: The Physical Science Basis. Contribution of Working Group14 I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Technical Summary; The Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2021.
- Xu, Z.X.; Gong, T.L.; Li, J.Y. Decadal trend of climate in the Tibetan Plateau—Regional temperature and precipitation. Hydrol. Process. Int. J. 2008, 22, 3056–3065. [Google Scholar] [CrossRef]
- Wan, W.; Xiao, P.; Feng, X.; Li, H.; Ma, R.; Duan, H.; Zhao, L. Monitoring lake changes of Qinghai-Tibetan Plateau over the past 30 years using satellite remote sensing data. Chin. Sci. Bull. 2014, 59, 1021–1035. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Xie, H.; Zhang, K.; Zhu, F. Lakes’ state and abundance across the Tibetan Plateau. Chin. Sci. Bull. 2014, 59, 3010–3021. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Xie, H.; Wang, W.; Yang, W. An inventory of glacial lakes in the Third Pole region and their changes in response to global warming. Glob. Planet. Change 2015, 131, 148–157. [Google Scholar] [CrossRef]
- Phan, V.H.; Lindenbergh, R.; Menenti, M. ICESat derived elevation changes of Tibetan lakes between 2003 and 2009. Int. J. Appl. Earth Obs. Geoinf. 2012, 17, 12–22. [Google Scholar] [CrossRef]
- Song, C.; Huang, B.; Ke, L.; Richards, K.S. Seasonal and abrupt changes in the water level of closed lakes on the Tibetan Plateau and implications for climate impacts. J. Hydrol. 2014, 514, 131–144. [Google Scholar] [CrossRef]
- Zhang, G.; Xie, H.; Kang, S.; Yi, D.; Ackley, S.F. Monitoring lake level changes on the Tibetan Plateau using ICESat altimetry data (2003–2009). Remote Sens. Environ. 2011, 115, 1733–1742. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, G.; Yang, R.; Liu, C.; Yang, K.; Qiao, B.; Han, B. Lake variations on Tibetan Plateau of recent 40 years and future changing tendency. Bull. Chin. Acad. Sci. 2019, 34, 1254–1263. [Google Scholar] [CrossRef]
- Qiao, B.; Zhu, L.; Yang, R. Temporal-spatial differences in lake water storage changes and their links to climate change throughout the Tibetan Plateau. Remote Sens. Environ. 2019, 222, 232–243. [Google Scholar] [CrossRef]
- Song, C.; Huang, B.; Ke, L. Modeling and analysis of lake water storage changes on the Tibetan Plateau using multi-mission satellite data. Remote Sens. Environ. 2013, 135, 25–35. [Google Scholar] [CrossRef]
- Zhang, G.; Luo, W.; Chen, W.; Zheng, G. A robust but variable lake expansion on the Tibetan Plateau. Sci. Bull. 2019, 64, 1306–1309. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Chen, W.; Xie, H. Tibetan Plateau’s lake level and storage changes from NASA’s ICESat/ICESat-2 and Landsat missions. Geophys. Res. Lett. 2019, 46, 13115–13116. [Google Scholar] [CrossRef]
- Yang, R.; Zhu, L.; Wang, J.; Ju, J.; Ma, Q.; Turner, F.; Guo, Y. Spatiotemporal variations in storage of closed lakes on the Tibetan Plateau and their climatic responses from 1976 to 2013. Clim. Change 2017, 140, 621–633. [Google Scholar] [CrossRef]
- Yao, F.; Wang, J.; Yang, K.; Wang, C.; Walter, B.A.; Crétaux, J.-F. Lake storage variation on the endorheic Tibetan Plateau and its attribution to climate change since the new millennium. Environ. Res. Lett. 2018, 13, 064011. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Shum, C.K.; Yi, S.; Yang, K.; Xie, H.; Feng, W.; Bolch, T.; Wang, L.; Behrangi, A.; et al. Lake volume and groundwater storage variations in Tibetan Plateau’s endorheic basin. Geophys. Res. Lett. 2017, 44, 5550–5560. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Peng, L.L.; Lin, Z.H. Progress on the projections of future climate change with various emission scenarios. Adv. Earth Sci. 2008, 23, 174–185. [Google Scholar]
- Zhou, T.; Chen, Z.; Zou, L.; Chen, X.; Yu, Y.; Wang, B.; Bao, Q.; Bao, Y.; Cao, J.; He, B.; et al. Development of climate and earth system models in China: Past achievements and new CMIP6 results. J. Meteorol. Res. 2020, 34, 1–19. [Google Scholar] [CrossRef]
- Eyring, V.; Cox, P.M.; Flato, G.M.; Gleckler, P.J.; Abramowitz, G.; Caldwell, P.; Collins, W.D.; Gier, B.K.; Hall, A.D.; Hoffman, F.M.; et al. Taking climate model evaluation to the next level. Nat. Clim. Change 2019, 9, 102–110. [Google Scholar] [CrossRef]
- Zhang, B.; Dai, X.G. Assessment of the deviation of China precipitation projected by CMIP5 models for 2006–2013. Chin. J. Atmos. Sci. 2016, 40, 981–994. [Google Scholar]
- Huang, X.; Le, Q.; Zhang, M. Future precipitation change in the Belt and Road Region under representative concentration Pathway Scenarios. J. Yangtze River Sci. Res. Inst. 2020, 37, 53–60. [Google Scholar]
- Kraaijenbrink, P.D.; Stigter, E.E.; Yao, T.; Immerzeel, W.W. Climate change decisive for Asia’s snow meltwater supply. Nat. Clim. Change 2021, 11, 591–597. [Google Scholar] [CrossRef]
- Lun, Y.; Liu, L.; Cheng, L.; Li, X.; Li, H.; Xu, Z. Assessment of GCMs simulation performance for precipitation and temperature from CMIP5 to CMIP6 over the Tibetan Plateau. Int. J. Clim. 2021, 41, 3994–4018. [Google Scholar] [CrossRef]
- Xu, X.; Wu, Q. Active Layer thickness variation on the Qinghai-Tibetan Plateau: Historical and projected trends. J. Geophys. Res. Atmos. 2021, 126, e2021JD034841. [Google Scholar] [CrossRef]
- Yin, G.A.; Niu, F.J.; Lin, Z.J.; Luo, J.; Liu, M.H. Data-driven spatiotemporal projections of shallow permafrost based on CMIP6 across the Qinghai–Tibet Plateau at 1 km2 scale. Adv. Clim. Change Res. 2021, 12, 814–827. [Google Scholar] [CrossRef]
- Wang, T.; Zhao, Y.; Xu, C.; Ciais, P.; Liu, D.; Yang, H.; Piao, S.; Yao, T. Atmospheric dynamic constraints on Tibetan Plateau freshwater under Paris climate targets. Nat. Clim. Change 2021, 11, 219–225. [Google Scholar] [CrossRef]
- Amengual, A.; Homar, V.; Romero, R.; Alonso, S.; Ramis, C. A Statistical adjustment of regional climate model outputs to local scales: Application to Platja de Palma, Spain. J. Clim. 2012, 25, 939–957. [Google Scholar] [CrossRef]
- Anderson, B.; Mackintosh, A. Controls on mass balance sensitivity of maritime glaciers in the Southern Alps, New Zealand: The role of debris cover. J. Geophys. Res. 2012, 117, F01003. [Google Scholar] [CrossRef]
- Yang, K.; He, J.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X. China meteorological forcing dataset (1979–2018). Big Earth Data Platf. Three Poles 2019. [Google Scholar] [CrossRef]
- He, J.; Yang, K.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X. The first high-resolution meteorological forcing dataset for land process studies over China. Sci. Data 2020, 7, 25. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; He, J.; Tang, W.; Qin, J.; Cheng, C.C. On downward shortwave and longwave radiations over high altitude regions: Observation and modeling in the Tibetan Plateau. Agric. For. Meteorol. 2010, 150, 38–46. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
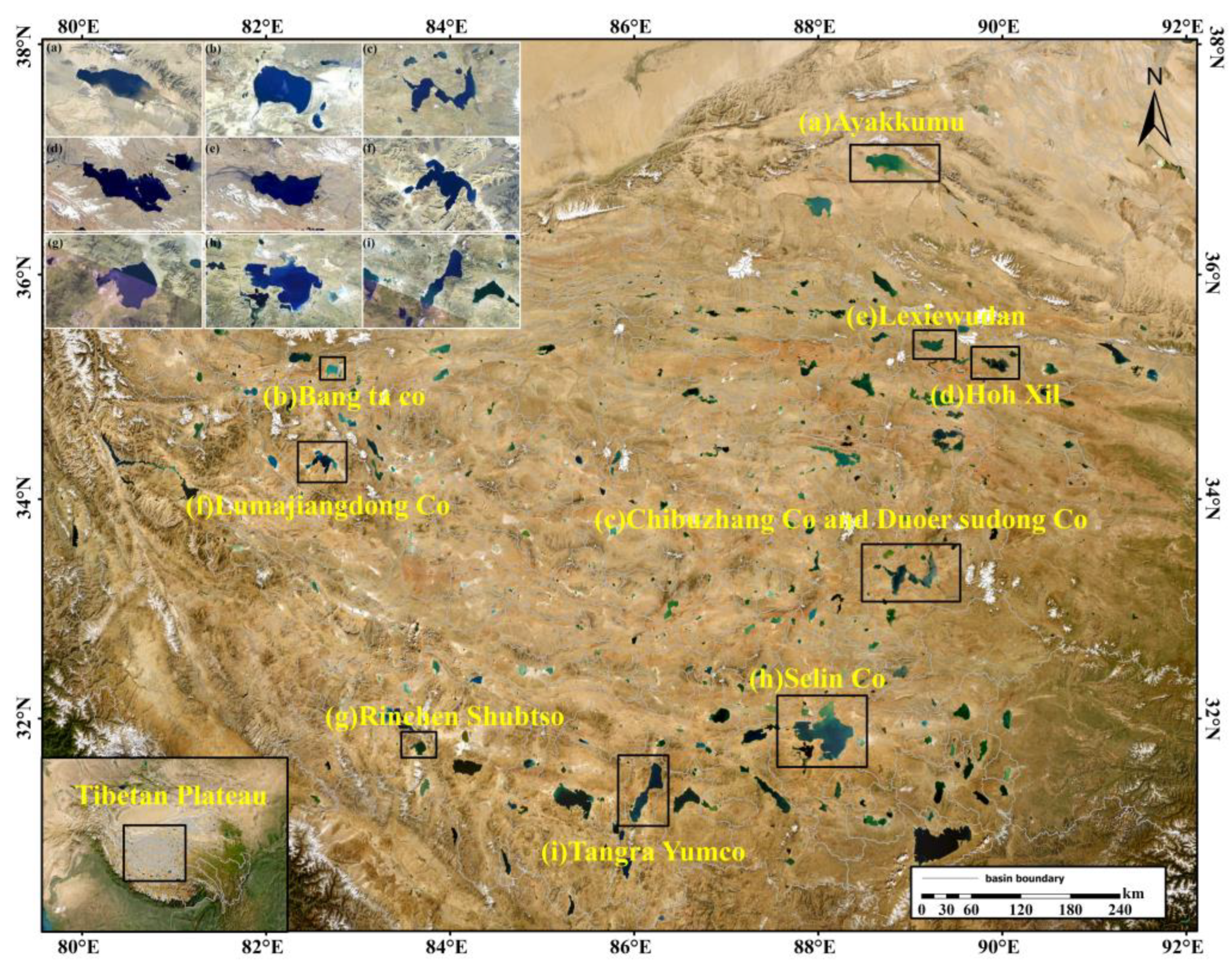

| Lake Name (Abbreviations) | Location | Average Temperature (°C) | Annual Precipitation (mm) | Annual Evaporation (mm) | Area (km2) |
|---|---|---|---|---|---|
| Ayakkumu (AY) | 37°25′–37°37′N, 89°03′–89°56′E | −7.5 | 116 | 363 | 537.6 |
| Bang da Co (BD) | 34°51′–35°N, 81°28′–81°42′E | −3.8 | 179 | 314 | 106.5 |
| Chibuzhang Co and Duoer sodong Co (CD) | 33°13′–33°40N′, 89°31′–90°25′E | −3.7 | 376 | 422 | 1065.6 |
| Hoh Xil (HX) | 35°29′–35°40′N, 90°55´–91°21′E | −9 | 314 | 430 | 299.9 |
| Lexiewudan (LX) | 35°41′–35°50′N, 90°–90°21′E | −9.5 | 324 | 415 | 229.2 |
| Lumajiangdong Co (LM) | 33°53′–34°07′N, 81°22′–81°49′E | −5 | 180 | 282 | 324.8 |
| Rinchen Shubtso (RC) | 31°12′–31°20′N, 83°19′–83°28′E | −1.5 | 197 | 359 | 187.1 |
| Selin Co (SL) | 31°32′–32°07′N, 88°45′–89°22′E | 0.8 | 313 | 434 | 2178 |
| TangraYum Co (TY) | 30°45′–31°21′N, 86°24′–86°48′E | −2.1 | 350 | 447 | 835.3 |
| Schema Name | Institution | Country | n (lat) × n (lon) |
|---|---|---|---|
| ACCESS-CM2 | Commonwealth Scientific and Industrial Research Organisation | Australia | 144 × 192 |
| ACCESS-ESM1-5 | Commonwealth Scientific and Industrial Research Organisation | Australia | 145 ×192 |
| BCC-CSM2-MR | Beijing Climate Center | China | 160 × 320 |
| CAS-ESM2-MR | Chinese Academy of Sciences | China | 128 × 256 |
| CESM2-WACCM | National Center for Atmospheric Research | USA | 192 × 288 |
| CMCC-CM2-SR5 | Fondazione Centro Euro-Mediterraneo sui Cambiamenti Climatici | Italy | 192 × 288 |
| CMCC-ESM2 | Fondazione Centro Euro-Mediterraneo sui Cambiamenti Climatici | Italy | 192 × 288 |
| EC-Earth3 | EC-Earth-Consortium | EU | 256 × 512 |
| EC-Earth3-Veg | EC-Earth-Consortium | EU | 256 × 512 |
| EC-Earth3-Veg-LR | EC-Earth-Consortium | EU | 160 × 320 |
| FGOALS-f3-L | Chinese Academy of Sciences | China | 180 × 288 |
| FGOALS-g3 | Chinese Academy of Sciences | China | 80 × 180 |
| FIO-ESM-2-0 | First Institute of Oceanography | China | 192 × 288 |
| GFDL-ESM4 | National Oceanic and Atmospheric Administration | USA | 180 × 288 |
| KACE-1.0-G | NIMS-KMA | Korea | 144 × 192 |
| MIROC6 | Japanese Research Community | Japan | 128 × 256 |
| MRI-ESM2-0 | MRI (Meteorological Research Institute) | Japan | 160 × 320 |
| NESM3 | Nanjing University of Information Science and Technology | China | 96 × 192 |
| NorESM2-LM | NorESM Climate Modeling Consortium | Norway | 96 × 144 |
| NorESM2-MM | NorESM Climate Modeling Consortium | Norway | 192 × 288 |
| Lake Name | AY | BD | CD | HX | LX | LM | RC | SL | TY |
|---|---|---|---|---|---|---|---|---|---|
| n_estimators | 159 | 105 | 16 | 12 | 81 | 6 | 16 | 15 | 91 |
| max_depth | 9 | 7 | 6 | 8 | 8 | 4 | 6 | 6 | 7 |
| max_features | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| Lake Name | R | PR | |||
|---|---|---|---|---|---|
| CCP | CCCP | OAP | SAMPBC (mm) | SAMPAC (mm) | |
| AY | 0.716 | 0.678 | 116.203 | 457.309 | 123.035 |
| BD | 0.609 | 0.582 | 179.575 | 486.169 | 175.832 |
| CD | 0.406 | 0.351 | 376.273 | 481.547 | 462.827 |
| HX | 0.720 | 0.634 | 303.900 | 674.722 | 300.518 |
| LX | 0.721 | 0.633 | 314.33 | 610.71 | 333.76 |
| LM | 0.669 | 0.593 | 180.07 | 350.27 | 214.19 |
| RC | 0.659 | 0.631 | 197.140 | 534.309 | 204.789 |
| SL | 0.844 | 0.809 | 313.458 | 466.914 | 331.013 |
| TY | 0.886 | 0.864 | 350.327 | 640.205 | 370.966 |
| Lake Name | Training Set | Test Set | ||||
|---|---|---|---|---|---|---|
| R2 | MAE (km3) | RMSE (km3) | R2 | MAE (km3) | RMSE (km3) | |
| AY | 0.819 | 0.065 | 0.085 | 0.802 | 0.031 | 0.041 |
| BD | 0.820 | 0.059 | 0.078 | 0.797 | 0.038 | 0.043 |
| CD | 0.834 | 0.083 | 0.117 | 0.830 | 0.057 | 0.074 |
| HX | 0.788 | 0.083 | 0.108 | 0.639 | 0.053 | 0.068 |
| LX | 0.854 | 0.052 | 0.085 | 0.797 | 0.028 | 0.039 |
| LM | 0.793 | 0.089 | 0.104 | 0.712 | 0.071 | 0.085 |
| RC | 0.705 | 0.067 | 0.103 | 0.585 | 0.023 | 0.032 |
| SL | 0.797 | 0.105 | 0.141 | 0.765 | 0.073 | 0.112 |
| TY | 0.789 | 0.067 | 0.088 | 0.641 | 0.101 | 0.135 |
| Lake Name | Rate of Change in Lake Storage (km3/y) | Changes in Lake Storage (km3) | Bias | ||||||
|---|---|---|---|---|---|---|---|---|---|
| SSP126 | SSP245 | SSP585 | SSP126 | SSP245 | SSP585 | SSP126 | SSP245 | SSP585 | |
| AY | 0.119 | 0.241 | 0.358 | 10.195 | 20.691 | 30.817 | 1.258 | 0.419 | 1.047 |
| BD | 0.124 | 0.100 | 0.086 | 10.685 | 8.627 | 7.432 | 0.656 | 0.557 | 0.176 |
| CD | 0.236 | 0.220 | 0.230 | 20.291 | 18.936 | 19.806 | 1.688 | 1.042 | 0.593 |
| HX | 0.120 | 0.160 | 0.174 | 10.316 | 13.781 | 14.981 | 2.368 | 1.879 | 0.894 |
| LX | 0.123 | 0.116 | 0.106 | 10.625 | 9.961 | 9.155 | 0.833 | 0.409 | 0.199 |
| LM | 0.227 | 0.211 | 0.221 | 19.486 | 18.107 | 18.969 | 0.474 | 0.417 | 0.265 |
| RC | 0.031 | 0.034 | 0.047 | 2.695 | 2.964 | 4.030 | 0.532 | 0.245 | 0.404 |
| SL | 0.966 | 0.863 | 0.715 | 83.065 | 74.268 | 61.495 | 6.187 | 3.856 | 1.280 |
| TY | 0.259 | 0.284 | 0.227 | 22.318 | 24.427 | 19.527 | 2.270 | 1.859 | 1.583 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, Y.; Zhu, L.; Qiao, B.; Zhang, R. Predicting Future Lake Water Storage Changes on the Tibetan Plateau under Different Climate Change Scenarios. Remote Sens. 2024, 16, 375. https://doi.org/10.3390/rs16020375
Hou Y, Zhu L, Qiao B, Zhang R. Predicting Future Lake Water Storage Changes on the Tibetan Plateau under Different Climate Change Scenarios. Remote Sensing. 2024; 16(2):375. https://doi.org/10.3390/rs16020375
Chicago/Turabian StyleHou, Yue, Liping Zhu, Baojin Qiao, and Run Zhang. 2024. "Predicting Future Lake Water Storage Changes on the Tibetan Plateau under Different Climate Change Scenarios" Remote Sensing 16, no. 2: 375. https://doi.org/10.3390/rs16020375
APA StyleHou, Y., Zhu, L., Qiao, B., & Zhang, R. (2024). Predicting Future Lake Water Storage Changes on the Tibetan Plateau under Different Climate Change Scenarios. Remote Sensing, 16(2), 375. https://doi.org/10.3390/rs16020375







