Beam-Space Post-Doppler Reduced-Dimension STAP Based on Sparse Bayesian Learning
Abstract
1. Introduction
- A novel RD STAP method based on the SBL algorithm is proposed, which has suboptimal clutter suppression performance in extremely heterogeneous clutter environments with only one training sample available.
- A novel angular Doppler domain RD channel selection algorithm is proposed, which maximizes the output SINR as a criterion for selecting auxiliary channels. In general, suboptimal clutter suppression performance can be achieved by selecting 3–8 auxiliary channels using the proposed algorithm.
2. STAP Model and GSC form Processor
2.1. STAP Model
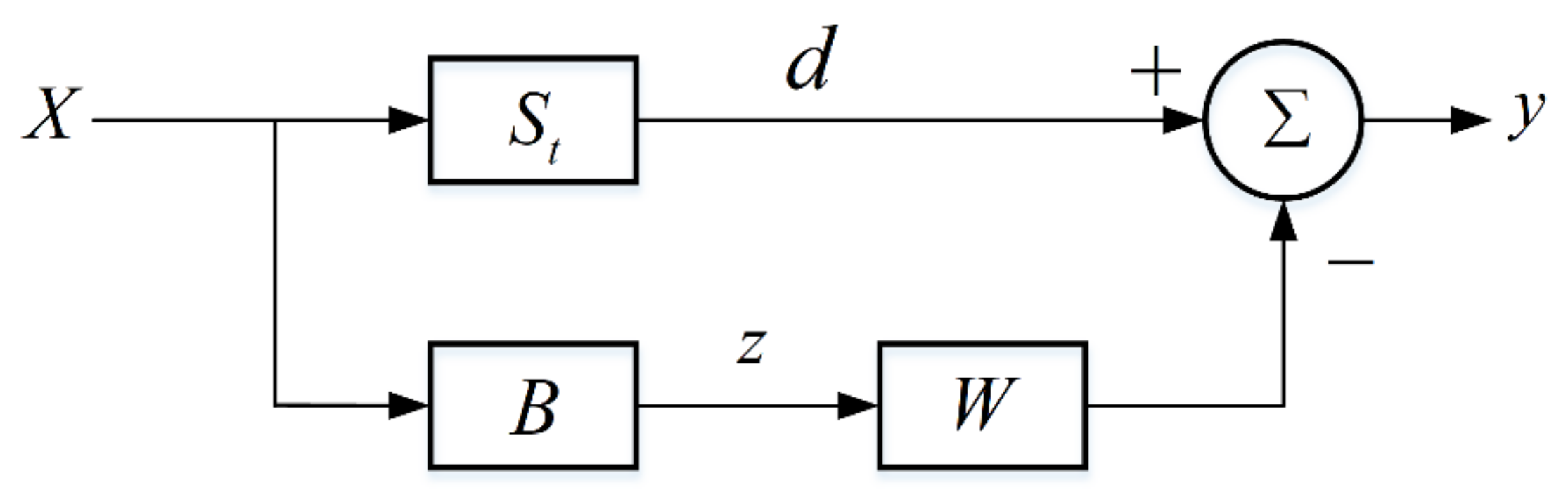
2.2. GSC form Processor
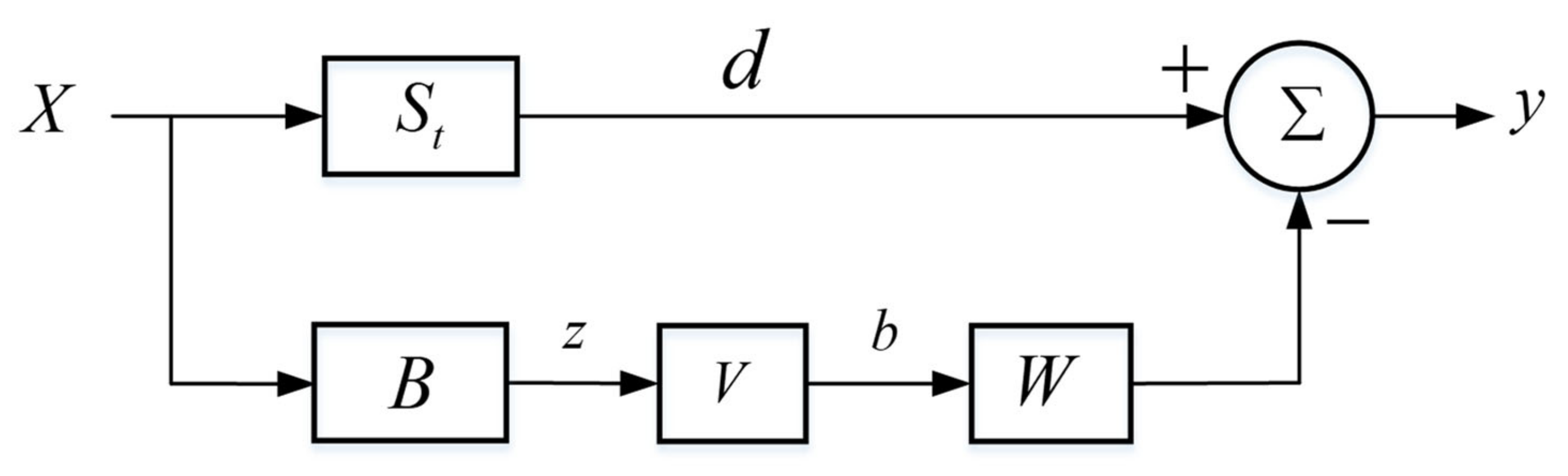
3. Proposed Algorithm
3.1. CNCM Estimation Method Based on SBL
| Algorithm 1. CNCM estimation method based on SBL. |
| Step1: Given the initial values , Step2: Compute the posterior moments Step3: Update the and using the EM rule Step4: Continue Step 2 and 3 until convergence Step5: Assuming Step6: Compute the CNCM by |
3.2. Channel Selection Algorithm Based on SINR Maximum Criterion
| Algorithm 2. The pseudo-code of the proposed channel selection algorithm. |
| Step1: Given the initial value: Estimated covariance matrix selection matrix blocking matrix B contains all candidate auxiliary channels total number of candidate channels Step2: Loop: end loop Step3: solve Let , and remove from candidate channel the number of remaining candidate channels Step4: Continue Step2 and Step3 until preset constraints are satisfied. Output: Selection matrix |
4. Numerical Simulation
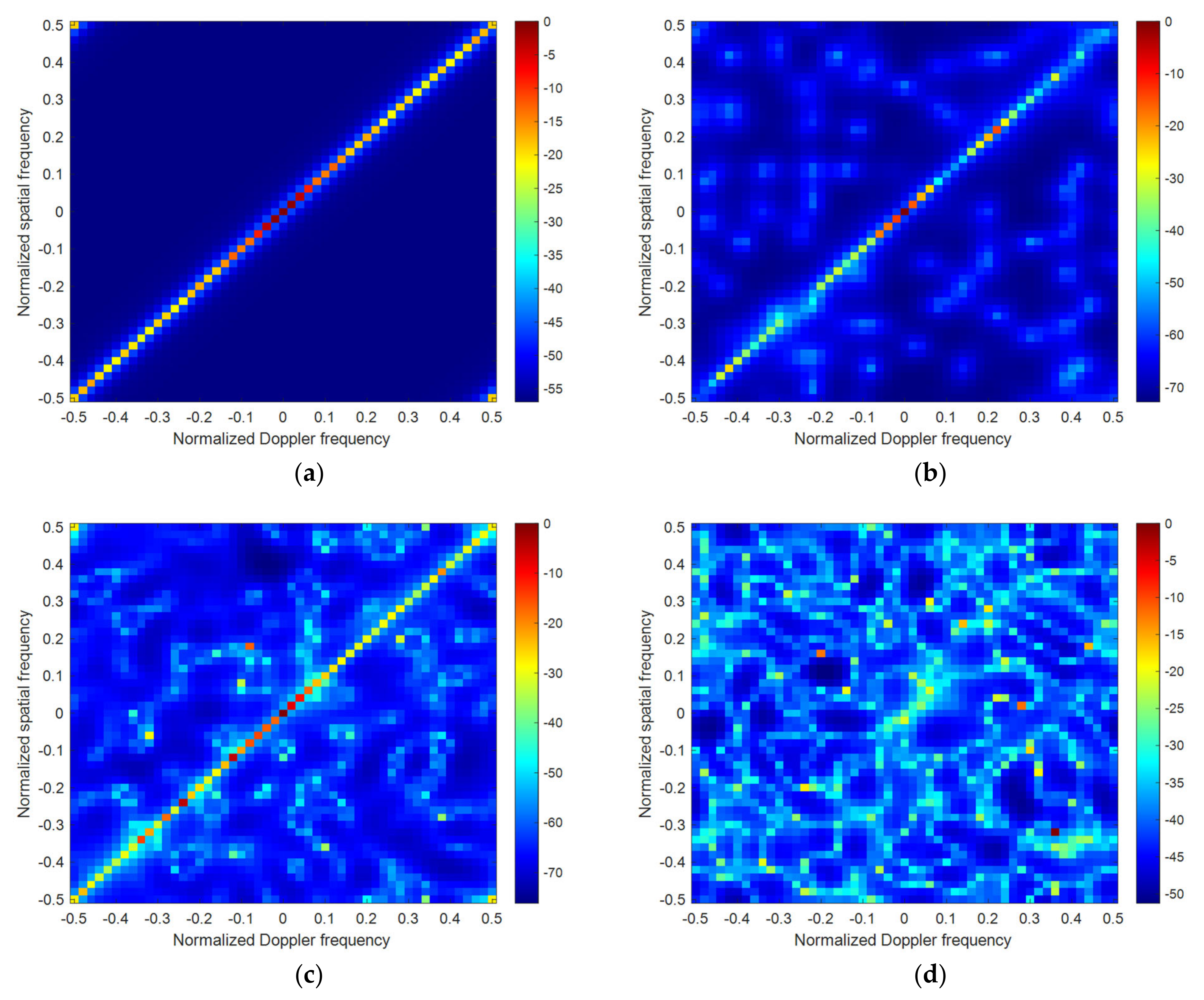
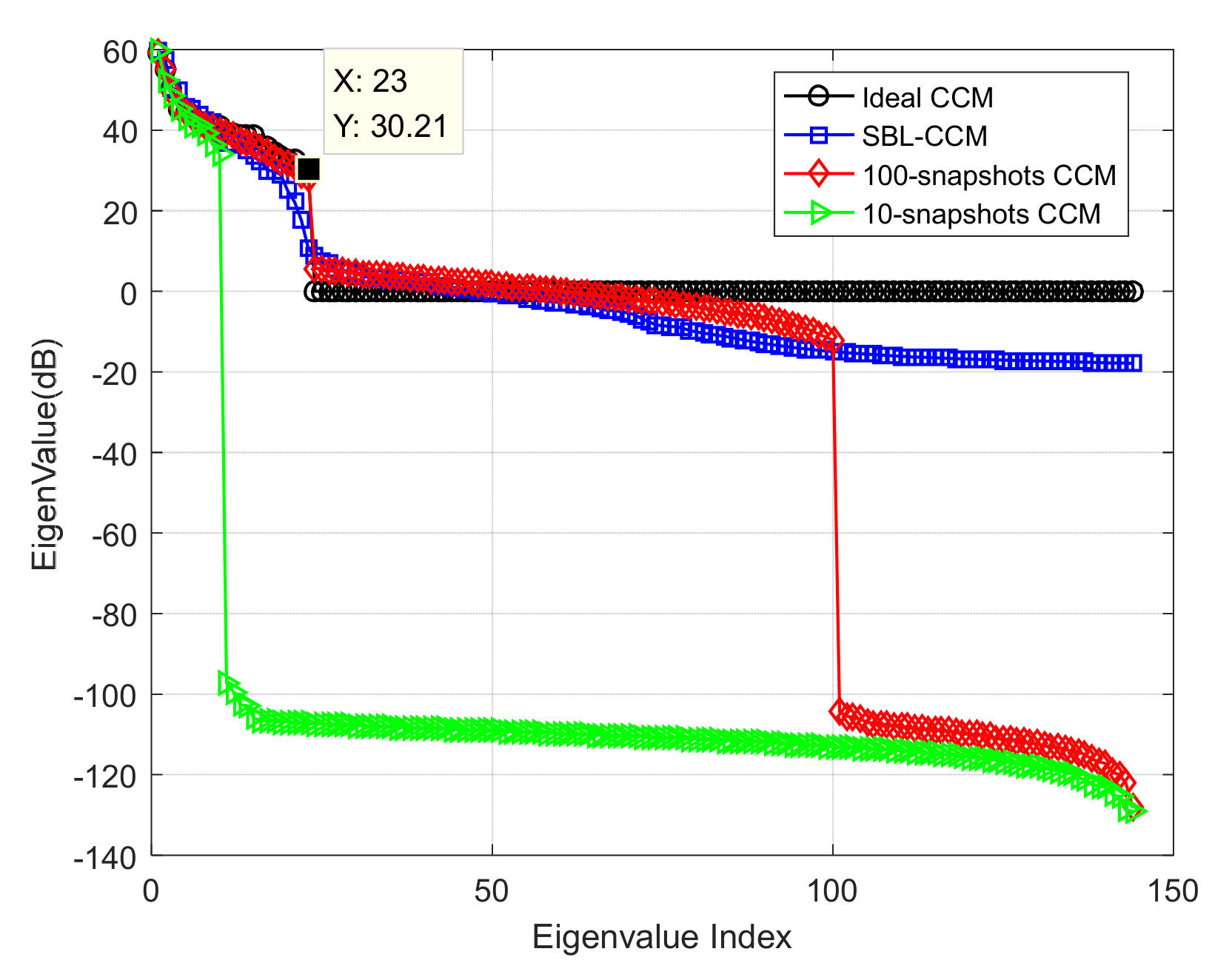
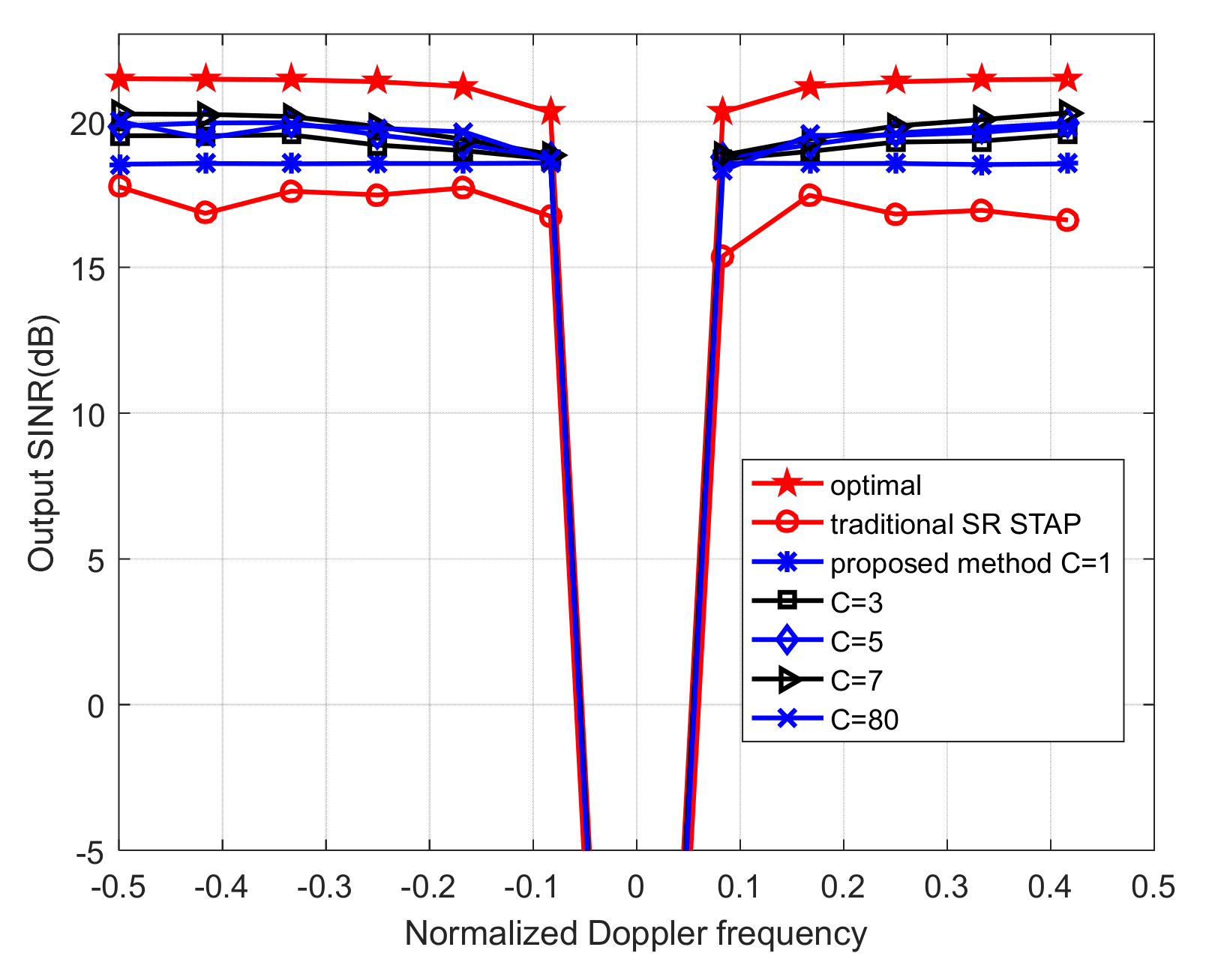
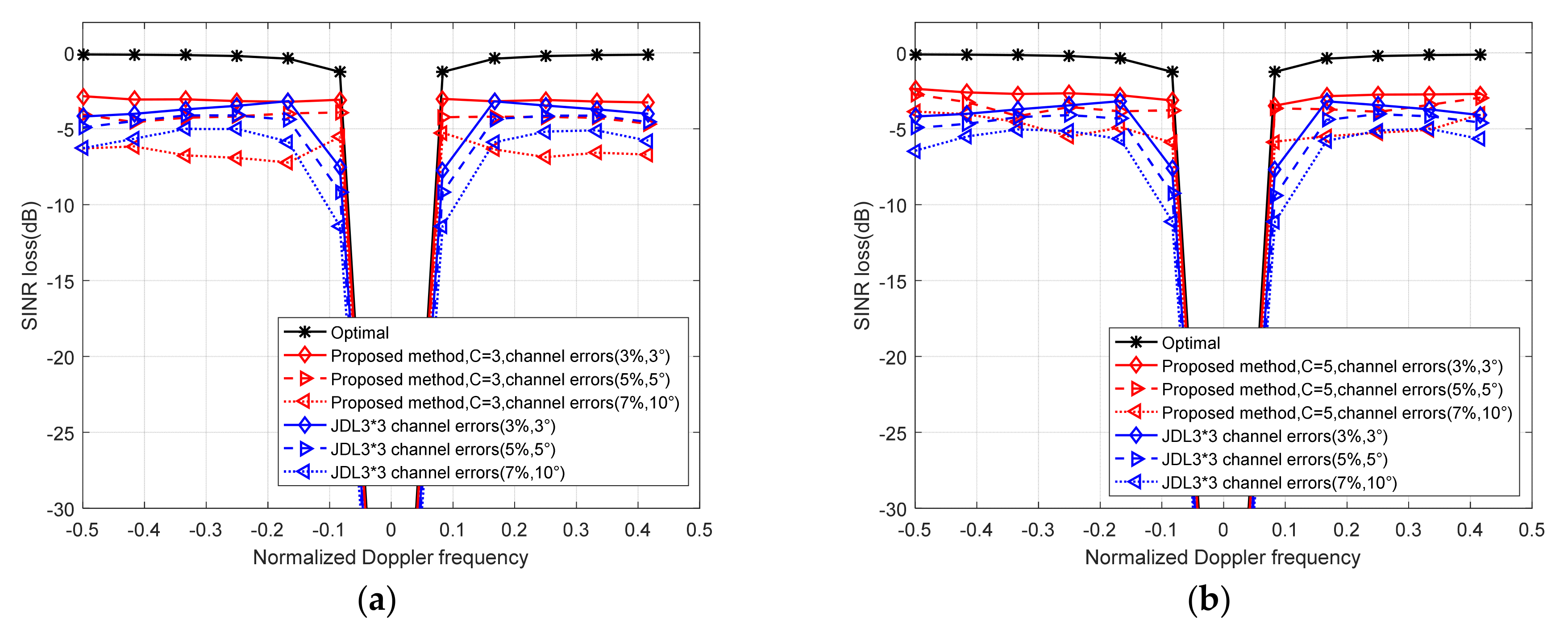
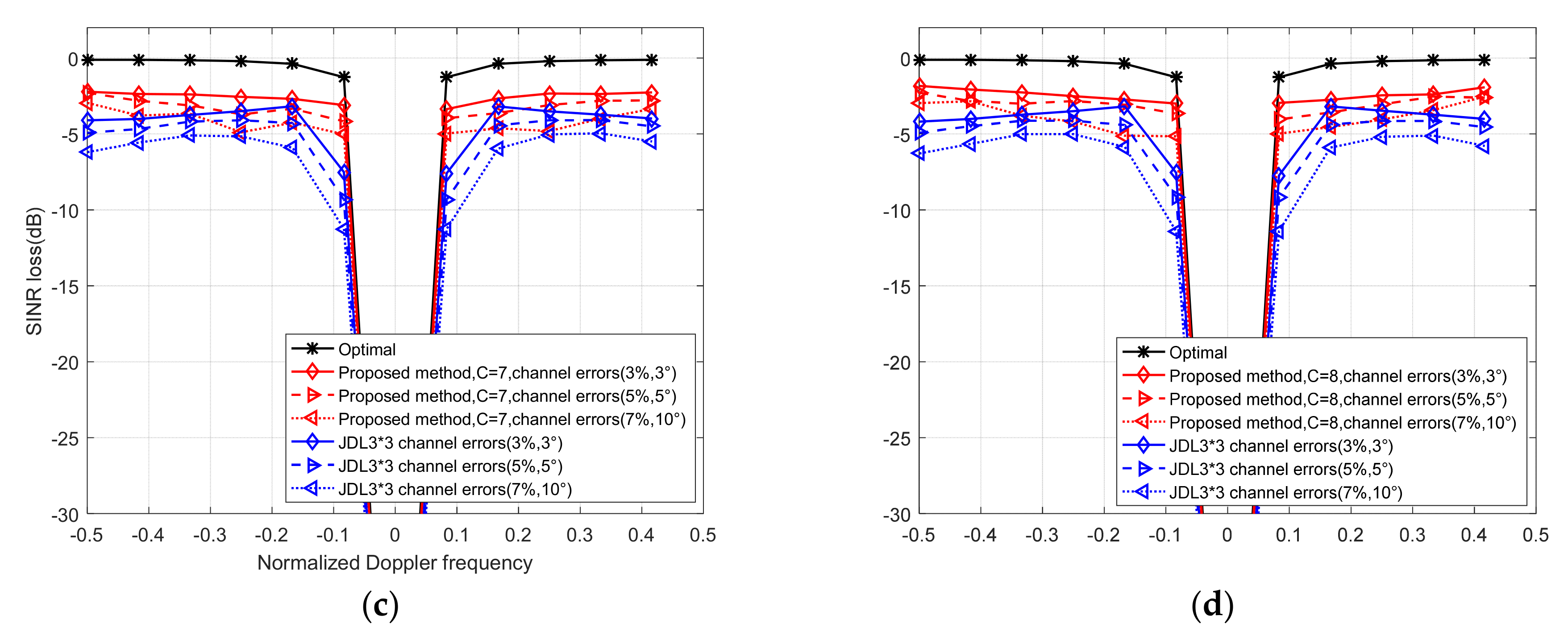
4.1. Performance Analysis Based on Simulation Data
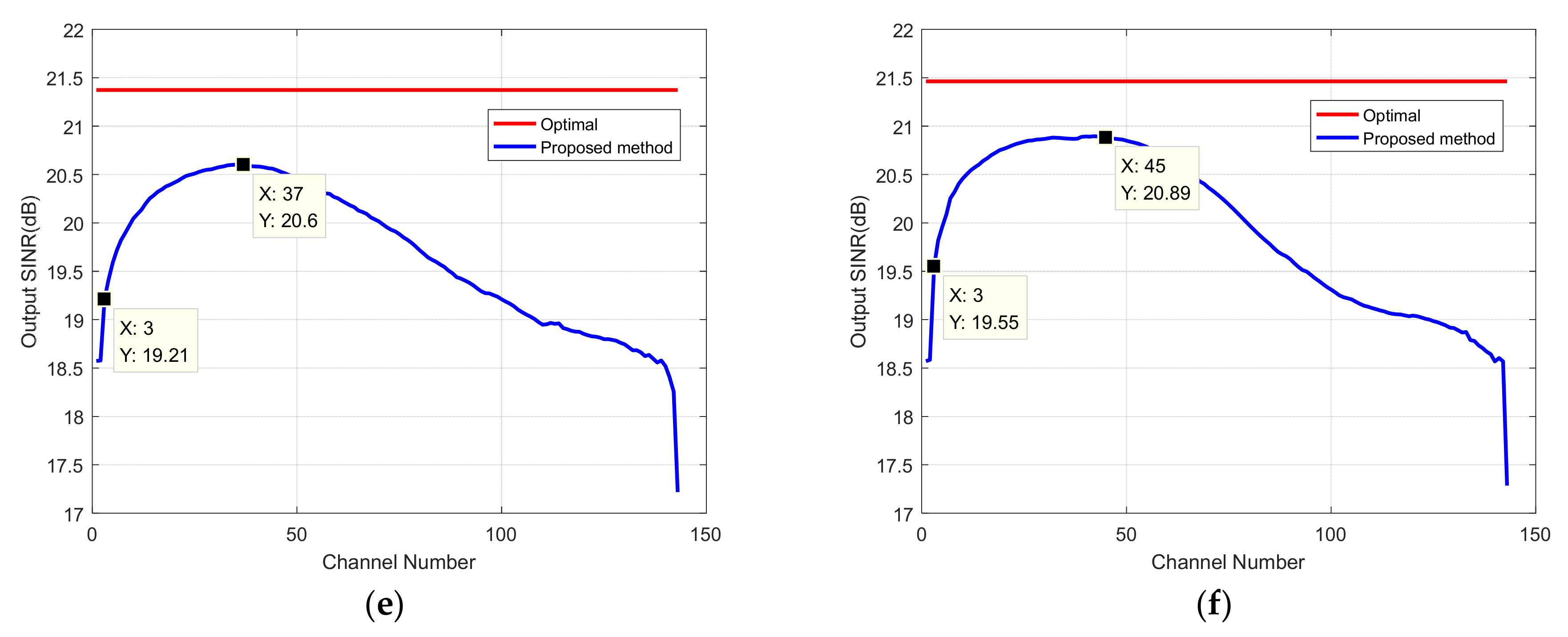
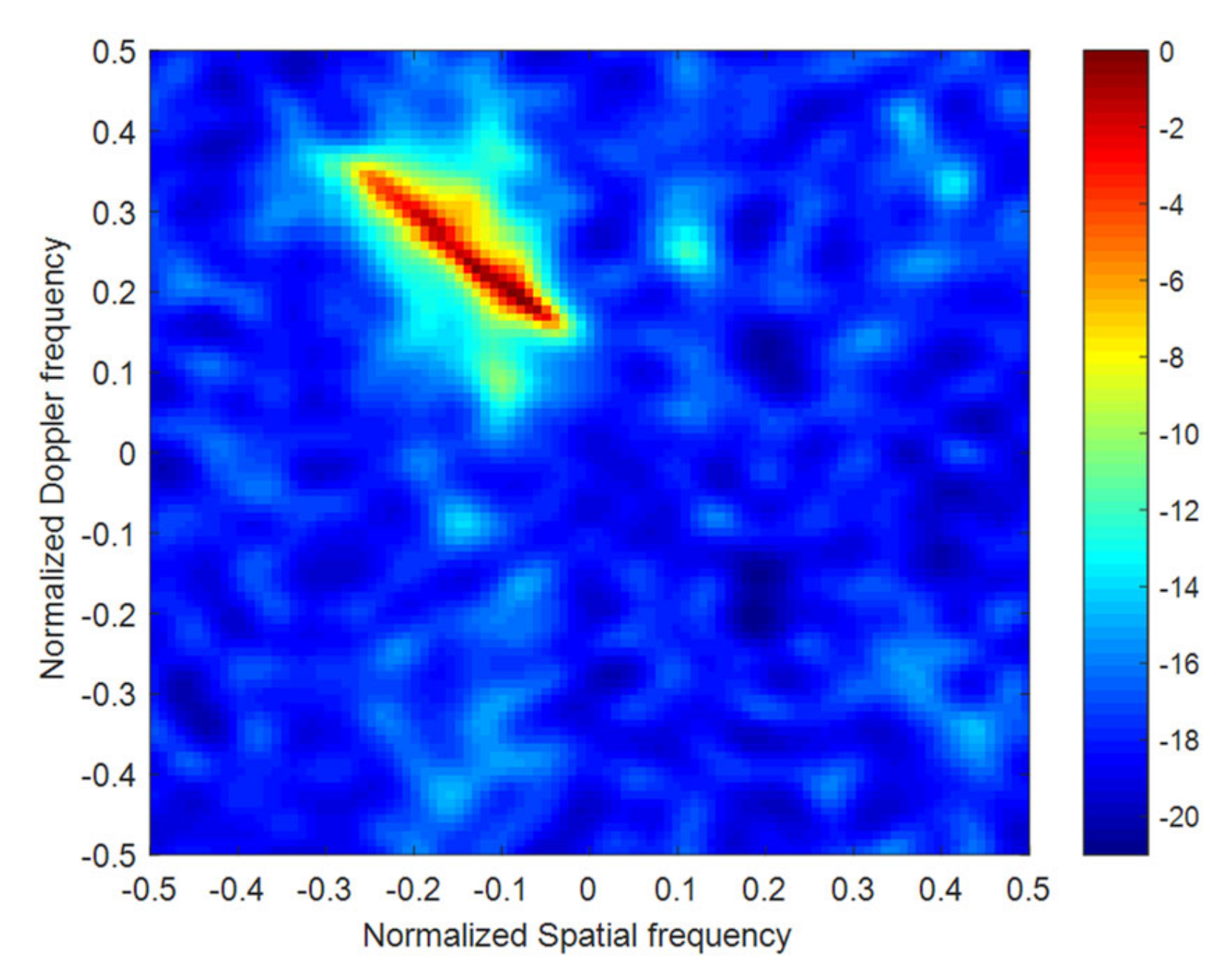
4.2. Performance Analysis Based on Measured Data
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ward, J. Space-Time Adaptive Processing for Airborne Radar; Technical Report, 1015; MIT Lincoln Laboratory: Lexington, MA, USA, 1994. [Google Scholar]
- Reed, I.S.; Mallett, J.D.; Brennan, L.E. Rapid Convergence Rate in Adaptive Arrays. IEEE Trans. Aerosp. Electron. Syst. 1974, 10, 853–863. [Google Scholar] [CrossRef]
- Klemm, R. Adaptive airborne MTI: An auxiliary channel approach. In IEE Proceedings F (Communications, Radar and Signal Processing); IET Digital Library: London, UK, 1987; Volume 134, pp. 269–276. [Google Scholar]
- Dipietro, R.C. Extended factored space-time processing for airborne radar systems. In Proceedings of the Conference Record of the Twenty-Sixth Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 26–28 October 1992; IEEE Computer Society: Pacific Grove, CA, USA, 1992; pp. 425–430. [Google Scholar]
- Wang, H.; Cai, L. On Adaptive Spatial-Temporal Processing for Airborne Surveillance Radar Systems. IEEE Trans. Aerosp. Electron. Syst. 1994, 7, 660–670. [Google Scholar] [CrossRef]
- Sun, K.; Zhang, H.; Li, G.; Meng, H.; Wang, X. A novel STAP algorithm using sparse recovery technique. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009. [Google Scholar]
- Yang, Z.; Li, X.; Wang, H.; Nie, L. Sparsity-Based Space-Time Adaptive Processing Using Complex-Valued Homotopy Technique. In Proceedings of the 2013 IEEE Radar Conference, Ottawa, ON, Canada, 29 April–3 May 2013. [Google Scholar]
- Sen, S. Low-Rank Matrix Decomposition and Spatial-Temporal Sparse Recovery for STAP Radar. IEEE J. Sel. Top. Signal Process. 2015, 12, 1510–1523. [Google Scholar] [CrossRef]
- Duan, K.; Wang, Z.; Xie, W. Sparsity-based STAP algorithm with multiple measurement vectors via sparse Bayesian learning strategy for airborne radar. IET Signal Process. 2016, 9, 544–553. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Gao, F. Clutter nulling space-time adaptive processing algorithm based on sparse representation for airborne radar. IET Radar Sonar Navig. 2017, 11, 177–184. [Google Scholar]
- Feng, W.; Guo, Y.; He, X. Jointly Iterative Adaptive Approach Based Space Time Adaptive Processing Using MIMO Radar. IEEE Access. 2018, 6, 26605–26616. [Google Scholar] [CrossRef]
- Wang, D.; Wang, T.; Cui, W.; Zhang, X. A Clutter Suppression Algorithm via Enhanced Sparse Bayesian Learning for Airborne Radar. IEEE Sens. J. 2023, 5, 10900–10911. [Google Scholar] [CrossRef]
- Fa, R.; De Lamare, R.C. Reduced-Rank STAP Algorithms using Joint Iterative Optimization of Filters. IEEE Trans. Aerosp. Electron. Syst. 2011, 7, 1668–1684. [Google Scholar] [CrossRef]
- Sun, K.; Meng, H.; Wang, Y. Direct Data Domain STAP using Sparse Representation of Clutter Spectrum. Signal Process. 2011, 4, 2222–2236. [Google Scholar] [CrossRef]
- Guo, Y.; Liao, G.; Feng, W. Sparse Representation Based Algorithm for Airborne Radar in Beam-Space Pose-Doppler Reduced-Dimension Space-Time Adaptive Processing. IEEE Access 2017, 4, 5896–5903. [Google Scholar] [CrossRef]
- Yang, Z.; de Lamare, R.C.; Li, X. L1-Regularized STAP Algorithms with a Generalized Sidelobe Canceler Architecture for Airborne Radar. IEEE Trans. Signal Process. 2012, 2, 674–686. [Google Scholar] [CrossRef]
- Zhang, W.; He, Z.; Li, J. A Method for Finding Best Channels in Beam-Space Post-Doppler Reduced-Dimension STAP. IEEE Trans. Aerosp. Electron. Syst. 2014, 1, 254–264. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian Learning and the Relevance Vector Machine. J. Mach. Learn. 2001, 1, 211–244. [Google Scholar]
- Shutin, D.; Buchgraber, T.; Kulkarni, S.R. Fast Variational Sparse Bayesian Learning with Automatic Relevance Determination for Superimposed Signals. IEEE Trans. Signal Process. 2011, 12, 6257–6261. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, H.-T.; Wang, J. An efficient Sparse Bayesian Learning Algorithm Based on Gaussian-Scale Mixtures. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1, 3065–3078. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; An, R.; He, N. Reduced Dimension STAP Based on Sparse Recovery in Heterogenous Clutter Environments. IEEE Trans. Aerosp. Electron. Syst. 2020, 2, 785–795. [Google Scholar] [CrossRef]
- Haimovich, A.M.; Berin, M. Eigenanalysis-based space-time adaptive radar: Performance analysis. IEEE Trans. Aerosp. Electron. Syst. 1997, 10, 1170–1179. [Google Scholar] [CrossRef]
- Sarkar, T.K.; Wang, H.; Park, S. A deterministic least-squares approach to space-time adaptive processing (STAP). IEEE Trans. Antennas Propag. 2001, 2, 91–103. [Google Scholar] [CrossRef]
- Wang, D.; Wang, T.; Cui, W. Adaptive Support-Driven Sparse Recovery STAP Method with Subspace Penalty. Remote Sens. 2022, 14, 4463. [Google Scholar] [CrossRef]
- Titi, G.W.; Marshall, D.F. The ARPA/NAVY mountaintop program: Adaptive signal processing for airborne early warning radar. In Proceedings of the 1996 IEEE International Conference on Acoustics, Speech, and Signal Processing Conference, Atlanta, GA, USA, 9 May 1996; IEEE: Piscataway, NJ, USA, 1996; Volume 5, pp. 1165–1168. [Google Scholar]






| Algorithm | Required Samples |
|---|---|
| EFA [4] | 6N |
| JDL(3*3) [5] | 18 |
| SBL-STAP [9] | 6 |
| Proposed method | 1 |
| Symbols | Parameters | Value |
|---|---|---|
| wavelength | 0.25 m | |
| element spacing | 0.125 m | |
| velocity | 125 m/s | |
| height | 8000 m | |
| number of pulses | 12 | |
| number of elements | 12 | |
| PRF | 2000 Hz | |
| sampling frequency | 1 MHz | |
| main lobe elevation angle | 0° | |
| main lobe azimuth angle | 90° | |
| CNR | 40 dB | |
| SNR | 10 dB | |
| Angular discretization | 4 N | |
| Doppler discretization | 4 M |
| Parameters | Value |
|---|---|
| Array number | 14 |
| Pulses number | 16 |
| PRF | 625 Hz |
| Bandwidth | 500 kHz |
| Range cell number | 403 |
| Range cell of target | 147 |
| Azimuth angle of target | 275° |
| Normalized Doppler frequency of target | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, J.; Wang, T.; Wang, D. Beam-Space Post-Doppler Reduced-Dimension STAP Based on Sparse Bayesian Learning. Remote Sens. 2024, 16, 307. https://doi.org/10.3390/rs16020307
Cao J, Wang T, Wang D. Beam-Space Post-Doppler Reduced-Dimension STAP Based on Sparse Bayesian Learning. Remote Sensing. 2024; 16(2):307. https://doi.org/10.3390/rs16020307
Chicago/Turabian StyleCao, Junxiang, Tong Wang, and Degen Wang. 2024. "Beam-Space Post-Doppler Reduced-Dimension STAP Based on Sparse Bayesian Learning" Remote Sensing 16, no. 2: 307. https://doi.org/10.3390/rs16020307
APA StyleCao, J., Wang, T., & Wang, D. (2024). Beam-Space Post-Doppler Reduced-Dimension STAP Based on Sparse Bayesian Learning. Remote Sensing, 16(2), 307. https://doi.org/10.3390/rs16020307





