Iterative Mamba Diffusion Change-Detection Model for Remote Sensing
Abstract
1. Introduction
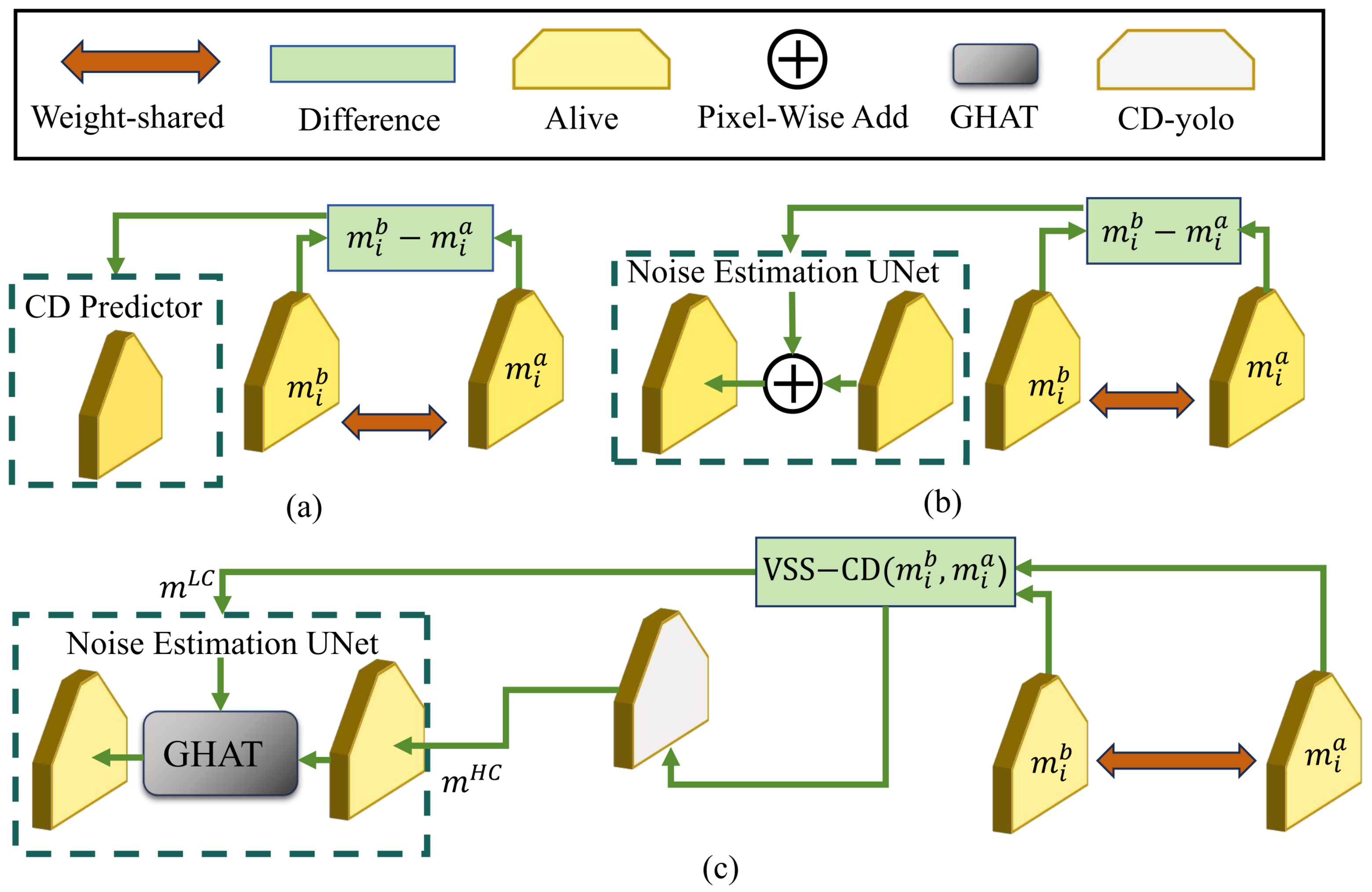
- We design a feature extractor, namely MCD, to capture long-frequency change information from pre- and post-change images while maintaining a linear computational complexity.
- The VSS-CD module within MCD is designed to train the change state representation, which effectively captures the long-frequency change feature, reducing information loss and improving CD fidelity. The difference feature extracted is iteratively fed into the DDPM, allowing for gradual refinement and more precise CD results.
- A Transformer-based GHAT is introduced into the generative framework to integrate high-dimensional CD features into the diffusion noise domain. Simultaneously, low-dimensional CD features are utilized to calibrate prior CD results at each iterative step, progressively refining the generated outcomes. These integration operations effectively enhance noise prediction, resulting in high-precision CD results.
2. Related Works
2.1. Traditional DL-Based Models in CD
2.2. DDPM-Based Models in CD
2.3. Mamba-Based Models in CD
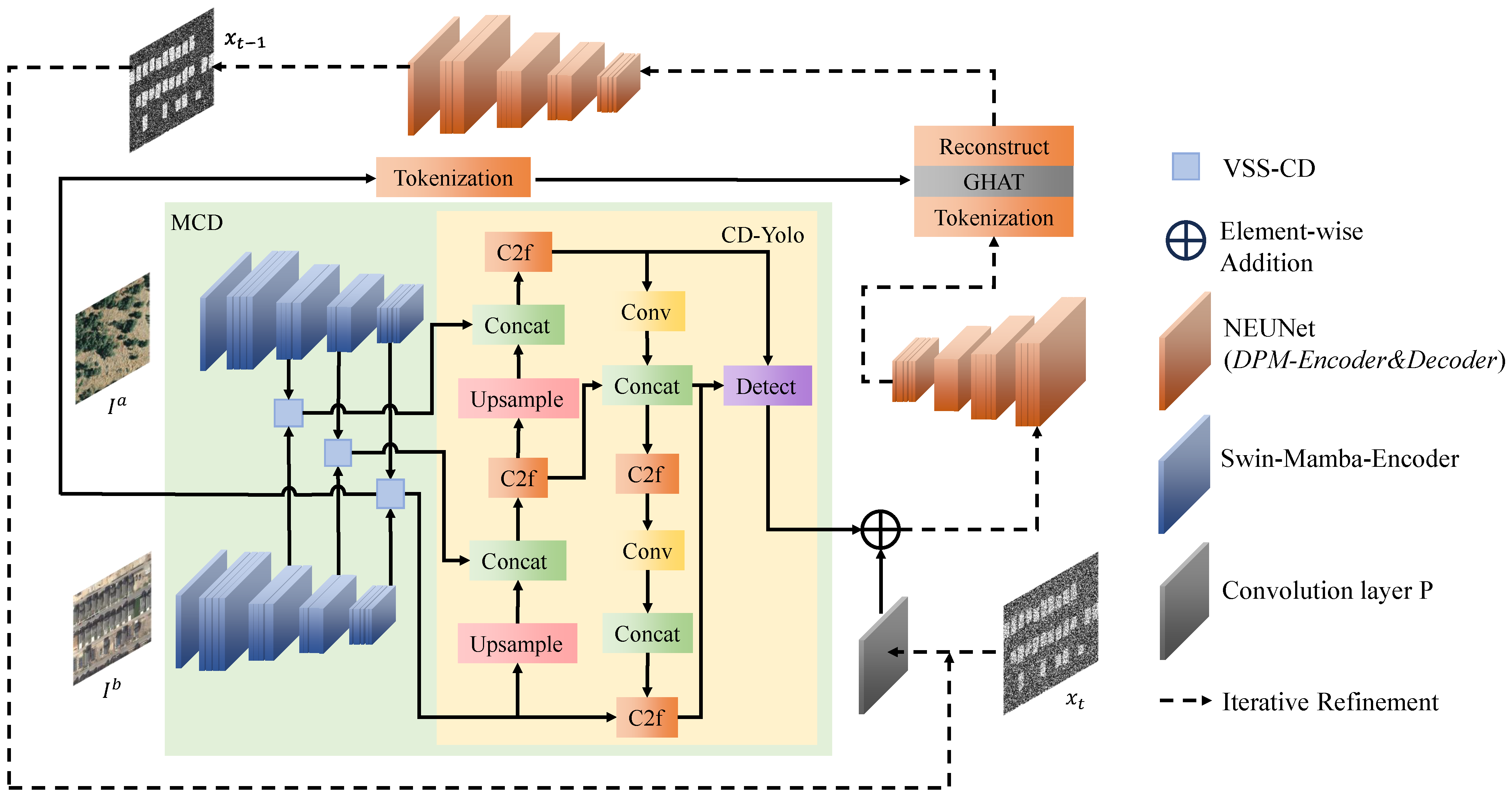
3. Methodology
3.1. Diffusion Model
3.1.1. Training Stage
3.1.2. Inference Stage
3.2. Network Details
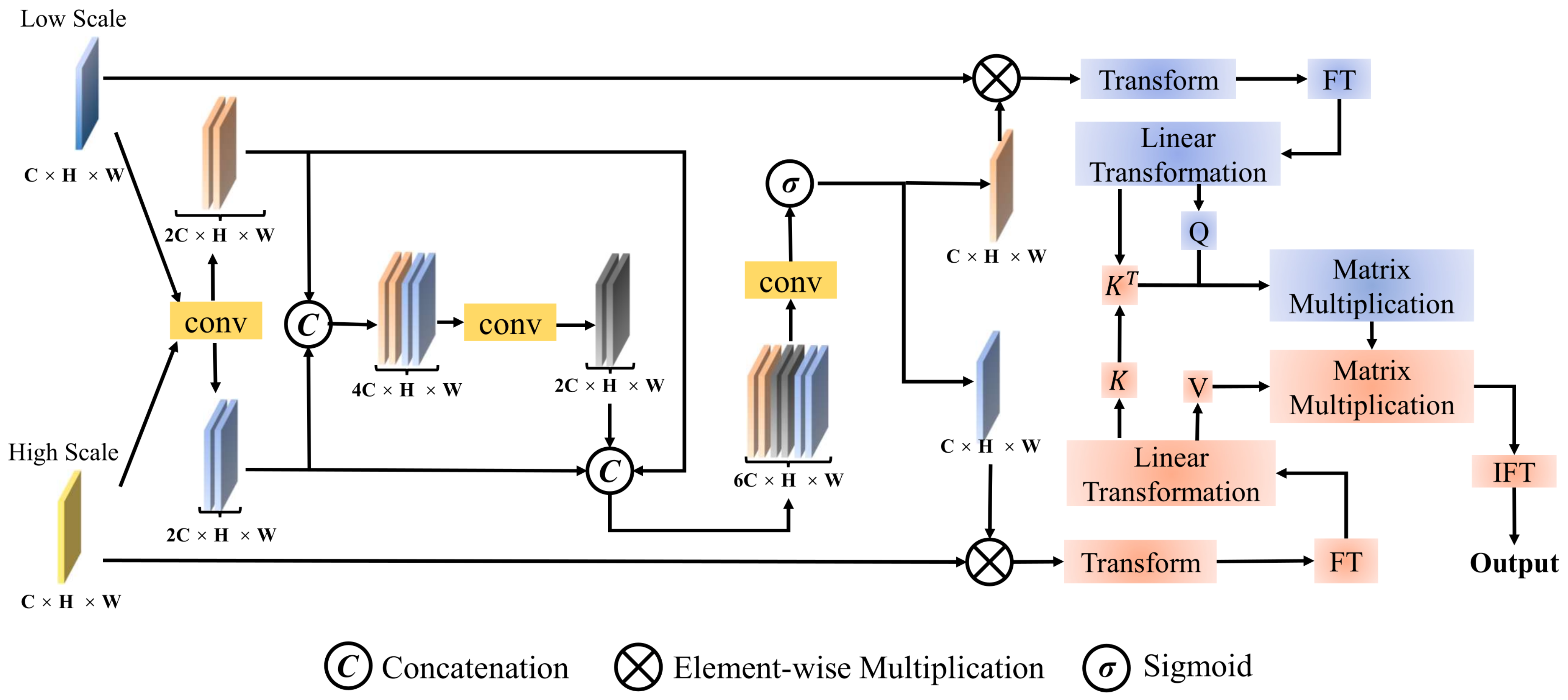
3.2.1. Mamba-CD Feature Extractor Module
3.2.2. NEUNet Architecture and Functionality
4. Performance Evaluation
4.1. Experimental Dataset
- CDD: The CDD is a high-resolution, four-season dataset designed for image-change-detection tasks. It provides an exceptionally high spatial resolution and high-resolution RGB imagery obtained from Google Earth, ranging from 3 to 100 cm/pixel, delivering highly detailed imagery essential for accurate and in-depth analysis. The CDD includes 10,000 training images, 3000 testing images, and 3000 validation images, all with dimensions of pixels. The inclusion of images from different seasons ensures diversity and robustness in detecting changes under various seasonal conditions. The CDD’s comprehensive and high-resolution imagery makes it an ideal resource for developing and evaluating algorithms in the field of computer vision, particularly for change-detection applications.
- WHU: WHU comprises high-resolution aerial imagery with a spatial resolution of cm/pixel, making it suitable for detailed analysis in various computer vision tasks. The dataset is divided into 6096 training patches, 762 testing patches, and 762 validation patches, each with dimensions of pixels. This structured division ensures a comprehensive and systematic approach to model training, testing, and validation. The high-resolution imagery provided by the WHU dataset facilitates the development and evaluation of advanced algorithms for applications such as image classification, segmentation, and change detection.
- LEVIR: LEVIR is a large-scale building CD dataset characterized by a high spatial resolution of m. It is meticulously segmented into 7120 training patches, 1024 validation patches, and 2048 testing patches, each with dimensions of pixels. The high resolution and comprehensive segmentation of the LEVIR dataset make it an invaluable resource in the field of RS.
- OSCD: OSCD is specifically designed to capture urban changes, including the emergence of new buildings and roads. Despite being a low-spatial-resolution dataset between 10 and 60 m, it is effectively structured into 14 training pairs and 10 test pairs with 13 spectral bands. This configuration makes the OSCD dataset particularly suitable for the development and evaluation of CD algorithms in the context of RS. Its focus on urban environments makes the OSCD dataset a valuable dataset for advancing the accuracy and efficiency of CD techniques in monitoring urban growth and infrastructure development.
4.2. Implementation Details
4.3. Evaluation Metrics
4.4. Comparison
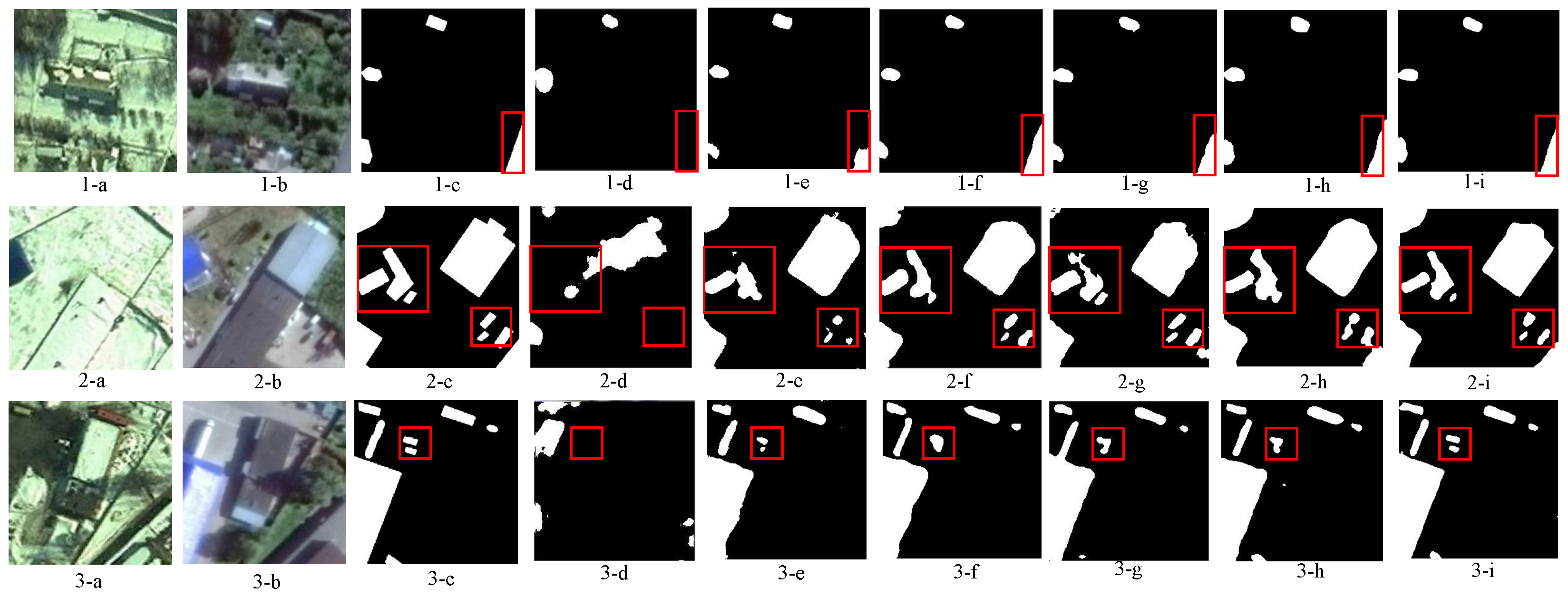
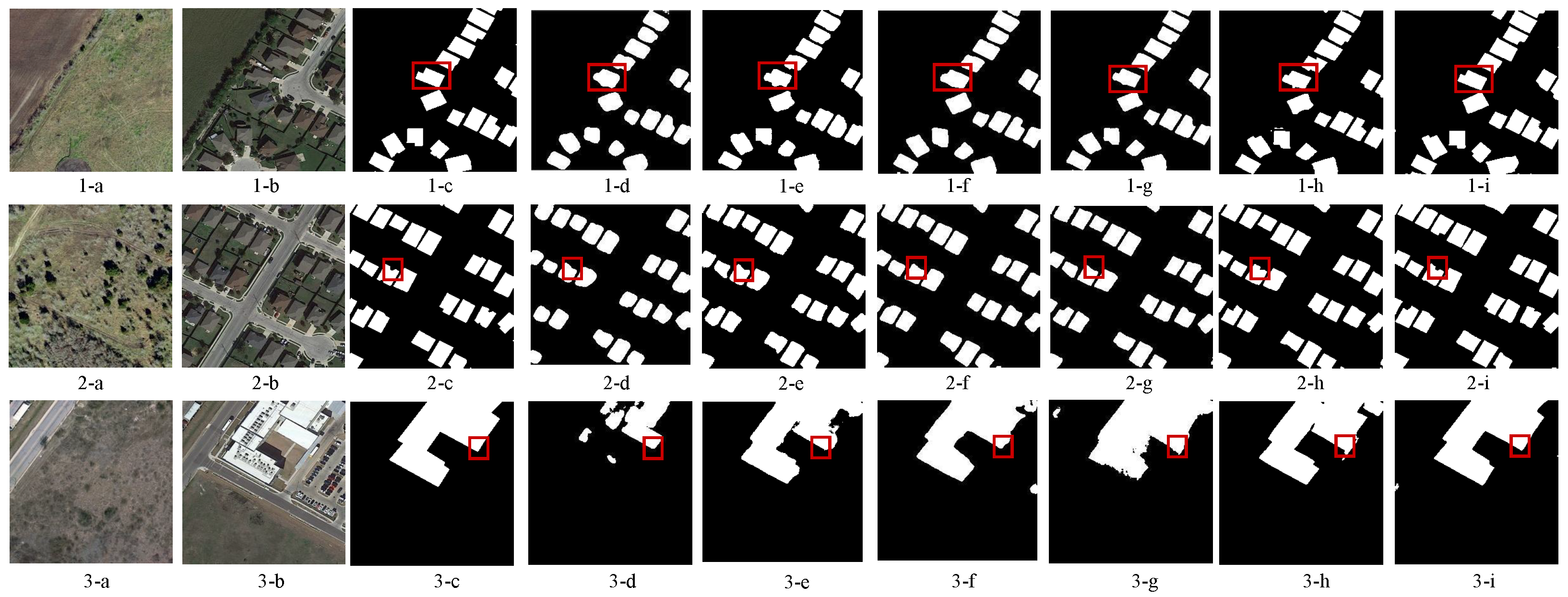
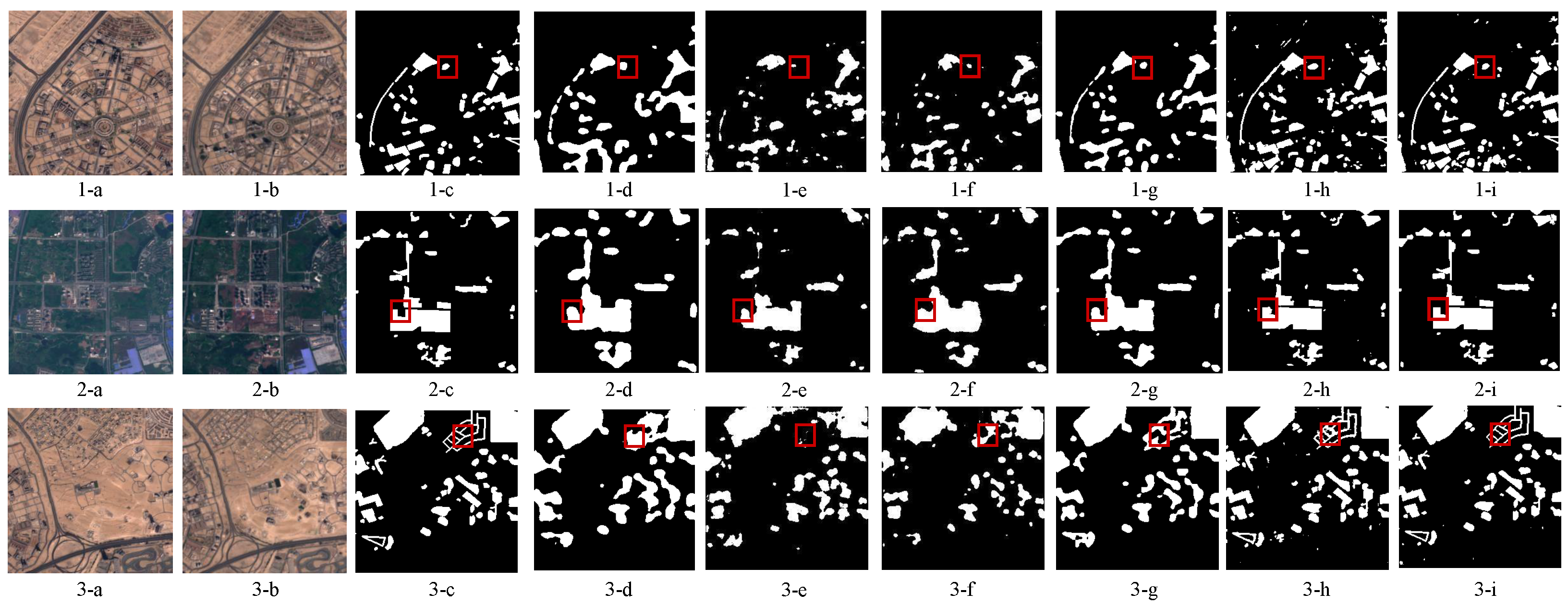
4.5. Experiments on CDDs
4.6. Experiments on WHU Datasets
4.7. Experiments on LEVIR Datasets
4.8. Experiments on OSCD Datasets
4.9. Multi-Scale Feature Visualization with Heatmaps
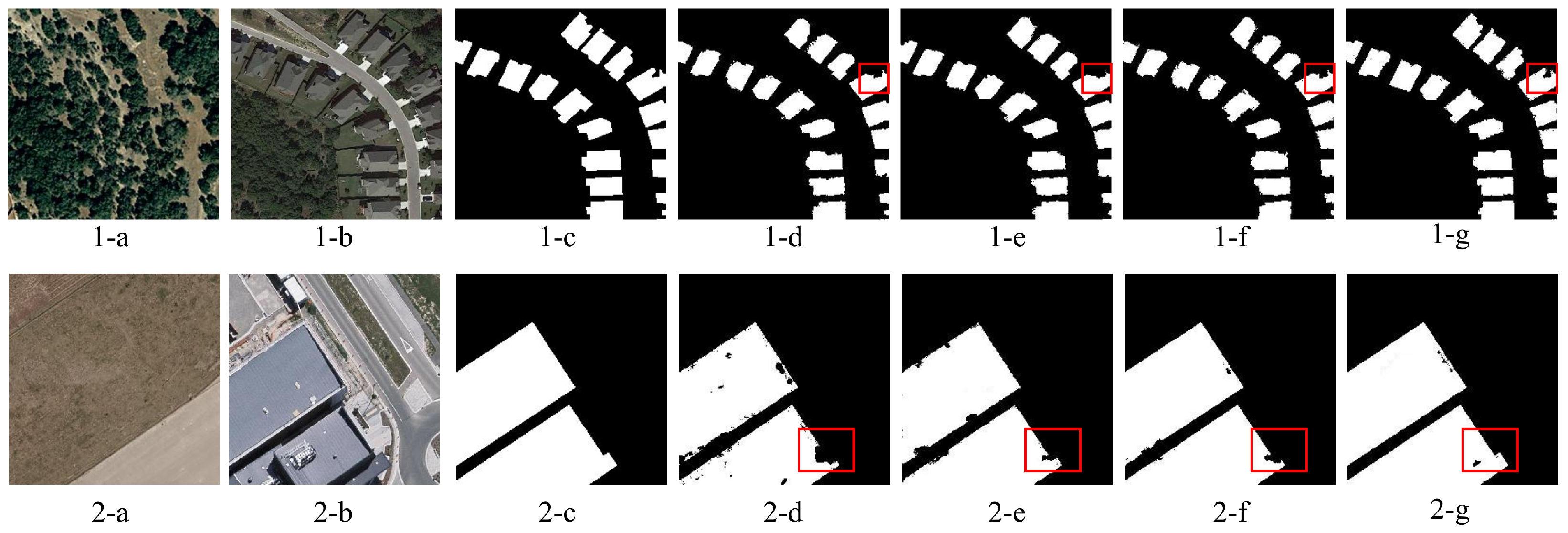
4.10. Ablation Study
4.11. Efficiency
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.; Wang, X.; Wu, W.; Li, G. Continuous Change Detection of Flood Extents with Multi-Source Heterogeneous Satellite Image Time Series. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4205418. [Google Scholar]
- Khan, S.H.; He, X.; Porikli, F.; Bennamoun, M. Forest change detection in incomplete satellite images with deep neural networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5407–5423. [Google Scholar] [CrossRef]
- Yu, D.; Fang, C. Urban Remote Sensing with Spatial Big Data: A Review and Renewed Perspective of Urban Studies in Recent Decades. Remote Sens. 2023, 15, 1307. [Google Scholar] [CrossRef]
- Jiang, H.; Peng, M.; Zhong, Y.; Xie, H.; Hao, Z.; Lin, J.; Ma, X.; Hu, X. A survey on deep learning-based change detection from high-resolution remote sensing images. Remote Sens. 2022, 14, 1552. [Google Scholar] [CrossRef]
- Wang, W.; Chen, Y.; Ghamisi, P. Transferring CNN with adaptive learning for remote sensing scene classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Bazi, Y.; Bashmal, L.; Rahhal, M.; Wang, F.; Yang, G. Vision transformers for remote sensing image classification. Remote Sens. 2021, 13, 516. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Y.; Yang, X.; Gao, S.; Li, F.; Kong, A.; Zu, D.; Sun, L. Improved remote sensing image classification based on multi-scale feature fusion. Remote Sens. 2020, 122, 213. [Google Scholar] [CrossRef]
- Lei, J.; Luo, X.; Fang, L.; Wang, M.; Gu, Y. Region-enhanced convolutional neural network for object detection in remote sensing images. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5693–5702. [Google Scholar] [CrossRef]
- Wu, H.; Huang, P.; Zhang, M.; Tang, W.; Yu, X. CMTFNet: CNN and multiscale transformer fusion network for remote sensing image semantic segmentation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 2004612. [Google Scholar] [CrossRef]
- Zhang, M.; Shi, W. A feature difference convolutional neural network-based change detection method. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7232–7246. [Google Scholar] [CrossRef]
- Hou, B.; Liu, Q.; Wang, H.; Wang, Y. From W-Net to CDGAN: Bitemporal change detection via deep learning techniques. IEEE Trans. Geosci. Remote Sens. 2019, 58, 1790–1802. [Google Scholar] [CrossRef]
- Zhan, Y.; Fu, K.; Yan, M.; Sun, X.; Wang, H.; Qiu, X. Change detection based on deep siamese convolutional network for optical aerial images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1845–1849. [Google Scholar] [CrossRef]
- Daudt, R.C.; Le Saux, B.; Boulch, A. Fully convolutional siamese networks for change detection. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 4063–4067. [Google Scholar]
- Bai, T.; Wang, L.; Yin, D.; Sun, K.; Chen, Y.; Li, W.; Li, D. Deep learning for change detection in remote sensing: A review. Geo-Spat. Inf. Sci. 2023, 26, 262–288. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, H.; Sun, W.; Li, S.; Wang, F.; Yang, G. A coarse-to-fine deep learning based land use change detection method for high-resolution remote sensing images. Remote Sens. 2020, 12, 1933. [Google Scholar] [CrossRef]
- Seydi, S.T.; Hasanlou, M.; Amani, M. A new end-to-end multi-dimensional CNN framework for land cover/land use change detection in multi-source remote sensing datasets. Remote Sens. 2020, 12, 2010. [Google Scholar] [CrossRef]
- Ye, Y.; Zhou, L.; Zhu, B.; Yang, C.; Sun, M.; Fan, J.; Fu, Z. Feature decomposition-optimization-reorganization network for building change detection in remote sensing images. Remote Sens. 2022, 14, 722. [Google Scholar] [CrossRef]
- Wu, Y.; Bai, Z.; Miao, Q.; Ma, W.; Yang, Y.; Gong, M. A classified adversarial network for multi-spectral remote sensing image change detection. Remote Sens. 2020, 12, 2098. [Google Scholar] [CrossRef]
- Xu, Q.; Chen, K.; Zhou, G.; Sun, X. Change capsule network for optical remote sensing image change detection. Remote Sens. 2021, 13, 2646. [Google Scholar] [CrossRef]
- Song, K.; Cui, F.; Jiang, J. An efficient lightweight neural network for remote sensing image change detection. Remote Sens. 2021, 13, 5152. [Google Scholar] [CrossRef]
- Ma, W.; Xiong, Y.; Wu, Y.; Yang, H.; Zhang, X.; Jiao, L. Change detection in remote sensing images based on image mapping and a deep capsule network. Remote Sens. 2019, 11, 626. [Google Scholar] [CrossRef]
- Chen, H.; Qi, Z.; Shi, Z. Remote sensing image change detection with transformers. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Gu, A.; Dao, T. Mamba: Linear-time sequence modeling with selective state spaces. arXiv 2023, arXiv:2312.00752. [Google Scholar]
- Hamilton, J.D. State-space models. Handb. Econom. 1994, 4, 3039–3080. [Google Scholar]
- Gu, A.; Goel, K.; Ré, C. Efficiently modeling long sequences with structured state spaces. arXiv 2021, arXiv:2111.00396. [Google Scholar]
- Zhang, M.; Yu, Y.; Gu, L.; Lin, T.; Tao, X. Vm-unet-v2 rethinking vision mamba unet for medical image segmentation. arXiv 2024, arXiv:2403.09157. [Google Scholar]
- Wang, Q.; Wang, C.; Lai, Z.; Zhou, Y. Insectmamba: Insect pest classification with state space model. arXiv 2024, arXiv:2404.03611. [Google Scholar]
- Ding, H.; Xia, B.; Liu, W.; Zhang, Z.; Zhang, J.; Wang, X.; Xu, S. A Novel Mamba Architecture with a Semantic Transformer for Efficient Real-Time Remote Sensing Semantic Segmentation. Remote Sens. 2024, 16, 2620. [Google Scholar] [CrossRef]
- Zhou, P.; An, L.; Wang, Y.; Geng, G. MLGTM: Multi-Scale Local Geometric Transformer-Mamba Application in Terracotta Warriors Point Cloud Classification. Remote Sens. 2024, 16, 2920. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhang, G.; Zou, X.; Wang, X.; Huang, J.; Li, X. ConvMambaSR: Leveraging State-Space Models and CNNs in a Dual-Branch Architecture for Remote Sensing Imagery Super-Resolution. Remote Sens. 2024, 16, 3254. [Google Scholar] [CrossRef]
- Chen, H.; Song, J.; Han, C.; Xia, J.; Yokoya, N. ChangeMamba: Remote Sensing Change Detection With Spatiotemporal State Space Model. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–12. [Google Scholar] [CrossRef]
- Wen, Y.; Ma, X.; Zhang, X.; Pun, M.O. GCD-DDPM: A generative change detection model based on difference-feature guided DDPM. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5404416. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Jocher, G.; Chaurasia, A.; Qiu, J. Ultralytics YOLO. 2023. Available online: https://github.com/ultralytics (accessed on 26 September 2024).
- Liu, R.; Kuffer, M.; Persello, C. The temporal dynamics of slums employing a CNN-based change detection approach. Remote Sens. 2019, 11, 2844. [Google Scholar] [CrossRef]
- Mopuri, K.R.; Garg, U.; Babu, R.V. CNN fixations: An unraveling approach to visualize the discriminative image regions. IEEE Trans. Image Process. 2018, 28, 2116–2125. [Google Scholar] [CrossRef]
- Mou, L.; Bruzzone, L.; Zhu, X.X. Learning spectral-spatial-temporal features via a recurrent convolutional neural network for change detection in multispectral imagery. IEEE Trans. Geosci. Remote Sens. 2018, 57, 924–935. [Google Scholar] [CrossRef]
- Liu, T.; Gong, M.; Lu, D.; Zhang, Q.; Zheng, H.; Jiang, F.; Zhang, M. Building change detection for VHR remote sensing images via local–global pyramid network and cross-task transfer learning strategy. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4704817. [Google Scholar] [CrossRef]
- Zhang, C.; Yue, P.; Tapete, D.; Jiang, L.; Shangguan, B.; Huang, L.; Liu, G. A deeply supervised image fusion network for change detection in high resolution bi-temporal remote sensing images. ISPRS J. Photogramm. Remote Sens. 2020, 166, 183–200. [Google Scholar] [CrossRef]
- Chen, J.; Yuan, Z.; Peng, J.; Chen, L.; Huang, H.; Zhu, J.; Liu, Y.; Li, H. DASNet: Dual attentive fully convolutional Siamese networks for change detection in high-resolution satellite images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 1194–1206. [Google Scholar] [CrossRef]
- Yang, L.; Chen, Y.; Song, S.; Li, F.; Huang, G. Deep Siamese networks based change detection with remote sensing images. Remote Sens. 2021, 13, 3394. [Google Scholar] [CrossRef]
- Zitzlsberger, G.; Podhorányi, M.; Svatoň, V.; Lazeckỳ, M.; Martinovič, J. Neural network-based urban change monitoring with deep-temporal multispectral and SAR remote sensing data. Remote Sens. 2021, 13, 3000. [Google Scholar] [CrossRef]
- Mandal, M.; Vipparthi, S.K. An empirical review of deep learning frameworks for change detection: Model design, experimental frameworks, challenges and research needs. IEEE Trans. Intell. Transp. Syst. 2021, 23, 6101–6122. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, L.; Cheng, S.; Li, Y. SwinSUNet: Pure transformer network for remote sensing image change detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Deng, Y.; Meng, Y.; Chen, J.; Yue, A.; Liu, D.; Chen, J. TChange: A Hybrid Transformer-CNN Change Detection Network. Remote Sens. 2023, 15, 1219. [Google Scholar] [CrossRef]
- Mao, Z.; Tong, X.; Luo, Z.; Zhang, H. MFATNet: Multi-scale feature aggregation via transformer for remote sensing image change detection. Remote Sens. 2022, 14, 5379. [Google Scholar] [CrossRef]
- Xia, L.; Chen, J.; Luo, J.; Zhang, J.; Yang, D.; Shen, Z. Building change detection based on an edge-guided convolutional neural network combined with a transformer. Remote Sens. 2022, 14, 4524. [Google Scholar] [CrossRef]
- Perera, M.V.; Nair, N.G.; Bandara, W.G.C.; Patel, V.M. SAR Despeckling using a Denoising Diffusion Probabilistic Model. IEEE Geosci. Remote Sens. Lett. 2023. [Google Scholar] [CrossRef]
- Nair, N.G.; Mei, K.; Patel, V.M. AT-DDPM: Restoring faces degraded by atmospheric turbulence using denoising diffusion probabilistic models. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 2–7 January 2023; pp. 3434–3443. [Google Scholar]
- Bandara, W.G.C.; Nair, N.G.; Patel, V.M. DDPM-CD: Remote sensing change detection using denoising diffusion probabilistic models. arXiv 2022, arXiv:2206.11892. [Google Scholar]
- Zhao, H.; Zhang, M.; Zhao, W.; Ding, P.; Huang, S.; Wang, D. Cobra: Extending mamba to multi-modal large language model for efficient inference. arXiv 2024, arXiv:2403.14520. [Google Scholar]
- Zhu, L.; Liao, B.; Zhang, Q.; Wang, X.; Liu, W.; Wang, X. Vision mamba: Efficient visual representation learning with bidirectional state space model. arXiv 2024, arXiv:2401.09417. [Google Scholar]
- Yue, Y.; Li, Z. Medmamba: Vision mamba for medical image classification. arXiv 2024, arXiv:2403.03849. [Google Scholar]
- Ma, X.; Zhang, X.; Pun, M.O. Rs3mamba: Visual state space model for remote sensing images semantic segmentation. arXiv 2024, arXiv:2404.02457. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, Y.; Zhao, Y.; Yu, H.; Xie, L.; Wang, Y.; Ye, Q.; Liu, Y. Vmamba: Visual state space model. arXiv 2024, arXiv:2401.10166. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Kingma, D.P.; Mohamed, S.; Jimenez Rezende, D.; Welling, M. Semi-supervised learning with deep generative models. Adv. Neural Inf. Process. Syst. 2014, 27, 3581–3589. [Google Scholar]
- Guo, Y.; Li, Y.; Wang, L.; Rosing, T. Depthwise convolution is all you need for learning multiple visual domains. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 8368–8375. [Google Scholar]
- Jocher, G.; Stoken, A.; Borovec, J.; Changyu, L.; Hogan, A.; Chaurasia, A.; Diaconu, L.; Ingham, F.; Colmagro, A.; Ye, H.; et al. Ultralytics/yolov5: v4. 0-nn. SiLU () activations, Weights & Biases logging, PyTorch Hub integration. Zenodo. 2021. Available online: https://zenodo.org/record/4418161 (accessed on 26 September 2024).
- Bandara, W.G.C.; Patel, V.M. Revisiting Consistency Regularization for Semi-supervised Change Detection in Remote Sensing Images. arXiv 2022, arXiv:2204.08454. [Google Scholar]
- Chen, H.; Shi, Z. A spatial-temporal attention-based method and a new dataset for remote sensing image change detection. Remote Sens. 2020, 12, 1662. [Google Scholar] [CrossRef]
- Lebedev, M.; Vizilter, Y.V.; Vygolov, O.; Knyaz, V.; Rubis, A.Y. Change Detection in Remote Sensing Images Using Conditional Adversarial Networks. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 565–571. [Google Scholar] [CrossRef]
- Daudt, R.C.; Le Saux, B.; Boulch, A.; Gousseau, Y. Urban change detection for multispectral earth observation using convolutional neural networks. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 2115–2118. [Google Scholar]
- Fang, S.; Li, K.; Shao, J.; Li, Z. SNUNet-CD: A densely connected Siamese network for change detection of VHR images. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Bandara, W.G.C.; Patel, V.M. A transformer-based siamese network for change detection. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium. IEEE, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 207–210. [Google Scholar]
- Li, K.; Li, Z.; Fang, S. Siamese NestedUNet networks for change detection of high resolution satellite image. In Proceedings of the 2020 1st International Conference on Control, Robotics and Intelligent System, Xiamen, China, 27–29 October 2020; pp. 42–48. [Google Scholar]
- Ma, X.; Zhang, X.; Pun, M.O. A crossmodal multiscale fusion network for semantic segmentation of remote sensing data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3463–3474. [Google Scholar] [CrossRef]



| Stage | Outputs |
|---|---|
| Convolution | |
| Linear Embedding + VSS Blocks | |
| Patch Merging + VSS Blocks | |
| Patch Merging + VSS Blocks | |
| Patch Merging + VSS Blocks |
| Method | Recall | Precision | OA | F1 | IoU |
|---|---|---|---|---|---|
| FC-SC [12] | 71.10 | 78.62 | 94.55 | 74.67 | 58.87 |
| SNUNet [66] | 80.29 | 84.52 | 95.73 | 82.35 | 69.91 |
| BIT [22] | 90.75 | 86.38 | 97.13 | 88.51 | 79.30 |
| ChangeFormer [67] | 93.64 | 94.54 | 98.45 | 94.09 | 88.94 |
| GCD-DDPM [32] | 95.10 | 94.76 | 98.87 | 94.93 | 90.56 |
| IMDCD | 96.73 | 97.49 | 99.34 | 97.11 | 94.12 |
| Method | Recall | Precision | OA | F1 | IoU |
|---|---|---|---|---|---|
| FC-SC [12] | 86.54 | 72.03 | 98.42 | 78.62 | 64.37 |
| SNUNet [66] | 81.33 | 85.66 | 98.68 | 83.44 | 71.39 |
| BIT [22] | 87.94 | 89.98 | 99.30 | 88.95 | 81.53 |
| ChangeFormer [67] | 86.43 | 89.69 | 98.95 | 88.03 | 78.46 |
| GCD-DDPM [32] | 92.29 | 92.79 | 99.39 | 92.54 | 86.52 |
| IMDCD | 93.27 | 93.85 | 99.51 | 93.56 | 88.39 |
| Method | Recall | Precision | OA | F1 | IoU |
|---|---|---|---|---|---|
| FC-SC [12] | 77.29 | 89.04 | 98.25 | 82.75 | 69.95 |
| SNUNet [66] | 84.33 | 88.55 | 98.70 | 86.39 | 76.11 |
| BIT [22] | 87.85 | 90.26 | 98.83 | 89.04 | 80.12 |
| ChangeFormer [67] | 87.73 | 89.39 | 98.81 | 88.56 | 79.34 |
| GCD-DDPM [32] | 91.24 | 90.68 | 99.14 | 90.96 | 83.56 |
| IMDCD | 91.12 | 91.56 | 99.21 | 91.34 | 84.66 |
| Method | Recall | Precision | OA | F1 | IoU |
|---|---|---|---|---|---|
| FC-SC [12] | 54.83 | 47.97 | 94.55 | 51.17 | 34.33 |
| SNUNet [66] | 60.49 | 48.62 | 94.63 | 53.91 | 36.13 |
| BIT [22] | 50.09 | 65.64 | 94.63 | 56.82 | 40.26 |
| ChangeFormer [67] | 49.37 | 62.90 | 95.20 | 55.32 | 38.10 |
| GCD-DDPM [32] | 73.94 | 50.60 | 95.84 | 60.08 | 43.29 |
| IMDCD | 58.39 | 67.21 | 96.37 | 62.49 | 45.52 |
| VSS-CD | High-Dimensional | Low-Dimensional | OA | F1 | IoU |
|---|---|---|---|---|---|
| ✓ | ✓ | 99.37 | 92.61 | 86.47 | |
| ✓ | ✓ | 99.41 | 92.73 | 87.04 | |
| ✓ | ✓ | 99.38 | 92.45 | 86.67 | |
| ✓ | ✓ | ✓ | 99.51 | 93.56 | 88.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Wen, Y.; Sun, J.; Zhu, P.; Mao, L.; Niu, G.; Li, J. Iterative Mamba Diffusion Change-Detection Model for Remote Sensing. Remote Sens. 2024, 16, 3651. https://doi.org/10.3390/rs16193651
Liu F, Wen Y, Sun J, Zhu P, Mao L, Niu G, Li J. Iterative Mamba Diffusion Change-Detection Model for Remote Sensing. Remote Sensing. 2024; 16(19):3651. https://doi.org/10.3390/rs16193651
Chicago/Turabian StyleLiu, Feixiang, Yihan Wen, Jiayi Sun, Peipei Zhu, Liang Mao, Guanchong Niu, and Jie Li. 2024. "Iterative Mamba Diffusion Change-Detection Model for Remote Sensing" Remote Sensing 16, no. 19: 3651. https://doi.org/10.3390/rs16193651
APA StyleLiu, F., Wen, Y., Sun, J., Zhu, P., Mao, L., Niu, G., & Li, J. (2024). Iterative Mamba Diffusion Change-Detection Model for Remote Sensing. Remote Sensing, 16(19), 3651. https://doi.org/10.3390/rs16193651






