Rotational Motion Compensation for ISAR Imaging Based on Minimizing the Residual Norm
Abstract
1. Introduction
- An iterative optimization method is designed to estimate rotational parameters independently to address the issue in RMC algorithms where high-order parameter errors lead to the incorrect estimation of low-order parameters, as well as to improve the RMC performance more robustly.
- The residual norm of compensated signal phases after phase linear fitting is used instead of the Shannon entropy to evaluate image quality, reducing the computational complexity.
- An inverse function expression is derived with better accuracy in order to accomplish RMC.
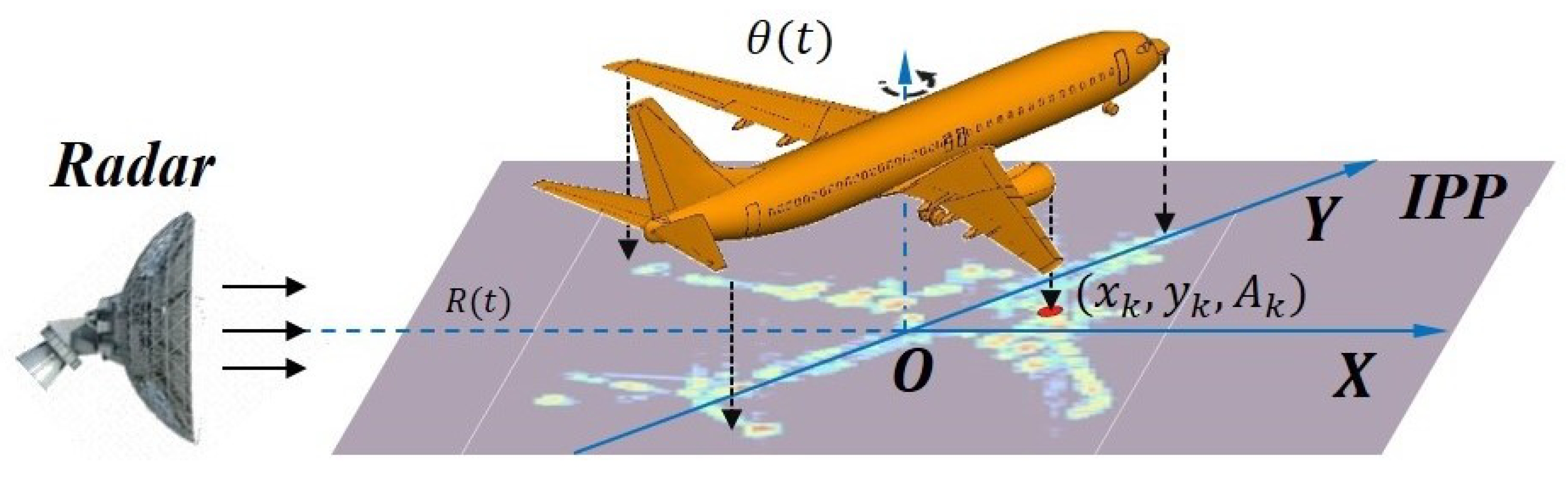
2. Signal Model
3. Proposed RMC Algorithm for ISAR Imaging
3.1. Rotational Motion Compensation Based on the Inverse Function Method
3.2. Rotational Parameter Estimation Based on the Minimum Residual Norm
3.3. Algorithm Summary
| Algorithm 1 Minimum residual norm search procedure |
|
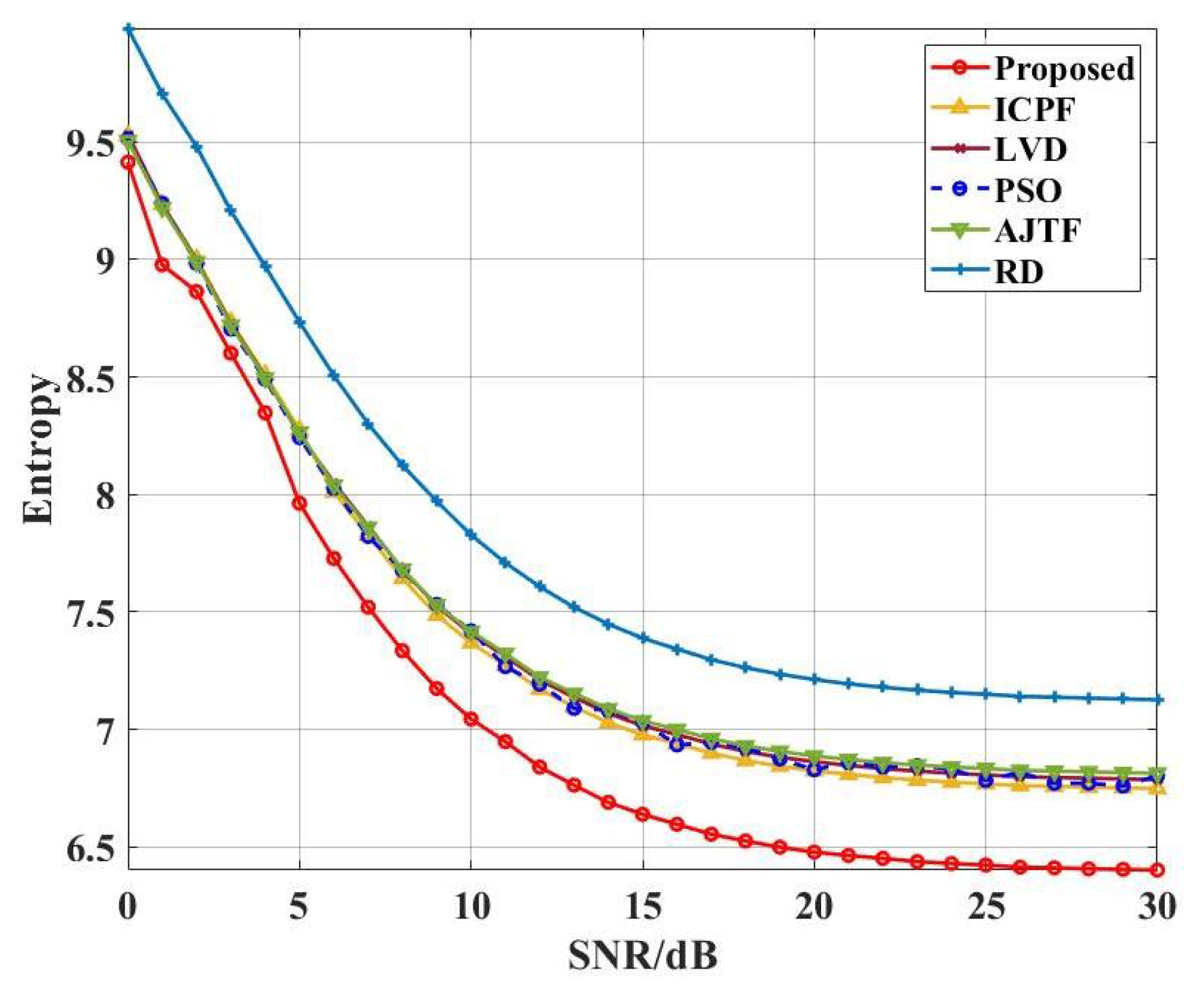
4. Simulation and Performance Evaluation and Verification
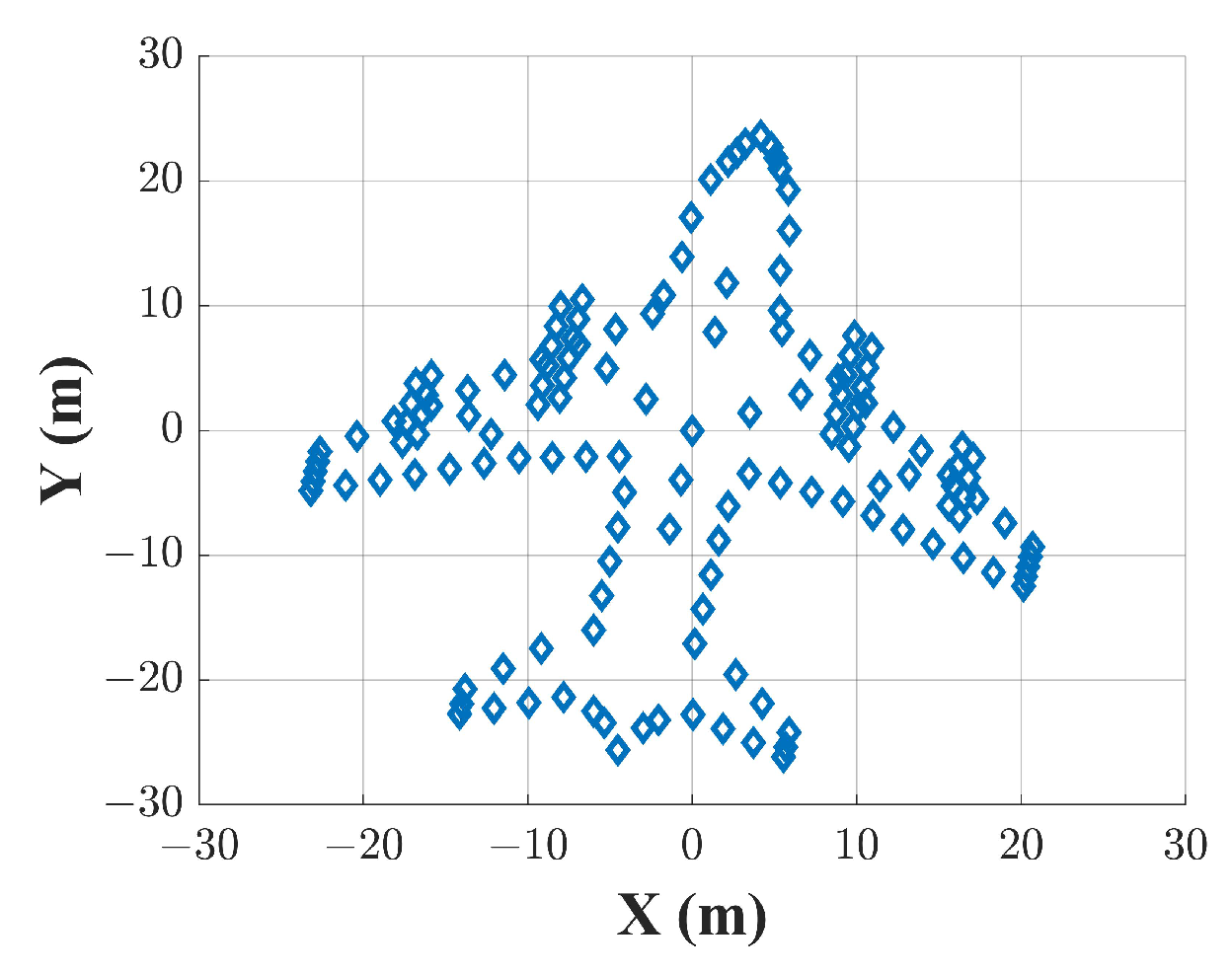
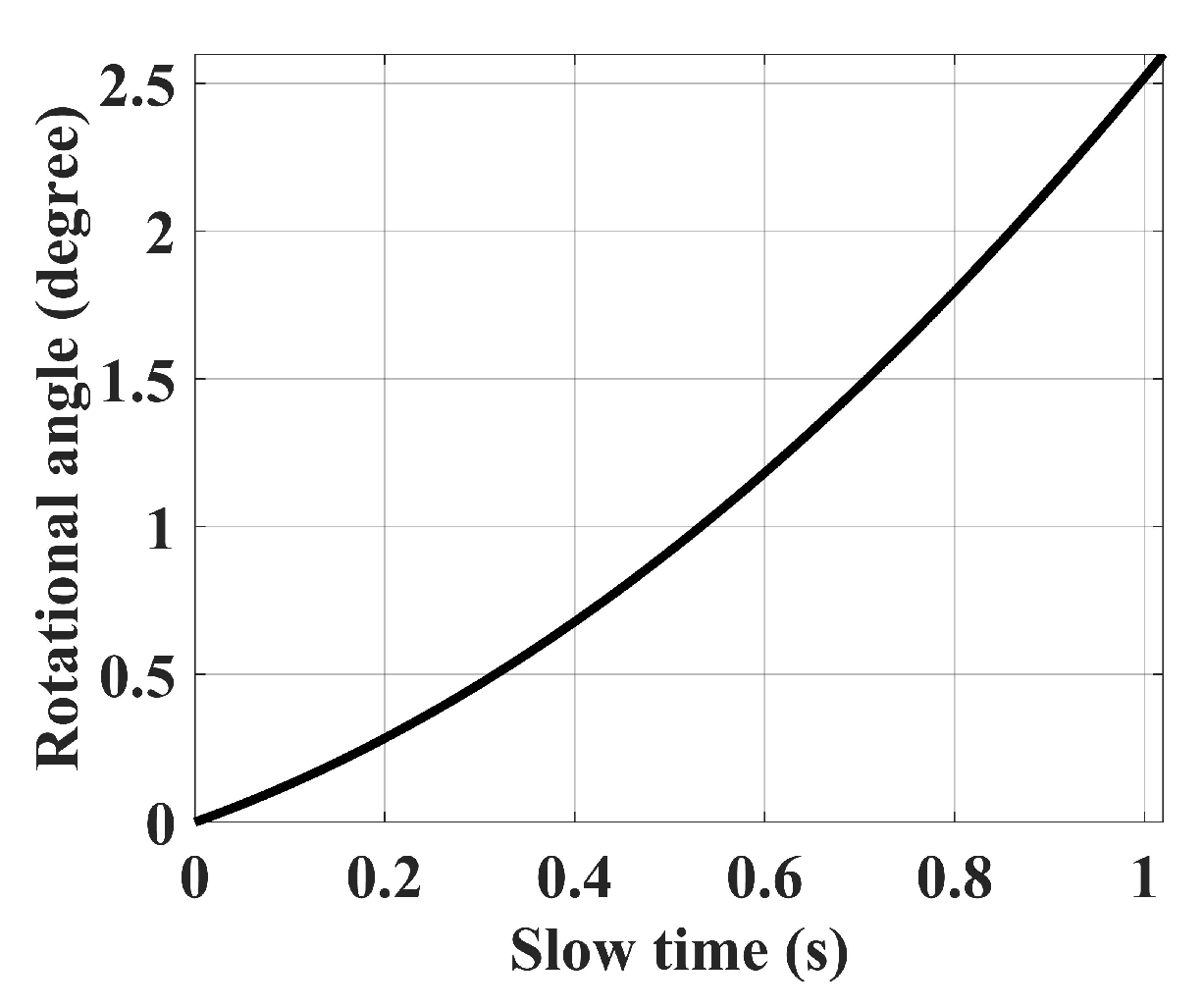
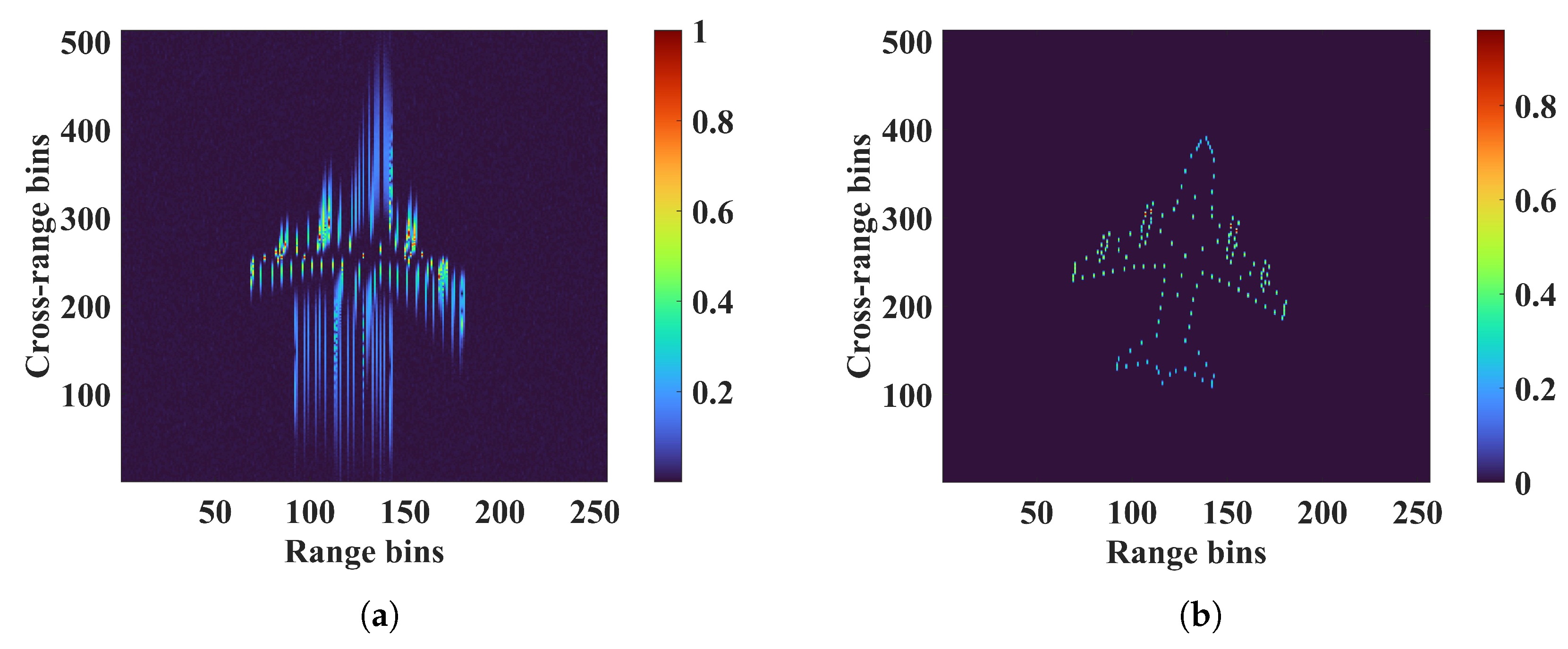
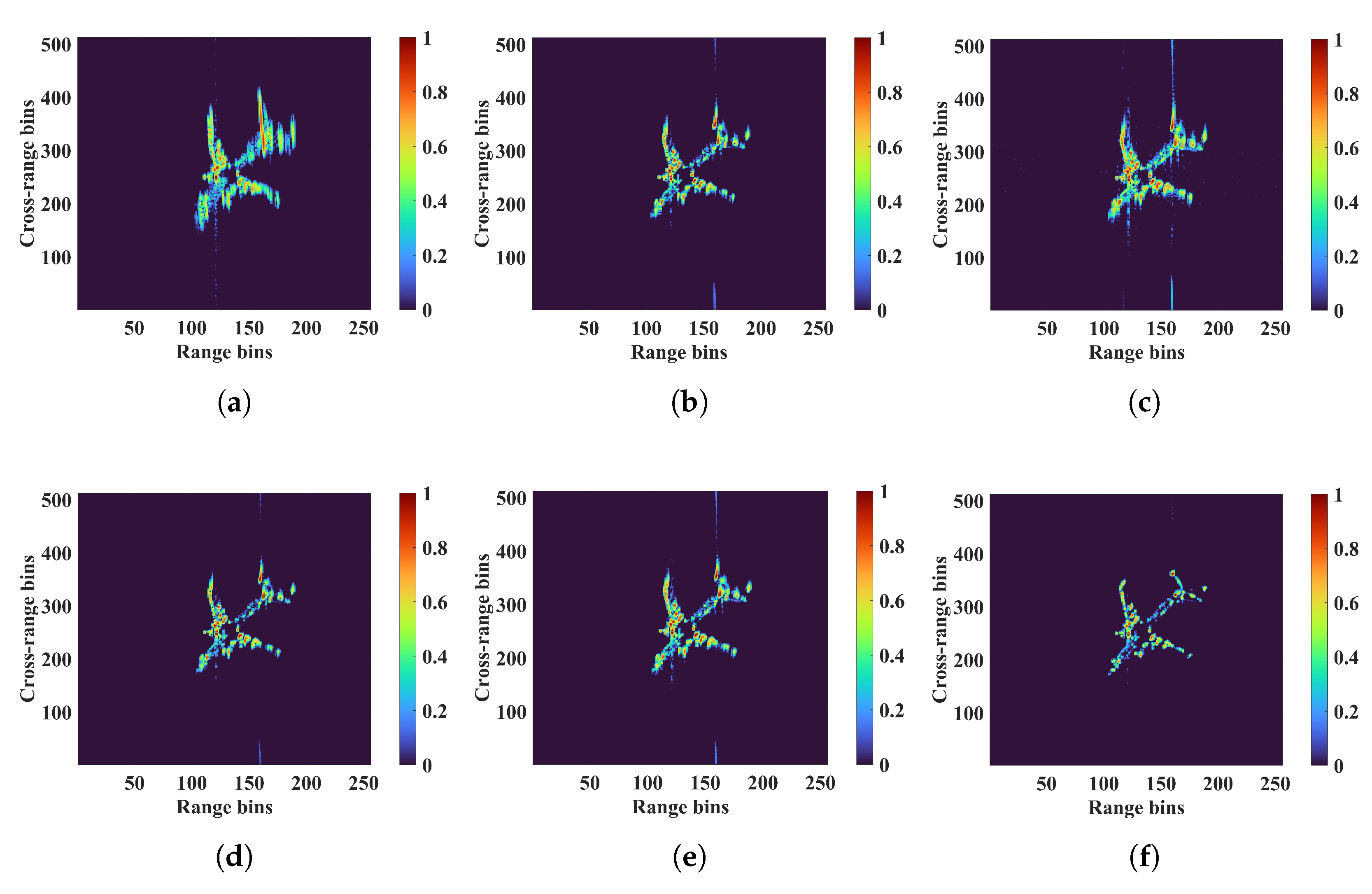
4.1. Simulation Data from an Ideal Point Scatter Target Model
4.2. Full-Wave Electromagnetic Simulation Data of an Airplane 3D Conducting Body Model
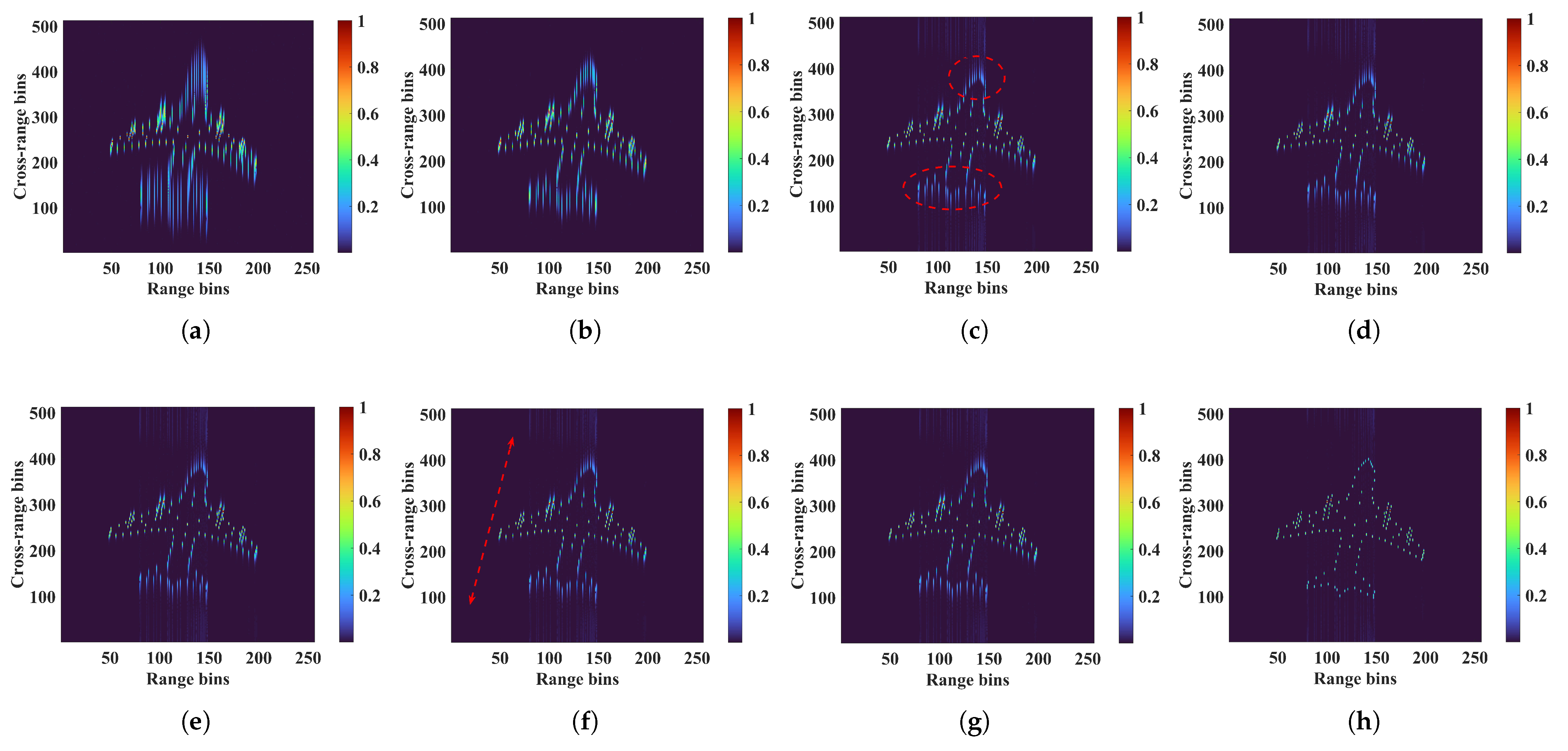
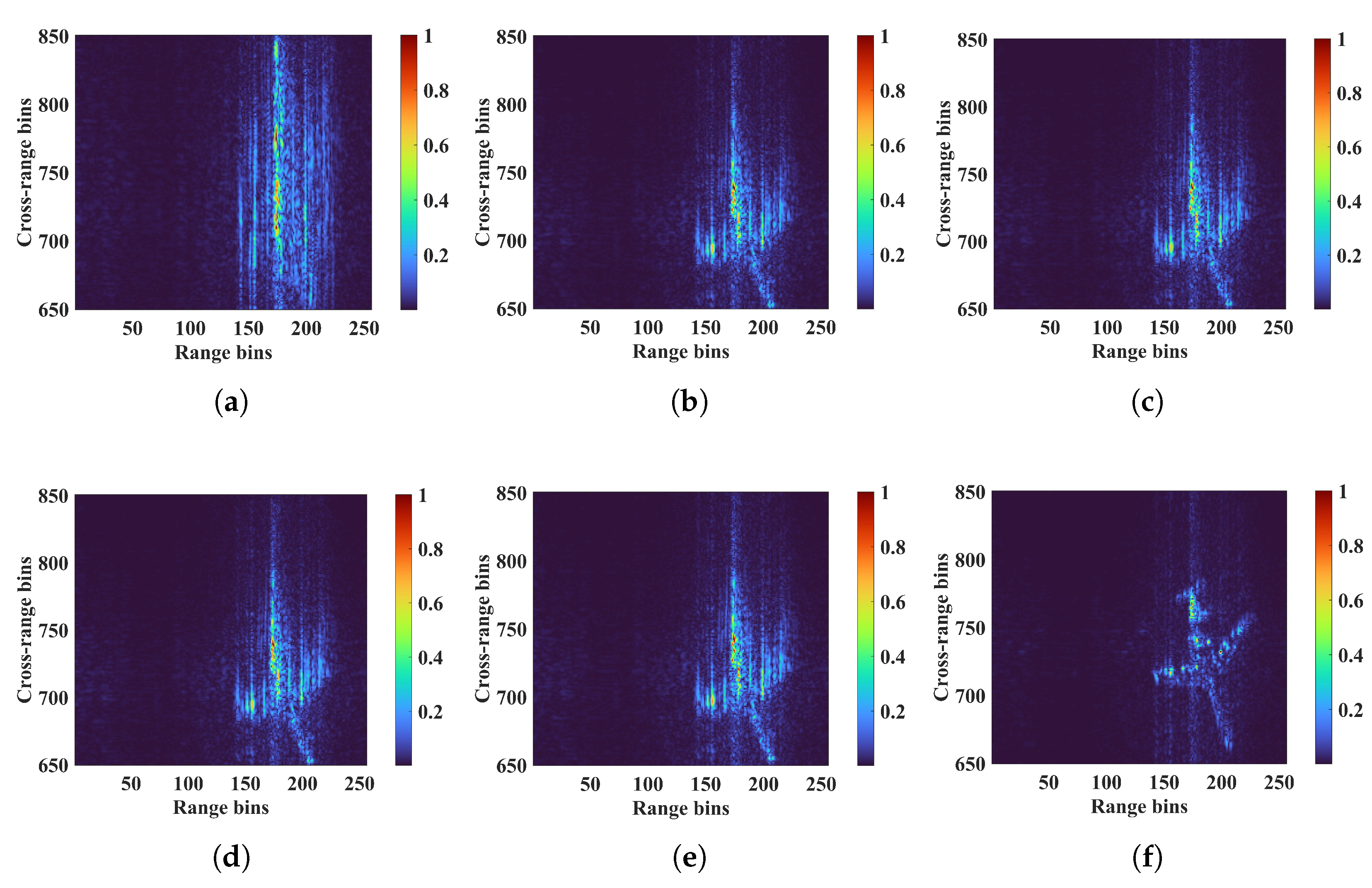
4.3. Actual Radar Measurement Data from an Aircraft Target
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Walker, J.L. Range-Doppler Imaging of Rotating Objects. IEEE Trans. Aerosp. Electron. Syst. 1980, AES–16, 23–52. [Google Scholar] [CrossRef]
- Berizzi, F.; Mese, E.D.; Diani, M.; Martorella, M. High-Resolution ISAR Imaging of Maneuvering Targets by Means of the Range Instantaneous Doppler Technique: Modeling and Performance Analysis. IEEE Trans. Image Process. 2001, 10, 1880–1890. [Google Scholar] [CrossRef]
- Li, J.; Wu, R.; Chen, V.C. Robust autofocus algorithm for ISAR imaging of moving targets. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 1056–1069. [Google Scholar] [CrossRef]
- Bai, X.; Tao, R.; Wang, Z.; Wang, Y. ISAR imaging of a ship target based on parameter estimation of multicomponent quadratic frequency-modulated signals. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1418–1429. [Google Scholar] [CrossRef]
- Guttavelli, A.; Rao, K. Comparison of various Algorithms for RD, RID and RIC methods using ISAR imaging. Int. J. Appl. Eng. Res. 2016, 11, 3364–3368. [Google Scholar]
- Zhu, D.; Wang, L.; Yu, Y.; Tao, Q.; Zhu, Z. Robust ISAR range alignment via minimizing the entropy of the average range profile. IEEE Geosci. Remote Sens. Lett. 2009, 6, 204–208. [Google Scholar]
- Kang, M.-S.; Bae, J.-H.; Lee, S.-H.; Kim, K.-T. Efficient ISAR autofocus via minimization of Tsallis Entropy. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2950–2960. [Google Scholar] [CrossRef]
- Xia, S.; Wang, Y.; Zhang, J.; Dai, F. High-Speed Maneuvering Target Inverse Synthetic Aperture Radar Imaging and Motion Parameter Estimation Based on Fast Spare Bayesian Learning and Minimum Entropy. Remote Sens. 2023, 15, 3376. [Google Scholar] [CrossRef]
- Liu, C.; Luo, Y.; Yu, Z.; Feng, J. ISAR Imaging of Non-Stationary Moving Target Based on Parameter Estimation and Sparse Decomposition. Remote Sens. 2023, 15, 2368. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, W.; Chen, Z.; Zhao, Z.; Hu, H.; Qi, C. A Novel Adaptive Joint Time Frequency Algorithm by the Neural Network for the ISAR Rotational Compensation. Remote Sens. 2018, 10, 334. [Google Scholar] [CrossRef]
- Li, W.; Yuan, Y.; Zhang, Y.; Luo, Y. Unblurring ISAR Imaging for Maneuvering Target Based on UFGAN. Remote Sens. 2022, 14, 5270. [Google Scholar] [CrossRef]
- Shi, H.; Yang, T.; Qiao, Z. ISAR Autofocus Imaging Algorithm for Maneuvering Targets Based on Phase Retrieval and Gabor Wavelet Transform. Remote Sens. 2018, 10, 1810. [Google Scholar] [CrossRef]
- Bao, Z.; Sun, C.; Xing, M. Time-frequency approaches to ISAR imaging of maneuvering targets and their limitations. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 1091–1099. [Google Scholar]
- Wang, Y. Inverse synthetic aperture radar imaging of manoeuvring target based on range-instantaneous-Doppler and range-instantaneous-chirp-rate algorithms. IET Radar Sonar Navig. 2012, 6, 921–928. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, X.; Zhang, Q. Rotation parameters estimation and cross-range scaling research for range instantaneous doppler ISAR images. IEEE Sens. J. 2020, 20, 7010–7020. [Google Scholar] [CrossRef]
- Kang, K.-B.; Kang, B.-S.; Park, S.-H.; Kim, K.-T. Efficient ISAR imaging approach for nonuniformly rotating targets based on ICPF-PPP. IEEE Trans. Image Process. 2022, 58, 5944–5953. [Google Scholar] [CrossRef]
- Li, D.; Gui, X.; Liu, H.; Su, J.; Xiong, H. An ISAR imaging algorithm for maneuvering targets with low SNR based on parameter estimation of multicomponent quadratic FM signals and nonuniform FFT. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5688–5702. [Google Scholar] [CrossRef]
- Huang, P.; Xia, X.-G.; Zhan, M.; Liu, X.; Liao, G.; Jiang, X. ISAR imaging of a maneuvering target based on parameter estimation of multicomponent cubic phase signals. IEEE Trans. Geosci. Remote Sens. 2022, 660, 1–18. [Google Scholar] [CrossRef]
- Li, D.; Zhan, M.; Zhang, X.; Fang, Z.; Liu, H. ISAR imaging of nonuniformly rotating target based on the multicomponent CPS model under low SNR environment. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1119–1135. [Google Scholar] [CrossRef]
- Lv, Q.; Su, T.; He, X. An ISAR imaging algorithm for nonuniformly rotating targets with low SNR based on modified bilinear parameter estimation of cubic phase signal. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 3108–3124. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Zheng, J.; Niu, J.; Zhou, Y.; Meng, N. ISAR imaging of nonuniformly rotating targets with low SNR based on third order autocorrelation function. IEEE Access 2020, 8, 74707–74719. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Zhou, Y.; Niu, J.; Wang, L.; Meng, N.; Zheng, J. ISAR imaging of nonuniformly rotating targets with low SNR based on coherently integrated nonuniform trilinear autocorrelation function. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1074–1078. [Google Scholar] [CrossRef]
- Wu, W.; Xu, S.; Hu, P.; Zou, J.; Chen, Z. Inverse Synthetic Aperture Radar Imaging of Targets with Complex Motion based on Optimized Non-Uniform Rotation Transform. Remote Sens. 2018, 10, 593. [Google Scholar] [CrossRef]
- Thayaparan, T.; Brinkman, W.; Lampropoulos, G. Inverse synthetic aperture radar image focusing using fast adaptive joint time-frequency and three-dimensional motion detection on experimental radar data. IET Radar Sonar Navig. 2010, 4, 382–394. [Google Scholar] [CrossRef]
- Brinkman, W.; Thayaparan, T. Focusing inverse synthetic aperture radar images with higher-order motion error using the adaptive joint-time frequency algorithm optimized with the genetic algorithm and the particle swarm optimization algorithm comparison and results. IET Signal Process. 2009, 3, 329–342. [Google Scholar]
- Liu, L.; Zhou, F.; Tao, M.L.; Zhao, B.; Zhang, Z.J. Cross-range scaling method of inverse synthetic aperture radar image based on discrete polynomial-phase transform. IET Radar Sonar Navig. 2015, 9, 333–341. [Google Scholar] [CrossRef]
- Kang, B.-S.; Bae, J.-H.; Lee, S.-J.; Kim, C.-H.; Kim, K.-T. Isar rotational motion compensation algorithm using polynomial phase transform. Microw. Opt. Technol. Lett. 2016, 58, 1551–1557. [Google Scholar] [CrossRef]
- Ozdemir, C. Inverse Synthetic Aperture Radar with MATLAB Algorithms, 2nd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- De Luigi, C.; Jauffret, C. Estimation and classification of FM signals using time frequency transforms. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 421–437. [Google Scholar] [CrossRef]
- Peleg, S.; Friedlander, B. The discrete polynomial-phase transform. IEEE Trans. Signal Process. 1995, 43, 1901–1914. [Google Scholar] [CrossRef]
- Wang, P.; Li, H.; Djurović, I.; Himed, B. Integrated Cubic Phase Function for Linear FM Signal Analysis. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 963–977. [Google Scholar] [CrossRef]
- Ramos, C.J.; Martins, A.P.; Carvalho, A.S. Frequency and Phase-Angle Estimation Using Ordinary Least Squares. IEEE Trans. Ind. Electron. 2015, 62, 5677–5688. [Google Scholar] [CrossRef]
- Long, T.; Jiao, W.; He, G. RPC Estimation via ℓ1-Norm-Regularized Least Squares (L1LS). IEEE Trans. Geosci. Remote Sens. 2015, 53, 4554–4567. [Google Scholar] [CrossRef]
- Zuo, L.; Wang, B. ISAR imaging of non-uniform rotating targets based on optimized matching Fourier transform. IEEE Access 2020, 8, 64324–64330. [Google Scholar] [CrossRef]
- Yun, T.; Pan, Q.; Hao, Y.; Xu, R. Target recognition algorithm based on HRRP time-spectrogram feature and multi-scale asymmetric convolutional neural network. J. Northwest. Polytech. Univ. 2023, 43, 537–545. [Google Scholar] [CrossRef]

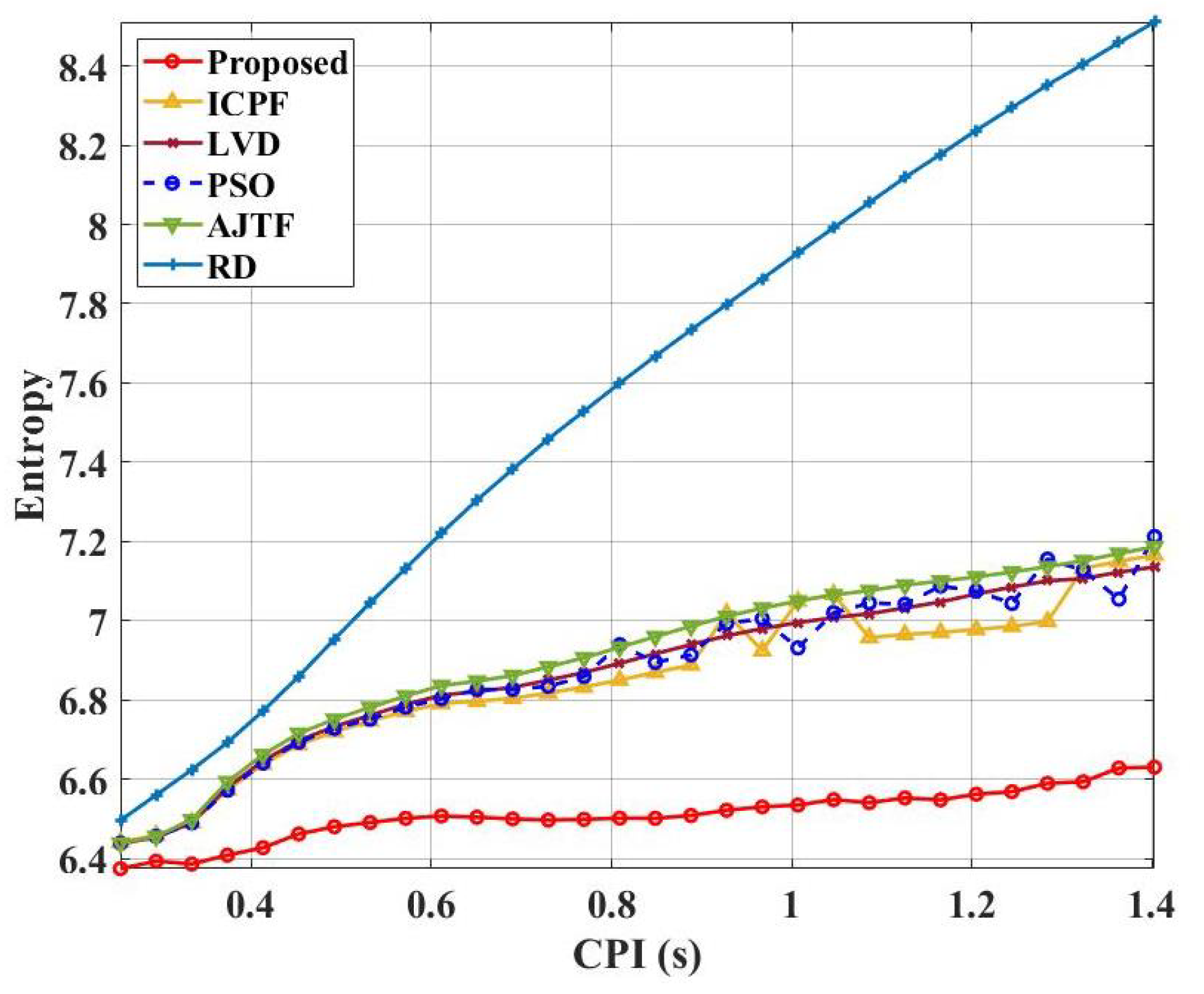
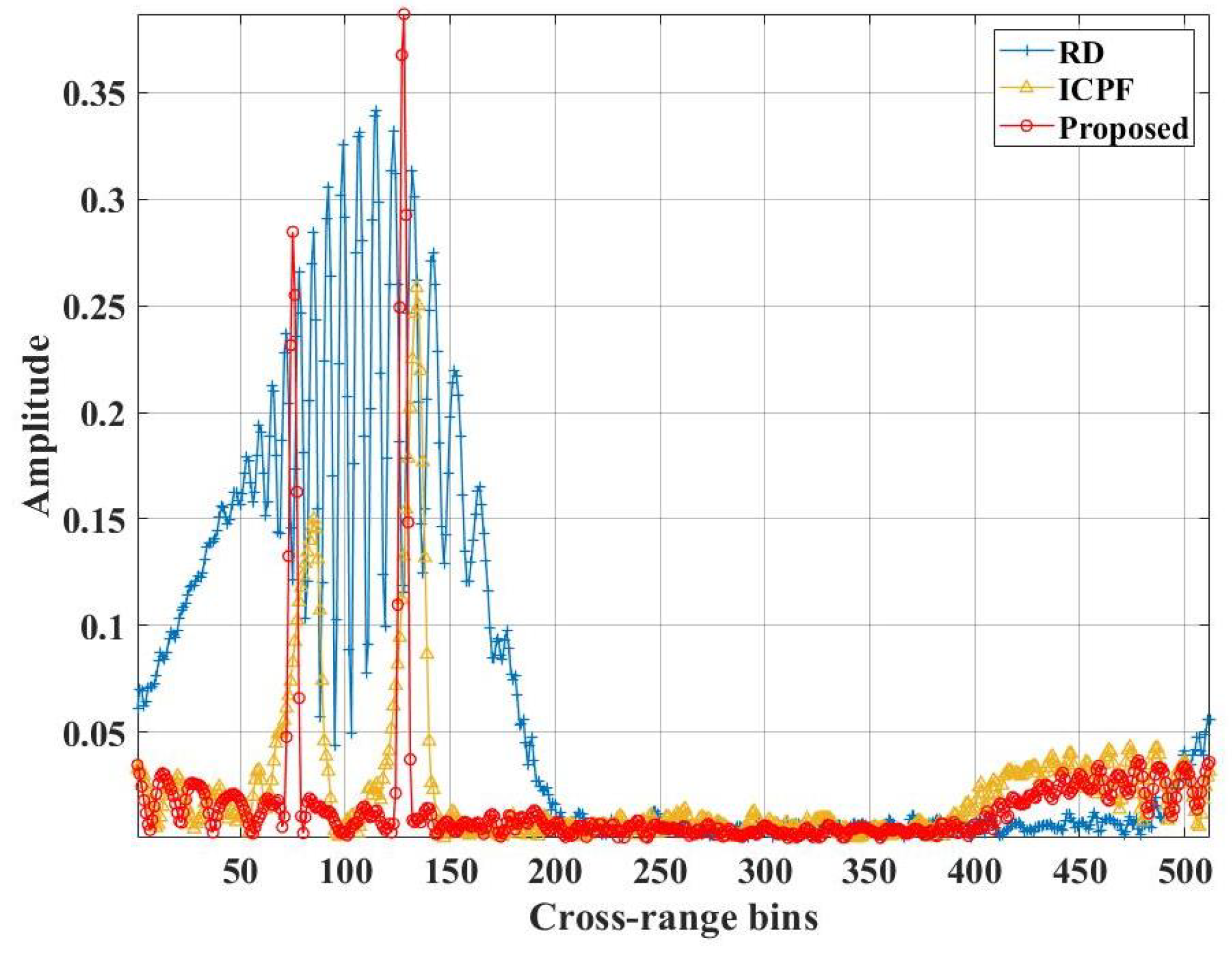
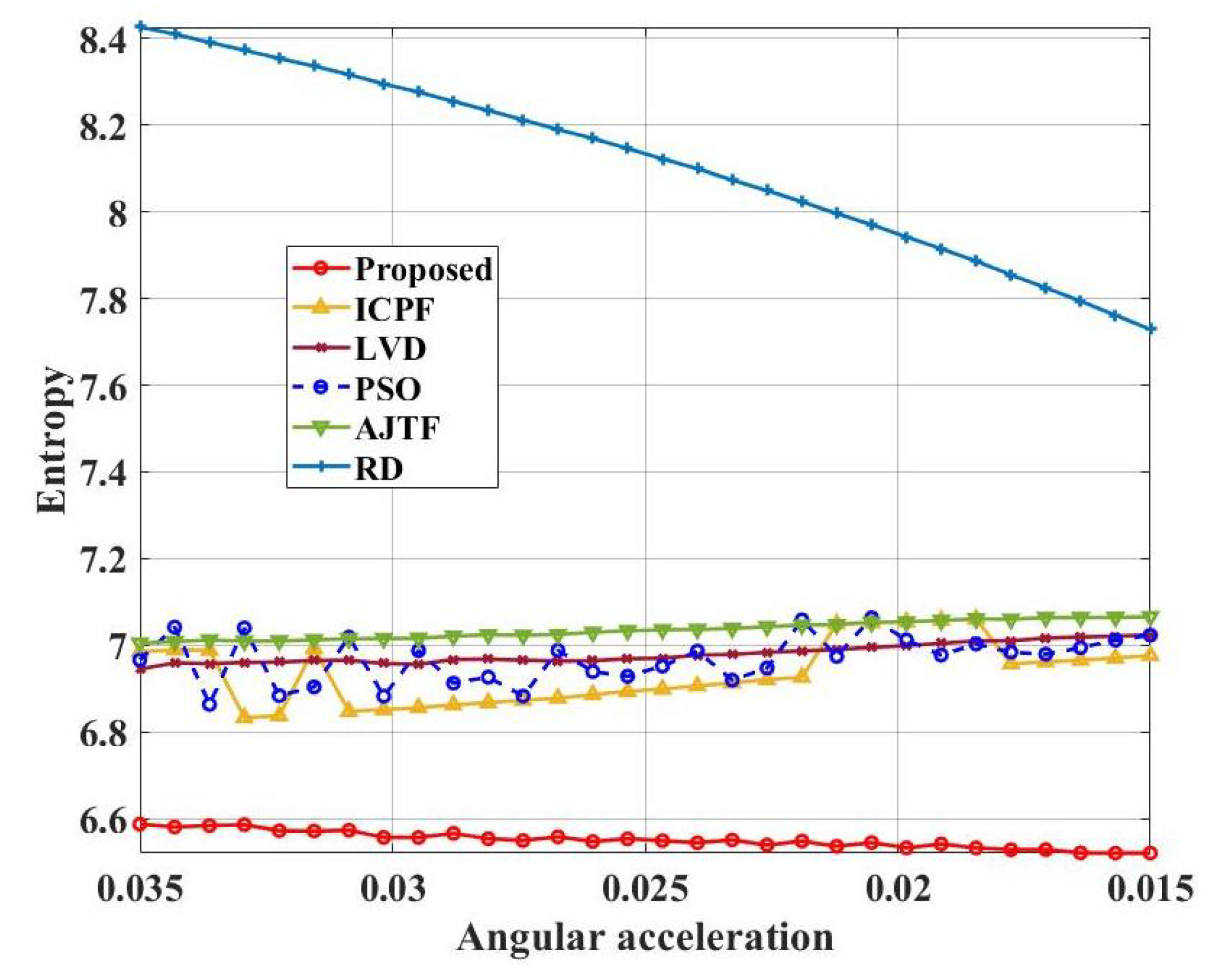

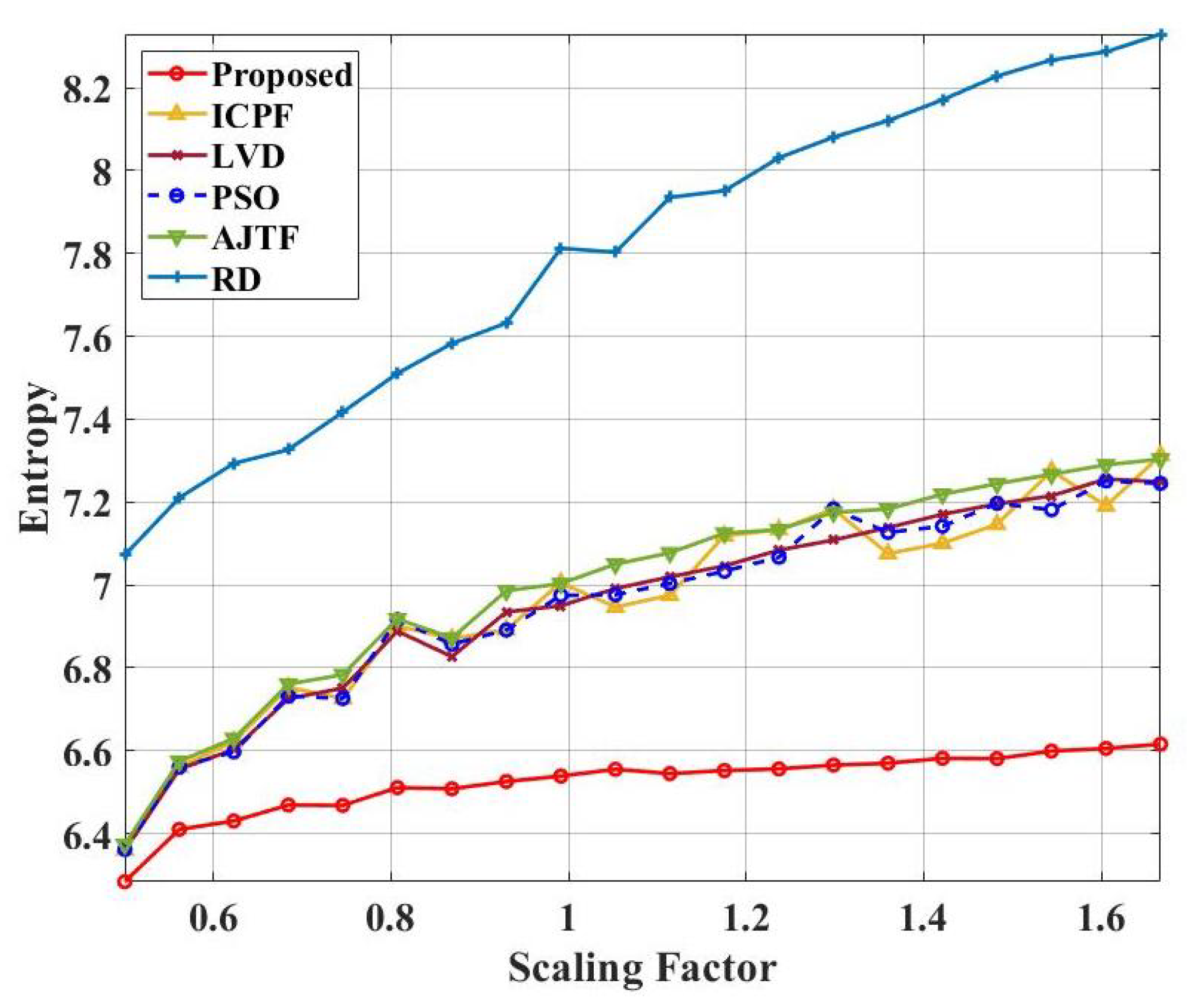


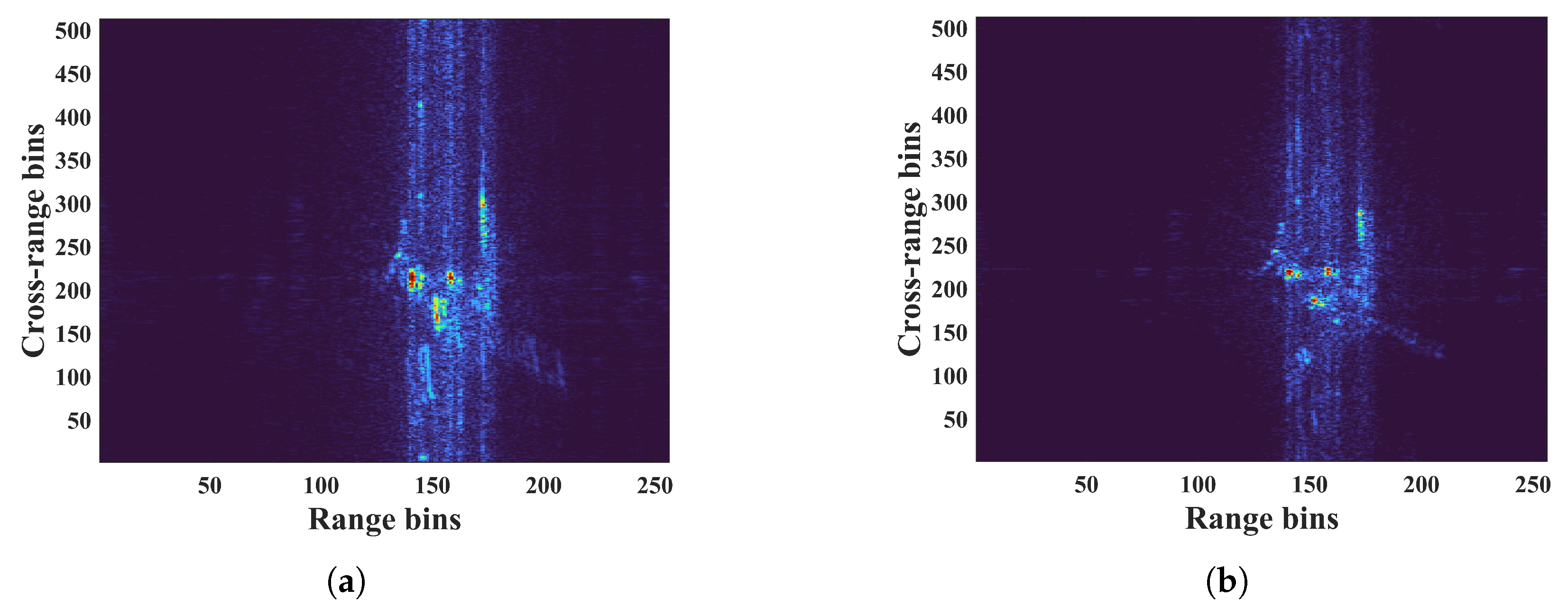
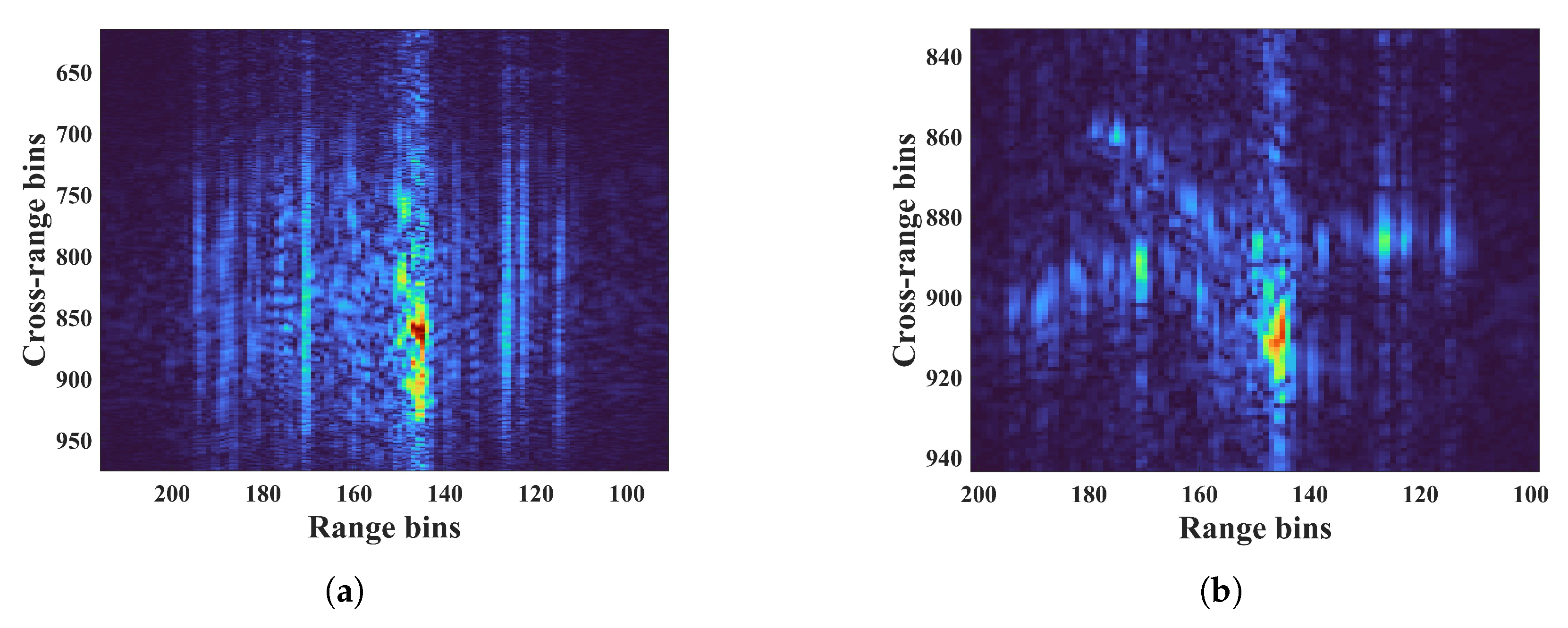
| Parameters | Values |
|---|---|
| Carrier frequency | 10 GHz |
| Range bandwidth | 400 MHz |
| CPI | 1.02 s |
| SNR | 20 dB |
| Pulse duration time | 4 ms |
| Number of bursts | 256 |
| Angular velocity | 0.020 rad/s |
| Angular acceleration | 0.048 rad/s2 |
| Algorithms | Stretched Values | Entropies | Computation Time |
|---|---|---|---|
| RD | 147.25 | 8.11 | / |
| RID | 121.96 | 7.74 | / |
| AJTF | 99.54 | 7.19 | 19.40 s |
| PSO | 87.91 | 7.18 | 6.83 s |
| LVD | 94.30 | 7.14 | 0.88 s |
| ICPF | 85.85 | 7.09 | 1.15 s |
| Replaced method | 91.65 | 7.07 | 0.42 s |
| Proposed | 11.35 | 6.49 | 0.52 s |
| Parameters | Values |
|---|---|
| Carrier frequency | 10 GHz |
| Range bandwidth | 400 MHz |
| CPI | 1.1475 s |
| SNR | 20 dB |
| Pulse duration time | 4.5 ms |
| Number of bursts | 256 |
| Angular velocity | 0.025 rad/s |
| Angular acceleration | 0.050 rad/s2 |
| Target wingspan | 28.45 m |
| Target length | 37.81 m |
| Target height | 11.1 m |
| Algorithms | Entropies | Computation Time |
|---|---|---|
| RD | 7.2140 | / |
| AJTF | 6.8873 | 20.3997 s |
| PSO | 6.8458 | 8.1070 s |
| LVD | 6.8625 | 0.8875 s |
| ICPF | 6.8250 | 0.9443 s |
| Proposed | 6.4782 | 0.9154 s |
| Algorithms | Entropies | Computation Time |
|---|---|---|
| RD | 9.1249 | / |
| AJTF | 8.6648 | 84.7111 s |
| PSO | 8.6624 | 8.6455 s |
| LVD | 8.6579 | 61.9058 s |
| ICPF | 8.6498 | 6.3751 s |
| Proposed | 8.0015 | 7.7714 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Sheng, W.; Xie, A.; Zhang, R. Rotational Motion Compensation for ISAR Imaging Based on Minimizing the Residual Norm. Remote Sens. 2024, 16, 3629. https://doi.org/10.3390/rs16193629
Yang X, Sheng W, Xie A, Zhang R. Rotational Motion Compensation for ISAR Imaging Based on Minimizing the Residual Norm. Remote Sensing. 2024; 16(19):3629. https://doi.org/10.3390/rs16193629
Chicago/Turabian StyleYang, Xiaoyu, Weixing Sheng, Annan Xie, and Renli Zhang. 2024. "Rotational Motion Compensation for ISAR Imaging Based on Minimizing the Residual Norm" Remote Sensing 16, no. 19: 3629. https://doi.org/10.3390/rs16193629
APA StyleYang, X., Sheng, W., Xie, A., & Zhang, R. (2024). Rotational Motion Compensation for ISAR Imaging Based on Minimizing the Residual Norm. Remote Sensing, 16(19), 3629. https://doi.org/10.3390/rs16193629






