Measuring Biophysical Parameters of Wheat Canopy with MHz- and GHz-Frequency Range Impulses Employing Contactless GPR
Abstract
1. Introduction
2. Methodology of In Situ and Remote Sensing Measurement
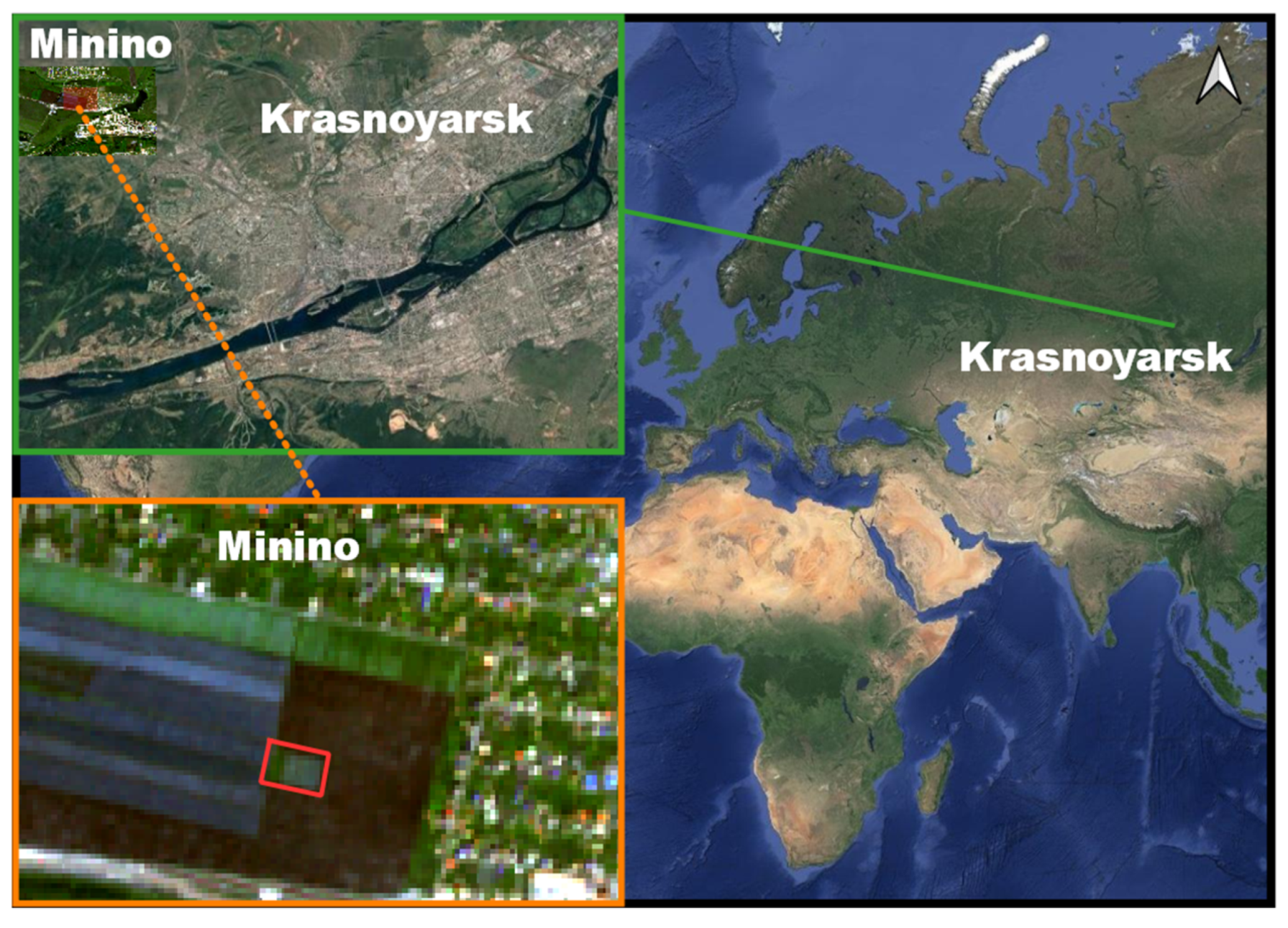
2.1. Test Field and In Situ Measurement
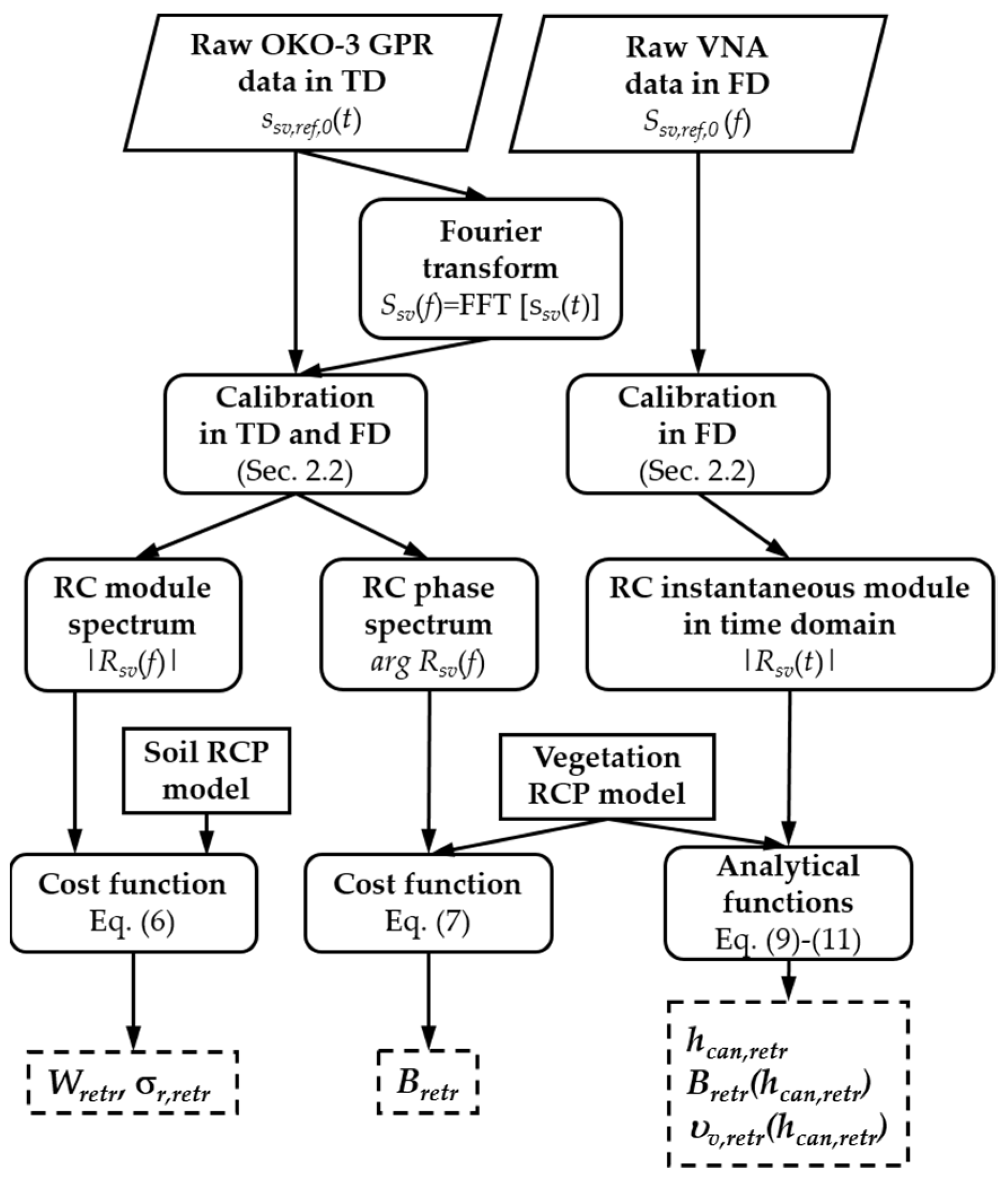
2.2. Methodology of Remote Sensing Measurement
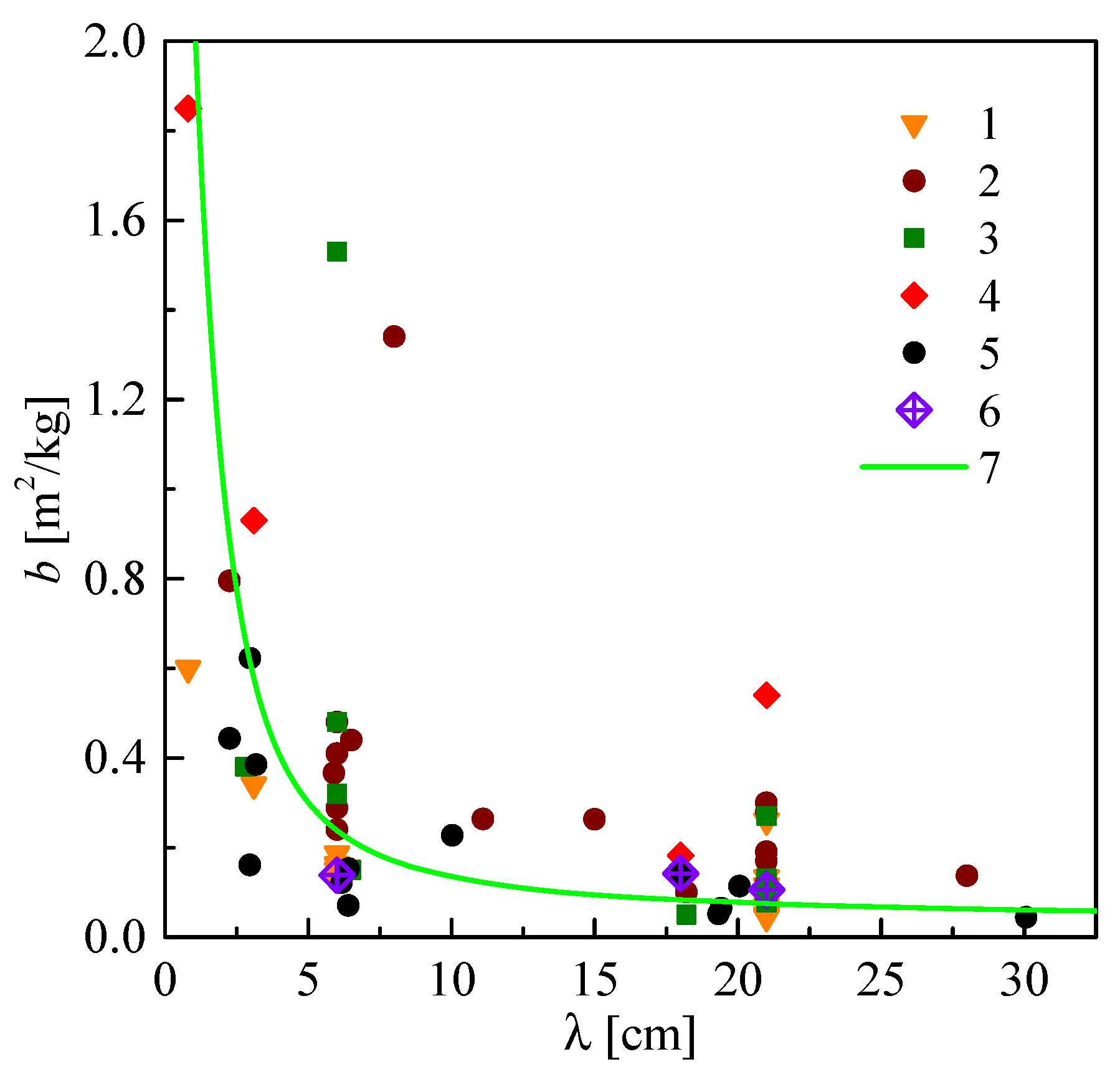
2.3. Model of the Reflection Coefficient and Dielectric Model of the Canopy
2.4. Algorithm for Measuring Soil Moisture and Surface Roughness, Canopy Height, and Biomass
3. Results
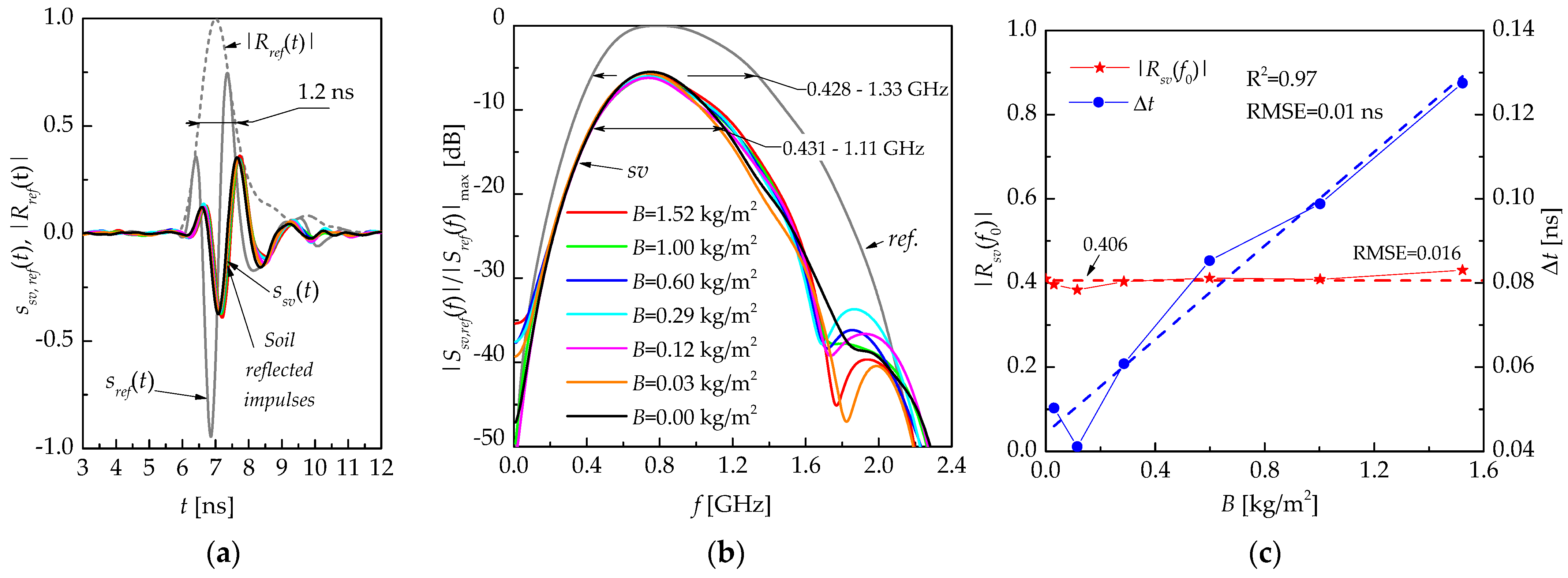
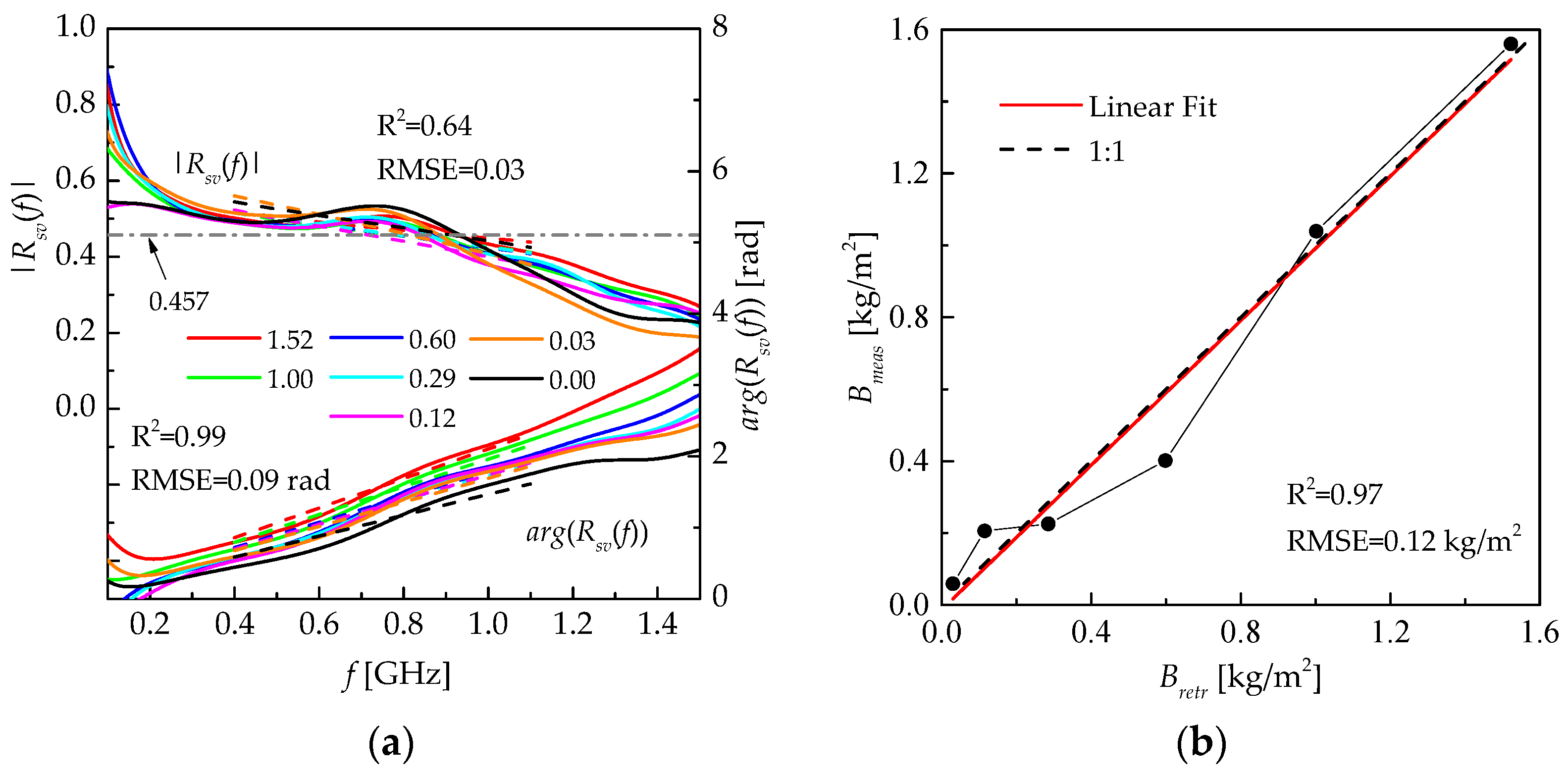
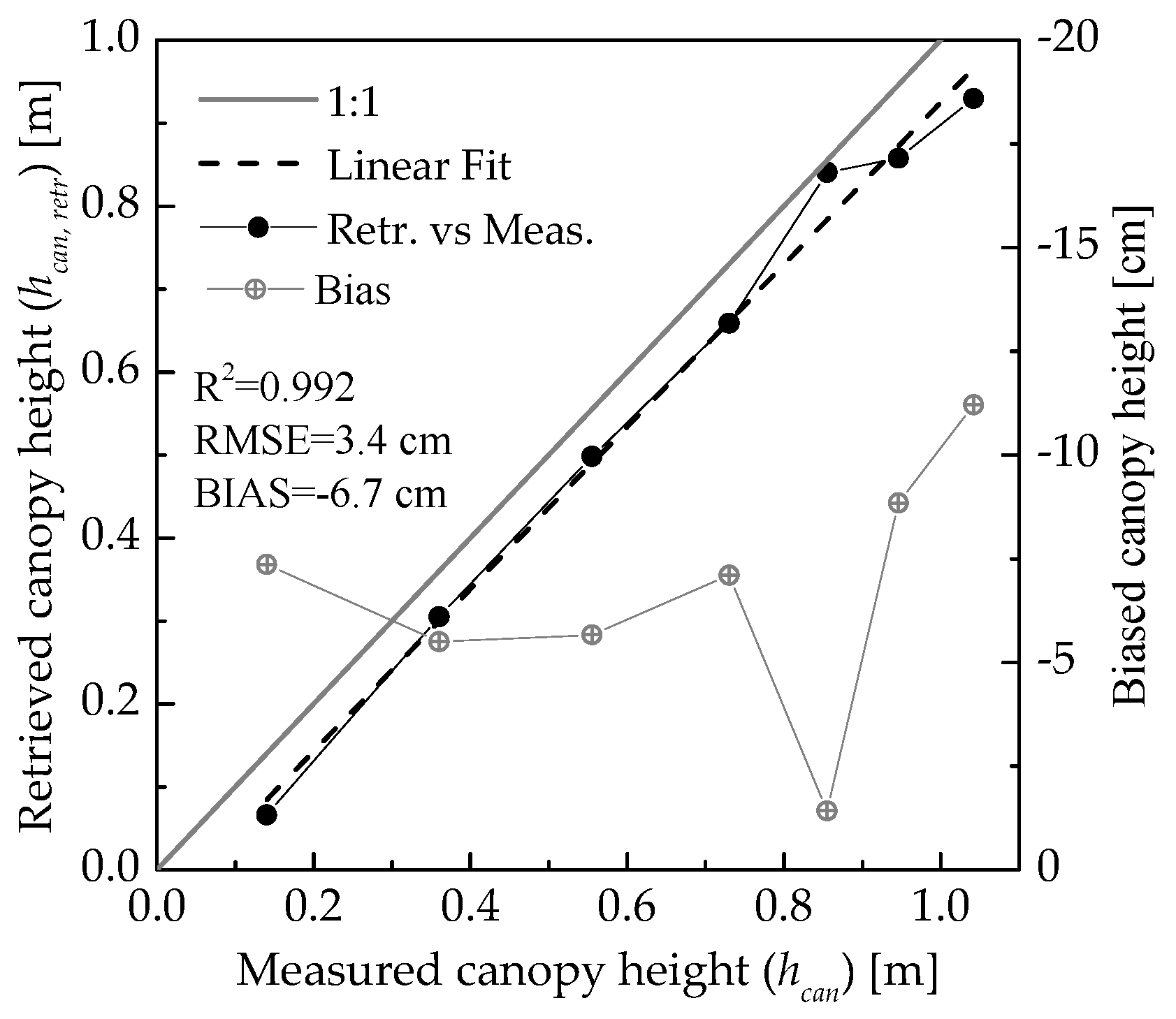
3.1. Experiment in the MHz-Frequency Range
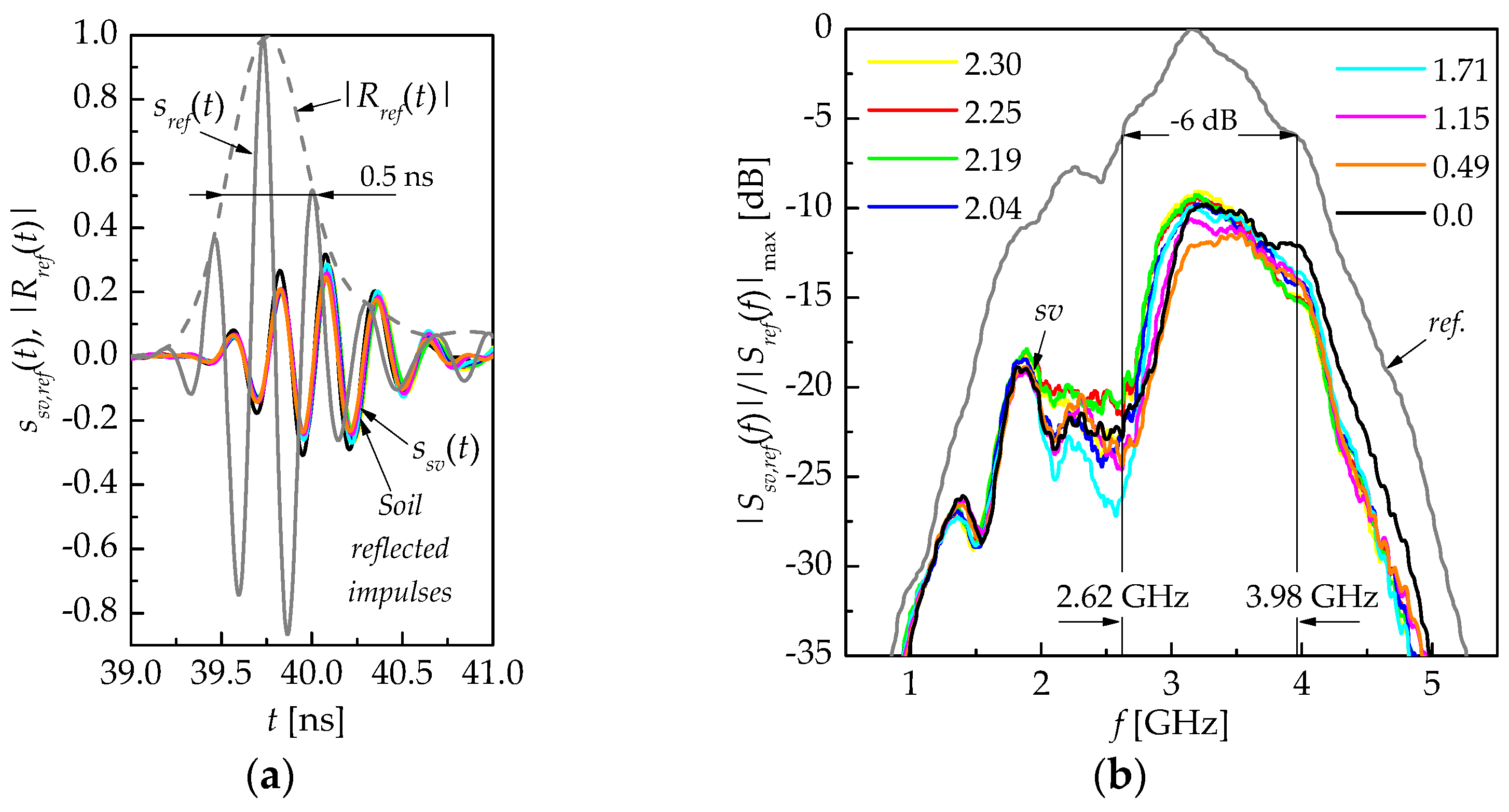
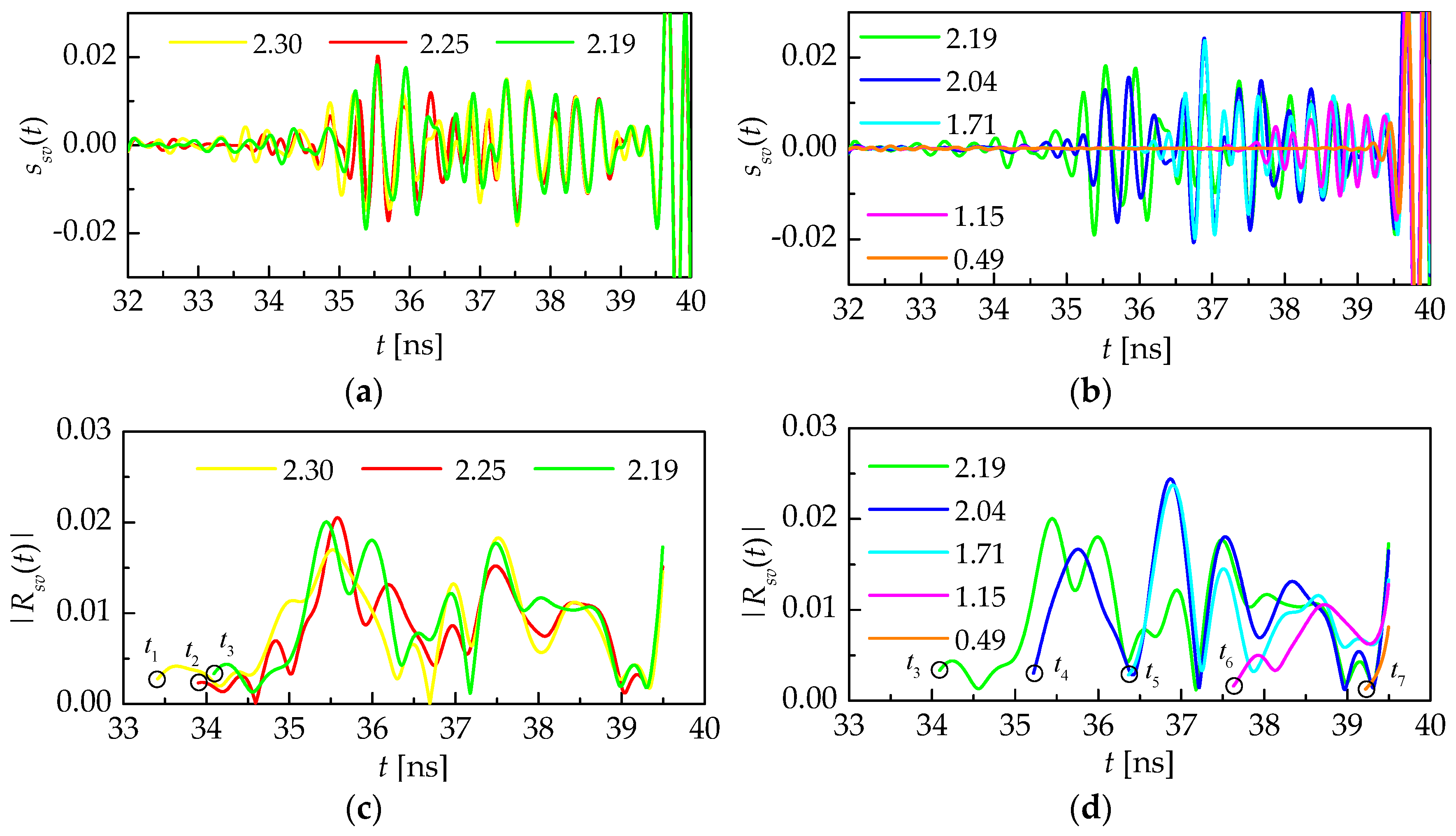
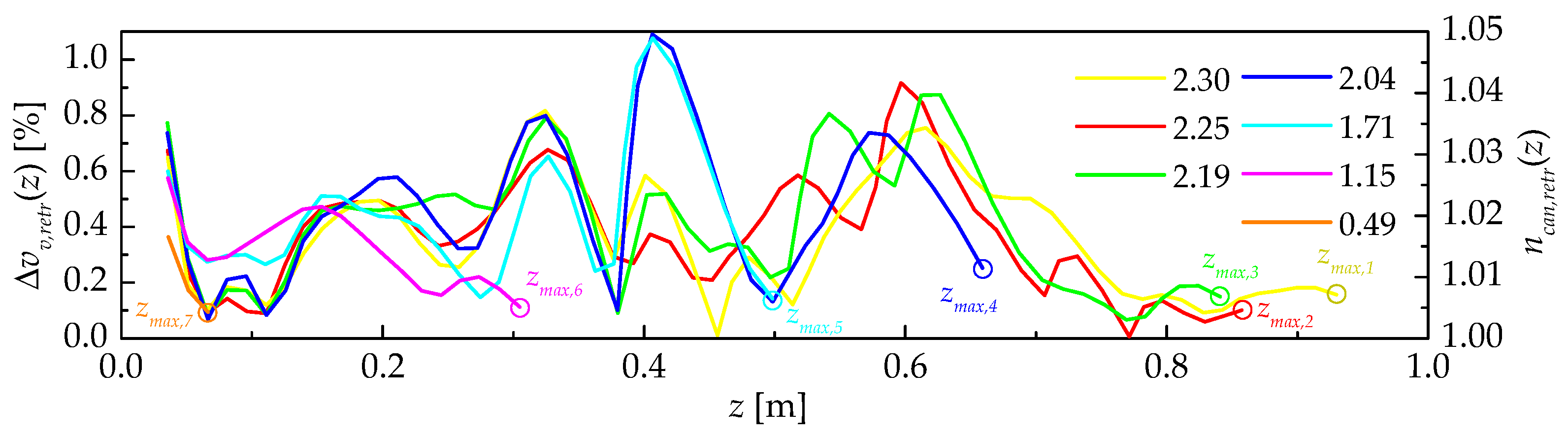
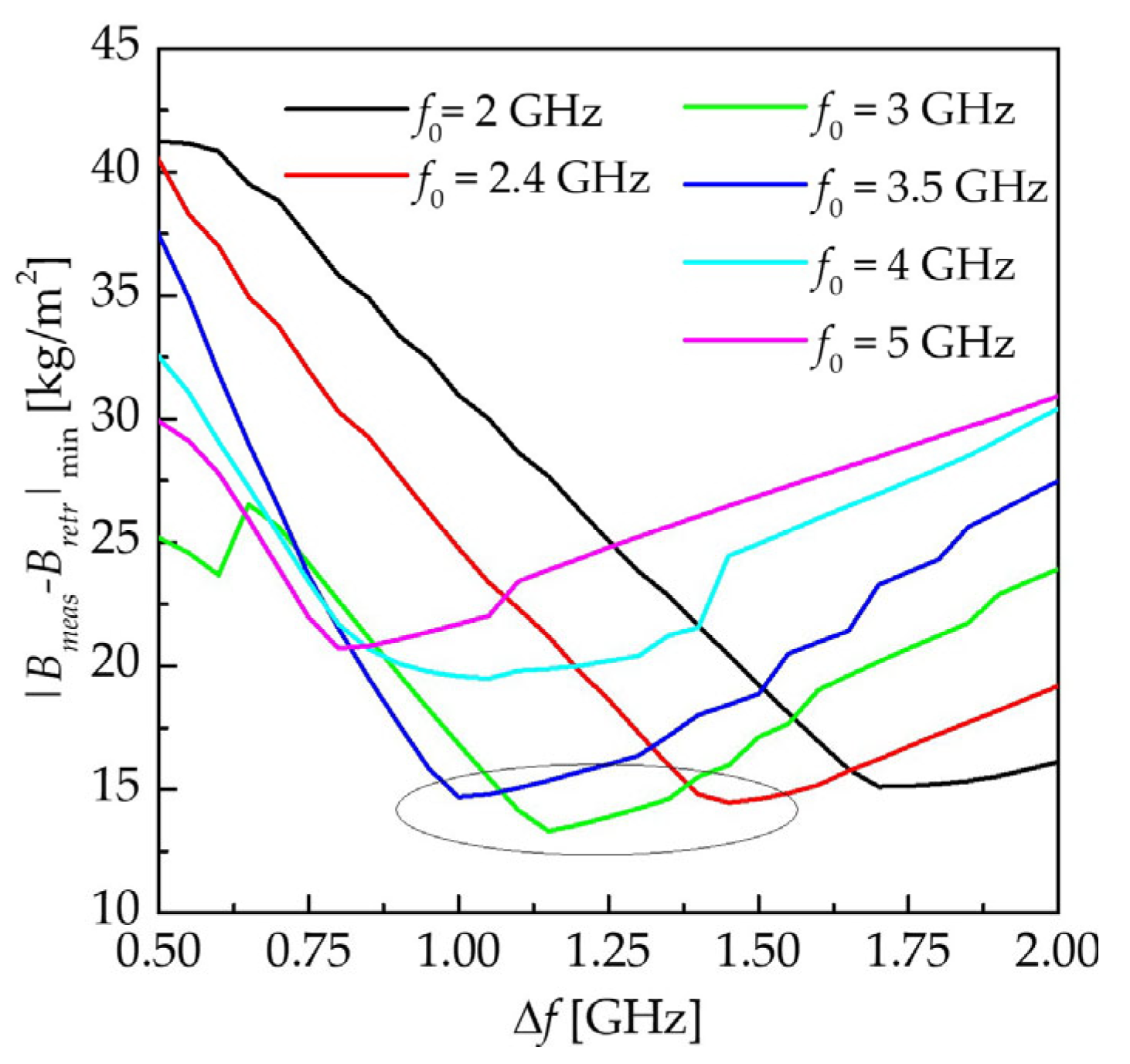
3.2. Experiment in GHz-Frequency Range
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khang, A. (Ed.) Handbook of Research on AI-Equipped IoT Applications in High-Tech Agriculture; IGI Global: Hershey, PA, USA, 2023; 473p. [Google Scholar]
- Zaman, Q. (Ed.) Precision Agriculture Evolution, Insights and Emerging Trends; Academic Press: Cambridge, MA, USA; Elsevier: Amsterdam, The Netherlands, 2023; 260p. [Google Scholar]
- Cognitive Technologies. Available online: https://cognitivepilot.com/breaking-news/vopros-otvet-o-rabote-novogo-avtopilota-na-traktorah-kirovecz-k-7m/ (accessed on 1 July 2024).
- Wang, D.; Li, R.; Zhu, B.; Liu, T.; Sun, C.; Guo, W. Estimation of Wheat Plant Height and Biomass by Combining UAV Imagery and Elevation Data. Agriculture 2023, 13, 9. [Google Scholar] [CrossRef]
- Kümmerer, R.; Noack, P.O.; Bauer, B. Using High-Resolution UAV Imaging to Measure Canopy Height of Diverse Cover Crops and Predict Biomass. Remote Sens. 2023, 15, 1520. [Google Scholar] [CrossRef]
- Shafiee, S.; Mroz, T.; Burud, I.; Lillemo, M. Evaluation of UAV multispectral cameras for yield and biomass prediction in wheat under different sun elevation angles and phenological stages. Comput. Electron. Agric. 2023, 210, 107874. [Google Scholar] [CrossRef]
- Harkel, J.T.; Bartholomeus, H.; Kooistra, L. Biomass and Crop Height Estimation of Different Crops Using UAV-Based Lidar. Remote Sens. 2020, 12, 17. [Google Scholar] [CrossRef]
- Bates, J.S.; Montzka, C.; Schmidt, M.; Jonard, F. Estimating Canopy Density Parameters Time-Series for Winter Wheat Using UAS Mounted LiDAR. Remote Sens. 2021, 13, 710. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Y.; Zhang, Q.; Duan, R.; Liu, J.; Qin, Y.; Wang, X. Toward Multi-Stage Phenotyping of Soybean with Multimodal UAV Sensor Data: A Comparison of Machine Learning Approaches for Leaf Area Index Estimation. Remote Sens. 2023, 15, 7. [Google Scholar] [CrossRef]
- Wang, T.; Liu, Y.; Wang, M.; Fan, Q.; Tian, H.; Qiao, X.; Li, Y. Applications of UAS in Crop Biomass Monitoring: A Review. Front. Plant Sci. 2021, 12, 616689. [Google Scholar] [CrossRef]
- Tang, Z.; Parajuli, A.; Chen, C.J.; Hu, Y.; Revolinski, S.; Medina, C.A.; Lin, S.; Zhang, Z.; Yu, L.-X. Validation of UAV-based alfalfa biomass predictability using photogrammetry with fully automatic plot segmentation. Sci. Rep. 2021, 11, 3336. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Zhu, S.; Yang, T.; Zhang, W.; Xu, Y.; Zhou, K.; Sun, J. Maize height estimation using combined unmanned aerial vehicle oblique photography and LIDAR canopy dynamic characteristics. Comput. Electron. Agric. 2024, 218, 108685. [Google Scholar] [CrossRef]
- Pittman, J.J.; Arnall, D.B.; Interrante, S.M.; Moffet, C.A.; Butler, T.J. Estimation of Biomass and Canopy Height in Bermudagrass, Alfalfa, and Wheat Using Ultrasonic, Laser, and Spectral Sensors. Sensors 2015, 15, 2920–2943. [Google Scholar] [CrossRef]
- Bertalan, L.; Holb, I.; Pataki, A.; Négyesi, G.; Szabó, G.; Szalóki, A.K.; Szabó, S. UAV-based multispectral and thermal cameras to predict soil water content–A machine learning approach. Comput. Electron. Agric. 2022, 200, 107262. [Google Scholar] [CrossRef]
- Guan, Y.; Grote, K. Assessing the Potential of UAV-Based Multispectral and Thermal Data to Estimate Soil Water Content Using Geophysical Methods. Remote Sens. 2024, 16, 61. [Google Scholar] [CrossRef]
- Lu, F.; Sun, Y.; Hou, F. Using UAV Visible Images to Estimate the Soil Moisture of Steppe. Water 2020, 12, 2334. [Google Scholar] [CrossRef]
- Kim, K.Y.; Zhu, Z.; Zhang, R.; Fang, B.; Cosh, M.H.; Russ, A.L.; Dai, E.; Elston, J.; Stachura, M.; Gasiewski, A.J.; et al. Precision Soil Moisture Monitoring With Passive Microwave L-Band UAS Mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 7684–7694. [Google Scholar] [CrossRef]
- Dai, E.; Gasiewski, A.J.; Venkitasubramony, A.; Stachura, M.; Elston, J. High Spatial Resolution Soil Moisture Mapping Using a Lobe Differencing Correlation Radiometer on a Small Unmanned Aerial System. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4062–4079. [Google Scholar] [CrossRef]
- Gleich, D. SAR UAV for soil moisture estimation. In Proceedings of the 2023 8th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Bali, Indonesia, 23–27 October 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Farhad, M.; Gurbuz, A.C.; Kurum, M.; Moorhead, R. Soil Moisture Mapper: A GNSS-R approach for soil moisture retrieval on UAV. In AI for Agriculture and Food Systems; Association for the Advancement of Artificial Intelligence: Menlo Park, CA, USA, 2021; pp. 1–4. [Google Scholar]
- Wu, K.; Rodriguez, G.A.; Zajc, M.; Jacquemin, E.; Clément, M.; De Coster, A.; Lambot, S. A new drone-borne GPR for soil moisture mapping. Remote Sens. Environ. 2019, 235, 111456. [Google Scholar] [CrossRef]
- Schreiber, L.V.; Atkinson Amorim, J.G.; Guimarães, L.; Motta Matos, D.; Maciel da Costa, C.; Parraga, A. Above-Ground Biomass Wheat Estimation: Deep Learning with UAV-Based RGB Images. Appl. Artif. Intell. 2022, 36, 2055392. [Google Scholar] [CrossRef]
- Zhai, W.; Li, C.; Cheng, Q.; Mao, B.; Li, Z.; Li, Y.; Ding, F.; Qin, S.; Fei, S.; Chen, Z. Enhancing Wheat Above-Ground Biomass Estimation Using UAV RGB Images and Machine Learning: Multi-Feature Combinations, Flight Height, and Algorithm Implications. Remote Sens. 2023, 15, 3653. [Google Scholar] [CrossRef]
- Dhakal, R.; Maimaitijiang, M.; Chang, J.; Caffe, M. Utilizing Spectral, Structural and Textural Features for Estimating Oat Above-Ground Biomass Using UAV-Based Multispectral Data and Machine Learning. Sensors 2023, 23, 9708. [Google Scholar] [CrossRef]
- Yue, J.; Yang, G.; Li, C.; Li, Z.; Wang, Y.; Feng, H.; Xu, B. Estimation of Winter Wheat Above-Ground Biomass Using Unmanned Aerial Vehicle-Based Snapshot Hyperspectral Sensor and Crop Height Improved Models. Remote Sens. 2017, 9, 708. [Google Scholar] [CrossRef]
- Yuan, W.; Li, J.; Bhatta, M.; Shi, Y.; Baenziger, P.S.; Ge, Y. Wheat Height Estimation Using LiDAR in Comparison to Ultrasonic Sensor and UAS. Sensors 2018, 18, 3731. [Google Scholar] [CrossRef]
- Hütt, C.; Bolten, A.; Hüging, H.; Bareth, G. UAV LiDAR Metrics for Monitoring Crop Height, Biomass and Nitrogen Uptake: A Case Study on a Winter Wheat Field Trial. J. Photogramm. Remote Sens. Geoinf. Sci. 2023, 91, 65–76. [Google Scholar] [CrossRef]
- Huisman, J.A.; Hubbard, S.S.; Redman, J.D.; Annan, A.P. Measuring soil water content with ground penetrating radar: A review. Vadose Zone J. 2003, 2, 476–491. [Google Scholar] [CrossRef]
- Tran, A.P.; Bogaert, P.; Wiaux, F.; Vanclooster, M.; Lambot, S. High-resolution space–time quantification of soil moisture along a hillslope using joint analysis of ground penetrating radar and frequency domain reflectometry data. J. Hydrol. 2015, 523, 252–261. [Google Scholar] [CrossRef]
- Dehem, M. Soil Moisture Mapping Using a Drone-Borne Ground Penetrating Radar. Master’s Thesis, Faculté des bioingénieurs, Université catholique de Louvain, Ottignies-Louvain-la-Neuve, Belgium, 2020; p. 67. Available online: https://dial.uclouvain.be/memoire/ucl/object/thesis:27331 (accessed on 21 September 2024).
- Di Mauro, A.; Scozzari, A.; Soldovieri, F. (Eds.) Instrumentation and Measurement Technologies for Water Cycle Management; Springer Water: Berlin/Heidelberg, Germany, 2022; 599p, pp. 417–436. [Google Scholar]
- Wu, K.; Desesquelles, H.; Cockenpot, R.; Guyard, L.; Cuisiniez, V.; Lambot, S. Ground-Penetrating Radar Full-Wave Inversion for Soil Moisture Mapping in Trench-Hill Potato Fields for Precise Irrigation. Remote Sens. 2022, 14, 6046. [Google Scholar] [CrossRef]
- Cheng, Q.; Su, Q.; Binley, A.; Liu, J.; Zhang, Z.; Chen, X. Estimation of surface soil moisture by a multi-elevation UAV-based ground penetrating radar. Water Resour. Res. 2023, 59, e2022WR032621. [Google Scholar] [CrossRef]
- Karpukhin, V.I.; Peshkov, A.N. Measurement of height and biomass of vegetation canopy by radar method. In Proceedings of Theory and Technology of Radar, Radio Navigation and Radio Communications in Civil Aviation; The Riga Institute of Civil Aviation Engineers: Riga, Latvia, 1985; pp. 69–73. [Google Scholar]
- Serbin, G.; Or, D. Near-surface soil water content measurements using horn antenna radar: Methodology and overview. Vadose Zone J. 2003, 2, 500–510. [Google Scholar]
- Serbin, G.; Or, D. Ground-penetrating radar measurement of crop and surface water content dynamics. Remote Sens. Environ. 2005, 96, 119–134. [Google Scholar] [CrossRef]
- Serbin, G.; Dani, O.R. Frequency-domain analyses of GPR waveforms: Enhancing near-surface observational capabilities. In Proceedings of the Symposium S7 Held during the Seventh IAHS Scientific Assembly, Foz do Iguaçu, Brazil, April 2005; IAHS Publ.: Wallingford, UK, 2006; Volume 303, pp. 274–285. Available online: https://iahs.info/uploads/dms/13440.36-274-285-S7-29-serbin.pdf (accessed on 21 September 2024).
- Ardekani, M.R.M.; Jacques, D.C.; Lambot, S. A Layered Vegetation Model for GPR Full-Wave Inversion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 18–28. [Google Scholar] [CrossRef]
- Ardekani, M.R.; Neyt, X.; Nottebaere, M.; Jacques, D.; Lambot, S. GPR data inversion for vegetation layer. In Proceedings of the 15th International Conference on Ground Penetrating Radar, Brussels, Belgium, 30 June–4 July 2014; pp. 170–175. [Google Scholar] [CrossRef]
- Carlson, N.L. Dielectric Constant of Vegetation at 8.5 GHz; Ohio State Univ., EiectroScience Lab.: Columbus, OH, USA, 1967. [Google Scholar]
- Da Silva, F.F.; Wallach, R.; Polak, A.; Chen, Y. Measuring water content of soil substitutes with time-domain reflectometry (TDR). J.-Am. Soc. Hortic. Sci. 1998, 123, 734–737. [Google Scholar] [CrossRef]
- Pramudita, A.A.; Wahyu, Y.; Rizal, S.; Prasetio, M.D.; Jati, A.N.; Wulansari, R.; Ryanu, H.H. Soil water content estimation with the presence of vegetation using ultra wideband radar-drone. IEEE Access 2022, 10, 85213–85227. [Google Scholar] [CrossRef]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- Jonard, F.; Weihermuller, L.; Jadoon, K.Z.; Schwank, M.; Vereecken, H.; Lambot, S. Mapping field-scale soil moisture with L-band radiometer and ground-penetrating radar over bare soil. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2863–2875. [Google Scholar] [CrossRef]
- Minet, J.; Wahyudi, A.; Bogaert, P.; Vanclooster, M.; Lambot, S. Mapping shallow soil moisture profiles at the field scale using full-waveform inversion of ground penetrating radar data. Geoderma 2011, 161, 225–237. [Google Scholar] [CrossRef]
- Jonard, F.; Weihermüller, L.; Vereecken, H.; Lambot, S. Accounting for soil surface roughness in the inversion of ultrawideband off-ground GPR signal for soil moisture retrieval. Geophysics 2012, 77, H1–H7. [Google Scholar] [CrossRef]
- André, F.; Jonard, F.; Jonard, M.; Vereecken, H.; Lambot, S. Accounting for Surface Roughness Scattering in the Characterization of Forest Litter with Ground-Penetrating Radar. Remote Sens. 2019, 11, 828. [Google Scholar] [CrossRef]
- Landron, O.; Feuerstein, M.J.; Rappaport, T.S. A comparison of theoretical and empirical reflection coefficients for typical exterior wall surfaces in a mobile radio environment. IEEE Trans. Antennas Propag. 1996, 44, 341–351. [Google Scholar] [CrossRef]
- Gómez-Dans, J.L.; Quegan, S.; Bennett, J.C. Indoor C-band polarimetric interferometry observations of a mature wheat canopy. IEEE Trans. Geosci. Remote Sens. 2006, 44, 768–777. [Google Scholar] [CrossRef]
- Brown, S.C.; Quegan, S.; Morrison, K.; Bennett, J.C.; Cookmartin, G. High-resolution measurements of scattering in wheat canopies-implications for crop parameter retrieval. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1602–1610. [Google Scholar] [CrossRef]
- Morrison, K.; Bennett, J. Tomographic Profiling—A Technique for Multi-Incidence-Angle Retrieval of the Vertical SAR Backscattering Profiles of Biogeophysical Targets. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1350–1355. [Google Scholar] [CrossRef]
- Geotech LLC. Available online: https://geotechru.com/products/geophysical-equipment/antenna/ (accessed on 1 July 2023).
- Nizhny Novgorod Scientific and Production Association named after M. V. Frunze. Available online: https://frunze.nt-rt.ru/price/product/443160 (accessed on 1 July 2023).
- Muzalevskiy, K. LPDA Calibration Using an UAV for Synthesizing UWB Impulses. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 2140–2144. [Google Scholar] [CrossRef]
- Muzalevskiy, K.; Mikhaylov, M.; Ruzicka, Z. Synthesizing of UltraWide Band Impulse by means of a Log-Periodic Dipole Antenna. Case Study for a Radar Stand Experiment. In Proceedings of the IEEE International Multi Conference on Engineering, Computer and Information Sciences (SIBIRCON), Yekaterinburg, Russia, 11–13 November 2022; pp. 1140–1143. [Google Scholar]
- Muzalevsky, K.V. Synthesis of an Ultra-Wideband Pulse by a Log-Periodic Antenna with Continuous Excitation by Harmonic Oscillations. Radiophys. Quantum Electron. 2023, 65, 615–623. [Google Scholar] [CrossRef]
- Mironov, L.; Bobrov, P.P.; Fomin, S.V. Dielectric model of moist soils with varying clay content in the 0.04 to 26.5 GHz frequency range. In Proceedings of the International Siberian Conference on Control and Communications (SIBCON), Tomsk, Russia, 12–13 September 2013; pp. 1–4. [Google Scholar]
- Romanov, A.N. Dielectric Properties of Water in Saline Soil and its Solonchak Vegetation at a Frequency of 1.41 GHz. IEEE Geosci. Remote Sens. Lett. 2021, 18, 2033–2037. [Google Scholar] [CrossRef]
- Romanov, A.N.; Kochetkova, T.D.; Suslyaev, V.I.; Shcheglova, A.S. Dielectric properties of marsh vegetation in a frequency range of 0.1–18 GHz under variation of temperature and moisture. Russ. Phys. J. 2017, 60, 803–811. [Google Scholar] [CrossRef]
- Mironov, V.L.; Mikhaylov, M.I.; Muzalevskiy, K.V.; Sorokin, A.V.; Fomin, S.V.; Karavayskiy, A.Y. Measurement of height and moisture of an agricultural vegetation using GPS/GLONASS receiver. Sib. Aerosp. J. 2014, 15, 88–97. [Google Scholar]
- Schmugge, T.J.; Jackson, T.J. A dielectric model of the vegetation effects on the microwave emission from soils. IEEE Trans. Geosci. Remote Sens. 1992, 30, 757–760. [Google Scholar] [CrossRef]
- Ulaby, F.T.; El-rayes, M.A. Microwave Dielectric Spectrum of Vegetation—Part II: Dual-Dispersion Model. IEEE Trans. Geosci. Remote Sens. 1987, GE-25, 550–557. [Google Scholar] [CrossRef]
- Liu, S.-F.; Liou, Y.-A.; Wang, W.-J.; Wigneron, J.-P.; Lee, J.-B. Retrieval of crop biomass and soil moisture from measured 1.4 and 10.65 GHz brightness temperatures. IEEE Trans. Geosci. Remote Sens. 2022, 40, 1260–1268. [Google Scholar] [CrossRef]
- Wigneron, J.P.; Calvet, J.C.; Chanzy, A.; Grosjean, O.; Laguerre, L. A composite discrete-continuous approach to model the microwave emission of vegetation. IEEE Trans. Geosci. Remote Sens. 1995, 33, 201–211. [Google Scholar] [CrossRef]
- Van de Griend, A.A.; Wigneron, J.P. On the measurement of microwave vegetation properties: Some guidelines for a protocol. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2277–2289. [Google Scholar] [CrossRef]
- Van de Griend, A.A.; Wigneron, J.P. The b-factor as a function of frequency and canopy type at H-polarization. IEEE Trans. Geosci. Remote Sens. 2004, 42, 786–794. [Google Scholar] [CrossRef]
- Chukhlantsev, A.A.; Golovachev, S.P. Attenuation of microwave radiation in vegetation [Oslablenie SVCH izlucheniya v rastitel’nom pokrove]. J. Commun. Technol. Electron. [Radiotekhnika I Elektron.] 1989, 34, 2269–2278. [Google Scholar]
- Gill, P.E.; Murray, W. Algorithms for Nonlinear Least-Squares Problem. SIAM J. Numer. Anal. 1978, 15, 977–992. [Google Scholar] [CrossRef]



| Soil Horizon ** | Depth [cm] | Organic Carbon [%] | Dry Bulk Density [g/cm3] | Soil Texture by Weight [%] | Clay Content by Weight [%] * | |
|---|---|---|---|---|---|---|
| <0.001 mm | <0.01 mm | |||||
| A1 | 0–10 | 6.9 | 1.0 | 35 | 54 | 39 |
| A2 | 10–22 | 4.8 | 1.1 | 34 | 50 | 37 |
| AB | 22–42 | 4.8 | 1.17 | 32 | 47 | 35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muzalevskiy, K.; Fomin, S.; Karavayskiy, A.; Leskova, J.; Lipshin, A.; Romanov, V. Measuring Biophysical Parameters of Wheat Canopy with MHz- and GHz-Frequency Range Impulses Employing Contactless GPR. Remote Sens. 2024, 16, 3547. https://doi.org/10.3390/rs16193547
Muzalevskiy K, Fomin S, Karavayskiy A, Leskova J, Lipshin A, Romanov V. Measuring Biophysical Parameters of Wheat Canopy with MHz- and GHz-Frequency Range Impulses Employing Contactless GPR. Remote Sensing. 2024; 16(19):3547. https://doi.org/10.3390/rs16193547
Chicago/Turabian StyleMuzalevskiy, Konstantin, Sergey Fomin, Andrey Karavayskiy, Julia Leskova, Alexey Lipshin, and Vasily Romanov. 2024. "Measuring Biophysical Parameters of Wheat Canopy with MHz- and GHz-Frequency Range Impulses Employing Contactless GPR" Remote Sensing 16, no. 19: 3547. https://doi.org/10.3390/rs16193547
APA StyleMuzalevskiy, K., Fomin, S., Karavayskiy, A., Leskova, J., Lipshin, A., & Romanov, V. (2024). Measuring Biophysical Parameters of Wheat Canopy with MHz- and GHz-Frequency Range Impulses Employing Contactless GPR. Remote Sensing, 16(19), 3547. https://doi.org/10.3390/rs16193547







