Automatic Radar Intra-Pulse Signal Modulation Classification Using the Supervised Contrastive Learning

Abstract

The modulation classification technology for radar intra-pulse signals is important in the electronic countermeasures field. As the high quality labeled radar signals are difficult to be captured in the real applications, the signal modulation classification base on the limited number of labeled samples is playing a more and more important role. To relieve the requirement of the labeled samples, many self-supervised learning (SeSL) models exist. However, as they cannot fully explore the information of the labeled samples and rely significantly on the unlabeled samples, highly time-consuming processing of the pseudo-labels of the unlabeled samples is caused. To solve these problems, a supervised learning (SL) model, using the contrastive learning (CL) method (SL-CL), is proposed in this paper, which achieves a high classification accuracy, even adopting limited number of labeled training samples. The SL-CL model uses a two-stage training structure, in which the CL method is used in the first stage to effectively capture the features of samples, then the multilayer perceptron is applied in the second stage for the classification. Especially, the supervised contrastive loss is constructed to fully exploring the label information, which efficiently increases the classification accuracy. In the experiments, the SL-CL outperforms the comparison models in the situation of limited number of labeled samples available, which reaches 94% classification accuracy using 50 samples per class at 5 dB SNR.

1. Introduction

In the electronic countermeasures field, the modulation classification of the radar intra-pulse signals is an important task, which provides the required information of the radar system, such as working mode, parameter setting, etc. [1]. However, with the development of the multi-system radar and the other advanced radar technologies, the difficulty of radar signal detection increases [2]. Many new types of radar signals are proposed; for example, the low probability intercept (LPI) radar signals are developed for anti-jamming and anti-interception, which have the properties of low power, frequency agility, and large time–width–bandwidth product [3]. A limited number of high-quality labeled signals can be captured due to the lower probability of intercepting these radar signals. So, the accurate classification of signals based on limited labeled samples is valuable for the interference applications and so on [4].

The traditional radar signal modulation classification methods usually extract features from the signals firstly, and then several thresholds for the feature parameters are set to classify the signals [5,6,7,8]. However, these methods mainly rely on the choice of signal features and the set thresholds, and they usually perform not very well or even fail to work in classifying the complex modulated signals or low signal-to-noise (SNR) signals. With highly developed artificial intelligence, significant achievements have been made in many applications, such as the image classification [9], image retrieval [10], natural language processing [11], etc. Compared to the traditional signal modulation classification methods, the deep learning-based methods can automatically obtain better signal features without setting thresholds.

Many deep learning models for the signal modulation classification have been proposed, and most of them are based on the supervised learning (SL) [12,13,14,15]. In [12], the convolutional neural network (CNN)-based model, AlexNet, is proposed, which uses the data augmentation and dropout operation to prevent the overfitting problem. Another CNN-based model, called OD-CNN, is proposed in [13], which utilizes multi-feature fusion method to construct a more complete signal feature representation for reducing the noise and frequency offset influences. Moreover, refs. [14,15] apply the transformer model to the signal modulation classification for automatically learning the global dependencies of the signals, which helps the model adaptively concentrate on the key signal features and leads to robust performance. In [16], the radar signal is preprocessed by the second-order short-time Fourier transformation, and then the modified CNN (MeNet) is applied to the classification. Some semi-supervised leaning (SSL) models are also proposed to increase the classification performance by predicting labels for the unlabeled samples, for example, the PLLW model in [17].

To decrease the requirement of labeled samples, the self-supervised learning (SeSL) models are proposed [18,19]. These models usually first need to be trained by a great number of unlabeled samples, and then fine-tuned with a few labeled samples. Furthermore, the performance of these models is affected by the quantity of the image augmentations, but more augmentation means a greater amount of computation. Contrastive learning (CL) is a typical SeSL method, which learns the similarity and dissimilarity between samples by contrasting different views of the same sample [20,21]. The CL extracts the effective image features by comparison, and only limited labeled samples are needed to fine-tune the classifier for better classification performance. The signal modulation classification method in [19] is based on the CL, but this method is easily affected by the quality of the unlabeled samples’ pseudo-labels.

A radar signal modulation classification, called SL-CL, which uses the CL strategy with the fully SL mode, is proposed in this paper, which adopts a two-stage training structure [22]. In the first training stage, the supervised contrastive loss adapting to the labeled samples is constructed, which is improved from the CL loss for the unlabeled samples, then the encoder is constrained by this loss for representing the sample features better. With the extracted features of the first stage, the samples are classified by the linear classifier of the second stage. Due to the strong ability of capturing the sample features, the requirement for the labeled samples is relieved when a high classification accuracy is achieved.

In the proposed SL-CL model, the SeSL-type contrastive learning model is changed into an SL model, which enhances the classification accuracy by utilizing labeled samples for training. The loss function is reconstructed according to the change, which increases the feature capture ability. Furthermore, the two-stage training structure with two different losses is adopted instead of the one-stage one, which further increases the classification accuracy.

There are six sections in this paper. In Section 2, The motivation and works related to the SL-CL model are presented. In Section 3, the signal model and the method of data preprocessing are presented. Then, the structure and details of the SL-CL model are shown in Section 4. Finally, the experiment performances of the SL-CL model are shown in Section 5, where the parameter settings are analyzed and the comparisons with the other models are executed. The conclusion of this paper is given in Section 6.

2. Motivation and Related Works

2.1. Motivation

Most existing methods for the signal modulation classification belong to the SL [23,24]. However, they usually trained with a great number of labeled data, and the normally used cross entropy loss ignores the relative relationships between the samples and their decision boundaries, which reduces the generalization performance.

Later, the SeSL model-based signal modulation classification methods are proposed, which usually use the unlabeled and labeled data for pre-training and fine-tuning, respectively [19,25]. However, they have to be trained by both a great number of unlabeled samples and a small number of labeled samples, and the performance of the model depends mainly on the augmentation strategies of generating the augmented samples from the unlabeled samples, which causes the classification performance decline easily for even slight defectiveness of the augmented data. As the CL is an SeSL model, it also has the above shortcomings.

The above problems can be solved by the proposed SL-CL model, which uses the SeSL method CL with the SL mode. The SL-CL only uses limited labeled samples for training, and the CL loss and single cross entropy loss are taken in the first and second training stage, respectively, which greatly increases the generalization performance. As the augmented data are not need at all, the potential errors caused by them are avoided.

2.2. Contrastive Learning

The CL loss function is defined by constructing the positive and negative sample pairs [26]. The general expression of the loss function ${\mathcal{L}}^{cl}$ is as follows:

$${\mathcal{L}}^{cl}=-\log {\displaystyle \frac{exp(\mathrm{sim}({\mathbf{x}}_i,{\mathbf{x}}_p)/\tau )}{exp(\mathrm{sim}({\mathbf{x}}_i,{\mathbf{x}}_p)/\tau )+{\sum }_{n\in R\left(n\right)}exp(\mathrm{sim}({\mathbf{x}}_i,{\mathbf{x}}_n)/\tau )}}$$

(1)

where ${\mathbf{x}}_i$, ${\mathbf{x}}_p$ and ${\mathbf{x}}_n$ represent the feature vectors of the input, positive and negative samples, respectively, $R\left(n\right)$ is the negative sample set, $\Sigma$ represents the summation operation, $\tau$ is a temperature scalar parameter, and $\mathrm{sim}(v1,v2)$ represents the similarity between the vectors $v1$ and $v2$, which can be Euclidean distance [27], Manhattan distance [28], etc.

The loss function learns the distinguishable and generalizable features of the samples through narrowing the distance between the positive sample pairs and expanding the distance between the negative sample pairs in the embedding space. The commonly used CL losses include the InfoNCE loss [29], NT-Xent loss [30], Triplet Loss [31], and ArcFace Loss [32].

3. Signal Model and Data Preprocessing

3.1. Signal Model

The signal model that is mainly used in the real world is written as

$$y\left(k\right)=A{e}^{j\phi \left(k\right)}+n\left(k\right)$$

(2)

where $y\left(k\right)$ represents the observed signal, A is the amplitude of the signal, $\phi (·)$ is the phase of the signal, $n\left(k\right)$ represents the addictive white Gaussian noise, and k is the sampling index.

The frequency modulation radar signals mainly include the linear and nonlinear frequency modulation ones (LFM and NLFM). The expressions of the phases of these two signals are shown in

Table 1. The phases of the frequency modulation signals.

Modulation Type	Parameter	Phase $\mathit{\phi }\left(\mathit{k}\right)$
LFM	$f_0$	$2\pi \left(f_{0}k\pm {\displaystyle \frac{\mu }{2}}{k}^2\right)$
	$\mu$
NLFM	$f_0$	$2\pi f_{0}k\pm \pi \mu {(k-{\displaystyle \frac{T}{2}})}^3$
	$\mu$

, where $f_0$ represents the carrier frequency, $\mu$ denotes the modulation slope, and T denotes the coding duration.

The binary phase shift keying signal (BPSK) and Frank-coded polyphase signal (Frank) are the phase-modulated radar signals, whose phases are shown in

Table 2. The phases of the phase modulation signals.

Modulation Type	Parameter	Phase $\mathit{\phi }\left(\mathit{k}\right)$
BPSK	$f_0$	$2\pi f_{0}k+\theta$
	$\theta$
Frank	M	$2\pi f_{0}k+{\displaystyle \frac{2\pi (i-1)(j-1)}{M}}$

. In the table, $\theta \in \{0,\pi \}$ indicates the initial phase, M is the frequency step number, and $i,j=1,2,\cdots ,M$ are the ordinal numbers of the code.

The LPI radar signals include the polyphase- and polytime-coded signals, and their phases are introduced in

Table 3. The phases of the polyphase-coded signals.

Modulation Type	Parameter	Phase $\mathit{\phi }\left(\mathit{k}\right)$
P1	M	$2\pi f_{0}k-\pi {\displaystyle \frac{[M-(2j-1\left)\right]\left[\right(j-1)M+(i-1\left)\right]}{M}}$
P2	M	$2\pi f_{0}k-\pi {\displaystyle \frac{(2i-1-M)(2j-1-M)}{2M}}$
P3	$N_c$	$2\pi f_{0}k+\pi {\displaystyle \frac{{(i-1)}^2}{N_c}}$
P4	$N_c$	$2\pi f_{0}k+\pi \left[{\displaystyle \frac{{(i-1)}^2}{N_c}}-(i-1)\right]$

and

Table 4. The phases of the polytime-coded signals.

Modulation Type	Parameter	Phase $\mathit{\phi }\left(\mathit{k}\right)$
T1	m	$2\pi f_{0}k+\mathrm{mod}\left\{{\displaystyle \frac{2\pi }{n}}\mathrm{INT}\left[(mk-jT){\displaystyle \frac{jn}{T}}\right],2\pi \right\}$
	T
	n
T2	m	$2\pi f_{0}k+\mathrm{mod}\left\{{\displaystyle \frac{2\pi }{n}}\mathrm{INT}\left[(mk-jT)\left({\displaystyle \frac{2j-m+1}{T}}\right){\displaystyle \frac{n}{2}}\right],2\pi \right\}$
	T
	n
T3	m	$2\pi f_{0}k+\mathrm{mod}\left\{{\displaystyle \frac{2\pi }{n}}\mathrm{INT}[mn{k}^2/\left(2T\right)],2\pi \right\}$
	T
	n
T4	m	$2\pi f_{0}k+\mathrm{mod}\left\{{\displaystyle \frac{2\pi }{n}}\mathrm{INT}[mn{k}^2/\left(2T\right)-nmt/2],2\pi \right\}$
	T
	n

, respectively. In Table 3, M is the number of Barker codes, $N_c$ is the pulse compression ratio, the numbers $i,j=1,2,\cdots ,M$ are for the P1 and P2 signals, and $i=1,2,\cdots ,N_c$ are for the P3 and P4 signals. In Table 4, $\mathrm{mod}\{·\}$ is the modular operation, $\mathrm{INT}[·]$ is the rounding operation, m is the number of phase states, n represents the number of phase segments, and the number $j=1,2,\cdots ,m-1$ is for the T1 and T2 signals.

3.2. Data Preprocessing

The proposed model requires the input data to be in the form of matrix, while the raw radar signal is in the form of vector, so the data preprocessing method should be applied firstly. The time frequency analysis methods are usually employed in the transformation of the signal sequences into the time frequency images.

Among the time frequency analysis methods, the Choi–Williams distribution (CWD) is good at describing the time frequency distribution, whose transform function $\mathrm{CWD}(t,f)$ is shown as follows:

$$\begin{array}{cc}\hfill \mathrm{CWD}(t,f)& =\int \int \sqrt{{\displaystyle \frac{\sigma }{4\pi {\delta }^2}}}G(u,\delta )\times y\left(u+{\displaystyle \frac{\delta }{2}}\right)y^{\ast }\left(u-{\displaystyle \frac{\delta }{2}}\right){\mathrm{e}}^{-\mathrm{j}2\pi f\delta }\mathrm{d}u\mathrm{d}\delta \hfill \end{array}$$

(3)

with

$$G(u,\delta )=exp\left[-{\displaystyle \frac{\sigma {(u-t)}^2}{4{\delta }^2}}\right]$$

(4)

where t denotes the time, f denotes the frequency, u is the independent variable of the signal $y\left(u\right)$, $\delta$ is the time shift, $G(u,\delta )$ represents the function of kernel, $\sigma$ denotes the attenuation factor, and ${(·)}^{\ast }$ denotes the conjugate transpose operation.

4. The Proposed SL-CL Model

4.1. Overview of the SL-CL Model

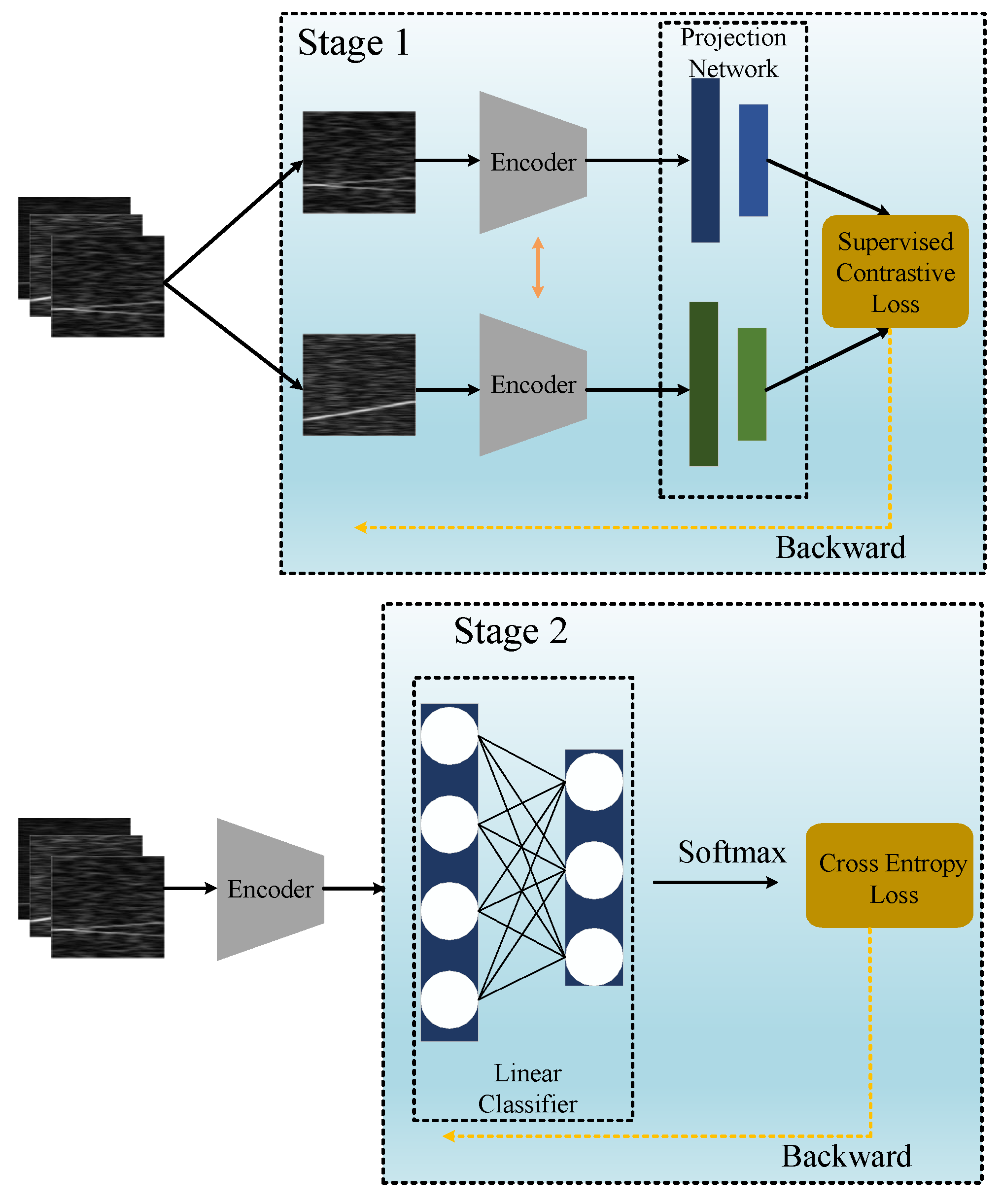
The architecture of the proposed SL-CL model is illustrated in Figure 1, which contains two stages. The first stage mainly extracts the features of the signals using the CL method, while the second stage implies the classification according to the features produced in the first stage.

The first stage consists of an encoder and a projection network. The encoder maps the time frequency image x to a feature vector r. Then, the projection network projects r to another vector z to reduce its dimension. The multi-layer perception is taken as the projection network in this paper. The supervised contrastive loss function used in this stage reformulates the contrastive loss with a supervised form, which enhances the features extraction ability.

The second stage is a linear classifier, which is constrained by the cross-entropy loss. The feature vector r is taken as the input of the linear classifier, and the softmax operation is performed to generate the classification results.

4.2. Encoder Module

In the CL method, the encoder module is a key component for mapping the input samples to the embedding space, which extracts the feature representation of the samples for the subsequent tasks. The commonly used encoder modules include the CNN, ResNet, etc.

ResNet learns the residual mappings instead of the underlying mappings, which alleviates the gradient vanishing problem from skip connections. ResNet is taken as the encoder in the first stage of the SL-CL, whose representation is

$$\mathrm{H}\left(x\right)=\mathrm{F}\left(x\right)+x$$

(5)

where x represents the input, $\mathrm{F}(·)$ is the transformation applied by the weight layer, and $\mathrm{H}(·)$ is the output.

ResNet contains multiple residual blocks. Each of the residual block includes multiple convolutional layers and skip connections, and is followed by a ReLU activation and a batch normalization operation. The general structure of the residual block is shown in Figure 2, which may vary a little in different networks. For example, ResNet-50 uses bottleneck blocks with 1 × 1, 3 × 3, and 1 × 1 convolutional kernels instead of a convolution block.

4.3. Supervised Contrastive Loss

In the first stage of the SL-CL model, the supervised contrastive loss is adopted, which is suitable to the situation of limited labeled samples available. The process of constructing the supervised contrastive loss is shown below.

Firstly, the similarity function $\mathrm{sim}(v1,v2)$ of the general CL loss function in Equation (1) is set as the inner production of vectors to cause the loss ${\mathcal{L}}^{sc{l}^{\prime }}$ to be written as

$${\mathcal{L}}^{sc{l}^{\prime }}=\sum _{i\in I}{\mathcal{L}}_i^{sc{l}^{\prime }}=-\sum _{i\in I}log{\displaystyle \frac{exp\left({\mathbf{z}}_i·{\mathbf{z}}_{j\left(i\right)}/\tau \right)}{{\sum }_{a\in A\left(i\right)}exp\left({\mathbf{z}}_i·{\mathbf{z}}_a/\tau \right)}}$$

(6)

where ${\mathcal{L}}_i^{sc{l}^{\prime }}$ denotes the loss of the ith sample, I represents the set of samples, $A\left(i\right)$ denotes the set of samples excluding the current ith sample, ${\mathbf{z}}_i$, ${\mathbf{z}}_{j\left(i\right)}$, and ${\mathbf{z}}_a$ are the current sample vector, positive sample vector, and the vector of all the samples exclude the current ith sample, respectively, and $\tau$ is still the temperature scalar parameter.

In this equation, only one positive sample vector (${\mathbf{z}}_{j\left(i\right)}$) is used to compare with the current sample vector (${\mathbf{z}}_i$). However, since the input samples of the SL-CL model are all labeled, there are multiple positive sample vectors, including the current sample. Thus, a more efficient loss is introduced, which fully uses all the positive sample vectors to compare with the current sample vector. This causes the current sample vector to be closer to all of the positive sample vectors, and the robustness of the model is enhanced. The supervised contrastive loss ${\mathcal{L}}^{scl}$ is then written as

$$\begin{array}{c}{\mathcal{L}}^{scl}={\displaystyle \sum _{i\in I}}{\mathcal{L}}_i^{scl}={\displaystyle \sum _{i\in I}}{\displaystyle \frac{-1}{\left|P\right(i\left)\right|}}{\displaystyle \sum _{p\in P\left(i\right)}}log{\displaystyle \frac{exp({\mathbf{z}}_i·{\mathbf{z}}_p/\tau )}{{\sum }_{a\in A\left(i\right)}exp\left({\mathbf{z}}_i·{\mathbf{z}}_a/\tau \right)}}\end{array}$$

(7)

where ${\mathcal{L}}_i^{scl}$ represents the loss of the ith sample, $P\left(i\right)$ represents all of the sets of positive samples, including the current ith sample, ${\mathbf{z}}_p$ is a positive sample vector, and $|·|$ denotes the module value operation.

4.4. Two-Stage Training

The training process of the SL-CL is given below, where the supervised contrastive loss and cross-entropy loss are adopted in the first and second stages, respectively.

In the first stage, the labeled samples are input into the encoder, then the output is transported to the projection network. The loss ${\mathcal{L}}^{scl}$ is used to optimize the encoder and projection network.

After the first-stage training, the parameters of the encoder are fixed; meanwhile, the projection network is discarded. The output of the encoder is taken as the input of the second stage to train a linear classifier using the cross-entropy loss. The cross-entropy loss is expressed as follows:

$${\mathcal{L}}^{ce}=\sum _{i\in I}{q}_{i}log\left(p_i\right)$$

(8)

where $q_i$ denotes the ground truth labels, and $p_i$ represents the predicted probabilities of the ith sample.

There is another, much easier way to train the SL-CL model in one stage, which is an end-to-end training method. Only the cross-entropy loss is used to train both the encoder and linear classifier in the same procedure. However, this way of training performs worse than the two-stage training, which will be shown in the experiment section later.

5. Experiments and Analysis

5.1. Datasets

There are 12 types of radar signals used in the following experiments, and the settings of them are shown in

Table 5. The parameter settings of the signals.

Modulation	Parameter	Range
-	$f_s$ (Sampling frequency)	200 MHz
	T (Time duration)	$[250/f_s,500/f_s]$
	$f_0$ (Carrier frequency)	$[3f_s/20,f_s/5]$
LFM, NLFM	$\mu$ (Modulation frequency)	$[f_s/20,f_s/10]$
BPSK	$\theta$ (Initial phase)	$\{0,\pi \}$
Frank, P1, P2	M (Number of codes)	$\{7,11,13\}$
	$N_c$ (Number of phase variations)	$\{20,21,22,23\}$
P3, P4	$N_c$(-)	$\{4,5,6\}$
T1, T2, T3, T4	m (Number of phase states)	$\{4,5,6\}$
	n (Number of phase segments)	$\left\{\right[1,m\left]\right\}$

, where $[·]$ represents a uniform random distribution and $\{·\}$ denotes a random parameter set. Figure 3 shows the time-frequency analysis of the signals at −5 dB.

5.2. Network Parameters and Training Strategies

In the proposed SL-CL model, the ResNet with 50 layers is taken as the encoder. The initial convolution layer is a 7 × 7 convolution kernel; then, a 3 × 3 max pooling layer follows. Subsequently, there are four residual blocks, which contain 3, 4, 6, and 3 residual units, respectively. Each unit is composed of a 1 × 1 convolution, a 3 × 3 convolution, and a 1 × 1 convolution. The output with size 1 × 1 × 2048 is through a global average pooling.

The SL-CL uses two-stage training, which includes the training of the encoder and linear classifier, respectively. The first-stage training uses the supervised contrast loss, and a projection network is added to reduce the dimension of the data. With the parameters are fixed and the projection network is abandoned in the first stage, the second-stage training uses the cross entropy loss to constrain the linear classifier.

5.3. Comparison Models

Seven comparison models are applied in this section. Among them, the OD-CNN [33], ResNet [34], VGG [35], AlexNet [36], and SL-CL-CE are all SL models, while the SIMCLR [18] and PLLW [17] are SeSL and SSL models, respectively. More details of the comparison models are given in

Table 6. The details of the models.

Model	Model Type	Two-Stage Training
SL-CL	SL	✓
VGG	SL	×
OD-CNN	SL	×
SIMCLR	SeSL	✓
SL-CL-CE	SL	×
ResNet	SL	×
AlexNet	SL	×
PLLW	SSL	×

.

The OD-CNN model is composed of an omni-dimensional dynamic convolution, a classifier, and a deep residual network. The model utilizes the omni-dimensional dynamic convolution to extract features from the signals.

ResNet is a commonly used residual connection network, which is composed of multiple residual blocks. The network used in the following experiments contains 18 layers.

VGG and AlexNet are both typical CNNs, which are good at capturing the fine details and complex features of the images.

SIMCLR is a simple SeSL model for the visual representation. The similarity between the SIMCLR and the proposed SL-CL is that they all use two-stage training. But, the SIMCLR uses the CL loss while the SL-CL uses the supervised contrastive loss in the first stage of training.

The structure of the SL-CL-CE model is the same as that of the SL-CL, but it uses end-to-end training. The cross-entropy loss is taken in this model.

PLLW is an SSL classification model based on CNN. The model selects high reliable prediction to label the unlabeled samples.

5.4. Parameter Analysis

In the following experiments, 50 and 100 labeled samples per type of signals for training and testing of the SL models are available, where the total number of signals are 600 and 1200, respectively. For the SeSL model SIMCLR, 50 unlabeled samples per type of signals are provided for training besides the labeled samples. The number of unlabeled samples used in the SSL model PLLW is the same as that of the labeled samples. All the experiment results are taken as the average value of 10 trials. In this section, several parameters are analyzed with the SNR setting as 0 dB.

In the supervised contrastive loss function, the key parameter affecting the classification accuracy is the temperature scalar parameter $\tau$, which controls the smoothness or sharpness of the probability distribution of the classes. With different settings of $\tau$, the results can be seen in Figure 4. It indicates that the classification accuracy increases as $\tau$ increases from 0.01 to 0.07, then the accuracy decreases with $\tau$ further increases. When $\tau$ equals to 0.07, the highest accuracy is achieved. If $\tau$ is too large, the relative distances between different samples will be reduced, which results in the decreasing of the discrimination between different samples. On the contrast, if $\tau$ is too small, the relative distances between the same samples will be magnified, which results in the over-emphasis of the differences in the same sample. That is the reason of the best performance happens at a medium value of $\tau$.

The batch size of the encoder is the number of samples processed simultaneously in the process of training. A larger batch size leads to higher training efficiency and more stable gradient estimation, but the memory requirement increases simultaneously. Meanwhile, a smaller batch size decreases the training efficiency and makes the the gradient estimation unstable. The classification results of varying batch sizes are shown in Figure 5. It can be observed that the classification accuracy improves as the batch size increases, where the accuracy improves from 89.33% to 89.67% with the batch size increases from 64 to 128. However, the memory requirement increases significantly with the batch size increases. Considering the computation efficiency, we select the batch size 64 in the following experiments.

The number of layers of the encoder is also analyzed. A greater number of layers is better for capturing the complex features, but more parameters will be generated and the overfitting problem may happens. The experimental results of different settings of the number of layers are given in

Table 7. Experimental results of the SL-CL model with a varying number of layers.

Number of layers	18	34	50	101
Accuracy (%)	$85.00$	$87.00$	89.33	$84.00$
Time cost per epoch (s)	$3.18$	$4.69$	8.38	$13.40$

. The best classification accuracy is achieved with a 50-layer encoder, which is 89.33%. The computation complexity or the time consuming increases with the number of layers increases, while the accuracy may decreases because of the overfitting problem. For example, the time consuming of a 101-layer encoder is nearly 5 s longer than that of the 50-layer encoder, but the accuracy of the 101-layer encoder is 5.33% less than the 50-layer encoder. So, the best setting of the number of layers is 50 in this experiment.

Additionally, the image resolution is an important factor for the classification. Although higher resolution of the image provides more detailed information, the time cost of training increases.

Table 8. Experimental results of the SL-CL model with a varying image resolution.

The image resolution	$32\times 32$	$64\times 64$	$128\times 128$	$256\times 256$
Accuracy (%)	$71.33$	89.33	$89.67$	$89.86$
Time cost per epoch (s)	$2.67$	6.90	$25.88$	$95.06$

presents the classification accuracy and time cost for different image resolutions, where $\tau$, batch size, and the number of layers are set as 0.07, 64 and 50, respectively. It can be observed that with the increasing of the image resolution, both the accuracy and time cost of training are all increased. The time costs per epoch with the image resolutions $128\times 128$ and $256\times 256$ are 25.88 and 89.86, respectively, which are much longer than that of the image resolution $64\times 64$; meanwhile, the accuracies increase only 0.34% and 0.53%, respectively. Therefore, considering both the classification accuracy and time cost, we choose the image resolution $64\times 64$ in the following experiments.

The effect of the number of epochs to the classification accuracy is analyzed, and the results are shown in Figure 6. The parameter settings are the same as the previous experiment. Since the second stage of training is a simple multi-layer perceptron, only the number of epochs of the first stage is tested. The number of epochs varies from 10 to 110 with an interval 10. It can be seen that the accuracy increases as the number of epochs increases. When the number of epochs reaches 110, the accuracy decreases a little, which is because too many epochs may cause over-fitting.

5.5. Performance Comparison

The comparison experiments of the SL-CL model are given below. The SL-CL is compared with the SIMCLR and SL-CL-CE models under different SNRs, and the performances are shown in Figure 7. The SL-CL outperforms the other two models at all the SNRs. Compared to the CL loss that used in the SIMCLR, the supervised contrastive loss used in the SL-CL model makes the samples with the same label more compact, which leads to a higher classification accuracy. The only difference between the SL-CL-CE and SL-CL models is the one-stage and two-stage training structures. As the performance of the SL-CL is better than that of the SL-CL-CE, it indicates that the two-stage training plays a promoting role in the classification.

Then, the comparison experiments between the SL-CL model and the other comparison models are given in

Table 9. Experiment results of models using 25 training samples per class at different SNRs.

Model∖SNR	$-5$ dB	$-4$ dB	$-3$ dB	$-2$ dB	$-1$ dB	0 dB	1 dB	2 dB	3 dB	4 dB	5 dB
OD-CNN	$52.78$	$58.68$	$60.07$	$62.84$	$64.58$	$69.09$	$70.83$	$73.95$	$76.32$	$79.67$	$80.00$
ResNet	$50.00$	$51.17$	$60.54$	$64.45$	$71.09$	$71.48$	$75.39$	$77.73$	$79.63$	$81.32$	$84.33$
VGG	$51.67$	$55.00$	$55.33$	$62.00$	$64.67$	$68.67$	$71.67$	$78.67$	$79.33$	$79.67$	$81.67$
AlexNet	$51.67$	$56.00$	$60.00$	$61.00$	$61.33$	$68.33$	$70.33$	$78.33$	$80.00$	$81.33$	$83.33$
SL-CL-CE	$36.00$	$43.33$	$44.33$	$53.00$	$53.33$	$58.00$	$59.67$	$69.00$	$73.33$	$75.67$	$76.76$
SIMCLR	$35.00$	$37.33$	$37.67$	$44.33$	$45.00$	$53.00$	$57.67$	$60.67$	$61.43$	$65.76$	$67.31$
PLLW	$35.50$	$38.27$	$43.21$	$47.78$	$50.00$	$55.37$	$59.67$	$62.00$	$64.00$	$66.67$	$68.00$
SL-CL	60.33	$\mathbf{60}.\mathbf{67}$	$\mathbf{61}.\mathbf{00}$	$\mathbf{68}.\mathbf{67}$	$\mathbf{72}.\mathbf{26}$	$\mathbf{76}.\mathbf{33}$	$\mathbf{79}.\mathbf{33}$	$\mathbf{79}.\mathbf{67}$	$\mathbf{81}.\mathbf{33}$	$\mathbf{83}.\mathbf{00}$	$\mathbf{85}.\mathbf{67}$

,

Table 10. Experimental results of models using 40 training samples per class at different SNRs.

Model∖SNR	$-5$ dB	$-4$ dB	$-3$ dB	$-2$ dB	$-1$ dB	0 dB	1 dB	2 dB	3 dB	4 dB	5 dB
OD-CNN	$61.11$	$66.32$	$70.33$	$74.65$	$76.04$	$76.04$	$80.35$	$80.35$	$83.33$	$86.61$	$87.67$
ResNet	$56.25$	$58.20$	$66.02$	$75.00$	$75.39$	$80.46$	$80.72$	$83.85$	$85.43$	$87.36$	$89.63$
VGG	$61.65$	$64.18$	$67.67$	$72.27$	$74.55$	$77.82$	$80.00$	$85.00$	$85.31$	$86.33$	$88.67$
AlexNet	$60.33$	$63.00$	$69.00$	$75.33$	$79.67$	$81.33$	$85.42$	$87.92$	$88.33$	$90.00$	$90.37$
SL-CL-CE	$47.00$	$48.33$	$52.00$	$56.00$	$66.33$	$73.33$	$74.58$	$76.76$	$80.00$	$82.33$	$83.31$
SIMCLR	$36.67$	$39.00$	$45.63$	$50.00$	$55.67$	$64.00$	$65.83$	$66.67$	$67.31$	$70.47$	$72.26$
PLLW	$38.50$	$40.33$	$47.78$	$54.52$	$57.80$	$63.25$	$65.62$	$68.34$	$75.00$	$78.78$	$83.19$
SL-CL	64.58	$\mathbf{70}.\mathbf{00}$	$\mathbf{72}.\mathbf{91}$	$\mathbf{75}.\mathbf{33}$	$\mathbf{80}.\mathbf{00}$	$\mathbf{83}.\mathbf{00}$	$\mathbf{86}.\mathbf{92}$	$\mathbf{88}.\mathbf{25}$	$\mathbf{89}.\mathbf{33}$	$\mathbf{90}.\mathbf{00}$	$\mathbf{91}.\mathbf{67}$

and

Table 11. Experimental results of models using 50 training samples per class at different SNRs.

Model∖SNR	$-5$ dB	$-4$ dB	$-3$ dB	$-2$ dB	$-1$ dB	0 dB	1 dB	2 dB	3 dB	4 dB	5 dB
OD-CNN	$66.31$	$70.83$	$72.91$	$78.51$	$80.90$	$81.00$	$81.94$	$87.15$	$90.20$	$91.32$	$93.40$
ResNet	$66.00$	$70.70$	$72.26$	$75.00$	$80.46$	$80.70$	$82.03$	$89.45$	$90.00$	$91.37$	$93.33$
VGG	$63.00$	$66.67$	$68.09$	$73.33$	$79.00$	$80.33$	$84.17$	$86.00$	$87.43$	$89.45$	$91.33$
AlexNet	$66.18$	$69.10$	$72.20$	$77.64$	$79.30$	$82.73$	$86.33$	$90.67$	$91.67$	$92.00$	$93.31$
SL-CL-CE	$56.67$	$60.00$	$67.00$	$68.00$	$69.14$	$74.95$	$75.67$	$82.33$	$84.00$	$90.67$	$92.00$
SIMCLR	$34.00$	$42.33$	$46.00$	$55.63$	$59.74$	$62.00$	$67.00$	$67.33$	$68.00$	$73.31$	$75.45$
PLLW	$43.01$	$48.10$	$52.65$	$60.17$	$66.98$	$72.43$	$74.51$	$76.92$	$80.54$	$82.10$	$83.47$
SL-CL	66.33	$\mathbf{72}.\mathbf{00}$	$\mathbf{73}.\mathbf{33}$	$\mathbf{79}.\mathbf{00}$	$\mathbf{85}.\mathbf{00}$	$\mathbf{89}.\mathbf{33}$	$\mathbf{90}.\mathbf{37}$	$\mathbf{91}.\mathbf{67}$	$\mathbf{92}.\mathbf{00}$	$\mathbf{93}.\mathbf{33}$	$\mathbf{94}.\mathbf{00}$

, in which the numbers of labeled samples for training are set as 25, 40, and 50, respectively. It can be observed that with the increasing of SNR, the overall classification accuracy increases accordingly. The classification accuracy of the SL-CL is always the highest among the comparison models at different SNRs and numbers of labeled samples. Even when the SNR is decreased as low as −5 dB, the accuracy of the SL-CL reaches 66.33% with 50 labeled training samples. The SIMCLR also uses two-stage training and CL method, but the first stage training uses the SeSL method. Although the cost of labeling is saved for the SIMCLR, the performance of classification decreases. In this experiment, the time costs of the SL-CL and SIMCLR are 10.7 s and 6.9 s per epoch, respectively. The time consumption of the SIMCLR is greater than that of the SL-CL, which indicates the SeSL model SIMCLR needs more time to process the pseudo-labels of the unlabeled samples. Besides the SIMCLR and SL-CL, the remaining models are all based on the one-stage training. Among these models, the performance of the SL-CL-CE is worse than the others, which is because the structure of the SL-CL-CE is the most complex one, which easily causes overfitting problem. The classification accuracy of the SSL model PLLW is much lower than that of the SL-CL, which is only a little higher than that of the SeSL model SIMCLR. As the PLLW chooses the labeled samples with higher confidence for training, it performs better than the SIMCLR using the unlabeled samples for training and the labeled samples for fine tuning. These models all perform worse than the SL-CL; the reason may be that they all use the single cross entropy loss while the SL-CL uses the supervised contrastive loss. As the feature capturing ability of the SL-CL is good, it performs well with a small number of labeled samples. With only 25 labeled samples per class and 5 dB SNR, the classification accuracy of the SL-CL is as high as 85.67%.

The confusion matrices are shown in Figure 8, where the diagonal values of the matrices are the ratios of the correct classifications. The classification accuracy increases as the SNR increases; meanwhile, the diagonal value of the matrix is more close to 1. In addition, the signals P1 and P4 is the most confused pair compared to the other signal pairs, which are recognized as each other about 35% of the time at −5 dB SNR.

6. Conclusions

The SL-CL model for the radar signal modulation classification is proposed in this paper, which uses the CL method with the SL mode. The model is trained by a two-stage training structure, where the first and second stages are used for capturing the signal features and classifying the samples, respectively. The supervised contrast loss is used to constrain the encoder in the first stage, which greatly improves the feature mining ability by paying attention to the relationships between samples of the same class. The SL-CL achieves higher accuracy and better robustness than the comparison models in the situation of limited number of labeled samples available, which provides a feasible method for the radar signal investigation. However, according to the experimental results, the ability of distinguishing similar samples under lower SNRs is still need to be improved for the SL-CL.