PGNN-Net: Parallel Graph Neural Networks for Hyperspectral Image Classification Using Multiple Spatial-Spectral Features
Abstract
1. Introduction
- We designed a HSI classification network with a parallel-style architecture called PGNN-Net, which enriches and develops the application of GNN in HSI classification.
- To compensate for the limitations of GCN in global spatial-spectral feature capture for HSI, we introduced ChebNet and adapted it, and finally constructed a more comprehensive representation of HSI features through a feature fusion strategy.
- We validate the effectiveness and sophistication of PGNN-Net on the four classical HSI datasets and analyze the performance of the model with different parameter settings.
2. Related Work
2.1. CNN-Based Classification
2.2. Transformer-Based Classification
2.3. GNN-Based Classification
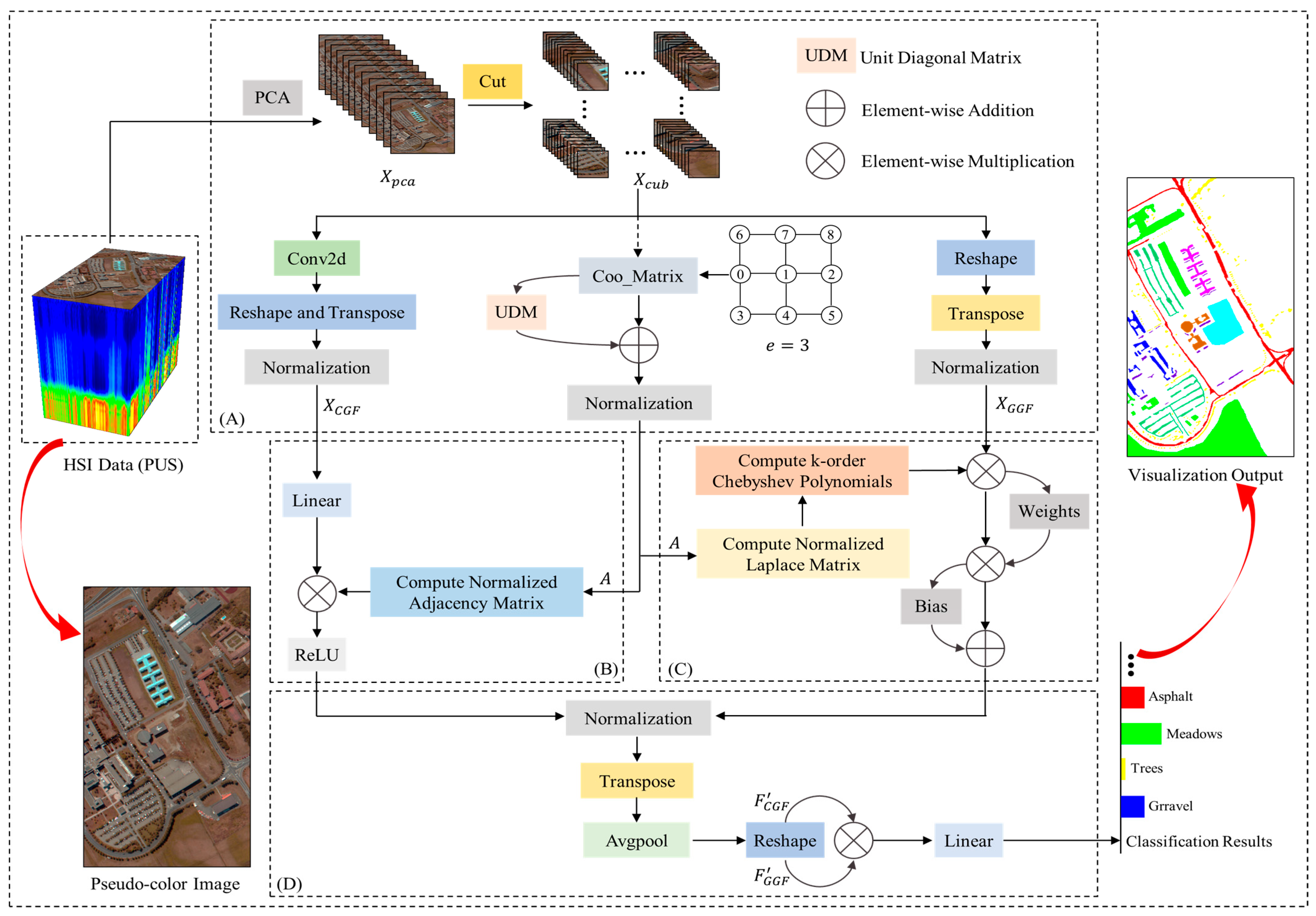
3. Methodology
3.1. Data Preprocessing
3.2. Local Spatial-Spectral Feature Extraction
3.3. Global Spatial-Spectral Feature Extraction
3.4. Feature Fusion and Classification
4. Results
4.1. Experimental Datasets
4.1.1. Indian Pines (IP)
4.1.2. Kennedy Space Center (KSC)
4.1.3. Pavia University Scene (PUS)
4.1.4. Botswana (BOT)
4.2. Evaluation Metrics
4.2.1. Overall Accuracy (OA)
4.2.2. Average Accuracy (AA)
4.2.3. Kappa
4.3. Experimental Settings
4.3.1. Platform Settings
4.3.2. Training Details
4.4. Experimental Results
4.4.1. Results for the IP
4.4.2. Results for the KSC
4.4.3. Results for the PUS
4.4.4. Results for the BOT
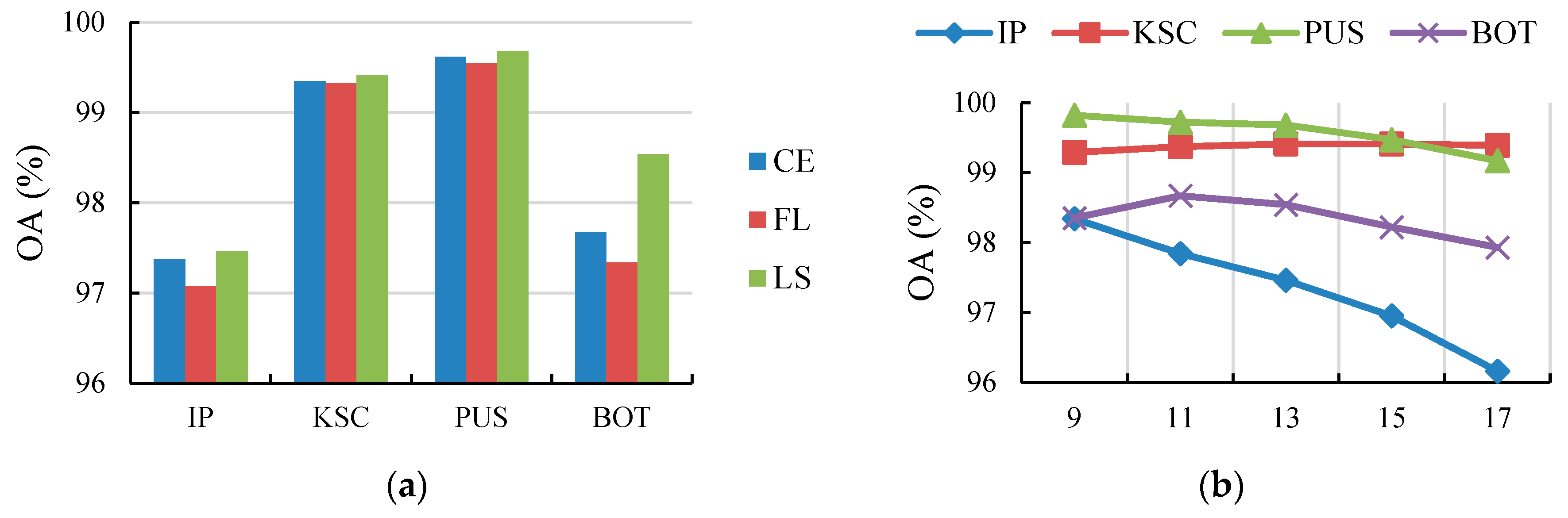
4.5. Ablation Study
4.5.1. Effect of the Edges in
4.5.2. Effect of k-Order in the CP
4.5.3. Effect of the Loss Function
4.5.4. Effect of the Cube Size
5. Discussion
5.1. Applicability
5.2. Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qian, S.E. Overview of hyperspectral imaging remote sensing from satellites. In Advances in Hyperspectral Image Processing Techniques; Wiley: Hoboken, NJ, USA, 2022; pp. 41–66. [Google Scholar]
- Stamford, J.; Aciksoz, S.B.; Lawson, T. Remote sensing techniques: Hyperspectral imaging and data analysis. In Photosynthesis: Methods and Protocols; Springer: Berlin/Heidelberg, Germany, 2024; pp. 373–390. [Google Scholar]
- Liu, H.; Li, W.; Xia, X.-G.; Zhang, M.; Gao, C.-Z.; Tao, R. Central attention network for hyperspectral imagery classification. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 8989–9003. [Google Scholar] [CrossRef] [PubMed]
- Lu, B.; Dao, P.D.; Liu, J.; He, Y.; Shang, J. Recent advances of hyperspectral imaging technology and applications in agriculture. Remote Sens. 2020, 12, 2659. [Google Scholar] [CrossRef]
- Agilandeeswari, L.; Prabukumar, M.; Radhesyam, V.; Phaneendra, K.L.B.; Farhan, A. Crop classification for agricultural applications in hyperspectral remote sensing images. Appl. Sci. 2022, 12, 1670. [Google Scholar] [CrossRef]
- Zhang, M.; Li, W.; Zhao, X.; Liu, H.; Tao, R.; Du, Q. Morphological transformation and spatial-logical aggregation for tree species classification using hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5501212. [Google Scholar] [CrossRef]
- Datta, D.; Mallick, P.K.; Bhoi, A.K.; Ijaz, M.F.; Shafi, J.; Choi, J. Hyperspectral image classification: Potentials, challenges, and future directions. Comput. Intell. Neurosci. 2022, 2022, 3854635. [Google Scholar] [CrossRef] [PubMed]
- Gewali, U.B.; Monteiro, S.T.; Saber, E. Machine learning based hyperspectral image analysis: A survey. arXiv 2018, arXiv:1802.08701. [Google Scholar]
- Huang, K.; Li, S.; Kang, X.; Fang, L. Spectral–spatial hyperspectral image classification based on KNN. Sens. Imaging 2016, 17, 1. [Google Scholar] [CrossRef]
- Wong, W.-T.; Hsu, S.-H. Application of SVM and ANN for image retrieval. Eur. J. Oper. Res. 2006, 173, 938–950. [Google Scholar] [CrossRef]
- Hasanlou, M.; Samadzadegan, F.; Homayouni, S. SVM-based hyperspectral image classification using intrinsic dimension. Arab. J. Geosci. 2015, 8, 477–487. [Google Scholar] [CrossRef]
- Yu, H.; Gao, L.; Li, J.; Li, S.S.; Zhang, B.; Benediktsson, J.A. Spectral-spatial hyperspectral image classification using subspace-based support vector machines and adaptive Markov random fields. Remote Sens. 2016, 8, 355. [Google Scholar] [CrossRef]
- Uchaev, D.; Uchaev, D. Small sample hyperspectral image classification based on the random patches network and recursive filtering. Sensors 2023, 23, 2499. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.J.; Khan, H.S.; Yousaf, A.; Khurshid, K.; Abbas, A. Modern trends in hyperspectral image analysis: A review. IEEE Access 2018, 6, 14118–14129. [Google Scholar] [CrossRef]
- Audebert, N.; Le Saux, B.; Lefèvre, S. Deep learning for classification of hyperspectral data: A comparative review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 159–173. [Google Scholar] [CrossRef]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep learning for hyperspectral image classification: An overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef]
- Li, X.; Li, Z.; Qiu, H.; Hou, G.; Fan, P. An overview of hyperspectral image feature extraction, classification methods and the methods based on small samples. Appl. Spectrosc. Rev. 2023, 58, 367–400. [Google Scholar] [CrossRef]
- Vaddi, R.; Manoharan, P. Hyperspectral image classification using CNN with spectral and spatial features integration. Infrared Phys. Technol. 2020, 107, 103296. [Google Scholar] [CrossRef]
- Lee, H.; Kwon, H. Going deeper with contextual CNN for hyperspectral image classification. IEEE Trans. Image Process. 2017, 26, 4843–4855. [Google Scholar] [CrossRef]
- Sun, M.; Song, Z.; Jiang, X.; Pan, J.; Pang, Y. Learning pooling for convolutional neural network. Neurocomputing 2017, 224, 96–104. [Google Scholar] [CrossRef]
- Yang, X.; Cao, W.; Lu, Y.; Zhou, Y. Hyperspectral image transformer classification networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5528715. [Google Scholar] [CrossRef]
- Qing, Y.; Liu, W.; Feng, L.; Gao, W. Improved transformer net for hyperspectral image classification. Remote Sens. 2021, 13, 2216. [Google Scholar] [CrossRef]
- Dubey, S.R.; Singh, S.K. Transformer-based generative adversarial networks in computer vision: A comprehensive survey. IEEE Trans. Artif. Intell. 2024, 1–16. [Google Scholar] [CrossRef]
- Liang, L.; Jin, L.; Xu, Y. Adaptive GNN for image analysis and editing. Adv. Neural Inf. Process. Syst. 2019, 32, 1–12. [Google Scholar]
- Yao, D.; Zhi-li, Z.; Xiao-feng, Z.; Wei, C.; Fang, H.; Yao-ming, C.; Cai, W.-W. Deep hybrid: Multi-graph neural network collaboration for hyperspectral image classification. Def. Technol. 2023, 23, 164–176. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Zhang, Y.; Shen, Q. Spectral-spatial classification of hyperspectral imagery using a dual-channel convolutional neural network. Remote Sens. Lett. 2017, 8, 438–447. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Fernandez-Beltran, R.; Plaza, J.; Plaza, A.J.; Pla, F. Deep pyramidal residual networks for spectral–spatial hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 57, 740–754. [Google Scholar] [CrossRef]
- He, M.; Li, B.; Chen, H. Multi-Scale 3D Deep Convolutional Neural Network for Hyperspectral Image Classification. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 3904–3908. [Google Scholar]
- Paoletti, M.E.; Moreno-Álvarez, S.; Xue, Y.; Haut, J.M.; Plaza, A. AAtt-CNN: Automatic attention-based convolutional neural networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5511118. [Google Scholar] [CrossRef]
- Mei, S.; Li, X.; Liu, X.; Cai, H.; Du, Q. Hyperspectral image classification using attention-based bidirectional long short-term memory network. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5509612. [Google Scholar] [CrossRef]
- Tang, H.; Li, Y.; Huang, Z.; Zhang, L.; Xie, W. Fusion of multidimensional CNN and handcrafted features for small-sample hyperspectral image classification. Remote Sens. 2022, 14, 3796. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A.; Chanussot, J. SpectralFormer: Rethinking hyperspectral image classification with transformers. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5518615. [Google Scholar] [CrossRef]
- Xu, H.; Zeng, Z.; Yao, W.; Lu, J. CS2DT: Cross spatial–spectral dense transformer for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2023, 20, 5510105. [Google Scholar] [CrossRef]
- Yang, L.; Yang, Y.; Yang, J.; Zhao, N.; Wu, L.; Wang, L.; Wang, T. FusionNet: A convolution–transformer fusion network for hyperspectral image classification. Remote Sens. 2022, 14, 4066. [Google Scholar] [CrossRef]
- Mei, S.; Song, C.; Ma, M.; Xu, F. Hyperspectral image classification using group-aware hierarchical transformer. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5539014. [Google Scholar] [CrossRef]
- Li, W.; Liu, Q.; Fan, S.; Xu, C.A.; Bai, H. Dual-stream GNN fusion network for hyperspectral classification. Appl. Intell. 2023, 53, 26542–26567. [Google Scholar] [CrossRef]
- Niruban, R.; Deepa, R. Graph neural network-based remote target classification in hyperspectral imaging. Int. J. Remote Sens. 2023, 44, 4465–4485. [Google Scholar] [CrossRef]
- Qin, A.; Shang, Z.; Tian, J.; Wang, Y.; Zhang, T.; Tang, Y.Y. Spectral–spatial graph convolutional networks for semisupervised hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2018, 16, 241–245. [Google Scholar] [CrossRef]
- Hu, H.; Yao, M.; He, F.; Zhang, F. Graph neural network via edge convolution for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2021, 19, 5508905. [Google Scholar] [CrossRef]
- Zhao, F.; Zhang, J.; Meng, Z.; Liu, H.; Chang, Z.; Fan, J. Multiple vision architectures-based hybrid network for hyperspectral image classification. Expert Syst. Appl. 2023, 234, 121032. [Google Scholar] [CrossRef]
- Liu, Q.; Dong, Y.; Zhang, Y.; Luo, H. A fast dynamic graph convolutional network and CNN parallel network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5530215. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. arXiv 2016, arXiv:1606.09375. [Google Scholar]
- Greenacre, M.; Groenen, P.J.; Hastie, T.; d’Enza, A.I.; Markos, A.; Tuzhilina, E. Principal component analysis. Nat. Rev. Methods Primers 2022, 2, 100. [Google Scholar] [CrossRef]
- Müller, R.; Kornblith, S.; Hinton, G.E. When does label smoothing help? arXiv 2019, arXiv:1906.02629. [Google Scholar]

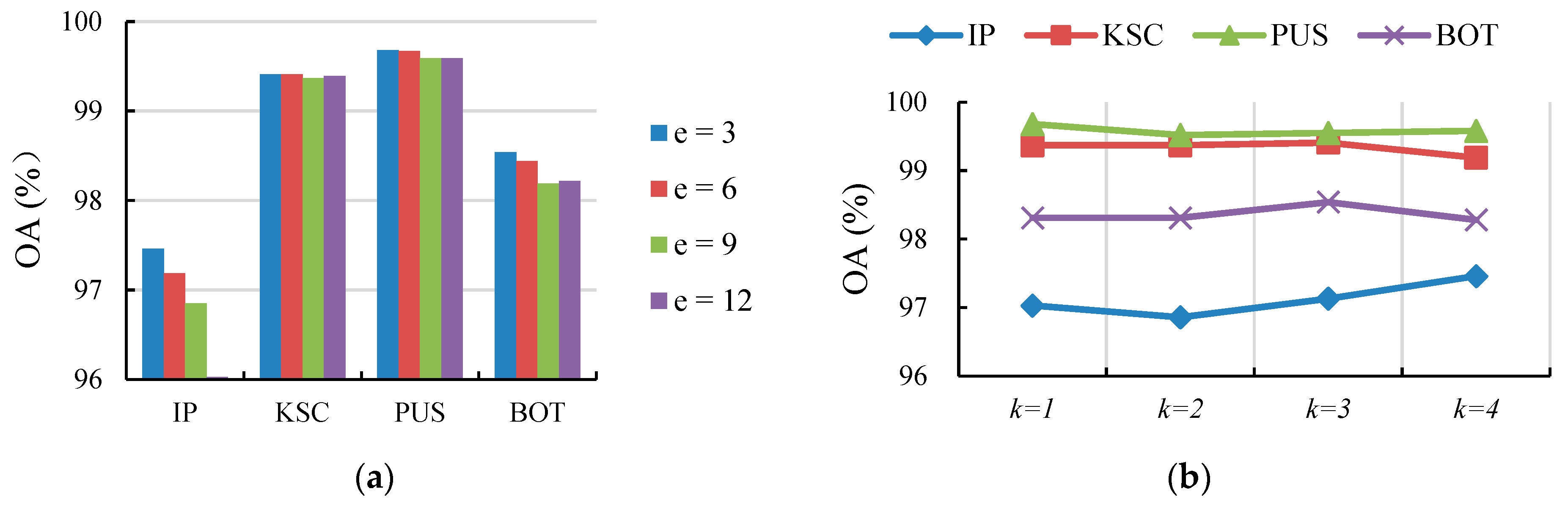
| Datasets | Size | |||
|---|---|---|---|---|
| Class | Pixel | Image | Band | |
| Indian Pines | 16 | 10,249 | 145 × 145 | 200 |
| Kennedy Space Center | 13 | 5211 | 512 × 614 | 176 |
| Pavia University Scene | 13 | 42,776 | 610 × 340 | 115 |
| Botswana | 14 | 3248 | 1476 × 256 | 145 |
| Class Number | Pixel Color | IP | KSC | ||
|---|---|---|---|---|---|
| Feature Name | Pixel Count | Feature Name | Pixel Count | ||
| 1 | Alfalfa | 46 | Scrub | 761 | |
| 2 | Corn-notill | 1428 | Willow-swamp | 243 | |
| 3 | Corn-mintill | 830 | CP-hammock | 256 | |
| 4 | Corn | 237 | CP/Oak | 252 | |
| 5 | Grass-pasture | 483 | Slash-pine | 161 | |
| 6 | Grass-trees | 730 | Oak/Broadleaf | 229 | |
| 7 | Grass-pasture-mowed | 28 | Hardwood-swamp | 105 | |
| 8 | Hay-windrowed | 478 | Graminoid-marsh | 431 | |
| 9 | Oats | 20 | Spartina-marsh | 520 | |
| 10 | Soybean-notill | 972 | Catiail-marsh | 404 | |
| 11 | Soybean-mintill | 2455 | Salt-marsh | 419 | |
| 12 | Soybean-clean | 593 | Mud-flats | 503 | |
| 13 | Wheat | 205 | Water | 927 | |
| 14 | Woods | 1265 | / | / | |
| 15 | Buildings-Grass-Trees-Drives | 386 | / | / | |
| 16 | Stone-Steel-Towers | 93 | / | / | |
| Class Number | Pixel Color | PUS | BOT | ||
|---|---|---|---|---|---|
| Feature Name | Pixel Count | Feature Name | Pixel Count | ||
| 1 | Asphalt | 6631 | Water | 270 | |
| 2 | Meadows | 18,649 | Hippo-grass | 101 | |
| 3 | Gravel | 2099 | Floodplain-grasses-1 | 251 | |
| 4 | Trees | 3064 | Floodplain-grasses-2 | 215 | |
| 5 | Painted metal sheets | 1345 | Reeds | 269 | |
| 6 | Bare Soil | 5029 | Riparian | 269 | |
| 7 | Bitumen | 1330 | Firescar | 259 | |
| 8 | Self-Blocking-Bricks | 3682 | Island-interior | 203 | |
| 9 | Shadows | 947 | Acacia-woodlands | 314 | |
| 10 | / | / | Acacia-shrublands | 248 | |
| 11 | / | / | Acacia-grasslands | 305 | |
| 12 | / | / | Short-mopane | 181 | |
| 13 | / | / | Mixed-mopane | 268 | |
| 14 | / | / | Chalcedony | 95 | |
| Class | SVM [10] | DPRN [27] | M3CNN [28] | GAHT [35] | SF [32] | CS2DT [33] | MVAHN [40] | Ours |
|---|---|---|---|---|---|---|---|---|
| 1 | 48.18 ± 18.50 | 28.64 ± 7.69 | 8.18 ± 2.32 | 80.00 ± 0.91 | 49.55 ± 0.91 | 32.73 ± 6.52 | 95.00 ± 5.45 | 100 ± 0.00 |
| 2 | 68.08 ± 2.57 | 85.06 ± 6.21 | 73.94 ± 2.36 | 96.57 ± 0.21 | 88.15 ± 0.03 | 95.42 ± 0.61 | 96.57 ± 0.11 | 96.71 ± 0.20 |
| 3 | 51.62 ± 1.20 | 78.05 ± 2.74 | 63.22 ± 2.86 | 97.74 ± 0.25 | 95.13 ± 0.26 | 95.44 ± 1.47 | 97.19 ± 0.39 | 94.63 ± 0.83 |
| 4 | 42.49 ± 8.38 | 57.60 ± 12.01 | 14.31 ± 4.41 | 96.53 ± 0.18 | 93.16 ± 0.36 | 88.80 ± 4.14 | 100 ± 0.00 | 96.98 ± 0.76 |
| 5 | 86.71 ± 1.14 | 79.26 ± 10.36 | 77.69 ± 3.03 | 92.07 ± 0.17 | 94.25 ± 0.22 | 92.07 ± 0.49 | 94.60 ± 1.94 | 94.81 ± 0.37 |
| 6 | 92.94 ± 3.92 | 92.58 ± 2.00 | 94.46 ± 2.02 | 97.86 ± 0.11 | 98.50 ± 0.07 | 98.21 ± 0.35 | 98.47 ± 0.30 | 96.88 ± 0.12 |
| 7 | 50.37 ± 25.21 | 22.22 ± 27.32 | 1.48 ± 2.96 | 79.26 ± 7.98 | 85.93 ± 1.48 | 5.19 ± 6.87 | 66.67 ± 22.22 | 94.81 ± 1.81 |
| 8 | 96.30 ± 0.46 | 92.47 ± 6.25 | 99.47 ± 0.11 | 100 ± 0.00 | 100 ± 0.00 | 99.87 ± 0.11 | 100 ± 0.00 | 100 ± 0.00 |
| 9 | 21.05 ± 11.76 | 16.84 ± 7.74 | 0.00 ± 0.00 | 66.32 ± 12.28 | 26.32 ± 0.00 | 5.26 ± 5.77 | 50.53 ± 17.49 | 61.05 ± 6.32 |
| 10 | 64.01 ± 2.51 | 79.98 ± 5.87 | 68.73 ± 4.62 | 93.78 ± 0.22 | 94.17 ± 0.04 | 92.48 ± 1.20 | 96.49 ± 0.20 | 97.12 ± 0.15 |
| 11 | 79.70 ± 2.36 | 93.41 ± 0.68 | 86.63 ± 2.40 | 97.05 ± 0.05 | 96.74 ± 0.07 | 97.64 ± 0.39 | 97.84 ± 0.10 | 98.69 ± 0.16 |
| 12 | 59.36 ± 3.51 | 58.79 ± 13.86 | 40.99 ± 4.74 | 89.38 ± 0.54 | 94.28 ± 0.17 | 92.54 ± 2.23 | 92.90 ± 1.87 | 94.78 ± 0.55 |
| 13 | 93.33 ± 2.60 | 86.36 ± 8.72 | 89.85 ± 6.55 | 95.90 ± 0.00 | 99.08 ± 0.21 | 99.28 ± 0.77 | 99.18 ± 0.89 | 100 ± 0.00 |
| 14 | 94.29 ± 1.63 | 95.26 ± 0.48 | 97.64 ± 0.73 | 98.50 ± 0.07 | 99.23 ± 0.12 | 99.62 ± 0.07 | 99.58 ± 0 | 99.20 ± 0.04 |
| 15 | 42.13 ± 7.68 | 67.68 ± 14.59 | 65.50 ± 11.50 | 99.18 ± 0.00 | 95.69 ± 0.11 | 97.33 ± 1.00 | 97.60 ± 0.61 | 98.53 ± 0.13 |
| 16 | 81.36 ± 4.43 | 82.73 ± 3.48 | 73.64 ± 17.01 | 77.95 ± 0.56 | 85.00 ± 1.11 | 77.50 ± 9.81 | 88.18 ± 1.70 | 90.23 ± 0.91 |
| OA | 74.71 ± 0.92 | 84.51 ± 4.72 | 77.44 ± 1.85 | 96.11 ± 0.04 | 94.93 ± 0.02 | 95.40 ± 0.09 | 97.19 ± 0.06 | 97.35 ± 0.09 |
| AA | 67.02 ± 2.34 | 69.81 ± 8.05 | 59.73 ± 2.24 | 91.13 ± 1.12 | 87.20 ± 0.14 | 79.34 ± 0.98 | 91.92 ± 2.54 | 94.65 ± 0.40 |
| Kappa | 71.00 ± 1.07 | 82.15 ± 5.50 | 74.02 ± 2.15 | 95.57 ± 0.05 | 94.21 ± 0.02 | 94.75 ± 0.10 | 96.80 ± 0.07 | 96.98 ± 0.10 |
| Class | SVM [10] | DPRN [27] | M3CNN [28] | GAHT [35] | SF [32] | CS2DT [33] | MVAHN [40] | Ours |
|---|---|---|---|---|---|---|---|---|
| 1 | 94.97 ± 1.50 | 99.42 ± 0.71 | 100 ± 0.00 | 99.89 ± 0.16 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 |
| 2 | 85.63 ± 1.05 | 89.01 ± 4.39 | 89.61 ± 2.31 | 99.05 ± 0.96 | 97.06 ± 0.69 | 95.15 ± 0.92 | 99.39 ± 1.01 | 100 ± 0.00 |
| 3 | 69.79 ± 12.35 | 85.93 ± 5.11 | 97.70 ± 0.33 | 97.61 ± 3.46 | 99.34 ± 0.33 | 97.45 ± 0.88 | 100 ± 0.00 | 100 ± 0.00 |
| 4 | 54.48 ± 8.07 | 58.08 ± 13.02 | 34.14 ± 4.63 | 93.47 ± 4.39 | 97.74 ± 0.20 | 88.20 ± 2.09 | 97.57 ± 2.43 | 100 ± 0.00 |
| 5 | 41.31 ± 20.39 | 38.95 ± 12.24 | 60.39 ± 2.43 | 78.43 ± 1.65 | 79.08 ± 0.00 | 73.86 ± 1.49 | 81.04 ± 0.00 | 81.05 ± 0.00 |
| 6 | 23.49 ± 13.17 | 54.13 ± 24.91 | 27.16 ± 8.72 | 93.58 ± 4.44 | 98.17 ± 0.00 | 96.79 ± 1.12 | 98.35 ± 0.55 | 99.72 ± 0.37 |
| 7 | 77.00 ± 8.57 | 78.00± 20.91 | 65.20 ± 6.97 | 98.20 ± 0.75 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 |
| 8 | 68.41 ± 10.12 | 87.09 ± 10.13 | 99.85 ± 0.29 | 98.88 ± 1.78 | 100 ± 0.00 | 100 ± 0.00 | 99.90 ± 0.20 | 100 ± 0.00 |
| 9 | 90.97 ± 5.01 | 96.72 ± 0.72 | 99.68 ± 0.10 | 99.76 ± 0.32 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 |
| 10 | 84.58 ± 2.34 | 100 ± 0.00 | 100 ± 0.00 | 99.79 ± 0.30 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 |
| 11 | 95.63 ± 1.43 | 97.09 ± 1.81 | 92.01 ± 1.29 | 99.80 ± 1.89 | 99.75 ± 0.00 | 99.40 ± 0.12 | 99.90 ± 0.20 | 100 ± 0.00 |
| 12 | 83.43 ± 2.23 | 92.01 ± 4.65 | 99.41 ± 0.20 | 99.79 ± 0.19 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 |
| 13 | 98.09 ± 0.55 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 |
| OA | 82.27 ± 1.78 | 89.94 ± 2.81 | 90.35 ± 0.85 | 98.35 ± 0.32 | 98.97 ± 0.05 | 98.08 ± 0.12 | 99.18 ± 0.10 | 99.40 ± 0.02 |
| AA | 74.44 ± 2.57 | 82.80 ± 4.89 | 81.93 ± 1.39 | 96.79 ± 0.50 | 97.78 ± 0.09 | 96.22 ± 0.23 | 98.17 ± 0.16 | 98.52 ± 0.03 |
| Kappa | 80.21 ± 1.98 | 88.74 ± 3.19 | 89.19 ± 0.96 | 98.16 ± 0.35 | 98.86 ± 0.06 | 97.86 ± 0.13 | 99.09 ± 0.11 | 99.33 ± 0.02 |
| Class | SVM [10] | DPRN [27] | M3CNN [28] | GAHT [35] | SF [32] | CS2DT [33] | MVAHN [40] | Ours |
|---|---|---|---|---|---|---|---|---|
| 1 | 93.22 ± 0.95 | 97.26 ± 0.38 | 97.82 ± 1.23 | 99.45 ± 0.06 | 97.35 ± 0.31 | 99.20 ± 0.22 | 99.42 ± 0.06 | 100 ± 0.00 |
| 2 | 98.45 ± 0.13 | 99.99 ± 0.01 | 99.69 ± 0.28 | 99.94 ± 0.01 | 99.89 ± 0.01 | 99.99 ± 0.00 | 99.98 ± 0.01 | 100 ± 0.00 |
| 3 | 77.92 ± 1.10 | 90.24 ± 1.75 | 83.55 ± 6.53 | 98.72 ± 0.67 | 94.74 ± 1.55 | 97.49 ± 1.27 | 99.59 ± 0.13 | 99.69 ± 0.02 |
| 4 | 92.52 ± 0.81 | 96.43 ± 0.30 | 97.08 ± 1.55 | 95.45 ± 0.21 | 96.65 ± 0.22 | 98.60 ± 0.07 | 97.33 ± 0.47 | 96.90 ± 0.19 |
| 5 | 99.44 ± 0.08 | 97.36 ± 2.13 | 99.97 ± 0.06 | 98.90 ± 0.51 | 99.83 ± 0.03 | 100 ± 0.00 | 99.64 ± 0.19 | 99.73 ± 0.12 |
| 6 | 84.17 ± 1.01 | 99.23 ± 0.28 | 98.02 ± 1.59 | 99.99 ± 0.01 | 99.92 ± 0.07 | 99.92 ± 0.02 | 100 ± 0.00 | 100 ± 0.00 |
| 7 | 82.99 ± 1.52 | 99.64 ± 0.55 | 96.01 ± 4.53 | 98.59 ± 0.71 | 100 ± 0.00 | 99.94 ± 0.08 | 99.97 ± 0.04 | 99.98 ± 0.03 |
| 8 | 88.77 ± 0.98 | 93.41 ± 1.78 | 93.73 ± 1.69 | 98.99 ± 0.07 | 92.85 ± 0.57 | 96.92 ± 0.35 | 98.90 ± 0.44 | 99.41 ± 0.04 |
| 9 | 99.82 ± 0.15 | 97.93 ± 0.75 | 98.04 ± 1.69 | 94.07 ± 0.78 | 98.09 ± 0.39 | 99.20 ± 0.29 | 95.71 ± 1.29 | 97.16 ± 0.45 |
| OA | 93.27 ± 0.05 | 98.04 ± 0.25 | 97.57 ± 1.08 | 99.20 ± 0.01 | 98.37 ± 0.06 | 99.36 ± 0.04 | 99.49 ± 0.02 | 99.64 ± 0.02 |
| AA | 90.81 ± 0.17 | 96.83 ± 0.38 | 95.99 ± 2.04 | 98.24 ± 0.03 | 97.70 ± 0.10 | 99.03 ± 0.12 | 98.95 ± 0.08 | 99.21 ± 0.06 |
| Kappa | 91.02 ± 0.07 | 97.40 ± 0.34 | 96.77 ± 1.44 | 98.94 ± 0.01 | 97.84 ± 0.05 | 99.15 ± 0.05 | 99.32 ± 0.02 | 99.52 ± 0.03 |
| Class | SVM [10] | DPRN [27] | M3CNN [28] | GAHT [35] | SF [32] | CS2DT [33] | MVAHN [40] | Ours |
|---|---|---|---|---|---|---|---|---|
| 1 | 98.98 ± 1.36 | 96.09 ± 3.13 | 80.47 ± 1.34 | 91.88 ± 5.50 | 93.52 ± 0.31 | 98.91 ± 0.57 | 98.05 ± 0.43 | 88.83 ± 0.84 |
| 2 | 84.79 ± 15.58 | 92.50 ± 11.96 | 55.63 ± 6.34 | 100 ± 0.00 | 99.58 ± 0.51 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 |
| 3 | 98.32 ± 1.30 | 91.85 ± 6.22 | 81.34 ± 1.54 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 |
| 4 | 90.39 ± 3.74 | 94.22 ± 8.87 | 88.92 ± 1.82 | 100 ± 0.00 | 100 ± 0.00 | 99.90 ± 0.20 | 100 ± 0.00 | 100 ± 0.00 |
| 5 | 81.17 ± 3.26 | 72.11 ± 7.69 | 68.91 ± 3.93 | 96.56 ± 2.97 | 87.50 ± 1.31 | 85.86 ± 2.57 | 98.83 ± 0.99 | 98.83 ± 0.43 |
| 6 | 67.73 ± 9.89 | 90.55 ± 10.92 | 71.17 ± 5.05 | 99.69 ± 0.16 | 89.53 ± 1.27 | 98.59 ± 0.80 | 98.44 ± 0.00 | 100 ± 0.00 |
| 7 | 95.12 ± 2.28 | 100 ± 0.00 | 95.20 ± 0.65 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 |
| 8 | 91.09 ± 7.81 | 93.58 ± 12.85 | 83.52 ± 1.52 | 100 ± 0.00 | 99.59 ± 0.21 | 99.69 ± 0.41 | 100 ± 0.00 | 100 ± 0.00 |
| 9 | 84.63 ± 1.84 | 99.33 ± 0.37 | 96.04 ± 1.17 | 100 ± 0.00 | 99.60 ± 0.13 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 |
| 10 | 88.39 ± 5.72 | 92.12 ± 3.00 | 78.31 ± 7.29 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 |
| 11 | 87.72 ± 2.67 | 85.59 ± 0.55 | 82.69 ± 1.61 | 91.45 ± 4.28 | 91.59 ± 1.10 | 92.62 ± 4.15 | 100 ± 0.00 | 100 ± 0.00 |
| 12 | 93.95 ± 2.54 | 89.77 ± 16.50 | 71.63 ± 4.93 | 100 ± 0.00 | 95.35 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 |
| 13 | 84.55 ± 4.65 | 93.25 ± 1.17 | 96.71± 1.80 | 98.98 ± 2.04 | 97.02 ± 0.31 | 100 ± 0.00 | 100 ± 0.00 | 100 ± 0.00 |
| 14 | 90.67 ± 11.62 | 76.89 ± 2.27 | 62.00 ± 1.09 | 93.11 ± 5.51 | 84.67 ± 1.78 | 82.22 ± 0.00 | 87.56 ± 0.44 | 82.22 ± 0.00 |
| OA | 88.08 ± 0.86 | 91.11 ± 3.38 | 81.81 ± 1.22 | 97.93 ± 0.39 | 95.74 ± 0.32 | 97.38 ± 0.11 | 99.25 ± 0.13 | 98.46 ± 0.07 |
| AA | 88.39 ± 1.42 | 90.56 ± 4.09 | 79.47 ± 1.37 | 97.98 ± 0.39 | 95.57 ± 0.20 | 96.99 ± 0.07 | 98.78 ± 0.13 | 97.85 ± 0.06 |
| Kappa | 87.09 ± 0.93 | 90.36 ± 3.68 | 80.26 ± 1.33 | 97.75 ± 0.42 | 95.38 ± 0.34 | 97.16 ± 0.11 | 99.19 ± 0.14 | 98.33 ± 0.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, N.; Jiang, M.; Wang, D.; Jia, Y.; Li, K.; Zhang, Y.; Wang, M.; Luo, J. PGNN-Net: Parallel Graph Neural Networks for Hyperspectral Image Classification Using Multiple Spatial-Spectral Features. Remote Sens. 2024, 16, 3531. https://doi.org/10.3390/rs16183531
Guo N, Jiang M, Wang D, Jia Y, Li K, Zhang Y, Wang M, Luo J. PGNN-Net: Parallel Graph Neural Networks for Hyperspectral Image Classification Using Multiple Spatial-Spectral Features. Remote Sensing. 2024; 16(18):3531. https://doi.org/10.3390/rs16183531
Chicago/Turabian StyleGuo, Ningbo, Mingyong Jiang, Decheng Wang, Yutong Jia, Kaitao Li, Yanan Zhang, Mingdong Wang, and Jiancheng Luo. 2024. "PGNN-Net: Parallel Graph Neural Networks for Hyperspectral Image Classification Using Multiple Spatial-Spectral Features" Remote Sensing 16, no. 18: 3531. https://doi.org/10.3390/rs16183531
APA StyleGuo, N., Jiang, M., Wang, D., Jia, Y., Li, K., Zhang, Y., Wang, M., & Luo, J. (2024). PGNN-Net: Parallel Graph Neural Networks for Hyperspectral Image Classification Using Multiple Spatial-Spectral Features. Remote Sensing, 16(18), 3531. https://doi.org/10.3390/rs16183531







