Salp Swarm Algorithm-Based Kalman Filter for Seamless Multi-Source Fusion Positioning with Global Positioning System/Inertial Navigation System/Smartphones

Abstract

With the rapid development of high-precision positioning service applications, there is a growing demand for accurate and seamless positioning services in indoor and outdoor (I/O) scenarios. To address the problem of low localization accuracy in the I/O transition area and the difficulty of achieving fast and accurate I/O switching, a Kalman filter based on the salp swarm algorithm (SSA) for seamless multi-source fusion positioning of global positioning system/inertial navigation system/smartphones (GPS/INS/smartphones) is proposed. First, an Android smartphone was used to collect sensor measurement data, such as light, magnetometer, and satellite signal-to-noise ratios in different environments; then, the change rules of the data were analyzed, and an I/O detection algorithm based on the SSA was used to identify the locations of users. Second, the proposed I/O detection service was used as an automatic switching mechanism, and a seamless indoor–outdoor localization scheme based on improved Kalman filtering with K-L divergence is proposed. The experimental results showed that the SSA-based I/O switching model was able to accurately recognize environmental differences, and the average accuracy of judgment reached 97.04%. The localization method achieved accurate and continuous seamless navigation and improved the average localization accuracy by 53.79% compared with a traditional GPS/INS system.

1. Introduction

With the rapid development of navigation technology, various navigation sensors and algorithms have emerged [1]. Global navigation satellite systems (GNSSs) are crucial for outdoor positioning. However, in indoor and outdoor (I/O) transition environments, GNSS signals are susceptible to interference from high-rise buildings [2], and the signal strength is significantly lower, which poses a serious challenge for seamless high-precision positioning.

To improve navigation performance in I/O transition areas, an increasing number of researchers are working on solving the problem of localization in occluded environments with weak GNSS signals. An inertial navigation system (INS) is an autonomous navigation system that does not depend on external information or radiate energy to the outside [3]. Its working principle is based on Newton’s laws of mechanics. Information such as velocity, yaw angle, and position in the navigation coordinate system can be obtained by integrating the acceleration of the measured carrier in the inertial reference frame against time and transforming it into the navigation coordinate system [4]. In the case of a poorly received GNSS signal in an occluded environment, such as an indoor environment, INS-assisted fusion Kalman filtering can be used to achieve localization; thus, combined GNSS/INS navigation is a better solution. El-Sheimy et al. proposed a dynamic error model based on an artificial neural network (ANN) to enhance the robustness of INS/GNSS [5]. By integrating navigation and positioning techniques, this method circumvents the limitation that the conventional Bayesian approach requires a priori knowledge to study GNSS signal interruptions, but it requires a large amount of high-quality data for training, and the training process may take a long time and many computational resources [6,7]. A tightly coupled method based on the GNSS carrier phase, an inertial measurement unit (IMU), and ultra-wideband (UWB) was proposed by Jiang et al. [8] and evaluated at predetermined static points, but this method requires a large number of UWB anchors to ensure that there is no rank loss. In [9], a tightly coupled PPP/INS/UWB filter was proposed by Z. Li et al. to improve the performance of PPP/INS. For common problems, such as drift occurring during interruptions of GNSS signals and multipath effects in urban regions [10], an adaptive extended Kalman filter (AKF) can be used for autonomous tuning to accurately analyze the mechanical properties and noise of the system [11,12]. Apart from linearization methods, the unscented Kalman filter (UKF) can handle large modeling errors and tolerate large initial attitude uncertainties through a given nonlinear transformation, but the performance of the UKF is sensitive to parameter settings and requires careful tuning to obtain optimal results [13,14,15]. Researchers have also proposed localization methods for indoor or other sheltered environments with poor GNSS signals, where mobile targets may receive signals with large coarse errors or cannot be positioned using satellites [16]. Because the power consumption and resource deployment of different positioning algorithms differ between indoor and outdoor environments, detecting the location of a smartphone user to apply the appropriate positioning method can improve positioning accuracy while saving resources. Therefore, I/O detection of a user’s location is necessary for better and more seamless positioning.

I/O detection is a step that connects indoor and outdoor environments for seamless positioning. To improve positioning accuracy and cut down power consumption, a multi-source converged localization system triggers specific localization fusion patterns based on I/O detection results [17]. Methods that focus on I/O detection in different environments can be divided into two categories: methods based on immutable detection principles or thresholds and methods based on machine learning. The first method uses immutable thresholds, where a mobile device is assumed to be in a certain environment when the sensor reading is compared with a certain value. P. Zhou et al. [18] used sensors within smartphones, including distance sensors, light sensors, accelerometers, magnetometers, and cellular tower RSS, to distinguish surroundings. However, it is difficult to adapt fixed detection rules or threshold-based methods to various circumstances and equipment. The second method extracts features from embedded smartphone sensors and detects I/O status using machine learning algorithms. MagI/O [19] used machine learning algorithms such as support vector machines (SVMs), gradient boosting machine (GBM), random forest (RF), k-nearest neighbor (kNN), and decision tree (DT) to process magnetic signals for I/O detection. Tests showed that some of the above methods could achieve an accuracy of more than 80% by using magnetic data exclusively. Of the two methods mentioned above, the first approach, which uses fixed thresholds, cannot adapt to different environments, and the second method is based on machine learning. Although the accuracy of the second method is improved to a certain extent compared with the conventional thresholds, it requires a large number of test sets, which greatly increases the workload. After investigation, there is no method for solving I/O detection with optimization algorithms; this is because most of the traditional optimization algorithms need more iterations to converge when dealing with realistic problems, which means slower speed. The salp swarm algorithm (SSA) is a relatively new optimization algorithm that was proposed in 2017 [20] and can quickly and easily solve all kinds of numerical problems in scientific research; it shows higher computational efficiency and convergence speed than those of traditional optimization algorithms, and this low latency and high efficiency are exactly what is needed for indoor and outdoor detection and localization application scenarios.

To solve the problems described above, this study presents an improved Kalman-filtered seamless GPS/INS positioning method based on the SSA. First, an indoor and outdoor switching algorithm based on salp swarm group optimization is proposed. The adaptive function of the SSA was designed, and the adaptive system between biological populations was used to randomly search for the global optimal solution that satisfied the objective function and transform the conventional fixed threshold into real-time dynamic switching parameters, which effectively completed the accurate detection of indoor and outdoor environments without test sets. Second, for transitional or indoor regions with poor-quality GNSS signals, this study achieved continuous localization and orientation across I/O regions by updating the Kalman filter based on combined GPS/INS navigation, and the similarity between the states and observations was assessed through Kullback–Leibler divergence (KL divergence) according to the physical meaning and properties of the data. This approach neither introduced a large dataset, as the neural network approach does, nor did it require the addition of physical devices to ensure localization accuracy, as other approaches do. The main contributions of this study can be summarized as follows:

(1)

A smartphone-based salp swarm-optimized I/O detection algorithm is proposed; it designs a suitable fitness function and searches for optimal dynamic switching parameters to achieve reliable detection in the presence of different devices and environments.

(2)

To perform the evaluation of the proposed algorithm in a classic I/O scenario, the proposed method was compared with several machine-learning- and sensor-data-based detection methods. The experimental results showed that the proposed algorithm achieved higher I/O detection accuracy in complex scenarios than the other algorithms in the test environment.

(3)

The proposed I/O detection service was used as an automatic switching mechanism to achieve accurate and seamless indoor–outdoor localization with an integrated solution based on Kalman filtering improved with Kullback–Leibler divergence.

In the second section of this article, the GPS/INS fusion localization model and the INS error model that serve as the foundation for the fusion algorithm’s design are presented. In addition, the state and observation models are elaborated upon. An I/O detection model based on the SSA as a key-switching algorithm for seamless I/O positioning is presented in Section 2.2. In Section 2.3, an improved Kalman filtering algorithm based on KL divergence is presented. In Section 2.4, the design of a seamless localization system by combining the architectures of the algorithms proposed in Section 2.2 and Section 2.3 is presented. Comparisons of the performance of the proposed scheme via experimental simulations and field experiments are described in Section 3.

2. Materials and Methods

2.1. GPS/INS Fusion Model

2.1.1. GPS/INS State Model

A system model for continuous-time Kalman filtering of the combined GPS/INS navigation system is as follows [21]:

$$\delta \dot{\mathit{x}}=\mathit{F}\delta \mathit{x}+\mathit{Gw}$$

(1)

where $\mathit{w}$ is the process noise, which describes random perturbations that are not considered in the dynamic modeling of the system. $\mathit{G}$ is a noise distribution vector containing the variance associated with the state vector. The following items represent the extent to which the noise source affects the position, velocity, attitude, gyroscope, and acceleration, respectively [22]:

$$\mathit{G}=\left[{\sigma }_{\mathit{r},\mathbf{1}\times \mathbf{3}},{\sigma }_{\mathit{v},\mathbf{1}\times \mathbf{3}},{\sigma }_{\epsilon ,\mathbf{1}\times \mathbf{3}},{\sigma }_{\omega ,\mathbf{1}\times \mathbf{3}},{\sigma }_{\mathit{f},\mathbf{1}\times \mathbf{3}}\right]$$

(2)

$\mathit{F}$ is a dynamic covariance matrix containing the components of the INS error model and can be summarized in the following form:

$$\mathit{F}=\left[\begin{array}{c}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathrm{F}}_{\mathit{r}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}\hfill \\ {\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathrm{F}}_{\mathit{v}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}\hfill \\ {\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathrm{F}}_{\epsilon }{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{R}}_{\mathrm{b}}^{\mathrm{l}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}\hfill \\ {\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathrm{F}}_{\omega }{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}\hfill \\ {\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathrm{F}}_{\mathit{f}}\hfill \end{array}\right]$$

(3)

The state vectors are the error components of the position, velocity, attitude, accelerometer, and gyroscope:

$$\delta {\mathrm{x}}_{\mathbf{15}\times \mathbf{1}}^{\mathit{l}}={\left[\delta {\mathit{r}}_{\mathbf{3}\times \mathbf{1}}^{\mathit{l}}\delta {\mathit{v}}_{\mathbf{3}\times \mathbf{1}}^{\mathit{l}}{\epsilon }_{\mathbf{3}\times \mathbf{1}}^{\mathit{l}}\delta {\omega }_{\mathbf{3}\times \mathbf{1}}\delta {\mathrm{f}}_{\mathbf{3}\times \mathbf{1}}\right]}^T$$

(4)

Therefore, the system model for combined INS/GPS navigation can be written as follows:

$$\begin{array}{c}\hfill \left[\begin{array}{c}\delta {\dot{\mathit{r}}}_{\mathbf{3}\times \mathbf{1}}^{\mathit{l}}\hfill \\ \delta {\dot{\mathit{v}}}_{\mathbf{3}\times \mathbf{1}}^{\mathit{l}}\hfill \\ {\dot{\epsilon }}_{\mathbf{3}\times \mathbf{1}}^{\mathit{l}}\hfill \\ \delta {\dot{\omega }}_{\mathbf{3}\times \mathbf{1}}\hfill \\ \delta {\dot{\mathrm{f}}}_{\mathbf{3}\times \mathbf{1}}\hfill \end{array}\right]=\left[\begin{array}{c}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathrm{F}}_{\mathit{r}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}\hfill \\ {\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathrm{F}}_{\mathit{v}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}\hfill \\ {\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathrm{F}}_{\epsilon }{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{R}}_{\mathrm{b}}^{\mathrm{l}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}\hfill \\ {\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathrm{F}}_{\omega }{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}\hfill \\ {\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathrm{F}}_{\mathit{f}}\hfill \end{array}\right]\ast \left[\begin{array}{c}\delta {\mathit{r}}_{\mathbf{3}\times \mathbf{1}}^{\mathit{l}}\hfill \\ \delta {\mathit{v}}_{\mathbf{3}\times \mathbf{1}}^{\mathit{l}}\hfill \\ {\epsilon }_{\mathbf{3}\times \mathbf{1}}^{\mathit{l}}\hfill \\ \delta {\omega }_{\mathbf{3}\times \mathbf{1}}\hfill \\ \delta {\mathrm{f}}_{\mathbf{3}\times \mathbf{1}}\hfill \end{array}\right]+\left[\begin{array}{c}{\sigma }_{\mathit{r},\mathbf{1}\times \mathbf{3}}\hfill \\ {\sigma }_{\mathit{v},\mathbf{1}\times \mathbf{3}}\hfill \\ {\sigma }_{\epsilon ,\mathbf{1}\times \mathbf{3}}\hfill \\ {\sigma }_{\omega ,\mathbf{1}\times \mathbf{3}}\hfill \\ {\sigma }_{\mathit{f},\mathbf{1}\times \mathbf{3}}\hfill \end{array}\right]\mathit{w}\end{array}$$

(5)

The above equation is discretized, and the system model in discrete time is

$$\delta {\mathrm{x}}_{\mathit{k}}=\left(\mathit{I}+\mathit{F}\Delta t\right)\delta {\mathrm{x}}_{\mathit{k}-\mathbf{1}}+\mathit{G}\Delta t{\mathit{w}}_{\mathit{k}-\mathbf{1}}$$

(6)

$$\begin{array}{c}\hfill \left[\begin{array}{c}\delta {\dot{\mathit{r}}}_{\mathbf{3}\times \mathbf{1}}^{\mathit{l}}\hfill \\ \delta {\dot{\mathit{v}}}_{\mathbf{3}\times \mathbf{1}}^{\mathit{l}}\hfill \\ {\dot{\epsilon }}_{\mathbf{3}\times \mathbf{1}}^{\mathit{l}}\hfill \\ \delta {\dot{\omega }}_{\mathbf{3}\times \mathbf{1}}\hfill \\ \delta {\dot{\mathrm{f}}}_{\mathbf{3}\times \mathbf{1}}\hfill \end{array}\right]=\left[\begin{array}{c}{\mathit{I}}_{\mathbf{3}\times \mathbf{3}}{\mathrm{F}}_{\mathit{r}}\Delta t{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}\hfill \\ {\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathit{I}}_{\mathbf{3}\times \mathbf{3}}{\mathrm{F}}_{\mathit{v}}\Delta t{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{R}}_b^l\Delta t\hfill \\ {\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathrm{F}}_{\epsilon }\Delta t{\mathit{I}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{R}}_{\mathrm{b}}^{\mathrm{l}}\Delta t{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}\hfill \\ {\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathit{I}}_{\mathbf{3}\times \mathbf{3}}+{\mathbf{F}}_{\omega }{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}\hfill \\ {\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathbf{0}}_{\mathbf{3}\times \mathbf{3}}{\mathit{I}}_{\mathbf{3}\times \mathbf{3}}+{\mathbf{F}}_{\mathit{f}}\Delta t\hfill \end{array}\right]\ast \left[\begin{array}{c}\delta {\mathit{r}}_{\mathbf{3}\times \mathbf{1}}^{\mathit{l}}\hfill \\ \delta {\mathit{v}}_{\mathbf{3}\times \mathbf{1}}^{\mathit{l}}\hfill \\ {\epsilon }_{\mathbf{3}\times \mathbf{1}}^{\mathit{l}}\hfill \\ \delta {\omega }_{\mathbf{3}\times \mathbf{1}}\hfill \\ \delta {\mathrm{f}}_{\mathbf{3}\times \mathbf{1}}\hfill \end{array}\right]+\left[\begin{array}{c}{\sigma }_{\mathit{r},\mathbf{1}\times \mathbf{3}}\hfill \\ {\sigma }_{\mathit{v},\mathbf{1}\times \mathbf{3}}\hfill \\ {\sigma }_{\epsilon ,\mathbf{1}\times \mathbf{3}}\hfill \\ {\sigma }_{\omega ,\mathbf{1}\times \mathbf{3}}\hfill \\ {\sigma }_{\mathit{f},\mathbf{1}\times \mathbf{3}}\hfill \end{array}\right]\mathit{w}\end{array}$$

(7)

where $\Delta t$ is the time interval between two consecutive state updates in a discrete-time model.

2.1.2. Inertial Navigation Model

GPS signals are used for the optimal estimation of navigation information, and the results of the optimal estimation are fed back to correct the INS to maintain a high accuracy [23]. Therefore, this study introduces the INS error model as the basis for designing the fusion model, which describes the position, velocity, and attitude errors due to a variety of error sources [24]. In most cases, these models are based on latitude, longitude, and altitude errors, as well as east, north, and vertical velocity errors.

The error state vector of the inertial control system is expressed as follows:

$${\mathrm{x}}_{\mathbf{15}\times \mathbf{1}}^{\mathit{l}}={\left[\delta {\mathit{r}}_{\mathbf{3}\times \mathbf{1}}^{\mathit{l}},\delta {\mathit{v}}_{\mathbf{3}\times \mathbf{1}}^{\mathit{l}},{\epsilon }_{\mathbf{3}\times \mathbf{1}}^{\mathit{l}},\delta {\omega }_{\mathbf{3}\times \mathbf{1}},\delta {\mathrm{f}}_{\mathbf{3}\times \mathbf{1}}\right]}^T$$

(8)

The error linearization model for each part of the above equation in the local-level frame (LLF) system is $\delta {\mathit{r}}^{\mathit{l}}={\left[\delta \phi ,\delta \lambda ,\delta h\right]}^T$, which is the location error vector referring to the error in the latitude, longitude, and elevation estimates of the geographic location.

$$\underset{\delta {\dot{\mathit{r}}}^{\mathit{l}}}{\underbrace{\left[\begin{array}{c}\delta \dot{\phi }\hfill \\ \delta \dot{\lambda }\hfill \\ \delta \dot{h}\hfill \end{array}\right]}}=\underset{{\mathit{F}}_{\mathit{r}}}{\underbrace{\left[\begin{array}{c}0{\displaystyle \frac{1}{\left(R_M+h\right)}}0\hfill \\ {\displaystyle \frac{1}{\left(R_N+h\right)cos\phi }}00\hfill \\ 001\end{array}\right]}}\underset{\delta {\mathit{v}}^{\mathit{l}}}{\underbrace{\left[\begin{array}{c}\delta v_e\hfill \\ \delta v_n\hfill \\ \delta v_u\hfill \end{array}\right]}}$$

(9)

$\delta {\mathit{v}}^{\mathit{l}}={\left[\delta v_e,\delta v_n,\delta v_u\right]}^T$ is a velocity error vector that omits smaller terms and can be succinctly expressed as follows:

$$\underset{\delta \dot{\mathit{v}}}{\underbrace{\left[\begin{array}{c}\delta {\dot{v}}_e\hfill \\ \delta {\dot{v}}_n\hfill \\ \delta {\dot{v}}_u\hfill \end{array}\right]}}=\underset{{\mathit{F}}_{\mathit{v}}}{\underbrace{\left[\begin{array}{c}0f_u-f_n\hfill \\ -f_{u}0f_e\hfill \\ f_n-f_{e}0\end{array}\right]}}\underset{\epsilon }{\underbrace{\left[\begin{array}{c}\delta p\hfill \\ \delta r\hfill \\ \delta A\hfill \end{array}\right]}}+\underset{{\mathit{R}}_{\mathit{b}}^{\mathit{l}}}{\underbrace{\left[\begin{array}{c}{R}_{11}{\mathrm{R}}_{12}{\mathrm{R}}_{13}\hfill \\ R_{21}{\mathrm{R}}_{22}{\mathrm{R}}_{23}\hfill \\ R_{31}{\mathrm{R}}_{32}{\mathrm{R}}_{33}\hfill \end{array}\right]}}\underset{\delta \mathrm{f}}{\underbrace{\left[\begin{array}{c}\delta f_x\hfill \\ \delta f_y\hfill \\ \delta f_z\hfill \end{array}\right]}}$$

(10)

${\epsilon }^{\mathit{l}}={\left[\delta p,\delta r,\delta A\right]}^T$ is the attitude error vector, which can usually be modeled by ignoring the inverse term of the Earth’s radius and the product term of the Earth’s rotation; therefore, the attitude angle error can be simplified by retaining only the first two terms:

$$\begin{array}{c}\hfill {\dot{\epsilon }}^{\mathit{l}}=\underset{{\dot{\epsilon }}^{\mathit{l}}}{\underbrace{\left[\begin{array}{c}\delta \dot{p}\hfill \\ \delta \dot{r}\hfill \\ \delta \dot{A}\hfill \end{array}\right]}}=\underset{{\mathit{F}}_{\epsilon }}{\underbrace{\left[\begin{array}{c}0{\displaystyle \frac{1}{\left(R_M+h\right)}}0\hfill \\ {\displaystyle \frac{-1}{\left(R_N+h\right)}}00\hfill \\ {\displaystyle \frac{-tan\phi }{\left(R_N+h\right)}}00\hfill \end{array}\right]}}\underset{\delta {\mathit{v}}^{\mathit{l}}}{\underbrace{\left[\begin{array}{c}\delta v_e\hfill \\ \delta v_n\hfill \\ \delta v_u\hfill \end{array}\right]}}+{\mathit{R}}_{\mathit{b}}^{\mathit{l}}\underset{\delta \omega }{\underbrace{\left[\begin{array}{c}\delta {\omega }_x\hfill \\ \delta {\omega }_y\hfill \\ \delta {\omega }_z\hfill \end{array}\right]}}\end{array}$$

(11)

$\delta \mathrm{f}={\left[\delta f_x,\delta f_y,\delta f_z\right]}^T$ is the accelerometer error vector, which can be calculated with the following equation:

$$\underset{\delta {\dot{\mathrm{f}}}^{\mathit{b}}}{\underbrace{\left[\begin{array}{c}\delta f_x\hfill \\ \delta f_y\hfill \\ \delta f_z\hfill \end{array}\right]}}=\underset{{\mathit{F}}_{\mathit{f}}}{\underbrace{\left[\begin{array}{c}-{\beta }_{fx}00\hfill \\ 0-{\beta }_{fy}0\hfill \\ 00-{\beta }_{fx}\end{array}\right]}}\underset{\delta {\mathrm{f}}^{\mathit{b}}}{\underbrace{\left[\begin{array}{c}\delta f_x\hfill \\ \delta f_y\hfill \\ \delta f_z\hfill \end{array}\right]}}+\underset{\sigma \mathit{f}}{\underbrace{\left[\begin{array}{c}\sqrt{2{\beta }_{fx}{\sigma }_{fx}^2}\hfill \\ \sqrt{2{\beta }_{fy}{\sigma }_{fy}^2}\hfill \\ \sqrt{2{\beta }_{fz}{\sigma }_{fz}^2}\hfill \end{array}\right]}}\mathit{w}\left(\mathit{t}\right)$$

(12)

$\delta \omega ={\left[\delta {\omega }_x,\delta {\omega }_y,\delta {\omega }_z\right]}^T$ is the gyroscope error vector. The drift error of the gyroscope is

$$\begin{array}{c}\hfill \delta \dot{\omega }=\underset{\delta \dot{\omega }}{\underbrace{\left[\begin{array}{c}\delta {\dot{\omega }}_x\hfill \\ \delta {\dot{\omega }}_y\hfill \\ \delta {\dot{\omega }}_z\hfill \end{array}\right]}}=\underset{{\mathit{F}}_{\mathit{f}}}{\underbrace{\left[\begin{array}{c}-{\beta }_{\omega x} 00\hfill \\ 0-{\beta }_{\omega y}0\hfill \\ 00-{\beta }_{\omega x}\end{array}\right]}}\underset{\delta \omega }{\underbrace{\left[\begin{array}{c}\delta {\omega }_x\hfill \\ \delta {\omega }_y\hfill \\ \delta {\omega }_z\hfill \end{array}\right]}}+\underset{\sigma \omega }{\underbrace{\left[\begin{array}{c}\sqrt{2{\beta }_{\omega x}{\sigma }_{\omega x}^2}\hfill \\ \sqrt{2{\beta }_{\omega y}{\sigma }_{\omega y}^2}\hfill \\ \sqrt{2{\beta }_{\omega z}{\sigma }_{\omega z}^2}\hfill \end{array}\right]}}\mathit{w}\left(\mathit{t}\right)\end{array}$$

(13)

2.1.3. GPS/INS Observation Model

The discrete KF measurement model is expressed as follows:

$$\delta {\mathit{z}}_{\mathit{k}}={\mathit{H}}_{\mathit{k}}\delta {\mathrm{x}}_{\mathit{k}}+{\eta }_{\mathit{k}}$$

(14)

where the second term on the right-hand side of the equation represents the zero-mean measurement noise with covariance ${\mathit{R}}_{\mathit{k}}$.

Because the state vector of the KF contains the error in the INS, the corresponding measurement vector consists of the difference between the velocity and position predicted with the INS and the position and velocity measured with GPS [25].

$$\delta {\mathit{z}}_{\mathit{k}}=\left[\begin{array}{c}{\mathit{r}}_{\mathit{INS}}^{\mathit{l}}-{\mathit{r}}_{\mathit{GPS}}^{\mathit{l}}\hfill \\ {\mathit{v}}_{\mathit{INS}}^{\mathit{l}}-{\mathit{v}}_{\mathit{GPS}}^{\mathit{l}}\hfill \end{array}\right]=\left[\begin{array}{c}{\phi }_{INS}-{\phi }_{GPS}\hfill \\ {\lambda }_{INS}-{\lambda }_{GPS}\hfill \\ h_{INS}-h_{GPS}\hfill \\ v_{e,INS}-v_{e,GPS}\hfill \\ v_{n,INS}-v_{n,GPS}\hfill \\ v_{u,INS}-v_{u,GPS}\hfill \end{array}\right]$$

(15)

${\mathit{H}}_{\mathit{k}}$ is the measurement matrix at time $t_k$, which describes the measured values obtained using a linear combination of the state variables without noise ${\mathit{z}}_{\mathit{k}}$, as follows:

$${\mathit{H}}_{\mathit{k}}=\left[{\mathit{I}}_{\mathbf{6}\times \mathbf{6}}{0}_{\mathbf{6}\times \mathbf{9}}\right]$$

(16)

The complete measurement model can then be written as follows:

$$\left[\begin{array}{c}{\mathit{r}}_{\mathit{INS}}^{\mathit{l}}-{\mathit{r}}_{\mathit{GPS}}^{\mathit{l}}\hfill \\ {\mathit{v}}_{\mathit{INS}}^{\mathit{l}}-{\mathit{v}}_{\mathit{GPS}}^{\mathit{l}}\hfill \end{array}\right]=\left[\begin{array}{c}{\mathit{I}}_{\mathbf{3}\times \mathbf{3}}{0}_{\mathbf{3}\times \mathbf{3}}{0}_{\mathbf{3}\times \mathbf{9}}\hfill \\ 0_{\mathbf{3}\times \mathbf{3}}{\mathrm{I}}_{\mathbf{3}\times \mathbf{3}}{0}_{\mathbf{3}\times \mathbf{9}}\hfill \end{array}\right]+\left[\begin{array}{c}{\eta }_{\mathit{r}}\hfill \\ {\eta }_{\mathit{v}}\hfill \end{array}\right]$$

(17)

It can be expanded to obtain the following:

$$\begin{array}{c}\hfill \left[\begin{array}{c}{\phi }_{INS}-{\phi }_{GPS}\hfill \\ {\lambda }_{INS}-{\lambda }_{GPS}\hfill \\ h_{INS}-h_{GPS}\hfill \\ v_{e,INS}-v_{e,GPS}\hfill \\ v_{n,INS}-v_{n,GPS}\hfill \\ v_{u,INS}-v_{u,GPS}\hfill \end{array}\right]={\left[{\mathit{I}}_{\mathbf{6}}{0}_{\mathbf{6}\times \mathbf{10}}\right]}_k+{\left[\begin{array}{c}{\eta }_{\phi }\hfill \\ {\eta }_{\lambda }\hfill \\ {\eta }_h\hfill \\ {\eta }_{ve}\hfill \\ {\eta }_{vn}\hfill \\ {\eta }_{vu}\hfill \end{array}\right]}_k\end{array}$$

(18)

In addition, there are two important covariance matrices: ${\mathit{R}}_{\mathit{k}}$ and ${\mathit{P}}_{\mathit{k}}$. ${\mathit{R}}_{\mathit{k}}$ contains the variance on the diagonal of the measured state, which is defined as

$${\mathit{R}}_{\mathit{k}}=diag({\sigma }_{\varphi }^2,{\sigma }_{\lambda }^2,{\sigma }_h^2,{\sigma }_{ve}^2,{\sigma }_{vn}^2,{\sigma }_{vu}^2)$$

(19)

The covariance of the predicted state $P_k$ is a diagonal matrix consisting of the variances on a diagonal.

$${\mathit{P}}_{\mathit{k}}=diag\left({\sigma }_{\mathit{r},\mathbf{3}\times \mathbf{3}}^{\mathbf{2}},{\sigma }_{\mathit{v},\mathbf{3}\times \mathbf{3}}^{\mathbf{2}},{\sigma }_{\epsilon ,\mathbf{3}\times \mathbf{3}}^{\mathbf{2}},{\sigma }_{\mathit{w},\mathbf{3}\times \mathbf{3}}^{\mathbf{2}},{\sigma }_{\mathit{f},\mathbf{3}\times \mathbf{3}}^{\mathbf{2}}\right)$$

(20)

where the variance term of each diagonal element is also a 3 × 3 diagonal matrix related to the position, velocity, attitude, gyroscope bias, and accelerometer bias.

Based on the mathematical model of combined GPS/INS navigation, to effectively manage the resources for rapid positioning and improve the positioning accuracy, according to the user’s location, indoor areas, outdoor areas, and the edge of the two (for rapid switching) are used to find the optimal positioning algorithm and to select the optimal positioning method; this study adopts an I/O detection algorithm based on salp swarm optimization to detect the user’s location in order to improve the response speed and accuracy of positioning.

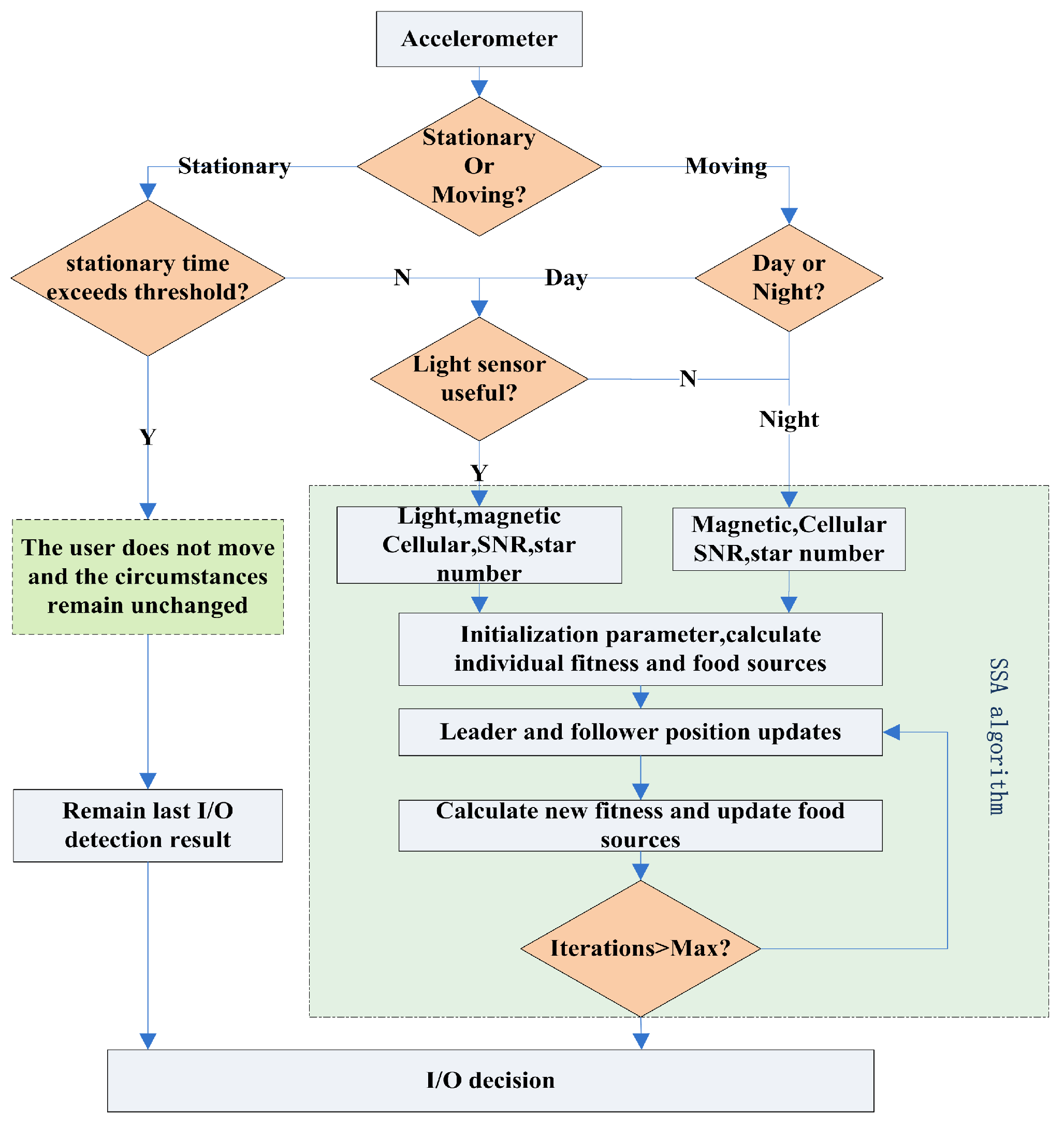
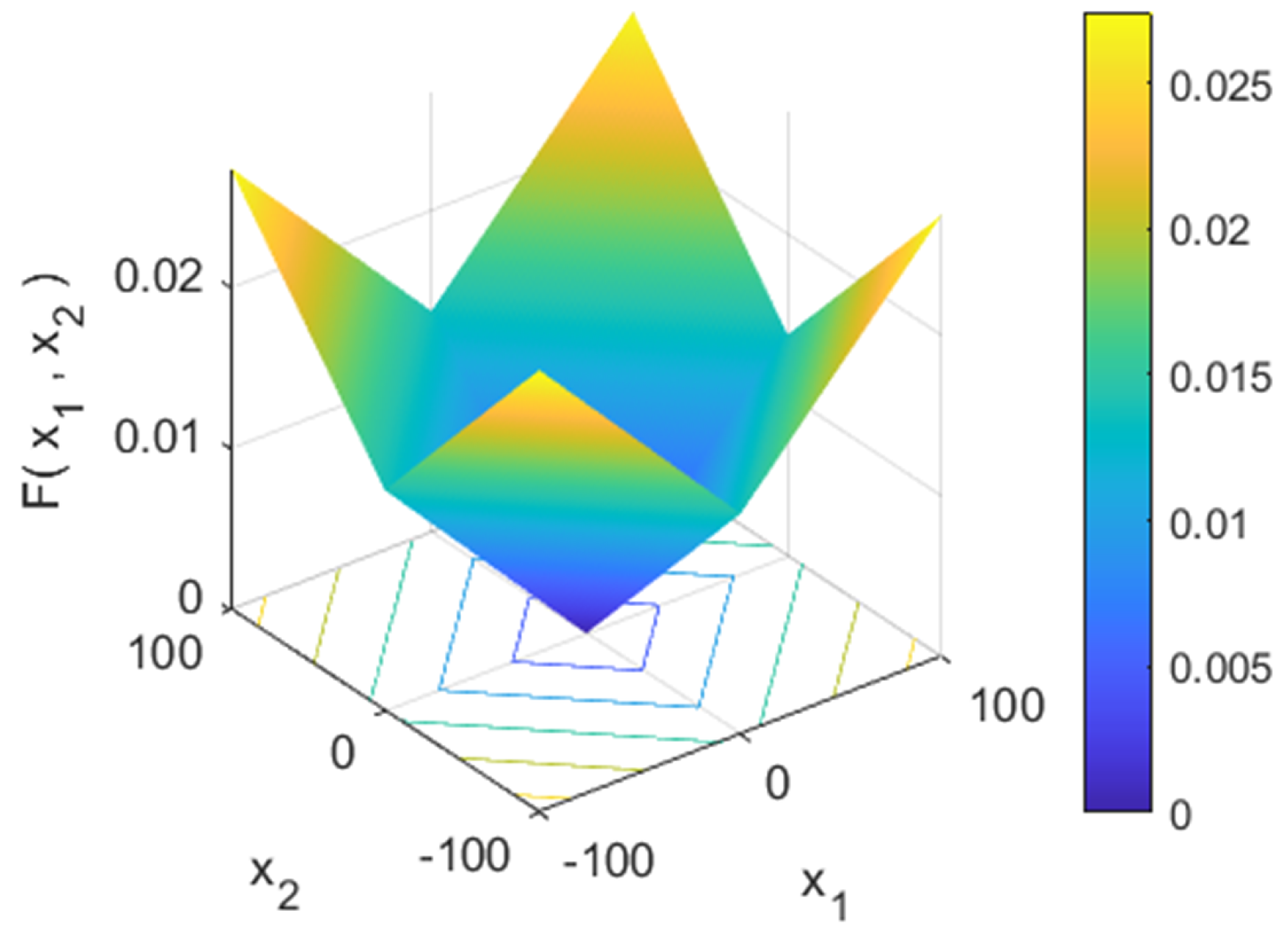
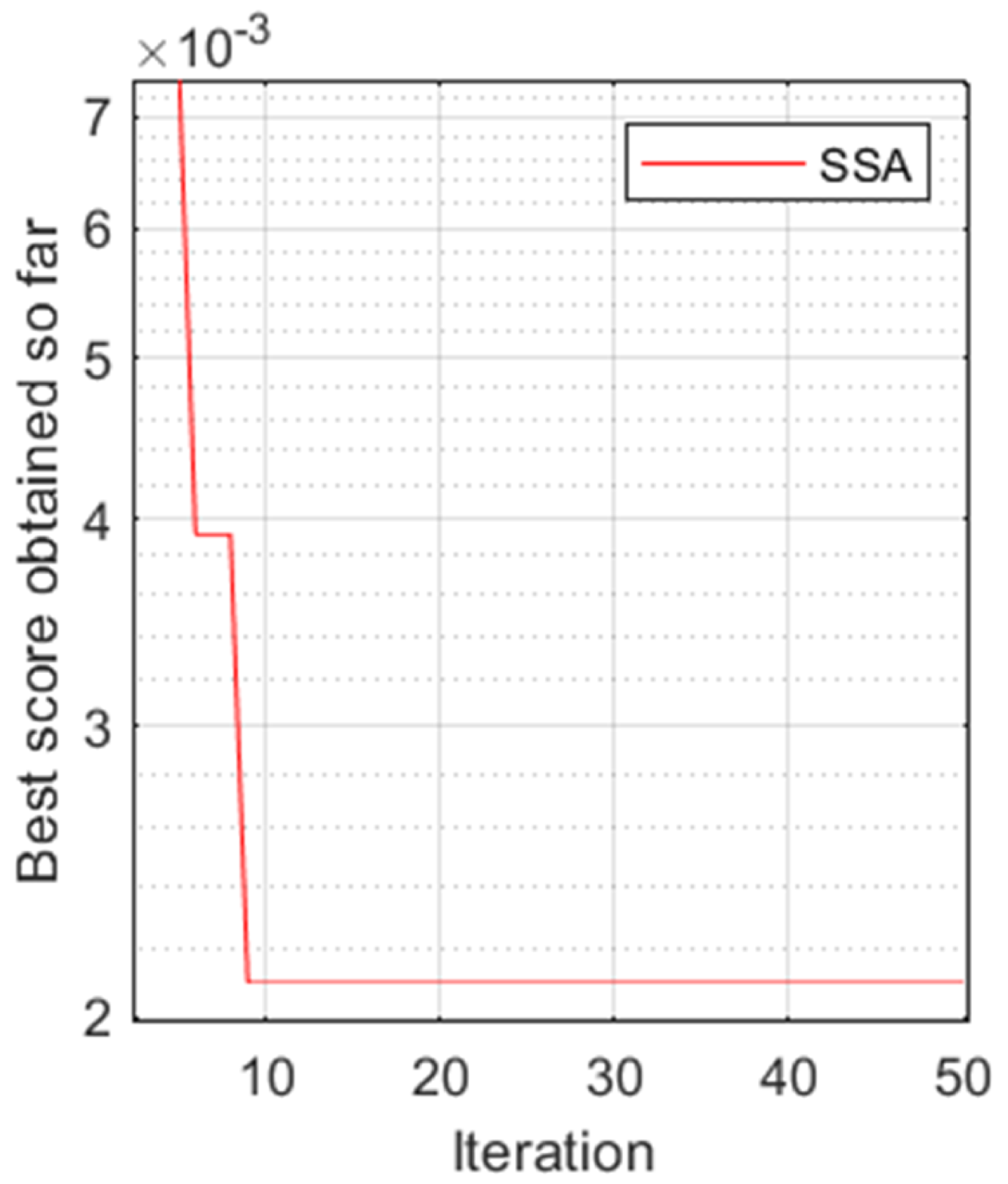
2.2. Indoor/Outdoor Detection Algorithm Based on Salp Swarm Optimization

When conducting I/O detection, existing algorithms, such as machine learning methods, not only require a large number of datasets for testing but also have a large time delay and low efficiency, while traditional threshold-switching algorithms have low accuracy and are not flexible enough; however, the SSA works quickly and easily to solve all kinds of numerical problems in scientific research, and it shows high computational efficiency and convergence speed compared with traditional optimization algorithms; this low latency and high efficiency are exactly what is needed for I/O detection and localization application scenarios. Therefore, this section proposes an I/O detection method based on swarm intelligence optimization as an important part of a seamless navigation system. In this study, the focus was on the localization problem on a two-dimensional plane. Therefore, the search space can be represented as $N\times 2$, N is the size of the salp swarm population, and j is the kinetic model dimension [26]. The food in the space can be represented as $\mathit{F}=\left[F_1,F_2\right]$, which represents the optimal parameter for switching between indoor and outdoor environments; the position matrix of the salp swarm in the candidate solution space is $\mathit{X}=\left[X_{n1},X_{n2}\right]$, the upper bound of the search space is $\mathit{ub}=\left[u{b}_1,u{b}_2\right]$, and the lower boundary is $\mathit{lb}=\left[l{b}_1,l{b}_2\right]$. The population initialization formula is as follows:

$$X_{j\times N}=rand\left(j,N\right)·\left(ub\left(j,N\right)-lb\left(j,N\right)\right)+lb\left(j,N\right)$$

(21)

where $X_j^i$ denotes the jth dimension of the ith follower individual because this study was conducted in two dimensions: $j=1,2,i=1,2,3,4,...,N$; N is the follower serial number.

When developing the adaptation function of the SSA, it was taken into account that it must be able to distinguish between different environments. Therefore, sensor data were selected for I/O environments with large differences or with a specific pattern of change.

According to observations, the main source of light in indoor environments comes from artificial light sources, such as incandescent and fluorescent lamps [27]. Outdoors, sunlight is the main source of light during the day. Therefore, the difference in light intensity between I/O scenarios is large, so it can be used as a basis for differentiation. Other sensor data selected in this study, such as the cellular RSSI, magnetic field strength, satellite signal-to-noise ratio, and the number of visible satellites, also have certain change patterns in I/O areas and in the transition area, which can be used to construct an objective function.

By constructing a correlation matrix based on the observation data obtained from each sensor and summarizing the principle of solving for the optimal switching coefficients in matrix form, the following relationship equation can be obtained:

$$\mathit{E}=\mathit{FY}$$

(22)

where $\mathit{Y}$ is the estimated weight, $\mathit{E}$ is the matrix of coefficients associated with each sensor, and $\mathit{F}$ is the correlation matrix of the collected data.

Owing to the effects of the measurement error, the above equation can be expressed as follows:

$$\widehat{\mathit{E}}=\widehat{\mathit{F}}\mathit{X}$$

(23)

Therefore, the problem of determining the optimal switching parameters can be treated as a problem of finding the optimal weights, which can be solved by applying an intelligent optimization algorithm.

The objective function can be constructed as follows:

$$min\mathit{Y}\left(\widehat{\mathit{D}},\mathit{x}\right)=\left({\displaystyle \frac{1}{\widehat{\mathit{D}}-\mathit{D}}}\times \left|\mathit{x}\right|\right){\left({\displaystyle \frac{1}{\widehat{\mathit{D}}-\mathit{D}}}\times \left|\mathit{x}\right|\right)}^T$$

(24)

The fitness function for evaluating the individuals in the SSA algorithm is, then,

$$f\left(X\right)=\sum _{i=1}^M{\left({\displaystyle \frac{1}{\widehat{{\mathit{D}}_{\mathit{i}}}-\mathit{D}}}\times \left|\mathit{x}\right|\right)\left({\displaystyle \frac{1}{\widehat{{\mathit{D}}_{\mathit{i}}}-\mathit{D}}}\times \left|\mathit{x}\right|\right)}^T$$

(25)

where ${\widehat{\mathit{D}}}_{\mathit{i}}$ is the measured value of the sensor at the ith moment, $\mathit{D}$ is the constant at which the sensor can distinguish between indoor and outdoor switching, and $\mathit{x}$ is the optimal solution found by the salp swarm; the weights are used to calculate the optimal parameters for I/O switching.

The SSA aims to find the optimal value by simulating the feeding and movement processes of salps. The population is divided into two types, leaders and followers, with each accounting for 50% of the total number of individuals in the swarm [28]. The two types of salp individuals use different methods to update their positions during the feeding process, with the leader’s position being updated as follows [29]:

$$x_i^j=\left\{\begin{array}{c}{F}_d+c_1\left(\left(ub-lb\right)c_2+lb\right){\mathrm{c}}_3\ge 0.5\hfill \\ F_d-c_1\left(\left(ub-lb\right)c_2+lb\right){\mathrm{c}}_3<0.5\hfill \end{array}\right.$$

(26)

where $F_d$ is the dth dimensional variable of the food location, and $c_2$ and $c_3$ are random numbers from 0 to 1. $c_2$ is the convergence factor, which controls the convergence speed and stability of the algorithm. $c_3$ determines the direction of movement of $x_i$, enhances diversity, and provides a global search function. $c_1$ stands for the boundary range, which determines the breadth of the algorithm’s search in the solution space. Whether the algorithm performs a global or local search is controlled by $c_1$; a global search is performed when $c_1>1$, and a local search is performed when $c_1<1$. $c_1$ is determined by the following equation:

$$c_1=2e^{-{\left({\displaystyle \frac{4t}{T_{max}}}\right)}^2}$$

(27)

where t is the current iteration number and $T_{max}$ is the maximum iteration number.

The movement of the follower salp individuals follows Newton’s second law of motion, and their positions change as follows:

$$X_d^{m^{\prime }}=X_d^m+{\displaystyle \frac{1}{2}}\left(X_d^{m-1}-X_d^m\right)={\displaystyle \frac{X_d^m+X_d^{m-1}}{2}}$$

(28)

where $X_d^m$ indicates that the mth follower was located in the dth dimension before the update, and $X_d^{m^{\prime }}$ represents the orientation of the follower after the update. The correction process for particles outside the value interval is performed as follows:

$$x_i^j\left(t\right)=j_{min}+rand\left(0,1\right)\left(j_{max}-j_{min}\right)$$

(29)

Based on the characteristics of I/O multi-sensors combined with the structural features of salps and search history information, the fitness function within the population constraint is optimized, and an I/O switching algorithm based on the salp swarm optimization algorithm is proposed. The specific steps are as follows:

Step 1: Initialize parameters: The maximum number of iterations is initialized; the number of salp populations represents the dimensional value of the number of sensors of multiple types, and the upper and lower bounds of the populations in each dimension space represent the upper and lower values of the variation in the weight ranges of each sensor.

Step 2: The individual fitness values are calculated, and the optimal solution is selected. The location of the salp swarm with the optimal adaptation value to be updated is selected as the food source, and it is used as the optimal solution; i.e., the weights of the current optimal switching parameters are calculated.

Step 3: The salp groups are divided into two parts: leaders and followers. The leaders are in the first half, and the followers are in the second half. The leaders update their positions according to (26), which makes it easier to explore and develop resources near the current optimal solution, and the followers update their positions according to (28).

Step 4: The fitness value is recalculated. After completing these steps, the fitness values of the salps are recalculated, the salp position corresponding to the optimal fitness value is selected, and the optimal solution is updated.

Step 5: The iteration conditions are determined. If it is greater than the maximum number of iterations, the optimal solution, i.e., the optimal fitness value and optimal position, is output, and the algorithm ends. If it was less than the maximum number of iterations, steps 3 and 4 are repeated.

Based on the salp swarm optimization model, a novel I/O detection model based on the fusion of smartphone sensors was proposed. The model consists of two main processing stages: in the first stage, data such as the light magnetic field of a user’s environment are collected using smartphone sensors, and in the second stage, the data collected from multiple sensors are input into the SSA model for prediction. A flowchart of the switching algorithm based on optimization with the SSA is shown in Figure 1.

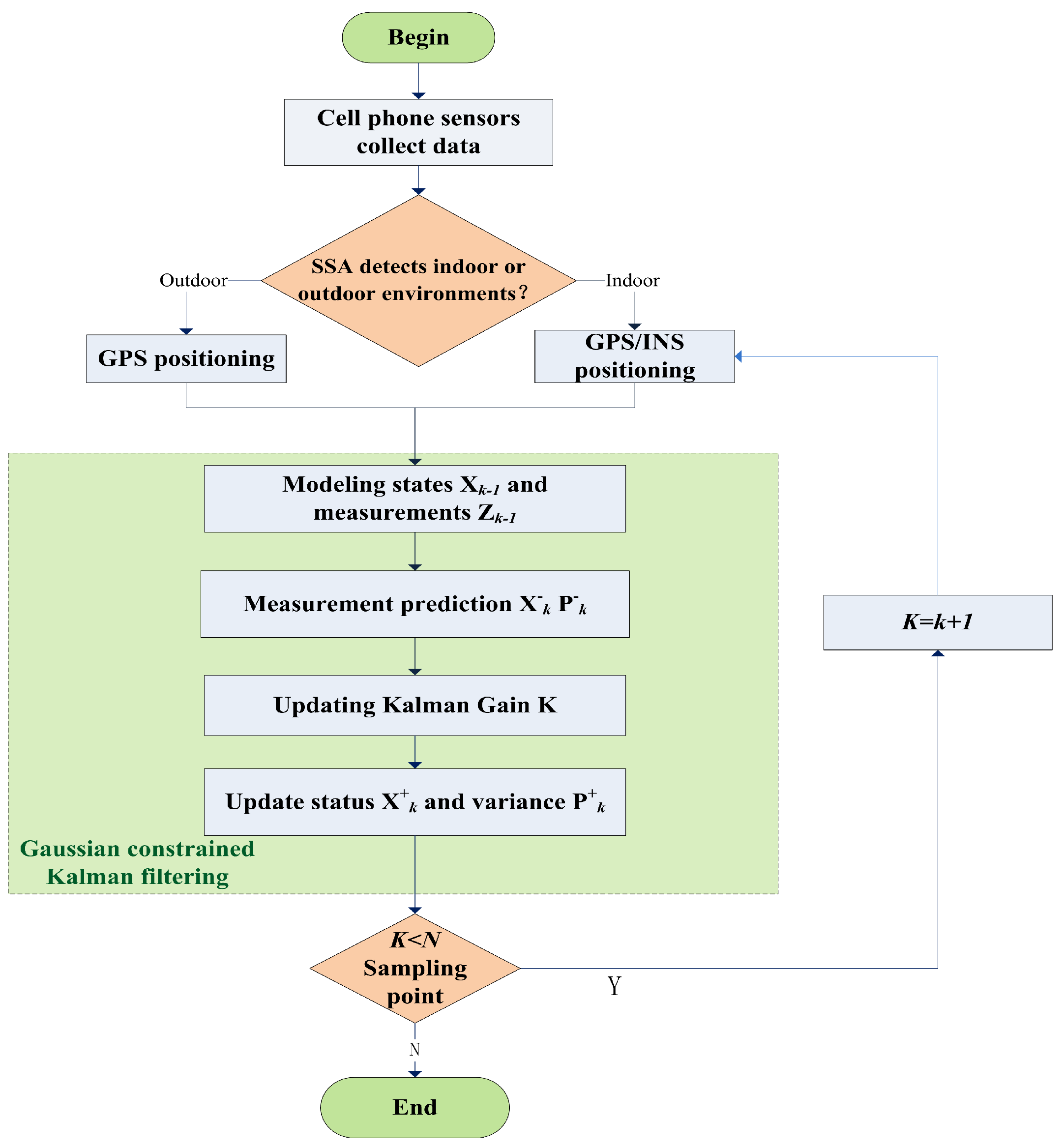
2.3. Improved Kalman Filtering Algorithm Based on Kullback–Leibler Divergence

To further improve the accuracy and reliability of fusion localization in indoor and outdoor transition regions, the a posteriori estimation of the Kalman filter was updated based on the physical meaning and characteristics of the data by evaluating the degree of similarity between the state and the observation, and the equations for updating the variables in the conventional Kalman filter were changed to improve the stability of the filter and the accuracy of the fusion localization.

By estimating the state of the system at moment k from the information at moment $k-1$, supposing that the system noise is zero-mean, the state estimate at moment k is expressed as follows [30]:

$${\widehat{\mathrm{x}}}_{\mathit{k}}\left(-\right)={\mathbf{\Phi }}_{\mathit{k},\mathit{k}-\mathbf{1}}{\widehat{\mathrm{x}}}_{\mathit{k}-\mathbf{1}}\left(+\right)$$

(30)

At the same time, Kalman filtering also transfers the uncertainty from the previous moment $k-1$ to the next moment k. The indeterminacy is expressed through the error covariance ${\mathit{P}}_{\mathit{k}}\left(-\right)$: [31]:

$${\mathit{P}}_{\mathit{k}}\left(-\right)={\mathbf{\Phi }}_{\mathit{k},\mathit{k}-\mathbf{1}}{\mathit{P}}_{\mathit{k}-\mathbf{1}}\left(+\right){\mathbf{\Phi }}_{\mathit{k},\mathit{k}-\mathbf{1}}^{\mathit{T}}+{\mathit{G}}_{\mathit{k}-\mathbf{1}}{\mathit{Q}}_{\mathit{k}-\mathbf{1}}{\mathit{G}}_{\mathit{k}-\mathbf{1}}^{\mathit{T}}$$

(31)

where $\mathit{P}$ is the state covariance matrix, and $\mathit{Q}$ is the input covariance matrix.

If the state ${\mathit{x}}_{\mathit{k}}$ follows a Gaussian distribution as follows:

$$f_x=N\left(x\left|\mu \left(-\right),p\left(-\right)\right.\right)$$

(32)

The posterior is then calculated according to the following formula:

$$f_{x\left|z\right.}\propto f_{x}N\left(z\left|\mathrm{\Phi },R\right.\right)$$

(33)

In the presence of additive noise, the a posteriori Kalman estimate is normally computed using general Gaussian filtering (GGF) equations [32]. In the GGF solution process, there exists an implicit condition: the state variables ${\mathit{x}}_{\mathit{k}}$ and the observed variables ${\mathit{z}}_{\mathit{k}}$ obey a joint Gaussian distribution. However, the variables ${\mathit{x}}_{\mathit{k}}$ and ${\mathit{z}}_{\mathit{k}}$ usually do not follow a strict Gaussian distribution, which makes the prediction error large and may lead to prediction bias. Therefore, the equations are updated by evaluating the similarity between ${\mathit{x}}_{\mathit{k}}$ and ${\mathit{z}}_{\mathit{k}}$ and then calculating the Kalman gain from it.

The Kullback–Leibler divergence (KL divergence) measures the degree of difference between two probability distributions; when the KL divergence is larger, it indicates a greater degree of difference between the two, while when the KL divergence is smaller, it indicates a greater degree of similarity between both. Given two distributions $p\left(x\left|y\right.\right)$ and $q\left(x\right)$, the forward KL divergence is defined as

$$D_{KL}\left(q∥p\right)=\int q\left(x\right)ln{\displaystyle \frac{q\left(x\right)}{p\left(x\left|y\right.\right)}}dx$$

(34)

For the nonlinear Kalman filtering problem, the posterior is on the latent state vector ${\mathit{x}}_{\mathit{k}}$ and, thus, is intractable. Therefore, as is often the case, $D_{KL}$ is not calculable. Instead, variational inference [33,34] uses the identity

$$lnp\left(y\right)=\mathcal{L}\left(q,p\left(y,x\right)\right)+KL\left[q\left(x\right)∥p\left(x\left|y\right.\right)\right]$$

(35)

where

$$\mathcal{L}\left(q,p\left(y,x\right)\right)=\int q\left(x\right)ln{\displaystyle \frac{p\left(y,x\right)}{q\left(x\right)}}dx$$

(36)

Paisley et al. [35] proposed a stochastic method for sampling unbiased gradients of $\mathcal{L}$, allowing for approximation-free minimization of the forward KL divergence using stochastic gradient descent. The following equation was obtained from the literature:

$$\mathcal{L}={}_q\left[f\left(x_t\right)\right]+{}_q\left[lnp\left(x_t\right)\right]-{}_q\left[lnq\left(x_t\right)\right]$$

(37)

$$f\left(x_t\right)=-{\displaystyle \frac{1}{2}}{\left(y_t-h\left(x_t\right)\right)}^T{R}^{-1}\left(y_t-h\left(x_t\right)\right)$$

(38)

Thus, the problem of finding the minimum of the divergence is transformed into finding the gradient of $\mathcal{L}$. By finding the gradient of the mean and variance of $\mathcal{L}$ separately such that ${\nabla }_{\widehat{\mu }}\mathcal{L}=0$ and ${\nabla }_{\widehat{\Sigma }}\mathcal{L}=0$, the a posteriori parameters can be derived.

The above is the process of using divergence to describe the degree of similarity between two variables—the state and the observation—and of solving for the Kalman posterior parameter by finding its minimum value.

According to [36], the degree of similarity between the state and the observation in Kalman filtering can be calculated as follows:

$$D_{KL}\left({\mathit{x}}_{\mathit{k}}\left|\right|{\mathit{z}}_{\mathit{k}}\right)={\displaystyle \frac{1}{2}}log\left|\mathit{I}+{\mathit{R}}^{-\mathbf{1}}\chi \right|$$

(39)

where

$$\chi =\sum _X\sum _Z\left(\left({\mathit{z}}_{\mathit{k}}-{\mathit{z}}_{\mathit{k}-\mathbf{1}}\right){\left({\mathit{z}}_{\mathit{k}}-{\mathit{z}}_{\mathit{k}-\mathbf{1}}\right)}^T-{\Psi }^T{\left(\mathit{P}\left(-\right)\right)}^{-1}\Psi \right)$$

(40)

The Kalman gain can be derived from the KL-divergence as follows:

$$\tilde{\mathit{K}}=\Psi {\varpi }^{\mathit{T}}{\left(\sum _Z\left({\mathit{z}}_{\mathit{k}}-{\mathit{z}}_{\mathit{k}-\mathbf{1}}\right){\left({\mathit{z}}_{\mathit{k}}-{\mathit{z}}_{\mathit{k}-\mathbf{1}}\right)}^T+\mathit{R}\right)}^{-1}$$

(41)

where

$$\Psi =\sum _X{\sum _Z\left({\mathit{x}}_{\mathit{k}}-\mu \left(-\right)\right)\left({\mathit{z}}_{\mathit{k}}-{\mathit{z}}_{\mathit{k}-\mathbf{1}}\right)}^T$$

(42)

$\tilde{\chi }$ is the diagonal matrix of $\chi$ and is defined as follows:

$$\tilde{\chi }=\varpi \chi {\varpi }^{\mathit{T}}$$

(43)

When a new measurement $z_k$ is acquired at moment $t_k$, it is compared with the predicted measurement ${\mathit{H}}_{\mathit{k}}{\widehat{\mathrm{x}}}_{\mathit{k}}\left(-\right)$ based on a priori state estimation.

$$\mathit{e}={\mathit{z}}_{\mathit{k}}-{\mathit{H}}_{\mathit{k}}{\widehat{\mathit{x}}}_{\mathit{k}}(-)$$

(44)

The two errors are weighted using $\mathit{K}$, and the state vector prediction is updated to produce the best estimate as follows:

$${\widehat{\mathrm{x}}}_{\mathit{k}}\left(+\right)={\widehat{\mathrm{x}}}_{\mathit{k}}\left(-\right)+{\mathit{K}}_{\mathit{k}}\left[{\mathit{z}}_{\mathit{k}}-{\mathit{H}}_{\mathit{k}}{\widehat{\mathrm{x}}}_{\mathit{k}}\left(-\right)\right]$$

(45)

In the update phase, the mean and variance of the posterior values are estimated as follows:

$$\mu \left(+\right)=\mu \left(-\right)+\mathit{K}\left({\mathit{Z}}_{\mathit{k}}-{\mathit{Z}}_{\mathit{k}-\mathbf{1}}\right)$$

(46)

$$\mathit{P}\left(+\right)=\mathit{P}\left(-\right)-\mathit{K}\sum _Z\left(\left({\mathit{z}}_{\mathit{k}}-{\mathit{z}}_{\mathit{k}-\mathbf{1}}\right){\left({\mathit{z}}_{\mathit{k}}-{\mathit{z}}_{\mathit{k}-\mathbf{1}}\right)}^T+\mathit{R}\right){\mathit{K}}^{\mathit{T}}$$

(47)

The improved Kalman filtering algorithm based on KL divergence continues the I/O detection algorithm proposed in the previous section. If the user’s location is detected as an I/O transition region, the algorithm establishes a dynamic model ${\widehat{\mathrm{x}}}_{k-1}\left(+\right)$ and a measurement model $Z_k$ based on the state vectors of the user’s position, velocity, etc., acquired by each sensor, in accordance with traditional Kalman filtering. Specifically, the a priori information in the prediction phase remains unchanged, and based on the state transfer equations and control inputs of the system, the next state’s ${\widehat{\mathrm{x}}}_k\left(-\right)$ is predicted, and the uncertainty of the predicted state is estimated, i.e., $P_k\left(-\right)$, (41) is used instead of the traditional Kalman gain K in the updating phase; the covariance matrices of the state estimation ${\widehat{\mathrm{x}}}_k\left(+\right)$ and the state uncertainty $P_k\left(+\right)$ are updated based on the values of K according to (45) and (47), respectively, to obtain the next moment of the user’s state information. A flowchart of the above algorithm is shown in Figure 2.

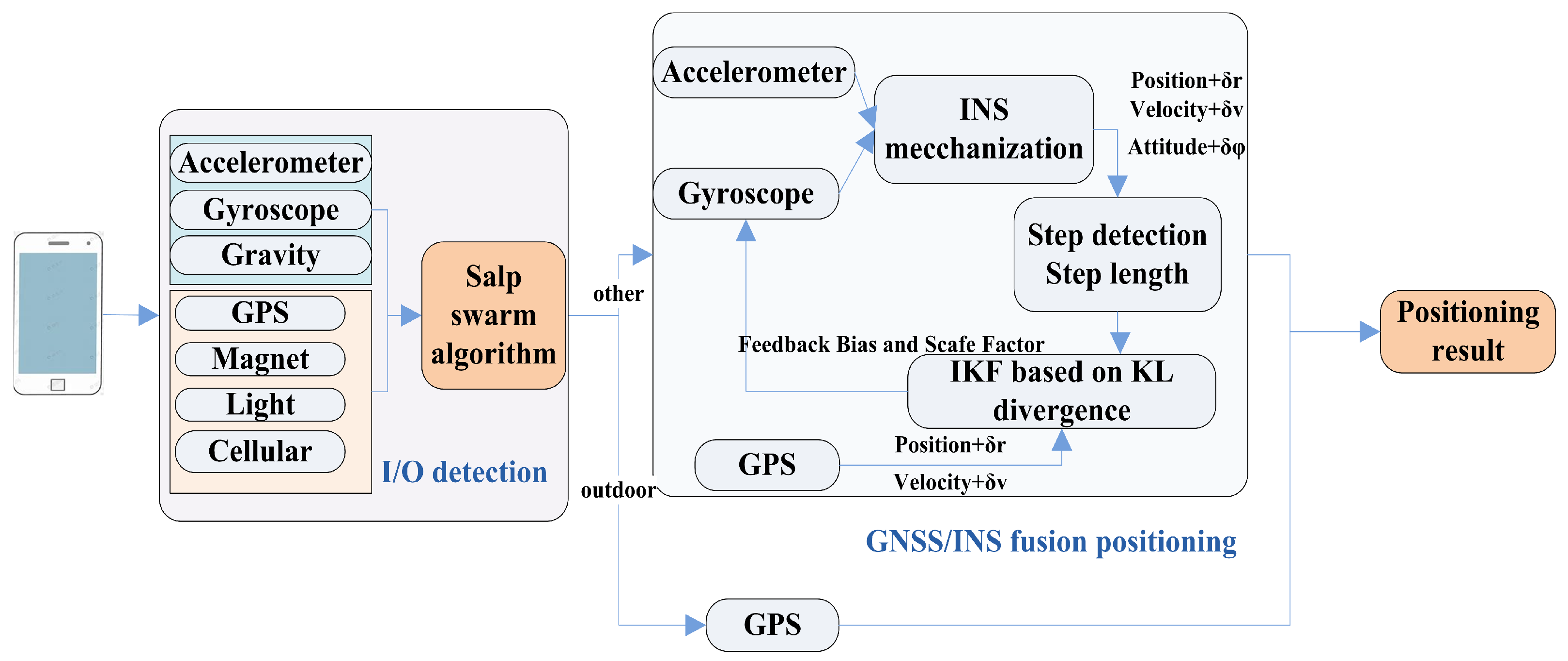
2.4. System Architecture

Considering the poor GPS signals in indoor and other sheltered environments, a moving target may receive signals with large coarseness or may not be able to use satellite positioning, which may significantly degrade navigation performance. Therefore, precise partitioning of I/O scenes is necessary to achieve robust localization. In this study, a seamless I/O positioning algorithm is proposed based on optimization with the SSA. Multiple sensors of a smartphone were used to collect data and analyze the rules. By constructing a suitable performance function, the salp swarm optimization algorithm was used to determine whether the user was indoors or outdoors. In outdoor environments, GPS was used for positioning, and the GPS signal was weakened in the transition area. In this case, the INS was used to assist the GPS data, and the positioning was realized with a fusion Kalman filter improved with KL divergence. An improved Kalman filter system model and a measurement model based on KL divergence were established, and the information about the user’s posture was obtained through integrated multi-sensor navigation. This method compensates for the shortcomings of single-navigation-system localization, such as lost locks in GPS satellite signals, low-frequency data updates, and an inability to obtain attitude information.

As shown in Figure 3, the seamless indoor–outdoor positioning system is divided into two parts. The first part is I/O detection, which includes GPS data collected from multiple sensors, magnetic field strength, light intensity, and other information to analyze the environment where the user is located using the SSA scheme, and the second part is the improved GPS/INS positioning, which matches the corresponding positioning algorithms based on the environmental results calculated in the previous step. If the detection result is outdoors, the traditional precise point positioning method using GPS fully provides the required accuracy for navigation; if the detection results are indoors or in a transition area, the fusion positioning method proposed in this study meets the accuracy requirement. The use of integrated GPS/INS schemes in environments with poor GPS signals together with improvement due to the use of the K-L divergence in the relationship between the state and the observation can improve the accuracy of localization indoors or in other complex environments where GPS signals are attenuated. The proposed algorithm improves the performance of conventional INS/GPS during seamless indoor and outdoor localization, and this integration scheme provides a theoretical basis for achieving higher performance with low-cost sensors.

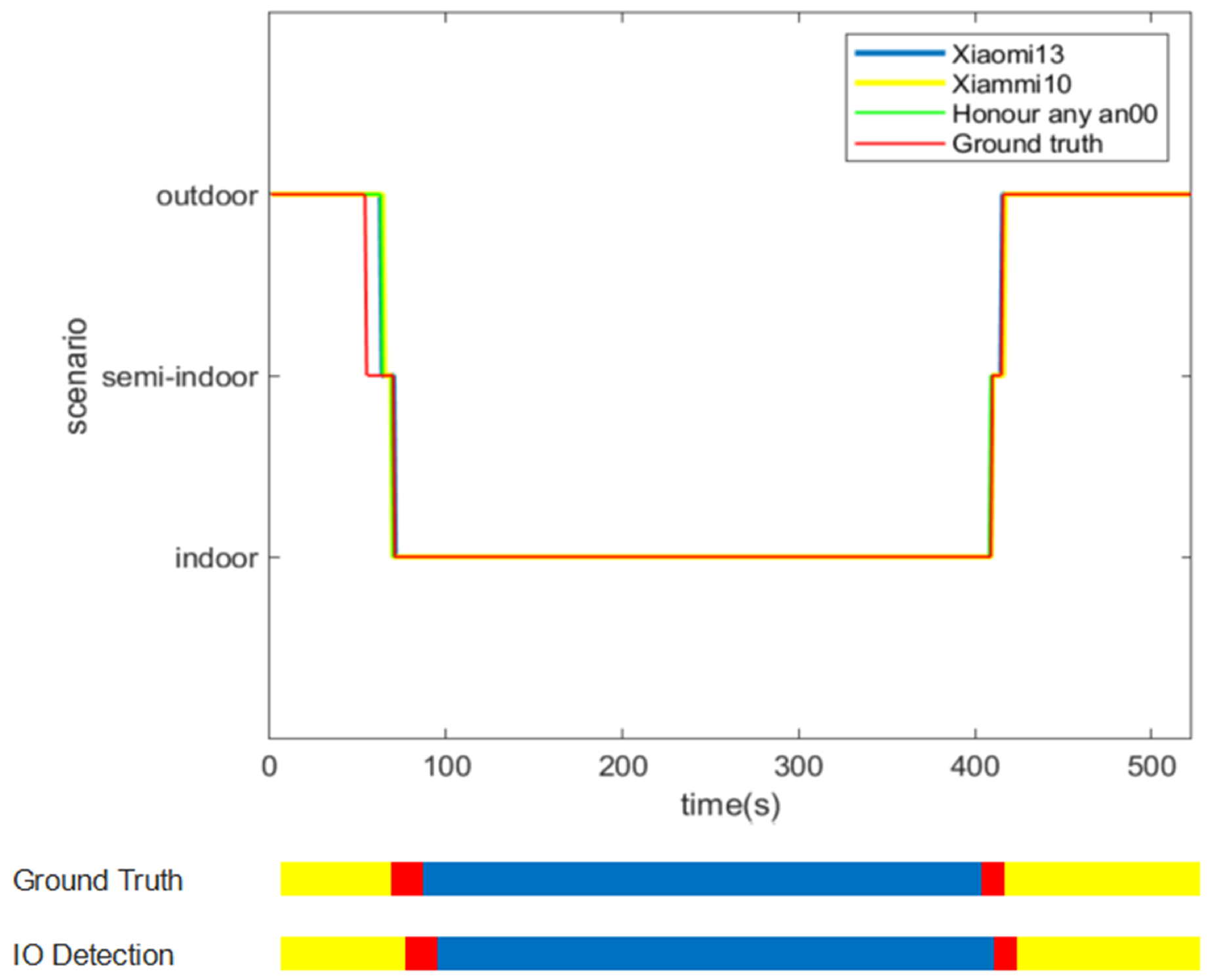
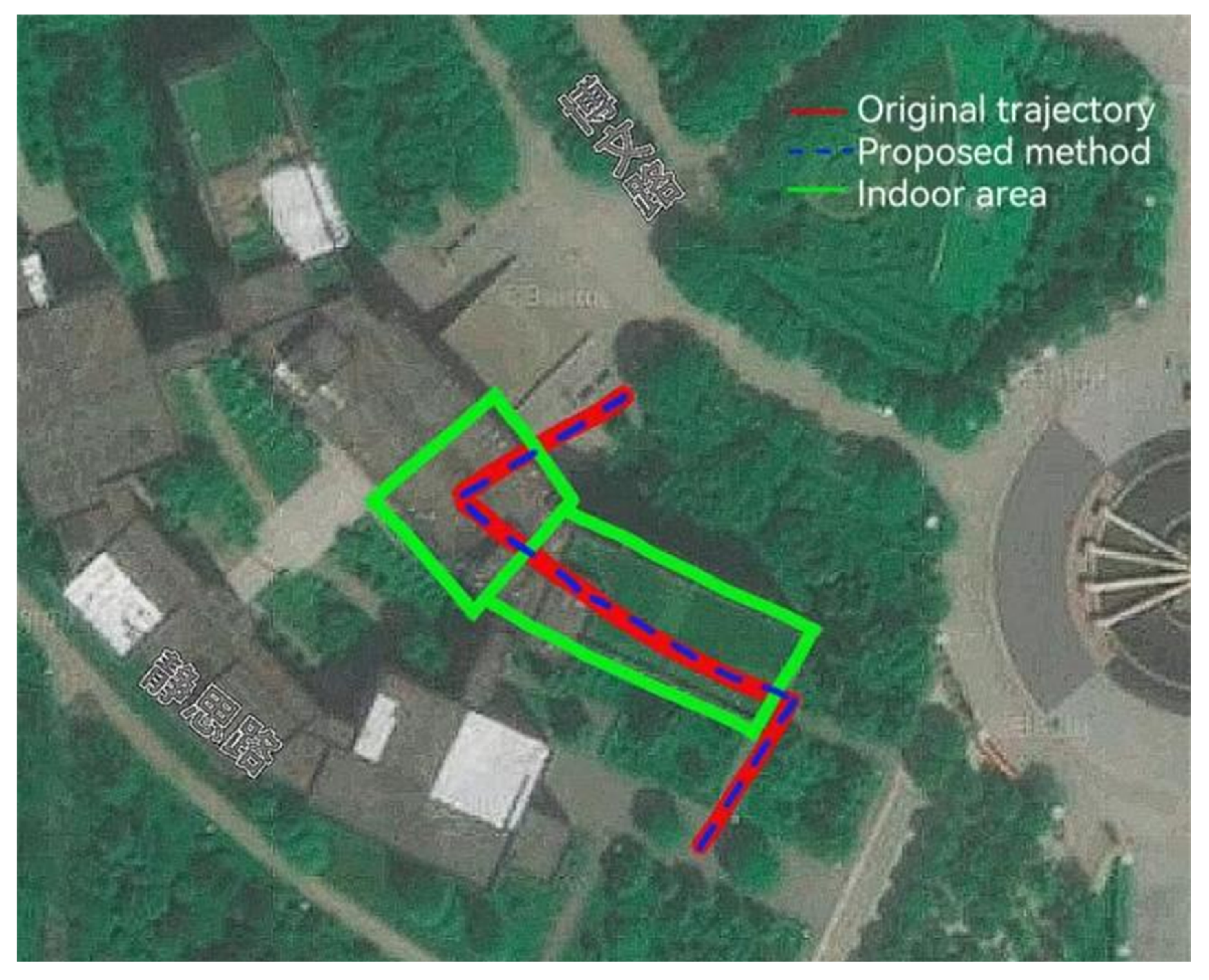
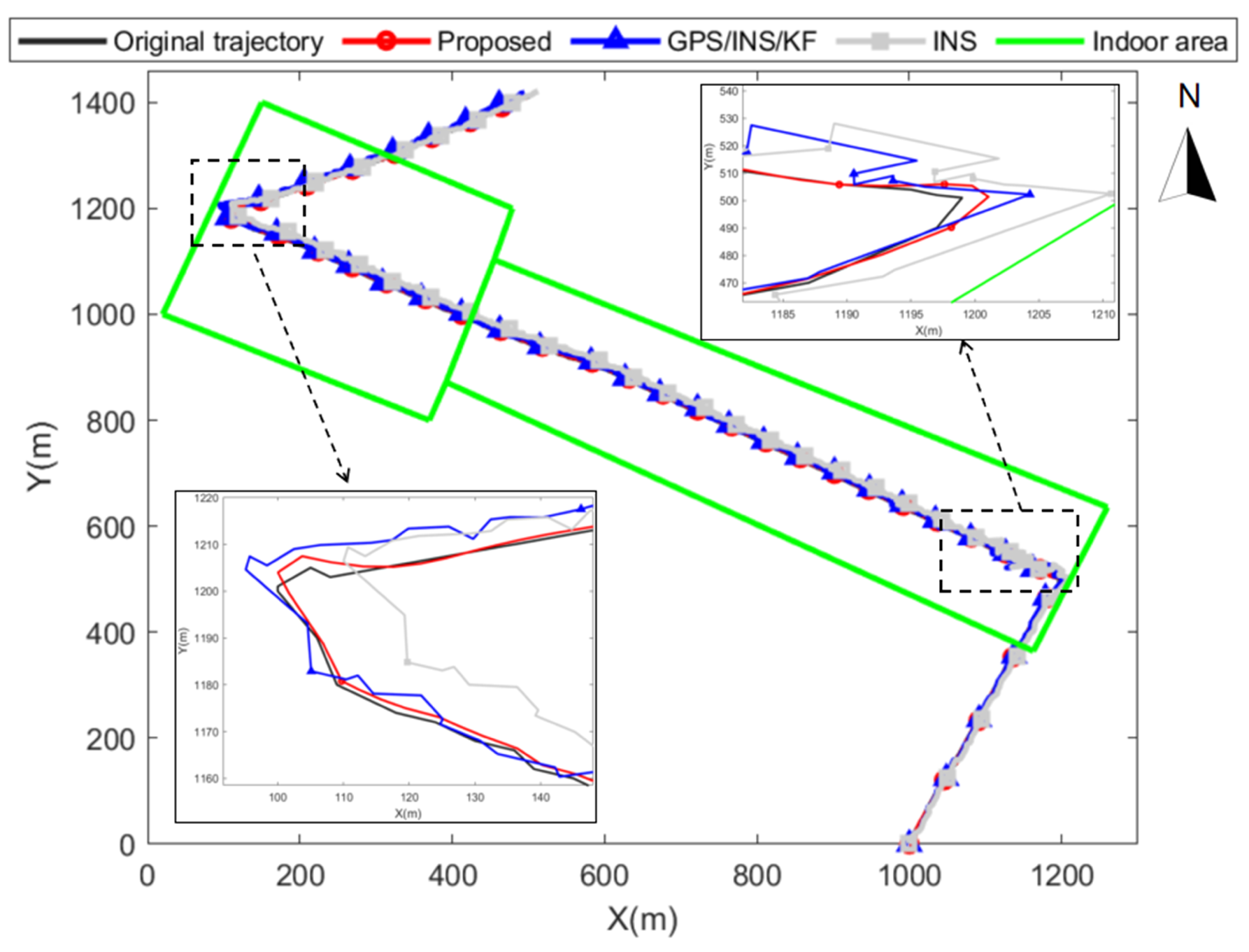
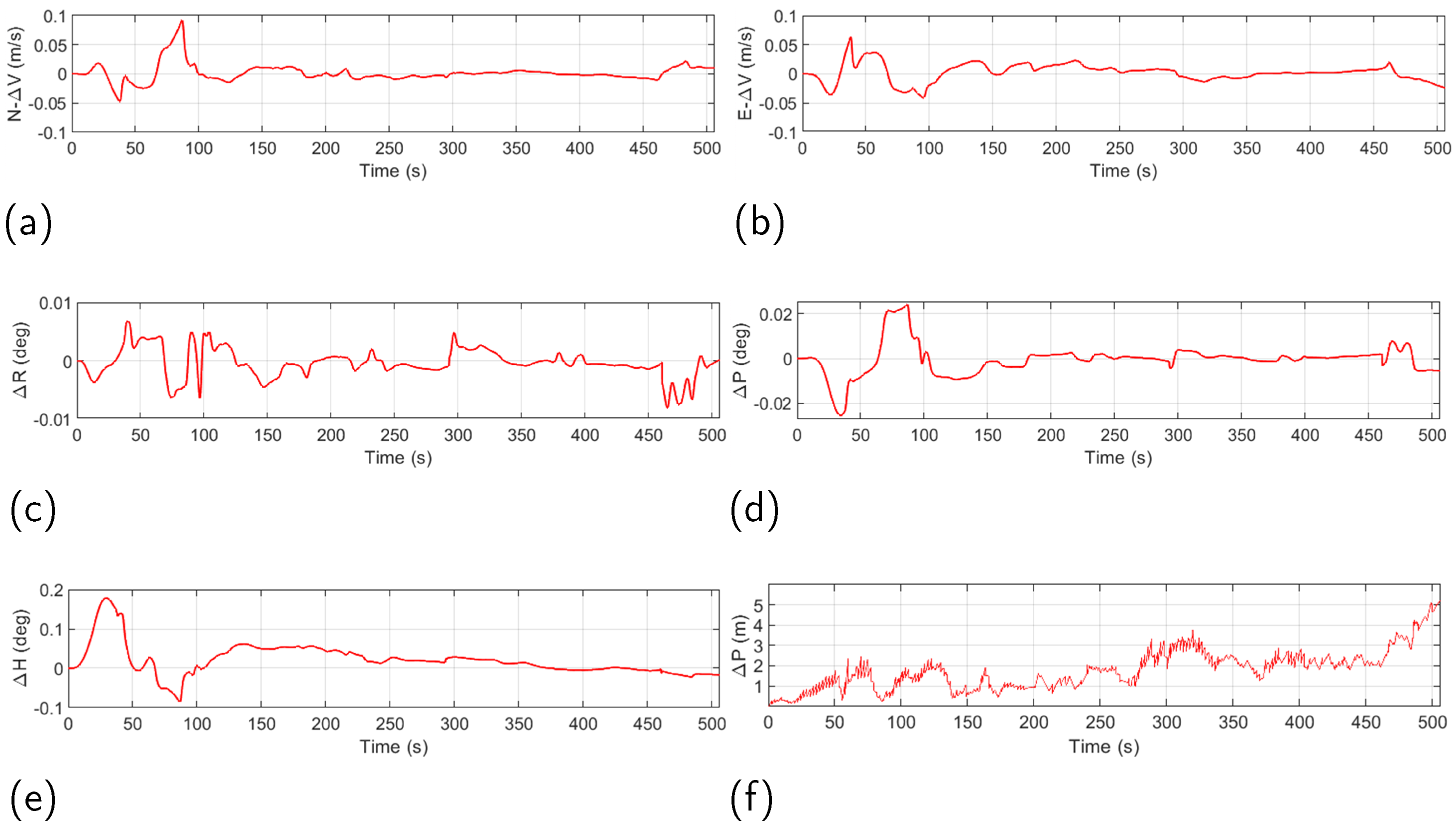
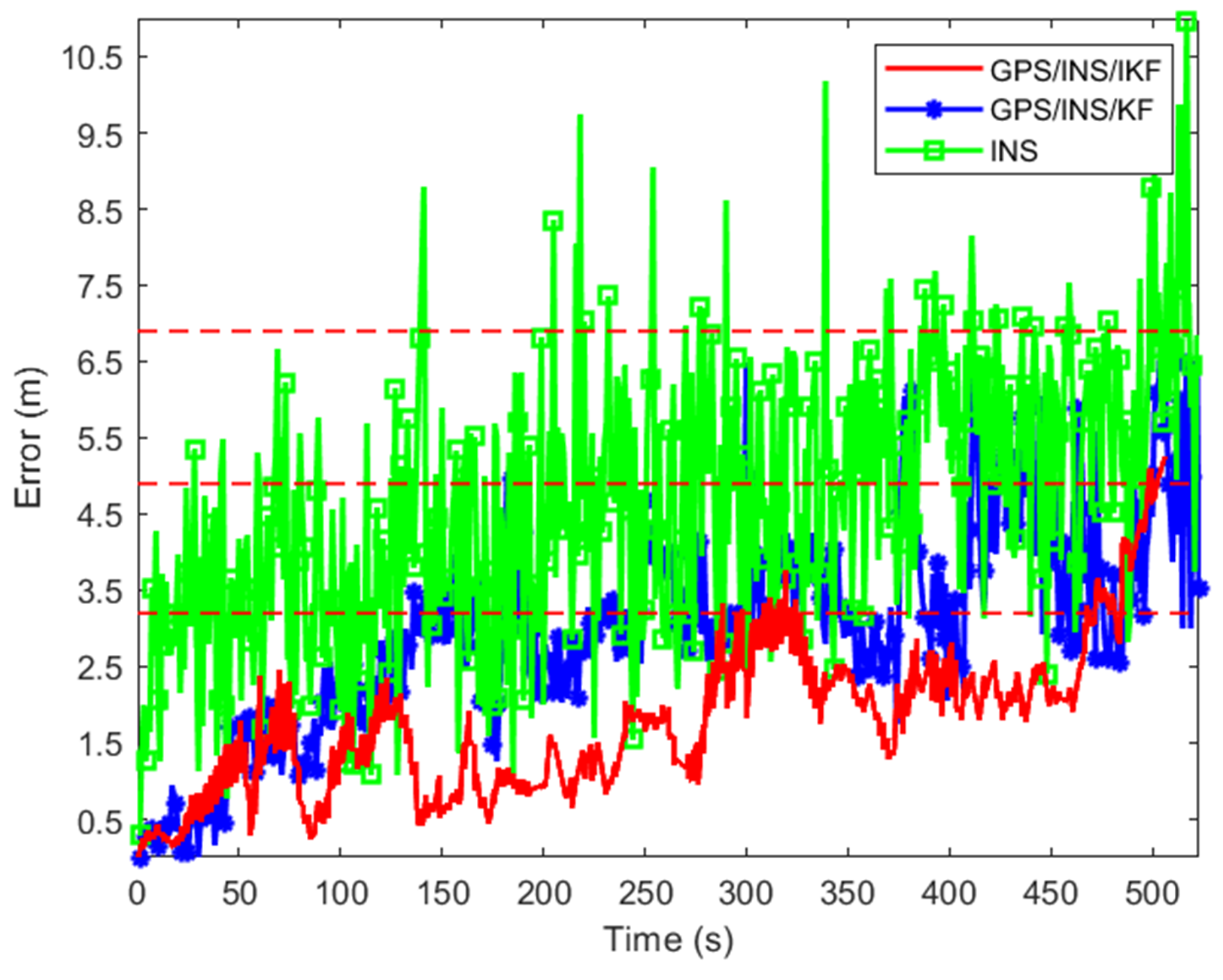
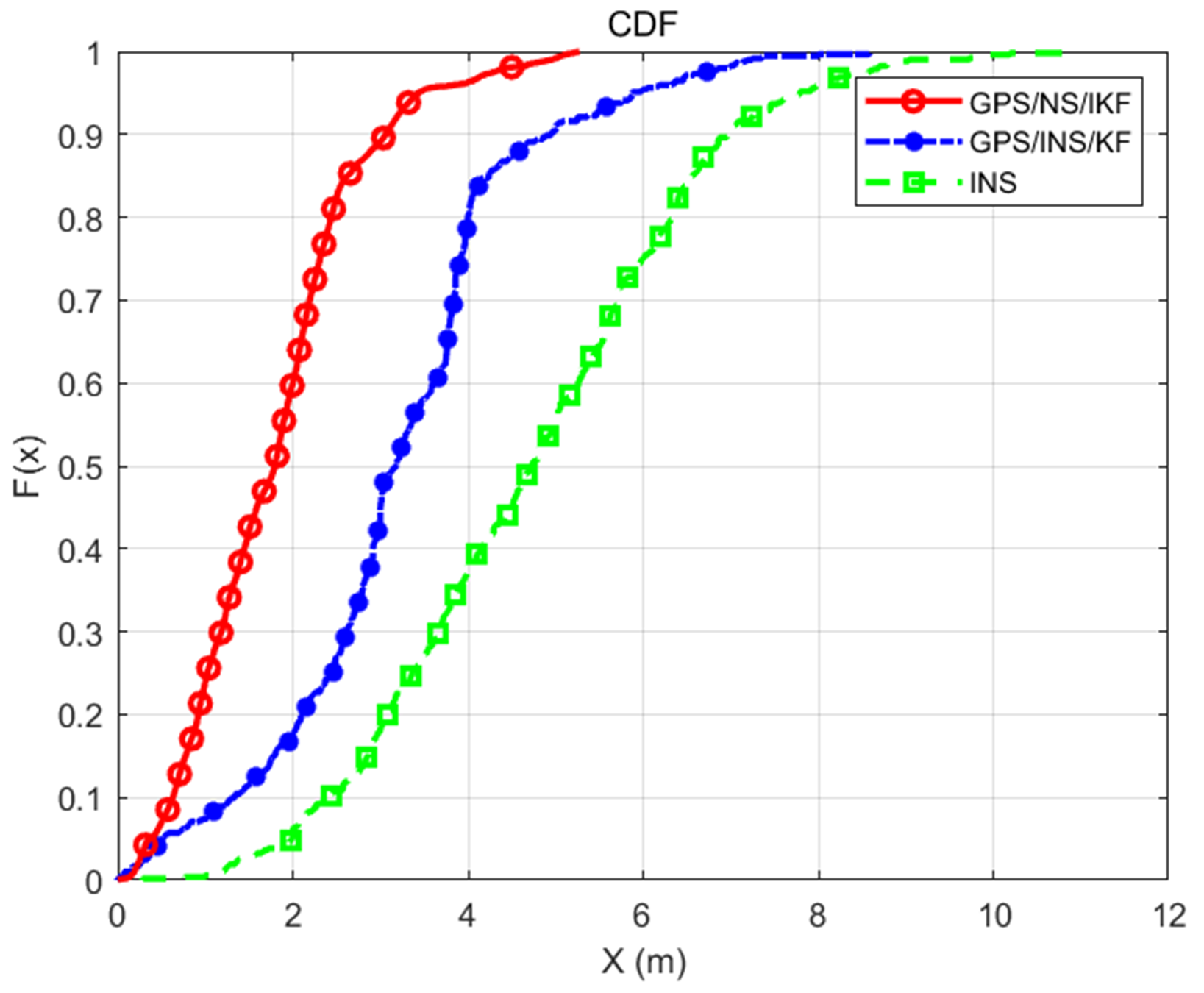
3. Experiment Results and Analysis

To verify the robustness of the algorithm and evaluate its performance in seamless switching, experiments were conducted using Xiaomi 13 (MI 13), Xiaomi 10 (MI 10), and Honor ANY (AN00) smartphones on the campus of Xi’an University of Posts and Telecommunications (XUPT), as shown in Figure 4. The experimenters carried three different types of smart mobile devices while walking along a preset trajectory. To prevent the influence of human behavioral differences on the sensor signal quality, the experimenters held the smartphones uniformly horizontally and received the signals at an appropriate height.

To construct a database for the indoor/outdoor detection (IOD) model in the indoor, outdoor, and semi-indoor (IOS) scenarios, a series of sensors were selected, such as GPS, Wi-Fi, light and magnets sensors, and their measurements were synchronously recorded via Android applications. As shown in

Table 1. Information on data acquisition.

Sensor	Frequency (Hz)	Measurement	Preprocess
GPS	1	$nu{m}_{sat}$, $snr$	GNSS outlier removal
Light	Unsteady	$nu{m}_l$	Linear interpolation
Magnet	50	$m_x$, $m_y$,$m_z$	/
Wi-Fi	1	$nu{m}_{\omega }$	/
Acc	50	$a_x$,$a_y$, $a_z$	Coordinate transformation, low-pass filtering, and cubic interpolation
Gyro	50	${\omega }_x$, ${\omega }_y$, ${\omega }_z$
Gravity	50	$g_x$, $g_y$, $g_z$

, due to the different sampling rates of the smartphones, the time window method was used to complete the data acquisition of each sensor separately. The signal-to-noise ratio and amount of visible satellite data in the GPS were measured at a frequency of once per second. For the light sensors, multiple (2–6) light intensity values per second were recorded via proximity sensor detection to avoid interference from clothing. For the magnetometers, three-axis magnetic values were collected. No coordinate conversion was used because the magnitude of the values in all three directions was a magnetometer. For Wi-Fi, callbacks were used as correlated signal indicators, and the RSSI was recorded for each periodic scan, which was controlled by the Android API. For behavioral sensors, such as accelerometers, gyroscopes, and gravity sensors, statistical metrics in the time and frequency domains were calculated from the raw time series as behavioral features. To counteract the effect of the smartphone pose, raw measurements were first converted into the world coordinate system using a rotation matrix in the smartphone output. A low-pass filter was then used to eliminate the noise. During information acquisition, anomalous or missing sensor readings required data cleaning or denoising methods to eliminate them. For data with low importance and a low rate of missing entries, this study did not apply additional processing; for those with high importance and a high rate of missing entries, similar values were obtained by repeating the experimental method; for those with high importance and low rate of missing entries, estimation was performed using empirical or theoretical knowledge. The software for cell phone data collection is SensorSense v4.0.5, and the app used to collect the GPS signal-to-noise ratio is GPS Test Plus v3.5.8.

Figure 5 and Figure 6 present the search space and the fitness function curves, respectively. As shown in Figure 5, the fitness function designed in this study was a multimodal test function with more than one optimal value, which prevented it from falling into local optima and benchmarked the explorative behavior of the optimization algorithm. Figure 6 shows that the fitness function decreased and tended to zero within 10 iterations, indicating that the function could search for the best switching parameters.

Figure 7 shows the detection effects of the three cell phones when using the SSA switching algorithm. In the figure, it can be seen that there were four I/O and transition region switches in this scene at the time points of 65 s, 75 s, 410 s, and 415 s. During these time periods, the user’s environment changed, and during the switching process, the sensor data inputted into the SSA changed differently (e.g., the light intensity changed drastically, while the RSSI may have changed only after a short delay), and this variability, as well as the difference in sensitivity of the sensors of each cell phone, led to a difference in the collected data, which explained why the lines did not overlap at the moment of switching. Most of the lines overlapped because it seemed that, although there were slight differences in the collected data, the overall trend of the sensor data was the same, which also showed that the SSA was effective in detecting the user’s location. Using the SSA to detect I/O conditions, the recognition effects of the three cell phones had small differences, a high accuracy, and a short delay.

Figure 8 shows the number of switching times for a single sensor in the scenario of Figure 7, from which it can be seen that the detection results of the light, GPS, and RSSI are all the same as the actual scenario (switching twice), of which GPS is the most accurate with the smallest switching delay, while RSSI has the largest switching delay. In addition, the magnetometer switched three times, which is more inaccurate compared to the other sensors, but the overall switching results match the experimental scenarios, verifying the robustness of the proposed algorithm.

Figure 9 and Figure 10 show the recognition accuracy for I/O areas and transition areas when using single and multiple sensors, respectively. In addition, the indoor and outdoor recognition accuracy for a single sensor was almost always greater than 90%, while the recognition accuracy in the transition region only reached above 80%, reflecting the necessity of using multiple sensors. In the multi-sensor recognition experiments, data were collected using three different smartphone brands. The I/O detection accuracy was over 95%, and the transition area accuracy was over 90%, which illustrated the general applicability of the proposed algorithm.

Table 2. Detection accuracy.

Android Cell Phones	Indoor	Outdoor	Semi-Indoor
Xiaomi10	99.42%	100%	91.67%
Honor any00	99.71%	99.41%	92.85%
Xiaomi13	99.41%	99.42%	92.31%

shows the combined detection accuracy of the sensors of the three cell phones, from which it can be seen that during the course of the experiments, the accuracy of the detection can reach 99% both indoors and outdoors, and the accuracy in the transition area can achieve more than 90%.

Table 3. Comparison of results for different I/O detection methods.

IOD Approach	Sensors Used for Detection	Indoor	Outdoor	Semi-Indoor	Complexities
[19]	Magnetometer	85.3%	85.3%	85.3%	Medium
[37]	Wi-Fi	96.8%	92.5%	90%	Low
[18]	Light, magnetometer, cellular	90%	92%	92%	High
[38]	Light, Wi-Fi, cellular, clocks, etc.	92.6%	93.74%	87.55%	Low
Proposed	Light, magnetometer, GPS, cellular	99.41%	99.42%	92.31%	Medium

presents a comparison of the performance of a detection method using machine learning, methods using fixed thresholds, and the detection method proposed in this study. Ashraf et al. [19] extracted different features of magnetic field data to distinguish I/O environments in a classifier based on machine learning, such as SVM and GBM, and the results of the detection were not satisfactory due to the singularity of the sensor data. To address the accuracy requirement, the authors of [37] designed an aggregated IOS detector based on the semi-Markov conditional random field (semi-CRF) algorithm. The sub-detector utilized only a WiFi sensor and a weak learner, making it easy to use and energy efficient. Zhou et al. [18] used three low-power sensors—light detectors, cellular detectors, and magnetometers—in combination with a Markov model to form a lightweight sensor for I/O detection. SenseIO [38] used measurements from sensor-rich smartphones to automatically infer the type of surroundings, with a detection accuracy of 91.30%. The proposed algorithm achieved an average combined detection accuracy of approximately 97.04% due to its highly explorative character and its ability to avoid local optima, and the simulated salp chain allowed the SSA to explore the search space and gradually move towards the global optimum. In this way, the problem of the low detection accuracy and reliability of existing IOD services is solved while reducing the complexity. In addition, the complexity evaluated in this study refers to the time complexity of the specific algorithms used in each article due to the requirement of low latency when switching between indoor and outdoor scenes.

Figure 11 and Figure 12 show the location–trajectory localization results for the two switching scenarios. In Figure 12, it is evident that the black dashed boxes mark the specific positions of the two switching points. In addition, the moving target started from the (1000, 0) position; when it reached the first switching point, the environment changed from outdoors to indoors, and the GPS signal became poorer and was gradually interrupted. At the same time, the three localization methods started to show large errors, and the localization error continuously increased after accumulation. The conventional GPS/INS method performed better in the first change in position, but the positioning error slowly increased with time, and a large error occurred during the second switching, indicating that the higher system accuracy requirements were not met. The improved solution proposed in this study tracked the user’s position more accurately in both of these cases, with only minor perturbations when large changes (e.g., turns) were generated, allowing precise, stable, highly accurate, and seamless localization.

Figure 13 shows the carrier motion trajectory for navigation simulation. It is evident that the combined navigation scheme proposed in this study can keep the attitude–velocity error at the usual GNSS level with a horizontal velocity error of almost less than 0.05 m/s, even in transition areas and indoor areas with poor GPS signals; thus, the horizontal attitude error was small, and the positioning error was approximately 3 m or less, indicating that maintain the attitude–velocity error could be maintained at the usual level of GPS. Thus, the improved Kalman filtering algorithm with the addition of INS in this study was able to correct the position error and stabilize the error.

In Figure 14, it can be seen that the error of the GPS/INS/IKF localization algorithm was basically within 3.2 m, while the error of the GPS/INS localization algorithm was within 4.9 m, and the INS algorithm’s localization error was basically within 6.9 m. In addition, the localization errors of the three algorithms increased when passing through I/O transition areas, and the use of the INS method produced obvious drift errors, which made it difficult to successfully achieve accurate indoor and outdoor localization. In contrast, the error of the proposed method did not exceed 5.2 m, indicating that a more accurate and stable navigation function can be realized.

Figure 15 shows a comparison of the cumulative distribution curves of the three algorithms. It is evident that there was a 90% probability that the error of the proposed algorithm was within 3.05 m, while the probability that the error of the GPS/INS method was within 3.05 m was 48.07%. That of the INS method was 19.45%, which showed that this method greatly improved the positioning accuracy for indoor/outdoor transition environments and successfully reduced the error. Both the GPS/INS algorithm and the proposed method were able to achieve continuous localization in severely degraded GNSS regions and indoor areas. However, the proposed algorithm had the best localization performance among the three algorithms, and the fused Kalman filter algorithm was improved by combining the relationship between states and observations to mitigate the interference of NLOS, multipath, and fault signals.

4. Conclusions

To accomplish fully precise and seamless indoor and outdoor navigation, a novel approach was suggested by using the salp swarm algorithm in conjunction with improved Kalman filtering in GPS/INS navigation. First, an I/O detection algorithm based on the SSA was proposed. The adaptive function of the SSA was designed, and an adaptive system between biological populations was used to randomly search for the global optimal solution that satisfied the objective function. The conventional fixed threshold was then converted into dynamic switching parameters, and smartphones were used to collect I/O sensor data for testing; then, accurate detection of indoor and outdoor environments was effectively achieved. In outdoor areas, GNSS technology can ensure highly accurate positioning. For transitional or indoor areas with poor GNSS signal quality, INS measurements were used as a complement, with KL divergence being introduced as an augmentation. Continuous localization in indoor and outdoor environments was possible thanks to the collaboration between inertial measurements and various sensors. The experimental results showed that the positioning results of the method proposed in this study were better than those of the traditional combined GPS/INS navigation method and the INS method in continuous indoor and outdoor scenes. The seamless positioning system with the improved Kalman-filtered GPS/INS based on the SSA was verified through field tests and simulations to achieve real-time positioning and provide users with highly reliable and continuous location services. In the future, this method can be applied to driverless vehicles and further optimized for their performance in a wide range of environments in order to further advance navigation technology.