Impact of Assimilating Geostationary Interferometric Infrared Sounder Observations from Long- and Middle-Wave Bands on Weather Forecasts with a Locally Cloud-Resolving Global Model
Abstract
1. Introduction
2. Methods
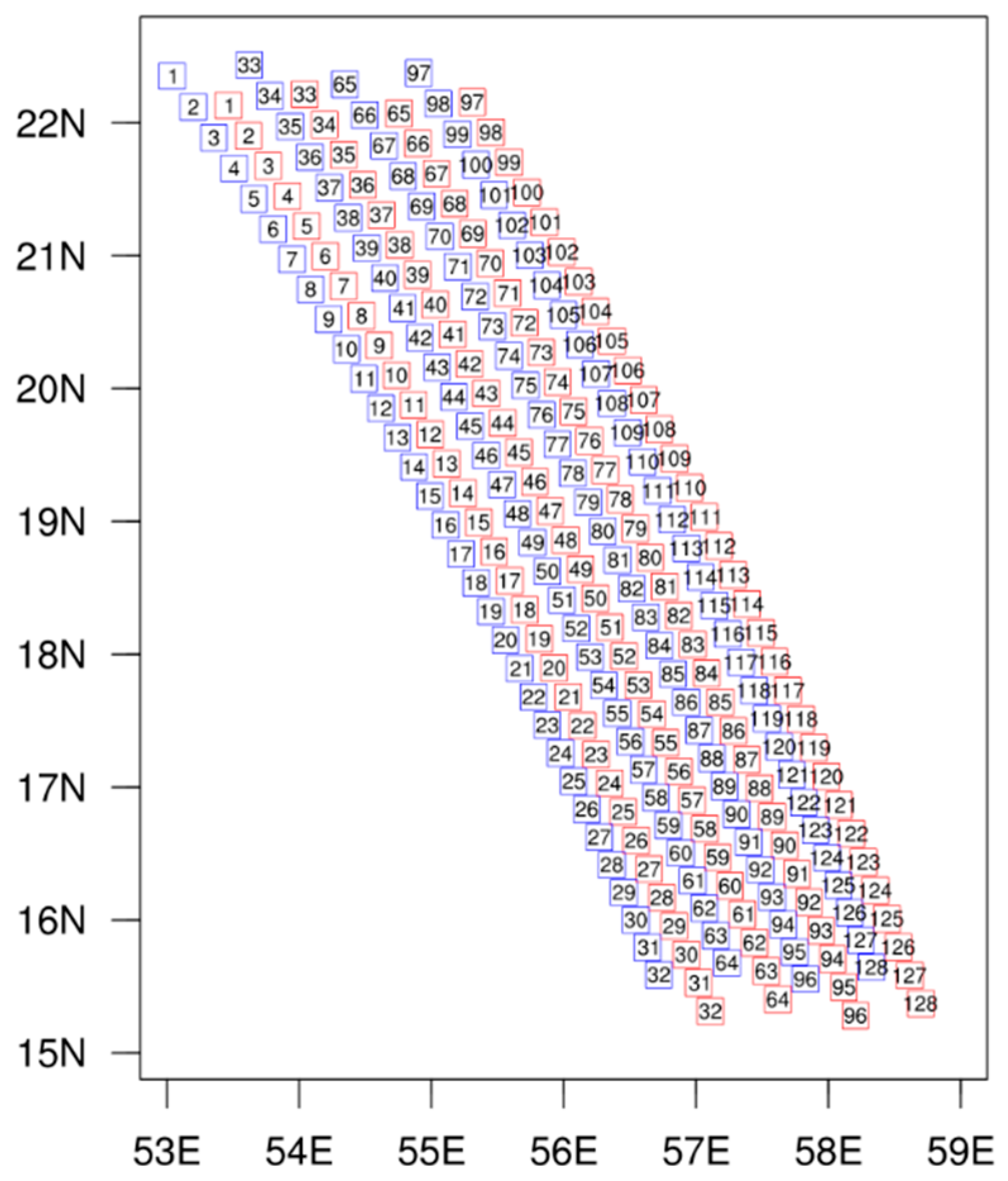
2.1. GIIRS/FY-4A Observations
2.2. SD3 Model
2.3. GSI Analysis System
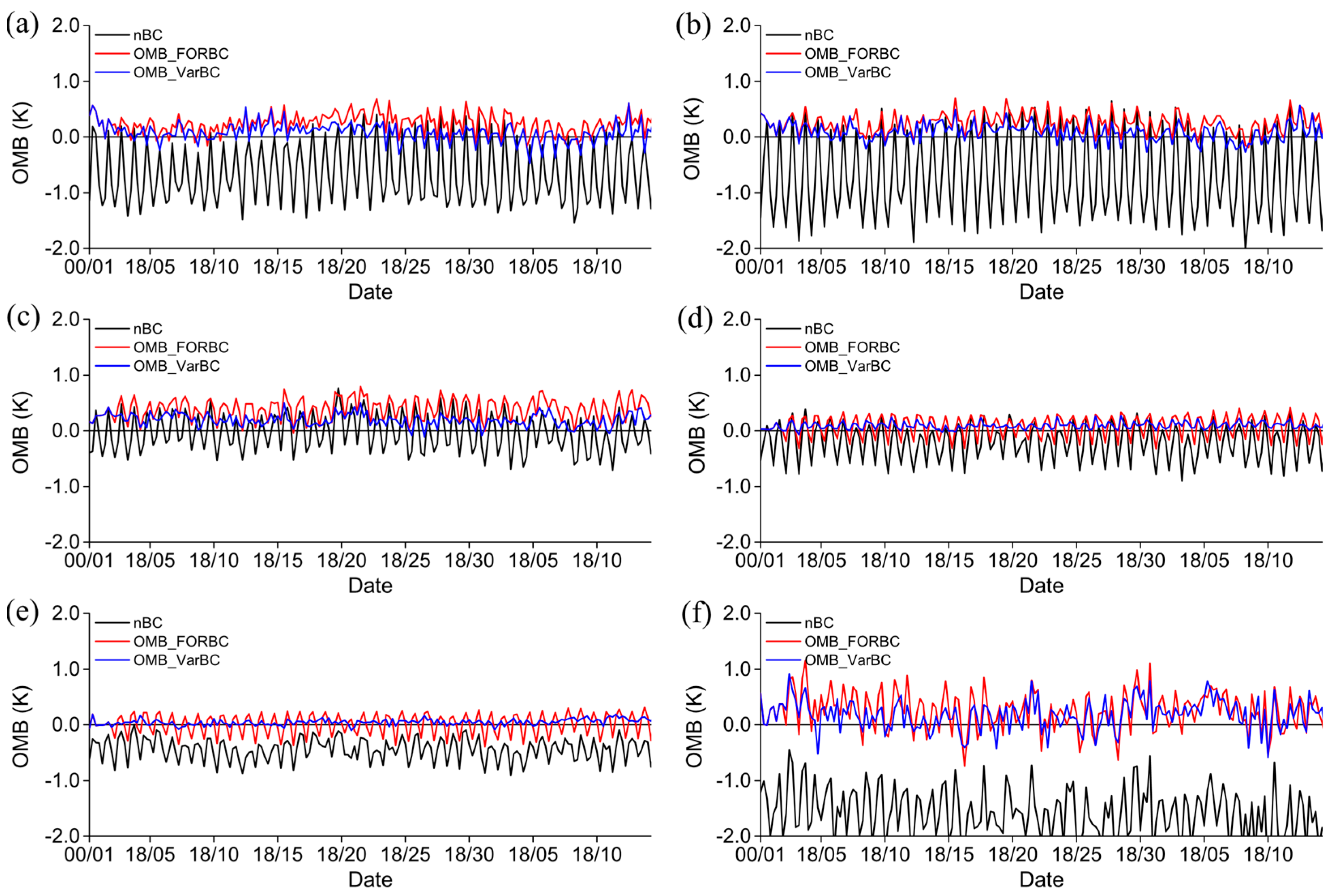
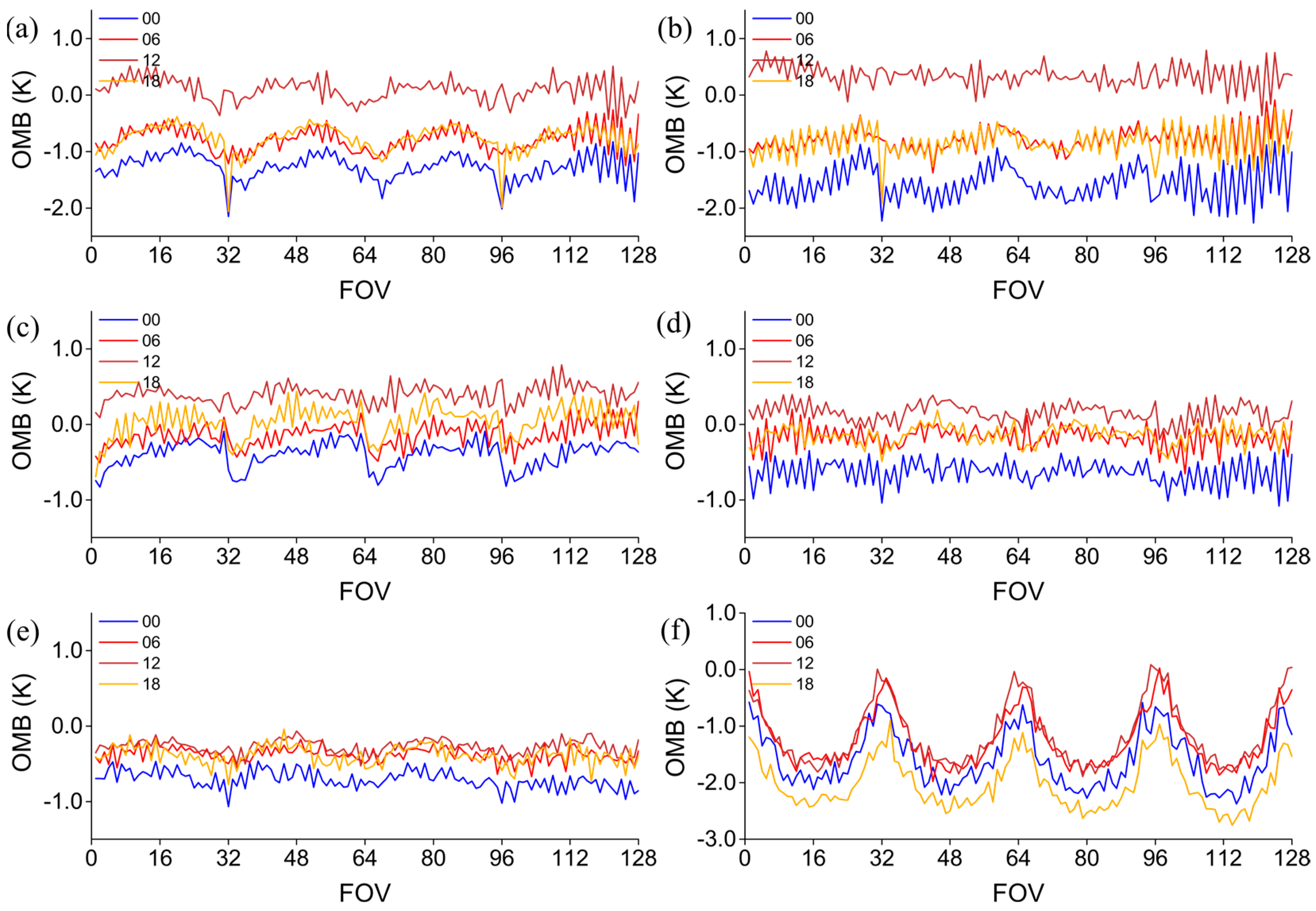
2.4. Bias Correction
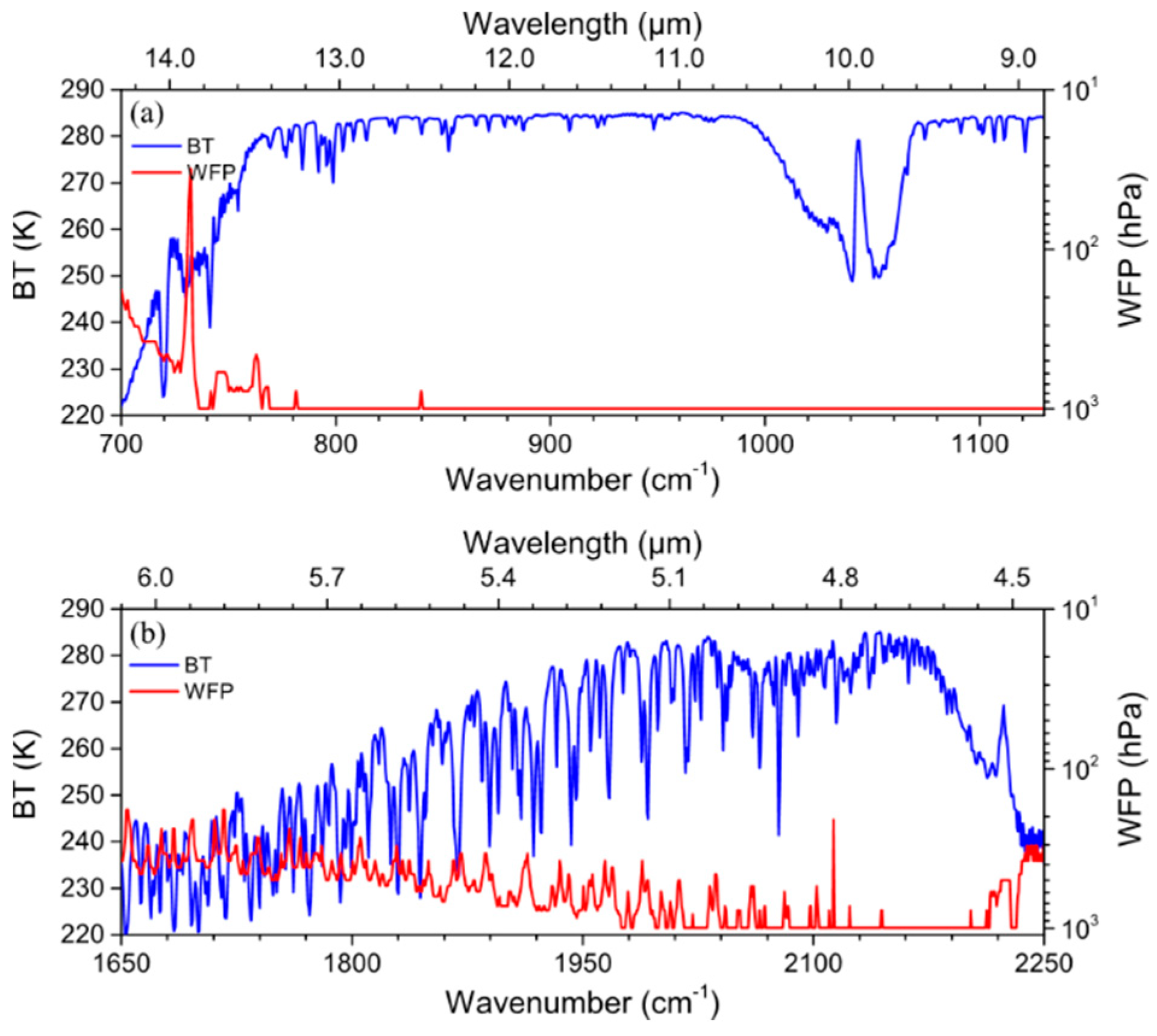
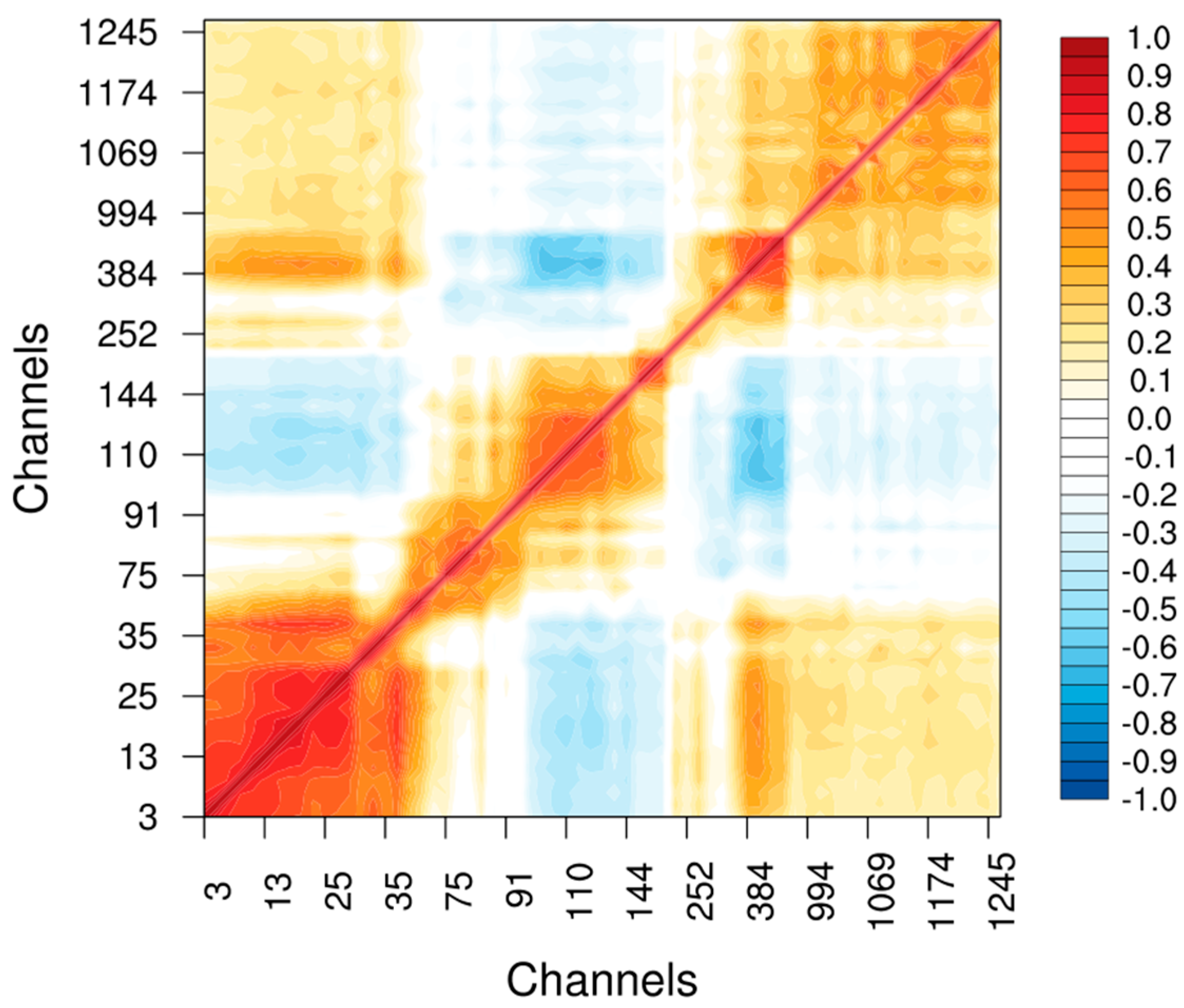
2.5. Observation Errors
2.6. Quality Control
3. Experimental Settings
4. Results
4.1. The Performance of SD3 Model
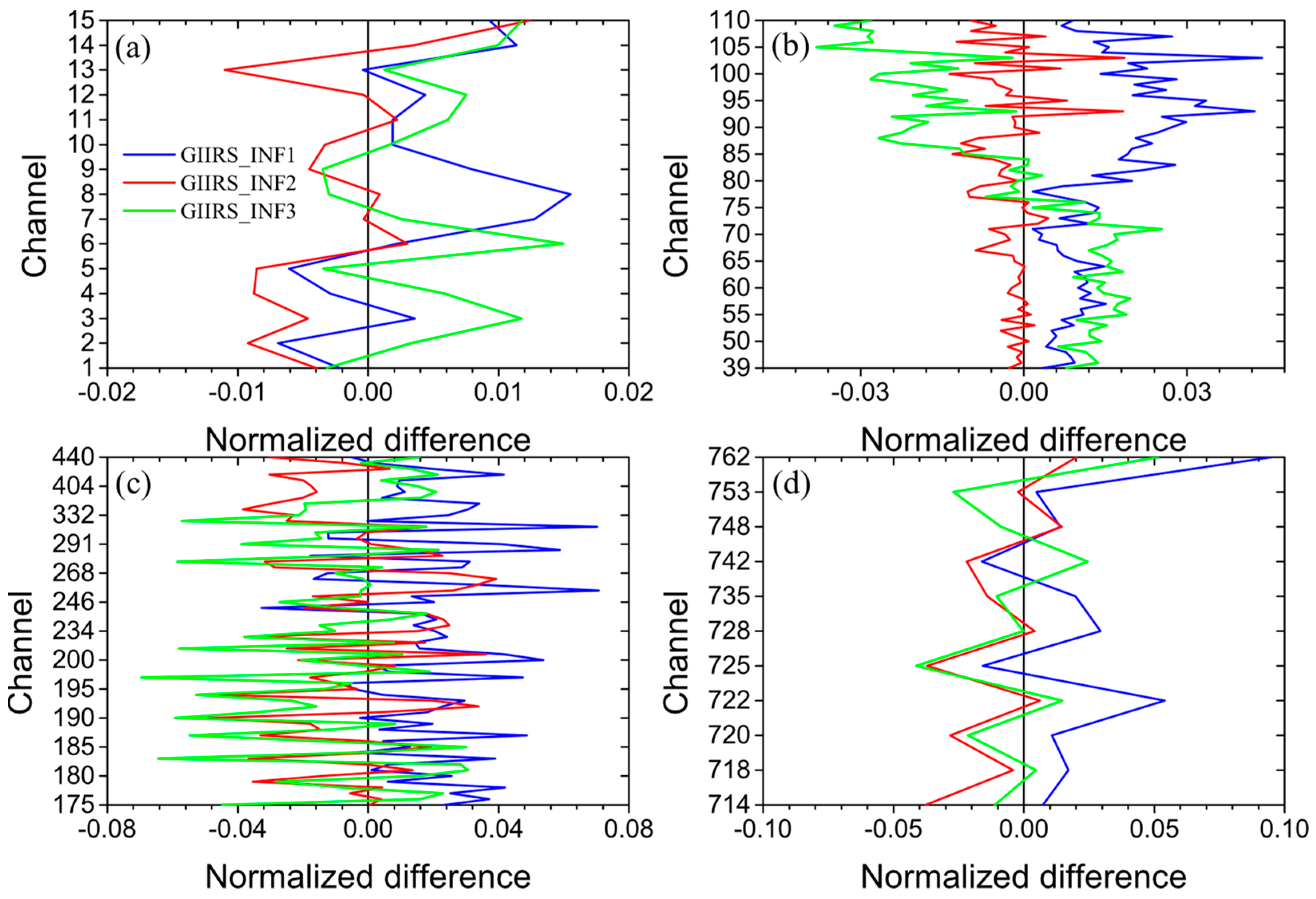
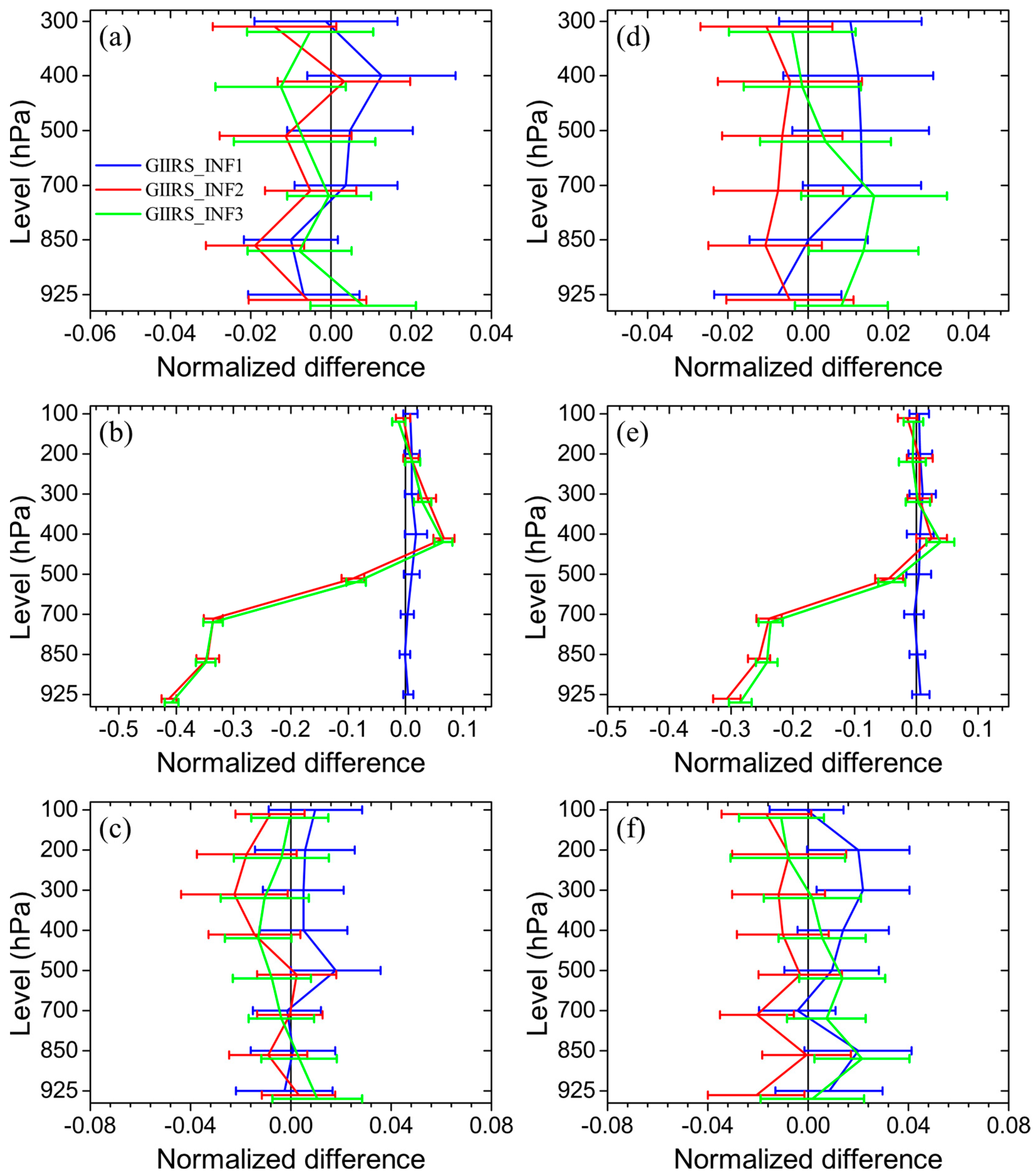
4.2. Short-Rang Forecast Impact
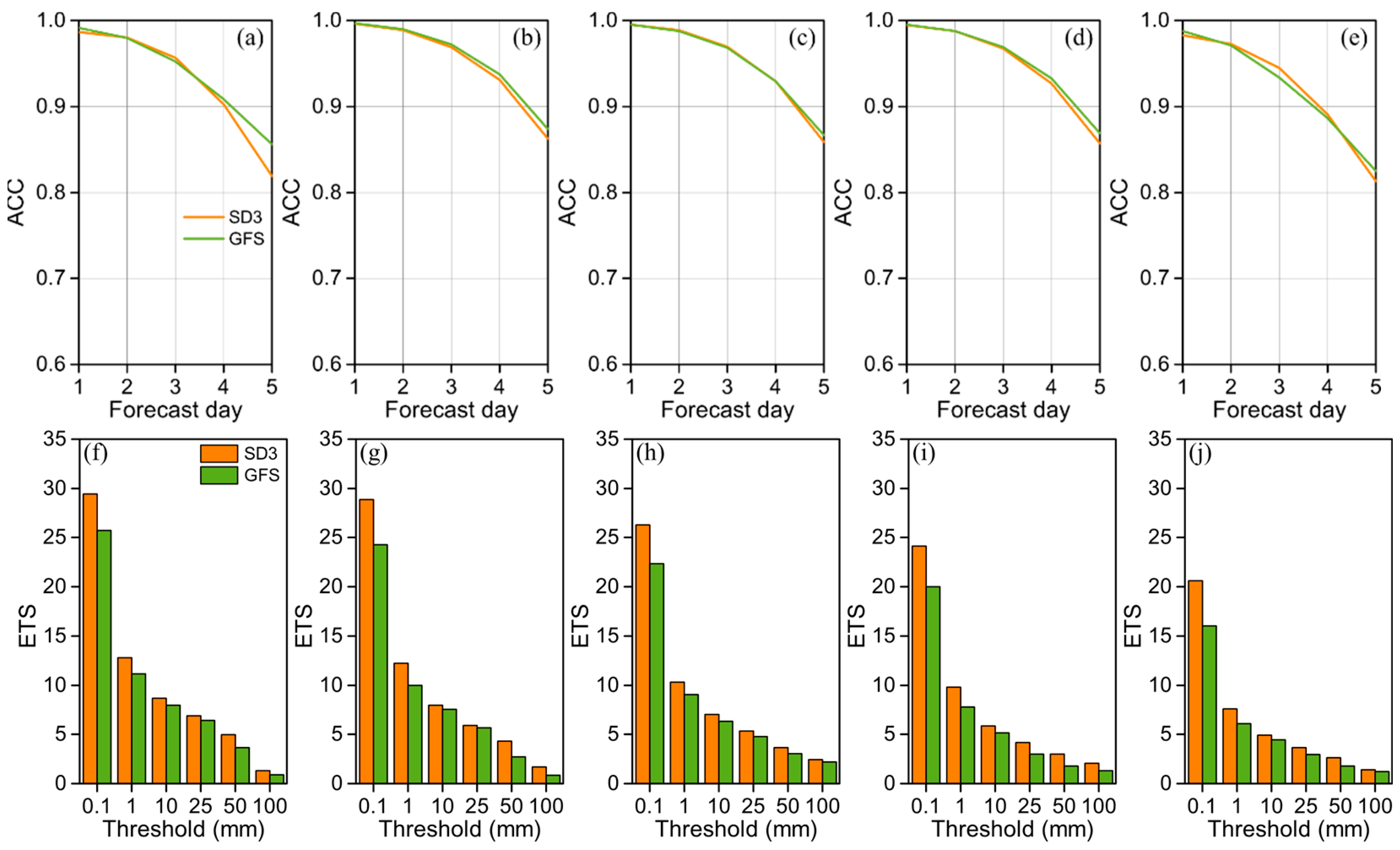
4.3. Middium-Rang Forecast Impact
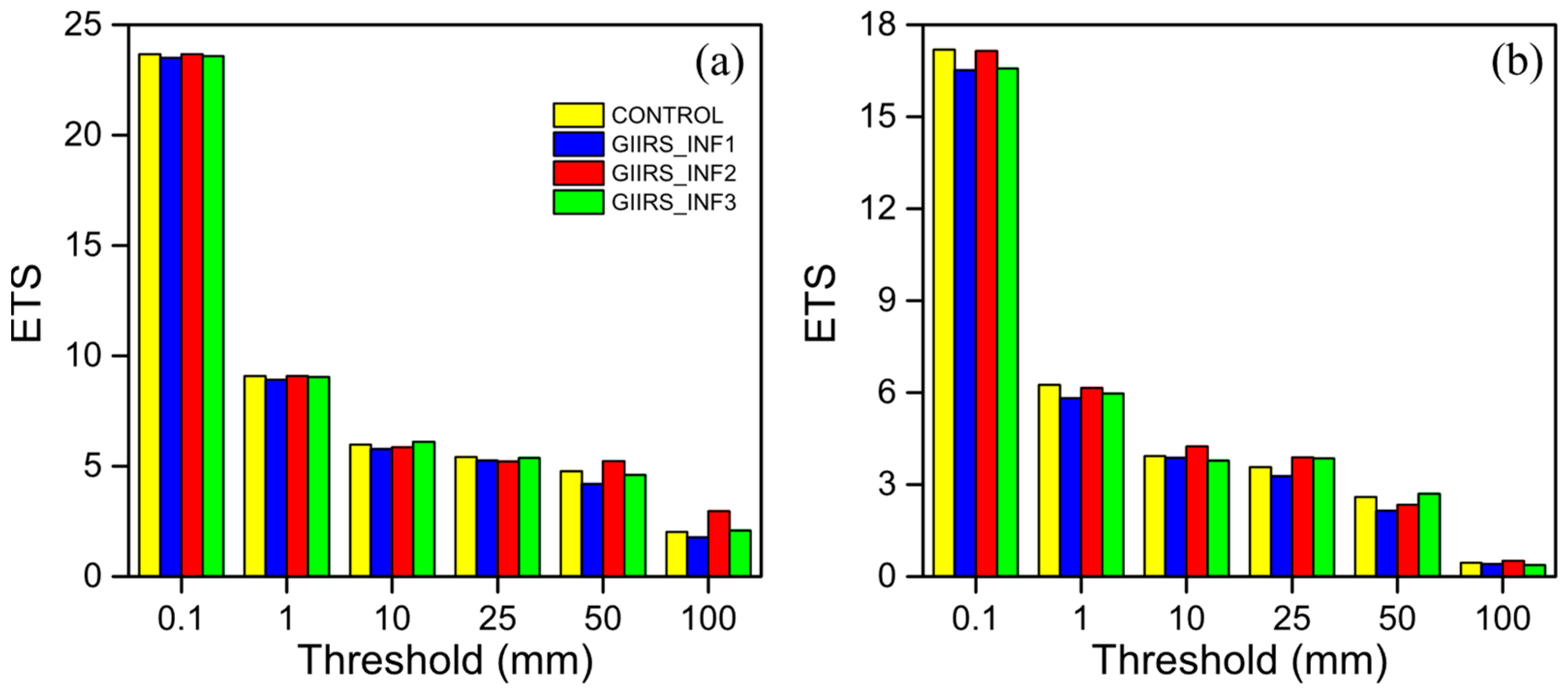
4.4. Precipitation Forecast Impact
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McNally, A.P.; Watts, P.D.; Smith, J.A.; Engelen, R.; Kelly, G.A.; Thépaut, J.N.; Matricardi, M. The assimilation of AIRS radiance data at ECMWF. Q. J. R. Meteorol. Soc. A J. Atmos. Sci. Appl. Meteorol. Phys. Oceanogr. 2016, 132, 935–957. [Google Scholar] [CrossRef]
- Collard, A.D.; McNally, A.P. The assimilation of infrared atmospheric sounding interferometer radiances at ECMWF. Q. J. R. Meteorol. Soc. 2009, 135, 1044–1058. [Google Scholar] [CrossRef]
- Hilton, F.; Atkinson, N.C.; English, S.J.; Eyre, J.R. Assimilation of IASI at the Met Office and assessment of its impact through observing system experiments. Q. J. R. Meteorol. Soc. 2009, 135, 495–505. [Google Scholar] [CrossRef]
- Guidard, V.; Fourrié, N.; Brousseau, P.; Rabier, F. Impact of IASI assimilation at global and convective scales and challenges for the assimilation of cloudy scenes. Q. J. R. Meteorol. Soc. 2011, 137, 1975–1987. [Google Scholar] [CrossRef]
- Smith, A.; Atkinson, N.; Bell, W.; Doherty, A. An initial assessment of observations from the Suomi-NPP satellite: Data from the Cross-track Infrared Sounder (CrIS). Atmos. Sci. Lett. 2015, 16, 260–266. [Google Scholar] [CrossRef]
- Eresmaa, R.; Letertre-Danczak, J.; Lupu, C.; Bormann, N.; McNally, A.P. The assimilation of Cross-track Infrared Sounder radiances at ECMWF. Q. J. R. Meteorol. Soc. 2017, 143, 3177–3188. [Google Scholar] [CrossRef]
- Wang, P.; Li, J.; Li, Z.; Lim, A.H.; Li, J.; Schmit, T.J.; Goldberg, M.D. The impact of Cross-track Infrared Sounder (CrIS) cloud-cleared radiances on Hurricane Joaquin (2015) and Matthew (2016) forecasts. J. Geophys. Res. Atmos. 2017, 122, 13–201. [Google Scholar] [CrossRef]
- Li, X.; Zou, X.; Zeng, M. An alternative bias correction scheme for CrIS data assimilation in a regional model. Mon. Weather Rev. 2019, 147, 809–839. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Otkin, J.; Schmit, T.J.; Liu, C.Y. Warning information in a preconvection environment from the geostationary advanced infrared sounding system—A simulation study using the IHOP case. J. Appl. Meteorol. Climatol. 2011, 50, 776–783. [Google Scholar] [CrossRef]
- Yin, R.; Han, W.; Gao, Z.; Di, D. The evaluation of FY4A’s Geostationary Interferometric Infrared Sounder (GIIRS) long-wave temperature sounding channels using the GRAPES global 4D-Var. Q. J. R. Meteorol. Soc. 2020, 146, 1459–1476. [Google Scholar] [CrossRef]
- Di, D.; Li, J.; Han, W.; Bai, W.; Wu, C.; Menzel, W.P. Enhancing the fast radiative transfer model for Fengyun-4 GIIRS by using local training profiles. J. Geophys. Res. Atmos. 2018, 123, 12–583. [Google Scholar] [CrossRef]
- Saunders, R.; Hocking, J.; Turner, E.; Rayer, P.; Rundle, D.; Brunel, P.; Vidot, J.; Roquet, P.; Matricardi, M.; Geer, A.; et al. An update on the RTTOV fast radiative transfer model (currently at version 12). Geosci. Model Dev. 2018, 11, 2717–2737. [Google Scholar] [CrossRef]
- Burrows, C. Assimilation of radiance observations from geostationary satellites: Third year report. In EUMETSAT/ECMWF Fellowship Programme Research Report; European Centre for Medium-Range Weather Forecasts: Reading, UK, 2020. [Google Scholar] [CrossRef]
- Dussarrat, P.; Burrows, C. Preparing for the exploitation of MTG-S IRS in NWP using FY4-A GIIRS observations. In ECMWF Technical Memoranda; European Centre for Medium-Range Weather Forecasts: Reading, UK, 2022. [Google Scholar] [CrossRef]
- Yin, R.; Han, W.; Gao, Z.; Li, J. Impact of high temporal resolution FY-4A Geostationary Interferometric Infrared Sounder (GIIRS) radiance measurements on Typhoon forecasts: Maria (2018) case with GRAPES global 4D-Var assimilation system. Geophys. Res. Lett. 2021, 48, 15. [Google Scholar] [CrossRef]
- Zhang, L.; Niu, Z.; Weng, F.; Dong, P.; Huang, W.; Zhu, J. Impacts of direct assimilation of the FY-4A/GIIRS long-wave temperature sounding channel data on forecasting Typhoon In-Fa (2021). Remote Sens. 2023, 15, 355. [Google Scholar] [CrossRef]
- Yin, R.; Han, W.; Wang, H.; Wang, J. Impacts of FY-4A GIIRS water vapor channels data assimilation on the forecast of “21·7” extreme rainstorm in Henan, China with CMA-MESO. Remote Sens. 2022, 14, 5710. [Google Scholar] [CrossRef]
- Kim, Y.; Evans, J.P.; Sharma, A. Multivariate bias correction of regional climate model boundary conditions. Clim. Dyn. 2023, 61, 3253–3269. [Google Scholar] [CrossRef]
- Benjamin, S.G.; Weygandt, S.S.; Brown, J.M.; Hu, M.; Alexander, C.R.; Smirnova, T.G.; Olson, J.B.; James, E.P.; Dowell, D.C.; Grell, G.A.; et al. A north American hourly assimilation and model forecast cycle: The Rapid Refresh. Mon. Weather Rev. 2016, 144, 1669–1694. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Z.; Wei, C.; Lu, F.; Guo, Q. Introducing the new generation of Chinese geostationary weather satellites, Fengyun-4. Bull. Am. Meteorol. Soc. 2017, 98, 1637–1658. [Google Scholar] [CrossRef]
- Harris, L.; Zhou, L.; Lin, S.J.; Chen, J.H.; Chen, X.; Gao, K.; Morin, M.; Rees, S.; Sun, Y.; Tong, M.; et al. GFDL SHiELD: A unified system for weather-to-seasonal prediction. J. Adv. Model. Earth Syst. 2020, 12, 10. [Google Scholar] [CrossRef]
- Chen, J.H.; Lin, S.J.; Zhou, L.; Chen, X.; Rees, S.; Bender, M.; Morin, M. Evaluation of tropical cyclone forecasts in the next generation global prediction system. Mon. Weather Rev. 2019, 147, 3409–3428. [Google Scholar] [CrossRef]
- Lin, S.-J.; Rood, R.B. An explicit flux-form semi-lagrangian shallow-water model on the sphere. Q. J. R. Meteorol. Soc. 1997, 123, 2477–2498. [Google Scholar]
- Lin, S.-J. A finite-volume integration method for computing pressure gradient force in general vertical coordinates. Q. J. R. Meteorol. Soc. 1997, 123, 1749–1762. [Google Scholar] [CrossRef]
- Lin, S.-J. A “vertically lagrangian” finite-volume dynamical core for global models. Mon. Weather Rev. 2004, 132, 2293–2307. [Google Scholar] [CrossRef]
- Kleist, D.T.; Parrish, D.F.; Derber, J.C.; Treadon, R.; Wu, W.S.; Lord, S. Introduction of the GSI into the NCEP global data assimilation system. Weather Forecast. 2009, 24, 1691–1705. [Google Scholar] [CrossRef]
- Parrish, D.F.; Derber, J.C. The National Meteorological Center’s spectral statistical-interpolation analysis system. Mon. Weather Rev. 1992, 120, 1747–1763. [Google Scholar] [CrossRef]
- Han, Y. JCSDA Community Radiative Transfer Model (CRTM)—Version 1. NOAA Tech. Rep. NESDIS 2006, 122, 33. [Google Scholar]
- Niu, Z.; Zhang, L.; Han, Y.; Dong, P.; Huang, W. Performances between the FY-4A/GIIRS and FY-4B/GIIRS Long-Wave Infrared (LWIR) channels under clear-sky and all-sky conditions. Q. J. R. Meteorol. Soc. 2023, 149, 1612–1628. [Google Scholar] [CrossRef]
- Zhu, Y.; Derber, J.; Collard, A.; Dee, D.; Treadon, R.; Gayno, G.; Jung, J.A. Enhanced radiance bias correction in the National Centers for Environmental Prediction’s Gridpoint Statistical Interpolation data assimilation system. Q. J. R. Meteorol. Soc. 2014, 140, 1479–1492. [Google Scholar] [CrossRef]
- Garand, L.; Heilliette, S.; Buehner, M. Interchannel error correlation associated with AIRS radiance observations: Inference and impact in data assimilation. J. Appl. Meteorol. 2007, 46, 714–725. [Google Scholar] [CrossRef]
- Bormann, N.; Collard, A.; Bauer, P. Estimates of spatial and interchannel observation-error characteristics for current sounder radiances for numerical weather prediction. II: Application to AIRS and IASI data. Q. J. R. Meteorol. Soc. 2010, 136, 1051–1063. [Google Scholar] [CrossRef]
- Stewart, L.; Dance, S.; Nichols, N.; Eyre, J.; Cameron, J. Estimating interchannel observation-error correlations for IASI radiance data in the Met Office system. Q. J. R. Meteorol. Soc. 2013, 140, 1236–1244. [Google Scholar] [CrossRef]
- Bormann, N.; Bonavita, M.; Dragani, R.; Eresmaa, R.; Matricardi, M.; McNally, A. Enhancing the impact of IASI observations through an updated observation-error covariance matrix. Q. J. R. Meteorol. Soc. 2016, 142, 1767–1780. [Google Scholar] [CrossRef]
- Desroziers, G.; Berre, L.; Chapnik, B.; Poli, P. Diagnosis of observation, background and analysis-error statistics in observation space. Q. J. R. Meteorol. Soc. 2005, 131, 3385–3396. [Google Scholar] [CrossRef]
- Bathmann, K.; Collard, A. Surface-dependent correlated infrared observation errors and quality control in the FV3 framework. Q. J. R. Meteorol. Soc. 2021, 147, 408–424. [Google Scholar] [CrossRef]
- Eyre, J.R.; Menzel, W.P. Retrieval of cloud parameters from satellite sounder data: A simulation study. J. Appl. Meteorol. Climatol. 1989, 28, 267–275. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xian, Z.; Zhu, J.; Lin, S.-J.; Liang, Z.; Chen, X.; Chen, K. Impact of Assimilating Geostationary Interferometric Infrared Sounder Observations from Long- and Middle-Wave Bands on Weather Forecasts with a Locally Cloud-Resolving Global Model. Remote Sens. 2024, 16, 3458. https://doi.org/10.3390/rs16183458
Xian Z, Zhu J, Lin S-J, Liang Z, Chen X, Chen K. Impact of Assimilating Geostationary Interferometric Infrared Sounder Observations from Long- and Middle-Wave Bands on Weather Forecasts with a Locally Cloud-Resolving Global Model. Remote Sensing. 2024; 16(18):3458. https://doi.org/10.3390/rs16183458
Chicago/Turabian StyleXian, Zhipeng, Jiang Zhu, Shian-Jiann Lin, Zhi Liang, Xi Chen, and Keyi Chen. 2024. "Impact of Assimilating Geostationary Interferometric Infrared Sounder Observations from Long- and Middle-Wave Bands on Weather Forecasts with a Locally Cloud-Resolving Global Model" Remote Sensing 16, no. 18: 3458. https://doi.org/10.3390/rs16183458
APA StyleXian, Z., Zhu, J., Lin, S.-J., Liang, Z., Chen, X., & Chen, K. (2024). Impact of Assimilating Geostationary Interferometric Infrared Sounder Observations from Long- and Middle-Wave Bands on Weather Forecasts with a Locally Cloud-Resolving Global Model. Remote Sensing, 16(18), 3458. https://doi.org/10.3390/rs16183458





