Solar Cycle Dependence of Migrating Diurnal Tide in the Equatorial Mesosphere and Lower Thermosphere
Abstract
1. Introduction
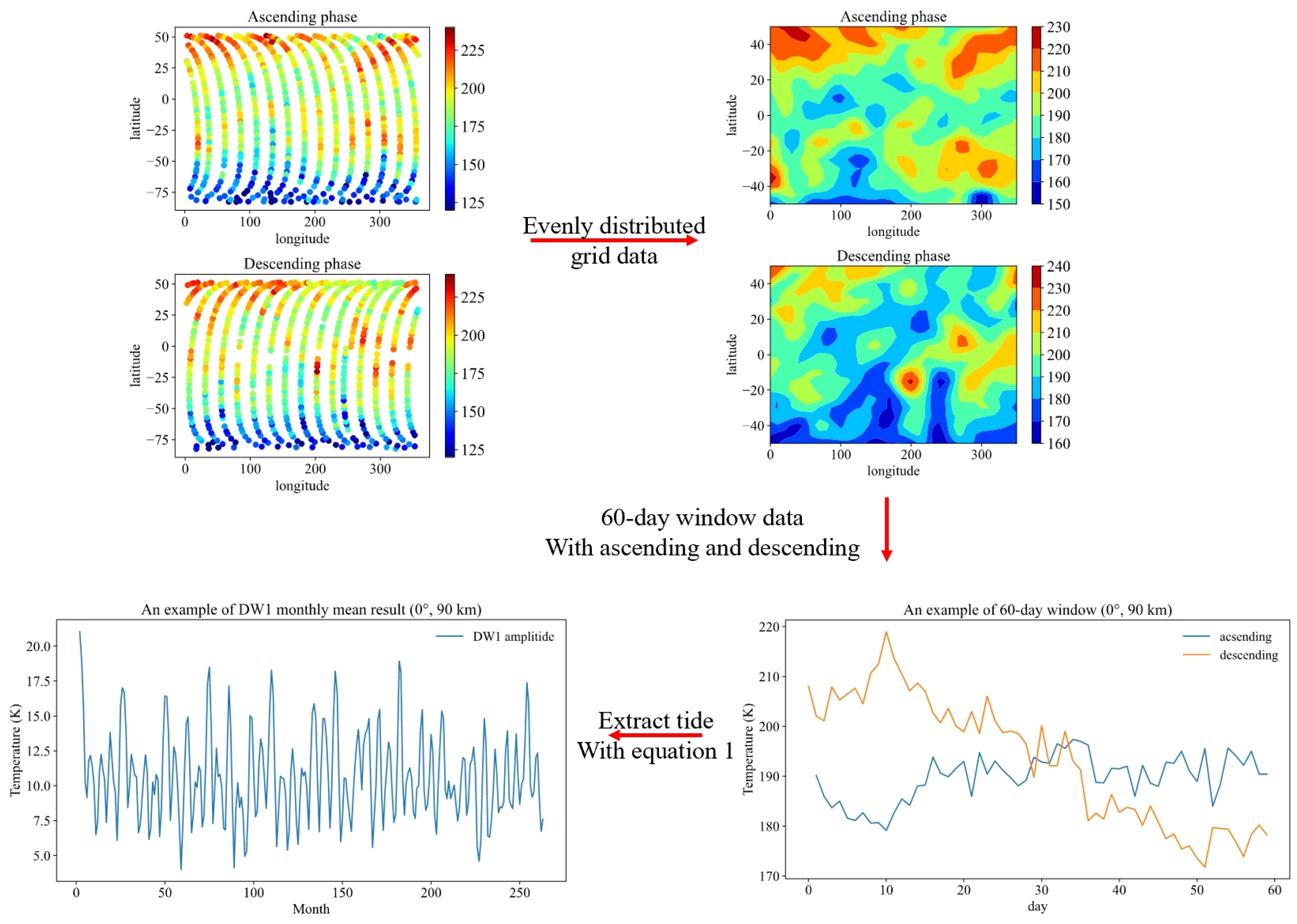
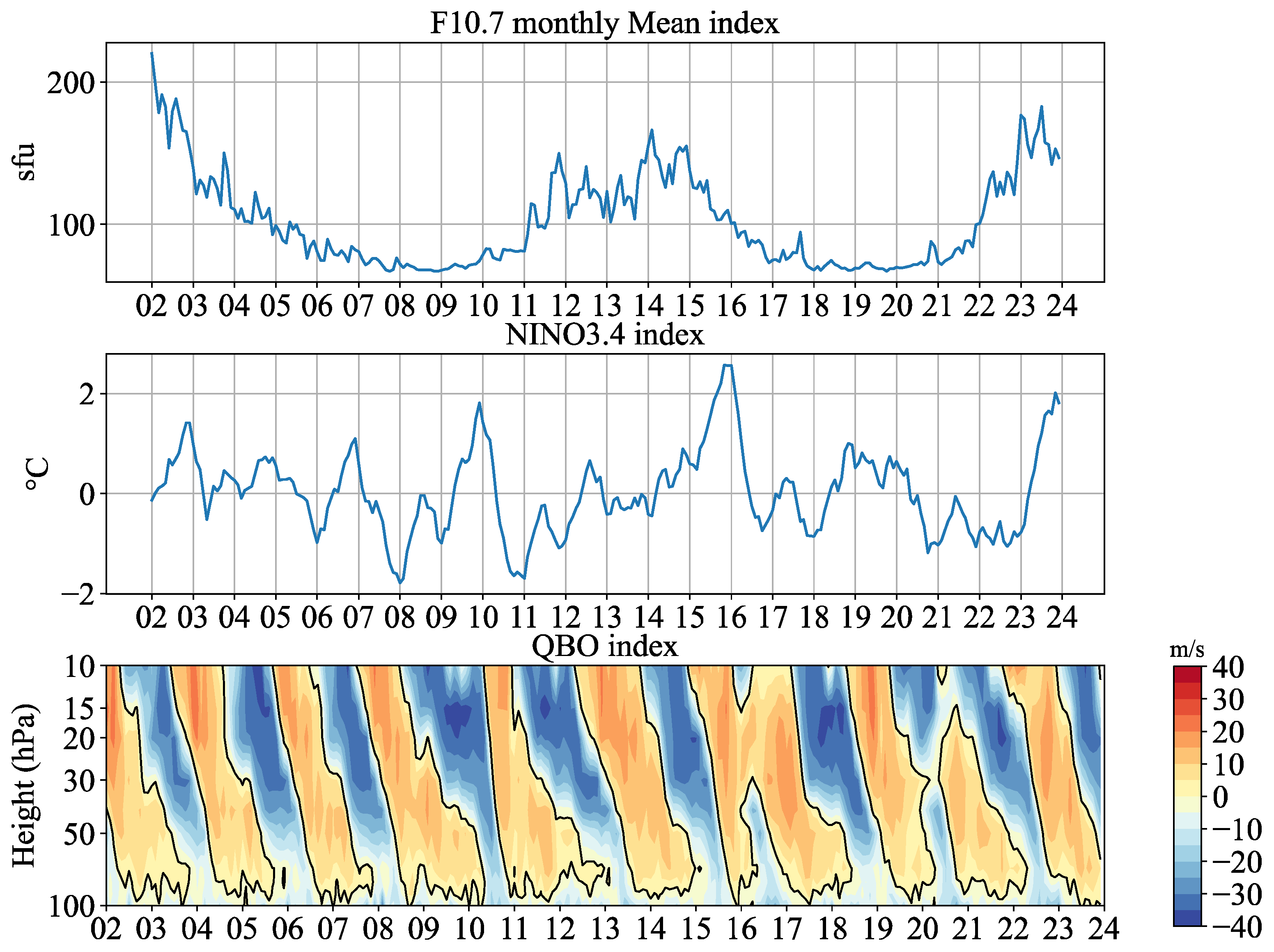
2. Data and Methods
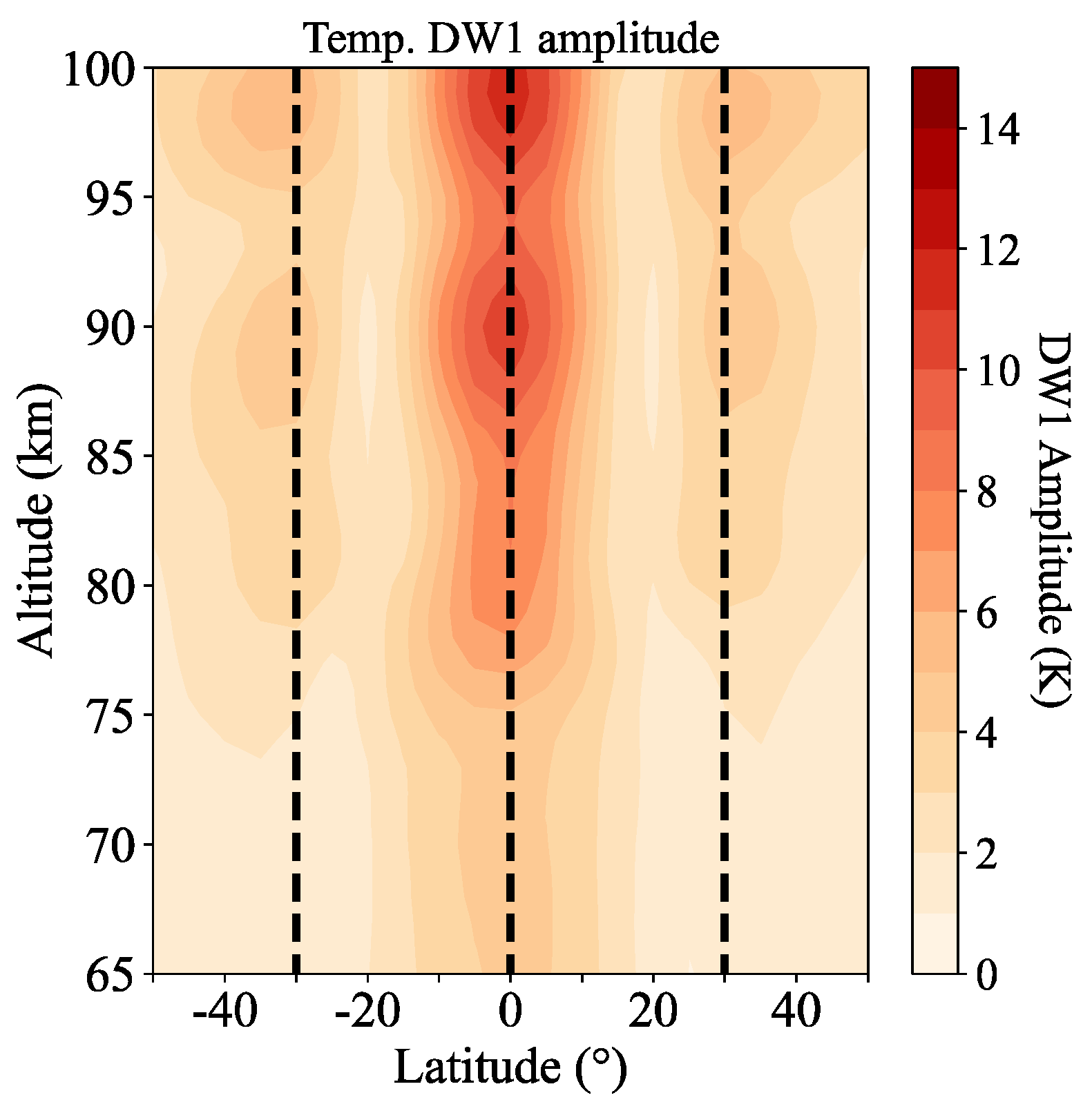
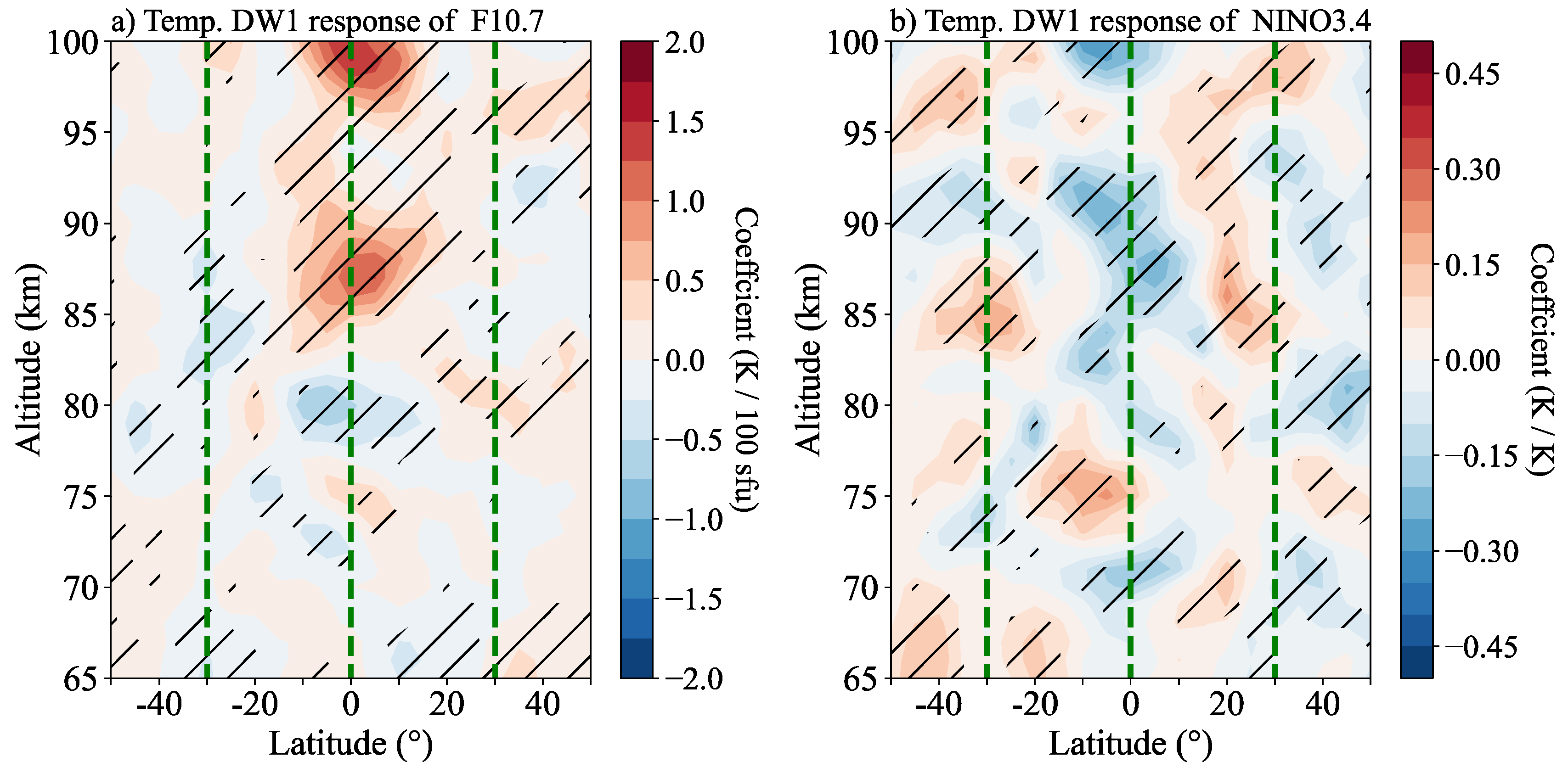
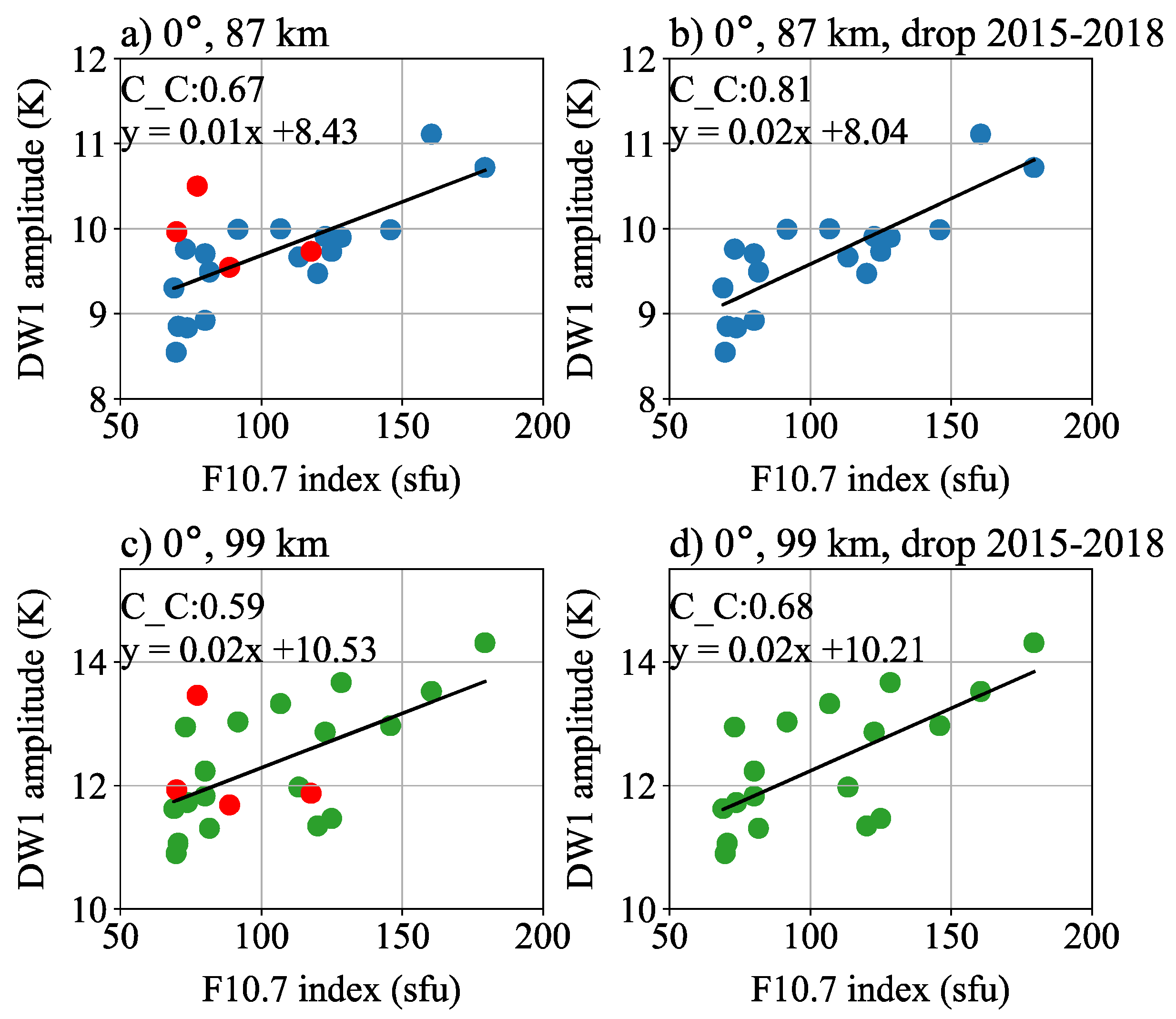
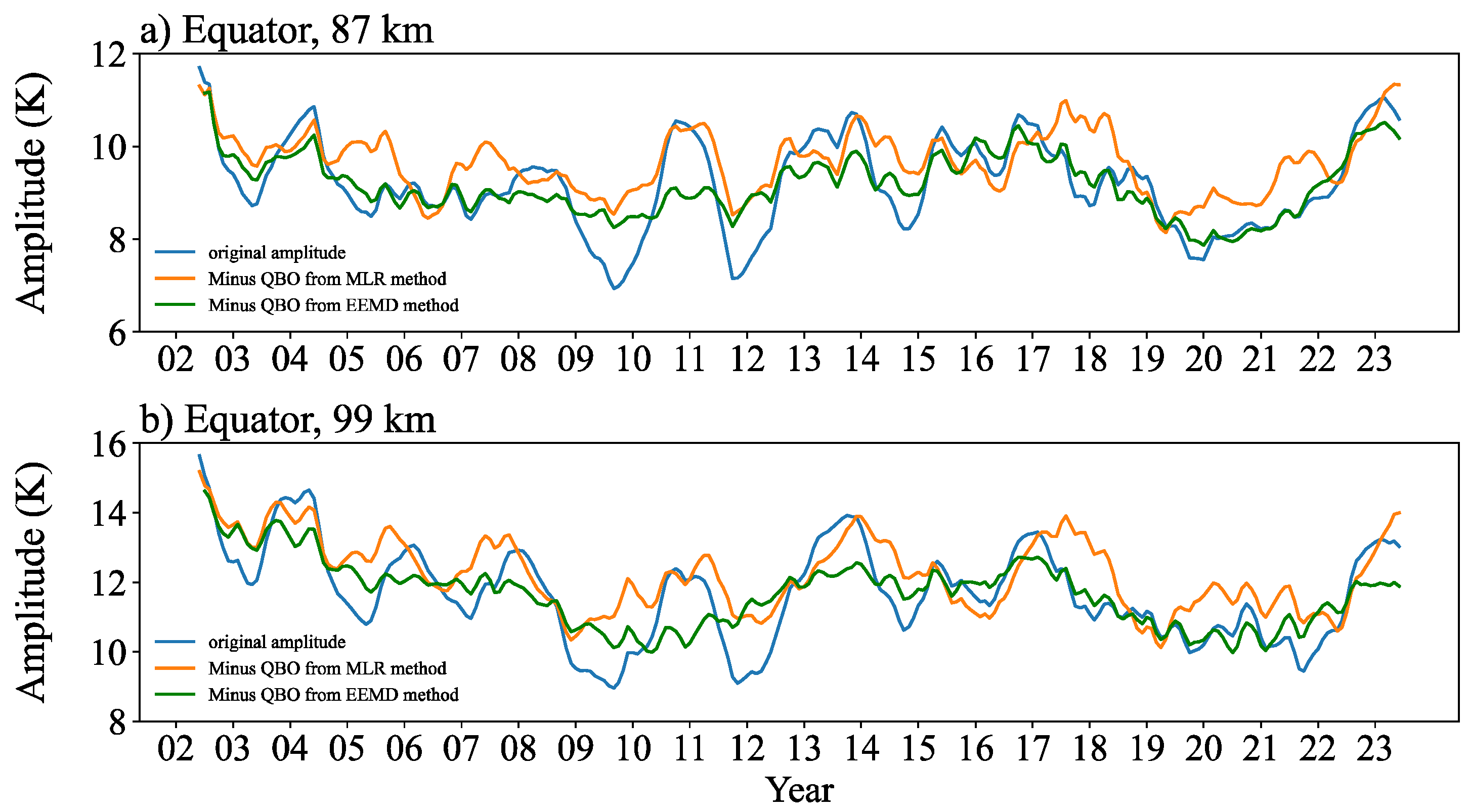
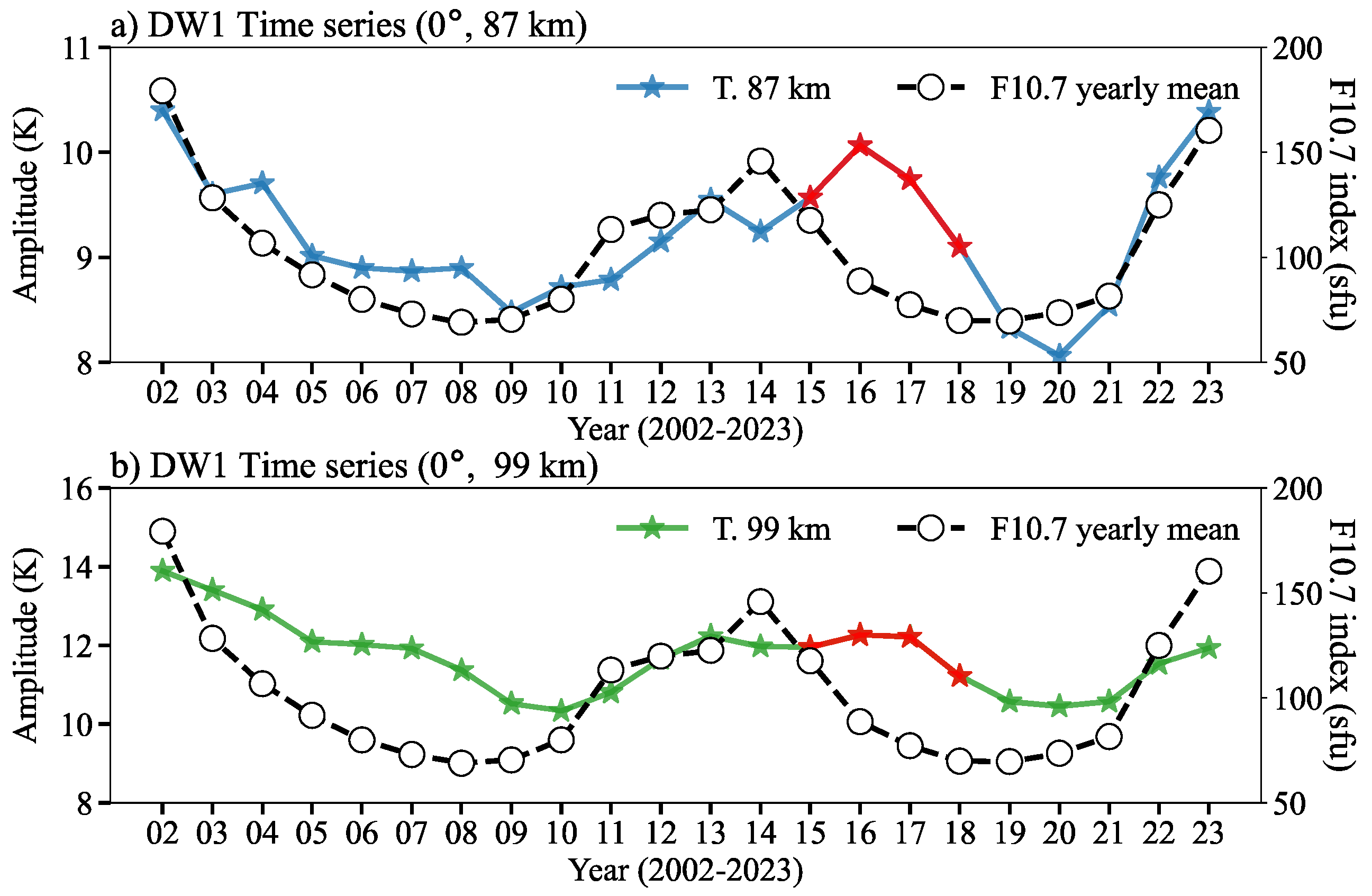
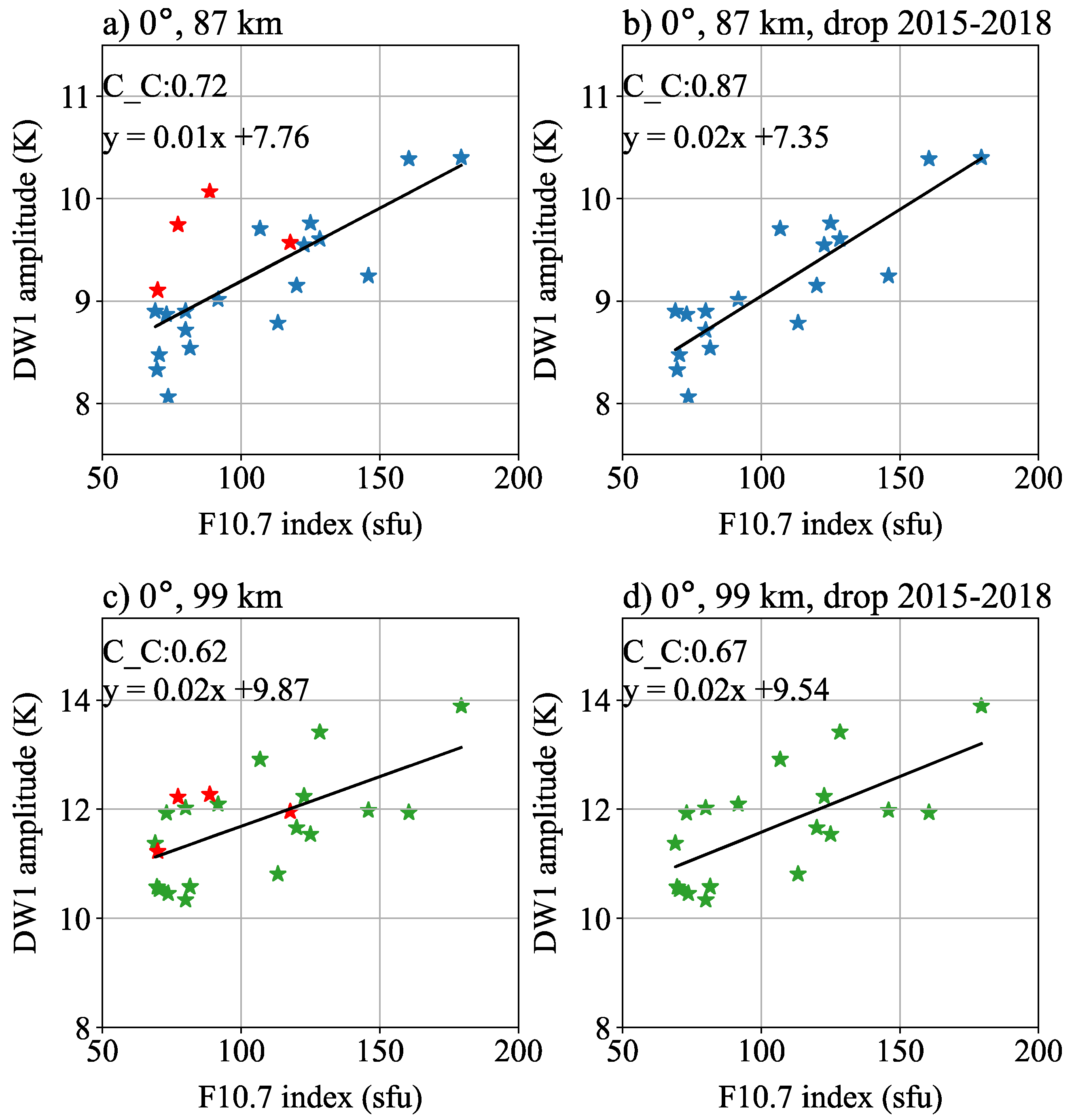
3. Solar Cycle Dependence of Temperature DW1
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Smith, A.K. Global Dynamics of the MLT. Surv. Geophys. 2012, 33, 1177–1230. [Google Scholar] [CrossRef]
- Lieberman, R.S.; Smith, A.K.; Franke, S.J.; Vincent, R.A.; Isler, J.R.; Manson, A.H.; Meek, C.E.; Fraser, G.J.; Fahrutdinova, A.; Thayaparan, T.; et al. Comparison of mesospheric and lower thermospheric residual wind with High Resolution Doppler Imager, medium frequency, and meteor radar winds. J. Geophys. Res. Atmos. 2000, 105, 27023–27035. [Google Scholar] [CrossRef]
- Garcia, R.R. On the Structure and Variability of the Migrating Diurnal Temperature Tide Observed by SABER. J. Atmos. Sci. 2023, 80, 687–704. [Google Scholar] [CrossRef]
- Cen, Y.; Yang, C.; Li, T.; Russell Iii, J.M.; Dou, X. Suppressed migrating diurnal tides in the mesosphere and lower thermosphere region during El Niño in northern winter and its possible mechanism. Atmos. Chem. Phys. 2022, 22, 7861–7874. [Google Scholar] [CrossRef]
- Dhadly, M.S.; Emmert, J.T.; Drob, D.P.; McCormack, J.P.; Niciejewski, R.J. Short-Term and Interannual Variations of Migrating Diurnal and Semidiurnal Tides in the Mesosphere and Lower Thermosphere. J. Geophys. Res. Space Phys. 2018, 123, 7106–7123. [Google Scholar] [CrossRef]
- Singh, D.; Gurubaran, S. Variability of diurnal tide in the MLT region over Tirunelveli (8.7°N), India: Consistency between ground- and space-based observations. J. Geophys. Res. Atmos. 2017, 122, 2696–2713. [Google Scholar] [CrossRef]
- Bremer, J.; Schminder, R.; Greisiger, K.M.; Hoffmann, P.; Kürschner, D.; Singer, W. Solar cycle dependence and long-term trends in the wind field of the mesosphere/lower thermosphere. J. Atmos. Sol. Terr. Phys. 1997, 59, 497–509. [Google Scholar] [CrossRef]
- Baumgaertner, A.J.G.; McDonald, A.J.; Fraser, G.J.; Plank, G.E. Long-term observations of mean winds and tides in the upper mesosphere and lower thermosphere above Scott Base, Antarctica. J. Atmos. Sol. Terr. Phys. 2005, 67, 1480–1496. [Google Scholar] [CrossRef]
- Sridharan, S.; Tsuda, T.; Gurubaran, S. Long-term tendencies in the mesosphere/lower thermosphere mean winds and tides as observed by medium-frequency radar at Tirunelveli (8.7°N, 77.8°E). J. Geophys. Res. 2010, 115, D08109. [Google Scholar] [CrossRef]
- Guharay, A.; Batista, P.P.; Andrioli, V.F. Investigation of solar cycle dependence of the tides in the low latitude MLT using meteor radar observations. J. Atmos. Sol. Terr. Phys. 2019, 193, 105083. [Google Scholar] [CrossRef]
- Andrioli, V.F.; Xu, J.; Batista, P.P.; Resende, L.C.A.; Da Silva, L.A.; Marchezi, J.P.; Li, H.; Wang, C.; Liu, Z.; Guharay, A. New Findings Relating Tidal Variability and Solar Activity in the Low Latitude MLT Region. J. Geophys. Res. Space Phys. 2022, 127, e2021JA030239. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, J.; Smith, A.K.; Liu, X. Seasonal and Interannual Variations of Global Tides in the Mesosphere and Lower Thermosphere Neutral Winds: I. Diurnal Tides. J. Geophys. Res. Space Phys. 2024, 129, e2023JA031887. [Google Scholar] [CrossRef]
- Wu, C.; Ridley, A.J.; Cullens, C.Y. Seasonal Dependency of the Solar Cycle, QBO, and ENSO Effects on the Interannual Variability of the Wind DW1 in the MLT Region. J. Geophys. Res. Space Phys. 2024, 129, e2024JA032472. [Google Scholar] [CrossRef]
- Vitharana, A.; Du, J.; Zhu, X.; Oberheide, J.; Ward, W.E. Numerical Prediction of the Migrating Diurnal Tide Total Variability in the Mesosphere and Lower Thermosphere. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029588. [Google Scholar] [CrossRef]
- Mertens, C.J.; Mlynczak, M.G.; López-Puertas, M.; Wintersteiner, P.P.; Picard, R.H.; Winick, J.R.; Gordley, L.L.; Russell, J.M. Retrieval of mesospheric and lower thermospheric kinetic temperature from measurements of CO215 µm Earth Limb Emission under non-LTE conditions. Geophys. Res. Lett. 2001, 28, 1391–1394. [Google Scholar] [CrossRef]
- Mertens, C.J. SABER observations of mesospheric temperatures and comparisons with falling sphere measurements taken during the 2002 summer MaCWAVE campaign. Geophys. Res. Lett. 2004, 31, L03105. [Google Scholar] [CrossRef]
- Dawkins, E.C.M.; Feofilov, A.; Rezac, L.; Kutepov, A.A.; Janches, D.; Höffner, J.; Chu, X.; Lu, X.; Mlynczak, M.G.; Russell, J. Validation of SABER v2.0 Operational Temperature Data With Ground-Based Lidars in the Mesosphere-Lower Thermosphere Region (75–105 km). J. Geophys. Res. Atmos. 2018, 123, 9916–9934. [Google Scholar] [CrossRef]
- Mlynczak, M.G.; Marshall, B.T.; Garcia, R.R.; Hunt, L.; Yue, J.; Harvey, V.L.; Lopez-Puertas, M.; Mertens, C.; Russell, J. Algorithm Stability and the Long-Term Geospace Data Record From TIMED/SABER. Geophys. Res. Lett. 2023, 50, e2022GL102398. [Google Scholar] [CrossRef]
- Xu, J.; Smith, A.K.; Yuan, W.; Liu, H.L.; Wu, Q.; Mlynczak, M.G.; Russell, J.M. Global structure and long-term variations of zonal mean temperature observed by TIMED/SABER. J. Geophys. Res. 2007, 112, D24106. [Google Scholar] [CrossRef]
- Xu, J.; Smith, A.K.; Liu, H.L.; Yuan, W.; Wu, Q.; Jiang, G.; Mlynczak, M.G.; Russell, J.M.; Franke, S.J. Seasonal and quasi-biennial variations in the migrating diurnal tide observed by Thermosphere, Ionosphere, Mesosphere, Energetics and Dynamics (TIMED). J. Geophys. Res. 2009, 114, D13107. [Google Scholar] [CrossRef]
- Liu, H.L. WACCM-X Simulation of Tidal and Planetary Wave Variability in the Upper Atmosphere. 2014, pp. 181–199. Available online: https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1002/9781118704417.ch16 (accessed on 1 May 2024).
- Huang, F.T.; Mayr, H.G.; Reber, C.A.; Russell, J.M.; Mlynczak, M.G.; Mengel, J.G. Ozone quasi-biennial oscillations (QBO), semiannual oscillations (SAO), and correlations with temperature in the mesosphere, lower thermosphere, and stratosphere, based on measurements from SABER on TIMED and MLS on UARS. J. Geophys. Res. Space Phys. 2008, 113, A01316. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Y.; Shen, B.-W. An Evaluation of the Parallel Ensemble Empirical Mode Decomposition Method in Revealing the Role of Downscaling Processes Associated with African Easterly Waves in Tropical Cyclone Genesis. J. Atmos. Oceanic Technol. 2016, 33, 1611–1628. [Google Scholar] [CrossRef]
- Zou, M.; Xiong, X.; Wu, Z.; Li, S.; Zhang, Y.; Chen, L. Increase of Atmospheric Methane Observed from Space-Borne and Ground-Based Measurements. Remote Sens. 2019, 11, 964. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2011, 1, 1–41. [Google Scholar] [CrossRef]
- Liu, M.; Xu, J.; Liu, H.; Liu, X. Possible modulation of migrating diurnal tide by latitudinal gradient of zonal wind observed by SABER/TIMED. Sci. China Earth Sci. 2015, 59, 408–417. [Google Scholar] [CrossRef]
- Gu, H.; Du, J. On the Roles of Advection and Solar Heating in Seasonal Variation of the Migrating Diurnal Tide in the Stratosphere, Mesosphere, and Lower Thermosphere. Atmosphere 2018, 9, 440. [Google Scholar] [CrossRef]
- Pramitha, M.; Kumar, K.K.; Ratnam, M.V.; Praveen, M.; Bhaskara Rao, S.V. Stratospheric Quasi Biennial Oscillation Modulations of Migrating Diurnal Tide in the Mesosphere and Lower Thermosphere Over the Low and Equatorial Latitudes. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028970. [Google Scholar] [CrossRef]
- Seidel, D.J.; Li, J.; Mears, C.; Moradi, I.; Nash, J.; Randel, W.J.; Saunders, R.; Thompson, D.W.J.; Zou, C.Z. Stratospheric temperature changes during the satellite era. J. Geophys. Res. Atmos. 2016, 121, 664–681. [Google Scholar] [CrossRef]
- Wang, Y.; Rao, J.; Lu, Y.; Ju, Z.; Yang, J.; Luo, J. A revisit and comparison of the quasi-biennial oscillation (QBO) disruption events in 2015/16 and 2019/20. Atmos. Res. 2023, 294, 106970. [Google Scholar] [CrossRef]
- Anstey, J.A.; Banyard, T.P.; Butchart, N.; Coy, L.; Newman, P.A.; Osprey, S.; Wright, C.J. Prospect of Increased Disruption to the QBO in a Changing Climate. Geophys. Res. Lett. 2021, 48, e2021GL093058. [Google Scholar] [CrossRef]
- Pramitha, M.; Kishore Kumar, K.; Venkat Ratnam, M.; Praveen, M.; Rao, S.V.B. Disrupted Stratospheric QBO Signatures in the Diurnal Tides Over the Low-Latitude MLT Region. Geophys. Res. Lett. 2021, 48, e2021GL093022. [Google Scholar] [CrossRef]
- Schieferdecker, T.; Lossow, S.; Stiller, G.P.; von Clarmann, T. Is there a solar signal in lower stratospheric water vapour? Atmos. Chem. Phys. 2015, 15, 9851–9863. [Google Scholar] [CrossRef]
- Sridharan, S.; Sandhya, M. Long-term (2004–2015) tendencies and variabilities of tropical UTLS water vapor mixing ratio and temperature observed by AURA/MLS using multivariate regression analysis. J. Atmos. Sol. Terr. Phys. 2016, 147, 156–165. [Google Scholar] [CrossRef]
- Ball, W.T.; Rozanov, E.V.; Alsing, J.; Marsh, D.R.; Tummon, F.; Mortlock, D.J.; Kinnison, D.; Haigh, J.D. The Upper Stratospheric Solar Cycle Ozone Response. Geophys. Res. Lett. 2019, 46, 1831–1841. [Google Scholar] [CrossRef]
- Nath, O.; Sridharan, S. Long-term variabilities and tendencies in zonal mean TIMED–SABER ozone and temperature in the middle atmosphere at 10–15° N. J. Atmos. Sol. Terr. Phys. 2014, 120, 1–8. [Google Scholar] [CrossRef]
- Woods, T.N.; Harder, J.W.; Kopp, G.; Snow, M. Solar-Cycle Variability Results from the Solar Radiation and Climate Experiment (SORCE) Mission. Sol. Phys. 2022, 297, 43. [Google Scholar] [CrossRef]
- Thuillier, G.; Zhu, P.; Snow, M.; Zhang, P.; Ye, X. Characteristics of solar-irradiance spectra from measurements, modeling, and theoretical approach. Light Sci Appl 2022, 11, 79. [Google Scholar] [CrossRef]
- Ortland, D.A. Daily estimates of the migrating tide and zonal mean temperature in the mesosphere and lower thermosphere derived from SABER data. J. Geophys. Res. Atmos. 2017, 122, 3754–3785. [Google Scholar] [CrossRef]
- McLandress, C. The Seasonal Variation of the Propagating Diurnal Tide in the Mesosphere and Lower Thermosphere. Part II: The Role of Tidal Heating and Zonal Mean Winds. J. Atmos. Sci. 2002, 59, 907–922. [Google Scholar] [CrossRef]
- Ramesh, K.; Smith, A.K.; Garcia, R.R.; Marsh, D.R.; Sridharan, S.; Kishore Kumar, K. Long-Term Variability and Tendencies in Middle Atmosphere Temperature and Zonal Wind From WACCM6 Simulations During 1850–2014. J. Geophys. Res. Atmos. 2020, 125, e2020JD033579. [Google Scholar] [CrossRef]
- Liu, X.; Xu, J.; Yue, J.; Yu, Y.; Batista, P.P.; Andrioli, V.F.; Liu, Z.; Yuan, T.; Wang, C.; Zou, Z.; et al. Global balanced wind derived from SABER temperature and pressure observations and its validations. Earth Syst. Sci. Data 2021, 13, 5643–5661. [Google Scholar] [CrossRef]
- Liu, X.; Xu, J.; Yue, J.; Andrioli, V.F. Variations in global zonal wind from 18 to 100 km due to solar activity and the quasi-biennial oscillation and El Niño–Southern Oscillation during 2002–2019. Atmos. Chem. Phys. 2023, 23, 6145–6167. [Google Scholar] [CrossRef]
- Iimura, H.; Fritts, D.C.; Riggin, D.M. Long-term oscillations of the wind field in the tropical mesosphere and lower thermosphere from Hawaii MF radar measurements. J. Geophys. Res. 2010, 115, D09112. [Google Scholar] [CrossRef]
- Remsberg, E.E.; Deaver, L.E. Interannual, solar cycle, and trend terms in middle atmospheric temperature time series from HALOE. J. Geophys. Res. Atmos. 2005, 110, D0610. [Google Scholar] [CrossRef]
- Hagan, M.E. Comparative effects of migrating solar sources on tidal signatures in the middle and upper atmosphere. J. Geophys. Res. Atmos. 1996, 101, 21213–21222. [Google Scholar] [CrossRef]
- Hagan, M.E.; Burrage, M.D.; Forbes, J.M.; Hackney, J.; Randel, W.J.; Zhang, X. GSWM-98: Results for migrating solar tides. J. Geophys. Res. Space Phys. 1999, 104, 6813–6827. [Google Scholar] [CrossRef]

| Two Layers | R-Square | Correlation Coefficient | Single Layer | R-Square |
|---|---|---|---|---|
| 30 hPa & 10 hPa | 0.44 | −0.12 | 70 hPa | 0.25 |
| 40 hPa & 15 hPa | 0.48 | −0.15 | 50 hPa | 0.13 |
| 50 hPa & 20 hPa | 0.45 | −0.27 | 40 hPa | 0.12 |
| 70 hPa & 30 hPa | 0.36 | −0.29 | 30 hPa | 0.27 |
| 20 hPa | 0.45 | |||
| 15 hPa | 0.43 | |||
| 10 hPa | 0.23 |
| Time Lag (Years) | −5 | −4 | −3 | −2 | −1 | 0 |
|---|---|---|---|---|---|---|
| 0°, 87 km | −0.31 | 0.06 | 0.39 | 0.62 * | 0.73 * | 0.72 * |
| 0°, 99 km | 0.06 | 0.46 * | 0.75 * | 0.90 * | 0.87 * | 0.62 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Jiang, G.; Luo, B.; Xu, J.; Lin, R.; Zhu, Y.; Liu, W. Solar Cycle Dependence of Migrating Diurnal Tide in the Equatorial Mesosphere and Lower Thermosphere. Remote Sens. 2024, 16, 3437. https://doi.org/10.3390/rs16183437
Liu S, Jiang G, Luo B, Xu J, Lin R, Zhu Y, Liu W. Solar Cycle Dependence of Migrating Diurnal Tide in the Equatorial Mesosphere and Lower Thermosphere. Remote Sensing. 2024; 16(18):3437. https://doi.org/10.3390/rs16183437
Chicago/Turabian StyleLiu, Shuai, Guoying Jiang, Bingxian Luo, Jiyao Xu, Ruilin Lin, Yajun Zhu, and Weijun Liu. 2024. "Solar Cycle Dependence of Migrating Diurnal Tide in the Equatorial Mesosphere and Lower Thermosphere" Remote Sensing 16, no. 18: 3437. https://doi.org/10.3390/rs16183437
APA StyleLiu, S., Jiang, G., Luo, B., Xu, J., Lin, R., Zhu, Y., & Liu, W. (2024). Solar Cycle Dependence of Migrating Diurnal Tide in the Equatorial Mesosphere and Lower Thermosphere. Remote Sensing, 16(18), 3437. https://doi.org/10.3390/rs16183437









