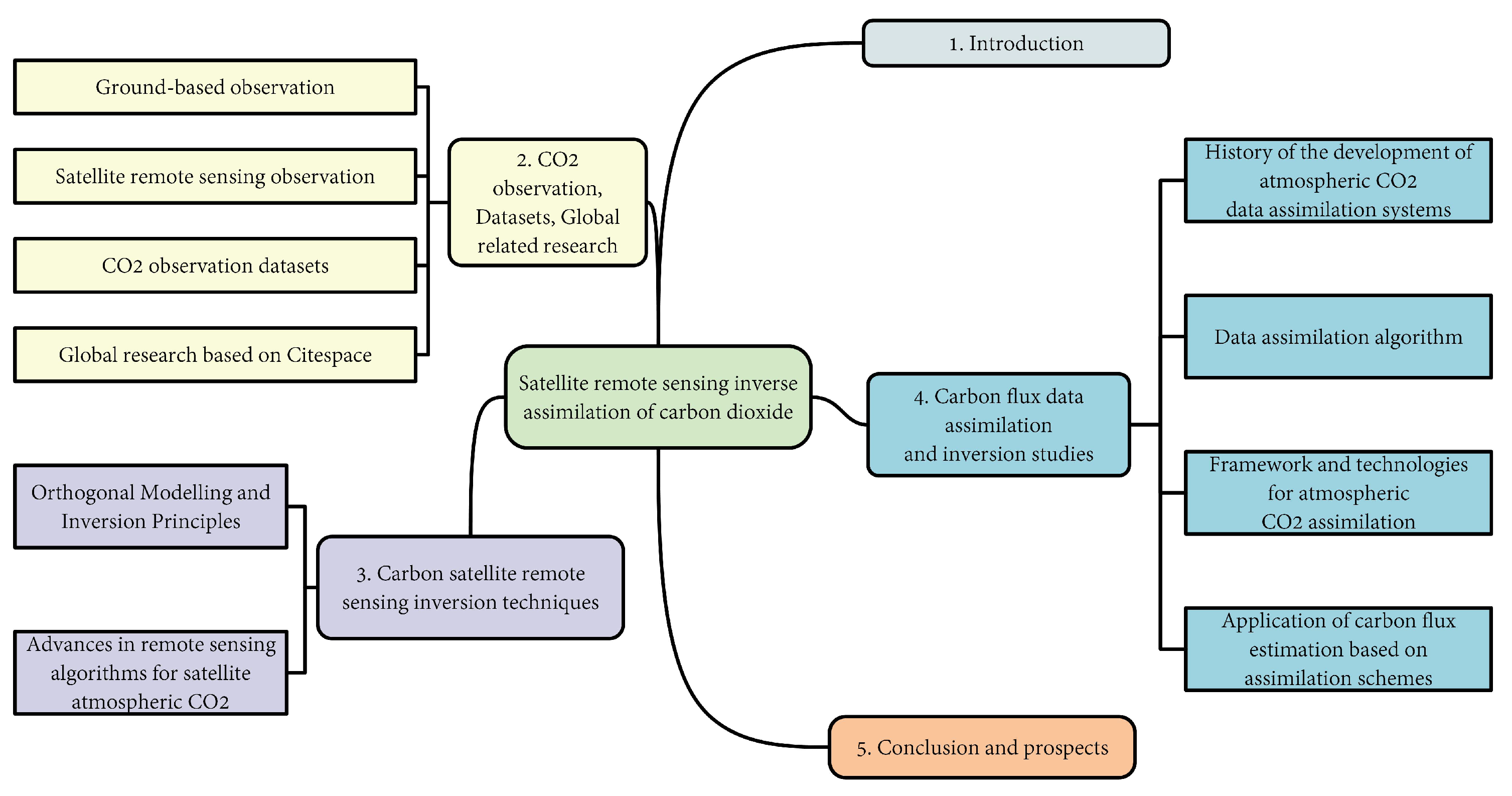
Review of Satellite Remote Sensing of Carbon Dioxide Inversion and Assimilation
Abstract
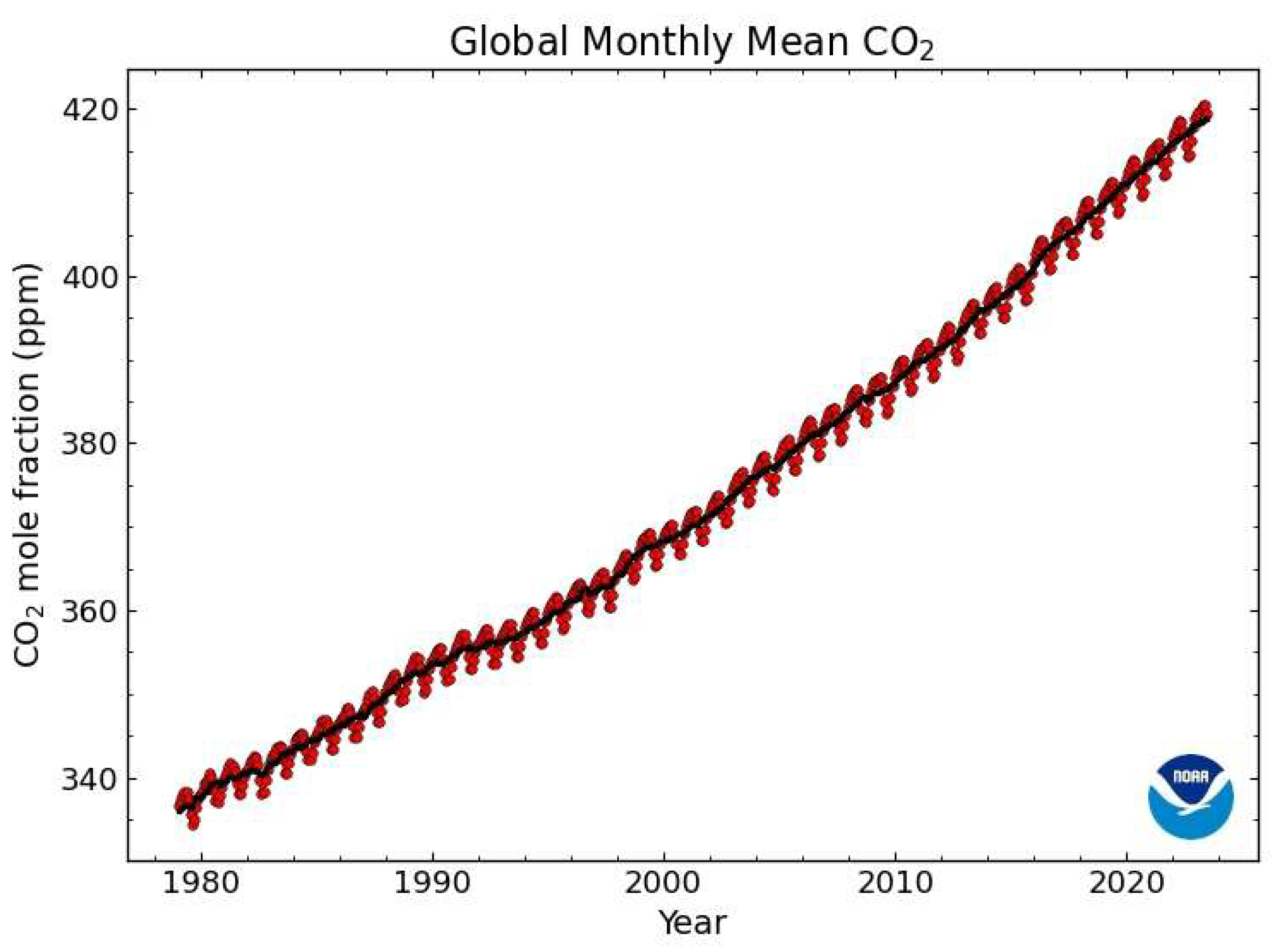
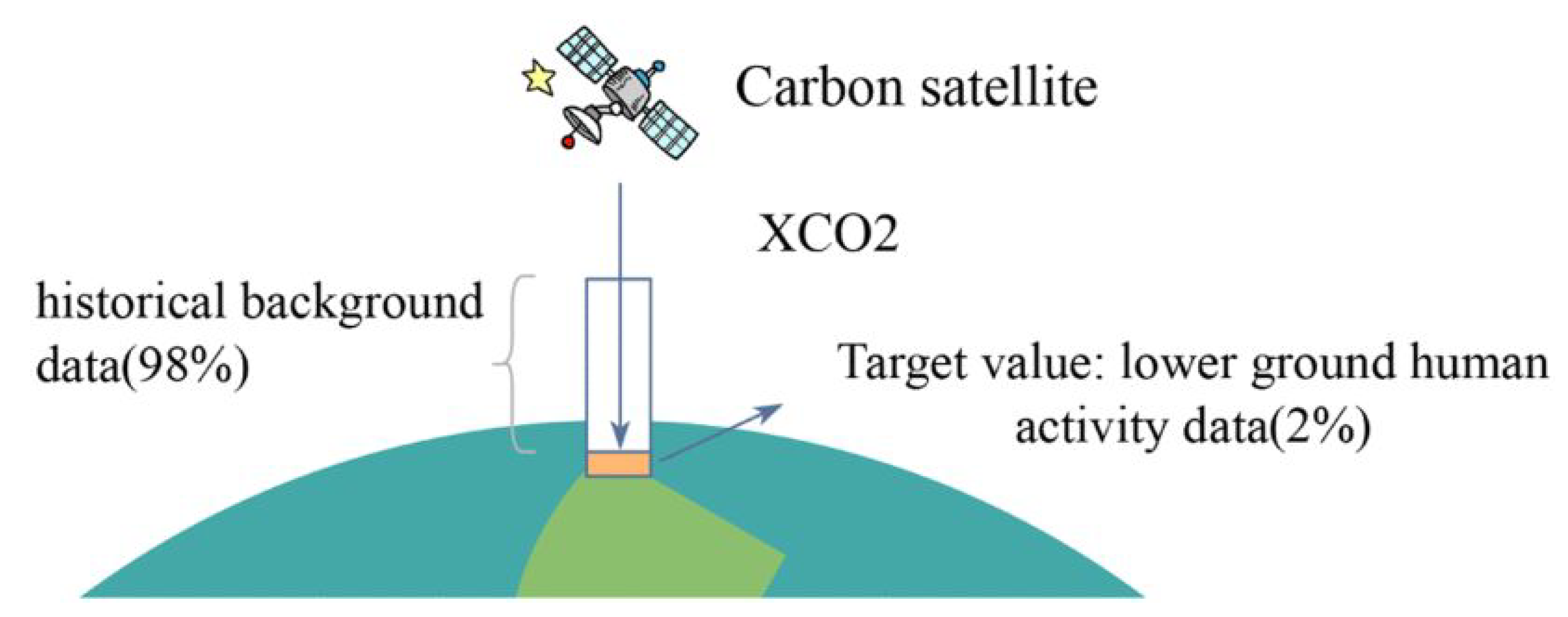
1. Introduction
- (1)
- An overview of CO2 satellite observation technologies, launched and planned CO2 satellites was presented.
- (2)
- Introduction to the principles and development of algorithms for various CO2 atmospheric transport models and inversion methods.
- (3)
- Introduction to carbon dioxide data-assimilation techniques and the global CO2-assimilation system, as well as the application of the assimilation program for carbon flux estimation.
2. CO2 Observation, Datasets, Global Related Research
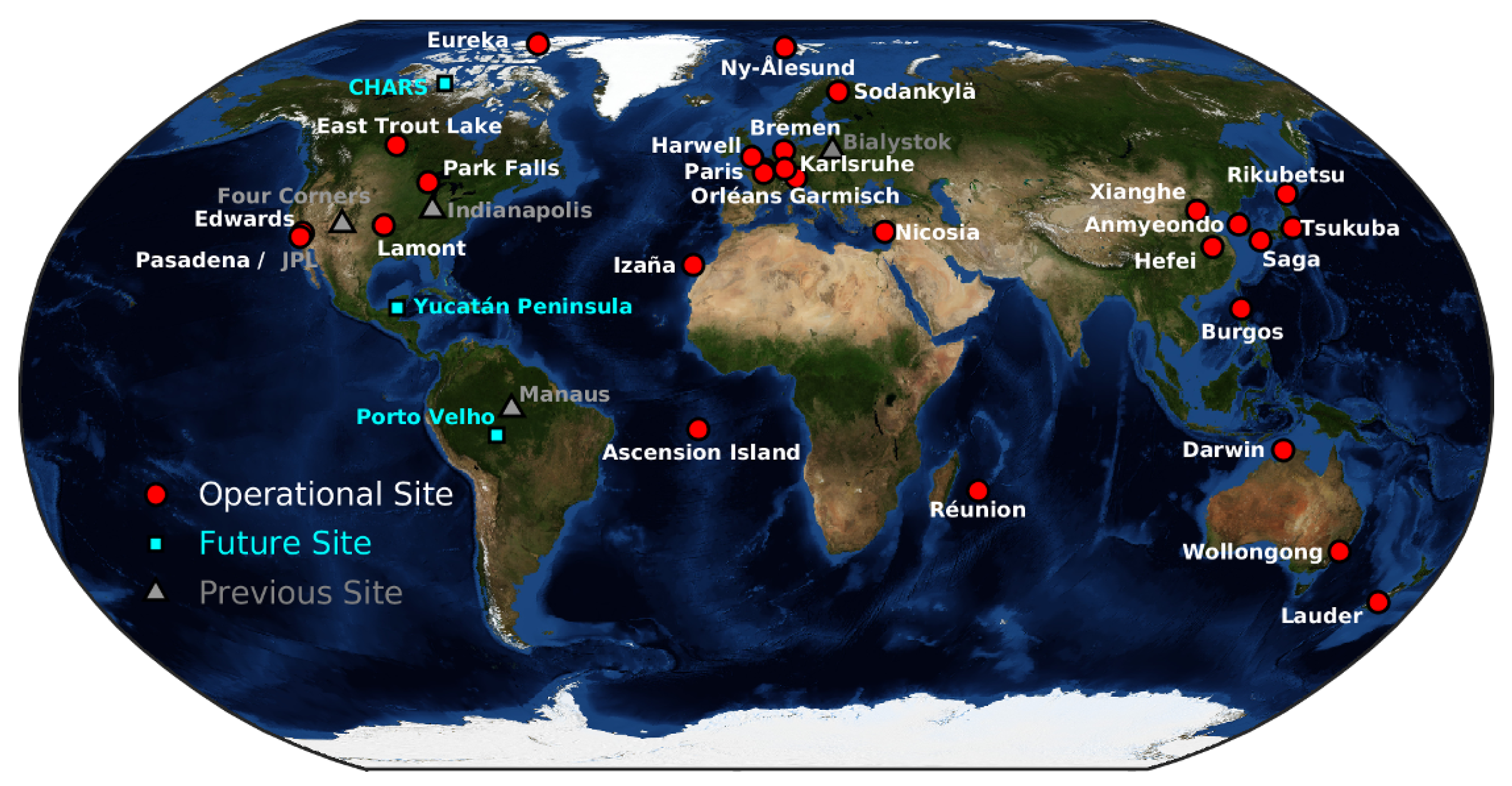
2.1. Ground-Based Observation
2.1.1. TCCON (Total Column Carbon Observation Network)
2.1.2. COCCON (COllaborative Carbon Column Observing Network)
2.2. Satellite Remote Sensing Observations
2.2.1. Development of Thermal Infrared Hyperspectral Sensors
2.2.2. Development of Short-Wave Infrared Hyperspectral Sensors
European Satellites
Japanese Satellites
United States Satellites
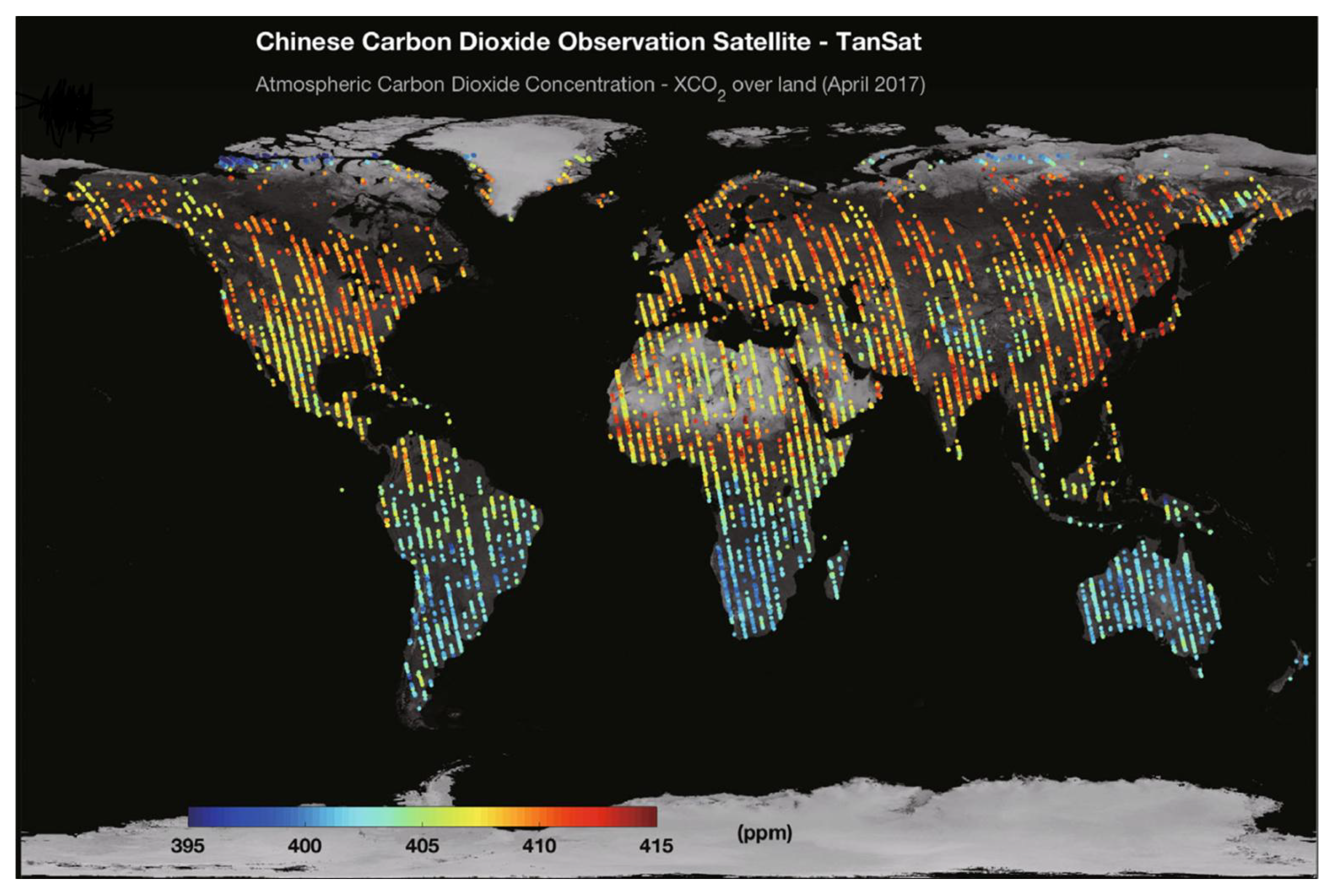
China Satellite
Planned Future Launches of Remote Sensing Satellites CO2
2.3. CO2 Observation Database
2.3.1. XCO2 Products
2.3.2. Anthropogenic Emissions Dataset
ODIAC Dataset
EDGAR Dataset
MEIC Dataset
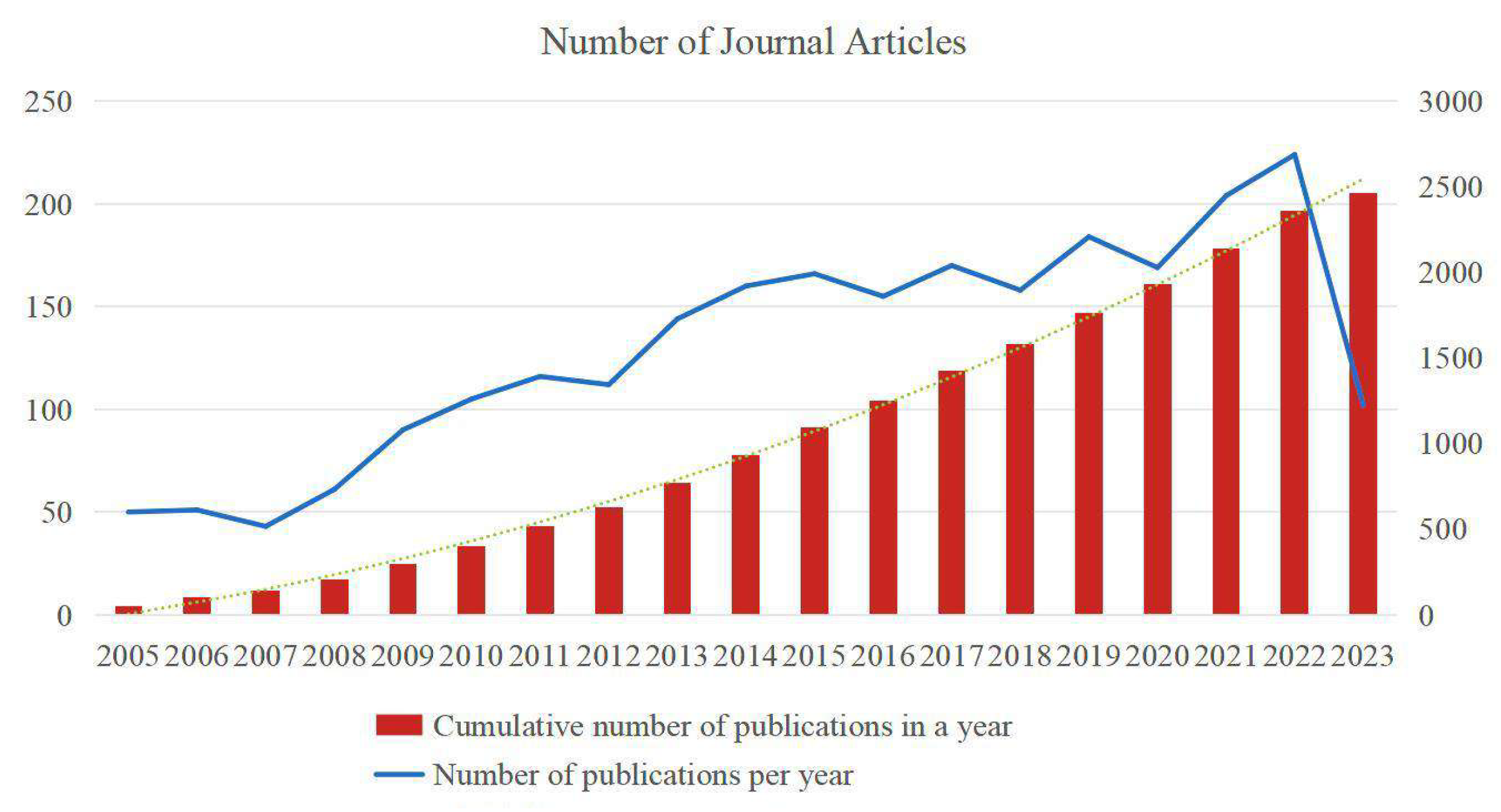
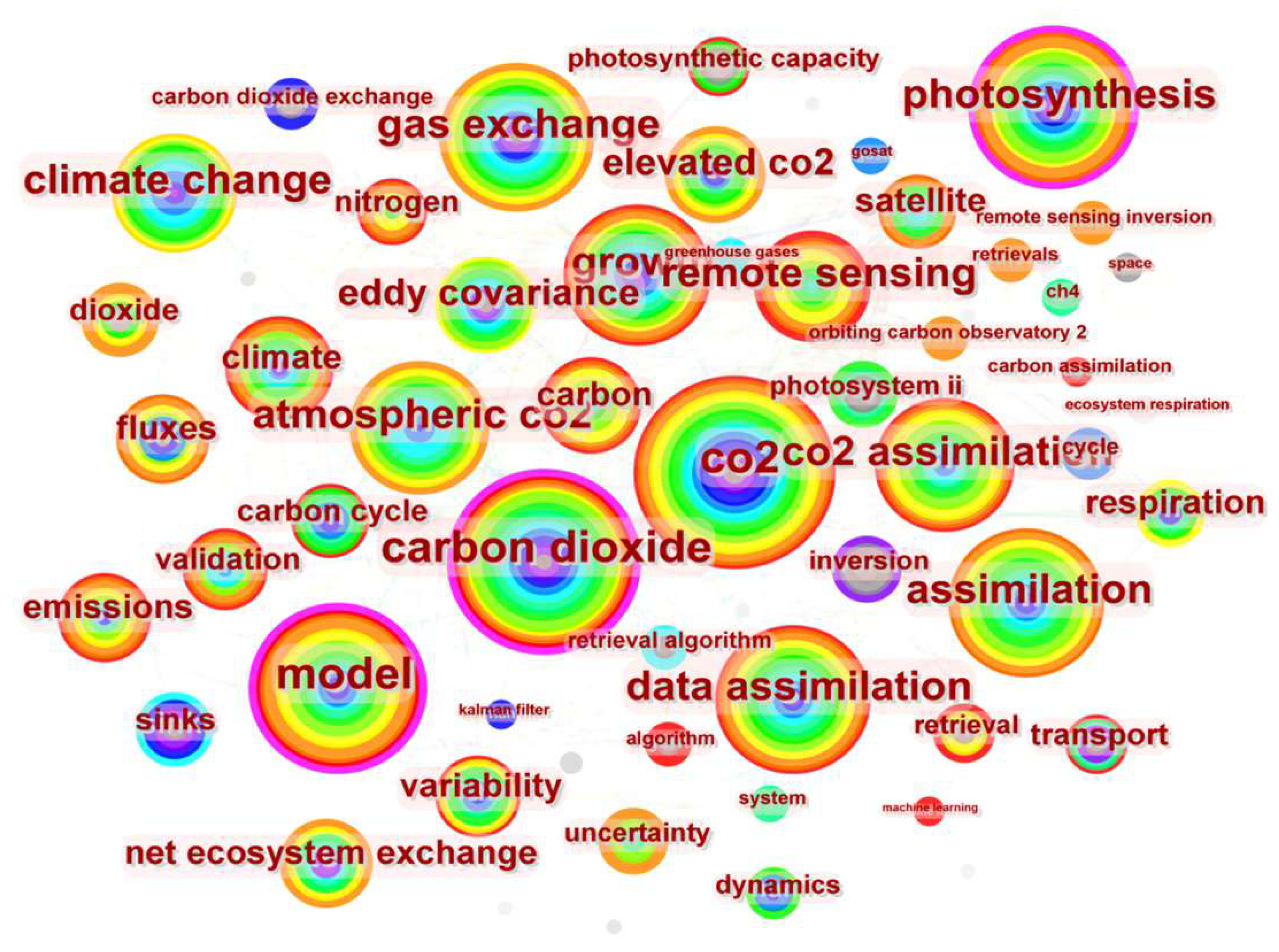
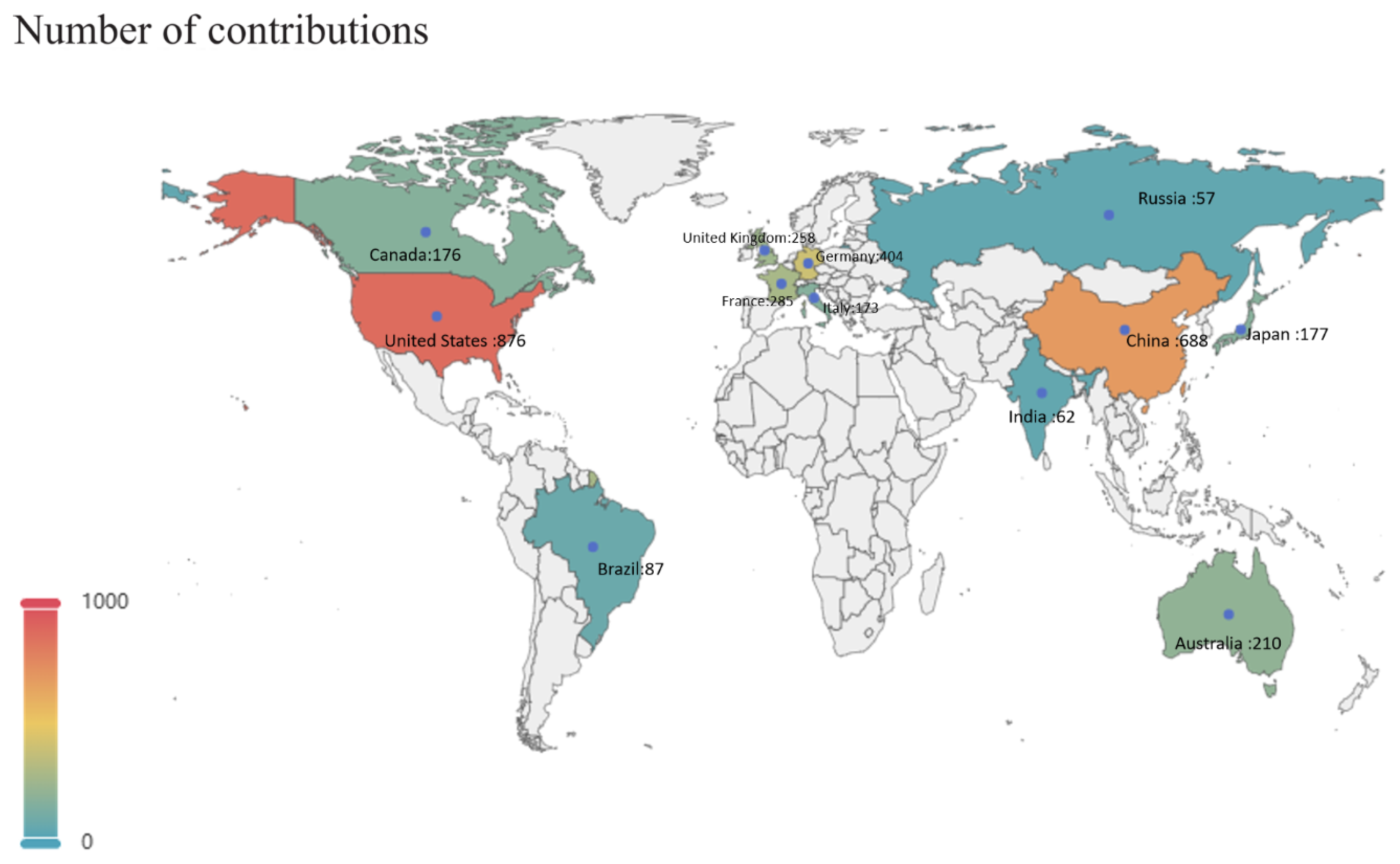
2.4. Citespace-Based Global Research
2.5. Section Summary
3. Carbon Satellite Remote Sensing Inversion Techniques
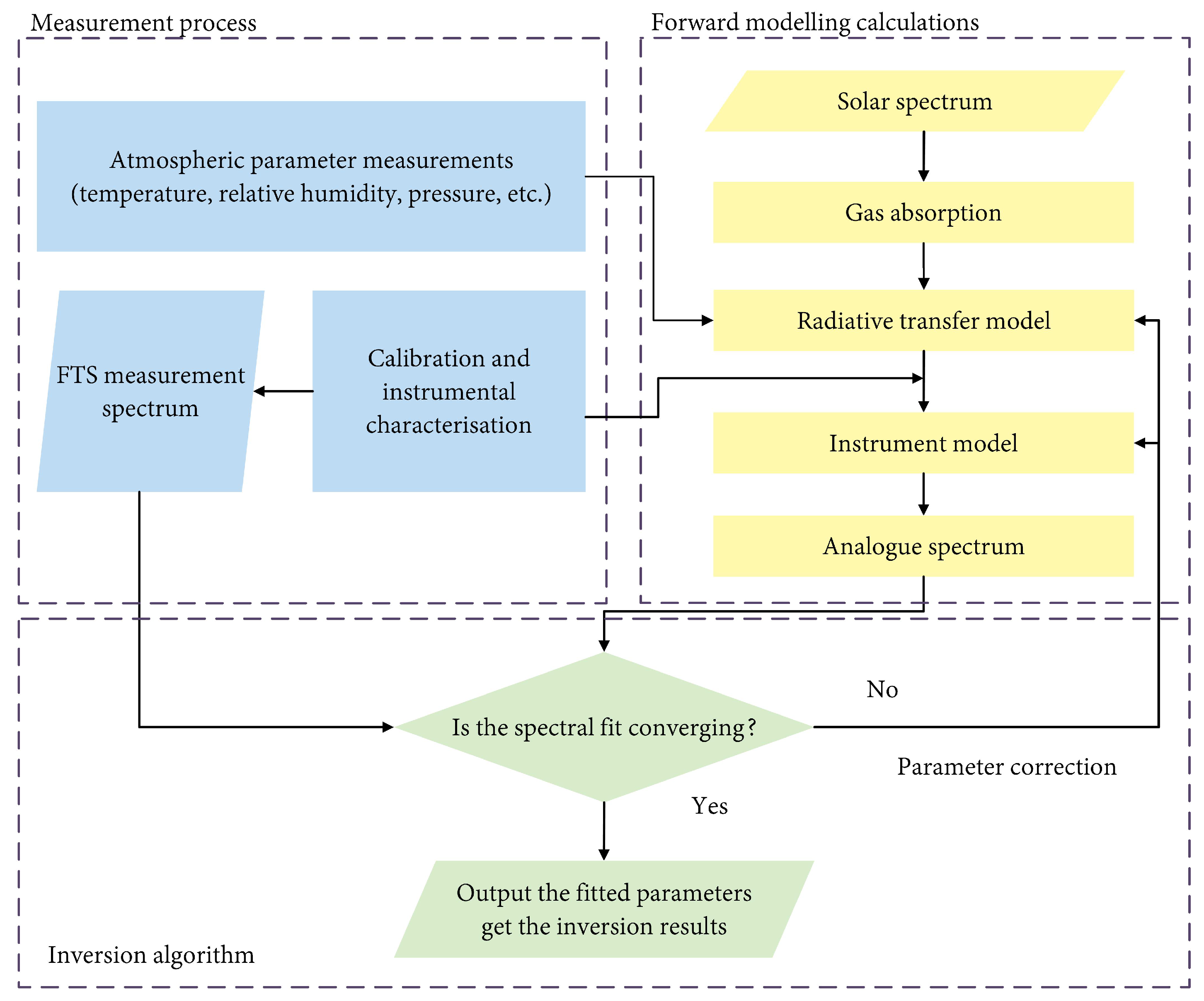
3.1. Orthogonal Modelling and Inversion Principles
3.1.1. Basic Principles of Remote Sensing Inversion
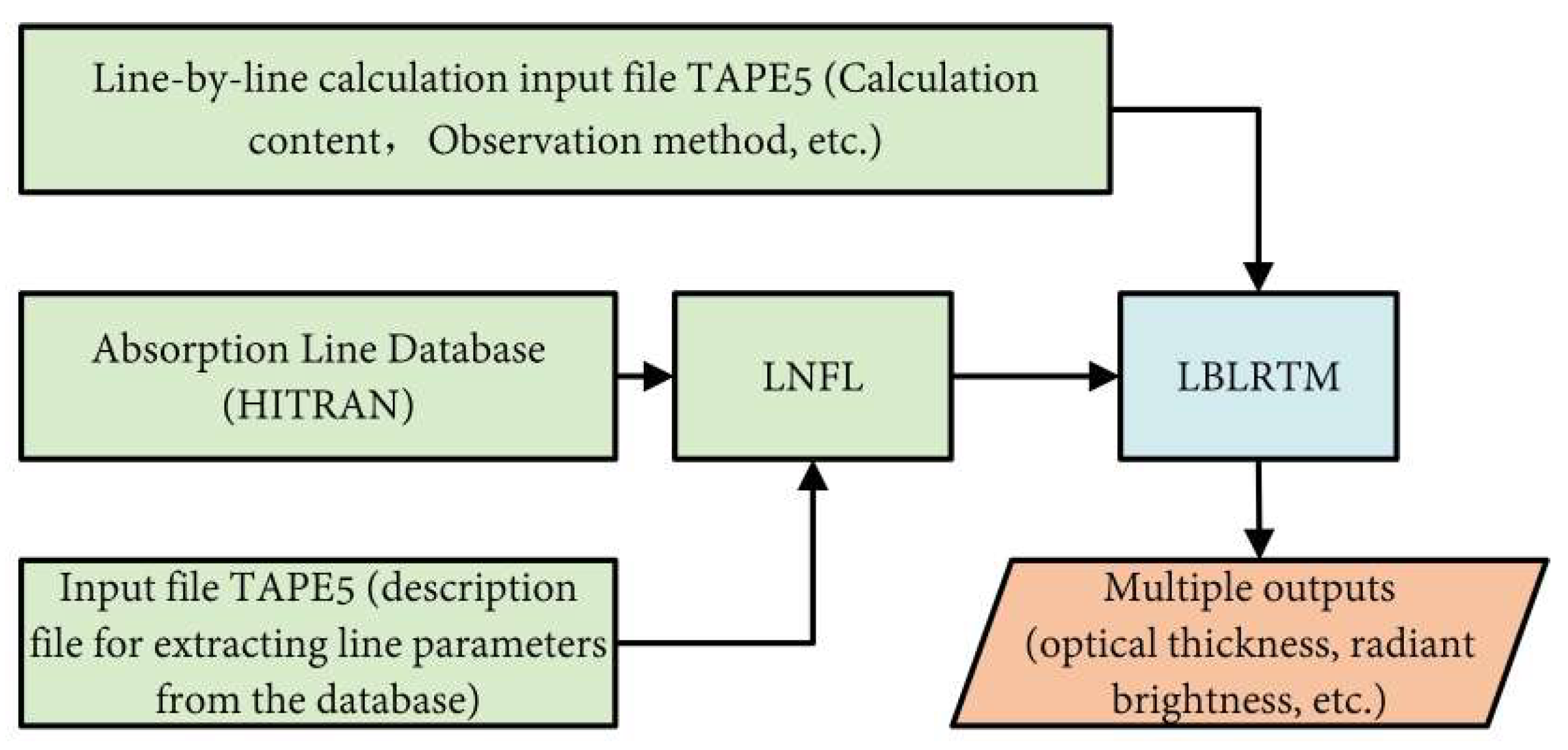
3.1.2. Selection of Forward Modelling
3.2. Advances in Remote Sensing Algorithms for Satellite Atmospheric CO2
3.2.1. Physical Inversion Algorithms
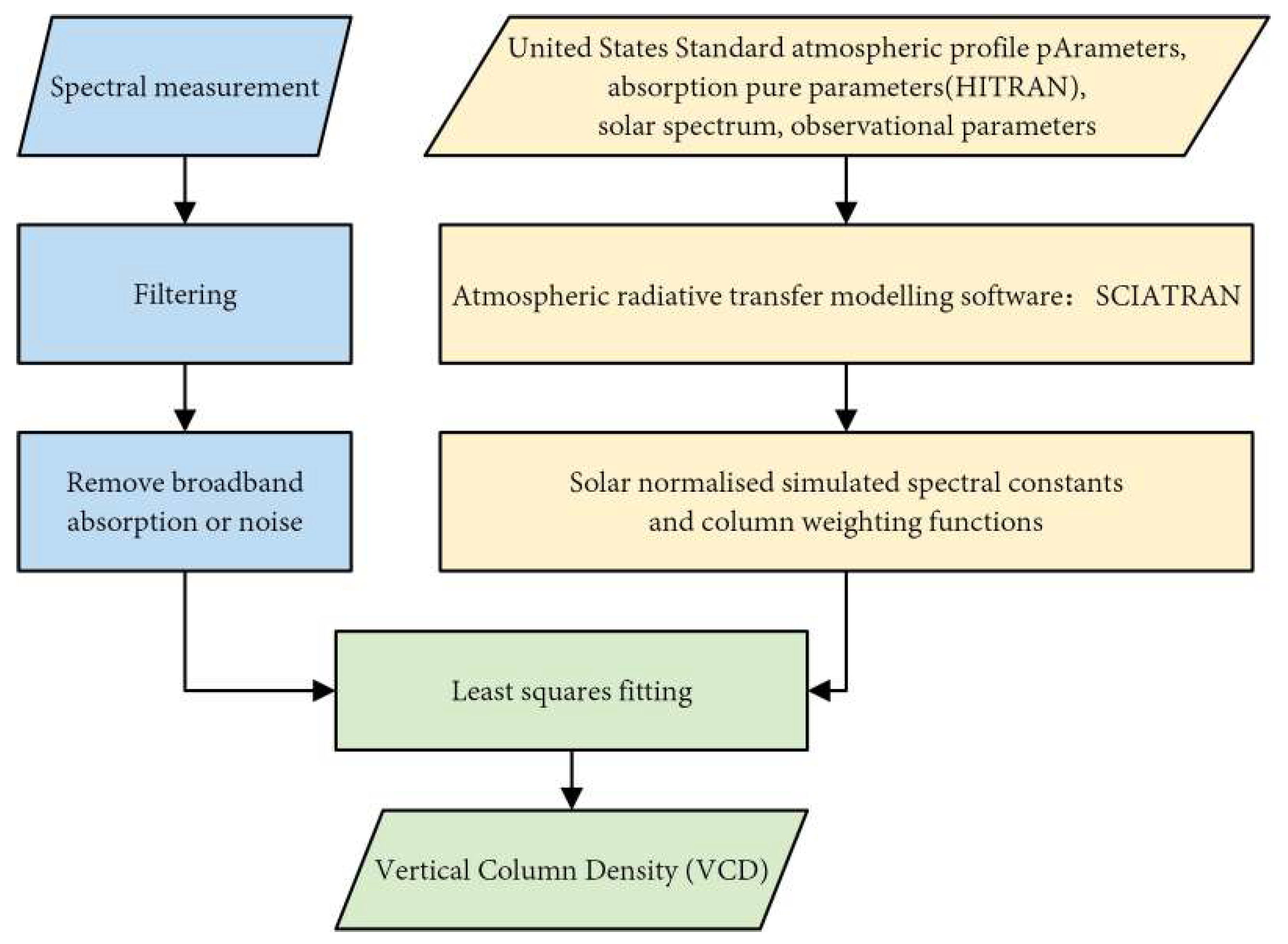
DOAS Algorithm
Optimal Estimation Algorithm
3.2.2. Photon Path Length Probability Density Function Algorithm
3.2.3. Statistical Methods for Principal Component Analysis (PCA)
3.2.4. Empirical Algorithms
Statistical Regression Inversion Algorithm
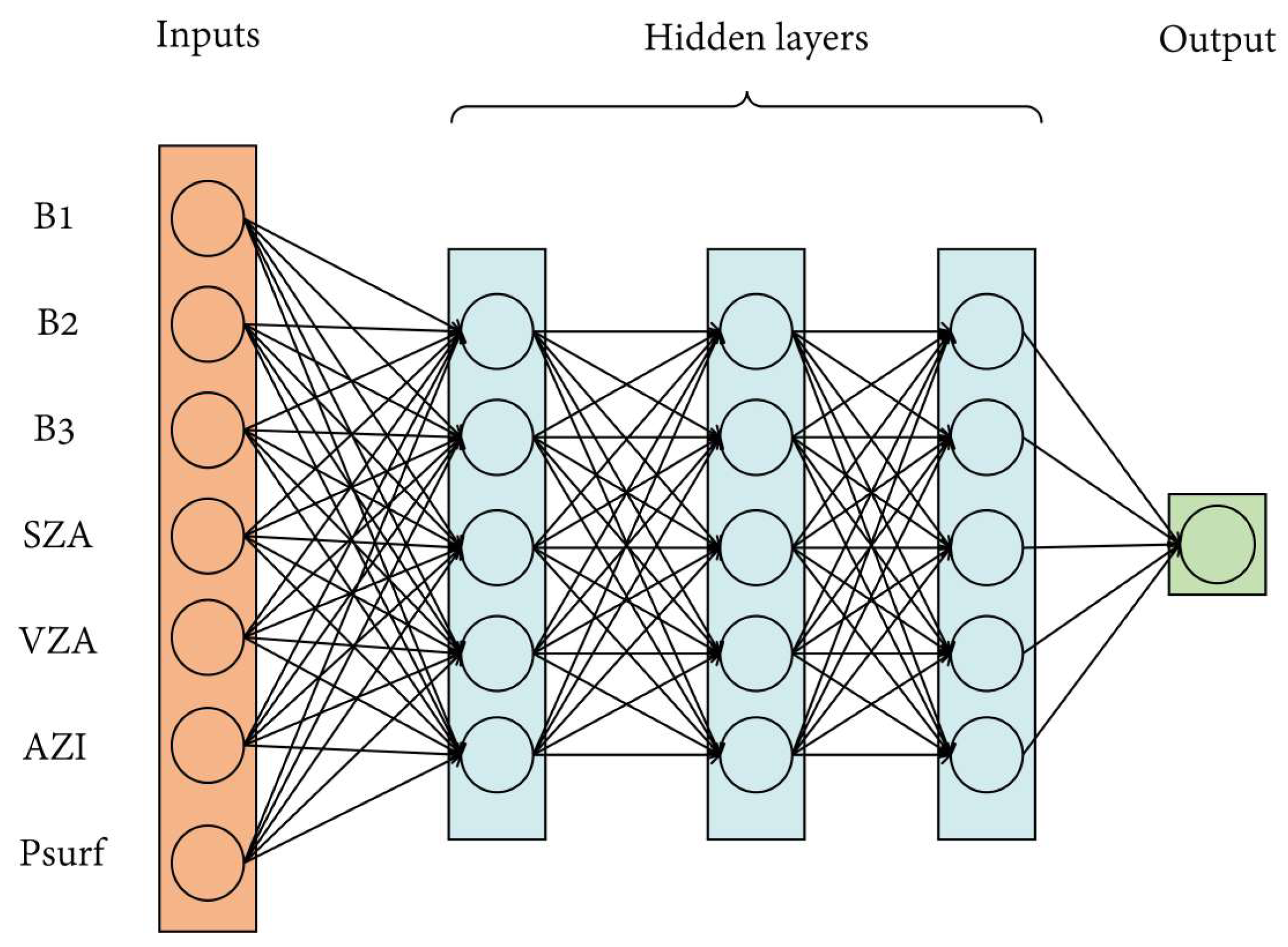
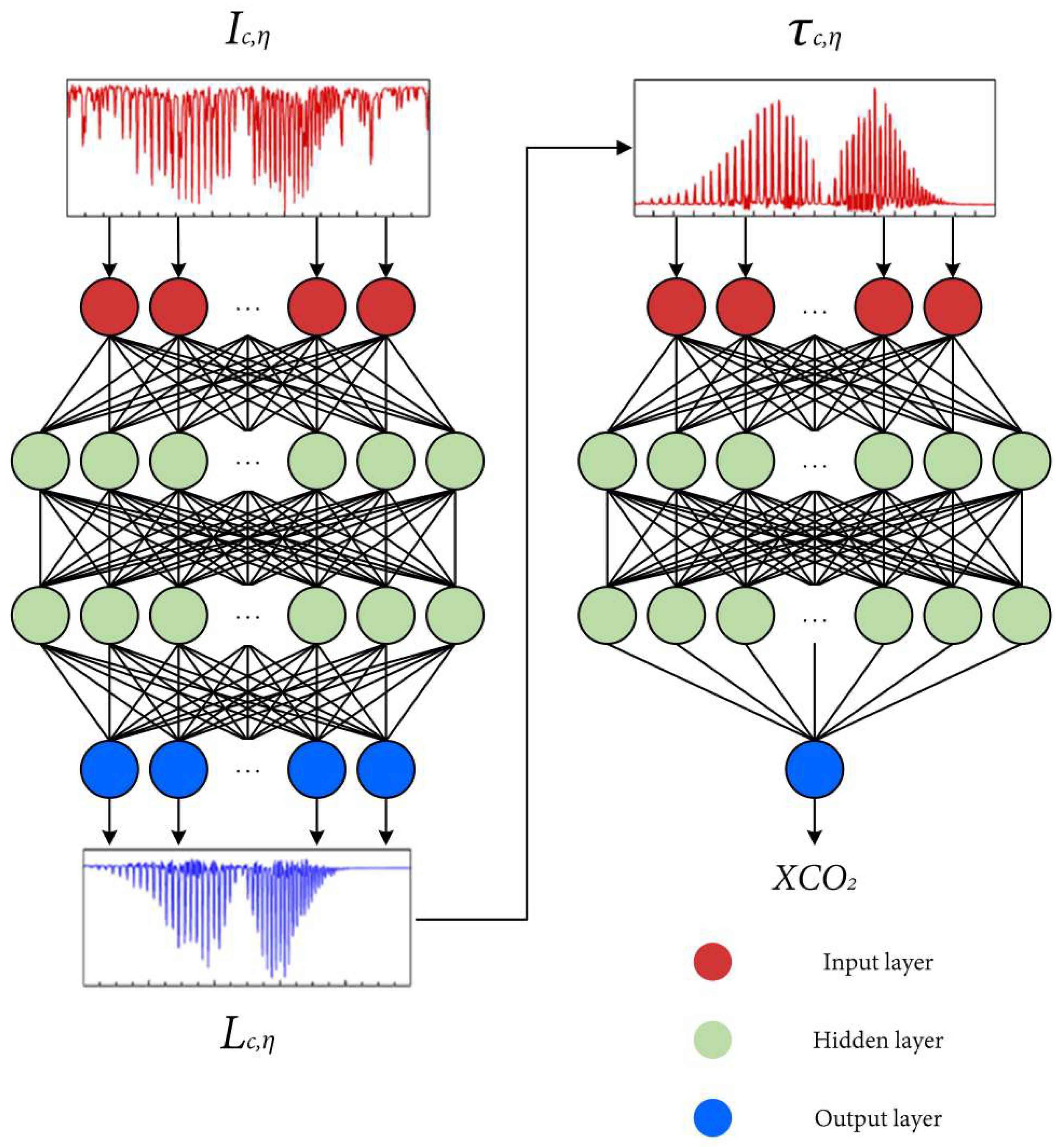
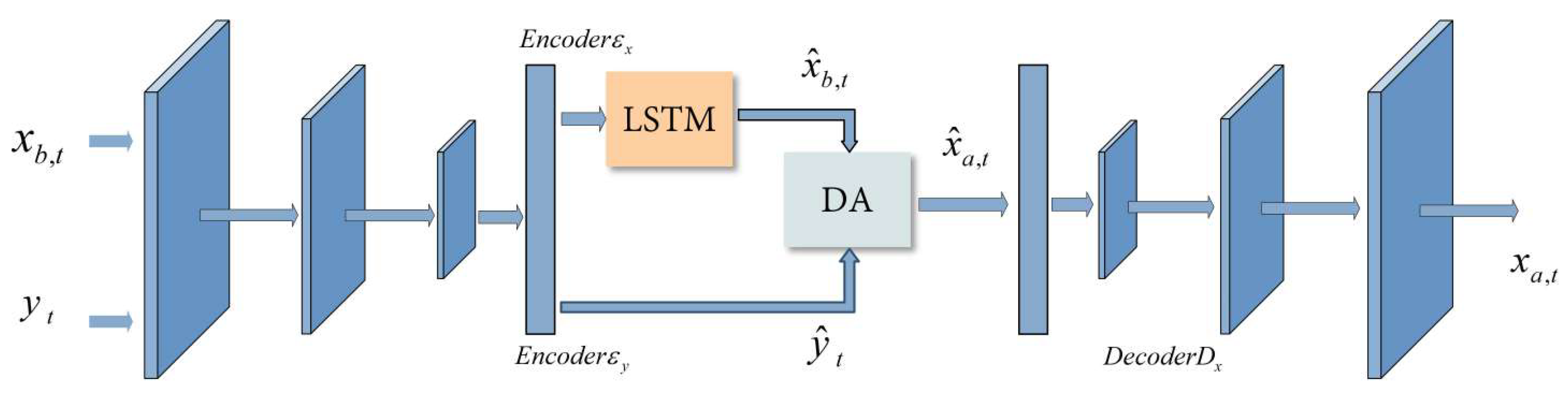
Neural Network Inversion Algorithm
3.2.5. NLS-4DVar Data-Assimilation Algorithm
3.3. Summary
4. Carbon Flux Data Assimilation and Inversion Studies
4.1. History of the Development of the Data-Assimilation System for Atmospheric CO2
4.2. Data-Assimilation Algorithms
4.2.1. Overview of Assimilation Data
4.2.2. Data-Assimilation Algorithms
3D-Var & 4D-Var
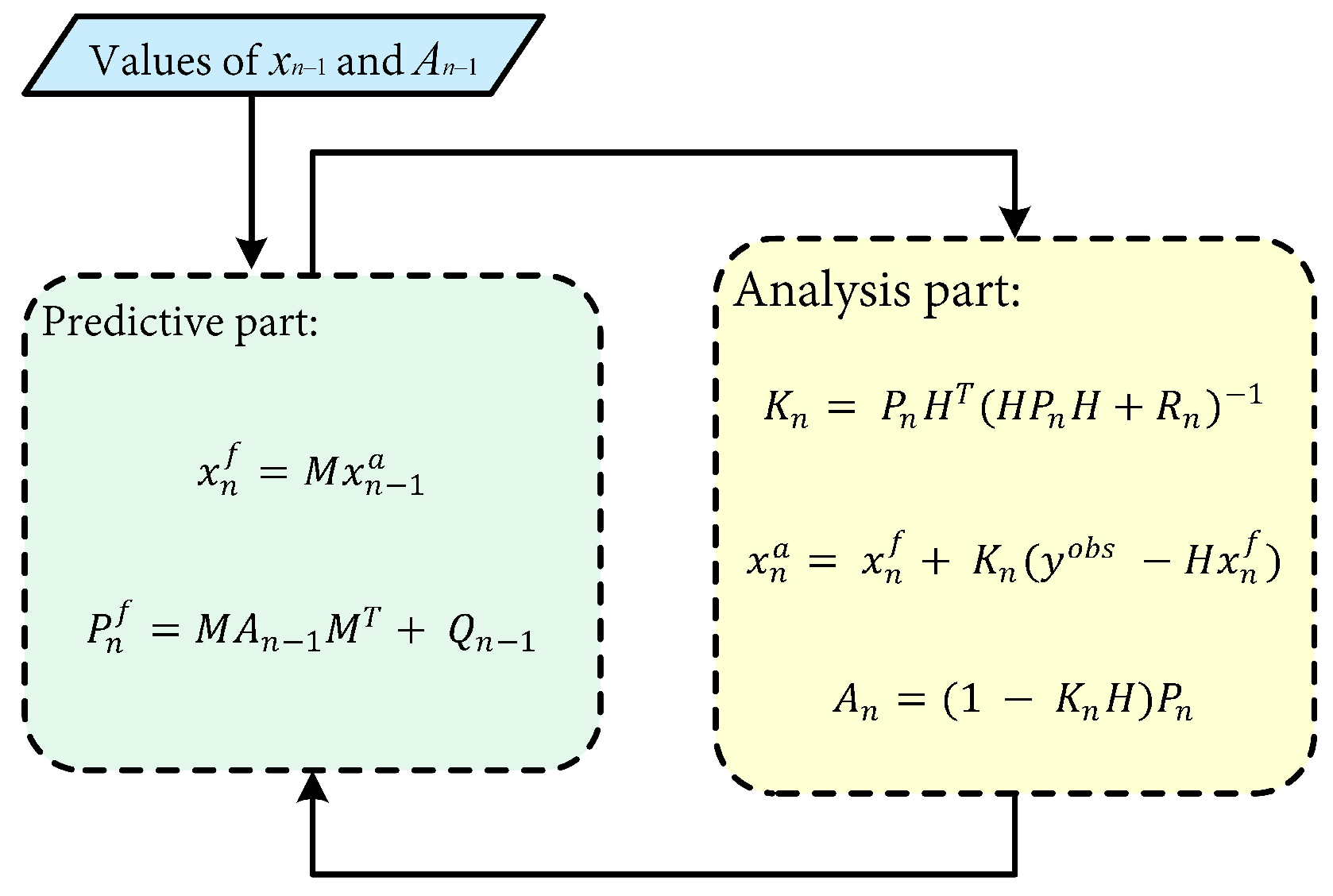
Kalman Filter Algorithm (KF)
Ensemble Kalman Filter Algorithm (EnKF)
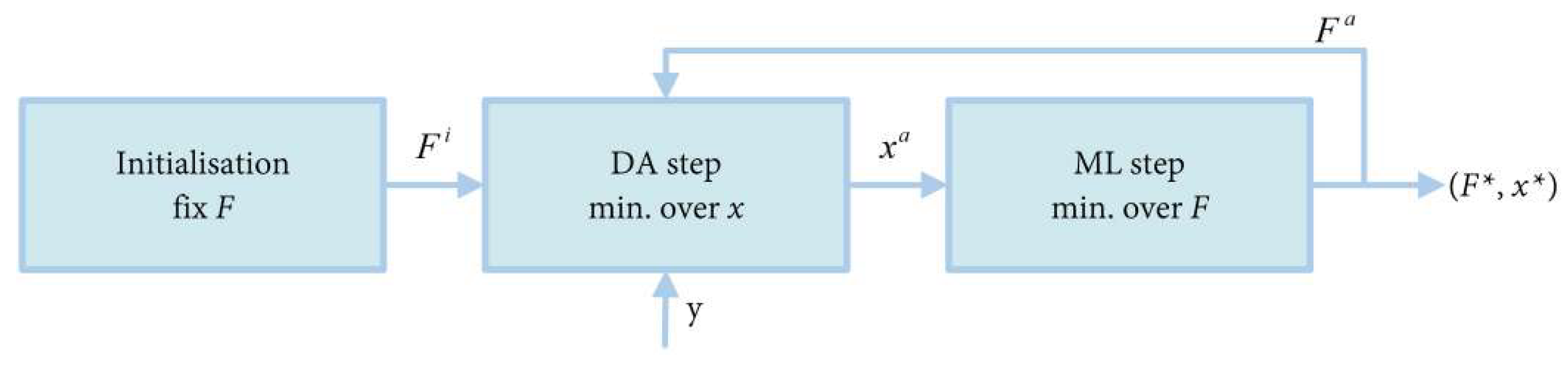
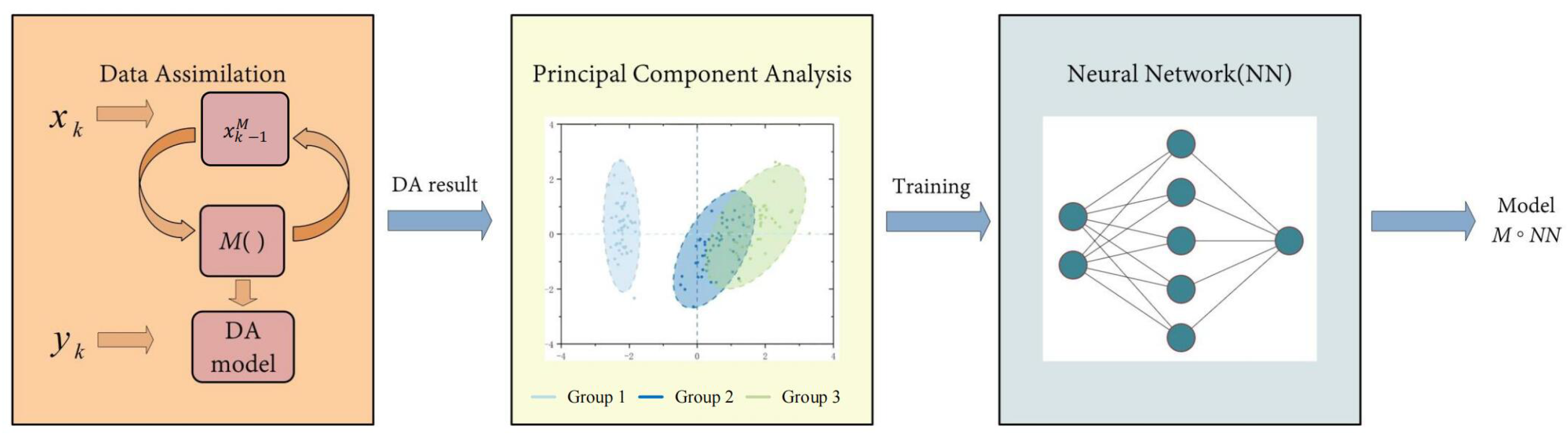
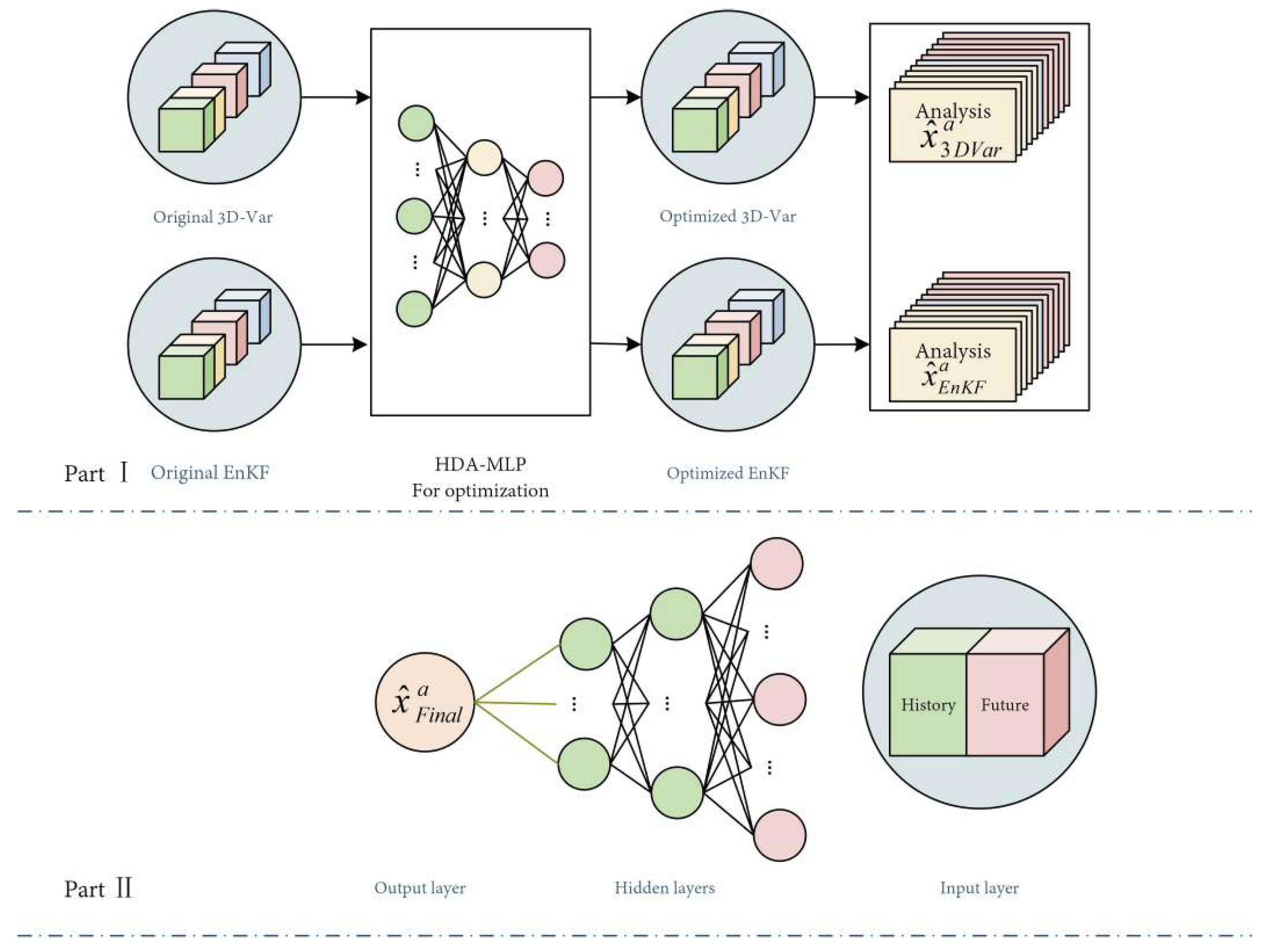
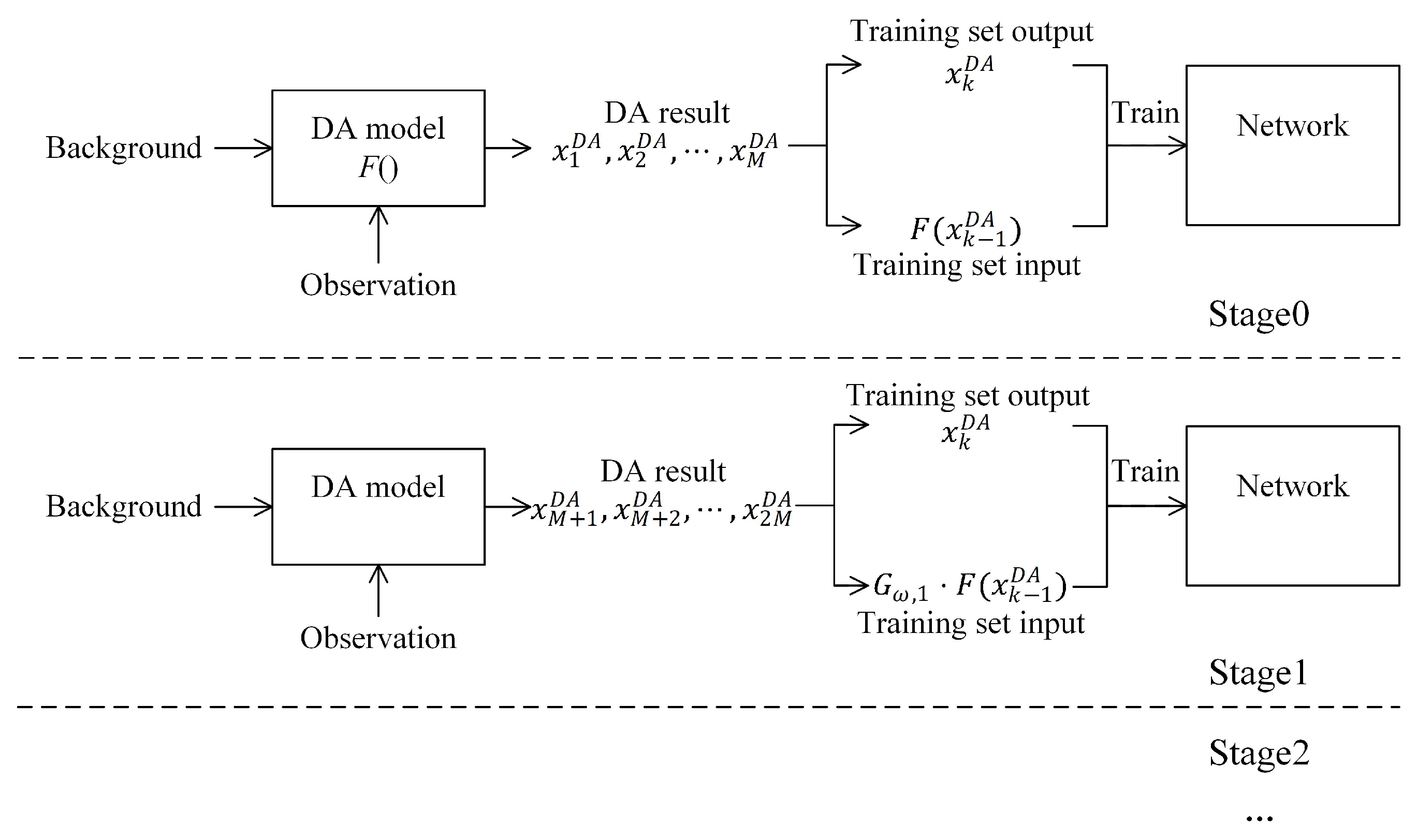
Machine Learning (ML) Algorithms
4.2.3. Summary of Data-Assimilation Algorithms
4.3. Framework and Techniques for Assimilation of Atmospheric CO2
4.3.1. Prior Flux
4.3.2. Atmospheric Transport Model
4.3.3. Satellite CO2 Column Concentration Data-Assimilation Process
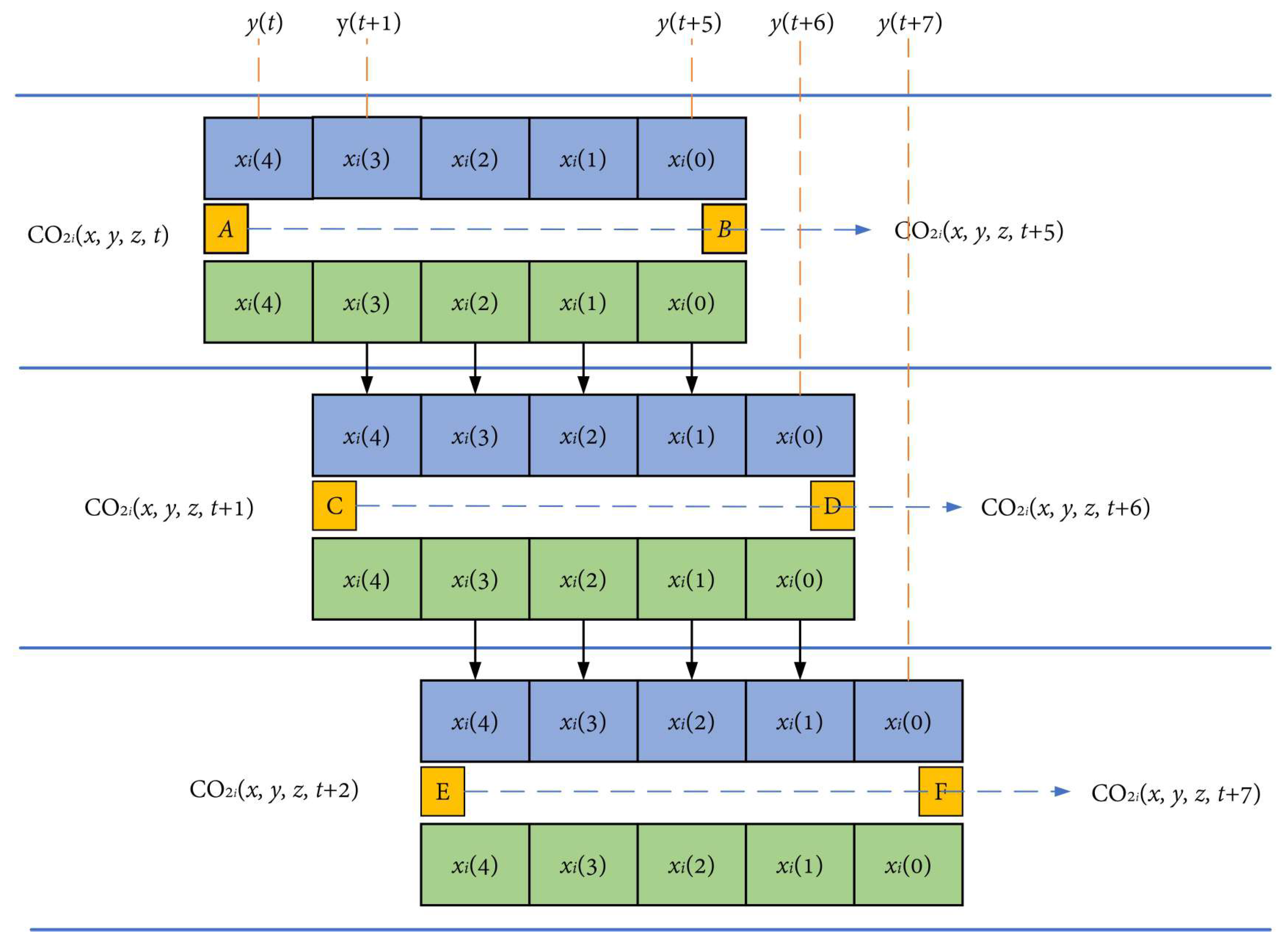
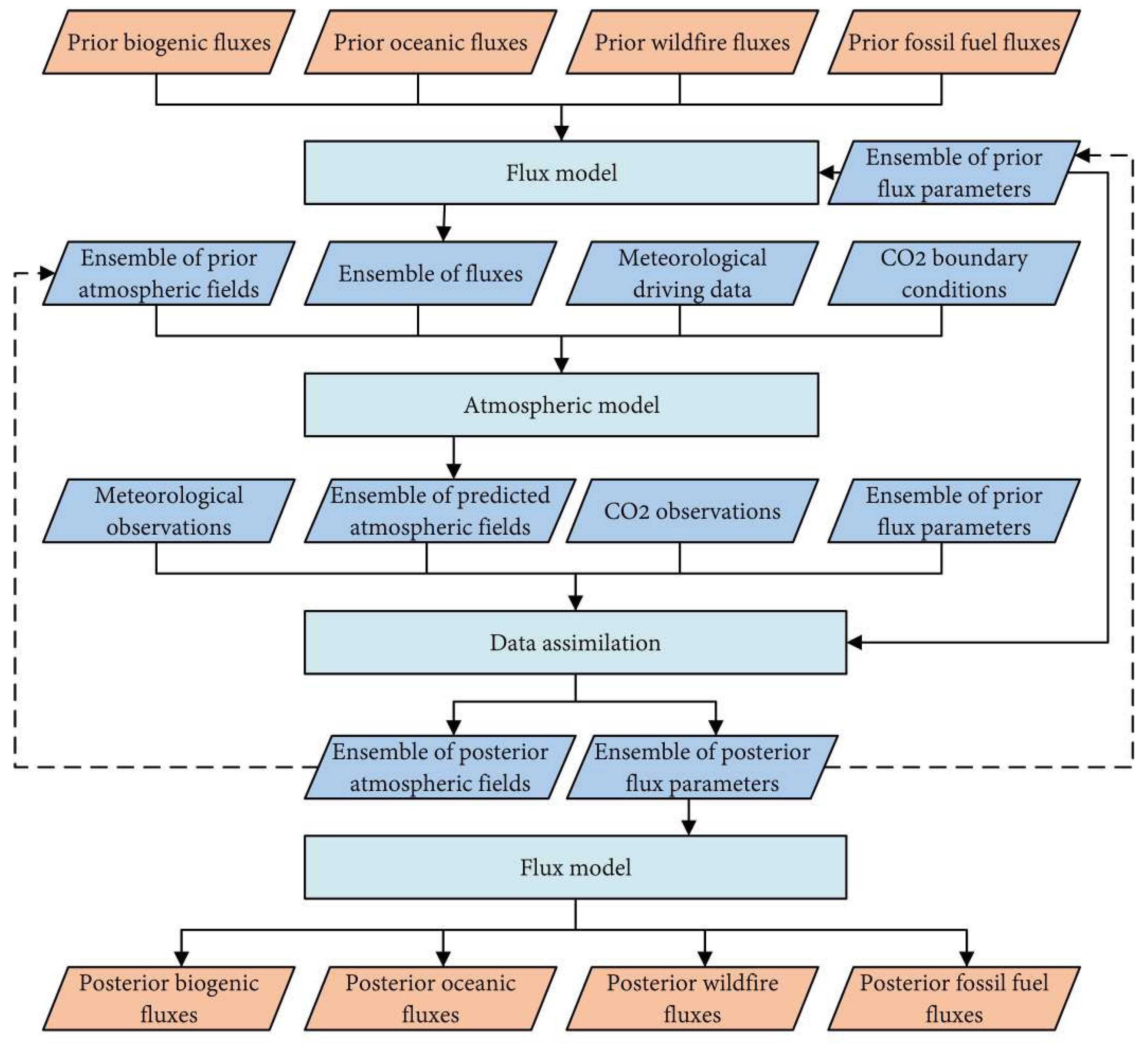
- (1)
- In the first analysis cycle, the background state vector is updated using observational data. At time t, the driving data (0, l, ⋯, 4) within the light blue box is used to drive the atmospheric transport model to simulate the CO2 concentration values from to for a period of 5 weeks. The simulated concentrations are sampled based on the temporal, spatial, and elevation information of the concentration observations ∼ to prepare for assimilation.
- (2)
- The assimilation process is performed on the state variables (average and deviation of CO2 flux) (0, l, ⋯, 4) at time t, according to the formula, to obtain the analyzed values of the state variables (CO2 flux) within the green box for the assimilation period of 5 weeks.
- (3)
- The (4) will not proceed to the next cycle at time . The optimized state vector (4) is used as the driving data to simulate the optimized concentration by the assimilation inversion module and the atmospheric transport model.
- (4)
- The analyzed field (0, 1, 2, 3) at time t becomes the background field for the next cycle at time . A new state variable (0) and new observation data enter the cycle to start a new assimilation process. Afterward, in each analysis cycle, the analysis state vector from the previous cycle is used as the background state vector for the current cycle.
4.4. Application of Carbon Flux Estimation Based on Assimilation Schemes
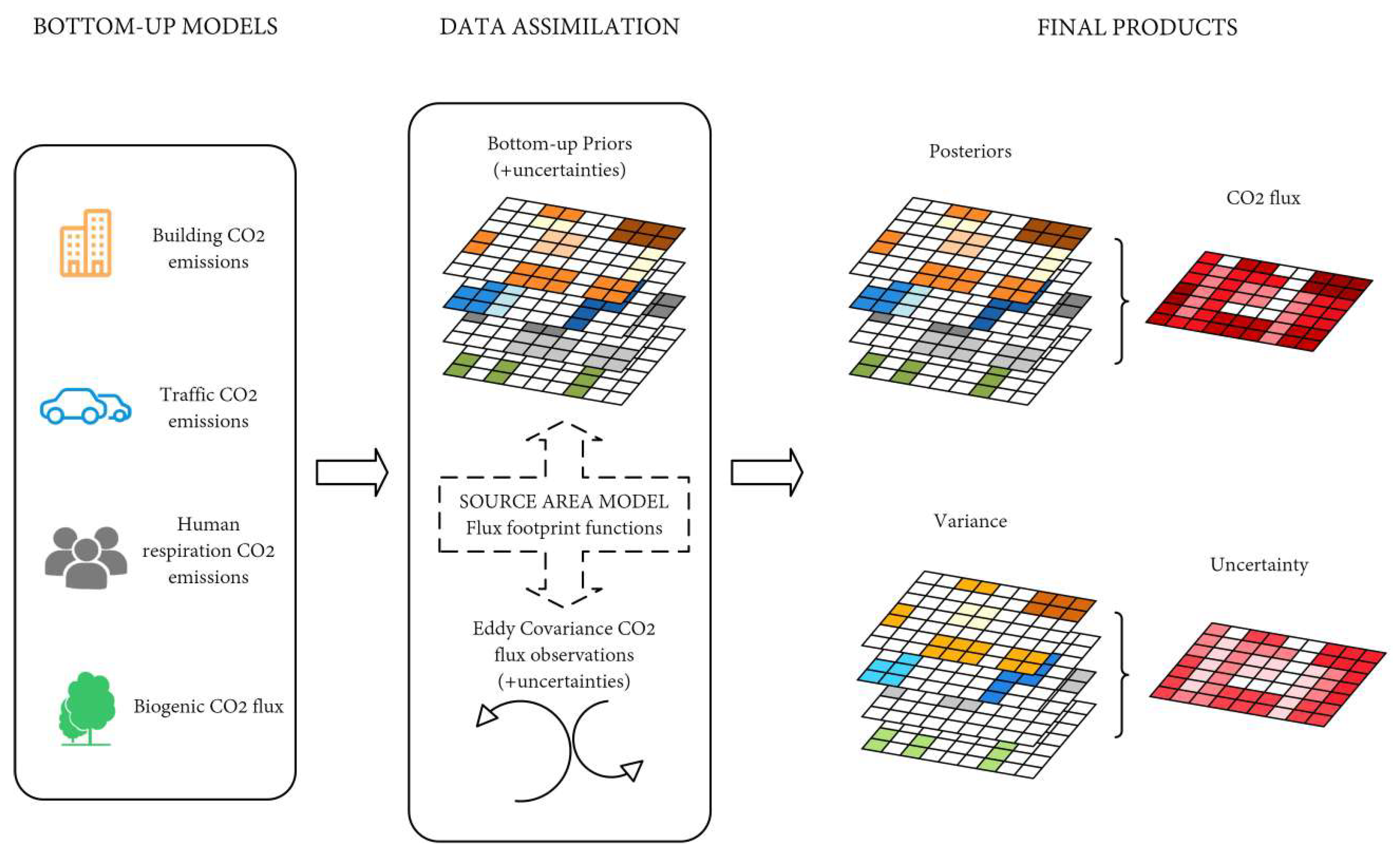
4.4.1. Optimising CO2 Emissions in Urban Areas
4.4.2. Assimilation of High-Resolution Carbon Fluxes Based on Satellite Observations
4.4.3. Assimilation Inversion Based on Regional Scale Models
4.5. Summary of Assimilation Research
5. Conclusions and Prospect
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Use of Artificial Intelligence
Acknowledgments
Conflicts of Interest
Abbreviations
| ACOS | Atmospheric CO2 Observations from Space |
| ADEOS | Advanced Earth Observing Satellite |
| AIRS | Atmospheric Infrared Sounder |
| AIUS | Atmospheric Infrared Ultraspectral Sounder |
| ANN | Artificial neural network |
| BESD | Bremen optimal Estimation DOAS |
| BRDF | Bidirectional Reflectance Distribution Function |
| CCDAS | Carbon-Cycle Data-Assimilation System |
| CDIAC | Carbon Dioxide Information Analysis Center |
| CMAQ | Community Multiscale Air Quality Modeling System |
| CO2M | European Copernicus anthropogenic CO2-monitoring mission |
| CTDAS | CarbonTracker Data-Assimilation Shell |
| CTMs | Chemical Transport Models |
| CrIS | Cross-track Infrared Sounder |
| DA | Data Assimilation |
| DDA | Deep Data Assimilation |
| DOAS | Differential Optical Absorption Spectroscopy |
| EC | Eddy Covariance |
| EnKF | Ensemble Kalman Filter |
| ENVISAT | European Environment Satellite |
| FTS | Fourier Transform Spectrometer |
| GAS | Greenhouse gases Absorption Spectrometer |
| GCAS | Global Carbon-Assimilation System |
| GLA | Generalized Latent Assimilation |
| GMI | Greenhouse gases Monitor Instrument |
| GOSAT | Greenhouse gases Observing Satellite |
| GRNN | Generalised regression neural networks |
| HIRAS | Hyperspectral Infrared Atmospheric Sounder |
| HIRS | High-Resolution Infrared Sounder |
| IAPCAS | Institute of Atmospheric Physics Carbon dioxide retrieval Algorithm for satellite observation |
| IASI | Infrared atmospheric detection interferometer |
| IMG | Interferometric Monitor for Greenhouse gases |
| IMAP-DOAS | Instrument for Measurements of Atmospheric Pollution DOAS |
| LSTM | Long Short-Term Memory Recurrent Neural Networks |
| MLP | Multilayer Perceptron |
| NARA | Nonlinear least squares four-dimensional variational data Assimilation (NLS-4DVar)-based CO2 (NLS-4DVar)-based CO2 Retrieval Algorithm |
| NIR | Near Infrared Spectroscopy |
| NIES | National Environmental Research Institute of Japan |
| NPP | National Polar-orbiting Partnership |
| OCO | Orbiting Carbon Observatory |
| ODIAC | Open-source Data Inventory for Anthropogenic CO2 |
| OI | Optimal Interpolation |
| PCA | Principal Component Analysis |
| PPDF | Photon Path Probability Distribution Function |
| SCIAMACHY | Scanning Imaging Absorption Spectrometer for Atmospheric Chartography |
| SCM | Stepwise Correction Method |
| SIF | Solar-Induced Fluorescence |
| SWIR | Short-Wave Infrared |
| TANSO | Thermal And Near-infrared Sensor for Carbon Observation |
| TES | Tropospheric Emission Spectrometer |
| TM5 | The Tracer Model version 5 |
| TROPOMI | Tropospheric Monitoring Instrument |
| WDCGG | World Data Centre for Greenhouse Gases |
| WFM-DOAS | Weighting Function Modified DOAS |
| WRF-STILT | Weather Research and Forecasting model Stochastic Time-Inverted Lagrangian Transport model |
| XCO2 | Column-averaged carbon dioxide dry-air mole fraction |
References
- Kiehl, J.; Trenberth, K. Earth’s Annual Global Mean Energy Budget. Bull. Am. Meteorol. Soc. 1997, 78, 197–208. [Google Scholar] [CrossRef]
- Friedlingstein, P.; O’Sullivan, M.; Jones, M.; Andrew, R.; Hauck, J.; Olsen, A.; Peters, G.; Peters, W.; Pongratz, J.; Sitch, S.; et al. Global Carbon Budget 2020. Earth Syst. Sci. Data 2020, 12, 3269–3340. [Google Scholar] [CrossRef]
- Friedlingstein, P.; O’Sullivan, M.; Jones, M.W.; Andrew, R.M.; Bakker, D.C.E.; Hauck, J.; Landschützer, P.; Le Quéré, C.; Luijkx, I.T.; Peters, G.P.; et al. Global Carbon Budget 2023. Earth Syst. Sci. Data 2023, 15, 5301–5369. [Google Scholar] [CrossRef]
- Cai, B.; Zhu, S.; Yu, S.; Dong, H.; Zhang, C.; Wang, C.; Zhu, J.; Gao, Q.; Fang, S.; Pan, X.; et al. Interpretation of “IPCC 2006 National Greenhouse Gas Inventory Guidelines 2019 Revised Edition”. Environ. Eng. 2019, 37, 4–14. [Google Scholar]
- Hu, K.; Zhang, Q.; Gong, S.; Zhang, F.; Weng, L.; Jiang, S.; Xia, M. A Review of Anthropogenic Ground-Level Carbon Emissions Based on Satellite Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 8339–8357. [Google Scholar] [CrossRef]
- Hu, K.; Zhang, Q.; Feng, X.; Liu, Z.; Shao, P.; Xia, M.; Ye, X. An Interpolation and Prediction Algorithm for XCO2 based on Multi-source Time Series Data. Remote Sens. 2024, 16, 1907. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Y.; Zou, M.; Xu, Q.; Li, L.; Li, X.; Tao, J. Overview of atmospheric CO2 remote sensing from space. J. Remote Sens. 2015, 19, 1–11. [Google Scholar]
- Yue, T.X.; Zhang, L.L.; Zhao, M.W.; Wang, Y.F.; Wilson, J. Space- and ground-based CO2 measurements: A review. Sci. China-Earth Sci. 2016, 59, 2089–2097. [Google Scholar] [CrossRef]
- Lee, E.; Zeng, F.W.; Koster, R.D.; Weir, B.; Ott, L.E.; Poulter, B. The impact of spatiotemporal variability in atmospheric CO2 concentration on global terrestrial carbon fluxes. Biogeosciences 2018, 15, 5635–5652. [Google Scholar] [CrossRef]
- Ito, A.; Inatomi, M.; Huntzinger, D.N.; Schwalm, C.; Michalak, A.M.; Cook, R.; King, A.W.; Mao, J.; Wei, Y.; Post, W.M.; et al. Decadal trends in the seasonal-cycle amplitude of terrestrial CO2 exchange resulting from the ensemble of terrestrial biosphere models. Tellus Chem. Phys. Meteorol. 2016, 68, 28968. [Google Scholar] [CrossRef]
- Poulter, B.; Frank, D.C.; Hodson, E.L.; Zimmermann, N.E. Impacts of land cover and climate data selection on understanding terrestrial carbon dynamics and the CO2 airborne fraction. Biogeosciences 2011, 8, 2027–2036. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J.; Che, K.; Cai, Z.; Yang, D.; Wu, L. Satellite remote sensing of greenhouse gases: Progress and trends. Yaogan Xuebao/J. Remote Sens. 2021, 25, 53–64. [Google Scholar] [CrossRef]
- Yang, X.; Wang, Z.; Pan, G.; Xiong, W.; Zhou, W.; Zhang, L.; Wang, Z.; Jiang, T.; Liu, J.; Dai, Y.; et al. Advances in atmospheric observation techniques for greenhouse gases by satellite remote sensing. J. Atmos. Environ. Opt. 2022, 17, 581–597. [Google Scholar]
- Liu, L.Y.; Chen, L.F.; Liu, Y.; Yang, D.X.; Zhang, X.Y.; Lu, N.M.; Ju, W.M.; Jiang, F.; Yin, Z.S.; Liu, G.H.; et al. Satellite remote sensing for global stocktaking: Methods, progress and perspectives. Natl. Remote Sens. Bull. 2022, 26, 243–267. [Google Scholar] [CrossRef]
- Frey, M.; Sha, M.K.; Hase, F.; Kiel, M.; Blumenstock, T.; Harig, R.; Surawicz, G.; Deutscher, N.M.; Shiomi, K.; Franklin, J.E.; et al. Building the COllaborative Carbon Column Observing Network (COCCON): Long-term stability and ensemble performance of the EM27/SUN Fourier transform spectrometer. Atmos. Meas. Tech. 2019, 12, 1513–1530. [Google Scholar] [CrossRef]
- Wunch, D.; Toon, G.C.; Blavier, J.F.L.; Washenfelder, R.A.; Notholt, J.; Connor, B.J.; Griffith, D.W.T.; Sherlock, V.; Wennberg, P.O. The Total Carbon Column Observing Network. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2011, 369, 2087–2112. [Google Scholar] [CrossRef]
- Hase, F.; Frey, M.; Kiel, M.; Blumenstock, T.; Harig, R.; Keens, A.; Orphal, J. Addition of a channel for XCO2 observations to a portable FTIR spectrometer for greenhouse gas measurements. Atmos. Meas. Tech. 2016, 9, 2303–2313. [Google Scholar] [CrossRef]
- Ogawa, T.; Shimoda, H.; Hayashi, M.; Imasu, R.; Ono, A.; Nishinomiya, S.; Kobayashi, H. IMG, interferometric measurement of greenhouse gases from space. Adv. Space Res. 1994, 14, 25–28. [Google Scholar] [CrossRef]
- Clerbaux, C.; Hadji-Lazaro, J.; Payan, S.; Camy-Peyret, C.; Megie, G. Retrieval of CO columns from IMG/ADEOS spectra. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1657–1661. [Google Scholar] [CrossRef]
- Lubrano, A.M.; Serio, C.; Clough, S.A.; Kobayashi, H. Simultaneous inversion for temperature and water vapor from IMG radiances. Geophys. Res. Lett. 2000, 27, 2533–2536. [Google Scholar] [CrossRef]
- Aumann, H.H.; Chahine, M.T.; Gautier, C.; Goldberg, M.D.; Kalnay, E.; McMillin, L.M.; Revercomb, H.; Rosenkranz, P.W.; Smith, W.L.; Staelin, D.H.; et al. AIRS/AMSU/HSB on the Aqua mission: Design, science objectives, data products, and processing systems. IEEE Trans. Geosci. Remote Sens. 2003, 41, 253–264. [Google Scholar] [CrossRef]
- Taylor, T.E.; Eldering, A.; Merrelli, A.; Kiel, M.; Somkuti, P.; Cheng, C.; Rosenberg, R.; Fisher, B.; Crisp, D.; Basilio, R.; et al. OCO-3 early mission operations and initial (vEarly) XCO2 and SIF retrievals. Remote Sens. Environ. 2020, 251, 112032. [Google Scholar] [CrossRef]
- Yang, D.X.; Liu, Y.; Cai, Z.N.; Chen, X.; Yao, L.; Lu, D.R. First Global Carbon Dioxide Maps Produced from TanSat Measurements. Adv. Atmos. Sci. 2018, 35, 621–623. [Google Scholar] [CrossRef]
- Rusli, S.P.; Hasekamp, O.; aan de Brugh, J.; Fu, G.; Meijer, Y.; Landgraf, J. Anthropogenic CO2 monitoring satellite mission: The need for multi-angle polarimetric observations. Atmos. Meas. Tech. 2021, 14, 1167–1190. [Google Scholar] [CrossRef]
- Dils, B.; Buchwitz, M.; Reuter, M.; Schneising, O.; Boesch, H.; Parker, R.; Guerlet, S.; Aben, I.; Blumenstock, T.; Burrows, J.P.; et al. The Greenhouse Gas Climate Change Initiative (GHG-CCI): Comparative validation of GHG-CCI SCIAMACHY/ENVISAT and TANSO-FTS/GOSAT CO2 and CH4 retrieval algorithm products with measurements from the TCCON. Atmos. Meas. Tech. 2014, 7, 1723–1744. [Google Scholar] [CrossRef]
- Buchwitz, M.; Reuter, M.; Schneising, O.; Boesch, H.; Guerlet, S.; Dils, B.; Aben, I.; Armante, R.; Bergamaschi, P.; Blumenstock, T.; et al. The Greenhouse Gas Climate Change Initiative (GHG-CCI): Comparison and quality assessment of near-surface-sensitive satellite-derived CO2 and CH4 global data sets. Remote Sens. Environ. 2015, 162, 344–362. [Google Scholar] [CrossRef]
- CO2_SCI_WFMD. Available online: https://catalogue.ceda.ac.uk/uuid/e493802d83c846c8b76f817866fb74cc (accessed on 25 June 2023).
- CO2_SCI_BESD. Available online: https://catalogue.ceda.ac.uk/uuid/294b4075ddbc4464bb06742816813bdc (accessed on 25 June 2023).
- CO2_GOS_OCFP. Available online: https://catalogue.ceda.ac.uk/uuid/9255faeb392f41debf5402caa40dada8 (accessed on 25 June 2023).
- CO2_EMMA. Available online: https://catalogue.ceda.ac.uk/uuid/9f002827ba7d48f59019fcfd3577a57e (accessed on 25 June 2023).
- CO2_GO2_ACOS. Available online: https://daac.gsfc.nasa.gov/datasets/ACOS_L2_Lite_FP_9r (accessed on 25 June 2024).
- CO2_GO2_SRFP. Available online: https://catalogue.ceda.ac.uk/uuid/169c76a05fa247eebc5ee53f239871a7 (accessed on 25 June 2023).
- CO2_GO2_NIES. Available online: https://data2.gosat.nies.go.jp (accessed on 25 June 2023).
- CO2_TAN_OCFP. Available online: https://catalogue.ceda.ac.uk/uuid/2cc63301f1854239aa61c70e58c61207 (accessed on 25 June 2023).
- CO2_OC2_ACOS. Available online: https://daac.gsfc.nasa.gov/datasets/OCO2_L2_Lite_FP_11.1r (accessed on 25 June 2024).
- CO2_OC2_FOCA. Available online: https://catalogue.ceda.ac.uk/uuid/070522ac6a5d4973a95c544beef714b4 (accessed on 25 June 2023).
- CO2_OC3_ACOS. Available online: https://daac.gsfc.nasa.gov/datasets/OCO3_L2_Lite_FP_10.4r (accessed on 25 June 2024).
- Oda, T.; Maksyutov, S. A very high-resolution (1 km × 1 km) global fossil fuel CO2 emission inventory derived using a point source database and satellite observations of nighttime lights. Atmos. Chem. Phys. 2011, 11, 543–556. [Google Scholar] [CrossRef]
- Minx, J.C.; Lamb, W.F.; Andrew, R.M.; Canadell, J.G.; Crippa, M.; Döbbeling, N.; Forster, P.M.; Guizzardi, D.; Olivier, J.; Peters, G.P.; et al. A comprehensive and synthetic dataset for global, regional, and national greenhouse gas emissions by sector 1970–2018 with an extension to 2019. Earth Syst. Sci. Data 2021, 13, 5213–5252. [Google Scholar] [CrossRef]
- Li, M.; Liu, H.; Geng, G.; Hong, C.; Liu, F.; Song, Y.; Tong, D.; Zheng, B.; Cui, H.; Man, H.; et al. Anthropogenic emission inventories in China: A review. Natl. Sci. Rev. 2017, 4, 834–866. [Google Scholar] [CrossRef]
- Chen, C.; Leydesdorff, L. Patterns of connections and movements in dual-map overlays: A new method of publication portfolio analysis. J. Assoc. Inf. Sci. Technol. 2014, 65, 334–351. [Google Scholar] [CrossRef]
- Chen, C.; Dubin, R.; Kim, M.C. Emerging trends and new developments in regenerative medicine: A scientometric update (2000–2014). Expert Opin. Biol. Ther. 2014, 14, 1295–1317. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; World Scientific: Singapore, 2000. [Google Scholar]
- Crisp, D.; Atlas, R.M.; Breon, F.M.; Brown, L.R.; Burrows, J.P.; Ciais, P.; Connor, B.J.; Doney, S.C.; Fung, I.Y.; Jacob, D.J.; et al. The Orbiting Carbon Observatory (OCO) mission. Adv. Space Res. 2004, 34, 700–709. [Google Scholar] [CrossRef]
- Connor, B.J.; Boesch, H.; Toon, G.; Sen, B.; Miller, C.; Crisp, D. Orbiting Carbon Observatory: Inverse method and prospective error analysis. J. Geophys. Res. Atmos. 2008, 113, D05305. [Google Scholar] [CrossRef]
- Jacquinet-Husson, N.; Scott, N.A.; Chédin, A.; Crépeau, L.; Armante, R.; Capelle, V.; Orphal, J.; Coustenis, A.; Boonne, C.; Poulet-Crovisier, N.; et al. The GEISA spectroscopic database: Current and future archive for Earth and planetary atmosphere studies. J. Quant. Spectrosc. Radiat. Transf. 2008, 109, 1043–1059. [Google Scholar] [CrossRef]
- Kotchenova, S.Y.; Vermote, E.F.; Matarrese, R.; Klemm, J.F.J. Validation of a vector version of the 6S radiative transfer code for atmospheric correction of satellite data. Part I: Path radiance. Appl. Opt. 2006, 45, 6762–6774. [Google Scholar] [CrossRef]
- Scott, N.A.; Chedin, A. A Fast Line-by-Line Method for Atmospheric Absorption Computations: The Automatized Atmospheric Absorption Atlas. J. Appl. Meteorol. Climatol. 1981, 20, 802–812. [Google Scholar] [CrossRef]
- Kneizys, F.X. Users Guide to LOWTRAN 7. Air Force Geophysics Lab. 1988. Available online: https://ui.adsabs.harvard.edu/abs/1988ugls.rept.....K (accessed on 25 June 2024).
- Berk, A.; Bernstein, L.S.; Anderson, G.P.; Acharya, P.K.; Robertson, D.C.; Chetwynd, J.H.; Adler-Golden, S.M. MODTRAN Cloud and Multiple Scattering Upgrades with Application to AVIRIS. Remote Sens. Environ. 1998, 65, 367–375. [Google Scholar] [CrossRef]
- Rozanov, A.; Rozanov, V.; Buchwitz, M.; Kokhanovsky, A.; Burrows, J.P. SCIATRAN 2.0—A new radiative transfer model for geophysical applications in the 175–2400 nm spectral region. Adv. Space Res. 2005, 36, 1015–1019. [Google Scholar] [CrossRef]
- Shephard, M.W.; Clough, S.A.; Payne, V.H.; Smith, W.L.; Kireev, S.; Cady-Pereira, K.E. Performance of the line-by-line radiative transfer model (LBLRTM) for temperature and species retrievals: IASI case studies from JAIVEx. Atmos. Chem. Phys. 2009, 9, 7397–7417. [Google Scholar] [CrossRef]
- Schulz, F.M.; Stamnes, K. Angular distribution of the Stokes vector in a plane-parallel, vertically inhomogeneous medium in the vector discrete ordinate radiative transfer (VDISORT) model. J. Quant. Spectrosc. Radiat. Transf. 2000, 65, 609–620. [Google Scholar] [CrossRef]
- Stamnes, K.; Tsay, S.C.; Wiscombe, W.; Jayaweera, K. Numerically stable algorithm for discrete-ordinate-method radiative transfer in multiple scattering and emitting layered media. Appl. Opt. 1988, 27, 2502–2509. [Google Scholar] [CrossRef]
- Schepers, D.; aan de Brugh, J.M.J.; Hahne, P.; Butz, A.; Hasekamp, O.P.; Landgraf, J. LINTRAN v2.0: A linearised vector radiative transfer model for efficient simulation of satellite-born nadir-viewing reflection measurements of cloudy atmospheres. J. Quant. Spectrosc. Radiat. Transf. 2014, 149, 347–359. [Google Scholar] [CrossRef]
- Saunders, R.; Hocking, J.; Turner, E.; Rayer, P.; Rundle, D.; Brunel, P.; Vidot, J.; Roquet, P.; Matricardi, M.; Geer, A.; et al. An update on the RTTOV fast radiative transfer model (currently at version 12). Geosci. Model Dev. 2018, 11, 2717–2737. [Google Scholar] [CrossRef]
- Platt, U.; Perner, D.; Pätz, H.W. Simultaneous measurement of atmospheric CH2O, O3, and NO2 by differential optical absorption. J. Geophys. Res. Ocean 1979, 84, 6329–6335. [Google Scholar] [CrossRef]
- Buchwitz, M.; Beek, R.; Noel, S.; Burrows, J.; Bovensmann, H. Carbon Monoxide, Methane and Carbon Dioxide over China Retrieved from SCIAMACHY/ENVISAT by WFM-DOAS; Special Publication, ESA SP; European Space Agency: Paris, France, 2006. [Google Scholar]
- Buchwitz, M.; de Beek, R.; Noël, S.; Burrows, J.P.; Bovensmann, H.; Bremer, H.; Bergamaschi, P.; Körner, S.; Heimann, M. Carbon monoxide, methane and carbon dioxide columns retrieved from SCIAMACHY by WFM-DOAS: Year 2003 initial data set. Atmos. Chem. Phys. 2005, 5, 3313–3329. [Google Scholar] [CrossRef]
- Buchwitz, M.; Rozanov, V.V.; Burrows, J.P. A near-infrared optimized DOAS method for the fast global retrieval of atmospheric CH4, CO, CO2, H2O, and N2O total column amounts from SCIAMACHY Envisat-1 nadir radiances. J. Geophys. Res. Atmos. 2000, 105, 15231–15245. [Google Scholar] [CrossRef]
- Sun, Y.W.; Xie, P.H.; Xu, J.; Zhou, H.J.; Liu, C.; Wang, Y.; Liu, W.Q.; Si, F.Q.; Zeng, Y. Measurement of atmospheric CO2 vertical column density using weighting function modified differential optical absorption spectroscopy. Acta Phys. Sin. 2013, 62, 130703. [Google Scholar] [CrossRef]
- Huo, Y. Ground-Based Observation and CO2 Retrieval of Ultra-Fine Solar Spectra in the Near-Infrared Band. Ph.D. Thesis, Lanzhou University, Lanzhou, China, 2015. [Google Scholar]
- Frankenberg, C.; Platt, U.; Wagner, T. Iterative maximum a posteriori (IMAP)-DOAS for retrieval of strongly absorbing trace gases: Model studies for CH4 and CO2 retrieval from near infrared spectra of SCIAMACHY onboard ENVISAT. Atmos. Chem. Phys. 2005, 5, 9–22. [Google Scholar] [CrossRef]
- Barkley, M.P.; Frieß, U.; Monks, P.S. Measuring atmospheric CO2 from space using Full Spectral Initiation (FSI) WFM-DOAS. Atmos. Chem. Phys. 2006, 6, 3517–3534. [Google Scholar] [CrossRef]
- Schneising, O.; Buchwitz, M.; Reuter, M.; Heymann, J.; Bovensmann, H.; Burrows, J.P. Long-term analysis of carbon dioxide and methane column-averaged mole fractions retrieved from SCIAMACHY. Atmos. Chem. Phys. 2011, 11, 2863–2880. [Google Scholar] [CrossRef]
- Oshchepkov, S.; Bril, A.; Yokota, T. An improved photon path length probability density function–based radiative transfer model for space-based observation of greenhouse gases. J. Geophys. Res. Atmos. 2009, 114, D19207. [Google Scholar] [CrossRef]
- Heymann, J.; Bovensmann, H.; Buchwitz, M.; Burrows, J.P.; Deutscher, N.M.; Notholt, J.; Rettinger, M.; Reuter, M.; Schneising, O.; Sussmann, R.; et al. SCIAMACHY WFM-DOAS XCO2: Reduction of scattering related errors. Atmos. Meas. Tech. 2012, 5, 2375–2390. [Google Scholar] [CrossRef]
- Heymann, J.; Reuter, M.; Hilker, M.; Buchwitz, M.; Schneising, O.; Bovensmann, H.; Burrows, J.P.; Kuze, A.; Suto, H.; Deutscher, N.M.; et al. Consistent satellite XCO2 retrievals from SCIAMACHY and GOSAT using the BESD algorithm. Atmos. Meas. Tech. 2015, 8, 2961–2980. [Google Scholar] [CrossRef]
- Yoshida, Y.; Ota, Y.; Eguchi, N.; Kikuchi, N.; Nobuta, K.; Tran, H.; Morino, I.; Yokota, T. Retrieval algorithm for CO2 and CH4 column abundances from short-wavelength infrared spectral observations by the Greenhouse gases observing satellite. Atmos. Meas. Tech. 2011, 4, 717–734. [Google Scholar] [CrossRef]
- Ishida, H.; Nakajima, T.Y. Development of an unbiased cloud detection algorithm for a spaceborne multispectral imager. J. Geophys. Res. Atmos. 2009, 114, D07206. [Google Scholar] [CrossRef]
- Oshchepkov, S.; Bril, A.; Yokota, T.; Wennberg, P.O.; Deutscher, N.M.; Wunch, D.; Toon, G.C.; Yoshida, Y.; O’Dell, C.W.; Crisp, D.; et al. Effects of atmospheric light scattering on spectroscopic observations of greenhouse gases from space. Part 2: Algorithm intercomparison in the GOSAT data processing for CO2 retrievals over TCCON sites. J. Geophys. Res. Atmos. 2013, 118, 1493–1512. [Google Scholar] [CrossRef]
- Someya, Y.; Yoshida, Y.; Ohyama, H.; Nomura, S.; Kamei, A.; Morino, I.; Mukai, H.; Matsunaga, T.; Laughner, J.L.; Velazco, V.A.; et al. Update on the GOSAT TANSO–FTS SWIR Level 2 retrieval algorithm. Atmos. Meas. Tech. 2023, 16, 1477–1501. [Google Scholar] [CrossRef]
- O’Dell, C.W.; Connor, B.; Bösch, H.; O’Brien, D.; Frankenberg, C.; Castano, R.; Christi, M.; Eldering, D.; Fisher, B.; Gunson, M.; et al. The ACOS CO2 retrieval algorithm—Part 1: Description and validation against synthetic observations. Atmos. Meas. Tech. 2012, 5, 99–121. [Google Scholar] [CrossRef]
- Crisp, D.; Fisher, B.M.; O’Dell, C.; Frankenberg, C.; Basilio, R.; Bösch, H.; Brown, L.R.; Castano, R.; Connor, B.; Deutscher, N.M.; et al. The ACOS CO2 retrieval algorithm—Part II: Global XCO2 data characterization. Atmos. Meas. Tech. 2012, 5, 687–707. [Google Scholar] [CrossRef]
- Taylor, T.E.; O’Dell, C.W.; Baker, D.; Bruegge, C.; Chang, A.; Chapsky, L.; Chatterjee, A.; Cheng, C.; Chevallier, F.; Crisp, D.; et al. Evaluating the consistency between OCO-2 and OCO-3 XCO2 estimates derived from the NASA ACOS version 10 retrieval algorithm. Atmos. Meas. Tech. 2023, 16, 3173–3209. [Google Scholar] [CrossRef]
- Boesch, H.; Baker, D.; Connor, B.; Crisp, D.; Miller, C. Global Characterization of CO2 Column Retrievals from Shortwave-Infrared Satellite Observations of the Orbiting Carbon Observatory-2 Mission. Remote Sens. 2011, 3, 270–304. [Google Scholar] [CrossRef]
- Cogan, A.J.; Boesch, H.; Parker, R.J.; Feng, L.; Palmer, P.I.; Blavier, J.F.L.; Deutscher, N.M.; Macatangay, R.; Notholt, J.; Roehl, C.; et al. Atmospheric carbon dioxide retrieved from the Greenhouse gases Observing SATellite (GOSAT): Comparison with ground-based TCCON observations and GEOS-Chem model calculations. J. Geophys. Res. Atmos. 2012, 117, D21301. [Google Scholar] [CrossRef]
- Butz, A.; Hasekamp, O.P.; Frankenberg, C.; Aben, I. Retrievals of atmospheric CO2 from simulated space-borne measurements of backscattered near-infrared sunlight: Accounting for aerosol effects. Appl. Opt. 2009, 48, 3322–3336. [Google Scholar] [CrossRef]
- Yang, D.; Liu, Y.; Cai, Z.; Deng, J. Study on the Spatiotemporal Distribution of Carbon Dioxide Concentration in China Based on GOSAT Inversion. J. Atmos. Sci. 2016, 40, 541–550. [Google Scholar]
- Schepers, D.; Guerlet, S.; Butz, A.; Landgraf, J.; Frankenberg, C.; Hasekamp, O.; Blavier, J.F.; Deutscher, N.M.; Griffith, D.W.T.; Hase, F.; et al. Methane retrievals from Greenhouse Gases Observing Satellite (GOSAT) shortwave infrared measurements: Performance comparison of proxy and physics retrieval algorithms. J. Geophys. Res. Atmos. 2012, 117, D10307. [Google Scholar] [CrossRef]
- Lu, S.; Landgraf, J.; Fu, G.; van Diedenhoven, B.; Wu, L.; Rusli, S.P.; Hasekamp, O.P. Simultaneous Retrieval of Trace Gases, Aerosols, and Cirrus Using RemoTAP—The Global Orbit Ensemble Study for the CO2M Mission. Front. Remote Sens. 2022, 3, 914378. [Google Scholar] [CrossRef]
- Yang, D.; Liu, Y.; Cai, Z.; Deng, J.; Wang, J.; Chen, X. An advanced carbon dioxide retrieval algorithm for satellite measurements and its application to GOSAT observations. Sci. Bull. 2015, 60, 2063–2066. [Google Scholar] [CrossRef][Green Version]
- Yang, D.; Liu, Y.; Boesch, H.; Yao, L.; Di Noia, A.; Cai, Z.; Lu, N.; Lyu, D.; Wang, M.; Wang, J.; et al. A New TanSat XCO2 Global Product towards Climate Studies. Adv. Atmos. Sci. 2021, 38, 8–11. [Google Scholar] [CrossRef]
- Thompson, D.R.; Chris Benner, D.; Brown, L.R.; Crisp, D.; Malathy Devi, V.; Jiang, Y.; Natraj, V.; Oyafuso, F.; Sung, K.; Wunch, D.; et al. Atmospheric validation of high accuracy CO2 absorption coefficients for the OCO-2 mission. J. Quant. Spectrosc. Radiat. Transf. 2012, 113, 2265–2276. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J.; Yao, L.; Chen, X.; Cai, Z.; Yang, D.; Yin, Z.; Gu, S.; Tian, L.; Lu, N.; et al. The TanSat mission: Preliminary global observations. Sci. Bull. 2018, 63, 1200–1207. [Google Scholar] [CrossRef]
- Oshchepkov, S.; Bril, A.; Yokota, T. PPDF-based method to account for atmospheric light scattering in observations of carbon dioxide from space. J. Geophys. Res. Atmos. 2008, 113, D23210. [Google Scholar] [CrossRef]
- Duan, F.; Wang, X.; Ye, H.; Jiang, Y.; Wu, H. A Method for Carbon Dioxide Retrieval Based on Statistics and Path Length Distribution. Acta Opt. Sin. 2017, 37, 26–32. [Google Scholar]
- Sang, H.; Wang, X.; Ye, H.; Jiang, Y. CO2 Statistical Inversion Method Based on Principal Component Analysis. J. Atmos. Environ. Opt. 2017, 12, 202–209. [Google Scholar]
- Noël, S.; Reuter, M.; Buchwitz, M.; Borchardt, J.; Hilker, M.; Bovensmann, H.; Burrows, J.P.; Di Noia, A.; Suto, H.; Yoshida, Y.; et al. XCO2 retrieval for GOSAT and GOSAT-2 based on the FOCAL algorithm. Atmos. Meas. Tech. 2021, 14, 3837–3869. [Google Scholar] [CrossRef]
- Ren, T.; Li, H.; Modest, M.F.; Zhao, C. Efficient two-dimensional scalar fields reconstruction of laminar flames from infrared hyperspectral measurements with a machine learning approach. J. Quant. Spectrosc. Radiat. Transf. 2021, 271, 107724. [Google Scholar] [CrossRef]
- Guo, M.; Wang, X.; Li, J.; Yi, K.; Zhong, G.; Tani, H. Assessment of Global Carbon Dioxide Concentration Using MODIS and GOSAT Data. Sensors 2012, 12, 16368–16389. [Google Scholar] [CrossRef] [PubMed]
- Sontag, E.D. Feedback stabilization using two-hidden-layer nets. IEEE Trans. Neural Netw. 1992, 3, 981–990. [Google Scholar] [CrossRef] [PubMed]
- Chédin, A.; Serrar, S.; Scott, N.A.; Crevoisier, C.; Armante, R. First global measurement of midtropospheric CO2 from NOAA polar satellites: Tropical zone. J. Geophys. Res. Atmos. 2003, 108, 4581. [Google Scholar] [CrossRef]
- Crevoisier, C.; Heilliette, S.; Chédin, A.; Serrar, S.; Armante, R.; Scott, N.A. Midtropospheric CO2 concentration retrieval from AIRS observations in the tropics. Geophys. Res. Lett. 2004, 31, L17106. [Google Scholar] [CrossRef]
- He, Z.; Lei, L.; Zhang, Y.; Sheng, M.; Wu, C.; Li, L.; Zeng, Z.C.; Welp, L.R. Spatio-Temporal Mapping of Multi-Satellite Observed Column Atmospheric CO2 Using Precision-Weighted Kriging Method. Remote Sens. 2020, 12, 576. [Google Scholar] [CrossRef]
- Turquety, S.; Hadji-Lazaro, J.; Clerbaux, C.; Hauglustaine, D.A.; Clough, S.A.; Cassé, V.; Schlüssel, P.; Mégie, G. Operational trace gas retrieval algorithm for the Infrared Atmospheric Sounding Interferometer. J. Geophys. Res. Atmos. 2004, 109, D21301. [Google Scholar] [CrossRef]
- Crevoisier, C.; Nobileau, D.; Fiore, A.M.; Armante, R.; Chédin, A.; Scott, N.A. Tropospheric methane in the tropics—First year from IASI hyperspectral infrared observations. Atmos. Chem. Phys. 2009, 9, 6337–6350. [Google Scholar] [CrossRef]
- Wu, M.; Jiang, X.; Tang, B. Rapid Algorithm for Hyperspectral Thermal Infrared Radiation Transmission Model Based on Neural Networks. J. Arid. Land Geogr. 2010, 33, 99–105. [Google Scholar]
- Zeng, J.; Nojiri, Y.; Landschützer, P.; Telszewski, M.; Nakaoka, S. A Global Surface Ocean fCO2 Climatology Based on a Feed-Forward Neural Network. J. Atmos. Ocean. Technol. 2014, 31, 1838–1849. [Google Scholar] [CrossRef]
- Siabi, Z.; Falahatkar, S.; Alavi, S.J. Spatial distribution of XCO2 using OCO-2 data in growing seasons. J. Environ. Manag. 2019, 244, 110–118. [Google Scholar] [CrossRef] [PubMed]
- Bril, A.; Maksyutov, S.; Belikov, D.; Oshchepkov, S.; Yoshida, Y.; Deutscher, N.M.; Griffith, D.; Hase, F.; Kivi, R.; Morino, I.; et al. EOF-based regression algorithm for the fast retrieval of atmospheric CO2 total column amount from the GOSAT observations. J. Quant. Spectrosc. Radiat. Transf. 2017, 189, 258–266. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X.; Ye, H.; Jiang, Y.; Duan, F.; Lv, S. Algorithm for Atmospheric CO2 Inversion of Beijing Urban Underlying Surface. J. Remote Sens. 2019, 23, 1223–1231. [Google Scholar]
- Shuai, Y.; Schaaf, C.B.; Strahler, A.H.; Liu, J.; Jiao, Z. Quality assessment of BRDF/albedo retrievals in MODIS operational system. Geophys. Res. Lett. 2008, 35, L05407. [Google Scholar] [CrossRef]
- Bréon, F.M.; David, L.; Chatelanaz, P.; Chevallier, F. On the potential of a neural-network-based approach for estimating XCO2 from OCO-2 measurements. Atmos. Meas. Tech. 2022, 15, 5219–5234. [Google Scholar] [CrossRef]
- David, L.; Bréon, F.M.; Chevallier, F. XCO2 estimates from the OCO-2 measurements using a neural network approach. Atmos. Meas. Tech. 2021, 14, 117–132. [Google Scholar] [CrossRef]
- Zhao, Z.; Xie, F.; Ren, T.; Zhao, C. Atmospheric CO2 retrieval from satellite spectral measurements by a two-step machine learning approach. J. Quant. Spectrosc. Radiat. Transf. 2022, 278, 108006. [Google Scholar] [CrossRef]
- Rothman, L.S.; Gordon, I.E.; Babikov, Y.; Barbe, A.; Chris Benner, D.; Bernath, P.F.; Birk, M.; Bizzocchi, L.; Boudon, V.; Brown, L.R.; et al. The HITRAN2012 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2013, 130, 4–50. [Google Scholar] [CrossRef]
- Zhu, M.; Zhang, F.; Li, W.; Wu, Y.; Xu, N. The impact of various HITRAN molecular spectroscopic databases on infrared radiative transfer simulation. J. Quant. Spectrosc. Radiat. Transf. 2019, 234, 55–63. [Google Scholar] [CrossRef]
- Xie, F.; Ren, T.; Zhao, Z.; Zhao, C. A machine learning based line-by-line absorption coefficient model for the application of atmospheric carbon dioxide remote sensing. J. Quant. Spectrosc. Radiat. Transf. 2023, 296, 108441. [Google Scholar] [CrossRef]
- Miao, Y.; Zou, M.; Sheng, S.; Zhu, K.; Ding, W.; Lin, J.; Qu, Z.; Li, D. CO2 satellite inversion methocl based on machine learning. China Environ. Sci. 2023, 43, 20–27. [Google Scholar]
- Wang, B.; Yang, Z.; Bian, G.; Wang, G.; Zhao, Y.; Xue, J.; Cheng, L. Implementation of Embedded CO2 Concentration Inversion Algorithm Based on Deep Learning. Laser J. 2023, 44, 42–46. [Google Scholar]
- Jin, Z.; Tian, X.; Duan, M.; Han, R. An Efficient Algorithm for Retrieving CO2 in the Atmosphere From Hyperspectral Measurements of Satellites: Application of NLS-4DVar Data Assimilation Method. Front. Earth Sci. 2021, 9, 688542. [Google Scholar] [CrossRef]
- Zhao, L. Remote Sensing Inversion of Atmospheric CO2 and CH4 Based on GOSAT Satellite. Ph.D. Thesis, Jilin University, Changchun, China, 2018. [Google Scholar]
- Deng, F.; Chen, J.M.; Ishizawa, M.; Yuen, C.W.; Mo, G.; Higuchi, K.; Chan, D.; Maksyutov, S. Global monthly CO2 flux inversion with a focus over North America. Tellus B 2007, 59, 179–190. [Google Scholar] [CrossRef]
- Peters, W.; Jacobson, A.R.; Sweeney, C.; Andrews, A.E.; Conway, T.J.; Masarie, K.; Miller, J.B.; Bruhwiler, L.M.P.; Pétron, G.; Hirsch, A.I.; et al. An atmospheric perspective on North American carbon dioxide exchange: CarbonTracker. Proc. Natl. Acad. Sci. USA 2007, 104, 18925–18930. [Google Scholar] [CrossRef]
- He, W.; van der Velde, I.R.; Andrews, A.E.; Sweeney, C.; Miller, J.; Tans, P.; van der Laan-Luijkx, I.T.; Nehrkorn, T.; Mountain, M.; Ju, W.; et al. CTDAS-Lagrange v1.0: A high-resolution data assimilation system for regional carbon dioxide observations. Geosci. Model Dev. 2018, 11, 3515–3536. [Google Scholar] [CrossRef]
- Chevallier, F.; Fisher, M.; Peylin, P.; Serrar, S.; Bousquet, P.; Bréon, F.M.; Chédin, A.; Ciais, P. Inferring CO2 sources and sinks from satellite observations: Method and application to TOVS data. J. Geophys. Res. Atmos. 2005, 110, D24309. [Google Scholar] [CrossRef]
- Kenea, S.T.; Oh, Y.S.; Rhee, J.S.; Goo, T.Y.; Byun, Y.H.; Li, S.; Labzovskii, L.D.; Lee, H.; Banks, R.F. Evaluation of Simulated CO2 Concentrations from the CarbonTracker-Asia Model Using In-situ Observations over East Asia for 2009–2013. Adv. Atmos. Sci. 2019, 36, 603–613. [Google Scholar] [CrossRef]
- Peters, W.; Krol, M.C.; van der Werf, G.R.; Houweling, S.; Jones, C.D.; Hughes, J.; Schaefer, K.; Masarie, K.A.; Jacobson, A.R.; Miller, J.B.; et al. Seven years of recent European net terrestrial carbon dioxide exchange constrained by atmospheric observations. Glob. Chang. Biol. 2010, 16, 1317–1337. [Google Scholar] [CrossRef]
- Zhang, H.F.; Chen, B.Z.; van der Laan-Luijk, I.T.; Machida, T.; Matsueda, H.; Sawa, Y.; Fukuyama, Y.; Langenfelds, R.; van der Schoot, M.; Xu, G.; et al. Estimating Asian terrestrial carbon fluxes from CONTRAIL aircraft and surface CO2 observations for the period 2006–2010. Atmos. Chem. Phys. 2014, 14, 5807–5824. [Google Scholar] [CrossRef]
- van der Laan-Luijkx, I.T.; van der Velde, I.R.; van der Veen, E.; Tsuruta, A.; Stanislawska, K.; Babenhauserheide, A.; Zhang, H.F.; Liu, Y.; He, W.; Chen, H.; et al. The CarbonTracker Data Assimilation Shell (CTDAS) v1.0: Implementation and global carbon balance 2001–2015. Geosci. Model Dev. 2017, 10, 2785–2800. [Google Scholar] [CrossRef]
- Kim, J.; Kim, H.M.; Cho, C.H.; Boo, K.O. Estimation of Surface CO2 Flux Using a Carbon Tracking System Based on Ensemble Kalman Filter. AGU Fall Meeting Abstracts. 2015. Available online: https://ui.adsabs.harvard.edu/abs/2015AGUFM.B23G0666K/abstract (accessed on 25 June 2024).
- Jiang, F.; Wang, H.W.; Chen, J.M.; Zhou, L.X.; Ju, W.M.; Ding, A.J.; Liu, L.X.; Peters, W. Nested atmospheric inversion for the terrestrial carbon sources and sinks in China. Biogeosciences 2013, 10, 5311–5324. [Google Scholar] [CrossRef]
- Zhang, S.; Yi, X.; Zheng, X.; Chen, Z.; Dan, B.; Zhang, X. Global carbon-assimilation system using a local ensemble Kalman filter with multiple ecosystem models. J. Geophys. Res. Biogeosci. 2014, 119, 2171–2187. [Google Scholar] [CrossRef]
- Tian, X.; Xie, Z.; Cai, Z.; Liu, Y.; Fu, Y.; Zhang, H. The Chinese carbon cycle data-assimilation system (Tan-Tracker). Chin. Sci. Bull. 2014, 59, 1541–1546. [Google Scholar] [CrossRef]
- Lu, L. Development of Regional High-Resolution Carbon Assimilation System and Research on Anthropogenic Carbon Emission Estimation. Ph.D. Thesis, China University of Mining and Technology, Beijing, China, 2020. [Google Scholar]
- Ma, J.; Qin, S. A Review of the Research Status of Data Assimilation Algorithms. Adv. Earth Sci. 2012, 27, 747–757. [Google Scholar]
- Zhao, L.; Shen, Z.; Li, C.; Gao, L.; Guo, M.; Sun, Y.; Peng, M. Advances in Observation, Simulation, and Assimilation of Surface Net Radiation Flux. J. Remote Sens. 2019, 23, 24–36. [Google Scholar]
- Zou, X. The Theory and Application of Data Assimilation; China Meteorological Press: Beijing, China, 2009. [Google Scholar]
- Panofsky, R.A. Objective weather-map analysis. J. Atmos. Sci. 1949, 6, 386–392. [Google Scholar] [CrossRef]
- Bergthorsson, P.; DÖÖs, B.R.; Fryklund, S.; Haug, O.; Lindquist, R. Routine Forecasting with the Barotropic Model. Tellus 1955, 7, 272–274. [Google Scholar] [CrossRef]
- Dimet, F.X.L.; Talagrand, O. Variational algorithms for analysis and assimilation of meteorological observations: Theoretical aspects. Tellus A 1986, 38A, 97–110. [Google Scholar] [CrossRef]
- Wang, B.; Zou, X.; Zhu, J. Data assimilation and its applications. Proc. Natl. Acad. Sci. USA 2000, 97, 11143–11144. [Google Scholar] [CrossRef] [PubMed]
- Ghil, M. Advances in Sequential Estimation for Atmospheric and Oceanic Flows (gtSpecial IssueltData Assimilation in Meteology and Oceanography: Theory and Practice). J. Meteorol. Soc. Jpn. 1997, 75, 289–304. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K.; Durrant-Whyte, H.F. A new approach for filtering nonlinear systems. In Proceedings of the 1995 American Control Conference—ACC’95, Seattle, WA, USA, 21–23 June 1995; Volume 3, pp. 1628–1632. [Google Scholar]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Bishop, C.H.; Etherton, B.J.; Majumdar, S.J. Adaptive Sampling with the Ensemble Transform Kalman Filter. Part I: Theoretical Aspects. Mon. Weather Rev. 2001, 129, 420–436. [Google Scholar] [CrossRef]
- Whitaker, J.S.; Hamill, T.M. Ensemble Data Assimilation without Perturbed Observations. Mon. Weather Rev. 2002, 130, 1913–1924. [Google Scholar] [CrossRef]
- Anderson, J.L. An Ensemble Adjustment Kalman Filter for Data Assimilation. Mon. Weather Rev. 2001, 129, 2884–2903. [Google Scholar] [CrossRef]
- Ott, E.; Hunt, B.R.; Szunyogh, I.; Zimin, A.V.; Kostelich, E.J.; Corazza, M.; Kalnay, E.; Patil, D.J.; Yorke, J.A. A local ensemble Kalman filter for atmospheric data assimilation. Tellus A 2004, 56, 415–428. [Google Scholar] [CrossRef]
- El Serafy, G.Y.H.; Mynett, A.E. Improving the operational forecasting system of the stratified flow in Osaka Bay using an ensemble Kalman filter–based steady state Kalman filter. Water Resour. Res. 2008, 44, W06416. [Google Scholar] [CrossRef]
- Parrish, D.F.; Derber, J.C. The National Meteorological Center’s Spectral Statistical-Interpolation Analysis System. Mon. Weather Rev. 1992, 120, 1747–1763. [Google Scholar] [CrossRef]
- Talagrand, O.; Courtier, P. Variational Assimilation of Meteorological Observations With the Adjoint Vorticity Equation. I: Theory. Q. J. R. Meteorol. Soc. 1987, 113, 1311–1328. [Google Scholar] [CrossRef]
- Ménard, R. Bias Estimation. In Data Assimilation: Making Sense of Observations; Lahoz, W., Khattatov, B., Menard, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 113–135. [Google Scholar]
- Peters, W.; Miller, J.B.; Whitaker, J.; Denning, A.S.; Hirsch, A.; Krol, M.C.; Zupanski, D.; Bruhwiler, L.; Tans, P.P. An ensemble data assimilation system to estimate CO2 surface fluxes from atmospheric trace gas observations. J. Geophys. Res. Atmos. 2005, 110, D24304. [Google Scholar] [CrossRef]
- Zhu, L. Application Research of Background Field Error Covariance Estimation Technique. Master’s Thesis, Nanjing University of Information Science and Technology, Nanjing, China, 2005. [Google Scholar]
- Evensen, G. Data Assimilation. The Ensemble Kalman Filter; Springer: Berlin/Heidelberg, Germany, 2005; Available online: https://link.springer.com/book/10.1007/978-3-642-03711-5 (accessed on 25 June 2024).
- Liang, S.; Li, X.; Xie, X. Land Surface Observation, Modeling, and Data Assimilation; World Scientific: Singapore, 2013. [Google Scholar] [CrossRef]
- Hamill, T.M.; Snyder, C. A Hybrid Ensemble Kalman Filter–3D Variational Analysis Scheme. Mon. Weather Rev. 2000, 128, 2905–2919. [Google Scholar] [CrossRef]
- Annan, J.D.; Hargreaves, J.C.; Edwards, N.R.; Marsh, R. Parameter estimation in an intermediate complexity earth system model using an ensemble Kalman filter. Ocean Model. 2005, 8, 135–154. [Google Scholar] [CrossRef]
- Hu, K.; Xu, K.; Xia, Q.; Li, M.; Song, Z.; Song, L.; Sun, N. An overview:Attention mechanisms in multi-agent reinforcement learning. Neurocomputing 2024, 598, 128105. [Google Scholar] [CrossRef]
- Hu, K.; Li, M.; Song, Z.; Xu, K.; Xia, Q.; Sun, N.; Zhou, P.; Xia, M. A Review of Research on Reinforcement Learning Algorithms for Multi-Agent. Neurocomputing 2024, 599, 128068. [Google Scholar] [CrossRef]
- Brajard, J.; Carrassi, A.; Bocquet, M.; Bertino, L. Combining data assimilation and machine learning to emulate a dynamical model from sparse and noisy observations: A case study with the Lorenz 96 model. J. Comput. Sci. 2020, 44, 101171. [Google Scholar] [CrossRef]
- Farchi, A.; Bocquet, M.; Laloyaux, P.; Bonavita, M.; Malartic, Q. A comparison of combined data assimilation and machine learning methods for offline and online model error correction. J. Comput. Sci. 2021, 55, 101468. [Google Scholar] [CrossRef]
- Bocquet, M.; Farchi, A.; Malartic, Q. Online learning of both state and dynamics using ensemble Kalman filters. Found. Data Sci. 2021, 3, 305–330. [Google Scholar] [CrossRef]
- Malartic, Q.; Farchi, A.; Bocquet, M. State, global, and local parameter estimation using local ensemble Kalman filters: Applications to online machine learning of chaotic dynamics. Q. J. R. Meteorol. Soc. 2022, 148, 2167–2193. [Google Scholar] [CrossRef]
- Farchi, A.; Chrust, M.; Bocquet, M.; Laloyaux, P.; Bonavita, M. Online Model Error Correction With Neural Networks in the Incremental 4D-Var Framework. J. Adv. Model. Earth Syst. 2023, 15, e2022MS003474. [Google Scholar] [CrossRef]
- Modares, H.; Alfi, A.; Fateh, M.M. Parameter identification of chaotic dynamic systems through an improved particle swarm optimization. Expert Syst. Appl. 2010, 37, 3714–3720. [Google Scholar] [CrossRef]
- Buizza, C.; Quilodrán Casas, C.; Nadler, P.; Mack, J.; Marrone, S.; Titus, Z.; Le Cornec, C.; Heylen, E.; Dur, T.; Baca Ruiz, L.; et al. Data Learning: Integrating Data Assimilation and Machine Learning. J. Comput. Sci. 2022, 58, 101525. [Google Scholar] [CrossRef]
- Chen, H.W.; Zhang, F.; Lauvaux, T.; Scholze, M.; Davis, K.J.; Alley, R.B. Regional CO2 Inversion Through Ensemble-Based Simultaneous State and Parameter Estimation: TRACE Framework and Controlled Experiments. J. Adv. Model. Earth Syst. 2023, 15, e2022MS003208. [Google Scholar] [CrossRef]
- Cheng, S.; Qiu, M. Observation error covariance specification in dynamical systems for data assimilation using recurrent neural networks. Neural Comput. Appl. 2022, 34, 13149–13167. [Google Scholar] [CrossRef]
- Huang, L.; Leng, H.; Li, X.; Ren, K.; Song, J.; Wang, D. A Data-Driven Method for Hybrid Data Assimilation with Multilayer Perceptron. Big Data Res. 2021, 23, 100179. [Google Scholar] [CrossRef]
- Zhu, J.; Hu, S.; Arcucci, R.; Xu, C.; Zhu, J.; Guo, Y. Model error correction in data assimilation by integrating neural networks. Big Data Min. Anal. 2019, 2, 83–91. [Google Scholar] [CrossRef]
- Peckham, S.E.; Grell, G.A.; McKeen, S.A.; Ahmadov, R.; Wong, K.Y.; Barth, M.; Pfister, G.; Wiedinmyer, C.; Fast, J.D.; Gustafson, W.I.; et al. WRF-Chem Version 3.8.1 User’s Guide. 2017. Available online: https://repository.library.noaa.gov/view/noaa/14945 (accessed on 25 June 2024). [CrossRef]
- Appel, K.W.; Napelenok, S.L.; Foley, K.M.; Pye, H.O.T.; Hogrefe, C.; Luecken, D.J.; Bash, J.O.; Roselle, S.J.; Pleim, J.E.; Foroutan, H.; et al. Description and evaluation of the Community Multiscale Air Quality (CMAQ) modeling system version 5.1. Geosci. Model Dev. 2017, 10, 1703–1732. [Google Scholar] [CrossRef]
- Mailler, S.; Menut, L.; Khvorostyanov, D.; Valari, M.; Couvidat, F.; Siour, G.; Turquety, S.; Briant, R.; Tuccella, P.; Bessagnet, B.; et al. CHIMERE-2017: From urban to hemispheric chemistry-transport modeling. Geosci. Model Dev. 2017, 10, 2397–2423. [Google Scholar] [CrossRef]
- Jacob, D.; Van den Hurk, B.J.J.M.; Andræ, U.; Elgered, G.; Fortelius, C.; Graham, L.P.; Jackson, S.D.; Karstens, U.; Köpken, C.; Lindau, R.; et al. A comprehensive model inter-comparison study investigating the water budget during the BALTEX-PIDCAP period. Meteorol. Atmos. Phys. 2001, 77, 19–43. [Google Scholar] [CrossRef]
- Bey, I.; Jacob, D.J.; Yantosca, R.M.; Logan, J.A.; Field, B.D.; Fiore, A.M.; Li, Q.; Liu, H.Y.; Mickley, L.J.; Schultz, M.G. Global modeling of tropospheric chemistry with assimilated meteorology: Model description and evaluation. J. Geophys. Res. Atmos. 2001, 106, 23073–23095. [Google Scholar] [CrossRef]
- Emmons, L.K.; Walters, S.; Hess, P.G.; Lamarque, J.F.; Pfister, G.G.; Fillmore, D.; Granier, C.; Guenther, A.; Kinnison, D.; Laepple, T.; et al. Description and evaluation of the Model for Ozone and Related chemical Tracers, version 4 (MOZART-4). Geosci. Model Dev. 2010, 3, 43–67. [Google Scholar] [CrossRef]
- Krol, M.; Houweling, S.; Bregman, B.; van den Broek, M.; Segers, A.; van Velthoven, P.; Peters, W.; Dentener, F.; Bergamaschi, P. The two-way nested global chemistry-transport zoom model TM5: Algorithm and applications. Atmos. Chem. Phys. 2005, 5, 417–432. [Google Scholar] [CrossRef]
- Hourdin, F.; Rio, C.; Grandpeix, J.Y.; Madeleine, J.B.; Cheruy, F.; Rochetin, N.; Jam, A.; Musat, I.; Idelkadi, A.; Fairhead, L.; et al. LMDZ6A: The Atmospheric Component of the IPSL Climate Model With Improved and Better Tuned Physics. J. Adv. Model. Earth Syst. 2020, 12, e2019MS001892. [Google Scholar] [CrossRef]
- Liu, J.; Bowman, K. A method for independent validation of surface fluxes from atmospheric inversion: Application to CO2. Geophys. Res. Lett. 2016, 43, 3502–3508. [Google Scholar] [CrossRef][Green Version]
- Yang, E.G.; Kort, E.A.; Wu, D.; Lin, J.C.; Oda, T.; Ye, X.; Lauvaux, T. Using Space-Based Observations and Lagrangian Modeling to Evaluate Urban Carbon Dioxide Emissions in the Middle East. J. Geophys. Res. Atmos. 2020, 125, e2019JD031922. [Google Scholar] [CrossRef]
- Boon, A.; Broquet, G.; Clifford, D.; Chevallier, F.; Butterfield, D.; Pison, I.; Ramonet, M.; Paris, J.D.; Ciais, P. Analysis of the potential of near-ground measurements of CO2 and CH4 in London, UK, for the monitoring of city-scale emissions using an atmospheric transport model. Atmos. Chem. Phys. 2016, 16, 6735–6756. [Google Scholar] [CrossRef]
- Staufer, J.; Broquet, G.; Bréon, F.M.; Puygrenier, V.; Chevallier, F.; Xueref-Remy, I.; Dieudonné, E.; Lopez, M.; Schmidt, M.; Ramonet, M.; et al. A first year-long estimate of the Paris region fossil fuel CO2 emissions based on atmospheric inversion. Atmos. Chem. Phys. Discuss. 2016, 16, 14703–14726. [Google Scholar] [CrossRef]
- Brophy, K.; Graven, H.; Manning, A.; White, E.; Arnold, T.; Fischer, M.; Jeong, S.; Cui, X.; Rigby, M. Characterizing uncertainties in atmospheric inversions of fossil fuel CO2 emissions in California. Atmos. Chem. Phys. 2019, 19, 2991–3006. [Google Scholar] [CrossRef]
- Super, I.; Denier van der Gon, H.A.C.; van der Molen, M.K.; Dellaert, S.N.C.; Peters, W. Optimizing a dynamic fossil fuel CO2 emission model with CTDAS (CarbonTracker Data Assimilation Shell, v1.0) for an urban area using atmospheric observations of CO2, CO, NOx, and SO2. Geosci. Model Dev. 2020, 13, 2695–2721. [Google Scholar] [CrossRef]
- Stagakis, S.; Feigenwinter, C.; Vogt, R.; Brunner, D.; Kalberer, M. A high-resolution monitoring approach of urban CO2 fluxes. Part 2—surface flux optimisation using eddy covariance observations. Sci. Total Environ. 2023, 903, 166035. [Google Scholar] [CrossRef]
- Stagakis, S.; Feigenwinter, C.; Vogt, R.; Kalberer, M. A high-resolution monitoring approach of urban CO2 fluxes. Part 1—bottom-up model development. Sci. Total Environ. 2023, 858, 160216. [Google Scholar] [CrossRef] [PubMed]
- Raupach, M.R.; Rayner, P.J.; Barrett, D.J.; DeFries, R.S.; Heimann, M.; Ojima, D.S.; Quegan, S.; Schmullius, C.C. Model–data synthesis in terrestrial carbon observation: Methods, data requirements and data uncertainty specifications. Glob. Chang. Biol. 2005, 11, 378–397. [Google Scholar] [CrossRef]
- Feng, L.; Palmer, P.I.; Bösch, H.; Dance, S. Estimating surface CO2 fluxes from space-borne CO2 dry air mole fraction observations using an ensemble Kalman Filter. Atmos. Chem. Phys. 2009, 9, 2619–2633. [Google Scholar] [CrossRef]
- Basu, S.; Guerlet, S.; Butz, A.; Houweling, S.; Hasekamp, O.; Aben, I.; Krummel, P.; Steele, P.; Langenfelds, R.; Torn, M.; et al. Global CO2 fluxes estimated from GOSAT retrievals of total column CO2. Atmos. Chem. Phys. 2013, 13, 8695–8717. [Google Scholar] [CrossRef]
- Maksyutov, S.; Takagi, H.; Valsala, V.K.; Saito, M.; Oda, T.; Saeki, T.; Belikov, D.A.; Saito, R.; Ito, A.; Yoshida, Y.; et al. Regional CO2 flux estimates for 2009–2010 based on GOSAT and ground-based CO2 observations. Atmos. Chem. Phys. 2013, 13, 9351–9373. [Google Scholar] [CrossRef]
- Chevallier, F.; Palmer, P.I.; Feng, L.; Boesch, H.; O’Dell, C.W.; Bousquet, P. Toward robust and consistent regional CO2 flux estimates from in situ and spaceborne measurements of atmospheric CO2. Geophys. Res. Lett. 2014, 41, 1065–1070. [Google Scholar] [CrossRef]
- Deng, F.; Jones, D.B.A.; O’Dell, C.W.; Nassar, R.; Parazoo, N.C. Combining GOSAT XCO2 observations over land and ocean to improve regional CO2 flux estimates. J. Geophys. Res. Atmos. 2016, 121, 1896–1913. [Google Scholar] [CrossRef]
- Maki, T.; Sekiyama, T.T.; Miyoshi, T.; Nakamura, T.; Iwasaki, T. Multiple Satellite Data Assimilation in Carbon Cycle Analysis Using a Local Ensemble Transform Kalman Filter (LETKF). AGU Fall Meeting Abstracts. 2016. Available online: https://ui.adsabs.harvard.edu/abs/2016AGUFM.A31E0085M/abstract (accessed on 25 June 2024).
- Monteil, G.; Broquet, G.; Scholze, M.; Lang, M.; Karstens, U.; Gerbig, C.; Koch, F.T.; Smith, N.E.; Thompson, R.L.; Luijkx, I.T.; et al. The regional European atmospheric transport inversion comparison, EUROCOM: First results on European-wide terrestrial carbon fluxes for the period 2006–2015. Atmos. Chem. Phys. 2020, 20, 12063–12091. [Google Scholar] [CrossRef]
- Jiang, F.; Wang, H.; Chen, J.M.; Ju, W.; Tian, X.; Feng, S.; Li, G.; Chen, Z.; Zhang, S.; Lu, X.; et al. Regional CO2 fluxes from 2010 to 2015 inferred from GOSAT XCO2 retrievals using a new version of the Global Carbon Assimilation System. Atmos. Chem. Phys. 2021, 21, 1963–1985. [Google Scholar] [CrossRef]
- Huang, Z.; Peng, Z.; Liu, H.; Zhang, M.; Ma, X.; Yang, S.C.; Lee, S.D.; Kim, S.Y. Development of CMAQ for East Asia CO2 data assimilation under an EnKF framework: A first result. Chin. Sci. Bull. 2014, 59, 3200–3208. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, M.; Wei, C.; Mizzi, A.P.; Huang, Y.; Gu, Q. Assimilation of OCO-2 retrievals with WRF-Chem/DART: A case study for the Midwestern United States. Atmos. Environ. 2021, 246, 118106. [Google Scholar] [CrossRef]
- Lauvaux, T.; Miles, N.L.; Deng, A.; Richardson, S.J.; Cambaliza, M.O.; Davis, K.J.; Gaudet, B.; Gurney, K.R.; Huang, J.; O’Keefe, D.; et al. High-resolution atmospheric inversion of urban CO2 emissions during the dormant season of the Indianapolis Flux Experiment (INFLUX). J. Geophys. Res. Atmos. 2016, 121, 5213–5236. [Google Scholar] [CrossRef] [PubMed]
- Thompson, R.L.; Patra, P.K.; Chevallier, F.; Maksyutov, S.; Law, R.M.; Ziehn, T.; van der Laan-Luijkx, I.T.; Peters, W.; Ganshin, A.; Zhuravlev, R.; et al. Top–down assessment of the Asian carbon budget since the mid 1990s. Nat. Commun. 2016, 7, 10724. [Google Scholar] [CrossRef]
- Kou, X.; Tian, X.; Zhang, M.; Peng, Z.; Zhang, X. Accounting for CO2 variability over East Asia with a regional joint inversion system and its preliminary evaluation. J. Meteorol. Res. 2017, 31, 834–851. [Google Scholar] [CrossRef]
- Zheng, T.; French, N.H.F.; Baxter, M. Development of the WRF-CO2 4D-Var assimilation system v1.0. Geosci. Model Dev. 2018, 11, 1725–1752. [Google Scholar] [CrossRef]
- Monteil, G.; Scholze, M. Regional CO2 inversions with LUMIA, the Lund University Modular Inversion Algorithm, v1.0. Geosci. Model Dev. 2021, 14, 3383–3406. [Google Scholar] [CrossRef]
- Baker, D.F.; Bell, E.; Davis, K.J.; Campbell, J.F.; Lin, B.; Dobler, J. A new exponentially decaying error correlation model for assimilating OCO-2 column-average CO2 data using a length scale computed from airborne lidar measurements. Geosci. Model Dev. 2022, 15, 649–668. [Google Scholar] [CrossRef]
- Tian, X.; Xie, Z.; Liu, Y.; Cai, Z.; Fu, Y.; Zhang, H.; Feng, L. A joint data assimilation system (Tan-Tracker) to simultaneously estimate surface CO2 fluxes and 3-D atmospheric CO2 concentrations from observations. Atmos. Chem. Phys. 2014, 14, 13281–13293. [Google Scholar] [CrossRef]
- Peng, Z.; Zhang, M.; Kou, X.; Tian, X.; Ma, X. A regional carbon data assimilation system and its preliminary evaluation in East Asia. Atmos. Chem. Phys. 2015, 15, 1087–1104. [Google Scholar] [CrossRef]
- Peng, Z.; Liu, Z.; Chen, D.; Ban, J. Improving PM2.5 forecast over China by the joint adjustment of initial conditions and source emissions with an ensemble Kalman filter. Atmos. Chem. Phys. 2017, 17, 4837–4855. [Google Scholar] [CrossRef]
- Peng, Z.; Lei, L.; Liu, Z.; Sun, J.; Ding, A.; Ban, J.; Chen, D.; Kou, X.; Chu, K. The impact of multi-species surface chemical observation assimilation on air quality forecasts in China. Atmos. Chem. Phys. 2018, 18, 17387–17404. [Google Scholar] [CrossRef]
- Peng, Z.; Lei, L.; Liu, Z.; Liu, H.; Chu, K.; Kou, X. Impact of Assimilating Meteorological Observations on Source Emissions Estimate and Chemical Simulations. Geophys. Res. Lett. 2020, 47, e2020GL089030. [Google Scholar] [CrossRef]
- Kou, X.; Peng, Z.; Zhang, M.; Hu, F.; Han, X.; Li, Z.; Lei, L. The carbon sink in China as seen from GOSAT with a regional inversion system based on the Community Multi-scale Air Quality (CMAQ) and ensemble Kalman smoother (EnKS). Atmos. Chem. Phys. 2023, 23, 6719–6741. [Google Scholar] [CrossRef]




| Sensor | Mounting Platform | Launching Time | Spectral Type | Spectral Range | Spectral Resolution/cm−1 | Spatial Resolution/km | Width/km |
|---|---|---|---|---|---|---|---|
| IMG | ADEOS | 1996 | Intervene | 600∼3030 | 0.15∼0.25 | 22 | - |
| AIRS | EOS-Aqua | 2002 | Encoder | 8.80∼15.4 µm | 0.55 | 13.5 | 1650 |
| 6.20∼8.22 µm | 1.2 | ||||||
| 3.74∼4.61 µm | 2.0 | ||||||
| TES | EOS-Aura | 2004 | Intervene | 3.2∼15.4 µm | 0.06 | 5 | 182 |
| IASI | METOP | 2006 | Intervene | 3.4∼15.5 µm | 0.35∼0.55 | 12 | 2200 |
| HIRAS | FY-3D | 2017 | Intervene | 8.8∼15.38 µm | 0.625 | 16 | 2250 |
| 5.71∼8.26 µm | 1.25 | ||||||
| 3.92∼4.64 µm | 2.5 | ||||||
| AIUS | GF-5 | 2018 | Intervene | 750∼4100 | 0.02 | - | 1850 |
| IRS | MTG | 2022 | Intervene | 8.26∼14.28 µm | 0.625 | 4 | - |
| 4.60∼6.25 µm | 10 |
| Country | Satellite | Detection Payload | Launching Time | Spatial Resolution/km | Spectral Band/µm | Spectral Resolution/cm−1 | Width/km |
|---|---|---|---|---|---|---|---|
| European Union | ENVISAT-1 | SCIAMACHY | 2002–2003 | 30 × 60 | 0.24∼2.4 | 4.2 | 960 |
| Japan | GOSAT | TANSO-FTS/CAI | 2009–2001 | 10.5 | 0.76∼14.3 | 0.6/0.27 | 640 |
| United States | OCO-2 | 3-band grating hyper spectrometer | 2014–2007 | 1.29 × 2.25 | 0.76∼2.08 | 0.043/0.083/0.104 | 10.6 |
| China | TANSAT | ACGS/CAPI | 2016–2012 | 2 × 2 | 0.76∼2.08 | 0.044/0.125/0.165 | 18 |
| China | FY-3D | GAS/FTS | 2017–2011 | 10 | 0.75∼2.38 | 0.6/0.27 | 2250 |
| China | GF-5 | GMI | 2018–2005 | 10.3 | 0.76∼2.06 | 0.6/0.27 | 865 |
| Japan | GOSAT-2 | TANSO-FTS-2/CAI-2 | 2018–2010 | 9.7 | 0.76∼14.3 | 0.6/0.27 | 632 |
| United States | OCO-3 | 3-band grating hyper spectrometer | 2019–2005 | 1.6 × 2.2 | 0.76∼2.08 | 0.044/0.084/0.108 | 10.6 |
| China | GF-5-02 | GMI | 2021–2009 | 10.3 | 0.76∼2.06 | 0.6/0.27 | 865 |
| France | MicroCarb | Infrared spectrometer | 2025 | 4.5 × 9 | 0.76∼2.06 | - | 13.5 |
| United States | Carbon Mapper | Hyperspectral imaging spectrometer | 2024 | 0.03 | 0.4∼2.5 | 0.05 | 18 |
| Japan | GOSAT-GW | TANSO-3 | 2024 | 10/1∼3 | 0.45∼1.6 | 0.05/0.02 | 911/90 |
| European Union | CO2M | CO2I/NO2I | 2025 | 2 × 2 | 0.74∼2.09 | 0.12/0.3/0.35 | 256 |
| China | TANSAT-2 | - | 2025 | 2 × 2 | - | - | — |
| Data Name | Algorithm | Version | Time Range | Download Website |
|---|---|---|---|---|
| SCIAMACHY WFMD | WFM-DOAS | V4.0 | 10.2002–04.2012 | [27] |
| SCIAMACHY BESD | DOAS-BESD | V2.1.2 | 01.2003–03.2012 | [28] |
| GOSAT OCFP | UOL-FP | V7.0 | 04.2009–12.2015 | [29] |
| CO2_EMMA | EMMA | V2.2 | 06.2009–06.2014 | [30] |
| GOSAT-2 ACOS | ACOS | V9r | 04.2009–08.2020 | [31] |
| GOSAT-2 SRFP | RemoTeC | V2.0.0 | 02.2019–08.2020 | [32] |
| GOSAT-2 NIES | NIES | V2.95 | 04.2009–08.2020 | [33] |
| Tansat OCFP | UOL-FP | V1.2 | 11.2017–12.2020 | [34] |
| OCO-2 ACOS | ACOS | V11.1r | 09.2014–08.2024 | [35] |
| OCO-2 FOCAL | FOCAL | V10 | 09.2014–05.2021 | [36] |
| OCO-3 ACOS | ACOS | V10.4r | 08.2019–08.2024 | [37] |
| Radiative Transfer Model | Band Range | Absorption Calculation Methods | Scattering | Polarization | Reference |
|---|---|---|---|---|---|
| 4A/OP | Near Infrared∼Thermal Infrared | Line by line | Supported | Supported | [48] |
| 6S | Visible Wave | Band pattern | Supported | Supported | [47] |
| LOWTRAN | 50,000 ∼Microwave | Band pattern | Supported | Unsupported | [49] |
| MODTRAN | 50,000 ∼Microwave | Band pattern/K-distribution | Supported | Supported | [50] |
| SCIATRAN | Ultraviolet∼Near Infrared | Line by line | Supported | Supported | [51] |
| LBLRTM/FASCODE | Ultraviolet∼Millimeter Wave | Line by line | Unsupported | Unsupported | [52] |
| VLIDORT | Ultraviolet∼Microwave | / | Supported | Supported | [53] |
| DISORT | Ultraviolet∼Microwave | / | Supported | Supported | [54] |
| LINTRAN | Visible Wave∼Thermal Infrared | Line by line | Supported | Supported | [55] |
| RTTOV | Near Infrared∼Thermal Infrared | Line by line | Supported | Unsupported | [56] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, K.; Feng, X.; Zhang, Q.; Shao, P.; Liu, Z.; Xu, Y.; Wang, S.; Wang, Y.; Wang, H.; Di, L.; et al. Review of Satellite Remote Sensing of Carbon Dioxide Inversion and Assimilation. Remote Sens. 2024, 16, 3394. https://doi.org/10.3390/rs16183394
Hu K, Feng X, Zhang Q, Shao P, Liu Z, Xu Y, Wang S, Wang Y, Wang H, Di L, et al. Review of Satellite Remote Sensing of Carbon Dioxide Inversion and Assimilation. Remote Sensing. 2024; 16(18):3394. https://doi.org/10.3390/rs16183394
Chicago/Turabian StyleHu, Kai, Xinyan Feng, Qi Zhang, Pengfei Shao, Ziran Liu, Yao Xu, Shiqian Wang, Yuanyuan Wang, Han Wang, Li Di, and et al. 2024. "Review of Satellite Remote Sensing of Carbon Dioxide Inversion and Assimilation" Remote Sensing 16, no. 18: 3394. https://doi.org/10.3390/rs16183394
APA StyleHu, K., Feng, X., Zhang, Q., Shao, P., Liu, Z., Xu, Y., Wang, S., Wang, Y., Wang, H., Di, L., & Xia, M. (2024). Review of Satellite Remote Sensing of Carbon Dioxide Inversion and Assimilation. Remote Sensing, 16(18), 3394. https://doi.org/10.3390/rs16183394







