Abstract
To address the high cost associated with acquiring hyperspectral data, spectral reconstruction (SR) has emerged as a prominent research area. However, contemporary SR techniques are more focused on image processing tasks in computer vision than on practical applications. Furthermore, the prevalent approach of employing single-dimensional features to guide reconstruction, aimed at reducing computational overhead, invariably compromises reconstruction accuracy, particularly in complex environments with intricate ground features and severe spectral mixing. Effectively utilizing both local and global information in spatial and spectral dimensions for spectral reconstruction remains a significant challenge. To tackle these challenges, this study proposes an integrated network of 3D CNN and U-shaped Transformer for heterogeneous spectral reconstruction, ICTH, which comprises a shallow feature extraction module (CSSM) and a deep feature extraction module (TDEM), implementing a coarse-to-fine spectral reconstruction scheme. To minimize information loss, we designed a novel spatial–spectral attention module (S2AM) as the foundation for constructing a U-transformer, enhancing the capture of long-range information across all dimensions. On three hyperspectral datasets, ICTH has exhibited remarkable strengths across quantitative, qualitative, and single-band detail assessments, while also revealing significant potential for subsequent applications, such as generalizability and vegetation index calculations) in two real-world datasets.
1. Introduction
Hyperspectral imaging technology integrates narrow-band imaging and spectroscopic techniques to detect real-world objects and acquire continuous spectral data. This approach facilitates the detection of numerous objects that are not discernible using broadband methods [1]. Leveraging this advantage, hyperspectral imaging finds extensive applications in medical imaging [2], remote sensing [3,4], target identification [5,6], and other domains. Nevertheless, acquiring hyperspectral images (HSIs) typically requires expensive imaging equipment and scanning techniques across spatial or spectral dimensions, making data acquisition time-consuming, labor-intensive, and financially burdensome.Furthermore, there is often a trade-off between spatial and spectral resolution during the acquisition process. Additionally, preprocessing hyperspectral data requires not only significant time and expertise but also precise calibration techniques, which are time-intensive.
To address these challenges, spectral super-resolution (SSR) and spectral reconstruction (SR) techniques have garnered considerable attention. Both approaches partially convert hardware and time costs into computational costs. SSR is achieved by fusing hyperspectral (HS) and multispectral (MS) images to mitigate low spatial resolution [7,8]; however, these methods still require the original HS image as input and do not address the inefficiencies in HS data acquisition. They can only reduce but not fundamentally resolve the various costs associated with hyperspectral data. As a cost-effective alternative, SR methods [9,10,11,12] have been proposed to generate HSIs by leveraging color information and identifiable spectral features within RGB images to estimate spectral response curves at individual pixel locations. Figure 1 illustrates the process of reconstructing an HSI from multispectral images (MSI). The key challenge is to learn the mapping function F. Compared to hyperspectral images, multispectral images contain limited information, posing a significant challenge in determining the appropriate mapping function F. The mapping function F is applied to multispectral images.
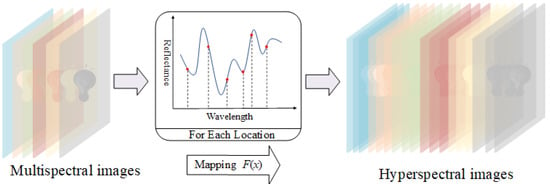
Figure 1.
Schematic representation of the SR.
Traditional SR methods primarily rely on model learning techniques such as matrix mapping and sparse coding [13,14]. Although these methods are fast, they exhibit limited reconstruction capability, poor generalization, and are unsuitable for large and complex scenes. Owing to the powerful feature extraction capabilities of deep learning, convolutional neural networks (CNNs) [15,16,17] and generative adversarial networks (GANs) [18,19] have been extensively applied in spectral reconstruction in recent years. While these methods have achieved remarkable results, they rely heavily on specifically designed modules and have limitations in capturing long-range dependencies. Transformer models [20] have recently emerged in the realm of computer vision, showing significant promise in addressing long-range dependencies and emphasizing global information. However, the existing methods, aiming to reduce computational complexity, frequently employ window-based multiple self-attention (W-MSA) or computational spectral MSA(S-MSA), each of which focus on a specific dimension. Additionally, the existing SR methods mainly focus on computer vision, often overlooking the impact of noise on reconstruction performance. In the field of remote sensing, however, limited spatial resolution and severe spectral mixing regions degrade SR performance. Furthermore, few methods effectively utilize both spatial and spectral information, and limited attention has been paid to high-frequency regions critical for practical applications. Consequently, achieving accurate SR in large-scale realistic scenes with complex ground features remains challenging.
To address these limitations, we propose a network based on the Integration of 3D CNN and U-shaped Transformer for heterogeneous spectral reconstruction (ICTH). This network integrates local and global spatial–spectral information to construct a high-precision SR model, refining from coarse to fine detail. We observe that directly using the Transformer network may lead to an emphasis on long-distance similarities due to the attention mechanism, resulting in the accumulation of computational errors. Consequently, we initially employ 3D CNN to gather local spatial–spectral information for preliminary reconstruction. This is followed by the utilization of the U-shaped Transformer architecture to achieve refined reconstruction, leveraging a two-dimensional attention mechanism to capture similarities among distant spectral bands.
The main contributions of this study are summarized as follows:
- (1)
- We propose ICTH for heterogeneous hyperspectral image reconstruction, combining a CNN and a Transformer to achieve a coarse-to-fine reconstruction scheme, demonstrating excellent results on three hyperspectral datasets;
- (2)
- We propose an efficient plug-and-play spatial–spectral attention mechanism (S2AM) that simultaneously extracts fine-grained features in both spatial and spectral dimensions while maintaining a linear relationship between complexity and spatial dimensions;
- (3)
- We have refined the pre-processing operations on heterogeneous image data to enhance SR accuracy;
- (4)
- We present a vegetation-index-based assessment of the effectiveness of spectral reconstruction.
2. Related Work
2.1. Hyperspectral Image Reconstruction
Current SRs can be classified into two categories: model-based methods and deep-learning-based methods. The former relies on manually crafted hyperspectral priors. Arad [21] employed sparse coding to derive the spectral dictionary; however, this approach neglected spatial constraints, resulting in low reconstruction quality. Gao [22] implemented SR by learning a low-rank dictionary for the overlapping regions of HS and MS images. Wan [23] explored the multilayer spatial–spectral prior of hyperspectral images using automatic weighted tensor ring decomposition with spectral quadratic variation regularization. However, these methods are constrained by the scene, do not thoroughly investigate interconnections between the data, and often overlook spatial information, resulting in poor model accuracy and limited generalization capability.
Recently, deep-learning-based SR methods have garnered increasing attention due to their excellent performance. Coded aperture snapshot spectral imaging (CASSI) produces a 2D snapshot estimation map on the camera after dispersion through a prism, subsequently deriving the mapping of discrete spectral bands from the 2D compressed image through specialized spectral reconstruction algorithms, culminating in the generation of 3D hyperspectral images [24,25]. Nevertheless, the equipment cost associated with CASSI remains considerable, prompting a growing shift towards RGB-HSI mapping tasks as researchers seek more cost-effective alternatives. Data-driven CNN-based models are extensively utilized to discern mapping relationships between images, enabling spectral super-resolution by statistically learning spatial context information [26,27,28,29]. For example, the HSCNN framework relies on spectral upsampling and residual learning enhancement to achieve the RGB to HSI reconstruction process [30]. Additionally, GANs with specifically designed architectures are employed to achieve SR through various adversarial training processes [31,32,33]. An prime example of this is the HSGAN model, which employs a specific four-level generator structure and a two-stage adversarial scheme to enhance the reconstruction accuracy of HSIs [34]. Compared to computer vision, spectral reconstruction in remote sensing places greater emphasis on complex environments and the extraction of edge features. However, approaches in both domains predominantly concentrate on short-range similarities, thereby exhibiting constraints in capturing non-local and long-range dependencies.
2.2. Vision Transformer
Since the introduction of Transformer models into computer vision, they have been extensively applied to advanced tasks such as image classification [35] and object detection [35], owing to their superior capability in capturing long-range spatial context.
As the pioneering visual transformer model in the domain of RGB-HSI spectral reconstruction, MST++ [20] constructs a U-shaped spectral long-range mapping architecture, comprising an encoder, a bottleneck, and a decoder. It addresses the limitations of CNNs in SR by mitigating information loss through operations such as multiple downsampling and upsampling, while also establishing skip connections. Of particular note is its novel spectral multi-attention mechanism, which diverges from traditional MSAs by computing self-attention in the spectral domain. Each spectral feature is treated as a marker, while global representation and self-attention are mapped as global spatial coordinates. This approach preserves a linear relationship between computational complexity and spatial dimensions, ensuring a global receptive field that is not confined to specific locations. Additionally, to accommodate variations in spectral density with wavelength, a learnable parameter is introduced to optimize the self-attention computation. The unique architecture, coupled with spectral attention, enables superior performance in handling high-dimensional data with multi-scale features.
Furthermore, Lin [36] developed a coarse-to-fine reconstruction model leveraging HSI sparsity. Zhao [37] incorporates an enhanced self-attention mechanism to significantly improve the performance of thermal infrared spectral reconstruction. To reduce computational cost, the existing models typically employ either single S-MSA or W-MSA to minimize computational complexity. However, these approaches often fail to simultaneously consider both spatial and spectral information, limiting their characterization capability, particularly for remote sensing images in complex environments, leading to significant reconstruction errors in high-frequency components.
3. Materials and Methods
3.1. Study Area and Experimental Design
An overview of the study area is presented in Figure 2. Two experimental fields were located at the China Rice Research Institute in Fuyang County, Hangzhou City, Zhejiang Province (30°04′45″N, 119°56′05″E), and a rice field on the outskirts of Jinhua City (30°02′86″N, 119°93′25″E). Experimental field No. 1 was divided into experimental zones and planted with the same rice variety at different times to enrich the sample diversity. Experimental field No. 2, covering an area of 3200 m², was sown with rice according to the usual schedule. Data from both plots were collected during the rice tasseling stage.
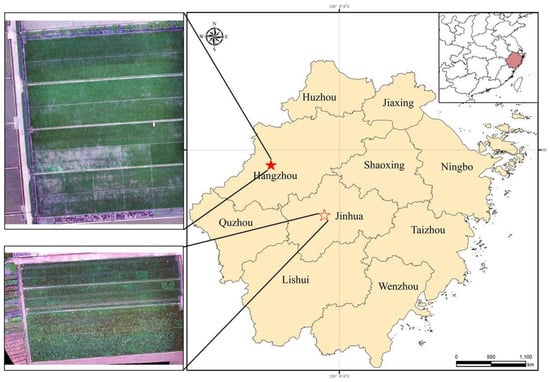
Figure 2.
Overview of the study areas.
3.2. Aerial Image Acquisition and Data Preprocessing
The aerial imagery was acquired in June 2023 at 12:00 PM utilizing unmanned aerial vehicle (UAV) platforms equipped with hyperspectral, multispectral, and RGB cameras. The hyperspectral imagery was obtained through a DJI Innovations Matrice 600 Pro hexacopter (DJI Technology Co., Ltd., Shenzhen, China) equipped with RTK and GNSS and a Specim FX10 hyperspectral push-broom scanner (Specim, Spectral Imaging Ltd., Oulu, Finland). The scanner is equipped with a 32 mm focal length lens, capturing 480 pixels and 300 spectral bands at 50 Hz, with wavelengths spanning from 385 to 1020 nm. The multispectral imagery was captured using a DJI Matrice 300 RTK drone, also equipped with RTK, carrying an MS600 V2 multispectral camera (Changguang Yuchen Information Technology & Equipment Co., Ltd., Qingdao, China). This camera offers a 48.8° field of view and captures images across six mono-spectral channels: blue (450 nm), green (555 nm), red (660 nm), red edge (720 nm), red edge (750 nm), and near-infrared (840 nm) at a trigger frequency of 1 Hz. Pre-flight mission planning for the UAV was executed using the DJI GS Pro application. The appropriate parameters were selected to ensure an overlap of hyperspectral and multispectral images exceeding 33%. The specific flight parameters are detailed in Table 1.

Table 1.
Results of ablation experiments on effects of different ingredients.
The Specim FX10 hyperspectral push-broom scanner was configured using the ISUZU_GR 2.5.0 software (Isuzu Optical Co., Ltd., Shanghai, China) to set the parameters and receive feedback. Additionally, the RGB images were acquired using a DJI Mavic Pro 2 quadcopter, equipped with a Hasselblad L1D-20C 20MP camera (Hasselblad, Gothenburg, Sweden). Figure 3 illustrates the UAV and camera hardware and software systems employed in this study.

Figure 3.
Overview of UAS and components used in the study. (a) DJI M600 Pro UAV System; (b) DJI M300 RTK UAV System; (c) DJI Mavic Pro 2; (d) Specim FX10 Hyperspectral camera; (e) MS600 V2 camera; (f) Hasselblad L1D-20C 20MP camera; (g) ISUZU_GR Software; (h) TQC Mapping Software 2.5.0; (i) DJI GS Pro 2.0.18.
3.3. Remote Sensing Image Preprocessing
3.3.1. RGB and Multispectral Image Mosaic
The ortho-mosaics of RGB and multispectral images obtained via UAVs were automatically processed using Pix4DMapper 4.4.12 software (Pix4D SA, Lausanne, Switzerland). This process included importing positional and geolocation information, aligning images, encrypting the point cloud, modeling the digital surface, and generating the ortho-mosaics. A total of 455 original RGB images and 2172 single-band multispectral images were utilized. For the multispectral images, ENVI (Exelis Visual Information Solution, Boulder, CO, USA) 5.6 software was employed for band fusion to generate a six-band ortho-mosaic.
3.3.2. Geometric Correction and Ortho-Stitching of Hyperspectral Data
The original airborne hyperspectral strips underwent preprocessing through the following steps, as illustrated in Figure 4a: (1) tracking linear features within the strips and applying geometric aberration correction via the single line correction method; (2) employing distinct features as ground control points to ensure precise alignment of the hyperspectral strips with the RGB ortho-photo basemap; and (3) determining the digital number (DN) values of the spectral dimensionality for overlapping areas of the strips during the final splicing process.
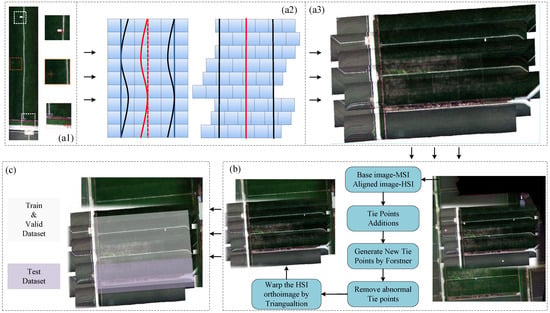
Figure 4.
Aerial image pre-processing process: (a) pre-processing process of hyperspectral strips: (a1) raw hyperspectral strips with control point selection, the red crosses are selected cases of ground control points, (a2) schematic of the process of geometric correction, (a3) hyperspectral ortho-stitching map; (b) geographic alignment process; (c) dataset production process.
3.4. Remote Sensing Image Alignment
Given that multispectral and hyperspectral images are acquired by different sensors with distinct geographic location information, it is crucial to calculate the feature points between the images to minimize geographic errors and prevent adverse effects on model reconstruction. The specific alignment process involves the following steps: (1) Use the multispectral image as the reference image and the hyperspectral image as the calibration image, ensuring that the resolution and scale remain consistent throughout the alignment process; (2) Utilize the cross-correlation algorithm [38] to match images based on the similarity of their spatial and partial spectral features, achieving optimal alignment results; (3) Apply rotation–scaling–translation (RST) as the transformation method and use the Forstner operator to obtain optimal matching points [39], ensuring an even distribution of control points by removing those with significant errors; (4) Employ triangulation [40] to warp the hyperspectral ortho-photo, achieving optimal image alignment and generating the aligned image; (5) Superimpose the two ortho-photos, setting the transmittance to greater than 50% to verify the alignment effect; (6) Manually crop the images to the same coverage area and remove the edges. All operations are depicted in the lower section of Figure 4.
3.5. Model Construction
3.5.1. Problem Formulation
Let denote MSI and denote HSI, where W is the width, H is the height, c is the number of bands in MSI X, C is the number of bands in HSI Y, and c < C. The spectral reconstruction of MSI is the inverse process of spectral dimensionality reduction, which is a high level problem, and it can be denoted as:
where M is the mapping matrix, and E is the residual term. To establish the optimal mapping between multispectral and hyperspectral bands, deep learning methods are typically employed to construct specific models aimed at minimizing . Consequently, this paper proposes a CNN-transformer model, ICTH, for HSI reconstruction. This model learns the MSI-HSI mapping M through two stages: shallow feature extraction and deep feature extraction, thus completing the spectral reconstruction from local to global.
3.5.2. Network Architecture
As illustrated in Figure 5a, ICTH is comprised of two components: a shallow feature extraction module (CSSM) and a deep feature extraction module (TDEM). The model initially stacks CSSMs, with each shallow feature extraction module composed of spatial–spectral Conv3D blocks (SSC3B), interconnected through residual connections, represented as follows:
where X is the input, and denotes the response of the SSC3B module. Subsequently, it is connected in series with deep feature extraction modules. Each deep feature extraction module comprises two encoders, one bottleneck, and two decoders arranged in a U-shaped Transformer structure. The computational formula can be denoted as follows:
where, stands for the response of the TDEM module, and stands for the output.
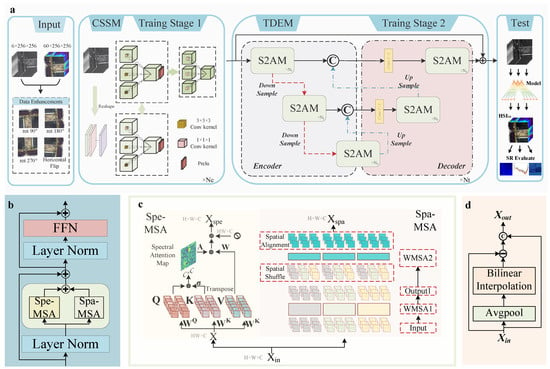
Figure 5.
Overall flow of the proposed solution: (a) overall structure of the network; (b) S2AM modules; (c) specific structure of the MSA; (d) structure of the HFE.
3.5.3. Spatial–Spectral Conv3D Block
The inherent ability of MSA to directly capture interrelationships between distant bands may lead to the model overlooking intricate details, producing a reconstructed image that is excessively smooth and deviates significantly from the original in regions with abrupt feature changes. The 3D convolution kernel effectively captures spatial and spectral features during shallow feature extraction. To address this issue without introducing excessive parameters, we propose SSC3B, which comprises multiple three-bit convolutions, as shown in Figure 5a. SSC3B utilizes a three-bit convolutional kernel to extract shallow features.
For a given feature map , we need to augment its dimensions to match the three-bit convolution kernel, denoting the augmented feature map as (p is set to 1 at input to reduce the impact on the original input). To mitigate excessive image smoothing and prevent a substantial increase in parameter count, a small convolution kernel is employed to extract finer spatial and spectral features. As illustrated in the CSSM section of Figure 5, we implement a cascade of two 3 × 3 × 3 convolutions during the initial stage to effectively capture details, subsequently employing a 1 × 1 × 1 convolution to eliminate redundant p dimensions. The specific process is defined as follows:
where is the 3D convolution kernel weights; N is the number of convolution kernels; C,H,W are the convolution kernel dimensions; is the bias; and is the activation function.
3.5.4. Spatial–Spectral Attention Mechanism
Hyperspectral images are rich in spatial–spectral features; however, to reduce the number of parameters in the model, the existing Transformer models often focus exclusively on either spatial or spectral information, leading to information loss. To address these challenges, we propose a Transformer-based 2D feature extraction module, named the spatial–spectral attention module (SSAM), which aims to extract both spatial and spectral features simultaneously, thereby enhancing the model’s learning capability. As illustrated in Figure 5c, the spatial–spectral attention mechanism (S2AM) comprises parallel spatial MSA and spectral MSA modules for computing spatial and spectral multi-head self-attention, respectively. The computational complexity of global MSA is quadratic with HW. To reduce the computational load of the spatial dimension, Liu [36] proposed spatial MSA based on windowed MSA (W-MSA). W-MSA partitions the input image into non-overlapping windows to reduce the computational load. However, this approach inevitably results in a lack of information interaction between these windows.
To alleviate this problem, we combine W-MSA with random window MSA to facilitate remote cross-window interaction. In brief, assuming the window size of W-MSA is M and the input comprises N tokens, the spatial dimensions of the output are initially reshaped to (M, N/M), then transposed and flattened to serve as input for the subsequent layer, namely, SW-MSA. This operation aggregates tokens from distant windows and establishes cross-window connections between remote regions. It is important to note that in the window shifting configuration of SW-MSA, the computational cost increases due to the expanded number of windows. The spatial shuffling operation effectively mitigates this issue; however, it can result in a batch window consisting of several sub-windows that are non-adjacent within the feature map. To prevent this, a masking mechanism is employed post-spatial shuffling to ensure that self-attention computation is confined to each sub-window, thereby maintaining a constant computational load. Subsequently, the spatial dimensions are reshaped to (N/M, M) using spatial alignment operations with relative positional offsets, followed by transposition and flattening to restore their original configurations.
Conversely, spectral MSA primarily processes spectral feature maps as markers and calculates self-attention along the spectral dimension, thus enhancing non-local spectral self-similarity and ensuring that its computational effort is linear with respect to spatial size. It is important to highlight that due to the significant variation in spectral density across different wavelengths, a learnable parameter, denoted as , is introduced to optimize the self-attention mechanism.
3.5.5. High-Frequency Extractor
The spectral reconstruction process requires multiple downsampling operations, which inevitably result in the loss of high-frequency information. Consequently, the reconstructed images exhibit increased smoothness and significant distortion of spectral curves in regions with substantial feature variations. To mitigate this issue, we introduce a high-frequency feature extractor (HFE) module (Figure 5d) in conjunction with S2AM at the encoder stage, aiming to capture high-frequency information.
As a learnable component, the HFE module conducts spatial downsampling on the given feature map X via average pooling, thereby attenuating detail information and local extrema in the image. To recover these detailed features, the feature map is first upsampled to its original size via bilinear interpolation. Subsequently, the difference between the original input and the post-processed feature map is calculated using the formula , where Y constitutes a feature map densely populated with high-frequency residual information. This feature map Y is subsequently aggregated with the original input and undergoes dimensional adjustment via convolutional layers to yield an output enriched with high-frequency residuals. Incorporating this enriched output into the multi-head attention mechanism facilitates the preservation of detailed features throughout the progressive downsampling in the encoder, thereby enhancing its applicability in scenarios involving complex features.
3.6. Model Performance Evaluation
To comprehensively assess the spectral reconstruction performance of the model and the utility of the reconstructed images in subsequent applications, we evaluate the model from two perspectives: visual effects and practical applications.
3.6.1. The Visual Effects Evaluation Indicators
The visual-effect-based assessment primarily relies on traditional evaluation metrics and band-specific error maps. Various evaluation metrics exist for reconstructed HSI, and this study employs five commonly used metrics: mean absolute relative error (MARE), root mean square error (RMSE), peak signal-to-noise ratio (PSNR), structural similarity (SSIM), and spectral angle (SAM). Let denote the ith band in the original HSI, denote the ith band in the reconstructed HSI, and n is the total number of spectral bands. The formulas for these five evaluation metrics are as follows:
These two metrics quantify the pixel error between the generated spectrum and the true spectrum in various ways.
In fields such as image restoration and denoising, PSNR is commonly used to measure the quality of signal reconstruction, which is derived from the mean square error (MSE). For HSI, PSNR needs to be calculated for each band separately, where MAXj is the maximum possible value of the actual HSI for the ith band.
Unlike RMSE and MARE, which measure error visibility, SSIM assesses the structural similarity between the two bands.
This metric reflects the spectral angular distance between the generated spectrum and the real spectrum, imposing greater constraints on the shape of the generated spectrum, thereby assessing the practical application value of the image.
Lower MARE, RMSE, and SAM, along with higher PSNR and SSIM, indicate superior model performance in spectral reconstruction.
3.6.2. The Application of Evaluation Indicators
Evaluation methods based on visual metrics can only broadly assess model performance, lacking full compatibility with human perception and failing to guarantee application performance in production activities. To prevent the reconstruction performance of the model from being confined to computer vision and to ensure its value in real-world production activities, we propose a validation method based on the vegetation index (VI). The VI is a crucial indicator of surface vegetation condition, containing over 90% of the remote sensing information related to vegetation. It enhances vegetation information while minimizing non-vegetation interference and has been widely used in fields such as yield prediction and crop monitoring. To differentiate multispectral data, we selected vegetation indices specific to hyperspectral images to validate their application value.
The fluorescence ratio index (FRI1) [41] is a significant indicator of the chlorophyll content in plant leaves, offering a potential advantage for precision agriculture management. Chlorophyll fluorescence is strongly influenced by pigment content and leaf absorption, making FRI1, calculated from spectra, a useful tool for farmers in field management. FRI1 is calculated as shown in Equation (10). To facilitate our next comparison, the VI values are scaled in [0, 1].
where represents the surface reflectance in this band of the image. Additionally, to facilitate calculation and evaluation, we categorize them into 5 levels, with level 1 designated for the removal of outliers arising from data processing or measurement errors. The specific gradient of this classification is detailed in Equation (11):
3.7. Training Setting
3.7.1. Dataset
In this study, one ideal dataset and two real-world datasets are utilized to evaluate the model’s performance. The dataset processing details are as follows: the NTIRE2022 dataset comprises 900 RGB-HSI pairs for training and 50 HSI pairs for validation. All HSI images have a spatial resolution of 482 × 512 and contain 31 channels ranging from 400 to 700 nm. We crop the image pairs to 100 × 100 for training to reduce memory requirements. The two self-constructed UAV low-altitude remote sensing rice field datasets were processed as described in Section 3.4, divided into training, validation, and test sets in the ratio of 7:1:2, and cropped to 256 × 256 for training.
3.7.2. Implementation Details
The experimental hardware configuration consisted of an AMD Ryzen 9 7950x CPU at 4.50 GHz and an NVIDIA GeForce GTX 4090 GPU. All models in this study were performed on the Pytorch platform under Windows and were briefly trained 300 times using the Adam optimizer ( = 0.9, = 0.999). The specific training parameters for ICTH were set to batch_size of 4, stride of 8, learning rate initialized to 0.0003, cosine annealing scheme using MARE as loss and applying random rotations and flips to augment the data during the training process, and and were set to 3 and 2 after several experiments.
4. Results
In this section, we compare ICTH with several state-of-the-art spectral reconstruction methods, namely, five natural image restoration models MIRNET [42], MPRNET [43], Restormer [44], HINET [45], EDSR [46], five SR algorithms HSCNN+ [47], HRNET [48], HDNET [49], AWAN [50], and MST++ [20]. All these methods are fully optimized on all three datasets under the same conditions to ensure fair competition and best performance.
4.1. Comparison with SOTA Methods
4.1.1. Quantitative Results
Table 2 presents the evaluation results of spectral reconstruction metrics on both the ideal and real-world datasets, with the best performance for each metric highlighted in bold. To validate the spectral reconstruction performance of the model, we conducted experiments on the NTIRE 2022 dataset. Our method achieved optimal results on most metrics and sub-optimal results on the SAM metric, with a difference of only 0.003 from the optimal value. Owing to our proposed local-to-global reconstruction framework, our model demonstrated excellent performance in spectral reconstruction under ideal conditions. To establish that the reconstruction capability of the model extends beyond the computer vision domain and can be applied to the remote sensing domain for heterogeneous spectral reconstruction, we conducted experiments on the UAV paddy field dataset. We achieved results comparable to those obtained with the ideal dataset, demonstrating the model’s generalization ability and its potential for application in remote sensing field production.

Table 2.
Comparison with 10 SOTA methods on two HSI datasets. The best and second-best methods are bolded and underlined.
To intuitively demonstrate the competitiveness of our model in spectral reconstruction of heterologous images, we present a MARE-Params-FLOPs comparison in Figure 6. The horizontal axis represents FLOPs (computational cost), the vertical axis denotes MARE (performance), and the radius of the circle indicates Params (memory cost). Our approach is positioned in the lower left corner, achieving an optimal balance between performance and efficiency. This is largely attributed to our shallow feature extraction module, which alleviates the burden on the 3D attention mechanism when handling long-range correlations, thereby preventing an increase in computational cost despite changes in attention.
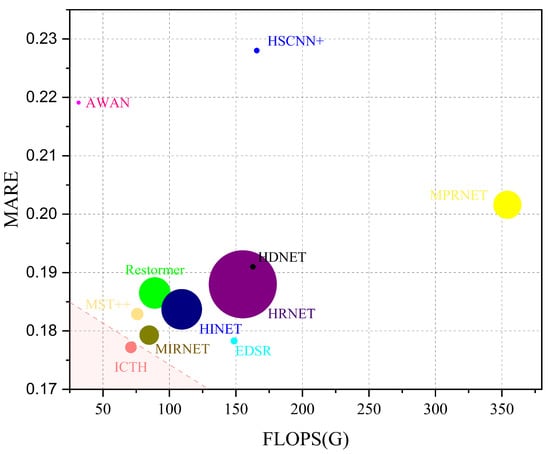
Figure 6.
Comparison of MARE-Params-FLOPS with other spectrum reconstruction algorithms. The calculated metrics are based on the applied realistic spectrum reconstruction task.
4.1.2. Qualitative Results
To visually assess the perceived quality of the hyperspectral reconstruction, we present the selection of three bands and the corresponding reconstruction error maps for the test set of the rice dataset in Figure 7. The error maps are computed as follows: a specific spectral band error (called error map ), computed as going where and represent the reconstructed image and ground truth image of the first band, respectively. According to the color bars, colors close to blue indicate values converging to 0. It is evident that the previous reconstruction methods struggle to maintain consistent granularity and eliminate distortions induced by manual manipulation, particularly in the high-frequency components (e.g., the bright spot in the lower left corner). In contrast, our method demonstrates a superior ability to accurately recover texture, largely due to our local-to-global reconstruction strategy. Additionally, the effective integration of the 3DCNN and the attention mechanism mitigates the effects of remote bands. It is important to emphasize that our method focuses on the rice field region (upper right region), which is crucial for production activities. Other methods exhibit noise, resulting in bright spots of varying sizes and densities in the rice field region. In contrast, our method integrates spatial and spectral dimensions to ensure improved spatial smoothing and spectral fidelity. To further demonstrate the reconstruction effectiveness in the rice planting area, we compare the reconstruction results of various methods with the ground truth values of the rice in the reconstructed image, as shown in the lower left corner. Our curves exhibit the highest correlation and overlap with the actual data.

Figure 7.
Comparison of reconstruction error maps for three bands at 500, 600, and 700 nm in experimental region 1. The spectral curve (lower left) corresponds to the selected red point in the RGB image.
4.1.3. Integrated Assessment
Previous quantitative assessments have relied on evaluation metrics for a holistic assessment of all bands, while qualitative experiments have used band error maps or single band reconstruction effects to demonstrate performance in only a few specific bands. To ensure our results perform well across all bands, not just specific ones, we employ two additional metrics for a comprehensive evaluation: mutual information and cross-entropy. We use mutual information and cross-entropy as additional metrics to evaluate the reconstruction of each single band relative to the original ground truth. Mutual information measures the dependence between two random variables, while cross-entropy measures the difference between the model’s predictions and the true distribution. Therefore, higher values of mutual information and lower cross-entropy indicate better reconstruction. To enhance the stability and diversity of the experimental setup, we carefully selected representative blocks in the test area, including road intersections and two types of vegetation areas. Comparing our model (red lines) with other state-of-the-art methods (various colored lines), our proposed method demonstrates near-optimal performance across almost all bands on both metrics, proving its superiority in full-band reconstruction.
Both metrics shown in Figure 8 exhibit a common characteristic: they display peaks or troughs around the 50th band. This observation may be attributed to the information present in the input bands. In the preceding section, we detailed the specific wavelengths of the six input bands. Notably, the red edge band includes two input wavelengths, whereas the wavelength intervals of the other bands exceed 100 nm. This results in richer spectral information within the red edge range compared to other regions. Consequently, under identical conditions, the increased input information enhances the accuracy of reconstruction for bands within this range relative to others. Therefore, the effectiveness of reconstruction is influenced not only by the model’s performance but also by the wavelengths of the input data.
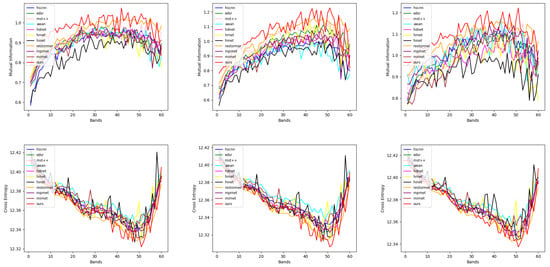
Figure 8.
Three representative blocks within the test area (roadway intersections, Vegetation 1, and Vegetation 2, in that order) were evaluated for the full band (Wavelength range between 460–800 nm).
4.2. Application Validation
The objective of the model designed in this study is to reconstruct heterogeneous HSI images using MSI remote sensing imagery and apply them to agricultural production practices. The comparison in the previous subsection has demonstrated the model’s excellent reconstruction performance, but it only proves success at the image processing level. To validate its real-world applicability, it is necessary not only to verify the reconstruction results on real datasets but also to evaluate subsequent production activities and generalizability.
4.2.1. Validation of the Application of VI
VIs are widely employed in agricultural remote sensing to assess and monitor vegetation cover, growth status, and yield prediction [51]. Therefore, VI distribution maps can significantly verify the subsequent application capability of the reconstructed images. To minimize computational cost, the generated test images are segmented into small pieces, lacking geographic information. To produce a VI distribution map encompassing the entire test area, it is necessary to incorporate the geographic location data from the multispectral dataset into the generated HSIs, and subsequently utilize this geographic information to assemble a complete ortho-photo map. Figure 9 presents the VI maps of the original HSI and those generated by various reconstruction methods, which will be analyzed in terms of overall restoration and detailed restoration. Except for the HINET and MIRNET methods, which failed to successfully generate VI maps, all other methods succeeded. Overall, our methods exhibit the highest similarity to the original VI distribution maps, both for the rice field and the concrete road between the fields. Among the green shrubs at the edge of the road, only our method achieved maximal restoration. In detail, a narrow horizontal line delineating the upper half of the rice field was also most clearly restored by our method.

Figure 9.
Comparison of VI profiles obtained by different methods.
Since the experimental dataset was mostly acquired at midday, variations in light intensity and other environmental factors can cause incidental differences in brightness and other aspects of the HSI images of consecutive strips. By training the model on the normal acquisition portion of the dataset, we can mitigate the negative effects of the acquisition environment to a certain extent, reconstructing the images to generate representations closer to the actual scene and producing accurate VI distribution maps.
4.2.2. Verification of Generalizability
While the feasibility of subsequent applications is crucial, the applicability of our method would be significantly limited if it were restricted to a specific study area. Therefore, the realistic generalization of the model is an essential indicator to consider. The results in Section 4.1.1 have demonstrated a certain degree of generalization capability of ICTH, but its generalization ability for realistic scenarios still requires verification. To address this, we applied the existing model data to Study Area 2, with the results presented in Table 3. Although the results differ slightly from those of Experimental Area I, our method still outperforms others, particularly in terms of MARE metrics. The stronger generalization performance ensures that the model proposed in this paper can be applied to more experimental sites, providing robust support for various agricultural remote sensing applications. The HRNET model, although not outperforming our model in Experimental Area 1, demonstrates stronger generalization. Conversely, other methods that have shown excellent performance in computer vision yield worse results.

Table 3.
Results of the generalizability comparison of the proposed method with other methods. The best and second-best methods are bolded and underlined.
4.3. Ablation Study
In this section, we conduct an extensive ablation study on the dataset used in Experiment 2 to analyze the reconstruction capabilities of various ICTH components.
4.3.1. Decomposition Ablation
To assess the influence of each module (CSSM and HFE), we initially performed decomposition ablation and present the quantitative findings in Table 4. From the second to the fourth row, it is evident that each module enhances reconstruction performance across all metrics. For instance, MARE exhibits enhancements of 15.4% and 8.6%, respectively, with continuous utilization of the module further elevating it to 17.4%, thereby underscoring the efficacy of these modules.

Table 4.
Results of ablation experiments on effects of different ingredients.
4.3.2. Attention Comparison
To further ascertain the effectiveness of our proposed spatial–spectral attention mechanism (S2AM), we compared it with single-dimensional attention. The results demonstrate that our spatial–spectral MSA outperforms single-dimensional attention in all aspects and has the capability to integrate with other independent modules for further performance enhancement.
5. Discussion
5.1. Importance of Geographic Alignment
The reconstruction results of the model presented in this paper outperform the state-of-the-art (SOTA) methods; however, some limitations remain, which are partly attributable to the dataset. Although the time difference between the acquisition of the two types of remote sensing images may be only a few tens of minutes, the sun’s illumination at midday can vary drastically, making it difficult to fully guarantee consistency. Additionally, discrepancies in the geographic information carried by the two sensors can cause location offsets, and geo-alignment is crucial in mitigating this deficiency. Table 5 presents a comparison of the reconstruction results of two UAV rice field hyperspectral datasets that have undergone alignment, where G represents the aligned image and w/o G represents the unaligned image. The unaligned dataset is much less effective in reconstruction compared to the aligned results, especially in Study Area 2, where the MARE value is clearly in an abnormal range. Location offsets may result in different corresponding pixels; for example, multispectral pixels on concrete roads may correspond to hyperspectral pixels on dirt or rice, which essentially offsets the reconstruction target. This not only hinders the model from achieving optimal results but may also lead to reconstruction failure. Therefore, implementing measures such as selecting obvious pixel points for matching to achieve geographic alignment helps improve the spectral reconstruction task. Although manual alignment cannot guarantee complete image alignment, it prevents inconsistencies in pixel–object correspondence.

Table 5.
Results of comparative experiments on the role of geographic alignment.
5.2. Scalability Challenges in Spectral Reconstruction of UAV Hyperspectral Imagery
The task of spectral reconstruction of heterologous hyperspectral images can effectively reduce the costs associated with hyperspectral image acquisition, eliminating the need for precise calibration techniques and extensive expertise in image processing. However, broader applications inevitably encounter challenges in adapting to agricultural scenes at varying spatial resolutions.
UAV-based methods provide higher spatial resolution and more accurate spectral representation of mixed pixels compared to traditional remote sensing techniques. Additionally, a single pixel in a satellite image may encompass an entire small-scale farmland, imposing limitations on subsequent agricultural activities. However, the relatively small coverage area of UAV remote sensing may be insufficient for large-scale farm applications.
For future work, we plan to further optimize the network structure to accommodate various scenarios, such as land changes due to seasonal variations, rainfall, or time of day. This is a challenging task that requires extensive UAV remote sensing data support.
6. Conclusions
In this study, our primary objective is to propose a novel model for efficiently reconstructing heterologous hyperspectral imagery, ensuring its effective application in subsequent agricultural production. To achieve this, we introduce an architecture that combines CNN and Transformer to extract spatial–spectral features from local to global scales, implementing a coarse-to-fine reconstruction scheme. We also propose the fusion spatial–spectral attention module (S2AM), which significantly enhances information extraction and fusion for cross-dimensional tasks. To address the challenges posed by different sensors in spectral reconstruction, we refine the data preprocessing operations for geographic alignment to minimize geographic offset issues in heterogeneous images. We validate the module’s effectiveness through ablation experiments, revealing outstanding performance across both ideal and diverse real-world HS datasets, which demonstrates robust generalization capabilities. Quantitative, qualitative, and single-band reconstruction evaluations further affirm the superiority of our method in image processing tasks. Moreover, application-specific metric evaluations corroborate the practical applicability of our approach, extending its relevance beyond the domain of computer vision.
Author Contributions
Conceptualization, W.S.; methodology, Z.H.; software, H.Z.; validation, Z.H.; resources, X.W.; data curation, Z.L.; writing—original draft, H.Z.; writing—review and editing, Z.L. and Y.Z.; visualization, H.Z. and X.W.; supervision, W.S. and Y.Z.; project administration, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by National Natural Science Foundation of China (NSFC), grant number: 61905219, Zhejiang Science and Technology Cooperation Plan, grant number: 2024SNJF071, China Agriculture Research System (CARS-01), Key Laboratory of Smart Agricultural Technology (Yangtze River Delta), Ministry of Agriculture and Rural Affairs, China, Nanjing, 210044, China.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to privacy.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Qureshi, R.; Uzair, M.; Khurshid, K.; Yan, H. Hyperspectral document image processing: Applications, challenges and future prospects. Pattern Recognit. 2019, 90, 12–22. [Google Scholar] [CrossRef]
- Meng, Z.; Qiao, M.; Ma, J.; Yu, Z.; Xu, K.; Yuan, X. Snapshot multispectral endomicroscopy. Opt. Lett. 2020, 45, 3897–3900. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Huang, W.; Dong, Y.; Liu, L.; Guo, A. Using UAV-based hyperspectral imagery to detect winter wheat fusarium head blight. Remote Sens. 2021, 13, 3024. [Google Scholar] [CrossRef]
- Miyoshi, G.T.; Arruda, M.d.S.; Osco, L.P.; Marcato Junior, J.; Gonçalves, D.N.; Imai, N.N.; Tommaselli, A.M.G.; Honkavaara, E.; Gonçalves, W.N. A novel deep learning method to identify single tree species in UAV-based hyperspectral images. Remote Sens. 2020, 12, 1294. [Google Scholar] [CrossRef]
- Tian, Q.; He, C.; Xu, Y.; Wu, Z.; Wei, Z. Hyperspectral Target Detection: Learning Faithful Background Representations via Orthogonal Subspace-Guided Variational Autoencoder. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5516714. [Google Scholar] [CrossRef]
- Chang, C.I. An effective evaluation tool for hyperspectral target detection: 3D receiver operating characteristic curve analysis. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5131–5153. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, W.; Wang, Q.; Li, X. SSR-NET: Spatial–spectral reconstruction network for hyperspectral and multispectral image fusion. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5953–5965. [Google Scholar] [CrossRef]
- Borsoi, R.A.; Imbiriba, T.; Bermudez, J.C.M. Super-resolution for hyperspectral and multispectral image fusion accounting for seasonal spectral variability. IEEE Trans. Image Process. 2019, 29, 116–127. [Google Scholar] [CrossRef]
- Yan, L.; Wang, X.; Zhao, M.; Kaloorazi, M.; Chen, J.; Rahardja, S. Reconstruction of hyperspectral data from RGB images with prior category information. IEEE Trans. Comput. Imaging 2020, 6, 1070–1081. [Google Scholar] [CrossRef]
- Hang, R.; Liu, Q.; Li, Z. Spectral super-resolution network guided by intrinsic properties of hyperspectral imagery. IEEE Trans. Image Process. 2021, 30, 7256–7265. [Google Scholar] [CrossRef]
- Xu, R.; Yao, M.; Chen, C.; Wang, L.; Xiong, Z. Continuous spectral reconstruction from rgb images via implicit neural representation. In Proceedings of the Computer Vision—ECCV 2022 Workshops: European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Cham, Switzerland, 2022; pp. 78–94. [Google Scholar] [CrossRef]
- Li, J.; Du, S.; Wu, C.; Leng, Y.; Song, R.; Li, Y. Drcr net: Dense residual channel re-calibration network with non-local purification for spectral super resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–20 June 2022; pp. 1259–1268. [Google Scholar] [CrossRef]
- Aeschbacher, J.; Wu, J.; Timofte, R. In defense of shallow learned spectral reconstruction from RGB images. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017; pp. 471–479. [Google Scholar]
- Akhtar, N.; Mian, A. Hyperspectral recovery from RGB images using Gaussian processes. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 42, 100–113. [Google Scholar] [CrossRef] [PubMed]
- Mei, S.; Jiang, R.; Li, X.; Du, Q. Spatial and spectral joint super-resolution using convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4590–4603. [Google Scholar] [CrossRef]
- Han, X.H.; Shi, B.; Zheng, Y. Residual HSRCNN: Residual hyper-spectral reconstruction CNN from an RGB image. In Proceedings of the 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 2664–2669. [Google Scholar]
- Koundinya, S.; Sharma, H.; Sharma, M.; Upadhyay, A.; Manekar, R.; Mukhopadhyay, R.; Karmakar, A.; Chaudhury, S. 2D-3D CNN based architectures for spectral reconstruction from RGB images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 844–851. [Google Scholar]
- Alvarez-Gila, A.; Van De Weijer, J.; Garrote, E. Adversarial networks for spatial context-aware spectral image reconstruction from RGB. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017; pp. 480–490. [Google Scholar]
- Zhang, Y.; Yang, W.; Zhang, W.; Yu, J.; Zhang, J.; Yang, Y.; Lu, Y.; Tang, W. Two-Step ResUp&Down Generative Adversarial Network to Reconstruct Multispectral Image from Aerial RGB Image. Comput. Electron. Agric. 2022, 192, 106617. [Google Scholar]
- Cai, Y.; Lin, J.; Lin, Z.; Wang, H.; Zhang, Y.; Pfister, H.; Timofte, R.; Van Gool, L. Mst++: Multi-stage spectral-wise transformer for efficient spectral reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–20 June 2022; pp. 745–755. [Google Scholar]
- Arad, B.; Ben-Shahar, O. Sparse recovery of hyperspectral signal from natural RGB images. In Proceedings of the Computer Vision—ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings Part VII 14. Springer: Berlin/Heidelberg, Germany, 2016; pp. 19–34. [Google Scholar]
- Gao, L.; Hong, D.; Yao, J.; Zhang, B.; Gamba, P.; Chanussot, J. Spectral superresolution of multispectral imagery with joint sparse and low-rank learning. IEEE Trans. Geosci. Remote Sens. 2020, 59, 2269–2280. [Google Scholar] [CrossRef]
- Wan, X.; Li, D.; Kong, F.; Lv, Y.; Wang, Q. Spectral Quadratic Variation Regularized Auto-Weighted Tensor Ring Decomposition for Hyperspectral Image Reconstruction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 9907–9921. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, W.; Xu, T.; Shi, G.; Zhou, S.; Liu, P.; Li, J. Spectral-wise implicit neural representation for hyperspectral image reconstruction. IEEE Trans. Circuits Syst. Video Technol. 2023, 34, 3714–3727. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhao, S.; Ma, X.; Zhang, T.; Arce, G.R. Hyperspectral image reconstruction via patch attention driven network. Opt. Express 2023, 31, 20221–20236. [Google Scholar] [CrossRef]
- Wang, L.; Sun, C.; Fu, Y.; Kim, M.H.; Huang, H. Hyperspectral image reconstruction using a deep spatial-spectral prior. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8032–8041. [Google Scholar]
- Fubara, B.J.; Sedky, M.; Dyke, D. RGB to spectral reconstruction via learned basis functions and weights. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 480–481. [Google Scholar]
- Zhang, L.; Lang, Z.; Wang, P.; Wei, W.; Liao, S.; Shao, L.; Zhang, Y. Pixel-aware deep function-mixture network for spectral super-resolution. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 12821–12828. [Google Scholar]
- Zhang, T.; Liang, Z.; Fu, Y. Joint spatial-spectral pattern optimization and hyperspectral image reconstruction. IEEE J. Sel. Top. Signal Process. 2022, 16, 636–648. [Google Scholar] [CrossRef]
- Xiong, Z.; Shi, Z.; Li, H.; Wang, L.; Liu, D.; Wu, F. HSCNN: CNN-based hyperspectral image recovery from spectrally undersampled projections. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017; pp. 518–525. [Google Scholar]
- Li, J.; Cui, R.; Li, B.; Song, R.; Li, Y.; Dai, Y.; Du, Q. Hyperspectral image super-resolution by band attention through adversarial learning. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4304–4318. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Zhu, Z.; Liu, H.; Hou, J.; Zeng, H.; Zhang, Q. Semantic-embedded unsupervised spectral reconstruction from single RGB images in the wild. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 2279–2288. [Google Scholar]
- Zhao, Y.; Po, L.M.; Lin, T.; Yan, Q.; Liu, W.; Xian, P. HSGAN: Hyperspectral reconstruction from rgb images with generative adversarial network. IEEE Trans. Neural Netw. Learn. Syst. 2023. early access. [Google Scholar] [CrossRef]
- Chen, C.F.R.; Fan, Q.; Panda, R. Crossvit: Cross-attention multi-scale vision transformer for image classification. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 357–366. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Zhao, E.; Qu, N.; Wang, Y.; Gao, C. Spectral Reconstruction from Thermal Infrared Multispectral Image Using Convolutional Neural Network and Transformer Joint Network. Remote Sens. 2024, 16, 1284. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.R. Distributed estimation fusion with unavailable cross-correlation. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 259–278. [Google Scholar] [CrossRef]
- Kenney, C.S.; Zuliani, M.; Manjunath, B. An axiomatic approach to corner detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 191–197. [Google Scholar]
- Oppermann, M. Triangulation—A methodological discussion. Int. J. Tour. Res. 2000, 2, 141–145. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H.; Shao, L. Learning enriched features for real image restoration and enhancement. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XXV 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 492–511. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H.; Shao, L. Multi-stage progressive image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14821–14831. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H. Restormer: Efficient transformer for high-resolution image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5728–5739. [Google Scholar]
- Chen, L.; Lu, X.; Zhang, J.; Chu, X.; Chen, C. Hinet: Half instance normalization network for image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 182–192. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Mu Lee, K. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 136–144. [Google Scholar]
- Shi, Z.; Chen, C.; Xiong, Z.; Liu, D.; Wu, F. Hscnn+: Advanced cnn-based hyperspectral recovery from rgb images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 939–947. [Google Scholar]
- Zhao, Y.; Po, L.M.; Yan, Q.; Liu, W.; Lin, T. Hierarchical regression network for spectral reconstruction from RGB images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 422–423. [Google Scholar]
- Hu, X.; Cai, Y.; Lin, J.; Wang, H.; Yuan, X.; Zhang, Y.; Timofte, R.; Van Gool, L. Hdnet: High-resolution dual-domain learning for spectral compressive imaging. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 17542–17551. [Google Scholar]
- Li, J.; Wu, C.; Song, R.; Li, Y.; Liu, F. Adaptive weighted attention network with camera spectral sensitivity prior for spectral reconstruction from RGB images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 462–463. [Google Scholar]
- Shen, Y.; Yan, Z.; Yang, Y.; Tang, W.; Sun, J.; Zhang, Y. Application of UAV-Borne Visible-Infared Pushbroom Imaging Hyperspectral for Rice Yield Estimation Using Feature Selection Regression Methods. Sustainability 2024, 16, 632. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).