Hyperspectral Estimation of Chlorophyll Content in Wheat under CO2 Stress Based on Fractional Order Differentiation and Continuous Wavelet Transforms
Abstract
1. Introduction
2. Materials and Methods
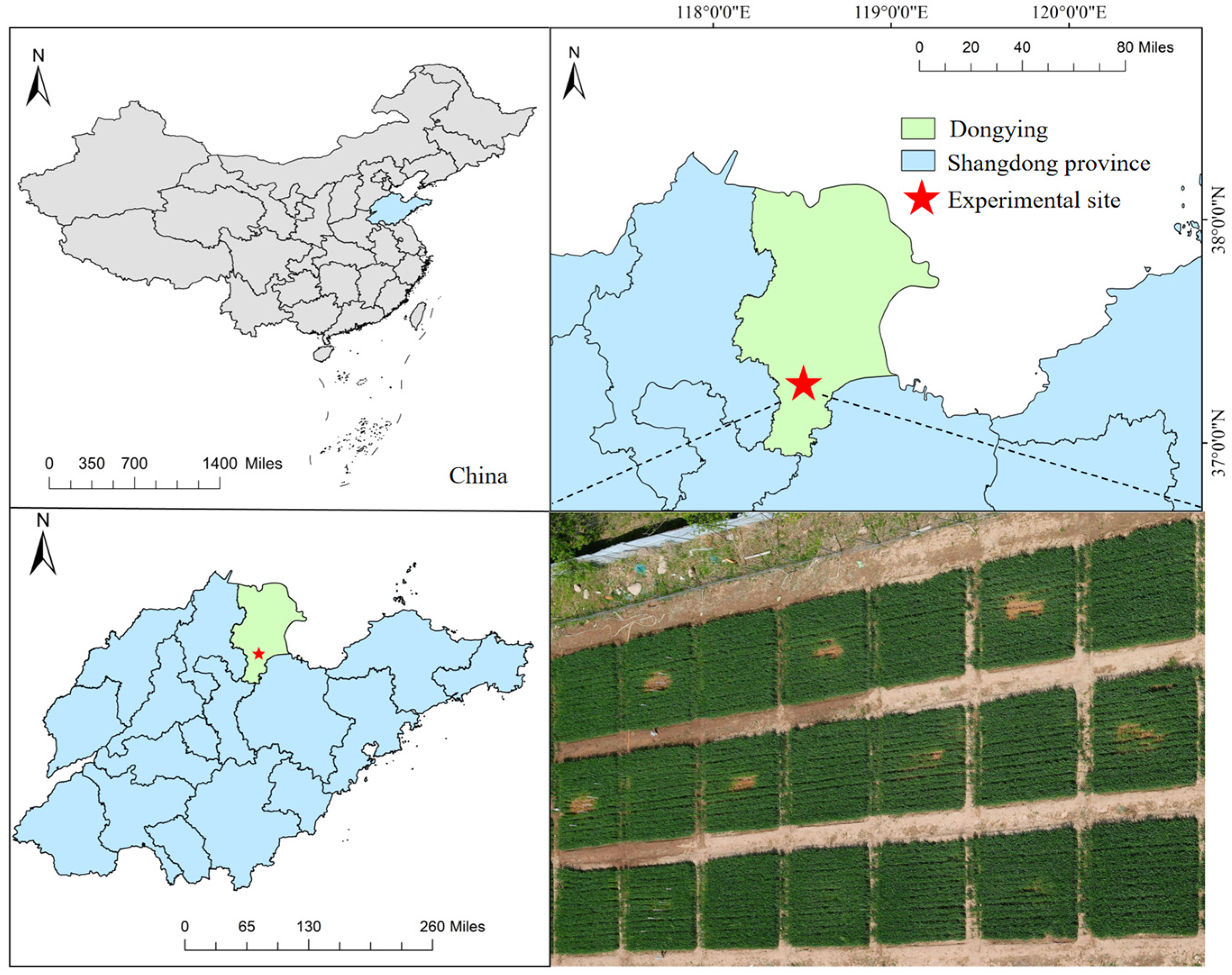
2.1. Study Area
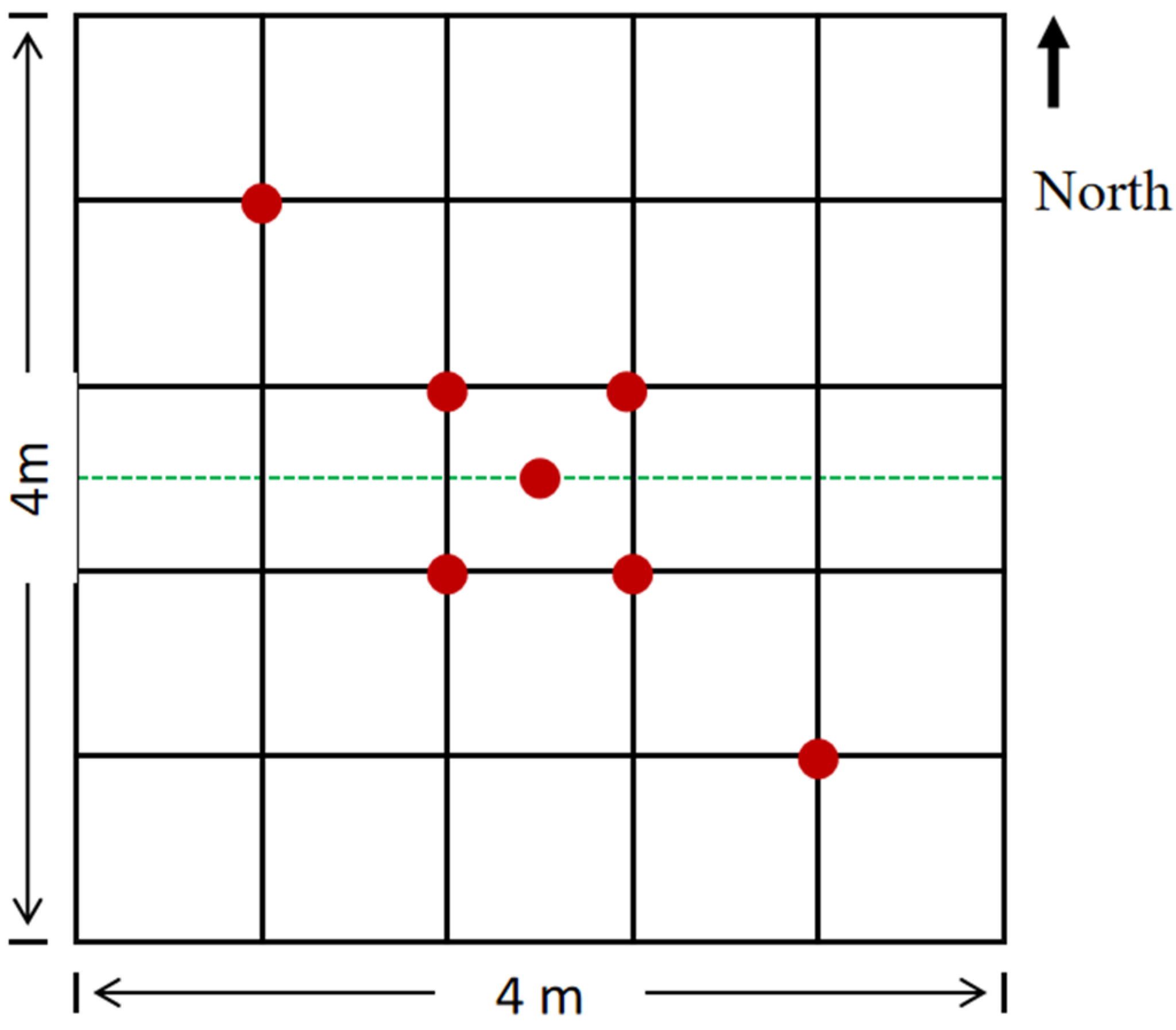
2.2. Experimental Field Design
2.3. Data Acquisition
2.3.1. Soil Gas Concentration Measurement
2.3.2. Spectral Measurement
2.3.3. Measurement of Chlorophyll
2.4. Methodologies
2.4.1. Fractional-Order Differentiation
2.4.2. Continuous Wavelet Transforms
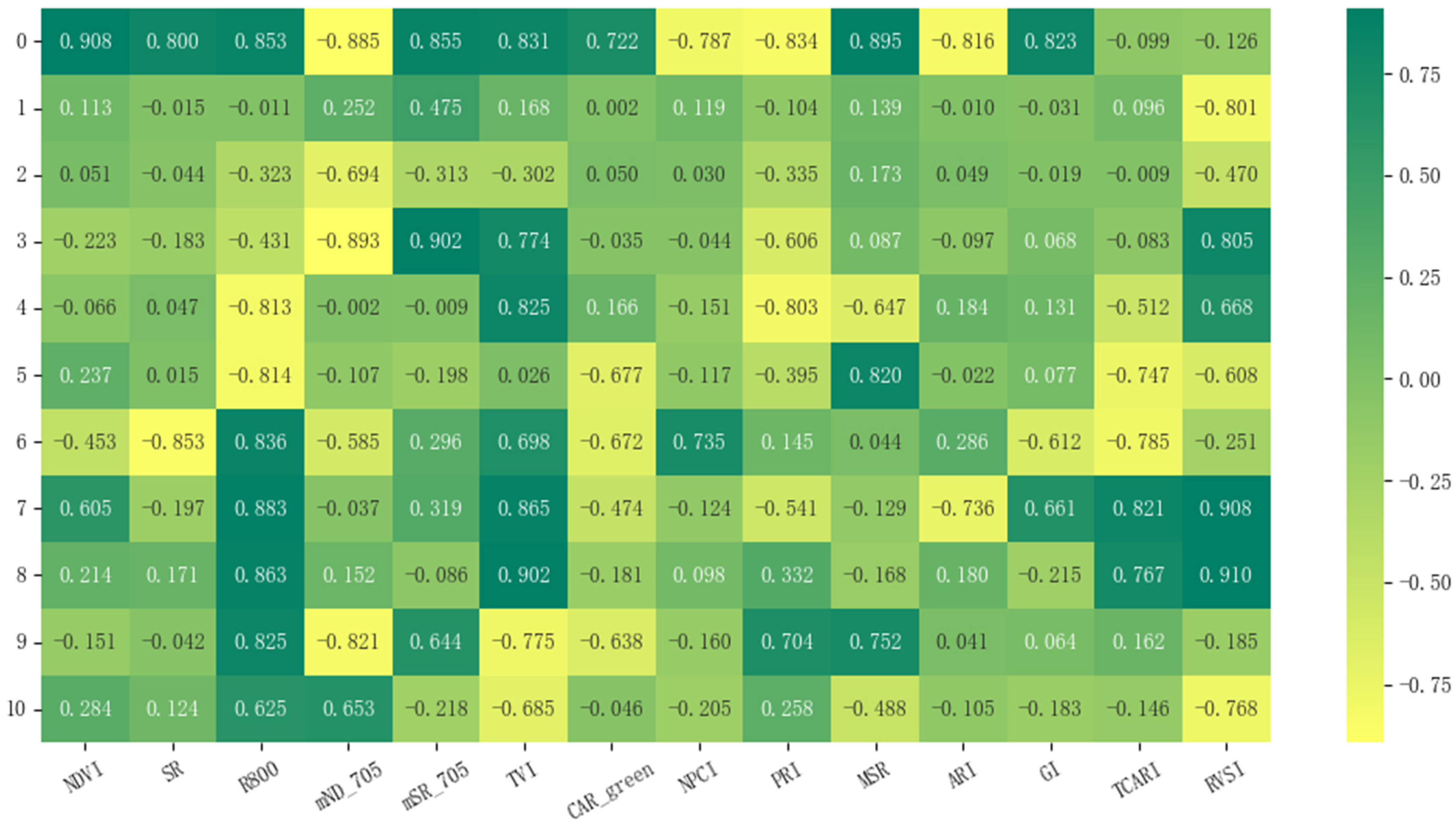
2.5. Constructing Multidimensional Vegetation Spectral Index
2.6. Integrated Estimation Models
2.7. Model Evaluation Methodology
3. Results
3.1. Dynamics of LCC Values in Wheat under CO2 Stress
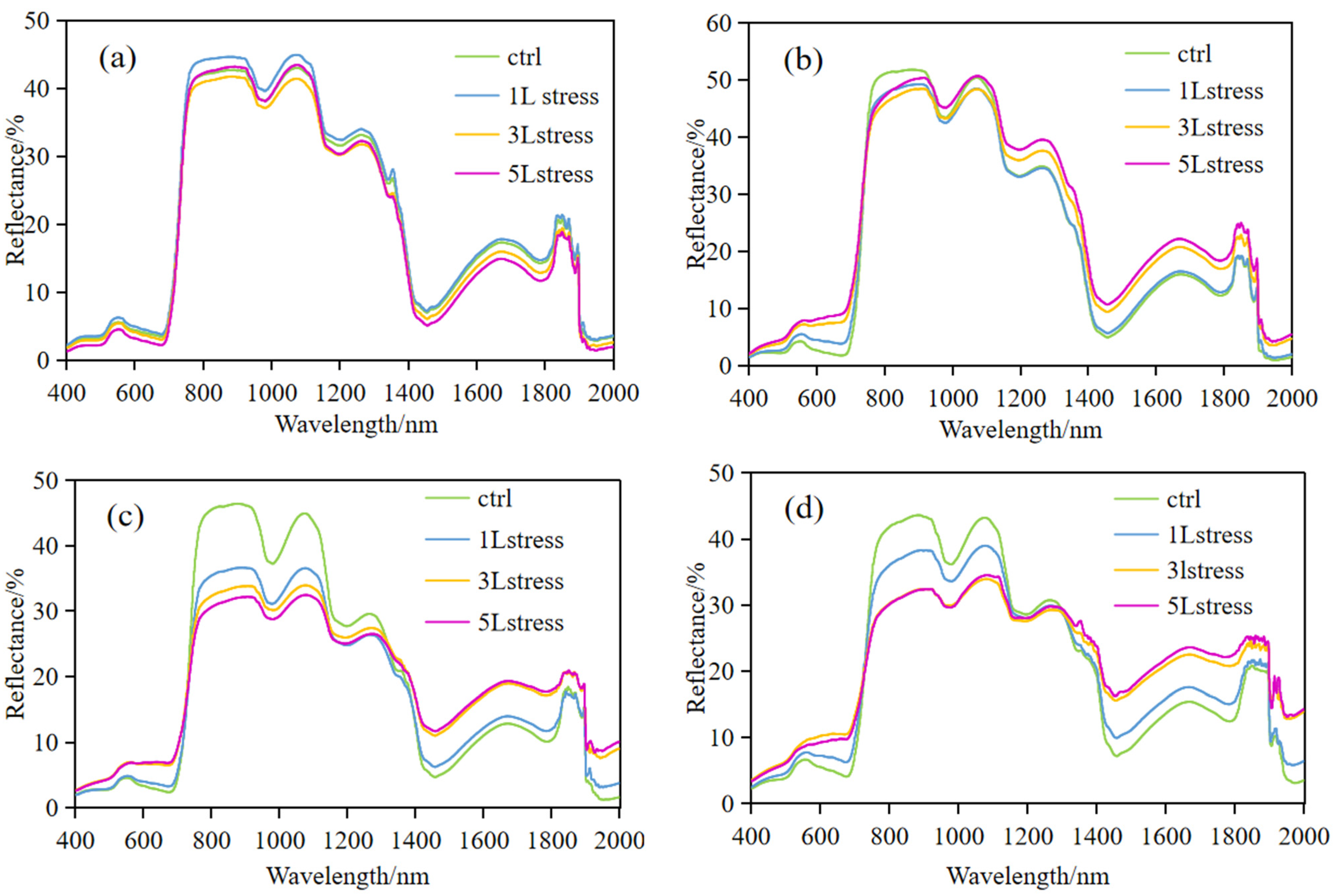
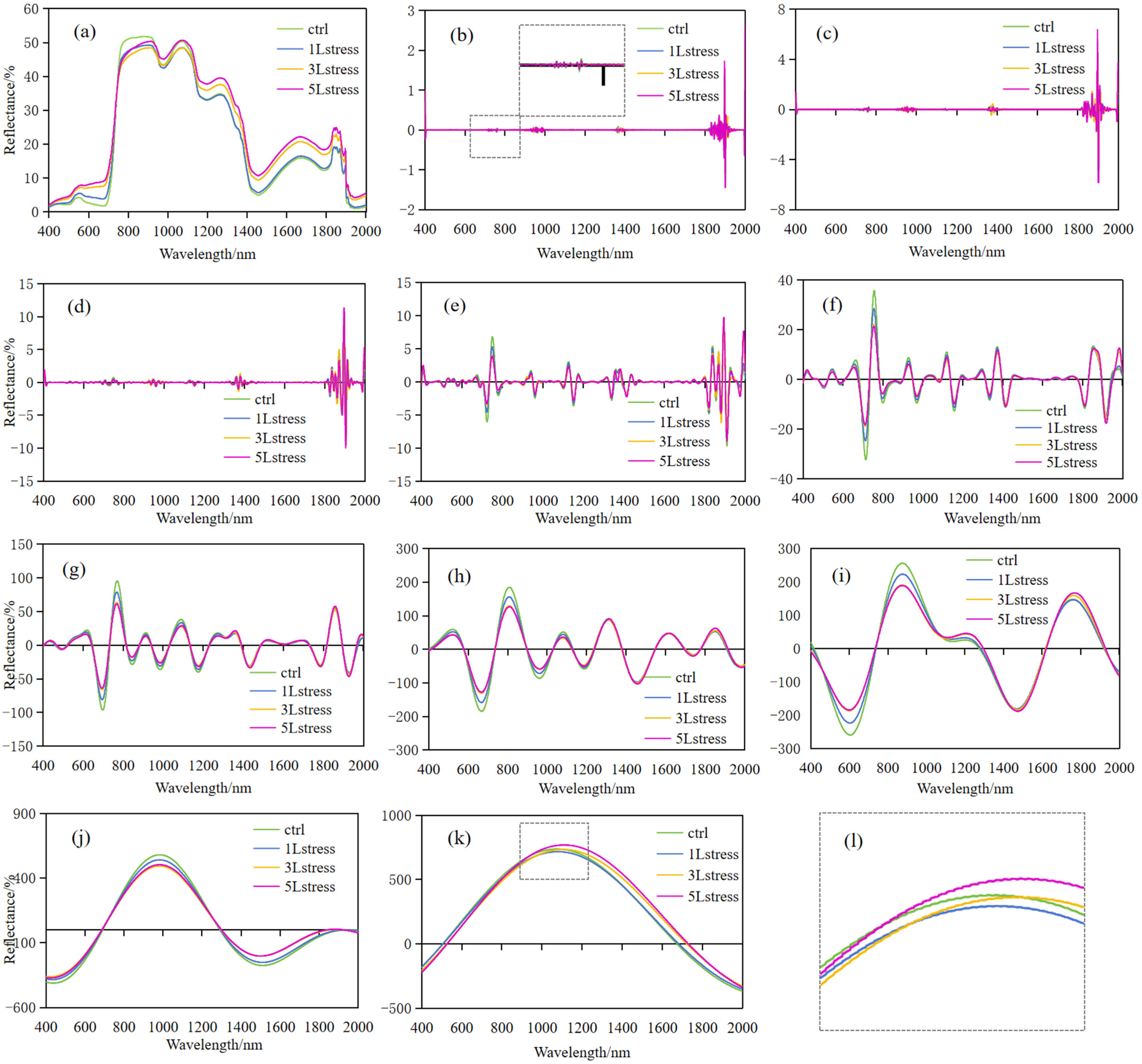
3.2. Dynamics of Reflectance Spectra of Wheat Canopies under CO2 Stress
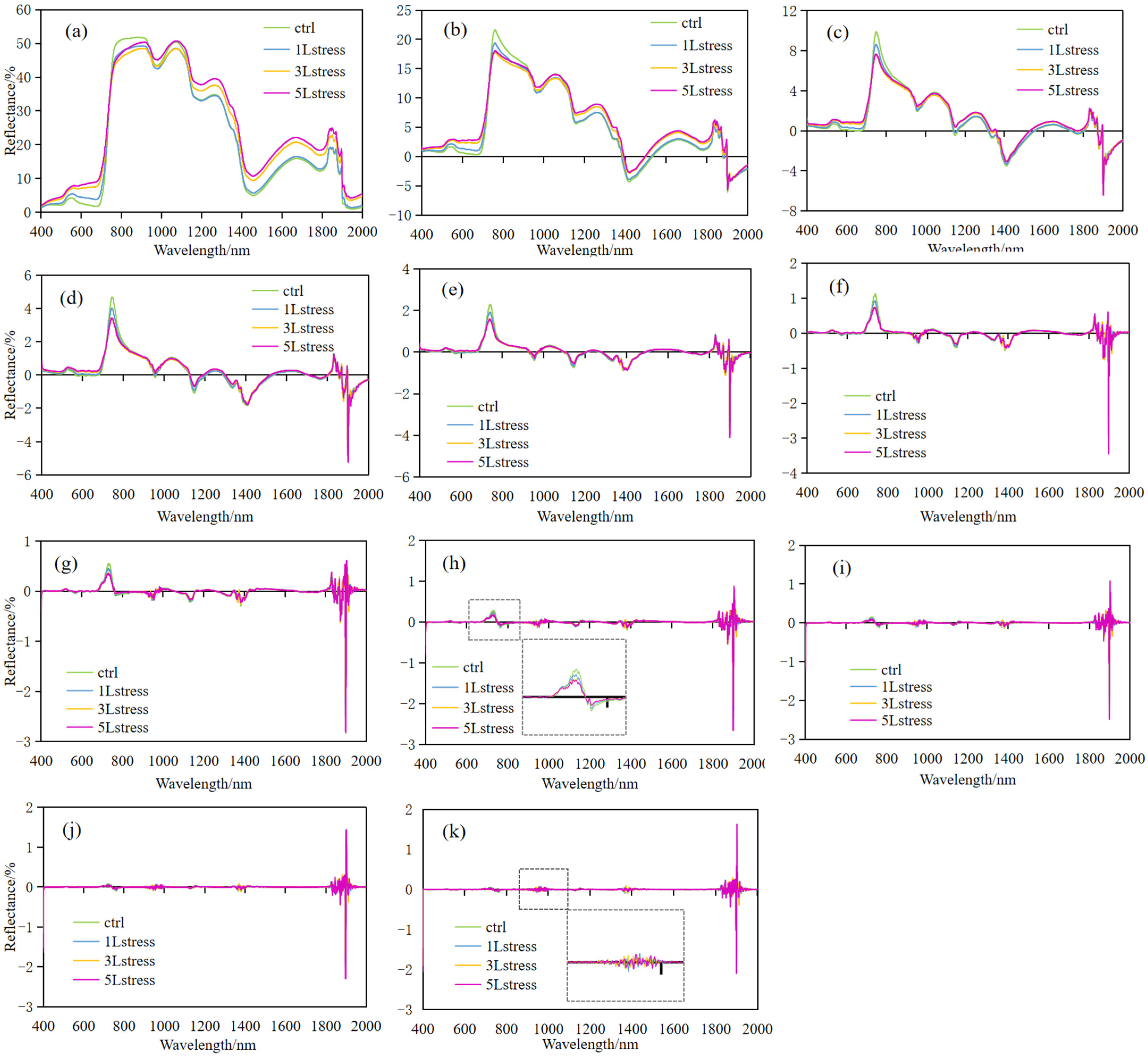
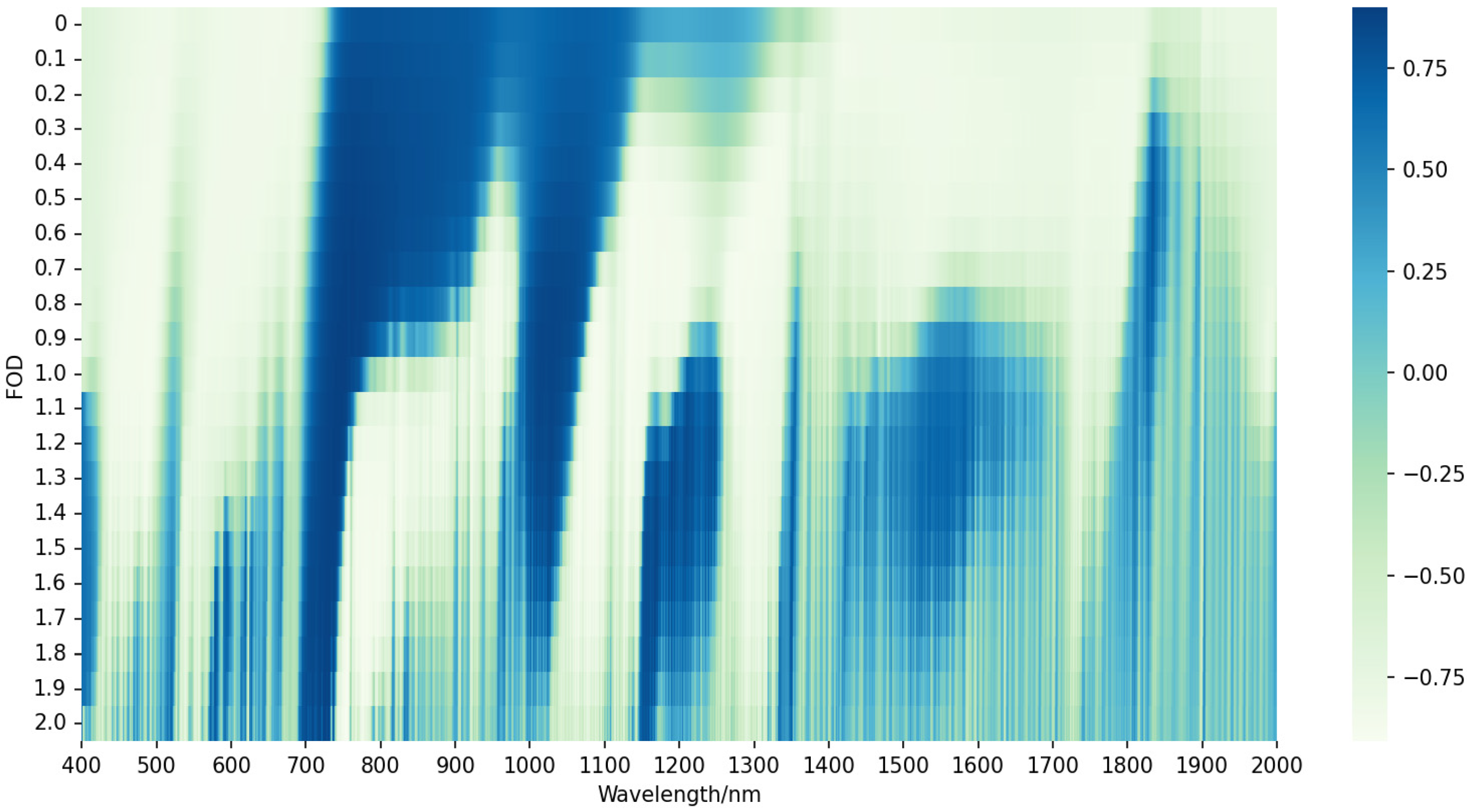
3.3. FOD-Based Analyses
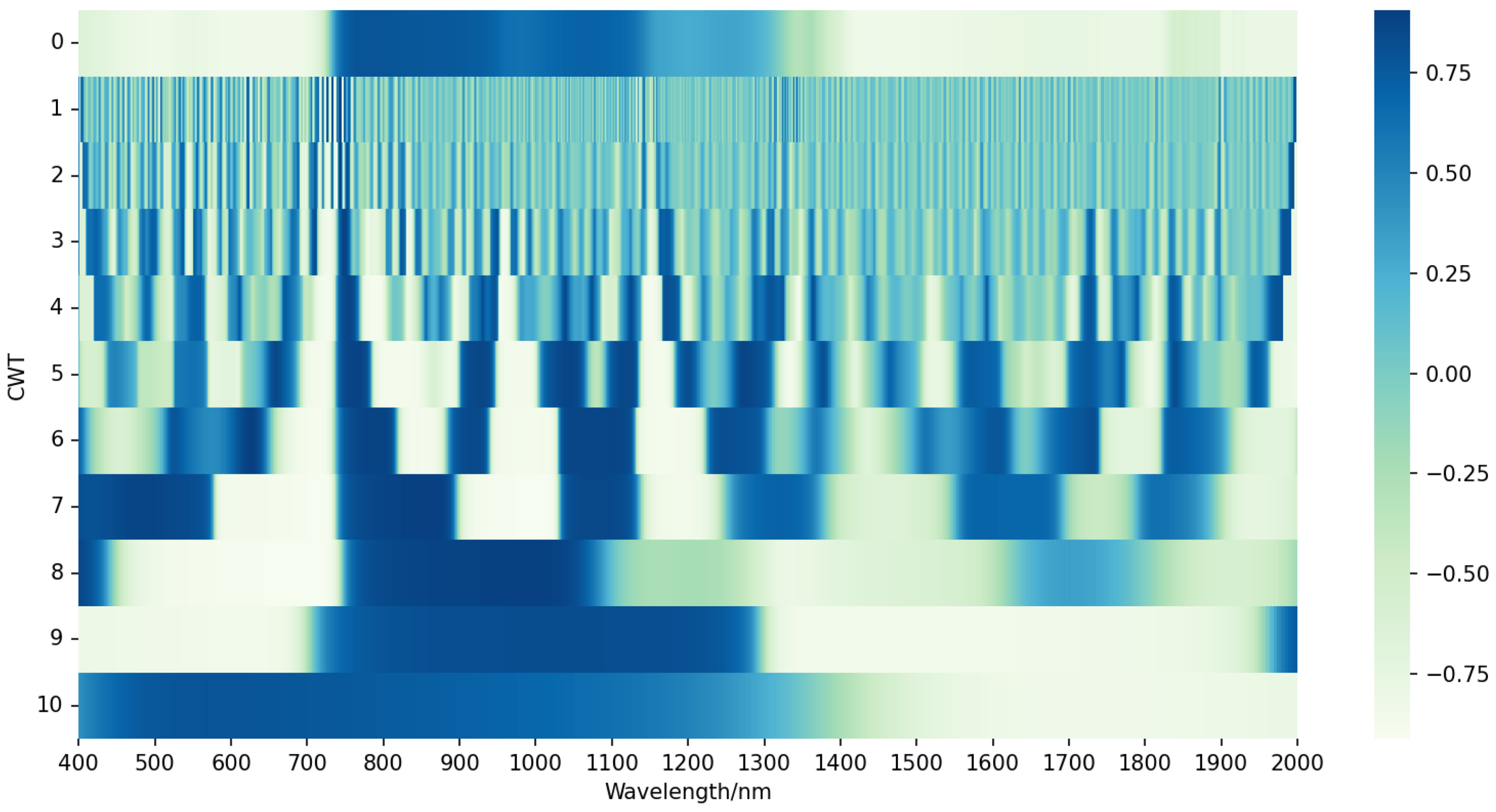
3.4. CWT-Based Analysis
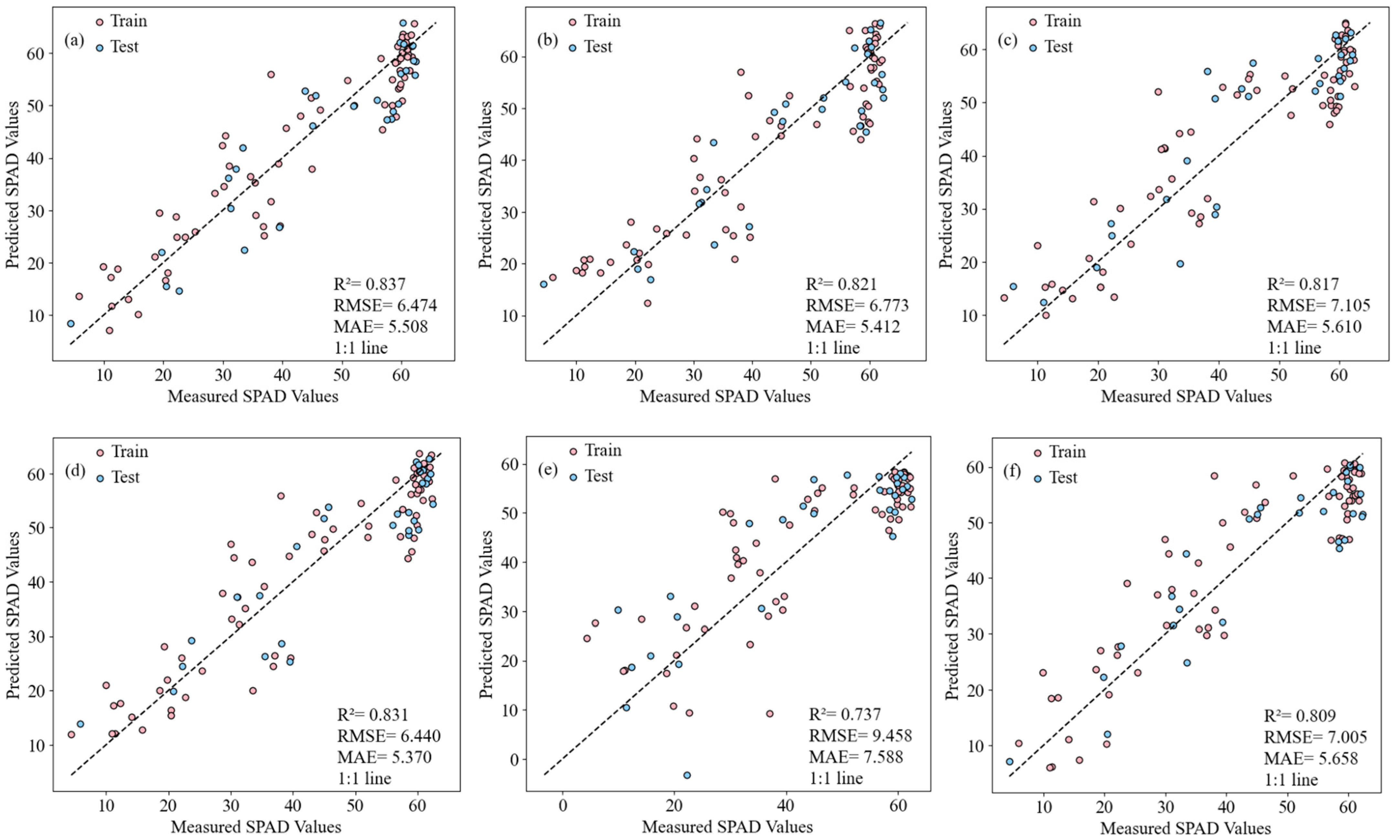
3.5. Comparison of LCC Estimation Based on FOD, CWT, and Raw Spectral Features
3.6. FOD-Based LCC Estimation
3.7. CWT-Based LCC Estimation
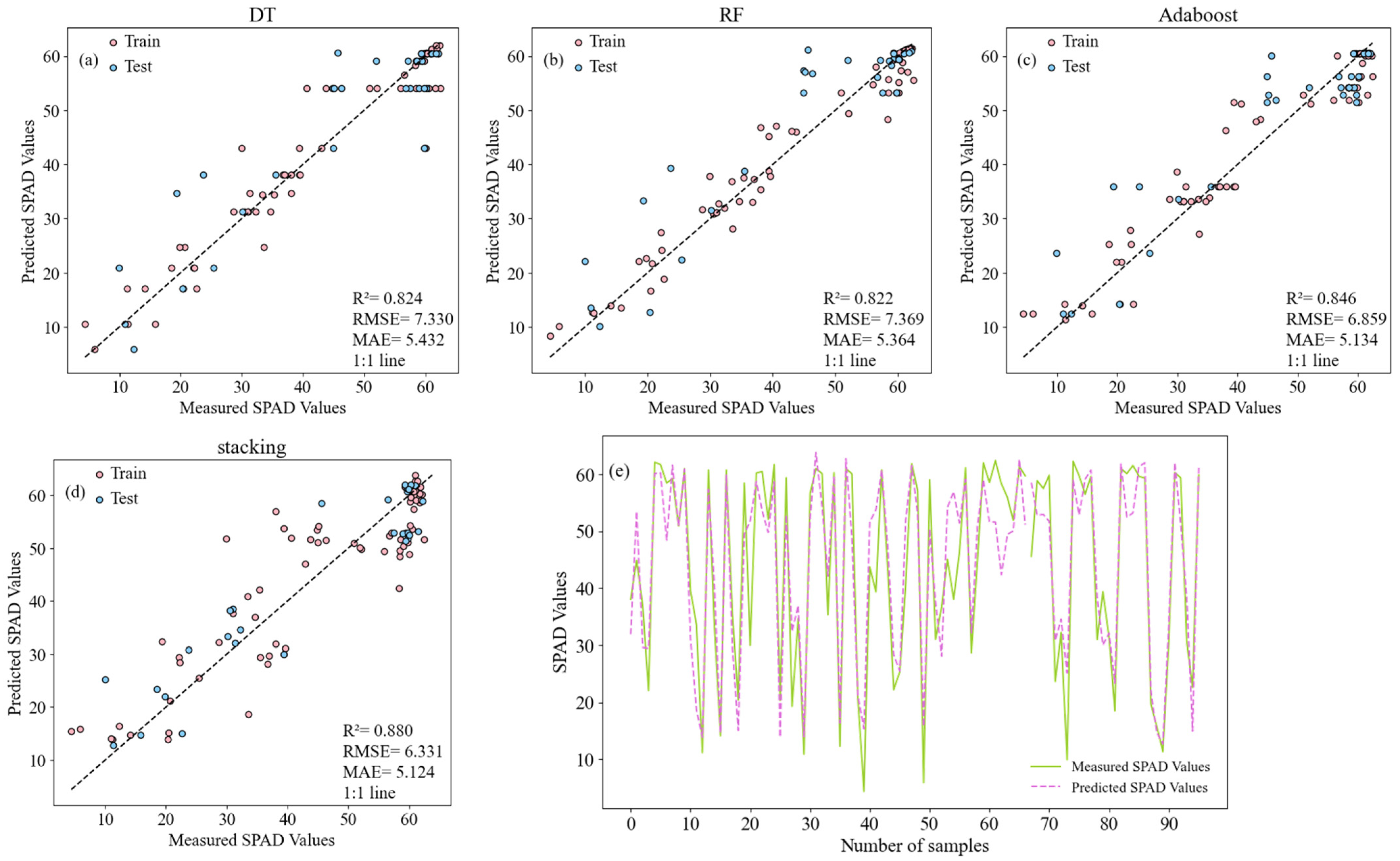
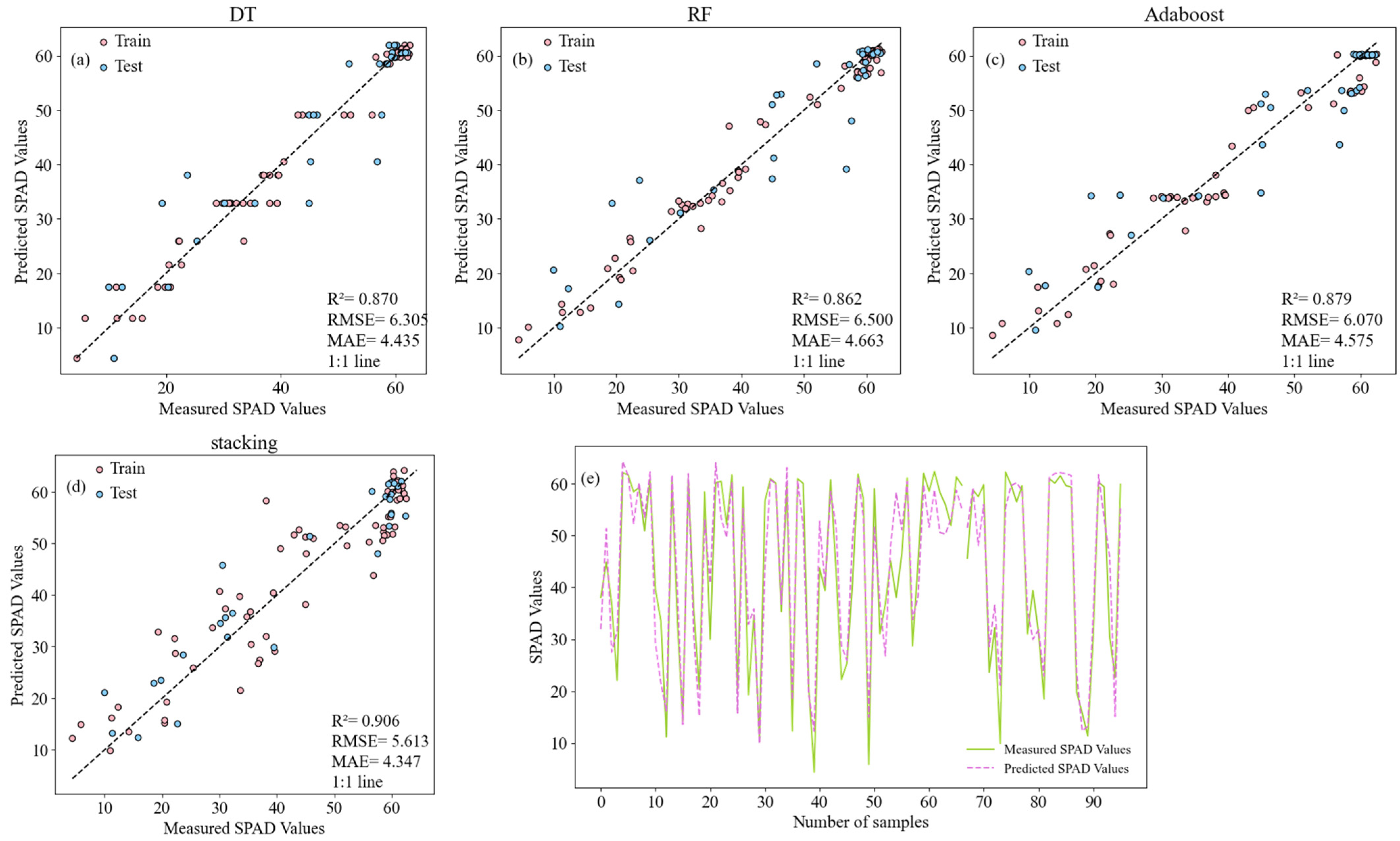
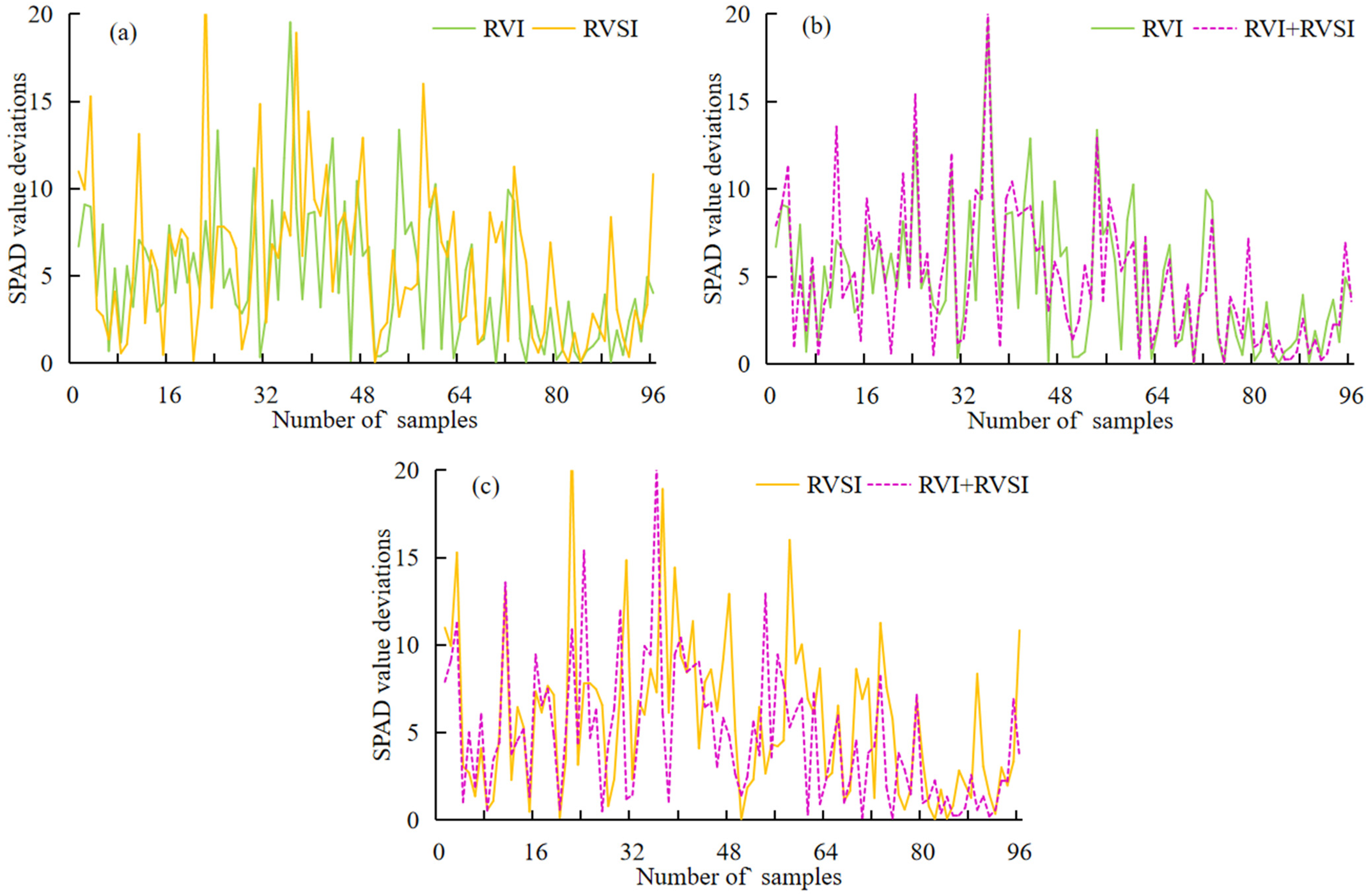
3.8. LCC Estimation Based on the Combination of FOD and CWT
4. Discussion
5. Conclusions
- Under CO2 stress conditions, the hyperspectral features of winter wheat changed significantly, as evidenced by the decrease in the LCC with the enhancement of stress, the enhancement of the reflectance of the green peak of the hyperspectral curve with the red shift, and the blue shift of the red edge, which accurately revealed the impact of CO2 on wheat physiology, and provided the scientific basis and technical support for the monitoring of the impact of large-scale CO2 on wheat yield by using the key spectral features of the band to assist in the precise management of agricultural responses to climate change.
- The effectiveness of the FOD and CWT spectral processing methods in weakening the baseline drift and overlapping peaks of the original spectra and enhancing the correlation between spectra and physiological indicators was also validated under CO2 stress conditions. This implies that these techniques are not only applicable to LCC estimation under normal growth conditions, but also can effectively support the accurate estimation of LCC under CO2 stress.
- The FOD-based dual-band combination is superior to the single band and can significantly improve the prediction of the LCC. The 1.2-order derivative dual-band RVI (R720, R522) showed excellent prediction ability under CO2 stress conditions (R2 = 0.901, RMSE = 5.798, MAE = 4.683), which realized a high precision estimation of the LCC.
- The application of CWT multi-scale analysis under CO2 stress has also achieved remarkable results. By analyzing the spectral data at different scales, we constructed the RVSI, which can reflect the effects of CO2 stress and achieve a reliable estimation of LCC (R2 = 0.880, RMSE = 6.331, and MAE = 5.124). The combination of sensitive spectral features based on FOD and CWT techniques enhances the estimation accuracy of LCC estimation under the stacking model (R2 = 0.906, RMSE = 5.613, MAE = 4.347).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Al-Traboulsi, M.; Sjögersten, S.; Colls, J.; Steven, M.; Craigon, J.; Black, C. Potential Impact of CO2 Leakage from Carbon Capture and Storage (CCS) Systems on Growth and Yield in Spring Field Bean. Environ. Exp. Bot. 2012, 80, 43–53. [Google Scholar] [CrossRef]
- Shang, Y.; Chen, X.; Yang, M.; Xing, X.; Jiao, J.; An, G.; Li, X.; Xiong, X. Comprehensive Review on Leakage Characteristics and Diffusion Laws of Carbon Dioxide Pipelines. Energy Fuels 2024, 38, 10456–10493. [Google Scholar] [CrossRef]
- Kim, Y.J.; He, W.; Ko, D.; Chung, H.; Yoo, G. Increased NO2 Emission by Inhibited Plant Growth in the CO2 Leaked Soil Environment: Simulation of CO2 Leakage from Carbon Capture and Storage (CCS) Site. Sci. Total Environ. 2017, 607–608, 1278–1285. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Ma, X.; Wu, Y.; Li, Y. Enhancement of Farmland Greenhouse Gas Emissions from Leakage of Stored CO2: Simulation of Leaked CO2 from CCS. Sci. Total Environ. 2015, 518–519, 78–85. [Google Scholar] [CrossRef]
- Zhou, X.; Lakkaraju, V.R.; Apple, M.; Dobeck, L.M.; Gullickson, K.; Shaw, J.A.; Cunningham, A.B.; Wielopolski, L.; Spangler, L.H. Experimental Observation of Signature Changes in Bulk Soil Electrical Conductivity in Response to Engineered Surface CO2 Leakage. Int. J. Greenh. Gas Control 2012, 7, 20–29. [Google Scholar] [CrossRef]
- Feitz, A.; Jenkins, C.; Schacht, U.; McGrath, A.; Berko, H.; Schroder, I.; Noble, R.; Kuske, T.; George, S.; Heath, C.; et al. An Assessment of near Surface CO2 Leakage Detection Techniques under Australian Conditions. Energy Procedia 2014, 63, 3891–3906. [Google Scholar] [CrossRef]
- Wang, P.; Xu, Y.; Song, S.; Shen, Y.; Li, S. Effect of Doubled Atmospheric CO2 and Nitrogen Application on Photosynthetic Rate and Chlorophyll Fluorescence Character of Winter Wheat. Acta Bot. Boreal-Occident Sin 2011, 31, 0144–0151. [Google Scholar]
- Xu, Y.; Jing, Y.; E, Y.; Ma, Y.; Li, S. Effect of Elevated Atmospheric CO2 Concentration on Leaf Characteristic and Evapotranspiration in Winter Wheat. Sci. Technol. Eng. 2014, 14, 17–22+55. [Google Scholar]
- Sakai, H.; Hasegawa, T.; Kobayashi, K. Enhancement of Rice Canopy Carbon Gain by Elevated CO2 is Sensitive to Growth Stage and Leaf Nitrogen Concentration. New Phytol. 2006, 170, 321–332. [Google Scholar] [CrossRef]
- Liu, C.; Hu, Z.; Islam, A.R.M.T.; Kong, R.; Yu, L.; Wang, Y.; Chen, S.; Zhang, X. Hyperspectral Characteristics and Inversion Model Estimation of Winter Wheat under Different Elevated CO2 Concentrations. Int. J. Remote Sens. 2021, 42, 1035–1053. [Google Scholar] [CrossRef]
- Wu, R.; Fan, Y.; Zhang, L.; Yuan, D.; Gao, G. Wheat Yield Estimation Study Using Hyperspectral Vegetation Indices. Appl. Sci. 2024, 14, 4245. [Google Scholar] [CrossRef]
- Xiao, B.; Li, S.; Dou, S.; He, H.; Fu, B.; Zhang, T.; Sun, W.; Yang, Y.; Xiong, Y.; Shi, J.; et al. Comparison of Leaf Chlorophyll Content Retrieval Performance of Citrus Using FOD and CWT Methods with Field-Based Full-Spectrum Hyperspectral Reflectance Data. Comput. Electron. Agric. 2024, 217, 108559. [Google Scholar] [CrossRef]
- Gregory, A.C. Ratios of Leaf Reflectances in Narrow Wavebands as Indicators of Plant Stress. Int. J. Remote Sens. 1994, 15, 697–703. [Google Scholar] [CrossRef]
- Carter, G.A. Reflectance Wavebands and Indices for Remote Estimation of Photosynthesis and Stomatal Conductance in Pine Canopies. Remote Sens. Environ. 1998, 63, 61–72. [Google Scholar] [CrossRef]
- Jiang, J.; Steven, M.D.; He, R.; Chen, Y.; Du, P.; Guo, H. Identifying the Spectral Responses of Several Plant Species under CO2 Leakage and Waterlogging Stresses2. Int. J. Greenh. Gas Control 2015, 37, 1–11. [Google Scholar] [CrossRef]
- Kong, Y.; Liu, Y.; Geng, J.; Huang, Z. Pixel-Level Assessment Model of Contamination Conditions of Composite Insulators Based on Hyperspectral Imaging Technology and a Semi-Supervised Ladder Network. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 326–335. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, F.; Gong, X.; Johnson, V. New Methods for Improving the Remote Sensing Estimation of Soil Organic Matter Content (SOMC) in the Ebinur Lake Wetland National Nature Reserve (ELWNNR) in Northwest China. Remote Sens. Environ. 2018, 218, 104–108. [Google Scholar] [CrossRef]
- Jiang, G.; Zhou, K.; Wang, J.; Sun, G.; Cui, S.; Chen, T.; Zhou, S.; Bai, Y.; Chen, X. Estimation of Rock Copper Content Based on Fractional-Order Derivative and Visible Near-Infrared–Shortwave Infrared Spectroscopy. Ore Geol. Rev. 2022, 150, 105092. [Google Scholar] [CrossRef]
- Li, L.; Geng, S.; Lin, D.; Su, G.; Zhang, Y.; Chang, L.; Ji, Y.; Wang, Y.; Wang, L. Accurate Modeling of Vertical Leaf Nitrogen Distribution in Summer Maize Using in Situ Leaf Spectroscopy via CWT and PLS-Based Approaches. Eur. J. Agron. 2022, 140, 126607. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, T.; Gu, X.; Yan, K.; Cong, W.; Chen, D.; Zhao, C. UAV-Borne Hyperspectral Estimation of Nitrogen Content in Tobacco Leaves Based on Ensemble Learning Methods. Comput. Electron. Agric. 2013, 211, 108008. [Google Scholar] [CrossRef]
- Zhang, L.; Yuan, D.; Fan, Y.; Yang, R. Hyperspectral Characteristics and SPAD Estimation of Wheat Leaves under CO2 Microleakage Stress. Sensors 2024, 24, 4776. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Jiang, J.; Li, K.; Xiong, K.; Du, Y.; Wang, X. Identificating Vegetation Stress under Natural Gas Micro-Leakage Based on Leaf Scale Temporal Hyperspectrum. Int. J. Remote Sens. 2023, 44, 6825–6844. [Google Scholar] [CrossRef]
- Abulaiti, Y.; Sawut, M.; Maimaitiaili, B.; Chunyue, M. A Possible Fractional Order Derivative and Optimized Spectral Indices for Assessing Total Nitrogen Content in Cotton. Comput. Electron. Agric. 2020, 171, 105275. [Google Scholar] [CrossRef]
- Hasan, U.; Jia, K.; Wang, L.; Wang, C.; Shen, Z.; Yu, W.; Sun, Y.; Jiang, H.; Zhang, Z.; Guo, J.; et al. Retrieval of Leaf Chlorophyll Contents (LCCs) in Litchi Based on Fractional Order Derivatives and VCPA-GA-ML Algorithms. Plants 2023, 12, 501. [Google Scholar] [CrossRef]
- Li, C.; Li, X.; Meng, X.; Xiao, Z.; Wu, X.; Wang, X.; Ren, L.; Li, Y.; Zhao, C.; Yang, C. Hyperspectral Estimation of Nitrogen Content in Wheat Based on Fractional Difference and Continuous Wavelet Transform. Agriculture 2023, 13, 1017. [Google Scholar] [CrossRef]
- Gao, G.; Zhang, L.; Wu, L.; Yuan, D. Estimation of Chlorophyll Content in Wheat Based on Optimal Spectral Index. Appl. Sci. 2024, 14, 703. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and Photographic Infrared Linear Combinations for Monitoring Vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of Leaf-Area Index from Quality of Light on the Forest Floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Yang, X.; Zhu, L.; Feng, Z. Hyperspectral characteristics and chlorophyll content estimation of winter wheat under ozone stress. Acta Ecol. Sin. 2023, 43, 3213–3223. [Google Scholar] [CrossRef]
- Sims, D.; Gamon, J. Relationships Between Leaf Pigment Content and Spectral Reflectance Across a Wide Range of Species, Leaf Structures and Developmental Stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing Prediction Power and Stability of Broadband and Hyperspectral Vegetation Indices for Estimation of Green Leaf Area Index and Canopy Chlorophyll Density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Ciganda, V.; Rundquist, D.C.; Arkebauer, T.J. Remote Estimation of Canopy Chlorophyll Content in Crops. Geophys. Res. Lett. 2005, 32, L08403. [Google Scholar] [CrossRef]
- Chen, J.M. Evaluation of Vegetation Indices and a Modified Simple Ratio for Boreal Applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Gitelson, A.; Merzlyak, M.N.; Chivkunova, O.B. Optical properties and nondestructive estimation of anthocyanin content in plant leaves. Photochem. Photobiol. 2001, 74, 38–45. [Google Scholar] [CrossRef] [PubMed]
- Merzlyak, M.N.; Gitelson, A.A.; Chivkunova, O.B.; Rakitin, V.Y.U. Non-Destructive Optical Detection of Pigment Changes during Leaf Senescence and Fruit Ripening. Physiol. Plant. 1999, 106, 135–141. [Google Scholar] [CrossRef]
- Devadas, R.; Lamb, D.; Simpfendorfer, S. Evaluating ten spectral vegetation indices for identifying rust infection in individual wheat leaves. Precis. Agric. 2009, 10, 459–470. [Google Scholar] [CrossRef]
- Ya, S.M.; Steven, M.; Foody, G. Remote sensing or barley stressed with CO2 and herbicide. Environ. Sci. Agric. Food Sci. 2011, 551–563. Available online: https://api.semanticscholar.org/CorpusID:131132759 (accessed on 19 August 2024).
- Keith, C.J.; Repasky, K.S.; Lawrence, R.L.; Jay, S.C.; Carlsten, J.L. Monitoring Effects of a Controlled Subsurface Carbon Dioxide Release on Vegetation Using a Hyperspectral Imager. Int. J. Greenh. Gas Control 2009, 3, 626–632. [Google Scholar] [CrossRef]
- Chen, Y.-H.; Jiang, J.-B.; Steven, M.; Gong, A.; Li, Y. Research on the Spectral Feature and Identification of the Surface Vegetation Stressed by Stored CO2 Underground Leakage. Guang Pu Xue Yu Guang Pu Fen Xi = Guang Pu 2012, 32, 1882–1885. [Google Scholar] [CrossRef]
- Gao, S.; Yan, K.; Liu, J.; Pu, J.; Zou, D.; Qi, J.; Mu, X.; Yan, G. Assessment of Remote-Sensed Vegetation Indices for Estimating Forest Chlorophyll Concentration. Ecol. Indic. 2024, 162, 112001. [Google Scholar] [CrossRef]
- Noomen, M.F.; Skidmore, A.K. The Effects of High Soil CO2 Concentrations on Leaf Reflectance of Maize Plants. Int. J. Remote Sens. 2009, 30, 481–497. [Google Scholar] [CrossRef]
- Vodnik, D.; Kastelec, D.; Pfanz, H.; Maček, I.; Turk, B. Small-Scale Spatial Variation in Soil CO2 Concentration in a Natural Carbon Dioxide Spring and Some Related Plant Responses. Geoderma 2006, 133, 309–319. [Google Scholar] [CrossRef]
- Gitelson, A.; Merzlyak, M.N. Spectral Reflectance Changes Associated with Autumn Senescence of Aesculus hippocastanum L. and Acer platanoides L. Leaves. Spectral Features and Relation to Chlorophyll Estimation. J. Plant Physiol. 1994, 143, 286–292. [Google Scholar] [CrossRef]
- Zhou, P.F.; Zhou, T.; Liu, X. Estimation of soil organic carbon and its uncertainty in Qinghai Province. Prog. Geogr. 2022, 41, 2327–2341. [Google Scholar] [CrossRef]



| Vegetation Indexes | Formulas | References |
|---|---|---|
| Normalized difference vegetation index (NDVI) | (R750 − R550)/(R750 + R550) | [27] |
| Simple Ratio (SR) | R800/R680 | [28] |
| Color content index (R800) | R800 − R550 | [29] |
| Modified normalized difference (mND 705) | (R700 − R705)/(R700 + R705 – 2 × R445) | [30] |
| Modified simple ratio (mSR_705) | (R750 − R445)/(R705 + R445) | [30] |
| Transformed Vegetation Index (TVl) | 0.5 × (120 × (R750 − R550)) – 200 × (R670 − R550) | [31] |
| Green carotenoid index (CAR_green) | (1/R510 − 1/R550) × R770 | [32] |
| Normalized chlorophyll ratio index (NPCI) | (R680 − R630)/(R680 + R630) | [33] |
| Photochemical vegetation index (PRI) | (R570 − R531)/(R570 + R531) | [29] |
| Improved odds index (MSR) | (R800/R670 − 1)/(R800/R670 + 1) | [31] |
| Anthocyanin reflectance index (ARI) | 1/R550 − 1/R700 | [34] |
| Greenness index (GI) | R554/R667 | [29] |
| Corrective chlorophyll absorption odds Index (TCARI) | 3 × (R700 − R675) − 0.2 × (R700 − R500) × R700/R670 | [35] |
| Red-edged vegetation stress index (RVSI) | (R712 − R670)/2 − R732 | [36] |
| FOD | Single Band | R | NDVI | R | RVI | R | DVI | R |
|---|---|---|---|---|---|---|---|---|
| original | R656 | −0.840 | (R721, R866) | −0.923 | (R726, R851) | −0.923 | (R730, R824) | −0.901 |
| 0.1 | R1420 | −0.845 | (R717, R856) | −0.922 | (R720, R851) | −0.921 | (R723, R856) | −0.904 |
| 0.2 | R764 | 0.842 | (R716, R805) | −0.920 | (R718, R806) | −0.919 | (R716, R868) | −0.906 |
| 0.3 | R763 | 0.859 | (R730, R731) | −0.919 | (R730, R731) | −0.919 | (R699, R1062) | −0.905 |
| 0.4 | R763 | 0.872 | (R730, R731) | −0.919 | (R730, R731) | −0.920 | (R553, R1073) | −0.907 |
| 0.5 | R762 | 0.882 | (R518, R1042) | −0.921 | (R721, R718) | 0.921 | (R553, R1055) | −0.918 |
| 0.6 | R762 | 0.891 | (R515, R1042) | −0.925 | (R721, R717) | 0.921 | (R553, R1042) | −0.921 |
| 0.7 | R762 | 0.898 | (R510, R1041) | −0.928 | (R722, R716) | 0.922 | (R506, R1073) | −0.925 |
| 0.8 | R762 | 0.900 | (R509, R1027) | −0.931 | (R720, R524) | 0.923 | (R500, R1072) | −0.927 |
| 0.9 | R752 | 0.895 | (R508, R1027) | −0.933 | (R720, R523) | 0.927 | (R504, R1028) | −0.924 |
| 1.0 | R749 | 0.894 | (R504, R1026) | −0.932 | (R720, R523) | 0.931 | (R500, R1026) | −0.921 |
| 1.1 | R1133 | −0.893 | (R504, R1026) | −0.930 | (R720, R522) | 0.933 | (R499, R1028) | −0.916 |
| 1.2 | R740 | 0.890 | (R503, R1026) | −0.922 | (R720, R522) | 0.935 | (R490, R1247) | −0.912 |
| 1.3 | R826 | −0.892 | (R500, R1194) | −0.906 | (R720, R522) | 0.935 | (R490, R1190) | −0.913 |
| 1.4 | R826 | −0.889 | (R693, R734) | −0.900 | (R720, R518) | 0.933 | (R490, R1190) | −0.914 |
| 1.5 | R731 | 0.885 | (R1900, R777) | −0.904 | (R719, R518) | 0.932 | (R767, R1351) | −0.910 |
| 1.6 | R756 | −0.887 | (R1900, R777) | −0.906 | (R754, R518) | −0.930 | (R767, R1351) | −0.913 |
| 1.7 | R756 | −0.895 | (R1900, R755) | −0.902 | (R754, R518) | −0.929 | (R767, R1348) | −0.914 |
| 1.8 | R755 | −0.900 | (R1899, R755) | −0.902 | (R753, R518) | −0.922 | (R755, R1168) | −0.913 |
| 1.9 | R755 | −0.906 | (R727, R753) | −0.905 | (R719, R509) | 0.913 | (R755, R1167) | −0.917 |
| 2.0 | R755 | −0.909 | (R727, R753) | −0.913 | (R750, R513) | −0.905 | (R755, R1159) | −0.920 |
| CWT | Origin | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| band | 656 | 737 | 738 | 749 | 788 | 764 | 626 | 720 | 708 | 1388 | 1727 |
| R | −0.840 | −0.878 | −0.873 | 0.890 | −0.891 | 0.884 | 0.901 | −0.909 | −0.911 | −0.857 | −0.837 |
| Original | FOD/CWT | |
|---|---|---|
| Single band | R656 = −0.840 | R755 = −0.909 |
| Dual band | NDVI (R721, R866) = −0.923 | RVI (R720, R522) = 0.935 |
| Vegetation index | NDVI = 0.908 | RVSI = 0.910 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Yuan, D.; Fan, Y.; Yang, R.; Zhao, M.; Jiang, J.; Zhang, W.; Huang, Z.; Ye, G.; Li, W. Hyperspectral Estimation of Chlorophyll Content in Wheat under CO2 Stress Based on Fractional Order Differentiation and Continuous Wavelet Transforms. Remote Sens. 2024, 16, 3341. https://doi.org/10.3390/rs16173341
Zhang L, Yuan D, Fan Y, Yang R, Zhao M, Jiang J, Zhang W, Huang Z, Ye G, Li W. Hyperspectral Estimation of Chlorophyll Content in Wheat under CO2 Stress Based on Fractional Order Differentiation and Continuous Wavelet Transforms. Remote Sensing. 2024; 16(17):3341. https://doi.org/10.3390/rs16173341
Chicago/Turabian StyleZhang, Liuya, Debao Yuan, Yuqing Fan, Renxu Yang, Maochen Zhao, Jinbao Jiang, Wenxuan Zhang, Ziyi Huang, Guidan Ye, and Weining Li. 2024. "Hyperspectral Estimation of Chlorophyll Content in Wheat under CO2 Stress Based on Fractional Order Differentiation and Continuous Wavelet Transforms" Remote Sensing 16, no. 17: 3341. https://doi.org/10.3390/rs16173341
APA StyleZhang, L., Yuan, D., Fan, Y., Yang, R., Zhao, M., Jiang, J., Zhang, W., Huang, Z., Ye, G., & Li, W. (2024). Hyperspectral Estimation of Chlorophyll Content in Wheat under CO2 Stress Based on Fractional Order Differentiation and Continuous Wavelet Transforms. Remote Sensing, 16(17), 3341. https://doi.org/10.3390/rs16173341








