A Space Object Optical Scattering Characteristics Analysis Model Based on Augmented Implicit Neural Representation
Abstract
1. Introduction
- By employing the method of AINRs, an innovative mapping between the geometric observation model and the satellite radiometric model has been established. This linkage facilitates a continuous and differentiable representation of both geometric and photometric transformations of satellites within a three-dimensional space. Additionally, the loss function has been reconstructed to overcome the drawbacks of traditional methods, such as high computational resource consumption, lack of interpretability, and susceptibility to uncertainties.
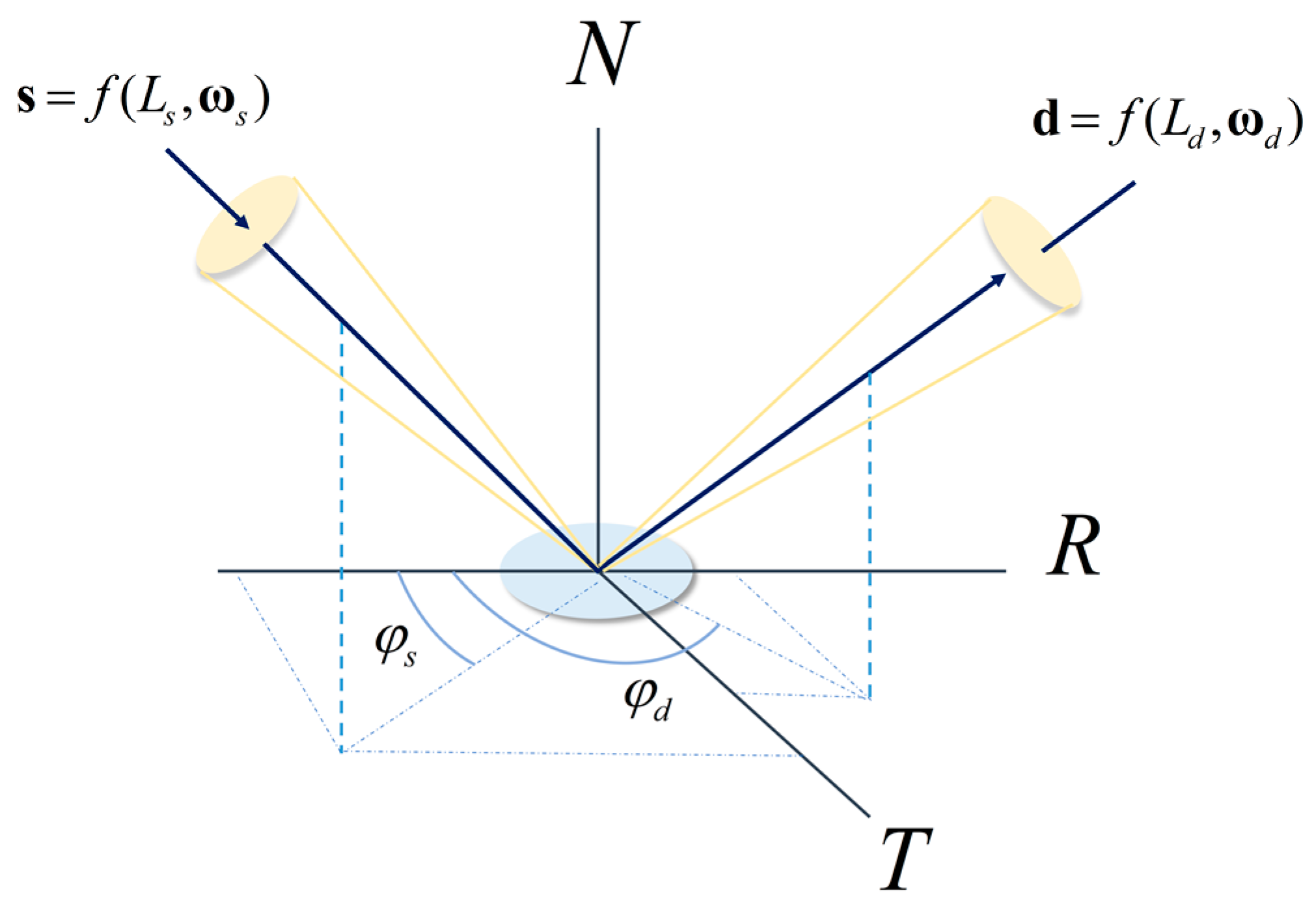
- In response to the uncertainties in boundary values of periodic angular data, which precipitate notable prediction errors such as “jumps” and “overturns”, this paper proposes a vector decomposition representation method based on the RTN coordinate system. This technique dissects the positional relationships observed in geometric measurements into unit vectors across three axes, which not only simplifies the preprocessing of normalized data but also enhances the adaptive learning capabilities of MLP.
- In the domain of experimental design, a comparative analysis was conducted to evaluate the effectiveness of three types of models, which were obtained based on S−net, R−net, and F−net. The model proposed in this discourse adopts a nested function approach meticulously refined with actual measurement data and complemented by data preprocessing and dropout mechanisms within the MLP to avoid the accumulation of errors engendered by atmospheric extinction. Simultaneously, comprehensive simulation data ameliorates the coverage limitations imposed by terrestrial observational constraints, such as Earth occultation, sky–ground shading, and observational field-of-view constraints. This approach enhances the generalization capability of the optical characteristic analysis model to real space data, thereby rendering the prediction results more substantiated and persuasive.
- The structure of this paper is organized as follows: Section 1 focuses on the development of the theories related to the optical scattering properties of space objects and discusses the constraints inherent in related research work. Section 2 describes the definition of spatial geometric observation, the modeling processes associated with AINRs and the structure of the MLP. Section 3 is dedicated to the construction of a pre-training model leveraging transfer learning techniques and delineates both the dataset utilized and the experimental configurations. Section 4 reveals a comprehensive performance evaluation of the experimental results. Finally, the conclusions drawn from this study are summarized in Section 5.
2. Problem Analysis
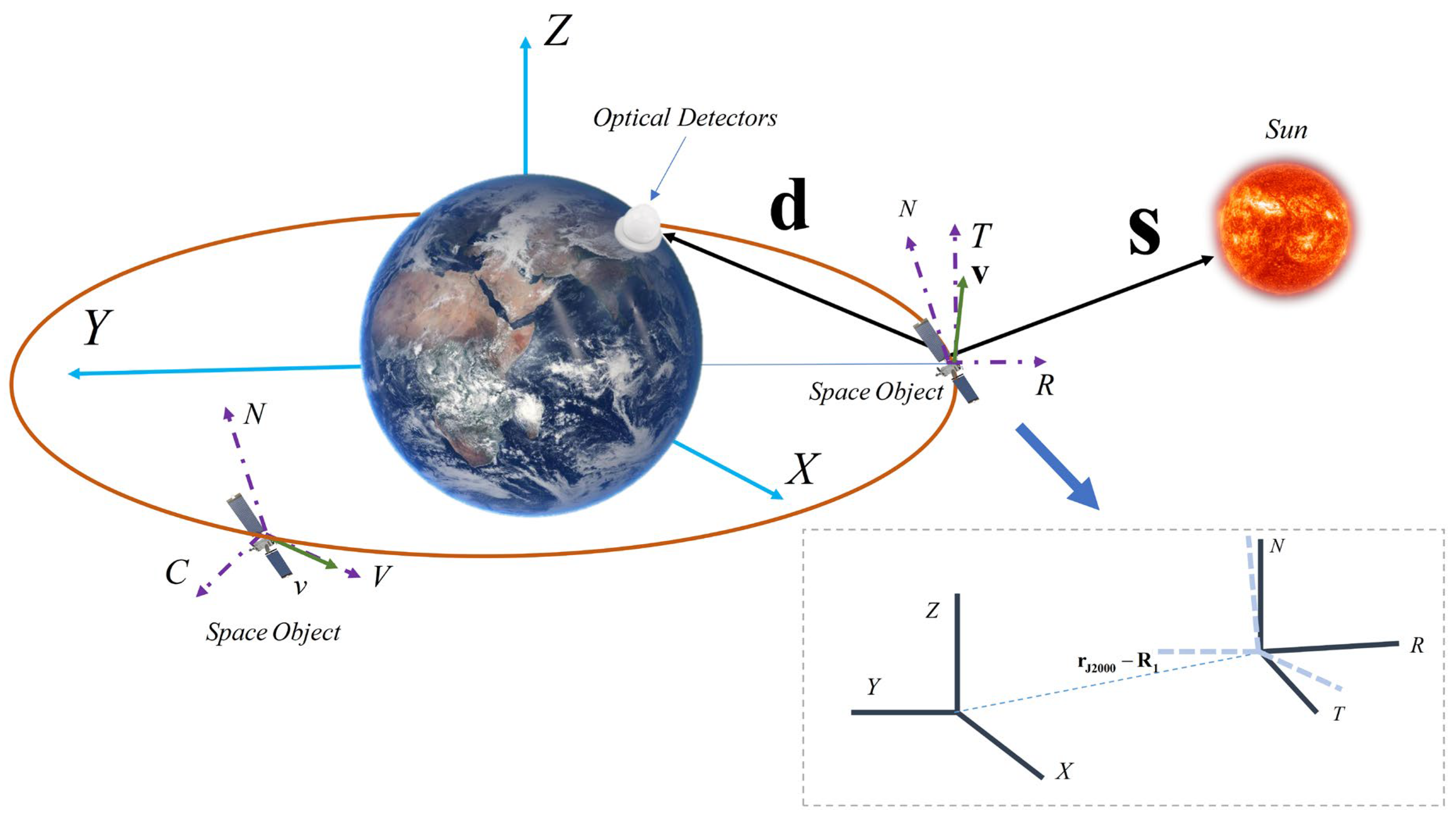
2.1. Geometric Observation Model
2.1.1. Transformation of Orbital Coordinates
- 1.
- VNC coordinate system: The V-axis is aligned with the direction of the velocity vector , the N-axis coincides with the direction of the orbital normal vector (), and the C-axis completes the orthogonal triad ().
- 2.
- RTN coordinate system: R (Radial) is the unit vector pointing from the Earth’s center toward the satellite, N (Normal) is the unit vector normal to the orbital plane, and T (Tangential) lies within the orbital plane, perpendicular to R.
- 3.
- VVLH coordinate system: The Z-axis is oriented along the negative position vector direction (), the Y-axis points along the negative orbital normal direction (), and the X-axis points in the direction of the velocity vector ().
2.1.2. Vector Calculations and Decomposition
- 1.
- The position and velocity of the satellite within the J2000 coordinate system are denoted as position and velocity ;
- 2.
- The position of the Sun is calculated and obtained through a coordinate rotation, with its position in the J2000 coordinate system denoted as ;
- 3.
- The position of the ground station is typically specified in geodetic coordinates, i.e., longitude, latitude, and altitude on the Earth’s surface. The position is converted into the inertial coordinate system by calculations from the geodetic coordinates and subsequently rotated to represent the position in the J2000 coordinate system, denoted as .
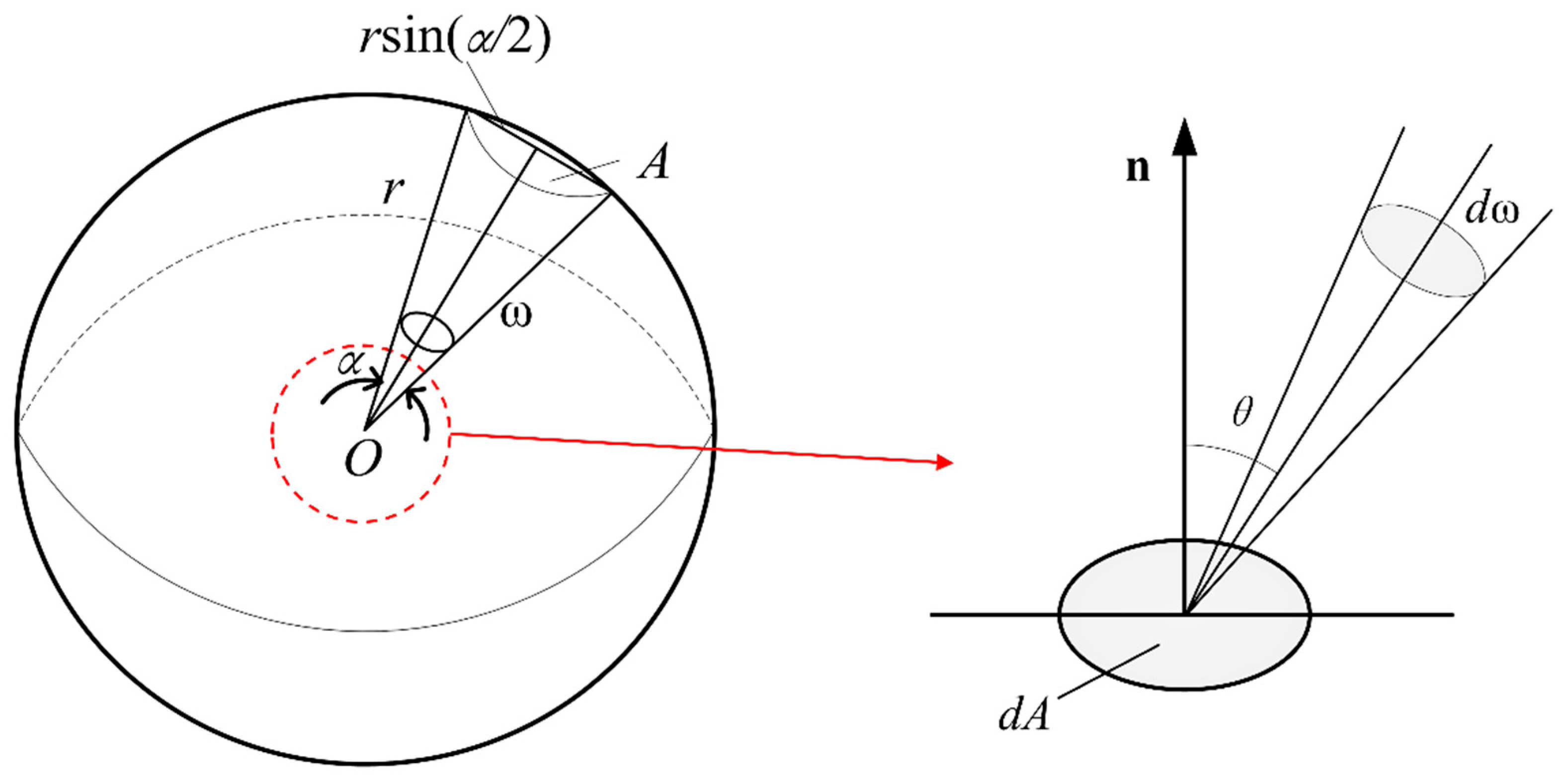
2.1.3. Observation Geometry Constraints
- 1.
- Evaluation of Elevation Angle;
- 2.
- Evaluation of Solar Eclipse Constraints and Earth Shadow Occlusion.
- The following formula is employed to determine whether the Earth obstructs the region between the satellite and the Sun. if , the path is unobscured, otherwise further judgment is required:
- The following formula was employed to calculate the distance between the center of the Earth and the line connecting the Sun to the object;
- To determine whether the sunlight is blocked by the Earth, the blocking height threshold is set to , with a value of 6380 km is uniformly specified in this paper. If , the observation data are deemed valid, otherwise they are considered invalid.
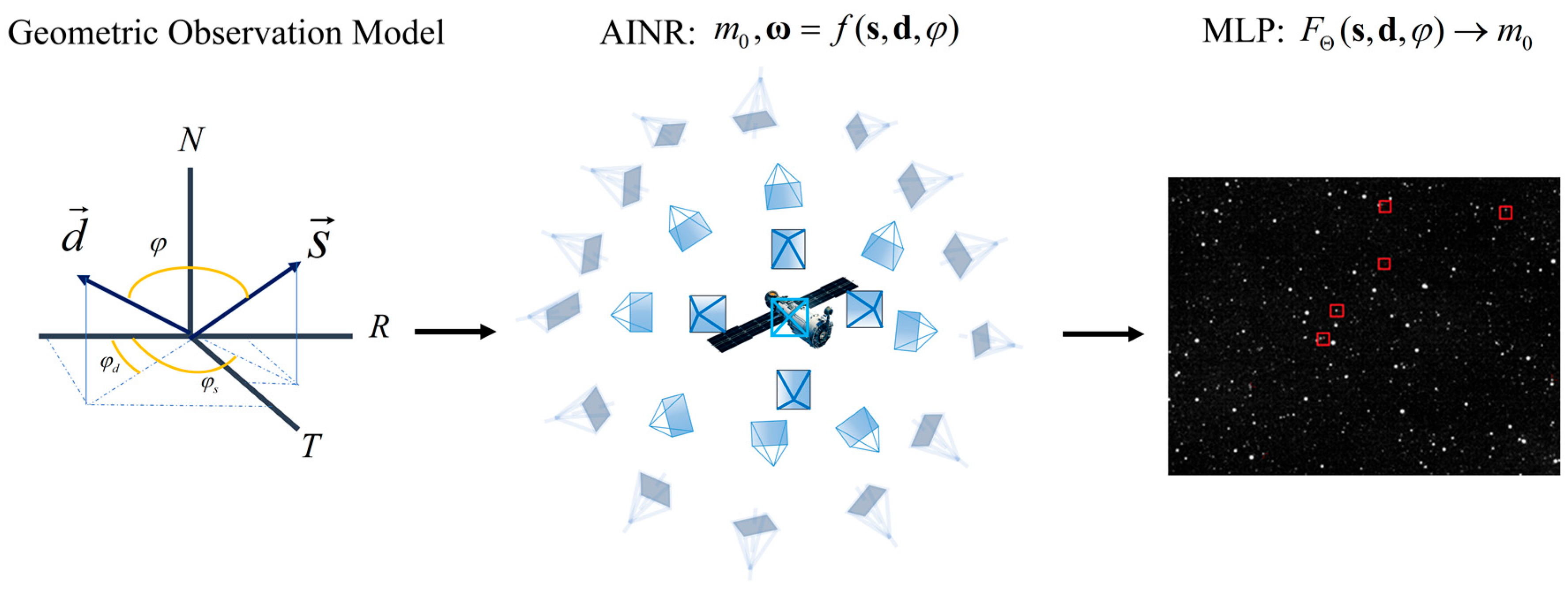
2.2. Photometric Prediction Based on AINRs
2.2.1. Implicit Neural Representation
2.2.2. Structure of MLP
2.2.3. Reconstructing the Loss Function
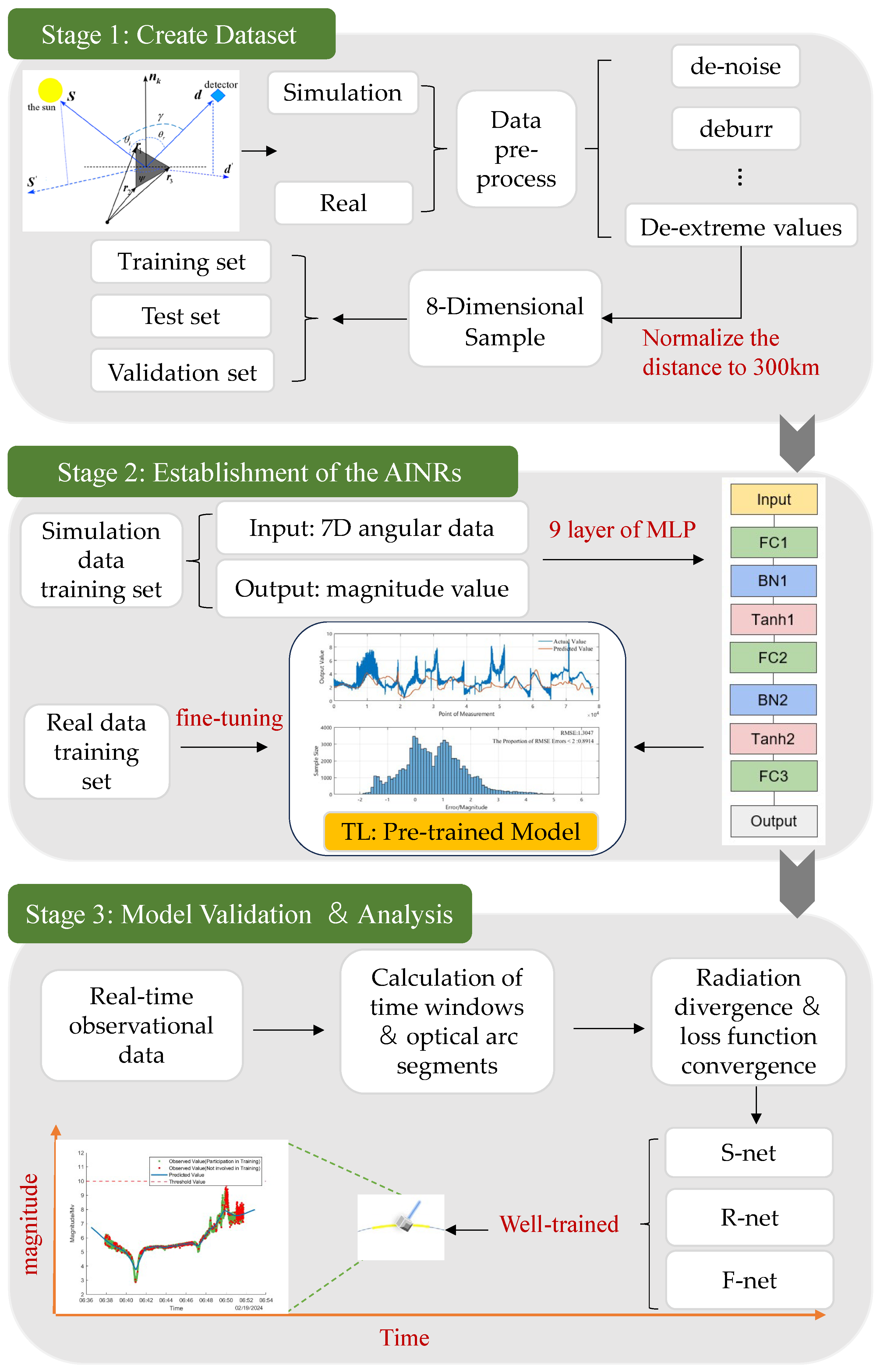
3. Modeling System Approach
3.1. Pre-Training Models Based on TL
3.2. Construction of Datasets
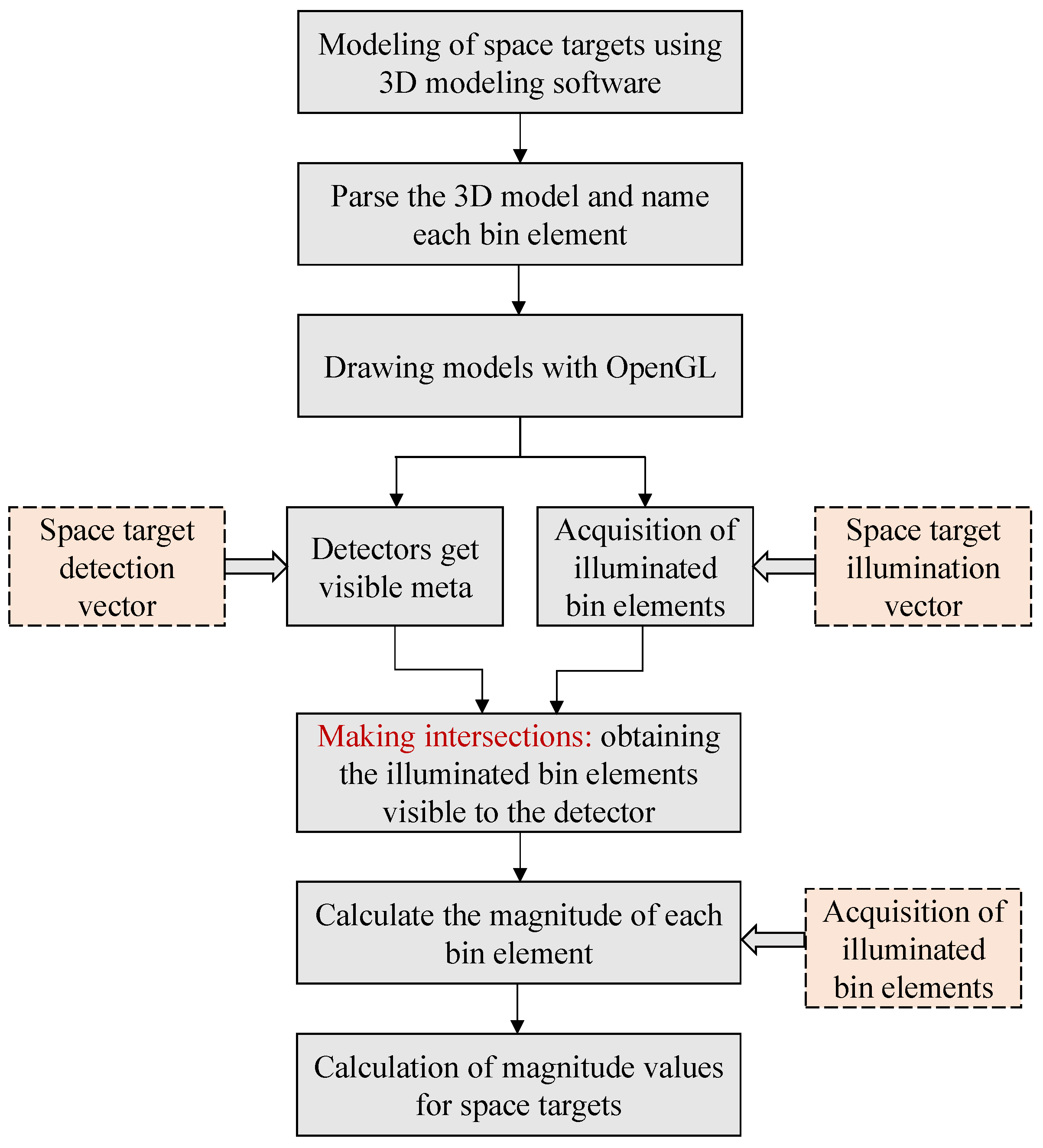
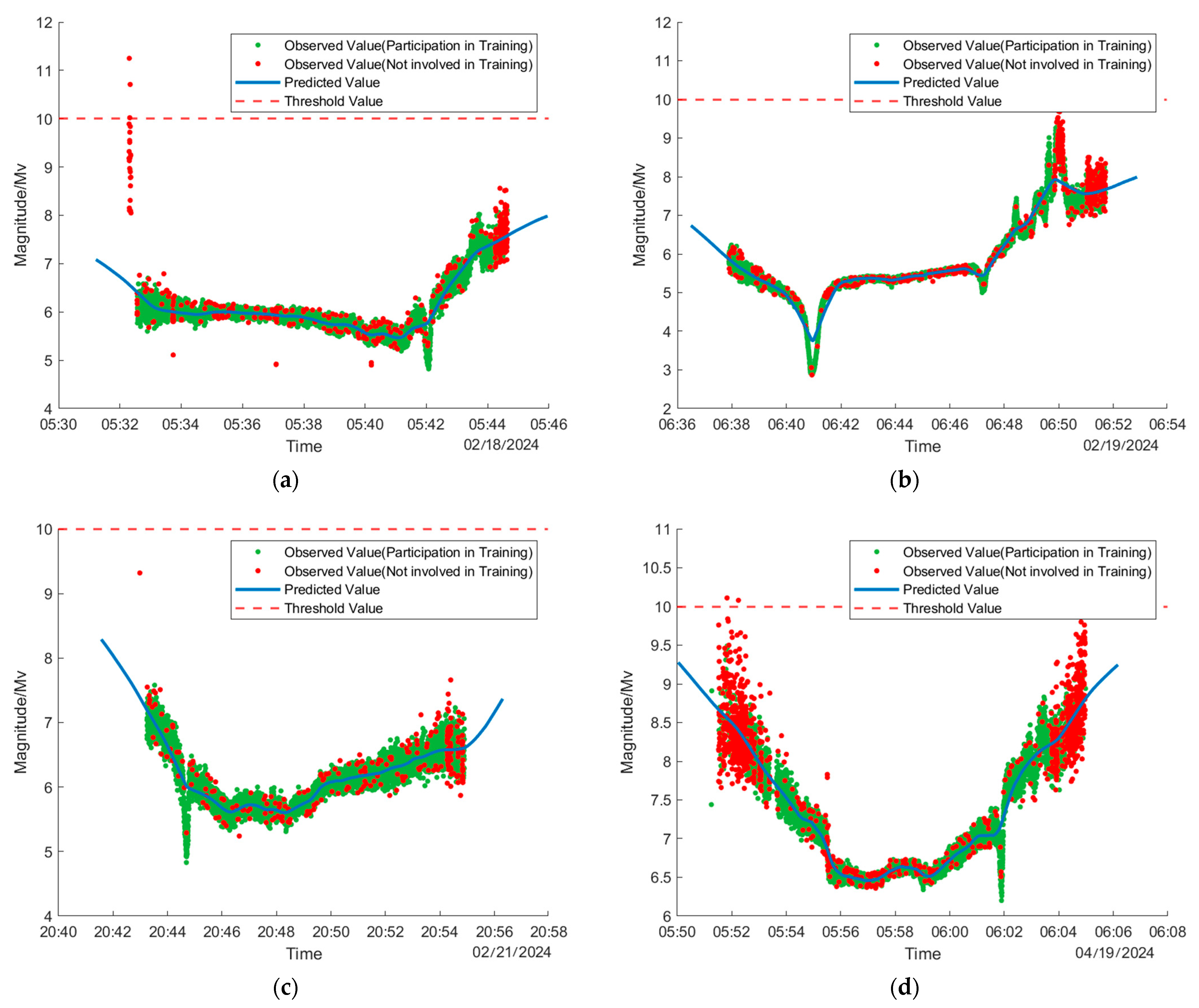
- The omnidirectional angle simulation data was generated from the ground-based optical observation simulation software. This data are crucial for analyzing the fundamental principle and numerical simulation process of the brightness of the optical scattering characteristics, as depicted in Figure 7, which illustrates the flowchart of the omnidirectional angle simulation software algorithm designed by our research team [29]. The primary steps in generating this data include constructing a three-dimensional model of the object based on the space object image acquired by optical telescope or high-resolution radar; determining the angular information corresponding to each face element of the space object under the orbital coordinate system; applying the actual BRDF model to components such as the sailplane, antenna, and other components, while other components are modeled based on the Lambertian body material, automatically optimizing and adjusting the object’s altitude, components, and the reflectivity of different face elements to compute object brightness; iteratively adjusting the above variables based on the prediction results until the error meets specified requirements [30].
- The experimental dataset originates from the Small Optoelectronic Innovation Practice Platform at the Space Engineering University. This platform is equipped to automatically interface with site meteorological monitoring equipment and operates in a preset multitasking mode, achieving unmanned equipment operation and data acquisition. The telescope utilized is a high-performance telescope with a 150 mm aperture (f/200) [31], positioned at geographical coordinates 116°40′4.79″E longitude, 40°21′22.36″N latitude, and an altitude of 87.41 m. To ensure the effectiveness of the satellite’s surface photometric characteristic inversion, the data are primarily derived from long-term observations of a three-axis stabilized artificial satellite by a single ground station, with the distance between the station and the satellite normalized to 300 km. The data produced by the platform also provide the potential for a myriad of other future research topics in space situational awareness, such as attitude control, and the platform will continue to drive research for years to come.
3.3. Evaluation Indicators
- 1.
- Root Mean Square Error (RMSE);
- 2.
- Mean Absolute Error (MAE);
4. Performance Evaluation
4.1. Input Parameters
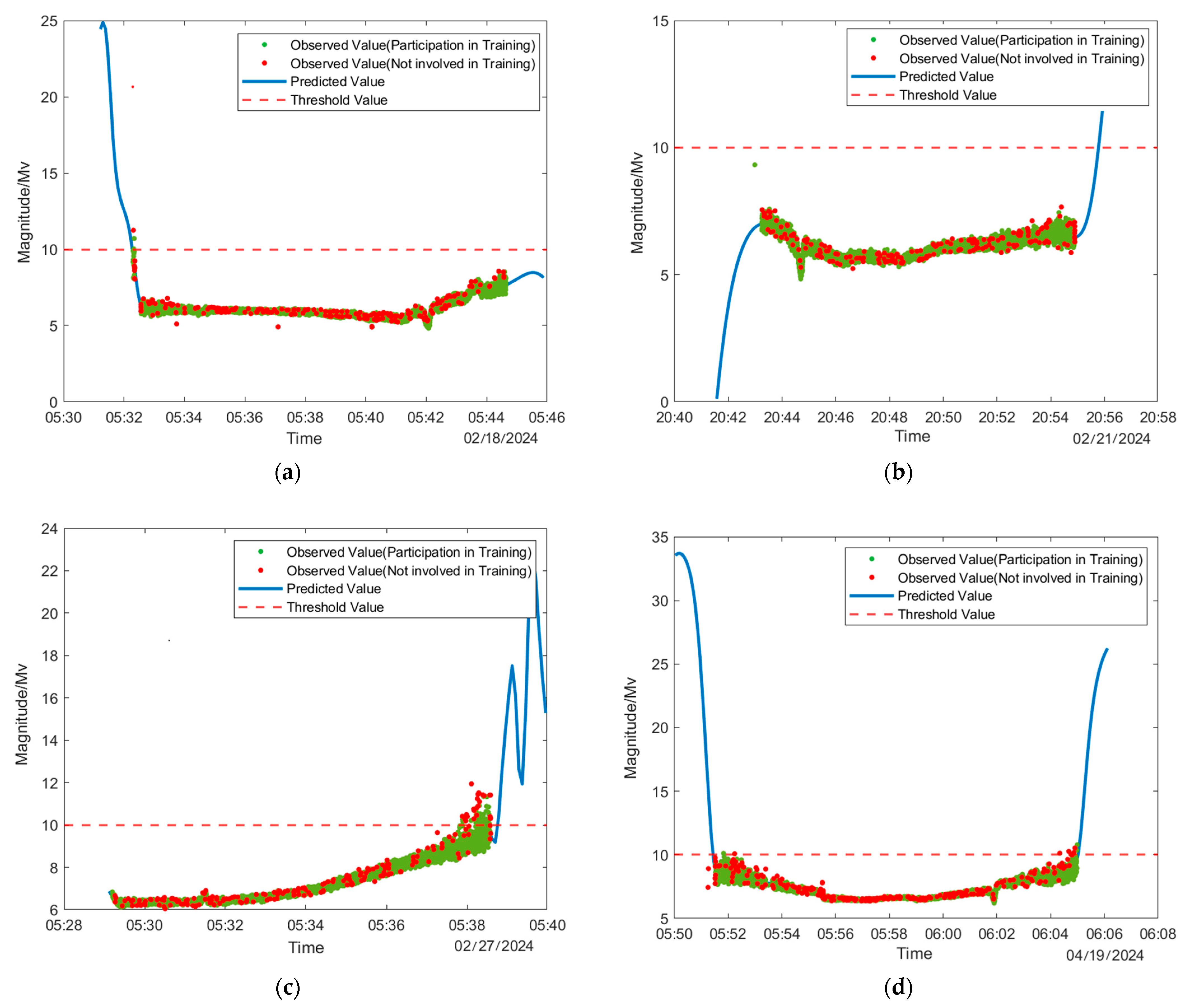
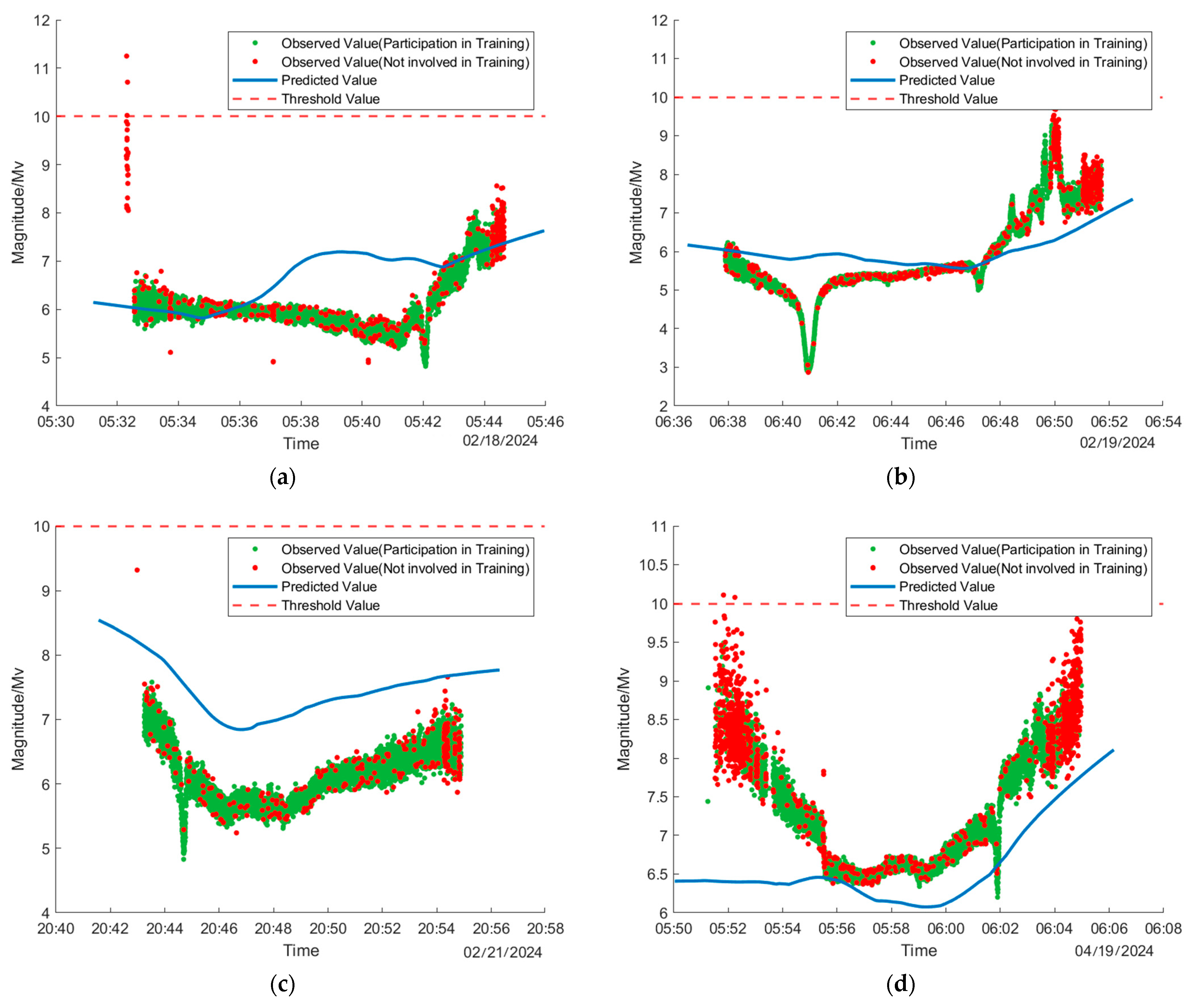
4.2. Model Predictions
- 1.
- S−net
- 2.
- R−net
- 3.
- F−net
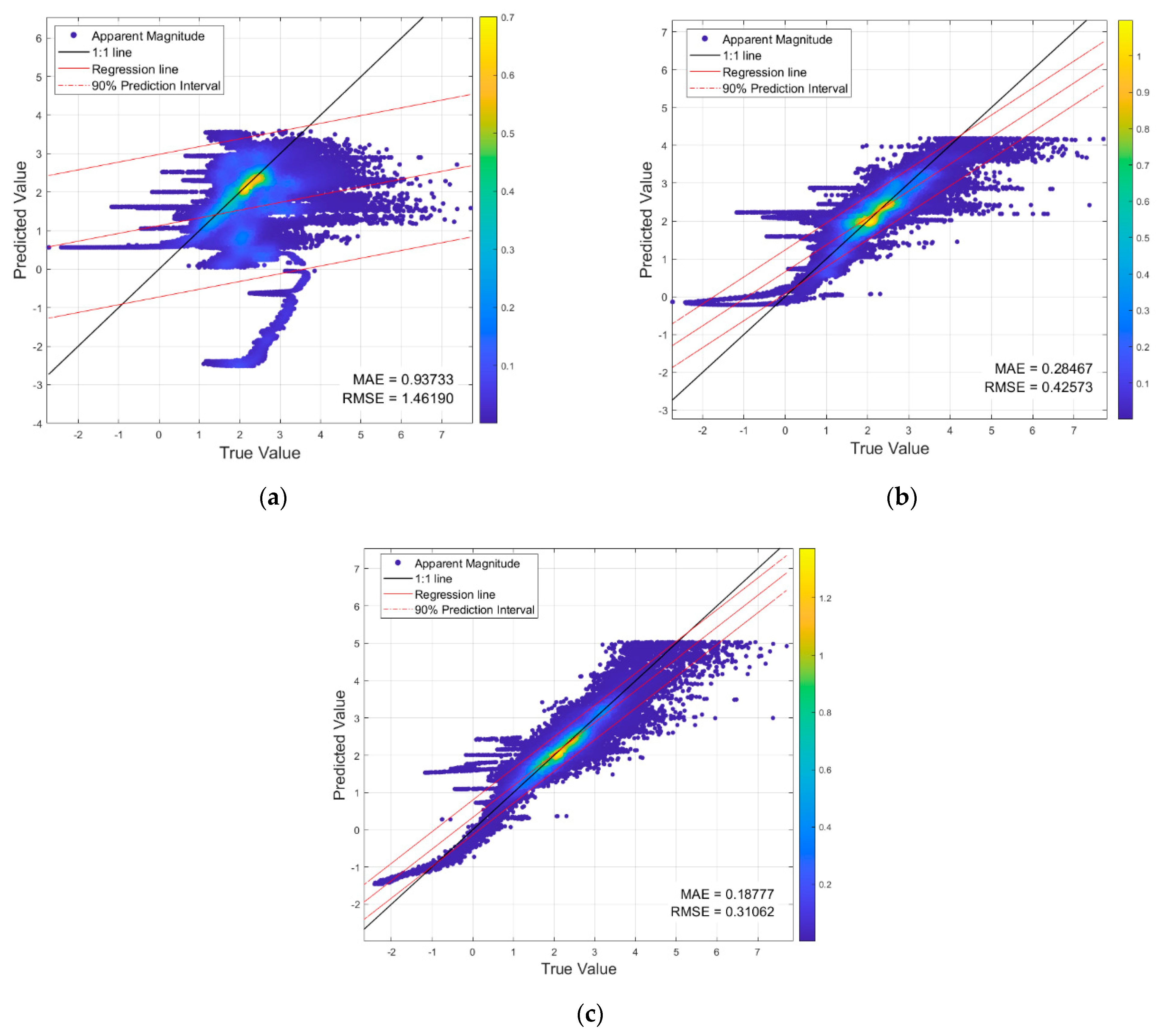
4.3. Comparison of Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AINRs | Augmented Implicit Neural Representations |
| MLP | Multi-Layer Perceptron |
| MAE | Mean Absolute Error |
| MSE | Mean Square Error |
| RMSE | Root Mean Square Error |
| RTN | Radial Transverse Normal |
| TL | Transfer Learning |
| TLE | Two-Line Element |
References
- Scott, R.L.; Thorsteinson, S.; Abbasi, V. On-Orbit Observations of Conjuncting Space Objects Prior to the Time of Closest Approach. J. Astronaut. Sci. 2020, 67, 1735–1754. [Google Scholar] [CrossRef]
- Ruo, M. Research on Key Feature Inversion Method for Space Objects Based on Ground Photometric Signals. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2021. [Google Scholar]
- Wang, X.; Huo, Y.; Fang, Y.; Zhang, F.; Wu, Y. ARSRNet: Accurate Space Object Recognition Using Optical Cross Section Curves. Appl. Opt. 2021, 60, 8956. [Google Scholar] [CrossRef] [PubMed]
- Friedman, A.M. Observability Analysis for Space Situational Awareness. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2022. [Google Scholar]
- Bieron, J.; Peers, P. An Adaptive BRDF Fitting Metric. Comput. Graph. Forum 2020, 39, 59–74. [Google Scholar] [CrossRef]
- Zhan, P. BRDF-Based Light Scattering Characterization of Random Rough Surfaces. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2024. [Google Scholar]
- Little, B.D. Optical Sensor Tasking Optimization for Space Situational Awareness. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2019. [Google Scholar]
- Rao, C.; Zhong, L.; Guo, Y.; Li, M.; Zhang, L.; Wei, K. Astronomical Adaptive Optics: A Review. PhotoniX 2024, 5, 16. [Google Scholar] [CrossRef]
- Liu, X.; Wu, J.; Man, Y.; Xu, X.; Guo, J. Multi-Objective Recognition Based on Deep Learning. Aircr. Eng. Aerosp. Technol. 2020, 92, 1185–1193. [Google Scholar] [CrossRef]
- Kerr, E.; Petersen, E.G.; Talon, P.; Petit, D.; Dorn, C.; Eves, S. Using AI to Analyze Light Curves for GEO Object Characterization. In Proceedings of the 22nd Advanced Maui Optical and Space Surveillance Technologies Conference (AMOS), Maui, HI, USA, 19–22 September 2021. [Google Scholar]
- Singh, N.; Brannum, J.; Ferris, A.; Horwood, J.; Borowski, H.; Aristoff, J. An Automated Indications and Warning System for Enhanced Space Domain Awareness. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference (AMOS), Maui, HI, USA, 16–18 September 2020. [Google Scholar]
- Dupree, W.; Penafiel, L.; Gemmer, T. Time Forecasting Satellite Light Curve Patterns Using Neural Networks. In Proceedings of the 22nd Advanced Maui Optical and Space Surveillance Technologies Conference (AMOS), Maui, HI, USA, 19–22 September 2021. [Google Scholar]
- Li, H. Space Object Optical Characteristic Calculation Model and Method in the Photoelectric Detection Object. Appl. Opt. 2016, 55, 3689. [Google Scholar] [CrossRef] [PubMed]
- Campiti, G.; Brunetti, G.; Braun, V.; Di Sciascio, E.; Ciminelli, C. Orbital Kinematics of Conjuncting Objects in Low-Earth Orbit and Opportunities for Autonomous Observations. Acta Astronaut. 2023, 208, 355–366. [Google Scholar] [CrossRef]
- Tao, X.; Li, Z.; Xu, C.; Huo, Y.; Zhang, Y. Track-to-Object Association Algorithm Based on TLE Filtering. Adv. Space Res. 2021, 67, 2304–2318. [Google Scholar] [CrossRef]
- Friedman, A.M.; Frueh, C. Observability of Light Curve Inversion for Shape and Feature Determination Exemplified by a Case Analysis. J. Astronaut. Sci. 2022, 69, 537–569. [Google Scholar] [CrossRef]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. Commun. ACM 2022, 65, 99–106. [Google Scholar] [CrossRef]
- Ford, E.B.; Seager, S.; Turner, E.L. Characterization of Extrasolar Terrestrial Planets from Diurnal Photometric Variability. Nature 2001, 412, 885–887. [Google Scholar] [CrossRef] [PubMed]
- Campbell, T.S. Astrometric and Photometric Data Fusion in Machine Learning-Based Characterization of Resident Space Objects. Ph.D. Thesis, University of Arizona, Tucson, AZ, USA, 2023. [Google Scholar]
- Cadmus, R.R. The Relationship between Photometric Measurements and Visual Magnitude Estimates for Red Stars. Astron. J. 2021, 161, 75. [Google Scholar] [CrossRef]
- Lei, X.; Lao, Z.; Liu, L.; Chen, J.; Wang, L.; Jiang, S.; Li, M. Telescopic Network of Zhulong for Orbit Determination and Prediction of Space Objects. Remote Sens. 2024, 16, 2282. [Google Scholar] [CrossRef]
- Chang, K.; Fletcher, J. Learned Satellite Radiometry Modeling from Linear Pass Observations. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference (AMOS), Maui, HI, USA, 19–22 September 2023. [Google Scholar]
- Baron, F.R.; Jefferies, S.M.; Shcherbik, D.V.; Hall, R.; Johns, D.; Hope, D.A. Hyper-Spectral Speckle Imaging of Resolved Objects. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference (AMOS), Maui, HI, USA, 19–22 September 2023. [Google Scholar]
- Lu, Y. Impact of Starlink Constellation on Early LSST: A Photometric Analysis of Satellite Trails with BRDF Model. arXiv 2024, arXiv:2403.11118. [Google Scholar]
- Vasylyev, D.; Semenov, A.A.; Vogel, W. Characterization of Free-Space Quantum Channels. In Proceedings of the Quantum Communications and Quantum Imaging XVI, San Diego, CA, USA, 19–23 August 2018; p. 31. [Google Scholar]
- Tancik, M. Object and Scene Reconstruction Using Neural Radiance Fields. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2023. [Google Scholar]
- Tancik, M.; Srinivasan, P.P.; Mildenhall, B.; Fridovich-Keil, S.; Raghavan, N.; Singhal, U.; Ramamoorthi, R.; Barron, J.T.; Ng, R. Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains. Adv. Neural Inf. Process. Syst. 2020, 33, 7537–7547. [Google Scholar]
- Yang, X.; Nan, X.; Song, B. D2N4: A Discriminative Deep Nearest Neighbor Neural Network for Few-Shot Space Target Recognition. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3667–3676. [Google Scholar] [CrossRef]
- Peng, L.; Li, Z.; Xu, C.; Fang, Y.; Zhang, F. Research on Space Object’s Materials Multi-Color Photometry Identification Based on the Extreme Learning Machine Algorithm. Spectrosc. Spectr. Anal. 2018, 39, 363–369. [Google Scholar]
- Xu, C.; Zhang, Y.; Li, P.; Li, J. Optical cross-sectional area calculation of spatial objects based on OpenGL pickup technique. J. Opt. 2017, 37, 218–227. [Google Scholar]
- Machine Vision Series Lenses for Telescopes. Available online: https://www.forecam.com/RicomCnSolutionShow.asp?Cls=%BB%FA%C6%F7%CA%D3%BE%F5%CF%B5%C1%D0%BE%B5%CD%B7 (accessed on 20 January 2024).
- Beirlant, J.; Dudewicz, E.J.; Györfi, L.; van der Meulen, E.C. Estimation of Shannon Differential Entropy: An Extensive Comparative Review. Entropy 1997, 19, 220–246. [Google Scholar]


| Number | Named Model | Description |
|---|---|---|
| 1 | S−net (Simulation) | The network model trained using omnidirectional angle simulated data; |
| 2 | R−net (Real) | The network model trained using ground-based telescope-measured data; |
| 3 | F−net (Fine-tuned) | Utilizing omnidirectional angle simulated data for pretraining the network and continually fine-tuning the network parameters with measured data to obtain the model; |
| Model | RMSE | Percentage Reduction | MAE | Percentage Reduction |
|---|---|---|---|---|
| S−net | 1.4619 | 0 | 0.93733 | 0 |
| R−net | 0.42573 | 0.7088 | 0.28467 | 0.6963 |
| F−net | 0.31062 | 0.7875 | 0.18777 | 0.7997 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Q.; Xu, C.; Zhao, S.; Tao, X.; Zhang, Y.; Tao, H.; Wang, X.; Fang, Y. A Space Object Optical Scattering Characteristics Analysis Model Based on Augmented Implicit Neural Representation. Remote Sens. 2024, 16, 3316. https://doi.org/10.3390/rs16173316
Zhu Q, Xu C, Zhao S, Tao X, Zhang Y, Tao H, Wang X, Fang Y. A Space Object Optical Scattering Characteristics Analysis Model Based on Augmented Implicit Neural Representation. Remote Sensing. 2024; 16(17):3316. https://doi.org/10.3390/rs16173316
Chicago/Turabian StyleZhu, Qinyu, Can Xu, Shuailong Zhao, Xuefeng Tao, Yasheng Zhang, Haicheng Tao, Xia Wang, and Yuqiang Fang. 2024. "A Space Object Optical Scattering Characteristics Analysis Model Based on Augmented Implicit Neural Representation" Remote Sensing 16, no. 17: 3316. https://doi.org/10.3390/rs16173316
APA StyleZhu, Q., Xu, C., Zhao, S., Tao, X., Zhang, Y., Tao, H., Wang, X., & Fang, Y. (2024). A Space Object Optical Scattering Characteristics Analysis Model Based on Augmented Implicit Neural Representation. Remote Sensing, 16(17), 3316. https://doi.org/10.3390/rs16173316







