Analysis of the Influence of Refraction-Parameter Deviation on Underwater Stereo-Vision Measurement with Flat Refraction Interface

Abstract

There has been substantial research on multi-medium visual measurement in fields such as underwater three-dimensional reconstruction and underwater structure monitoring. Addressing the issue where traditional air-based visual-measurement models fail due to refraction when light passes through different media, numerous studies have established refraction-imaging models based on the actual geometry of light refraction to compensate for the effects of refraction on cross-media imaging. However, the calibration of refraction parameters inevitably contains errors, leading to deviations in these parameters. To analyze the impact of refraction-parameter deviations on measurements in underwater structure visual navigation, this paper develops a dual-media stereo-vision measurement simulation model and conducts comprehensive simulation experiments. The results indicate that to achieve high-precision underwater-measurement outcomes, the calibration method for refraction parameters, the distribution of the targets in the field of view, and the distance of the target from the camera must all be meticulously designed. These findings provide guidance for the construction of underwater stereo-vision measurement systems, the calibration of refraction parameters, underwater experiments, and practical applications.

1. Introduction

Multi-medium visual measurement is a crucial branch of the visual-measurement field. Common multi-media visual-measurement scenarios include situations where light traverses two mediums, such as air–water, or three mediums, such as air–glass–air and air–glass–water [1,2,3]. Examples of such scenarios include the visual measurement of thermal deformation of alumina ceramic plates and stainless-steel plates under radiant heating [4] as well as the three-dimensional shape measurement of underwater bridge piers [5].

Multi-medium visual measurement has garnered extensive attention in areas such as underwater deformation monitoring and three-dimensional reconstruction [1,5,6,7,8]. In addition, it can also be applied to underwater navigation and positioning. In underwater engineering, such as immersed tunnels, the precise alignment of prefabricated elements requires high-precision underwater navigation and positioning [9]. Similarly, the autonomous recovery of autonomous underwater vehicles (AUVs) necessitates accurate navigation [10]. For navigation scenarios involving the docking of underwater structures at close range, visual measurement becomes a crucial method due to its rich information and high accuracy [11,12].

In underwater visual measurement, cameras are either placed in waterproof housings or positioned above the water surface. Consequently, a significant characteristic is that light propagation undergoes refraction at the interfaces of different media, causing the light rays to deviate from a straight-line path. Therefore, traditional air-based stereo-vision measurement models are no longer applicable under multi-media conditions [13]. When the camera images an object through a sealed housing’s transparent window, the interface typically comes in shapes such as planar, hemispherical, and cylindrical [14,15,16]. Hemispherical ports counteract the refraction effect through their specific shapes, do not reduce the field of view, and can withstand high pressure in deep water, but they may induce image blurring and have higher manufacturing requirements [17,18]. Cylindrical interfaces have the advantage of allowing a larger field of view (in one direction) and are relatively simple and cost-effective to manufacture [19]. Although flat interfaces can significantly reduce the field of view and may introduce chromatic aberration, they are well-studied and have lower manufacturing costs [17]. Therefore, the focus of this paper is on underwater visual measurement with a flat interface.

The basic problems of underwater photogrammetry with a flat interface, including the basic formulas and the methods of automatic reduction to one perspective, were explored decades ago [20,21,22]. Since no later than the 1960s, researchers have proposed numerous methods for refractive compensation in planar underwater visual measurement. Broadly, these methods can be categorized into three solutions. The first approach involves placing two auxiliary calibration grids or a calibration frame within the object space, utilizing the calibration structure to determine the direction of light prior to its incident [23]. However, this method necessitates the customization of specific calibration grids or frames, making the implementation process relatively complex. The second approach entails focal length compensation or refraction absorption, wherein the pixel offset error induced by refraction is approximated as an error stemming from changes in lens focal length or distortion. By calibrating the camera’s lens or distortion parameters, the influence of refraction can be mitigated [24,25,26]. Nevertheless, due to the nonlinearity of the refractive effect and the dependence of the refraction error’s magnitude on the object’s position and the angle of incidence, these methods only approximate the elimination of refraction effects [13,27]. The final method is geometric refraction correction, which involves establishing an underwater refraction imaging model through geometric analysis to explicitly account for the refractive effects, thereby theoretically ensuring the accuracy of the measurement results [8,28,29,30,31,32,33,34,35,36,37].

Research on geometric refraction correction primarily focuses on the development of calibration methods and measurement models. The two-stage underwater camera calibration represents a groundbreaking advancement in the field [29]. The optimization method can also be employed to calibrate parameters such as the normal vector of the refraction interface and the distance from the interface to the camera. However, it is essential to assign appropriate initial values in advance [30]. Leveraging the geometric property that two incident light rays from the same object entering the stereo camera lie on the same plane, the calibration parameters can also be optimized through 3D point remapping [33]. The refractive index varies with different light frequencies. The parameters of the underwater camera can be calibrated by calculating the offset in the imaging position of different light frequencies emitted by a specially designed calibration plate placed at the same location [31]. To eliminate measurement errors caused by the spherical refraction interface, an underwater calibration algorithm based on an advanced non-dominated sorting genetic algorithm is proposed. This approach, utilizing an integrated geometric refraction model, significantly enhances the performance of underwater visual measurement [35].

Regarding the influence of refraction on visual measurements, for multi-view (more than two views) underwater 3D reconstruction, the influence on the accuracy of the 3D reconstruction is evaluated quantitatively and systematically in [25]. Tong [38] used simulation and real experiments to analyze the influence of different refraction parameters and proposed measures to reduce the influence. However, due to the inevitability of measurement errors, the calibrated refraction parameters must contain deviations. When using the refraction-measurement model for refraction compensation, the impact of the parameter deviation on the visual measurement results is also worth studying. In addition, conducting underwater experiments is relatively challenging, so performing relevant analyses through simulation experiments is a preferable option. To the best of our knowledge, current research does not provide specific algorithms for simulation analysis. To investigate the impact of refraction-parameter deviations on stereo-visual measurement in dual-media conditions, this paper first established a simulation model for stereo-visual measurement in the air–water scenario. Then, a thorough analysis of the relationship between the stereo-visual measurement model and refraction-parameter deviations using simulation experiments was conducted. The conclusions can provide guidance for the construction of underwater stereo-vision measurement systems, refraction parameter calibration, underwater experiments, and practical applications.

The subsequent structure of the paper is arranged as follows. Section 2 introduces the light refraction geometry and measurement model for multi-media stereo vision, establishes a simulation algorithm for dual-media stereo-visual measurement and provides a simulation experimental design. The experimental results are presented and discussed in Section 3 and Section 4, respectively. Section 5 presents the conclusions.

2. Methods

2.1. Measurement Model

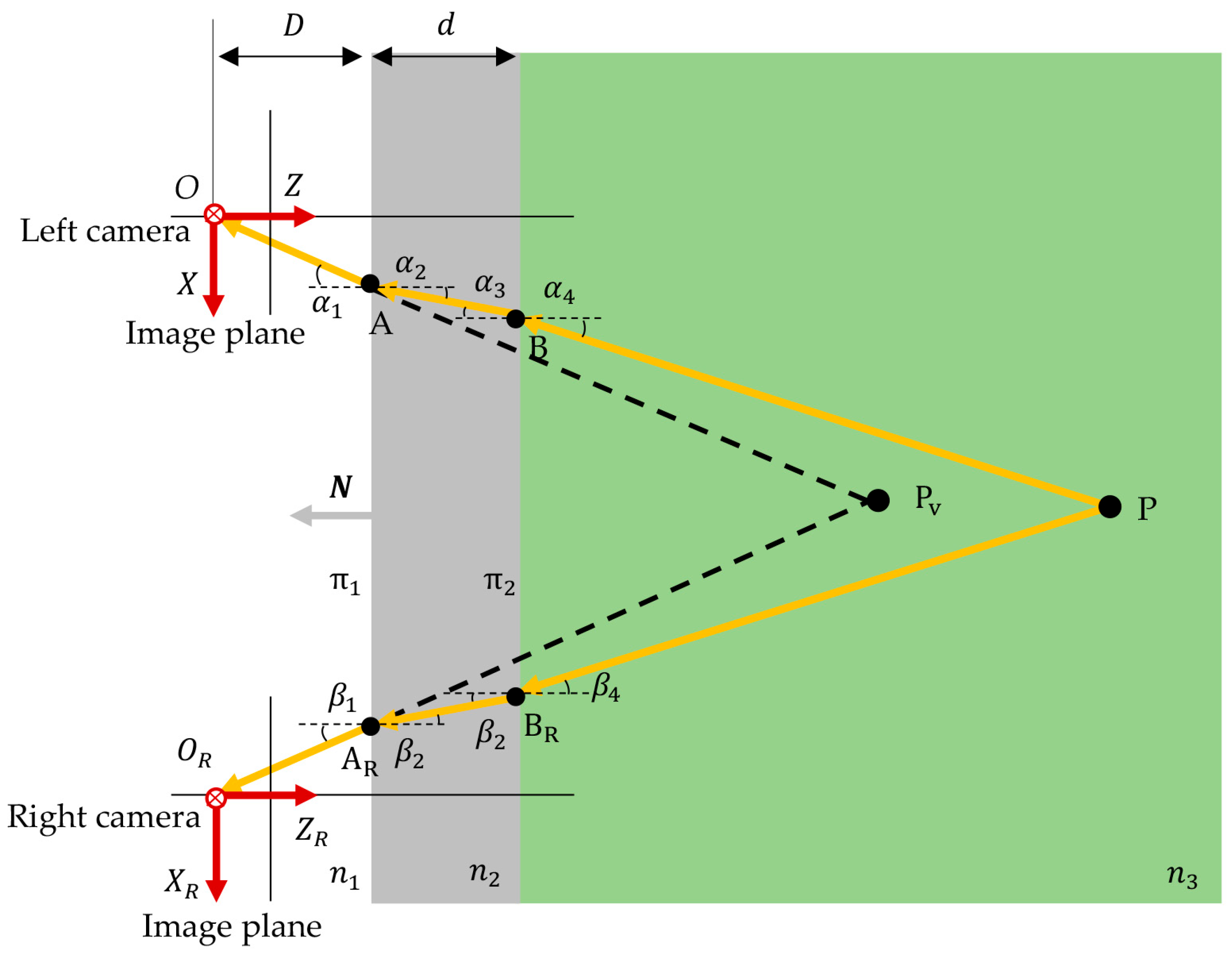
The stereo-vision measurement system includes left and right cameras. It is assumed that the cameras image the target through a transparent window inside a watertight cabin. The material of the transparent window is generally glass. The light reflected or emitted by the underwater target reaches the camera through three mediums and two refraction interfaces. Both interfaces are assumed to be planar and parallel to each other. The refraction geometry is shown in Figure 1.

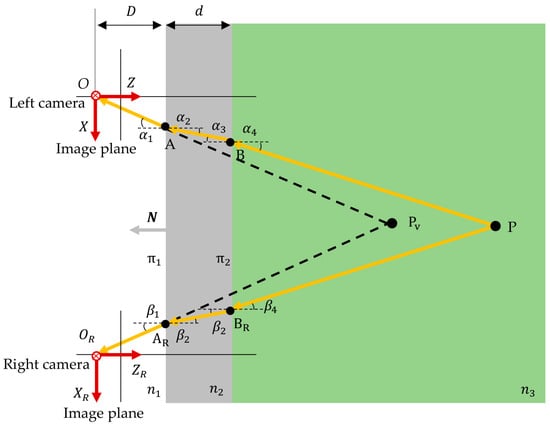
Figure 1. Refractive geometry for air–glass–water medium with two flat interfaces.

The camera coordinate system of the left camera $O—XYZ$ is used as the reference coordinate system. P is the target point underwater and its coordinate is $\left(X, Y, Z\right)$. The two refraction interfaces are denoted as ${\mathrm{\pi }}_1$ and ${\mathrm{\pi }}_2$. The distance from the left camera optical center to the interface ${\mathrm{\pi }}_1$ is D, and the thickness of the glass layer is d. Due to refraction, the optical paths between P and the cameras are not straight lines, but the broken lines $\mathrm{PB}—\mathrm{BA}—\mathrm{AO}$ and ${\mathrm{PB}}_{\mathrm{R}}—{\mathrm{B}}_{\mathrm{R}}{\mathrm{A}}_{\mathrm{R}}—{\mathrm{A}}_{\mathrm{R}}{\mathrm{O}}_{\mathrm{R}}$ according to Snell’s law. The refraction angles of the two rays are denoted by ${\alpha }_i$ and ${\beta }_i$. It is assumed that both cameras have been carefully calibrated. The camera coordinate system of the right camera is $O_R—X_R{Y}_R{Z}_R$, and the coordinates of the origin $O_R$ in the reference coordinate system are denoted as $\mathit{t}=\left(t_x, t_y, t_z\right)$, which is the translation vector of the right camera with respect to the left camera.

The target point P is the intersection point of the lines BP and ${\mathrm{B}}_{\mathrm{R}}\mathrm{P}$. If the equations of two lines are found, the intersection point is the coordinate of P. The derivation of the equations for the lines BP and ${\mathrm{B}}_{\mathrm{R}}\mathrm{P}$ is detailed below [1].

After obtaining two images from the left and right cameras and completing target recognition and matching, the point ${\mathrm{P}}_{\mathrm{v}}$ is obtained using conventional triangulation. The points O, A, and ${\mathrm{P}}_{\mathrm{v}}$ are collinear. The points ${\mathrm{O}}_{\mathrm{R}}$, ${\mathrm{A}}_{\mathrm{R}}$, and ${\mathrm{P}}_{\mathrm{v}}$ are also collinear. The coordinates of the points O, ${\mathrm{O}}_{\mathrm{R}}$, and ${\mathrm{P}}_{\mathrm{v}}$ are known. Therefore, the unit direction vectors of the lines OA and ${\mathrm{O}}_{\mathrm{R}}{\mathrm{A}}_{\mathrm{R}}$ can be obtained as

$$\left\{\begin{array}{c}{\mathit{\zeta }}^1=\left({\zeta }_x^1, {\zeta }_y^1, {\zeta }_z^1\right)=\frac{{\mathit{P}}_{\mathrm{v}}-\mathit{O}}{‖{\mathit{P}}_{\mathrm{v}}-\mathit{O}‖}\\ {\mathit{\xi }}^1=\left({\xi }_x^1, {\xi }_y^1, {\xi }_z^1\right)=\frac{{\mathit{P}}_{\mathrm{v}}-{\mathit{O}}_{\mathrm{R}}}{‖{\mathit{P}}_{\mathrm{v}}-{\mathit{O}}_{\mathrm{R}}‖}\end{array}\right.$$

(1)

In terms of the direction vector of the line and a point on the line, the equations for the lines OA and ${\mathrm{O}}_{\mathrm{R}}{\mathrm{A}}_{\mathrm{R}}$ are

$$\left\{\begin{array}{c}\frac{X}{{\zeta }_x^1}=\frac{Y}{{\zeta }_y^1}=\frac{Z}{{\zeta }_z^1}\\ \frac{X-t_x}{{\xi }_x^1}=\frac{Y-t_y}{{\xi }_y^1}=\frac{Z-t_z}{{\xi }_z^1}\end{array}\right.$$

(2)

The points A and ${\mathrm{A}}_{\mathrm{R}}$ are the intersections of the lines OA and ${\mathrm{O}}_{\mathrm{R}}{\mathrm{A}}_{\mathrm{R}}$ with the interface ${\mathrm{\pi }}_1$. Assuming that the normal vector $\mathit{N}=\left(N_x,N_y, N_z\right)$ of ${\mathrm{\pi }}_1$ is known, the equation for ${\mathrm{\pi }}_1$ can be expressed as

$$\mathit{N}{\mathit{X}}^T+D=0$$

(3)

Combining Equations (2) and (3), the coordinates of the points A and ${\mathrm{A}}_{\mathrm{R}}$ can be obtained as

$$\left\{\begin{array}{c}\mathit{A}=\left(A_x,A_y,A_z\right)=-\frac{D}{\mathit{N}{\left({\mathit{\zeta }}^1\right)}^{\mathrm{T}}}{\mathit{\zeta }}^1\\ {\mathit{A}}_R=-\frac{\mathit{N}{\mathit{t}}^T+D}{\mathit{N}{\left({\mathit{\xi }}^1\right)}^T}{\mathit{\xi }}^1+\mathit{t}\end{array}\right.$$

(4)

According to the vector inner product formula, the angles ${\alpha }_1$ and ${\beta }_1$ are

$$\left\{\begin{array}{c}{\alpha }_1=\frac{\mathit{N}·{\mathit{\zeta }}^1}{‖\mathit{N}‖‖{\mathit{\zeta }}^1‖}\\ {\beta }_1=\frac{\mathit{N}·{\mathit{\xi }}^1}{‖\mathit{N}‖‖{\mathit{\xi }}^1‖}\end{array}\right.$$

(5)

Based on Snell’s law, the angles ${\alpha }_2$ and ${\beta }_2$ are

$$\left\{\begin{array}{c}{\alpha }_2={\sin }^{-1} \left(\frac{n_1·\sin {\alpha }_1}{n_2}\right)\\ {\beta }_2={\sin }^{-1} \left(\frac{n_1·\sin {\beta }_1}{n_2}\right)\end{array}\right.$$

(6)

For the left camera, the lines OA, AB, and the camera optical axis are coplanar, so the normal vector of this plane is

$$\left\{\begin{array}{c}{\mathit{n}}_{\mathrm{l}}=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]\\ \mathit{k}={\mathit{\zeta }}^1\times {\mathit{n}}_{\mathrm{l}}=\left[\begin{array}{ccc}{k}_1& k_2& k_3\end{array}\right]\end{array}\right.$$

(7)

where ${\mathit{n}}_{\mathrm{l}}$ is the unit direction vector of the left camera optical axis. Through Rodriguez’s formula, the rotation matrix ${\mathit{R}}_{\mathrm{A}}$ and the unit direction vector ${\mathit{\zeta }}^2$ of the line AB are determined as

$$\left\{\begin{array}{c}{\mathit{R}}_{\mathrm{A}}=\mathit{I}+{\left[\mathit{k}\right]}_{\times }\sin {\alpha }_2+{\left[\mathit{k}\right]}_{\times }^2\left(1-\cos {\alpha }_2\right)\\ {\left[\mathit{k}\right]}_{\times }=\left[\begin{array}{ccc}0& -k_3& k_2\\ k_3& 0& -k_1\\ -k_2& k_1& 0\end{array}\right]\\ {\mathit{\zeta }}^2=\left({\zeta }_x^2, {\zeta }_y^2, {\zeta }_z^2\right)=\frac{{\left({\mathit{R}}_{\mathrm{A}}{\mathit{n}}_{\mathrm{l}}\right)}^T}{‖{\left({\mathit{R}}_{\mathrm{A}}{\mathit{n}}_{\mathrm{l}}\right)}^T‖}\end{array}\right.$$

(8)

where $\mathit{I}$ is the unit matrix and ${\left[\mathit{k}\right]}_{\times }$ is the antisymmetric matrix generated by $\mathit{k}$.

Considering the thickness $d$ of the glass layer, we can obtain the coordinates of point B

$$\mathit{B}=\left(B_x,B_y,B_z\right)=\mathit{A}+\frac{d}{\cos {\alpha }_2}{\mathit{\zeta }}^2$$

(9)

Because ${\alpha }_2={\alpha }_3$, similar to Equations (6) and (8), the angle ${\alpha }_4$ and the unit direction vector of line BP can be calculated as

$$\left\{\begin{array}{c}{\alpha }_4={\sin }^{-1}\left(\frac{n_2·\sin {\alpha }_2}{n_3}\right)\\ {\mathit{R}}_{\mathrm{B}}=\mathit{I}+{\left[\mathit{k}\right]}_{\times }\sin {\alpha }_4+{\left[\mathit{k}\right]}_{\times }^2\left(1-\cos {\alpha }_4\right)\\ {\mathit{\zeta }}^3=\left({\zeta }_x^3, {\zeta }_y^3, {\zeta }_z^3\right)=\frac{{\left({\mathit{R}}_{\mathrm{B}}{\mathit{n}}_{\mathrm{l}}\right)}^T}{‖{\left({\mathit{R}}_{\mathrm{B}}{\mathit{n}}_{\mathrm{l}}\right)}^T‖}\end{array}\right.$$

(10)

For the line BP, the direction vector ${\mathit{\zeta }}^3$ and a point on the line, B, are known; therefore, its equation is

$$\frac{X-B_x}{{\zeta }_x^3}=\frac{Y-B_y}{{\zeta }_y^3}=\frac{Z-B_z}{ {\zeta }_z^3}$$

(11)

For the right camera, the equation of the line ${\mathrm{B}}_{\mathrm{R}}\mathrm{P}$ can be obtained following a similar derivation process

$$\frac{X-B_{Rx}}{{\xi }_x^3}=\frac{Y-B_{Ry}}{{\xi }_y^3}=\frac{Z-B_{Rz}}{{\xi }_z^3}$$

(12)

In theory, the intersection of the lines BP and ${\mathrm{B}}_{\mathrm{R}}\mathrm{P}$ is point P, which is to be determined. However, the lines BP and ${\mathrm{B}}_{\mathrm{R}}\mathrm{P}$ may not intersect due to the errors. Suppose there exists a point H on the line BP and a point M on the line ${\mathrm{B}}_{\mathrm{R}}\mathrm{P}$ and the line from H to M forms the vector Q

$$\left\{\begin{array}{c}\mathit{H}=\mathit{B}+s_1{\mathit{\zeta }}^3\\ \mathit{M}={\mathit{B}}_{\mathrm{R}}+s_2{\mathit{\xi }}^3\\ \mathit{Q}=\mathit{H}-\mathit{M}\end{array}\right.$$

(13)

where $s_1$ and $s_2$ are the coefficients. Our aim is to minimize the length of Q. The length of the common perpendicular segment of two lines is the smallest. If Q is perpendicular to both lines BP and ${\mathrm{B}}_{\mathrm{R}}\mathrm{P}$, we have

$$\left\{\begin{array}{c}\mathit{Q}·{\mathit{\zeta }}^3=0\\ \mathit{Q}·{\mathit{\xi }}^3=0\end{array}\right.$$

(14)

According to Equation (14), $s_1$ and $s_2$ can be calculated, and then $\mathit{H}$ and $\mathit{M}$ can be obtained. The average of $\mathit{H}$ and $\mathit{M}$ is considered to be point P

$$\mathit{P}=\frac{\mathit{H}+\mathit{M}}{2}$$

(15)

The model is derived for a three-medium scenario, but with minor adjustments, it is equally applicable to a two-medium scenario.

2.2. Dual-Medium Simulation Model

The refraction parameters involved in the above measurement model include the distance from the camera to the refraction interface, the normal direction of the refraction interface, and the refractive indices of different mediums. Calibration errors of these parameters may impact the measurement results. Therefore, it is necessary to assess the impact of refractive parameter deviations on measurement results. However, conducting such evaluations through underwater experiments is relatively complex. In contrast, simulation experiments are more efficient. Consequently, this paper investigates a simulation model for underwater stereo-visual measurement. For simplicity, the camera is placed in the air and the target in the water, constituting an air–water scenario.

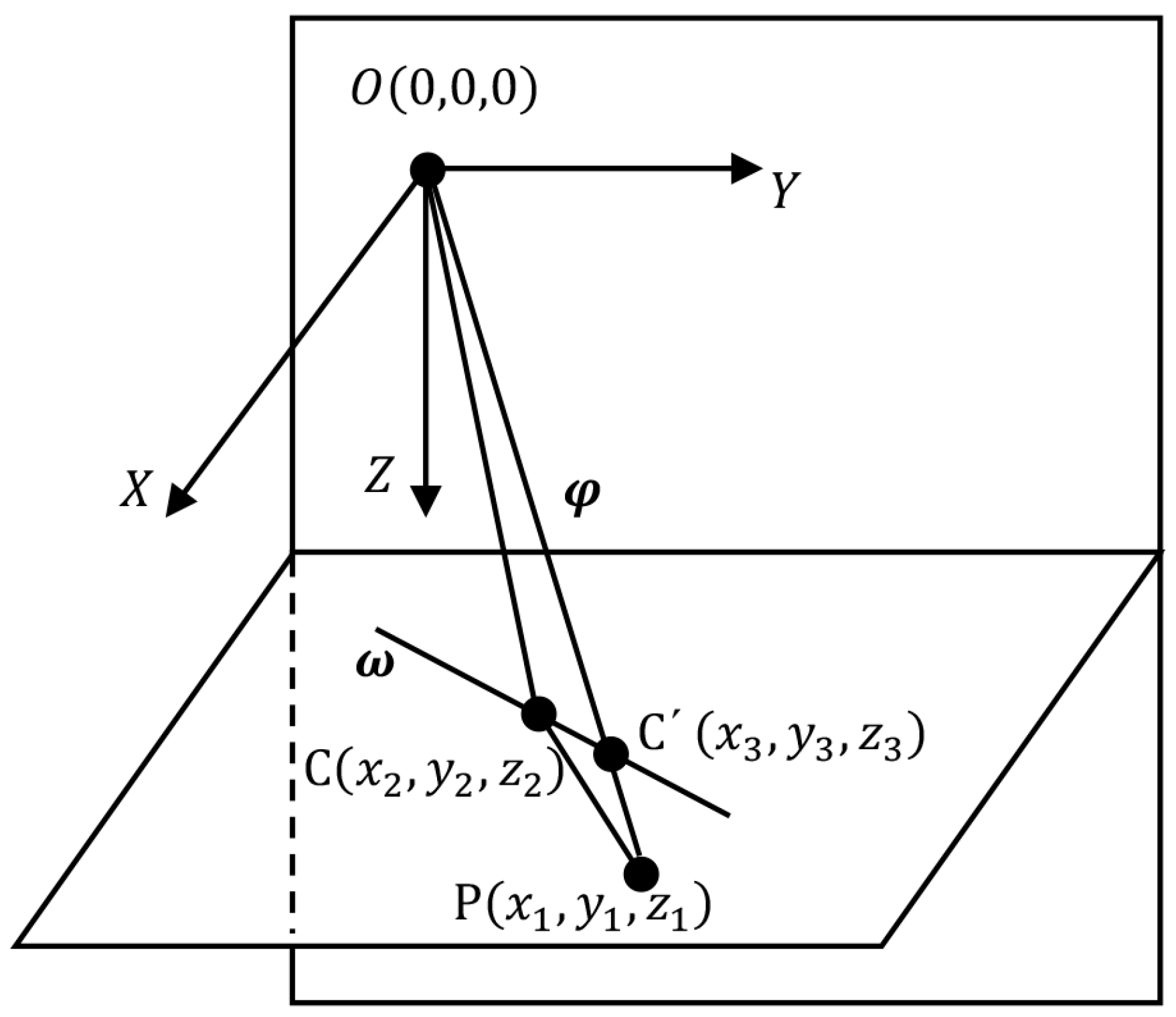
Taking the left camera coordinate system as the reference coordinate system. Given the coordinate of the target P is $\left(x_1,y_1,z_1\right)$; the distance from the left camera to the refractive interface is $D$, and the normal vector of the refractive interface is N. The camera is in the air. The target is in the water. The refractive indices of air and water are $n_1$ and $n_2$, respectively.

For the left camera, the refraction geometry is shown in Figure 2. $O$ represents the camera’s optical center. P is the target. C is the refraction point. C′ is the intersection of the line OP with the refractive interface. The objective is to calculate the coordinate of point C.

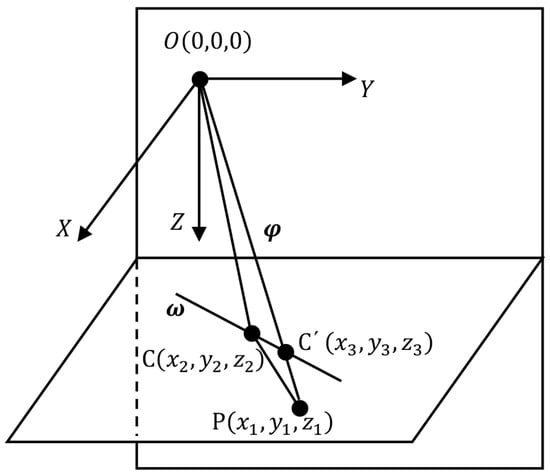
Figure 2. Refracted light in the dual-medium scenario.

The direction vector $\mathit{\phi }$ of line OP is

$$\mathit{\phi }=\mathit{P}-\mathit{O}$$

(16)

The entire refracted light PC-CO is in a refraction plane. Since PC and CO are coplanar with the normal vector N of the refraction interface, the normal vector of the refraction plane is

$$\mathit{\chi }=\frac{\mathit{\phi }\times \mathit{N}}{‖\mathit{\phi }\times \mathit{N}‖}=\left[\begin{array}{ccc}{\chi }_1& {\chi }_2& {\chi }_3\end{array}\right]$$

(17)

where $\times$ denotes the cross-product. The unit normal vector of the intersection CC′ of the refraction plane and the refractive interface is

$$\mathit{\omega }=\frac{\mathit{\chi }\times \mathit{N}}{‖\mathit{\chi }\times \mathit{N}‖}=\left[\begin{array}{ccc}{\omega }_1& {\omega }_2& {\omega }_3\end{array}\right]$$

(18)

Determine the coordinate of a point on line CC′, denoted as $\left(x_0,y_0,z_0\right)$. Then, the line CC′ can be expressed as

$$\left\{\begin{array}{c}x=x_0+\lambda {\mathit{\omega }}_1\\ y=y_0+\lambda {\mathit{\omega }}_2\\ z=z_0+\lambda {\mathit{\omega }}_3\end{array}\right.$$

(19)

where $\lambda$ is the coefficient.

According to the relationship between refractive index and the speed of light, if the speed of light in vacuum is c, the speeds of light in the air and water are

$$\left\{\begin{array}{c}{v}_a=\frac{c}{n_1}\\ v_w=\frac{c}{n_2}\end{array}\right.$$

(20)

Let the coordinate of point C be $\left(x_2,y_2,z_2\right)$. The lengths of the two optical paths OC and CP are

$$\left\{\begin{array}{c}{l}_{OC}=\sqrt{x_2^2+y_2^2+z_2^2}\\ l_{CP}=\sqrt{{\left(x_1-x_2\right)}^2+{\left(y_1-y_2\right)}^2+{\left(z_1-z_2\right)}^2}\end{array}\right.$$

(21)

According to the relationship between speed, time, and distance, the propagation time of the light between O and P is

$$t=\frac{l_{OC}}{v_a}+\frac{l_{CP}}{v_w}$$

(22)

The refraction point C is a point that satisfies Equation (19). When all refraction parameters are known, Equation (22) is a function of coefficient $\lambda$. According to Fermat’s principle, the actual path of light passing between two fixed points in space is always the shortest optical path (or propagation time). So, the derivative of $t$ is equal to 0, which is

$$f\left(\lambda \right)=\frac{dt}{d\lambda }=0$$

(23)

Solving the above formula, we can get the value of $\lambda$. Combining it with Equation (19), the coordinate of point C can be obtained. So, the complete propagation path of the light is established. For the right camera, the simulation process is similar, the only difference is that $l_{OC}$ in Equation (21) is transformed into the following form

$$l_{OC}=\sqrt{{\left(x_R-x_2\right)}^2+{\left(y_R-y_2\right)}^2+{\left(z_R-z_2\right)}^2}$$

(24)

where $\left(x_R,y_R,z_R\right)$ is the coordinate of the origin of the right camera coordinate system in the reference coordinate system.

The target pixel coordinate can be easily calculated based on the coordinate of point C and the camera parameters using the perspective imaging model, thus realizing the simulation of the imaging process.

2.3. Simulation Experimental Design

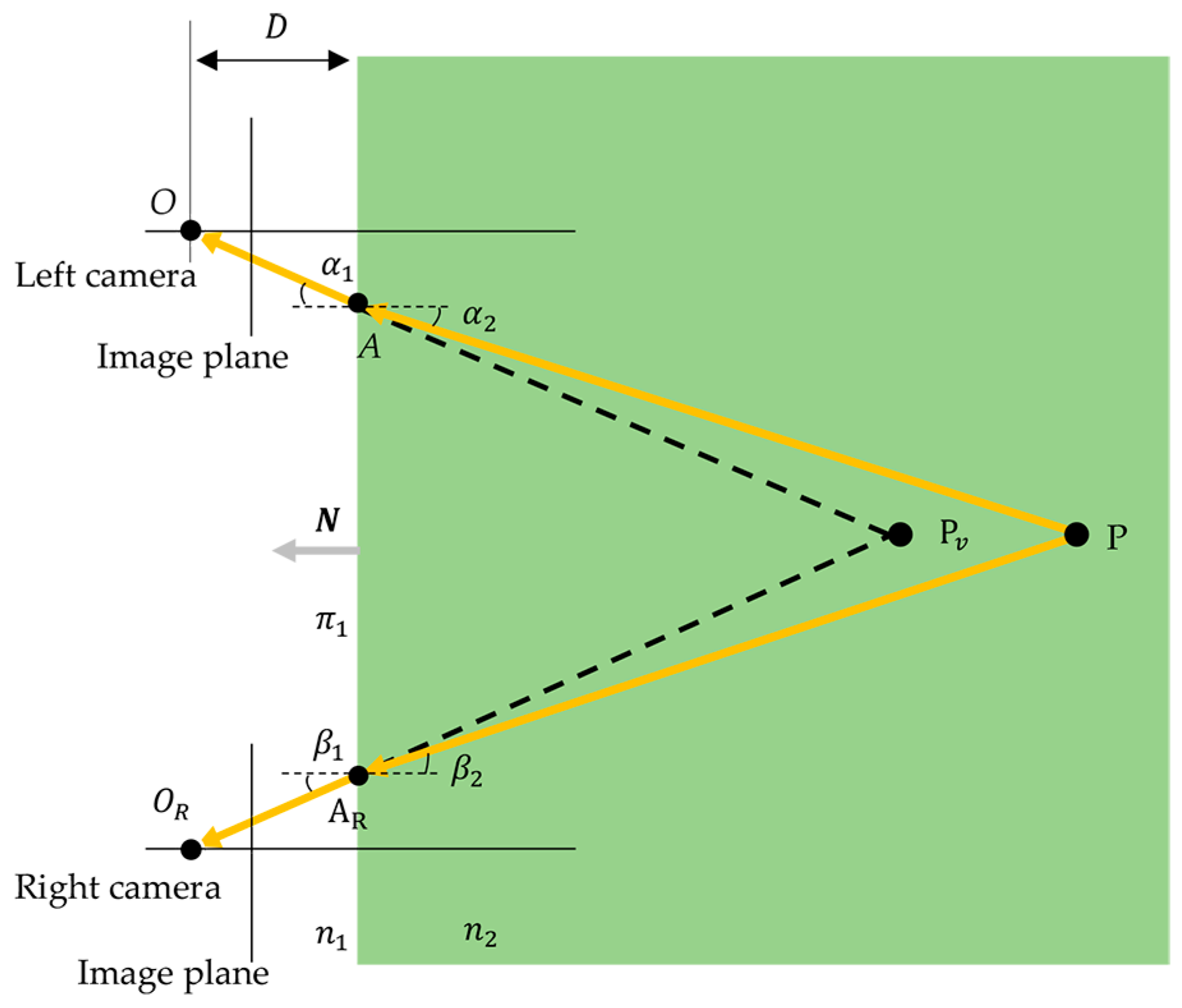
The purpose of the simulation experiments is to evaluate the impact of the deviations of the refraction parameters in the measurement model on the results and to provide guidance for the calibration of the refraction parameters and the construction of the measurement system. The cameras are placed in the air and the target in the water, as shown in Figure 3. The intrinsic and external parameters of the left and right cameras are known. The two cameras share the same refraction interface. The refraction parameters that affect the measurement model are the distance D between the left camera and the refraction interface, the medium refractive indices $n_1$ and $n_2$, and the refraction interface normal N. Since the refraction angle of the light depends on the relative refractive index, the relative refractive index $n_r=n_1/n_2$ is discussed in the simulation experiments.

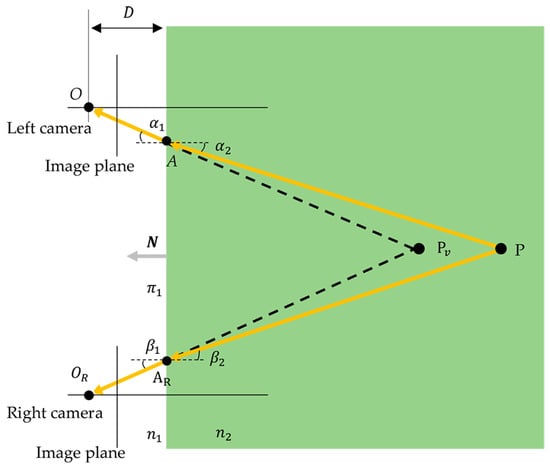
Figure 3. Air–water dual-medium visual-measurement scenario with one flat interface.

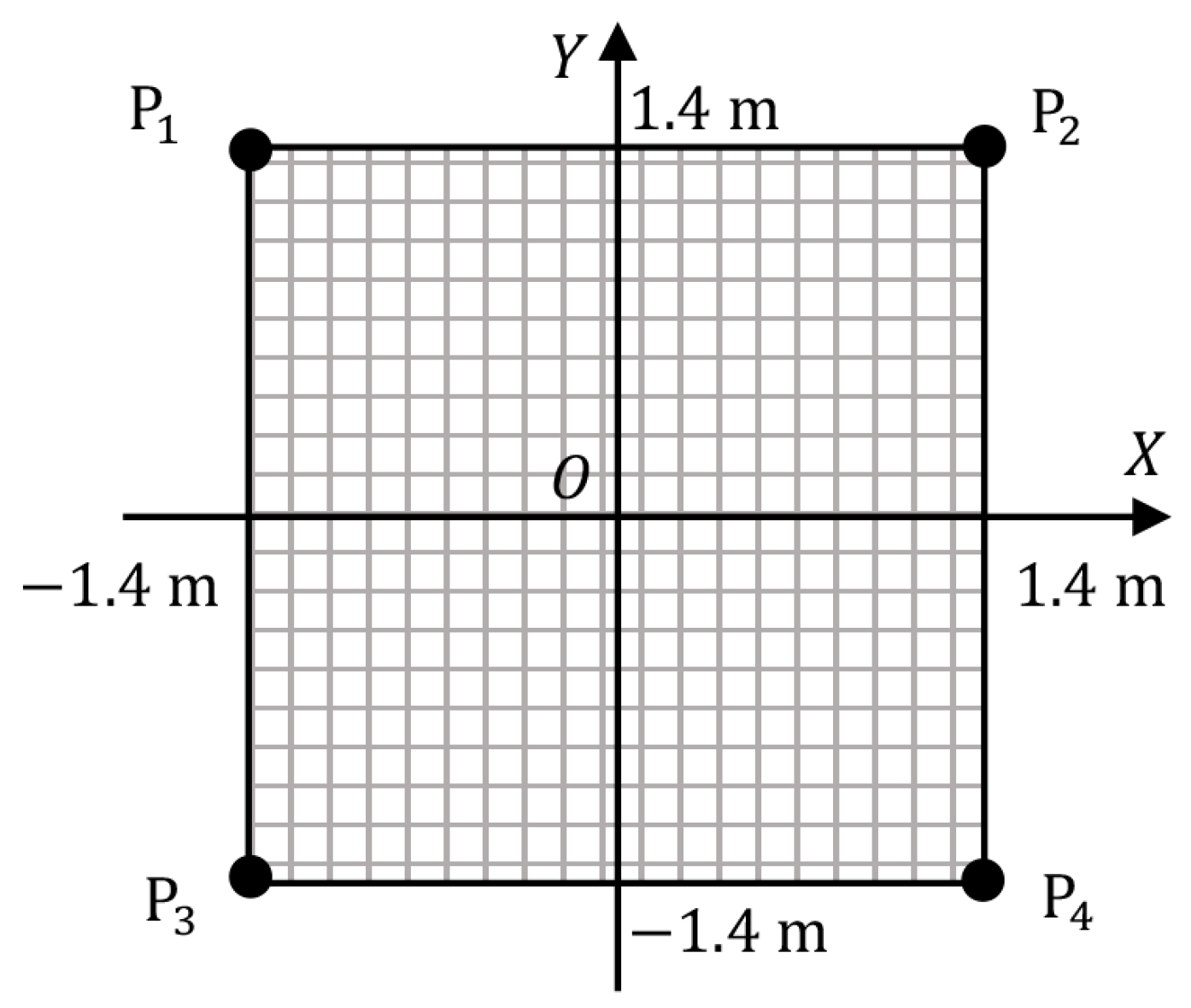
Take the left camera coordinate system as the reference coordinate system. We simulated a $2.8\times 2.8{ \mathrm{m}}^2$ square area and its distribution in the XOY plane of the left camera coordinate system is shown in Figure 4. The $Z$ coordinate of the square area can take different values.

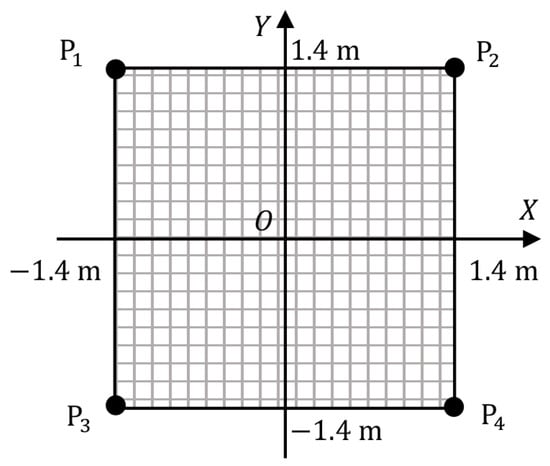
Figure 4. Target area and four feature points.

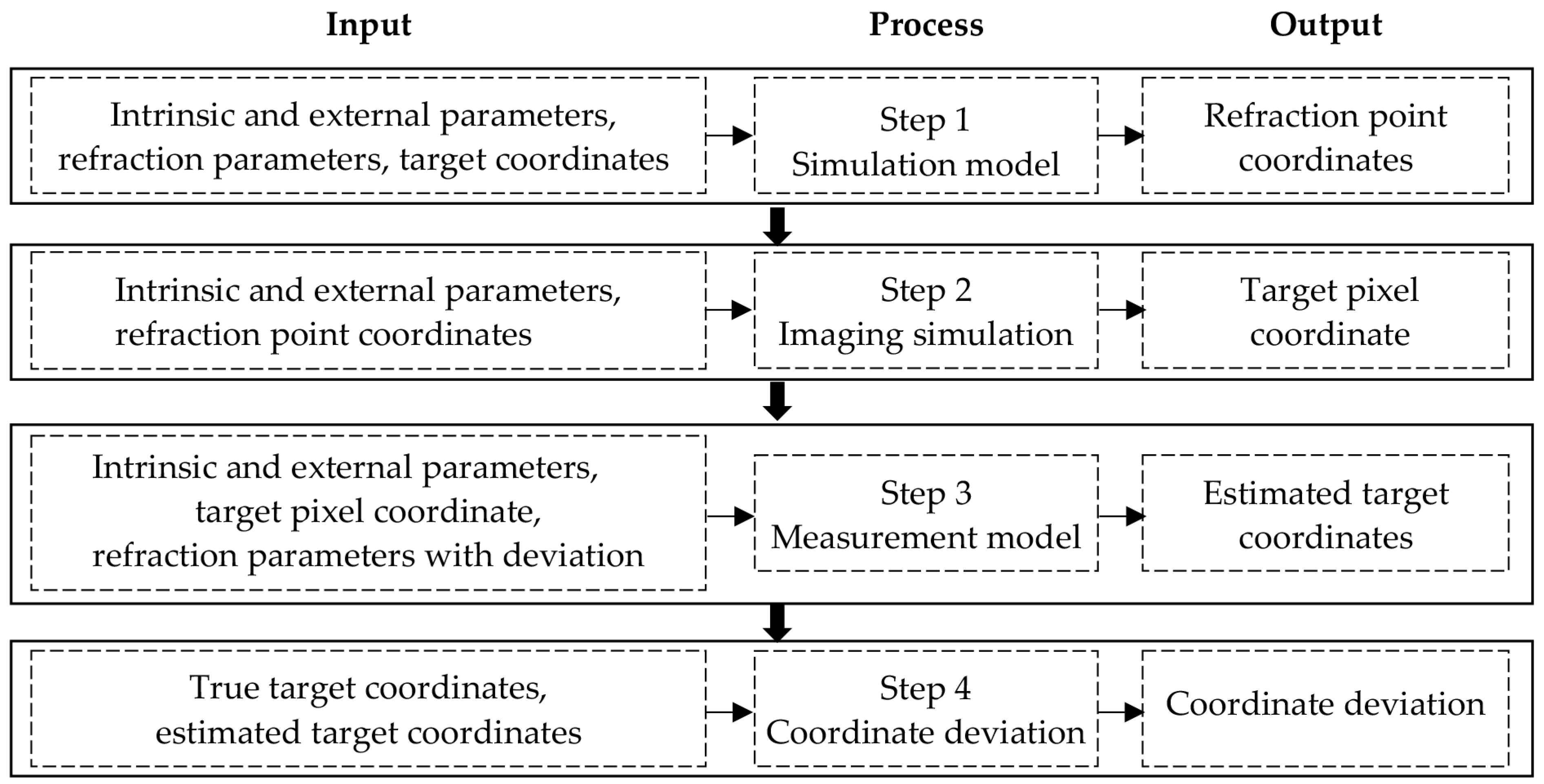
The intrinsic and external parameters of the left and right cameras and the target coordinates are known. The true values of the refraction parameters are set as shown in Table 1. The simulation process is shown in Figure 5. The experiments consist of four steps. (1) In step 1, based on the camera parameters, the refraction parameters without deviations, and the target coordinates, the simulation model proposed in Section 2.2 is used to simulate the coordinate of the refraction point. (2) In step 2, based on the camera parameters and the refraction point coordinate, the corresponding pixel coordinate is obtained using the perspective imaging model. (3) In step 3, based on the camera parameters, the target pixel coordinate, and the refraction parameters with certain deviations, the refractive measurement model described in Section 2.1 is used to estimate the target coordinate. (4) In step 4, the deviation between the estimated and the true coordinates of the target is calculated. The true coordinate of the target is $\left(X, Y, Z\right)$, and the estimated coordinate obtained in step 3 is $\left(X^e, Y^e,Z^e\right)$. The coordinate deviations are denoted as $d_x$, $d_y$, and $d_z$, respectively.

$$\left\{\begin{array}{c}{d}_x=X^e-X\\ d_y=Y^e-Y\\ d_z=Z^e-Z\end{array}\right.$$

(25)

Table 1. True values of the refraction parameters.

D	${\mathit{n}}_{\mathit{r}}$	N
10 cm	${\displaystyle \frac{n_1}{n_2}}={\displaystyle \frac{1}{1.33}}$	$\left(0,0,1\right)$

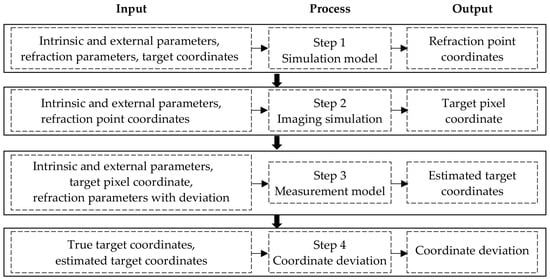
Figure 5. Simulation process.

The total coordinate deviation is given by $d_p$, where $d_p=\sqrt{d_x^2+d_y^2+d_z^2}$. Since the pixel coordinate of the target is obtained through the imaging model in step 2, they do not contain any errors. The refraction parameters used in step 3 are added with a certain amount of deviation, with the requirement that the deviation is added to only one parameter at a time. Three experiments were conducted. Experiment 1 discussed the sensitivity of the measurement model to the refraction parameters. Experiment 2 analyzed the influence of the fixed refraction-parameter deviation on the targets at different distances. Experiment 3 studied the change in the measurement results of fixed targets with the refraction parameter.

3. Results

3.1. Experiment 1

The aim of this experiment is to analyze the sensitivity of the dual-medium visual measurement model to deviations in refraction parameters. All targets are on the same plane with a $Z$-distance of 5 m as shown in Figure 4. After intentionally introducing deviations in the refraction parameters, the measured coordinates of the targets will differ from their true values, resulting in coordinate discrepancies. Sequentially introduce deviations in different refraction parameters until the maximum $d_p$ reaches 1 cm.

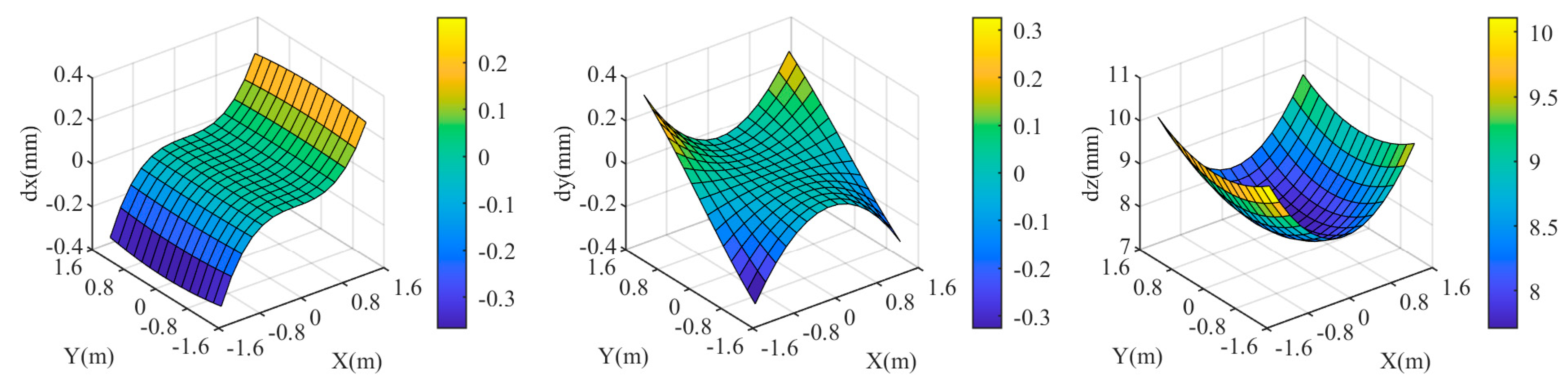
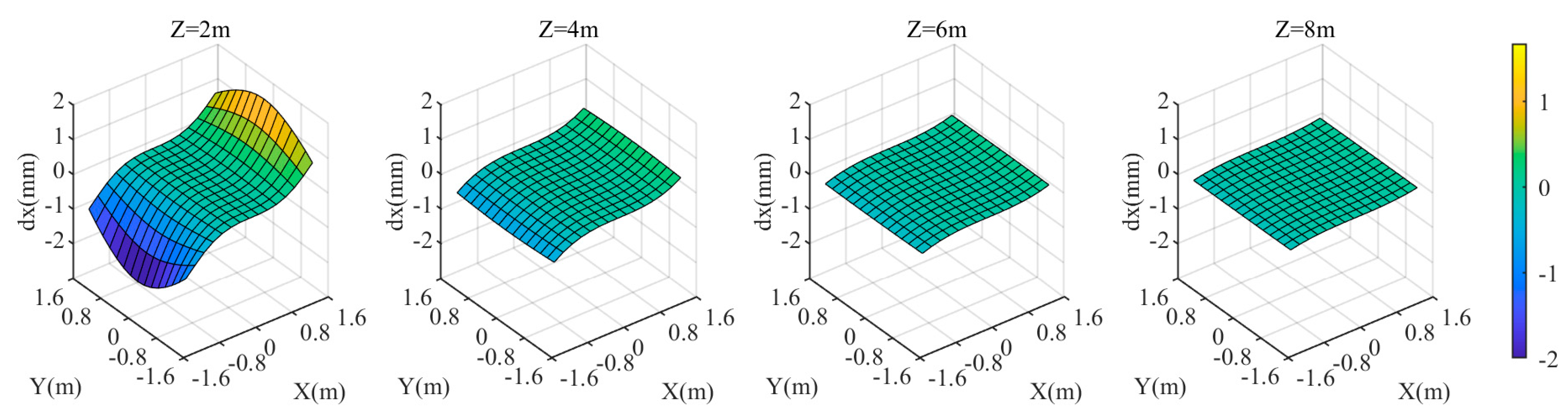
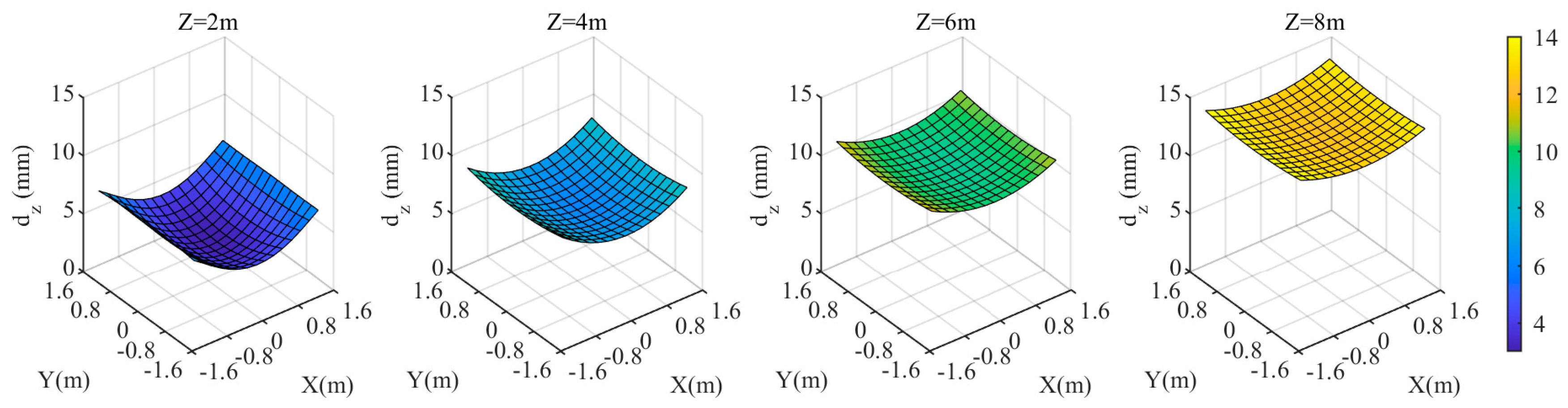
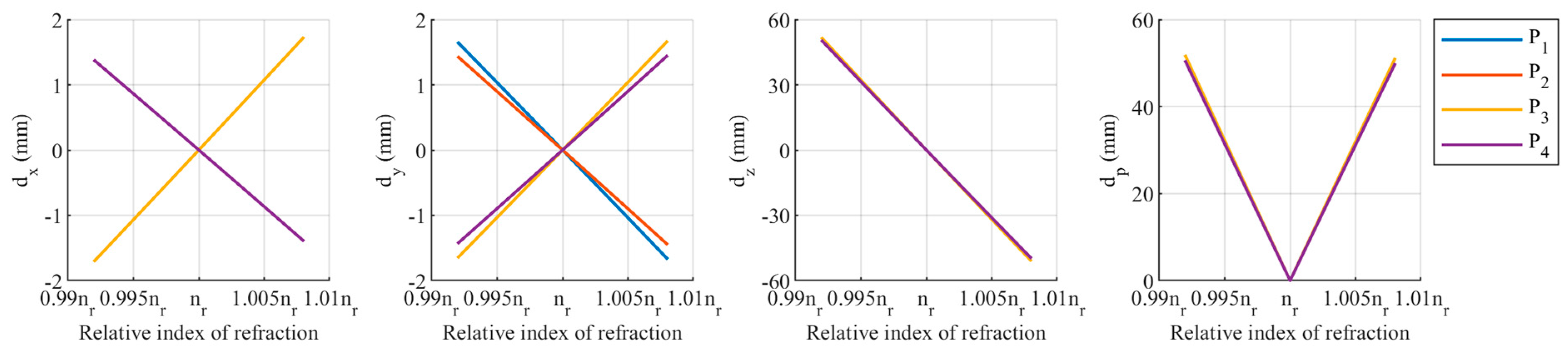
First, analyze the impact of deviation in the relative refractive index. The true value of the relative refractive index is $n_r$. When the relative refractive index changes to 0.99843$n_r$, the maximum $d_p$ is 10 mm, as shown in Figure 6. In this case, the discrepancies in $X$ and $Y$ coordinate components are minimal, less than 0.5 mm, and $d_p$ primarily depends on the discrepancy in $Z$ coordinate component. Relative refractive index deviation is more likely to cause $Z$ coordinate deviation. The maximum coordinate discrepancy occurs at the four corners in Figure 4.

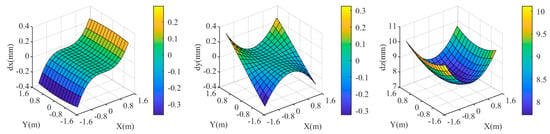
Figure 6. Coordinate deviation of the target area at $Z=5 \mathrm{m}$ when the relative refraction is 0.99843$n_r$. $\max \left(d_p\right)=10 \mathrm{mm}$.

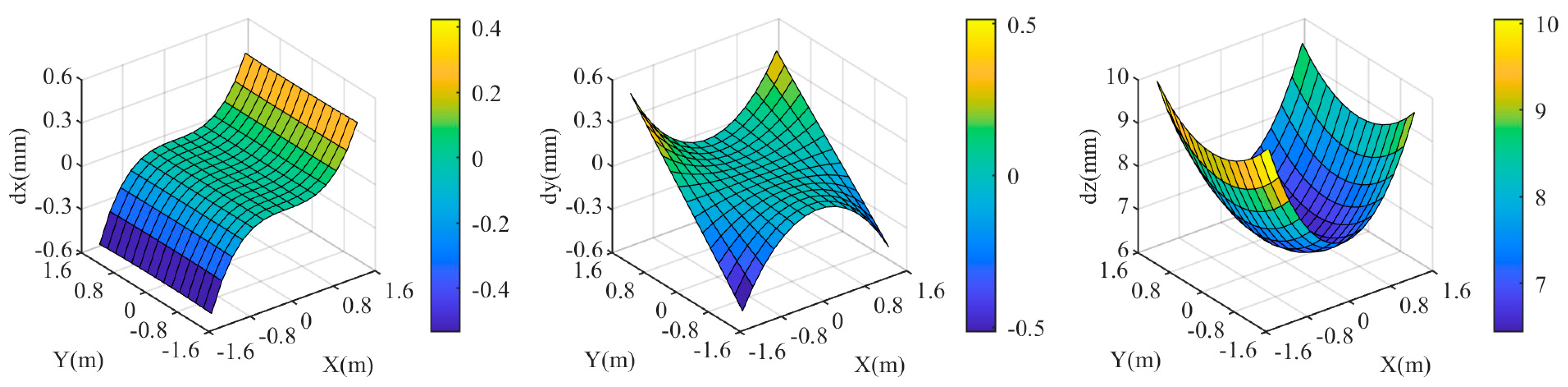
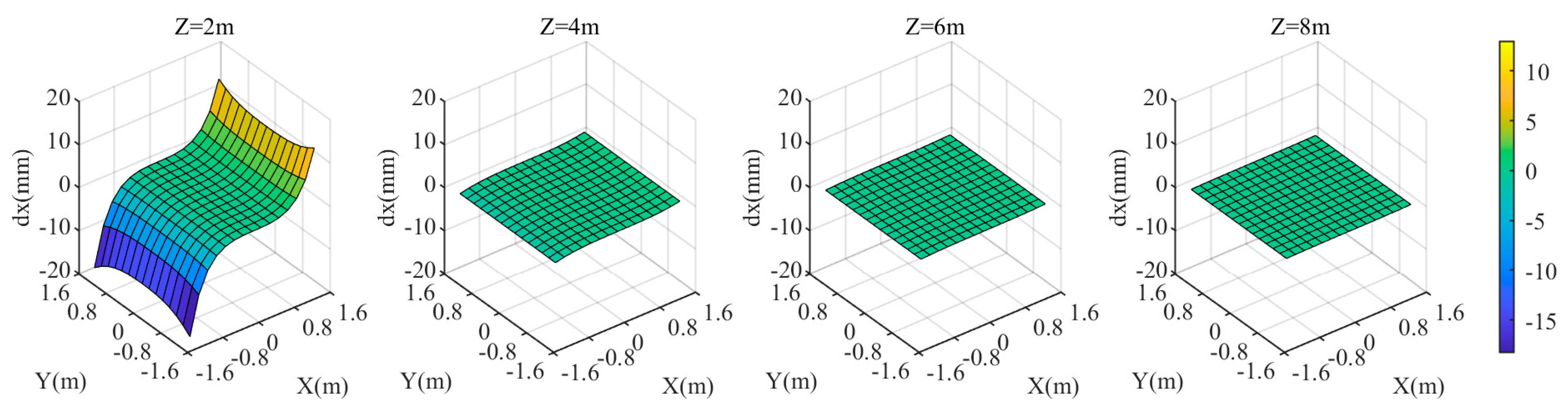
Next, analyze the impact of deviation in the distance from the camera to the refractive interface. The true value of this distance is denoted as D. When the distance changes to 0.805D, the maximum $d_p$ is 10 mm, as shown in Figure 7. The deviation in D has a minimal impact on $X$ and $Y$ coordinate components of the target, less than 1 mm. It is more likely to cause discrepancies in the $Z$ coordinate component, with $d_p$ primarily depending on the discrepancy in the $Z$ coordinate component. The maximum coordinate discrepancy occurs at the four corners in Figure 4.

Figure 7. Coordinate deviation of the target area at $Z=5 \mathrm{m}$ when the distance is $0.805D$. $\max \left(d_p\right)=10 \mathrm{mm}$.

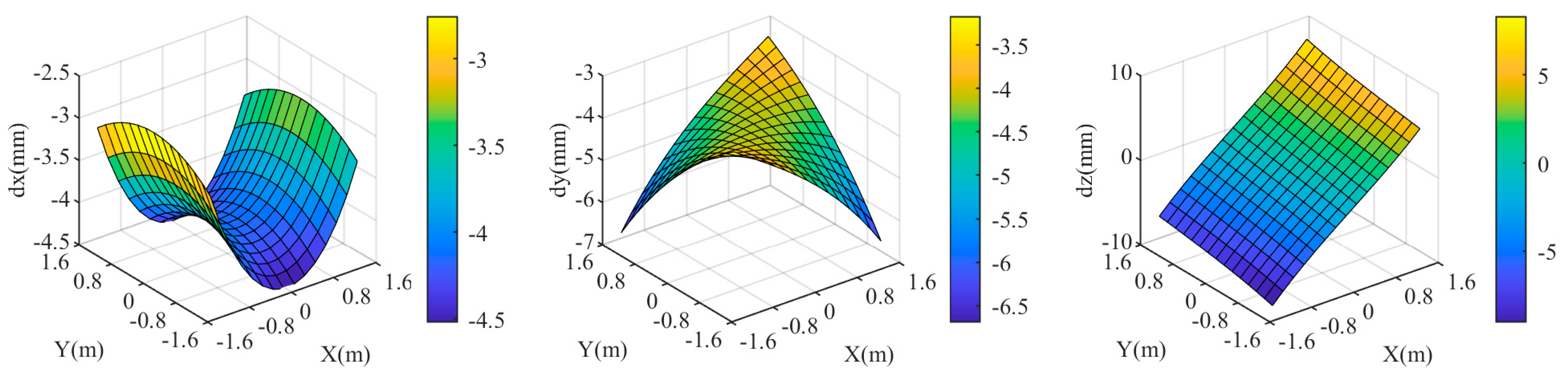
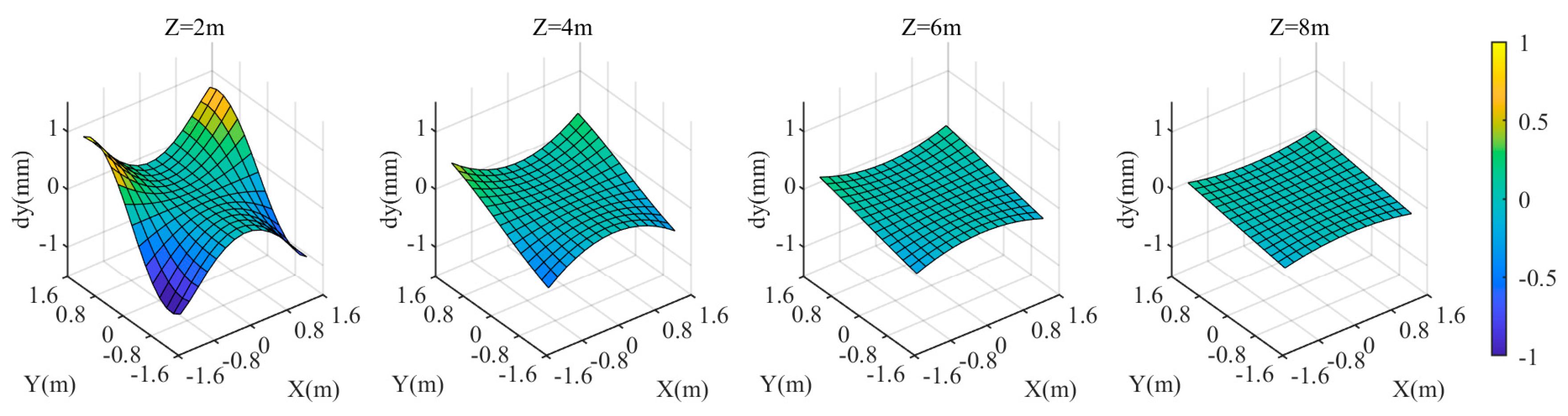
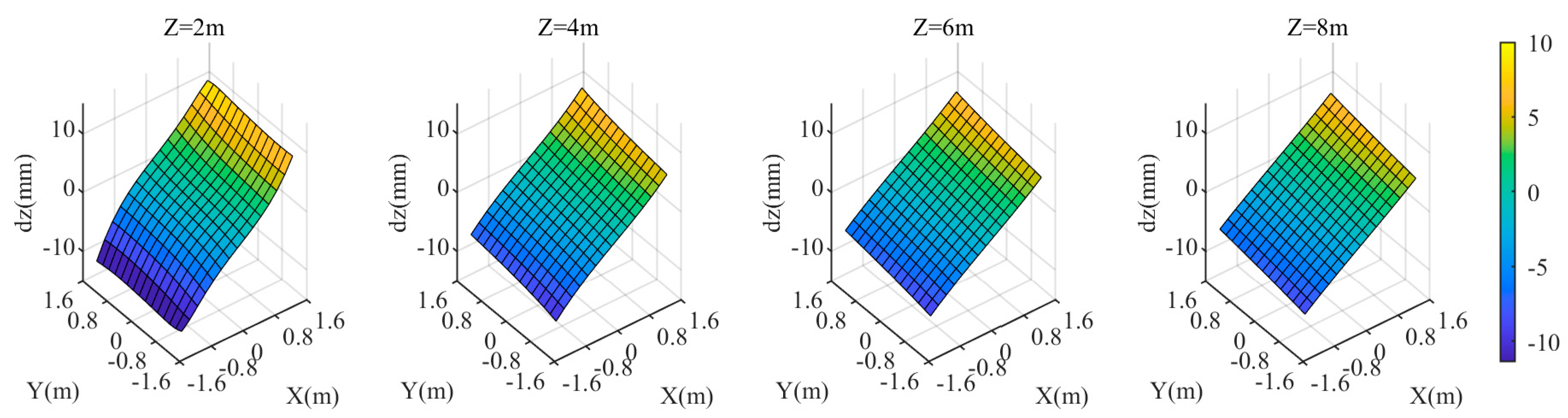
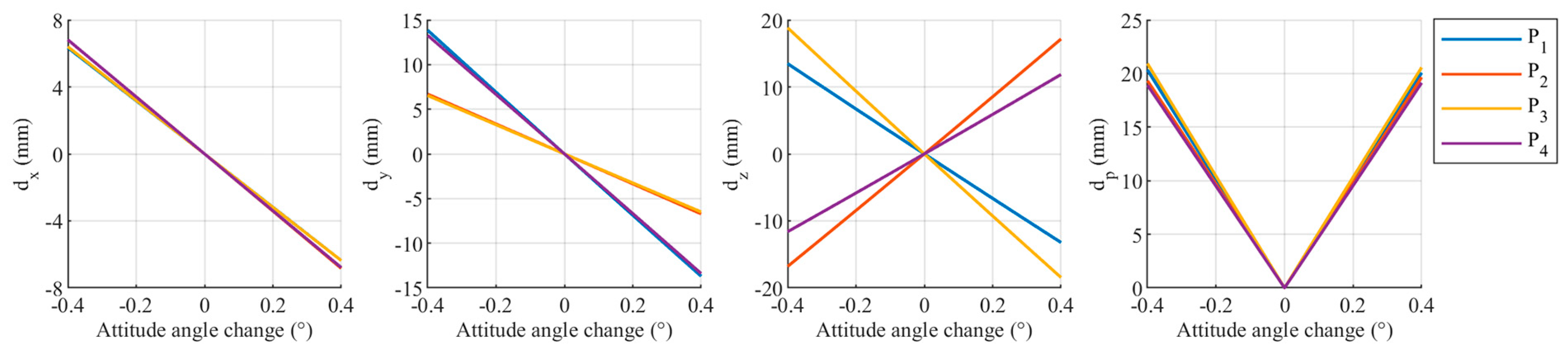
Finally, analyze the impact of deviation in the normal direction of the refractive surface. The theoretical direction of the refractive surface normal is parallel to the optical axis of the left camera. The normal direction deviation is represented by the simultaneous rotation of its three attitude angles by the same angle. When the rotation angle is 0.195°, the maximum $d_p$ is 10 mm, as shown in Figure 8. Deviations in the normal direction have a significant impact on all three coordinate components of the targets, especially the $Y$ and $Z$ coordinates. The extent of the impact varies across different points in the target area; points closer to the center are less affected, while points closer to the four corners are more affected.

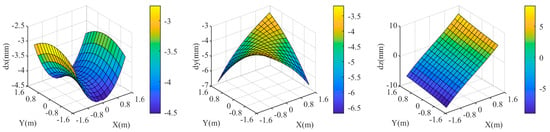
Figure 8. Coordinate deviation of the target area at $Z=5 \mathrm{m}$ when the rotation angle of the normal direction of the refractive surface is 0.195°. $\max \left(d_p\right)=10 \mathrm{mm}$.

Combining Figure 6, Figure 7 and Figure 8, it is evident that the dual-medium stereo-vision measurement model is highly sensitive to deviations in the relative refractive index. Even a deviation of 0.157% can result in a maximum comprehensive coordinate deviation of up to 10 mm in the target area. In contrast, the measurement model is less sensitive to deviations in the distance from the camera to the refractive interface and the normal direction of the refractive interface. This indicates that in underwater experiments or practical applications, special attention must be given to the calibration of the refractive indices of different mediums.

3.2. Experiment 2

In Experiment 1, we fixed the target area at $Z=5 \mathrm{m}$. However, with the same deviations in refraction parameters, the coordinate deviations of the target might differ if the distance between the target and the camera varies. Four different $Z$ values were set at intervals of 2 m, ranging from 2 m to 8 m. Deviations were sequentially introduced in different refraction parameters: the relative refractive index changed to 0.99843$n_r$, the distance from the camera to the refractive interface changed to 0.805D, and the rotation angle of the refractive surface normal was 0.195°.

3.2.1. Target Plane

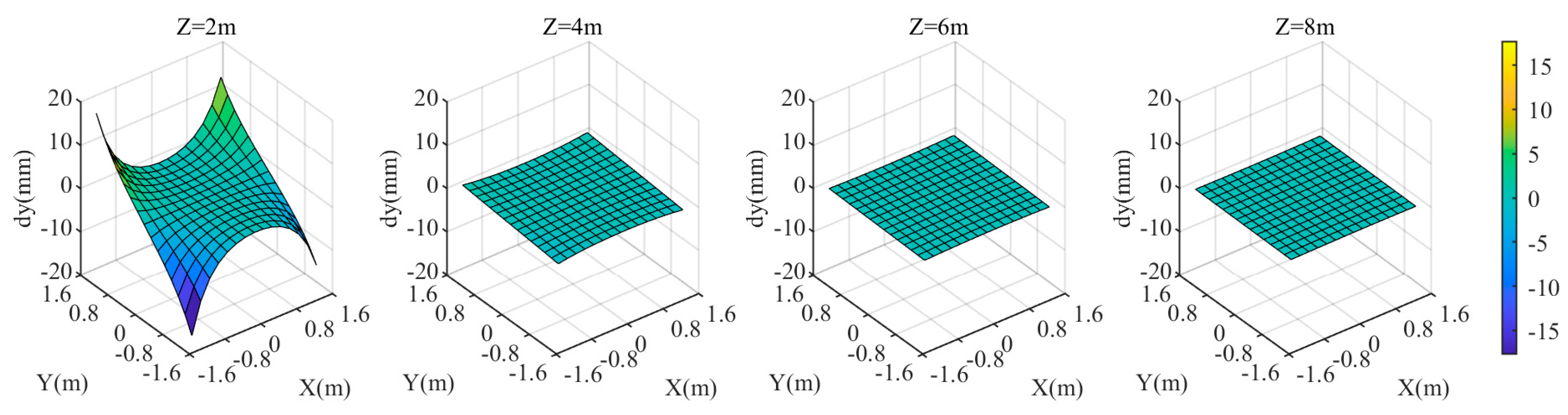
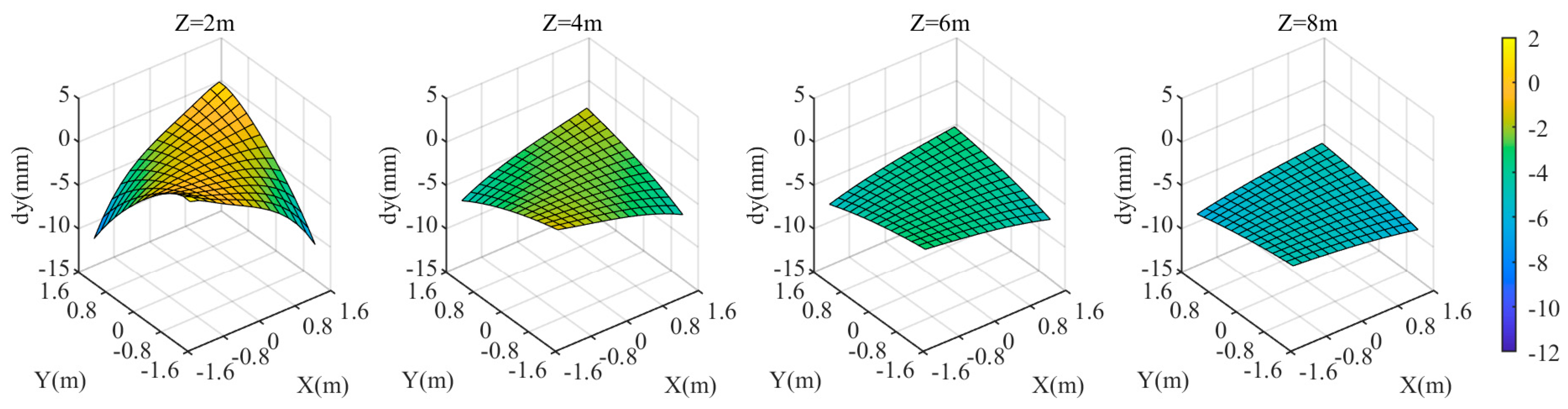
When the relative refractive index is 0.99843$n_r$, the coordinate discrepancies of the three components in the target area are shown in Figure 9, Figure 10 and Figure 11. For different $Z$ values, the discrepancies in $X$ and $Y$ coordinate components remain relatively small. However, the smaller the $Z$ value, the relatively larger the $d_x$ and $d_y$ discrepancies. At $Z=2 \mathrm{m}$, the maximum values of $d_x$ and $d_y$ are approximately ±2 mm and ±1 mm, respectively. The discrepancy in $Z$ coordinate component, $d_z$, exhibits a significantly different variation pattern. The larger the $Z$ value, the larger the $d_z$. At $Z=2 \mathrm{m}$, $d_z$ is the smallest, with a maximum value of approximately 7.4 mm in the edge of the target area; at $Z$ = 8 m, $d_z$ is the largest, with both the maximum and minimum values of $d_z$ in the target area being approximately 14 mm. Since $d_z$ is significantly larger than $d_x$ and $d_y$, when the relative refractive index deviation is constant, the closer the target is to the camera, the smaller the resulting $d_p$. The closer the target is to the center of the region, the smaller its $d_p$ is.

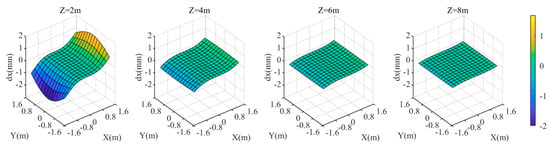
Figure 9. $X$ coordinate deviation of the target area at different distances from the camera when the relative refraction is 0.99843$n_r$.

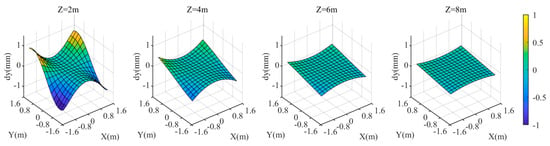
Figure 10. $Y$ coordinate deviation of the target area at different distances from the camera when the relative refraction is 0.99843$n_r$.

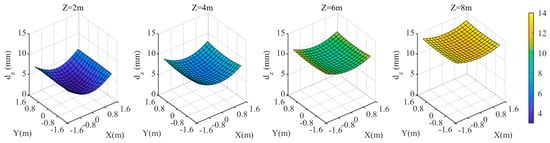
Figure 11. $Z$ coordinate deviation of the target area at different distances from the camera when the relative refraction is 0.99843$n_r$.

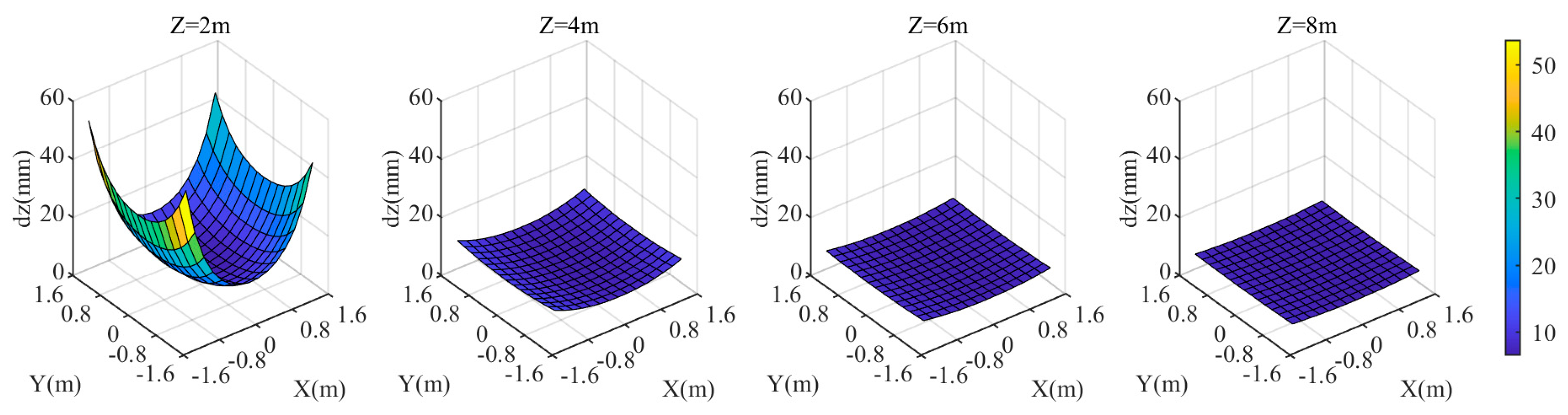
When the distance from the camera to the refractive interface is 0.805D, the coordinate discrepancies of the three components in the target area are shown in Figure 12, Figure 13 and Figure 14. When $Z$ is greater than 4 m, as $Z$ value increases, $d_x$, $d_y$, and $d_z$ gradually decrease. At $Z=2 \mathrm{m}$, the maximum values of $d_x$ and $d_y$ are approximately ±18 mm, and the maximum value of $d_z$ is approximately 54 mm, occurring at the four corners of the area. Overall, the farther the target plane is from the camera, the smaller the values of $d_x$, $d_y$, and $d_z$, resulting in a smaller $d_p$. Additionally, the closer the target is to the center of the area, the smaller the $d_p$.

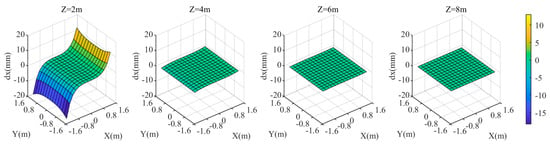
Figure 12. $X$ coordinate deviation of the target area at different distances from the camera when the distance is $0.805D$.

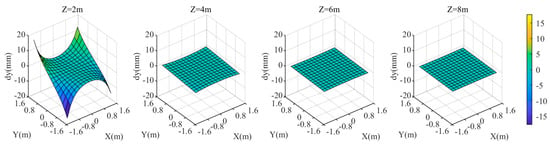
Figure 13. $Y$ coordinate deviation of the target area at different distances from the camera when the distance is $0.805D$.

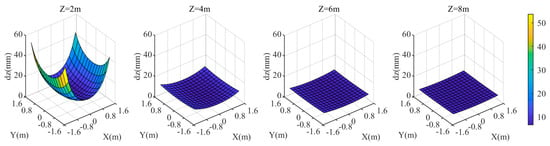
Figure 14. $Z$ coordinate deviation of the target area at different distances from the camera when the distance is $0.805D$.

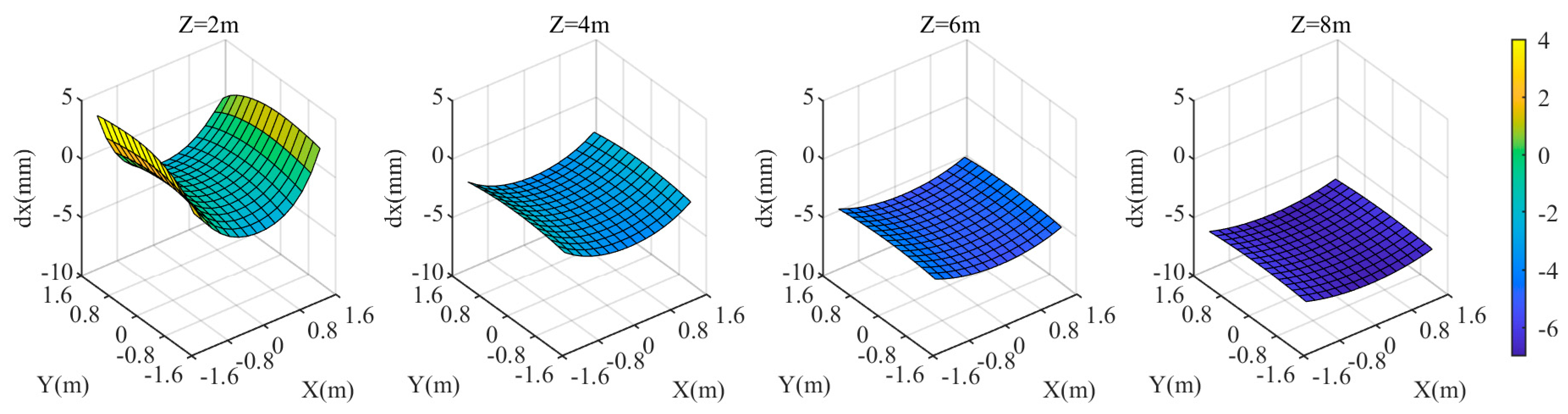
When the three attitude angles of the refractive interface normal all change by 0.195°, the coordinate discrepancies of the three components in the target area are shown in Figure 15, Figure 16 and Figure 17. As the $Z$ value increases from 2 m to 8 m, $d_x$ changes from positive to negative, and its absolute value generally increases. At $Z$ = 2 m, there is a noticeable variation in $d_x$ among different points in the target area, with $d_x$ decreasing towards the center of the area. As the $Z$ value increases, the variation in $d_x$ among different points in the target area gradually diminishes. At $Z$ = 8 m, $d_x$ reaches −7 mm. The $d_y$ component exhibits a similar trend with changes in $Z$; the larger the $Z$ value, the greater the absolute value of $d_y$. At $Z$ = 2 m, there is a noticeable variation in $d_y$ among different points in the target area, with $d_y$ decreasing towards the center of the area. The relationship between $d_z$ and $Z$ is relatively less pronounced. As $Z$ increases from 2 m to 8 m, $d_z$ slightly decreases. However, there are noticeable differences in $d_z$ among different points in the target area.

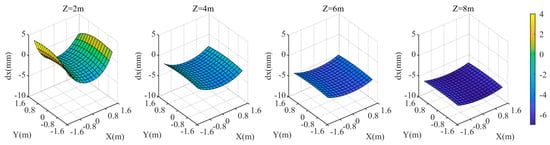
Figure 15. $X$ coordinate deviation of the target area at different distances from the camera when the rotation angle of the normal direction of the refractive surface is 0.195°.

Figure 16. $Y$ coordinate deviation of the target area at different distances from the camera when the rotation angle of the normal direction of the refractive surface is 0.195°.

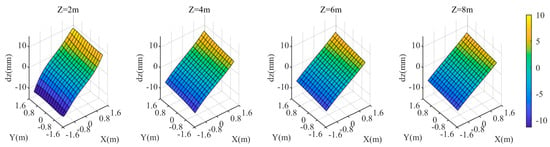
Figure 17. $Z$ coordinate deviation of the target area at different distances from the camera when the rotation angle of the normal direction of the refractive surface is 0.195°.

3.2.2. Fixed Points

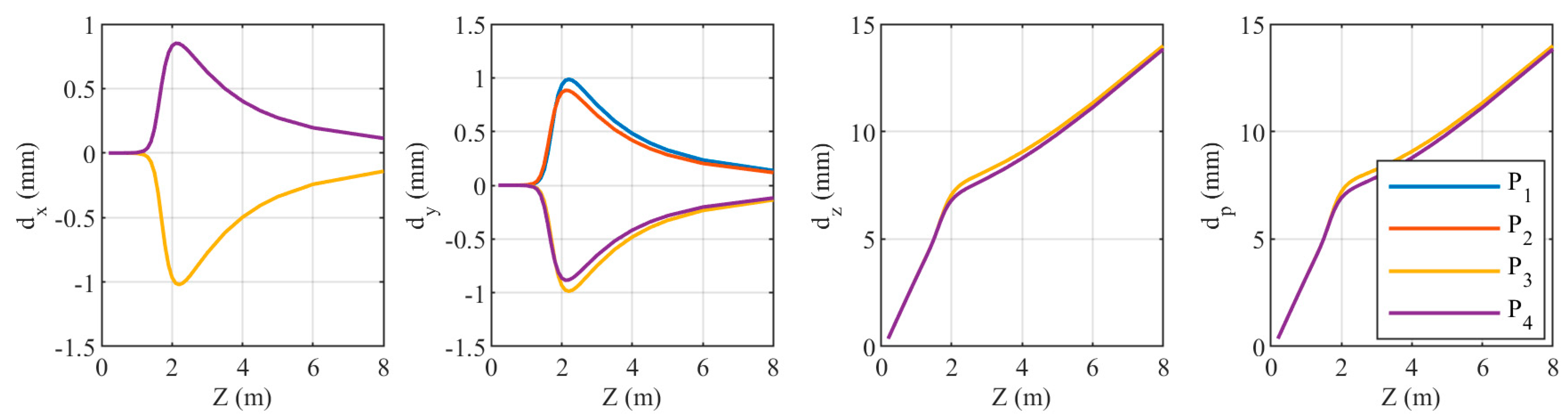
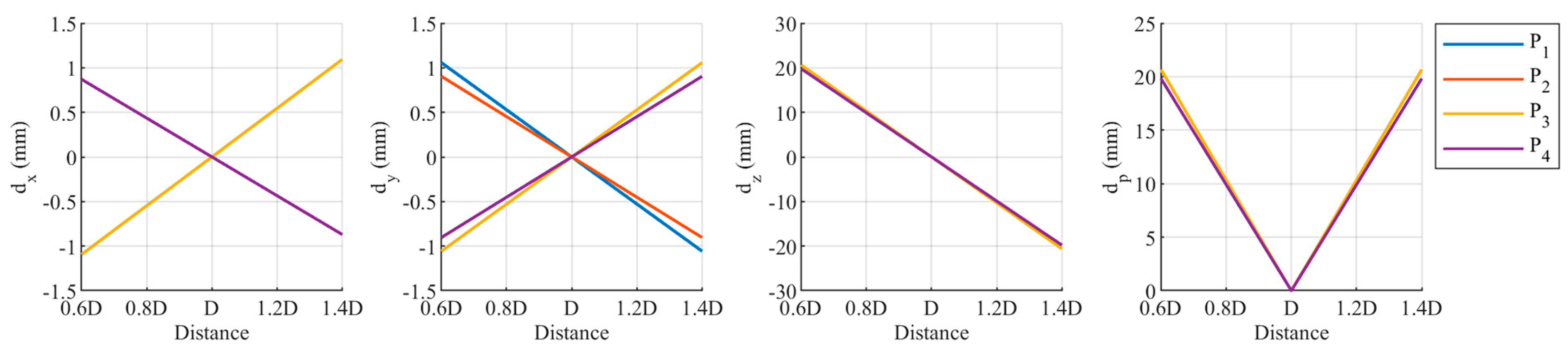
To further analyze the relationship between the coordinate deviations of the target and $Z$ value, we selected the four corners of the target area shown in Figure 4 as feature points for the experiment. The $Z$ values range from 0.5 m to 8 m. Based on the previous analysis, we know that when $Z$ value is fixed, these four points have the largest $d_p$ within the entire target area. We sequentially analyzed different refraction parameters, maintaining the same deviation magnitudes as discussed earlier.

When the relative refractive index is 0.99843$n_r$, the coordinate discrepancies of the four points are shown in Figure 18. As $Z$ increases, $d_x$ and $d_y$ exhibit similar trends: both initially increase rapidly, then decrease, with the rate of decrease being fast at first and then slowing down. The maximum values of $d_x$ and $d_y$ occur around $Z$ = 2.2 m, about ±1 mm. For $d_x$, the trends for ${\mathrm{P}}_1$ and ${\mathrm{P}}_3$, as well as ${\mathrm{P}}_2$ and ${\mathrm{P}}_4$, are completely consistent. For $d_y$, the trends for ${\mathrm{P}}_1$ and ${\mathrm{P}}_2$, as well as ${\mathrm{P}}_3$ and ${\mathrm{P}}_4$, are very similar. $d_z$ increases with increasing $Z$. Since $d_z$ is much larger than $d_x$ and $d_y$, $d_p$ mainly depends on the magnitude of $d_z$. The trends for $d_z$ and $d_p$ are consistent for all four points.

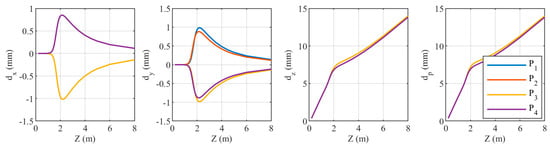
Figure 18. Relationship between the coordinate components of the four target points and $Z$ when the relative refraction is 0.99843$n_r$.

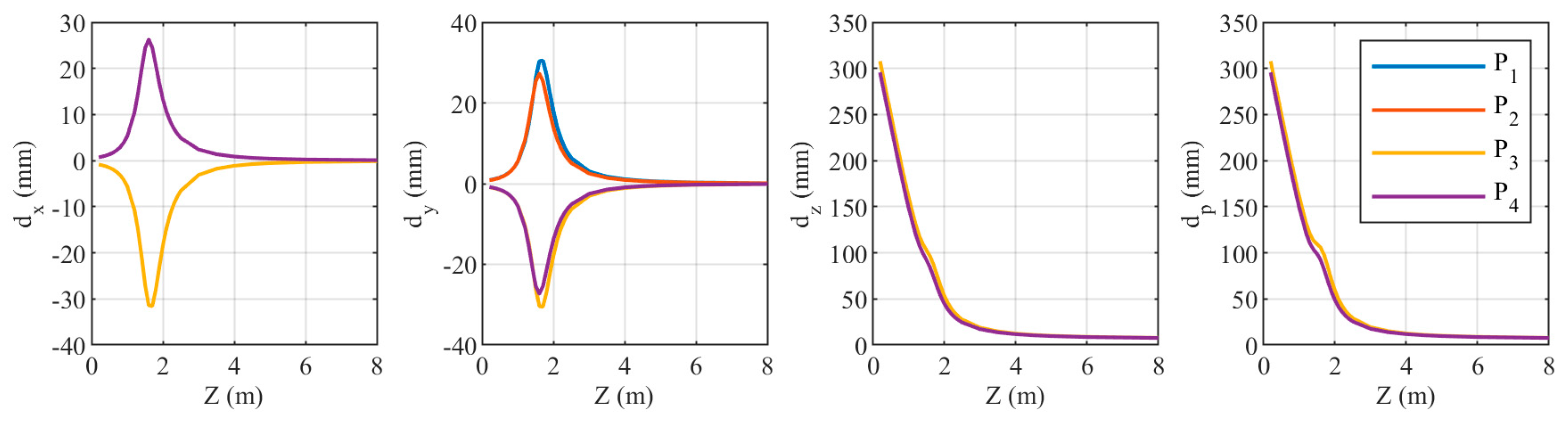
When the distance from the camera to the refractive interface is $0.805D$, the coordinate discrepancies of the four points are shown in Figure 19. Similar to Figure 18, as $Z$ increases, $d_x$ and $d_y$ exhibit similar trends: both initially increase rapidly, then decrease, with the rate of decrease being fast at first and then slowing down. However, the maximum values of $d_x$ and $d_y$ occur around $Z=1.7 \mathrm{m}$, reaching approximately ±30 mm. For $d_x$, the trends for ${\mathrm{P}}_1$ and ${\mathrm{P}}_3$, as well as for ${\mathrm{P}}_2$ and ${\mathrm{P}}_4$, are consistent. For $d_y$, the trends for ${\mathrm{P}}_1$ and ${\mathrm{P}}_2$, as well as for ${\mathrm{P}}_3$ and ${\mathrm{P}}_4$, are similar. $d_z$ decreases with increasing $Z$, with the rate of decrease being fast at first and then slowing down, with an inflection point around $Z=3 \mathrm{m}$. Although the values of $d_x$ and $d_y$ around $Z=1.7 \mathrm{m}$ exceed ±20 mm, they are still an order of magnitude smaller than $d_z$. Therefore, $d_p$ mainly depends on the magnitude of $d_z$. The trends for $d_z$ and $d_p$ are consistent for all four points; as $Z$ value increases, $d_p$ decreases.

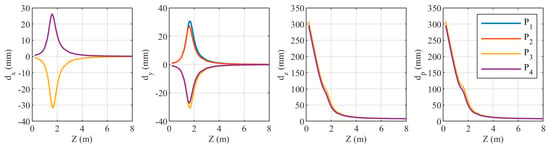
Figure 19. Relationship between the coordinate components of the four target points and $Z$ when the distance is $0.805D$.

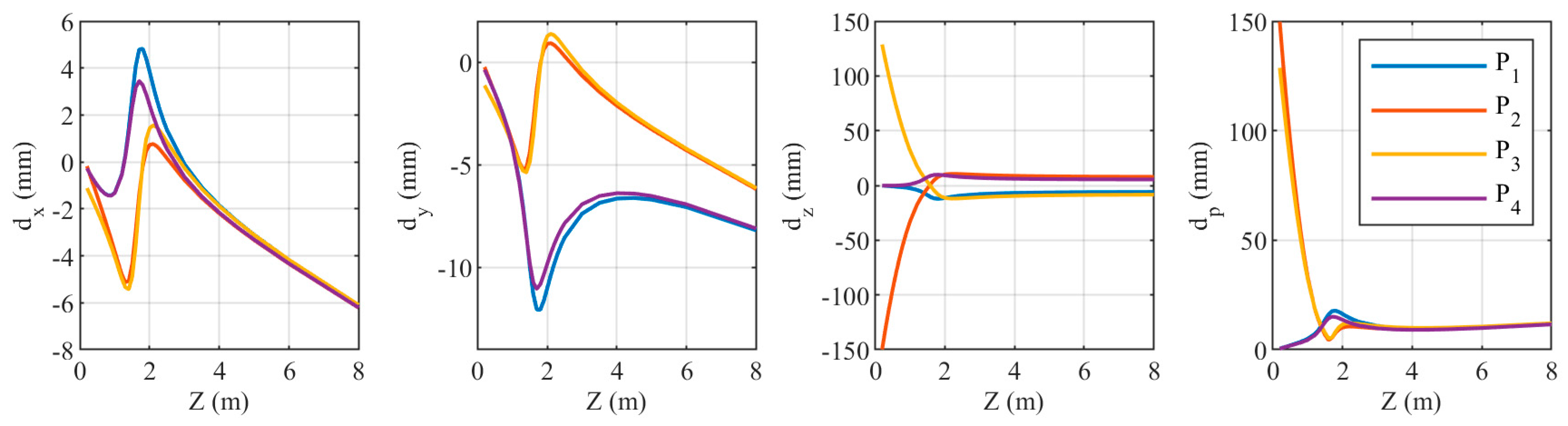
When the three attitude angles of the refraction interface normal change by 0.195°, the coordinate component deviations of the four points are shown in Figure 20. For $Z$ less than 3 m, the variation trends of the three coordinate component deviations are quite complex. The variation trends of $d_z$ differ significantly among different points. For points ${\mathrm{P}}_2$ and ${\mathrm{P}}_3$, $d_z$ is significantly larger than $d_x$ and $d_y$. In contrast, for points ${\mathrm{P}}_1$ and ${\mathrm{P}}_4$, the deviations in all three coordinate components are relatively small. When $Z$ is greater than 3 m, $d_x$ and $d_y$ generally increase with increasing $Z$, while $d_z$ shows no obvious variation. Additionally, $d_x$ and $d_y$ are similar in magnitude and significantly larger than $d_z$. For points ${\mathrm{P}}_2$ and ${\mathrm{P}}_3$, when $Z$ is small, the deviation $d_p$ is mainly determined by $d_z$. However, when $Z$ is large, $d_p$ is primarily influenced by $d_x$ and $d_y$. For points ${\mathrm{P}}_1$ and ${\mathrm{P}}_4$, $d_p$ is affected by all three coordinate components, and as $Z$ increases, the influence of $d_x$ and $d_y$ becomes more significant.

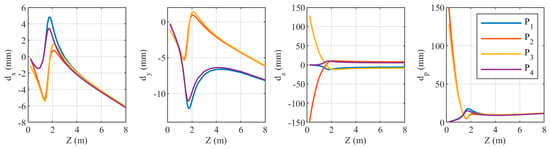
Figure 20. Relationship between the coordinate components of the four target points and $Z$ when the rotation angle of the normal direction of the refractive surface is 0.195°.

3.3. Experiment 3

In the aforementioned experiments, we fixed the deviation of the refraction parameters. However, as the deviations of the refraction parameters vary, the target-coordinate deviations also change accordingly. Therefore, we conducted this experiment to investigate the relationship between target-coordinate deviations and refraction-parameter deviations. In this experiment, we continued to select the four feature points shown in Figure 4 as targets and set $Z$ to 5 m. We then sequentially introduced deviation sequences into different refraction parameters.

The relationship between the deviations of the target coordinate and the three refraction-parameter deviations—relative refractive index, the distance from the camera to the refraction interface, and the direction of the refraction interface normal—is shown in Figure 21, Figure 22 and Figure 23. $d_x$, $d_y$, and $d_z$ all exhibit a linear relationship with the refraction-parameter deviations. The $d_p$ plot displays a symmetric distribution with the true value of the refraction parameters as the axis of symmetry, indicating that both positive and negative deviations in the refraction parameters have the same effect on $d_p$. The smaller the deviation in the refraction parameters, the closer $d_x$, $d_y$, $d_z$, and $d_p$ are to zero.

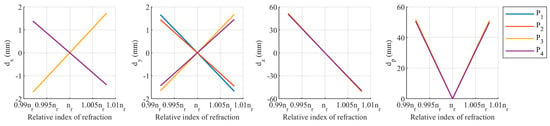
Figure 21. Relationship between target-coordinate deviation and relative refractive index deviation.

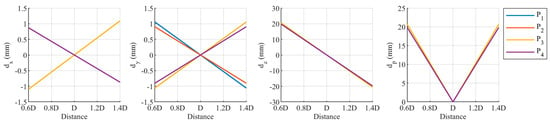
Figure 22. Relationship between target-coordinate deviation and camera-to-refractive-interface distance deviation.

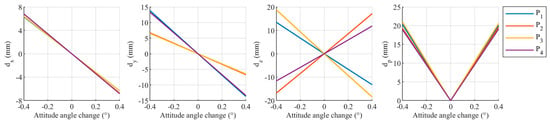
Figure 23. Relationship between target-coordinate deviation and normal direction of refraction interface.

4. Discussion

When the cameras are in the air and the target is in the water, the light path from the target to the camera undergoes refraction, causing the light to deviate from a straight line. In order to compensate for refraction in stereo-vision measurement, a theoretically rigorous approach is to use the refraction-measurement model. However, the refraction-measurement model involves refraction parameters such as the refractive indices of the medium, the distance from the camera to the refractive interface, and the normal of the refractive interface. These parameters generally require calibration. Due to the presence of errors, the calibrated refraction parameters inevitably differ from their true values. The experimental results in Section 3 demonstrate the impact of deviations in refraction parameters on stereo-vision measurement.

The impact of different refraction-parameter deviations on stereo-vision measurement varies, and the magnitude of this impact is related to the distribution of the target within the plane. Deviations in the relative refractive index and the distance between the target and the camera are more likely to cause discrepancies in the Z coordinate, while their effect on the X and Y coordinates is relatively minor. The total coordinate deviation of the target is primarily determined by the Z-coordinate deviation, and the closer the target is to the edge of the field of view, the greater its coordinate deviation. Deviations in the orientation of the refractive interface normal significantly affect all three coordinate components of the target. Regardless of the type of refraction-parameter deviation, the overall trend shows that the closer the target is to the edge of the field of view, the greater the coordinate deviation. A deviation of 0.157% in the relative refractive index can result in a maximum target-coordinate deviation of up to 1 cm, indicating that the stereo-visual measurement model is highly sensitive to deviations in the relative refractive index in the air–water condition. In underwater experiments or practical applications, special attention must be paid to the calibration of refractive indices of different media.

The impact of refraction-parameter deviations on stereo-visual measurement is related to the distance between the target and the camera, and the influence of different refraction parameters varies with the distance. When the deviation in the relative refractive index is constant, the closer the target is to the camera, the smaller the total coordinate deviation of the targets. When the deviation in the distance between the camera and the refractive interface is constant, as the distance between the target and the camera increases, the deviations in X and Y coordinates first increase rapidly, then decrease rapidly, and finally stabilize, while the deviation in Z coordinate decreases rapidly and gradually stabilizes. The deviation in the Z coordinate is an order of magnitude greater than that in the X and Y coordinates, so the overall coordinate deviation is determined by the Z coordinate deviation. For points at different positions within the field of view, the overall coordinate deviations caused by the deviations in the relative refractive index and the camera-refractive interface distance with the changes in the Z coordinate are approximately consistent. The impact of deviations in the orientation of the refractive interface normal varies more complexly with changes in the Z coordinate and is related to the distribution of the target. In underwater experiments or practical applications to mitigate the impact of deviations in the orientation of the refractive interface normal, attention must be paid to the distribution of the target within the field of view.

For the fixed targets, changes in the refraction parameters deviations result in linear variations in the X, Y, Z, and overall coordinate deviations. The larger the deviation in the refraction parameters, the greater the coordinate deviations. Whether the refraction parameter is greater or less than its true value, the impact on the overall coordinate deviation remains the same.

According to the experimental results, targets closer to the edge of the field of view are more susceptible to the influence of refraction-parameter deviations. This indicates that the current refraction-measurement model performs better for targets near the center of the field of view, while it may not fully eliminate refraction errors for targets near the edges.

5. Conclusions

This paper introduces a refraction-based visual-measurement model, establishes a stereo-vision simulation model, and conducts specific simulation experiments to study in detail the impact of deviations in various refraction parameters on stereo-visual measurement. The simulation accurately determines the coordinates of the refraction points based on the positions of the cameras and the targets, thereby obtaining the corresponding pixel coordinates used to estimate the targets’ position. Experimental results demonstrate that the influence of different refraction-parameter deviations on stereo-visual measurement varies and is related to the distribution of the target within the field of view and the distance between the target and the camera. The overall coordinate deviation of the target is not necessarily minimized by simply increasing or decreasing the distance between the target and the camera; it must be determined based on the magnitude of the deviation in each refraction parameter. The stereo-visual measurement model is particularly sensitive to deviations in the relative refractive index in the air–water condition. Therefore, in underwater experiments or practical applications, careful calibration of the refractive indices of different media and attention to the distribution of targets within the field of view are crucial. The work and conclusions presented in this paper provide guidance for the construction of underwater stereo-vision measurement systems, refraction parameter calibration, underwater experiments, and practical applications. However, this study primarily conducted research by developing a simulation model and performing simulated experiments. Future work should include underwater experiments to validate the conclusions of this paper. In addition, the current refraction-measurement model is more suitable for targets located near the center of the field of view, whereas its effectiveness for targets at the edges is less than ideal, indicating the need for further optimization of the refraction-measurement model in the future.