UVIO: Adaptive Kalman Filtering UWB-Aided Visual-Inertial SLAM System for Complex Indoor Environments
Abstract
1. Introduction
2. Related Work
- In this paper, we introduce a new method to improve accuracy and reduce noise in evaluating position through UWB in NLOS localization scenarios. An adaptive Kalman filter (AKF) will be used to process UWB data, and the received signal strength indicator (RSSI) between the tag and each of the four base stations, as well as IMU signals, will be processed in real-time during the measurement. Meanwhile, the degree of fluctuation over a window frame, known as the estimation of precision (EOP), will be computed. A new RSSI-EOP factor, considering all these inputs, is then used to update the noise covariance matrix (which directly influences the adjustment of the Kalman gain matrix) in the AKF to indicate the reliability of the UWB signals based on the signal strength and fluctuation degree. Instead of setting a threshold for the dilution of precision and excluding measurements in a particular interval, our strategy utilizes both UWB and IMU signals. When fluctuation is large, particularly under NLOS scenarios, it can lead to larger errors when updating the Kalman gain. With this RSSI-EOP factor, most NLOS data in the measurement vector can be immediately identified and assigned lower confidence, allowing the prediction to emphasize IMU (state extrapolation equation) over UWB measurements (measurement equation). Compared to completely excluding outlier data from the measurement vector, which can easily lead to poor positioning results, this factor ensures a better and more stable transition between previous and current postures. Experimental results show that the NLOS identification and correction method proposed in this paper is effective and practical, significantly enhancing the robustness and accuracy of the fusion system in complex indoor environments.
- Second, this paper proposes a fusion strategy based on factor graph optimization (FGO) to fuse a binocular camera, a six-DOF IMU, and UWB information to further refine the pose estimation. Since AKF only considers a relatively short period, the estimated pose could still suffer from large fluctuations (partially due to noise and interference). In this work, a visual-based localization method is also integrated into pose estimation. Compared to the traditional fusion-based methods, this method considers historical measurement data to infer current pose information to help improve the accuracy of the prediction. In FGO, every pose, including both position and orientation in a global frame, is represented as a node. To solve the timestamp synchronization problem, we propose using the local frame VIO rotation matrix as the edge to constrain the relative motion between two consecutive nodes. Moreover, we applied the corrected UWB position as the state (node), which means that we trust the global (world) position of UWB more in the long term. This proposed approach is highly rational as it can effectively address the typical cumulative errors in visual SLAM methods. Meanwhile, we can compensate for signal drift from UWB by leveraging short-term localization constraints through visual-inertial odometry (VIO).
3. UWB Positioning Methodology
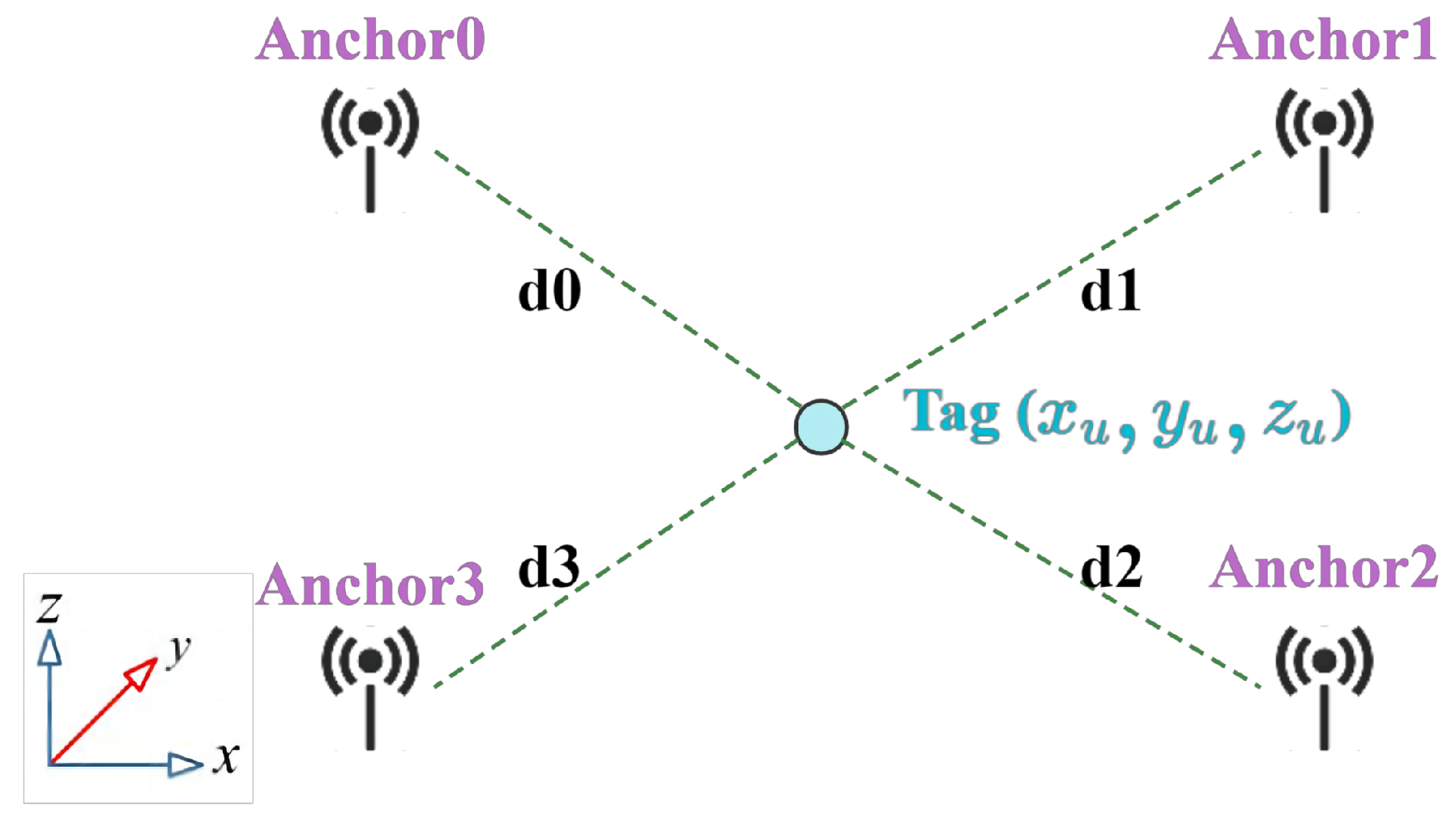
3.1. Base Station Layout
3.2. UWB Ranging Principle
3.3. Algorithm Selection
3.4. LM Parameters Setting
3.5. Analysis of Results
4. Data Fusion Strategy
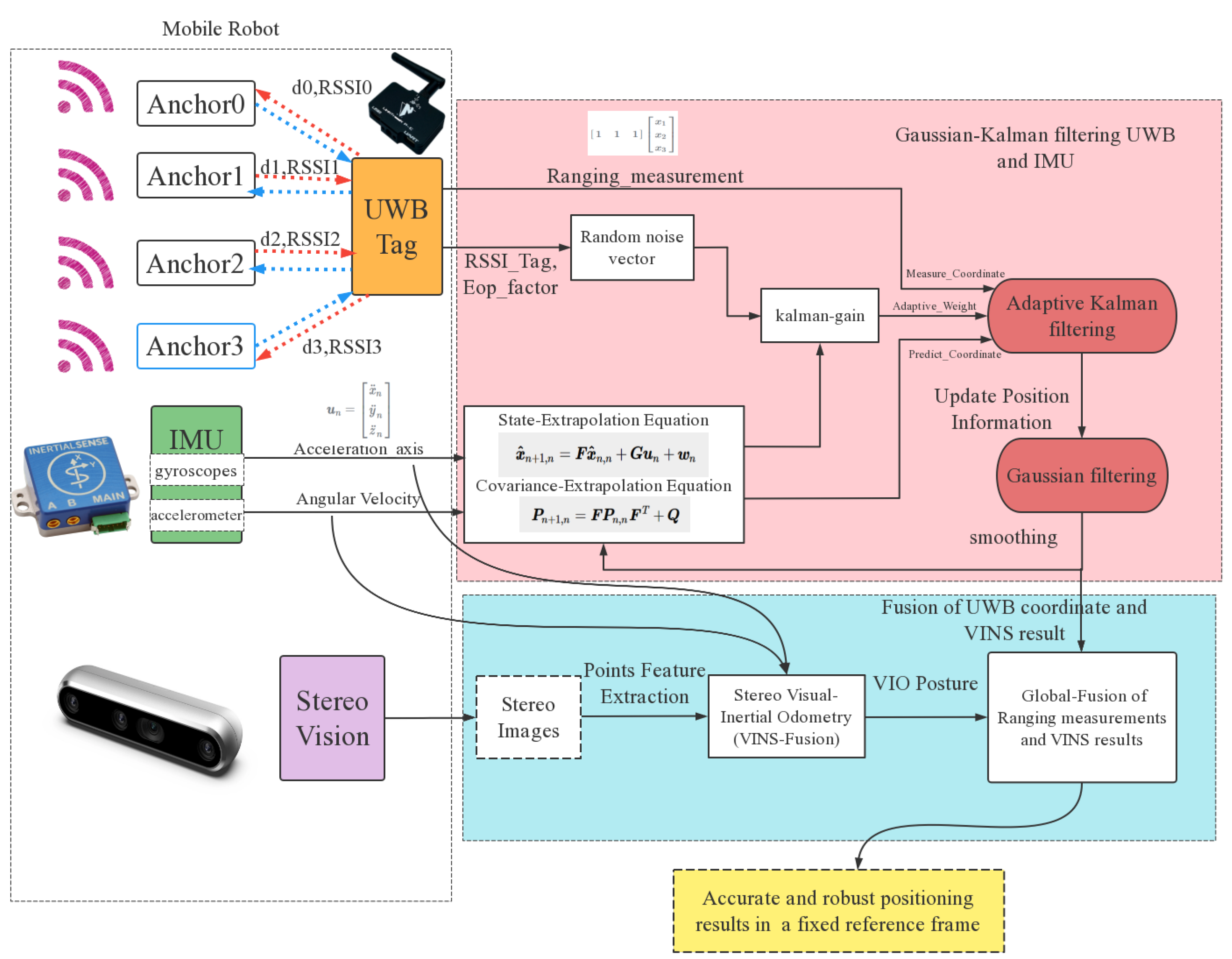
4.1. System Structure Design
4.2. Adaptive Kalman Filtering Model Design
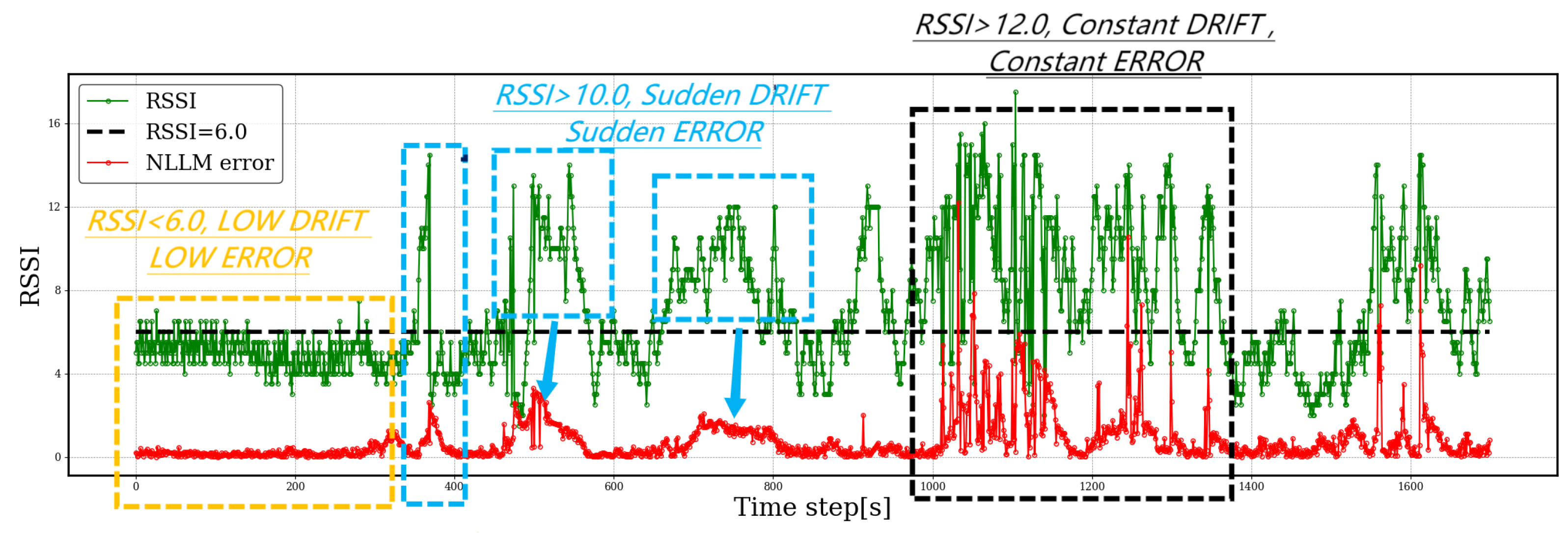
4.3. Channel Power Diagnostics Based on RSSI-EOP Factor
4.4. Experimental Study and Analysis of Results
Hardware Setup and Experiment Scene
4.5. Analysis of Results
| Algorithm 1: Outlier Detection |
Require: Outlier threshold
|
5. UWB/IMU-Visual SLAM Integrated Model Based on Factor Graph Optimization
5.1. Factor Graph Optimization Model
5.2. Evaluation of the UWB/IMU/Visual-SLAM Integrated Positioning Algorithm
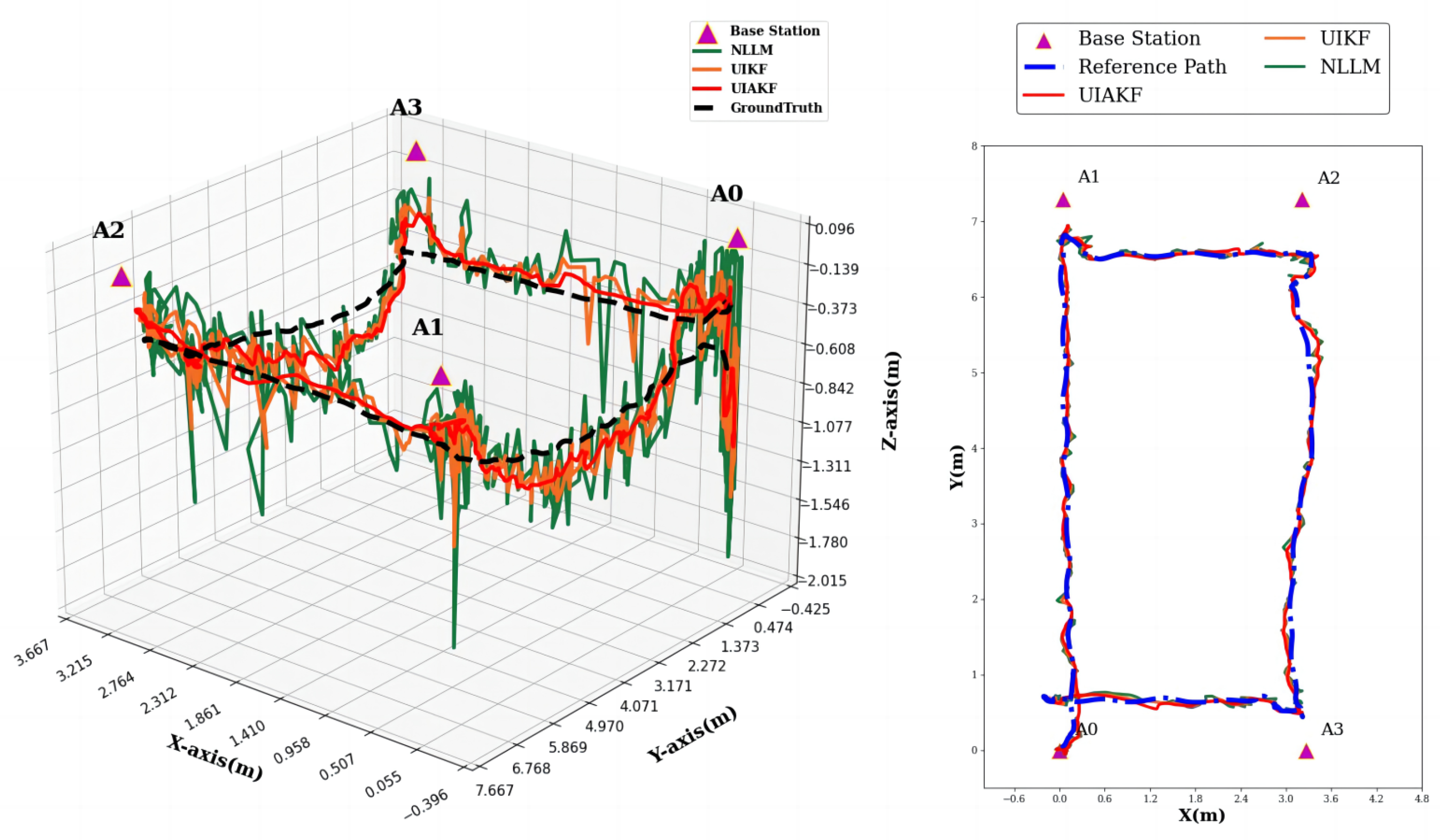
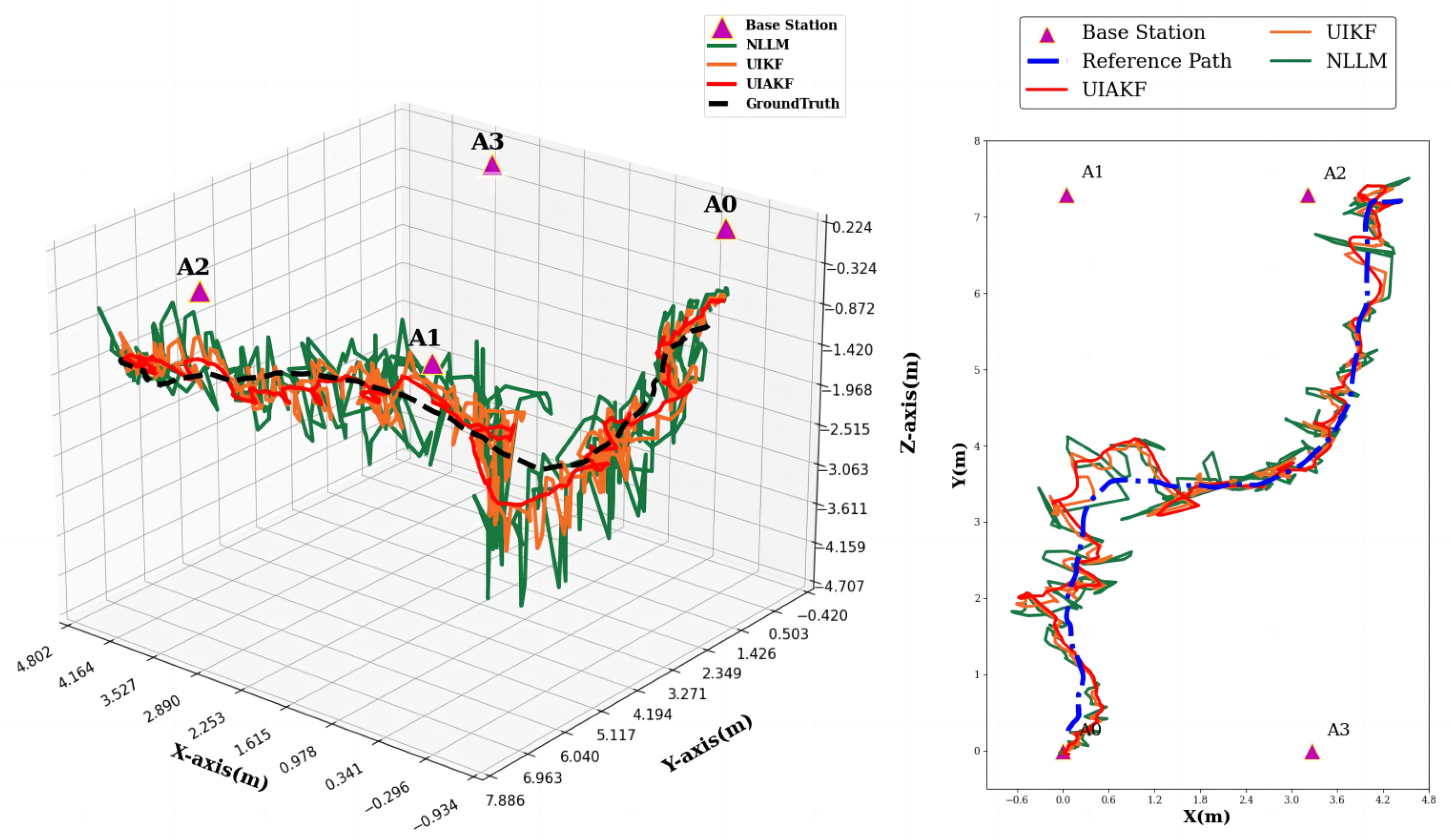
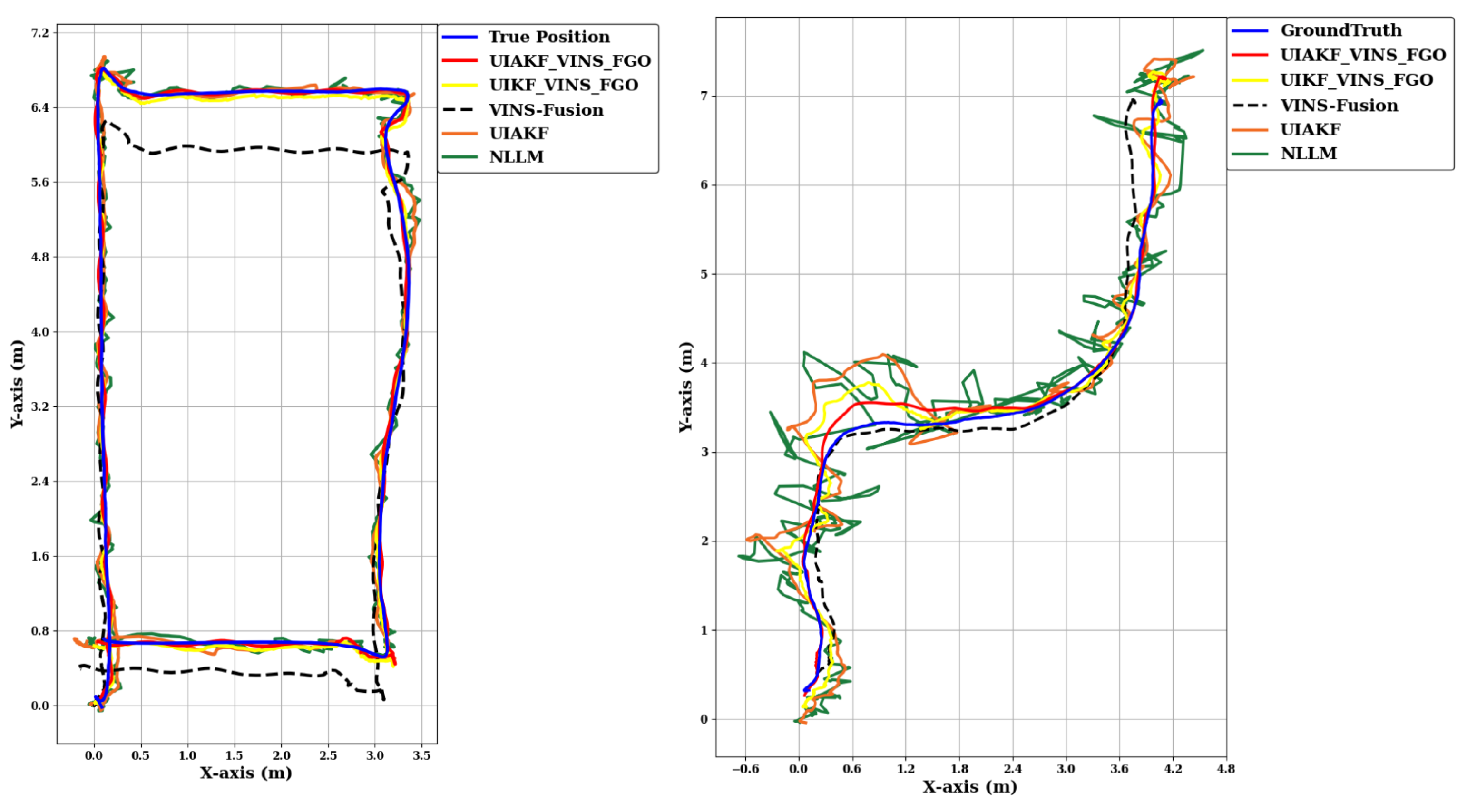
- Levenberg–Marquardt method positioning + NLOS outlier correction (NLLM) (green);
- Levenberg–Marquardt method positioning + NLOS outlier correction + adaptive Kalman filtering of IMU (UIAKF) (orange);
- Visual-IMU odometry (VINS-Fusion) (black);
- FGO-Based VINS-Fusion + UIKF Fusion (UIKF-VINS-FGO) (yellow);
- FGO-Based VINS-Fusion + UIAKF Fusion (UIAKF-VINS-FGO) (red);
- Ground truth (blue);
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mur-Artal, R.; Tardós, J.D. ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo, and RGB-D Cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Geneva, P.; Eckenhoff, K.; Lee, W.; Yang, Y.; Huang, G. OpenVINS: A Research Platform for Visual-Inertial Estimation. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 4666–4672. [Google Scholar] [CrossRef]
- Qin, T.; Li, P.; Shen, S. VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Zhuang, Y.; El-Sheimy, N. Tightly-Coupled Integration of WiFi and MEMS Sensors on Handheld Devices for Indoor Pedestrian Navigation. IEEE Sens. J. 2016, 16, 224–234. [Google Scholar] [CrossRef]
- Qin, T.; Cao, S.; Pan, J.; Shen, S. A General Optimization-based Framework for Global Pose Estimation with Multiple Sensors. arXiv 2019, arXiv:1901.03642. [Google Scholar]
- Gomez-Ojeda, R.; Moreno, F.A.; Zuñiga-Noël, D.; Scaramuzza, D.; Gonzalez-Jimenez, J. PL-SLAM: A Stereo SLAM System Through the Combination of Points and Line Segments. IEEE Trans. Robot. 2019, 35, 734–746. [Google Scholar] [CrossRef]
- Li, S.; Hedley, M.; Bengston, K.; Humphrey, D.; Johnson, M.; Ni, W. Passive Localization of Standard WiFi Devices. IEEE Syst. J. 2019, 13, 3929–3932. [Google Scholar] [CrossRef]
- Hu, S.; He, K.; Yang, X.; Peng, S. Bluetooth Fingerprint based Indoor Localization using Bi-LSTM. In Proceedings of the 2022 31st Wireless and Optical Communications Conference (WOCC), Shenzhen, China, 11–12 August 2022; pp. 161–165. [Google Scholar] [CrossRef]
- Watthanawisuth, N.; Tuantranont, A.; Kerdcharoen, T. Design of mobile robot for real world application in path planning using ZigBee localization. In Proceedings of the 2014 14th International Conference on Control, Automation and Systems (ICCAS 2014), Gyeonggi-do, Republic of Korea, 22–25 October 2014; pp. 1600–1603. [Google Scholar] [CrossRef]
- Sun, W.; Xue, M.; Yu, H.; Tang, H.; Lin, A. Augmentation of Fingerprints for Indoor WiFi Localization Based on Gaussian Process Regression. IEEE Trans. Veh. Technol. 2018, 67, 10896–10905. [Google Scholar] [CrossRef]
- Zhang, M.; Jia, J.; Chen, J.; Deng, Y.; Wang, X.; Aghvami, A.H. Indoor Localization Fusing WiFi With Smartphone Inertial Sensors Using LSTM Networks. IEEE Internet Things J. 2021, 8, 13608–13623. [Google Scholar] [CrossRef]
- Silva, B.; Pang, Z.; Åkerberg, J.; Neander, J.; Hancke, G. Experimental study of UWB-based high precision localization for industrial applications. In Proceedings of the 2014 IEEE International Conference on Ultra-WideBand (ICUWB), Paris, France, 1–3 September 2014; pp. 280–285. [Google Scholar] [CrossRef]
- Chan, Y.; Ho, K. A simple and efficient estimator for hyperbolic location. IEEE Trans. Signal Process. 1994, 42, 1905–1915. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, X.; Bo, X.; Yang, Z.; Zhao, Z. Ultra-wideband high precision positioning system based on SDS-TWR algorithm. In Proceedings of the 2021 International Applied Computational Electromagnetics Society (ACES-China) Symposium, Chengdu, China, 28–31 July 2021; pp. 1–2. [Google Scholar] [CrossRef]
- Hol, J.D.; Dijkstra, F.; Luinge, H.; Schon, T.B. Tightly coupled UWB/IMU pose estimation. In Proceedings of the 2009 IEEE International Conference on Ultra-Wideband, Vancouver, BC, Canada, 9–11 September 2009; pp. 688–692. [Google Scholar] [CrossRef]
- Dwek, N.; Birem, M.; Geebelen, K.; Hostens, E.; Mishra, A.; Steckel, J.; Yudanto, R. Improving the Accuracy and Robustness of Ultra-Wideband Localization Through Sensor Fusion and Outlier Detection. IEEE Robot. Autom. Lett. 2020, 5, 32–39. [Google Scholar] [CrossRef]
- Wen, K.; Yu, K.; Li, Y.; Zhang, S.; Zhang, W. A New Quaternion Kalman Filter Based Foot-Mounted IMU and UWB Tightly-Coupled Method for Indoor Pedestrian Navigation. IEEE Trans. Veh. Technol. 2020, 69, 4340–4352. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, A.; Sui, X.; Wang, C.; Wang, S.; Gao, J.; Shi, Z. Improved-UWB/LiDAR-SLAM Tightly Coupled Positioning System with NLOS Identification Using a LiDAR Point Cloud in GNSS-Denied Environments. Remote Sens. 2022, 14, 1380. [Google Scholar] [CrossRef]
- Zeng, Q.; Liu, D.; Lv, C. UWB/Binocular VO Fusion Algorithm Based on Adaptive Kalman Filter. Sensors 2019, 19, 4044. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.H.; Nguyen, T.M.; Xie, L. Range-Focused Fusion of Camera-IMU-UWB for Accurate and Drift-Reduced Localization. IEEE Robot. Autom. Lett. 2021, 6, 1678–1685. [Google Scholar] [CrossRef]
- Yang, B.; Li, J.; Zhang, H. UVIP: Robust UWB aided Visual-Inertial Positioning System for Complex Indoor Environments. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 5454–5460. [Google Scholar] [CrossRef]
- Ding, L.; Zhu, X.; Zhou, T.; Wang, Y.; Jie, Y.; Su, Y. Research on UWB-Based Indoor Ranging Positioning Technolog and a Method to Improve Accuracy. In Proceedings of the 2018 IEEE Region Ten Symposium (Tensymp), Sydney, NSW, Australia, 4–6 July 2018; pp. 69–73. [Google Scholar] [CrossRef]
- Mazraani, R.; Saez, M.; Govoni, L.; Knobloch, D. Experimental results of a combined TDOA/TOF technique for UWB based localization systems. In Proceedings of the 2017 IEEE International Conference on Communications Workshops (ICC Workshops), Paris, France, 21–25 May 2017; pp. 1043–1048. [Google Scholar] [CrossRef]
- Gu, Y.; Yang, B. Clock Compensation Two-Way Ranging (CC-TWR) Based on Ultra-Wideband Communication. In Proceedings of the 2018 Eighth International Conference on Instrumentation & Measurement, Computer, Communication and Control (IMCCC), Harbin, China, 19–21 July 2018; pp. 1145–1150. [Google Scholar] [CrossRef]
- Cheung, K.; So, H.; Ma, W.K.; Chan, Y. Least squares algorithms for time-of-arrival-based mobile location. IEEE Trans. Signal Process. 2004, 52, 1121–1130. [Google Scholar] [CrossRef]
- Malyavej, V.; Udomthanatheera, P. RSSI/IMU sensor fusion-based localization using unscented Kalman filter. In Proceedings of the The 20th Asia-Pacific Conference on Communication (APCC2014), Pattaya, Thailand, 1–3 October 2014; pp. 227–232. [Google Scholar] [CrossRef]
- Fakharian, A.; Gustafsson, T.; Mehrfam, M. Adaptive Kalman filtering based navigation: An IMU/GPS integration approach. In Proceedings of the 2011 International Conference on Networking, Sensing and Control, Delft, The Netherlands, 11–13 April 2011; pp. 181–185. [Google Scholar] [CrossRef]
- Tardif, J.P.; George, M.; Laverne, M.; Kelly, A.; Stentz, A. A new approach to vision-aided inertial navigation. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 4161–4168. [Google Scholar] [CrossRef]
- Lee, Y.; Lim, D. Vision/UWB/IMU sensor fusion based localization using an extended Kalman filter. In Proceedings of the 2019 IEEE Eurasia Conference on IOT, Communication and Engineering (ECICE), Yunlin, Taiwan, 3–6 October 2019; pp. 401–403. [Google Scholar] [CrossRef]
- Zhang, R.; Fu, D.; Chen, G.; Dong, L.; Wang, X.; Tian, M. Research on UWB-Based Data Fusion Positioning Method. In Proceedings of the 2022 28th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Nanjing, China, 16–18 November 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Sabatelli, S.; Galgani, M.; Fanucci, L.; Rocchi, A. A double stage Kalman filter for sensor fusion and orientation tracking in 9D IMU. In Proceedings of the 2012 IEEE Sensors Applications Symposium Proceedings, Brescia, Italy, 7–9 February 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Wymeersch, H.; Marano, S.; Gifford, W.M.; Win, M.Z. A Machine Learning Approach to Ranging Error Mitigation for UWB Localization. IEEE Trans. Commun. 2012, 60, 1719–1728. [Google Scholar] [CrossRef]
- Maranò, S.; Gifford, W.M.; Wymeersch, H.; Win, M.Z. NLOS identification and mitigation for localization based on UWB experimental data. IEEE J. Sel. Areas Commun. 2010, 28, 1026–1035. [Google Scholar] [CrossRef]
- Decawave. Dw1000 Metrics for Estimation of Non Line of Sight Operating Conditions; Technical Report aps013 Part 3 Application Note; Decawave: Dublin, Ireland, 2016. [Google Scholar]
- Qin, C.; Ye, H.; Pranata, C.E.; Han, J.; Zhang, S.; Liu, M. LINS: A Lidar-Inertial State Estimator for Robust and Efficient Navigation. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 8899–8906. [Google Scholar] [CrossRef]

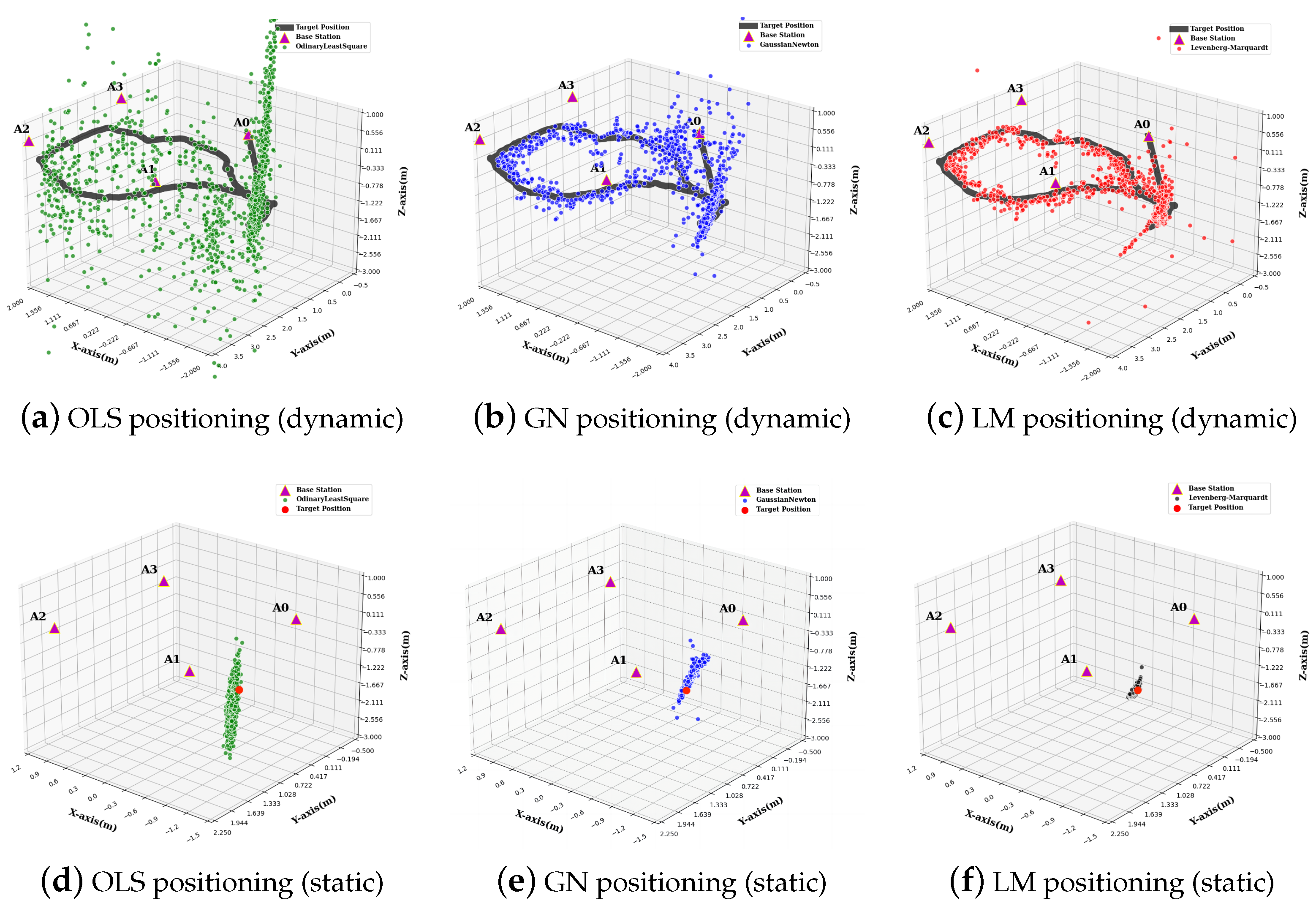




| RMSE | OLS | GN | LM | |
|---|---|---|---|---|
| X (m) | 0.0524 | 0.03903 | 0.0288 | |
| LOS | Y (m) | 0.03178 | 0.051 | 0.0195 |
| Z (m) | 0.638 | 0.1328 | 0.0905 | |
| Position (m) | 0.64 | 0.1475 | 0.097 | |
| X (m) | 0.191 | 0.155 | 0.118 | |
| NLOS | Y (m) | 0.1305 | 0.1552 | 0.157 |
| Z (m) | 1.69 | 0.858 | 0.617 | |
| Position (m) | 1.706 | 0.886 | 0.74 |
| NLLM | UIKF | UIAKF | |||
|---|---|---|---|---|---|
| X | 0.0784 | 0.0607 | 0.06956 | ||
| RMSE (m) | Y | 0.06457 | 0.0577 | 0.06477 | |
| Z | 0.265 | 0.185 | 0.1546 | ||
| LOS | X | 0.34882 | 0.199 | 0.2267 | |
| Max (m) | Y | 0.2968 | 0.1709 | 0.13386 | |
| Z | 1.14795 | 0.78 | 0.47739 | ||
| Availability (±0.2 m) | – | 52.313% | 68.74% | 75.917% | |
| X | 0.29 | 0.224 | 0.213 | ||
| RMSE (m) | Y | 0.199 | 0.173 | 0.177 | |
| Z | 0.466 | 0.284 | 0.193 | ||
| NLOS | X | 0.769 | 0.656 | 0.63163 | |
| Max (m) | Y | 0.439 | 0.384 | 0.378 | |
| Z | 1.9788 | 1.086 | 0.512 | ||
| Availability (±0.2 m) | – | 17.1206% | 27.237% | 40.645% |
| NLLM | UIAKF | VINS | UIKF_VINS_FGO | UIAKF_VINS_FGO | |||
|---|---|---|---|---|---|---|---|
| X | 0.088 | 0.0801 | 0.086 | 0.0497 | 0.0244 | ||
| RMSE (m) | Y | 0.07938 | 0.0728 | 0.229 | 0.0531 | 0.0218 | |
| Z | 0.264 | 0.148 | 0.433 | 0.0639 | 0.0192 | ||
| LOS | X | 0.358 | 0.259 | 0.198 | 0.152 | 0.0553 | |
| Max (m) | Y | 0.28 | 0.264 | 0.327 | 0.139 | 0.052 | |
| Z | 1.18 | 0.5521 | 1.38 | 0.37 | 0.122 | ||
| Availability (±0.2 m) | – | 54.545% | 77.02% | 52.033% | 91.17% | 100.0% | |
| X | 0.283 | 0.203 | 0.353 | 0.151 | 0.095 | ||
| RMSE (m) | Y | 0.286 | 0.18 | 0.31 | 0.173 | 0.1178 | |
| Z | 0.472 | 0.301 | 0.456 | 0.261 | 0.2112 | ||
| NLOS | X | 0.746 | 0.546 | 0.88 | 0.431 | 0.2553 | |
| Max (m) | Y | 0.418 | 0.353 | 0.47 | 0.371 | 0.2953 | |
| Z | 2.029 | 0.518 | 0.375 | 0.51 | 0.3853 | ||
| Availability(±0.2 m) | – | 16.536% | 42.21% | 57.02% | 73.37% | 89.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Wang, S.; Hao, J.; Ma, B.; Chu, H.K. UVIO: Adaptive Kalman Filtering UWB-Aided Visual-Inertial SLAM System for Complex Indoor Environments. Remote Sens. 2024, 16, 3245. https://doi.org/10.3390/rs16173245
Li J, Wang S, Hao J, Ma B, Chu HK. UVIO: Adaptive Kalman Filtering UWB-Aided Visual-Inertial SLAM System for Complex Indoor Environments. Remote Sensing. 2024; 16(17):3245. https://doi.org/10.3390/rs16173245
Chicago/Turabian StyleLi, Junxi, Shouwen Wang, Jiahui Hao, Biao Ma, and Henry K. Chu. 2024. "UVIO: Adaptive Kalman Filtering UWB-Aided Visual-Inertial SLAM System for Complex Indoor Environments" Remote Sensing 16, no. 17: 3245. https://doi.org/10.3390/rs16173245
APA StyleLi, J., Wang, S., Hao, J., Ma, B., & Chu, H. K. (2024). UVIO: Adaptive Kalman Filtering UWB-Aided Visual-Inertial SLAM System for Complex Indoor Environments. Remote Sensing, 16(17), 3245. https://doi.org/10.3390/rs16173245






