Abstract
The simplicity of the so-called triangle method allows estimates of evapotranspiration and soil water content to be made without ancillary data external to the image and with just a few simple algebraic calculations. Drawing on many examples in the literature showing that the pixel distribution in temperature/fractional vegetation cover (NDVI) space closely resembles a right triangle, this paper shows that adoption of a right triangle shape further simplifies the triangle model. Moreover, it allows one to mostly avoid the problem of sparse or low-resolution data. A time dimension can be included showing that trajectories inside the triangle can provide additional information on root zone soil water content. After discussing some of the ambiguities in the triangle method, and the advantageous properties of the right triangle, a proposal is made to illuminate the relationship between thermal/optical measurements and root zone water content within the right triangle framework.
1. The Triangle Method
Since 1990, at least 68 papers based on the so-called triangle method for estimating the evapotranspiration and surface soil water content remotely using optical/thermal measurements have appeared in the published literature [1]. Many more papers have been written about remote sensing of soil water content [2,3]. The advantage of the triangle method is that no ancillary data external to the image are required for obtaining these essential parameters and almost no calculations are necessary. Solutions for these variables are based on the configuration of pixels in fractional vegetation cover/surface radiometric temperature space. Basically, a triangle configuration occurs because vegetation tends to exhibit a much more uniform temperature pattern than soils do [4]. Accordingly, the plant canopy temperature decreases with increasing fractional vegetation cover wherein the soil surface becomes virtually invisible to the radiometer over a dense vegetation cover. The simplest version of the triangle shape is a right triangle, which has major advantages over the general case of the triangle [5].
Cited weaknesses of the triangle method are (1) its implementation requires sufficient points to define the triangular shape, and (2) visual construction is highly subjective. These perceived impediments have led to a proliferation of different types of configurations including various trapezoid models whose boundaries were determined quantitatively. (In the interest of brevity, the sheer volume of publications on this subject is unnecessary to cite here, but recent papers pertaining to the triangle model are [1,6,7].
This paper approaches the problem of remote sensing of soil water content based on a right triangle model using remotely sensed optical/thermal measurements. It will focus on the simplicity of its geometry which permits one to specify the triangle’s vertices based on selection of temperature and NDVI values at only two points in the larger image. In so doing, discussion will focus on how the right triangle concept avoids the problem of sparse data and how selection of a trapezoid alternate to the triangle may be due to insufficient data. Finally, the paper will show how the congruency of the right triangle allows inclusion of a time dimension.
2. The Right Triangle
An example of right triangle configuration is shown in Figure 1. While a target of a study may consist of part of an image, input information defined below is obtained from the entire (or greater) image. In the figure, derived from the greater image, the fractional vegetation cover Fr is plotted against a scaled surface infrared temperature T*. Surface radiometric temperature (Tir) is scaled between the maximum value in the greater image (Tmax, appropriate to a dry bare surface, such as a parking lot) and its minimum value in the image (Tmin, appropriate to a field of dense vegetation such as a forest canopy). T* is defined as
T* = (Tmax − Tir)/(Tmax − Tmin)
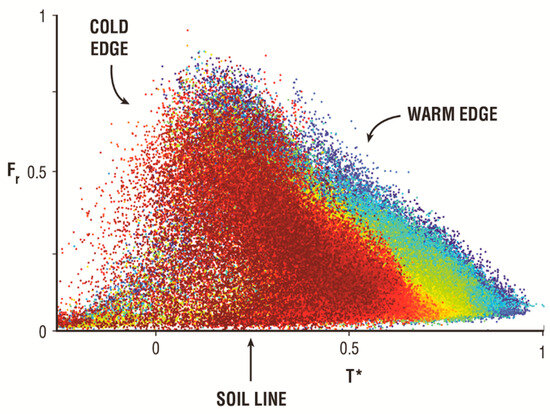
Figure 1.
Scatterplot of pixels from a Senntinel-3 image over Spain, where Fr is the fractional vegetation cover and T* is the scaled radiometric surface temperature. The color scheme is meant to aid in visualization. (Figure courtesy of George Petropoulos.)
Similarly, Fr is defined as
Fr = [(NDVI − NDVIo)/(NDVIs − NDVIo)]n
NDVIo is the value of NDVI for bare soil, corresponding to the location of Tmax, and NDVIs is the value of NDVI for dense vegetation, corresponding to the location of Tmin. Thus, this input data are obtained from just two locations on the greater image. In many papers, the exponent n has been obtained as 2.0 but a closer inspection of the original data for which this relationship was created suggests that 1.6 might be a better fit with the measurements.
A salient feature of these images is well-defined edges to the pixel envelope. Sharp edges in nature or in data generally reflect some external constraint. No less true for the triangle, its three sides correspond to physical limits of vegetation and soil water content.
One such limit is zero vegetation cover, the bottom face of the triangle in Figure 1. It is called the ‘soil line’, which is typically linear. Similarly, the ‘warm edge, the hypotenuse,’ corresponds to the limit of maximum soil surface radiometric temperature as a function of Fr. It is also constructed as a straight line (e.g., [5]). Mallick et al. [8] adopted the right triangle shape and presented many examples of a straight warm edge in their Figure 3. Tang et al. [9] made use of this empirical fact by defining their warm edge objectively, using a linear regression equation through the warmest pixels in each interval of Fr.
The left face of the triangle, defined as the ‘cold edge’ (or moist edge), is often less well-defined than the warm edge. In this case, the scatter of points is at least partly due to interference by cloud or standing water, notably the tail of points near the lower left corner of Figure 1.
The cold edge is drawn as a straight line perpendicularly to the soil line at T* = 0 extending through the fuzz of pixels to meet the warm edge near the upper vertex of the triangle as in [5,10,11]. The cold edge represents an effective upper limit of surface soil water content, essentially that at field capacity. Although no fundamental reason exists for the cold edge being a straight line, hundreds of examples exist in the literature showing a straight line orthogonal to the soil line.
Points inside the triangle therefore correspond to values of relative soil water content (defined as Mo), whose values range from zero (some lower limit of dryness at the warm edge) to 1.0, representing an upper limit of soil water content. Evapotranspiration fraction (EF, the ratio of evapotranspiration to the net radiation or, alternately, to the net radiation minus the ground heat flux) is equal to 1.0 at the cold edge but does not vanish at the warm edge because it depends on the amount of vegetation present, which can transpire even over dry soil.
Solutions for EF and Mo are represented in Figure 2 by assuming linearity across the domain. A comparison with numerical simulations [6] shows that Mo is closely representative of nonlinear solutions for this parameter, while EF usually differs by less than 20%, the greatest differences found near the cold edge.
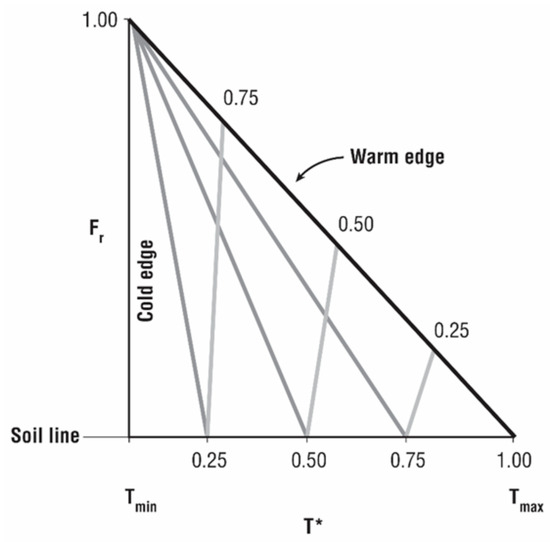
Figure 2.
Interior linear solution of right triangle, such as that shown in Figure 1, for surface soil moisture availability (Mo; solid lines) and evapotranspiration fraction (EF; dashed lines).
Currently, evapotranspiration (ET or EF) estimates reported in the literature using remotely determined optical/thermal measurements show quite good agreement with field measurements because the variables influencing the estimates of this variable do not depend very sensitively on root zone soil water content. For soil water content in the root zone, however, agreement with ground truth is much poorer using optical/thermal measurements, with R-square (R2) values typically ranging from about 0.1 to 0.4.
3. Measurement Uncertainties; Surface Radiometric Temperature
The reason for this poor agreement in root zone soil water content can be best explained by looking closely at what is being measured with a radiometer, specifically the radiometric surface temperature. This is illustrated by the schematic illustration in Figure 3.
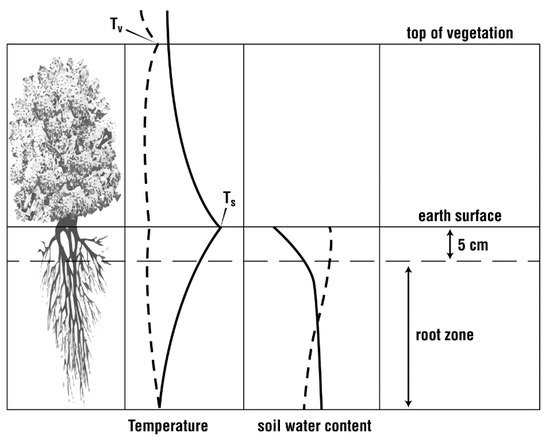
Figure 3.
Schematic representation of a typical vertical profile of temperature throughout the plant and substrate layer including the leaf temperature at the top of the canopy (Tv) and the skin temperature of the sunlit bare soil around the plants (Ts) and the vertical variation of the soil water content in the substrate over bare soil (solid profiles) and over vegetation (dashed profiles).
Although schematic, the profiles of temperature and soil moisture in Figure 3 conform closely to this author’s own observations of these two quantities in sunlit conditions. Here the root zone is arbitrarily separated into two layers, a near-surface layer (nominally 5 cm deep) and a deeper one below where most of the roots are located.
Over vegetation, the radiant temperature of the upper leaf surfaces is typically about 1 °C higher than that of the air immediately above the canopy, while over bare soil, the surface radiometric temperature under sunlight can be considerably elevated above the air temperature. Within the canopy radiometric, temperature varies little with height as it does below the surface, while decreasing with decreasing height above the bare soil surface and with depth below the surface.
In the bare soil patches, soil water is depleted over a shallow substrate layer (typically less than 5 cm) but may remain only slightly depleted below the top few centimeters [12]. In vegetated areas, the soil water is depleted more uniformly over the root zone and so may show only a small depletion at any level with time. Thus, elevated temperatures over dry soil may mask moist conditions below the top few cm, leading to a false estimation of root zone soil water content [12,13,14].
That the soil can remain relatively moist below a drying surface is well known to farmers who avoid plowing their fields in times of drought lest water from the moister substrate can be exposed and allowed to evaporate. Lack of coupling between root zone water content and that at the surface has led some researchers [15] to conclude that agreement between measured soil water content and that estimated from thermal/optical remote sensing is better over a densely vegetated area, as would be the case if, as in Figure 3, the soil water content at the surface and deeper substrate are similar. Conversely, Kasim et al. [16] found the opposite, that agreement improves with decreasing vegetation cover when soil water measurements are made over the top 5 cm.
Another problem in estimating root zone soil water content is the way plants respond to root zone drying. Unlike soils, plants will not allow themselves to be heated so strongly. As the root zone dries out, the demand for transpiration (T) may begin to exceed the ability of the plant to furnish the required moisture, at which time stomates partially close for a period until the demand lessens due to decreased solar input. In response, the transpiration curve (Tv versus time) flattens and the stomatal closure increases in duration during the stress period, while the sensible heat flux and radiant temperature of the plants show an increase during this same period. This effect, illustrated in Figure 4, has been well documented using both model simulations and field measurements [17,18,19].
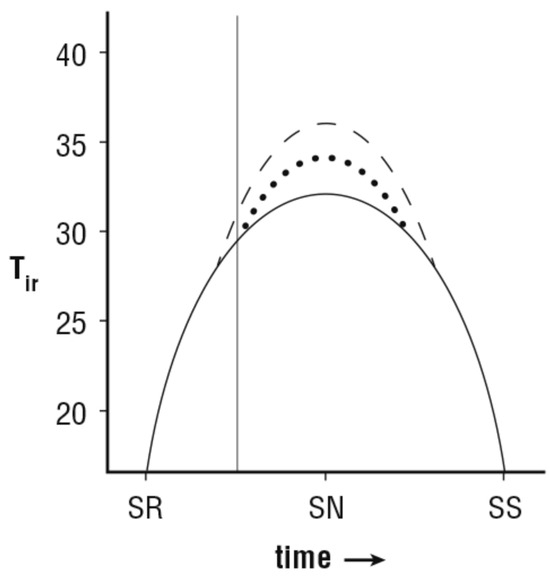
Figure 4.
Schematic illustration of the radiometric temperature (Tir) versus time at the top of a plant canopy undergoing progressive root zone water depletion over several days. As water content there diminishes (solid line changing to dotted and then to dashed), the period during which plant stress occurs lengthens. The vertical line represents the time of measurement made by a polar orbiting satellite. SR, SN, and SS refer, respectively, to sunrise, solar noon, and sunset.
Now, the problem for the plant is that the flattening of the transpiration curve implies an increase in leaf temperature. Yet, observations show that the rise in temperature of a plant canopy caused by water stress in the root zone seldom exceeds just a few degrees C, at least up to the point of plant collapse [18] when the transpiration plateau extends throughout much of the day, The figure emphasizes the fact that the satellite measurements, having been made an hour or more from the time of maximum stress (solar noon), show less (or a vanishing) increase in temperature at local satellite overpass time, e.g., 1100.
In response to the increased stress caused by an excessive demand on the plant to supply water to the leaves, further measures are taken by the plant to avoid a destructive rise in leaf temperature. Rather than let the leaves suffer cell damage due to high temperatures, the plant can orientate the leaves so that they lie parallel to the sun’s rays, curl the leaves, or allow the leaves, at least those undergoing stress, to drop to the ground. In such cases, the reaction to water stress would take the form of a decrease in leaf area, in which more of the sun’s rays reach bare soil, thereby effectively reducing the apparent fractional vegetation cover while the soil temperature newly exposed to the sun’s direct rays increases.
Although measurements made by satellites such as Landsat, occurring an hour or so before solar noon, may not show significant increases in vegetation temperature (as suggested by Figure 4), a significant change in both surface radiometric temperature and fractional vegetation cover over the canopy may occur because of the secondary effects of water stress on the change in Fr.
4. Triangle or Trapezoid
Beginning around 2012, trapezoid models began to replace the triangular concept in the literature. These models emerged in response to perceived difficulties with the triangle model. Pixel distributions often failed to show a well-defined upper vertex or well-defined boundaries, suggesting that the configuration of pixels might be a trapezoid and not a triangle. Moreover, in view of the ambiguity in defining the pixel envelope, it seemed more objective to solve for the boundaries mathematically using various physical relationships such as the flux equations and the energy balance constraint. The various mathematical constructs allowed for a reasonable estimate of EF, if not root zone soil water content.
It is this author’s opinion, however, that the quantitatively derived endpoints are generally poor representations of the pixel borders. Frequently, the derived borders of the polygon appear to conflict with the visual borders. Even Long et al., whose many papers employ mathematical solutions for the figure’s trapezoidal end points (e.g., [20]), concede better results for EF using the triangle model with observed edges, as does [21] (see their Figures 10 and 11). Inaccurately specifying the end points objectively undoubtedly arises from inputs into the various physical relationships used in the quantitative formulation. As Long et al. [20] point out, these endpoints are highly sensitive to poorly known input parameters (such as canopy resistances) and to variables requiring precise field measurements whose uncertainties greatly impact the accuracy of all input variables [22].
Having looked at hundreds of examples in the literature, this author could see that, in most cases, the pixel envelopes can be visualized with little imagination as right triangles given the removal of extraneous pixels (such as those found over standing water or affected by cloud cover). Indeed, many examples of pixel envelopes represented by trapezoids, can be redrawn as right triangles. For example, despite adopting the trapezoid model, Long et al. [20] present such an example in their Figure 3a,b, which could easily be redrawn as right triangles.
Two reasons for the perceived appearance of a trapezoid are (1) insufficient number of pixels to resolve a triangle, notably at high fractional vegetation cover. For example, in the absence of pixels in the upper part of the triangle in Figure 2, the shape reduces to a trapezoid; (2) the result of plant water stress in which pixels representing stressed plants cause points near the upper part of the triangle to spill over the warm edge where small changes in temperature correspond to large changes in Mo in Figure 2), creating a second triangle, the unshaded area in Figure 5.
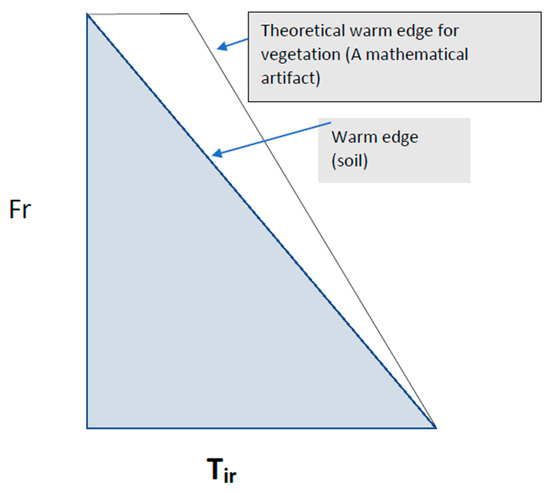
Figure 5.
Right triangle depicting the two-phase model with pixel spillage. The unshaded triangle contains pixels that represent vegetation experiencing water stress due to root zone water depletion. The warm edge in the shaded triangle still represents the dryness limit for the bare soil, whereas the warm edge in the unshaded triangle constitutes the limit for plant water stress.
Whether this spillage of pixels past the warm edge, referred to by [3,21] as ‘oversaturation’, is due to plant water stress as these authors contend or to internal or measurement error is yet to be determined. They chose to represent the pixel distribution in Fr/Tir space as a trapezoid comprising two internal triangles, referred to as the’ two phase’ model (Figure 5). Note, that as Fr decreases, oversaturation becomes less likely, as small increases in leaf temperature in the interior of the shaded triangle may fail to reach the warm edge.
5. Constructing the Right Triangle with Limited Pixel Cover
An advantage in adopting a right triangle, besides the greater simplicity, is that it enables a triangle to be constructed in the presence of sparse data. It is possible to construct a right triangle from just the four endpoints Tmax, Tmin, NDVIo, and NDVIs, which are determined from the larger image [13]. Then, if part of the warm edge is visible in the data, it is extended to the soil line at Tmax and to the cold edge; subsequently, the figure can be adjusted to insure compatibility of the projected warm edge with the predetermined endpoints, notably NDVIs. Except for a dense canopy of trees, most vegetated surfaces will exhibit some pare patches such that few pixels appear near the upper vertex of the triangle, where the fractional vegetation cover is defined as 1.0, resulting in an underestimate of NDVIs. Zhang et al. [23] attribute the sparsity of pixels near the upper vertex of the triangle to the resolution of the radiometer, so that some bare patches are contained within the most vegetated pixels.
To illustrate, consider the schematic depiction in Figure 6 of a triangle created with a sparse distribution of pixels. The triangle’s base, the soil line, is initially set between Tmax and Tmin. Noting that a series of points appear to resemble part of the warm edge (denoted by a bracket), a line can be drawn from Tmax through these points to intersect the soil line on one end and the cold edge on the other.
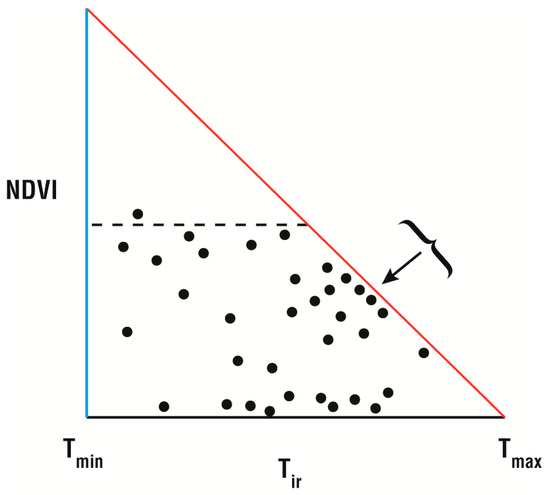
Figure 6.
A schematic triangle showing sparse pixel distribution (dots) plotted against the surface infrared temperature (Tir) and the normalized difference vegetation index (ND VI), where Tmax and Tmin define the soil line. In the absence of pixels near the upper vertex, the horizontal dashed line incorrectly defines the figure as a trapezoid. The series of dotes designated by the arrow with bracket lies along a fragment of the dry edge (red bracket), from which the full warm edge can be constructed. The green border is the wet edge.
It is understandable that the triangle can be mistaken for a trapezoid. Figure 6 shows that in the absence of pixels near the upper vertex, one could easily represent the pixel distribution in this figure by drawing the dashed line across the triangle, as shown in the figure.
6. Adding a Third Dimension to the Triangle
A single value for a crop moisture index based on temperature alone, such as Mo, is unable to provide specific information on plant water status. As argued here, NDVI or Fr may react more strongly to variations in soil water content than just temperature. Yet, a point within the triangle in two-dimensional Tir/Fr space is also not a very specific index of crop water stress. What may be more important are the time changes in these two variables. One can imagine (Figure 7) a three-dimensional triangle with coordinates (T*, Fr, time) in which the track of a pixel at a specific ground location would reflect the changing state of soil moisture at that point.
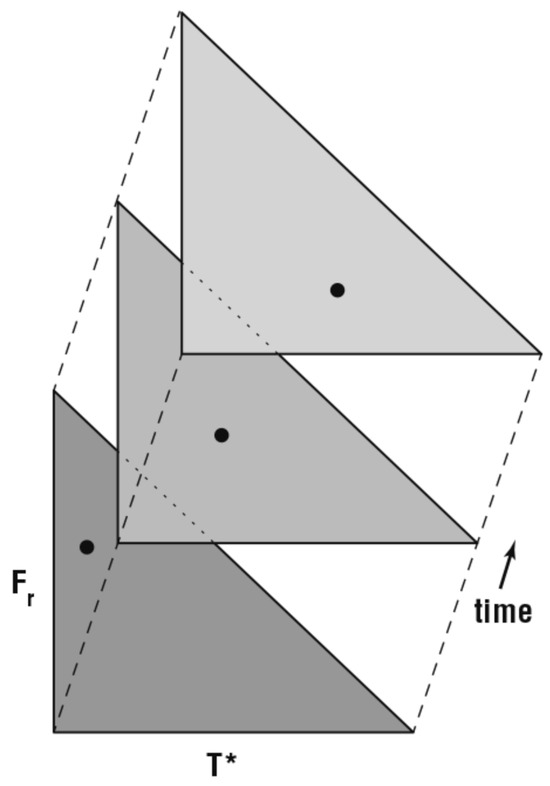
Figure 7.
Schematic illustration of a trajectory showing the time change within the right triangle, of a point on the surface in scaled surface radiometric temperature (T*) and fractional vegetation cover (Fr) as it migrates toward lower Fr and higher T*.
In the context of triangle space, root zone drying would show pixels migrating toward lower Fr and higher surface radiometric temperature, that is toward the lower right-hand vertex of the triangle (ref. Figure 2 and Figure 7). This kind of track was shown in [24] for progressive urbanization in San Jose’ Costa Rica. Whereas measurement error and instrument noise may obscure the value of Mo near the upper vertex, a trajectory over time could help resolve its true movement within the triangle.
A more illuminating crop moisture index would take the form of a four-component linear or higher-order regression equation, wherein the index would regress on T*, Fr, ΔT*, and ΔFr, where the symbol Δ refers to a time change in the variable T* or Fr over some period, such as a few days.
7. Recommendations
It is this author’s opinion that the present state of assessing root zone soil water content with the aid of thermal/optical sensors has reached an impasse with a risk of copycat repetition in which more and more complex models yield no improvement in assessing root zone soil water content.
I recommend a tightly coordinated program between the field operations and the modelers—between those making the measurements on the ground and those interpreting the measurements using the triangle/trapezoid framework. During the field program, soil water content measurements would be made over different parts of a vegetated domain of at least several acres in size. Substrate soil water measurements would be obtained over at least two depths (e.g., 0–5 cm and 5–20 cm). Daily assessments of vegetation state would be made at various locations in the field, such as the state of the leaves, and the density of plants. Satellite and other measurements would be made every several days over a period of a month or two during the height of the growing season. Satellite images would be georeferenced in real time so that the triangles could be constructed to allow constructive feedback to reach those in the field.
An object of the program would be to address questions such as the following:
- Is there any systematic variation in root zone (or surface) soil water content across the domain of the triangle?
- How likely is the root zone soil water content near field capacity along the cold edge or near wilting along the warm edge?
- Does spillage of pixel past the warm edges especially near the upper vertex of the triangle signify plant water stress or are these pixels usually the result of spurious conditions?
- Does measurement error overwhelm the signal near the upper vertex of the triangle and, if so, how far from that vertex does this ‘noise’ overwhelm the signal?
- Finally, the challenge still remains to estimate the two key temperature values (Tmax and Tmin and their associated NDVI values) in a reliable and routine fashion from the larger image.
8. Conclusions
The right triangle is easy to construct; it requires no information external to the image, the specification of two temperatures and two values of NDV from only two locations in the greater image (as opposed to a selected target area), and almost no computation. Further, it largely avoids sparse data or resolution problems.
Successive right triangles being essentially congruent, its geometry lends itself to the addition of a time dimension which could yield a more complete assessment of plant water stress, wherein changes in fractional vegetation cover and surface radiometric temperature constitute additional predictors of soil water content changes. If, in future tests, the right triangle method emerges as roughly as accurate as (or more so) existing models employing thermal/optical measurements, its advantages in simplicity should warrant its general application.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Carlson, T.N. A critique of the triangle method and a version suitable for estimating soil moisture from satellite imagery. J. Geogr. Environ. Earth Sci. Int. 2023, 27, 1–16. [Google Scholar] [CrossRef]
- Alburn, N.E. Evaluation of a Surface Energy Balance Method Based on Optical and Thermal Satellite Imagery to Estimate Root Zone Soil Moisture. Master’s Thesis, Department of Civil Engineering, Colorado State University, Ft Collins, CO, USA, 2014; p. 45. [Google Scholar]
- Babaeian, E.; Sadeghi, H.; Jones, S.; Montzka, C.; Vereecken, H.; Tuller, M. Ground, proximal and satellite remote sensing of soil moisture. Rev. Geophys. 2019, 57, 530–616. [Google Scholar] [CrossRef]
- Piles, M.; Camps, A.; Vall-Llossera, M.; Corbella, I.; Panciera, R.; Rudiger, C.; Kerr, Y.H.; Walker, J. SMOS-derived soil moisture using MODIS visible/infrared data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3156–3166. [Google Scholar] [CrossRef]
- Jiang, L.; Islam, S. Estimation of surface evaporation map over southern Great Plains using remote sensing data. Water Resour. Res. 2001, 37, 329–340. [Google Scholar] [CrossRef]
- Carlson, T.N.; Petropoulos, G.P. A new method for estimating evapotranspiration and surface soil moisture from optical and thermal infrared measurements: The simplified triangle. Int. J. Remote Sens. 2019, 40, 7716–7729. [Google Scholar] [CrossRef]
- Carlson, T.N. A brief analysis of the triangle method and a proposal for its operational implementation. Remote Sens. 2020, 12, 3832. [Google Scholar] [CrossRef]
- Mallick, K.; Bhattacharya, B.K.; Patel, N.K. Estimating volumetric surface moisture content for cropped soils using a soil wetness index based on surface temperature and NDVI. Agric. Forest. Meteorol. 2009, 149, 1327–1342. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.-L.; Tang, B. A application of the Ts-VI triangle method with enhanced edges determination for evapotranspiration estimation from MODIS data in arid and semi-arid regions: Implementation and validation. Remote Sens. Environ. 2010, 114, 540–551. [Google Scholar] [CrossRef]
- Yang, Y.; Shang, S.A. Hybrid and dua-source scheme and trapezoid framework-based evapotranspiration model (HTEM)using satellite images: Algorithm and model test. J Geophys. Res 2013, 228, 2284–2300. [Google Scholar] [CrossRef]
- Nguyen, H.H.; Cho, S.; Choi, M. Synergy of SAR and optical/thermal and infrared remote sensing of soil moisture estimation in agro-pastoral transitional zones. Agric. For. Meteorol. 2022, 312, 108719. [Google Scholar] [CrossRef]
- Capehart, W.J.; Carlson, T.N. Decoupling of surface and near-surface soil water content: A remote sensing perspective. Water Resour. Res. 1997, 33, 1383–1395. [Google Scholar] [CrossRef]
- Rahimzadeh, B.; Berg, P.; Champagne, A.A.; Omasa, K. Estimation of soil moisture using optical/thermal infrared remote sensing in the Canadian prairies. ISPRS J. Photogramm. Remote Sens. 2013, 83, 94–103. [Google Scholar] [CrossRef]
- Wang, W.; Huang, D.; Wang, X.G.; Liu, Y.R.; Zhou, E. Estimation of soil moisture using trapezoidal relationship between remotely sensed land surface temperature and vegetation index. Hydrol. Earth Syst. Sci. 2011, 15, 1699–1712. [Google Scholar] [CrossRef]
- Wang, S.; Garcia, M.; Ibrom, A.; Jacobsen, J.; Koppl, C.J.; Mallick, K.; Loomis, M.C.; Bauer-Gottwein, P. Mapping root-zone soil noisture using a temperature-vegetation triangle approach with an unmanned aerial system incorporating surface roughness from structure and motion. Remote Sens. 2018, 10, 1978. [Google Scholar] [CrossRef]
- Kasim, A.; Carlson, T.N.; Usman, S. Limitations in validating derived soil water content from thermal/optical measurements using the simplified triangle method. Remote Sens. 2020, 12, 1155. [Google Scholar] [CrossRef]
- Lynn, B.H.; Carlson, T.N. Stomatal resistance model illustrating plant vs external control of transpiration. Agric. For. Meteorol. 1990, 52, 5–43. [Google Scholar] [CrossRef]
- Carlson, T.N.; Belles, J.R.; Gillies, R.R. Transient water stress in a vegetation canopy: Simulations and measurements. Remote Sens. Environ. 1991, 33, 175–186. [Google Scholar] [CrossRef]
- Olioso, A.; Carlson, T.N.; Bresson, N. Simulations of diurnal transpiration and diurnal photosynthesis of a water stressed soybean crop. Agric. For. Meteor. 1996, 81, 41–59. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.; Scanlon, B. Deriving theoretical boundaries to address scale dependencies of triangle models for evapotranspiration estimation. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Sadeghi, M.; Babaeian, E.; Tuller, M.; Jones, S.B. The optical trapezoid model. A novel approach to remote sensing of soil moisture applied to Sentinel-2 and Lansat-8 observations. Remote Sens. Environ. 2017, 198, 52–68. [Google Scholar] [CrossRef]
- Peng, J.; Liu, Y.; Zhao, X.; Loew, A. Estimation of evapotranspiration from MODIS radiances in the Poyang Lake Basin, China. Hydrol. Earth Syst. Sci. 2013, 17, 1431. [Google Scholar] [CrossRef]
- Zhang, H.; Gorelik, S.M.; Avisse, N.; Tilmant, N.; Rasekar, D.; Yoon, J. A new temperature-vegetation triangle algorithm with variable edges (TAVE) for satellite-based actual evapotranspiration estimation. Remote Sens. 2016, 8, 735. [Google Scholar] [CrossRef]
- Carlson, T.N.; Sanchez-Azofeifa, A. Satellite remote sensing of land use changes in and around San Jose’, Costa Rica. Remote Sens. Environ. 1999, 70, 247–256. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).