Atmospheric Water Vapor Variability over Houston: Continuous GNSS Tomography in the Year of Hurricane Harvey (2017)
Abstract
1. Introduction
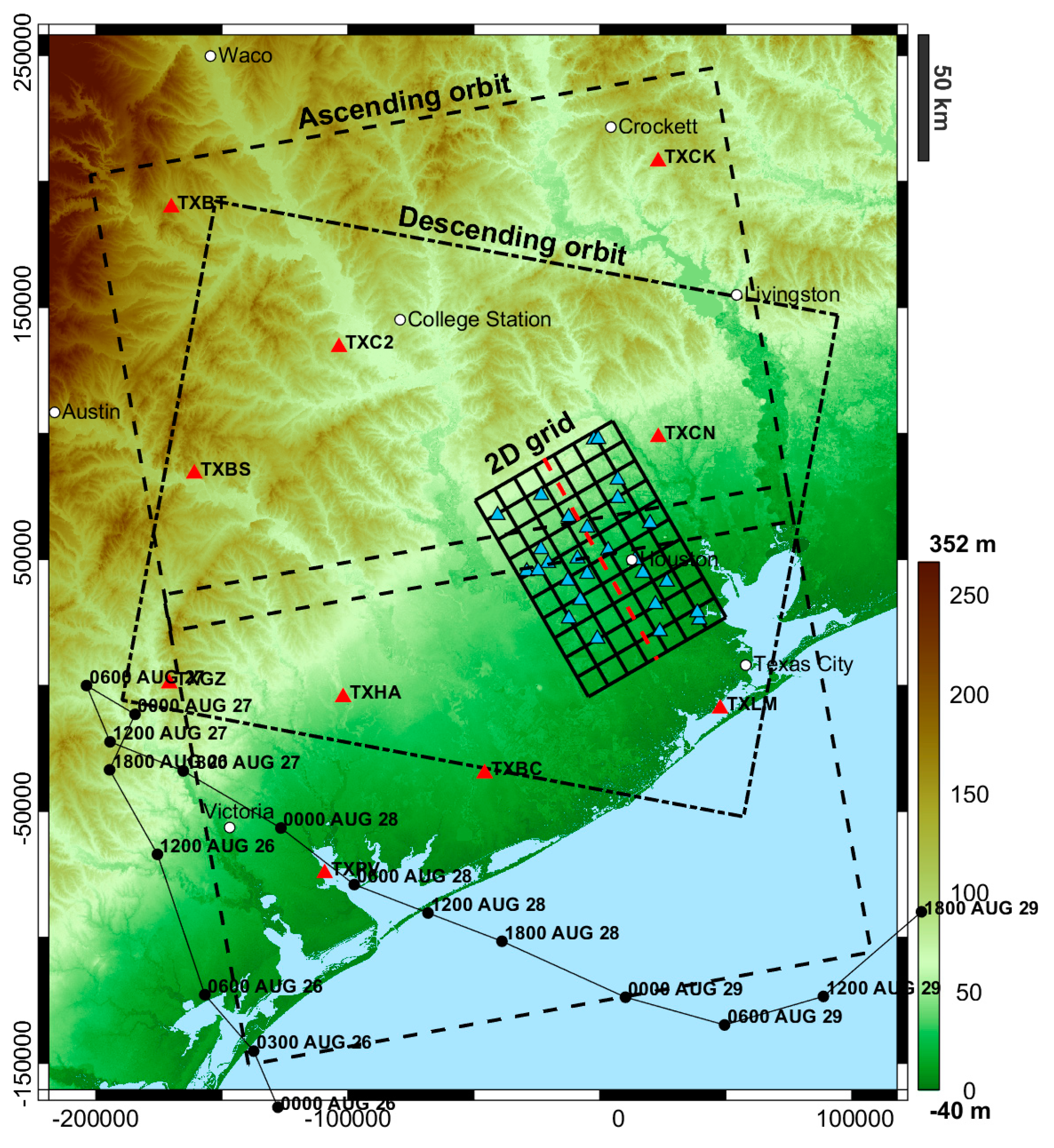
2. Materials and Methods
2.1. ERA5 Dataset
2.2. WRF Dataset
2.3. GNSS-RO Dataset
2.4. InSAR Dataset
2.5. GNSS Dataset
2.6. GNSS Tomographic Algorithm
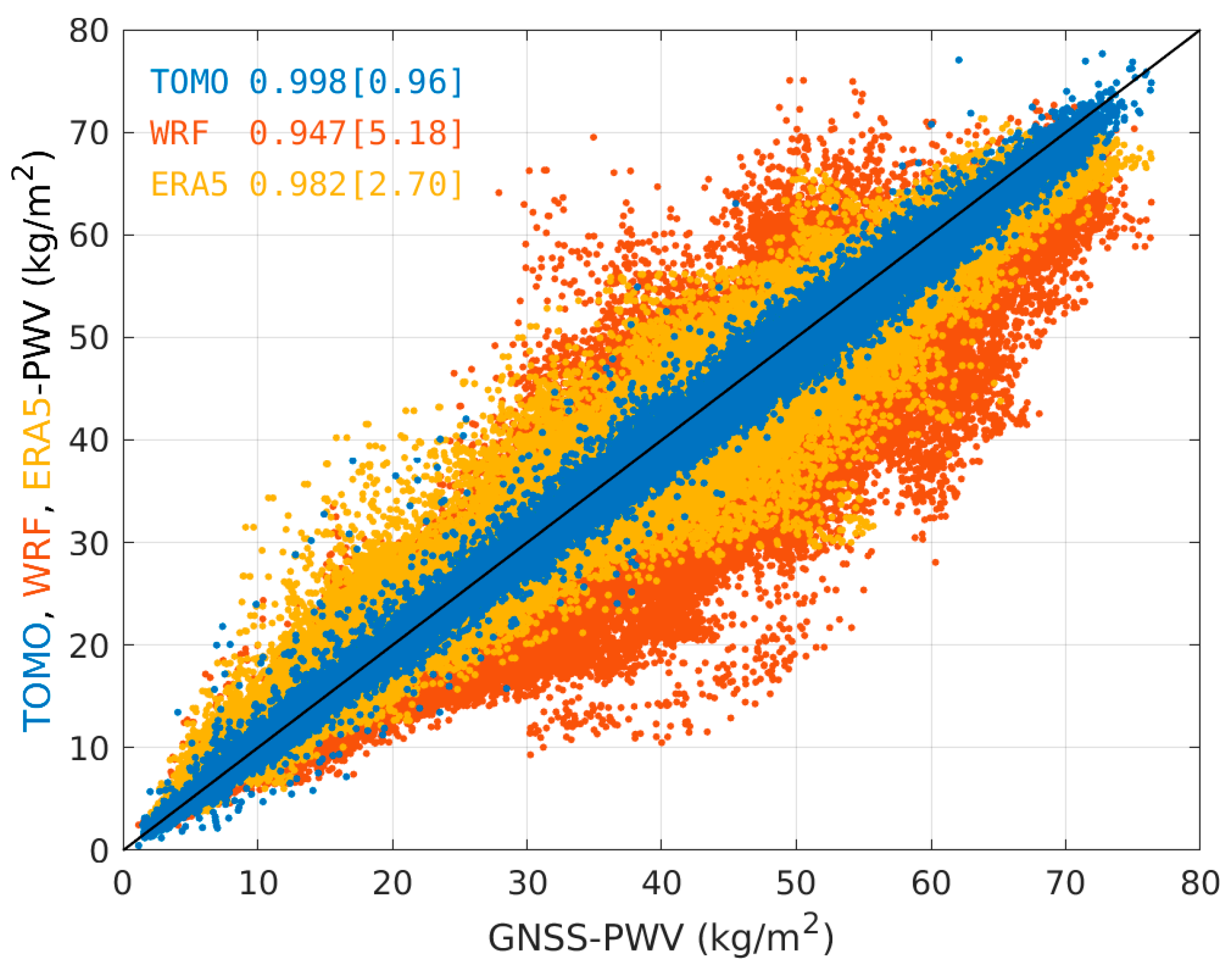
2.7. Validation Tools
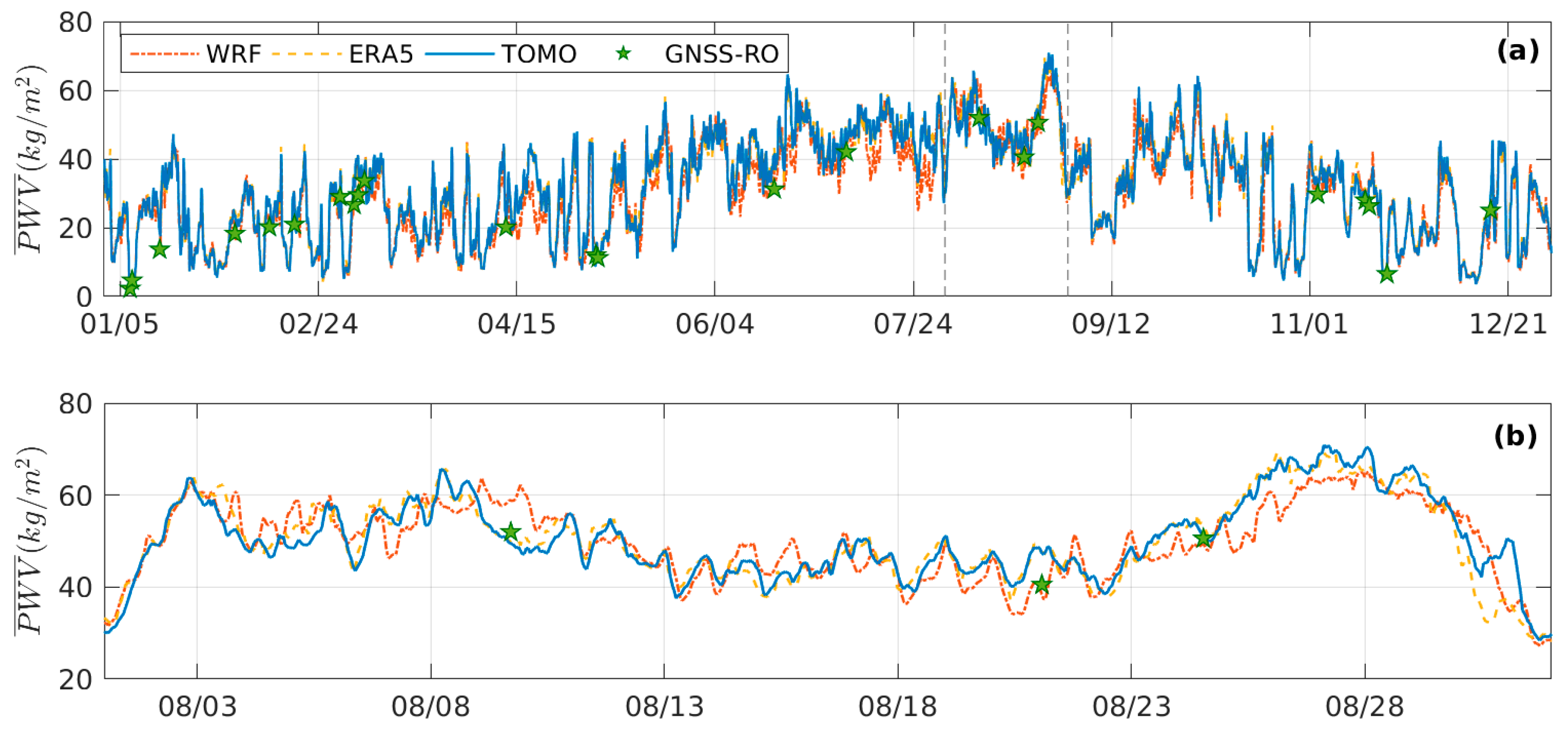
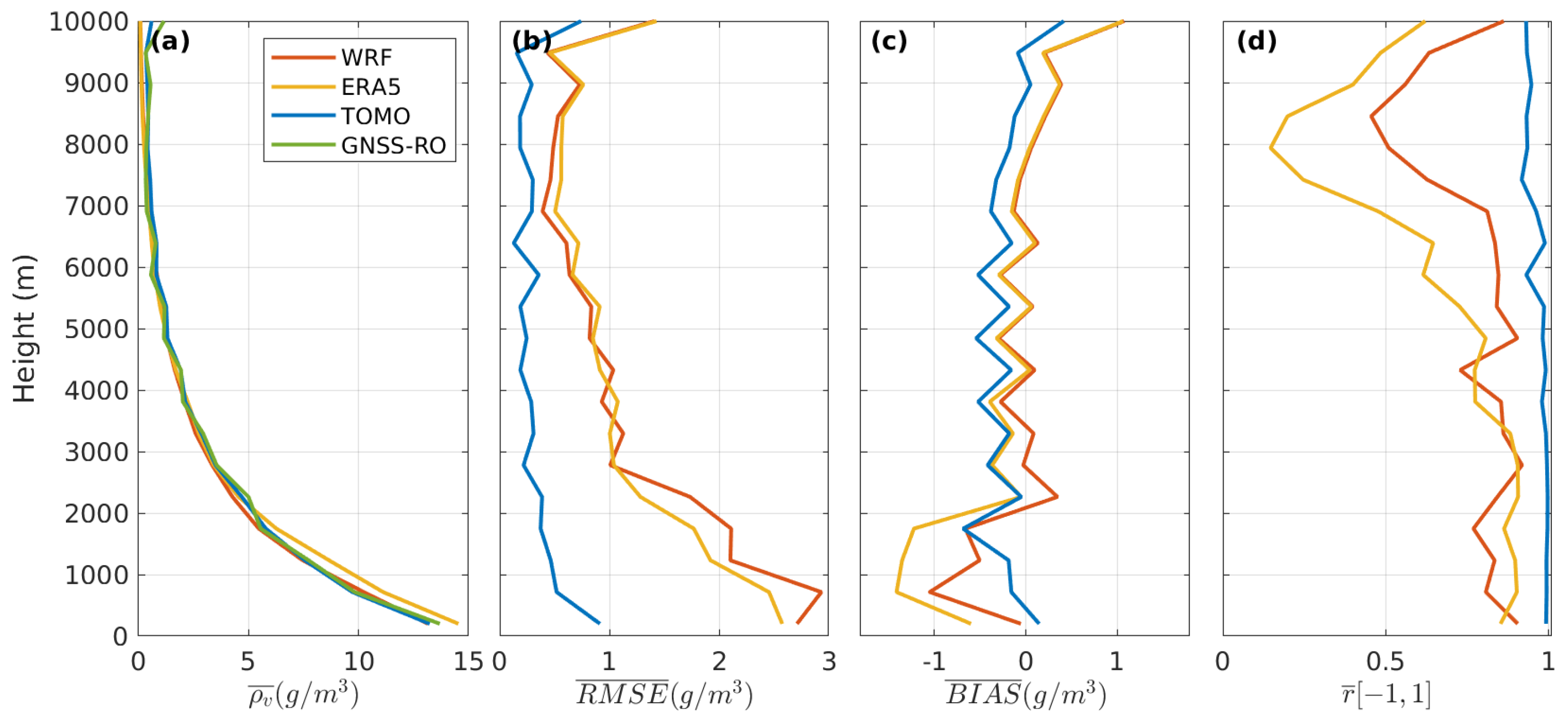
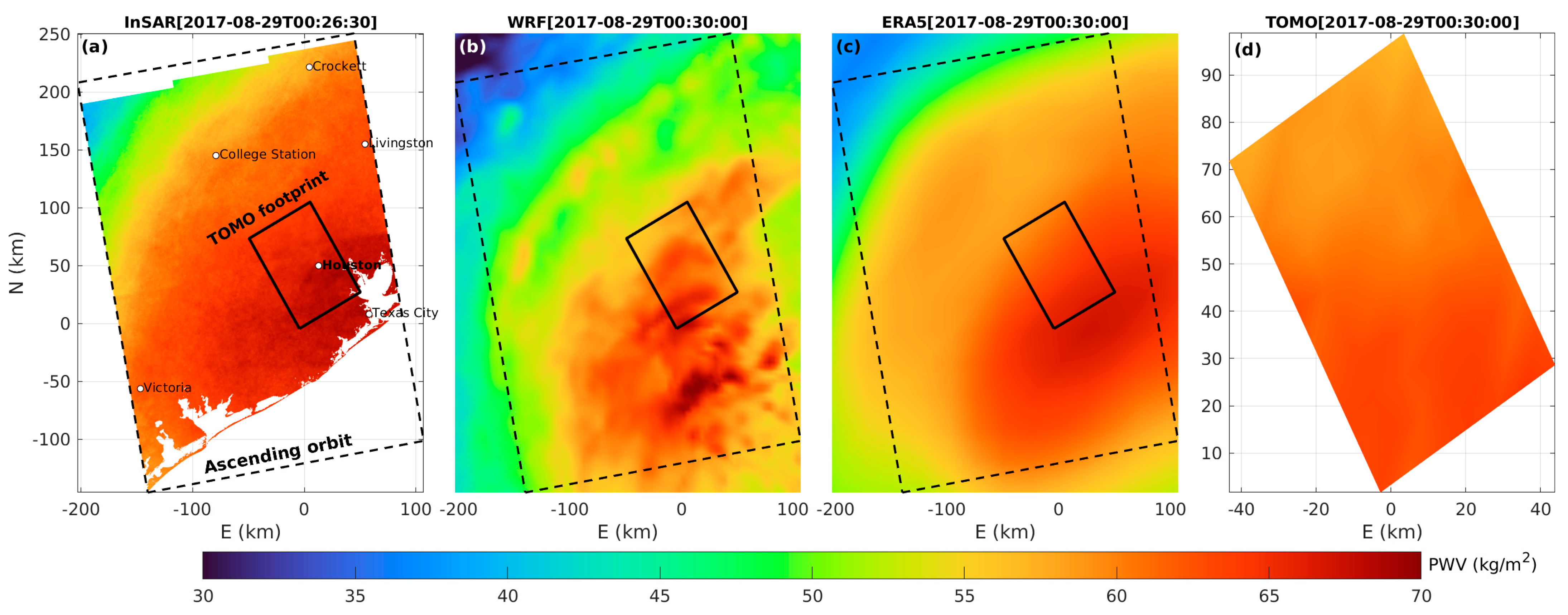
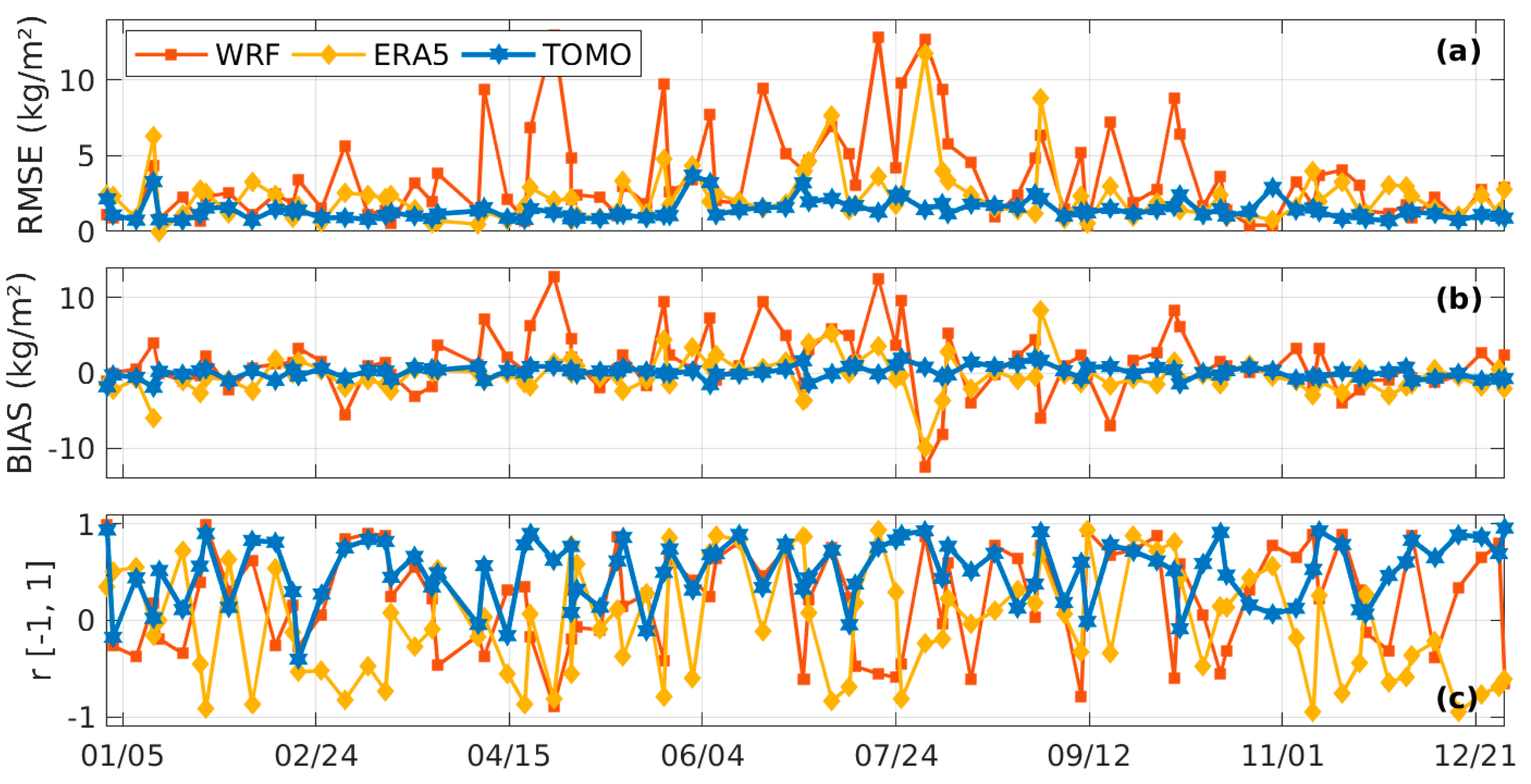
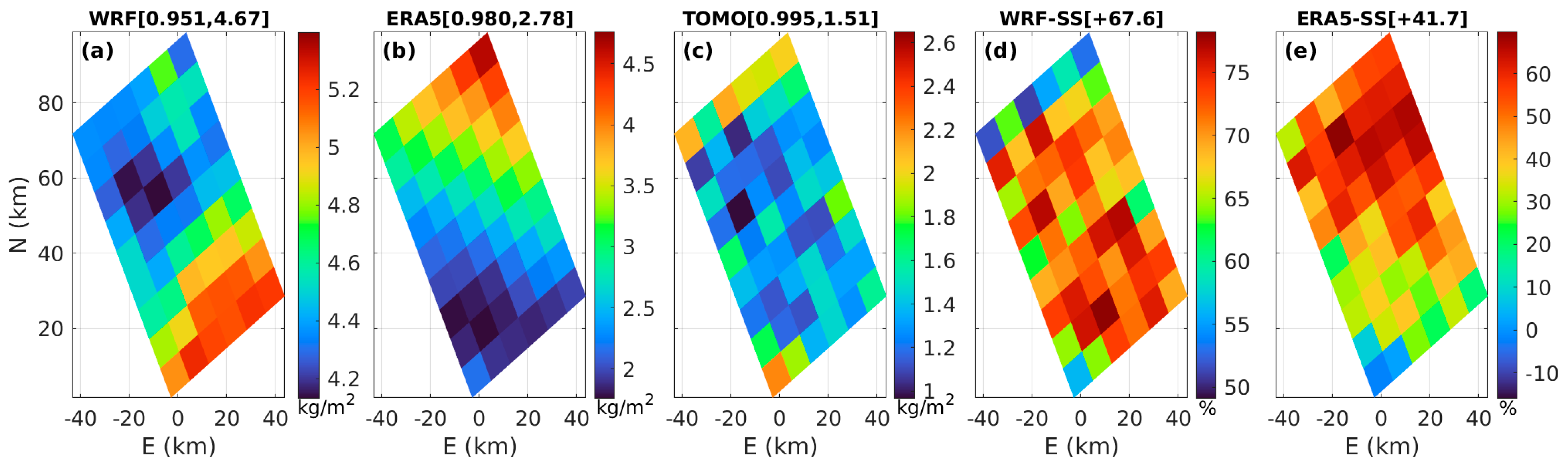
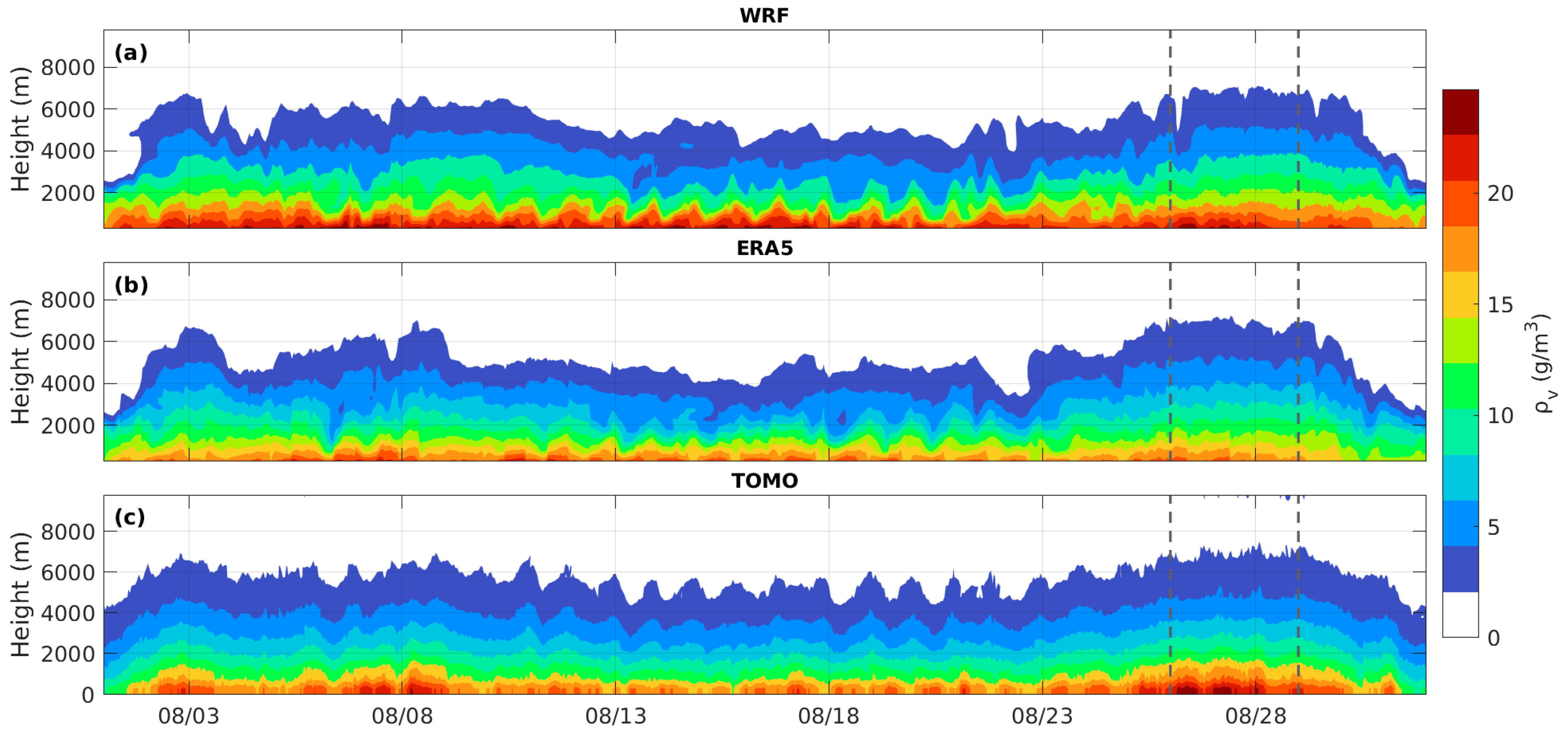
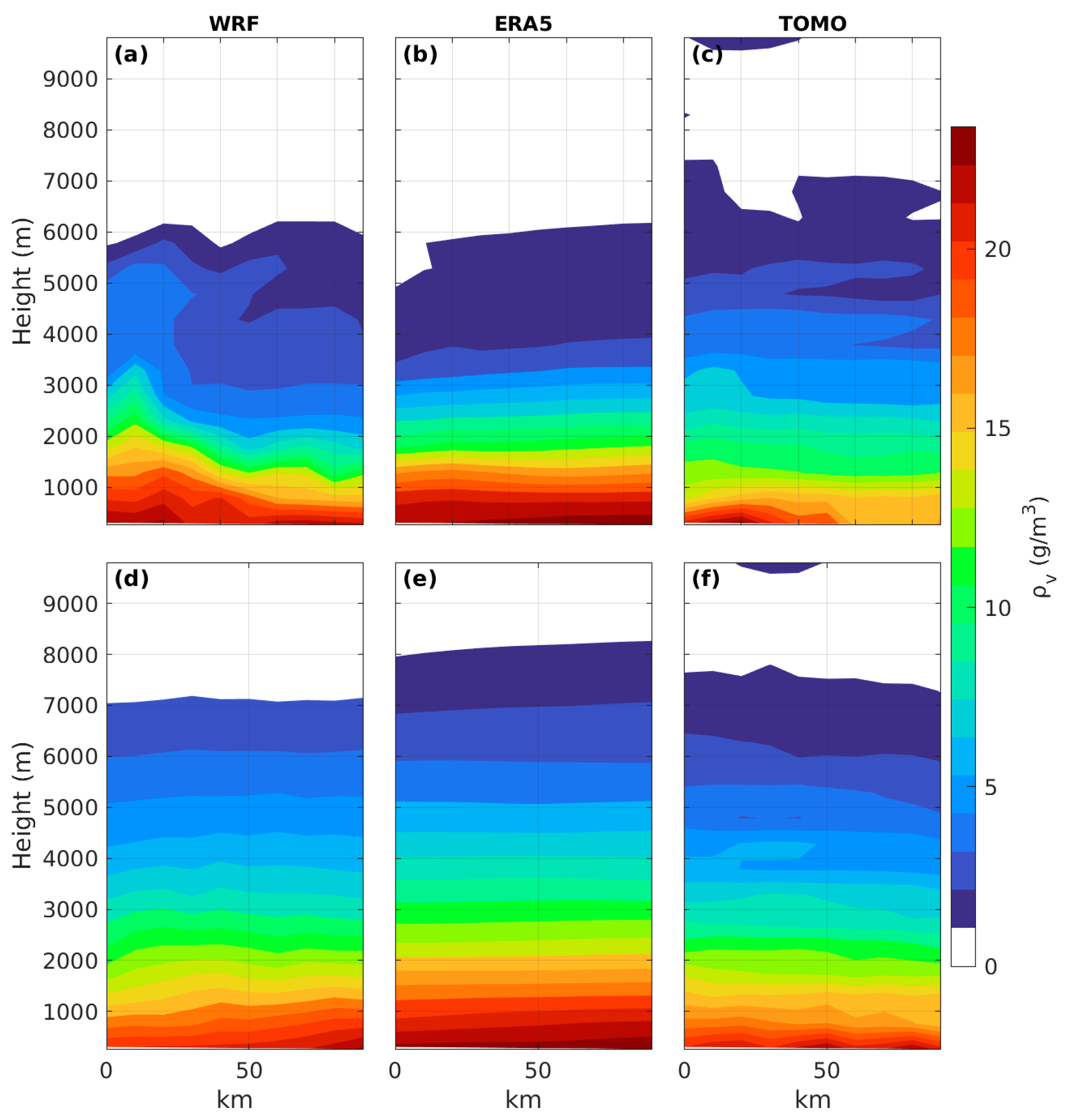
3. Results and Discussion
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Georgiev, C.G.; Santurette, P.; Maynard, K. Diagnosis of Thermodynamic Environment of Deep Convection. In Weather Analysis and Forecasting; Academic Press: Cambridge, MA, USA, 2016; pp. 157–222. [Google Scholar] [CrossRef]
- Flores, A.; Ruffini, G.; Rius, A. 4D Tropospheric Tomography Using GPS Slant Wet Delays. Ann. Geophys. 2000, 18, 223–234. [Google Scholar] [CrossRef]
- Rohm, W.; Bosy, J. The Verification of GNSS Tropospheric Tomography Model in a Mountainous Area. Adv. Space Res. 2011, 47, 1721–1730. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Yao, W.; Xia, P. An Optimal Tropospheric Tomography Approach with the Support of an Auxiliary Area. Ann. Geophys. 2018, 36, 1037–1046. [Google Scholar] [CrossRef]
- Yang, F.; Guo, J.; Shi, J.; Meng, X.; Zhao, Y.; Zhou, L.; Zhang, D. A GPS Water Vapour Tomography Method Based on a Genetic Algorithm. Atmos. Meas. Tech. 2020, 13, 355–371. [Google Scholar] [CrossRef]
- Benevides, P.; Catalao, J.; Miranda, P.M.A. On the Inclusion of GPS Precipitable Water Vapour in the Nowcasting of Rainfall. Nat. Hazards Earth Syst. Sci. 2015, 15, 2605–2616. [Google Scholar] [CrossRef]
- Benevides, P.; Catalao, J.; Nico, G.; Miranda, P.M.A. 4D Wet Refractivity Estimation in the Atmosphere Using GNSS Tomography Initialized by Radiosonde and AIRS Measurements: Results from a 1-Week Intensive Campaign. GPS Solut. 2018, 22, 91. [Google Scholar] [CrossRef]
- Chen, B.; Liu, Z. Assessing the Performance of Troposphere Tomographic Modeling Using Multi-Source Water Vapor Data during Hong Kong’s Rainy Season from May to October 2013. Atmos. Meas. Tech. 2016, 9, 5249–5263. [Google Scholar] [CrossRef]
- Xia, P.; Cai, C.; Liu, Z. GNSS Troposphere Tomography Based on Two-Step Reconstructions Using GPS Observations and COSMIC Profiles. Ann. Geophys. 2013, 31, 1805–1815. [Google Scholar] [CrossRef]
- Notarpietro, R.; Cucca, M.; Gabella, M.; Venuti, G.; Perona, G. Tomographic Reconstruction of Wet and Total Refractivity Fields from GNSS Receiver Networks. Adv. Space Res. 2011, 47, 898–912. [Google Scholar] [CrossRef]
- Trzcina, E.; Hanna, N.; Kryza, M.; Rohm, W. TOMOREF Operator for Assimilation of GNSS Tomography Wet Refractivity Fields in WRF DA System. J. Geophys. Res. Atmos. 2020, 125, e2020JD032451. [Google Scholar] [CrossRef]
- Haji-Aghajany, S.; Amerian, Y.; Verhagen, S. B-Spline Function-Based Approach for GPS Tropospheric Tomography. GPS Solut. 2020, 24, 88. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y. An Improved Troposphere Tomographic Approach Considering the Signals Coming from the Side Face of the Tomographic Area. Ann. Geophys. 2017, 35, 87–95. [Google Scholar] [CrossRef]
- Yang, F.; Guo, J.; Shi, J.; Zhou, L.; Xu, Y.; Chen, M. A Method to Improve the Distribution of Observations in GNSS Water Vapor Tomography. Sensors 2018, 18, 2526. [Google Scholar] [CrossRef] [PubMed]
- Adavi, Z.; Mashhadi-Hossainali, M. 4D Tomographic Reconstruction of the Tropospheric Wet Refractivity Using the Concept of Virtual Reference Station, Case Study: Northwest of Iran. Meteorol. Atmos. Phys. 2014, 126, 193–205. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, C.; Xu, C. A New GNSS-Derived Water Vapor Tomography Method Based on Optimized Voxel for Large GNSS Network. Remote Sens. 2020, 12, 2306. [Google Scholar] [CrossRef]
- Miranda, P.M.A.; Mateus, P. A New Unconstrained Approach to GNSS Atmospheric Water Vapor Tomography. Geophys. Res. Lett. 2021, 48, e2021GL094852. [Google Scholar] [CrossRef]
- Miranda, P.M.A.; Mateus, P. Improved GNSS Water Vapor Tomography With Modified Mapping Functions. Geophys. Res. Lett. 2022, 49, e2022GL100140. [Google Scholar] [CrossRef]
- Miranda, P.M.A.; Adams, D.K.; Tomé, R.; Fernandes, R.; Mateus, P. Optimizing Boundary Conditions in GNSS Tomography: A Continuous 7-Month Case Study in the Amazon. Geophys. Res. Lett. 2023, 50, e2023GL105030. [Google Scholar] [CrossRef]
- Haji-Aghajany, S.; Amerian, Y. Hybrid Regularized GPS Tropospheric Sensing Using 3-D Ray Tracing Technique. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1475–1479. [Google Scholar] [CrossRef]
- Flores, A.; De Arellano, J.V.G.; Gradinarsky, L.P.; Rius, A. Tomography of the Lower Troposphere Using a Small Dense Network of GPS Receivers. IEEE Trans. Geosci. Remote Sens. 2001, 39, 439–447. [Google Scholar] [CrossRef]
- Champollion, C.; Masson, F.; Bouin, M.N.; Walpersdorf, A.; Doerflinger, E.; Bock, O.; Van Baelen, J. GPS Water Vapour Tomography: Preliminary Results from the ESCOMPTE Field Experiment. Atmos. Res. 2005, 74, 253–274. [Google Scholar] [CrossRef]
- Bender, M.; Dick, G.; Ge, M.; Deng, Z.; Wickert, J.; Kahle, H.G.; Raabe, A.; Tetzlaff, G. Development of a GNSS Water Vapour Tomography System Using Algebraic Reconstruction Techniques. Adv. Space Res. 2011, 47, 1704–1720. [Google Scholar] [CrossRef]
- Foken, T. (Ed.) Springer Handbook of Atmospheric Measurements; Springer Handbooks; Springer International Publishing: Cham, Switzerland, 2021; ISBN 978-3-030-52170-7. [Google Scholar]
- Rohm, W.; Yuan, Y.; Biadeglgne, B.; Zhang, K.; Marshall, J. Le Ground-Based GNSS ZTD/IWV Estimation System for Numerical Weather Prediction in Challenging Weather Conditions. Atmos. Res. 2014, 138, 414–426. [Google Scholar] [CrossRef]
- Perler, D.; Geiger, A.; Hurter, F. 4D GPS Water Vapor Tomography: New Parameterized Approaches. J. Geod. 2011, 85, 539–550. [Google Scholar] [CrossRef]
- Yang, F.; Gong, X.; Wang, Y.; Liu, M.; Li, J.; Xu, T.; Hao, R. GNSS Water Vapor Tomography Based on Kalman Filter with Optimized Noise Covariance. GPS Solut. 2023, 27, 181. [Google Scholar] [CrossRef]
- Bonafoni, S.; Biondi, R.; Brenot, H.; Anthes, R. Radio Occultation and Ground-Based GNSS Products for Observing, Understanding and Predicting Extreme Events: A Review. Atmos. Res. 2019, 230, 104624. [Google Scholar] [CrossRef]
- Saxena, S.; Dwivedi, R. GNSS Ground-Based Tomography: State-of-the-Art and Technological Challenges. Int. J. Remote Sens. 2023, 44, 5313–5343. [Google Scholar] [CrossRef]
- Yang, F.; Sun, Y.; Meng, X.; Guo, J.; Gong, X. Assessment of Tomographic Window and Sampling Rate Effects on GNSS Water Vapor Tomography. Satell. Navig. 2023, 4, 7. [Google Scholar] [CrossRef]
- Penrose, R. A Generalized Inverse for Matrices. Math. Proc. Camb. Philos. Soc. 1955, 51, 406–413. [Google Scholar] [CrossRef]
- Lawson, C.L.; Hanson, R.J. Solving Least Squares Problems; Society for Industrial and Applied Mathematics; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1995; ISBN 978-0-89871-356-5. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Liu, Z.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Barker, D.M.; et al. A Description of the Advanced Research WRF Model Version 4.3 (No. NCAR/TN-556+STR). Available online: https://opensky.ucar.edu/islandora/object/opensky:2898 (accessed on 1 August 2024).
- Anthes, R.A. Exploring Earth’s Atmosphere with Radio Occultation: Contributions to Weather, Climate and Space Weather. Atmos. Meas. Tech. 2011, 4, 1077–1103. [Google Scholar] [CrossRef]
- Mateus, P.; Miranda, P.M.A. Using InSAR Data to Improve the Water Vapor Distribution Downstream of the Core of the South American Low-Level Jet. J. Geophys. Res. Atmos. 2022, 127, e2021JD036111. [Google Scholar] [CrossRef]
- Mateus, P.; Miranda, P.M.A.; Nico, G.; Catalao, J. Continuous Multitrack Assimilation of Sentinel-1 Precipitable Water Vapor Maps for Numerical Weather Prediction: How Far Can We Go With Current InSAR Data? J. Geophys. Res. Atmos. 2021, 126, e2020JD034171. [Google Scholar] [CrossRef]
- Hoffmann, L.; Günther, G.; Li, D.; Stein, O.; Wu, X.; Griessbach, S.; Heng, Y.; Konopka, P.; Müller, R.; Vogel, B.; et al. From ERA-Interim to ERA5: The Considerable Impact of ECMWF’s next-Generation Reanalysis on Lagrangian Transport Simulations. Atmos. Chem. Phys. 2019, 19, 3097–3124. [Google Scholar] [CrossRef]
- Stull, R.B. Practical Meteorology: An Algebra-Based Survey of Atmospheric Science; 1.02b.; Sundog Publishing, LLC: Vancouver, BC, Canada, 2017. [Google Scholar]
- Neiman, P.J.; Ralph, F.M.; Wick, G.A.; Kuo, Y.-H.; Wee, T.-K.; Ma, Z.; Taylor, G.H.; Dettinger, M.D. Diagnosis of an Intense Atmospheric River Impacting the Pacific Northwest: Storm Summary and Offshore Vertical Structure Observed with COSMIC Satellite Retrievals. Mon. Weather Rev. 2008, 136, 4398–4420. [Google Scholar] [CrossRef]
- Palmer, P.I.; Barnett, J.J.; Eyre, J.R.; Healy, S.B. A Nonlinear Optimal Estimation Inverse Method for Radio Occultation Measurements of Temperature, Humidity, and Surface Pressure. J. Geophys. Res. Atmos. 2000, 105, 17513–17526. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry, Data Interpretation and Error Analysis; Remote Sensing and Digital Image Processing; Springer: Dordrecht, The Netherlands, 2001; Volume 2, ISBN 978-0-7923-6945-5. [Google Scholar]
- Kinoshita, Y.; Shimada, M.; Furuya, M. InSAR Observation and Numerical Modeling of the Water Vapor Signal during a Heavy Rain: A Case Study of the 2008 Seino Event, Central Japan. Geophys. Res. Lett. 2013, 40, 4740–4744. [Google Scholar] [CrossRef]
- Brenot, H.; Ducrocq, V.; Walpersdorf, A.; Champollion, C.; Caumont, O. GPS Zenith Delay Sensitivity Evaluated from High-Resolution Numerical Weather Prediction Simulations of the 8–9 September 2002 Flash Flood over Southeastern France. J. Geophys. Res. Atmos. 2006, 111, 15105. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar Interferogram Filtering for Geophysical Applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Nico, G.; Fortuny, J. Using the Matrix Pencil Method to Solve Phase Unwrapping. IEEE Trans. Signal Process. 2003, 51, 886–888. [Google Scholar] [CrossRef]
- Bevis, M. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable Water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Jean Rüeger, A.M. Refractive Index Formulae for Radio Waves. In Proceedings of the FIG XXII International Congress, Washington, DC, USA, 19–26 April 2002; pp. 19–26. [Google Scholar]
- Mateus, P.; Nico, G.; Catalão, J. Maps of PWV Temporal Changes by SAR Interferometry: A Study on the Properties of Atmosphere’s Temperature Profiles. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2065–2069. [Google Scholar] [CrossRef]
- Mendes, V.B. Modeling the Neutral-Atmospheric Propagation Delay in Radiometric Space Techniques; University of New Brunswick: Fredericton, NB, Canada, 1999; p. 353. Available online: https://gge.ext.unb.ca/Pubs/TR199.pdf (accessed on 1 August 2024).
- Mateus, P.; Catalão, J.; Nico, G.; Benevides, P. Mapping Precipitable Water Vapor Time Series from Sentinel-1 Interferometric SAR. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1373–1379. [Google Scholar] [CrossRef]
- Mateus, P.; Catalão, J.; Nico, G. Improving the Accuracy and Spatial Resolution of ERA5 Precipitable Water Vapor Using InSAR Data. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1001905. [Google Scholar] [CrossRef]
- Meroni, A.N.; Montrasio, M.; Venuti, G.; Barindelli, S.; Mascitelli, A.; Manzoni, M.; Monti-Guarnieri, A.V.; Gatti, A.; Lagasio, M.; Parodi, A.; et al. On the Definition of the Strategy to Obtain Absolute InSAR Zenith Total Delay Maps for Meteorological Applications. Front. Earth Sci. 2020, 8, 359. [Google Scholar] [CrossRef]
- Remy, D.; Chen, Y.; Froger, J.L.; Bonvalot, S.; Cordoba, L.; Fustos, J. Revised Interpretation of Recent InSAR Signals Observed at Llaima Volcano (Chile). Geophys. Res. Lett. 2015, 42, 3870–3879. [Google Scholar] [CrossRef]
- Wadge, G.; Webley, P.W.; James, I.N.; Bingley, R.; Dodson, A.; Waugh, S.; Veneboer, T.; Puglisi, G.; Mattia, M.; Baker, D.; et al. Atmospheric Models, GPS and InSAR Measurements of the Tropospheric Water Vapour Field over Mount Etna. Geophys. Res. Lett. 2002, 29, 11. [Google Scholar] [CrossRef]
- Zebker, H.A.; Rosen, P.A.; Hensley, S. Atmospheric Effects in Interferometric Synthetic Aperture Radar Surface Deformation and Topographic Maps. J. Geophys. Res. Solid Earth 1997, 102, 7547–7563. [Google Scholar] [CrossRef]
- Mateus, P.; Catalão, J.; Nico, G. Sentinel-1 Interferometric SAR Mapping of Precipitable Water Vapor over a Country-Spanning Area. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2993–2999. [Google Scholar] [CrossRef]
- Mateus, P.; Miranda, P.M.A.; Nico, G.; Catalão, J.; Pinto, P.; Tomé, R. Assimilating InSAR Maps of Water Vapor to Improve Heavy Rainfall Forecasts: A Case Study with Two Successive Storms. J. Geophys. Res. Atmos. 2018, 123, 3341–3355. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; Floyd, M.A.; McClusky, S.C. GAMIT Reference Manual Reference Manual GPS Analysis at MIT; Department of Earth, Atmospheric, and Planetary Sciences Institute of Technology: Cambridge, MA, USA, 2018; Available online: http://geoweb.mit.edu/gg/docs.php (accessed on 1 August 2024).
- Chen, G.; Herring, T.A. Effects of Atmospheric Azimuthal Asymmetry on the Analysis of Space Geodetic Data. J. Geophys. Res. Solid Earth 1997, 102, 20489–20502. [Google Scholar] [CrossRef]
- Gal-Chen, T.; Somerville, R.C.J. On the Use of a Coordinate Transformation for the Solution of the Navier-Stokes Equations. J. Comput. Phys. 1975, 17, 209–228. [Google Scholar] [CrossRef]
- Tomasi, C. Vertical Distribution Features of Atmospheric Water Vapor in the Mediterranean, Red Sea, and Indian Ocean. J. Geophys. Res. Atmos. 1984, 89, 2563–2566. [Google Scholar] [CrossRef]
- Prein, A.F.; Rasmussen, R.; Castro, C.L.; Dai, A.; Minder, J. Special Issue: Advances in Convection-Permitting Climate Modeling. Clim. Dyn. 2020, 55, 1–2. [Google Scholar] [CrossRef]
| Name of Strategy | Strategy Setting |
|---|---|
| Approach | DD (Double Difference) |
| Choice of observable | LC (Linear Combination of L1 and L2) |
| Cut-off elevation angle | 5° |
| Sampling interval | 30 s |
| Dry a priori model | SAAS (Saastamoinen model) |
| Dry and Wet mapping function | VMF3 |
| Ocean tidal model | FES2004 |
| Solid tide models | IERS10 |
| Orbit and clock | IGS final products |
| Satellite and antenna phase center | IGS14 ANTEX file |
| Tropospheric Gradient Estimation | 2 h |
| Tropospheric delay | |
| Ionosphere effect | 1-order (LC), 2- and 3-order correction |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mateus, P.; Catalão, J.; Fernandes, R.; Miranda, P.M.A. Atmospheric Water Vapor Variability over Houston: Continuous GNSS Tomography in the Year of Hurricane Harvey (2017). Remote Sens. 2024, 16, 3205. https://doi.org/10.3390/rs16173205
Mateus P, Catalão J, Fernandes R, Miranda PMA. Atmospheric Water Vapor Variability over Houston: Continuous GNSS Tomography in the Year of Hurricane Harvey (2017). Remote Sensing. 2024; 16(17):3205. https://doi.org/10.3390/rs16173205
Chicago/Turabian StyleMateus, Pedro, João Catalão, Rui Fernandes, and Pedro M. A. Miranda. 2024. "Atmospheric Water Vapor Variability over Houston: Continuous GNSS Tomography in the Year of Hurricane Harvey (2017)" Remote Sensing 16, no. 17: 3205. https://doi.org/10.3390/rs16173205
APA StyleMateus, P., Catalão, J., Fernandes, R., & Miranda, P. M. A. (2024). Atmospheric Water Vapor Variability over Houston: Continuous GNSS Tomography in the Year of Hurricane Harvey (2017). Remote Sensing, 16(17), 3205. https://doi.org/10.3390/rs16173205







