Spatio-Temporal Pruning for Training Ultra-Low-Latency Spiking Neural Networks in Remote Sensing Scene Classification
Abstract
1. Introduction
- Inspired by the concept of transfer learning, we introduce a novel spatio-temporal pruning method designed to train ultra-low-latency SNNs. This approach effectively integrates the temporal dynamics characteristic of SNNs with the static feature extraction capabilities of CNNs. Consequently, this method significantly enhances the performances of ultra-low-latency SNNs and effectively reduces the performance gap with ANNs.
- Since residual connections allow information to cross layers, the influence of network structures (such as VGG and ResNet) on feature extraction varies differently. To investigate the effectiveness of our method across different network structures, we analyze the impact of the position of the fundamental module (the module subject to pruning) on feature expression and determine the optimal pruning strategy accordingly.
- To validate the efficacy of our method, we construct an ultra-low-latency SNN training framework based on the leak integrate-and-fire (LIF) neuron model. Through evaluation in a remote sensing scene classification task, our method not only achieves state-of-the-art performance but also successfully reduces the latency of SNNs to one time step, which is 200 times lower than those of other advanced approaches.
2. Related Works
2.1. Remote Sensing Scene Classification
2.2. Methods of Training Ultra-Low-Latency SNNs
2.2.1. ANN-SNN Conversion
2.2.2. Direct Training
2.2.3. Hybrid Training
3. Proposed Method
3.1. Overall Workflow of the Proposed Spatio-Temporal Pruning Method
| Algorithm 1: Spatio-Temporal Pruning Method |
| Input: the number of Unit (M), the location of Unit (AS), ANN model (Na, Nb), SNN model (Sa, Sb). |
| for m in M do |
| if n == AS then // the nth layer is the location of Unit |
| Nb (n,m) ← Add_Unit(n,m,Na) // Step1 |
| Sb (n,m) ← Nb (n,m) // TP method;Step2 |
| Sa ← Sb (n,m) // Algorithm 2; Step3 |
| end for |
| Algorithm 2: Spatial pruning from SNNb to SNNa |
| Input: the number of layers in Sa (La), SNNa weights (Wa), SNNb weights (Wb), SNNa threshold (va), SNNb threshold vb, SNNa membrane leak (λa), SNNa membrane leak (λb). |
| for i = 0 in range(La) do |
| if i < AS then |
| Wa [i] ← Wb [i] |
| va [i] ← vb [i] |
| λa [i] ← λb [i] |
| else |
| Wa [i] ← Wb [i+ M] |
| va [i] ← vb [i+ M] |
| λa [i] ← λb [i+ M] |
| end for |
3.2. Deep Networks with the Structure of Unit
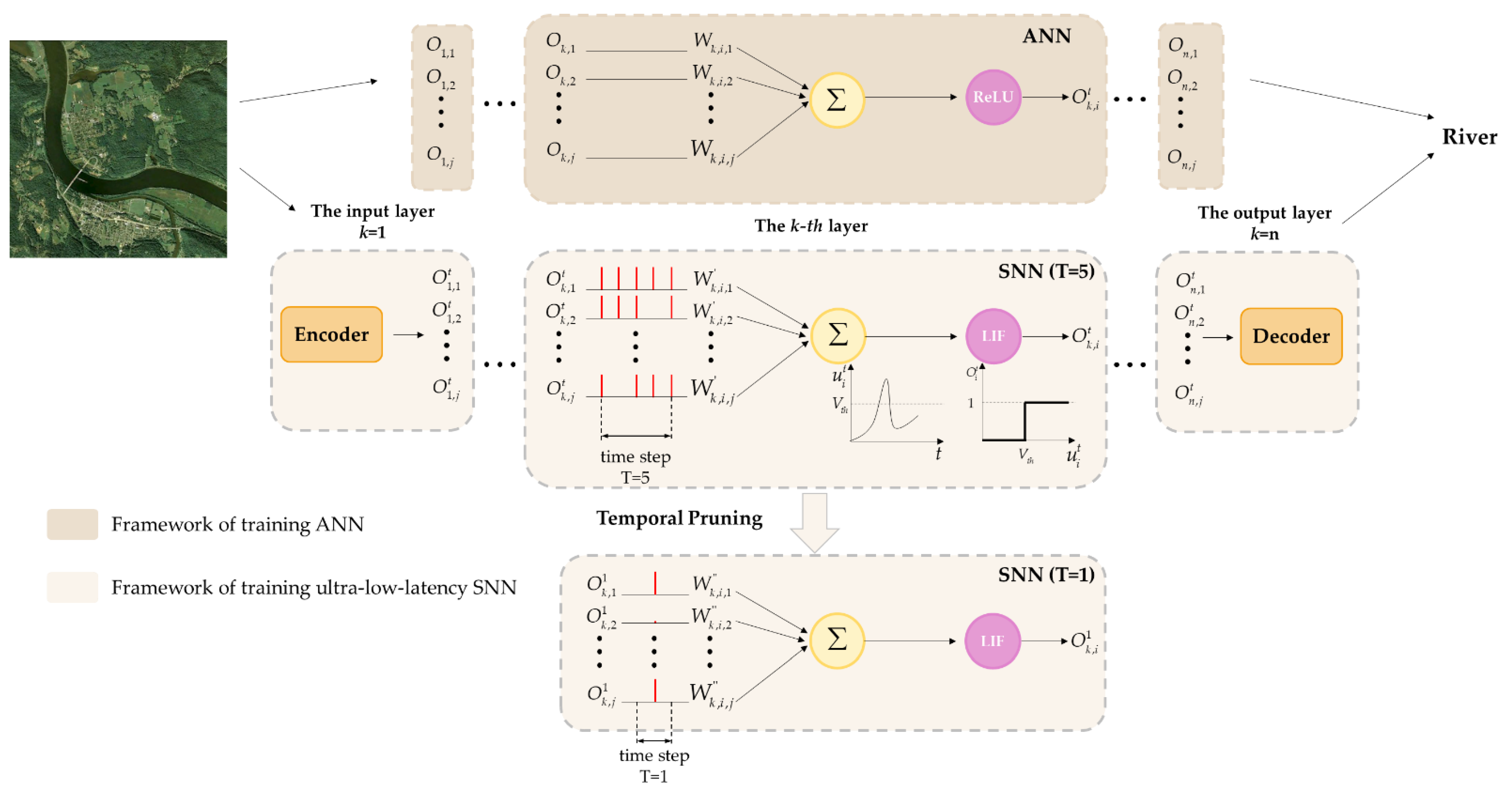
3.3. The Framework of Training Ultra-Low-Latency SNNs
3.3.1. Spiking Neuron Model
3.3.2. Surrogate Gradient
3.3.3. Input Layer and Direct Encoding
3.3.4. Output Layer and Loss Function
3.3.5. Conversion of Batch Normalization Layers
3.3.6. Temporal Pruning
4. Experiment and Discussion
4.1. Datasets and Evaluation Metrics
4.1.1. Datasets
4.1.2. Evaluation Metrics
4.2. Implementation Details
4.2.1. Networks
4.2.2. Hyperparameters Setting
4.3. Experimental Results of Performance
4.3.1. Comparison with ANN
4.3.2. Comparison with State-of-the-Art Methods
4.3.3. Ablation Study
4.3.4. Analysis of Unit Location Impact
4.4. Experimental Results of Energy Efficiency
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sang, X.; Xue, L.; Ran, X.; Li, X.; Liu, J.; Liu, Z. Intelligent High-Resolution Geological Mapping Based on SLIC-CNN. ISPRS Int. J. Geo-Inf. 2020, 9, 99. [Google Scholar] [CrossRef]
- Zhao, W.; Bo, Y.; Chen, J.; Tiede, D.; Blaschke, T.; Emery, W.J. Exploring Semantic Elements for Urban Scene Recognition: Deep Integration of High-Resolution Imagery and OpenStreetMap (OSM). ISPRS J. Photogramm. Remote Sens. 2019, 151, 237–250. [Google Scholar] [CrossRef]
- Cervone, G.; Sava, E.; Huang, Q.; Schnebele, E.; Harrison, J.; Waters, N. Using Twitter for Tasking Remote-Sensing Data Collection and Damage Assessment: 2013 Boulder Flood Case Study. Int. J. Remote Sens. 2016, 37, 100–124. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Lu, X. Remote Sensing Image Scene Classification: Benchmark and State of the Art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Cheng, G.; Yang, C.; Yao, X.; Guo, L.; Han, J. When Deep Learning Meets Metric Learning: Remote Sensing Image Scene Classification via Learning Discriminative CNNs. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2811–2821. [Google Scholar] [CrossRef]
- Li, E.; Xia, J.; Du, P.; Lin, C.; Samat, A. Integrating Multilayer Features of Convolutional Neural Networks for Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5653–5665. [Google Scholar] [CrossRef]
- Zhou, W.; Newsam, S.; Li, C.; Shao, Z. PatternNet: A Benchmark Dataset for Performance Evaluation of Remote Sensing Image Retrieval. ISPRS J. Photogramm. Remote Sens. 2018, 145, 197–209. [Google Scholar] [CrossRef]
- Maass, W. Networks of Spiking Neurons: The Third Generation of Neural Network Models. Neural Netw. 1997, 10, 1659–1671. [Google Scholar] [CrossRef]
- Zheng, H.; Wu, Y.; Deng, L.; Hu, Y.; Li, G. Going Deeper with Directly-Trained Larger Spiking Neural Networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 35, pp. 11062–11070. [Google Scholar]
- Kim, S.; Park, S.; Na, B.; Yoon, S. Spiking-Yolo: Spiking Neural Network for Energy-Efficient Object Detection. In Proceedings of the AAAI Conference on Artificial Intelligence, Midtown, NY, USA, 7–12 February 2020; Volume 34, pp. 11270–11277. [Google Scholar]
- Wu, S.; Li, J.; Qi, L.; Liu, Z.; Gao, X. Remote Sensing Imagery Scene Classification Based on Spiking Neural Network. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 2795–2798. [Google Scholar]
- Niu, L.-Y.; Wei, Y.; Liu, Y. Event-Driven Spiking Neural Network Based on Membrane Potential Modulation for Remote Sensing Image Classification. Eng. Appl. Artif. Intell. 2023, 123, 106322. [Google Scholar] [CrossRef]
- Chowdhury, S.S.; Rathi, N.; Roy, K. Towards Ultra Low Latency Spiking Neural Networks for Vision and Sequential Tasks Using Temporal Pruning. In Proceedings of the Computer Vision—ECCV 2022, Tel Aviv, Israel, 23–27 October 2022; Avidan, S., Brostow, G., Cissé, M., Farinella, G.M., Hassner, T., Eds.; Springer Nature: Cham, Switzerland, 2022; pp. 709–726. [Google Scholar]
- Hao, Z.; Ding, J.; Bu, T.; Huang, T.; Yu, Z. Bridging the Gap between Anns and Snns by Calibrating Offset Spikes. arXiv 2023, arXiv:2302.10685. [Google Scholar]
- Bu, T.; Fang, W.; Ding, J.; Dai, P.; Yu, Z.; Huang, T. Optimal ANN-SNN Conversion for High-Accuracy and Ultra-Low-Latency Spiking Neural Networks. arXiv 2023, arXiv:2303.04347. [Google Scholar]
- Guo, Y.; Liu, X.; Chen, Y.; Zhang, L.; Peng, W.; Zhang, Y.; Huang, X.; Ma, Z. Rmp-Loss: Regularizing Membrane Potential Distribution for Spiking Neural Networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–3 October 2023; pp. 17391–17401. [Google Scholar]
- Li, Y.; Guo, Y.; Zhang, S.; Deng, S.; Hai, Y.; Gu, S. Differentiable Spike: Rethinking Gradient-Descent for Training Spiking Neural Networks. Adv. Neural Inf. Process. Syst. 2021, 34, 23426–23439. [Google Scholar]
- Guo, Y.; Peng, W.; Chen, Y.; Zhang, L.; Liu, X.; Huang, X.; Ma, Z. Joint A-SNN: Joint Training of Artificial and Spiking Neural Networks via Self-Distillation and Weight Factorization. Pattern Recognit. 2023, 142, 109639. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Y.; Xu, C.; Shi, B.; Xu, C.; Tian, Q.; Xu, C. AdderNet: Do We Really Need Multiplications in Deep Learning? In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1465–1474. [Google Scholar]
- Li, W.; Chen, H.; Huang, M.; Chen, X.; Xu, C.; Wang, Y. Winograd Algorithm for Addernet. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 6307–6315. [Google Scholar]
- Sakr, C.; Choi, J.; Wang, Z.; Gopalakrishnan, K.; Shanbhag, N. True Gradient-Based Training of Deep Binary Activated Neural Networks via Continuous Binarization. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 2346–2350. [Google Scholar]
- Diffenderfer, J.; Kailkhura, B. Multi-Prize Lottery Ticket Hypothesis: Finding Accurate Binary Neural Networks by Pruning a Randomly Weighted Network. arXiv 2021, arXiv:2103.09377. [Google Scholar]
- Datta, G.; Liu, Z.; Beerel, P.A. Can We Get the Best of Both Binary Neural Networks and Spiking Neural Networks for Efficient Computer Vision? In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of Oriented Gradients for Human Detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 886–893. [Google Scholar]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Oliva, A.; Torralba, A. Modeling the Shape of the Scene: A Holistic Representation of the Spatial Envelope. Int. J. Comput. Vis. 2001, 42, 145–175. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehen-sive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Luus, F.P.; Salmon, B.P.; Van den Bergh, F.; Maharaj, B.T.J. Multiview Deep Learning for Land-Use Classification. IEEE Geo-Sci. Remote Sens. Lett. 2015, 12, 2448–2452. [Google Scholar] [CrossRef]
- Zhang, F.; Du, B.; Zhang, L. Scene Classification via a Gradient Boosting Random Convolutional Network Framework. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1793–1802. [Google Scholar] [CrossRef]
- Zhang, W.; Tang, P.; Zhao, L. Remote Sensing Image Scene Classification Using CNN-CapsNet. Remote Sens. 2019, 11, 494. [Google Scholar] [CrossRef]
- Guo, X.; Hou, B.; Ren, B.; Ren, Z.; Jiao, L. Network Pruning for Remote Sensing Images Classification Based on Interpretable CNNs. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
- Kucik, A.S.; Meoni, G. Investigating Spiking Neural Networks for Energy-Efficient on-Board Ai Applications. A Case Study in Land Cover and Land Use Classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 2020–2030. [Google Scholar]
- Deng, S.; Gu, S. Optimal Conversion of Conventional Artificial Neural Networks to Spiking Neural Networks. arXiv 2021, arXiv:2103.00476. [Google Scholar]
- Ding, J.; Yu, Z.; Tian, Y.; Huang, T. Optimal ANN-SNN Conversion for Fast and Accurate Inference in Deep Spiking Neural Networks. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence; International Joint Conferences on Artificial Intelligence Organization, Montreal, QC, Canada, 19–27 August 2021; pp. 2328–2336. [Google Scholar]
- Han, B.; Roy, K. Deep Spiking Neural Network: Energy Efficiency through Time Based Coding. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 388–404. [Google Scholar]
- Li, Y.; Deng, S.; Dong, X.; Gong, R.; Gu, S. A Free Lunch from ANN: Towards Efficient, Accurate Spiking Neural Networks Calibration. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 6316–6325. [Google Scholar]
- Yan, Z.; Zhou, J.; Wong, W.-F. Near Lossless Transfer Learning for Spiking Neural Networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 10577–10584. [Google Scholar]
- Li, Y.; He, X.; Dong, Y.; Kong, Q.; Zeng, Y. Spike Calibration: Fast and Accurate Conversion of Spiking Neural Network for Object Detection and Segmentation. arXiv 2022, arXiv:2207.02702. [Google Scholar]
- Han, B.; Srinivasan, G.; Roy, K. RMP-SNN: Residual Membrane Potential Neuron for Enabling Deeper High-Accuracy and Low-Latency Spiking Neural Network. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 13555–13564. [Google Scholar]
- Hao, Z.; Bu, T.; Ding, J.; Huang, T.; Yu, Z. Reducing Ann-Snn Conversion Error through Residual Membrane Potential. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 11–21. [Google Scholar]
- Rathi, N.; Roy, K. Diet-Snn: A Low-Latency Spiking Neural Network with Direct Input Encoding and Leakage and Threshold Optimization. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 3174–3182. [Google Scholar] [CrossRef]
- Neftci, E.O.; Mostafa, H.; Zenke, F. Surrogate Gradient Learning in Spiking Neural Networks: Bringing the Power of Gradient-Based Optimization to Spiking Neural Networks. IEEE Signal Process. Mag. 2019, 36, 51–63. [Google Scholar] [CrossRef]
- Wu, Y.; Deng, L.; Li, G.; Zhu, J.; Xie, Y.; Shi, L. Direct Training for Spiking Neural Networks: Faster, Larger, Better. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 1311–1318. [Google Scholar]
- Zhang, W.; Li, P. Temporal Spike Sequence Learning via Backpropagation for Deep Spiking Neural Networks. Adv. Neural Inf. Process. Syst. 2020, 33, 12022–12033. [Google Scholar]
- Shrestha, S.B.; Orchard, G. Slayer: Spike Layer Error Reassignment in Time. Adv. Neural Inf. Process. Syst. 2018, 31, 1419–1428. [Google Scholar]
- Wu, Y.; Deng, L.; Li, G.; Shi, L. Spatio-Temporal Backpropagation for Training High-Performance Spiking Neural Networks. Front. Neurosci. 2018, 12, 323875. [Google Scholar] [CrossRef]
- Fang, W.; Yu, Z.; Chen, Y.; Masquelier, T.; Huang, T.; Tian, Y. Incorporating Learnable Membrane Time Constant to Enhance Learning of Spiking Neural Networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 2661–2671. [Google Scholar]
- Kim, Y.; Panda, P. Revisiting Batch Normalization for Training Low-Latency Deep Spiking Neural Networks from Scratch. Front. Neurosci. 2021, 15, 773954. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, Y.; Zhang, L.; Wang, Y.; Liu, X.; Tong, X.; Ou, Y.; Huang, X.; Ma, Z. Reducing Information Loss for Spiking Neural Networks. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 36–52. [Google Scholar]
- Guo, Y.; Chen, Y.; Zhang, L.; Liu, X.; Wang, Y.; Huang, X.; Ma, Z. IM-Loss: Information Maximization Loss for Spiking Neural Networks. Adv. Neural Inf. Process. Syst. 2022, 35, 156–166. [Google Scholar]
- Guo, Y.; Tong, X.; Chen, Y.; Zhang, L.; Liu, X.; Ma, Z.; Huang, X. Recdis-Snn: Rectifying Membrane Potential Distribution for Directly Training Spiking Neural Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 326–335. [Google Scholar]
- Guo, Y.; Zhang, Y.; Chen, Y.; Peng, W.; Liu, X.; Zhang, L.; Huang, X.; Ma, Z. Membrane Potential Batch Normalization for Spiking Neural Networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 19420–19430. [Google Scholar]
- Rathi, N.; Srinivasan, G.; Panda, P.; Roy, K. Enabling Deep Spiking Neural Networks with Hybrid Conversion and Spike Timing Dependent Backpropagation. arXiv 2020, arXiv:2005.01807. [Google Scholar]
- Xu, Q.; Li, Y.; Shen, J.; Liu, J.K.; Tang, H.; Pan, G. Constructing Deep Spiking Neural Networks from Artificial Neural Networks with Knowledge Distillation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 7886–7895. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Burkitt, A.N. A Review of the Integrate-and-Fire Neuron Model: I. Homogeneous Synaptic Input. Biol. Cybern. 2006, 95, 1–19. [Google Scholar] [CrossRef]
- Esser, S.K.; Merolla, P.A.; Arthur, J.V.; Cassidy, A.S.; Appuswamy, R.; Andreopoulos, A.; Berg, D.J.; McKinstry, J.L.; Melano, T.; Barch, D.R.; et al. Convolutional Networks for Fast, Energy-Efficient Neuromorphic Computing. Proc. Natl. Acad. Sci. USA 2016, 113, 11441–11446. [Google Scholar] [CrossRef]
- Rueckauer, B.; Lungu, I.-A.; Hu, Y.; Pfeiffer, M.; Liu, S.-C. Conversion of Continuous-Valued Deep Networks to Efficient Event-Driven Networks for Image Classification. Front. Neurosci. 2017, 11, 294078. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S. Bag-of-Visual-Words and Spatial Extensions for Land-Use Classification. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010; pp. 270–279. [Google Scholar]
- Xia, G.-S.; Hu, J.; Hu, F.; Shi, B.; Bai, X.; Zhong, Y.; Zhang, L. AID: A Benchmark Dataset for Performance Evaluation of Aerial Scene Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3965–3981. [Google Scholar] [CrossRef]
- Horowitz, M. 1.1 Computing’s Energy Problem (and What We Can Do about It). In Proceedings of the 2014 IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC), San Francisco, CA, USA, 9–13 February 2014; pp. 10–14. [Google Scholar]
- Lu, X.; Sun, H.; Zheng, X. A Feature Aggregation Convolutional Neural Network for Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7894–7906. [Google Scholar] [CrossRef]
- Dong, Z.; Gu, Y.; Liu, T. UPetu: A Unified Parameter-Efficient Fine-Tuning Framework for Remote Sensing Foundation Model. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5616613. [Google Scholar] [CrossRef]
- Bi, Q.; Qin, K.; Li, Z.; Zhang, H.; Xu, K.; Xia, G.-S. A Multiple-Instance Densely-Connected ConvNet for Aerial Scene Classification. IEEE Trans. Image Process. 2020, 29, 4911–4926. [Google Scholar] [CrossRef] [PubMed]
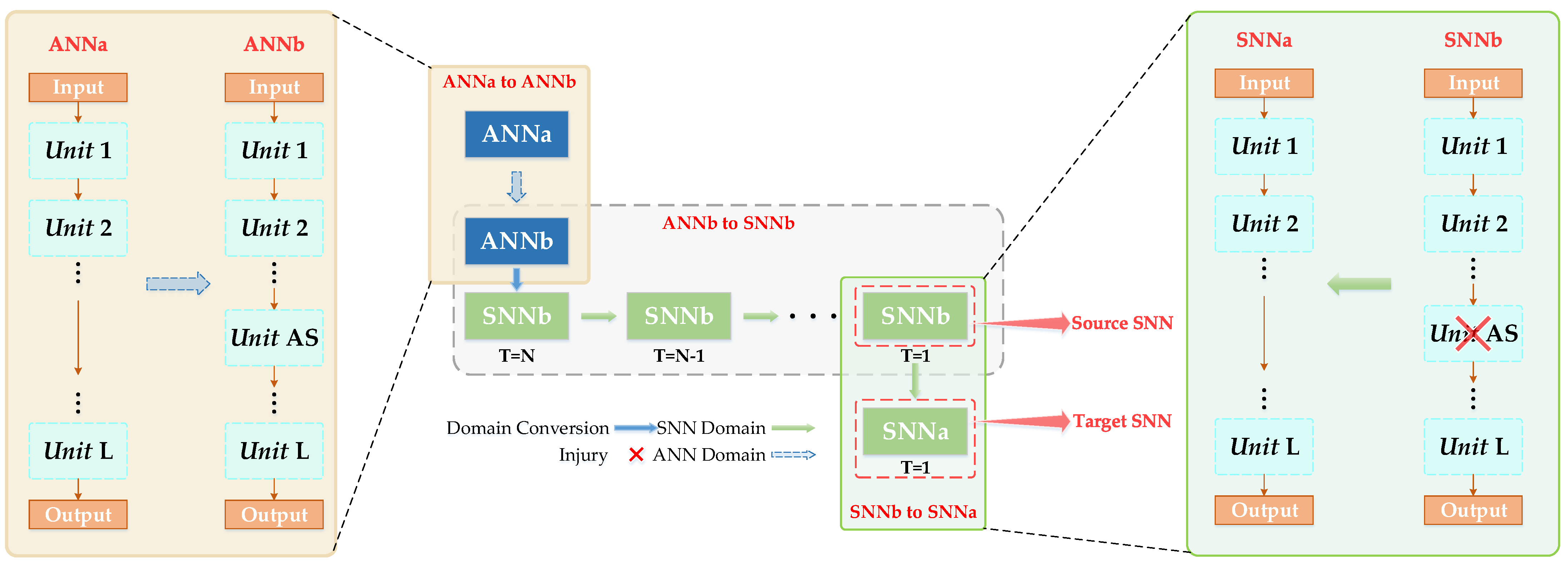












| Target SNN | Source SNN | Target SNN | Source SNN |
|---|---|---|---|
| VGG11_Base | VGG11_AS | VGG14_Base | VGG14_AS |
| conv3-64 | conv3-64 | conv3-64 | conv3-64 |
| conv3-64 | conv3-64 | ||
| averagepool | |||
| conv3-128 | conv3-128 | conv3-128 | conv3-128 |
| conv3-128 | conv3-128 | ||
| averagepool | |||
| conv3-256 | conv3-256 | conv3-256 | conv3-256 |
| conv3-256 | conv3-256 | conv3-256 | conv3-256 |
| conv3-256 | conv3-256 | ||
| averagepool | |||
| conv3-512 | conv3-512 | conv3-512 | conv3-512 |
| conv3-512 | conv3-512 | conv3-512 | conv3-512 |
| conv3-512 | conv3-512 | ||
| averagepool | |||
| conv3-512 | conv3-512 | conv3-512 | conv3-512 |
| conv3-512 | conv3-512 | conv3-512 | conv3-512 |
| conv3-512 | conv3-512 | conv3-512 | |
| conv3-512 | |||
| averagepool | |||
| FC-4096 | FC-10 | ||
| FC-4096 | |||
| FC-10 | |||
| Target SNN | Source SNN | |||
|---|---|---|---|---|
| ResNet18_Base | ResNet18_AS1 | ResNet18_AS 2 | ResNet18_AS 3 | ResNet18_AS 4 |
| conv7-64-2 | ||||
| Adaptive Average pool | ||||
| FC | ||||
| Target SNN | Source SNN | ||||
|---|---|---|---|---|---|
| VGG11_Base | VGG11_AS1 | VGG11_AS2 | VGG11_AS3 | VGG11_AS4 | VG11_AS5 |
| conv3-64 | conv3-64 | conv3-64 | conv3-64 | conv3-64 | conv3-64 |
| conv3-64 | |||||
| averagepool | |||||
| conv3-128 | conv3-128 | conv3-128 | conv3-128 | conv3-128 | conv3-128 |
| conv3-128 | |||||
| averagepool | |||||
| conv3-256 | conv3-256 | conv3-256 | conv3-256 | conv3-256 | conv3-256 |
| conv3-256 | conv3-256 | conv3-256 | conv3-256 | conv3-256 | conv3-256 |
| conv3-256 | conv3-256 | ||||
| averagepool | |||||
| conv3-512 | conv3-512 | conv3-512 | conv3-512 | conv3-512 | conv3-512 |
| conv3-512 | conv3-512 | conv3-512 | conv3-512 | conv3-512 | conv3-512 |
| conv3-512 | |||||
| averagepool | |||||
| conv3-512 | conv3-512 | conv3-512 | conv3-512 | conv3-512 | conv3-512 |
| conv3-512 | conv3-512 | conv3-512 | conv3-512 | conv3-512 | conv3-512 |
| conv3-512 | |||||
| averagepool | |||||
| FC-4096 | |||||
| FC-4096 | |||||
| FC | |||||
| Dataset | Method | Model | Time Step | Accuracy (%) |
|---|---|---|---|---|
| UCM (TR = 80%) | FACNN [62] | VGG-16(ANN) | - | 98.81 |
| UPetu [63] | ANN | - | 99.05 | |
| TF-reset [12] | VGG-15(SNN) | >200 | 99.00 | |
| Multi-bit spiking [11] | VGG-20(SNN) | >200 | 98.81 | |
| STP (ours) | VGG-14(SNN) | 1 | 98.81 | |
| AID (TR = 80%) | TF-reset [12] | VGG-15(SNN) | >200 | 94.82 |
| STP (ours) | VGG-14(SNN) | 1 | 95.6 | |
| AID (TR = 50%) | MIDC-Net_CS [64] | ANN | - | 92.95 |
| STP (ours) | VGG-14(SNN) | 1 | 94.72 |
| Dataset | Method | Model | Time Step | Accuracy (%) |
|---|---|---|---|---|
| UCM (TR = 80%) | IM-Loss [50] | VGG14 | 2 | 93.10 |
| DIET-SNN [41] | 2 | 93.81 | ||
| TP [13] | 2 | 94.05 | ||
| STP (ours) | 2 | 95.24 | ||
| WHU-RS19 (TR = 80%) | IM-Loss [50] | VGG11 | 1 | 92.37 |
| DIET-SNN [41] | 1 | 92.86 | ||
| TP [13] | 1 | 93.37 | ||
| STP (ours) | 1 | 94.9 |
| Dataset | Model | Method | SNN T2 | SNN T1 |
|---|---|---|---|---|
| UCM (TR = 80%) | VGG14 | TP [13] | 94.17 ± 1.10 | 93.89 ± 0.43 |
| VGG14 | STP (ours) | 95.33 ± 0.65 | 95.06 ± 0.69 | |
| ResNet18 | TP [13] | 93.10 ± 0.45 | 93.20 ± 0.31 | |
| ResNet18 | STP (ours) | 93.63 ± 0.35 | 93.75 ± 0.31 | |
| AID (TR = 20%) | VGG11 | TP [13] | 81.62 ± 0.18 | 81.37 ± 0.31 |
| VGG11 | STP (ours) | 83.48 ± 0.18 | 83.16 ± 0.17 | |
| ResNet18 | TP [13] | 76.76 ± 0.16 | 76.40 ± 0.22 | |
| ResNet18 | STP (ours) | 77.25 ± 0.24 | 76.51 ± 0.25 |
| Network | Dataset | Base [13] | AS1 | AS2 | AS3 | AS4 | AS5 |
|---|---|---|---|---|---|---|---|
| ResNet18 | UCM (TR = 80%) | 93.10 ± 0.23 | 93.75 ± 0.31 | 93.22 ± 0.26 | 92.80 ± 0.52 | 93.04 ± 0.35 | - |
| VGG11 | WHU-RS19 (TR = 80%) | 92.99 ± 0.66 | 59.95 ± 0.26 | 90.06 ± 1.55 | 89.04 ± 0.85 | 91.67 ± 0.24 | 94.26 ± 0.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Xu, M.; Chen, H.; Liu, W.; Chen, L.; Xie, Y. Spatio-Temporal Pruning for Training Ultra-Low-Latency Spiking Neural Networks in Remote Sensing Scene Classification. Remote Sens. 2024, 16, 3200. https://doi.org/10.3390/rs16173200
Li J, Xu M, Chen H, Liu W, Chen L, Xie Y. Spatio-Temporal Pruning for Training Ultra-Low-Latency Spiking Neural Networks in Remote Sensing Scene Classification. Remote Sensing. 2024; 16(17):3200. https://doi.org/10.3390/rs16173200
Chicago/Turabian StyleLi, Jiahao, Ming Xu, He Chen, Wenchao Liu, Liang Chen, and Yizhuang Xie. 2024. "Spatio-Temporal Pruning for Training Ultra-Low-Latency Spiking Neural Networks in Remote Sensing Scene Classification" Remote Sensing 16, no. 17: 3200. https://doi.org/10.3390/rs16173200
APA StyleLi, J., Xu, M., Chen, H., Liu, W., Chen, L., & Xie, Y. (2024). Spatio-Temporal Pruning for Training Ultra-Low-Latency Spiking Neural Networks in Remote Sensing Scene Classification. Remote Sensing, 16(17), 3200. https://doi.org/10.3390/rs16173200





