Perpendicular Electrical Conductivity in the Topside Ionosphere Derived from Swarm Measurements
Abstract
1. Introduction
2. Data and Methods
2.1. Swarm Observations and Preliminary Analysis
2.2. Electrical Conductivity Perpendicular to the Geomagnetic Field in the Topside Ionosphere
3. Results
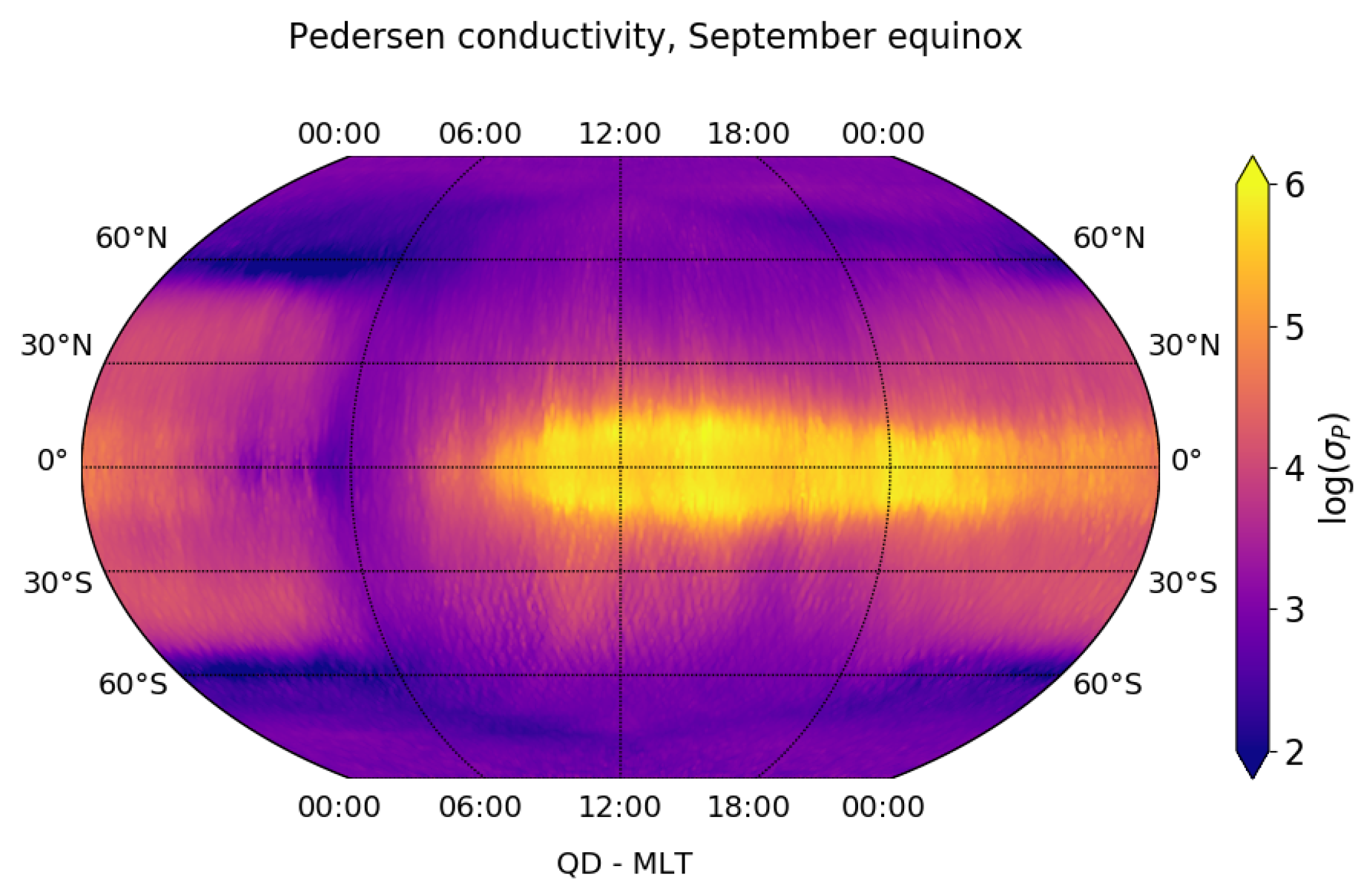
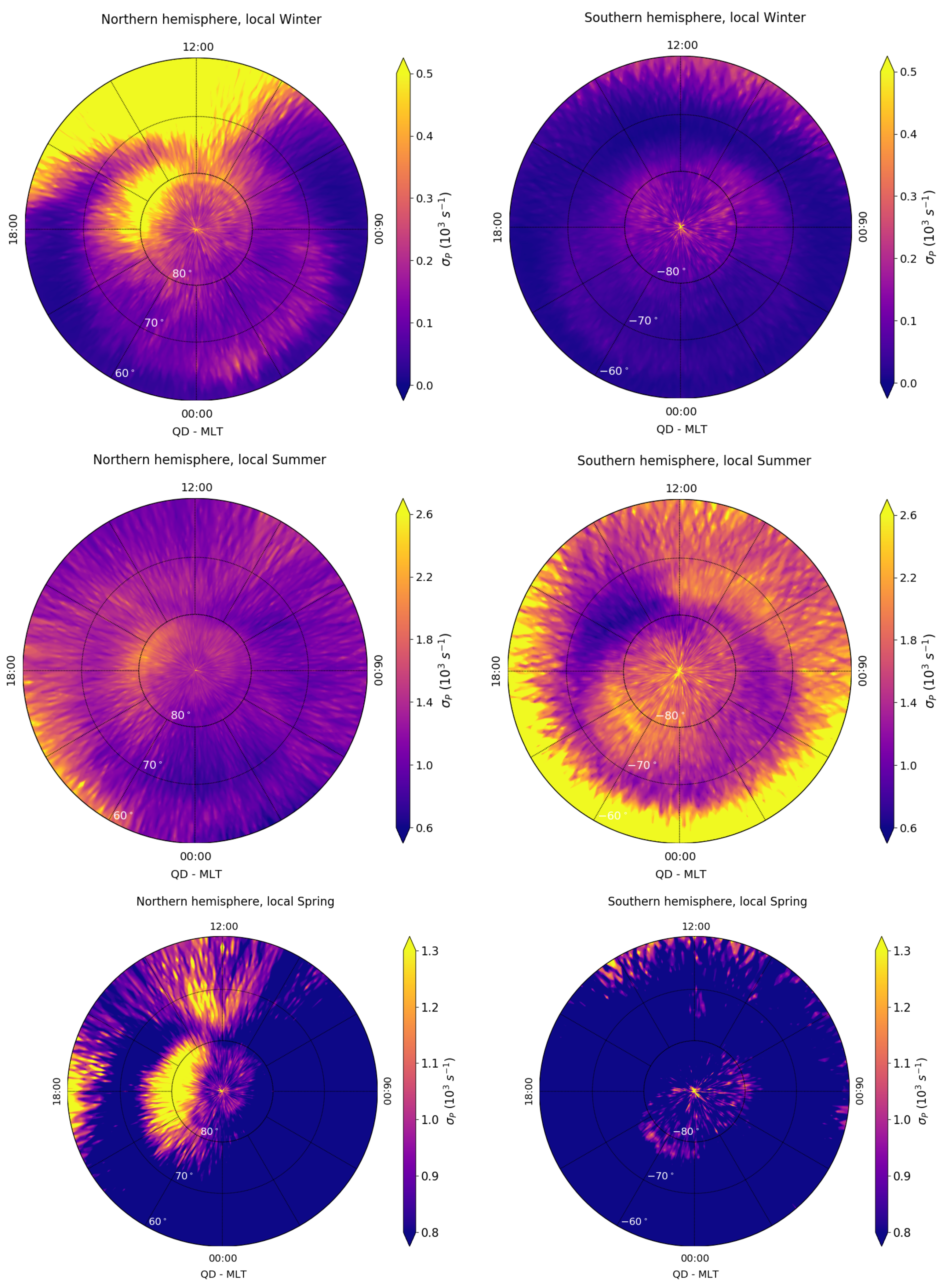
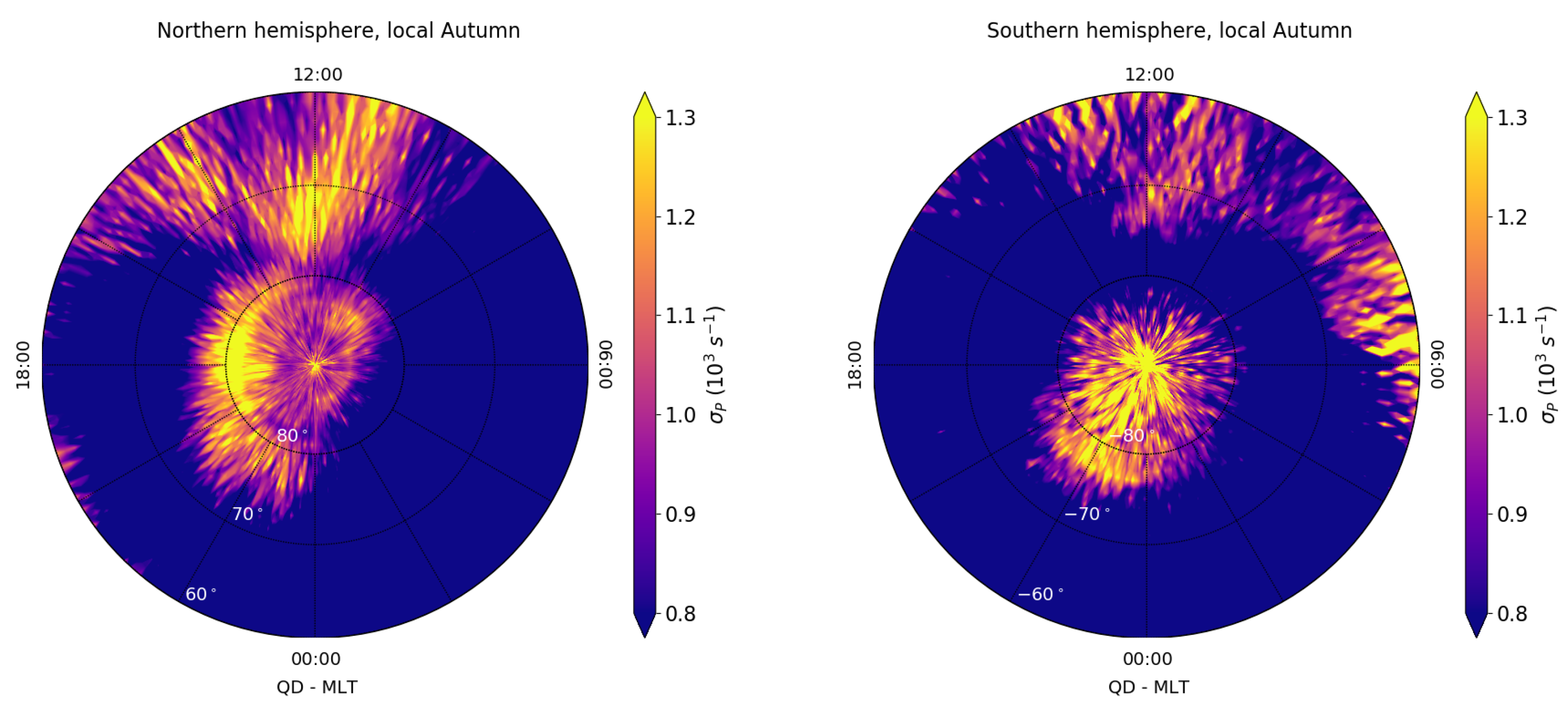
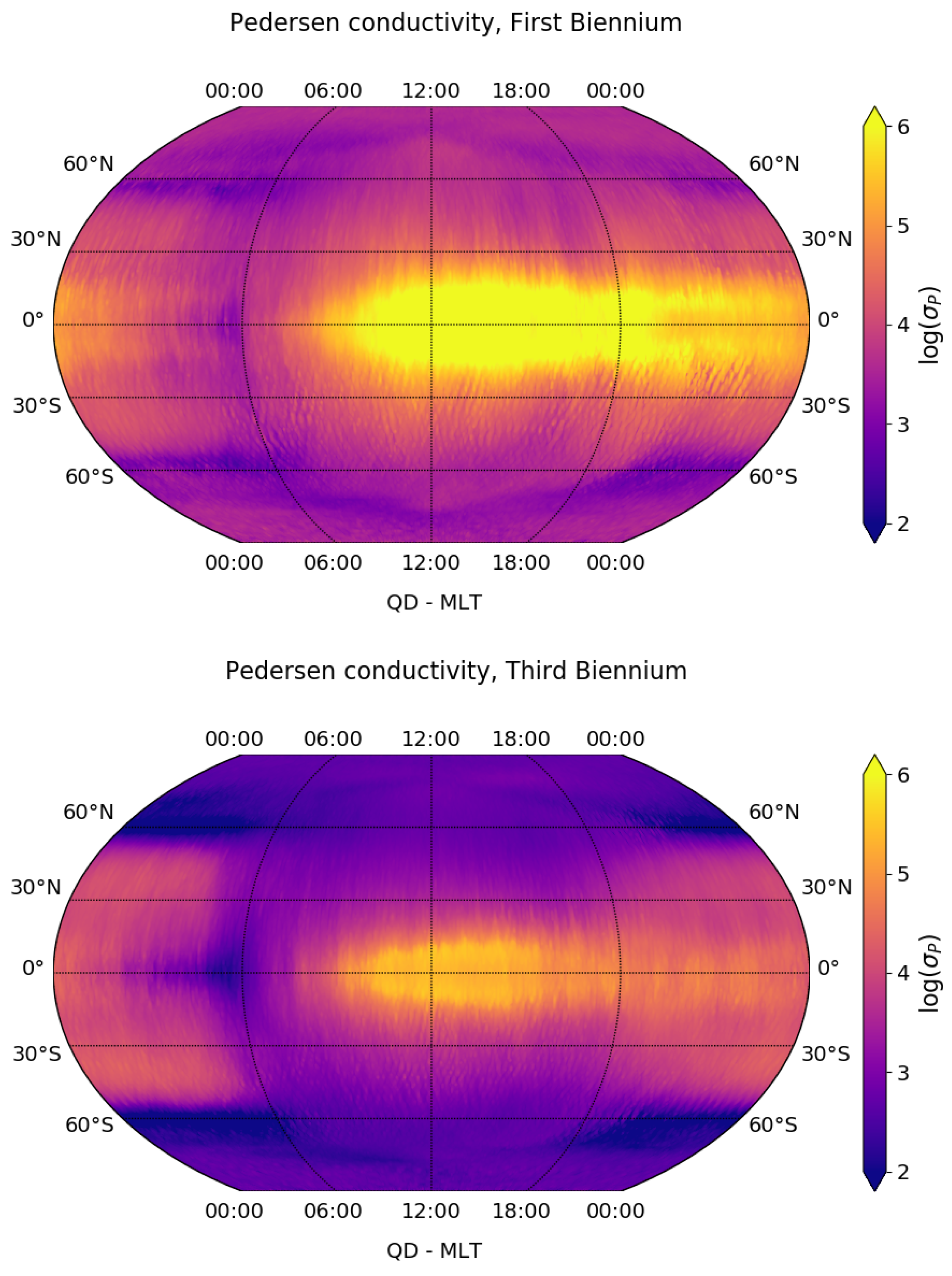
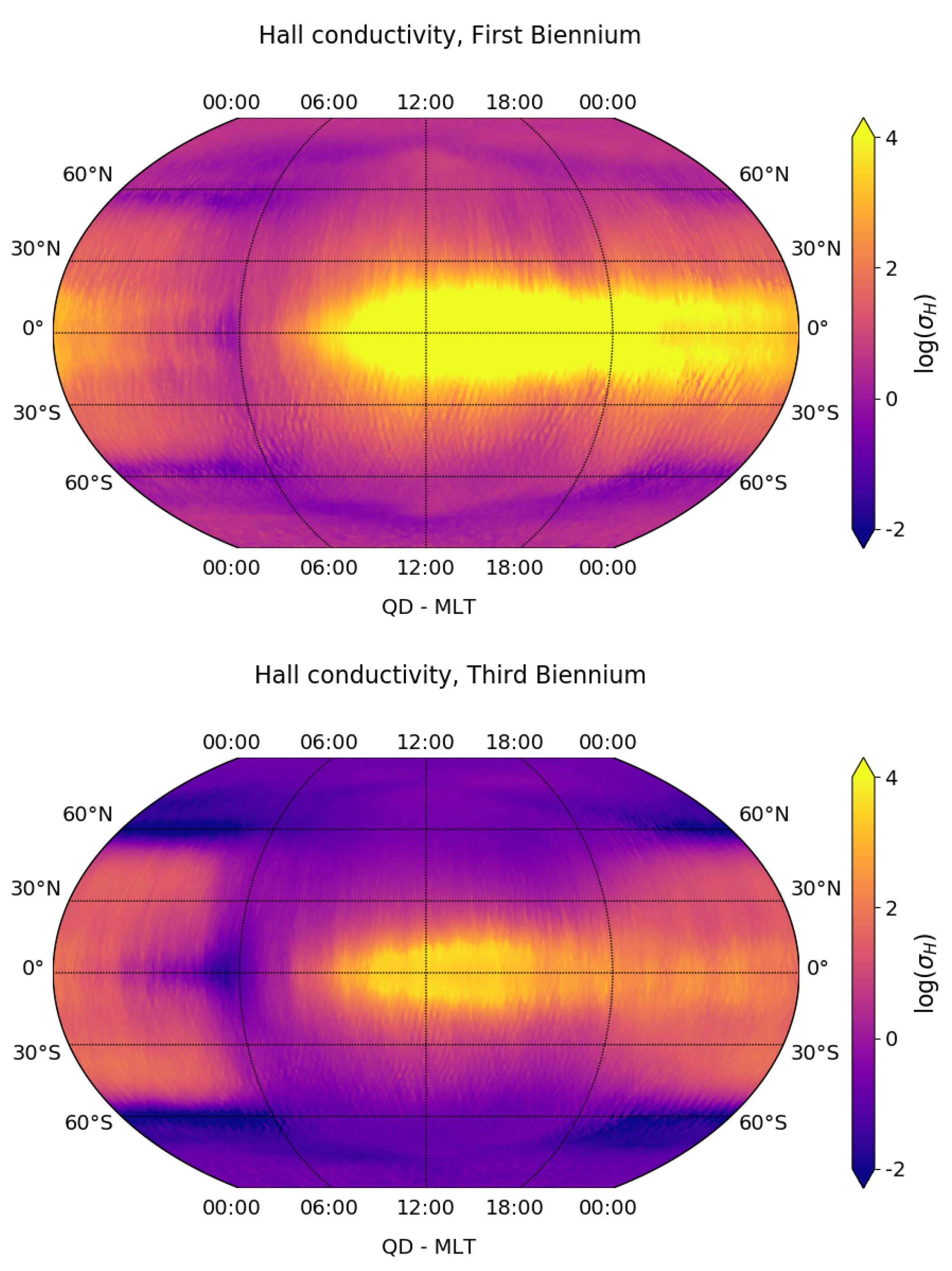
3.1. Climatological Behaviour of Electrical Conductivity Perpendicular to the Geomagnetic Field
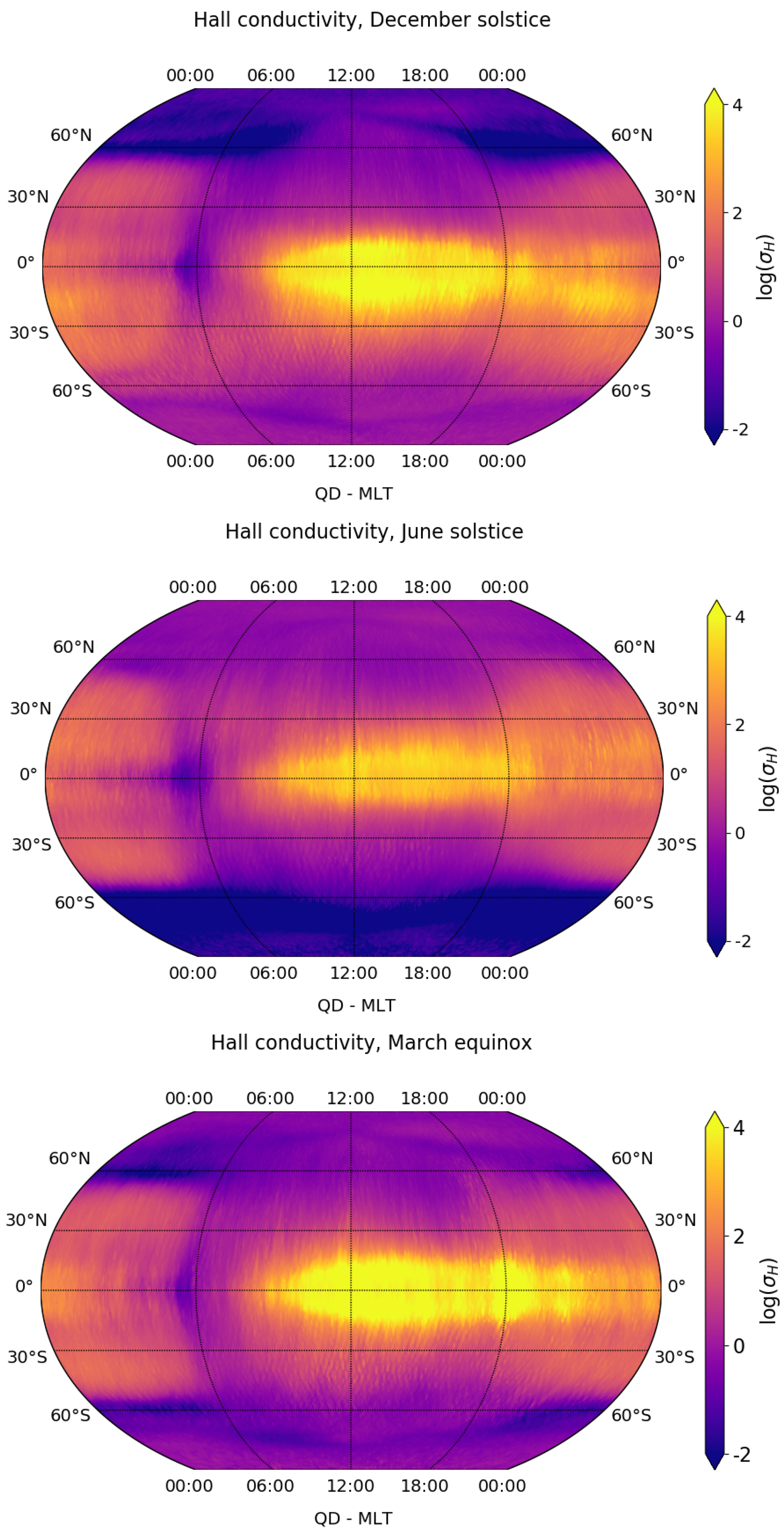
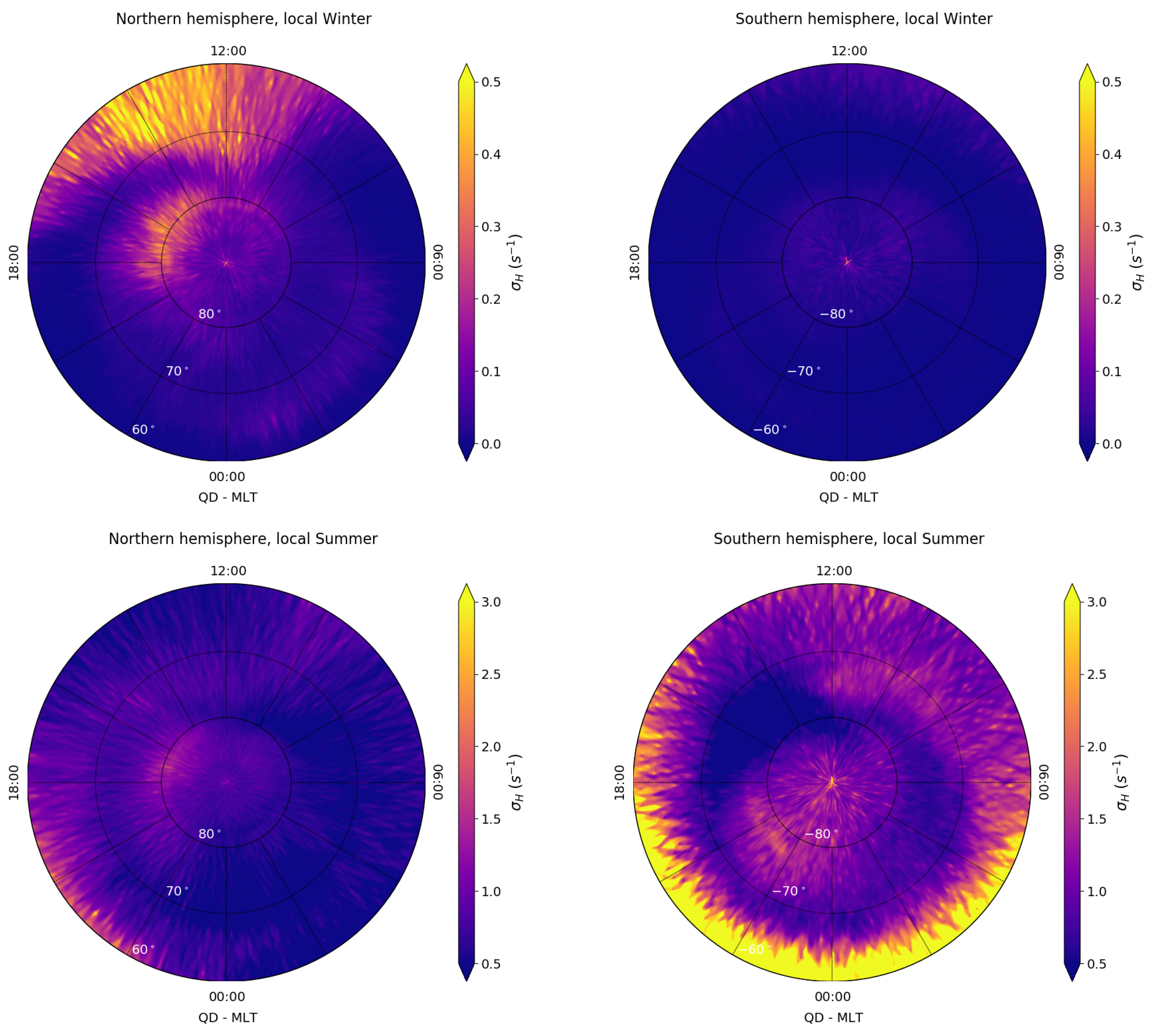
3.2. Seasonal Variation of Electrical Conductivity Perpendicular to the Geomagnetic Field
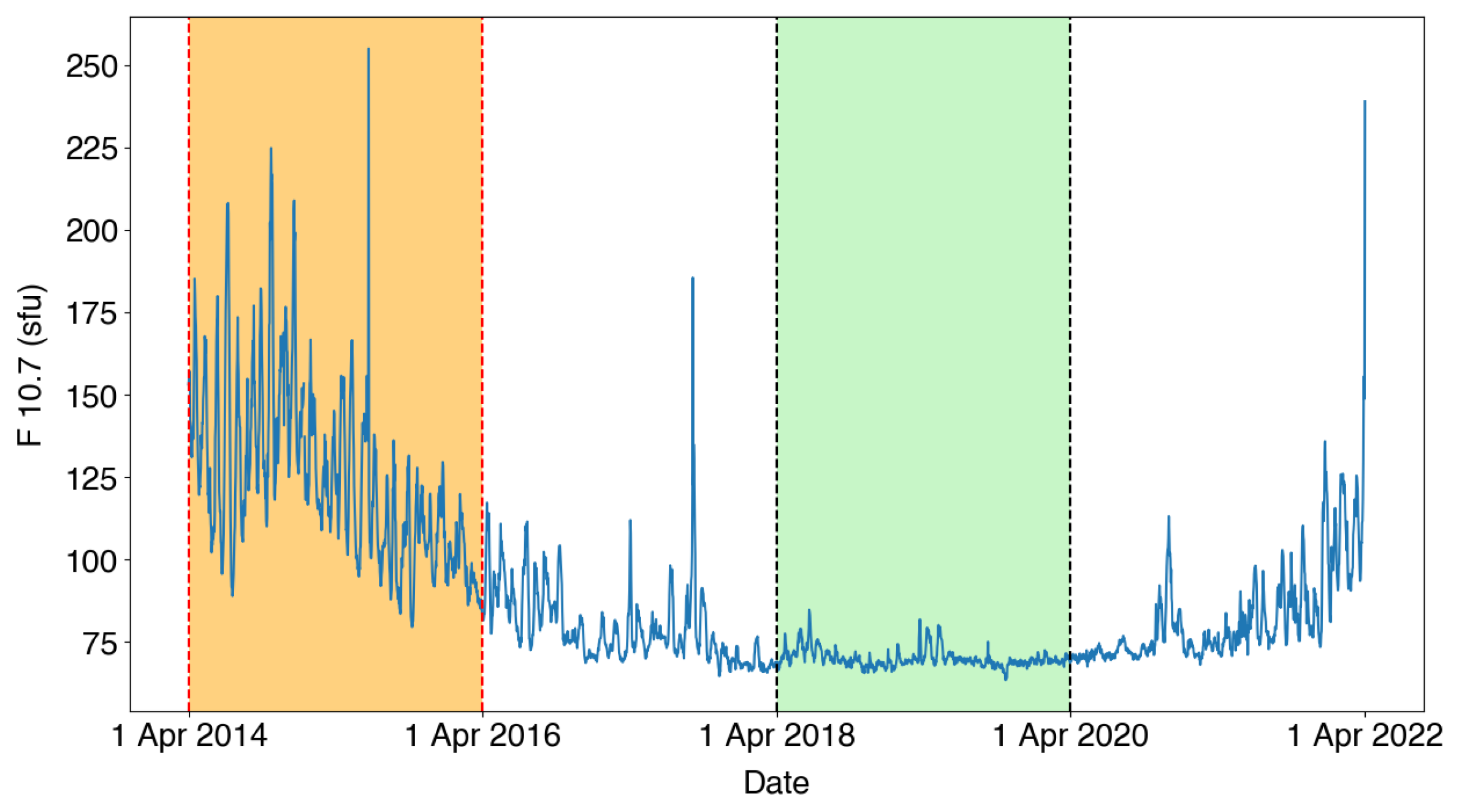
3.3. Electrical Conductivity Variation Perpendicular to the Geomagnetic Field Due to Solar Activity
4. Discussion
- The average altitude of Swarm A is 450 km, sensibly below the indicated upper transition height of 500 km. Thus, even in the specific case of winter night during very low solar activity, the dominant ion species at Swarm A altitude should still be O+.
- The specific case mentioned should only affect the third biennium of the data set used in this work [112,113]. As explained in the text, the choice of selecting biennia guarantees an even sampling of seasons. Thus, winter nights in the third biennium cover only a fraction of the data set used to pursue our statistical study. Therefore, the specific case may be limiting for local rather than statistical studies.
- Most important of all, the relevant features of perpendicular conductivity emerging from our study are mainly located on the day side, where O+ is definitely the dominant species at the Swarm altitude.
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ASM | Absolute Scalar Magnetometer |
| CDF | Cumulative Distribution Function |
| EEJ | Equatorial Electrojet |
| EIA | Equatorial Ionisation Anomaly |
| ESA | European Space Agency |
| EUV | Extreme Ultra Violet |
| FAC | Field-Aligned Current |
| GOL | Generalised Ohm Law |
| IHFAC | Inter-Hemispheric Field-Aligned Current |
| LP | Langmuir Probe |
| MLT | Magnetic Local Time |
| QD | Quasi Dipole |
| RHS | Right Hand Side |
| UTC | Universal Time Coordinated |
References
- Poedjono, B.; Beck, N.; Buchanan, A.; Borri, L.; Maus, S.; Finn, C.A.; Worthington, E.W.; White, T. Improved Geomagnetic Referencing in the Arctic Environment. In Proceedings of the SPE Arctic and Extreme Environments Conference & Exhibition, Moscow, Russia, 15–17 October 2013. [Google Scholar]
- Pezzopane, M.; Pignalberi, A.; Coco, I.; Consolini, G.; De Michelis, P.; Giannattasio, F.; Marcucci, M.F.; Tozzi, R. Occurrence of GPS Loss of Lock Based on a Swarm Half-Solar Cycle Dataset and Its Relation to the Background Ionosphere. Remote Sens. 2021, 13, 2209. [Google Scholar] [CrossRef]
- De Michelis, P.; Consolini, G.; Pignalberi, A.; Lovati, G.; Pezzopane, M.; Tozzi, R.; Giannattasio, F.; Coco, I.; Marcucci, M.F. Ionospheric Turbulence: A Challenge for GPS Loss of Lock Understanding. Space Weather 2022, 20, e2022SW003129. [Google Scholar] [CrossRef]
- Boteler, D.H.; Pirjola, R.J.; Nevanlinna, H. The effects of geomagnetic disturbances on electrical systems at the Earth’s surface. Adv. Space Res. 1998, 22, 17–27. [Google Scholar] [CrossRef]
- Boteler, D.H.; Pirjola, R.J. Modeling geomagnetically induced currents. Space Weather 2017, 15, 258–276. [Google Scholar] [CrossRef]
- Liu, H.; Lühr, H. Strong disturbance of the upper thermospheric density due to magnetic storms: CHAMP observations. J. Geophys. Res. Space Phys. 2005, 110, A04301. [Google Scholar] [CrossRef]
- Pirjola, R.; Kauristie, K.; Lappalainen, H.; Viljanen, A.; Pulkkinen, A. Space weather risk. Space Weather 2005, 3. [Google Scholar] [CrossRef]
- Moldwin, M. An Introduction to Space Weather; Cambridge University Press: Cambdrige, UK, 2008. [Google Scholar] [CrossRef]
- Zmuda, A.J.; Martin, J.H.; Heuring, F.T. Transverse magnetic disturbances at 1100 km in the auroral region. J. Geophys. Res. (1896–1977) 1966, 71, 5033–5045. [Google Scholar] [CrossRef]
- Zmuda, A.J.; Armstrong, J.C. The diurnal flow pattern of field-aligned currents. J. Geophys. Res. (1896–1977) 1974, 79, 4611–4619. [Google Scholar] [CrossRef]
- Iijima, T.; Potemra, T.A. Large-scale characteristics of field-aligned currents associated with substorms. J. Geophys. Res. Space Phys. 1978, 83, 599–615. [Google Scholar] [CrossRef]
- Amm, O. Ionospheric Elementary Current Systems in Spherical Coordinates and Their Application. J. Geomagn. Geoelectr. 1997, 49, 947–955. [Google Scholar] [CrossRef]
- Kamide, Y.; Baumjohann, W. Magnetosphere-Ionosphere Coupling; Springer: Berlin/Heidelberg, Germany, 1993; Volume 23. [Google Scholar] [CrossRef]
- Sugiura, M.; Poros, D.J. An improved model equatorial electrojet with a meridional current system. J. Geophys. Res. Space Phys. 1969, 74, 4025–4034. [Google Scholar] [CrossRef]
- Fambitakoye, O.; Mayaud, P.N. Equatorial electrojet and regular daily variation S/R/. I—A determination of the equatorial electrojet parameters. II—The centre of the equatorial electrojet. J. Atmos. Terr. Phys. 1976, 38, 1–17. [Google Scholar] [CrossRef]
- Mayaud, P. The equatorial counter-electrojet—A review of its geomagnetic aspects. J. Atmos. Terr. Phys. 1977, 39, 1055–1070. [Google Scholar] [CrossRef]
- Marriott, R.; Richmond, A.D.; Venkateswaran, S. The Quiet-Time Equatorial Electrojet and Counter-Electrojet. J. Geomagn. Geoelectr. 1979, 31, 311–340. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Maute, A. Sq and EEJ—A Review on the Daily Variation of the Geomagnetic Field Caused by Ionospheric Dynamo Currents. Space Sci. Rev. 2017, 206, 299–405. [Google Scholar] [CrossRef]
- Takeda, M.; Maeda, H. F-region dynamo in the evening—Interpretation of equatorial Delta D anomaly found by MAGSAT. J. Atmos. Terr. Phys. 1983, 45, 401–408. [Google Scholar] [CrossRef]
- Langel, R.A.; Purucker, M.; Rajaram, M. The equatorial electrojet and associated currents as seen in Magsat data. J. Atmos. Terr. Phys. 1993, 55, 1233–1269. [Google Scholar] [CrossRef]
- Van Sabben, D. Magnetospheric currents, associated with the NS asymmetry of Sq. J. Atmos. Terr. Phys. 1966, 28, 965–982. [Google Scholar] [CrossRef]
- Lühr, H.; Kervalishvili, G.; Michaelis, I.; Rauberg, J.; Ritter, P.; Park, J.; Merayo, J.M.G.; Brauer, P. The interhemispheric and F region dynamo currents revisited with the Swarm constellation. Geophys. Res. Lett. 2015, 42, 3069–3075. [Google Scholar] [CrossRef]
- Cravens, T.E. Physics of Solar System Plasmas; Cambridge Atmospheric and Space Science Series; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]
- Pedersen, P.O. The Propagation of Radio Waves along the Surface of the Earth and in the Atmosphere; Number 15; Danmarks naturvidenskabelige Samfund: Copenhagen, Denmark, 1927. [Google Scholar]
- Cowling, T.G. The Electrical Conductivity of an Ionized Gas in a Magnetic Field, with Applications to the Solar Atmosphere and the Ionosphere. Proc. R. Soc. Lond. Ser. A 1945, 183, 453–479. [Google Scholar] [CrossRef]
- Baker, W.G. Conductivity of the Ionosphere. Nature 1952, 170, 1090–1092. [Google Scholar] [CrossRef]
- Baker, W.G.; Martyn, D.F. Electric currents in the ionosphere-The conductivity. Philos. Trans. R. Soc. Lond. Ser. Math. Phys. Sci. 1953, 246, 281–294. [Google Scholar] [CrossRef]
- Cowling, T.G.; Borger, R. Electrical conductivity in the ionosphere. Nature 1948, 162, 142. [Google Scholar]
- Takeda, M.; Araki, T. Electric conductivity of the ionosphere and nocturnal currents. J. Atmos. Terr. Phys. 1985, 47, 601–609. [Google Scholar] [CrossRef]
- Pulkkinen, A.; Amm, O.; Viljanen, A. Ionospheric equivalent current distributions determined with the method of spherical elementary current systems. J. Geophys. Res. Space Phys. 2003, 108. [Google Scholar] [CrossRef]
- Weygand, J.M.; Amm, O.; Viljanen, A.; Angelopoulos, V.; Murr, D.; Engebretson, M.J.; Gleisner, H.; Mann, I. Application and validation of the spherical elementary currents systems technique for deriving ionospheric equivalent currents with the North American and Greenland ground magnetometer arrays. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Zossi, B.S.; Elias, A.G.; Fagre, M. Ionospheric Conductance Spatial Distribution During Geomagnetic Field Reversals. J. Geophys. Res. Space Phys. 2018, 123, 2379–2397. [Google Scholar] [CrossRef]
- Kamide, Y.; Richmond, A.D.; Matsushita, S. Estimation of ionospheric electric fields, ionospheric currents, and field-aligned currents from ground magnetic records. J. Geophys. Res. Space Phys. 1981, 86, 801–813. [Google Scholar] [CrossRef]
- Robinson, R.; Tsunoda, R.T.; Vickrey, J.F.; Guerin, L. Sources of F region ionization enhancements in the nighttime auroral zone. J. Geophys. Res. Space Phys. 1985, 90, 7533–7546. [Google Scholar] [CrossRef]
- Robinson, R.; Vondrak, R.R.; Potemra, T.A. Auroral zone conductivities within the field-aligned current sheets. J. Geophys. Res. Space Phys. 1985, 90, 9688–9696. [Google Scholar] [CrossRef]
- Mende, S.B.; Eather, R.H.; Rees, M.H.; Vondrak, R.R.; Robinson, R.M. Optical mapping of ionospheric conductance. J. Geophys. Res. Space Phys. 1984, 89, 1755–1763. [Google Scholar] [CrossRef]
- Germany, G.A.; Torr, D.G.; Richards, P.G.; Torr, M.R.; John, S. Determination of ionospheric conductivities from FUV auroral emissions. J. Geophys. Res. Space Phys. 1994, 99, 23297–23305. [Google Scholar] [CrossRef]
- Takeda, M. The correlation between the variation in ionospheric conductivity and that of the geomagnetic Sq field. J. Atmos. Sol. Terr. Phys. 2002, 64, 1617–1621. [Google Scholar] [CrossRef]
- Föpl, H.; Haerendel, G.; Haser, L.; Lüst, R.; Melzner, F.; Meyer, B.; Neuss, H.; Rabben, H.H.; Rieger, E.; Stöcker, J.; et al. Preliminary results of electric field measurements in the auroral zone. J. Geophys. Res. (1896–1977) 1968, 73, 21–26. [Google Scholar] [CrossRef]
- Marklund, G.; Sandahl, I.; Opgenoorth, H. A study of the dynamics of a discrete auroral arc. Planet. Space Sci. 1982, 30, 179–197. [Google Scholar] [CrossRef]
- Holzworth, R.H.; Kelley, M.C.; Siefring, C.L.; Hale, L.C.; Mitchell, J.D. Electrical measurements in the atmosphere and the ionosphere over an active thunderstorm: 2. Direct current electric fields and conductivity. J. Geophys. Res. Space Phys. 1985, 90, 9824–9830. [Google Scholar] [CrossRef]
- Mozer, F.S.; Serlin, R. Magnetospheric electric field measurements with balloons. J. Geophys. Res. (1896–1977) 1969, 74, 4739–4754. [Google Scholar] [CrossRef]
- Fuller-Rowell, T.J.; Evans, D.S. Height-integrated Pedersen and Hall conductivity patterns inferred from the TIROS-NOAA satellite data. J. Geophys. Res. Space Phys. 1987, 92, 7606–7618. [Google Scholar] [CrossRef]
- Spiro, R.W.; Reiff, P.H.; Maher, L.J., Jr. Precipitating electron energy flux and auroral zone conductances-An empirical model. J. Geophys. Res. Space Phys. 1982, 87, 8215–8227. [Google Scholar] [CrossRef]
- Kirkwood, S.; Opgenoorth, H.; Murphree, J. Ionospheric conductivities, electric fields and currents associated with auroral substorms measured by the EISCAT radar. Planet. Space Sci. 1988, 36, 1359–1380. [Google Scholar] [CrossRef]
- Moen, J.; Brekke, A. The solar flux influence on quiet time conductances in the auroral ionosphere. Geophys. Res. Lett. 1993, 20, 971–974. [Google Scholar] [CrossRef]
- Amm, O.; Vanhamäki, H.; Kauristie, K.; Stolle, C.; Christiansen, F.; Haagmans, R.; Masson, A.; Taylor, M.G.G.T.; Floberghagen, R.; Escoubet, C.P. A method to derive maps of ionospheric conductances, currents, and convection from the Swarm multisatellite mission. J. Geophys. Res. Space Phys. 2015, 120, 3263–3282. [Google Scholar] [CrossRef]
- Olsen, N. A new tool for determining ionospheric currents from magnetic satellite data. Geophys. Res. Lett. 1996, 23, 3635–3638. [Google Scholar] [CrossRef]
- Mobley, F.; Eckard, L.; Fountain, G.; Ousley, G. MAGSAT—A new satellite to survey the earth’s magnetic field. IEEE Trans. Magn. 1980, 16, 758–760. [Google Scholar] [CrossRef]
- Juusola, L.; Amm, O.; Viljanen, A. One-dimensional spherical elementary current systems and their use for determining ionospheric currents from satellite measurements. Earth Planets Space 2006, 58, 667–678. [Google Scholar] [CrossRef]
- Tozzi, R.; Pezzopane, M.; De Michelis, P.; Piersanti, M. Applying a curl-B technique to Swarm vector data to estimate nighttime F region current intensities. Geophys. Res. Lett. 2015, 42, 6162–6169. [Google Scholar] [CrossRef]
- Aakjær, C.D.; Olsen, N.; Finlay, C.C. Determining polar ionospheric electrojet currents from Swarm satellite constellation magnetic data. Earth Planets Space 2016, 68, 140. [Google Scholar] [CrossRef]
- Reigber, C.; Schwintzer, P. CHAMP—A Challenging Microsatellite Payload for Geophysical Research and Application. In Proceedings of the Kleinsatelliten-Ein Vielversprechender Weg in der Weltraumforschung und Raumfahrttechnik, Dresden, Germany, 3–4 May 1995. [Google Scholar]
- Friis-Christensen, E.; Lühr, H.; Hulot, G. SWARM: A constellation to study the Earth’s magnetic field. Earth Planets Space 2006, 58, 351–358. [Google Scholar] [CrossRef]
- Giannattasio, F.; De Michelis, P.; Pignalberi, A.; Coco, I.; Consolini, G.; Pezzopane, M.; Tozzi, R. Parallel Electrical Conductivity in the Topside Ionosphere Derived From Swarm Measurements. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028452. [Google Scholar] [CrossRef]
- Giannattasio, F.; Pignalberi, A.; De Michelis, P.; Coco, I.; Consolini, G.; Pezzopane, M.; Tozzi, R. Dependence of Parallel Electrical Conductivity in the Topside Ionosphere on Solar and Geomagnetic Activity. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029138. [Google Scholar] [CrossRef]
- Giannattasio, F.; Pignalberi, A.; De Michelis, P.; Coco, I.; Pezzopane, M.; Tozzi, R.; Consolini, G. Parallel Electrical Conductivity at Low and Middle Latitudes in the Topside Ionosphere Derived from CSES-01 Measurements. Remote Sens. 2022, 14, 5079. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, X.; Yuan, S.; Wang, L.; Cao, J.; Huang, J.; Zhu, X.; Piergiorgio, P.; Dai, J. The state-of-the-art of the China Seismo-Electromagnetic Satellite mission. Sci. China Technol. Sci. 2018, 61, 634–642. [Google Scholar] [CrossRef]
- Giannattasio, F.; Consolini, G.; Coco, I.; De Michelis, P.; Pezzopane, M.; Pignalberi, A.; Tozzi, R. Dissipation of field-aligned currents in the topside ionosphere. Sci. Rep. 2022, 12, 17202. [Google Scholar] [CrossRef]
- Consolini, G.; Quattrociocchi, V.; D’Angelo, G.; Alberti, T.; Piersanti, M.; Marcucci, M.F.; De Michelis, P. Electric Field Multifractal Features in the High-Latitude Ionosphere: CSES-01 Observations. Atmosphere 2021, 12, 646. [Google Scholar] [CrossRef]
- Piersanti, M.; Ubertini, P.; Battiston, R.; Bazzano, A.; D’Angelo, G.; Rodi, J.; Diego, P.; Zhima, Z.; Ammendola, R.; Badoni, D.; et al. Nature Evidence of an upper ionospheric electric field perturbation correlated with a gamma ray burst. Nat. Commun. 2023, 14, 7013. [Google Scholar] [CrossRef] [PubMed]
- Schunk, R.; Nagy, A. Ionospheres: Physics, Plasma Physics, and Chemistry; Cambridge University Press: Cambdrige, UK, 2009. [Google Scholar] [CrossRef]
- Knudsen, D.J.; Burchill, J.K.; Buchert, S.C.; Eriksson, A.I.; Gill, R.; Wahlund, J.E.; Åhlen, L.; Smith, M.; Moffat, B. Thermal ion imagers and Langmuir probes in the Swarm electric field instruments. J. Geophys. Res. Space Phys. 2017, 122, 2655–2673. [Google Scholar] [CrossRef]
- Catapano, F.; Buchert, S.; Qamili, E.; Nilsson, T.; Bouffard, J.; Siemes, C.; Coco, I.; D’Amicis, R.; Tøffner-Clausen, L.; Trenchi, L.; et al. Swarm Langmuir probes’ data quality validation and future improvements. Geosci. Instrum. Methods Data Syst. 2022, 11, 149–162. [Google Scholar] [CrossRef]
- Lomidze, L.; Knudsen, D.J.; Burchill, J.; Kouznetsov, A.; Buchert, S.C. Calibration and Validation of Swarm Plasma Densities and Electron Temperatures Using Ground-Based Radars and Satellite Radio Occultation Measurements. Radio Sci. 2018, 53, 15–36. [Google Scholar] [CrossRef]
- Smirnov, A.; Shprits, Y.; Zhelavskaya, I.; Lühr, H.; Xiong, C.; Goss, A.; Prol, F.S.; Schmidt, M.; Hoque, M.; Pedatella, N.; et al. Intercalibration of the Plasma Density Measurements in Earth’s Topside Ionosphere. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029334. [Google Scholar] [CrossRef]
- Larson, B.; Koustov, A.V.; Kouznetsov, A.F.; Lomidze, L.; Gillies, R.G.; Reimer, A.S. A Comparison of the Topside Electron Density Measured by the Swarm Satellites and Incoherent Scatter Radars Over Resolute Bay, Canada. Radio Sci. 2021, 56, e2021RS007326. [Google Scholar] [CrossRef]
- Pignalberi, A.; Giannattasio, F.; Truhlik, V.; Coco, I.; Pezzopane, M.; Consolini, G.; De Michelis, P.; Tozzi, R. On the Electron Temperature in the Topside Ionosphere as Seen by Swarm Satellites, Incoherent Scatter Radars, and the International Reference Ionosphere Model. Remote Sens. 2021, 13, 4077. [Google Scholar] [CrossRef]
- Pignalberi, A.; Pezzopane, M.; Coco, I.; Piersanti, M.; Giannattasio, F.; De Michelis, P.; Tozzi, R.; Consolini, G. Inter-Calibration and Statistical Validation of Topside Ionosphere Electron Density Observations Made by CSES-01 Mission. Remote Sens. 2022, 14, 4679. [Google Scholar] [CrossRef]
- Pakhotin, I.P.; Burchill, J.K.; Förster, M.; Lomidze, L. The swarm Langmuir probe ion drift, density and effective mass (SLIDEM) product. Earth Planets Space 2022, 74, 109. [Google Scholar] [CrossRef]
- Xiong, C.; Jiang, H.; Yan, R.; Lühr, H.; Stolle, C.; Yin, F.; Smirnov, A.; Piersanti, M.; Liu, Y.; Wan, X.; et al. Solar Flux Influence on the In-Situ Plasma Density at Topside Ionosphere Measured by Swarm Satellites. J. Geophys. Res. Space Phys. 2022, 127, e2022JA030275. [Google Scholar] [CrossRef]
- Burchill, J.K.; Lomidze, L. Calibration of Swarm Ion Density, Drift, and Effective Mass Measurements. Earth Space Sci. 2024, 11, e2023EA003463. [Google Scholar] [CrossRef]
- Pignalberi, A.; Truhlik, V.; Giannattasio, F.; Coco, I.; Pezzopane, M. Mid- and High-Latitude Electron Temperature Dependence on Solar Activity in the Topside Ionosphere through the Swarm B Satellite Observations and the International Reference Ionosphere Model. Atmosphere 2024, 15, 490. [Google Scholar] [CrossRef]
- Richmond, A.D. Ionospheric Electrodynamics Using Magnetic Apex Coordinates. J. Geomagn. Geoelectr. 1995, 47, 191–212. [Google Scholar] [CrossRef]
- Emmert, J.T.; Richmond, A.D.; Drob, D.P. A computationally compact representation of Magnetic-Apex and Quasi-Dipole coordinates with smooth base vectors. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef]
- Laundal, K.M.; Richmond, A.D. Magnetic Coordinate Systems. Space Sci. Rev. 2017, 206, 27–59. [Google Scholar] [CrossRef]
- Kelley, M. The Earth’s Ionosphere: Plasma Physics and Electrodynamics, 2nd ed.; International Geophysics Book Series; Academic Press: Cambridge, MA, USA; Elsevier Science: Amsterdam, The Netherlands, 2009; Volume 96. [Google Scholar]
- Chapman, S.; Cowling, T. The Mathematical Theory of Non-Uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction, and Diffusion in Gases; Cambridge University Press: Cambdrige, UK, 1958. [Google Scholar]
- Nicolet, M. The collision frequency of electrons in the ionosphere. J. Atmos. Terr. Phys. 1953, 3, 200–211. [Google Scholar] [CrossRef]
- Singh, R.N. The effective electron collision frequency in the lower F region of the ionosphere. Proc. Phys. Soc. 1966, 87, 425–428. [Google Scholar] [CrossRef]
- Aggarwal, K.; Nath, N.; Setty, C. Collision frequency and transport properties of electrons in the ionosphere. Planet. Space Sci. 1979, 27, 753–768. [Google Scholar] [CrossRef]
- Vickrey, J.F.; Vondrak, R.R.; Matthews, S.J. The diurnal and latitudinal variation of auroral zone ionospheric conductivity. J. Geophys. Res. Space Phys. 1981, 86, 65–75. [Google Scholar] [CrossRef]
- Rishbeth, H. The ionospheric E-layer and F-layer dynamos—A tutorial review. J. Atmos. Sol. Terr. Phys. 1997, 59, 1873–1880. [Google Scholar] [CrossRef]
- Nishino, M.; Nozawa, S.; Holtet, J.A. Daytime ionospheric absorption features in the polar cap associated with poleward drifting F-region plasma patches. Earth Planets Space 1998, 50, 107–117. [Google Scholar] [CrossRef]
- Třísková, L.; Truhlík, V.; Šmilauer, J. An empirical model of ion composition in the outer ionosphere. Adv. Space Res. 2003, 31, 653–663. [Google Scholar] [CrossRef]
- Richards, P.G.; Bilitza, D.; Voglozin, D. Ion density calculator (IDC): A new efficient model of ionospheric ion densities. Radio Sci. 2010, 45, 1–11. [Google Scholar] [CrossRef]
- Stolle, C.; Liu, H.; Truhlík, V.; Lühr, H.; Richards, P.G. Solar flux variation of the electron temperature morning overshoot in the equatorial F region. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Milan, S.; Clausen, L.; Coxon, J.; Carter, J.; Walach, M.T.; Laundal, K.M.; Østgaard, N.; Tenfjord, P.; Reistad, J.; Snekvik, K.; et al. Overview of Solar Wind–Magnetosphere–Ionosphere–Atmosphere Coupling and the Generation of Magnetospheric Currents. Space Sci. Rev. 2017, 206, 547–573. [Google Scholar] [CrossRef]
- Appleton, E.V. Two Anomalies in the Ionosphere. Nature 1946, 157, 691. [Google Scholar] [CrossRef]
- Mitra, S.K. Geomagnetic Control of Region F2 of the Ionosphere. Nature 1946, 158, 668–669. [Google Scholar] [CrossRef]
- Duncan, R. The equatorial F-region of the ionosphere. J. Atmos. Terr. Phys. 1960, 18, 89–100. [Google Scholar] [CrossRef]
- Balan, N.; Liu, L.; Le, H. A brief review of equatorial ionization anomaly and ionospheric irregularities. Earth Planet. Phys. 2018, 2, 257–275. [Google Scholar] [CrossRef]
- Pignalberi, A.; Giannattasio, F.; Truhlik, V.; Coco, I.; Pezzopane, M.; Alberti, T. Investigating the Main Features of the Correlation Between Electron Density and Temperature in the Topside Ionosphere Through Swarm Satellites Data. J. Geophys. Res. Space Phys. 2024, 129, e2023JA032201. [Google Scholar] [CrossRef]
- Bilitza, D.; Pezzopane, M.; Truhlik, V.; Altadill, D.; Reinisch, B.W.; Pignalberi, A. The International Reference Ionosphere Model: A Review and Description of an Ionospheric Benchmark. Rev. Geophys. 2022, 60, e2022RG000792. [Google Scholar] [CrossRef]
- Mayr, H.G.; Mahajan, K.K. Seasonal variation in the F 2 region. J. Geophys. Res. (1896–1977) 1971, 76, 1017–1027. [Google Scholar] [CrossRef]
- Millward, G.H.; Rishbeth, H.; Fuller-Rowell, T.J.; Aylward, A.D.; Quegan, S.; Moffett, R.J. Ionospheric F 2 layer seasonal and semiannual variations. J. Geophys. Res. Space Phys. 1996, 101, 5149–5156. [Google Scholar] [CrossRef]
- Balan, N.; Otsuka, Y.; Fukao, S.; Abdu, M.; Bailey, G. Annual variations of the ionosphere: A review based on MU radar observations. Adv. Space Res. 2000, 25, 153–162. [Google Scholar] [CrossRef]
- Zou, L.; Rishbeth, H.; Müller-Wodarg, I.C.F.; Aylward, A.D.; Millward, G.H.; Fuller-Rowell, T.J.; Idenden, D.W.; Moffett, R.J. Annual and semiannual variations in the ionospheric F2-layer. I. Modelling. Ann. Geophys. 2000, 18, 927–944. [Google Scholar] [CrossRef]
- Rishbeth, H.; Müller-Wodarg, I.C.F.; Zou, L.; Fuller-Rowell, T.J.; Millward, G.H.; Moffett, R.J.; Idenden, D.W.; Aylward, A.D. Annual and semiannual variations in the ionospheric F2-layer: II. Physical discussion. Ann. Geophys. 2000, 18, 945–956. [Google Scholar] [CrossRef]
- Sai Gowtam, V.; Tulasi Ram, S. Ionospheric annual anomaly—New insights to the physical mechanisms. J. Geophys. Res. Space Phys. 2017, 122, 8816–8830. [Google Scholar] [CrossRef]
- Ma, R.; Xu, J.; Liao, H. The features and a possible mechanism of semiannual variation in the peak electron density of the low latitude F2 Layer. J. Atmos. Sol. Terr. Phys. 2003, 65, 47–57. [Google Scholar] [CrossRef]
- Bailey, G.J.; Su, Y.Z.; Oyama, K.I. Yearly variations in the low-latitude topside ionosphere. Ann. Geophys. 2000, 18, 789–798. [Google Scholar] [CrossRef]
- Lomidze, L.; Knudsen, D.J.; Shepherd, M.; Huba, J.D.; Maute, A. Equinoctial Asymmetry in the Upper Ionosphere: Comparison of Satellite Observations and Models. J. Geophys. Res. Space Phys. 2023, 128, e2022JA031123. [Google Scholar] [CrossRef]
- Tapping, K.F. The 10.7 cm solar radio flux (F10.7). Space Weather 2013, 11, 394–406. [Google Scholar] [CrossRef]
- Maeda, K. Conductivity and drifts in the ionosphere. J. Atmos. Terr. Phys. 1977, 39, 1041–1053. [Google Scholar] [CrossRef]
- Lovati, G.; De Michelis, P.; Consolini, G.; Berrilli, F. Pressure-Gradient Current at High Latitude from Swarm Measurements. Remote Sens. 2022, 14, 1428. [Google Scholar] [CrossRef]
- Heelis, R.A.; Coley, W.R.; Burrell, A.G.; Hairston, M.R.; Earle, G.D.; Perdue, M.D.; Power, R.A.; Harmon, L.L.; Holt, B.J.; Lippincott, C.R. Behavior of the O+/H+ transition height during the extreme solar minimum of 2008. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Klenzing, J.; Simoes, F.; Ivanov, S.; Heelis, R.A.; Bilitza, D.; Pfaff, R.; Rowland, D. Topside equatorial ionospheric density and composition during and after extreme solar minimum. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Klenzing, J.; Burrell, A.G.; Heelis, R.A.; Huba, J.D.; Pfaff, R.; Simões, F. Exploring the role of ionospheric drivers during the extreme solar minimum of 2008. Ann. Geophys. 2013, 31, 2147–2156. [Google Scholar] [CrossRef]
- Huba, J.D.; Heelis, R.; Maute, A. Large-Scale O+ Depletions Observed by ICON in the Post-Midnight Topside Ionosphere: Data/Model Comparison. Geophys. Res. Lett. 2021, 48, e2020GL092061. [Google Scholar] [CrossRef]
- Vaishnav, R.; Jin, Y.; Mostafa, M.G.; Aziz, S.R.; Zhang, S.R.; Jacobi, C. Study of the upper transition height using ISR observations and IRI predictions over Arecibo. Adv. Space Res. 2021, 68, 2177–2185. [Google Scholar] [CrossRef]
- Aponte, N.; Brum, C.G.M.; Sulzer, M.P.; González, S.A. Measurements of the O+ to H+ transition height and ion temperatures in the lower topside ionosphere over Arecibo for equinox conditions during the 2008–2009 extreme solar minimum. J. Geophys. Res. Space Phys. 2013, 118, 4465–4470. [Google Scholar] [CrossRef]
- Kotov, D.V.; Truhlik, V.; Richards, P.G.; Stankov, S.; Bogomaz, O.V.; Chernogor, L.F.; Domnin, I.F. Night-time light ion transition height behaviour over the Kharkiv (50 °N, 36 °E) IS radar during the equinoxes of 2006–2010. J. Atmos. Sol.-Terr. Phys. 2015, 132, 1–12. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International Reference Ionosphere 2016: From ionospheric climate to real-time weather predictions. Space Weather 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Lizunov, G.; Skorokhod, T.; Hayakawa, M.; Korepanov, V. Formation of Ionospheric Precursors of Earthquakes—Probable Mechanism and Its Substantiation. Open J. Earthq. Res. 2020, 09, 142–169. [Google Scholar] [CrossRef]
- Banks, P.; Kockarts, G. Chapter 9—Collision Processes. In Aeronomy; Banks, P., Kockarts, G., Eds.; Academic Press: Cambridge, MA, USA, 1973; pp. 184–239. [Google Scholar] [CrossRef]
- Rees, D.; Fuller-Rowell, T. The CIRA theoretical thermosphere model. Adv. Space Res. 1988, 8, 27–106. [Google Scholar] [CrossRef]
- Guo, J.; Wan, W.; Forbes, J.M.; Sutton, E.; Nerem, R.S.; Bruinsma, S. Interannual and latitudinal variability of the thermosphere density annual harmonics. J. Geophys. Res. Space Phys. 2008, 113. [Google Scholar] [CrossRef]
- Qian, L.; Solomon, S.C.; Kane, T.J. Seasonal variation of thermospheric density and composition. J. Geophys. Res. Space Phys. 2009, 114. [Google Scholar] [CrossRef]
- Emmert, J. Thermospheric mass density: A review. Adv. Space Res. 2015, 56, 773–824. [Google Scholar] [CrossRef]
- Afraimovich, E.L.; Astafyeva, E.I.; Oinats, A.V.; Yasukevich, Y.V.; Zhivetiev, I.V. Global electron content: A new conception to track solar activity. Ann. Geophys. 2008, 26, 335–344. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, L.; Le, H. Solar activity variations of nighttime ionospheric peak electron density. J. Geophys. Res. Space Phys. 2008, 113. [Google Scholar] [CrossRef]
- Chakraborty, S.; Hajra, R. Solar control of ambient ionization of the ionosphere near the crest of the equatorial anomaly in the Indian zone. In Proceedings of the Annales Geophysicae; Copernicus Publications: Göttingen, Germany, 2008; Volume 26, pp. 47–57. [Google Scholar]
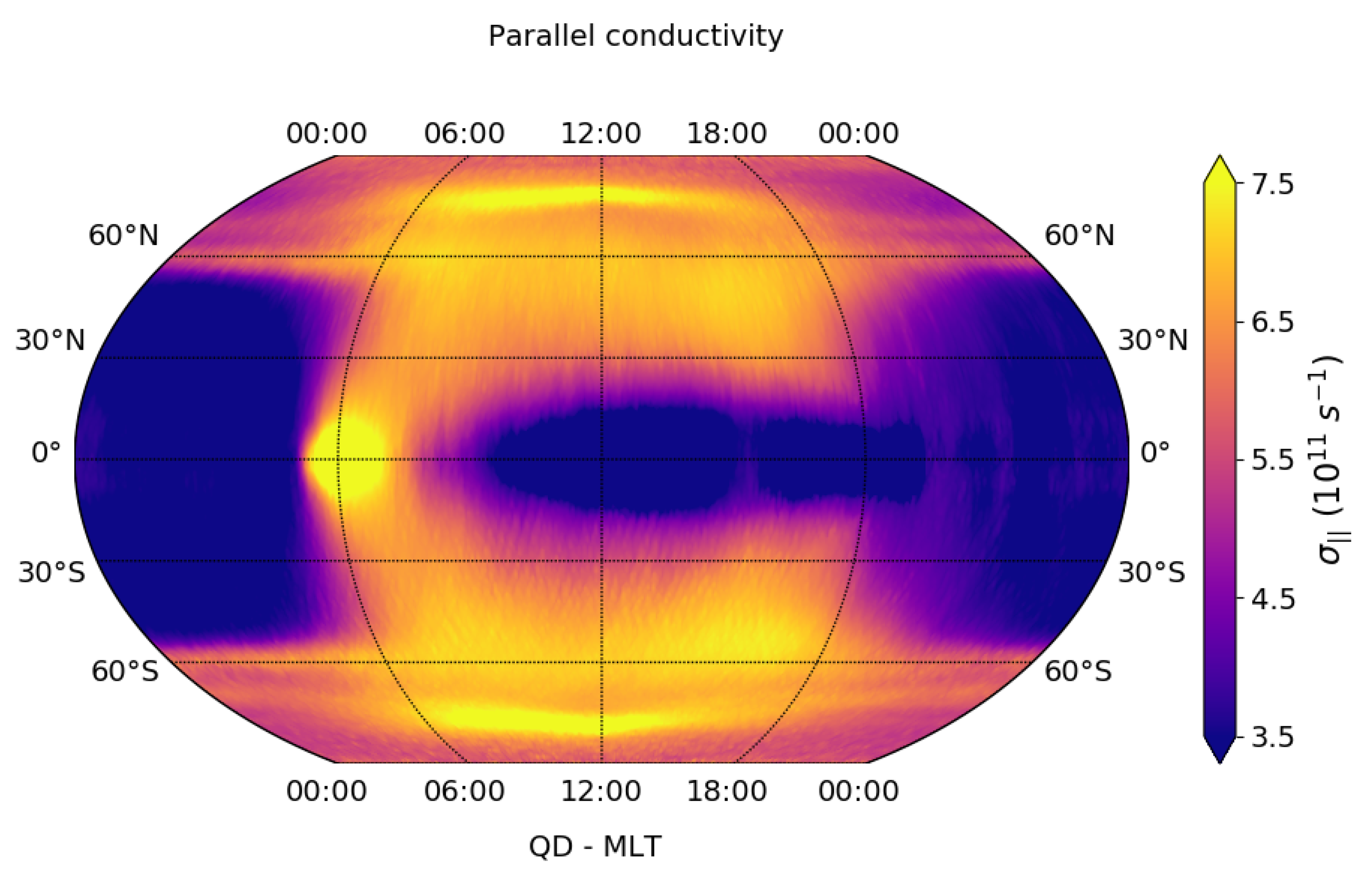
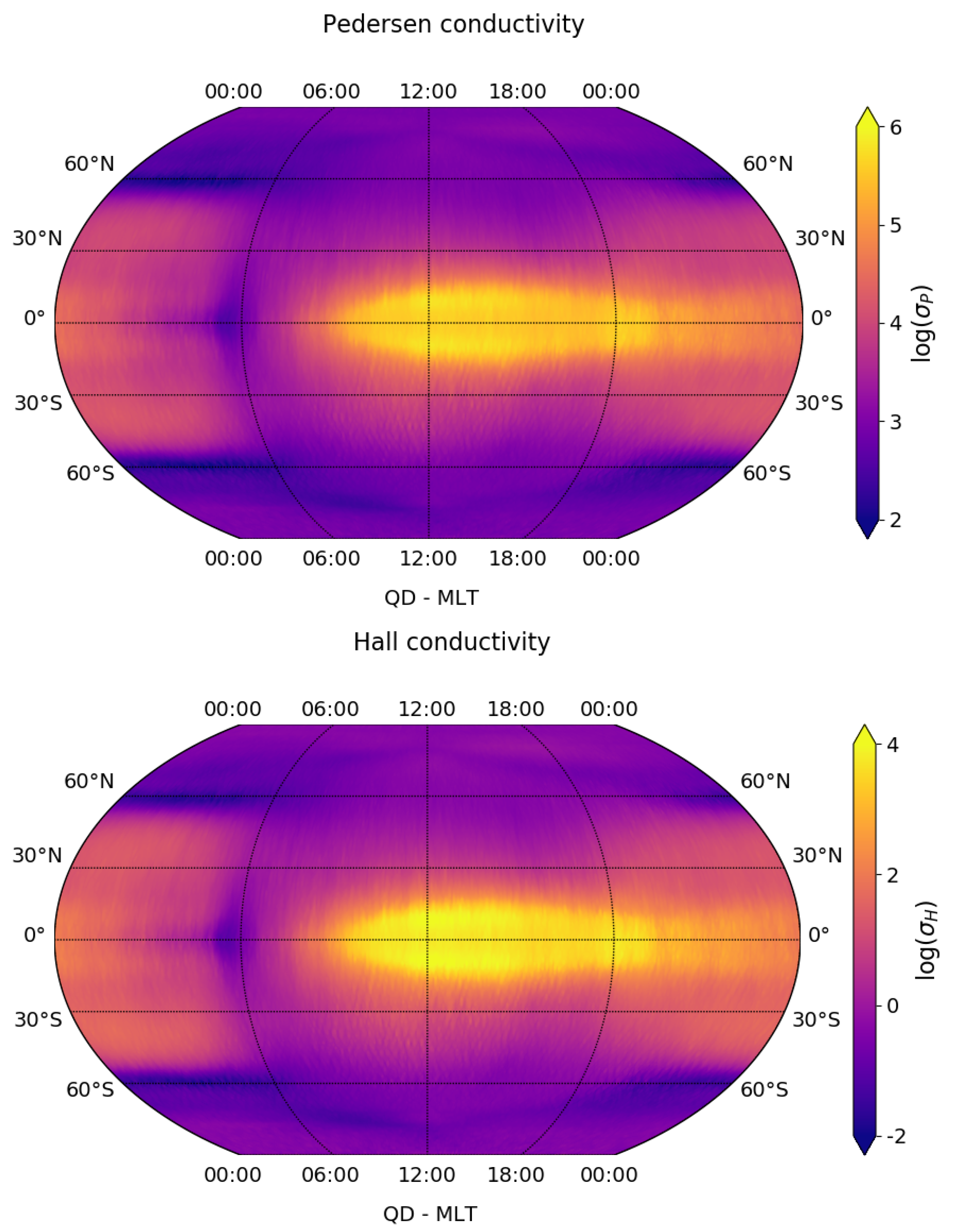

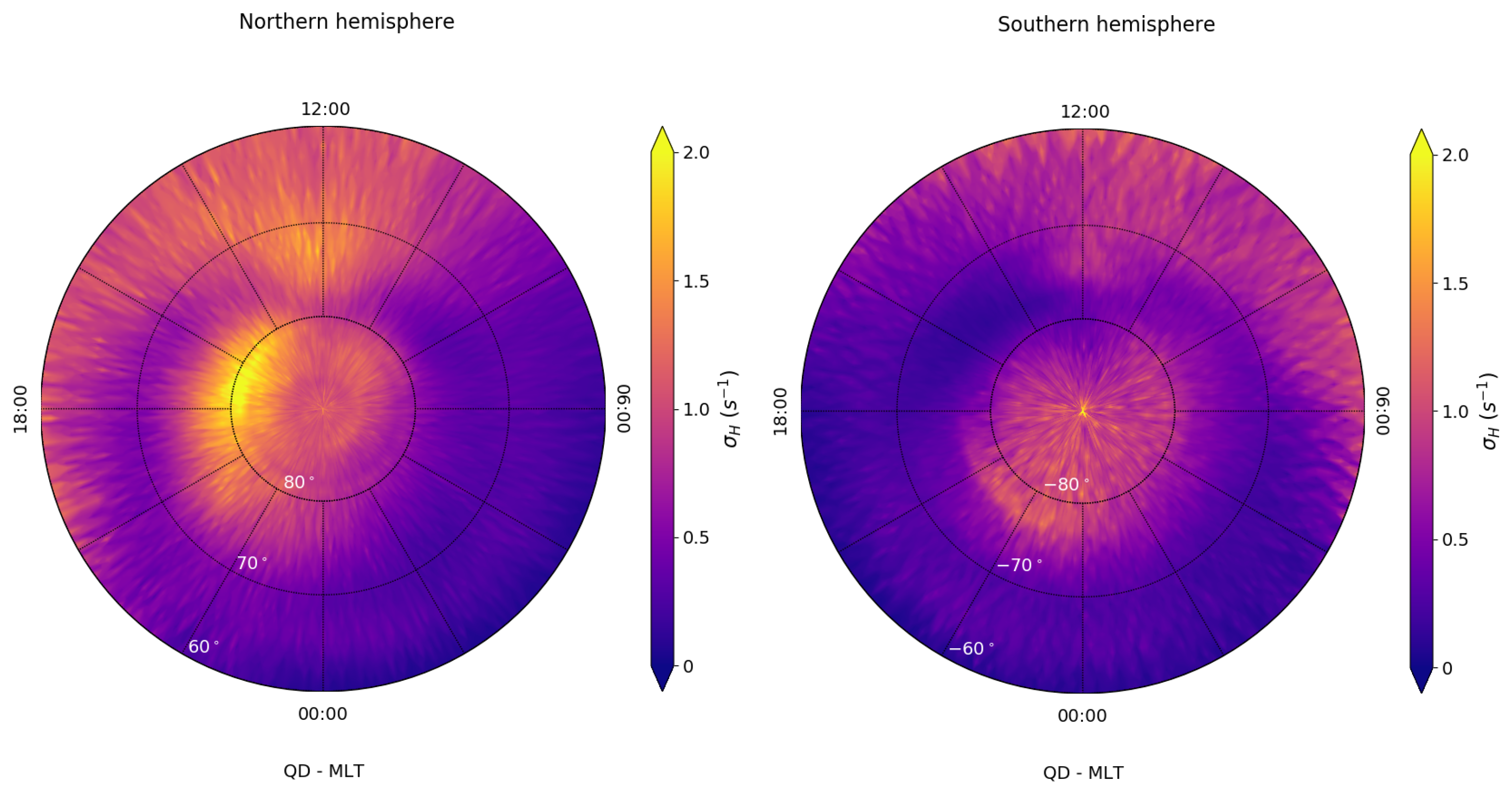
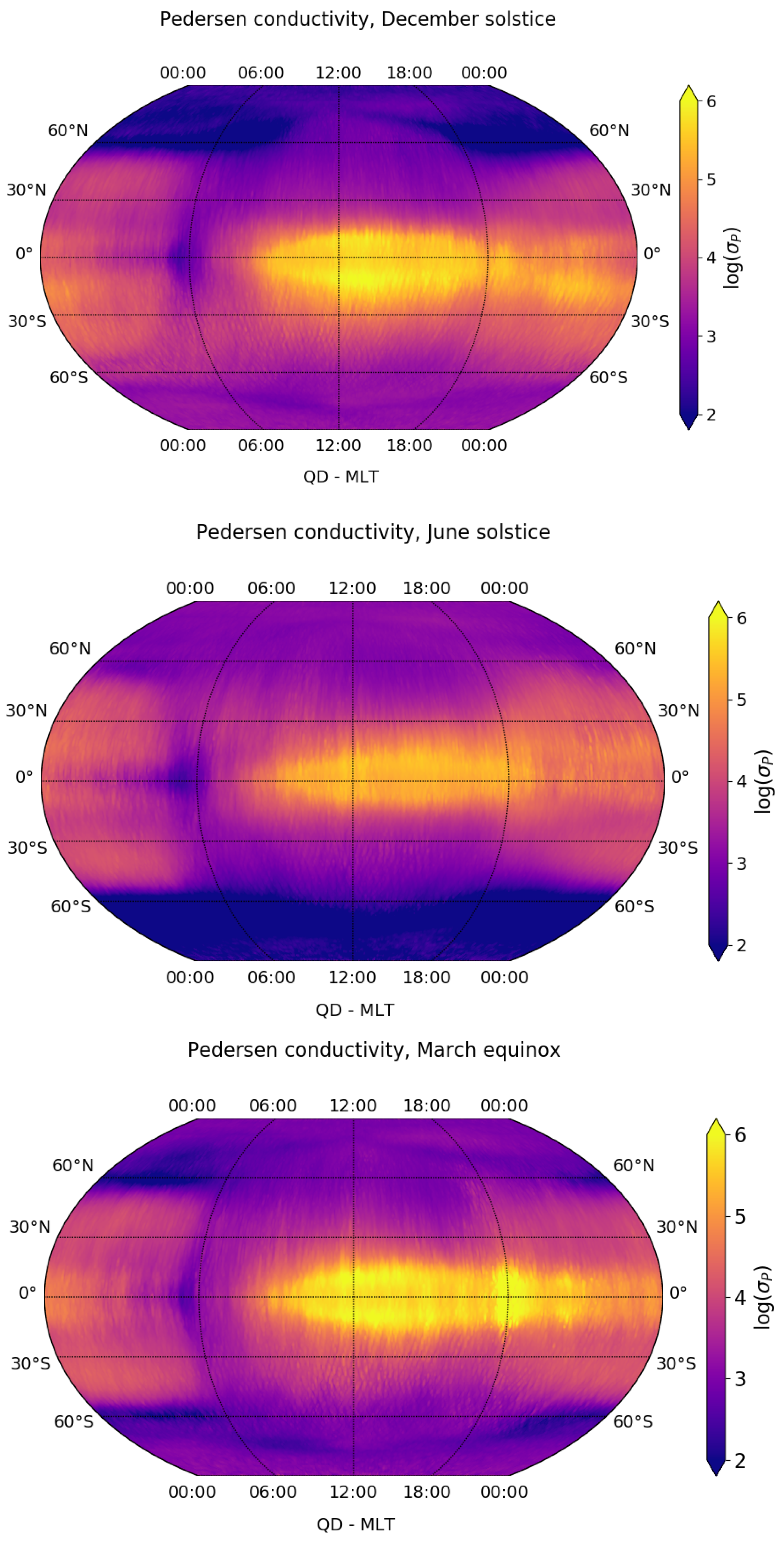


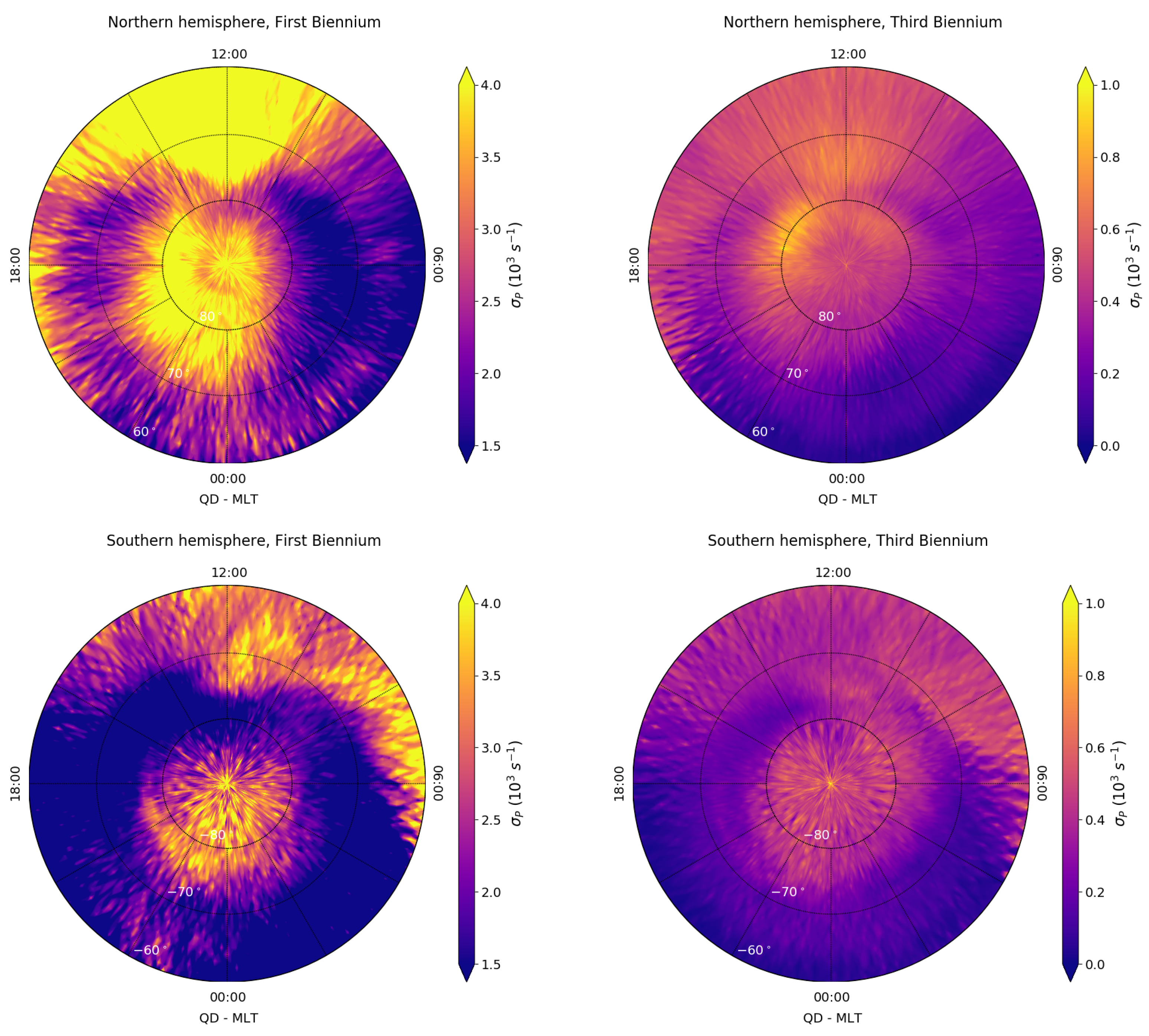
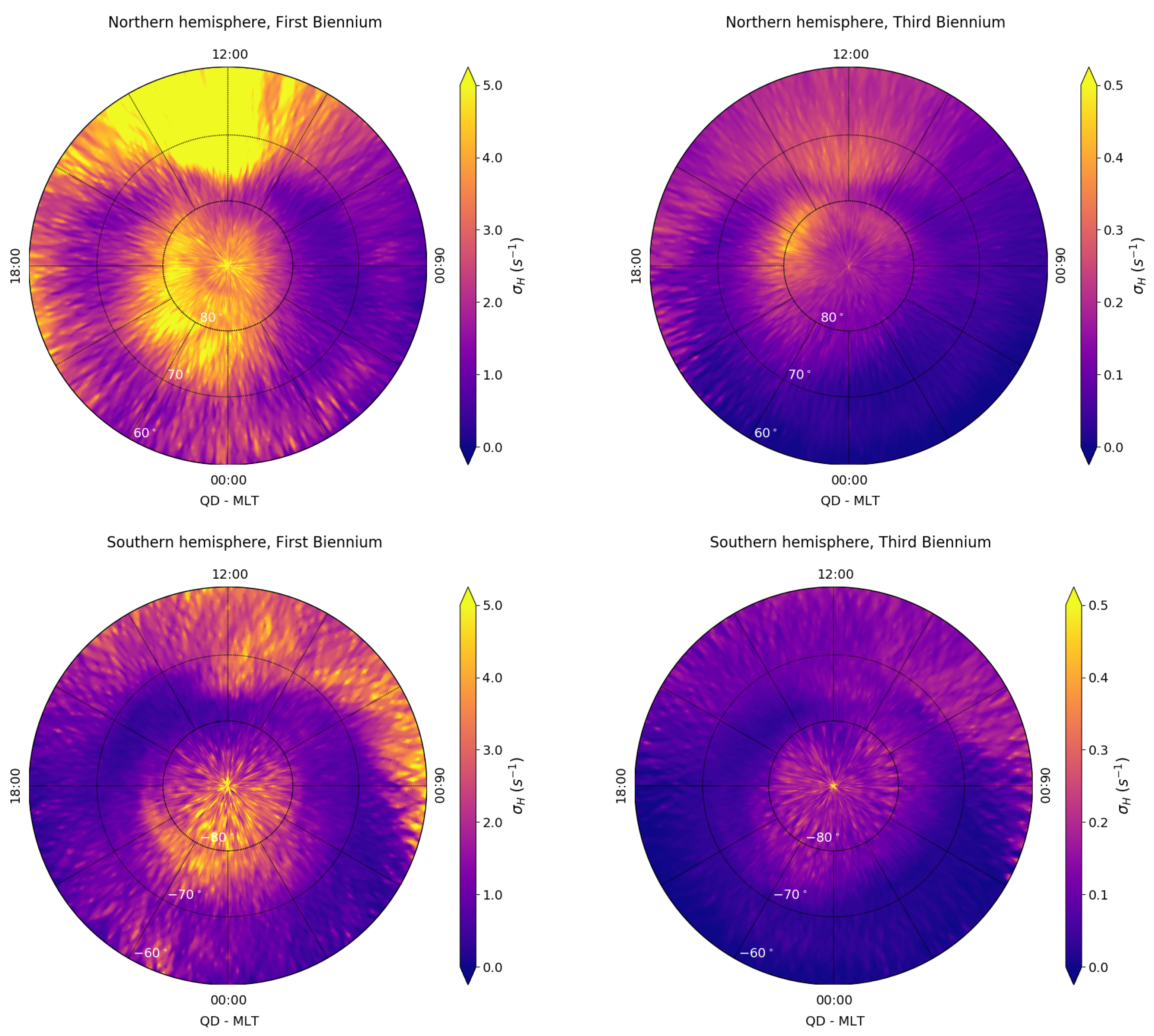
| Minimum Value (s−1) | Maximum Value (s−1) | Minimum Uncertainty (%) | Maximum Uncertainty (%) | Maximum Conditioned Uncertainty (%) | |
|---|---|---|---|---|---|
| 61 | 7 × 105 | 0.6 | 25.5 | 2.4 | |
| 10−2 | 1.3 × 104 | 0.8 | 29.3 | 2.6 |
| Minimum Value (s−1) | Maximum Value (s−1) | Minimum Uncertainty (%) | Maximum Uncertainty (%) | Maximum Conditioned Uncertainty (%) | |
|---|---|---|---|---|---|
| December solstice | 4.6 | 1.2 × 106 | 0.7 | 59.4 | 4.7 |
| June solstice | 0.1 | 4.3 × 105 | 0.7 | 70.7 | 5.2 |
| March equinox | 15.4 | 1.9 × 106 | 0.8 | 70.7 | 4.9 |
| September equinox | 19.9 | 1.1 × 106 | 0.4 | 70.7 | 4.9 |
| Minimum Value (s−1) | Maximum Value (s−1) | Minimum Uncertainty (%) | Maximum Uncertainty (%) | Maximum Conditioned Uncertainty (%) | |
|---|---|---|---|---|---|
| December solstice | 0.0 | 3.1 × 104 | 1.0 | 66.7 | 5.1 |
| June solstice | 0.0 | 5.5 × 103 | 1.0 | 70.7 | 5.9 |
| March equinox | 0.0 | 6.5 × 104 | 1.0 | 70.7 | 5.1 |
| September equinoxes | 0.0 | 3.0 × 104 | 1.0 | 70.7 | 5.5 |
| Minimum Value (s−1) | Maximum Value (s−1) | Minimum Uncertainty (%) | Maximum Uncertainty (%) | Maximum Conditioned Uncertainty (%) | |
|---|---|---|---|---|---|
| First Biennium | 10.7 | 2.8 × 106 | 0.9 | 70.6 | 4.7 |
| Third Biennium | 0.6 | 3.7 × 105 | 0.5 | 70.5 | 5.0 |
| Minimum Value (s−1) | Maximum Value (s−1) | Minimum Uncertainty (%) | Maximum Uncertainty (%) | Maximum Conditioned Uncertainty (%) | |
|---|---|---|---|---|---|
| First Biennium | 0.0 | 1.1 × 105 | 1.1 | 99.7 | 4.9 |
| Third Biennium | 0.0 | 5.3 × 103 | 0.8 | 109.4 | 5.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giannattasio, F.; Pignalberi, A.; Tozzi, R.; De Michelis, P.; Mestici, S.; Consolini, G.; Coco, I.; Pezzopane, M. Perpendicular Electrical Conductivity in the Topside Ionosphere Derived from Swarm Measurements. Remote Sens. 2024, 16, 3129. https://doi.org/10.3390/rs16173129
Giannattasio F, Pignalberi A, Tozzi R, De Michelis P, Mestici S, Consolini G, Coco I, Pezzopane M. Perpendicular Electrical Conductivity in the Topside Ionosphere Derived from Swarm Measurements. Remote Sensing. 2024; 16(17):3129. https://doi.org/10.3390/rs16173129
Chicago/Turabian StyleGiannattasio, Fabio, Alessio Pignalberi, Roberta Tozzi, Paola De Michelis, Simone Mestici, Giuseppe Consolini, Igino Coco, and Michael Pezzopane. 2024. "Perpendicular Electrical Conductivity in the Topside Ionosphere Derived from Swarm Measurements" Remote Sensing 16, no. 17: 3129. https://doi.org/10.3390/rs16173129
APA StyleGiannattasio, F., Pignalberi, A., Tozzi, R., De Michelis, P., Mestici, S., Consolini, G., Coco, I., & Pezzopane, M. (2024). Perpendicular Electrical Conductivity in the Topside Ionosphere Derived from Swarm Measurements. Remote Sensing, 16(17), 3129. https://doi.org/10.3390/rs16173129









