A New Approximation Modeling Method for the Triaxial Induction Logging in Planar-Stratified Biaxial Anisotropic Formations
Abstract
1. Introduction
2. Physics of Triaxial Induction Logging
3. Computation of Primary TIL Response in Homogeneous Formation
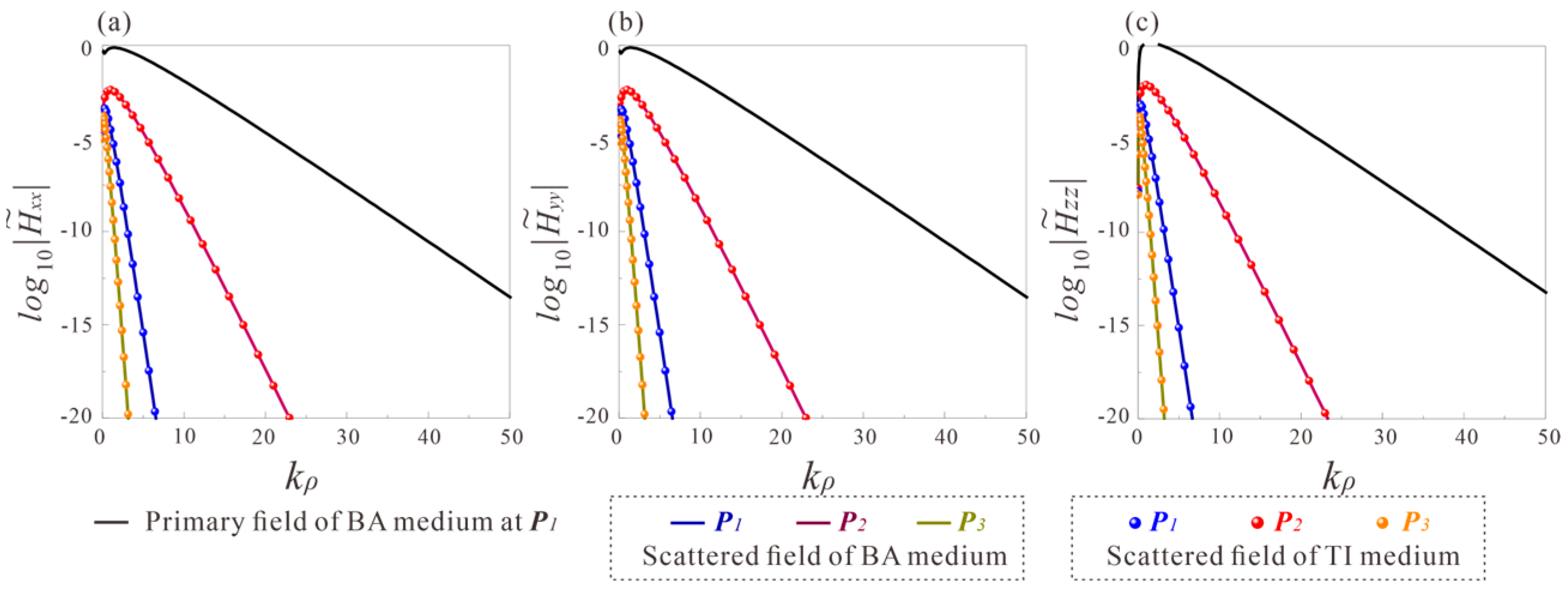
3.1. Spectral Primary Field in Homogeneous BA Medium
3.2. The Two-Level Subtraction of Spectral Primary Fields
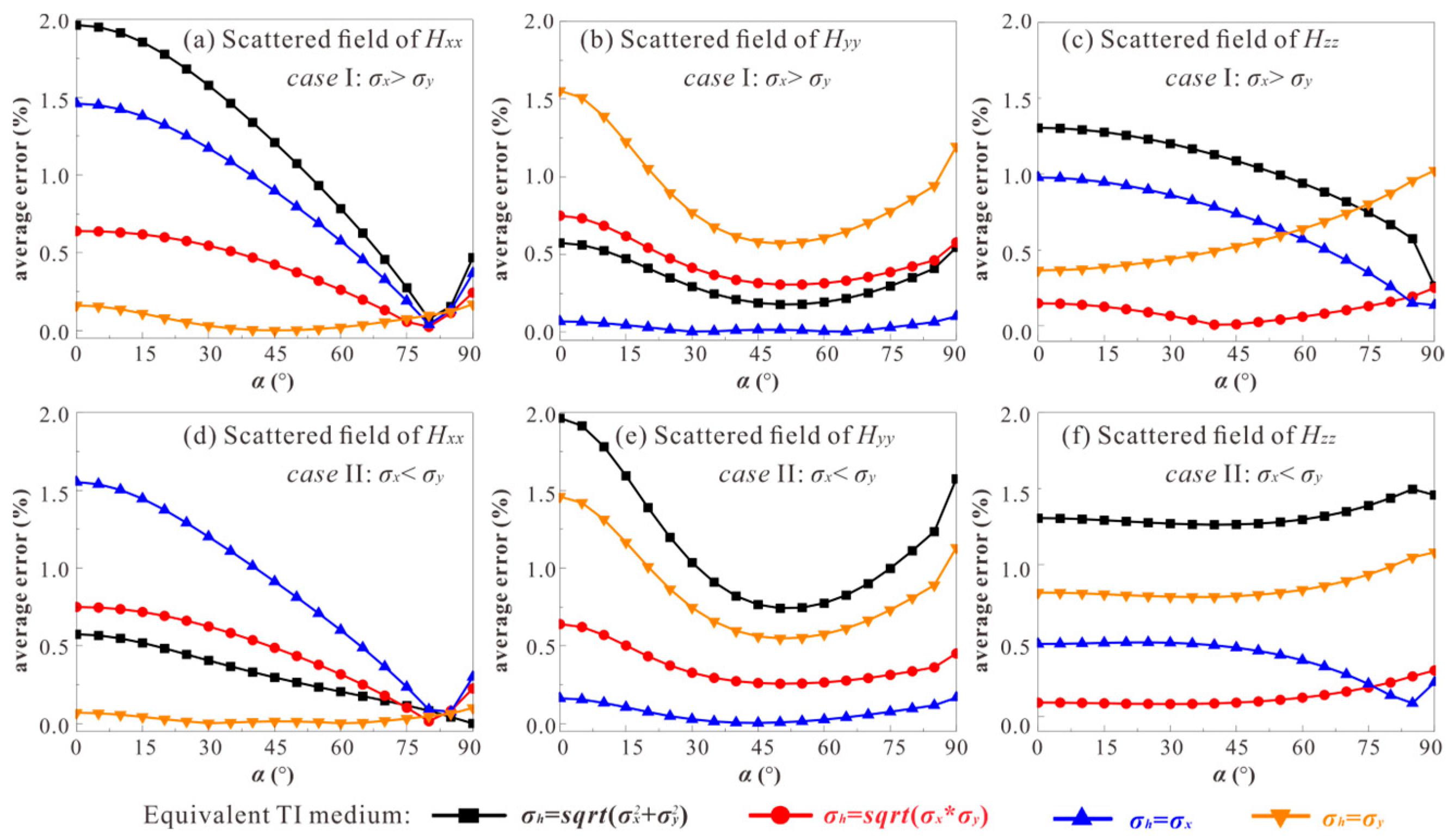
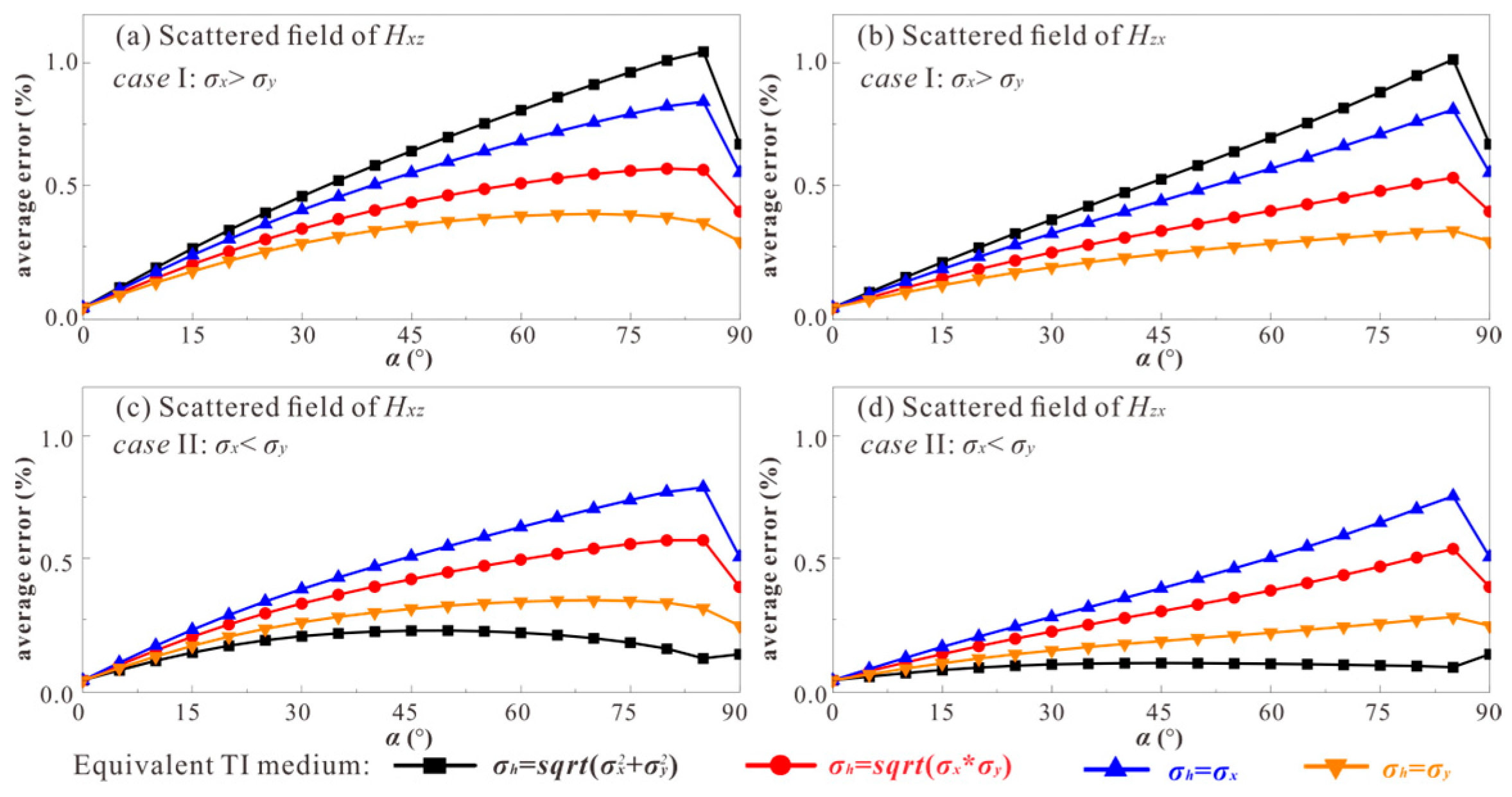
3.3. Optimal Construction of Equivalent TI Medium
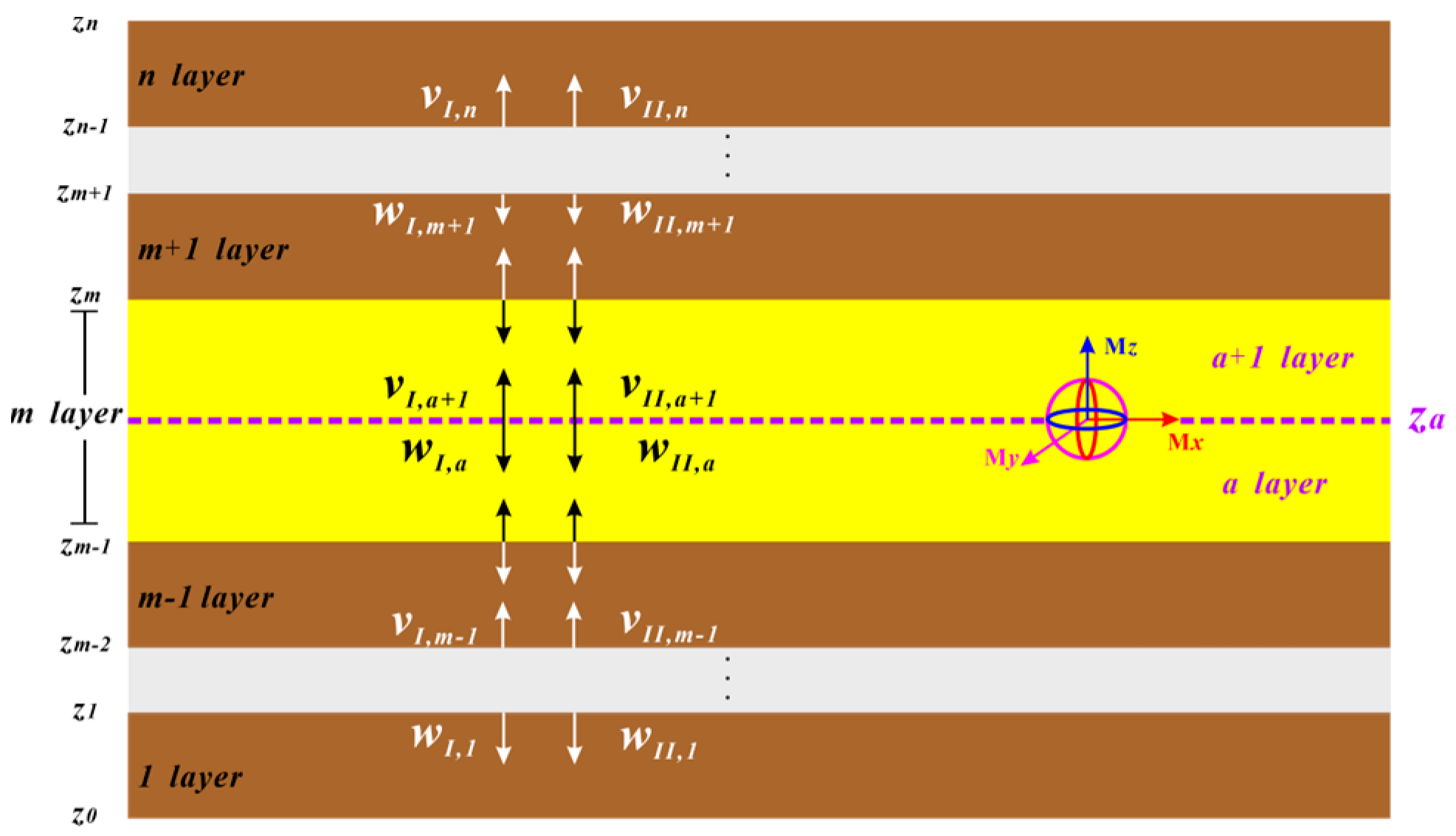
4. Rapid Computation of Scattered Fields in Layered BA Formations
4.1. The Modified Amplitude Propagator Matrix (MAPM) Algorithm
4.2. Approximating the Scattered Fields with Layered TI Model
4.3. Best Approximation Model Analysis
5. Numerical Examples
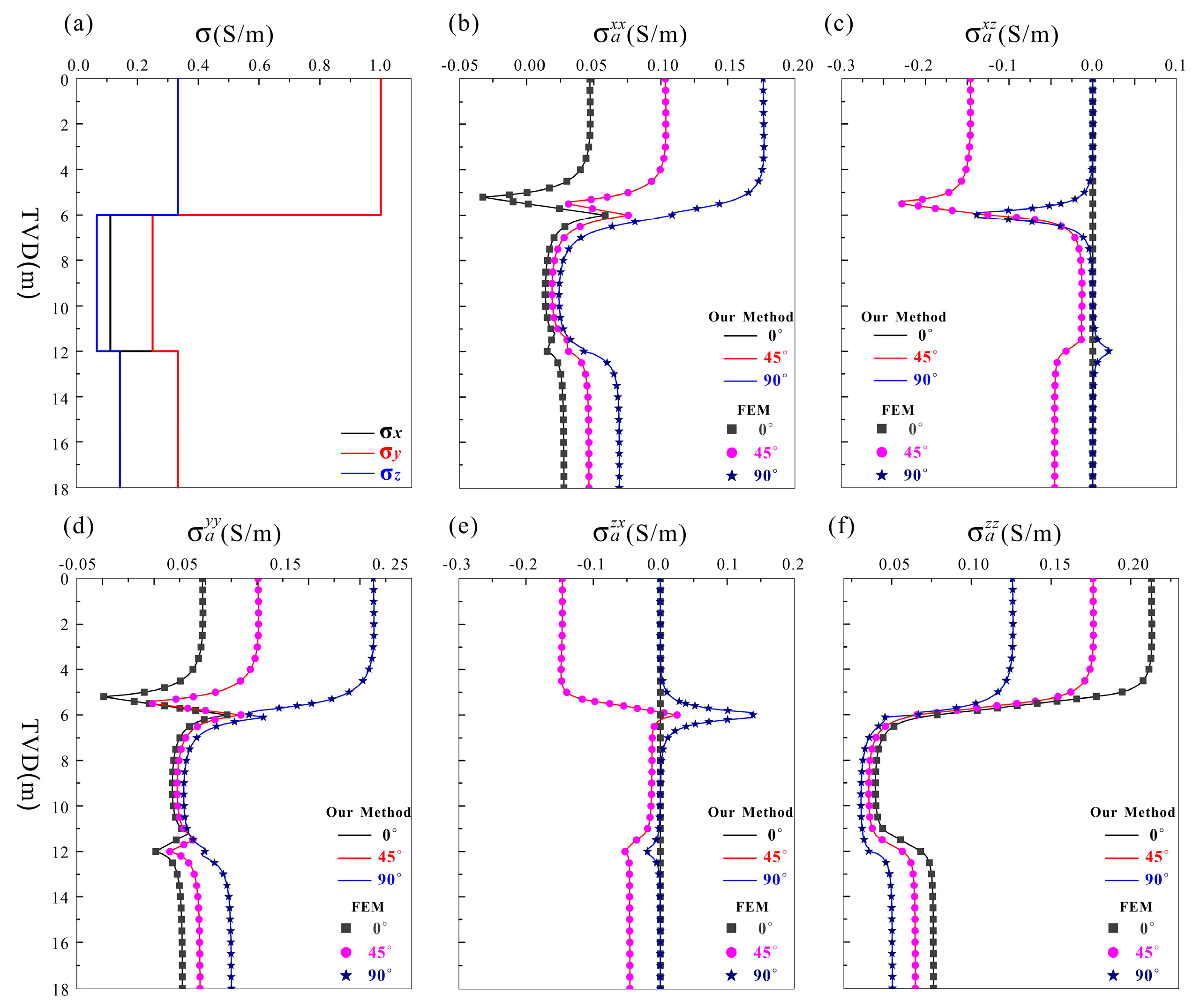
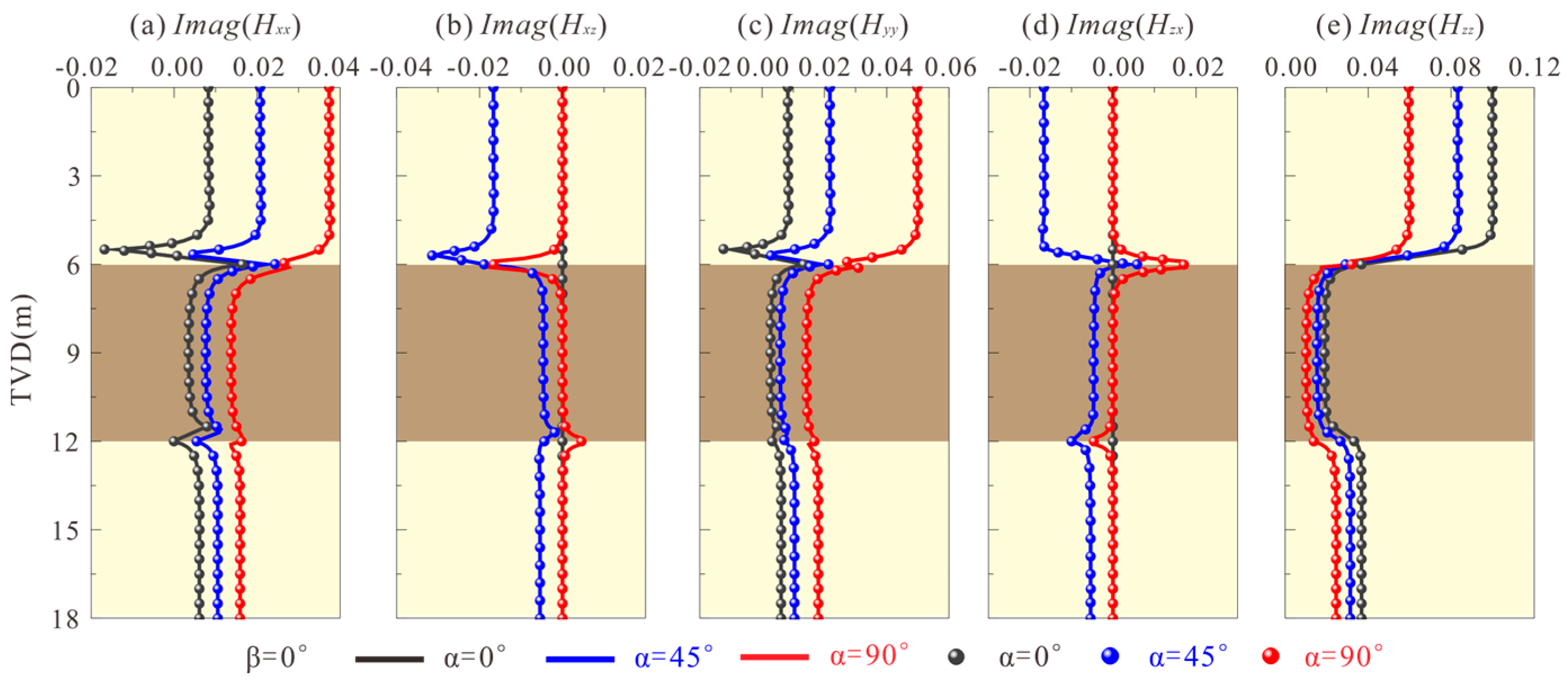
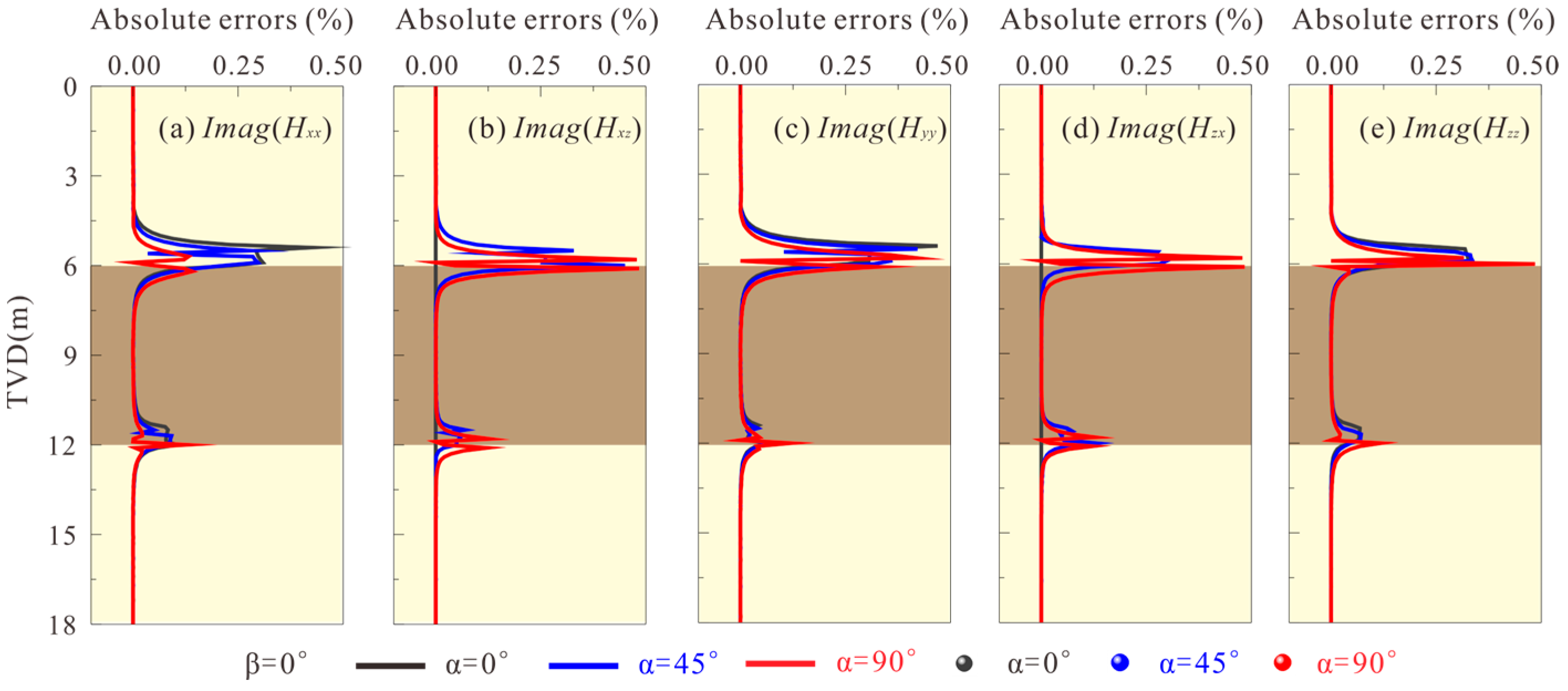
5.1. Accuracy Analysis
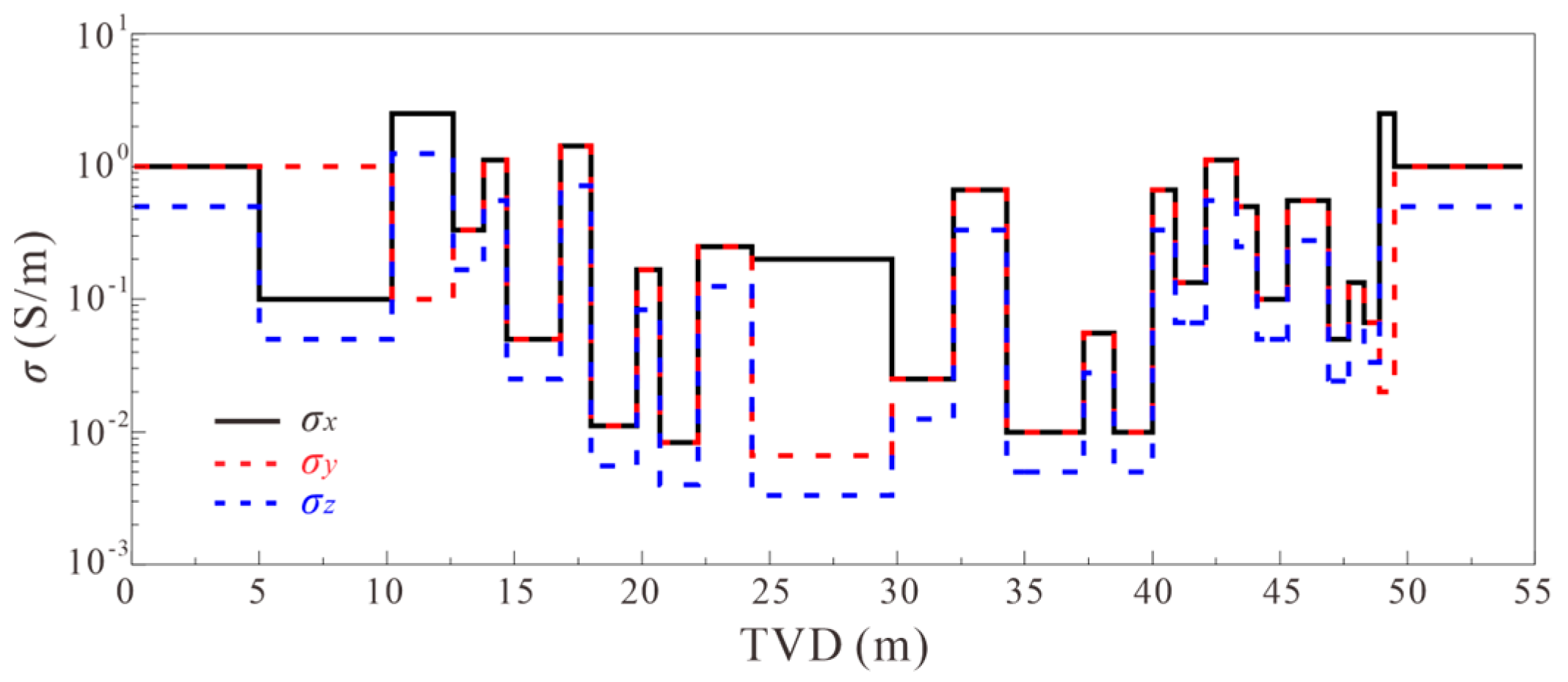
5.2. Applicability Analysis
6. Discussion
6.1. Advantages
- The new approximation method is at least two orders of magnitude faster than the current modeling approach while maintaining a computational precision error within 0.5% after processing the primary and scattered fields, making real-time data processing possible.
- The new approximation method is highly applicable to a wide range of formation conditions (including dip angle, thickness, and anisotropy) and tool parameters (such as frequency and spacing).
- In addition to the approximation method, this paper also presents a concise and stable MAPM algorithm for the rigorous solution of scattered fields in layered BA media. This algorithm can be extended to more complex anisotropic models, such as cross anisotropy, full anisotropy.
6.2. Limits
- The approximation method is currently applicable only to layered BA formations and is not yet suitable for more complex anisotropic cases, such as cross anisotropy and full anisotropy. Additionally, the method is designed for actual formations where the coefficient of horizontal anisotropy is small due to formation development and depositional features. As a result, it may not be applicable to anisotropic models in other fields.
- The coil system of commercial TIL tools is typically designed with a single transmitter and two receivers. Due to the varying distances between the transmitting coil and the two receiving coils, it is necessary to separately approximate the formations at the locations of the two coils during the measurement process, making the procedure quite complex.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anderson, B.I.; Barber, T.D.; Luling, M.G. The Response of Induction Tools to Dipping, Anisotropic Formations. In Proceedings of the Transactions of the SPWLA 36th Annual Logging Symposium Paper D, Paris, France, 26–29 June 1995. [Google Scholar]
- Gao, L.; Gianzero, S.; Kennedy, D.; SanMartin, L. The Response of a Triaxial Induction Sonde in a Biaxial Anisotropy Medium. Petrophysics 2002, 43, 172–184. [Google Scholar]
- Kang, Z.M.; Zhang, Y.; Hou, B.B.; Chen, G.; Hao, X.; Qin, H.; Qin, W. Using the Multi-component Induction Logging Data to Evaluate the Geometric Parameters of the Hydraulic Fracture. J. Geophys. Eng. 2022, 19, 1163–1179. [Google Scholar] [CrossRef]
- Hagiwara, T. Apparent Dip and Apparent Anisotropy from Multifrequency Triaxial Induction Measurements. Geophysics 2011, 76, F1–F13. [Google Scholar] [CrossRef]
- Fang, L.Q.; Bai, Y.X.; Guo, S.Y.; Liu, X.; Tang, S.; Li, X.; Xiao, J. Anisotropy Evaluation and Interface Detection Based on 3D Holographic Azimuthal Electromagnetic Resistivity Logging Instrument. J. Geophys. Eng. 2023, 20, 763–773. [Google Scholar] [CrossRef]
- Wu, Z.G.; Li, H.; Yue, X.Z. 2.5-Dimensional modeling of EM logging-while-drilling tool in anisotropic medium on a Lebedev grid. Pet. Sci. 2023, 20, 249–260. [Google Scholar] [CrossRef]
- Kriegshauser, B.; Fanini, O.; Forgang, S.; Itskovich, G.; Rabinovich, M.; Tabarovsky, L.; Vd Horst, J. A New Multicomponent Induction Logging Tool to Resolve Anisotropic Formations. In Proceedings of the SPWLA 41st Annual Logging Symposium, Dallas, TX, USA, 4–7 June 2000. [Google Scholar]
- Georgi, D.; Schoen, J.; Rabinovich, M. Biaxial Anisotropy: Its Occurrence and Measurement with Multicomponent Induction Tools. In Proceedings of the SPE Annual Technical Conference and Exhibition, USE Society of Petroleum Engineers, Denver, CO, USA, 21–24 September 2008. [Google Scholar]
- Michael, Z.; David, K.; Ertan, P. Foundations of Tensor Induction Well-Logging. Petrophysics 2001, 42, 588–610. [Google Scholar]
- Davydycheva, S.; Wang, T. A Fast Modeling Method to Solve Maxwell’s Equations in 1D Layered Biaxial Anisotropic Medium. Geophysics 2011, 76, F293–F302. [Google Scholar] [CrossRef]
- Cheryauka, A.B.; Zhdanov, M.S. Focusing Inversion of Tensor Induction Logging Data in Anisotropic Formations and Deviated Well. In Proceedings of the 71st Annual International Meeting, SEG, Expanded Abstracts, San Antonio, TX, USA, 9–14 September 2001; pp. 357–360. [Google Scholar]
- Kerry, K. Is the Fast Hankel Transform Faster Than Quadrature? Geophysics 2012, 77, F21–F30. [Google Scholar]
- Wang, L.; Qiao, P.; Zhao, W.N. A New Propagator Matrix Algorithm to Compute Electromagnetic Fields in Multilayered Formations with Full Anisotropy. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–11. [Google Scholar] [CrossRef]
- Chen, J.F. A Semianalytical Finite Element Analysis of Electromagnetic Propagation Stratified Media. Microw. Opt. Technol. Lett. 2015, 57, 15–18. [Google Scholar] [CrossRef]
- Hu, Y.Y.; Sun, Q.T. Modeling of triaxial induction logging responses in multilayered anisotropic formations. Geophysics 2021, 86, E305–E314. [Google Scholar] [CrossRef]
- Kang, Z.Z.; Wang, H.N.; Yin, C.C. Semi-Analytic Sensitivity of the MCIL Responses in Homogeneous Biaxial Anisotropic Media. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Zhou, Y.G.; Wang, L.J.; Ren, Q.; Liang, B.; Liu, Q.H. Simulation of Electromagnetic Waves in Magnetized Cold Plasma by a Novel BZT-DGTD Method. IEEE Trans. Antennas Propag. 2023, 71, 9233–9244. [Google Scholar] [CrossRef]
- Kong, J.A. Electromagnetic Fields Due to Dipole Antennas Over Stratified Anisotropic Media. Geophysics 1972, 37, 985–996. [Google Scholar] [CrossRef]
- Chew, W.C. Waves and Fields in Inhomogeneous Media; IEEE Press: New York, NY, USA, 1995. [Google Scholar]
- Løseth, L.; Ursin, B. Electromagnetic Fields in Planarly Layered Anisotropic Media. Geophys. J. Int. 2007, 170, 44–80. [Google Scholar] [CrossRef]
- Yuan, N.; Nie, X.C.; Liu, R.; Qiu, C.W. Simulation of Full Responses of a Triaxial Induction Tool in a Homogeneous Biaxial Anisotropic Formation. Geophysics 2010, 75, E101–E114. [Google Scholar] [CrossRef][Green Version]
- Wang, G.L.; Barber, T.; Wu, P.; Allen, D.; Abubakar, A. Fast Inversion of Triaxial Induction Data in Dipping Crossbedded Formations. Geophysics 2017, 82, 31–45. [Google Scholar] [CrossRef]
- Hong, D.C.; Li, N.; Han, W.; Zhan, Q.; Zeyde, K.; Liu, Q.H. An Analytic Algorithm for Dipole Electromagnetic Field in Fully Anisotropic Planar-Stratified Media. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9120–9131. [Google Scholar] [CrossRef]
- Guptasarma, D.; Singh, B. New Digital Linear Filters for Hankel J0 and J1 Transforms. Geophys. Prospect. 1997, 45, 745–762. [Google Scholar] [CrossRef]
- Simsek, E.; Liu, Q.H.; Wei, B. Singularity Subtraction for Evaluation of Green’s Functions for Multilayer Media. IEEE Trans. Microw. Theory Techn. 2006, 54, 216–225. [Google Scholar] [CrossRef]
- Liu, T.L.; Xing, G.L.; Zhang, X.C. Electromagnetic Fields Computation of Planar-Distribution Sources in Anisotropic Planar-Stratified Media with an Equivalent Boundary Approach. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–13. [Google Scholar] [CrossRef]
- Hu, Y.Y.; Yuan, F.; Wang, D.Z.; Zhong, Y.; Liu, Q.H. Electromagnetic Waves in Multilayered Generalized Anisotropic Media. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5758–5766. [Google Scholar] [CrossRef]
- Li, N.; Hong, D.C.; Han, W.; Liu, Q.H. An Analytic Algorithm for Electromagnetic Field in Planar-Stratified Biaxial Anisotropic Formation. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1644–1653. [Google Scholar] [CrossRef]
- Deng, S.G.; Liu, T.L.; Wang, L. Analytical Solution of Multicomponent Induction Logging Response in Biaxial Anisotropy Medium. Chin. J. Geophys. 2020, 63, 362–373. (In Chinese) [Google Scholar]
- Wang, L.; Qiao, P.; Li, Z.Q. A New Semi-Analytical Algorithm for Rapid Simulation of Triaxial Electromagnetic Logging Responses in Multilayered Biaxial Anisotropic Formation. Geophysics 2023, 88, D115–D129. [Google Scholar] [CrossRef]
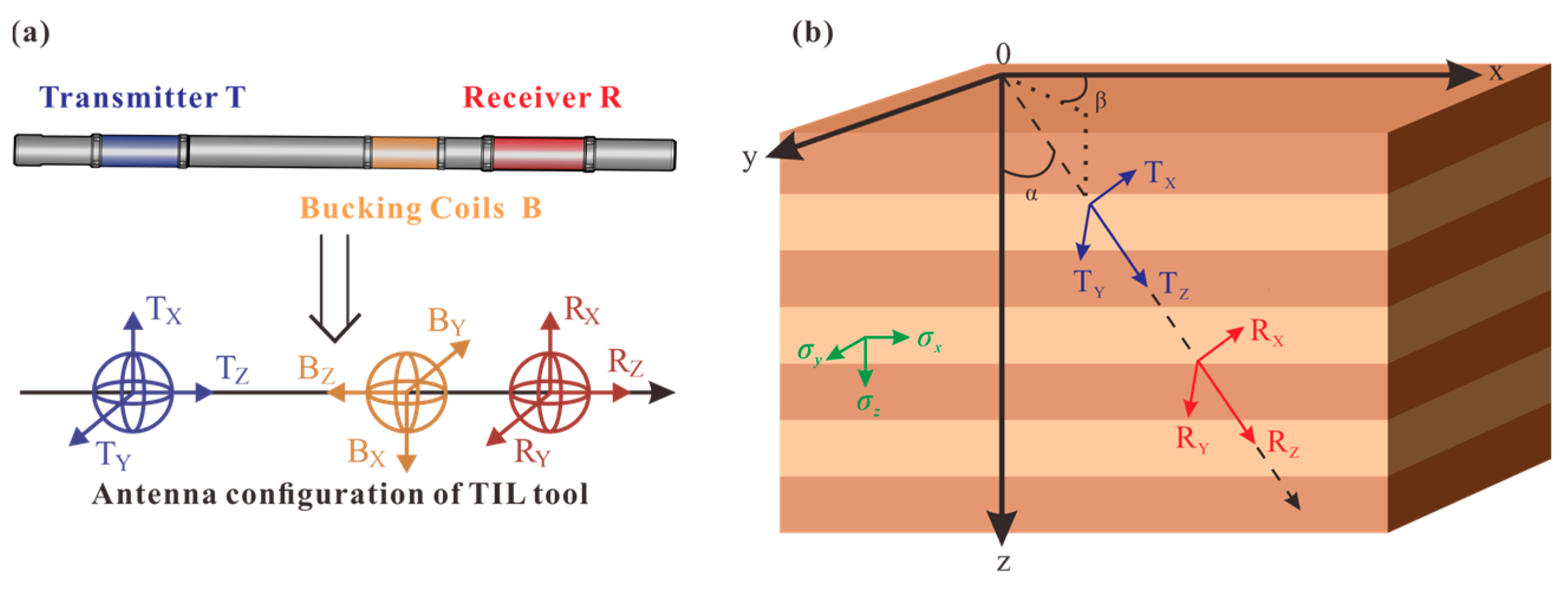
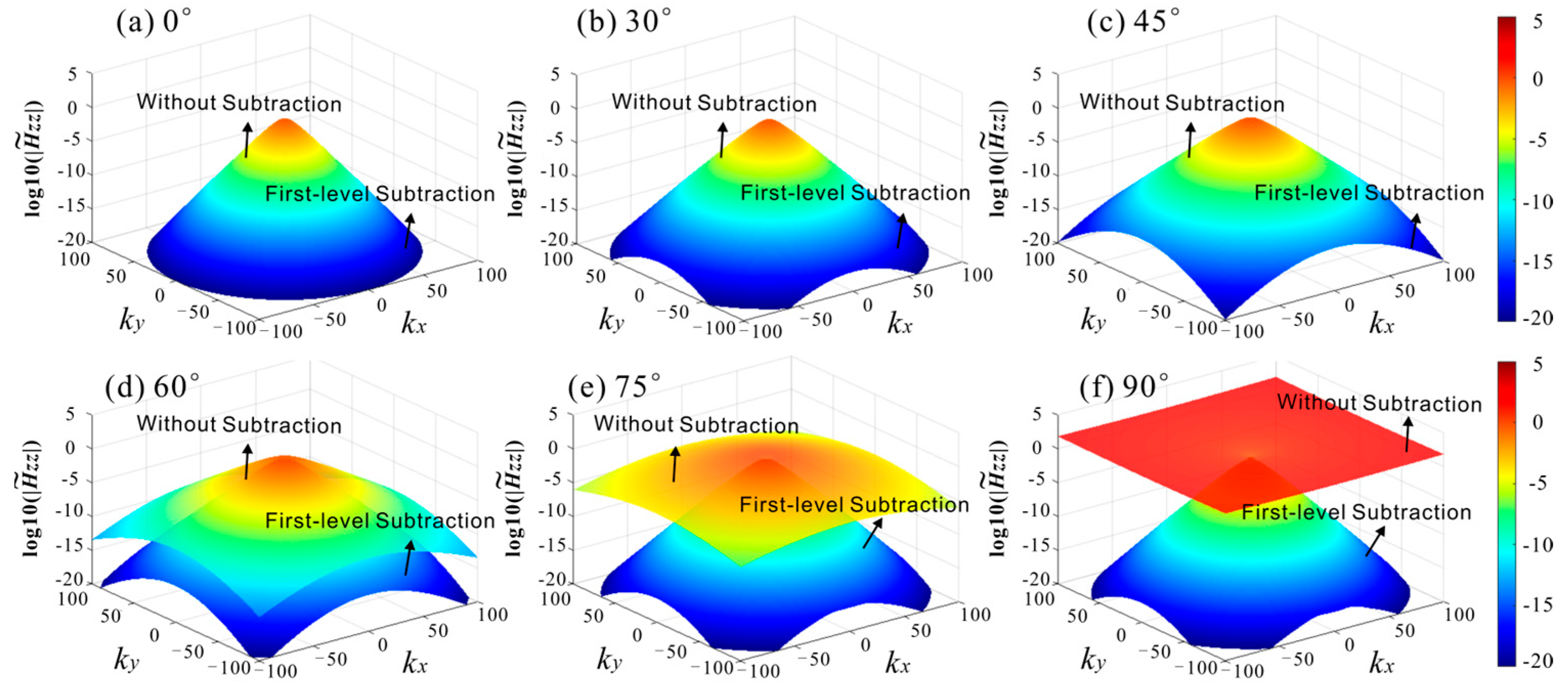

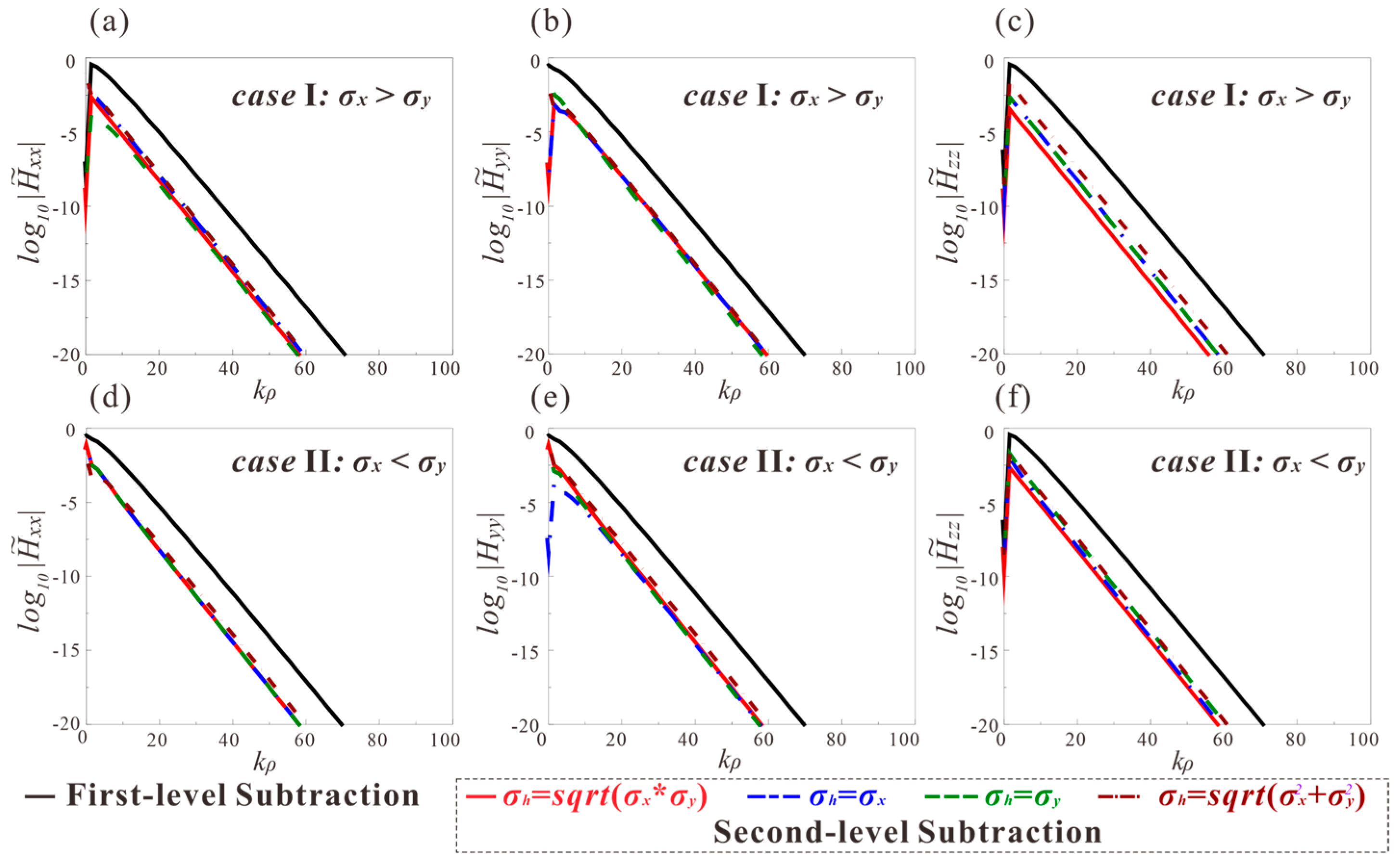
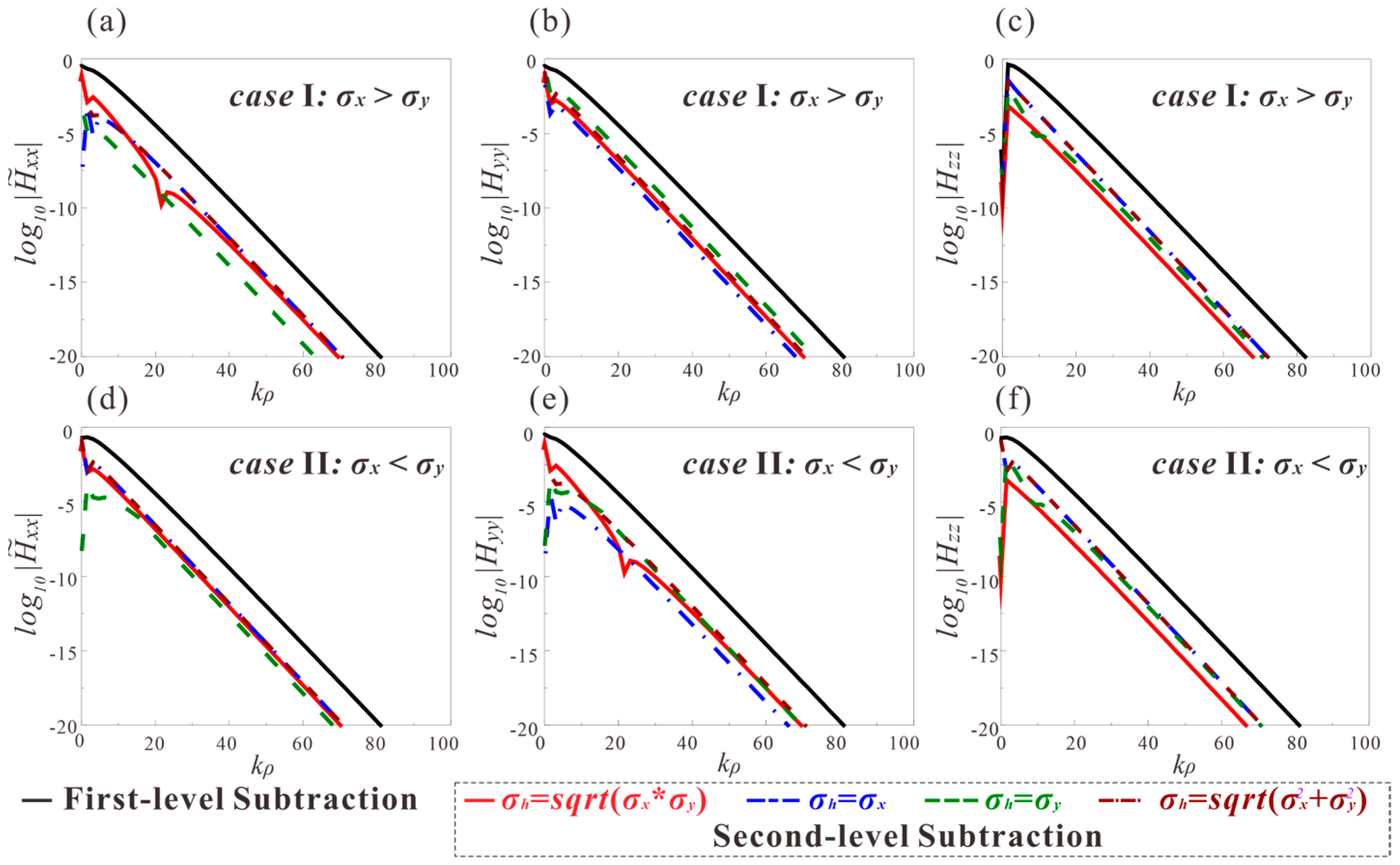



| Components | |||||||
|---|---|---|---|---|---|---|---|
| Quadrants | |||||||
| 1st | +1 | +1 | +1 | +1 | +1 | +1 | |
| 2nd | −1 | −1 | −1 | +1 | +1 | −1 | |
| 3rd | +1 | +1 | +1 | +1 | −1 | −1 | |
| 4th | −1 | −1 | −1 | +1 | −1 | +1 | |
| Components | |||||
|---|---|---|---|---|---|
| Cases | |||||
| σx > σy | σh = σy | σh = σx | σh = σy | ||
| σx < σy | |||||
| α, β (°) | Average Errors (%) | Relative Time Cost (MAPM (s)) | Relative Time Cost (Approximation(s)) | Speed-Up Factor | ||||
|---|---|---|---|---|---|---|---|---|
| 0, 0 | 0.203 | 0.212 | 0.198 | 0.221 | 0.224 | 0.0321 | 0.0008 | 41.25 |
| 45, 0 | 0.234 | 0.231 | 0.222 | 0.262 | 0.260 | 0.0382 | 0.0010 | 37.34 |
| 90, 0 | 0.257 | 0.248 | 0.242 | 0.277 | 0.269 | 0.0739 | 0.0022 | 33.56 |
| 80, 30 | 0.264 | 0.252 | 0.245 | 0.279 | 0.271 | 0.0858 | 0.0025 | 33.89 |
| 80, 45 | 0.268 | 0.257 | 0.247 | 0.280 | 0.272 | 0.0937 | 0.0029 | 32.51 |
| 80, 75 | 0.276 | 0.267 | 0.253 | 0.284 | 0.275 | 0.1309 | 0.0044 | 30.05 |
| α, β (°) | Minimum Errors (%) | Maximum Errors (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0, 0 | 0.022 | 0.023 | 0.022 | 0.024 | 0.024 | 0.448 | 0.468 | 0.437 | 0.488 | 0.495 |
| 45, 0 | 0.025 | 0.025 | 0.024 | 0.028 | 0.028 | 0.468 | 0.462 | 0.444 | 0.524 | 0.52 |
| 90, 0 | 0.028 | 0.027 | 0.026 | 0.030 | 0.029 | 0.514 | 0.496 | 0.484 | 0.554 | 0.538 |
| 80, 30 | 0.028 | 0.028 | 0.027 | 0.030 | 0.029 | 0.528 | 0.504 | 0.49 | 0.558 | 0.542 |
| 80, 45 | 0.029 | 0.028 | 0.027 | 0.030 | 0.029 | 0.536 | 0.514 | 0.494 | 0.56 | 0.544 |
| 80, 75 | 0.030 | 0.029 | 0.0275 | 0.030 | 0.029 | 0.552 | 0.534 | 0.506 | 0.568 | 0.551 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, P.; Wang, L.; Yuan, X.; Deng, S. A New Approximation Modeling Method for the Triaxial Induction Logging in Planar-Stratified Biaxial Anisotropic Formations. Remote Sens. 2024, 16, 3076. https://doi.org/10.3390/rs16163076
Qiao P, Wang L, Yuan X, Deng S. A New Approximation Modeling Method for the Triaxial Induction Logging in Planar-Stratified Biaxial Anisotropic Formations. Remote Sensing. 2024; 16(16):3076. https://doi.org/10.3390/rs16163076
Chicago/Turabian StyleQiao, Ping, Lei Wang, Xiyong Yuan, and Shaogui Deng. 2024. "A New Approximation Modeling Method for the Triaxial Induction Logging in Planar-Stratified Biaxial Anisotropic Formations" Remote Sensing 16, no. 16: 3076. https://doi.org/10.3390/rs16163076
APA StyleQiao, P., Wang, L., Yuan, X., & Deng, S. (2024). A New Approximation Modeling Method for the Triaxial Induction Logging in Planar-Stratified Biaxial Anisotropic Formations. Remote Sensing, 16(16), 3076. https://doi.org/10.3390/rs16163076








