Distributed Phased Multiple-Input Multiple-Output Radars for Early Warning: Observation Area Generation
Abstract
:1. Introduction
1.1. Related Works and Motivation
1.2. Contributions
- A mathematical model for evaluating the detection performance of distributed MIMO radars with widely separated phased array antennas is developed. This model considers the correlation of target echoes received in different channels by extending the target model in [29] from circle to sphere. Meanwhile, it also considers a ground clutter environment based on the bistatic radar clutter model in [30].
- An optimization strategy for the generation of observation areas is presented. There is an inherent trade-off under fixed detection coverage and performance requirements: a shorter beam dwell time demands increased transmit power. Although a shorter dwell time accelerates target detection, increased transmit power raises the risk of intercept. To balance radar detection efficiency and survivability, our optimization strategy minimizes the transmit power and beam dwell time of the nodes. In addition, we consider the worst case for targets to be detected, similar to [7].
- A two-stage method for solving the problem of observation area generation is proposed. To separately optimize the beamforming weights and the beam dwell time, we introduce the signal-to-clutter-plus-noise ratio (SCNR) as a criterion and a power factor as a variable. The first stage jointly optimizes the transmit and receive beamforming weights to balance the SCNRs of all transmit–receive channels at all cells under test (CUT) within an observation area. Linearized successive convex approximation (SCA) and trust region techniques [31] are used to solve this optimization problem. The second stage optimizes the power factor under various beam dwell times to scale down the transmit beamforming weights. A binary search method is used to build a Pareto solution set for the original problem.
2. System Model and Detection Performance
- Each node is equipped with a uniform planar array antenna and has an identical number of elements.
- For each node, the far-field assumption is valid, i.e., all elements of a node share the same beam propagation direction towards any target or CUT.
- The radar system is assumed to be perfectly calibrated, for example, using GPS satellites [32], allowing for the ignoring of time synchronization errors between different nodes.

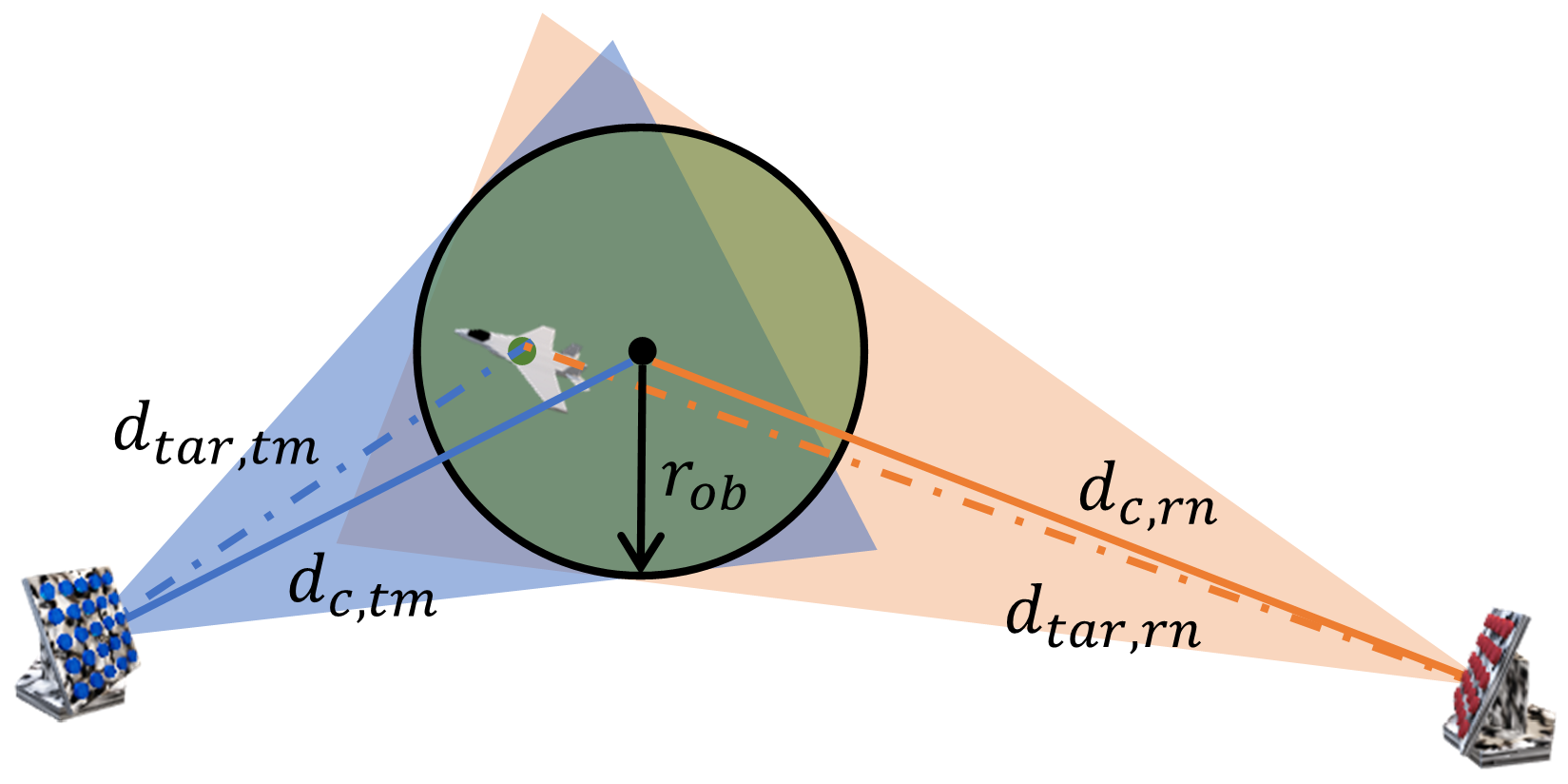
2.1. Target Echo Model
2.2. Ground Clutter Echo Model
2.3. Radar Detection Performance
3. Optimization Problem and Solving Method
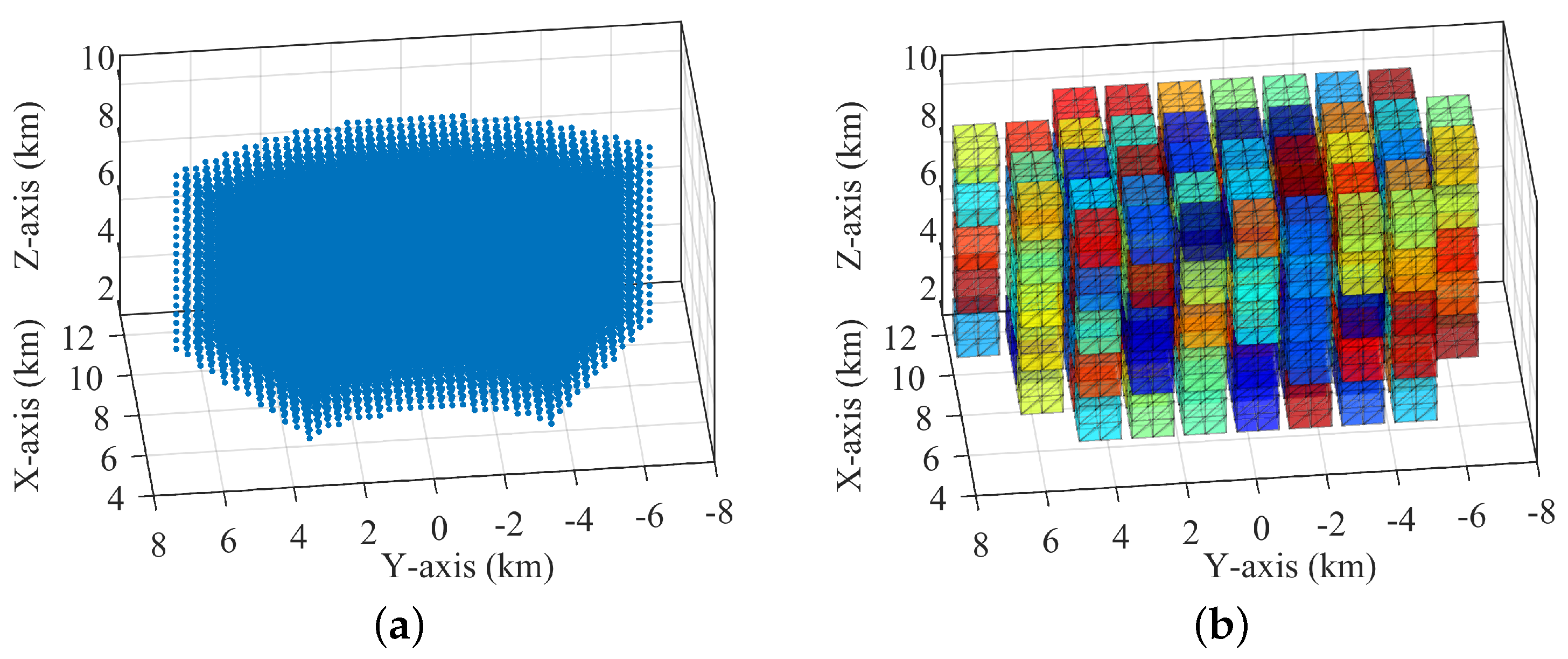
3.1. Observation Area Generation Problem
- Targets with a small RCS produce a low-power echo, making them less detectable.
- Targets moving at low speeds are more difficult to distinguish from ground clutter.
- Small targets produce high-correlated echoes, which can degrade the performance of a non-coherent accumulation detector.
3.2. Observation Area Generation Method
3.2.1. Local Similarity of Target Echo Power
3.2.2. Balanced SCNR Strategy
3.2.3. Selection of Initial Expansion Point
3.2.4. Linearization Method
3.2.5. Optimization of Transmit and Receive Beamforming Weights
- or .
- The iteration count has reached its maximum value.
| Algorithm 1: SCA-based method for the optimization of beamforming weights |
 |
3.2.6. Optimization of Transmit Power and Pulse Number
| Algorithm 2: Binary search for optimization of transmit power and pulse number |
 |
| Algorithm 3: Summary of the proposed method |
 |
3.2.7. Time Complexity
4. Simulation Result and Analysis
4.1. Influence of Initial Beamforming Weights
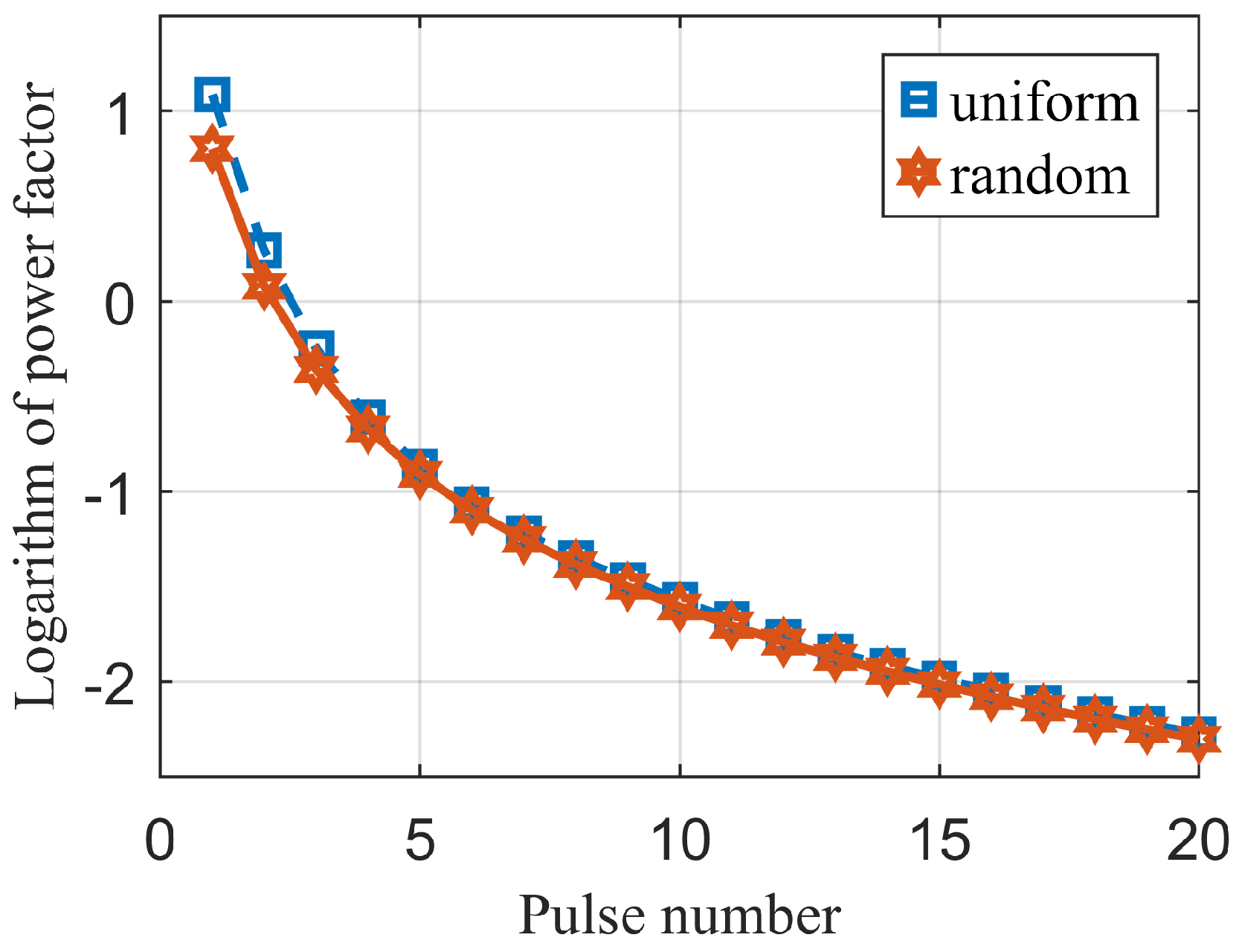
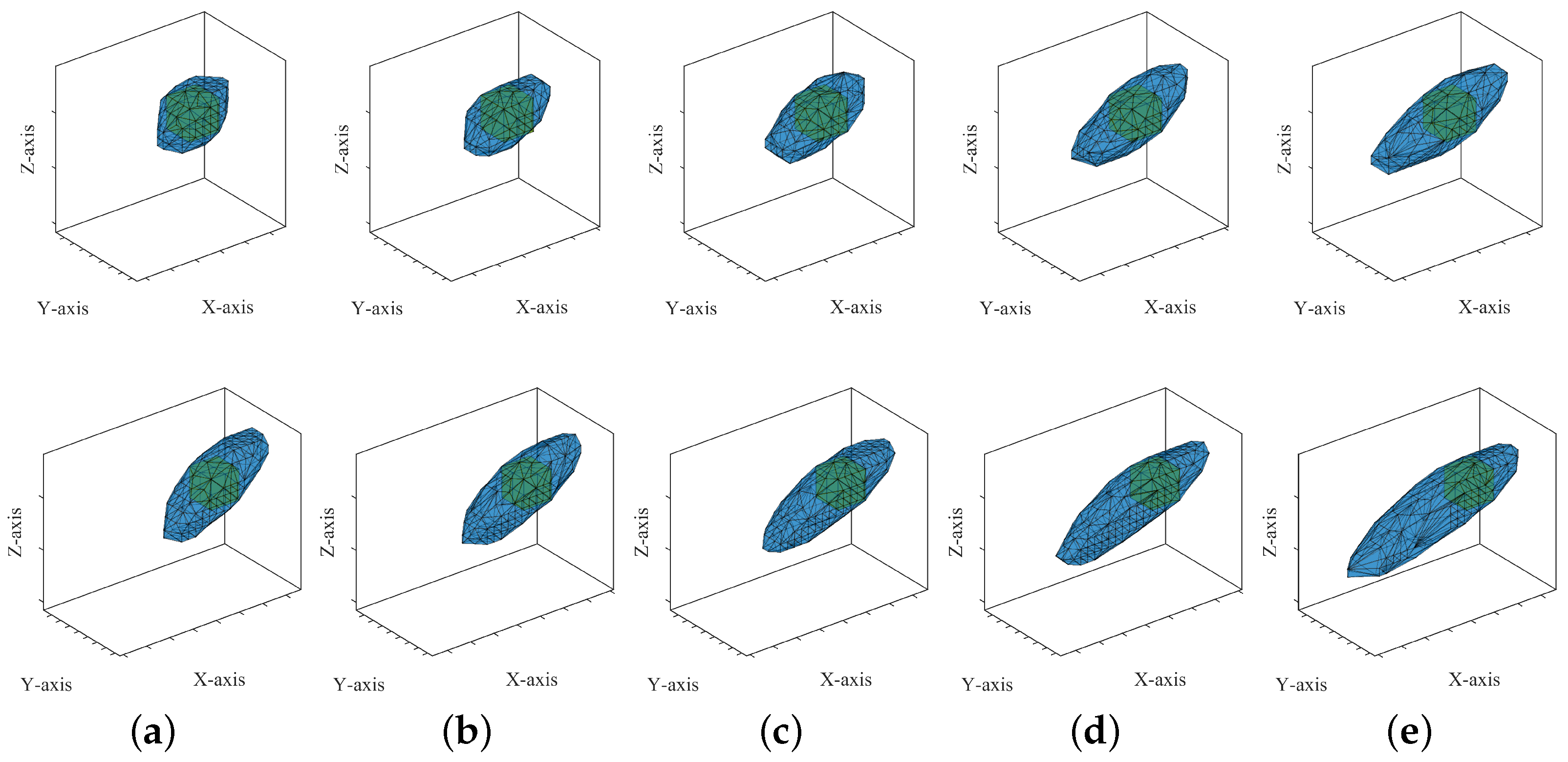
4.2. Influence of Pulse Number
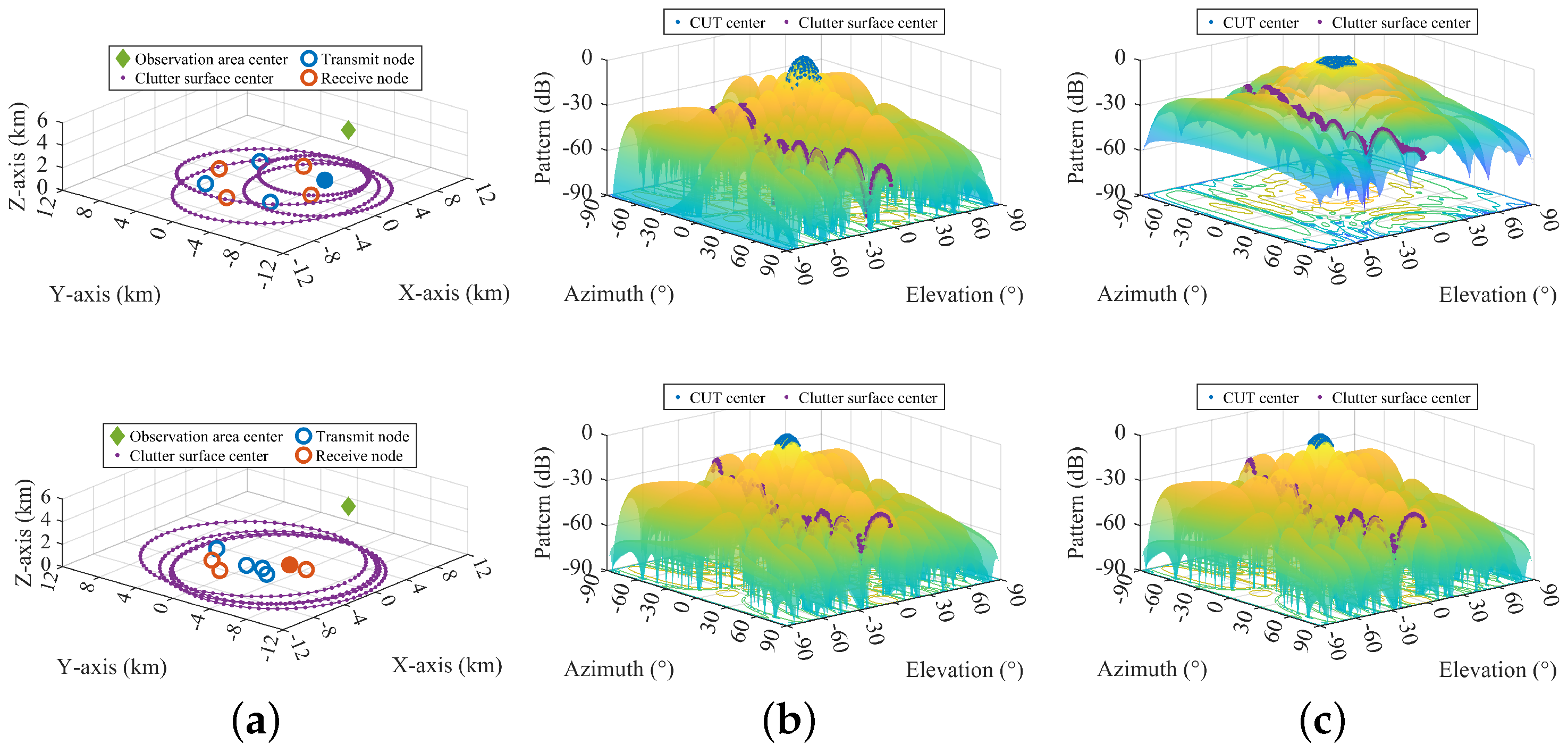
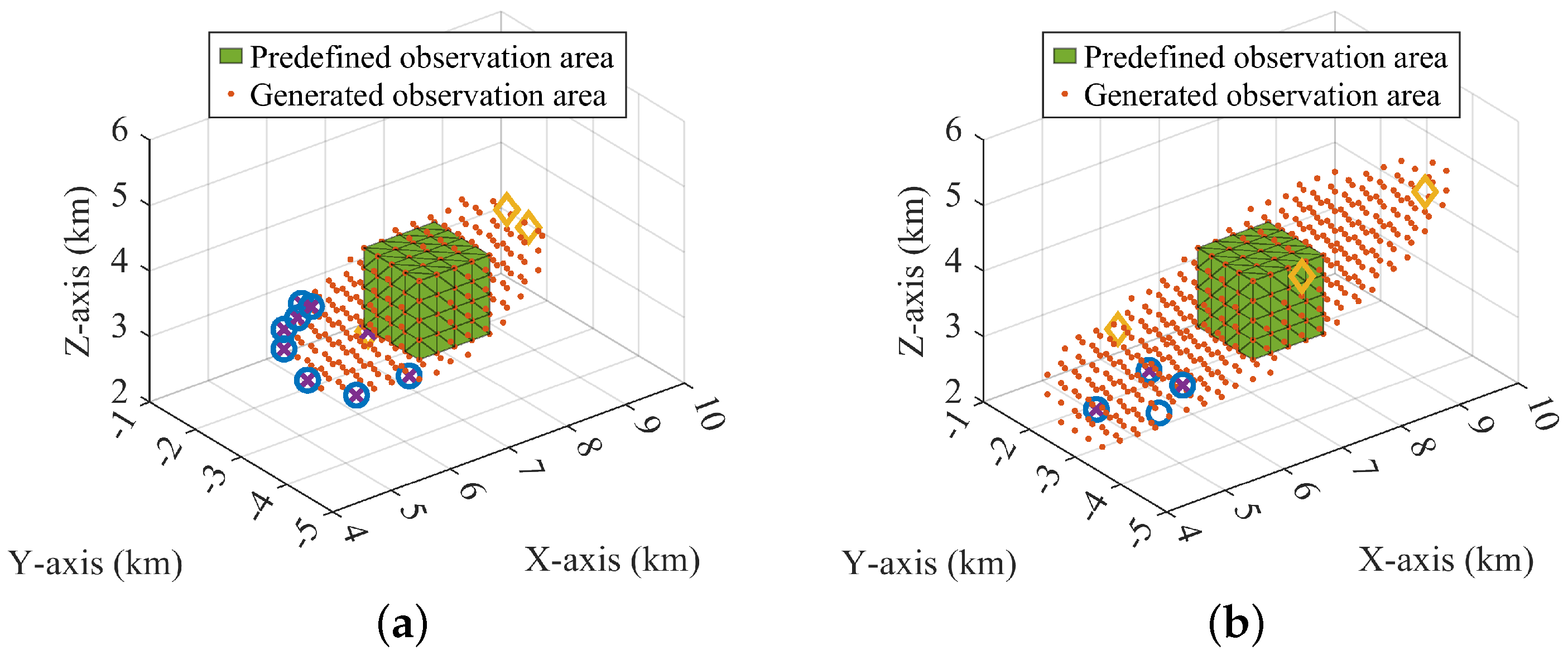
4.3. Influence of Observation Area Locations
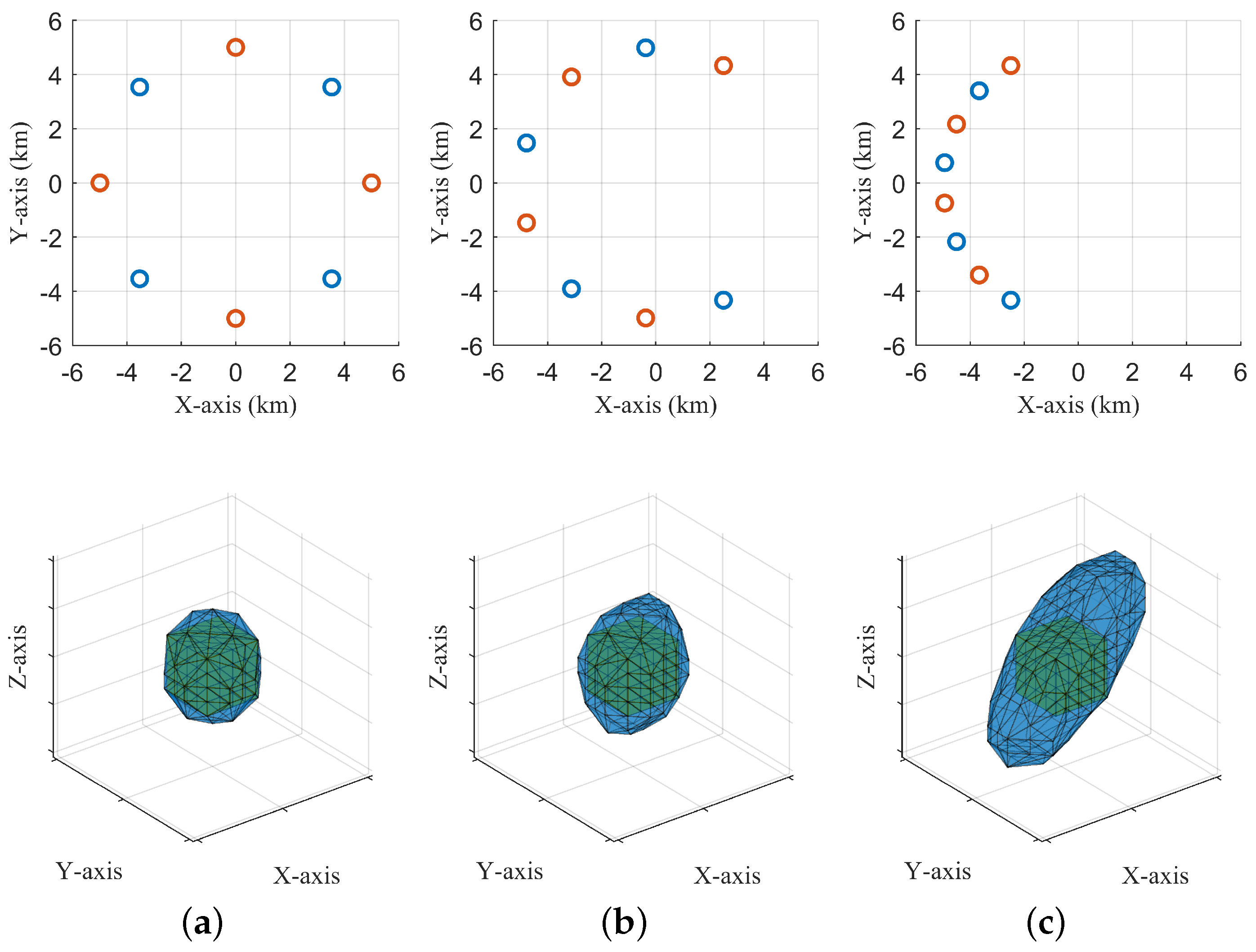
4.4. Influence of Node Location
5. Discussion
5.1. The Effectiveness of the Balanced SCNR Strategy
5.2. A Trade-Off between Beam Energy Utilization Efficiency and Scheduling Convenience
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Covariance of Matched Filter Outputs of Target Echo
Appendix A.1. Expression of
Appendix A.2. Analytical Form of
References
- Fishler, E.; Haimovich, A.; Blum, R.; Cimini, L.; Chizhik, D.; Valenzuela, R. Spatial diversity in radars-models and detection performance. IEEE Trans. Signal Process. 2006, 54, 823–838. [Google Scholar] [CrossRef]
- Haimovich, A.M.; Blum, R.S.; Cimini, L.J. MIMO radar with widely separated antennas. IEEE Signal Process. Mag. 2008, 25, 116–129. [Google Scholar] [CrossRef]
- Aittomaki, T.; Koivunen, V. Performance of MIMO radar with angular diversity under swerling. IEEE J. Sel. Top. Signal Process. 2010, 4, 101–114. [Google Scholar] [CrossRef]
- Qi, C.; Xie, J.; Zhang, H.; Ding, Z.; Yang, X. Optimal configuration of array elements for hybrid distributed PA-MIMO radar system based on target detection. Remote Sens. 2022, 14, 4129. [Google Scholar] [CrossRef]
- Sadeghi, M.; Behnia, F.; Amiri, R.; Farina, A. Target localization geometry gain in distributed MIMO Radar. IEEE Trans. Signal Process. 2021, 69, 1642–1652. [Google Scholar] [CrossRef]
- Rabideau, D.; Parker, P. Ubiquitous MIMO multifunction digital array radar. In Proceedings of the Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003; pp. 1057–1064. [Google Scholar]
- Luo, D.; Wen, G.; Liang, Y.; Zhu, L.; Song, H. Beam scheduling for early warning with distributed MIMO radars. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 6044–6058. [Google Scholar] [CrossRef]
- Chen, H.; Ta, S.; Sun, B. Cooperative game approach to power allocation for target tracking in distributed MIMO radar sensor networks. IEEE Syst. J. 2015, 15, 5423–5432. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.; Xie, J.; Zhang, Z.; Lu, W. Joint subarray selection and power allocation for cognitive target tracking in large-scale MIMO radar networks. IEEE Syst. J. 2020, 14, 2569–2580. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.; Zhang, Z.; Lu, W.; Xie, J. Joint target assignment and power allocation in multiple distributed MIMO radar networks. IEEE Syst. J. 2021, 15, 694–704. [Google Scholar] [CrossRef]
- Lu, X.; Yi, W.; Kong, L. LPI-Based transmit resource scheduling for target tracking with distributed MIMO radar systems. IEEE Trans. Veh. 2023, 72, 14230–14244. [Google Scholar] [CrossRef]
- Liang, Y.; Wen, G.; Zhu, L.; Luo, D.; Song, H. Detection power of a distributed MIMO radar system. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3463–3479. [Google Scholar] [CrossRef]
- Richards, M.A. Fundamentals of Radar Signal Processing; McGraw-Hill: New York, NY, USA, 2009. [Google Scholar]
- Fielding, J.E. Beam overlap impact on phased-array target detection. IEEE Trans. Aerosp. Electron. Syst. 1993, 29, 404–411. [Google Scholar] [CrossRef]
- Lu, J.; Hu, W.; Xiao, H.; Yu, W. Novel cued search strategy based on information gain for phased array radar. J. Syst. Eng. Electron. 2008, 19, 292–297. [Google Scholar]
- Hansen, R.C. Phased Array Antennas; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Mailloux, R.J. Phased Array Antenna Handbook; Artech House: Norwood, MA, USA, 2018. [Google Scholar]
- Wang, H.; Xu, L.; Yan, Z.; Gulliver, T.A. Low complexity MIMO-FBMC sparse channel parameter estimate for industrial big data communications. IEEE Trans. Ind. Informat. 2021, 17, 3422–3430. [Google Scholar] [CrossRef]
- Wu, J.; Shi, C.; Zhang, W.; Zhou, J. Joint beamforming design and power control game for a MIMO radar system in the presence of multiple jammers. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 759–773. [Google Scholar] [CrossRef]
- Ding, Z.; Xie, J. Joint transmit and receive beamforming for cognitive FDA-MIMO radar with moving target. IEEE Sens. J. 2021, 21, 20878–20885. [Google Scholar] [CrossRef]
- Zhou, J.; Li, H.; Cui, W. Joint design of transmit and receive beamforming for transmit subaperturing MIMO radar. IEEE Signal Process Lett. 2019, 26, 1648–1652. [Google Scholar] [CrossRef]
- Zhou, J.; Li, H.; Cui, W. Low-Complexity joint transmit and receive beamforming for MIMO radar with multi-targets. IEEE Signal Process Lett. 2022, 27, 1410–1414. [Google Scholar] [CrossRef]
- Faghand, E.; Mehrshahi, E.; Ghorashi, S.A. Complexity reduction in beamforming of uniform array antennas for MIMO radars. IEEE Trans. Radar Syst. 2023, 59, 413–422. [Google Scholar] [CrossRef]
- Huang, J.; Su, H.; Yang, Y. Robust adaptive beamforming for MIMO radar in the presence of covariance matrix estimation error and desired signal steering vector mismatch. IET Radar Sonar Navig. 2020, 14, 118–126. [Google Scholar] [CrossRef]
- Liu, R. Transmit-Receive beamforming for distributed phased-MIMO radar system. IEEE Trans. Veh. 2022, 71, 1439–1453. [Google Scholar] [CrossRef]
- Zhang, R.; Cheng, L.; Wang, S.; Lou, Y.; Gao, Y.; Wu, W.; Ng, D.W.K. Integrated sensing and communication with massive MIMO: A unified tensor approach for channel and target parameter estimation. IEEE Trans. Wirel. Commun. 2024, 23, 8571–8587. [Google Scholar] [CrossRef]
- Yu, X.; Alhujaili, K.; Cui, G.; Monga, V. MIMO radar waveform design in the presence of multiple targets and practical constraints. IEEE Trans. Signal Process. 2020, 68, 1974–1989. [Google Scholar] [CrossRef]
- Wang, X.; Guo, Y.; Wen, F. EMVS-MIMO radar with sparse Rx geometry: Tensor modeling and 2D direction finding. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 8062–8075. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, H.; Zhao, Y.; Hu, L. Target spatial and frequency scattering diversity property for diversity MIMO radar. Signal Process. 2011, 91, 269–276. [Google Scholar] [CrossRef]
- Pola, M.; Bezousek, P.; Pidanic, J. Model comparison of bistatic radar clutter. In Proceedings of the 2013 Conference on Microwave Techniques (COMITE), Pardubice, Czech Republic, 17–18 April 2013; pp. 182–185. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer: New York, NY, USA, 2006. [Google Scholar]
- Weiss, M. Synchronization of bistatic radar systems. In Proceedings of the IGARSS 2004, 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; pp. 1750–1753. [Google Scholar]
- Goldstein, H.; Poole, C.P.; Safko, J.L. Classical Mechanics; Wesley: San Francisco, CA, USA, 2002. [Google Scholar]
- Agatonović, M.; Stanković, Z.; Dončov, N.; Sit, L.; Milovanović, B.; Zwick, T. Application of artificial neural networks for efficient high-resolution 2D DOA estimation. Radioengineering 2012, 21, 1178–1186. [Google Scholar]
- Barton, D.K. Radar Equations for Modern Radar; Artech House: Boston, MA, USA, 2013. [Google Scholar]
- Zhang, H.; Xie, J.; Shi, J.; Zhang, Z.; Fu, X.; Zwick, T. Sensor scheduling and resource allocation in distributed MIMO radar for joint target tracking and detection. IEEE Access 2019, 7, 62387–62400. [Google Scholar] [CrossRef]
- Bodenham, D.A.; Adams, M.N. A comparison of efficient approximations for a weighted sum of chi-squared random variables. Stat. Comput. 2016, 26, 917–928. [Google Scholar] [CrossRef]
- Yang, S.; Yi, W.; Jakobsson, A. Multitarget detection strategy for distributed MIMO radar with widely separated antennas. IEEE Trans. Geosci. 2022, 60, 5113516. [Google Scholar] [CrossRef]
- Radmard, M.; Chitgarha, M.M.; Majd, M.N.; Nayebi, M.M. Anenna placement and power allocation optimization in mimo detection. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1468–1478. [Google Scholar] [CrossRef]
- Hu, Q.; Su, H.; Zhou, S.; Liu, Z. Target detection with SNR diversity for distributed MIMO radar. In Proceedings of the 2015 IEEE Radar Conference, Johannesburg, South Africa, 27–30 October 2015; pp. 87–90. [Google Scholar]
- Liu, H.; Zhou, S.; Su, H.; Yu, Y. Detection performance of spatial-frequency diversity MIMO radar. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 3137–3155. [Google Scholar]
- Yang, Y.; Cui, G.; Yi, W. Distributed MIMO radar detection with channel evaluation and selection strategy. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 1214–1217. [Google Scholar]
- Dinkelbach, W. On nonlinear fractional programming. Manag. Sci. 1967, 13, 492–498. [Google Scholar] [CrossRef]
- Rajagopal, S. Beam broadening for phased antenna arrays using multi-beam subarrays. In Proceedings of the 2012 IEEE International Conference on Communications (ICC), Ottawa, ON, Canada, 10–15 June 2012; pp. 3637–3642. [Google Scholar]
- Remmert, R. Theory of Complex Functions; Springer: New York, NY, USA, 1991. [Google Scholar]
- Long, M.W. Radar Reflectivity of Land and Sea; Artech House: Boston, MA, USA, 2001. [Google Scholar]
- Lishchenko, V.; Khudov, H.; Tahyan, K.; Sapegin, E.; Zvonko, A.; Serdiuk, O. Method of the detection quality improving by complexing of the same synchronous radars into multi-radar system. In Proceedings of the 2022 IEEE 41st International Conference on Electronics and Nanotechnology (ELNANO), Kyiv, Ukraine, 10–14 October 2022; pp. 496–499. [Google Scholar]
- Barkat, M.; Varshney, P.K. Decentralized CFAR signal detection. IEEE Trans. Aerosp. Electron. Syst. 1989, 25, 141–149. [Google Scholar] [CrossRef]






| Notation | Meaning |
| conjugate operation | |
| conjugate transpose operation | |
| transpose operation | |
| extract the maximum element | |
| extract the minimum element | |
| round down to the closest integer | |
| arc cosine function | |
| arc tangent function | |
| ⊗ | Kronecker product |
| ⊙ | element-wise multiplication |
| statistical expectation | |
| block diagonal matrix created by the elements | |
| Symbol | Meaning |
| a set of positive integers | |
| a set of complex numbers | |
| global rectangular coordinates | |
| local rectangular coordinates | |
| spherical coordinates (in a node coordinate system) | |
| spherical coordinates (in a target coordinate system) | |
| global azimuth angle | |
| global elevation angle | |
| unit matrix/identity matrix |
| NODE | Symbol | Meaning | Value |
| element number in column | 10 | ||
| element number in row | 10 | ||
| U | total element number | 100 | |
| 3 dB beam width in elevation | 180° | ||
| 3 dB beam width in azimuth | 180° | ||
| element maximum transmit power | 50 W | ||
| carrier frequency | 1 GHz | ||
| pulse repetition interval | 1 ms | ||
| system loss | 4 dB | ||
| noise bandwidth | 0.5 MHz | ||
| TARGET | Symbol | Meaning | Value |
| minimum velocity | 170 km/h | ||
| maximum velocity | 1080 km/h | ||
| minimum RCS | 1 m2 | ||
| target size | 1 m | ||
| OTHERS | Symbol | Meaning | Value |
| angle interval of clutter surfaces | 5° | ||
| edge length of CUTs | 300 m | ||
| wind speed | 1.25 m/h | ||
| threshold of detection performance | 0.9 | ||
| false alarm probability | 1 × 10−6 | ||
| normalized reflectivity parameter | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, D.; Wen, G. Distributed Phased Multiple-Input Multiple-Output Radars for Early Warning: Observation Area Generation. Remote Sens. 2024, 16, 3052. https://doi.org/10.3390/rs16163052
Luo D, Wen G. Distributed Phased Multiple-Input Multiple-Output Radars for Early Warning: Observation Area Generation. Remote Sensing. 2024; 16(16):3052. https://doi.org/10.3390/rs16163052
Chicago/Turabian StyleLuo, Dengsanlang, and Gongjian Wen. 2024. "Distributed Phased Multiple-Input Multiple-Output Radars for Early Warning: Observation Area Generation" Remote Sensing 16, no. 16: 3052. https://doi.org/10.3390/rs16163052
APA StyleLuo, D., & Wen, G. (2024). Distributed Phased Multiple-Input Multiple-Output Radars for Early Warning: Observation Area Generation. Remote Sensing, 16(16), 3052. https://doi.org/10.3390/rs16163052






