Downscaling TRMM Monthly Precipitation in Cloudy and Rainy Regions and Analyzing Spatiotemporal Variations: A Case Study in the Dongting Lake Basin
Abstract
:1. Introduction
2. Materials and Methods
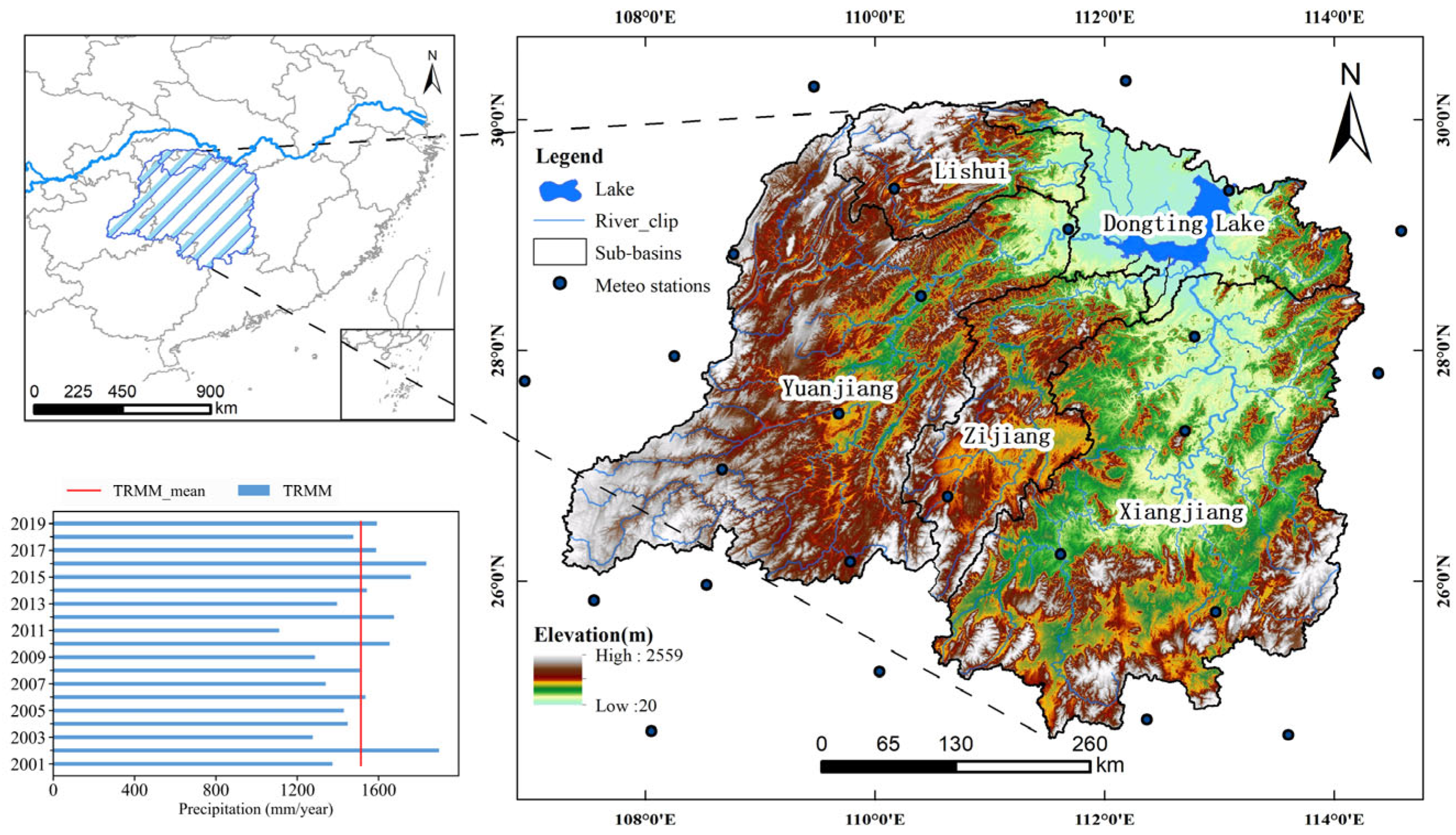
2.1. Overview of the Study Area
2.2. Data Sources
2.2.1. Satellite Precipitation Data
2.2.2. Vegetation Data
2.2.3. Cloud Cover Data
2.2.4. Topographic Data
2.2.5. Meteorological Station Precipitation Observation Data
2.3. Research Methods
2.3.1. Downscaling Algorithm
2.3.2. Downscaling Framework
2.3.3. Downscaling Evaluation Method
2.3.4. Precipitation Trend Analysis Method
3. Results and Analysis
3.1. Feature Importance
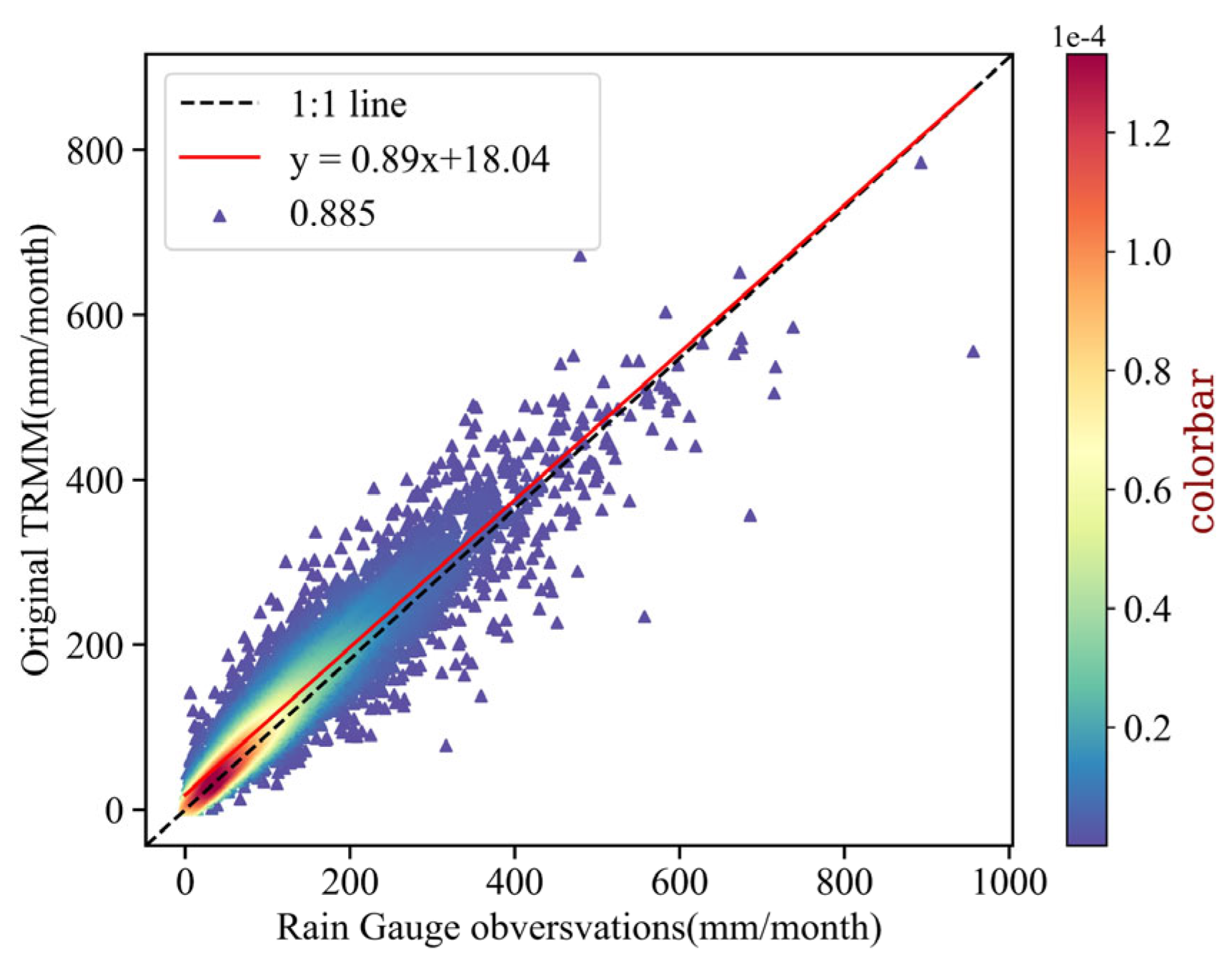
3.2. Suitability Analysis of Original TRMM Data
3.3. Accuracy Evaluation Analysis of Different Downscaling Strategies
3.4. Downscaling Results and Their Spatiotemporal Distribution Characteristics
3.5. Precipitation Variation Trends in the Dongting Lake Basin
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Langella, G.; Basile, A.; Bonfante, A.; Terribile, F. High-Resolution Space–Time Rainfall Analysis Using Integrated ANN Inference Systems. J. Hydrol. 2010, 387, 328–342. [Google Scholar] [CrossRef]
- Li, M.; Shao, Q. An Improved Statistical Approach to Merge Satellite Rainfall Estimates and Raingauge Data. J. Hydrol. 2010, 385, 51–64. [Google Scholar] [CrossRef]
- Wu, C.; Chen, J.M. The Use of Precipitation Intensity in Estimating Gross Primary Production in Four Northern Grasslands. J. Arid Environ. 2012, 82, 11–18. [Google Scholar] [CrossRef]
- Li, Q.; Cao, Y.; Miao, S.; Huang, X. Spatiotemporal Characteristics of Drought and Wet Events and Their Impacts on Agriculture in the Yellow River Basin. Land 2022, 11, 556. [Google Scholar] [CrossRef]
- Brunner, M.I.; Swain, D.L.; Wood, R.R.; Willkofer, F.; Done, J.M.; Gilleland, E.; Ludwig, R. An Extremeness Threshold Determines the Regional Response of Floods to Changes in Rainfall Extremes. Commun. Earth Environ. 2021, 2, 173. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical Approaches for Incorporating Elevation into the Spatial Interpolation of Rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Ly, S.; Charles, C.; Degré, A. Different Methods for Spatial Interpolation of Rainfall Data for Operational Hydrology and Hydrological Modeling at Watershed Scale: A Review. Biotechnol. Agron. Société Environ. 2013, 17, 392–406. [Google Scholar]
- Jiang, S.; Ren, L.; Hong, Y.; Yong, B.; Yang, X.; Yuan, F.; Ma, M. Comprehensive Evaluation of Multi-Satellite Precipitation Products with a Dense Rain Gauge Network and Optimally Merging Their Simulated Hydrological Flows Using the Bayesian Model Averaging Method. J. Hydrol. 2012, 452–453, 213–225. [Google Scholar] [CrossRef]
- Henn, B.; Newman, A.J.; Livneh, B.; Daly, C.; Lundquist, J.D. An Assessment of Differences in Gridded Precipitation Datasets in Complex Terrain. J. Hydrol. 2018, 556, 1205–1219. [Google Scholar] [CrossRef]
- Gao, Z.; Long, D.; Tang, G.; Zeng, C.; Huang, J.; Hong, Y. Assessing the Potential of Satellite-Based Precipitation Estimates for Flood Frequency Analysis in Ungauged or Poorly Gauged Tributaries of China’s Yangtze River Basin. J. Hydrol. 2017, 550, 478–496. [Google Scholar] [CrossRef]
- Hu, Q.; Li, Z.; Wang, L.; Huang, Y.; Wang, Y.; Li, L. Rainfall Spatial Estimations: A Review from Spatial Interpolation to Multi-Source Data Merging. Water 2019, 11, 579. [Google Scholar] [CrossRef]
- Skaugen, T.; Andersen, J. Simulated Precipitation Fields with Variance-Consistent Interpolation. Hydrol. Sci. J. 2010, 55, 676–686. [Google Scholar] [CrossRef]
- Xu, S.; Wu, C.; Wang, L.; Gonsamo, A.; Shen, Y.; Niu, Z. A New Satellite-Based Monthly Precipitation Downscaling Algorithm with Non-Stationary Relationship between Precipitation and Land Surface Characteristics. Remote Sens. Environ. 2015, 162, 119–140. [Google Scholar] [CrossRef]
- Zhang, T.; Li, B.; Yuan, Y.; Gao, X.; Sun, Q.; Xu, L.; Jiang, Y. Spatial Downscaling of TRMM Precipitation Data Considering the Impacts of Macro-Geographical Factors and Local Elevation in the Three-River Headwaters Region. Remote Sens. Environ. 2018, 215, 109–127. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Petersen, W.A.; Berg, W.; Kidd, C.; Stocker, E.F.; Kirschbaum, D.B.; Kakar, R.; Braun, S.A.; Huffman, G.J.; Iguchi, T.; et al. The Global Precipitation Measurement (GPM) Mission for Science and Society. Bull. Am. Meteorol. Soc. 2017, 98, 1679–1695. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Arkin, P.; Chang, A.; Ferraro, R.; Gruber, A.; Janowiak, J.; McNab, A.; Rudolf, B.; Schneider, U. The Global Precipitation Climatology Project (GPCP) Combined Precipitation Dataset. Bull. Am. Meteorol. Soc. 1997, 78, 5–20. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Kubota, T.; Shige, S.; Hashizume, H.; Aonashi, K.; Takahashi, N.; Seto, S.; Hirose, M.; Takayabu, Y.N.; Ushio, T.; Nakagawa, K.; et al. Global Precipitation Map Using Satellite-Borne Microwave Radiometers by the GSMaP Project: Production and Validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Sanchez-Moreno, J.F.; Mannaerts, C.M.; Jetten, V. Applicability of Satellite Rainfall Estimates for Erosion Studies in Small Offshore Areas: A Case Study in Cape Verde Islands. CATENA 2014, 121, 365–374. [Google Scholar] [CrossRef]
- Liu, X.C.; Zhao, J.J.; Zhang, H.Y.; Guo, X.Y.; Zhang, Z.X.; Fu, Y.Y. Accuracy Verification and Application of TRMM Precipitation Data in Northeast China. J. Nat. Resour. 2015, 30, 1047–1056. [Google Scholar] [CrossRef]
- Fang, J.; Yang, W.; Luan, Y.; Du, J.; Lin, A.; Zhao, L. Evaluation of the TRMM 3B42 and GPM IMERG Products for Extreme Precipitation Analysis over China. Atmos. Res. 2019, 223, 24–38. [Google Scholar] [CrossRef]
- Gebremichael, M.; Krajewski, W.F.; Over, T.M.; Takayabu, Y.N.; Arkin, P.; Katayama, M. Scaling of Tropical Rainfall as Observed by TRMM Precipitation Radar. Atmos. Res. 2008, 88, 337–354. [Google Scholar] [CrossRef]
- Sorooshian, S.; AghaKouchak, A.; Arkin, P.; Eylander, J.; Foufoula-Georgiou, E.; Harmon, R.; Hendrickx, J.M.H.; Imam, B.; Kuligowski, R.; Skahill, B.; et al. Advanced Concepts on Remote Sensing of Precipitation at Multiple Scales. Bull. Am. Meteorol. Soc. 2011, 92, 1353–1357. [Google Scholar] [CrossRef]
- Yan, X.; Chen, H.; Tian, B.; Sheng, S.; Wang, J.; Kim, J.-S. A Downscaling–Merging Scheme for Improving Daily Spatial Precipitation Estimates Based on Random Forest and Cokriging. Remote Sens. 2021, 13, 2040. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Rutten, M.M.; Droogers, P. Spatial Downscaling of TRMM Precipitation Using Vegetative Response on the Iberian Peninsula. Remote Sens. Environ. 2009, 113, 362–370. [Google Scholar] [CrossRef]
- Ghorbanpour, A.K.; Hessels, T.; Moghim, S.; Afshar, A. Comparison and Assessment of Spatial Downscaling Methods for Enhancing the Accuracy of Satellite-Based Precipitation over Lake Urmia Basin. J. Hydrol. 2021, 596, 126055. [Google Scholar] [CrossRef]
- Wang, H.; Zang, F.; Zhao, C.; Liu, C. A GWR Downscaling Method to Reconstruct High-Resolution Precipitation Dataset Based on GSMaP-Gauge Data: A Case Study in the Qilian Mountains, Northwest China. Sci. Total Environ. 2022, 810, 152066. [Google Scholar] [CrossRef]
- Elnashar, A.; Zeng, H.; Wu, B.; Zhang, N.; Tian, F.; Zhang, M.; Zhu, W.; Yan, N.; Chen, Z.; Sun, Z.; et al. Downscaling TRMM Monthly Precipitation Using Google Earth Engine and Google Cloud Computing. Remote Sens. 2020, 12, 3860. [Google Scholar] [CrossRef]
- Arshad, A.; Zhang, W.; Zhang, Z.; Wang, S.; Zhang, B.; Cheema, M.J.M.; Shalamzari, M.J. Reconstructing High-Resolution Gridded Precipitation Data Using an Improved Downscaling Approach over the High Altitude Mountain Regions of Upper Indus Basin (UIB). Sci. Total Environ. 2021, 784, 147140. [Google Scholar] [CrossRef] [PubMed]
- Foody, G.M. Geographical Weighting as a Further Refinement to Regression Modelling: An Example Focused on the NDVI–Rainfall Relationship. Remote Sens. Environ. 2003, 88, 283–293. [Google Scholar] [CrossRef]
- Li, B.; Tao, S.; Dawson, R.W. Relations between AVHRR NDVI and Ecoclimatic Parameters in China. Int. J. Remote Sens. 2002, 23, 989–999. [Google Scholar] [CrossRef]
- Quiroz, R.; Yarlequé, C.; Posadas, A.; Mares, V.; Immerzeel, W.W. Improving Daily Rainfall Estimation from NDVI Using a Wavelet Transform. Environ. Model. Softw. 2011, 26, 201–209. [Google Scholar] [CrossRef]
- Xu, K.J.; Zeng, H.D.; Zhang, Z.D.; Xie, J.S.; Yang, Y.S. Remote Sensing Analysis of the Correlation Between Forest Growing Season and Temperature and Precipitation in Subtropical Fujian Province. J. Geoinf. Sci. 2015, 17, 1249–1259. [Google Scholar]
- Zhang, Q.; Li, Y.Q.; Yang, Y.Y. Review of Research Progress on Cloud Cover and Its Relationship with Precipitation in China. Plateau Mt. Meteorol. Res. 2011, 31, 79–83. [Google Scholar] [CrossRef]
- Braga, R.C.; Rosenfeld, D.; Krüger, O.O.; Ervens, B.; Holanda, B.A.; Wendisch, M.; Krisna, T.; Pöschl, U.; Andreae, M.O.; Voigt, C.; et al. Linear Relationship between Effective Radius and Precipitation Water Content near the Top of Convective Clouds: Measurement Results from ACRIDICON–CHUVA Campaign. Atmos. Chem. Phys. 2021, 21, 14079–14088. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Feingold, G. On the Relationship between Open Cellular Convective Cloud Patterns and the Spatial Distribution of Precipitation. Atmos. Chem. Phys. 2015, 15, 1237–1251. [Google Scholar] [CrossRef]
- Liu, Y.; Xi, D.-G.; Li, Z.-L.; Shi, C.-X. Analysis and Application of the Relationship between Cumulonimbus (Cb) Cloud Features and Precipitation Based on FY-2C Image. Atmosphere 2014, 5, 211–229. [Google Scholar] [CrossRef]
- Mahmoud, M.T.; Mohammed, S.A.; Hamouda, M.A.; Mohamed, M.M. Impact of Topography and Rainfall Intensity on the Accuracy of IMERG Precipitation Estimates in an Arid Region. Remote Sens. 2020, 13, 13. [Google Scholar] [CrossRef]
- Badas, M.G.; Deidda, R.; Piga, E. Orographic Influences in Rainfall Downscaling. Adv. Geosci. 2005, 2, 285–292. [Google Scholar] [CrossRef]
- Kileshye Onema, J.-M.; Taigbenu, A. NDVI–Rainfall Relationship in the Semliki Watershed of the Equatorial Nile. Phys. Chem. Earth Parts A/B/C 2009, 34, 711–721. [Google Scholar] [CrossRef]
- Jia, S.; Zhu, W.; Lű, A.; Yan, T. A Statistical Spatial Downscaling Algorithm of TRMM Precipitation Based on NDVI and DEM in the Qaidam Basin of China. Remote Sens. Environ. 2011, 115, 3069–3079. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Hamed, K.H.; Rao, A.R. A Modified Mann-Kendall Trend Test for Autocorrelated Data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Hamed, K.H. Trend Detection in Hydrologic Data: The Mann–Kendall Trend Test under the Scaling Hypothesis. J. Hydrol. 2008, 349, 350–363. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Ji, X.; Luo, X.; Li, X. Fine-Resolution Precipitation Mapping in a Mountainous Watershed: Geostatistical Downscaling of TRMM Products Based on Environmental Variables. Remote Sens. 2018, 10, 119. [Google Scholar] [CrossRef]
- Peng, S.; Ding, Y.; Liu, W.; Li, Z. 1 Km Monthly Temperature and Precipitation Dataset for China from 1901 to 2017. Earth Syst. Sci. Data 2019, 11, 1931–1946. [Google Scholar] [CrossRef]
- Jing, W.; Yang, Y.; Yue, X.; Zhao, X. A Spatial Downscaling Algorithm for Satellite-Based Precipitation over the Tibetan Plateau Based on NDVI, DEM, and Land Surface Temperature. Remote Sens. 2016, 8, 655. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W.G.M. First Results from Version 7 TRMM 3B43 Precipitation Product in Combination with a New Downscaling–Calibration Procedure. Remote Sens. Environ. 2013, 131, 1–13. [Google Scholar] [CrossRef]
- Ji, L.; Peters, A.J. Lag and Seasonality Considerations in Evaluating AVHRR NDVI Response to Precipitation. Photogramm. Eng. Remote Sens. 2005, 71, 1053–1061. [Google Scholar] [CrossRef]
- Shen, Z.; Yong, B. Downscaling the GPM-Based Satellite Precipitation Retrievals Using Gradient Boosting Decision Tree Approach over Mainland China. J. Hydrol. 2021, 602, 126803. [Google Scholar] [CrossRef]
- Mutanga, O.; Masenyama, A.; Sibanda, M. Spectral Saturation in the Remote Sensing of High-Density Vegetation Traits: A Systematic Review of Progress, Challenges, and Prospects. ISPRS J. Photogramm. Remote Sens. 2023, 198, 297–309. [Google Scholar] [CrossRef]
- Garroutte, E.L.; Hansen, A.J.; Lawrence, R.L. Using NDVI and EVI to Map Spatiotemporal Variation in the Biomass and Quality of Forage for Migratory Elk in the Greater Yellowstone Ecosystem. Remote Sens. 2016, 8, 404. [Google Scholar] [CrossRef]
- Shi, Y.; Song, L.; Xia, Z.; Lin, Y.; Myneni, R.B.; Choi, S.; Wang, L.; Ni, X.; Lao, C.; Yang, F. Mapping Annual Precipitation across Mainland China in the Period 2001–2010 from TRMM3B43 Product Using Spatial Downscaling Approach. Remote Sens. 2015, 7, 5849–5878. [Google Scholar] [CrossRef]










| Month | Lon | Lat | Cloud_freq | EVI | NDVI | Elev |
|---|---|---|---|---|---|---|
| 1 | 36.76% | 40.87% | 7.79% | 2.92% | 6.64% | 5.03% |
| 2 | 26.81% | 60.52% | 3.38% | 2.22% | 2.95% | 4.12% |
| 3 | 33.34% | 55.97% | 3.08% | 2.11% | 2.48% | 3.02% |
| 4 | 36.75% | 48.67% | 4.14% | 2.55% | 2.82% | 5.08% |
| 5 | 42.31% | 34.88% | 9.83% | 3.57% | 3.72% | 5.68% |
| 6 | 49.17% | 31.49% | 7.38% | 2.55% | 3.25% | 6.17% |
| 7 | 43.83% | 39.24% | 6.70% | 3.02% | 2.45% | 4.76% |
| 8 | 39.84% | 38.99% | 5.56% | 3.62% | 3.34% | 8.65% |
| 9 | 35.03% | 41.26% | 6.22% | 4.57% | 4.11% | 8.82% |
| 10 | 36.56% | 37.89% | 15.26% | 2.13% | 4.77% | 3.39% |
| 11 | 39.14% | 41.24% | 10.00% | 1.92% | 3.35% | 4.35% |
| 12 | 35.62% | 44.43% | 7.55% | 3.48% | 4.04% | 4.87% |
| Month | ccoef | RMSE |
|---|---|---|
| 1 | 0.822778 | 17.4107 |
| 2 | 0.866163 | 18.9472 |
| 3 | 0.879001 | 26.51058 |
| 4 | 0.849754 | 36.51156 |
| 5 | 0.826795 | 47.1467 |
| 6 | 0.894293 | 48.53282 |
| 7 | 0.886362 | 44.43203 |
| 8 | 0.803994 | 44.53409 |
| 9 | 0.808776 | 32.59009 |
| 10 | 0.866147 | 19.80569 |
| 11 | 0.86226 | 21.33393 |
| 12 | 0.838474 | 14.87215 |
| Strategy | Monthly | Multi-Year Monthly |
|---|---|---|
| Description | The downscaling model is trained using the sample data from each month of the current year. Twelve models are trained annually, one for each month, to downscale precipitation for the corresponding periods. | All samples from 2001 to 2019 are aggregated. The model for each month is trained using the long-term sample set of that month, resulting in twelve models in total, each applied to the corresponding month’s precipitation downscaling for each year. |
| H | Variation Types | ||
|---|---|---|---|
| <−0.0005 | ≥1.96 | >0.5 | Significantly reduced |
| <−0.0005 | −1.96~1.96 | >0.5 | Slightly reduced |
| −0.0005–0.0005 | −1.96~1.96 | >0.5 | Stable and unchanged |
| ≥0.0005 | −1.96~1.96 | >0.5 | Slight increase |
| ≥0.0005 | <−1.96 | >0.5 | Significant increase |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, H.; Peng, H.; Zhai, J.; Gao, H.; Jin, D.; Xiao, S. Downscaling TRMM Monthly Precipitation in Cloudy and Rainy Regions and Analyzing Spatiotemporal Variations: A Case Study in the Dongting Lake Basin. Remote Sens. 2024, 16, 2959. https://doi.org/10.3390/rs16162959
Xia H, Peng H, Zhai J, Gao H, Jin D, Xiao S. Downscaling TRMM Monthly Precipitation in Cloudy and Rainy Regions and Analyzing Spatiotemporal Variations: A Case Study in the Dongting Lake Basin. Remote Sensing. 2024; 16(16):2959. https://doi.org/10.3390/rs16162959
Chicago/Turabian StyleXia, Haonan, Huanhua Peng, Jun Zhai, Haifeng Gao, Diandian Jin, and Sijia Xiao. 2024. "Downscaling TRMM Monthly Precipitation in Cloudy and Rainy Regions and Analyzing Spatiotemporal Variations: A Case Study in the Dongting Lake Basin" Remote Sensing 16, no. 16: 2959. https://doi.org/10.3390/rs16162959
APA StyleXia, H., Peng, H., Zhai, J., Gao, H., Jin, D., & Xiao, S. (2024). Downscaling TRMM Monthly Precipitation in Cloudy and Rainy Regions and Analyzing Spatiotemporal Variations: A Case Study in the Dongting Lake Basin. Remote Sensing, 16(16), 2959. https://doi.org/10.3390/rs16162959







