MGCET: MLP-mixer and Graph Convolutional Enhanced Transformer for Hyperspectral Image Classification
Abstract
1. Introduction
Motivation and Contribution
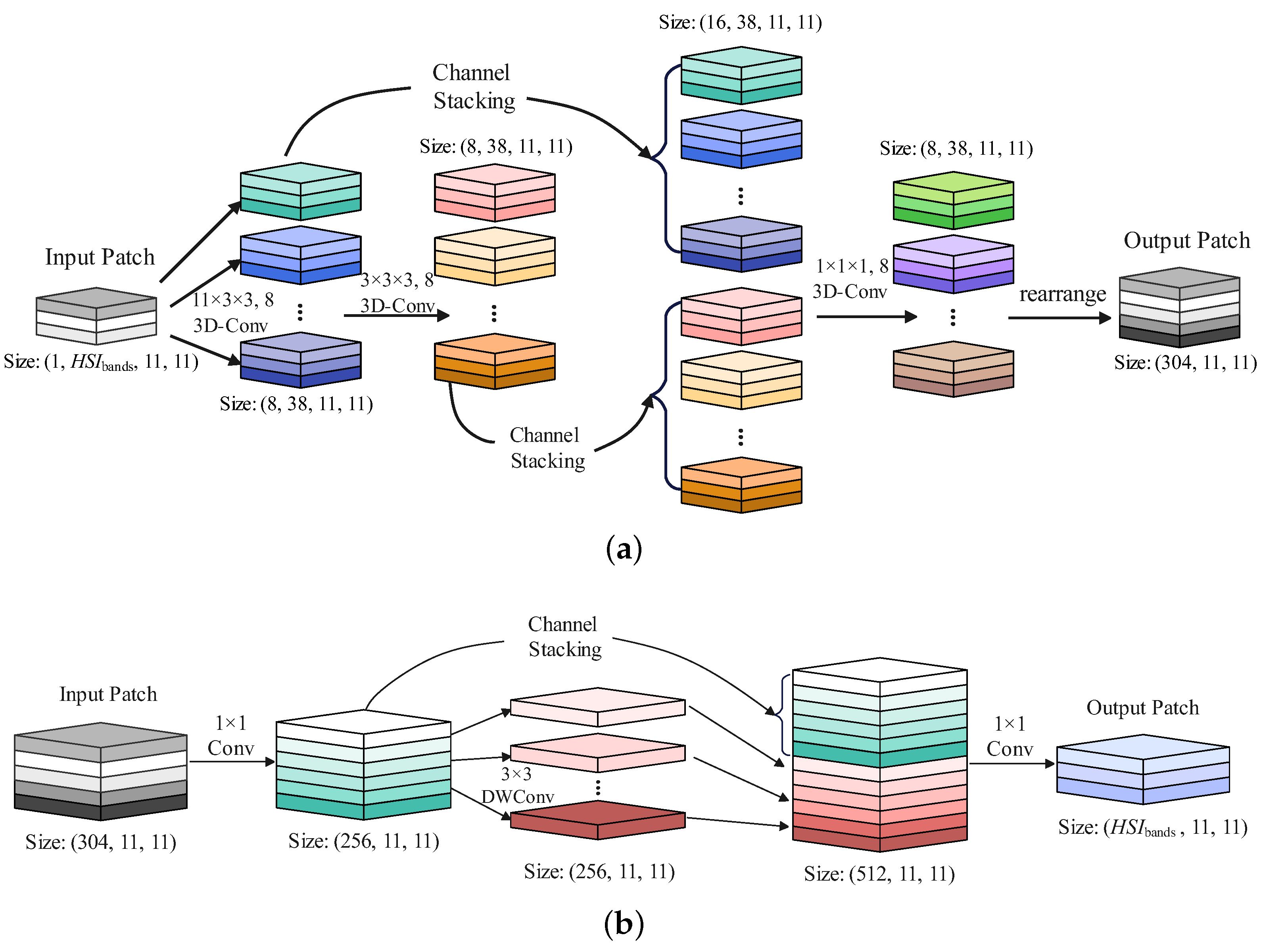
- A spatial-spectral extraction block (SSEB) module for efficient extraction of spatial-spectral features is suggested, to extract deep spatial-spectral features and localized spatial-spectral features using a 3D-convolution module and a 2D-convolution module, respectively.
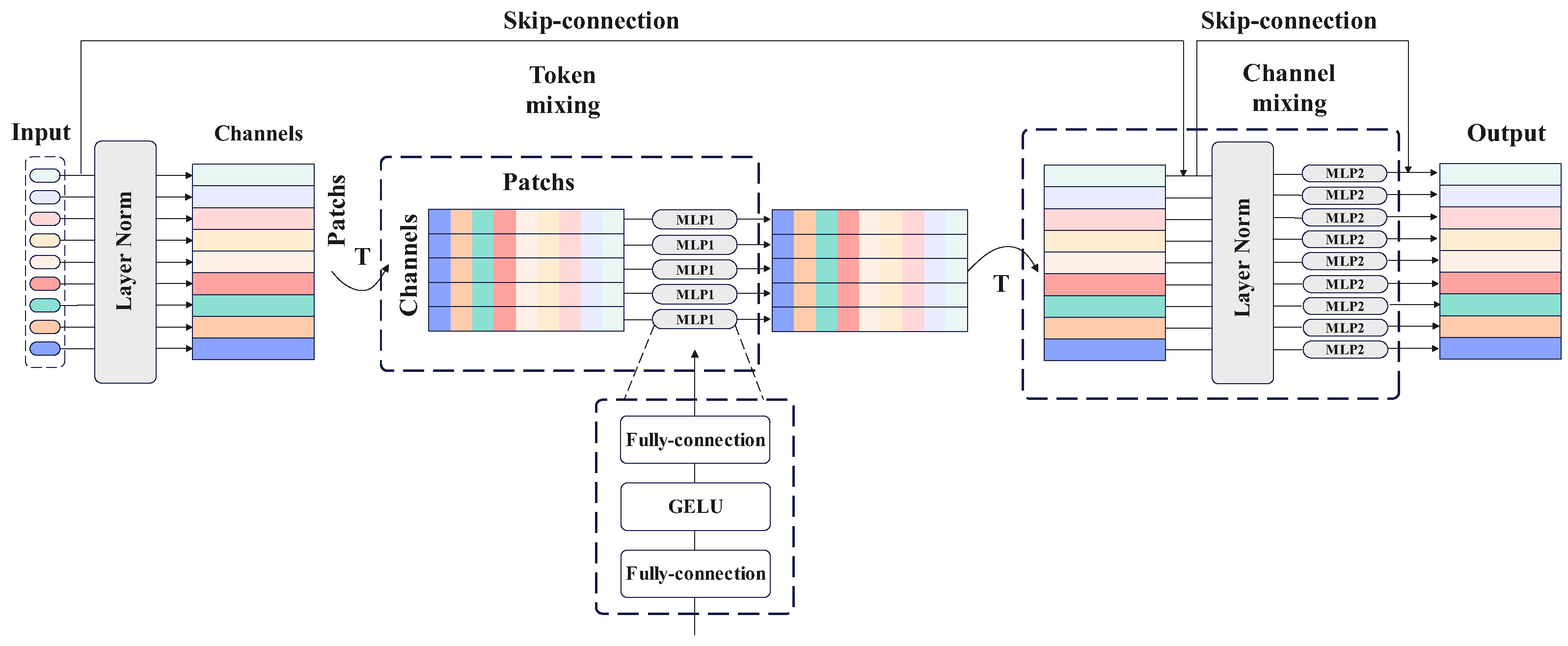
- The spatial spectral features obtained from the SSEB are further mined using the token-mixing MLP module and channel-mixing MLP module of the MLP-mixer, respectively, and feature maps containing more information are obtained under the condition that the output feature maps are guaranteed to be unchanged from the output.
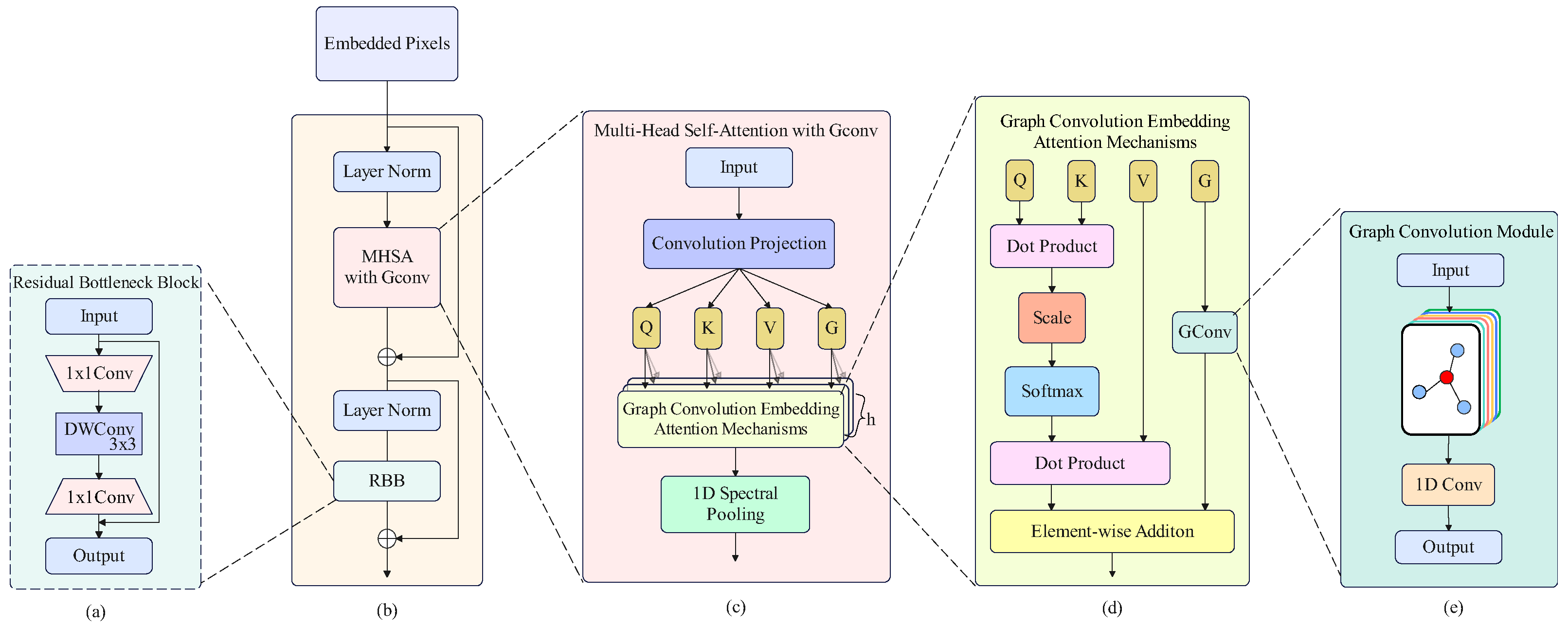
- The graph convolutional enhanced transformer (GCET) introduces graph convolutional into the ViT, which overcomes the shortcomings of MHSA’s overly dispersed attention, while fully exploiting the spatial relationships and similarities between pixels.
- MGCET was subjected to a large number of ablation and comparison experiments on four datasets. The results showed that MGCET had good classification accuracy compared to several state-of-the-art approaches.
2. Methodology
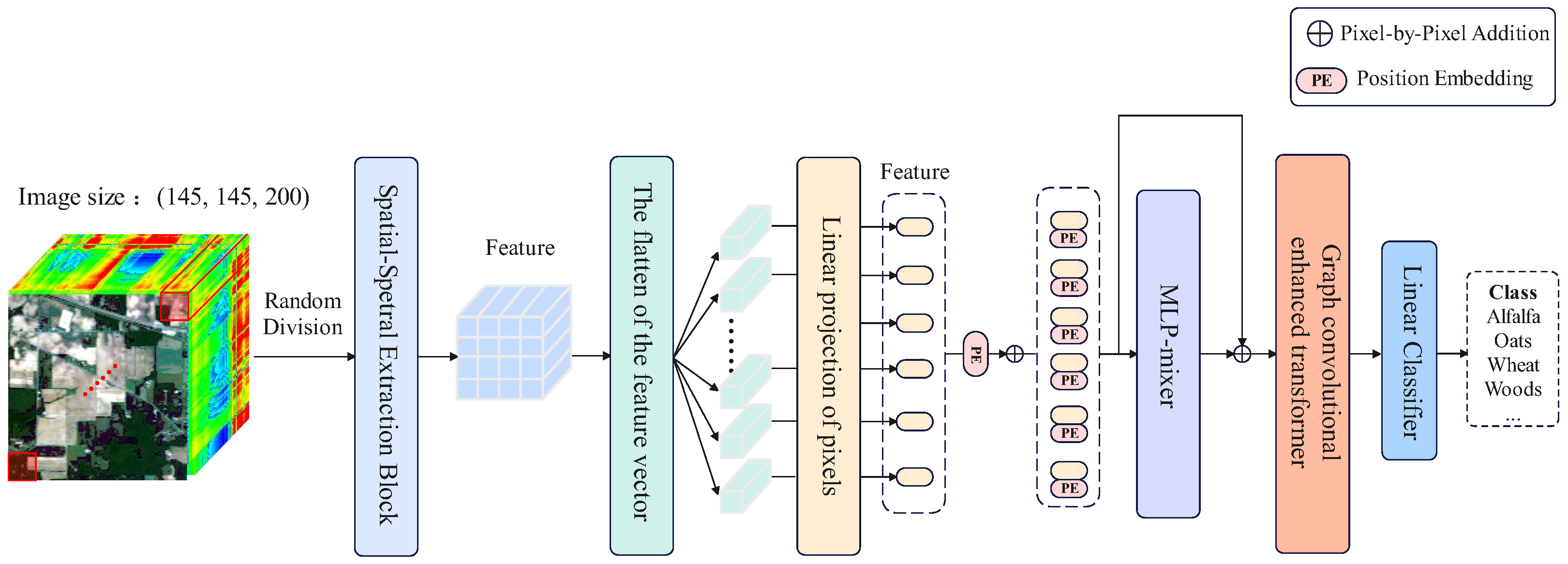
2.1. Overview of MLP-mixer and Graph Convolutional Enhanced Transformer
2.2. Spatial-Spectral Extraction Block
2.3. MLP-mixer
2.4. Graph Convolutional Enhanced Transformer
2.5. System Model
- 1:
- Split HSI dataset into 3D-patches with the same size.
- 2:
- Spatial-spectral extraction block is utilized to obtain feature .
- 3:
- Flattened and projected feature to obtain sequence data .
- 4:
- The spatial and channel features are further extracted using a token-mixer MLP and channel-mixer MLP, respectively, to obtain the feature .
- 5:
- The graph convolution module embedded in MHSA is employed to obtain a feature , which contains the similarity between the sequence data.
- 6:
- Output features of MHSAG: .
- 7:
- Feature is the final output of the entire model.
- 8:
- The final classification result is obtained through AvgPooling and a linear classifier.
3. Experiments
3.1. Dataset Description
3.1.1. Indian Pines (IP) Dataset
3.1.2. Pavia University (PU) Dataset
3.1.3. Salinas Valley (SA)
3.1.4. Kennedy Space Center (KSC)
3.2. Experimental Settings
- (1)
- SVM-RBF: As a traditional machine learning method, it employs a nonlinear mapping through radial basis function (RBF) for extracting the spectral information of HSI and then selects the optimal penalty coefficients and kernel function parameter through a grid search.
- (2)
- 3D-CNN: The 3D-CNN model comprises two 3D-CNN with 3 × 3 × 3 convolution kernels, three 3D-CNN with 3 × 1 × 1 convolution kernels, one 3D-CNN with 2 × 3 × 3 convolution kernel, four ReLU activation layers, and a fully connected layer.
- (3)
- RSSAN (residual spectral-spatial attention network) is comprised of two primary modules: the spectral-spatial attention learning module, and the spectral-spatial feature module. The former incorporates spatial and spectral attention, while the latter comprises two residual spectral spatial attention modules (containing two convolutional layers and one attention layer).
- (4)
- DBDA (double-branch dual-attention mechanism network) mainly consists of spectral and spatial branches. The former comprises a series of three-dimensional convolutional layers and channel attention, while the latter comprises a series of 3D convolutional layers and spatial attention.
- (5)
- SSRN (spectral-spatial residual network) is comprised of two blocks for spectral residuals and the same for spatial residuals. The former comprises 3D convolutional layers with a 1 × 1 × 7 kernel size and residuals. Similarly, the latter comprises 3D convolutional layers with a 3 × 3 × 128 kernel size and residuals.
- (6)
- ViT (vision transformer) divides an image into patches, subsequently employing the linear embedding sequences of these image blocks as input to the transformer for the purpose of training an image classification model in a supervised manner.
- (7)
- SSFTT (spectral-spatial feature tokenization transformer) is comprised of three modules: a spectral-spatial feature extraction, a Gaussian weighted feature tokenizer, and a transformer encoder. The MHSA in the transformer encoder has four heads with an embedding dimension of 256.
- (8)
- GAHT: Group-aware hierarchical transformer comprises three grouped pixel embedding and three transformer encoders. The heads of the MHSA in the transformer encoder are 8, 4, 2, with embedding dimensions of 256, 128, 64.
- (9)
- SpectralFormer: SpectralFormer primarily comprises two modules: the groupwise spectral embedding and the cross-layer adaptive fusion. The embedding dimensions are 256.
- (10)
- IFormer: IFormer primarily consists of a ghost module and inception transformer encoder. The inception transformer encode includes high-frequency feature extraction, low-frequency feature extraction, and feature fusion. The embedding dimensions of the transformer encode are 256.
- (11)
- MGECT: MLP-mixer and transformer fusion network is mainly composed of a joint GCN and transformer (JGT) structure, the MLP-mixer module, and a spatial-spectral feature extraction module. The JGT consists of a residual bottleneck block and a transformer encoder with graph convolution embedding. The MHSA in the transformer encoder has four heads, with an embedding dimension of 256.
3.3. Performance Evaluation Indicators
3.4. Experimental Results and Analysis
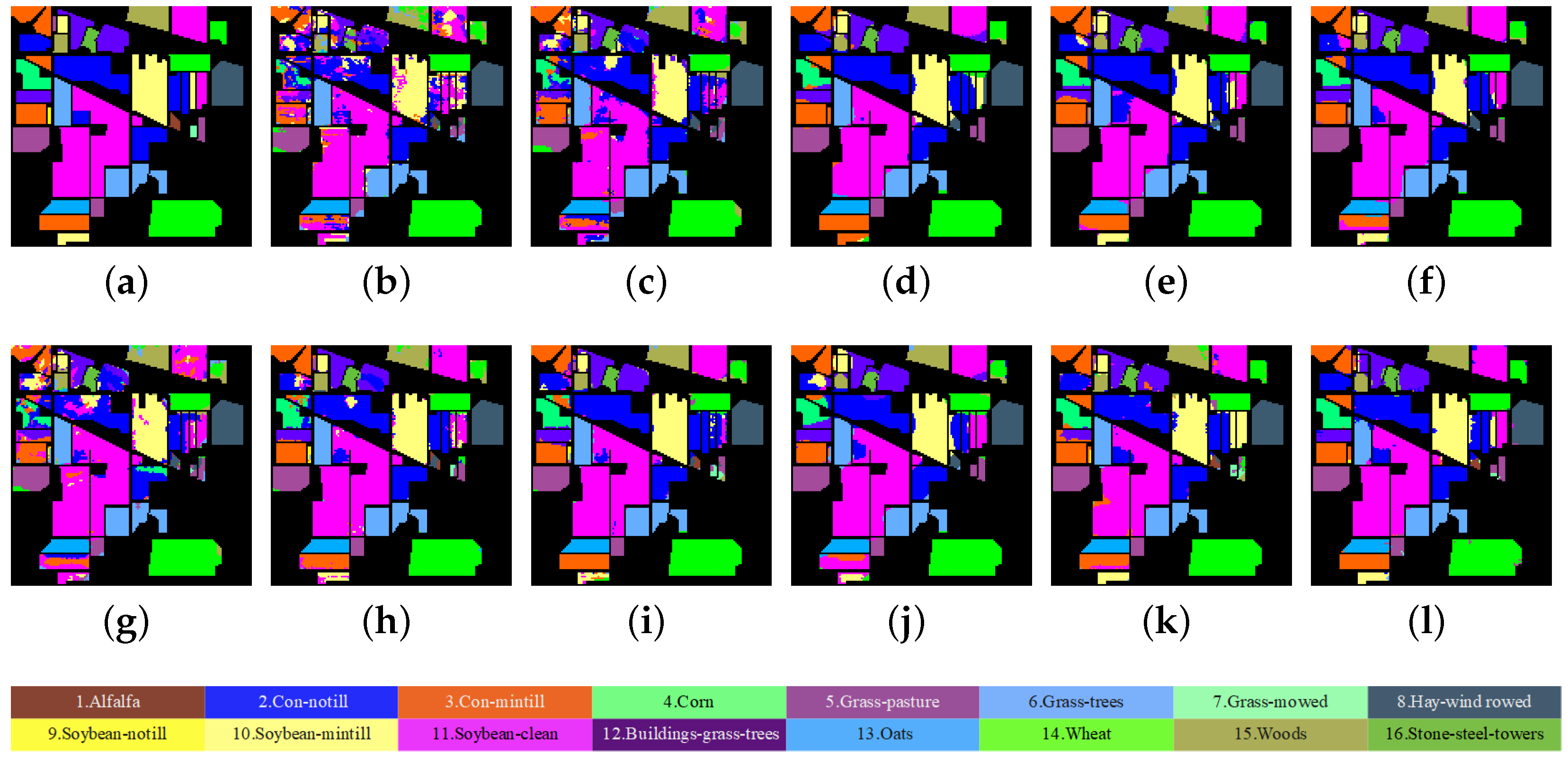
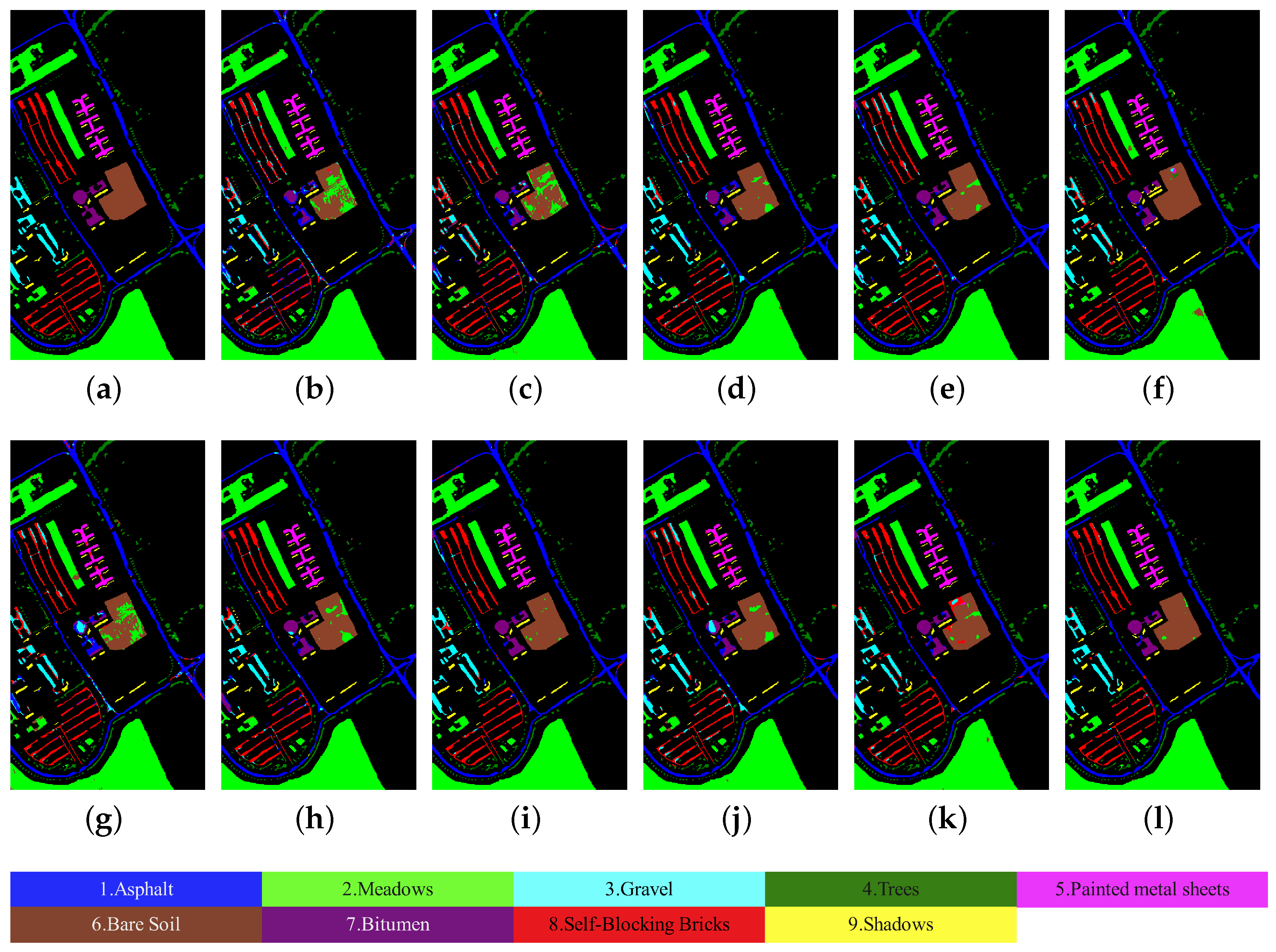
3.4.1. Results of Comparative Experiments
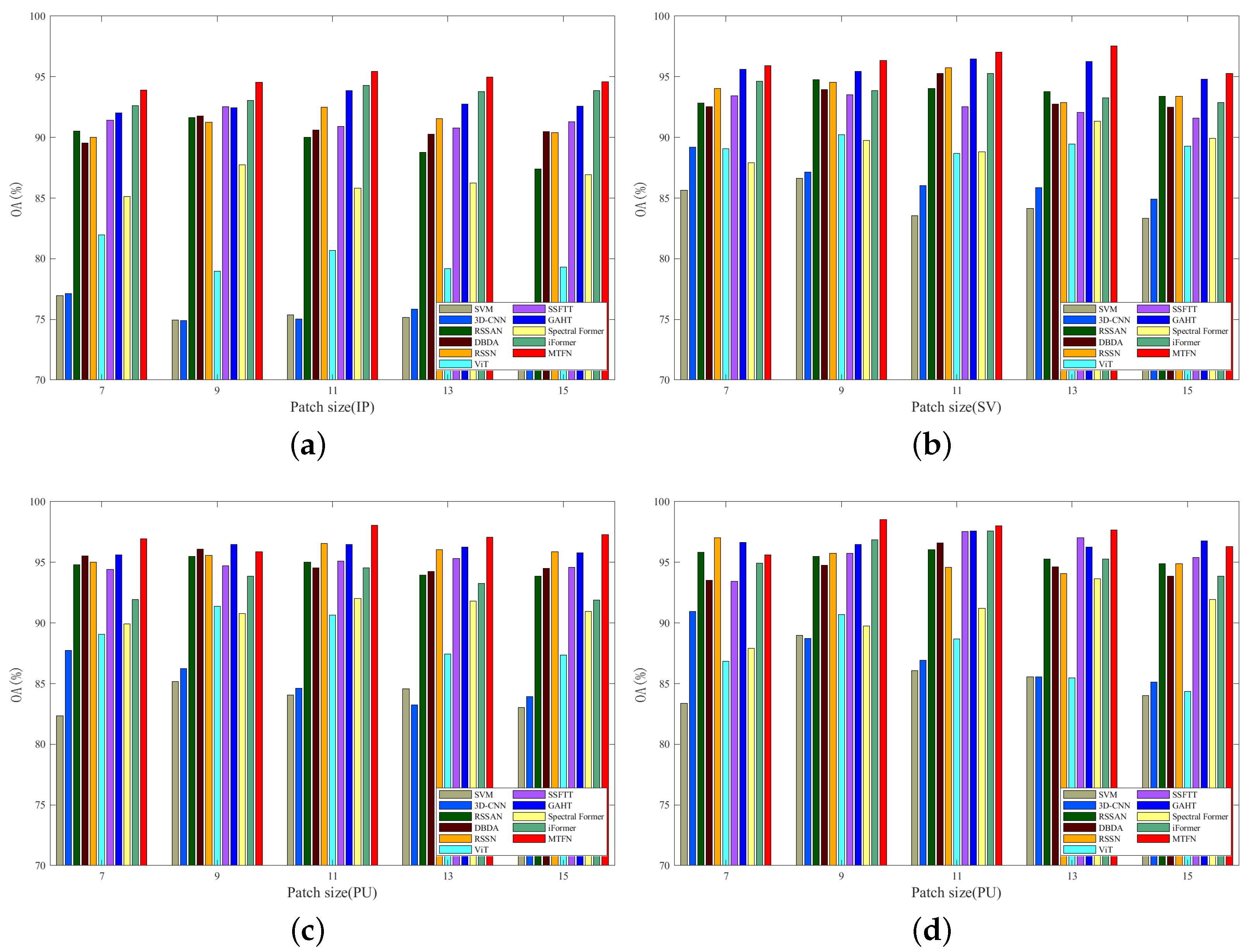
3.4.2. Image Patch Size Analysis
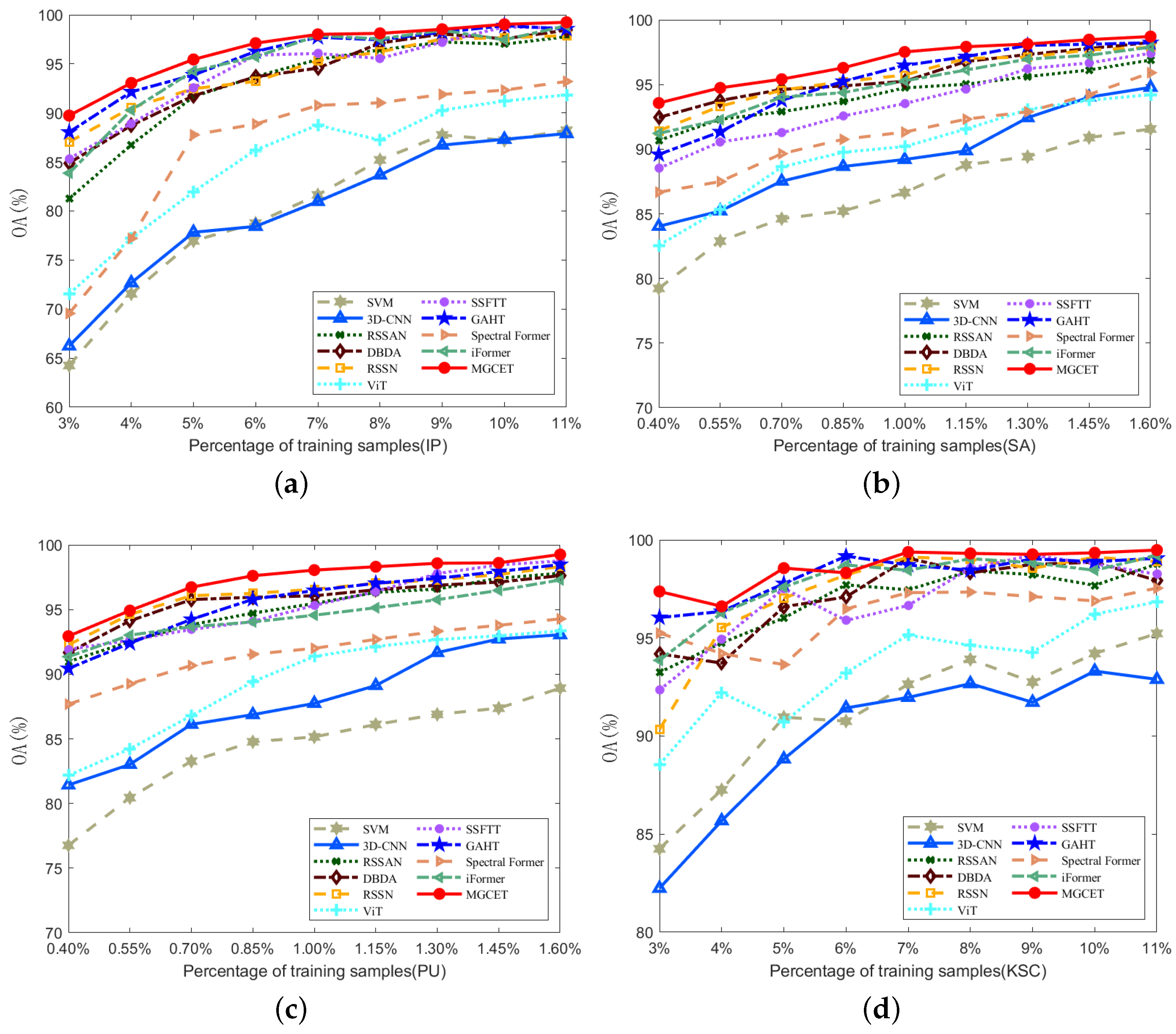
3.4.3. Analysis of Training Samples
4. Discussion
4.1. Analysis of Different Modules
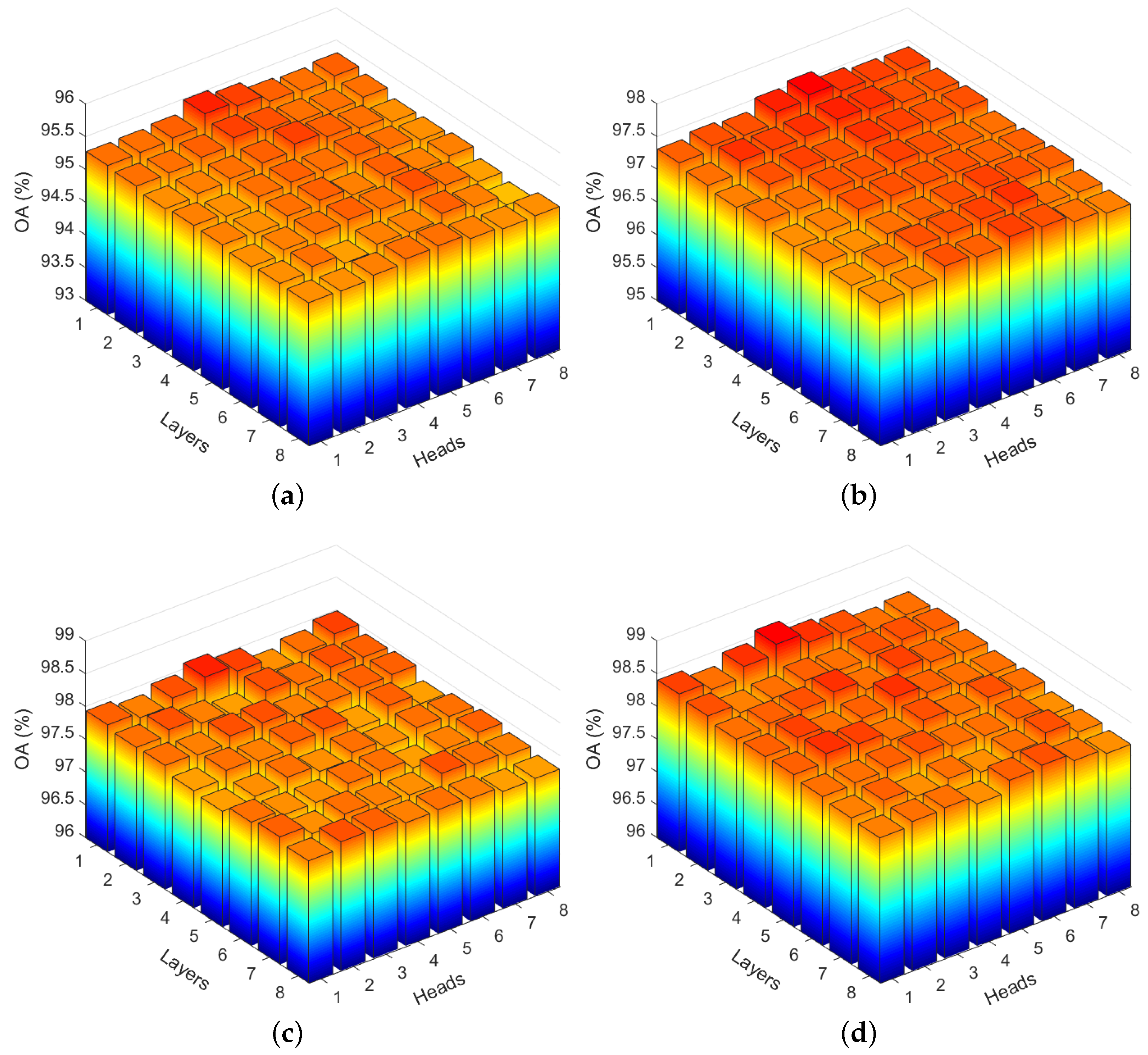
4.2. Analysis of Attention Mechanism
4.3. Analysis of Model Architecture
- Structure-1: parallel and additive fusion;
- Structure-2: parallel and multiplicative fusion;
- Structure-3: series and MLP-mixer preceded GCET;
- Structure-4: Series and GCET preceded MLP-mixer.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Feng, X.; He, L.; Cheng, Q.; Long, X.; Yuan, Y. Hyperspectral and multispectral remote sensing image fusion based on endmember spatial information. Remote Sens. 2020, 12, 1009. [Google Scholar] [CrossRef]
- Gao, A.F.; Rasmussen, B.; Kulits, P.; Scheller, E.L.; Greenberger, R.; Ehlmann, B.L. Generalized unsupervised clustering of hyperspectral images of geological targets in the near infrared. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 4294–4303. [Google Scholar]
- Zhao, X.; Li, W.; Zhang, M.; Tao, R.; Ma, P. Adaptive iterated shrinkage thresholding-based lp-norm sparse representation for hyperspectral imagery target detection. Remote Sens. 2020, 12, 3991. [Google Scholar] [CrossRef]
- Sun, G.; Jiao, Z.; Zhang, A.; Li, F.; Fu, H.; Li, Z. Hyperspectral image-based vegetation index (HSVI): A new vegetation index for urban ecological research. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102529. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Y.; Mei, X.; Dai, X.; Ma, J. Multifeature-based discriminative label consistent K-SVD for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4995–5008. [Google Scholar] [CrossRef]
- Ma, L.; Crawford, M.M.; Tian, J. Local manifold learning-based k-nearest-neighbor for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4099–4109. [Google Scholar] [CrossRef]
- Ge, H.; Pan, H.; Wang, L.; Liu, M.; Li, C. Self-training algorithm for hyperspectral imagery classification based on mixed measurement k-nearest neighbor and support vector machine. J. Appl. Remote Sens. 2021, 15, 042604. [Google Scholar] [CrossRef]
- Okwuashi, O.; Ndehedehe, C.E. Deep support vector machine for hyperspectral image classification. Pattern Recognit. 2020, 103, 107298. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Ye, Q.; Huang, P.; Zhang, Z.; Zheng, Y.; Fu, L.; Yang, W. Multiview learning with robust double-sided twin SVM. IEEE Trans. Cybern. 2021, 52, 12745–12758. [Google Scholar] [CrossRef] [PubMed]
- Haut, J.; Paoletti, M.; Paz-Gallardo, A.; Plaza, J.; Plaza, A.; Vigo-Aguiar, J. Cloud implementation of logistic regression for hyperspectral image classification. In Proceedings of the 17th International Conference on Computational and Mathematical Methods in Science and Engineering, CMMSE, Rota, Spain, 4–8 July 2017; Volume 3, pp. 1063–2321. [Google Scholar]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Spectral–spatial hyperspectral image segmentation using subspace multinomial logistic regression and Markov random fields. IEEE Trans. Geosci. Remote Sens. 2011, 50, 809–823. [Google Scholar] [CrossRef]
- Khodadadzadeh, M.; Li, J.; Plaza, A.; Bioucas-Dias, J.M. A subspace-based multinomial logistic regression for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2105–2109. [Google Scholar] [CrossRef]
- Ghamisi, P.; Maggiori, E.; Li, S.; Souza, R.; Tarablaka, Y.; Moser, G.; De Giorgi, A.; Fang, L.; Chen, Y.; Chi, M.; et al. New frontiers in spectral-spatial hyperspectral image classification: The latest advances based on mathematical morphology, Markov random fields, segmentation, sparse representation, and deep learning. IEEE Geosci. Remote Sens. Mag. 2018, 6, 10–43. [Google Scholar] [CrossRef]
- Luo, F.; Huang, H.; Ma, Z.; Liu, J. Semisupervised sparse manifold discriminative analysis for feature extraction of hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6197–6211. [Google Scholar] [CrossRef]
- Peng, J.; Li, L.; Tang, Y.Y. Maximum likelihood estimation-based joint sparse representation for the classification of hyperspectral remote sensing images. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 1790–1802. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Hong, Q.; Zhong, X.; Chen, W.; Zhang, Z.; Li, B. Hyperspectral Image Classification Network Based on 3D Octave Convolution and Multiscale Depthwise Separable Convolution. ISPRS Int. J. Geo-Inf. 2023, 12, 505. [Google Scholar] [CrossRef]
- Li, H.; Xiong, X.; Liu, C.; Ma, Y.; Zeng, S.; Li, Y. SFFNet: Staged Feature Fusion Network of Connecting Convolutional Neural Networks and Graph Convolutional Neural Networks for Hyperspectral Image Classification. Appl. Sci. 2024, 14, 2327. [Google Scholar] [CrossRef]
- Zahisham, Z.; Lim, K.M.; Koo, V.C.; Chan, Y.K.; Lee, C.P. 2SRS: Two-stream residual separable convolution neural network for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Meng, Z.; Zhang, J.; Zhao, F.; Liu, H.; Chang, Z. Residual dense asymmetric convolutional neural network for hyperspectral image classification. In Proceedings of the IGARSS 2022 —2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 3159–3162. [Google Scholar]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep recurrent neural networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Hong, D.; Cai, W.; Yu, C.; Yang, N.; Cai, W. Multi-feature fusion: Graph neural network and CNN combining for hyperspectral image classification. Neurocomputing 2022, 501, 246–257. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yao, J.; Zhang, B.; Plaza, A.; Chanussot, J. Graph convolutional networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5966–5978. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, Y.; Zhao, X.; Siye, L.; Yang, N.; Cai, Y.; Zhan, Y. Multireceptive field: An adaptive path aggregation graph neural framework for hyperspectral image classification. Expert Syst. Appl. 2023, 217, 119508. [Google Scholar] [CrossRef]
- Wang, X.; Sun, L.; Lu, C.; Li, B. A novel transformer network with a CNN-enhanced cross-attention mechanism for hyperspectral image classification. Remote Sens. 2024, 16, 1180. [Google Scholar] [CrossRef]
- Qing, Y.; Liu, W.; Feng, L.; Gao, W. Improved transformer net for hyperspectral image classification. Remote Sens. 2021, 13, 2216. [Google Scholar] [CrossRef]
- Dalal, A.A.; Cai, Z.; Al-Qaness, M.A.; Dahou, A.; Alawamy, E.A.; Issaka, S. Compression and reinforce variation with convolutional neural networks for hyperspectral image classification. Appl. Soft Comput. 2022, 130, 109650. [Google Scholar]
- Dalal, A.A.; Cai, Z.; Al-qaness, M.A.; Alawamy, E.A.; Alalimi, A. ETR: Enhancing transformation reduction for reducing dimensionality and classification complexity in hyperspectral images. Expert Syst. Appl. 2023, 213, 118971. [Google Scholar]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep convolutional neural networks for hyperspectral image classification. J. Sens. 2015, 2015, 258619. [Google Scholar] [CrossRef]
- Hamida, A.B.; Benoit, A.; Lambert, P.; Amar, C.B. 3-D deep learning approach for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4420–4434. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Ma, L.; Jiang, H.; Zhao, H. Deep residual networks for hyperspectral image classification. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2107; IEEE: Piscataway, NJ, USA, 2017; pp. 1824–1827. [Google Scholar]
- Paoletti, M.E.; Haut, J.M.; Fernandez-Beltran, R.; Plaza, J.; Plaza, A.J.; Pla, F. Deep pyramidal residual networks for spectral–spatial hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 57, 740–754. [Google Scholar] [CrossRef]
- Meng, Z.; Li, L.; Jiao, L.; Feng, Z.; Tang, X.; Liang, M. Fully dense multiscale fusion network for hyperspectral image classification. Remote Sens. 2019, 11, 2718. [Google Scholar] [CrossRef]
- Zhu, M.; Jiao, L.; Liu, F.; Yang, S.; Wang, J. Residual spectral–spatial attention network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 449–462. [Google Scholar] [CrossRef]
- Li, R.; Zheng, S.; Duan, C.; Yang, Y.; Wang, X. Classification of hyperspectral image based on double-branch dual-attention mechanism network. Remote Sens. 2020, 12, 582. [Google Scholar] [CrossRef]
- Lin, J.; Gao, F.; Shi, X.; Dong, J.; Du, Q. SS-MAE: Spatial–spectral masked autoencoder for multisource remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Wang, M.; Gao, F.; Dong, J.; Li, H.C.; Du, Q. Nearest neighbor-based contrastive learning for hyperspectral and LiDAR data classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar] [CrossRef]
- Wang, J.; Gao, F.; Dong, J.; Du, Q. Adaptive DropBlock-enhanced generative adversarial networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5040–5053. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A.; Chanussot, J. SpectralFormer: Rethinking hyperspectral image classification with transformers. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, G.; Zheng, Y.; Wu, Z. Spectral–spatial feature tokenization transformer for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Mei, S.; Song, C.; Ma, M.; Xu, F. Hyperspectral image classification using group-aware hierarchical transformer. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Ren, Q.; Tu, B.; Liao, S.; Chen, S. Hyperspectral image classification with iformer network feature extraction. Remote Sens. 2022, 14, 4866. [Google Scholar] [CrossRef]
- Yang, A.; Li, M.; Ding, Y.; Hong, D.; Lv, Y.; He, Y. GTFN: GCN and transformer fusion with spatial-spectral features for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
- Zhao, F.; Zhang, J.; Meng, Z.; Liu, H.; Chang, Z.; Fan, J. Multiple vision architectures-based hybrid network for hyperspectral image classification. Expert Syst. Appl. 2023, 234, 121032. [Google Scholar] [CrossRef]
- Cui, Y.; Shao, C.; Luo, L.; Wang, L.; Gao, S.; Chen, L. Center weighted convolution and GraphSAGE cooperative network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar] [CrossRef]
- Shi, C.; Yue, S.; Wang, L. A dual branch multiscale Transformer network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–20. [Google Scholar] [CrossRef]
- Zhuo, R.; Guo, Y.; Guo, B. A hyperspectral image classification method based on 2-d compact variational mode decomposition. IEEE Trans. Geosci. Remote Sens. 2023, 20, 1–5. [Google Scholar] [CrossRef]





| Module | Layer | Configuration [Output Size] (Kernel)(Stride) (Padding) |
|---|---|---|
| 3D Convolution Module | 3-D Conv-1 | [8, 38, 11, 11]; (11, 3, 3); (5, 1, 1); (0, 1, 1) |
| 3-D Conv-2 | [8, 38, 11, 11]; (3, 3, 3); (1, 1, 1); (1, 1, 1) | |
| 3-D Conv-3 | [8, 38, 11, 11]; (1, 1, 1); (1, 1, 1); (0, 0, 0) | |
| Rearrange | [304, 11, 11](–)(–)(–) | |
| 2D Convolution Module | 2-D Conv-1 | [256, 11, 11]; (1 × 1); (1, 1); (0, 0) |
| 2-D DWConv-2 | [256, 11, 11]; (3 × 3); (1, 1); (0, 0) | |
| 2-D Conv-3 | [, 11, 11]; (1 × 1); (1, 1); (0, 0) | |
| Patch Embeddings | nn.Flatten() | [121, ](–)(–)(–) |
| nn.Linear() | [121, 256](–)(–)(–) | |
| Postional Embeddings | nn.Parameter() | [121, 256](–)(–)(–) |
| MLP-mixer | nn.LayerNorm() | [121, 256](–)(–)(–) |
| token-mixing MLP | [121, 256](–)(–)(–) | |
| nn.LayerNorm() | [121, 256](–)(–)(–) | |
| channel-mixing MLP | [121, 256](–)(–)(–) | |
| Graph convolutional Enhanced Transformer Encoder | nn.LayerNorm() | [121, 256](–)(–)(–) |
| GConv | [121, 512](–)(–)(–) | |
| MHSAG | [121, 512](–)(–)(–) | |
| 1-D AdaptiveAvgPool | [121, 256](–)(–)(–) | |
| nn.LayerNorm() | [121, 256](–)(–)(–) | |
| Residual Bottleneck Block | 2-D Conv-5 | [11, 11, 64]; (1 × 1); (1 × 1); (0, 0) |
| 2-D DWConv-6 | [11, 11, 64]; (3 × 3); (1 × 1); (1, 1) | |
| 2-D Conv-7 | [11, 11, 256]; (1 × 1); (1 × 1); (0, 0) | |
| Classifier | Dropout | Output Size: [121, 256] |
| Avg Pooling | [1, 256](–)(–)(–) | |
| nn.LayerNorm() | [1, 256](–)(–)(–) | |
| nn.Linear() | [1, Classes](–)(–)(–) |
| Class No. | Class Name | Training | Testing |
|---|---|---|---|
| 1 | Alfalfa | 2 | 44 |
| 2 | Con-notill | 71 | 1357 |
| 3 | Con-mintill | 41 | 789 |
| 4 | Corn | 12 | 225 |
| 5 | Grass-pasture | 24 | 459 |
| 6 | Grass-trees | 37 | 693 |
| 7 | Grass-pasture-mowed | 1 | 27 |
| 8 | Hay-windrowed | 24 | 454 |
| 9 | Oats | 1 | 19 |
| 10 | Soybean-notill | 49 | 923 |
| 11 | Soybean-mintill | 123 | 2332 |
| 12 | Soybean-clean | 30 | 563 |
| 13 | Wheat | 10 | 195 |
| 14 | Woods | 63 | 1203 |
| 15 | Buildings-grass-trees-drivers | 19 | 367 |
| 16 | Stone-steel-towers | 5 | 88 |
| Total | 512 | 9737 |
| Class No. | Class Name | Training | Testing |
|---|---|---|---|
| 1 | Asphalt | 66 | 6565 |
| 2 | Meadows | 186 | 18,463 |
| 3 | Gravel | 21 | 2078 |
| 4 | Trees | 31 | 3033 |
| 5 | Painted metal sheets | 13 | 1332 |
| 6 | Bare Soil | 50 | 4979 |
| 7 | Bitumen | 13 | 1317 |
| 8 | Self-Blocking Bricks | 37 | 3645 |
| 9 | Shadows | 10 | 937 |
| Total | 427 | 42,349 |
| Class No. | Class Name | Training | Testing |
|---|---|---|---|
| 1 | Brocoli-green-weeds-1 | 20 | 1989 |
| 2 | Brocoli-green-weeds-2 | 37 | 3689 |
| 3 | Fallow | 20 | 1956 |
| 4 | Fallow-rough-plow | 14 | 1380 |
| 5 | Fallow-smooth | 27 | 2651 |
| 6 | Stubble | 39 | 3920 |
| 7 | Celery | 36 | 3543 |
| 8 | Grapes-untrained | 113 | 11,158 |
| 9 | Soil-vinyard-develop | 62 | 6141 |
| 10 | Corn-senesced-green-weeds | 33 | 3245 |
| 11 | Lettuce-romaine-4wk | 11 | 1057 |
| 12 | Lettuce-romaine-5wk | 19 | 1908 |
| 13 | Lettuce-romaine-6wk | 9 | 907 |
| 14 | Lettuce-romaine-7wk | 11 | 1059 |
| 15 | Vinyard-untrained | 72 | 7196 |
| 16 | Vinyard-vertical-trellis | 18 | 1789 |
| Total | 541 | 53,588 |
| Class No. | Class Name | Training | Testing |
|---|---|---|---|
| 1 | Scrub | 38 | 723 |
| 2 | Willow Swamp | 12 | 231 |
| 3 | CP Hammock | 13 | 243 |
| 4 | Slash Pine | 13 | 239 |
| 5 | 0ak/Broadleaf | 8 | 153 |
| 6 | Hardwood swamp | 11 | 218 |
| 7 | Swap | 5 | 100 |
| 8 | Graminoid Marsh | 22 | 409 |
| 9 | Spartina Marsh | 26 | 494 |
| 10 | Cattail Marsh | 20 | 384 |
| 11 | Salt Marsh | 21 | 398 |
| 12 | Mud Flats | 25 | 478 |
| 13 | Water | 46 | 881 |
| Total | 260 | 4951 |
| Class No. | SVM-RBF | 3D-CNN | RSSAN | DBDA | RSSN | ViT | SSFTT | GAHT | Spectral Former | iFormer | MGCET |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 71.36 ± 3.65 | 81.01 ± 3.10 | 78.29 ± 1.34 | 76.00 ± 2.01 | 75.91 ± 2.74 | 74.52 ± 4.06 | 77.11 ± 0.70 | 79.63 ± 0.32 | 70.52 ± 3.15 | 76.48 ± 3.35 | 79.08 ± 1.03 |
| 2 | 68.16 ± 7.99 | 71.18 ± 6.81 | 87.69 ± 1.44 | 83.28 ± 9.17 | 84.61 ± 7.02 | 81.89 + 3.72 | 89.08 ± 1.87 | 91.30 ± 0.88 | 86.89 ± 5.53 | 93.19 ± 4.14 | 94.70 ± 1.51 |
| 3 | 61.12 ± 5.52 | 66.92 ± 8.72 | 89.87 ± 0.45 | 88.17 ± 6.21 | 81.39 ± 5.31 | 79.46 ± 8.19 | 92.87 ± 3.21 | 93.59 ± 0.86 | 91.30 ± 3.83 | 92.51 ± 0.23 | 93.30 ± 1.61 |
| 4 | 60.90 ± 11.75 | 68.89 ± 2.40 | 90.98 ± 1.99 | 100.00 ± 0.00 | 96.42 ± 0.91 | 85.51 ± 4.89 | 98.55 ± 0.41 | 97.71 ± 1.61 | 95.53 ± 2.34 | 87.29 ± 3.03 | 94.48 ± 0.93 |
| 5 | 73.18 ± 0.69 | 73.36 ± 6.93 | 93.23 ± 1.29 | 95.52 ± 5.21 | 97.05 ± 0.17 | 85.75 ± 3.16 | 97.12 ± 1.84 | 96.19 ± 1.08 | 87.51 ± 4.01 | 95.47 ± 3.61 | 95.25 ± 1.01 |
| 6 | 91.13 ± 1.14 | 88.29 ± 4.15 | 96.61 ± 0.37 | 97.37 ± 1.13 | 97.42 ± 1.11 | 81.81 ± 7.71 | 96.37 ± 0.93 | 96.71 ± 1.15 | 99.32 ± 0.13 | 99.16 ± 0.66 | 99.36 ± 0.39 |
| 7 | 64.18 ± 10.37 | 75.00 ± 2.11 | 76.87 ± 3.62 | 83.24 ± 1.47 | 79.30 ± 0.71 | 75.48 ± 4.01 | 79.70 ± 0.31 | 76.87 ± 1.67 | 84.81 ± 5.01 | 84.81 ± 11.08 | 83.69 ± 0.04 |
| 8 | 95.79 ± 1.35 | 97.02 ± 1.00 | 97.00 ± 0.00 | 98.77 ± 0.78 | 100.00 ± 0.00 | 73.76 ± 5.72 | 98.47 ± 0.48 | 99.05 ± 0.21 | 83.18 ± 7.78 | 99.76 ± 0.32 | 97.90 ± 2.12 |
| 9 | 58.17 ± 1.37 | 78.00 ± 0.71 | 75.00 ± 0.33 | 79.90 ± 0.04 | 77.29 ± 1.20 | 83.76 ± 4.72 | 77.36 ± 4.27 | 79.78 ± 3.67 | 73.76 ± 1.94 | 77.55 ± 2.51 | 84.27 ± 3.02 |
| 10 | 66.76 ± 2.69 | 77.93 ± 3.73 | 88.39 ± 1.13 | 86.24 ± 4.53 | 97.63 ± 0.59 | 89.30 ± 2.19 | 92.24 ± 2.33 | 94.04 ± 1.71 | 93.77 ± 0.13 | 97.36 ± 1.28 | 96.68 ± 1.82 |
| 11 | 73.59 ± 3.41 | 59.64 ± 3.73 | 85.79 ± 0.76 | 83.03 ± 3.39 | 81.21 ± 6.71 | 77.68 ± 6.24 | 84.21 ± 4.91 | 87.18 ± 1.42 | 93.17 ± 0.42 | 96.99 ± 2.11 | 97.97 ± 1.26 |
| 12 | 56.22 ± 5.87 | 62.94 ± 5.66 | 89.16 ± 0.88 | 86.98 ± 7.12 | 88.30 ± 4.19 | 86.36 ± 2.91 | 92.98 ± 3.72 | 90.70 ± 0.71 | 82.48 ± 10.72 | 93.29 ± 6.13 | 96.61 ± 2.42 |
| 13 | 86.97 ± 0.51 | 89.05 ± 0.27 | 97.00 ± 1.10 | 96.61 ± 1.53 | 97.37 ± 2.12 | 94.62 + 2.16 | 98.61 ± 1.53 | 99.02 ± 0.34 | 90.82 ± 4.73 | 99.94 ± 0.07 | 99.95 ± 0.03 |
| 14 | 94.43 ± 0.82 | 83.13 ± 0.60 | 92.58 ± 0.13 | 97.78 ± 0.07 | 96.67 ± 2.64 | 93.77 ± 1.41 | 98.18 ± 0.77 | 99.03 ± 0.39 | 81.49 ± 7.17 | 98.10 ± 1.14 | 97.69 ± 1.77 |
| 15 | 61.70 ± 2.47 | 80.43 ± 6.91 | 88.59 ± 0.69 | 98.17 ± 0.51 | 96.90 ± 1.13 | 96.51 ± 2.38 | 99.17 ± 0.89 | 98.16 ± 0.71 | 91.26 ± 3.61 | 97.91 ± 1.73 | 95.35 ± 4.46 |
| 16 | 83.17 ± 8.52 | 100.00 ± 0.00 | 92.41 ± 2.10 | 98.77 ± 0.35 | 100.00 ± 0.00 | 94.30 ± 3.26 | 95.47 ± 2.35 | 97.47 ± 1.25 | 100.00 ± 0.00 | 96.78 ± 2.06 | 97.72 ± 1.09 |
| OA(%) | 76.96 ± 2.25 | 77.83 ± 1.78 | 91.66 ± 3.63 | 91.75 ± 3.84 | 92.47 ± 2.46 | 81.96 ± 3.21 | 92.55 ± 2.81 | 93.87 ± 0.27 | 87.76 ± 1.81 | 94.28 ± 0.76 | 95.45 ± 0.87 |
| AA(%) | 72.30 ± 1.66 | 79.12 ± 1.21 | 93.13 + 1.08 | 94.21 ± 2.47 | 93.17 ± 0.78 | 81.55 ± 2.07 | 93.71 + 1.74 | 95.23 ± 0.48 | 87.81 ± 2.01 | 93.22 ± 2.06 | 95.35 ± 1.96 |
| Kappa(%) | 84.81 ± 3.22 | 74.38 ± 1.99 | 89.32 ± 0.78 | 91.03 ± 3.47 | 80.03 ± 3.83 | 85.71 ± 3.29 | 93.33 ± 3.67 | 94.15 ± 1.23 | 84.19 ± 4.22 | 93.47 ± 2.73 | 95.22 ± 0.91 |
| Class No. | SVM-RBF | 3D-CNN | RSSAN | DBDA | RSSN | ViT | SSFTT | GAHT | Spectral Former | iFormer | MGCET |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 79.73 ± 6.65 | 80.47 ± 4.31 | 97.81 ± 1.36 | 98.80 ± 0.51 | 100.00 ± 0.00 | 85.47 ± 7.16 | 100.00 ± 0.00 | 99.84 ± 0.17 | 93.17 ± 2.05 | 98.42 ± 0.65 | 97.14 ± 3.13 |
| 2 | 89.09 ± 4.99 | 89.59 ± 3.71 | 97.97 ± 1.07 | 98.21 ± 0.19 | 99.91 ± 0.05 | 92.59 + 1.96 | 98.66 ± 0.81 | 96.12 ± 1.03 | 97.48 ± 0.59 | 99.08 ± 0.61 | 100.00 ± 0.00 |
| 3 | 82.50 ± 6.52 | 88.17 ± 6.02 | 96.80 ± 1.41 | 98.07 ± 0.29 | 96.61 ± 3.11 | 88.17 ± 4.49 | 94.79 ± 2.12 | 97.59 ± 1.01 | 95.19 ± 0.86 | 98.31 ± 0.48 | 99.46 ± 0.36 |
| 4 | 87.20 ± 6.75 | 88.89 ± 4.41 | 95.72 ± 3.01 | 97.63 ± 1.06 | 95.81 ± 1.41 | 88.81 ± 3.19 | 99.22 ± 0.32 | 97.91 ± 1.06 | 92.55 ± 3.04 | 98.48 ± 0.07 | 98.73 ± 1.08 |
| 5 | 87.59 ± 3.69 | 90.99 ± 3.51 | 95.14 ± 4.19 | 96.21 ± 3.41 | 96.51 ± 1.97 | 87.99 ± 5.06 | 95.59 ± 0.81 | 98.48 ± 1.03 | 91.20 ± 2.71 | 95.47 ± 1.10 | 98.94 ± 1.13 |
| 6 | 88.69 ± 3.24 | 93.65 ± 3.19 | 98.65 ± 1.37 | 99.07 ± 0.33 | 97.99 ± 1.61 | 93.65 ± 2.17 | 98.69 ± 1.03 | 100.00 ± 0.00 | 96.42 ± 1.36 | 98.15 ± 0.06 | 99.86 ± 0.15 |
| 7 | 89.95 ± 1.37 | 93.61 ± 5.22 | 98.99 ± 0.63 | 96.89 ± 2.01 | 98.45 ± 0.79 | 89.61 ± 2.11 | 99.10 ± 0.11 | 98.18 ± 1.77 | 92.25 ± 2.91 | 99.19 ± 0.28 | 99.96 ± 0.03 |
| 8 | 75.58 ± 7.15 | 86.04 ± 7.01 | 92.27 ± 4.88 | 94.77 ± 3.04 | 93.33 ± 2.70 | 91.04 ± 1.02 | 85.59 ± 3.08 | 92.18 ± 3.01 | 81.97 ± 3.01 | 93.14 ± 3.29 | 94.02 ± 2.52 |
| 9 | 92.73 ± 4.37 | 96.46 ± 1.02 | 99.36 ± 0.04 | 99.95 ± 0.03 | 98.60 ± 0.28 | 89.46 ± 2.02 | 97.91 ± 2.07 | 98.97 ± 0.16 | 91.76 ± 3.91 | 99.15 ± 1.15 | 99.87 ± 0.12 |
| 10 | 85.95 ± 3.29 | 91.52 ± 2.35 | 95.63 ± 1.71 | 96.01 ± 3.38 | 98.34 ± 0.99 | 92.51 ± 2.51 | 93.51 ± 3.13 | 97.08 ± 1.74 | 86.64 ± 6.01 | 93.47 ± 2.84 | 97.54 ± 1.68 |
| 11 | 90.58 ± 2.41 | 93.73 ± 2.03 | 96.57 ± 1.71 | 94.23 ± 4.03 | 97.01 ± 2.79 | 95.73 ± 0.54 | 96.70 ± 1.92 | 99.26 ± 0.49 | 87.05 ± 1.49 | 97.62 ± 1.69 | 99.18 ± 0.36 |
| 12 | 93.24 ± 3.15 | 96.92 ± 2.36 | 99.32 ± 0.71 | 98.98 ± 0.02 | 98.19 ± 0.29 | 94.92 ± 1.19 | 98.88 ± 1.02 | 99.44 ± 0.61 | 95.47 ± 0.74 | 99.06 ± 0.53 | 99.95 ± 0.06 |
| 13 | 94.37 ± 1.31 | 97.18 ± 0.81 | 99.81 ± 0.08 | 97.79 ± 1.04 | 97.57 ± 1.08 | 94.88 + 0.12 | 96.88 ± 0.58 | 95.79 ± 1.24 | 92.61 ± 0.82 | 95.28 ± 1.37 | 100.00 ± 0.00 |
| 14 | 95.35 ± 1.02 | 90.82 ± 2.11 | 95.97 ± 2.03 | 96.08 ± 1.02 | 98.57 ± 0.66 | 90.82 ± 3.10 | 91.80 ± 1.07 | 97.57 ± 1.59 | 97.97 ± 1.16 | 96.51 ± 1.48 | 99.20 ± 0.51 |
| 15 | 73.66 ± 8.07 | 68.08 ± 4.99 | 85.05 ± 3.03 | 87.17 ± 3.59 | 85.68 ± 6.23 | 75.08 ± 9.08 | 84.42 ± 6.09 | 91.28 ± 3.72 | 79.07 ± 8.31 | 90.65 ± 2.37 | 92.76 ± 2.75 |
| 16 | 96.08 ± 3.22 | 96.86 ± 0.11 | 99.91 ± 0.10 | 92.72 ± 0.41 | 98.46 ± 0.44 | 94.76 ± 0.26 | 96.09 ± 1.55 | 96.87 ± 1.65 | 87.12 ± 3.05 | 94.13 ± 2.71 | 99.37 ± 0.61 |
| OA(%) | 86.64 ± 4.05 | 89.20 ± 3.17 | 94.74 ± 2.93 | 95.25 ± 1.89 | 95.73 ± 1.06 | 90.20 ± 1.28 | 93.53 ± 1.13 | 96.48 ± 1.22 | 91.32 ± 1.81 | 95.28 ± 0.37 | 97.52 ± 0.37 |
| AA(%) | 84.46 ± 4.61 | 90.91 ± 2.75 | 95.77 + 2.12 | 96.01 ± 1.38 | 96.17 ± 0.78 | 92.19 ± 3.01 | 95.08 + 0.74 | 96.89 ± 1.08 | 93.48 ± 2.01 | 95.74 ± 1.20 | 98.52 ± 0.34 |
| Kappa(%) | 85.24 ± 1.52 | 90.19 ± 4.09 | 95.76 ± 2.18 | 95.26 ± 0.78 | 91.11 ± 2.38 | 94.01 ± 1.92 | 96.44 ± 0.69 | 95.34 ± 1.23 | 90.34 ± 3.89 | 94.68 ± 0.71 | 97.04 ± 0.41 |
| Class No. | SVM-RBF | 3D-CNN | RSSAN | DBDA | RSSN | ViT | SSFTT | GAHT | Spectral Former | iFormer | MGCET |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 82.40 ± 1.81 | 83.02 ± 2.77 | 91.93 ± 0.98 | 93.54 ± 1.05 | 94.24 ± 1.08 | 89.45 ± 2.81 | 95.61 ± 1.49 | 95.54 ± 0.23 | 88.73 ± 0.61 | 96.01 ± 0.46 | 97.37 ± 1.64 |
| 2 | 83.34 ± 3.05 | 88.12 ± 4.17 | 94.63 ± 0.27 | 96.43 ± 0.62 | 98.03 ± 0.89 | 90.54 ± 4.35 | 96.36 ± 0.63 | 97.43 ± 0.71 | 95.88 ± 0.72 | 97.75 ± 0.82 | 99.55 ± 0.53 |
| 3 | 86.37 ± 3.01 | 84.61 ± 3.82 | 88.68 ± 2.49 | 89.44 ± 1.51 | 90.44 ± 1.12 | 85.05 ± 6.95 | 90.38 ± 2.12 | 92.44 ± 1.37 | 89.40 ± 2.01 | 84.11 ± 7.12 | 93.65 ± 3.77 |
| 4 | 82.92 ± 1.91 | 90.11 ± 1.44 | 96.91 ± 1.05 | 94.93 ± 1.12 | 94.52 ± 0.51 | 94.77 ± 0.71 | 96.36 ± 0.82 | 96.93 ± 1.30 | 95.97 ± 1.24 | 97.92 ± 0.27 | 97.36 ± 1.14 |
| 5 | 92.03 ± 1.25 | 93.48 ± 0.92 | 97.69 ± 0.69 | 98.07 ± 0.35 | 98.57 ± 0.61 | 94.12 ± 0.53 | 97.68 ± 1.21 | 98.07 ± 0.71 | 94.88 ± 1.79 | 98.39 ± 0.77 | 99.12 ± 1.10 |
| 6 | 94.21 ± 0.32 | 81.94 ± 9.12 | 96.32 ± 2.12 | 97.72 ± 1.28 | 96.62 ± 1.47 | 89.91 ± 1.67 | 92.37 ± 2.47 | 97.12 ± 0.44 | 85.29 ± 3.06 | 87.26 ± 8.13 | 97.96 ± 0.42 |
| 7 | 93.81 ± 1.64 | 86.38 ± 4.02 | 97.40 ± 1.33 | 98.71 ± 0.23 | 97.04 ± 0.96 | 94.29 ± 2.72 | 94.49 ± 1.61 | 98.51 ± 0.35 | 87.45 ± 3.14 | 97.12 ± 1.08 | 98.10 ± 3.51 |
| 8 | 90.46 ± 1.72 | 95.97 ± 1.59 | 96.39 ± 1.08 | 97.37 ± 0.19 | 97.17 ± 0.62 | 97.01 ± 1.06 | 95.94 ± 0.31 | 98.17 ± 0.17 | 94.38 ± 1.01 | 94.96 ± 0.12 | 96.44 ± 2.49 |
| 9 | 89.82 ± 0.98 | 93.62 ± 0.92 | 97.65 ± 0.08 | 97.97 ± 0.43 | 98.27 ± 0.59 | 94.84 ± 1.82 | 97.31 ± 0.76 | 98.27 ± 0.11 | 95.25 ± 1.12 | 96.95 ± 0.48 | 97.88 ± 1.70 |
| OA(%) | 85.15 ± 1.08 | 87.74 ± 1.73 | 95.47 ± 0.72 | 96.07 ± 0.33 | 96.57 ± 0.23 | 91.37 ± 3.17 | 95.32 ± 0.91 | 96.47 ± 0.31 | 92.00 ± 1.42 | 94.56 ± 0.97 | 98.05 ± 0.41 |
| AA(%) | 89.89 ± 1.11 | 86.70 ± 3.12 | 95.91 + 0.95 | 95.98 ± 0.47 | 96.38 ± 1.01 | 92.12 ± 1.99 | 94.39 ± 1.35 | 96.28 ± 0.26 | 91.37 ± 1.92 | 93.41 ± 1.03 | 96.99 ± 1.19 |
| Kappa(%) | 83.04 ± 1.78 | 83.69 ± 3.41 | 93.71 ± 0.58 | 95.24 ± 0.92 | 95.64 ± 1.02 | 90.80 ± 3.08 | 93.94 ± 3.23 | 95.74 ± 0.40 | 92.96 ± 1.91 | 91.23 ± 0.71 | 97.56 ± 0.81 |
| Class No. | SVM-RBF | 3D-CNN | RSSAN | DBDA | RSSN | ViT | SSFTT | GAHT | Spectral Former | iFormer | MGCET |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 88.40 ± 4.00 | 93.40 ± 1.30 | 98.20 ± 0.36 | 100.00 ± 0.00 | 99.86 ± 0.12 | 92.08 ± 0.50 | 100.00 ± 0.00 | 99.82 ± 0.21 | 94.31 ± 0.51 | 100.00 ± 0.00 | 100.00 ± 0.00 |
| 2 | 82.28 ± 7.69 | 86.28 ± 4.69 | 96.46 ± 1.08 | 97.42 ± 2.98 | 97.02 ± 1.82 | 87.21 ± 3.68 | 98.66 ± 0.81 | 99.05 ± 0.72 | 87.63 ± 2.02 | 99.24 ± 0.71 | 96.10 ± 2.72 |
| 3 | 85.80 ± 6.52 | 85.80 ± 3.71 | 97.60 ± 2.12 | 92.61 ± 3.05 | 97.33 ± 1.51 | 90.08 ± 7.00 | 94.79 ± 2.12 | 98.16 ± 0.71 | 86.59 ± 1.72 | 97.97 ± 2.17 | 98.68 ± 1.21 |
| 4 | 70.71 ± 2.64 | 75.71 ± 4.77 | 91.32 ± 3.62 | 87.32 ± 8.27 | 92.67 ± 2.62 | 77.02 ± 9.14 | 94.22 ± 0.32 | 88.04 ± 10.09 | 92.10 ± 3.22 | 91.32 ± 6.90 | 92.55 ± 3.46 |
| 5 | 76.22 ± 6.85 | 69.22 ± 4.64 | 84.41 ± 6.02 | 94.41 ± 4.77 | 86.86 ± 7.05 | 84.96 ± 8.33 | 95.59 ± 0.81 | 90.72 ± 2.21 | 72.52 ± 8.26 | 90.55 ± 4.18 | 88.72 ± 3.21 |
| 6 | 93.34 ± 2.20 | 87.34 ± 3.85 | 93.45 ± 4.01 | 95.01 ± 4.08 | 93.74 ± 5.59 | 91.69 ± 3.60 | 98.69 ± 1.03 | 92.41 ± 4.12 | 94.54 ± 2.83 | 98.54 ± 2.32 | 97.43 ± 0.81 |
| 7 | 89.34 ± 6.40 | 94.34 ± 4.20 | 92.37 ± 5.06 | 87.37 ± 2.46 | 97.92 ± 0.52 | 93.75 ± 0.93 | 99.10 ± 0.11 | 94.00 ± 1.24 | 93.12 ± 3.24 | 88.62 ± 0.17 | 99.41 ± 0.39 |
| 8 | 87.75 ± 1.48 | 89.75 ± 2.09 | 95.90 ± 0.82 | 96.90 ± 1.19 | 98.21 ± 1.62 | 86.88 ± 4.66 | 90.59 ± 3.08 | 99.95 ± 0.19 | 96.90 ± 0.97 | 97.33 ± 0.93 | 99.80 ± 0.08 |
| 9 | 91.01 ± 2.09 | 95.01 ± 3.40 | 96.51 ± 1.10 | 97.01 ± 0.62 | 99.72 ± 0.26 | 91.99 ± 3.48 | 97.91 ± 2.07 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.19 ± 0.67 | 99.95 ± 0.07 |
| 10 | 91.63 ± 4.38 | 93.03 ± 1.08 | 100.00 ± 0.00 | 99.76 ± 0.38 | 99.53 ± 0.50 | 91.48 ± 0.69 | 93.51 ± 3.13 | 99.91 ± 0.29 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 |
| 11 | 93.93 ± 2.41 | 95.33 ± 2.19 | 98.14 ± 0.52 | 99.61 ± 0.46 | 98.84 ± 0.70 | 92.78 ± 4.23 | 96.70 ± 1.92 | 98.28 ± 0.02 | 95.49 ± 0.17 | 99.29 ± 0.15 | 99.94 ± 0.10 |
| 12 | 95.56 ± 3.15 | 92.02 ± 4.38 | 96.87 ± 1.38 | 98.87 ± 1.02 | 97.15 ± 3.02 | 92.24 ± 2.98 | 98.88 ± 1.02 | 100.00 ± 0.00 | 94.23 ± 2.85 | 99.56 ± 0.33 | 99.03 ± 1.04 |
| 13 | 96.32 ± 2.13 | 98.23 ± 0.81 | 99.20 ± 0.81 | 99.82 ± 0.12 | 100.00 ± 0.00 | 97.35 ± 3.12 | 96.88 ± 0.58 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 | 100.00 ± 0.00 |
| OA(%) | 88.96 ± 1.23 | 90.97 ± 1.07 | 96.02 ± 0.41 | 96.59 ± 0.53 | 97.03 ± 0.65 | 90.71 ± 0.83 | 97.52 ± 0.48 | 97.77 ± 0.60 | 93.64 ± 0.82 | 97.59 ± 0.58 | 98.52 ± 0.78 |
| AA(%) | 86.61 ± 1.88 | 88.01 ± 2.75 | 94.56 + 1.12 | 94.06 ± 1.24 | 95.26 ± 1.40 | 88.94 ± 1.17 | 95.62 + 1.09 | 96.45 ± 1.18 | 92.58 ± 1.91 | 96.88 ± 1.47 | 97.38 ± 1.60 |
| Kappa(%) | 89.94 ± 1.37 | 91.21 ± 0.29 | 96.04 ± 1.04 | 96.21 ± 0.59 | 96.82 ± 0.73 | 89.66 ± 0.92 | 96.95 ± 0.53 | 97.30 ± 1.23 | 92.59 ± 0.68 | 96.02 ± 0.93 | 98.47 ± 0.86 |
| Network | GCET | MLP-mixer | Metric | IP | SA | PU | KSC |
|---|---|---|---|---|---|---|---|
| Net-1 | ✕ | ✕ | OA | 83.82 ± 4.76 | 88.80 ± 1.13 | 82.22 ± 6.71 | 90.26 ± 0.71 |
| AA | 78.18 ± 5.16 | 89.24 ± 1.58 | 84.55 ± 4.57 | 89.76 ± 2.32 | |||
| Kappa | 82.20 ± 5.32 | 88.69 ± 1.32 | 82.59 ± 4.79 | 91.25 ± 1.66 | |||
| Net-2 | ✕ | ✓ | OA | 93.36 ± 2.08 | 95.23 ± 0.50 | 95.52 ± 2.11 | 96.91 ± 0.42 |
| AA | 92.05 ± 2.29 | 96.17 ± 1.51 | 96.33 ± 0.93 | 94.78 ± 0.11 | |||
| Kappa | 91.57 ± 2.15 | 95.98 ± 0.68 | 97.34 ± 1.26 | 97.12 ± 0.30 | |||
| Net-3 | ✓ | ✕ | OA | 94.41 ± 1.18 | 96.35 ± 0.71 | 97.21 ± 1.17 | 97.72 ± 0.18 |
| AA | 92.45 ± 1.88 | 96.45 ± 0.31 | 95.75 ± 0.83 | 96.30 ± 0.70 | |||
| Kappa | 92.49 ± 1.84 | 95.77 ± 0.86 | 96.02 ± 1.02 | 96.91 ± 0.12 | |||
| Net-4 | ✓ | ✓ | OA | 95.45 ± 0.91 | 97.57 ± 0.42 | 98.05 ± 0.41 | 98.52 ± 0.07 |
| AA | 93.99 ± 1.28 | 97.22 ± 0.60 | 97.78 ± 0.20 | 97.74 ± 0.34 | |||
| Kappa | 94.73 ± 1.06 | 97.49 ± 0.68 | 97.49 ± 0.68 | 98.04 ± 0.55 |
| Network | Metric | IP | SA | PU | KSC |
|---|---|---|---|---|---|
| MHSA | OA | 94.92 ± 0.76 | 96.88 ± 0.83 | 97.82 ± 0.71 | 98.36 ± 0.41 |
| AA | 93.58 ± 0.52 | 97.04 ± 0.08 | 96.55 ± 1.07 | 96.76 ± 0.52 | |
| Kappa | 93.32 ± 1.12 | 96.69 ± 0.41 | 96.29 ± 0.72 | 97.75 ± 0.16 | |
| MHSAG | OA | 95.45 ± 0.91 | 97.57 ± 0.42 | 98.05 ± 0.41 | 98.52 ± 0.07 |
| AA | 93.99 ± 1.28 | 97.22 ± 0.60 | 97.78 ± 0.20 | 97.74 ± 0.34 | |
| Kappa | 94.73 ± 1.06 | 97.49 ± 0.68 | 97.49 ± 0.68 | 98.04 ± 0.55 |
| Structure | Metric | IP | SA | PU | KSC |
|---|---|---|---|---|---|
| Structure-1 | OA | 94.57 ± 0.76 | 96.97 ± 0.47 | 97.59 ± 0.21 | 97.79 ± 0.65 |
| AA | 93.51 ± 0.82 | 97.11 ± 0.24 | 95.97 ± 0.51 | 95.97 ± 1.38 | |
| Kappa | 94.13 ± 0.89 | 96.52 ± 0.52 | 96.81 ± 0.28 | 97.53 ± 0.72 | |
| Structure-2 | OA | 94.29 ± 0.60 | 96.68 ± 0.83 | 97.25 ± 0.60 | 98.01 ± 0.27 |
| AA | 92.74 ± 1.17 | 97.31 ± 0.25 | 95.52 ± 1.02 | 96.50 ± 1.83 | |
| Kappa | 92.89 ± 0.69 | 96.31 ± 0.93 | 96.36 ± 0.80 | 97.79 ± 1.09 | |
| Structure-3 | OA | 95.45 ± 0.91 | 97.57 ± 0.42 | 98.05 ± 0.41 | 98.52 ± 0.07 |
| AA | 93.99 ± 1.28 | 97.22 ± 0.60 | 97.78 ± 0.20 | 97.74 ± 0.34 | |
| Kappa | 94.73 ± 1.06 | 97.49 ± 0.68 | 97.49 ± 0.68 | 98.04 ± 0.55 | |
| Structure-4 | OA | 95.14 ± 0.31 | 97.18 ± 0.26 | 97.78 ± 0.26 | 98.11 ± 0.41 |
| AA | 93.66 ± 2.21 | 97.59 ± 0.16 | 96.51 ± 0.42 | 97.35 ± 0.95 | |
| Kappa | 94.80 ± 0.35 | 96.86 ± 0.28 | 96.66 ± 0.18 | 97.78 ± 0.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-qaness, M.A.A.; Wu, G.; AL-Alimi, D. MGCET: MLP-mixer and Graph Convolutional Enhanced Transformer for Hyperspectral Image Classification. Remote Sens. 2024, 16, 2892. https://doi.org/10.3390/rs16162892
Al-qaness MAA, Wu G, AL-Alimi D. MGCET: MLP-mixer and Graph Convolutional Enhanced Transformer for Hyperspectral Image Classification. Remote Sensing. 2024; 16(16):2892. https://doi.org/10.3390/rs16162892
Chicago/Turabian StyleAl-qaness, Mohammed A. A., Guoyong Wu, and Dalal AL-Alimi. 2024. "MGCET: MLP-mixer and Graph Convolutional Enhanced Transformer for Hyperspectral Image Classification" Remote Sensing 16, no. 16: 2892. https://doi.org/10.3390/rs16162892
APA StyleAl-qaness, M. A. A., Wu, G., & AL-Alimi, D. (2024). MGCET: MLP-mixer and Graph Convolutional Enhanced Transformer for Hyperspectral Image Classification. Remote Sensing, 16(16), 2892. https://doi.org/10.3390/rs16162892









