Angle Estimation Using Learning-Based Doppler Deconvolution in Beamspace with Forward-Looking Radar
Abstract
1. Introduction
- An end-to-end learning-based FLR target angle estimation framework is established, which omits the computationally expensive iterative optimization.
- A regression strategy is adopted, which can avoid the off-grid effects.
- A semi-supervised mechanism is introduced in learning through the manifold regularization framework to avoid building overly large FLR target positioning datasets.
2. Methods
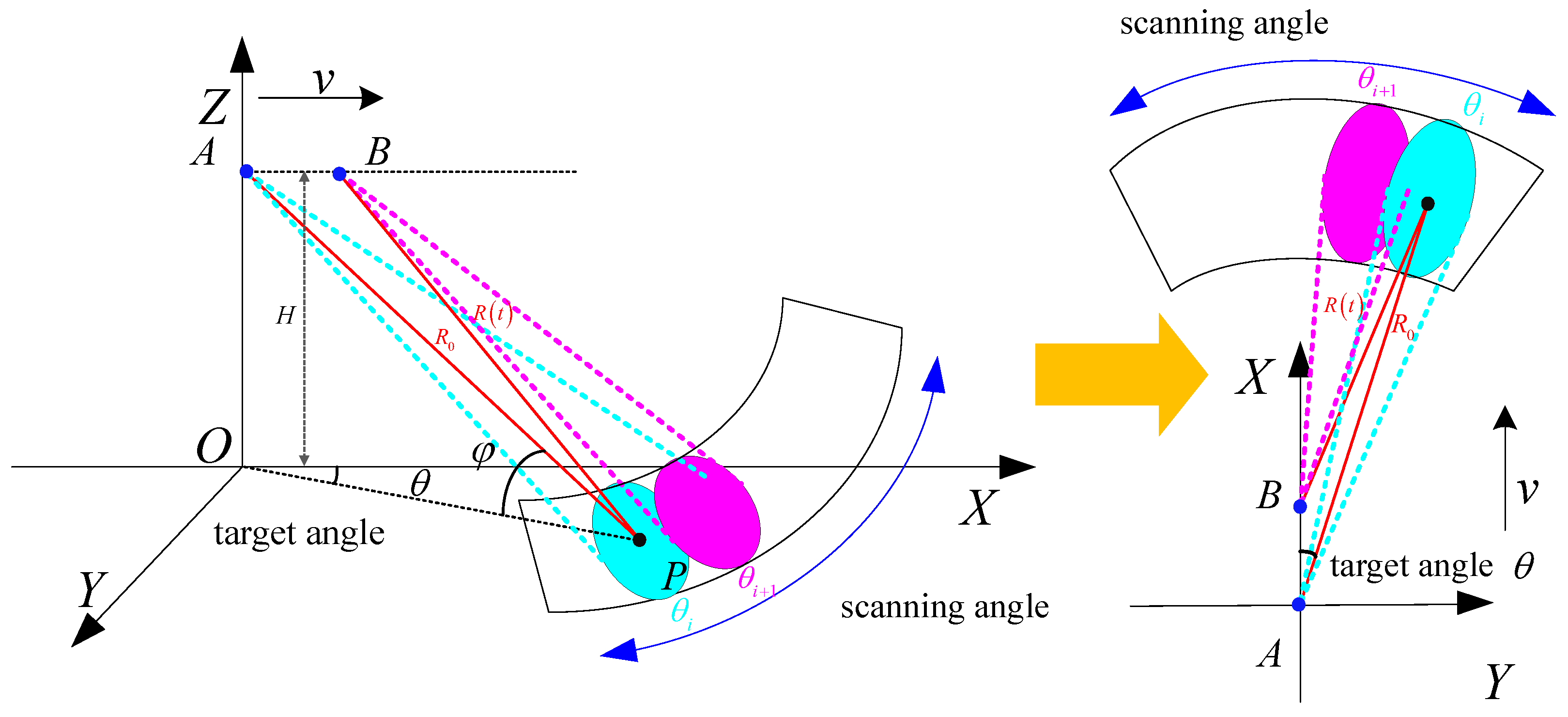
2.1. Mathematical Model
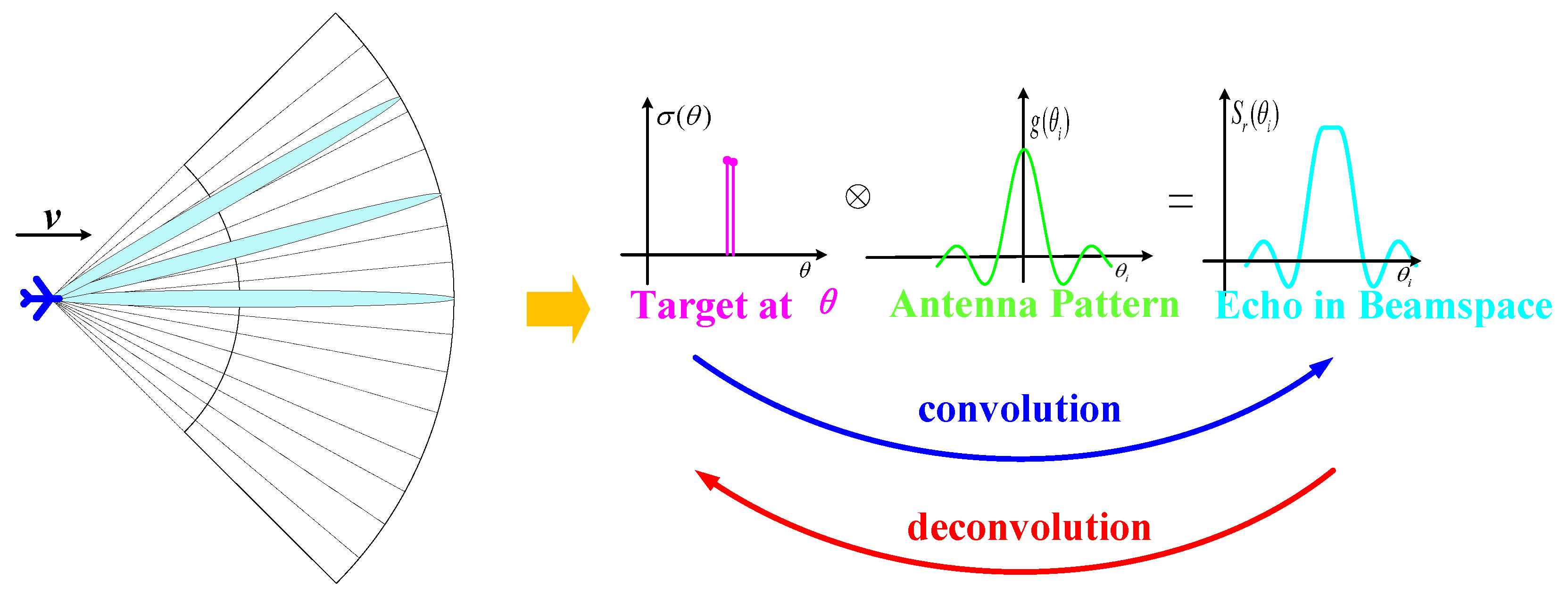
2.2. Angle Estimation Using SSL-FAE
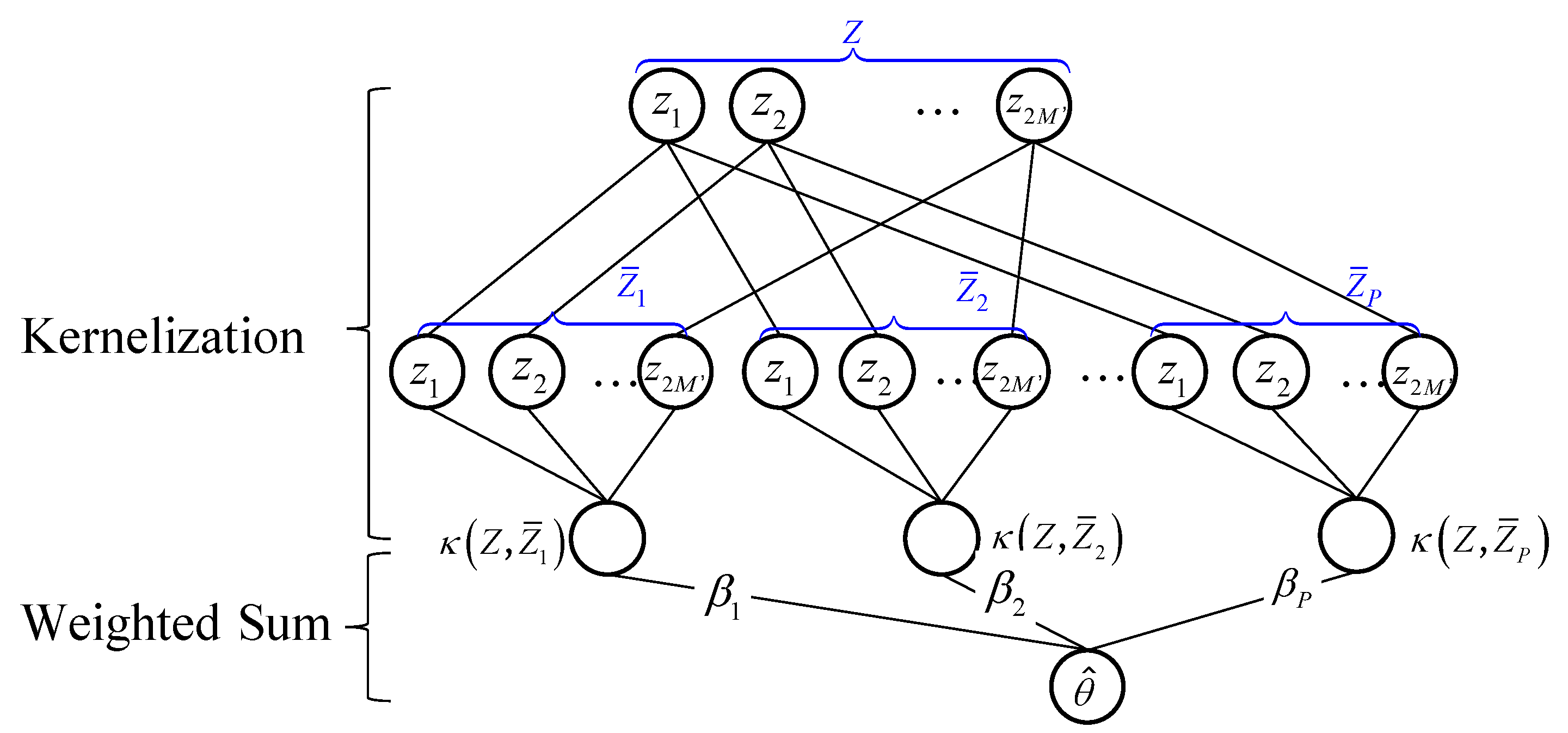
2.3. Training SSL-FAE
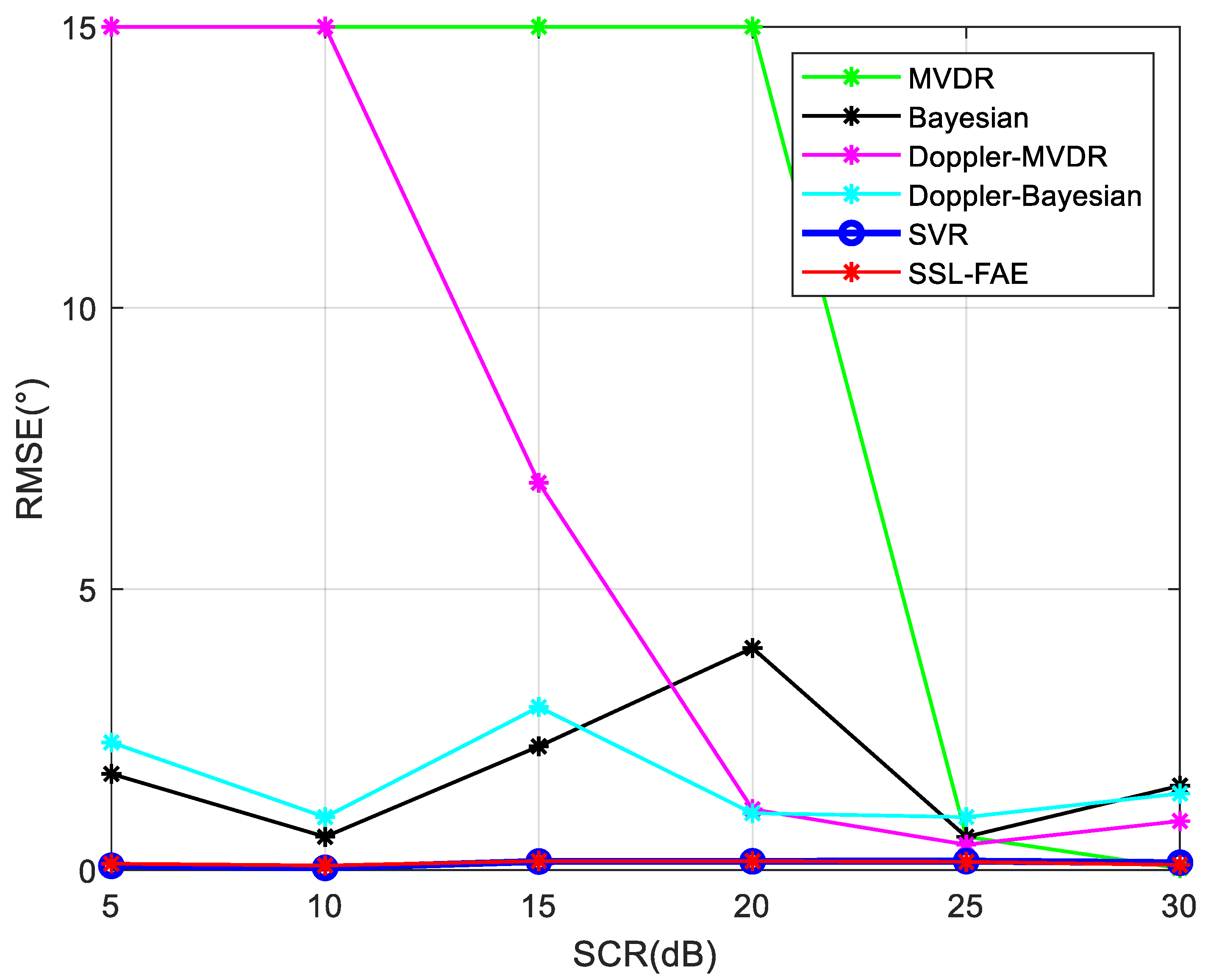
3. Numerical Simulations and Results
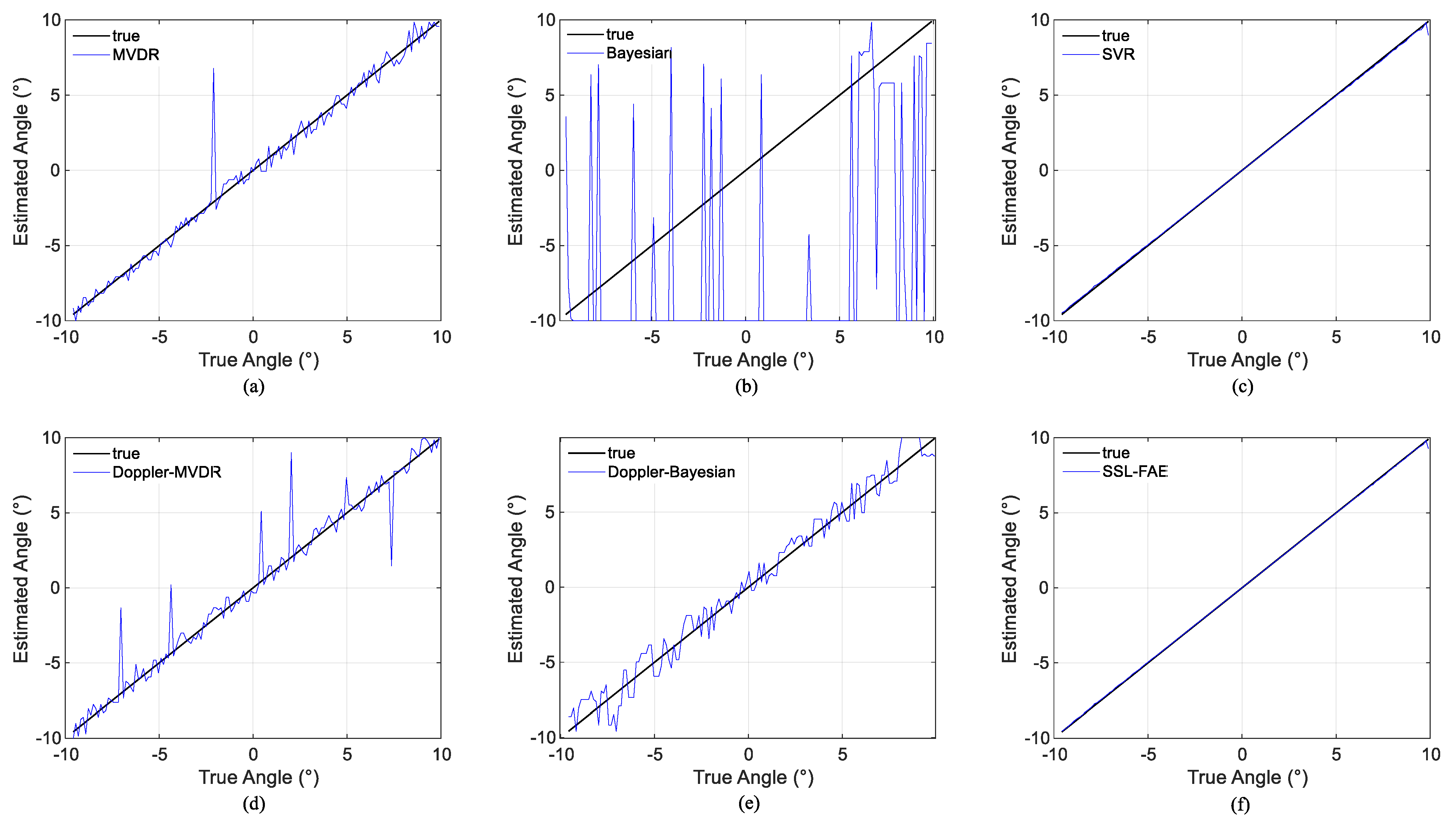
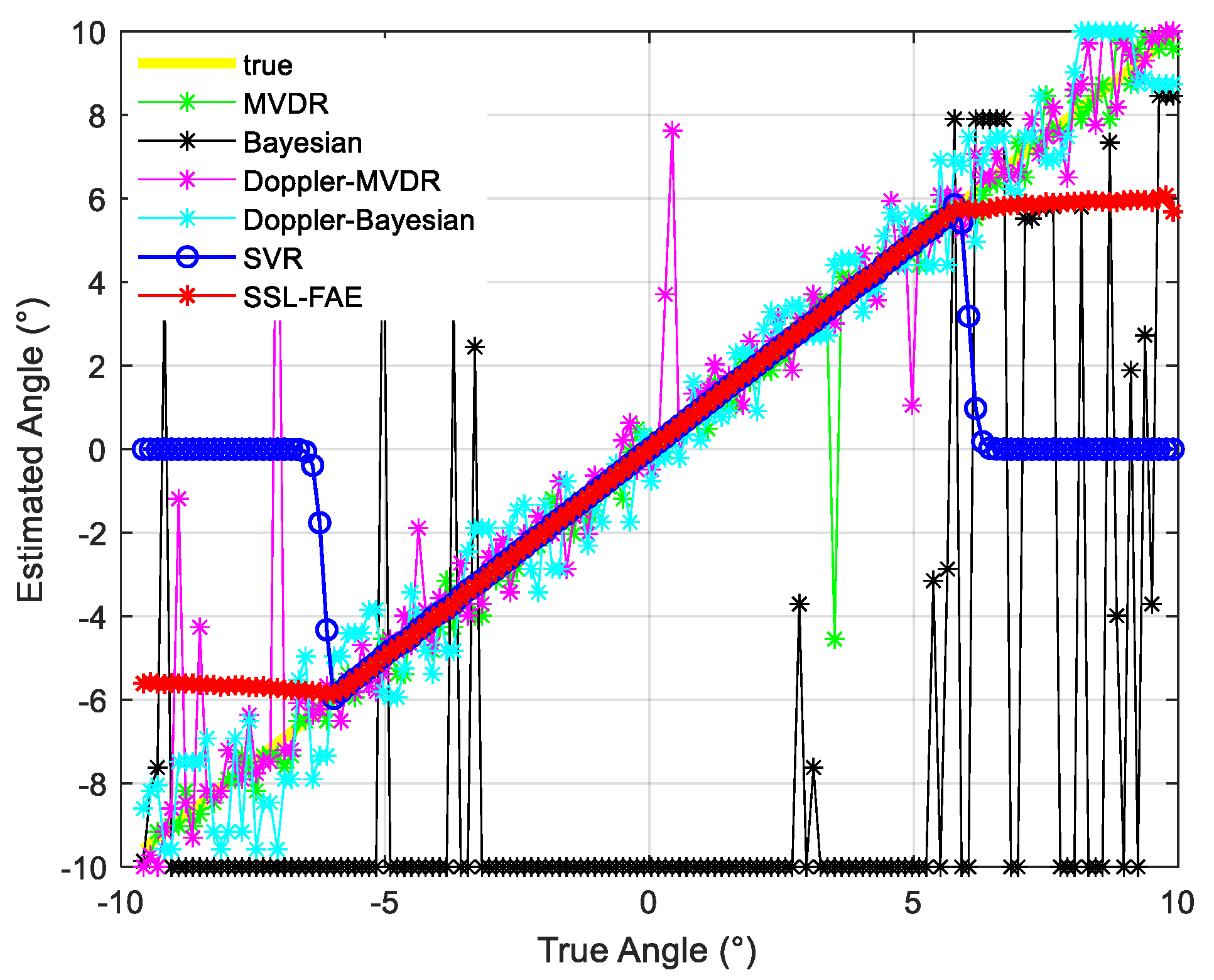
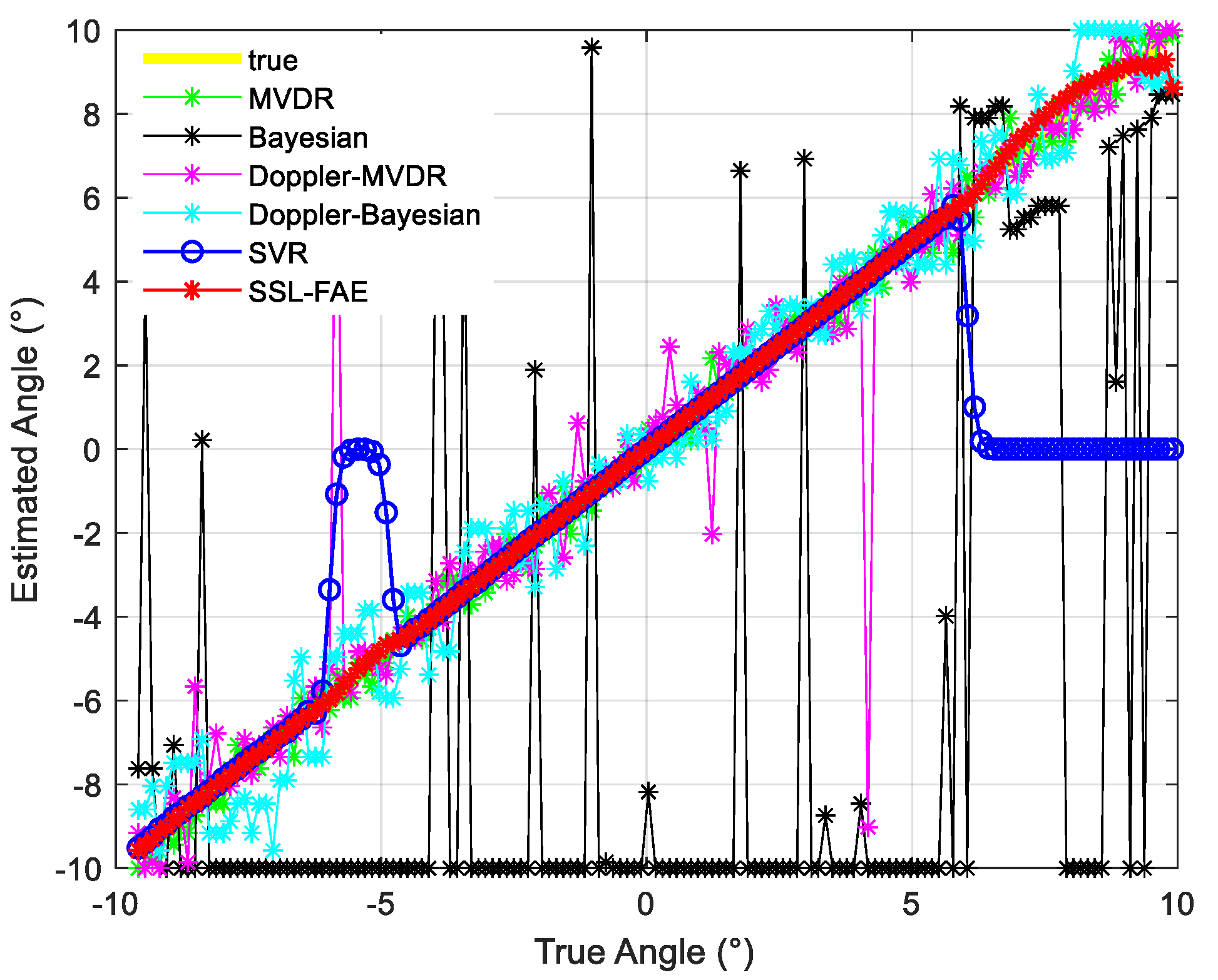
3.1. Experiment 1
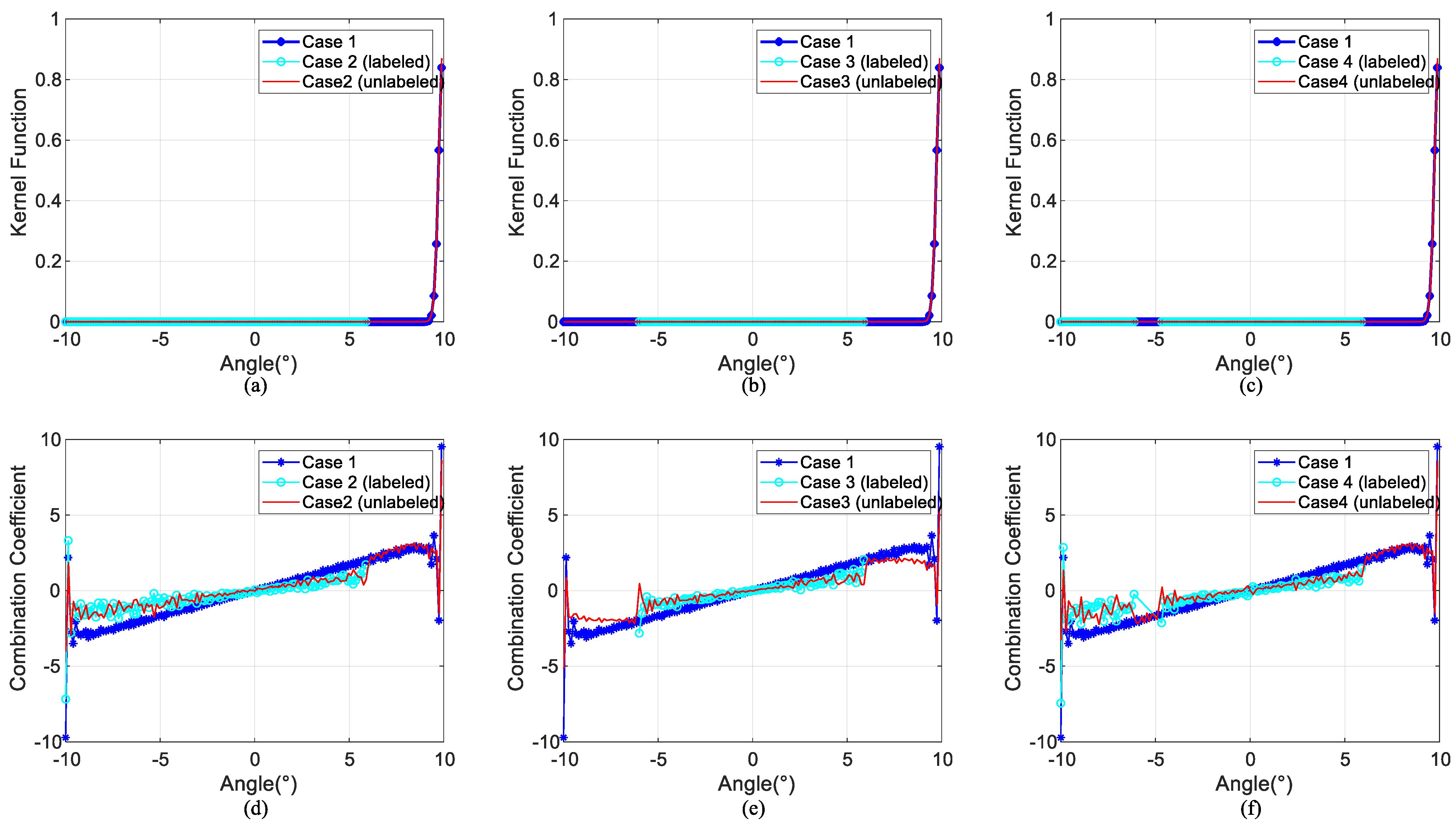
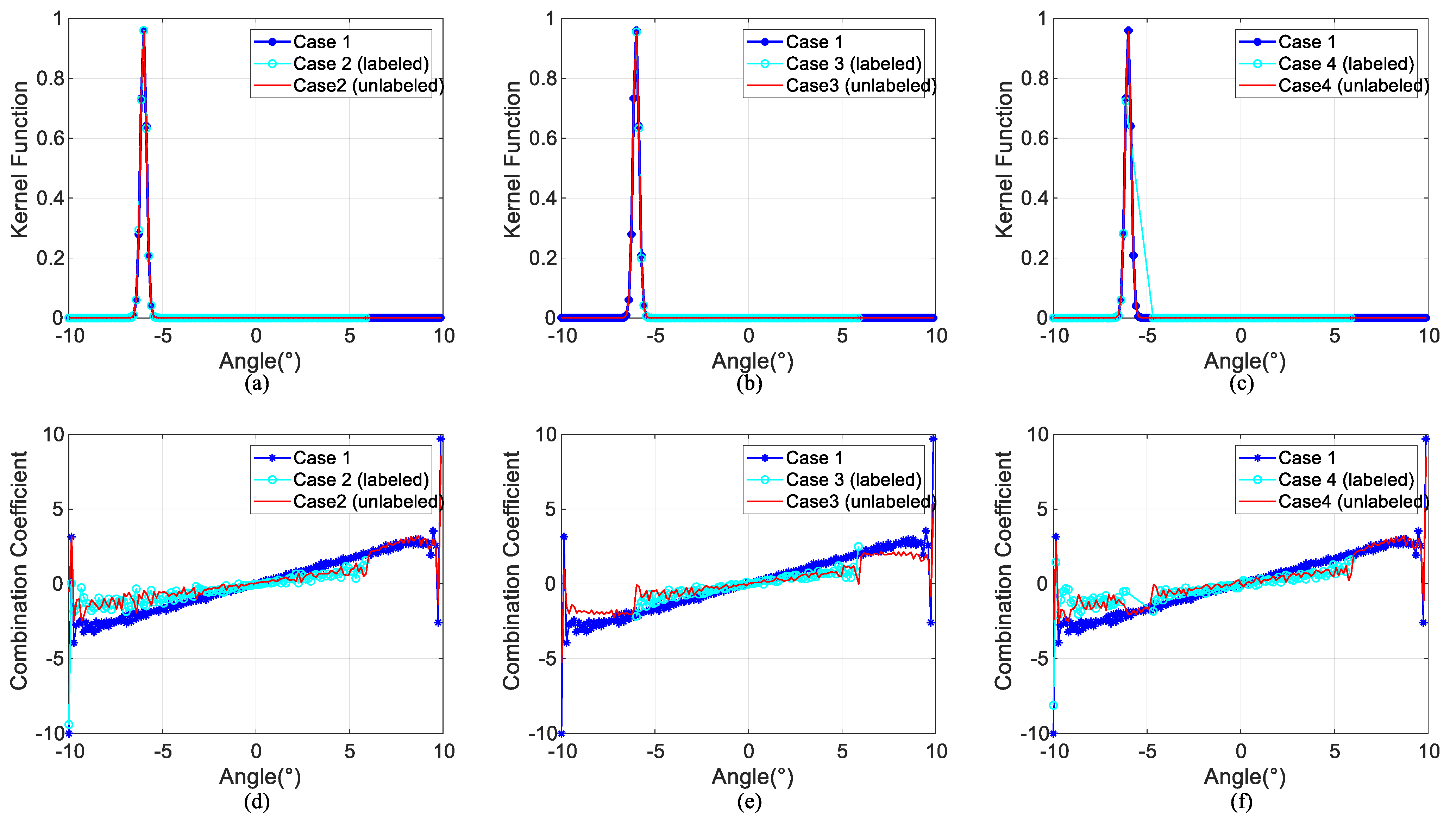
3.1.1. Case 1
3.1.2. Case 2
3.1.3. Case 3
3.1.4. Case 4
3.1.5. Case 5
3.2. Experiment 2
3.3. Experiment 3
3.4. Experiment 4
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FLR | Forward-looking radar |
| SVR | Support vector regression |
| SNR | Signal-to-noise ratio |
| APD | Antenna pattern deconvolution |
| SVM | Support vector machines |
| ASP | Array signal processing |
| SSL-FAE | Semi-supervised learning framework for FLR angle estimation |
| MVDR | Minimum variance distortionless response |
| CS | Compressive sensing |
| RKHS | Reproducing kernel Hilbert space |
| RBF | Radial basis function |
| SCR | Signal-to-clutter ratio |
References
- Chen, H.; Li, Y.; Gao, W.; Zhang, W.; Sun, H.; Guo, L.; Yu, J. Bayesian Forward-Looking Superresolution Imaging Using Doppler Deconvolution in Expanded Beam Space for High-Speed Platform. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Huang, Y.; Li, W.; Yang, J. Angular Superresolution for Scanning Radar with Improved Regularized Iterative Adaptive Approach. IEEE Trans. Geosci. Remote Sens. 2016, 13, 846–850. [Google Scholar] [CrossRef]
- Chen, H.M.; Li, M.; Wang, Z.; Lu, Y.; Zhang, P.; Wu, Y. Sparse Super-resolution Imaging for Airborne Single Channel Forward-looking Radar in Expanded Beam Space via l p Regularisation. Electron. Lett. 2015, 51, 863–865. [Google Scholar] [CrossRef]
- Dropkin, H.; Ly, C. Superresolution for scanning antenna. In Proceedings of the 1997 IEEE National Radar Conference, Syracuse, New York, NY, USA, 13–15 May 1997; pp. 306–308. [Google Scholar]
- Li, Y.; Liu, J.; Jiang, X.; Huang, X. Angular Superresol for Signal Model in Coherent Scanning Radars. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 3103–3116. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Li, W.; Huang, Y.; Yang, J. Super-Resolution Surface Mapping for Scanning Radar: Inverse Filtering Based on the Fast Iterative Adaptive Approach. IEEE Trans. Geosci. Remote Sens. 2018, 56, 127–144. [Google Scholar] [CrossRef]
- Zhang, Y.; Jakobsson, A.; Zhang, Y.; Huang, Y.; Yang, J. Wideband Sparse Reconstruction for Scanning Radar. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6055–6068. [Google Scholar] [CrossRef]
- Zhu, R.; Wen, J.; Xiong, X. Forward-looking imaging algorithm for airborne radar based on beam-space multiple signal classification. In Proceedings of the 2020 IEEE 20th International Conference on Communication Technology (ICCT), Nanning, China, 28–31 October 2020; pp. 1276–1280. [Google Scholar]
- Zha, Y.; Huang, Y.; Sun, Z.; Wang, Y.; Yang, J. Bayesian Deconvolution for Angular Super-Resolution in Forward-Looking Scanning Radar. Sensors 2015, 15, 6924–6946. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhang, Q.; Li, C.; Zhang, Y.; Huang, Y.; Yang, J. Sea-Surface Target Angular Superresolution in Forward-Looking Radar Imaging Based on Maximum A Posteriori Algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2822–2834. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, Y.; Huang, Y.; Zhang, Y. Azimuth Superresolution of Forward-Looking Radar Imaging Which Relies on Linearized Bregman. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2032–2043. [Google Scholar] [CrossRef]
- Yang, J.; Kang, Y.; Zhang, Y.; Huang, Y.; Zhang, Y. A Bayesian angular superresolution method with lognormal constraint for sea-surface target. IEEE Access 2020, 8, 13419–13428. [Google Scholar] [CrossRef]
- Duarte, M.F.; Baraniuk, R.G. Spectral compressive sensing. Appl. Comput. Harmon. Anal. 2013, 35, 111–129. [Google Scholar] [CrossRef]
- Chi, Y.; Scharf, L.L.; Pezeshki, A.; Calderbank, A.R. Sensitivity to basis mismatch in compressed sensing. IEEE Trans. Signal Process. 2011, 59, 2182–2195. [Google Scholar] [CrossRef]
- Herman, M.A.; Strohmer, T. General deviants: An analysis of perturbations in compressed sensing. IEEE J. Sel. Top. Signal Process. 2010, 4, 342–349. [Google Scholar] [CrossRef]
- Wang, M.; Yang, S.; Wu, S.; Luo, F. A RBFNN Approach for DoA Estimation of Ultra Wideband Antenna Array. Neurocomputing 2008, 71, 631–640. [Google Scholar] [CrossRef]
- Xiao, X.; Zhao, S.; Zhong, X.; Jones, D.L.; Chng, E.S.; Li, H. A Learning-Based Approach to Direction of Arrival Estimation in Noisy and Reverberant Environments. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, QLD, Australia, 19–24 April 2015; pp. 2814–2818. [Google Scholar] [CrossRef]
- Chakrabarty, S.; Habets, E.A.P. Broadband Doa Estimation Using Convolutional Neural Networks Trained with Noise Signals. In Proceedings of the 2017 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 15–18 October 2017; pp. 136–140. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, J.; Yuen, C.; Rahardja, S. Indoor Sound Source Localization with Probabilistic Neural Network. IEEE Trans. Ind. Electron. 2018, 65, 6403–6413. [Google Scholar] [CrossRef]
- Liu, Z.M.; Zhang, C.; Yu, P.S. Direction-of-Arrival Estimation Based on Deep Neural Networks with Robustness to Array Imperfections. IEEE Trans. Antennas Propag. 2018, 66, 7315–7327. [Google Scholar] [CrossRef]
- Lo, T.; Leung, H.; Litva, J. Radial Basis Function Neural Network for Direction-of-Arrivals Estimation. IEEE Signal Process. Lett. 1994, 1, 45–47. [Google Scholar] [CrossRef]
- El Zooghby, A.; Christodoulou, C.; Georgiopoulos, M. A Neural Network-Based Smart Antenna for Multiple Source Tracking. IEEE Trans. Antennas Propag. 2000, 48, 768–776. [Google Scholar] [CrossRef]
- Randazzo, A.; Abou-Khousa, M.A.; Pastorino, M.; Zoughi, R. Direction of Arrival Estimation Based on Support Vector Regression: Experimental Validation and Comparison with MUSIC. IEEE Antennas Wirel. Propag. Lett. 2007, 6, 379–382. [Google Scholar] [CrossRef]
- Dehghanpour, M.; Vakili, V.T.; Farrokhi, A. DOA Estimation Using Multiple Kernel Learning SVM Considering Mutual Coupling. In Proceedings of the 2012 Fourth International Conference on Intelligent Networking and Collaborative Systems, Bucharest, Romania, 19–21 September 2012; pp. 55–61. [Google Scholar] [CrossRef]
- Ashok, C.; Venkateswaran, N. Support Vector Regression Based DOA Estimation in Heavy Tailed Noise Environment. In Proceedings of the 2016 International Conference on Wireless Communications, Signal Processing and Networking (WiSPNET), Chennai, India, 23–25 March 2016; pp. 99–102. [Google Scholar] [CrossRef]
- Venkateswaran, N.; Ashok, C. DOA Estimation of Near-Field Sources Using Support Vector Regression. In Proceedings of the 2016 IEEE Region 10 Conference (TENCON), Singapore, 22–25 November 2016; pp. 1570–1574. [Google Scholar] [CrossRef]
- Kabaoglu, N. Target Tracking Using Particle Filters with Support Vector Regression. IEEE Trans. Veh. Technol. 2009, 58, 2569–2573. [Google Scholar] [CrossRef]
- Ozer, S.; Cirpan, H.; Kabaoglu, N. Support Vector Machines Based Target Tracking Techniques. In Proceedings of the 2006 IEEE 14th Signal Processing and Communications Applications, Antalya, Turkey, 17–19 April 2006; pp. 1–4. [Google Scholar] [CrossRef]
- Kabaoğlu, N.; Çırpan, H.A. Wideband Target Tracking by Using SVR-based Sequential Monte Carlo Method. Signal Process. 2008, 88, 2804–2816. [Google Scholar] [CrossRef]
- Wu, L.L.; Huang, Z.T. Coherent SVR Learning for Wideband Direction-of-Arrival Estimation. IEEE Signal Process. Lett. 2019, 26, 642–646. [Google Scholar] [CrossRef]
- Wu, L. Array Signal Processing Based on Machine Learning. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2022. [Google Scholar]
- Perry, R.P.; DiPietro, R.C.; Fante, R.L. Coherent Integration with Range Migration Using Keystone Formatting. In Proceedings of the 2007 IEEE Radar Conference, Waltham, MA, USA, 17–20 April 2007; pp. 863–868. [Google Scholar] [CrossRef]
- Li, W.; Li, M.; Zuo, L.; Chen, H.; Wu, Y. Real aperture radar forward-looking imaging based on variational Bayesian in presence of outliers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Z.; Zhang, Y.; Jin, X.; Gao, W.; Yu, J. Data-driven airborne bayesian forward-looking superresolution imaging based on generalized Gaussian distribution. Front. Signal Process. 2023, 3, 1093203. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y. A generalized MVDR spectrum. IEEE Signal Process. Lett. 2005, 12, 827–830. [Google Scholar] [CrossRef]
- Wen, X.; Kuang, G.; Hu, J.; Zhan, R.; Zhang, J. Forward-looking imaging of scanning phased array radar based on the compressed sensing. Prog. Electromagn. Res. 2013, 143, 575–604. [Google Scholar] [CrossRef]
- Chen, L.; Tsang, I.W.; Xu, D. Laplacian Embedded Regression for Scalable Manifold Regularization. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 902–915. [Google Scholar] [CrossRef] [PubMed]
- Hernández, N.; Biscay, R.J.; Talavera, I. Support Vector Regression Methods for Functional Data. In Progress in Pattern Recognition, Image Analysis and Applications; Rueda, L., Mery, D., Kittler, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 4756, pp. 564–573. [Google Scholar] [CrossRef]
- Shen, X.J.; Dong, Y.; Gou, J.P.; Zhan, Y.Z.; Fan, J. Least Squares Kernel Ensemble Regression in Reproducing Kernel Hilbert Space. Neurocomputing 2018, 311, 235–244. [Google Scholar] [CrossRef]
- Beale, R.; Jackson, T. Neural Computing—An Introduction; CRC Press: Boca Raton, FL, USA, 1990. [Google Scholar]



| Parameter | Symbol | Value |
|---|---|---|
| frequency | 77 GHz | |
| bandwidth | 2 GHz | |
| pulsewidth | T | 2 s |
| pulse repetition frequency | PRF | 10 kHz |
| altitude | H | 100 m |
| velocity | v | 0–250 km/h |
| Symbol | Value |
|---|---|
| 0.1 | |
| 0.1 |
| 10 m/s | 40 m/s | 70 m/s | 100 m/s | 130 m/s | 160 m/s | |
|---|---|---|---|---|---|---|
| SVR | ||||||
| SSL-FAE |
| MVDR | Bayesian | Doppler–MVDR | Doppler–Bayesian | SVR | SSL-FAE | |
|---|---|---|---|---|---|---|
| Training | - | - | - | - | 0.3399 s | 1.5508 s |
| Estimation | 0.0874 s | 0.0055 s | 0.4118 s | 0.0073 s | 0.0016 s | 0.0028 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Xu, X.; Xu, Y.; Luan, Y.; Tang, H.; Chen, L.; Zhang, F.; Liu, J.; Yu, J. Angle Estimation Using Learning-Based Doppler Deconvolution in Beamspace with Forward-Looking Radar. Remote Sens. 2024, 16, 2840. https://doi.org/10.3390/rs16152840
Li W, Xu X, Xu Y, Luan Y, Tang H, Chen L, Zhang F, Liu J, Yu J. Angle Estimation Using Learning-Based Doppler Deconvolution in Beamspace with Forward-Looking Radar. Remote Sensing. 2024; 16(15):2840. https://doi.org/10.3390/rs16152840
Chicago/Turabian StyleLi, Wenjie, Xinhao Xu, Yihao Xu, Yuchen Luan, Haibo Tang, Longyong Chen, Fubo Zhang, Jie Liu, and Junming Yu. 2024. "Angle Estimation Using Learning-Based Doppler Deconvolution in Beamspace with Forward-Looking Radar" Remote Sensing 16, no. 15: 2840. https://doi.org/10.3390/rs16152840
APA StyleLi, W., Xu, X., Xu, Y., Luan, Y., Tang, H., Chen, L., Zhang, F., Liu, J., & Yu, J. (2024). Angle Estimation Using Learning-Based Doppler Deconvolution in Beamspace with Forward-Looking Radar. Remote Sensing, 16(15), 2840. https://doi.org/10.3390/rs16152840






