Abstract
Topography critically affects the occurrence of soil erosion, and computing slope spectrum information entropy (SSIE) allows for the convenient mirroring of the patterns of macroscopic topographic variation. However, whether SSIE can be effectively utilized for the quantitative assessment of soil erosion across various types of water-erosion areas and the specific methodology for its application remain unclear. This study focused on the quantitative relationship between SSIE, the slope length and slope steepness (LS) factor within various types of water-erosion areas across different spatial scales in China using multi-source geographic information data and technical tools such as remote sensing and geographic information systems. The results revealed (1) clear consistency in the spatial patterns of SSIE and the LS factor, which both displayed a distinct three-step distribution pattern from south to north. (2) The power model (Y = A·X^B) demonstrated a superior capacity to explaining the relationship between SSIE and the LS factors compared to the linear or exponential models, as evidenced by a higher coefficient of determination (R2). R2 values of different evaluation units (second-grade water-erosion area, third-grade water-erosion area, 30 km × 30 km grid, and 15 km × 15 km grid) were 0.88, 0.88, 0.81, and 0.79, respectively. (3) Despite a range of variances across various spatial scale evaluation units and different types of water-erosion areas, no significant disparities were evident within the power model. These findings offer a new topographic factor that can be incorporated into models designed for the expedited evaluation of soil erosion rates across water-erosion areas. Information about the proximity of the SSIE to the LS factor is valuable for enhancing the practical utilization of SSIE in the quantitative evaluation of soil erosion.
1. Introduction
Soil erosion has progressively emerged as a crucial hindrance to the sustainable development of the global economy and society [1,2,3]. Compared to wind and freeze–thaw erosion, water erosion has evolved into the most significant and widespread form of soil erosion and surface dynamic processes [4,5]. According to statistics, approximately 1000 hectares of farmland are impacted by soil erosion globally each year [6]. China’s extensive geographical expanse and the complexity of its natural, economic, and social conditions have facilitated extensive and diverse soil erosion across various regions. The water-erosion areas in China can be divided into six first-grade water-erosion areas [7], namely, the Northeastern Mollison (NEM), North earth-Stone (NS), Northwestern Loess Plateau (NWL), South red Soil (SR), Southwestern purple Soil (SWP), and Southwestern karst (SWK). Soil erosion remains one of the most pressing ecological and environmental concerns, particularly in the NEM [8,9], NWL [10,11,12], SR [13], and SWK [14,15,16]. Climatic conditions are the primary factor determining variations in natural environmental conditions on the earth’s surface. Topography is vital in controlling the redistribution of surface materials and energy [17] and influencing the intensity of human activities. It also has a crucial effect on regional soil erosion. Hence, choosing topographic factors capable of rapidly estimating the amount of soil erosion and assessing soil erosion intensity can contribute to a novel scientific approach for monitoring and evaluating the ecological impacts of soil and water conservation efforts.
Researchers in China and internationally have extensively investigated the mechanisms and influencing factors of the soil erosion process. They have established comprehensive foundational databases for soil erosion and have made substantial advancements in soil erosion model research, and the outcomes are useful. Soil erosion prediction models are vital for the quantitative forecasting and prediction of soil erosion [18]. They are paramount in soil and water conservation as well as ecological environment development and construction. The slope length and slope steepness (LS) factor [19] serves as a metric for assessing the impact of topographic characteristics on soil erosion and is essential for conducting regional soil erosion assessments and estimating soil erosion using both the Universal Soil Loss Equation [20,21] and Revised Universal Soil Loss Equation (RUSLE) [22,23]. Nonetheless, acquiring the LS factor is intricate and fraught with significant uncertainty [24,25,26,27]. This complexity makes it unsuitable for rapidly estimating the amount and intensity of soil erosion at the macro-scale.
In 2003, Tang et al. [28] introduced the slope spectrum theory while investigating the optimal digital elevation model (DEM) resolution for extracting slope values on the Loess Plateau (China). This theory effectively captures the undulation patterns of the regional macro topology [29]. Research on the slope spectrum theory has produced notable findings, particularly in the Loess Plateau region [30,31]. This encompasses the exploration of the impact of various classification methods and classification variances in the surface slope spectrum [32], as well as the revelation of fundamental conditions for the extraction and application of the slope spectrum [33]. Moreover, it introduces the concept of slope spectrum information entropy (SSIE) to quantify slope spectrum characteristics. The findings also demonstrate that SSIE can effectively depict surface complexity [34] and exhibits a power function relationship with the gully density [35]. At present, based on the DEM, some scholars have analyzed the slope spectrum characteristics of areas with severe soil erosion, such as the Pisha sandstone areas [36], the purple soil area [37], and the rocky mountain area [38]. The slope spectrum theory has been used to quantify the slope spectrum uniformity using the SSIE method, and the spatial difference in SSIE has been discussed, the relationship between SSIE and LS factors clarified, and the application field of the slope spectrum broadened. However, the relationship between SSIE and LS factors and soil erosion intensity in different types of water-erosion areas has not yet been fully elucidated, and the application and promotion of SSIE at different spatial scales have not been effectively verified.
Hence, a systematic analysis of the relationship between SSIE and the LS factor, as well as soil erosion intensity in various types of water-erosion areas in China, is vital. This analysis is conducted using Advanced Spaceborne Thermal Emission and Reflection Radiometer Global Digital Elevation Model (ASTER GDEM) data with a 30 m resolution and soil erosion data estimated using the RUSLE model. It aims to address the uncertainties associated with LS factor calculations. The objectives of this research are as follows: (1) Identify the spatial distribution patterns of SSIE and LS factors within different water-erosion areas in China. (2) Assess the performance of diverse models (i.e., linear, power, and exponential models) in simulating the correlation between SSIE and the LS factor. (3) Determine the best regression model for SSIE and LS factors in each water-erosion area. This study aims to comprehensively elucidate the spatial patterns of topographic undulations in various types of water-erosion areas across China using SSIE. The analysis seeks to elucidate the distinct topographic and geomorphological characteristics present in these diverse water-erosion areas. This research presents novel scientific approaches for assessing and predicting soil erosion within different water-erosion areas in China. Meanwhile, it holds relevance as a reference for the swift quantitative evaluation of soil erosion in diverse global regions.
2. Materials and Methods
2.1. Study Area
This study focuses on the six first-grade water-erosion areas [7] designated by the Ministry of Water Resources of the People’s Republic of China. These regions (Figure 1) are identified as the NEM, NS, NWL, SR, SWP, and SWK. The NEM region is one of the three major black soil regions globally [39], covering approximately 12% of the total global black soil [40]. This region features a remarkably high forest coverage rate and is vital in commercial grain production within China [41]. However, the region has faced significant challenges due to prolonged and extensive deforestation, as well as excessive land reclamation. The NS area is characterized by mountainous and hilly landscapes within a temperate, semi-humid, and semi-arid climate. The high gravel content in the soil in this region predisposes it to erosion, especially during heavy summer rainfall [38,42]. The NWL is considered one of the most severely eroded regions in the world, primarily due to its extensive distribution and the deep layers of loose loess soil [12]. The SWP is known for its distinctive soil resource, purple soil. This type of soil has a loose structure [43,44] and faces challenges due to limited arable land per capita in the region and over-cultivation. Consequently, this has led to significant soil and water loss problems in hilly areas and under forests [45]. The SWK is the most extensively developed among the three major karst landforms globally [46,47], and it features the largest exposed expanse of carbonate rock. Owing to its unique geological, hydrological, and climatic characteristics [48], coupled with the significant challenges posed by human activities and land resource management [49], the rate of soil erosion in this region markedly exceeds that of soil formation. The specific characteristics of the six first-grade water-erosion areas in China are detailed in Table 1.
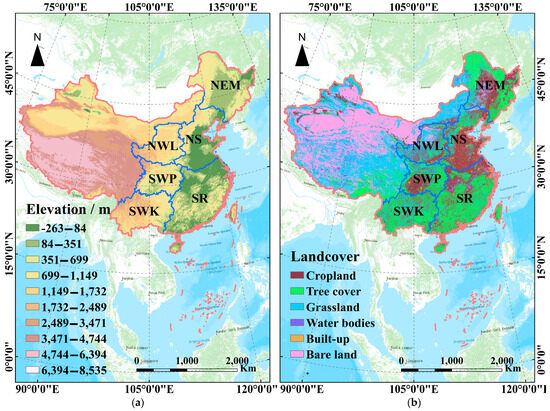
Figure 1.
Elevation (a) and landcover map (b) of water-erosion areas in China. NEM: Northeastern Mollison, NS: North earth-stone, NWL: Northwestern Loess Plateau, SR: South red soil, SWP: Southwestern purple soil, SWK: Southwestern karst. Note: The elevation data (https://www.resdc.cn/data.aspx?DATAID=123, accessed on 7 July 2023) and the 2020 landcover data (https://www.resdc.cn/DOI/DOI.aspx?DOIID=54, accessed on 7 July 2023) were downloaded from Resource and Environment Science and Data Center.

Table 1.
Overview of Water-Erosion Areas in China.
2.2. Data Collection and Preprocessing
The elevation data for the water-erosion areas were obtained from ASTER GDEM and downloaded from the Geospatial Data Cloud of the Chinese Academy of Sciences (https://www.gscloud.cn/, accessed on 7 July 2023). The data have a spatial resolution of 30 m. In this paper, the spatial reference of all layers was “WGS_1984_Lambert_Conformal_Conic”.
The soil erosion data for water-erosion areas were sourced from the 2015 soil erosion grid dataset of China, which was estimated by Li et al. [50] using the RUSLE model. This dataset had a spatial resolution of 1 km, with units expressed as t hm−2 a−1. The soil erosion intensity for each grid was categorized based on the Soil Erosion Classification and Grading Standard (SL190-2007) issued by the Ministry of Water Resources, People’s Republic of China [51]. The classification comprised six levels: very slight, slight, moderate, severe, very severe, and extremely severe.
To enhance the robustness and practicality of the research outcomes, a total of 4626 grids, each covering an area of 900 km2, along with 20,177 grids spanning 225 km2, were generated within China’s water-erosion areas. The study investigated the potential of SSIE to express soil erosion intensity and LS factor within four spatial scale evaluation units (second-grade water-erosion areas, third-grade water-erosion areas, 30 km × 30 km grid, and 15 km × 15 km grid).
2.3. Extraction of the Slope Spectrum and Calculation of Slope Spectrum Information Entropy
A slope spectrum curve is a graphical representation that displays the proportion of the area covered by each grade of slope segment within a particular statistical area. The slope spectrum curve generated using the 3° isometric classification method accurately portrays the collective attributes of ground slope [32]. Its calculation formula is presented in Equation (1):
represents the area frequency of the Grade i slope segment; stands for the area of the Grade i slope segment; and n represents the total area of a particular statistical area.
Wang et al. [52] indicated that a region must have an area greater than 30 km2 to acquire stable and dependable slope spectrum information. The smallest evaluation unit used in this study covered an area of 225 km2, which aligned with the requirements for slope spectrum information research.
In this paper, we utilized the SSIE, as defined by Li et al. [35], to gauge the variation in data frequencies among different groups within the slope spectrum curve. Its calculation formula is presented in Equation (2):
H represents the SSIE; n stands for the classification number in the 3° isometric classification method; represents the area frequency of the Grade i slope segment.
2.4. Calculation of Slope Length and Steepness Factor
This study computed the LS factor for the water-erosion area using DEM data, following the method employed in the comprehensive survey of soil and water conservation in China. The calculation formula is presented in Equations (3)–(6):
where L represents the slope length factor, λ signifies the slope length value extracted from DEM data, m denotes the slope length index, θ represents the slope value extracted from DEM data, and S represents the slope factor.
L = (λ/22.1) m
LS = L × S
2.5. Methods for Data Analysis
Regression analysis was used to analyze the relationship between SSIE and the LS factor. The selection of the optimal regression model for SSIE and LS factor was based on the determination coefficient (R2) of the regression model (linear model Y = A·X + B, power model Y = A·X^B, and exponential model Y = A·e^B·X). The formula for R2 is shown in Equation (7):
where N is the sample number, represents the true value of the slope length factor, represents the predicted value of the slope length factor obtained through regression analysis, and represents the average value of the true slope length factor values.
All statistical analysis and regression predictions were implemented in MATLAB R2022a [53] and Origin 2022.
3. Results
3.1. Distribution Characteristics of Slope Spectrum Curve and Topographic Factors
3.1.1. Characteristics of Slope Spectrum Curves in Various Types and Spatial Scales of Water-Erosion Areas
Apart from the two peaks observed in the slope spectrum within the SWK, all other slope spectrums of first-grade water-erosion areas are unimodal (Figure 2). These peaks generally fall within the range of 0–3°, although the peak values vary significantly between different regions. The order of peaks, ranging from the highest to the lowest, is as follows: the NS (51.09%), NEM (45.70%), SR (30.41%), NWL (22.98%), and SWP (10.89%) (Figure 2). This sequence corresponds to the overall topographical gradient, which transitions from gentle terrain to steeper landscapes. The variation in the slope spectrum curve can effectively reflect the difference in geomorphology of different types of water-erosion areas. No significant disparities were observed in the slope spectrum of the respective second-grade water-erosion areas (Figure 3) within the first-grade water-erosion areas. Notably, the slope spectrum curves of the corresponding second-grade water-erosion areas in the NEM and the NS exhibited substantial overlap. This suggests that the geomorphological features of the NEM resemble those of the second-grade water-erosion areas in the NS.
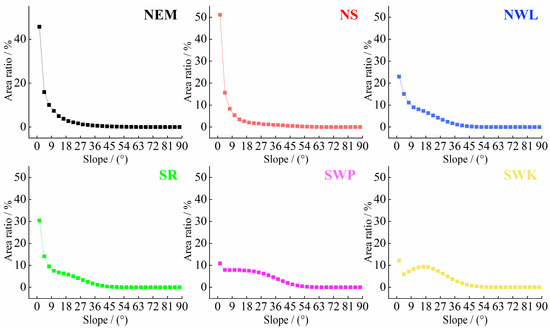
Figure 2.
Slope spectrum curves of the first-grade water-erosion areas. NEM: Northeastern Mollison, NS: North earth-stone, NWL: Northwestern Loess Plateau, SR: South red soil, SWP: Southwestern purple soil, SWK: Southwestern karst.
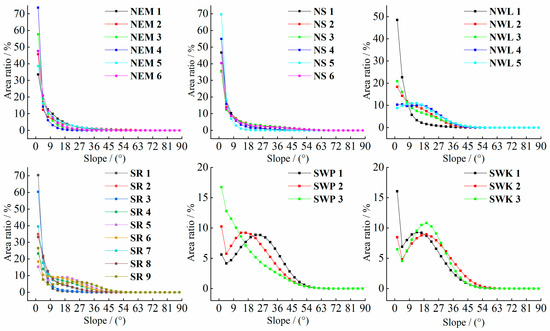
Figure 3.
Slope spectrum curves of the second-grade water-erosion areas. NEM: Northeastern Mollison, NS: North earth-stone, NWL: Northwestern Loess Plateau, SR: South red soil, SWP: Southwestern purple soil, SWK: Southwestern karst. The legend (e.g., NEM 1, NS 1, NWL 1) denotes the second-grade water-erosion areas within various first-grade water-erosion areas.
3.1.2. Spatial Patterns of SSIE in Different Types of Water-Erosion Areas
Generally, the SSIE values exhibit a spatial distribution pattern characterized by an increase from north to south and a decrease from the western to the eastern coast (Figure 4). High values occurred in the southern non-coastal area of the SR, the marginal area of the SWP, and the SWK. Low SSIE values were observed in several regions, including the Northeast China Plain in the middle of the NEM, the North China Plain within the NS, the relatively flat Ordos Plateau in the northwest portion of the NWL, and the Jianghuai Plains with numerous lakes in the northeastern part of the SR. The mean value of SSIE across China’s first-grade water-erosion areas exhibited a distinct three-step distribution pattern from south to north. The highest mean SSIE values are in the SWK and SWP, measuring 2.64 and 2.63 nat, respectively. Conversely, the lowest mean SSIE values are in the NEM and the NS, with values of 1.74 and 1.76 nat, respectively. The mean SSIE values for the NWL and the SR fall between 2.24 and 1.99 nat, respectively. The values of SSIE exhibit the highest degree of variability (with a standard deviation of 0.63) in the SR. Across this area, the values decrease gradually from the southeast to the northeast, ranging from 2.71 to 0.55 nat. Conversely, the SWK displays the lowest level of dispersion in its values (with a standard deviation of 0.09). In this region, the SSIE consistently exhibits high values.
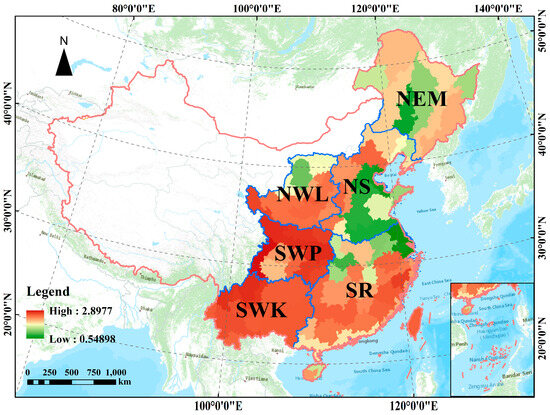
Figure 4.
Spatial distribution pattern of slope spectrum information entropy in water-erosion regions. NEM: Northeastern Mollison, NS: North earth-stone, NWL: Northwestern Loess Plateau, SR: South red soil, SWP: Southwestern purple soil, SWK: Southwestern karst.
3.1.3. Spatial Patterns of LS Factor in Different Types of Water-Erosion Areas
The spatial distribution of LS factors in various types of water-erosion areas in China was mapped using the methodology outlined in the fourth soil erosion census of China. Spatially, the distribution pattern of the LS factor and SSIE exhibit a high degree of consistency (Figure 4 and Figure 5), with pronounced north–south variations. High values of the LS factor are primarily concentrated in several regions: the Loess Plateau area with significant soil erosion; the southeastern hilly area within one of China’s three major hilly regions, the western, northern, and eastern regions of the SWP; and the Yunnan–Guizhou Plateau area, which is one of the three major karst landforms globally. Conversely, low values of the LS factor were primarily concentrated in the northeast plain of the NEM area and the North China plain of the NS. The mean values (<2, ≈6, >10) of LS factors and their main distribution ratios are similar (Figure 6a) in three groups (group 1: the NEM and the NS; group 2: the NWL and the SR; group 3: the SWP and the SWK). Specifically, the proportions of 0–5 (87.51–89.96%, 62.35–64.81%, 43.58–44.07%), 5–10 (4.91–6.93%, 12.57–13.22%, 14.05–15.69%), and >20 (0.60–0.98%, 10.07–10.76%, and 21.79–23.64%) in the three groups exhibit a similar distribution pattern.
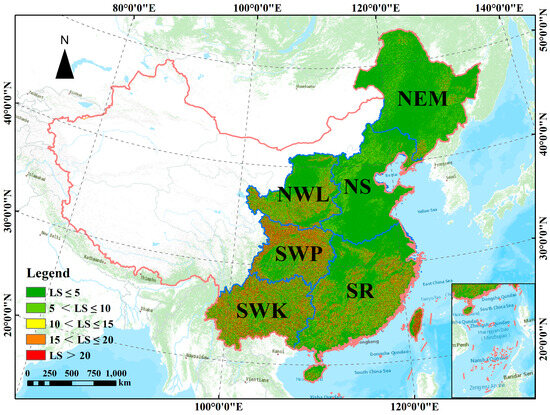
Figure 5.
Spatial distribution pattern of slope length and steepness factor in water-erosion regions. NEM: Northeastern Mollison, NS: North earth-stone, NWL: Northwestern Loess Plateau, SR: South red soil, SWP: Southwestern purple soil, SWK: Southwestern karst.
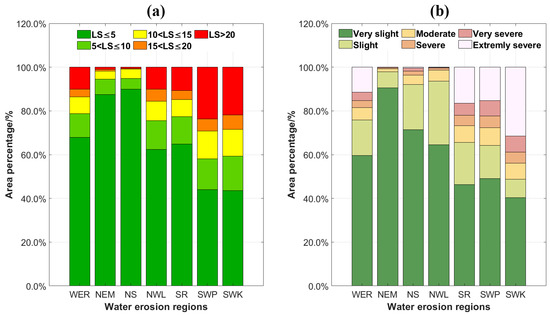
Figure 6.
Grade proportion of the slope length and steepness factor (a) and the soil erosion intensity (b). WER: Water-Erosion Regions, NEM: Northeastern Mollison, NS: North earth-stone, NWL: Northwestern Loess Plateau, SR: South red soil, SWP: Southwestern purple soil, SWK: Southwestern karst.
3.1.4. Identification of Spatial Hotspots of Soil Erosion in Various Water-Erosion Areas
The spatial distribution map (Figure 7) of soil erosion intensity in water-erosion areas was created based on soil erosion data estimated by the RUSLE model [50], following the guidelines outlined in the Soil Erosion Classification and Grading Standard (SL190-2007).
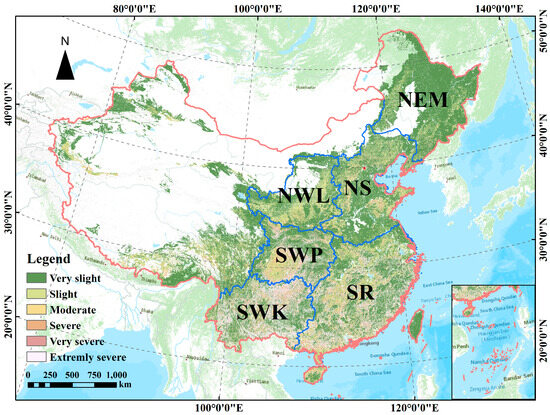
Figure 7.
Spatial distribution pattern of soil erosion intensity in water-erosion regions. NEM: Northeastern Mollison, NS: North earth-stone, NWL: Northwestern Loess Plateau, SR: South red soil, SWP: Southwestern purple soil, SWK: Southwestern karst.
A notable disparity in soil erosion intensity is observed between the water-erosion areas in northern China and those in southern China. Specifically, in the northern water-erosion areas, erosion is very slight and slight, covering 92.14–97.90% of the total area, with extremely severe occupying a minimal portion. Conversely, in the southern water-erosion area, the combined area of very slight and slight erosion corresponds to a narrower range, namely 48.78–65.56% of the total area. However, the area affected by extremely severe erosion constitutes a broader spectrum, ranging from 15.25% to 31.44%. The soil erosion hotspots are concentrated in specific regions, including the Greater Khingan Mountains and Changbai Mountains in the NEM area, the Shandong hills in the eastern part of the NS area, the NWL area, the southeastern hills in the SR area, the Sichuan Basin in the SWP area, and the Yunnan–Guizhou Plateau in the SWK area. Furthermore, there is some consistency between the distribution ratio of the LS factor and soil erosion intensity in the first-grade water-erosion area (Figure 6).
3.2. The Capacity of SSIE to Elucidate the Soil Erosion Intensity
The SSIE for various spatial scale evaluation units (second-grade water-erosion area, third-grade water-erosion area, 30 km × 30 km grid, and 15 km × 15 km grid) is limited in its capacity to elucidate soil erosion intensity, with a goodness of fit score lower than 0.30 (Figure 8). Likewise, even when differentiating between various types of water-erosion areas, the goodness of fit (R2) for the two spatial scale evaluation units remains low (Figures S1 and S2). The above analysis results demonstrate that SSIE is not effective in explaining soil erosion intensity.
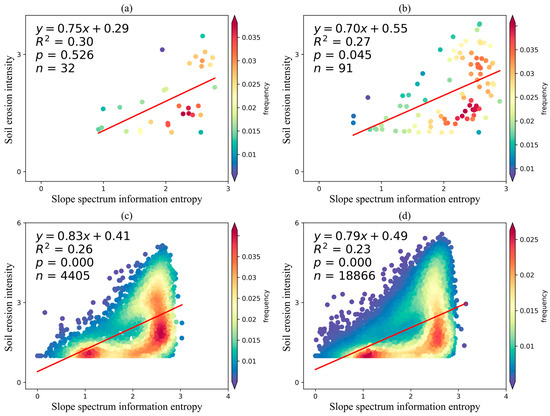
Figure 8.
Capacity of slope spectrum information entropy to elucidate the soil erosion intensity in different spatial scale evaluation units. Second-grade water-erosion area (a), third-grade level water-erosion area (b), 30 km × 30 km sample zone (c), 15 km × 15 km sample zone (d). Red line represents the linear regression line.
3.3. Capacity of SSIE to Elucidate the LS Factor
3.3.1. Capacity of SSIE to Elucidate the LS Factor in Different Evaluation Units
The SSIE-LS power model (Y = AX^B) can effectively elucidate the relationship between SSIE and LS factors within the second-grade water-erosion areas, the third-grade water-erosion areas, as well as the 30 km × 30 km and 15 km × 15 km sample zones (Figure 9). In particular, R2 values of second-grade and third-grade water-erosion areas are close to 0.9. Despite substantial variations in scale and sample sizes across distinct evaluation units, no significant differences are observed in the SSIE-LS power model among the four specific evaluation units. The corresponding A values are 0.07, 0.15, 0.16, and 0.18, respectively, with corresponding B values of 5.12, 4.37, 4.33, and 4.20. The SSIE-LS power models derived from 4626 sample zones of 30 km × 30 km and 20,177 sample zones of 15 km × 15 km exhibit the least difference. Meanwhile, the SSIE-LS power model with the second-grade and third-grade water-erosion areas as evaluation units has a higher application value.
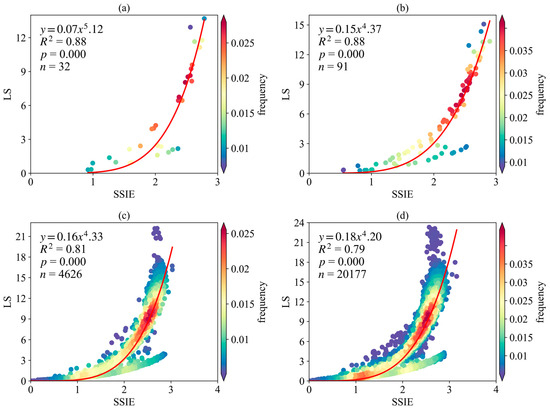
Figure 9.
Capacity of slope spectrum information entropy to elucidate the slope length and steepness factor in different evaluation units. (a): second-grade water-erosion area, (b): third-grade level water-erosion area, (c): 30 km × 30 km sample zone, (d): 15 km × 15 km sample zone. Red line represents the fitted curve.
3.3.2. Capacity of SSIE to Elucidate the LS Factor in Various Types of Water-Erosion Areas
The SSIE-LS power models for each water-erosion area were developed (Figure 10 and Figure 11) based on the disparities in geological structures and geomorphic categories across distinct water-erosion areas (Table 1). This process relied on data derived from the corresponding water-erosion areas and utilized two evaluation units—the 30 km × 30 km sample zone and the 15 km × 15 km sample zone to enhance the goodness of fit (R2) within the SSIE-LS power models. Relative to the SSIE-LS power model spanning the entirety of the water-erosion region, the accuracy of the four distinct water-erosion area models exhibits varying degrees of improvement under the two evaluation units. Specifically, the average increase in R2 is 0.04, 0.16, 0.12, and 0.07 for NS, SR, NWL, and SWP, respectively (Figure 9c and Figure 10b–e; Figure 9d and Figure 11b–e). However, the strength (R2) of the SSIE-LS power model within the NEM and SWK does not demonstrate a substantial enhancement when contrasted with the comprehensive model spanning the entirety of the water-erosion area (Figure 9c,d, Figure 10a,b and Figure 11a,b).
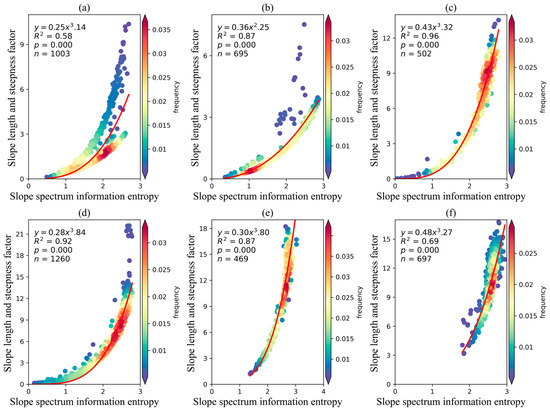
Figure 10.
Capacity of slope spectrum information entropy to elucidate the slope length and slope steepness factor in various types of water-erosion areas under the evaluation unit of the 30 km × 30 km sample zone. Northeastern Mollison (a), North earth-stone (b), Northwestern Loess Plateau (c), South red soil (d), Southwestern purple soil (e), Southwestern karst (f). Red line represents the fitted curve.
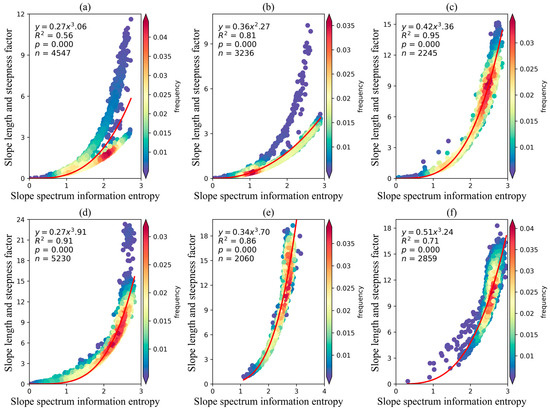
Figure 11.
Relationship between slope spectrum information entropy and slope length and steepness factor in various types of water-erosion areas under the evaluation unit of the 15 km × 15 km sample zone. Northeastern Mollison (a), North earth-stone (b), Northwestern Loess Plateau (c), South red soil (d), Southwestern purple soil (e), Southwestern karst (f). Red line represents the fitted curve.
For the same water-erosion area, the strength of the SSIE-LS power models, as measured by coefficient A and coefficient B, remained similar under the two evaluation units. Except for a notable discrepancy in R2 of up to 0.06 within the SRN, the variations within the other five water-erosion zones remain low, ranging from 0.01 (NWL, SR, and SWP) to 0.02 (NEM and SWK). Regarding coefficient A, the ascending order of differences is as follows: NS (0.00), NWL (0.01), SR (0.01), NEM (0.02), SWK (0.02), and SWP (0.04). For coefficient B, the ascending sequence of differences is as follows: NS (0.02), SWK (0.03), NWL (0.04), SR (0.07), NEM (0.08), and SWP (0.10).
Generally, compared to the linear or exponential models, the power model demonstrates a superior capacity to explain the relationship between SSIE and LS (Figure 12). Specifically, the power model of SSIE-LS outperforms the linear model in all 16 different scenarios (Figure 12a). Although the difference in the simulation effect between the power model and the exponential model is small (Figure 12b), the power model slightly outperforms the exponential model in 10 out of 16 scenarios. Therefore, the power model may be robust enough to simulate the relationship between SSIE and LS.
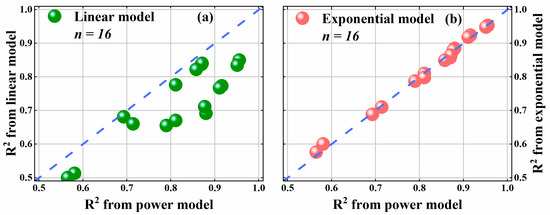
Figure 12.
Comparison of goodness of fit (R2) of power and linear (a)/exponential (b) SSIE-LS models for 16 different scenarios with 4 evaluation units (i.e., second-grade water-erosion area, third-grade level water-erosion area, 30 km × 30 km grid, and 15 km × 15 km grid). The 1:1 line is shown as dashed line.
4. Discussion
This study shows that slope spectrum curves characterizing various types of water-erosion areas in China primarily exhibit “L”, “near-L”, and “near-S” types. This phenomenon is chiefly attributed to the elevated surface fragmentation and more substantial slope variations in the SWP and the SWK of southwestern China when compared to the other four water-erosion areas. These outcomes closely align with the slope spectrum curves observed in mountainous areas with significant topography [54] and in the Pisha sandstone areas with severe soil erosion [36], underscoring that the slope spectrum curves in mountainous regions with deep mountain gullies are more diverse than those in flat plains. The peak values of slope spectrum curves in the five second-grade water-erosion areas districts located in the NWL primarily fall within the range of 0–3° and 12–15°. This differs from the peak values of 25–30° reported by Zhu Mei and colleagues [32] in the hilly and gully region in the northern part of the NWL. The variation can be attributed to the distinctive characteristics of the northern hilly region, which serves as a representative area of the NWL [55]. This region is characterized by an abundance of ravines and complex and diverse landforms, which leads to inherently higher peak values in the slope spectrum curve compared to the entirety of the NWL.
The spatial distribution pattern of SSIE, the LS factor, and soil erosion intensity were strongly consistent within China’s water-erosion areas. This consistency aligns with the actual topographical and geomorphological features of these areas. Typically, mountainous regions, characterized by intricate and rugged terrain, exhibit higher values, whereas plains with relatively flat terrain tend to exhibit lower values [38]. Furthermore, the average LS factor values within the first-grade water-erosion areas in this study show the following ranking from high to low: the SWP (11.03), SWK (10.56), SR (6.18), NWL (6.16), NEM (1.79), and NS (1.37). Notably, these results differ starkly from those of Guo et al. [56], who conducted their research on a 30 km × 30 km scale typical sample area. This disparity can be attributed to the substantial difference in spatial scale between their research and the present study.
The functional relationship between SSIE and soil erosion intensity is not ideal across various spatial scale evaluation units and different types of water-erosion areas. This observation essentially corresponds with the relationship observed in different Pisha sandstone areas concerning soil erosion modulus [36,57]. Notably, soil erosion intensity is influenced by numerous factors, including the natural geographical environment (precipitation intensity, topography effect, and soil types) and human activities [58,59]. Consequently, the functional relationship between SSIE and soil erosion intensity remains uncertain. Nonetheless, the connection between SSIE and the LS factor typically exhibits a notable power function relationship. However, the goodness of fit of the power function model varies across various spatial scale evaluation units and types of water-erosion areas. This aligns with the power function relationship observed by Li et al. [35] in the Loess Plateau of northern Shaanxi when examining the relationship between SSIE and gully density based on mathematical statistics. This finding is incongruent with the logarithmic function model relationship between SSIE and LS factor derived from statistical analysis using counties of various geomorphic types as units of measurement [54]. The disparity in results can be attributed to the different roles of SSIE in constructing the functional relationship models. In the former study, it served as the dependent variable, whereas in this investigation, it was employed as the independent variable in the construction of the functional model. This research aimed to offer insights into the utilization of SSIE in soil erosion studies. Thus, it is in alignment with the research requirements to employ SSIE as an independent variable in the construction of the functional model.
The scatterplot depicting the relationship between SSIE and LS factor exhibits a branching pattern, which is notably pronounced in the NEM and the NS. In future studies, the utilization of big data and advanced machine learning methods, in conjunction with more detailed soil and water conservation zoning and a wider range of topographic factors, can facilitate more comprehensive research on the prediction model for the LS factor. In addition, the use of SSIE to calculate RUSLE instead of LS for the quantitative assessment of soil erosion and the exploration of the differences between the results of LS and SSIE calculations will be key in the next study.
5. Conclusions
This paper employed SSIE as an evaluation index to comprehensively analyze the topographical and geomorphic characteristics of various types of water-erosion areas in China. It quantified the quantitative relationships between SSIE and soil erosion intensity, as well as soil erosion topographic factors, across different water-erosion areas and multi-spatial scale systems (second-grade water-erosion area, third-grade level water-erosion area, 30 km × 30 km grid, and the 15 km × 15 km grid). The main conclusions are as follows.
Within the water-erosion areas of China, a marked coherence was observed in the spatial distribution patterns of SSIE and the LS factor, characterized by a three-step distribution from south to north. Specifically, the southern (i.e., SWP and SWK) and northern water-erosion areas (i.e., NEM and NS) exhibited high and low values, respectively. The fitting relationship between SSIE and soil erosion intensity was weak (R2 < 0.30) across various spatial scale evaluation units and diverse water-erosion areas. Furthermore, to unveil the precise practical utility of SSIE in soil erosion research, a multiscale analysis encompassing 16 distinct scenarios was employed. This analysis quantified the intricate coupling dynamics between SSIE and the LS factor. Notably, the power model (Y = AX^B) exhibited an exceptional capability to elucidate the intricate relationship between these two factors, with an average R2 of 0.82. The LS factor for each water-erosion area could be calculated using the regression equation provided in Section 2. Lastly, while there are variations between different spatial scale evaluation units and different types of water-erosion zones, these differences are not distinctly apparent within the power model.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/rs16152816/s1, Figure S1: The capacity of slope spectrum information entropy to elucidate the soil erosion intensity in various types of water erosion areas under the evaluation unit of the 30 km × 30 km sample zone. Northeastern Mollison (a), North earth-stone (b), Northwestern losses plateau (c), South red soil (d), Southwestern purple soil (e), Southwestern karst (f); Figure S2: The capacity of slope spectrum information entropy to elucidate the soil erosion intensity in various types of water erosion areas under the evaluation unit of the 15 km × 15 km sample zone. Northeastern Mollison (a), North earth-stone (b), Northwestern losses plateau (c), South red soil (d), Southwestern purple soil (e), Southwestern karst (f).
Author Contributions
Conceptualization, F.X., W.Z. and T.Y.; methodology, F.X., W.Z. and G.Z.; software, F.X. and W.Z.; validation, F.X. and W.Z.; formal analysis, F.X. and W.Z.; investigation, F.X.; resources, W.Z., W.Q. and N.F.; data curation, F.X. and W.Z.; writing—original draft preparation, F.X.; writing—review and editing, F.X., W.Z. and C.X.; visualization, F.X.; supervision, W.Z. and C.X.; project administration, W.Z.; funding acquisition, W.Q., W.Z. and T.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Natural Science Foundation of China (41907050, 41877073); the Natural Science Foundation of Shandong Province (ZR2023QD030, ZR2019MD031).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors thank Junchen Long and Lin Li for their assistance with data processing.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, K.; Wang, L.; Wang, Z.; Hu, Y.; Zeng, Y.; Yan, H.; Xu, B.; Li, C.; Cui, H.; Yu, S.; et al. Multiple Perspective Accountings of Cropland Soil Erosion in China Reveal Its Complex Connection with Socioeconomic Activities. Agric. Ecosyst. Environ. 2022, 337, 108083. [Google Scholar] [CrossRef]
- Tong, L.S.; Fang, N.F.; Xiao, H.B.; Shi, Z.H. Sediment Deposition Changes the Relationship between Soil Organic and Inorganic Carbon: Evidence from the Chinese Loess Plateau. Agric. Ecosyst. Environ. 2020, 302, 107076. [Google Scholar] [CrossRef]
- Pimentel, D.; Kounang, N. Ecology of Soil Erosion in Ecosystems. Ecosystems 1998, 1, 416–426. [Google Scholar] [CrossRef]
- Li, H.; Zhu, H.; Wei, X.; Liu, B.; Shao, M. Soil Erosion Leads to Degradation of Hydraulic Properties in the Agricultural Region of Northeast China. Agric. Ecosyst. Environ. 2021, 314, 107388. [Google Scholar] [CrossRef]
- Lal, R. Soil Erosion and the Global Carbon Budget. Environ. Int. 2003, 29, 437–450. [Google Scholar] [CrossRef] [PubMed]
- Pimentel, D.; Burgess, M. Soil Erosion Threatens Food Production. Agriculture 2013, 3, 443–463. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, C.; Sun, B.; Ji, Q.; Wang, C. Overview of national soil and water conservation zoning. Soil Water Conserv. China 2015, 12, 12–17. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, G.; Wang, C. How Does Straw-Incorporation Rate Reduce Runoff and Erosion on Sloping Cropland of Black Soil Region? Agric. Ecosyst. Environ. 2023, 357, 108676. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, G.; Zhu, P.; Wang, C.; Wan, Y. Impact of Slope Position on Soil Erodibility Indicators in Rolling Hill Regions of Northeast China. Catena 2022, 217, 106475. [Google Scholar] [CrossRef]
- Liu, C.; Jia, X.; Ren, L.; Zhao, C.; Yao, Y.; Zhang, Y.; Shao, M. Cropland-to-Shrubland Conversion Reduces Soil Water Storage and Contributes Little to Soil Carbon Sequestration in a Dryland Area. Agric. Ecosyst. Environ. 2023, 354, 108572. [Google Scholar] [CrossRef]
- Zhao, J.; Vanmaercke, M.; Chen, L.; Govers, G. Vegetation Cover and Topography Rather than Human Disturbance Control Gully Density and Sediment Production on the Chinese Loess Plateau. Geomorphology 2016, 274, 92–105. [Google Scholar] [CrossRef]
- Zhu, Y.; Jia, X.; Qiao, J.; Shao, M. What Is the Mass of Loess in the Loess Plateau of China? Sci. Bull. 2019, 64, 534–539. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Qin, X.; Qiu, Q.; Yu, R.; Yao, Y.; Li, H.; Shao, M.; Wei, X. Soil and Water Conservation Measures Reduce Erosion but Result in Carbon and Nitrogen Accumulation of Red Soil in Southern China. Agric. Ecosyst. Environ. 2023, 346, 108346. [Google Scholar] [CrossRef]
- Li, S.-L.; Liu, C.-Q.; Chen, J.-A.; Wang, S.-J. Karst Ecosystem and Environment: Characteristics, Evolution Processes, and Sustainable Development. Agric. Ecosyst. Environ. 2021, 306, 107173. [Google Scholar] [CrossRef]
- Li, C.; Wang, Z.; Li, Z.; Xu, X. Soil Erosion Impacts on Nutrient Deposition in a Typical Karst Watershed. Agric. Ecosyst. Environ. 2021, 322, 107649. [Google Scholar] [CrossRef]
- Duan, X.; Bai, Z.; Rong, L.; Li, Y.; Ding, J.; Tao, Y.; Li, J.; Li, J.; Wang, W. Investigation Method for Regional Soil Erosion Based on the Chinese Soil Loss Equation and High-Resolution Spatial Data: Case Study on the Mountainous Yunnan Province, China. Catena 2020, 184, 104237. [Google Scholar] [CrossRef]
- Duarte, L.; Cunha, M.; Teodoro, A.C. Comparing Hydric Erosion Soil Loss Models in Rainy Mountainous and Dry Flat Regions in Portugal. Land 2021, 10, 554. [Google Scholar] [CrossRef]
- Zhang, K.; Yu, Y.; Dong, J.; Yang, Q.; Xu, X. Adapting & Testing Use of USLE K Factor for Agricultural Soils in China. Agric. Ecosyst. Environ. 2019, 269, 148–155. [Google Scholar] [CrossRef]
- Van Remortel, R.D.; Maichle, R.W.; Hickey, R.J. Computing the LS Factor for the Revised Universal Soil Loss Equation through Array-Based Slope Processing of Digital Elevation Data Using a C++ Executable. Comput. Geosci. 2004, 30, 1043–1053. [Google Scholar] [CrossRef]
- Wischmeier, W.H. Predicting Rainfall Erosion Losses—A Guide to Conservation Planning. In Agriculture Handbook; Department of Agriculture, Science and Education Administration: Port Antonio, Jamaica, 1978; Volume 537. [Google Scholar]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall-Erosion Losses from Cropland East of the Rocky Mountains. In Agricultural Handbook; Agricultural Research Service, US Department of Agriculture: Washington, DC, USA, 1965; Volume 282. [Google Scholar]
- Renard, K.; Foster, G.R.; Weesies, G.; Mccool, D.; Yoder, D. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); US Department of Agriculture, Agricultural Research Service: Washington, DC, USA, 1997.
- Renard, K.G.; Freimund, J.R. Using Monthly Precipitation Data to Estimate the R-Factor in the Revised USLE. J. Hydrol. 1994, 157, 287–306. [Google Scholar] [CrossRef]
- Tang, G. Exploration and Practice of Digital Terrain Analysis on Loess Plateau; China Science Publishing & Media Ltd.: Beijing, China, 2015. [Google Scholar]
- Fairfield, J.; Leymarie, P. Drainage Networks from Grid Digital Elevation Models. Water Resour. Res. 1991, 27, 709–717. [Google Scholar] [CrossRef]
- Qin, W.; Zhu, Q.; Zhang, Y. Advance in researches on slope length factor in universal soil loss equation. Sci. Soil Water Conserv. 2010, 8, 117–124. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, Q.; Li, R.; Liu, Q. Estimation methods of slope gradient and slope length in watershed based on GIS and multiple flow direction algorithm. Trans. Chin. Soc. Agric. Eng. 2012, 28, 159–164. [Google Scholar]
- Tang, G.; Zhao, M.; Li, T.; Liu, Y.; Xie, Y. Modeling slope uncertainty derived from DEMs in Loess Plateau. Acta Geogr. Sin. 2003, 58, 824–830. [Google Scholar]
- Tang, G.; Li, F.; Liu, X.; Long, Y.; Yang, X. Research on the Slope Spectrum of the Loess Plateau. Sci. China Ser. E-Technol. Sci. 2008, 51, 175–185. [Google Scholar] [CrossRef]
- Li, F.; Tang, G.; Wang, C.; Cui, L.; Zhu, R. Slope Spectrum Variation in a Simulated Loess Watershed. Front. Earth Sci. 2016, 10, 328–339. [Google Scholar] [CrossRef]
- Tang, G.; Song, X.; Li, F.; Zhang, Y.; Xiong, L. Slope Spectrum Critical Area and Its Spatial Variation in the Loess Plateau of China. J. Geogr. Sci. 2015, 25, 1452–1466. [Google Scholar] [CrossRef]
- Zhu, M.; Li, F. Influence of slope classification on slope spectrum. Sci. Surv. Mapp. 2009, 34, 165–167. [Google Scholar]
- Wang, C.; Tang, G.; Li, F.; Yang, X.; Ge, S. Fundamental Conditions of Slope Spectrum Abstraction and Application. Sci. Geogr. Sin. 2007, 27, 587–592. [Google Scholar]
- Liu, S.; Li, F.; Jiang, R.; Chang, R.; Liu, W. A Method of Loess LandformAutomatic Recognition Based on Slope Spectrum. J. Geo-Inf. Sci. 2015, 17, 1234–1242. [Google Scholar]
- Li, F.; Tang, G.; Jia, Y.; Cao, Z. Scale Effect and Spatial Distribution of Slope Spectrum’s Information Entropy. J. Geo-Inf. Sci. 2007, 9, 13–18. [Google Scholar]
- Wu, S.; Rao, L. Characteristics and spatial differentiation of slope spectrum in different areas of Pisha Sandstone Areas. Trans. Chin. Soc. Agric. Eng. 2021, 37, 125–132+341. [Google Scholar]
- Zhao, W.; Dong, Q.; Yan, T.; Qin, W.; Zhu, Q. Relationship between slope spectrum’s information entropy and terrain factors in water erosion areas of purple soil in southwest China. Trans. Chin. Soc. Agric. Eng. 2020, 36, 160–167+342. [Google Scholar]
- Xu, F.; Zhao, W.; Yan, T.; Qin, W.; Chen, H. Can Slope Spectrum Information Entropy Replace Slope Length and Steepness Factor: A Case Study of the Rocky Mountain Area in Northern China. Catena 2022, 212, 106047. [Google Scholar] [CrossRef]
- Fan, H.; Cai, Q.; Chen, G.; Cui, M. Comparative study of the soil erosion and control in the three major black soil regions in the world. J. Nat. Resour. 2005, 20, 387–393. [Google Scholar]
- Liang, A.; Zhang, Y.; Chen, X.; Zhang, S.; Huang, D.; Yang, X.; Zhang, X.; Li, X.; Tian, C.; Mclaughlin, N.B.; et al. Development and effects of conservation tillage in the black soil region of Northeast China. Sci. Geogr. Sin. 2022, 42, 1325–1335. [Google Scholar] [CrossRef]
- Liu, X.; Guo, M.; Zhang, X.; Zhang, S.; Zhou, P.; Chen, Z.; Qi, J.; Shen, Q. Morphological Characteristics and Volume Estimation Model of Permanent Gullies and Topographic Threshold of Gullying in the Rolling Hilly Mollisols Region of Northeast China. Catena 2023, 231, 107323. [Google Scholar] [CrossRef]
- Zhang, G.; Zhao, W.; Yan, T.; Qin, W.; Miao, X. Estimation of Gully Growth Rate and Erosion Amount Using UAV and Worldview-3 Images in Yimeng Mountain Area, China. Remote Sens. 2022, 15, 233. [Google Scholar] [CrossRef]
- Zhu, X.; Fu, S.; Wu, Q.; Wang, A. Soil Detachment Capacity of Shallow Overland Flow in Earth-Rocky Mountain Area of Southwest China. Geoderma 2020, 361, 114021. [Google Scholar] [CrossRef]
- Wang, X.; Li, Z.; Cai, C.; Shi, Z.; Xu, Q.; Fu, Z.; Guo, Z. Hydrological Response of Sloping Farmlands with Different Rock Fragment Covers in the Purple Soil Area of China. J. Hydrol. Eng. 2013, 18, 446–456. [Google Scholar] [CrossRef]
- Stolte, J.; Shi, X.; Ritsema, C. Introduction: Soil Erosion and Nutrient Losses in the Hilly Purple Soil Area in China. Soil Tillage Res. 2009, 105, 283–284. [Google Scholar] [CrossRef]
- Hartmann, A.; Goldscheider, N.; Wagener, T.; Lange, J.; Weiler, M. Karst Water Resources in a Changing World: Review of Hydrological Modeling Approaches: Karst Water Resources Prediction. Rev. Geophys. 2014, 52, 218–242. [Google Scholar] [CrossRef]
- Gutiérrez, F.; Parise, M.; De Waele, J.; Jourde, H. A Review on Natural and Human-Induced Geohazards and Impacts in Karst. Earth-Sci. Rev. 2014, 138, 61–88. [Google Scholar] [CrossRef]
- Liu, C.; Lv, D.; Chen, H.; Nie, Y. Causes for the eco-enviromental vulnerability of the karst areas in southwest China. J. Geol. Hazards Environ. Preserv. 2014, 25, 49–53. [Google Scholar]
- Cai, Y. Preliminary research on ecological reconsrution in Karst mountain poverty areas of southwest China. Adv. Earth Sci. 1996, 11, 84–88. [Google Scholar]
- Li, J.; Sun, R.; Xiong, M.; Yang, G. Estimation of soil erosion based on the RUSLE model in China. Acta Ecol. Sin. 2020, 40, 3473–3485. [Google Scholar]
- SL190-2007; The Soil Erosion Classification and Grading Standard. Ministry of Water Resources of the People’s Republic of China; China Water & Power Press: Beijing, China, 2008.
- Wang, C. The Uncertainty of Slope Spectrum Derived from DEM in The Loess Plateau of Northern Shaanxi Province. Master’s Thesis, Northwest University, Xi’an, China, 2005. [Google Scholar]
- Gilbert, J.R.; Moler, C.; Schreiber, R. Sparse Matrices in MATLAB: Design and Implementation. SIAM J. Matrix Anal. Appl. 1992, 13, 333–356. [Google Scholar] [CrossRef]
- Jv, Z.; Zhang, J.; Bai, Z. Investigation on relationship between slope spectrum’s information entropy and topographical factor influencing soil loss in the mountainous region. Sci. Surv. Mapp. 2019, 44, 86–90. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.; Zhu, Q.; Yang, S.; Li, H.; Ma, H. A Gully Erosion Assessment Model for the Chinese Loess Plateau Based on Changes in Gully Length and Area. Catena 2017, 148, 195–203. [Google Scholar] [CrossRef]
- Guo, M.; Yang, Q.; Wang, C. Analysis on erosional terrain characteristics of typical samples in main water erosion region of China. Trans. Chin. Soc. Agric. Eng. 2013, 29, 81–89+307–308. [Google Scholar]
- Wang, Y.; Wu, Y.; Kou, Q.; Min, D.; Chang, Y.; Zhang, R. Definition of arsenic rock zone borderline and its classification. Sci. Soil Water Conserv. 2007, 5, 14–18. [Google Scholar] [CrossRef]
- Borrelli, P.; Robinson, D.A.; Fleischer, L.R.; Lugato, E.; Ballabio, C.; Alewell, C.; Meusburger, K.; Modugno, S.; Schütt, B.; Ferro, V.; et al. An Assessment of the Global Impact of 21st Century Land Use Change on Soil Erosion. Nat. Commun. 2017, 8, 2013. [Google Scholar] [CrossRef] [PubMed]
- Borrelli, P.; Robinson, D.A.; Panagos, P.; Lugato, E.; Yang, J.E.; Alewell, C.; Wuepper, D.; Montanarella, L.; Ballabio, C. Land Use and Climate Change Impacts on Global Soil Erosion by Water (2015–2070). Proc. Natl. Acad. Sci. USA 2020, 117, 21994–22001. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).