Abstract
Land cover classification of Synthetic Aperture Radar (SAR) imagery is a significant research direction in SAR image interpretation. However, due to the unique imaging methodology of SAR, interpreting SAR images presents numerous challenges, and land cover classification using SAR imagery often lacks innovative features. Distributed scatterers interferometric synthetic aperture radar (DS-InSAR), a common technique for deformation extraction, generates several intermediate parameters during its processing, which have a close relationship with land features. Therefore, this paper utilizes the coherence matrix, the number of statistically homogeneous pixels (SHPs), and ensemble coherence, which are involved in DS-InSAR as classification features, combined with the backscatter intensity of multi-temporal SAR imagery, to explore the impact of these features on the discernibility of land objects in SAR images. The results indicate that the adopted features improve the accuracy of land cover classification. SHPs and ensemble coherence demonstrate significant importance in distinguishing land features, proving that these proposed features can serve as new attributes for land cover classification in SAR imagery.
1. Introduction
Land cover classification using Synthetic Aperture Radar (SAR) imagery is a major research topic in Earth observation studies [1]. Over the past few decades, optical remote sensing technology has been a robust tool for surveilling land use and land cover in urban regions. However, its efficacy is often compromised by cloud cover and adverse weather conditions, hindering the acquisition of usable imagery in every revisit cycle. With the deepening of research, Song et al. [2] discovered that approximately 80% of non-urban land in urban areas becomes urbanized within three years. Similarly, Li et al. [3] found that most vegetated areas turn into impervious surfaces (ISs) within a period of 2–3 years. These findings highlight the necessity of increasing the frequency of land monitoring for a better comprehension of land use and land cover dynamics. In this context, SAR emerges as a formidable alternative imaging system. SAR’s ability to penetrate cloud cover, smoke, and haze allows for the provision of imagery under all weather conditions and during both day and night, as referenced in [4,5,6]. This capability positions SAR as an attractive data source for land use and cover mapping, particularly when optical data are unavailable or of substandard quality due to various reasons. However, the interpretation of SAR imagery remains a challenging task, owing to its unique imaging geometry [7], complex scattering processes [8], and the presence of speckle noise.
SAR signals exhibit the following two significant properties: (1) sensitivity of the backscatter coefficient to the target’s geometric shape and dielectric constant; (2) the coherence properties of electromagnetic pulses that allow for interferometric measurements [9]. Numerous scholars have leveraged these attributes of SAR signals to study various terrestrial environments [10,11,12]. Michael et al. [13] use time-series SAR/InSAR data for characterizing arctic tundra hydro-ecological conditions. Their assessment showed that the predictive capability of SAR intensity is superior to coherence, and the accuracy improves when both intensity and coherence are used together. Luca et al. [14] analyzed the role of interferometric coherence in detecting flood disasters in urban and agricultural areas. Their results show that the analysis of the multi-temporal of the coherence is useful for the interpretation of SAR data since it enables a considerable reduction in classification errors that could be committed considering intensity data only. Fariba et al. [15] studied the multi-temporal coherence and SAR backscatter of wetlands. The results of this study confirmed the potential of incorporating SAR and InSAR features for mapping wetlands with similar ecological characteristics. Previous studies typically opt for coherence combinations with the shortest temporal baselines, as these combinations are believed to effectively preserve information about terrain changes [16,17,18]. However, for a set of N images, it is possible to generate an N × N coherence matrix that includes all baseline combinations. These non-shortest baseline combinations may also contain hidden information about the terrain. Consequently, this paper endeavors to investigate the role of coherence from all baseline combinations in the coherence matrix for terrain classification. Compared to its applications in interpreting other land features, SAR is relatively less advanced in urban areas. Urban regions are among the most complex environments on Earth, where a mix of man-made structures and natural elements of various shapes and sizes co-exist. The interaction between radar signals and diverse urban characteristics makes it challenging to effectively interpret urban land features based solely on the properties of the radar signals.
With the increase in the number of SAR satellites being launched, a vast amount of SAR data have become available, leading to the emergence of Multi-Temporal Interferometric SAR (MT-InSAR) [18]. This technique has become the standard method for detecting subtle deformations [19]. Before detecting deformations, radar pixels are differentiated. Based on different scattering types, image pixels can be categorized into Permanent Scatterer (PS) pixels [20] and Distributed Scatterer (DS) pixels.
In the process of selecting DS points, identifying statistically homogeneous pixels is crucial. Two pixels are defined as part of the same statistically homogeneous pixel family if their data stacks over time come from the same probability distribution function. In the real physical world, similar land features exhibit similar scattering characteristics. From a time-series perspective, a particular land feature usually does not undergo significant changes over time, aligning with the consistency of its scattering properties. This means that time-series pixel stacks representing the same land feature will exhibit similar statistical properties. Therefore, pixels judged to be part of the same SHP family are likely to represent the same land feature in the real world.
After the selection of SHPs, a further selection of DS points can be carried out. For deterministic radar targets like PS pixels, all non-diagonal elements of the coherence matrix are redundant in phase. However, this is not applicable for DS pixels. For DS pixels, it is necessary to process N(n − 1)/2 interferometric phase values, rather than merely n, as in the case of PS pixels. Ferretti [21] introduced the PTA algorithm to assess the optimum phase value , which can be seen as an extension of the temporal coherence widely used in PS analysis. The phase stability of DS points over time can be evaluated through γ. The closer the value of is to 1, the more stable the phase value of that point. This indicates that DS pixels with higher γ values correspond to real-world land features that also exhibit relatively stable scattering properties over time.
In summary, the entire DS-InSAR computational process involves the calculation of the coherence matrix, the selection of statistically homogeneous pixels (SHPs), and the estimation of ensemble coherence. Theoretically, these steps are all associated with surface objects. Therefore, this study hypothesizes that integrating DS-InSAR attributes can improve the accuracy of land cover classification in SAR images. To test this hypothesis, we designed a set of combined experiments, incorporating the coherence matrix, the number of statistically homogeneous pixels, and ensemble coherence as classification features alongside traditional backscatter intensity. We used a Random Forest classifier for training, and analyzed the importance of the selected features compared to traditional backscatter features. Subsequently, we employed various evaluation metrics to assess the impact of these features on classification accuracy and their inter-relationships. Finally, we conducted land feature mapping within the study and evaluated the potential of the introduced features for surface feature mapping.
2. Materials and Methods
In this paper, we proposed the use of a coherence matrix, the number of statistically homogeneous pixels, and ensemble coherence as classification features for SAR image land feature classification. By combining these with the traditional SAR backscatter intensity and employing a Random Forest classifier, we conducted classification experiments on the feature combinations and assessed the results using evaluation methods. This section will detail the underlying principles of the features utilized and the methods adopted.
2.1. Selected Features
2.1.1. Backscatter Intensity
The SAR backscatter intensity of ground targets is a function of several factors, including SAR wavelength, image acquisition geometry, local topography, surface roughness, and the dielectric constant of the target [15]. In SAR imagery, a higher backscatter intensity usually corresponds to the intensity of radar wave reflection off the target surface, which can be utilized to differentiate various land types, detect changes, and more. In modern urban settings, the vertical structures of tall buildings may cause multiple reflections of radar waves in the vertical direction, resulting in strong reflective intensity [22]. For roads, the surface is usually smooth, leading to primary reflection rather than the scattering of radar waves [23]. Water typically exhibits a lower backscatter intensity due to its smooth surfaces and absorption of radar waves [24]. Dense canopy vegetation may show a higher scattering intensity due to the complex structure of branches and leaves causing multiple scatterings [25]. However, low vegetation like grassland, with its uniform surface, might display a lower backscatter intensity. Therefore, this paper leverages the varying reflective characteristics of different land features to radar waves as classification features.
2.1.2. Coherence Matrix
For a given pair of Single Look Complex (SLC) SAR images, interferometric coherence is defined as the magnitude of the complex cross-correlation coefficient, quantifying the similarity between the two SAR images. Interferometric coherence is often used as a parameter to assess the stability of the phase in interferograms [26]. Moreover, interferometric coherence can also reflect changes in surface ground targets between two time periods, making it a viable parameter for classification [27]. Coherence can be expressed as follows:
where represents the coherence, andare the radar signals received at the same location but at two different times, anddenotes the complex conjugate.
When a time series of N SAR images is available, the potential combinations of pairs of SAR images to derive the coherence is equal to N(N − 1)/2. The selection of baseline combinations plays a significant role in deriving temporal interferometric coherence information, sensitivity to different temporal phenomena of each land cover, and in influencing classification rates [28]. It is also possible to define the Hermitian positive semidefinite coherence matrix for the complete interferometric stack as follows:
where represents the coherence matrix.
The coherence matrix in (2) contains, on the main diagonal, the self-coherence combinations, and the off-diagonal terms contain all possible interferometric combinations of the SAR stack of images. Assuming a constant image acquisition sampling, the closer the interferometric combination is to the mean diagonal, the shorter the temporal baseline.
2.1.3. Statistically Homogeneous Pixels
Given a set of N SAR images, assuming they are appropriately resampled on the same master grid, let Z be the complex data vector.
where T indicates transposition, P is a generic image pixel, and Zi(P) is the complex reflectivity value of the ith image of the data stack corresponding to pixel P.
For distributed radar targets, where no dominant scatterer can be identified within a resolution cell, Z is a (complex) random vector. If two pixels are considered homogeneous, then the two data vectors z(P1) and z(P2) should originate from the same probability distribution function. In practice, a window of a certain size is centered on the pixel under analysis, and a statistical test is performed on all the pixels within this window to select a homogeneous statistical population. The two-sample Kolmogorov–Smirnov (KS) test is a commonly used method for this purpose. However, the method’s sensitivity to small stack sizes and its empirical function’s sensitivity to data distribution inevitably lead to a decrease in image resolution and quality. Furthermore, as the time stack increases, the computational cost of calculating SHPs also grows.
In this study, we employ the FaSHPS algorithm [29] proposed by Jiang et al. for the extraction of homogeneous points. The algorithm first requires obtaining the mean amplitude of M pixels and using the Lilliefors test to verify the normality of in homogeneous regions. Next, is separated into non-overlapping small blocks. The pixel with the median mean amplitude among all pixels in each block is selected as the mean . The coefficient of variation is then calculated by regressing the scatter plot of the sample STD. Subsequently, potentially abnormal values induced by temporal variability are discarded from the time-wise vector using a revised boxplot method. Finally, a fixed window is defined for each central pixel p, and SHPs are selected based on the confidence interval.
This algorithm’s primary feature is that it transforms the hypothesis testing problem into an estimation of confidence intervals, thereby improving the speed of selecting homogeneous points. More specifically, for a stack of N SAR images , the mean for pixel P is estimated as . According to the Central Limit Theorem (CLT), as the size N increases, tends towards a normal distribution. . According to the statistical theory of distributed targets in SAR imagery, in uniform regions, single-look intensity images conform to a Rayleigh distribution. The coefficient of variation, which remains constant, is a key characteristic of this distribution. Consequently, a specific interval can be derived as follows:
In this context, P{ } denotes probability, and is the quantile point of the standard normal distribution. When is known, Equation (4) becomes a definite interval. Assume the reference pixel is , and the number of pixels to be tested is K. Then, the sample mean is taken as the true value for . Subsequently, the sample means of the remaining pixels are estimated and compared individually with Equation (4). All the sample means that fall within this interval are preliminarily considered as homogeneous points, without considering the connectivity of the pixels. When K-1 pixels have been tested, those falling within the interval are considered to have the same statistical properties and are referred to as the same statistically homogeneous pixel family. The size of this family is referred to in this study as the number of statistically homogeneous pixels. In other words, it is the number of pixels within the window constructed around the central pixel that have the same statistical properties. This number is used as a classification feature and serves as an input to the model in this study.
2.1.4. Ensemble Coherence
For a deterministic radar target, such as a PS pixel, the phase values of all off-diagonal elements of the coherence matrix are redundant, whereby the N(N − 1)/2 phase values (the matrix is Hermitian) are simply the difference in phase values of the N available SAR scenes.
However, this is not applicable for DS pixel points. For DS pixel targets, it is necessary to process n(n − 1)/2 interferometric phase values. After obtaining the optimum solution through maximum likelihood phase estimation, the quality of the phase value is then assessed. The measure can be formulated as follows:
where γ is the goodness of fit index, an extension of the temporal coherence; ϕnk denotes the interferometric phase of the item at row m and column n of the sampled coherence matrix; and θm and θn are the estimated optimal phases. It is worth noting that all phases here are wrapped phases, as using unwrapped phases would cause errors to propagate into the estimation of ensemble coherence. The DS candidates will be further weeded according to the goodness of fit index. Only those candidates exhibiting a γ value higher than a predefined threshold will be selected as the final DS targets. Therefore, targets identified via this method are likely to be more indicative of the attributes of DS points. This suggests that they are typically constituted of smaller-scale surface features, like rocks, sections of buildings, or areas covered in vegetation. Given these traits, this study incorporates the ensemble coherence of DS points as a key feature for classification purposes.
2.2. Random Forest Modeling
In this study, classical machine learning algorithms, specifically Random Forest (RF), were employed for the synergistic classification of SAR backscatter intensity images and other features. This algorithm is highly popular in remote sensing applications [30] due to its unique advantages for remote sensing imagery. These include (1) The capability to handle high-dimensional data. Remote sensing data often have high-dimensional features, and Random Forest can effectively process such data without being significantly impacted by the curse of dimensionality [31]. (2) Random Forest, by integrating multiple decision trees, reduces overfitting to specific datasets, thereby enhancing generalizability [32]. (3) Random Forest can effectively handle data with missing values and offers relatively fast training and prediction speeds [33], making it suitable for processing large-scale remote sensing datasets.
Although RF is a complex model, its output can be interpreted through the contributions of individual decision trees, which is particularly important for the analysis of remote sensing data. In classification tasks, RF determines the final category through a “majority voting” approach. That is, each tree provides a prediction, and the most common category is selected as the final result. Due to its multi-tree structure, Random Forest exhibits a strong resistance to outliers and noise. Therefore, many scholars have utilized this algorithm for classification research. For instance, Sonobe et al. [34] employed RF classification with multi-temporal TerraSAR-X dual-polarization data to identify crop types. Wohlfart et al. [35], in a review of most articles published in the past decade, incorporated TerraSAR-X data into wetland studies, demonstrating the success of using the Random Forest algorithm for TerraSAR-X data classification.
In this study, we first used backscatter intensity as the basic feature input to the classifier, employing stratified random sampling to select the training and test sets. To ensure the stability of the training and test sets, we conducted 5-fold cross-validation, resulting in accuracies of 70.86%, 69.86%, 69.16%, 68.76%, and 68.93%. By calculating the mean accuracy and standard deviation, we obtained an average accuracy of 69.51% with a standard deviation of 0.77%. Additionally, the 95% confidence interval was calculated to be [68.61%, 70.41%], ensuring the stability of the selected samples. Subsequently, using the determined samples, we performed a grid search to identify the optimal parameter combination, which included 100 trees and a maximum tree depth of 10. With these parameters established, we constructed five experimental combinations, each representing a combination of backscatter intensity with different features. By comparing these various feature combinations, we aim to evaluate the discriminative capabilities of the land features represented by the selected features.
2.3. Accuracy Assessment
To validate the models, we employed overall accuracy (OA), Kappa coefficient (Kappa), average accuracy (AA), Producer’s Accuracy (PA), and User’s Accuracy (UA) [36] for a quantitative evaluation of the classification accuracy. The statistical formulas for these metrics are as follows:
Overall accuracy (OA): This is a measure of the overall correctness of a classification model. It is calculated as the ratio of correctly classified instances to the total number of instances.
Average accuracy (AA): AA provides an average of accuracies obtained for each class, ensuring that all classes are equally represented in the accuracy assessment. It is calculated by averaging the individual accuracies of each class.
where N is the number of classes, and Acci is the accuracy for class i, calculated as the number of correctly classified instances of class i divided by the total number of instances of class i.
Kappa coefficient: The Kappa coefficient is a statistical measure that accounts for chance agreement in classification accuracy. It compares the observed accuracy with the expected accuracy (random chance).
where P0 is the observed agreement (the relative observed agreement among raters), and Pe is the hypothetical probability of chance agreement.
Producer’s Accuracy (PA) is a measure of the accuracy from the perspective of the data producer. It quantifies the probability that a certain class in the ground truth (actual data) is correctly classified in the predicted dataset. In essence, PA evaluates the omission error and is crucial for understanding how effectively the classification model captures the real-world instances of each class. The formula for calculating Producer’s Accuracy is:
User’s Accuracy (UA) provides an assessment from the user’s standpoint. It measures the probability that a pixel classified into a particular class in the predicted dataset truly belongs to that class in reality. This metric is pivotal for evaluating the commission error and indicates the reliability of the classification results for end-users. The User’s Accuracy is calculated using the following formula:
Confusion Matrix: A confusion matrix is a specific table layout that allows for the visualization of the performance of an algorithm, typically a supervised learning one. The matrix compares the actual target values with those predicted by the model, allowing for an easy assessment of errors.
Feature Importance: Feature importance refers to techniques that assign a score to input features based on how useful they are at predicting a target variable.
The Pearson correlation coefficient, also known as the Pearson product-moment correlation coefficient, is a statistical measure of the linear correlation between two variables. Its value ranges from −1 to 1, where 1 indicates a perfect positive correlation, −1 indicates a perfect negative correlation, and 0 indicates no linear correlation. The formula for calculating the Pearson correlation coefficient is:
where and are the observed values of the two variables, and are their mean values, and n is the number of observations.
Feature correlation analysis measures the redundancy of information between two features. The Pearson correlation coefficient is an excellent measure of linear correlation within variables. Therefore, calculating the Pearson correlation coefficient for SAR features allows for an analysis of the correlation between features.
3. Study Area
Our research took place in Shenzhen, a densely populated megacity in Southern China (Figure 1). The study area, located in the central part of Shenzhen, spans about 45 square kilometers and encompasses a variety of typical urban elements, including skyscrapers, densely packed buildings, bridges, overpasses, and urban parks, making it an excellent location for land use classification. The dataset for this study included 24 TerraSAR satellite SAR images. These images were obtained in Stripmap mode with a spatial resolution of 3 m × 3 m and were collected over the period from 12 February 2019 to 11 November 2020. The dataset was categorized into the following five classes: water bodies, roads, built-up areas, vegetation, and grass. For ground truth creation, we manually selected some pixels that were clear and reliable based on the averaged SAR intensity image. To prevent overlap between the training and testing datasets, we divided the samples, assigning 70% to the training set and the remaining 30% to the test set. The specific numbers of training and testing samples are detailed in Table 1.
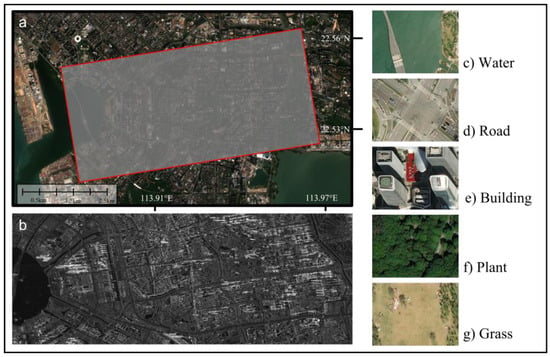
Figure 1.
Research area and schematic diagram of classified land features. (a) Optical image. The red frame indicates the research area. (b) Averaged SAR intensity image. (c–g) represent the optical images of classified land features within the research area.

Table 1.
The number of training and testing samples for different categories in the dataset.
4. Results and Discussion
4.1. Assessment of Accuracy
To assess the discriminative capability of the three features adopted in this study for land features within the research area, we designed five feature combinations. These are backscatter intensity (Mli); Mli plus coherence matrix (CohM); Mli plus the number of homogeneous points (Bro); Mli plus ensemble coherence (Pcoh); and a combination that covers all features—Mli+CohM+Bro+Pcoh. To mitigate the impact of training sample variations, all reported results are the averages of five runs with different training samples. The classification results were then objectively evaluated using OA, AA, Kappa, PA, and UA [37].
The experimental results are shown in Table 2. Overall, using only intensity information for the classification of study land features resulted in an overall accuracy of just 69.35%, an average classification accuracy of 56.51%, and a Kappa coefficient of 0.63. By introducing other features, the overall classification accuracy of the model improved. Notably, after incorporating the coherence matrix as a feature, the classification accuracy increased the most, reaching 85.03%, with an average accuracy of 76.68%, and a Kappa coefficient of 0.81. The number of homogeneous pixels ranked second in overall accuracy, and ensemble coherence features were third.

Table 2.
The OA, AA, and Kappa coefficient for the five classification combinations.
To assess the discriminative ability of the features we used for different land cover categories, we provide the PA, UA, and confusion matrices for the aforementioned feature combinations. First, we observe the accuracy changes for five types of land features from the perspectives of PA and UA (Figure 2). It is observed that buildings and water bodies have a high PA and UA across different feature combinations. Water, roads, and buildings achieve the highest PA and UA in the combination of coherence and backscatter intensity. For grass, the other three feature combinations all yield an accuracy improvement over using backscatter intensity alone. For vegetation, the combination of ensemble coherence and backscatter intensity achieves the highest PA, while coherence achieves the highest UA. Overall, the combinations involving coherence show significant improvements in both PA and UA across all types of land features.
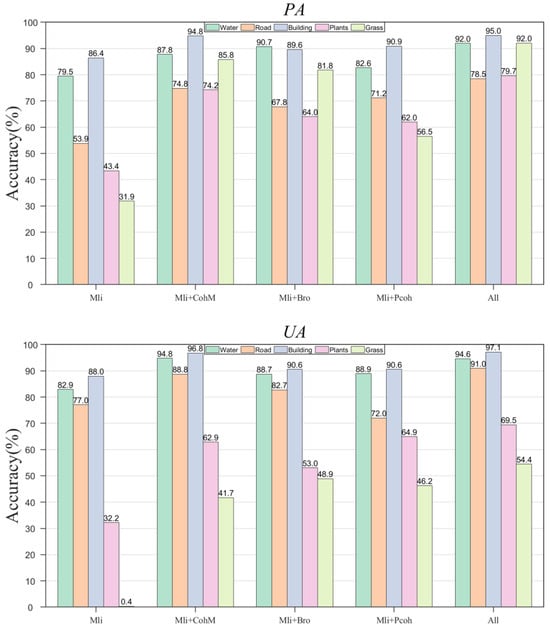
Figure 2.
The PA and UA for different land feature categories under the five feature combinations.
Figure 3 displays the confusion matrices for the five feature combinations. The elements on the main diagonal indicate the degree of agreement between the mapped categories and the actual ground truth, while the off-diagonal elements represent misclassifications allocated to other land cover categories. When only using backscatter intensity as the classification feature, buildings are well-differentiated, with only a few instances being misclassified as vegetation or roads. Water is also relatively well classified, with most points correctly categorized. However, grass is almost indistinguishable in this scenario.
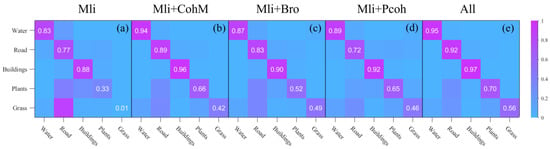
Figure 3.
The confusion matrices for the five feature combinations. (a) Time-series backscatter intensity feature combination (Mli). (b) Backscatter and coherence matrix combination (Mli + CohM). (c) Backscatter and statistically homogeneous pixel number combination (Mli + Bro). (d) Backscatter and ensemble coherence combination (Mli + Pcoh). (e) Combination of all features: backscatter, coherence matrix, statistically homogeneous pixel number, and ensemble coherence (Mli + CohM + Bro + Pcoh).
After incorporating the coherence matrix as a feature, the number of correctly classified instances for each land cover type improved, especially for grass, which saw a significant rise from almost no correct predictions to a considerable number of correctly predicted samples. Compared to other land features, roads experienced the most confusion with other categories, while water had the least confusion. When the homogeneous points feature and ensemble coherence feature were separately added, buildings, water, and grass showed almost the same predictive ability. However, for roads and vegetation, they each exhibited different predictive capabilities; homogeneous points tended to favor roads, whereas ensemble coherence leaned towards vegetation. Yet, relative to coherence, these two features did not significantly stand out in identifying buildings.
To better reveal the relationships between the features used, we calculated the Pearson correlation matrix between them. Given that the coherence matrix generated a 552-dimensional feature vector by separating the real and imaginary parts, we employed PCA (Principal Component Analysis) to reduce the dimensionality of this high-dimensional data, selecting the top 8 dimensions with the highest scores for input to compute the Pearson correlation matrix. Figure 4 shows a high positive correlation among scattering intensities, a negative correlation relative to Bro, a positive correlation with Pcoh, and almost no correlation with coherence. Bro and Pcoh exhibited a strong negative correlation between each other, but both showed almost no correlation with coherence.
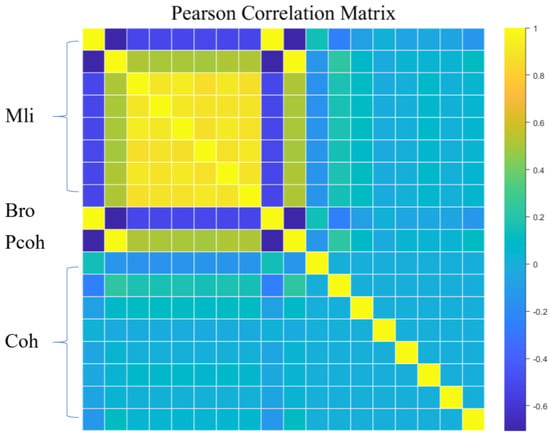
Figure 4.
The Pearson correlation matrix for the selected features. Mli represents the time−series backscatter, Bro represents the number of statistically homogeneous pixels, Pcoh represents the ensemble coherence, and Coh represents the PCA−processed coherence.
Figure 5 presents the mapping results using the five feature combinations. Figure 5a shows a significant distinction for water and roads, but for other land features, most are misclassified as roads, particularly grass, which is almost indistinguishable. Figure 5b, which uses the coherence matrix for mapping, shows improved vegetation recognition compared to Figure 5a, better identification of grass, and more precise recognition of buildings. Figure 5c, using the number of homogeneous pixels for mapping, significantly improves the identification of grass compared to Figure 5a and Figure 5b, though vegetation recognition is not as effective. Figure 5d, representing the mapping results of ensemble coherence, offers a clearer identification of urban buildings and better outcomes for vegetation, but there are slight differences in identifying grass. Figure 5e, which utilizes all features for training, demonstrates more significant effects in vegetation classification, building recognition, and grass identification compared to the previous results.
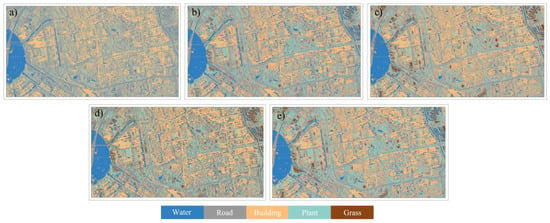
Figure 5.
The mapping results of the five feature combinations. (a) Time-series backscatter intensity feature mapping (Mli). (b) Backscatter and coherence matrix combination mapping (Mli + CohM). (c) Backscatter and statistically homogeneous pixel number combination mapping (Mli + Bro). (d) Backscatter and ensemble coherence combination mapping (Mli + Pcoh). (e) Mapping with all features combined: backscatter, coherence matrix, statistically homogeneous pixel number, and ensemble coherence (Mli + CohM + Bro + Pcoh).
4.2. Feature Importance and t-Test
To evaluate how the adopted features compare to backscatter intensity in land feature classification, we established the importance relationship between each feature and backscatter intensity. Figure 6a shows the feature importance results when only using time-series intensity as the classification feature. It is observed that SAR image scattering intensities at different times vary in their discriminative ability, but overall, there is not a significant difference in importance scores. Figure 6b illustrates the relationship between backscatter intensity and the coherence matrix. The real and imaginary parts of coherence were input into the classifier separately, and their feature importance scores were calculated. The scores show that the difference in feature importance between backscatter intensity and coherence is minimal. Some coherence features stand out with relatively higher scores, but overall scores are low, indicating little difference between coherence and backscatter intensity. Figure 6c shows the feature importance relationship between homogeneous pixels and backscatter intensity. The results indicate that homogeneous pixels have higher and more distinct importance scores compared to backscatter intensity, suggesting that they offer greater discriminative power in classifying land features. Figure 6d presents the feature importance relationship between ensemble coherence and backscatter intensity. Like homogeneous pixels, ensemble coherence also exhibits higher importance scores than backscatter, with a significant difference from the scores of other time-series backscatter intensities. Figure 6e shows the results of combining all features. Homogeneous pixels demonstrate the highest importance, followed by ensemble coherence, with the scattering intensity at time point one ranking third. This suggests that compared to traditional features, the number of homogeneous pixels and ensemble coherence exhibit a more significant importance in classification.
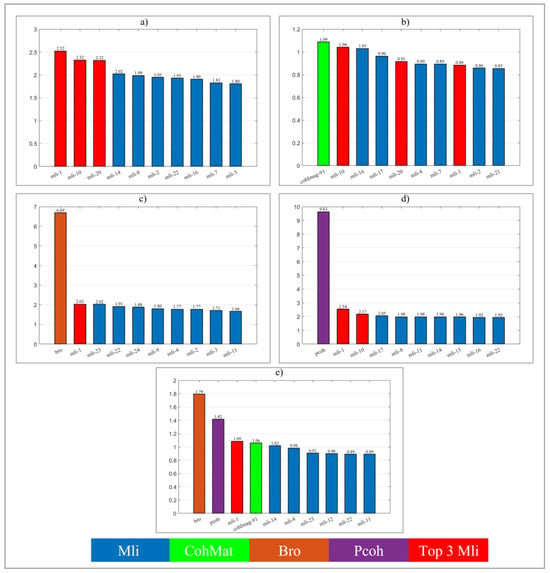
Figure 6.
The feature importance of the five combinations. (a) Time-series backscatter intensity feature importance (Mli); red represents the top three most important intensity features. (b) Backscatter and coherence matrix combination feature importance (Mli + CohM); green represents the highest-scoring coherence features. (c) Backscatter and statistically homogeneous pixel number combination feature importance (Mli + Bro); brown represents the scores for the number of statistically homogeneous pixels. (d) Backscatter and ensemble coherence combination feature importance (Mli + Pcoh); purple represents the scores for ensemble coherence. (e) Feature importance for the combination of all features: backscatter, coherence matrix, statistically homogeneous pixel number, and ensemble coherence (Mli + CohM + Bro + Pcoh).
To further validate the effectiveness of the proposed features in improving classification accuracy, we used t-tests to evaluate whether the differences in classification tasks were statistically significant. Specifically, we conducted 10 training runs for each experimental combination and recorded the results. We then performed t-tests comparing the new feature combinations with the control group using only backscatter features. The results are shown in Table 3. All proposed feature combinations had p-values significantly less than 0.05, reaching the level of significance. This indicates that the selected features statistically significantly improve classification performance, meaning the improvement is not due to random factors but is real. Additionally, the confidence intervals for all feature combinations did not include 0, further indicating that the impact of the proposed features on classification performance is significant.

Table 3.
Different feature combinations t-test results.
4.3. Time-Series Backscatter Intensity of Different Terrains
To further explore the discriminative ability of intensity features for different land features, we compared the time-series backscatter intensity of different land covers. Figure 7 reveals significant variations in the backscatter values for some types of land cover. For water, due to the strong absorption capability of water molecules to electromagnetic waves (especially in optical and microwave bands), the backscatter coefficient is relatively low. In contrast, buildings, particularly modern ones, are often composed of hard materials like concrete, metal, bricks, and glass. These materials strongly reflect electromagnetic waves, resulting in higher backscatter. Compared to natural environments, buildings have large vertical surfaces, increasing the reflective area for electromagnetic waves, especially for side-looking radar. Therefore, buildings have a relatively high backscatter coefficient. However, vegetation in urban areas exhibits different scattering properties. Plant structures, such as leaves, stems, and branches, are complex in shape and internal structure, leading to multiple scattering, reflection, and refraction phenomena. Most plants contain significant amounts of water, affecting their electromagnetic properties, positioning the scattering intensity curve of vegetation between buildings and water bodies. However, urban areas also have man-made roads and grass. Their intensity curves are quite similar and even overlap at certain times, making it challenging to distinguish these two land features based solely on backscatter intensity.

Figure 7.
The time-series scattering intensity of the five types of land features.
4.4. The Impact of Coherence over Small Time Spans
Coherence describes the similarity between two or more images acquired at different times. Due to seasonal changes, SAR image results may vary, leading to differences in coherence. Therefore, this section discusses the discriminative ability of coherence combinations for land features in different seasonal scenarios and time spans.
Table 4 presents eight combinations of different seasons and time spans. Across all image sets, the time span is from 12 February 2019 to 11 November 2020, covering a year and nine months, including seasonal changes. However, our study area is in Shenzhen, where the temperature is mild throughout the year, so the entire year is divided into three seasons—spring, summer, and autumn. Based on historical temperatures in Shenzhen, the period from 12 February 2019 to 19 April 2019, with four images, is defined as spring, as the average temperature during this period is below 22 degrees Celsius. The period from 11 May 2019 to 3 November 2019, is defined as summer, as the average temperature during these months is above 22 degrees Celsius. The period from 25 November 2019 to 21 February 2020, is defined as autumn, as the temperature during this period is below 22 degrees Celsius but above 10 degrees Celsius. Each of these periods includes four images, with six coherence combinations. As seen in the table, the overall accuracy (OA) for spring and autumn is higher compared to the two phases of summer. Overall, there is not a significant difference in accuracy between different seasons.

Table 4.
Classification accuracy of coherence combinations for different seasons and time spans.
Since Shenzhen has high temperatures throughout the year and a long summer season, we explored the impact of different time spans on classification accuracy by selecting images taken in the summer. The first set of images was taken from 24 June 2019 to 3 November 2019, with six images and 15 coherence combinations. In comparison, the images taken from 30 May 2020 to 11 November 2020, also include six images and 15 coherence combinations. The OA results for these two periods are similar, and both have a higher accuracy compared to the four-image combinations. Next, we compared the eight images taken from 11 May 2019 to 3 November 2019, and found that this combination resulted in an even higher accuracy. Finally, using all 24 images, the classification accuracy reached 84.90%. This indicates that coherence combinations over longer time spans provide better classification results.
In summary, different seasonal coherence combinations lead to varying classification results, but the overall differences are not significant, likely because Shenzhen does not have a distinct winter season, resulting in minimal changes in vegetation. On the other hand, as the time span increases and more coherence combinations are included, classification accuracy improves. This suggests that coherence combinations can be beneficial for land feature classification and that coherence matrices have great potential in this field.
4.5. Coherence Component Analysis on Classification Accuracy
Typically, multi-temporal SAR imagery generates N(N − 1)/2 complex coherence values. The combinations with the shortest temporal baseline are usually selected as classification features to describe land features or their changes. However, this does not mean that other temporal baseline combinations cannot convey land feature information. Therefore, a more comprehensive coherence matrix may also contain additional information about land features. Coherence refers to the correlation between two complex SAR images, meaning it is composed of complex data with real and imaginary parts. In our experiments, we found that using the real and imaginary parts of coherence as separate features in the classifier, as opposed to using the magnitude of coherence, results in different accuracies, as shown in Table 5. Generally, treating the real and imaginary parts as separate features leads to relatively higher accuracies, suggesting that they may contain more information that is relevant to land feature classification.

Table 5.
The classification accuracy of different coherence part combinations.
Although the coherence matrix offers a more comprehensive combination, it inevitably includes redundancy and decorrelation. Therefore, dimensionality reduction is a common approach when dealing with high-dimensional data. Principal Component Analysis (PCA) is a well-established technique in remote sensing for reducing the dimensionality of multi-dimensional data. It reduces redundancy in multi-band or multi-temporal images, enhances the signal-to-noise ratio, and facilitates change detection using multi-temporal datasets. Hence, we conducted dimensionality reduction experiments using PCA on both the real–imaginary part combination and the magnitude group. We selected the top 24 features with the highest scores from the real–imaginary combination and the top 12 features from the magnitude group. These selected features were then combined with backscatter intensity to form new feature combinations, which are subsequently used for training the models.
The results revealed that the accuracy of the magnitude group post-PCA reduction was approximately 2% higher than the SEG group, which is a stark contrast to the data before PCA was applied. Furthermore, the highest accuracy reached was around 85%. This suggests that the PCA-reduced magnitude data extracted features more representative of land feature categories. Consequently, this not only reduced training time but also maintained accuracy. The experimental findings highlight that the coherence matrix may contain a lot of useful information. Perhaps the phase and amplitude information of coherence also hides different land feature characteristics. However, as this is not the main focus of this paper, it will not be discussed further.
4.6. Comparison of Different SHP Selection Windows
During the determination process for SHPs, an estimation window centered on each pixel P is defined, followed by the identification of pixels sharing the same statistical characteristics as P. This implies that the definition of window size can impact the number of SHP families identified. Moreover, for SAR images with different resolutions, the land feature information represented by a single pixel can vary. Appropriate window sizes for different land features might select more suitable SHP families. Therefore, we used five different window sizes in combination with backscatter intensity, inputting them into the classifier. The results in Table 6 revealed that as the window size increased, the OA also rose. The OA reached its maximum when the window size was 13 × 13. When the window was further enlarged, the accuracy slightly decreased, indicating that the size of the window indeed affects the accuracy of land feature classification.

Table 6.
The OA, AA, and Kappa coefficient for different window sizes in the selection of SHPs.
From the perspective of PA and UA in Figure 8, the accuracy for all land features, generally reaches its peak when the window size is set to 13 × 13. For water and vegetation, their scattering characteristics are quite stable over time, allowing for distinction based on scattering intensity. However, for the other three land features—buildings, roads, and bare land—their scattering intensities are similar across the time series, leading to similar statistical properties. Therefore, they are prone to misclassification as a single family during SHP selection. Moreover, the FaSHPS algorithm performs well in areas with significant textural differences, helping to avoid confusion with scatterers that differ in reflectance intensity from the central pixel. Hence, the appropriate window size has a considerable impact on the discrimination ability for SAR imagery of different resolutions and for different land features.
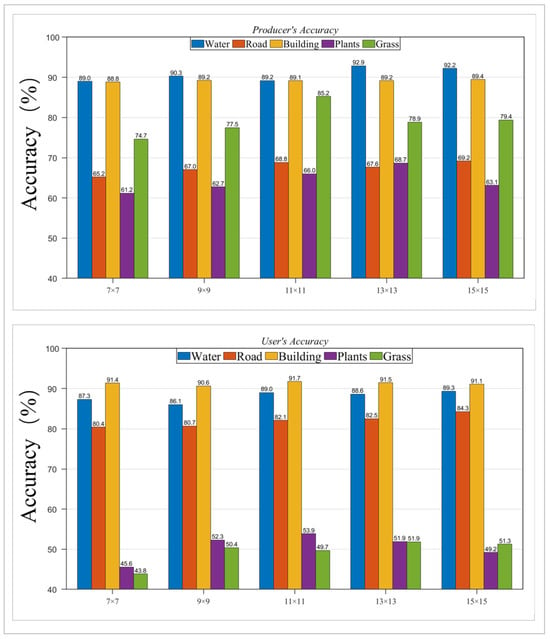
Figure 8.
PA and UA of five kinds of ground objects under windows of different sizes with homogenous particles.
4.7. Comparison of Different Classifiers
In land classification and mapping, the accuracy of various classifiers can differ when tasked with classifying different types of land cover. Some classifiers are better suited for specific land cover types, leading to an enhanced performance in those categories. In light of this, to assess how well our newly adopted features adapt to different classifiers, we chose to conduct comparative tests using XGBoost and SVM. XGBoost is a tree-based ensemble algorithm that builds multiple decision tree models iteratively, with each tree attempting to correct the errors of the previous one. This ensemble approach enables XGBoost to construct robust models that exhibit high accuracy. On the other hand, the primary objective of SVM (Support Vector Machine) is to identify an optimal decision boundary (or hyperplane) that separates data points of different categories. This boundary is chosen to maximize the distance to the nearest data points (support vectors). SVM is also a powerful supervised learning algorithm known for its effectiveness in classification tasks [38].
The experimental results in Table 7 indicate that for the combinations of Mli, Mli + Bro, and Mli + Pcoh, a similar OA was observed across the various classifiers. However, different classifiers exhibited distinct PA and UA values for different types of land cover, suggesting that each classifier has varying abilities to distinguish between different land covers. The integration of the coherence matrix, particularly in combinations with more classification features like Mli + cohM and All, showed that XGB performed better than RF. This aligns with XGB’s reputation as an advanced ensemble tree model, demonstrating a superior classification performance, although its PA and UA values varied across different land covers. For instance, in the Mli + cohM combination, RF excelled in classifying water and roads, while all three classifiers showed a comparable performance in identifying buildings. XGB, however, demonstrated stronger discriminative power for vegetation and grass. In summary, XGB exhibited the most outstanding performance with high-dimensional data, while RF outperformed SVM. Nonetheless, when facing various land covers, different classifiers showed varying levels of performance.

Table 7.
The results of OA, AA, Kappa coefficient, PA, and UA for five experimental combinations using three different machine learning classifiers.
5. Conclusions
This study primarily investigates the impact of adopting various features on the classification of ground objects in SAR imagery. For traditional SAR image classification, backscatter intensity and coherence are the most commonly utilized features. In dealing with surface cover changes caused by seasonal variations, such as flooding, combinations with the shortest temporal baselines are typically chosen. However, the non-shortest temporal baseline combinations also contain information on land cover changes. Therefore, this paper initially employs the coherence matrix as one of the classification features to explore its capability in land cover classification. The findings reveal that while the coherence matrix significantly enhances classification accuracy, it does not play a substantially more critical role than the backscatter intensity feature. Notably, coherence is a complex number; normalizing it between 0 and 1 is a standard practice, but its real and imaginary components can also be used individually as features in classification. For the coherence matrix of all temporal baseline combinations, redundant and irrelevant information can be hidden, especially for multi-temporal SAR images where coherence combinations are numerous. Thus, when considering the extraction of more effective features, PCA is a common technique used. This paper also examines the effect on land cover classification capability when the modulus of coherence and its real and imaginary parts are used as separate features, and contrasts this with the use of PCA for dimensionality reduction in the modulus. The results indicate that using the real and imaginary parts of coherence as separate features, along with PCA reduction in the modulus, achieves the highest classification accuracy.
This study focuses on two main features derived from the DS-InSAR process. When used in combination with backscatter intensity, both the number of SHPs and the ensemble coherence were found to significantly improve land cover classification capabilities, with comparable precision between two groups. This enhancement is because the selection of DS points relies initially on SHP determination, which infers that pixel points maintain similar scattering properties over time. As previously discussed, uniform scattering properties suggest identical land cover, thus underscoring their substantial importance as features. A comprehensive set of experiments conclusively demonstrated the outstanding performance and significant importance of homogeneous points and ensemble coherence in classification, affirming the discernment capabilities of the proposed features for ground objects within SAR imagery. It is important to note that the number of SHPs and the ensemble coherence are not based on SAR image intensity. They possess a comprehensive mathematical derivation in their processing, making them more reliable choices for land cover classification features. Future research could delve into the statistical properties of these features and their relationship with land cover to assess their classification potential for an expanded array of ground objects.
Author Contributions
Conceptualization, M.W. and C.W.; methodology, M.W. and C.W.; software, M.W.; investigation, M.W. and C.W.; formal analysis, M.W. and C.W.; writing—original draft preparation, M.W.; writing—review and editing, M.W., C.W., Y.L. and C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The work is jointly supported by the National Natural Science Foundation of China (42374018 and 42304012), the Shenzhen Scientific Research and the Development Funding Programmes (RCYX20210706092140076 and JCYJ20220531101409021), and Open Research Fund of State Key Laboratory of Subtropical Building and Urban Science (2022ZB04).
Data Availability Statement
The data generated and analyzed during this study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Liu, S.; Su, H.; Cao, G.; Wang, S.; Guan, Q. Learning from data: A post classification method for annual land cover analysis in urban areas. ISPRS J. Photogramm. Remote Sens. 2019, 154, 202–215. [Google Scholar] [CrossRef]
- Song, X.-P.; Sexton, J.O.; Huang, C.; Channan, S.; Townshend, J.R. Characterizing the magnitude, timing and duration of urban growth from time series of Landsat-based estimates of impervious cover. Remote Sens. Environ. 2016, 175, 1–13. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Zhu, Z.; Liang, L.; Yu, B.; Cao, W. Mapping annual urban dynamics (1985–2015) using time series of Landsat data. Remote Sens. Environ. 2018, 216, 674–683. [Google Scholar] [CrossRef]
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Xiang, D.; Tang, T.; Hu, C.; Li, Y.; Su, Y. A kernel clustering algorithm with fuzzy factor: Application to SAR image segmentation. IEEE Geosci. Remote Sens. Lett. 2013, 11, 1290–1294. [Google Scholar] [CrossRef]
- Li, Y.; Zuo, X.; Zhu, D.; Wu, W.; Yang, X.; Guo, S.; Shi, C.; Huang, C.; Li, F.; Liu, X. Identification and analysis of landslides in the Ahai reservoir area of the Jinsha River Basin using a combination of DS-InSAR, optical images, and field surveys. Remote Sens. 2022, 14, 6274. [Google Scholar] [CrossRef]
- Wang, C.; Wei, M.; Qin, X.; Li, T.; Chen, S.; Zhu, C.; Liu, P.; Chang, L. Three-dimensional lookup table for more precise SAR scatterers positioning in urban scenarios. ISPRS J. Photogramm. Remote Sens. 2024, 209, 133–149. [Google Scholar] [CrossRef]
- Wang, C.; Chang, L.; Wang, X.-S.; Zhang, B.; Stein, A. Interferometric synthetic aperture radar statistical inference in deformation measurement and geophysical inversion: A review. IEEE Geosci. Remote Sens. Mag. 2024, 12, 8–35. [Google Scholar] [CrossRef]
- Bruzzone, L.; Marconcini, M.; Wegmuller, U.; Wiesmann, A. An advanced system for the automatic classification of multitemporal SAR images. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1321–1334. [Google Scholar] [CrossRef]
- Karlson, M.; Gålfalk, M.; Crill, P.; Bousquet, P.; Saunois, M.; Bastviken, D. Delineating northern peatlands using Sentinel-1 time series and terrain indices from local and regional digital elevation models. Remote Sens. Environ. 2019, 231, 111252. [Google Scholar] [CrossRef]
- Li, Z.; Chen, H.; White, J.C.; Wulder, M.A.; Hermosilla, T. Discriminating treed and non-treed wetlands in boreal ecosystems using time series Sentinel-1 data. Int. J. Appl. Earth Obs. Geoinf. 2020, 85, 102007. [Google Scholar] [CrossRef]
- Millard, K.; Kirby, P.; Nandlall, S.; Behnamian, A.; Banks, S.; Pacini, F. Using growing-season time series coherence for improved peatland mapping: Comparing the contributions of Sentinel-1 and RADARSAT-2 coherence in full and partial time series. Remote Sens. 2020, 12, 2465. [Google Scholar] [CrossRef]
- Merchant, M.A.; Obadia, M.; Brisco, B.; DeVries, B.; Berg, A. Applying machine learning and time-series analysis on Sentinel-1A SAR/InSAR for characterizing Arctic tundra hydro-ecological conditions. Remote Sens. 2022, 14, 1123. [Google Scholar] [CrossRef]
- Pulvirenti, L.; Chini, M.; Pierdicca, N.; Boni, G. Use of SAR data for detecting floodwater in urban and agricultural areas: The role of the interferometric coherence. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1532–1544. [Google Scholar] [CrossRef]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Brisco, B.; Motagh, M. Multi-temporal, multi-frequency, and multi-polarization coherence and SAR backscatter analysis of wetlands. ISPRS J. Photogramm. Remote Sens. 2018, 142, 78–93. [Google Scholar] [CrossRef]
- Corbane, C.; Lemoine, G.; Pesaresi, M.; Kemper, T.; Sabo, F.; Ferri, S.; Syrris, V. Enhanced automatic detection of human settlements using Sentinel-1 interferometric coherence. Int. J. Remote Sens. 2018, 39, 842–853. [Google Scholar] [CrossRef]
- Li, Y.; Martinis, S.; Wieland, M.; Schlaffer, S.; Natsuaki, R. Urban flood mapping using SAR intensity and interferometric coherence via Bayesian network fusion. Remote Sens. 2019, 11, 2231. [Google Scholar] [CrossRef]
- Chang, S.; Deng, Y.; Zhang, Y.; Zhao, Q.; Wang, R.; Zhang, K. An advanced scheme for range ambiguity suppression of spaceborne SAR based on blind source separation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5230112. [Google Scholar] [CrossRef]
- Wang, C.; Wang, X.-S.; Xu, Y.; Zhang, B.; Jiang, M.; Xiong, S.; Zhang, Q.; Li, W.; Li, Q. A new likelihood function for consistent phase series estimation in distributed scatterer interferometry. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5227314. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Jeyachandran, I.; Burian, S.J.; Stetson, S.W. Estimating urban canopy parameters using synthetic aperture radar data. J. Appl. Meteorol. Climatol. 2010, 49, 732–747. [Google Scholar] [CrossRef]
- Babu, A.; Baumgartner, S.V.; Krieger, G. Approaches for road surface roughness estimation using airborne polarimetric SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3444–3462. [Google Scholar] [CrossRef]
- Kasischke, E.S.; Smith, K.B.; Bourgeau-Chavez, L.L.; Romanowicz, E.A.; Brunzell, S.; Richardson, C.J. Effects of seasonal hydrologic patterns in south Florida wetlands on radar backscatter measured from ERS-2 SAR imagery. Remote Sens. Environ. 2003, 88, 423–441. [Google Scholar] [CrossRef]
- Patel, P.; Srivastava, H.S.; Panigrahy, S.; Parihar, J.S. Comparative evaluation of the sensitivity of multi-polarized multi-frequency SAR backscatter to plant density. Int. J. Remote Sens. 2006, 27, 293–305. [Google Scholar] [CrossRef]
- Chul Jung, H.; Alsdorf, D. Repeat-pass multi-temporal interferometric SAR coherence variations with Amazon floodplain and lake habitats. Int. J. Remote Sens. 2010, 31, 881–901. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.; Zhang, H.; Tang, Y.; Liu, X. Analysis of permafrost region coherence variation in the Qinghai–Tibet Plateau with a high-resolution TerraSAR-X image. Remote Sens. 2018, 10, 298. [Google Scholar] [CrossRef]
- Jacob, A.W.; Vicente-Guijalba, F.; Lopez-Martinez, C.; Lopez-Sanchez, J.M.; Litzinger, M.; Kristen, H.; Mestre-Quereda, A.; Ziółkowski, D.; Lavalle, M.; Notarnicola, C. Sentinel-1 InSAR coherence for land cover mapping: A comparison of multiple feature-based classifiers. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 535–552. [Google Scholar] [CrossRef]
- Jiang, M.; Ding, X.L.; Hanssen, R.F.; Malhotra, R.; Chang, L. Fast Statistically Homogeneous Pixel Selection for Covariance Matrix Estimation for Multitemporal InSAR. Ieee Trans. Geosci. Remote Sens. 2015, 53, 1213–1224. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Kloiber, S.M.; Macleod, R.D.; Smith, A.J.; Knight, J.F.; Huberty, B.J. A semi-automated, multi-source data fusion update of a wetland inventory for east-central Minnesota, USA. Wetlands 2015, 35, 335–348. [Google Scholar] [CrossRef]
- Guan, H.; Li, J.; Chapman, M.; Deng, F.; Ji, Z.; Yang, X. Integration of orthoimagery and lidar data for object-based urban thematic mapping using random forests. Int. J. Remote Sens. 2013, 34, 5166–5186. [Google Scholar] [CrossRef]
- Miao, X.; Heaton, J.S.; Zheng, S.; Charlet, D.A.; Liu, H. Applying tree-based ensemble algorithms to the classification of ecological zones using multi-temporal multi-source remote-sensing data. Int. J. Remote Sens. 2012, 33, 1823–1849. [Google Scholar] [CrossRef]
- Sonobe, R.; Tani, H.; Wang, X.; Kobayashi, N.; Shimamura, H. Random forest classification of crop type using multi-temporal TerraSAR-X dual-polarimetric data. Remote Sens. Lett. 2014, 5, 157–164. [Google Scholar] [CrossRef]
- Wohlfart, C.; Winkler, K.; Wendleder, A.; Roth, A. TerraSAR-X and wetlands: A review. Remote Sens. 2018, 10, 916. [Google Scholar] [CrossRef]
- Liu, J.; Li, P.; Tu, C.R.; Wang, H.J.; Zhou, Z.W.; Feng, Z.X.; Shen, F.; Li, Z.H. Spatiotemporal Change Detection of Coastal Wetlands Using Multi-Band SAR Coherence and Synergetic Classification. Remote Sens. 2022, 14, 2610. [Google Scholar] [CrossRef]
- Guan, D.; Xiang, D.; Tang, X.; Wang, L.; Kuang, G. Covariance of textural features: A new feature descriptor for SAR image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3932–3942. [Google Scholar] [CrossRef]
- Gašparović, M.; Dobrinić, D. Comparative assessment of machine learning methods for urban vegetation mapping using multitemporal sentinel-1 imagery. Remote Sens. 2020, 12, 1952. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).