Predictions of Aboveground Herbaceous Production from Satellite-Derived APAR Are More Sensitive to Ecosite than Grazing Management Strategy in Shortgrass Steppe
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Ground-Based Measurements
2.3. Remotely Sensed Measurements
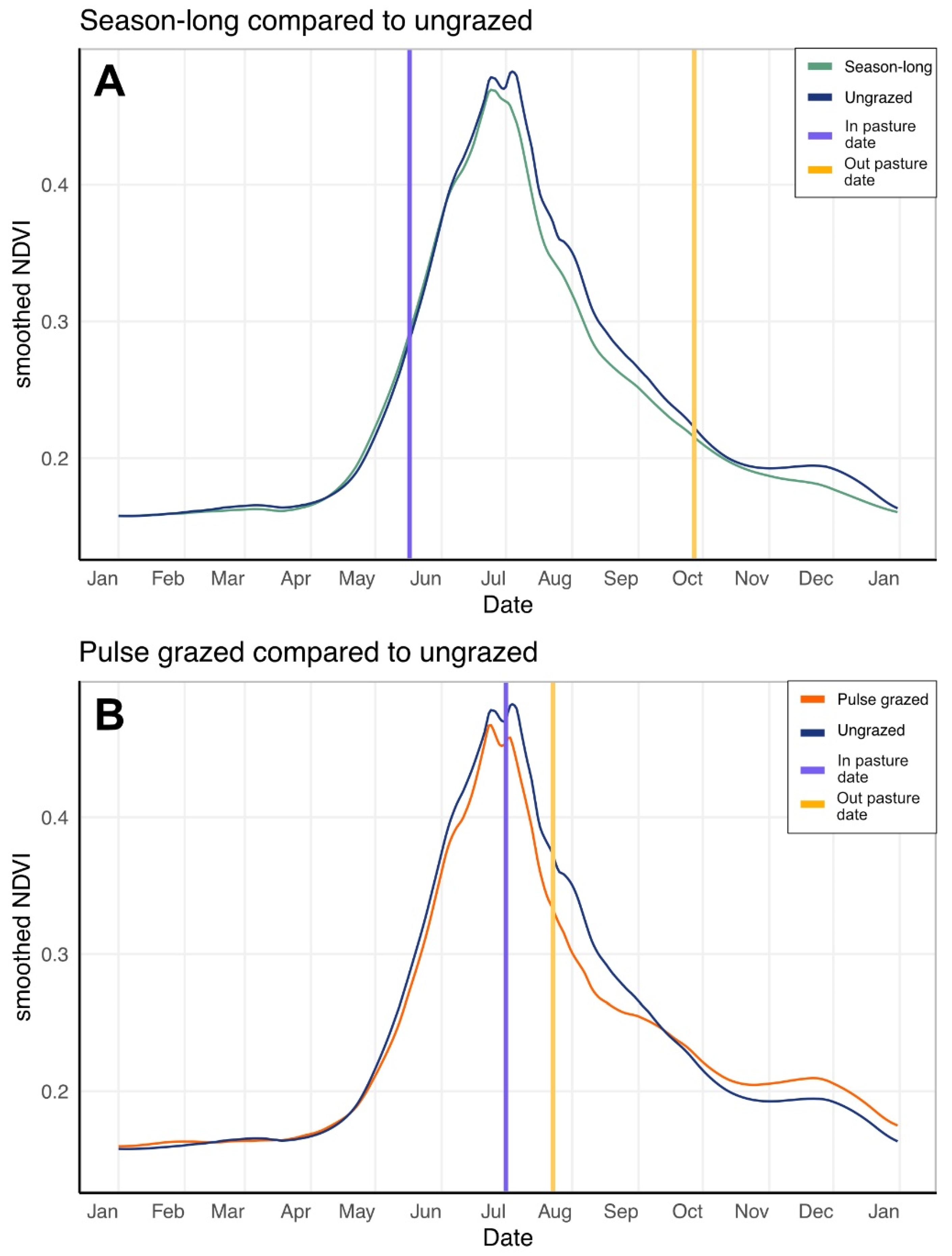
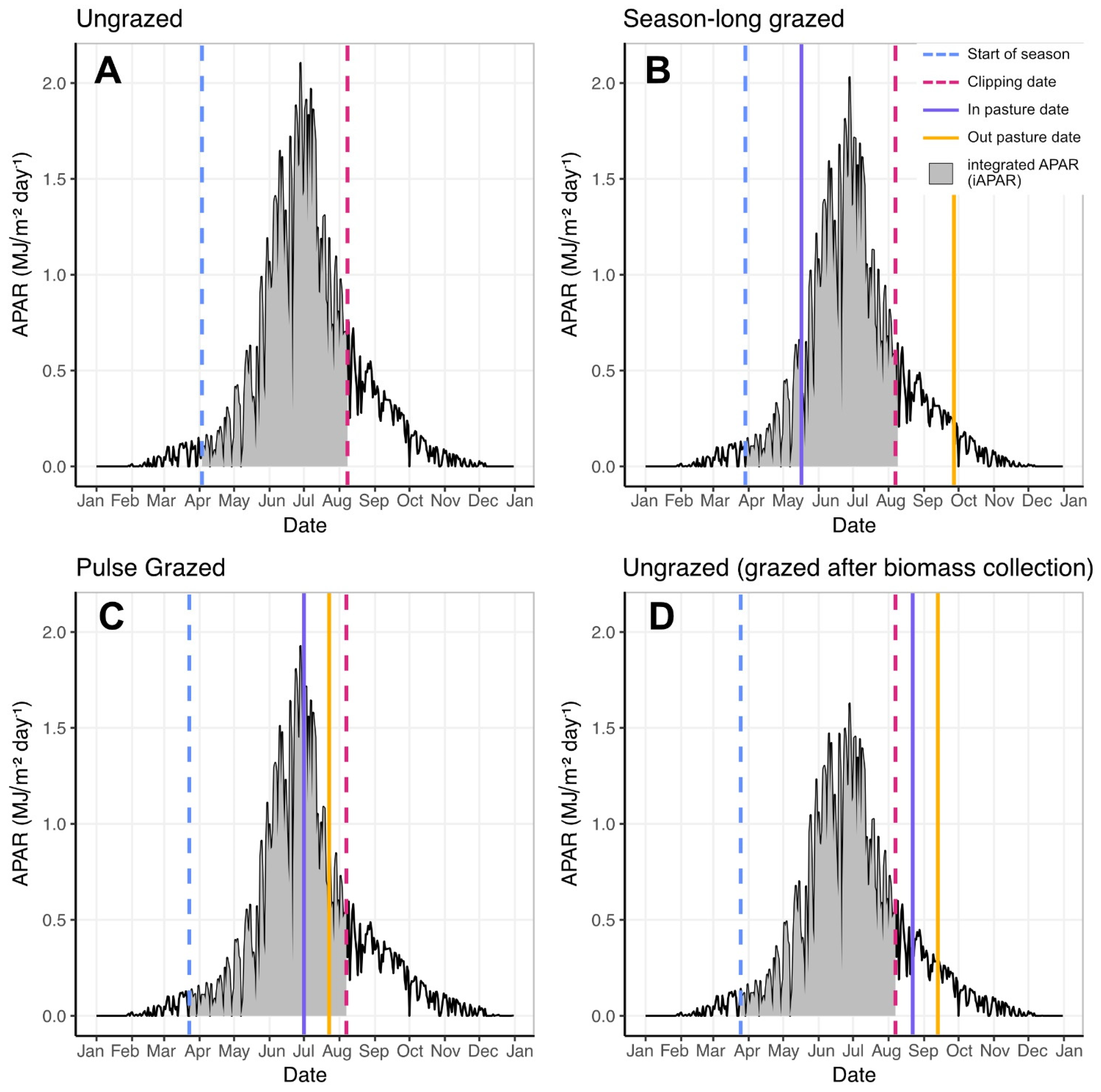
2.3.1. Calculating iAPAR
2.3.2. Extracting Rangeland Analysis Platform Estimates
2.3.3. Estimating ANHP from iAPAR
2.4. Comparing RAP and iAPAR Model Results
3. Results
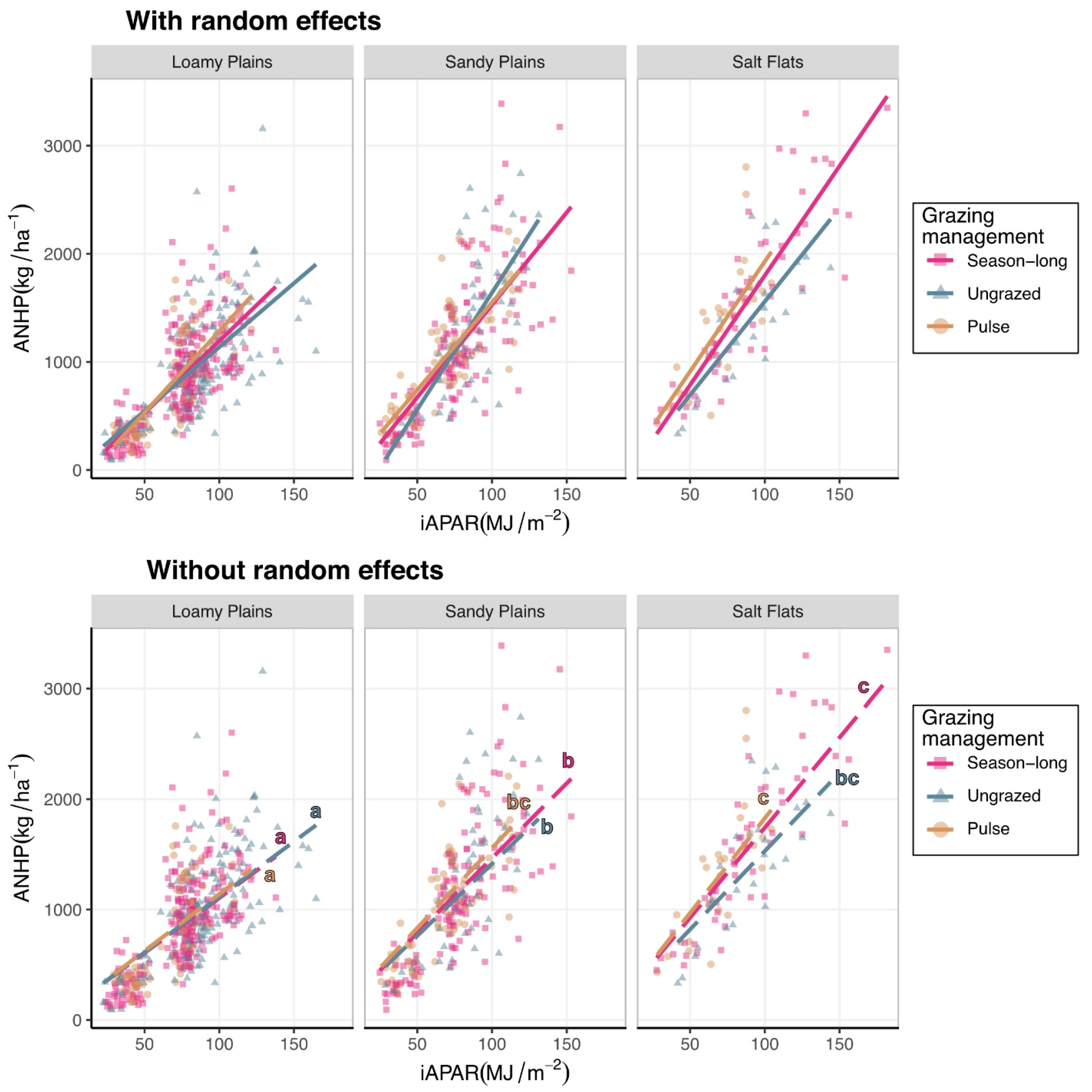
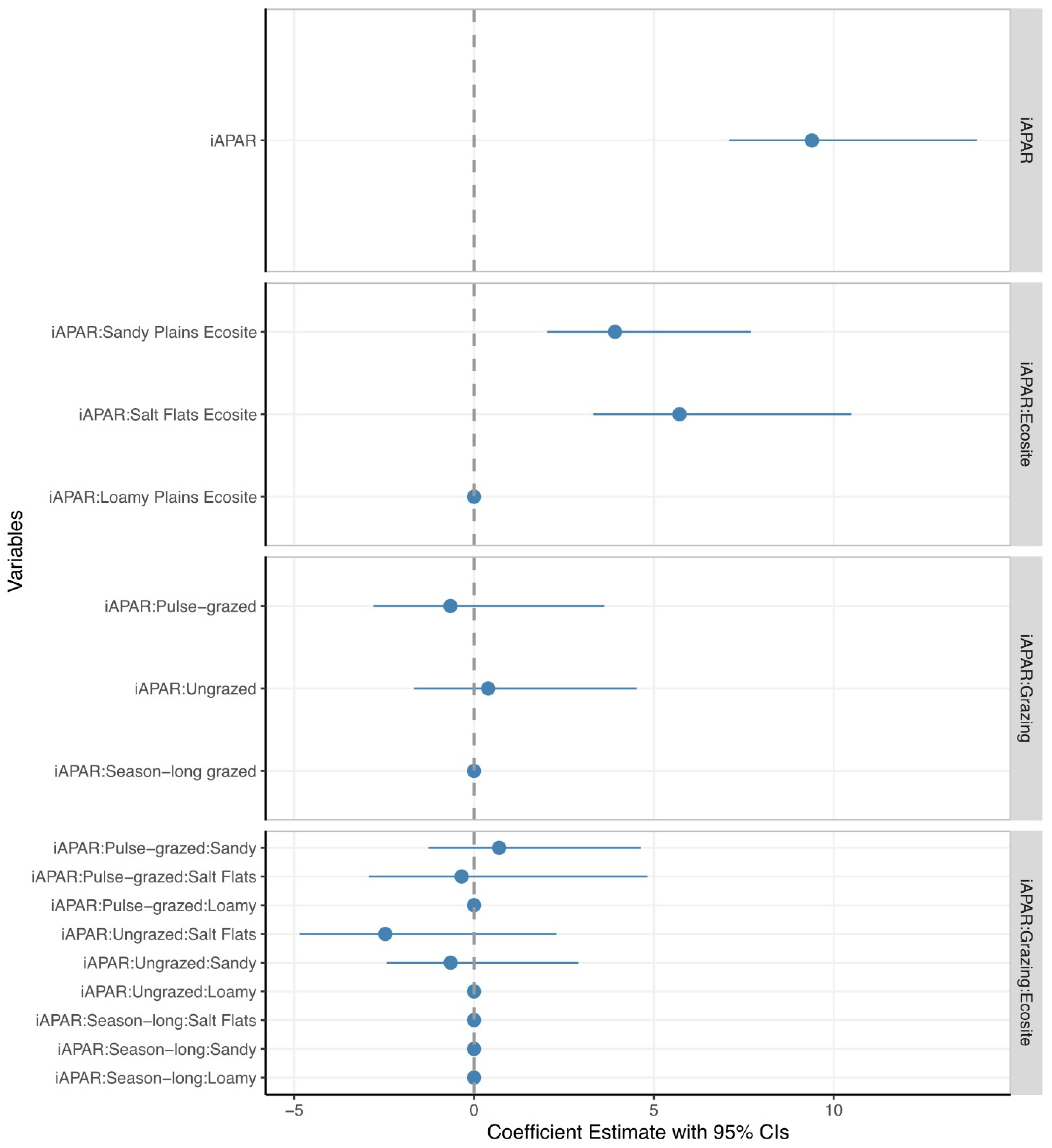
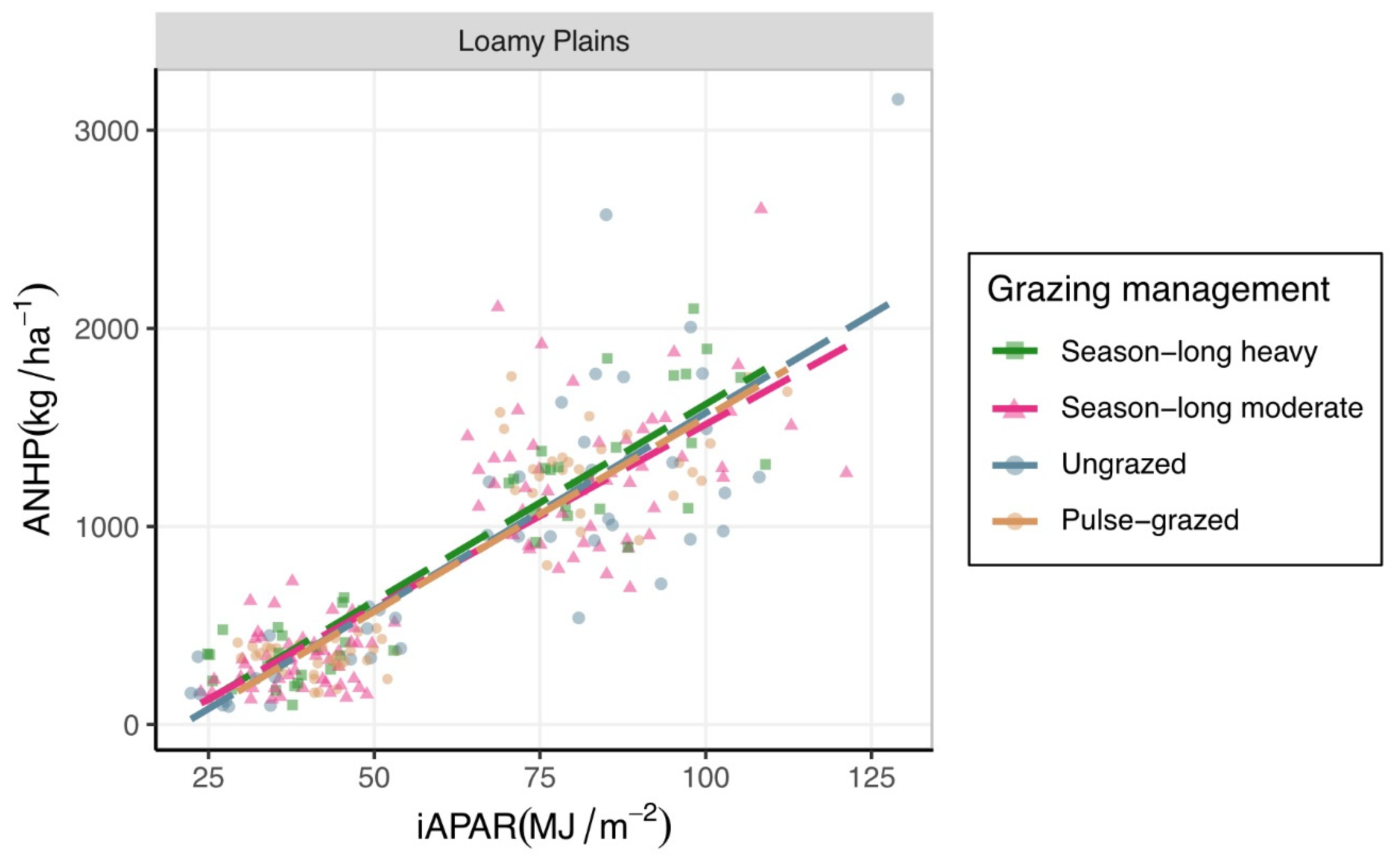
3.1. Estimating ANHP from iAPAR
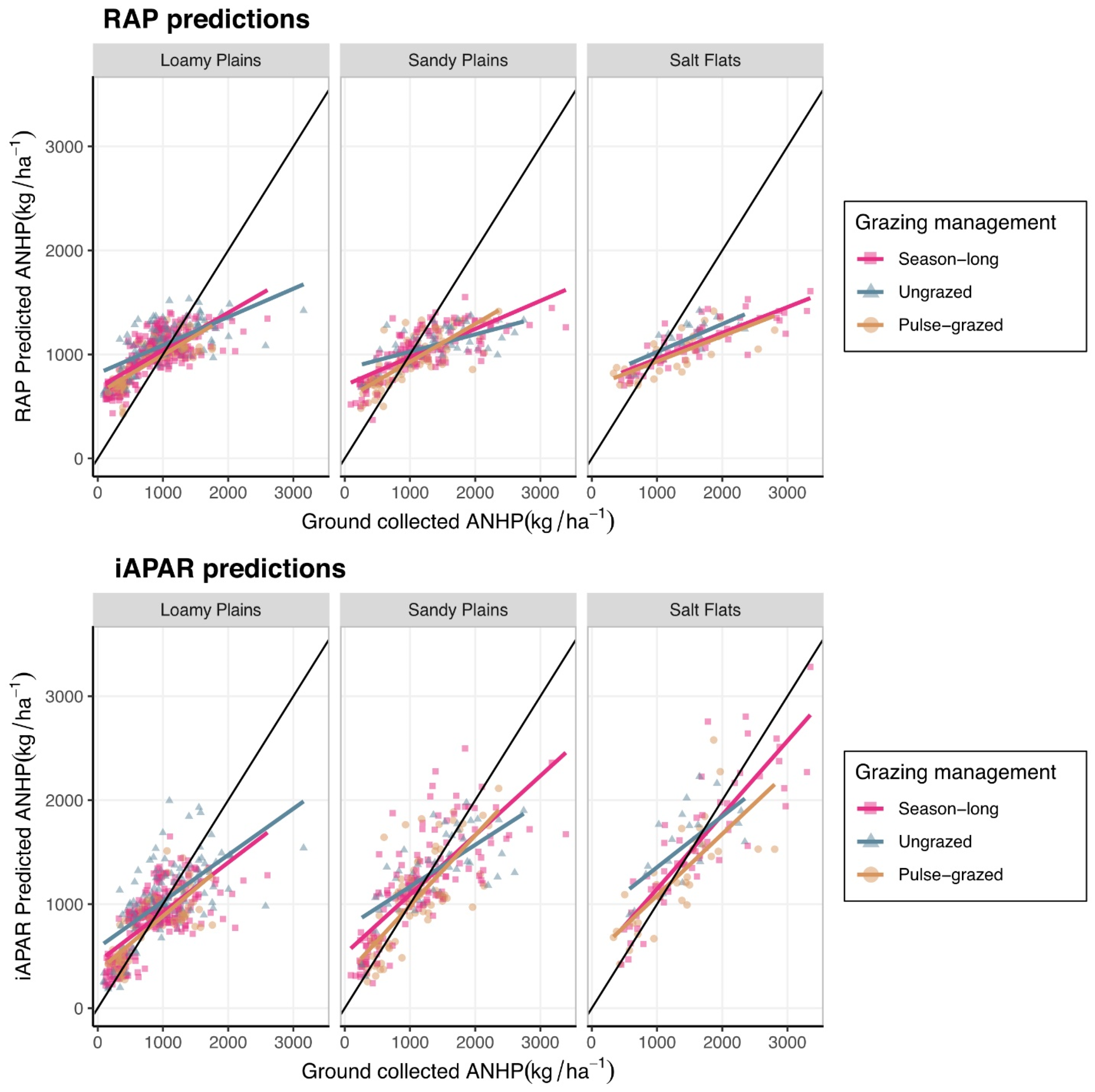
3.2. iAPAR and RAP Model Comparison
4. Discussion
4.1. Effects of Ecosite
4.2. Effects of Grazing Management
4.3. Process-Based vs. Empirical Modeling
4.4. Implications
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Holechek, J.; Pieper, R.D.; Herbel, C.H. Range Management: Principles and Practices, 6th ed.; Prentice Hall: Boston, MA, USA, 2011; ISBN 978-0-13-501416-5. [Google Scholar]
- Holechek, J.L. Global Trends in Population, Energy Use and Climate: Implications for Policy Development, Rangeland Management and Rangeland Users. Rangel. J. 2013, 35, 117. [Google Scholar] [CrossRef]
- Grigera, G.; Oesterheld, M.; Pacín, F. Monitoring Forage Production for Farmers’ Decision Making. Agric. Syst. 2007, 94, 637–648. [Google Scholar] [CrossRef]
- Hoover, D.L.; Pfennigwerth, A.A.; Duniway, M.C. Drought Resistance and Resilience: The Role of Soil Moisture–Plant Interactions and Legacies in a Dryland Ecosystem. J. Ecol. 2021, 109, 3280–3294. [Google Scholar] [CrossRef]
- Porensky, L.M.; Derner, J.D.; Augustine, D.J.; Milchunas, D.G. Plant Community Composition After 75 Yr of Sustained Grazing Intensity Treatments in Shortgrass Steppe. Rangel. Ecol. Manag. 2017, 70, 456–464. [Google Scholar] [CrossRef]
- Charles, G.K.; Porensky, L.M.; Riginos, C.; Veblen, K.E.; Young, T.P. Herbivore Effects on Productivity Vary by Guild: Cattle Increase Mean Productivity While Wildlife Reduce Variability. Ecol. Appl. 2017, 27, 143–155. [Google Scholar] [CrossRef] [PubMed]
- Hannusch, H.J.; Rogers, W.E.; Lodge, A.G.; Starns, H.D.; Tolleson, D.R. Semi-arid Savanna Herbaceous Production and Diversity Responses to Interactive Effects of Drought, Nitrogen Deposition, and Fire. J. Veg. Sci. 2020, 31, 255–265. [Google Scholar] [CrossRef]
- Augustine, D.J.; Derner, J.D.; Fernández-Giménez, M.E.; Porensky, L.M.; Wilmer, H.; Briske, D.D. Adaptive, Multipaddock Rotational Grazing Management: A Ranch-Scale Assessment of Effects on Vegetation and Livestock Performance in Semiarid Rangeland. Rangel. Ecol. Manag. 2020, 73, 796–810. [Google Scholar] [CrossRef]
- Monroe, P.H.M.; Barreto-Garcia, P.A.B.; Barros, W.T.; de Oliveira, F.G.R.B.; Pereira, M.G. Physical Protection of Soil Organic Carbon through Aggregates in Different Land Use Systems in the Semi-Arid Region of Brazil. J. Arid Environ. 2021, 186, 104427. [Google Scholar] [CrossRef]
- Reinermann, S.; Asam, S.; Kuenzer, C. Remote Sensing of Grassland Production and Management—A Review. Remote Sens. 2020, 12, 1949. [Google Scholar] [CrossRef]
- Myneni, R.B.; Ramakrishna, R.; Nemani, R.; Running, S.W. Estimation of Global Leaf Area Index and Absorbed Par Using Radiative Transfer Models. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1380–1393. [Google Scholar] [CrossRef]
- Gaffney, R.; Porensky, L.; Gao, F.; Irisarri, J.; Durante, M.; Derner, J.; Augustine, D. Using APAR to Predict Aboveground Plant Productivity in Semi-Aid Rangelands: Spatial and Temporal Relationships Differ. Remote Sens. 2018, 10, 1474. [Google Scholar] [CrossRef]
- Tucker, C.J.; Fung, I.Y.; Keeling, C.D.; Gammon, R.H. Relationship between Atmospheric CO2 Variations and a Satellite-Derived Vegetation Index. Nature 1986, 319, 195–199. [Google Scholar] [CrossRef]
- Smith, W.; Reed, S.C.; Cleveland, C.C.; Ballantyne, A.P.; Anderegg, W.R.L.; Wieder, W.R.; Liu, Y.Y.; Running, S.W. Large Divergence of Satellite and Earth System Model Estimates of Global Terrestrial CO2 Fertilization. Nat. Clim. Chang. 2016, 6, 306–310. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A Continuous Satellite-Derived Measure of Global Terrestrial Primary Production. BioScience 2004, 54, 547. [Google Scholar] [CrossRef]
- Robinson, N.P.; Allred, B.W.; Smith, W.K.; Jones, M.O.; Moreno, A.; Erickson, T.A.; Naugle, D.E.; Running, S.W. Terrestrial Primary Production for the Conterminous United States Derived from Landsat 30 m and MODIS 250 m. Remote Sens. Ecol. Conserv. 2018, 4, 264–280. [Google Scholar] [CrossRef]
- Jones, M.O.; Robinson, N.P.; Naugle, D.E.; Maestas, J.D.; Reeves, M.C.; Lankston, R.W.; Allred, B.W. Annual and 16-Day Rangeland Production Estimates for the Western United States. Rangel. Ecol. Manag. 2021, 77, 112–117. [Google Scholar] [CrossRef]
- McNaughton, S.J. Compensatory Plant Growth as a Response to Herbivory. Oikos 1983, 40, 329. [Google Scholar] [CrossRef]
- Milchunas, D.G.; Lauenroth, W.K. Quantitative Effects of Grazing on Vegetation and Soils Over a Global Range of Environments: Ecological Archives M063-001. Ecol. Monogr. 1993, 63, 327–366. [Google Scholar] [CrossRef]
- Ramula, S.; Paige, K.N.; Lennartsson, T.; Tuomi, J. Overcompensation: A 30-year Perspective. Ecology 2019, 100, e02667. [Google Scholar] [CrossRef]
- McNaughton, S.J.; Milchunas, D.G.; Frank, D.A. How Can Net Primary Productivity Be Measured in Grazing Ecosystems? Ecology 1996, 77, 974–977. [Google Scholar] [CrossRef]
- Duniway, M.C.; Bestelmeyer, B.T.; Tugel, A. Soil Processes and Properties That Distinguish Ecological Sites and States. Rangelands 2010, 32, 9–15. [Google Scholar] [CrossRef]
- United States Department of Agriculture, N.R.C.S. Ecological Site Description for Loamy Plains (R067BY002CO). Available online: https://edit.jornada.nmsu.edu/catalogs/esd/067B/R067BY002CO (accessed on 11 March 2024).
- United States Department of Agriculture, N.R.C.S. Ecological Site Description for Sandy Plains (R067BY024CO). Available online: https://edit.jornada.nmsu.edu/catalogs/esd/067B/R067BY024CO (accessed on 11 March 2024).
- United States Department of Agriculture, N.R.C.S. Ecological Site Description for Salt Flat (R067BY033CO). Available online: https://edit.jornada.nmsu.edu/catalogs/esd/067B/R067BY033CO (accessed on 11 March 2024).
- Milchunas, D.G.; Lauenroth, W.K. Effects of Grazing on Vegetation. In Ecology of the Shortgrass Steppe; Oxford University Press: Oxford, UK, 2008; ISBN 978-0-19-513582-4. [Google Scholar]
- Spiegal, S.; Bestelmeyer, B.T.; Archer, D.W.; Augustine, D.J.; Boughton, E.H.; Boughton, R.K.; Cavigelli, M.A.; Clark, P.E.; Derner, J.D.; Duncan, E.W.; et al. Evaluating Strategies for Sustainable Intensification of US Agriculture through the Long-Term Agroecosystem Research Network. Environ. Res. Lett. 2018, 13, 034031. [Google Scholar] [CrossRef]
- Lauenroth, W.K.; Burke, I.C. Ecology of the Shortgrass Steppe: A Long-Term Perspective; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Fernández-Giménez, M.E.; Augustine, D.J.; Porensky, L.M.; Wilmer, H.; Derner, J.D.; Briske, D.D.; Stewart, M.O. Complexity Fosters Learning in Collaborative Adaptive Management. Ecol. Soc. 2019, 24, art29. [Google Scholar] [CrossRef]
- Wilmer, H.; Augustine, D.J.; Derner, J.D.; Fernández-Giménez, M.E.; Briske, D.D.; Roche, L.M.; Tate, K.W.; Miller, K.E. Diverse Management Strategies Produce Similar Ecological Outcomes on Ranches in Western Great Plains: Social-Ecological Assessment. Rangel. Ecol. Manag. 2018, 71, 626–636. [Google Scholar] [CrossRef]
- Davis, K.P.; Augustine, D.J.; Monroe, A.P.; Derner, J.D.; Aldridge, C.L. Adaptive Rangeland Management Benefits Grassland Birds Utilizing Opposing Vegetation Structure in the Shortgrass Steppe. Ecol. Appl. 2020, 30, e02020. [Google Scholar] [CrossRef]
- R Core Team. In R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023.
- Gao, F.; Hilker, T.; Zhu, X.; Anderson, M.; Masek, J.; Wang, P.; Yang, Y. Fusing Landsat and MODIS Data for Vegetation Monitoring. IEEE Geosci. Remote Sens. Mag. 2015, 3, 47–60. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the Blending of the Landsat and MODIS Surface Reflectance: Predicting Daily Landsat Surface Reflectance. IEEE Trans. Geosci. REMOTE Sens. 2006, 44, 2207–2218. [Google Scholar]
- Claverie, M.; Ju, J.; Masek, J.G.; Dungan, J.L.; Vermote, E.F.; Roger, J.-C.; Skakun, S.V.; Justice, C. The Harmonized Landsat and Sentinel-2 Surface Reflectance Data Set. Remote Sens. Environ. 2018, 219, 145–161. [Google Scholar] [CrossRef]
- Kearney, S.P.; Porensky, L.M.; Augustine, D.J.; Gaffney, R.; Derner, J.D. Monitoring Standing Herbaceous Biomass and Thresholds in Semiarid Rangelands from Harmonized Landsat 8 and Sentinel-2 Imagery to Support within-Season Adaptive Management. Remote Sens. Environ. 2022, 271, 112907. [Google Scholar] [CrossRef]
- Bates, D.; Machler, M.; Bolker, B.M.; Walker, S.C. Fitting Linear Mixed-Effects Models Using Lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Augustine, D.J.; Dijkstra, F.A.; William Hamilton Iii, E.; Morgan, J.A. Rhizosphere Interactions, Carbon Allocation, and Nitrogen Acquisition of Two Perennial North American Grasses in Response to Defoliation and Elevated Atmospheric CO2. Oecologia 2011, 165, 755–770. [Google Scholar] [CrossRef] [PubMed]
- Irisarri, J.G.N.; Derner, J.D.; Porensky, L.M.; Augustine, D.J.; Reeves, J.L.; Mueller, K.E. Grazing Intensity Differentially Regulates ANPP Response to Precipitation in North American Semiarid Grasslands. Ecol. Appl. 2016, 26, 1370–1380. [Google Scholar] [CrossRef] [PubMed]
- Augustine, D.J.; Derner, J.D.; Milchunas, D.; Blumenthal, D.; Porensky, L.M. Grazing Moderates Increases in C3 Grass Abundance over Seven Decades across a Soil Texture Gradient in Shortgrass Steppe. J. Veg. Sci. 2017, 28, 562–572. [Google Scholar] [CrossRef]
- Boughton, E.H.; Gomez-Casanovas, N.; Swain, H.; Bernacchi, C.; Boughton, R.K.; Brinsko, K.; Li, H.; Rivero, A.; DeLucia, E.H.; Sparks, J. Patch-Burn Grazing Impacts Forage Resources in Subtropical Humid Grazing Lands. Rangel. Ecol. Manag. 2022, 84, 10–21. [Google Scholar] [CrossRef]
- Schoenecker, K.A.; Zeigenfuss, L.C.; Augustine, D.J. Can Grazing by Elk and Bison Stimulate Herbaceous Plant Productivity in Semiarid Ecosystems? Ecosphere 2022, 13, e4025. [Google Scholar] [CrossRef]
- Gaffney, R.; Augustine, D.J.; Kearney, S.P.; Porensky, L.M. Using Hyperspectral Imagery to Characterize Rangeland Vegetation Composition at Process-Relevant Scales. Remote Sens. 2021, 13, 4603. [Google Scholar] [CrossRef]


| Dependent Variable: | |
|---|---|
| ANHP (SE) (kg/ha −1) | |
| iAPAR | 9.39 *** (1.17) |
| Grazing management: Ungrazed | −11.96 (92.45) |
| Grazing management: Pulse-grazed | 55.44 (78.54) |
| Ecosite Sandy Plains | −28.11 (77.39) |
| Ecosite Salt Flats | 94.16 (110.03) |
| iAPAR: Grazing management: Ungrazed | 0.39 (1.05) |
| iAPAR: Grazing management: Pulse-grazed | −0.65 (1.09) |
| iAPAR: Ecosite Sandy Plains | 3.92 *** (0.96) |
| iAPAR: Ecosite Salt Flats | 5.71 *** (1.22) |
| iAPAR: Grazing management: Ungrazed: Ecosite Sandy Plains | −0.65 (0.90) |
| iAPAR: Grazing management: Pulse-grazed: Ecosite Sandy Plains | 0.69 (1.00) |
| iAPAR: Grazing management: Ungrazed: Ecosite Salt Flats | −2.46 * (1.21) |
| iAPAR: Grazing management: Pulse-grazed: Ecosite Salt Flats | −0.34 (1.32) |
| Constant | 149.95 (119.99) |
| Observations | 852 |
| Log Likelihood | −6037.74 |
| Akaike Inf. Crit. | 12,109.50 |
| Bayesian Inf. Crit. | 12,190.20 |
| Source | Ecosite | MAE (kg/ha−1) | MAE% | MPE% | MAPE% | R2 | r |
|---|---|---|---|---|---|---|---|
| iAPAR | All | 268.51 | 25.60 | −14.97 | 32.64 | 0.62 | 0.78 |
| RAP | 343.08 | 32.71 | −28.57 | 49.59 | 0.40 | 0.72 | |
| iAPAR | Loamy Plains | 249.21 | 28.00 | −17.16 | 35.51 | 0.49 | 0.70 |
| Sandy Plains | 290.58 | 25.32 | −13.94 | 31.60 | 0.58 | 0.76 | |
| Salt Flats | 295.75 | 19.92 | −8.14 | 22.86 | 0.67 | 0.82 | |
| RAP | Loamy Plains | 301.77 | 33.90 | −47.98 | 59.67 | 0.40 | 0.72 |
| Sandy Plains | 354.08 | 30.85 | −12.08 | 39.76 | 0.36 | 0.74 | |
| Salt Flats | 494.03 | 33.27 | 13.40 | 31.02 | 0.07 | 0.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peirce, E.S.; Kearney, S.P.; Santamaria, N.; Augustine, D.J.; Porensky, L.M. Predictions of Aboveground Herbaceous Production from Satellite-Derived APAR Are More Sensitive to Ecosite than Grazing Management Strategy in Shortgrass Steppe. Remote Sens. 2024, 16, 2780. https://doi.org/10.3390/rs16152780
Peirce ES, Kearney SP, Santamaria N, Augustine DJ, Porensky LM. Predictions of Aboveground Herbaceous Production from Satellite-Derived APAR Are More Sensitive to Ecosite than Grazing Management Strategy in Shortgrass Steppe. Remote Sensing. 2024; 16(15):2780. https://doi.org/10.3390/rs16152780
Chicago/Turabian StylePeirce, Erika S., Sean P. Kearney, Nikolas Santamaria, David J. Augustine, and Lauren M. Porensky. 2024. "Predictions of Aboveground Herbaceous Production from Satellite-Derived APAR Are More Sensitive to Ecosite than Grazing Management Strategy in Shortgrass Steppe" Remote Sensing 16, no. 15: 2780. https://doi.org/10.3390/rs16152780
APA StylePeirce, E. S., Kearney, S. P., Santamaria, N., Augustine, D. J., & Porensky, L. M. (2024). Predictions of Aboveground Herbaceous Production from Satellite-Derived APAR Are More Sensitive to Ecosite than Grazing Management Strategy in Shortgrass Steppe. Remote Sensing, 16(15), 2780. https://doi.org/10.3390/rs16152780







