Multi-Feature Cross Attention-Induced Transformer Network for Hyperspectral and LiDAR Data Classification
Abstract
1. Introduction
2. Materials and Methods
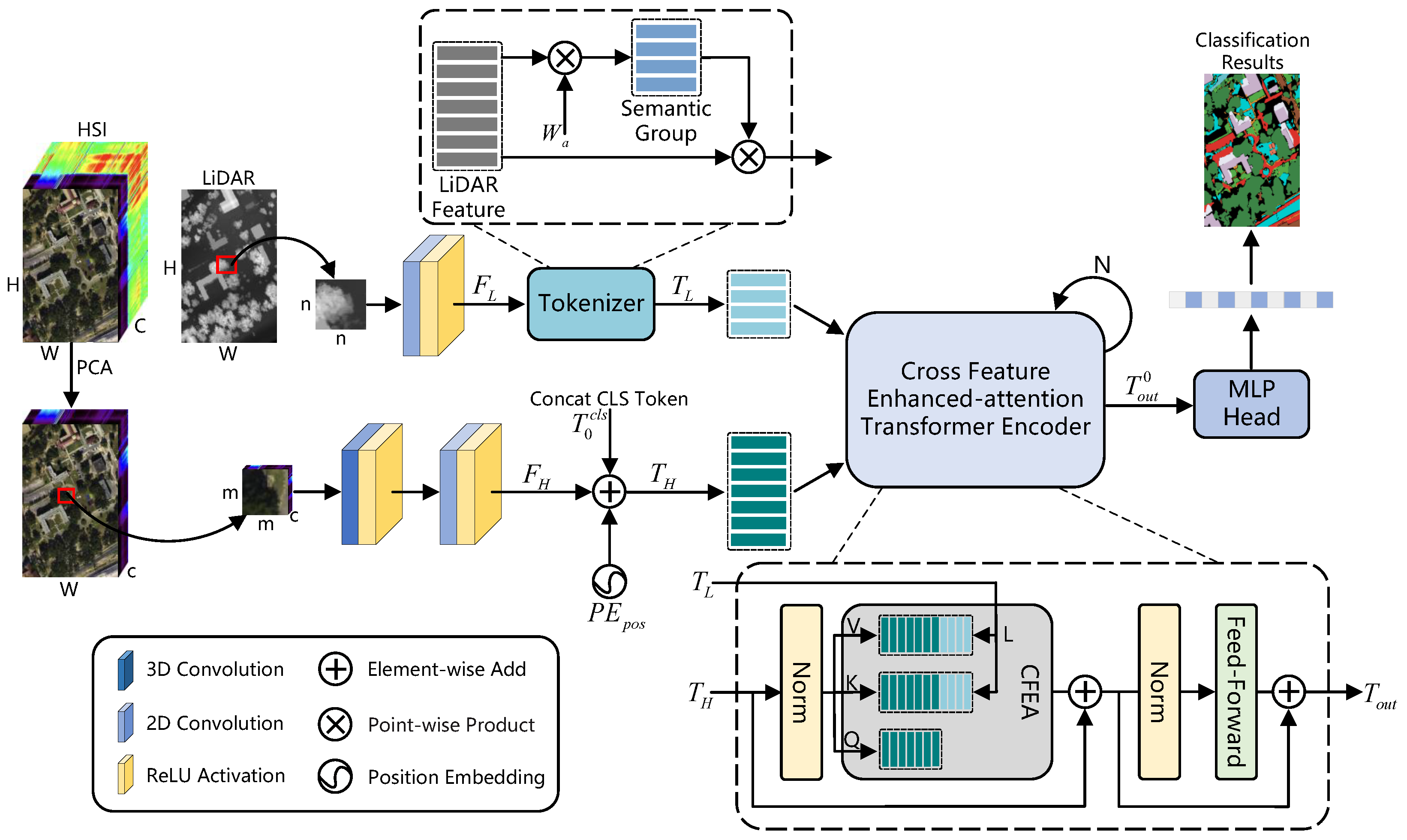
2.1. HSI and LiDAR-Data Preprocessing
2.2. Shallow CNN Feature-Extraction Module
2.3. HSI Semantic Tokenizer and LiDAR Gaussian-Weighted Feature Tokenizer
2.4. Cross-Feature Enhanced-Attention Transformer Encoder
2.5. Classification Head
| Algorithm 1 MCAITN network. |
| Require: HSI data , LiDAR data ; PCA bands number c; patch size S; train rate . Ensure: Predicted labels of the test set.
|
3. Experiments
3.1. Dataset Description
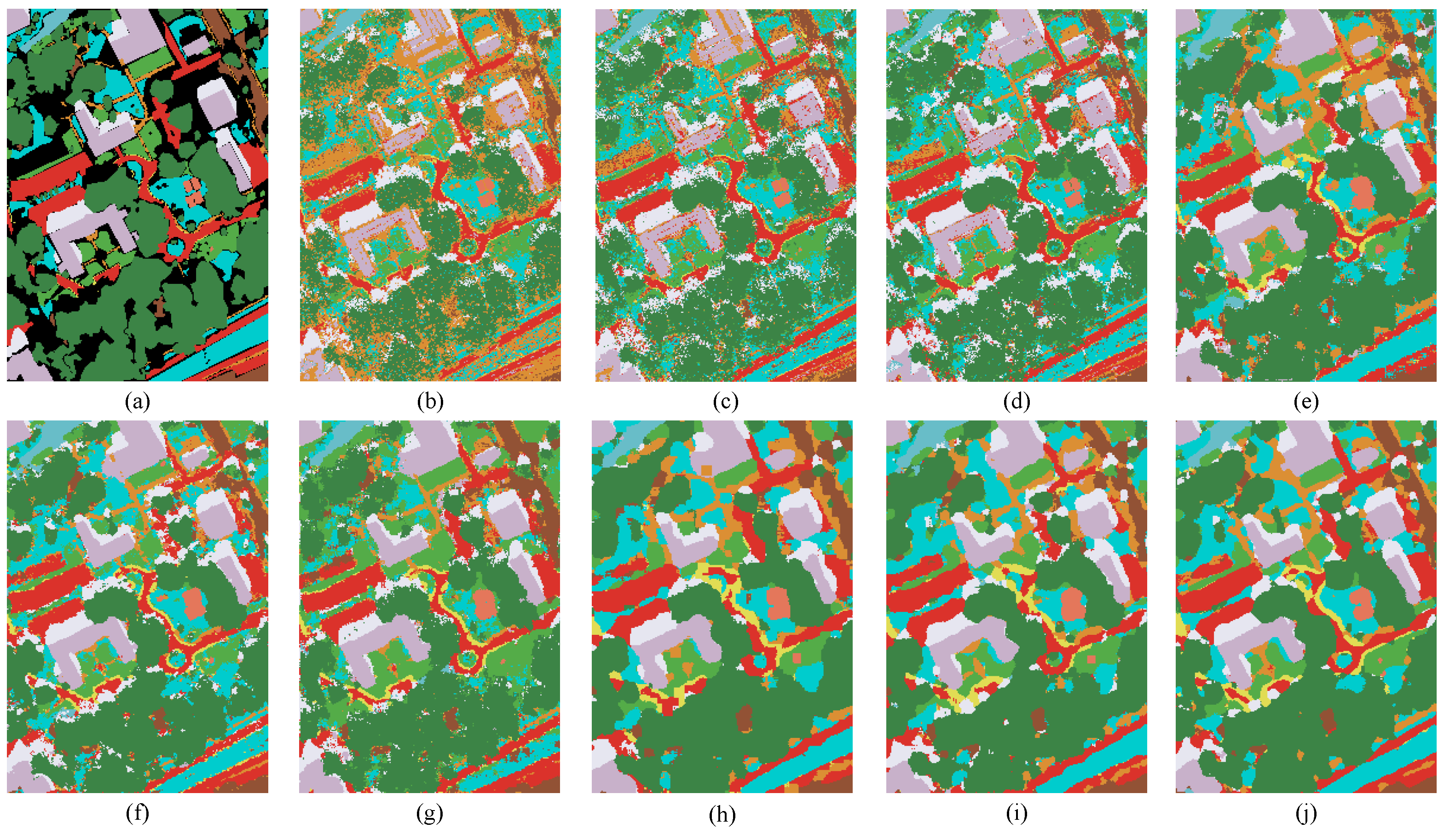
3.1.1. MUUFL
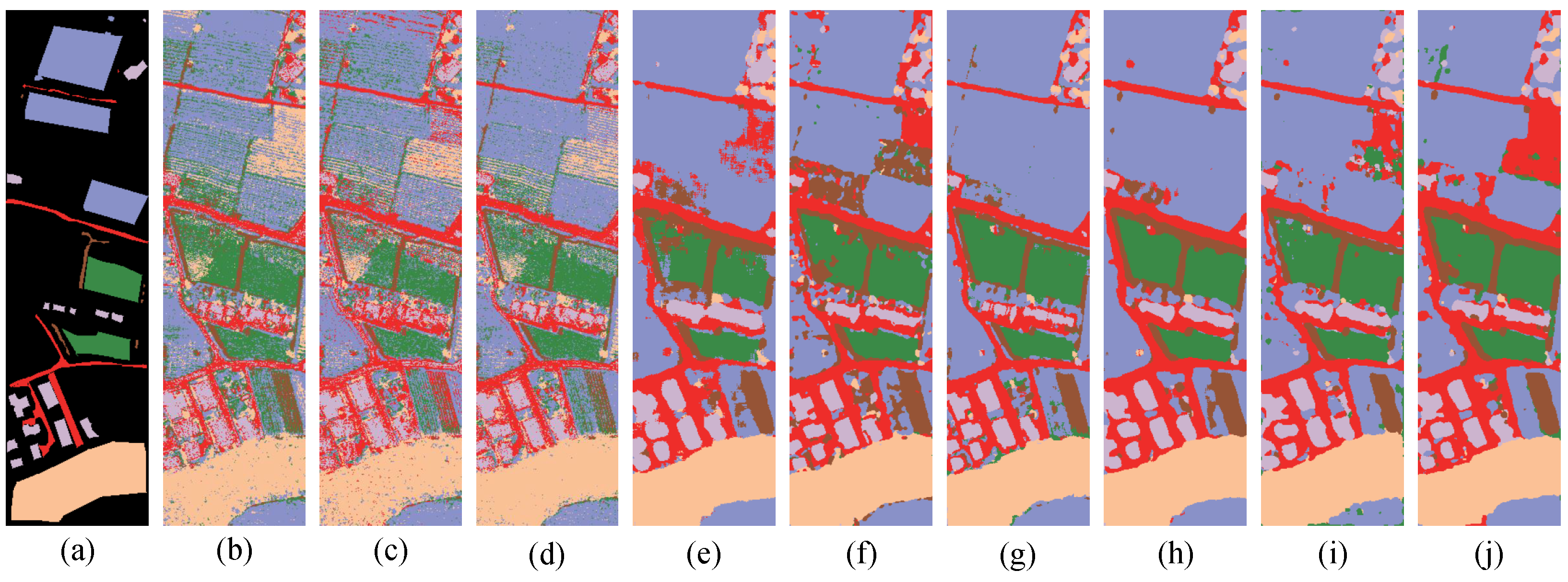
3.1.2. Trento
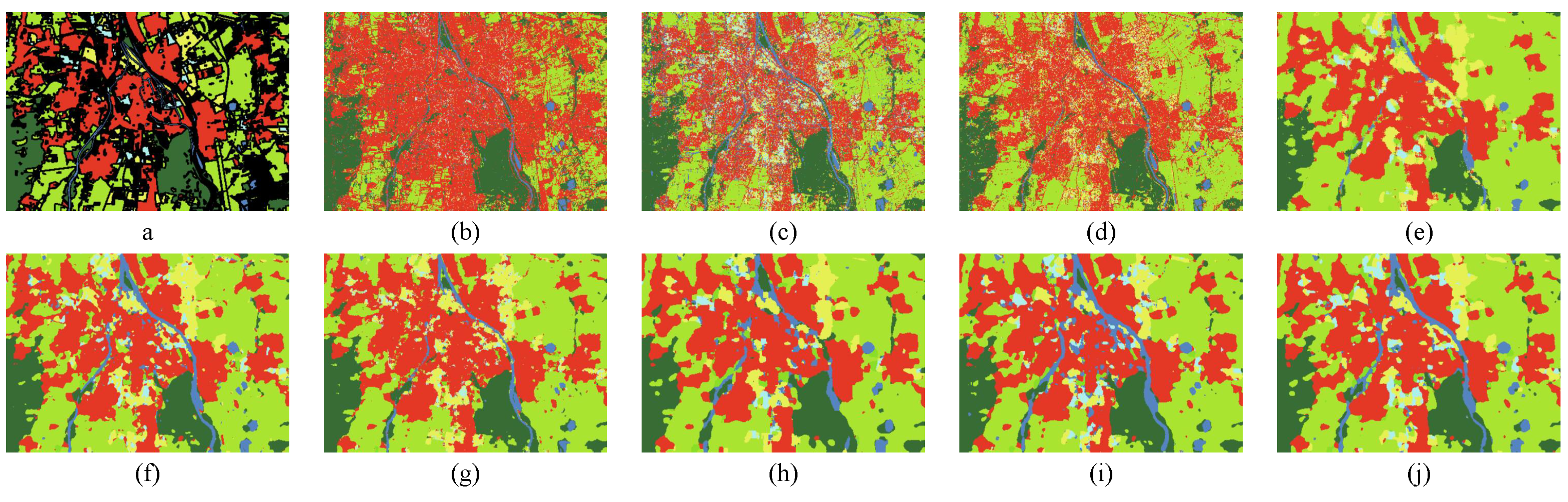
3.1.3. Augsburg
3.2. Experimental Setup
3.2.1. Evaluation Indicators
3.2.2. Configurations
3.3. Classification Results and Analysis
3.3.1. Quantitative Results and Analysis
3.3.2. Visual Evaluation and Analysis
4. Discussion
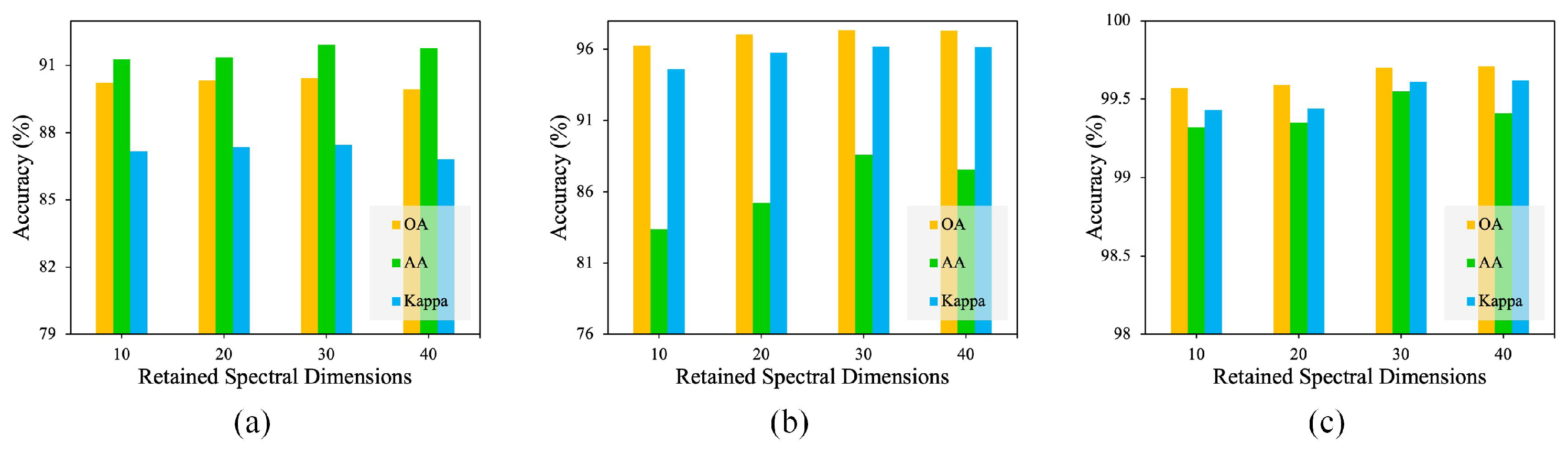
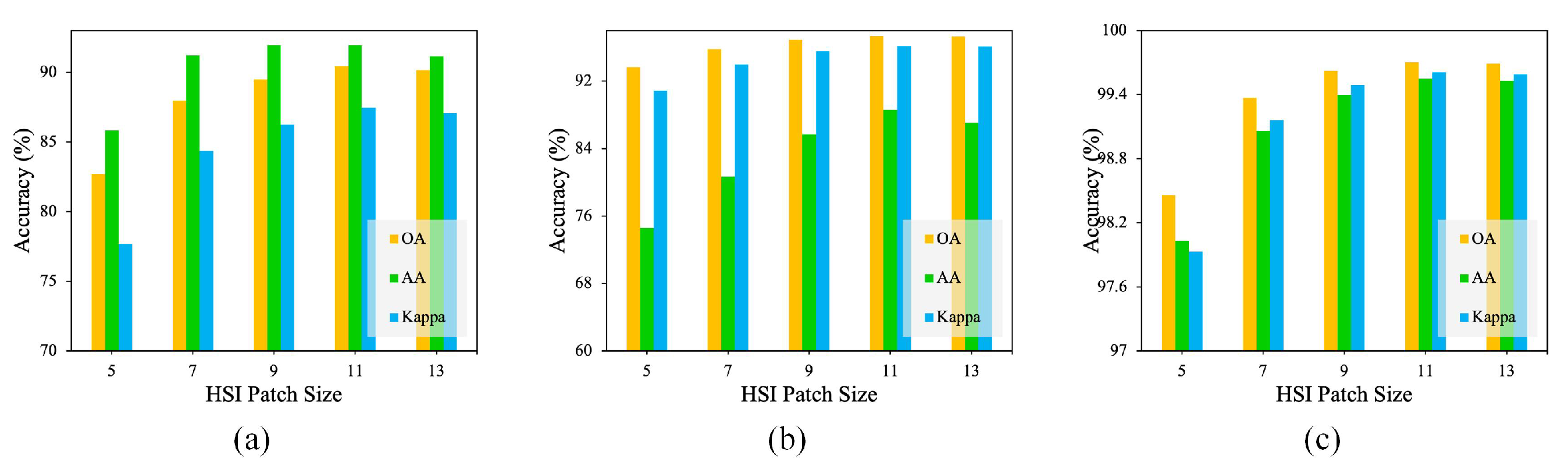
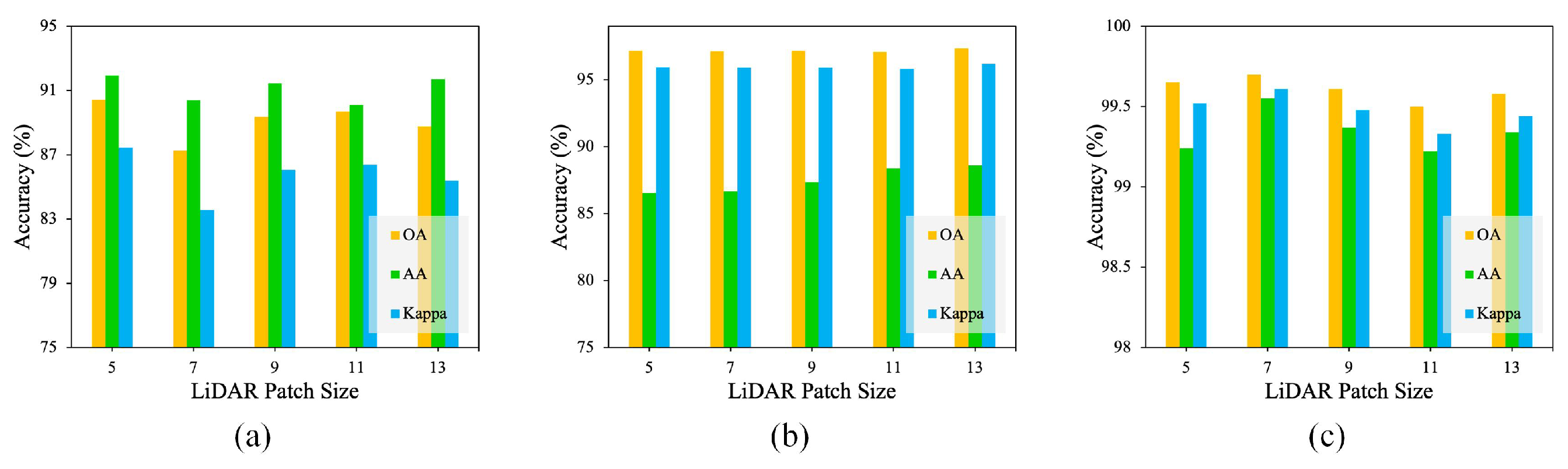
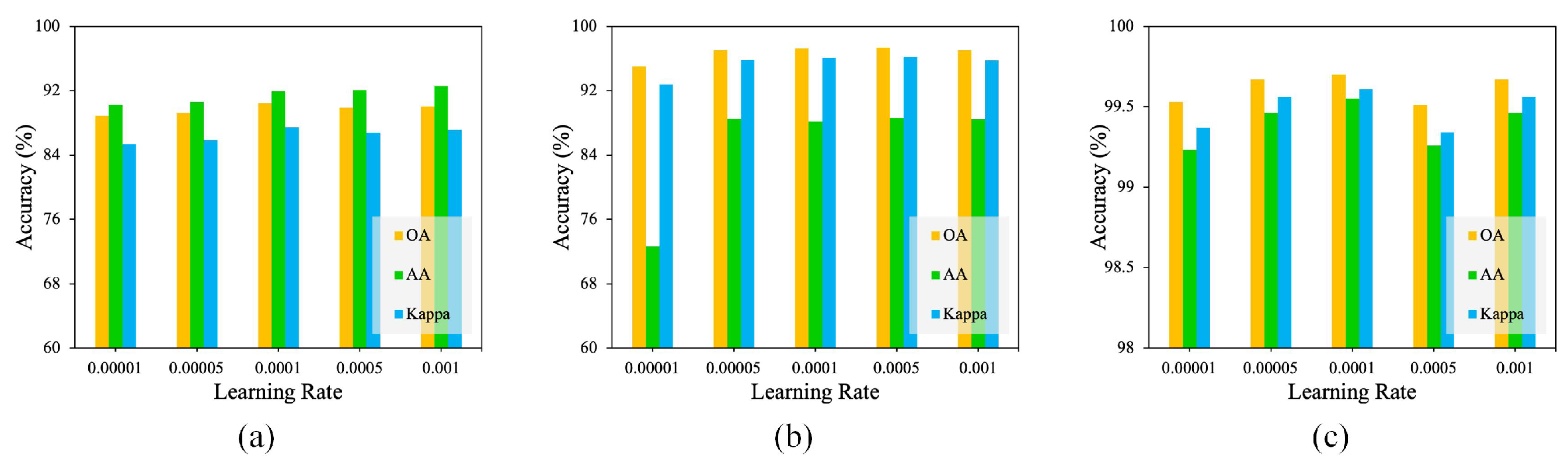
4.1. Parameter Analysis
4.2. Ablation Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MCAITN | Multi-feature, cross-attention-induced transformer network |
| CNNs | Convolutional neural networks |
| SVN | Support vector machine |
| RF | Random forest |
| RNNs | Recurrent neural networks |
| GANs | generative adversarial networks |
| LSTM | Long short-term memory |
| HSI | Hyperspectral image |
| HSIC | Hyperspectral image classification |
| IP-CNN | Interleaving perception convolutional neural network |
| Sal2RN | Saliency reinforcement network |
| DSHFNet | Dynamic-scale hierarchical fusion network |
| AMSSE-Net | Adaptive multiscale spatial–spectral enhancement network |
| CMSE | Cross-modal semantic enhancement |
| SAEs | Autoencoders |
| GCNs | Graph convolutional networks |
| CFEA | Cross-feature enhanced attention |
| FFN | Feed-forward network |
| MLP | Multi-layer perceptron |
| FC | Fully connected |
References
- He, L.; Li, J.; Liu, C.; Li, S. Recent Advances on Spectral–Spatial Hyperspectral Image Classification: An Overview and New Guidelines. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1579–1597. [Google Scholar] [CrossRef]
- Teke, M.; Deveci, H.S.; Haliloğlu, O.; Gürbüz, S.Z.; Sakarya, U. A short survey of hyperspectral remote sensing applications in agriculture. In Proceedings of the 2013 6th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, 12–14 June 2013; pp. 171–176. [Google Scholar] [CrossRef]
- Agilandeeswari, L.; Prabukumar, M.; Radhesyam, V.; Phaneendra, K.L.N.B.; Farhan, A. Crop Classification for Agricultural Applications in Hyperspectral Remote Sensing Images. Appl. Sci. 2022, 12, 1670. [Google Scholar] [CrossRef]
- Lu, B.; Dao, P.D.; Liu, J.; He, Y.; Shang, J. Recent Advances of Hyperspectral Imaging Technology and Applications in Agriculture. Remote Sens. 2020, 12, 2659. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Tuia, D.; Bruzzone, L.; Benediktsson, J.A. Advances in Hyperspectral Image Classification: Earth Monitoring with Statistical Learning Methods. IEEE Signal Process. Mag. 2014, 31, 45–54. [Google Scholar] [CrossRef]
- Stuart, M.B.; Davies, M.; Hobbs, M.J.; Pering, T.D.; McGonigle, A.J.S.; Willmott, J.R. High-Resolution Hyperspectral Imaging Using Low-Cost Components: Application within Environmental Monitoring Scenarios. Sensors 2022, 22, 4652. [Google Scholar] [CrossRef]
- Weber, C.; Aguejdad, R.; Briottet, X.; Avala, J.; Fabre, S.; Demuynck, J.; Zenou, E.; Deville, Y.; Karoui, M.; Benhalouche, F.; et al. Hyperspectral Imagery for Environmental Urban Planning. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1628–1631. [Google Scholar] [CrossRef]
- Brabant, C.; Alvarez-Vanhard, E.; Laribi, A.; Morin, G.; Thanh Nguyen, K.; Thomas, A.; Houet, T. Comparison of Hyperspectral Techniques for Urban Tree Diversity Classification. Remote Sens. 2019, 11, 1269. [Google Scholar] [CrossRef]
- Nisha, A.; Anitha, A. Current Advances in Hyperspectral Remote Sensing in Urban Planning. In Proceedings of the 2022 Third International Conference on Intelligent Computing Instrumentation and Control Technologies (ICICICT), Kannur, India, 11–12 August 2022; pp. 94–98. [Google Scholar] [CrossRef]
- Shimoni, M.; Haelterman, R.; Perneel, C. Hypersectral Imaging for Military and Security Applications: Combining Myriad Processing and Sensing Techniques. IEEE Geosci. Remote Sens. Mag. 2019, 7, 101–117. [Google Scholar] [CrossRef]
- Zhao, J.; Zhou, B.; Wang, G.; Ying, J.; Liu, J.; Chen, Q. Spectral Camouflage Characteristics and Recognition Ability of Targets Based on Visible/Near-Infrared Hyperspectral Images. Photonics 2022, 9, 957. [Google Scholar] [CrossRef]
- Zhao, G.; Ye, Q.; Sun, L.; Wu, Z.; Pan, C.; Jeon, B. Joint Classification of Hyperspectral and LiDAR Data Using a Hierarchical CNN and Transformer. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar] [CrossRef]
- Sun, L.; He, C.; Zheng, Y.; Wu, Z.; Jeon, B. Tensor cascaded-rank minimization in subspace: A unified regime for hyperspectral image low-level vision. IEEE Trans. Image Process. 2022, 32, 100–115. [Google Scholar] [CrossRef]
- Sun, L.; Cao, Q.; Chen, Y.; Zheng, Y.; Wu, Z. Mixed noise removal for hyperspectral images based on global tensor low-rankness and nonlocal SVD-aided group sparsity. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–17. [Google Scholar] [CrossRef]
- Song, T.; Zeng, Z.; Gao, C.; Chen, H.; Li, J. Joint Classification of Hyperspectral and LiDAR Data Using Height Information Guided Hierarchical Fusion-and-Separation Network. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–15. [Google Scholar] [CrossRef]
- Ahmad, M.; Shabbir, S.; Roy, S.K.; Hong, D.; Wu, X.; Yao, J.; Khan, A.M.; Mazzara, M.; Distefano, S.; Chanussot, J. Hyperspectral Image Classification—Traditional to Deep Models: A Survey for Future Prospects. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 968–999. [Google Scholar] [CrossRef]
- Song, W.; Li, S.; Fang, L.; Lu, T. Hyperspectral Image Classification with Deep Feature Fusion Network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3173–3184. [Google Scholar] [CrossRef]
- Yang, H.; Yu, H.; Zheng, K.; Hu, J.; Tao, T.; Zhang, Q. Hyperspectral Image Classification Based on Interactive Transformer and CNN With Multilevel Feature Fusion Network. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Yang, J.; Li, A.; Qian, J.; Qin, J.; Wang, L. A Hyperspectral Image Classification Method Based on Pyramid Feature Extraction with Deformable–Dilated Convolution. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Cao, X.; Yao, J.; Xu, Z.; Meng, D. Hyperspectral Image Classification with Convolutional Neural Network and Active Learning. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4604–4616. [Google Scholar] [CrossRef]
- Xue, Z.; Yu, X.; Tan, X.; Liu, B.; Yu, A.; Wei, X. Multiscale Deep Learning Network with Self-Calibrated Convolution for Hyperspectral and LiDAR Data Collaborative Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Baassou, B.; He, M.; Mei, S. An accurate SVM-based classification approach for hyperspectral image classification. In Proceedings of the 2013 21st International Conference on Geoinformatics, Kaifeng, China, 20–22 June 2013; pp. 1–7. [Google Scholar] [CrossRef]
- Xie, L.; Li, G.; Xiao, M.; Peng, L.; Chen, Q. Hyperspectral Image Classification Using Discrete Space Model and Support Vector Machines. IEEE Geosci. Remote Sens. Lett. 2017, 14, 374–378. [Google Scholar] [CrossRef]
- Amini, S.; Homayouni, S.; Safari, A. Semi-supervised classification of hyperspectral image using random forest algorithm. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 2866–2869. [Google Scholar] [CrossRef]
- Wang, S.; Dou, A.; Yuan, X.; Zhang, X. The airborne hyperspectral image classification based on the random forest algorithm. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 2280–2283. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, G.; Li, X.; Wang, B. Cascaded Random Forest for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1082–1094. [Google Scholar] [CrossRef]
- Yang, X.; Ye, Y.; Li, X.; Lau, R.Y.K.; Zhang, X.; Huang, X. Hyperspectral Image Classification with Deep Learning Models. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5408–5423. [Google Scholar] [CrossRef]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep Learning for Hyperspectral Image Classification: An Overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef]
- Ullah, F.; Ullah, I.; Khan, R.U.; Khan, S.; Khan, K.; Pau, G. Conventional to Deep Ensemble Methods for Hyperspectral Image Classification: A Comprehensive Survey. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 3878–3916. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Generative Adversarial Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5046–5063. [Google Scholar] [CrossRef]
- Deng, X.; Dragotti, P.L. Deep Convolutional Neural Network for Multi-Modal Image Restoration and Fusion. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3333–3348. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Wang, X.; Zheng, Y.; Wu, Z.; Fu, L. Multiscale 3-D–2-D Mixed CNN and Lightweight Attention-Free Transformer for Hyperspectral and LiDAR Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–16. [Google Scholar] [CrossRef]
- Fang, Y.; Ye, Q.; Sun, L.; Zheng, Y.; Wu, Z. Multiattention Joint Convolution Feature Representation with Lightweight Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Liang, L.; Zhang, S.; Li, J. Multiscale DenseNet Meets With Bi-RNN for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 5401–5415. [Google Scholar] [CrossRef]
- Hu, W.S.; Li, H.C.; Pan, L.; Li, W.; Tao, R.; Du, Q. Spatial–Spectral Feature Extraction via Deep ConvLSTM Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4237–4250. [Google Scholar] [CrossRef]
- Huang, L.; Chen, Y. Dual-Path Siamese CNN for Hyperspectral Image Classification with Limited Training Samples. IEEE Geosci. Remote Sens. Lett. 2021, 18, 518–522. [Google Scholar] [CrossRef]
- Yu, C.; Han, R.; Song, M.; Liu, C.; Chang, C.I. Feedback Attention-Based Dense CNN for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Bhatti, U.A.; Yu, Z.; Chanussot, J.; Zeeshan, Z.; Yuan, L.; Luo, W.; Nawaz, S.A.; Bhatti, M.A.; Ain, Q.U.; Mehmood, A. Local Similarity-Based Spatial—Spectral Fusion Hyperspectral Image Classification with Deep CNN and Gabor Filtering. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Song, R.; Li, Y.; Han, K.; Du, Q. Sal2RN: A Spatial—Spectral Salient Reinforcement Network for Hyperspectral and LiDAR Data Fusion Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, S.; Hong, D.; Gao, H.; Zhang, C.; Bi, M.; Li, C. Multimodal Transformer Network for Hyperspectral and LiDAR Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–17. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, J.; Feng, Y.; Wang, L. MS2CANet: Multiscale Spatial—Spectral Cross-Modal Attention Network for Hyperspectral Image and LiDAR Classification. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Gao, H.; Feng, H.; Zhang, Y.; Xu, S.; Zhang, B. AMSSE-Net: Adaptive Multiscale Spatial–Spectral Enhancement Network for Classification of Hyperspectral and LiDAR Data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–17. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Hang, R.; Zhang, B.; Chanussot, J. Deep Encoder—Decoder Networks for Classification of Hyperspectral and LiDAR Data. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Du, X.; Zheng, X.; Lu, X.; Doudkin, A.A. Multisource Remote Sensing Data Classification with Graph Fusion Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10062–10072. [Google Scholar] [CrossRef]
- Dam, T.; Anavatti, S.G.; Abbass, H.A. Mixture of Spectral Generative Adversarial Networks for Imbalanced Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, Y.; Tu, B.; Liu, Y. Local Information Interaction Transformer for Hyperspectral and LiDAR Data Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 1130–1143. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, H.; Zheng, Y.; Wu, Z.; Ye, Z.; Zhao, H. MASSFormer: Memory-Augmented Spectral-Spatial Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 8257–8268. [Google Scholar] [CrossRef]
- Fu, L.; Zhang, D.; Ye, Q. Recurrent thrifty attention network for remote sensing scene recognition. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–17. [Google Scholar] [CrossRef]
- Ding, K.; Lu, T.; Fu, W.; Li, S.; Ma, F. Global–Local Transformer Network for HSI and LiDAR Data Joint Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Zhang, M.; Gao, F.; Zhang, T.; Gan, Y.; Dong, J.; Yu, H. Attention Fusion of Transformer-Based and Scale-Based Method for Hyperspectral and LiDAR Joint Classification. Remote Sens. 2023, 15, 650. [Google Scholar] [CrossRef]
- Ni, K.; Wang, D.; Zheng, Z.; Wang, P. MHST: Multiscale Head Selection Transformer for Hyperspectral and LiDAR Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 5470–5483. [Google Scholar] [CrossRef]
- Yang, J.X.; Zhou, J.; Wang, J.; Tian, H.; Liew, A.W.C. LiDAR-Guided Cross-Attention Fusion for Hyperspectral Band Selection and Image Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–15. [Google Scholar] [CrossRef]
- Roy, S.K.; Sukul, A.; Jamali, A.; Haut, J.M.; Ghamisi, P. Cross Hyperspectral and LiDAR Attention Transformer: An Extended Self-Attention for Land Use and Land Cover Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–15. [Google Scholar] [CrossRef]
- Hong, D.; Hu, J.; Yao, J.; Chanussot, J.; Zhu, X.X. Multimodal remote sensing benchmark datasets for land cover classification with a shared and specific feature learning model. ISPRS J. Photogramm. Remote Sens. 2021, 178, 68–80. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yokoya, N.; Yao, J.; Chanussot, J.; Du, Q.; Zhang, B. More Diverse Means Better: Multimodal Deep Learning Meets Remote-Sensing Imagery Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4340–4354. [Google Scholar] [CrossRef]
- Feng, M.; Gao, F.; Fang, J.; Dong, J. Hyperspectral and Lidar Data Classification Based on Linear Self-Attention. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 2401–2404. [Google Scholar] [CrossRef]
- Wu, X.; Hong, D.; Chanussot, J. Convolutional Neural Networks for Multimodal Remote Sensing Data Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–10. [Google Scholar] [CrossRef]
- Hang, R.; Li, Z.; Ghamisi, P.; Hong, D.; Xia, G.; Liu, Q. Classification of Hyperspectral and LiDAR Data Using Coupled CNNs. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4939–4950. [Google Scholar] [CrossRef]



| No. | MUUFL | Augsburg | Trento | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Class | Training. | Test. | Class | Training. | Test. | Class | Training. | Test. | |
| C01 | Trees | 150 | 23,096 | Forest | 675 | 12,832 | Apple Trees | 129 | 3905 |
| C02 | Mostly Grass | 150 | 4120 | Residential Area | 1516 | 28,813 | Buildings | 125 | 2778 |
| C03 | Mixed Ground Surface | 150 | 6732 | Industrial Area | 192 | 3659 | Ground | 105 | 374 |
| C04 | Dirt and Sand | 150 | 1676 | Low Plants | 1342 | 25,515 | Woods | 154 | 8969 |
| C05 | Road | 150 | 6537 | Allotment | 28 | 547 | Vineyard | 184 | 10,317 |
| C06 | Water | 150 | 316 | Commercial Area | 82 | 1563 | Roads | 122 | 3052 |
| C07 | Buildings Shadow | 150 | 2083 | Water | 76 | 1454 | |||
| C08 | Buildings | 150 | 6090 | ||||||
| C09 | Sidewalk | 150 | 1235 | ||||||
| C10 | Yellow Curb | 150 | 33 | ||||||
| C11 | Cloth Panels | 150 | 119 | ||||||
| - | Total | 1650 | 52,037 | Total | 3911 | 74,383 | Total | 819 | 29,395 |
| No. | SVM [22] | S2FL [55] | EndNet [44] | MDL [56] | LSAF [57] | CCRNet [58] | CoupledCNN [59] | HCT [12] | MCAITN |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 74.81 ± 01.79 | 81.02 ± 00.74 | 84.21 ± 00.96 | 89.42 ± 03.88 | 88.70 ± 00.99 | 84.81 ± 01.91 | 89.16 ± 01.85 | 91.12 ± 01.43 | 91.75 ± 01.57 |
| 2 | 72.94 ± 01.91 | 76.99 ± 02.36 | 83.28 ± 02.09 | 74.57 ± 13.12 | 85.29 ± 02.48 | 85.81 ± 01.57 | 86.96 ± 00.94 | 85.47 ± 02.35 | 86.62 ± 03.42 |
| 3 | 57.59 ± 02.06 | 66.16 ± 01.51 | 71.85 ± 02.07 | 77.96 ± 04.67 | 78.97 ± 02.26 | 66.15 ± 03.63 | 81.60 ± 02.32 | 81.53 ± 04.88 | 82.21 ± 03.20 |
| 4 | 63.39 ± 01.34 | 82.56 ± 02.98 | 87.65 ± 01.49 | 90.83 ± 09.13 | 97.16 ± 01.41 | 94.39 ± 02.98 | 94.36 ± 02.97 | 96.07 ± 00.44 | 96.92 ± 00.89 |
| 5 | 79.06 ± 00.93 | 84.46 ± 01.22 | 88.96 ± 01.86 | 75.93 ± 04.39 | 87.72 ± 01.28 | 85.77 ± 02.63 | 89.66 ± 02.69 | 87.57 ± 04.96 | 89.26 ± 01.97 |
| 6 | 92.51 ± 01.31 | 94.49 ± 00.62 | 94.38 ± 01.53 | 99.79 ± 00.18 | 100 ± 00.00 | 99.03 ± 00.64 | 98.92 ± 00.64 | 99.45 ± 00.69 | 99.50 ± 00.48 |
| 7 | 82.45 ± 01.03 | 84.19 ± 01.23 | 88.70 ± 01.52 | 90.01 ± 07.08 | 94.46 ± 01.40 | 88.54 ± 01.82 | 91.84 ± 01.65 | 94.23 ± 00.42 | 93.64 ± 01.78 |
| 8 | 66.16 ± 01.50 | 79.49 ± 01.72 | 80.56 ± 02.05 | 96.32 ± 02.05 | 95.59 ± 00.35 | 94.48 ± 00.72 | 96.71 ± 01.29 | 95.15 ± 02.92 | 96.84 ± 00.84 |
| 9 | 79.48 ± 01.73 | 71.55 ± 02.78 | 75.39 ± 03.02 | 70.23 ± 11.80 | 77.14 ± 02.78 | 65.45 ± 02.27 | 72.71 ± 02.56 | 78.38 ± 01.55 | 80.53 ± 02.33 |
| 10 | 82.93 ± 03.49 | 92.33 ± 03.89 | 97.31 ± 02.48 | 84.85 ± 08.02 | 93.94 ± 05.25 | 87.72 ± 03.08 | 94.32 ± 02.85 | 95.45 ± 02.62 | 95.67 ± 04.58 |
| 11 | 75.09 ± 02.46 | 85.82 ± 02.53 | 98.18 ± 01.18 | 100.00 ± 00.00 | 99.72 ± 00.48 | 97.95 ± 01.81 | 98.47 ± 00.59 | 99.02 ± 01.06 | 98.44 ± 01.32 |
| OA (%) | 72.23 ± 01.37 | 78.31 ± 00.18 | 82.92 ± 00.64 | 85.58 ± 00.45 | 88.18 ± 00.43 | 83.12 ± 01.01 | 88.73 ± 00.39 | 88.93 ± 00.97 | 90.43 ± 00.67 |
| AA (%) | 75.13 ± 01.53 | 81.73 ± 01.85 | 86.41 ± 00.87 | 86.36 ± 01.23 | 90.79 ± 00.50 | 86.37 ± 00.99 | 90.43 ± 01.34 | 91.22 ± 01.57 | 91.94 ± 00.52 |
| 65.41 ± 01.42 | 72.47 ± 00.33 | 77.82 ± 01.04 | 81.17 ± 00.37 | 84.60 ± 00.52 | 78.25 ± 01.17 | 85.16 ± 01.03 | 85.29 ± 00.85 | 87.45 ± 00.83 |
| No. | SVM [22] | S2FL [55] | EndNet [44] | MDL [56] | LSAF [57] | CCRNet [58] | CoupledCNN [59] | HCT [12] | MCAITN |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 95.78 ± 00.39 | 97.18 ± 00.15 | 92.49 ± 00.49 | 95.56 ± 03.04 | 99.15 ± 00.21 | 96.44 ± 00.97 | 97.47 ± 00.97 | 98.98 ± 00.17 | 98.97 ± 00.27 |
| 2 | 89.41 ± 01.27 | 72.29 ± 01.26 | 88.61 ± 00.53 | 93.82 ± 03.88 | 98.53 ± 00.05 | 96.69 ± 00.76 | 97.71 ± 00.65 | 98.69 ± 00.26 | 98.82 ± 00.29 |
| 3 | 06.47 ± 01.35 | 32.25 ± 03.09 | 41.38 ± 03.13 | 79.42 ± 07.18 | 89.22 ± 03.02 | 82.76 ± 03.83 | 84.71 ± 03.57 | 88.33 ± 04.20 | 88.92 ± 03.16 |
| 4 | 67.32 ± 01.39 | 87.45 ± 01.04 | 94.25 ± 00.53 | 99.74 ± 00.06 | 99.22 ± 00.31 | 98.02 ± 00.41 | 97.56 ± 00.53 | 98.94 ± 00.29 | 99.07 ± 00.25 |
| 5 | 06.86 ± 01.82 | 40.34 ± 05.19 | 31.75 ± 03.13 | 56.26 ± 13.26 | 87.08 ± 05.64 | 41.69 ± 06.06 | 69.43 ± 03.05 | 80.04 ± 08.55 | 86.66 ± 08.75 |
| 6 | 10.90 ± 01.87 | 39.97 ± 02.81 | 28.32 ± 04.21 | 57.34 ± 21.99 | 54.36 ± 05.16 | 33.38 ± 05.05 | 72.84 ± 02.36 | 70.38 ± 02.06 | 74.89 ± 03.78 |
| 7 | 53.27 ± 01.85 | 70.35 ± 01.29 | 50.65 ± 02.07 | 47.58 ± 12.57 | 70.02 ± 02.64 | 59.39 ± 06.24 | 61.98 ± 02.58 | 72.81 ± 04.62 | 72.91 ± 03.00 |
| OA (%) | 76.01 ± 00.83 | 78.77 ± 00.37 | 86.77 ± 00.56 | 93.50 ± 01.46 | 96.85 ± 00.23 | 94.35 ± 00.74 | 95.59 ± 00.75 | 97.08 ± 00.21 | 97.34 ± 00.15 |
| AA (%) | 47.15 ± 00.78 | 62.83 ± 01.06 | 61.06 ± 00.95 | 75.68 ± 00.51 | 85.37 ± 01.33 | 72.63 ± 02.80 | 83.1 ± 01.90 | 86.88 ± 01.07 | 88.61 ± 01.14 |
| 64.82 ± 01.09 | 70.87 ± 00.71 | 80.73 ± 00.58 | 90.63 ± 02.08 | 95.48 ± 00.33 | 93.09 ± 00.61 | 93.92 ± 00.79 | 95.82 ± 00.29 | 96.18 ± 00.21 |
| No. | SVM [22] | S2FL [55] | EndNet [44] | MDL [56] | LSAF [57] | CCRNet [58] | CoupledCNN [59] | HCT [12] | MCAITN |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 80.05 ± 01.08 | 80.35 ± 00.71 | 87.52 ± 00.62 | 98.06 ± 01.39 | 99.66 ± 00.09 | 99.13 ± 00.91 | 99.32 ± 00.21 | 99.59 ± 00.17 | 99.41 ± 00.44 |
| 2 | 77.03 ± 03.13 | 80.32 ± 01.23 | 87.43 ± 00.82 | 99.37 ± 00.74 | 98.85 ± 00.79 | 96.74 ± 01.41 | 97.87 ± 00.29 | 98.49 ± 01.15 | 99.32 ± 00.32 |
| 3 | 85.64 ± 02.57 | 90.47 ± 00.71 | 98.22 ± 01.04 | 99.07 ± 00.27 | 97.86 ± 00.92 | 94.17 ± 02.11 | 98.39 ± 00.31 | 100.00 ± 00.00 | 100.00 ± 00.00 |
| 4 | 92.48 ± 01.23 | 93.14 ± 00.31 | 98.37 ± 00.32 | 100.00 ± 00.00 | 100.00 ± 00.00 | 99.97 ± 00.04 | 100.00 ± 00.00 | 100.00 ± 00.00 | 100.00 ± 00.00 |
| 5 | 82.43 ± 01.01 | 82.14 ± 00.39 | 93.66 ± 00.36 | 99.98 ± 00.03 | 99.87 ± 00.19 | 99.95 ± 00.05 | 100.00 ± 00.00 | 99.98 ± 00.02 | 100.00 ± 00.00 |
| 6 | 82.21 ± 01.39 | 80.78 ± 01.22 | 86.68 ± 01.65 | 96.16 ± 02.14 | 98.31 ± 00.60 | 96.46 ± 01.49 | 97.96 ± 00.89 | 97.96 ± 01.01 | 98.56 ± 01.01 |
| OA (%) | 84.43 ± 00.51 | 85.14 ± 00.48 | 93.01 ± 00.31 | 99.27 ± 00.19 | 99.31 ± 00.19 | 98.68 ± 00.63 | 99.04 ± 00.33 | 99.59 ± 00.09 | 99.70 ± 00.09 |
| AA (%) | 83.31 ± 01.72 | 84.53 ± 00.31 | 91.98 ± 00.80 | 98.78 ± 00.30 | 99.09 ± 00.08 | 97.74 ± 00.81 | 98.92 ± 00.25 | 99.34 ± 00.15 | 99.55 ± 00.14 |
| 79.45 ± 00.68 | 80.25 ± 00.65 | 90.55 ± 00.29 | 99.02 ± 00.26 | 99.23 ± 00.13 | 98.19 ± 00.57 | 98.97 ± 00.26 | 99.44 ± 00.12 | 99.61 ± 00.12 |
| Cases | Component | Indicators | |||||
|---|---|---|---|---|---|---|---|
| Conv3D | Conv2D | Lidar-Branch | CFEA-TE | OA (%) | AA (%) | ||
| 1 | √ | - | √ | √ | 87.57 | 88.14 | 83.75 |
| 2 | - | √ | √ | √ | 86.89 | 87.78 | 82.93 |
| 3 | - | - | √ | TE | 55.61 | 50.44 | 43.16 |
| 4 | √ | √ | - | TE | 88.69 | 90.63 | 85.19 |
| 5 | √ | √ | √ | √ | 90.43 | 91.94 | 87.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Liu, R.; Sun, L.; Zheng, Y. Multi-Feature Cross Attention-Induced Transformer Network for Hyperspectral and LiDAR Data Classification. Remote Sens. 2024, 16, 2775. https://doi.org/10.3390/rs16152775
Li Z, Liu R, Sun L, Zheng Y. Multi-Feature Cross Attention-Induced Transformer Network for Hyperspectral and LiDAR Data Classification. Remote Sensing. 2024; 16(15):2775. https://doi.org/10.3390/rs16152775
Chicago/Turabian StyleLi, Zirui, Runbang Liu, Le Sun, and Yuhui Zheng. 2024. "Multi-Feature Cross Attention-Induced Transformer Network for Hyperspectral and LiDAR Data Classification" Remote Sensing 16, no. 15: 2775. https://doi.org/10.3390/rs16152775
APA StyleLi, Z., Liu, R., Sun, L., & Zheng, Y. (2024). Multi-Feature Cross Attention-Induced Transformer Network for Hyperspectral and LiDAR Data Classification. Remote Sensing, 16(15), 2775. https://doi.org/10.3390/rs16152775








