Random Forest—Based Identification of Factors Influencing Ground Deformation Due to Mining Seismicity
Abstract
1. Introduction
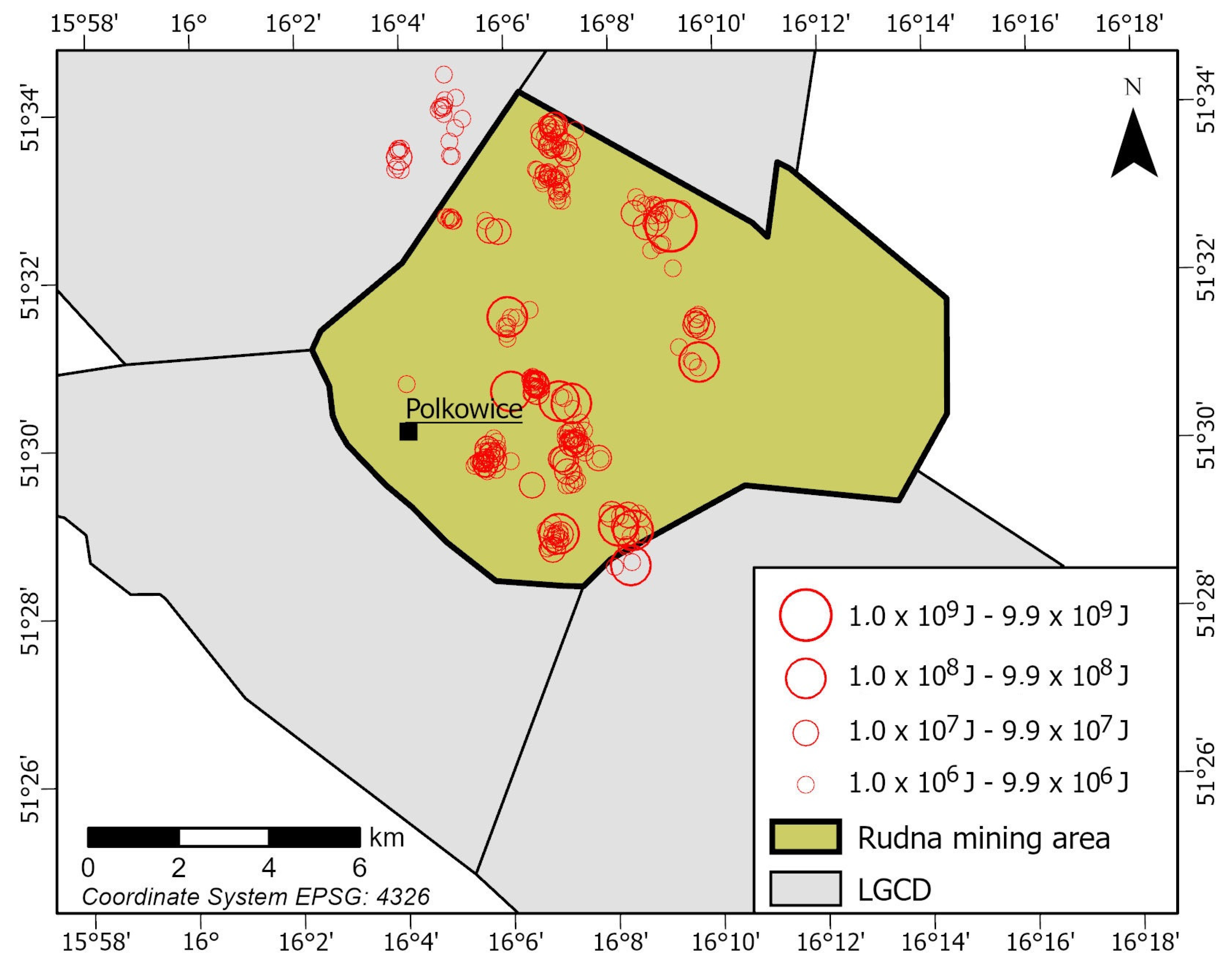
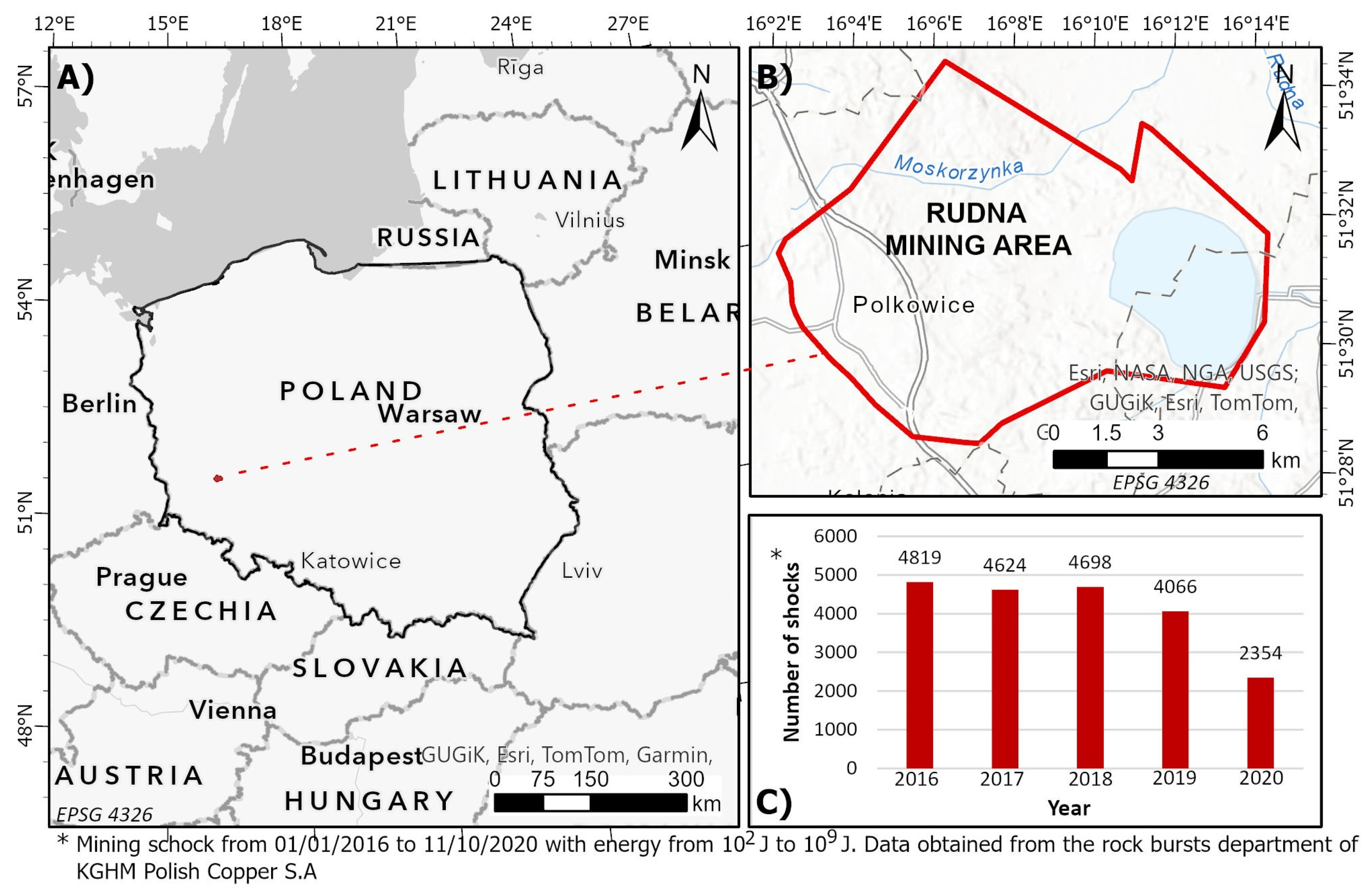
2. Area of Interest
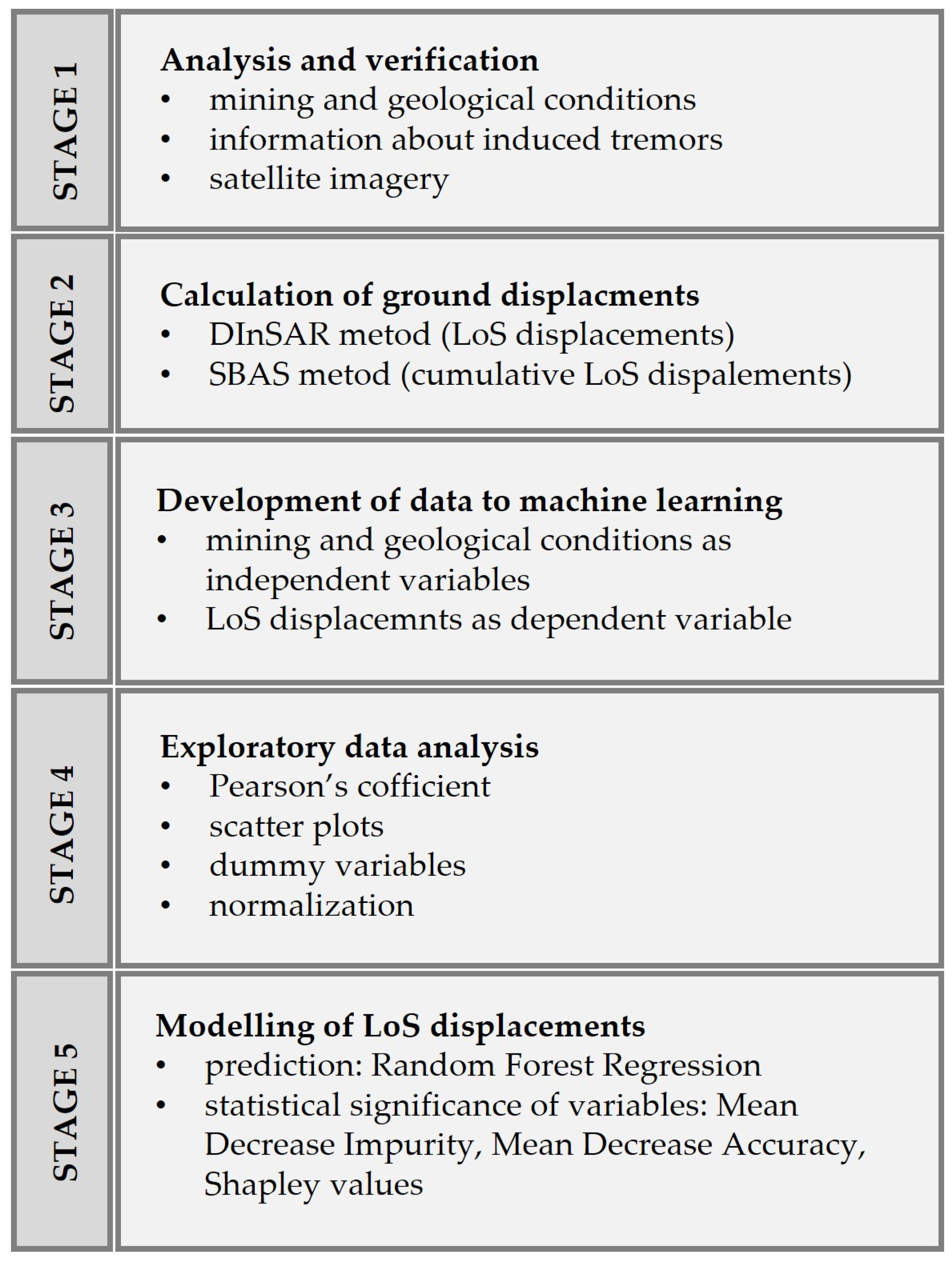
3. Data and Methods
3.1. Data
- Differential InSAR for the period from 28/11/2016 to 22/12/2019—104 images,
- SBAS InSAR for the period from 11/10/2016 to 26/02/2020—189 images,
| Data | Time | Energy (J) | Magnitude 1 | X | Y | Z |
|---|---|---|---|---|---|---|
| 29 November 2016 | 21:09:40 | 1.00 × 108 | 3.50 | 5,709,717 | 5,580,593 | −963 |
| 16 December 2016 | 7:46:50 | 9.50 × 107 | 3.50 | 5,707,594 | 5,578,375 | −790 |
| 22 January 2017 | 20:08:15 | 1.10 ×107 | 3.01 | 5,708,119 | 5,577,792 | −810 |
| 9 April 2017 | 0:23:11 | 6.60 ×107 | 3.40 | 5,709,224 | 5,576,982 | −816 |
| 10 November 2017 | 12:19:06 | 2.30 × 107 | 3.17 | 5,709,245 | 5,576,989 | −806 |
| 7 December 2017 | 18:42:49 | 5.00 × 107 | 3.34 | 5,707,653 | 5,576,009 | −775 |
| 26 December 2017 | 12:15:29 | 1.20 × 108 | 3.54 | 5,709,065 | 5,576,432 | −824 |
| 15 September 2018 | 18:35:14 | 3.00 × 108 | 3.74 | 5,705,223 | 5,579,084 | −649 |
| 20 November 2018 | 7:15:55 | 3.00 × 107 | 3.23 | 5,706,339 | 5,579,021 | −717 |
| 29 January 2019 | 13:53:43 | 3.10 × 108 | 3.75 | 5,708,800 | 5,577,770 | −773 |
| 30 November 2019 | 5:58:32 | 4.50 × 107 | 3.32 | 5,707,506 | 5,577,645 | −799 |
3.2. Calculation of Ground Displacements
3.3. Identification of Ground Displacement Factors
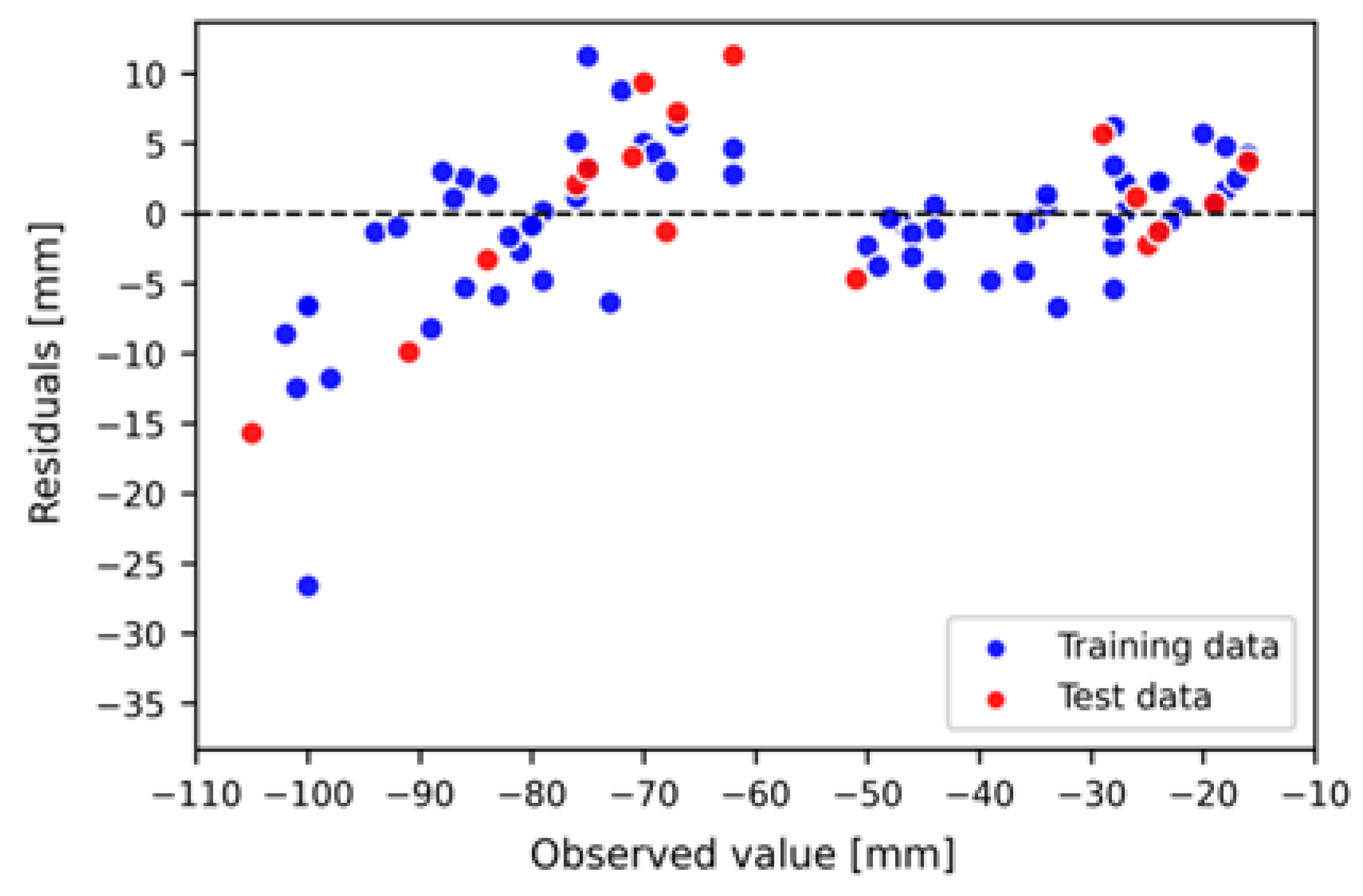
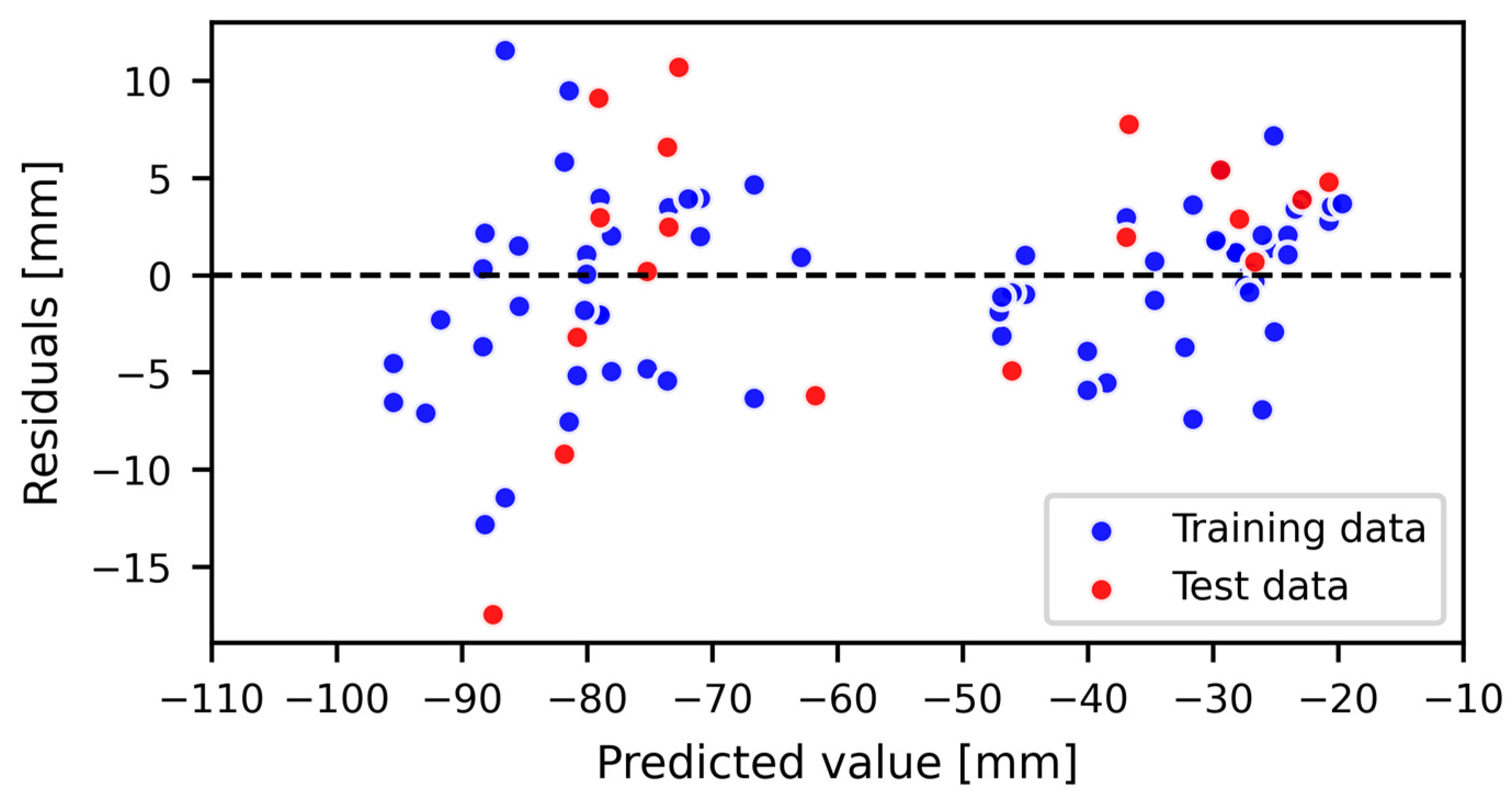
4. Results
5. Discussion
6. Conclusions
- The RFR method enabled modeling the relationship between LOS displacements caused by high-energy tremors, i.e., ≥107 J, and a set of explanatory variables characterizing mining and geological conditions.
- The best-performing final model was characterized by RMSE = 7 mm, R2 = 0.93, and most of the residual values were within the range of ±5 mm.
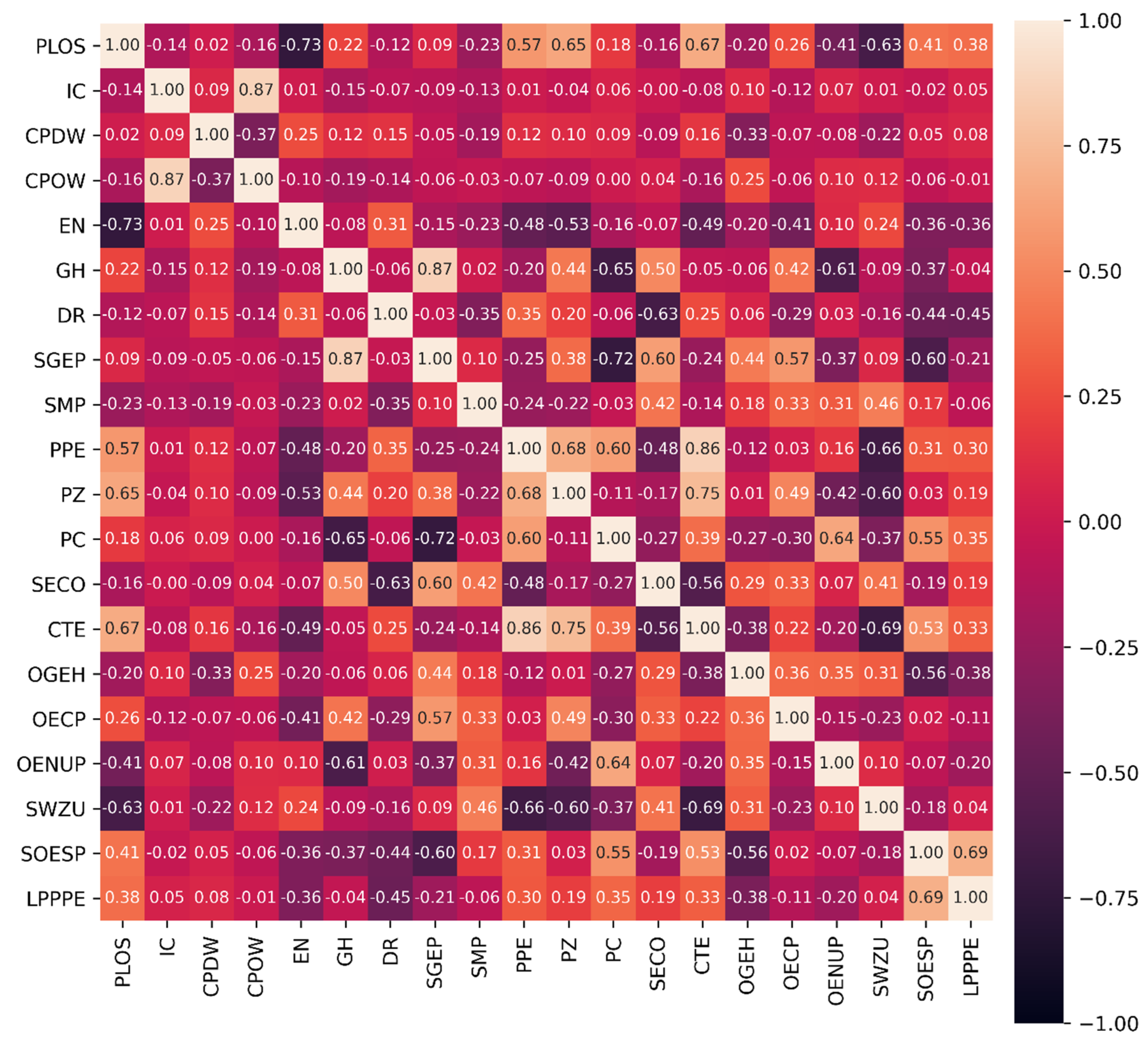
- The identified statistically significant explanatory variables behind the observed LOS displacements caused by induced tremors tested independently with three methods (MDI, MDA, and SHAP) included CTE, as well as SOESP, PPE, LEC, EN, PZ, SLWUS, SGEP, SWZU, LEF, OGEH, CPOW, and CPDW.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| No. | Variables | Symbol | Range of Value |
|---|---|---|---|
| 1. | LOS displacements (mm; dependent variable). (Displacements calculated using InSAR methods.) | PLOS | −111 to −16 |
| 2. | Time interval between imagery dates (days). (The number of days between a pair of images used to calculate LOS displacements.) | IC | 6, 12, 18, or 24 |
| 3. | Time between the reference image date and shock date (days). (The number of days between the pre-shock reference image date and the shock date.) | CPDW | 0 to 17 |
| 4. | Time between shock date and slave image (days). (Number of days between the shock date and the post-shock image date.) | CPOW | 1 to 24 |
| 5. | Energy (J). (Registered energy of the seismic events obtained from the Mine Geophysics Station of the Rudna mine.) | EN | 1.10 × 107 to 3.10 × 108 |
| 6. | Hypocenter depth (m b.s.l.). (The values come from the list of mining tremors recorded by the Mine Geophysics Station of the Rudna mine.) | GH | −1090 to −841 |
| 7. | Annual deformations (mm). (The ground deformation values determined on the basis of leveling measurement campaigns conducted by the mine.) | DR | −250 to 100 |
| 8. | Location of the epicenter in the unexploited part of the field. 1 (Occurrence of an epicenter in unexploited parts of the copper field.) | LEC | 0 or 1 |
| 9. | Location of the epicenter—front. 1 (Occurrence of an epicenter at the mine operation front.) | LEF | 0 or 1 |
| 10. | Average depth of field exploitation (m b.s.l.). (The depth at which exploitation is carried out.) | SGEP | −1099.4 to 895.3 |
| 11. | Average thickness in the field (m). (Variable representing the thickness of the copper field, determined from mining excavation maps.) | SMP | 4.8 to 9.8 |
| 12. | The direction of the advance of the front NW. 1 (Direction of the NW mining front.) | PFNW | 0 or 1 |
| 13. | The direction of the advance of the front SE. 1 (Direction of the SE mining front.) | PFSE | 0 or 1 |
| 14. | The area of the exploitation field (ha). (Variable representing the area of a given copper-mining field calculated from mining excavation maps.) | PPE | 11.8692 to 46.2168 |
| 15. | Goaf area (ha). (Variable representing the area of goaf calculated from mining excavation maps.) | PZ | 0 to 21.7382 |
| 16. | The unexploited area of the field (ha). (Variable representing the area of the unmined part of the copper field calculated from mining excavation maps.) | PC | 0 to 35.5129 |
| 17. | The ratio of the exploited area to the area of the department. (Variable representing the ratio of the exploited area in the field where the shock occurred to the area of the entire department.) | SECO | 0.19 to 0.69 |
| 18. | Operation status in progress. 1 (Variable representing the present status of the exploitation in the field where the shock occurred.) | SET | 0 or 1 |
| 19. | Operation status complete. 1 (Variable representing completed status of the operation in the field where the shock occurred.) | SEZ | 0 or 1 |
| 20. | Method of liquidation of the excavation—partial dry filling. 1 (Liquidation of an excavation with partial dry backfill in the field where the shock occurred.) | SLWCPS | 0 or 1 |
| 21. | The method of liquidation of the excavation with the deflection of the roof. 1 (Liquidation of an excavation with a deflection of the roof in the field where the shock occurred.) | SLWUS | 0 or 1 |
| 22. | Method of liquidation of the excavation—hydraulic backfilling. 1 (Liquidation of the excavation and hydraulic backfilling in the field where the shock occurred.) | SLWPH | 0 or 1 |
| 23. | Duration of exploitation (years). (Variable representing the number of years of operation in the field where the shock occurred.) | CTE | 0 to 10 |
| 24. | Distance between the depth of exploitation and the hypocenter (m). (Variable representing the distance measured between variables #6 and #10.) | OGEH | −115 to 20 |
| 25. | Distance between the epicenter and the centroid of the exploitation field (m). (Variable representing the distance measured from the epicenter to the centroid of the field where the epicenter appeared.) | OECP | 121 to 320 |
| 26. | Distance between the epicenter and the nearest fault in the exploitation field (m). (Variable representing the distance measured from the epicenter to the nearest fault.) | OENUP | 6 to 328 |
| 27. | Average value of a fault’s throw in the exploitation field (m). (Variable representing the average throw of a fault within the mining field where the shock occurred, calculated on the basis of information contained in mining excavation maps.) | SWZU | 2 to 8.4 |
| 28. | Average distance between the epicenter and adjacent exploitation fields (m). (Variable representing the distance measured from the epicenter to the edge of the adjacent exploitation field.) | SOESP | 0 to 520 |
| 29. | Number of exploitation fields adjacent to the exploitation field from the epicenter. (Variable determined on the basis of information contained in maps of mining excavations. The number of exploitation fields bordering the field in which the shock occurred.) | LPPPE | 0 to 6 |
References
- Kratzsch, H. Mining Subsidence Engineering; Springer: Berlin/Heidelberg, Germany, 1983; ISBN 978-3-642-81925-4. [Google Scholar]
- Whittaker, B.N.; Reddish, D.J. Subsidence: Occurrence, Prediction and Control; Elsevier: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Sokoła-Szewioła, V. Method of Prediction the Probability of a Strong Tremor on the Basis of Observed Changes of Mining Ground Subsidences. Arch. Min. Sci. 2009, 54, 725–737. [Google Scholar]
- Temporim, F.A.; Gama, F.F.; Mura, J.C.; Paradella, W.R.; Silva, G.G.; Temporim, F.A.; Gama, F.F.; Mura, J.C.; Paradella, W.R.; Silva, G.G. Application of Persistent Scatterers Interferometry for Surface Displacements Monitoring in N5E Open Pit Iron Mine Using TerraSAR-X Data, in Carajás Province, Amazon Region. Braz. J. Geol. 2017, 47, 225–235. [Google Scholar] [CrossRef]
- Milczarek, W.; Kopeć, A.; Głąbicki, D. Estimation of Tropospheric and Ionospheric Delay in DInSAR Calculations: Case Study of Areas Showing (Natural and Induced) Seismic Activity. Remote Sens. 2019, 11, 621. [Google Scholar] [CrossRef]
- Mutke, G. Oddziaływanie Górniczych Wstrząsów Sejsmicznych Na Powierzchnię; Główny Instytut Górnictwa: Katowice, Poland, 2019. [Google Scholar]
- Gibowicz, G. Seismicity in Mines; Pageoph Topical Volumes; Birkhäuser: Basel, Switzerland, 1989; ISBN 978-3-7643-2273-1. [Google Scholar]
- Gibowicz, S.J. Seismicity Induced by Mining: An Overview. In Monitoring a Comprehensive Test Ban Treaty; Husebye, E.S., Dainty, A.M., Eds.; NATO ASI Series; Springer: Berlin/Heidelberg, Germany, 1996; pp. 385–409. ISBN 978-94-011-0419-7. [Google Scholar]
- Larsson, K. Seismicity in Mines: A Review; Luleå University of Technology, Department of Civil and Environmental Engineering Division of Rock Mechanics: Luleå, Sweden, 2004; p. 118. [Google Scholar]
- Verdon, J.P.; Kendall, J.-M.; Butcher, A.; Luckett, R.; Baptie, B.J. Seismicity Induced by Longwall Coal Mining at the Thoresby Colliery, Nottinghamshire, U.K. Geophys. J. Int. 2018, 212, 942–954. [Google Scholar] [CrossRef]
- Foulger, G.R.; Wilson, M.P.; Gluyas, J.G.; Julian, B.R.; Davies, R.J. Global Review of Human-Induced Earthquakes. Earth-Sci. Rev. 2018, 178, 438–514. [Google Scholar] [CrossRef]
- Tama, A.; Guzy, A.; Witkowski, W.T.; Hejmanowski, R.; Malinowska, A. Mapping Vertical Ground Movement Caused by Human-Induced Seismicity Applying Satellite Radar Interferometry and Geostatistics. In Proceedings of the ResearchGate, Vienna, Austria, 31 October–2 November 2018. [Google Scholar]
- Hejmanowski, R.; Malinowska, A.A.; Witkowski, W.T.; Guzy, A. An Analysis Applying InSAR of Subsidence Caused by Nearby Mining-Induced Earthquakes. Geosciences 2019, 9, 490. [Google Scholar] [CrossRef]
- Wang, S.; Jiang, G.; Weingarten, M.; Niu, Y. InSAR Evidence Indicates a Link Between Fluid Injection for Salt Mining and the 2019 Changning (China) Earthquake Sequence. Geophys. Res. Lett. 2020, 47, e2020GL087603. [Google Scholar] [CrossRef]
- GMTSAR. Available online: https://topex.ucsd.edu/gmtsar/downloads/ (accessed on 5 July 2024).
- Science Toolbox Exploitation Platform. Available online: https://step.esa.int/main/download/snap-download/ (accessed on 23 July 2024).
- Kubanek, J.; Liu, Y.; Harrington, R.M.; Samsonov, S. Observation of Surface Deformation Associated with Hydraulic Fracturing in Western Canada Using InSAR. In Proceedings of the EUSAR 2018; 12th European Conference on Synthetic Aperture Radar, Aachen, Germany, 5–7 June 2018; pp. 1–6. [Google Scholar]
- Milczarek, W. Application of a Small Baseline Subset Time Series Method with Atmospheric Correction in Monitoring Results of Mining Activity on Ground Surface and in Detecting Induced Seismic Events. Remote Sens. 2019, 11, 1008. [Google Scholar] [CrossRef]
- Malinowska, A.; Witkowski, W.T.; Guzy, A.; Hejmanowski, R. Study of Dynamic Displacement Phenomena with the Use of Imaging Radars from the Sentinel Mission. Zesz. Nauk. Inst. Gospod. Surowcami Miner. I Energią PAN 2017, 101, 229–246. [Google Scholar]
- Krawczyk, A.; Grzybek, R. An Evaluation of Processing InSAR Sentinel-1A/B Data for Correlation of Mining Subsidence with Mining Induced Tremors in the Upper Silesian Coal Basin (Poland). E3S Web Conf. 2018, 26, 00003. [Google Scholar] [CrossRef]
- Barnhart, W.D.; Yeck, W.L.; McNamara, D.E. Induced Earthquake and Liquefaction Hazards in Oklahoma, USA: Constraints from InSAR. Remote Sens. Environ. 2018, 218, 1–12. [Google Scholar] [CrossRef]
- Deng, F.; Dixon, T.H.; Xie, S. Surface Deformation and Induced Seismicity Due to Fluid Injection and Oil and Gas Extraction in Western Texas. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018962. [Google Scholar] [CrossRef]
- Wang, G.; Zhu, S.; Zhang, X.; Wen, Y.; Zhu, Z.; Zhu, Q.; Xie, L.; Li, J.; Tan, Y.; Yang, T.; et al. Prediction of Mining-Induced Seismicity and Damage Assessment of Induced Surface Buildings in Thick and Hard Key Stratum Working Face: A Case Study of Liuhuanggou Coal Mine in China. Front. Earth Sci. 2023, 11, 1238055. [Google Scholar] [CrossRef]
- Cieślik, K.; Milczarek, W.; Warchala, E.; Kosydor, P.; Rożek, R. Identifying Factors Influencing Surface Deformations from Underground Mining Using SAR Data, Machine Learning, and the SHAP Method. Remote Sens. 2024, 16, 2428. [Google Scholar] [CrossRef]
- Wang, X.; Chen, S.; Xia, Y.; Niu, Y.; Gong, J.; Yang, Y. Analysis of Surface Deformation and Related Factors over Mining Areas Based on InSAR: A Case Study of Fengcheng Mine. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2024, XLVIII-1–2024, 697–712. [Google Scholar] [CrossRef]
- Cieślik, K.; Milczarek, W. Application of Machine Learning in Forecasting the Impact of Mining Deformation: A Case Study of Underground Copper Mines in Poland. Remote Sens. 2022, 14, 4755. [Google Scholar] [CrossRef]
- Kopeć, A.; Bugajska, N.; Milczarek, W.; Głąbicki, D. Long-term monitoring of the impact of the impact of mining operations on the ground surface at the regional scale based on the InSAR-SBAS technique, the Upper Silesian Coal Basin (Poland). Case study. Acta Geodyn. Et Geomater. 2022, 19, 93–110. [Google Scholar] [CrossRef]
- Sui, L.; Ma, F.; Chen, N. Mining Subsidence Prediction by Combining Support Vector Machine Regression and Interferometric Synthetic Aperture Radar Data. ISPRS Int. J. Geo-Inf. 2020, 9, 390. [Google Scholar] [CrossRef]
- Xi, N.; Mei, G.; Liu, Z.; Xu, N. Automatic Identification of Mining-Induced Subsidence Using Deep Convolutional Networks Based on Time-Series InSAR Data: A Case Study of Huodong Mining Area in Shanxi Province, China. Bull. Eng. Geol. Env. 2023, 82, 78. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Dixon, B. GIS-Based Groundwater Potential Mapping Using Boosted Regression Tree, Classification and Regression Tree, and Random Forest Machine Learning Models in Iran. Environ. Monit Assess 2015, 188, 44. [Google Scholar] [CrossRef]
- Jaiswal, J.K.; Samikannu, R. Application of Random Forest Algorithm on Feature Subset Selection and Classification and Regression. In Proceedings of the 2017 World Congress on Computing and Communication Technologies (WCCCT), Tiruchirappalli, India, 2–4 February 2017; pp. 65–68. [Google Scholar]
- Lagomarsino, D.; Tofani, V.; Segoni, S.; Catani, F.; Casagli, N. A Tool for Classification and Regression Using Random Forest Methodology: Applications to Landslide Susceptibility Mapping and Soil Thickness Modeling. Environ. Model Assess 2017, 22, 201–214. [Google Scholar] [CrossRef]
- Izquierdo-Verdiguier, E.; Zurita-Milla, R. An Evaluation of Guided Regularized Random Forest for Classification and Regression Tasks in Remote Sensing. Int. J. Appl. Earth Obs. Geoinf. 2020, 88, 102051. [Google Scholar] [CrossRef]
- Belmokre, A.; Mihoubi, M.K.; Santillán, D. Analysis of Dam Behavior by Statistical Models: Application of the Random Forest Approach. KSCE J. Civ. Eng. 2019, 23, 4800–4811. [Google Scholar] [CrossRef]
- Dai, B.; Gu, C.; Zhao, E.; Qin, X. Statistical Model Optimized Random Forest Regression Model for Concrete Dam Deformation Monitoring. Struct. Control Health Monit. 2018, 25, e2170. [Google Scholar] [CrossRef]
- Li, X.; Su, H.; Hu, J. The Prediction Model of Dam Uplift Pressure Based on Random Forest. IOP Conf. Ser. Mater. Sci. Eng. 2017, 229, 012025. [Google Scholar] [CrossRef]
- Guo, Z.; Huang, H. Application of RS-RF Model in Deformation Prediction of Concrete Dam. IOP Conf. Ser. Earth Environ. Sci. 2020, 474, 072003. [Google Scholar] [CrossRef]
- Li, X.; Wen, Z.; Su, H. An Approach Using Random Forest Intelligent Algorithm to Construct a Monitoring Model for Dam Safety. Eng. Comput. 2021, 37, 39–56. [Google Scholar] [CrossRef]
- Su, Y.; Weng, K.; Lin, C.; Zheng, Z. An Improved Random Forest Model for the Prediction of Dam Displacement. IEEE Access 2021, 9, 9142–9153. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Wang, J.; Pradhan, B.; Hong, H.; Bui, D.T.; Duan, Z.; Ma, J. A Comparative Study of Logistic Model Tree, Random Forest, and Classification and Regression Tree Models for Spatial Prediction of Landslide Susceptibility. Catena 2017, 151, 147–160. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Tien Bui, D.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Khosravi, K.; Yang, Y.; Pham, B.T. Assessment of Advanced Random Forest and Decision Tree Algorithms for Modeling Rainfall-Induced Landslide Susceptibility in the Izu-Oshima Volcanic Island, Japan. Sci. Total Environ. 2019, 662, 332–346. [Google Scholar] [CrossRef]
- Sun, D.; Wen, H.; Wang, D.; Xu, J. A Random Forest Model of Landslide Susceptibility Mapping Based on Hyperparameter Optimization Using Bayes Algorithm. Geomorphology 2020, 362, 107201. [Google Scholar] [CrossRef]
- Rahmati, O.; Kornejady, A.; Deo, R.C. Spatial Prediction of Landslide Susceptibility Using Random Forest Algorithm. In Intelligent Data Analytics for Decision-Support Systems in Hazard Mitigation: Theory and Practice of Hazard Mitigation; Deo, R.C., Samui, P., Kisi, O., Yaseen, Z.M., Eds.; Springer Transactions in Civil and Environmental Engineering; Springer: Singapore, 2021; pp. 281–292. ISBN 9789811557729. [Google Scholar]
- Hu, X.; Wu, S.; Zhang, G.; Zheng, W.; Liu, C.; He, C.; Liu, Z.; Guo, X.; Zhang, H. Landslide Displacement Prediction Using Kinematics-Based Random Forests Method: A Case Study in Jinping Reservoir Area, China. Eng. Geol. 2021, 283, 105975. [Google Scholar] [CrossRef]
- Ilia, I.; Loupasakis, C.; Tsangaratos, P. Land Subsidence Phenomena Investigated by Spatiotemporal Analysis of Groundwater Resources, Remote Sensing Techniques, and Random Forest Method: The Case of Western Thessaly, Greece. Environ. Monit Assess 2018, 190, 623. [Google Scholar] [CrossRef]
- Chen, Y.; Tong, Y.; Tan, K. Coal Mining Deformation Monitoring Using SBAS-InSAR and Offset Tracking: A Case Study of Yu County, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6077–6087. [Google Scholar] [CrossRef]
- Kohestani, V.R.; Bazarganlari, M.R.; Asgari Marnani, J. Prediction of Maximum Surface Settlement Caused by Earth Pressure Balance Shield Tunneling Using Random Forest. J. AI Data Min. 2017, 5, 127–135. [Google Scholar] [CrossRef]
- Limbeck, J.; Bisdom, K.; Lanz, F.; Park, T.; Barbaro, E.; Bourne, S.; Kiraly, F.; Bierman, S.; Harris, C.; Nevenzeel, K.; et al. Using Machine Learning for Model Benchmarking and Forecasting of Depletion-Induced Seismicity in the Groningen Gas Field. Comput Geosci 2021, 25, 529–551. [Google Scholar] [CrossRef]
- Rouet-Leduc, B.; Hulbert, C.; Lubbers, N.; Barros, K.; Humphreys, C.J.; Johnson, P.A. Machine Learning Predicts Laboratory Earthquakes. Geophys. Res. Lett. 2017, 44, 9276–9282. [Google Scholar] [CrossRef]
- Amini, A. Investigation of Induced Seismicity Mechanisms and Magnitude Distributions under Different Stress Regimes, Geomechanical Factors, and Fluid Injection Parameters. Ph.D. Dissertation, University of British Columbia, Kelowna, BC, Canada, 2020. [Google Scholar]
- Miao, T.Y.; Wang, M. Susceptibility Analysis of Earthquake-Induced Landslide Using Random Forest Method; Atlantis Press: Amsterdam, The Netherlands, 2015; pp. 771–775. [Google Scholar]
- Zhou, Y.; Li, S.; Zhou, C.; Luo, H. Intelligent Approach Based on Random Forest for Safety Risk Prediction of Deep Foundation Pit in Subway Stations. J. Comput. Civ. Eng. 2019, 33, 05018004. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, R.; Wu, C.; Goh, A.T.C.; Wang, L. Assessment of Basal Heave Stability for Braced Excavations in Anisotropic Clay Using Extreme Gradient Boosting and Random Forest Regression. Undergr. Space 2020, 7, 233–241. [Google Scholar] [CrossRef]
- Furuya, M. SAR Interferometry. In Encyclopedia of Solid Earth Geophysics; Gupta, H.K., Ed.; Springer: Dordrecht, The Netherlands, 2011; pp. 1041–1049. ISBN 978-90-481-8702-7. [Google Scholar]
- Bürgmann, R.; Rosen, P.A.; Fielding, E.J. Synthetic Aperture Radar Interferometry to Measure Earth’s Surface Topography and Its Deformation. Annu. Rev. Earth Planet. Sci. 2000, 28, 169–209. [Google Scholar] [CrossRef]
- Dąbski, J.; Dunaj, A.; Markiewicz, M.; Mikoda, A.; Paździor, J.; Rydzewski, A.; Siewierski, S. Historia Rozwoju KGHM Polska Miedź S.A. In MONOGRAFIA KGHM Polska Miedź S.A.; KGHM CUPRUM Sp. z o.o. CBR; Lubin: Wrocław, Poland, 2007. [Google Scholar]
- Butra, J. Eksploatacja Złoża rud Miedzi w Warunkach Zagrożenia Tąpaniami i Zawałami; Cuprum Centrum Badawczo-Rozwojowe: Wrocław, Poland, 2010; ISBN 978-83-929275-8-7. [Google Scholar]
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping Small Elevation Changes over Large Areas: Differential Radar Interferometry. J. Geophys. Res. Solid Earth 1989, 94, 9183–9191. [Google Scholar] [CrossRef]
- Hartl, P.; Thiel, K.-H. Fields of Experiments in ERS-1 SAR Interferometry in Bonn and Naples; Proc. Of Symposium “From Optics to Radar: SPOT and ERS Applications”, Cépaduès- Èditions: Paris, France, 1993. [Google Scholar]
- Huang, J.; Xie, M.; Farooq, A.; Williams, E.J. DInSAR Technique for Slow-Moving Landslide Monitoring Based on Slope Units. Surv. Rev. 2019, 51, 70–77. [Google Scholar] [CrossRef]
- Govorčin, M.; Herak, M.; Matoš, B.; Pribičević, B.; Vlahović, I. Constraints on Complex Faulting during the 1996 Ston–Slano (Croatia) Earthquake Inferred from the DInSAR, Seismological, and Geological Observations. Remote Sens. 2020, 12, 1157. [Google Scholar] [CrossRef]
- Wajs, J.; Milczarek, W.J. Detection of Surface Subsidence Using SAR SENTINEL 1A Imagery and the DInSAR Method—A Case Study of the Belchatow Open Pit Mine, Central Poland. EDP Sci. 2018, 55, 00004. [Google Scholar] [CrossRef]
- Novellis, V.D.; Atzori, S.; Luca, C.D.; Manzo, M.; Valerio, E.; Bonano, M.; Cardaci, C.; Castaldo, R.; Bucci, D.D.; Manunta, M.; et al. DInSAR Analysis and Analytical Modeling of Mount Etna Displacements: The December 2018 Volcano-Tectonic Crisis. Geophys. Res. Lett. 2019, 46, 5817–5827. [Google Scholar] [CrossRef]
- Nela, B.R.; Bandyopadhyay, D.; Singh, G.; Glazovsky, A.F.; Lavrentiev, I.I.; Kromova, T.E.; Arigony-Neto, J. Glacier Flow Dynamics of the Severnaya Zemlya Archipelago in Russian High Arctic Using the Differential SAR Interferometry (DInSAR) Technique. Water 2019, 11, 2466. [Google Scholar] [CrossRef]
- Ferretti, A.; Savio, G.; Barzaghi, R.; Borghi, A.; Musazzi, S.; Novali, F.; Prati, C.; Rocca, F. Submillimeter Accuracy of InSAR Time Series: Experimental Validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1142–1153. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Yastika, P.E.; Shimizu, N.; Verbovšek, T. A Case Study on Landslide Displacement Monitoring by SBAS DInSAR in the Vipava River Valley, Slovenia. In Proceedings of the OnePetro, The 5th ISRM Young Scholars’ Symposium on Rock Mechanics and International Symposium on Rock Engineering for Innovative Future, Okinawa, Japan, 1–4 December 2019. [Google Scholar]
- Huang, J.; Khan, S.D.; Ghulam, A.; Crupa, W.; Abir, I.A.; Khan, A.S.; Kakar, D.M.; Kasi, A.; Kakar, N. Study of Subsidence and Earthquake Swarms in the Western Pakistan. Remote Sens. 2016, 8, 956. [Google Scholar] [CrossRef]
- Gama, F.F.; Cantone, A.; Mura, J.C.; Pasquali, P.; Paradella, W.R.; dos Santos, A.R.; Silva, G.G. Monitoring Subsidence of Open Pit Iron Mines at Carajás Province Based on SBAS Interferometric Technique Using TerraSAR-X Data. Remote Sens. Appl. 2017, 8, 199–211. [Google Scholar] [CrossRef]
- Grzesiak, K.; Milczarek, W.J. LOS Displacements of Mauna Loa Volcano, Hawaii Island, as Determined Using SBAS-InSAR. E3S Web Conf. 2018, 55, 00006. [Google Scholar] [CrossRef]
- Brencher, G.; Handwerger, A.L.; Munroe, J.S. InSAR-Based Characterization of Rock Glacier Movement in the Uinta Mountains, Utah, USA. Cryosphere 2021, 15, 4823–4844. [Google Scholar] [CrossRef]
- Breiman, L. Out-of-Bag Estimation. Statistics Department. University of California: Berkeley, CA, USA, 1996. [Google Scholar]
- Breiman, L. Bagging Predictors. Mach. Learn 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Han, S.; Kim, H. On the Optimal Size of Candidate Feature Set in Random Forest. Appl. Sci. 2019, 9, 898. [Google Scholar] [CrossRef]
- Raschka, S.; Mirjalili, V. Python Uczenie Maszynowe, 2nd ed.; Helion SA: Boston, MA, USA, 2019. [Google Scholar]
- Zhao, X.; Yu, B.; Liu, Y.; Chen, Z.; Li, Q.; Wang, C.; Wu, J. Estimation of Poverty Using Random Forest Regression with Multi-Source Data: A Case Study in Bangladesh. Remote Sens. 2019, 11, 375. [Google Scholar] [CrossRef]
- Kohavi, R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection. Ijcai 1995, 14, 1137–1145. [Google Scholar]
- Breiman, L. Manual on Setting Up, Using, And Understanding Random Forests V3.1.; UC Berkeley, Department of Statistics: Berkeley, CA, USA, 2002. [Google Scholar]
- Lundberg, S.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Rawlings, J.O.; Pantula, S.G.; Dickey, D.A. Applied Regression Analysis: A Research Tool; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; ISBN 978-0-387-98454-4. [Google Scholar]
- Li, Y.; Zou, C.; Berecibar, M.; Nanini-Maury, E.; Chan, J.C.W.; van den Bossche, P.; Van Mierlo, J.; Omar, N. Random Forest Regression for Online Capacity Estimation of Lithium-Ion Batteries. Appl. Energy 2018, 232, 197–210. [Google Scholar] [CrossRef]
- Kumar, V.; Venkataraman, G. SAR Interferometric Coherence Analysis for Snow Cover Mapping in the Western Himalayan Region. Int. J. Digit. Earth 2011, 4, 78–90. [Google Scholar] [CrossRef]
- Rahmati, O.; Falah, F.; Naghibi, S.A.; Biggs, T.; Soltani, M.; Deo, R.C.; Cerdà, A.; Mohammadi, F.; Tien Bui, D. Land Subsidence Modelling Using Tree-Based Machine Learning Algorithms. Sci. Total Environ. 2019, 672, 239–252. [Google Scholar] [CrossRef]
- Du, S.; Feng, G.; Wang, J.; Feng, S.; Malekian, R.; Li, Z. A New Machine-Learning Prediction Model for Slope Deformation of an Open-Pit Mine: An Evaluation of Field Data. Energies 2019, 12, 1288. [Google Scholar] [CrossRef]
- Ren, M.; Cheng, G.; Zhu, W.; Nie, W.; Guan, K.; Yang, T. A Prediction Model for Surface Deformation Caused by Underground Mining Based on Spatio-Temporal Associations. Geomat. Nat. Hazards Risk 2022, 13, 94–122. [Google Scholar] [CrossRef]
- Li, J.; Gao, F.; Lu, J.; Tao, T. Deformation Monitoring and Prediction for Residential Areas in the Panji Mining Area Based on an InSAR Time Series Analysis and the GM-SVR Model. Open Geosci. 2019, 11, 58. [Google Scholar] [CrossRef]
- Iannace, G.; Ciaburro, G.; Trematerra, A. Wind Turbine Noise Prediction Using Random Forest Regression. Machines 2019, 7, 69. [Google Scholar] [CrossRef]
- Gibowicz, S.J.; Lasocki, S. Seismicity Induced by Mining: Ten Years Later. In Advances in Geophysics; Dmowska, R., Saltzman, B., Eds.; Elsevier: Amsterdam, The Netherlands, 2001; Volume 44, pp. 39–181. [Google Scholar]
- Guha, S.K. Mining Induced Seismicity. In Induced Earthquakes; Guha, S.K., Ed.; Springer: Dordrecht, The Netherlands, 2000; pp. 159–215. ISBN 978-94-015-9452-3. [Google Scholar]


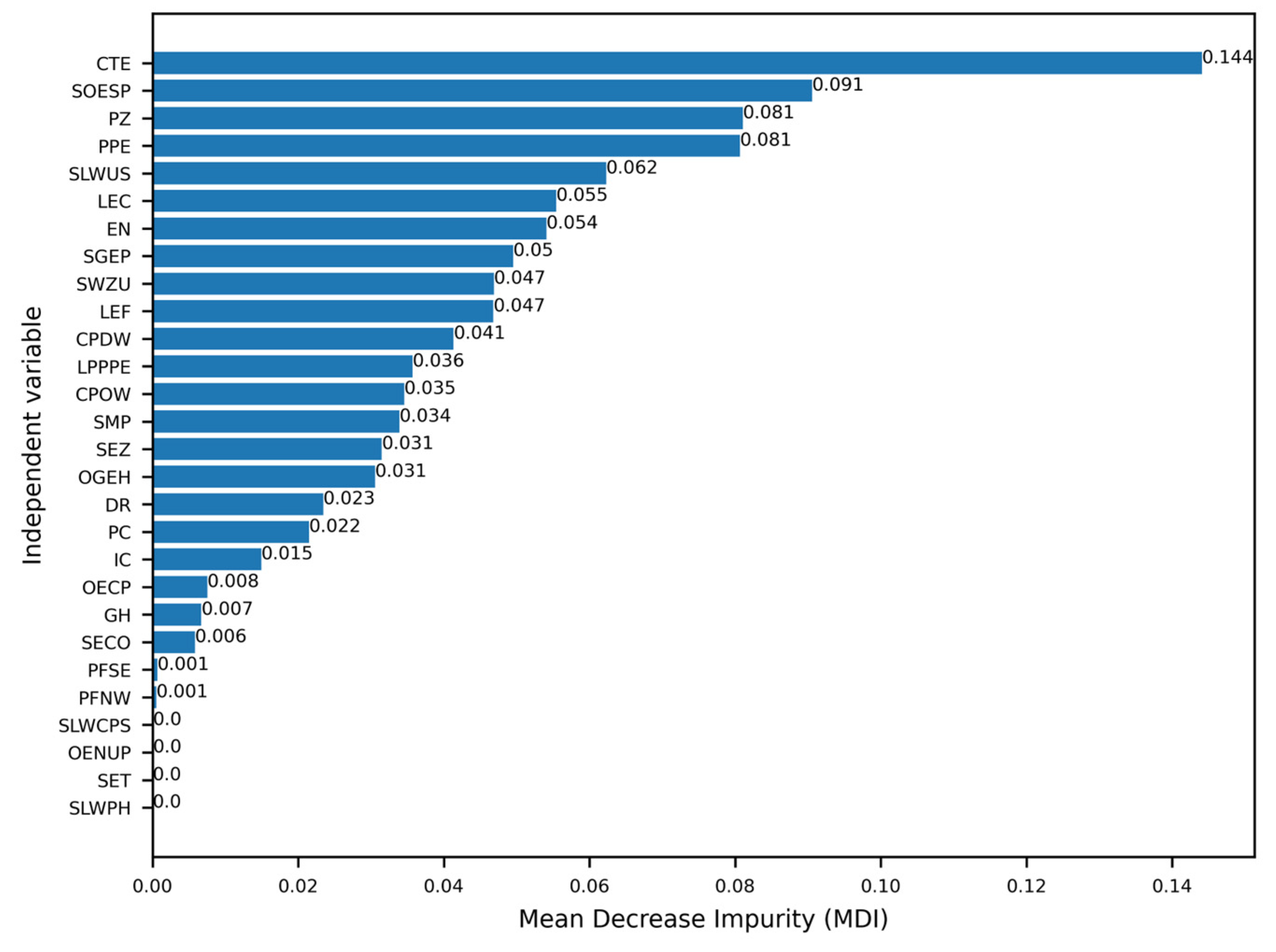
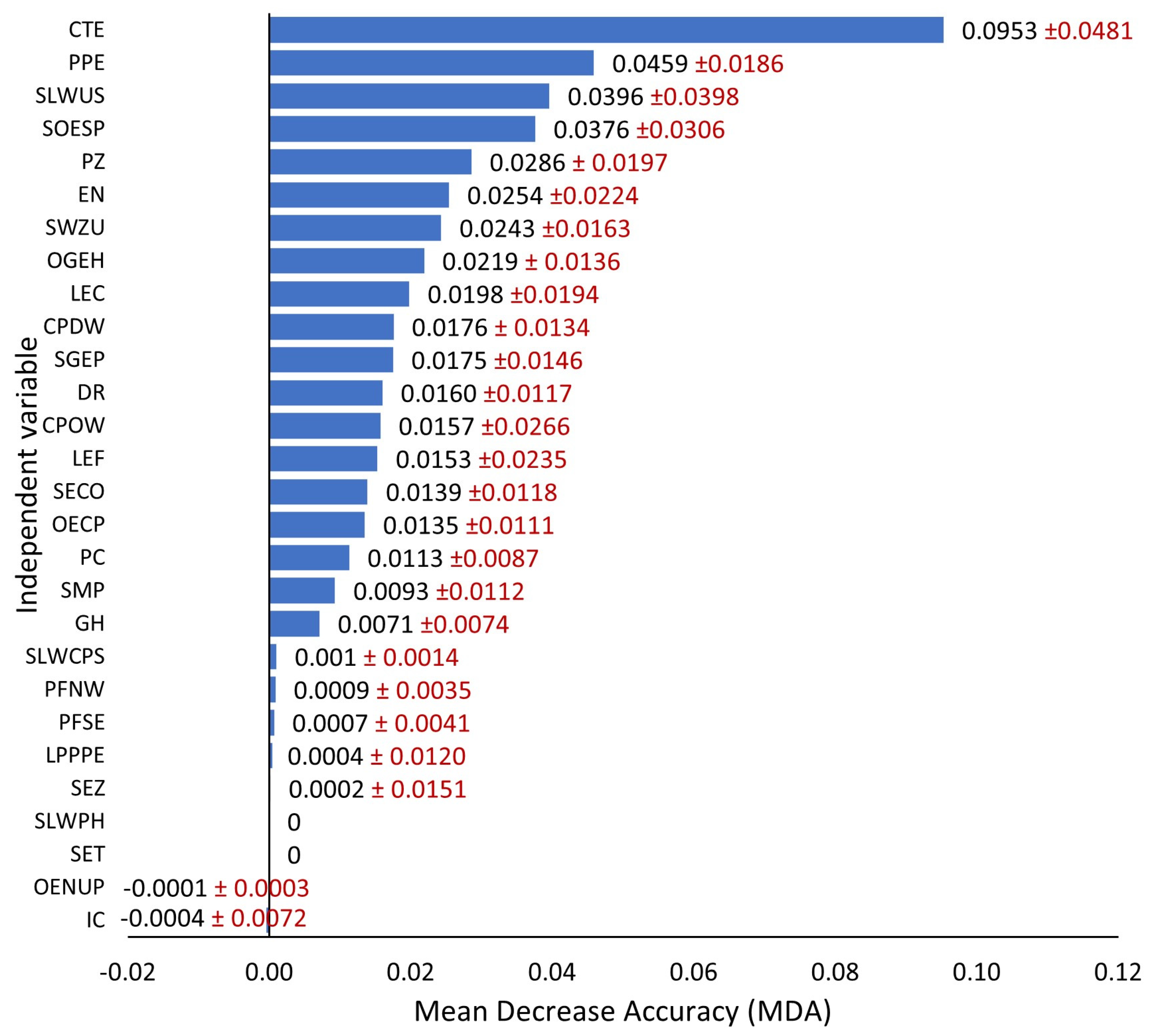

| No. | Parameter Name | Parameter Values |
|---|---|---|
| 1. | n_estimators 1 | {10, 20, 30, 40, 50, 60, 70, 80, 90, 100} |
| 2. | max_depth 2 | {4, 6, 8, 10} |
| 3. | min_samples_split 3 | {2, 4, 6, 8} |
| 4. | min_samples_leaf 4 | {1, 3, 5, 7} |
| 5. | max_features 5 | {4, 5, 6, 28} |
| No. | Parameter Name | Optimal Values |
|---|---|---|
| 1. | n_estimators | 10 |
| 2. | max_depth | 6 |
| 3. | min_samples_split | 2 |
| 4. | min_samples_leaf | 1 |
| 5. | max_features | 5 |
| Error | Model with Outliers | Model without Outliers | ||
|---|---|---|---|---|
| Training Dataset | Test Dataset | Training Dataset | Test Dataset | |
| MSE | 29 mm2 | 112 mm2 | 20 mm2 | 48 mm2 |
| RMSE | 5 mm | 11 mm | 5 mm | 7 mm |
| MAE | 4 mm | 7 mm | 4 mm | 6 mm |
| R2 | 0.95 | 0.87 | 0.97 | 0.93 |
| ME | 27 mm | 36 mm | 13 mm | 17 mm |
| MAPE | 7.4% | 10.7% | 7.8% | 12.0% |
| OOB | 18% | 13% | ||
| No. | Statistical Significance of Independent Variables | ||
|---|---|---|---|
| MDI Method | MDA Method | SHAP Method | |
| 1. | CTE | CTE | CTE |
| 2. | SOESP | PPE | EN |
| 3. | PZ | SLWUS | SWZU |
| 4. | PPE | SOESP | SOESP |
| 5. | SLWUS | PZ | LEC |
| 6. | LEC | EN | CPOW |
| 7. | EN | SWZU | SGEP |
| 8. | SGEP | OGEH | LEF |
| 9. | SWZU | LEC | IC |
| 10. | LEF | CPDW | PPE |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Owczarz, K.; Blachowski, J. Random Forest—Based Identification of Factors Influencing Ground Deformation Due to Mining Seismicity. Remote Sens. 2024, 16, 2742. https://doi.org/10.3390/rs16152742
Owczarz K, Blachowski J. Random Forest—Based Identification of Factors Influencing Ground Deformation Due to Mining Seismicity. Remote Sensing. 2024; 16(15):2742. https://doi.org/10.3390/rs16152742
Chicago/Turabian StyleOwczarz, Karolina, and Jan Blachowski. 2024. "Random Forest—Based Identification of Factors Influencing Ground Deformation Due to Mining Seismicity" Remote Sensing 16, no. 15: 2742. https://doi.org/10.3390/rs16152742
APA StyleOwczarz, K., & Blachowski, J. (2024). Random Forest—Based Identification of Factors Influencing Ground Deformation Due to Mining Seismicity. Remote Sensing, 16(15), 2742. https://doi.org/10.3390/rs16152742









