A Waveform Design for Integrated Radar and Jamming Based on Smart Modulation and Complementary Coding
Abstract
1. Introduction
- Proposing a waveform design and processing method for integrated radar and jamming based on smart modulation and complementary coding, solving the issue of high sidelobes in traditional integrated radar and jamming waveforms;
- Theoretical derivation and analysis of the influence of phase angles of coding sequences on the detection and jamming effects of integrated waveform are provided. A method for adjusting detection and jamming performance is proposed, allowing for the flexible control of the jamming effect by changing the phase angles;
- The superior detection and jamming performance of the proposed waveforms is demonstrated through experimental results.
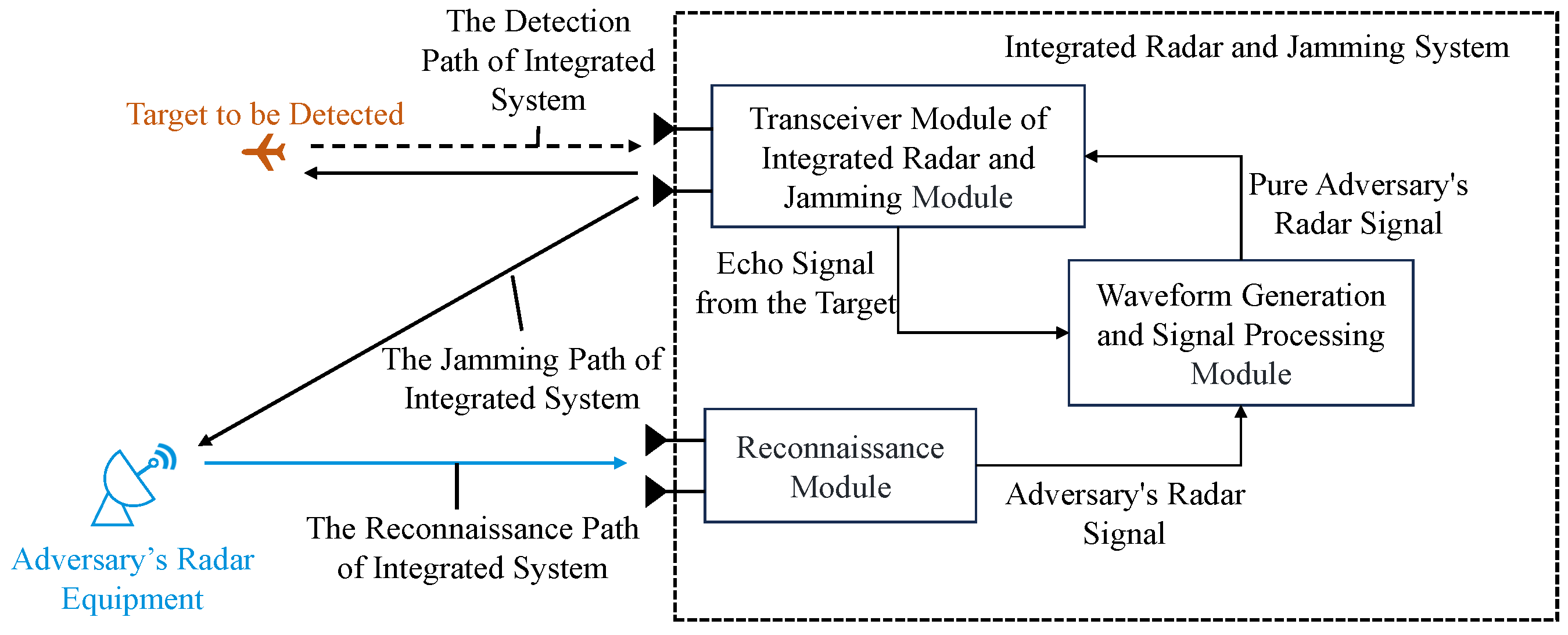
2. The Working Scenarios of Integrated Radar and Jamming Systems
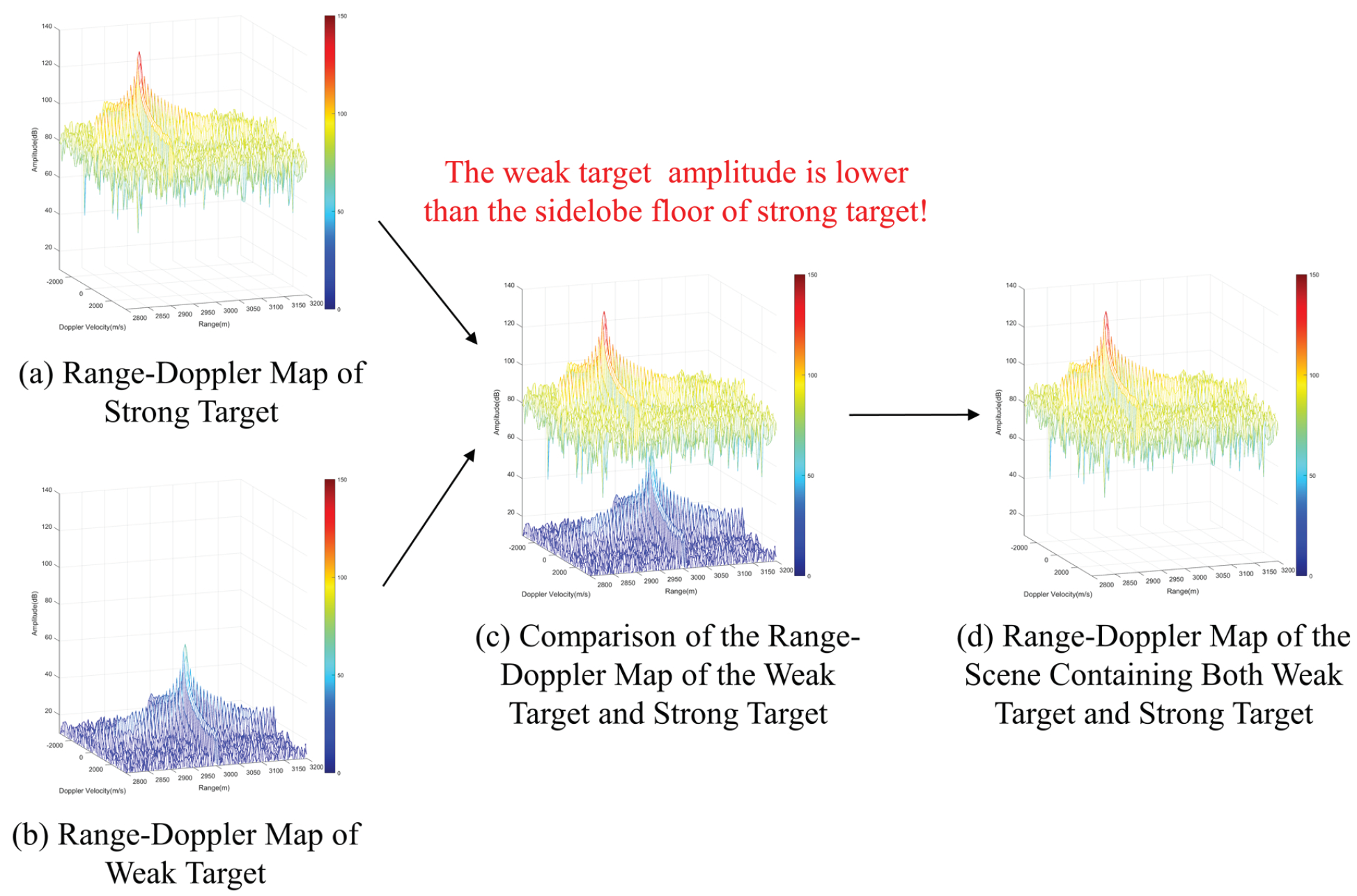
3. Limitations of Traditional Integrated Radar and Jamming Waveforms and Signal Processing Methods
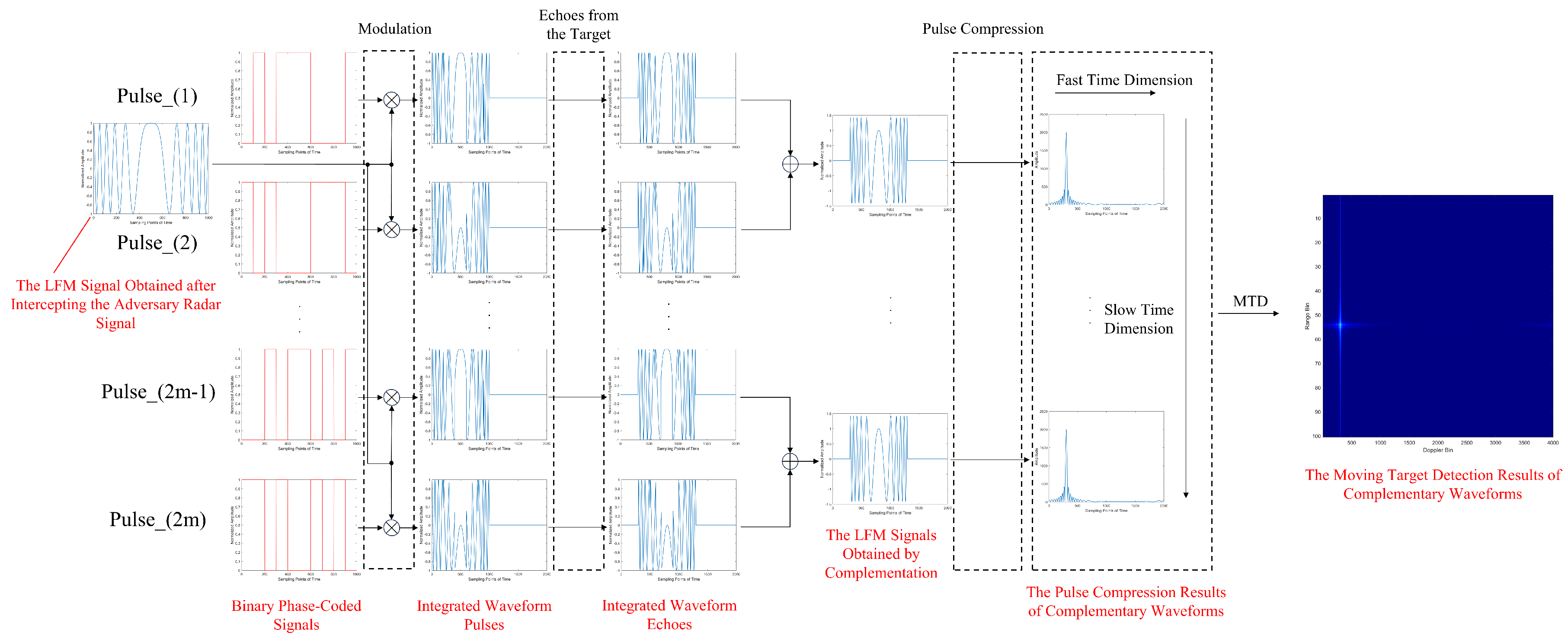
4. Design and Processing Model of Integrated Radar and Jamming Waveform Based on Smart Modulation and Complementary Coding
- 1.
- The coding sequences used in this integrated waveform have complementary relationships between pulses, which can be added to obtain a complete LFM signal with a constant modulus, while the coding sequences used in the traditional integrated waveforms are completely random, which severely affects the detection performance of the integrated waveform.
- 2.
- The phase of the coding sequence is not limited to 0 and , but can be arbitrarily selected, ensuring flexible and variable detection and jamming effects.
5. Waveform Detection and Jamming Performance Control
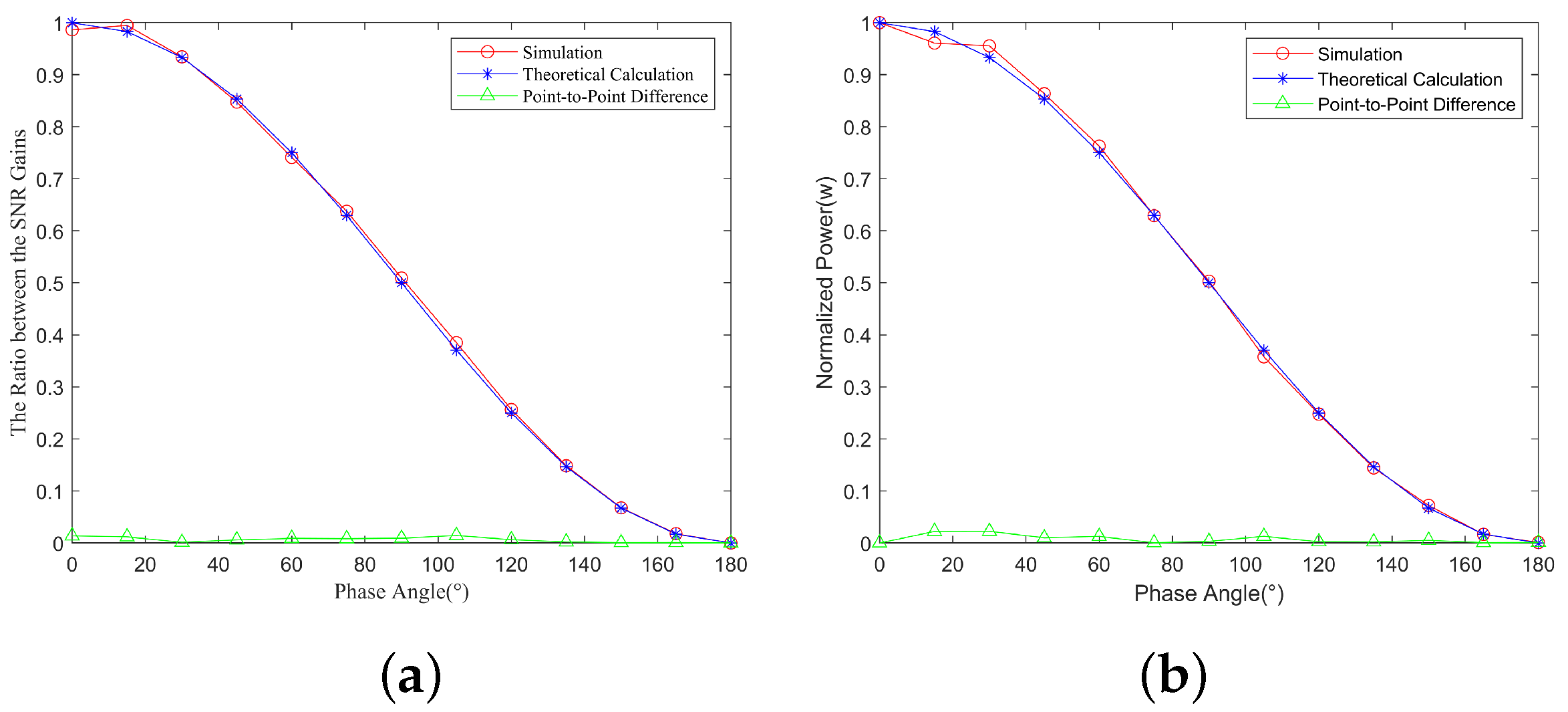
5.1. The Influence of Phase Angle on Detection Effect
5.2. The Influence of Phase Angle on Jamming Effect
6. Simulation Analysis
6.1. Analysis of Point Target Detection Performance
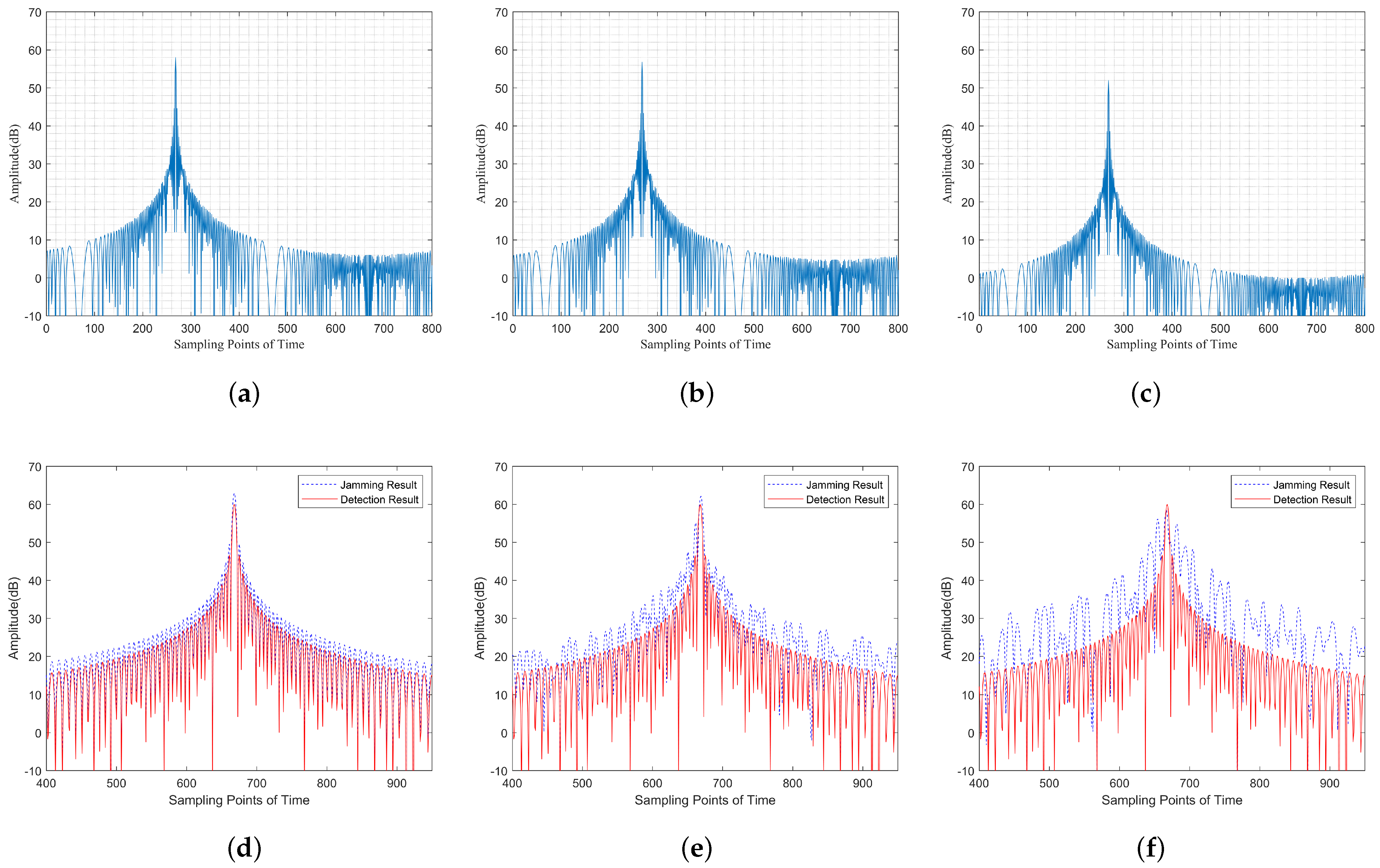
6.2. The Influence of Phase Angle on Detection and Jamming Effects
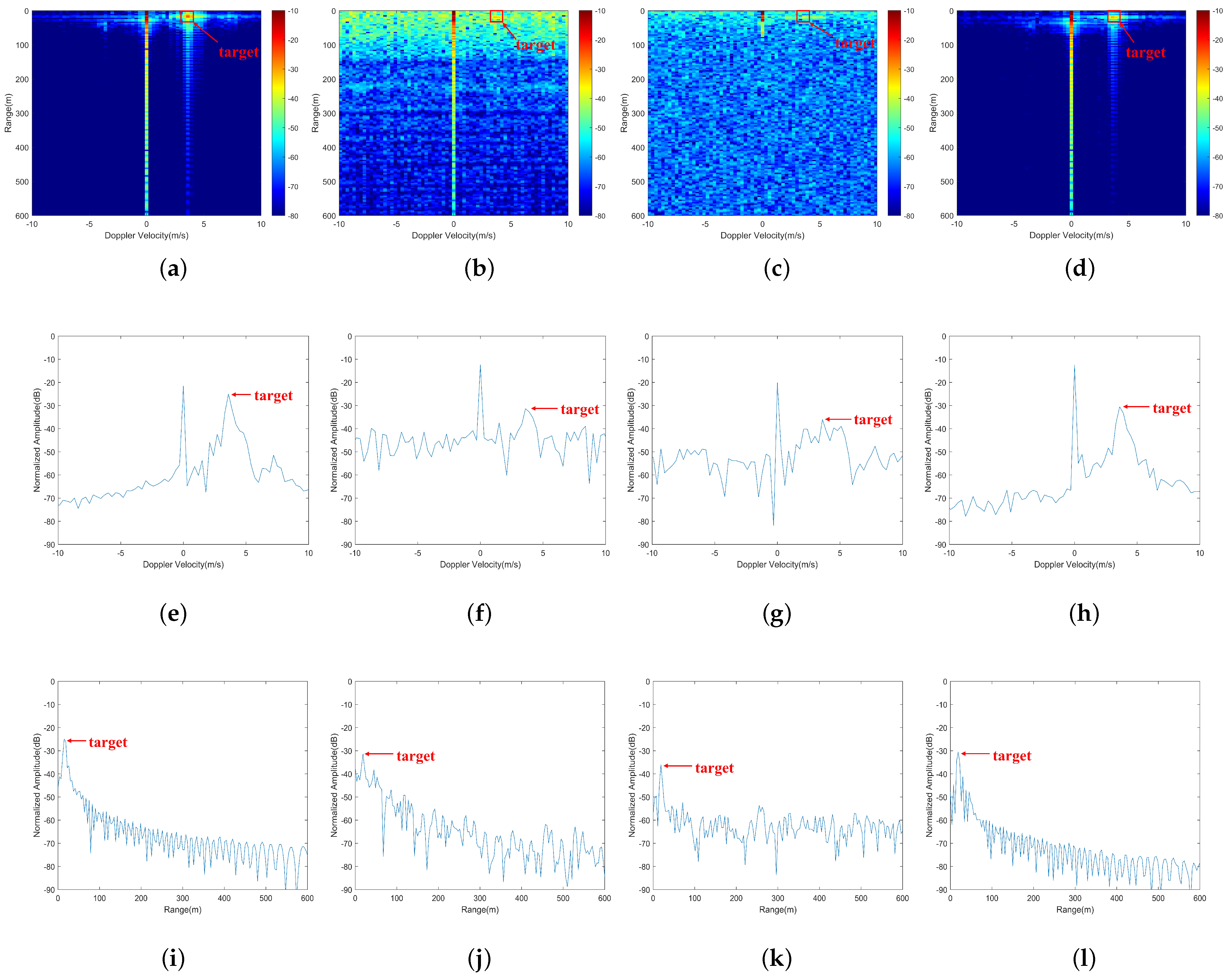
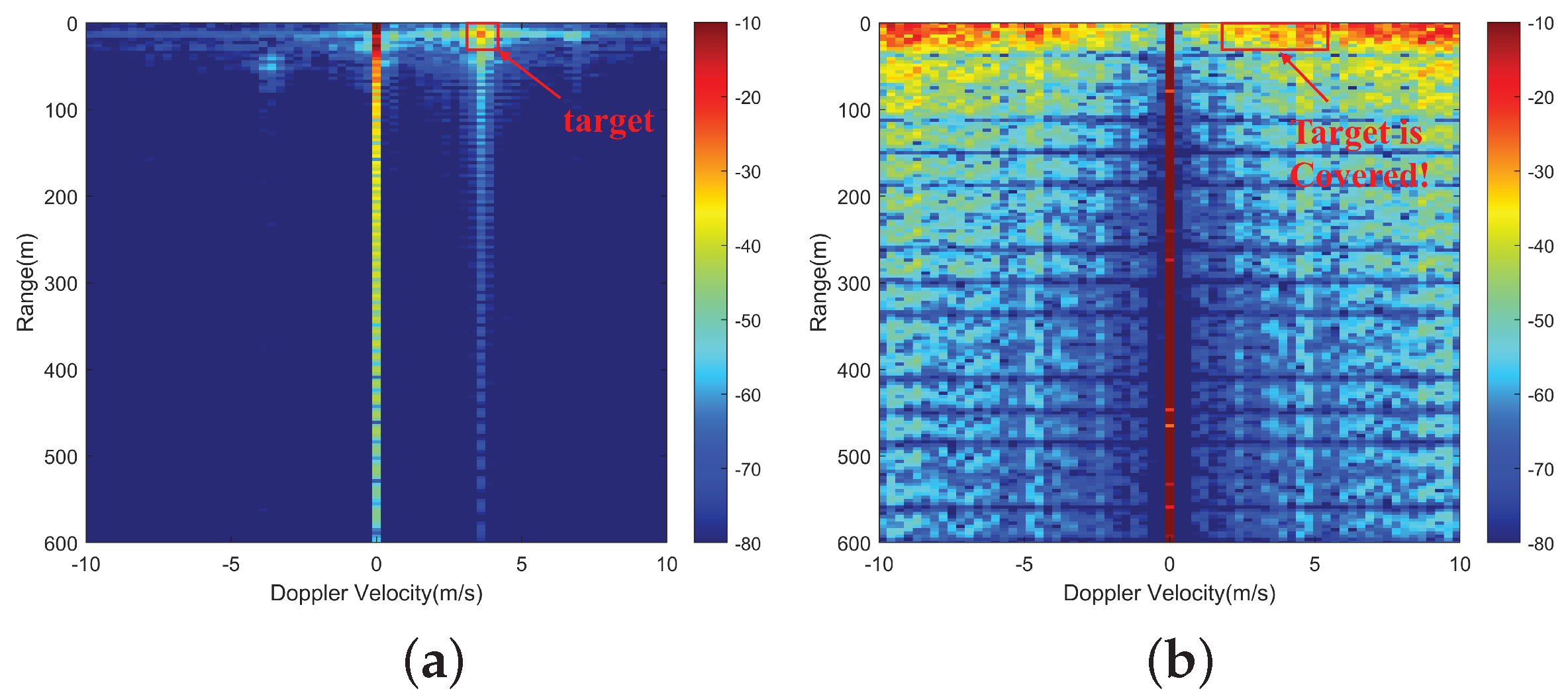
7. Data Processing for Experimental Results
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LFM | linear frequency modulation |
| EW | electronic warfare |
| NFM | noise frequency modulation |
| SNR | signal-to-noise ratio |
| MTD | moving target detection |
| CPI | coherent processing interval |
| PRI | pulse repetition interval |
| ISLR | integration sidelobe ratio |
| USRP | universal software radio peripheral |
| RF | radio frequency |
| SCNR | signal-to-clutter-noise ratio |
References
- Zhang, C.; Wang, L.; Jiang, R.; Hu, J.; Xu, S. Radar jamming decision-making in cognitive electronic warfare: A review. IEEE Sens. J. 2023, 23, 11383–11403. [Google Scholar] [CrossRef]
- Liu, G.; Huang, Z.; Zhang, Q.; Mu, B.; Guo, H. Joint Radar Jamming and Communication System Design Based on Universal Filtered Multicarrier Chirp Waveform. Remote Sens. 2024, 16, 1383. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, Y.; Yeo, T.S.; Cheng, Y.; Fu, J. Robust Multiplexing Waveform Design for Integrated OFDM Radar and Communication via Complex Weight Optimization. Remote Sens. 2023, 15, 4438. [Google Scholar] [CrossRef]
- Zhang, L.; Luo, Y.; Wang, H.; Zhang, Q. Detection of False Targets in a Full Polarization Radar Network under Deception Jamming. IEEE Sens. J. 2023, 24, 3368–3379. [Google Scholar] [CrossRef]
- Xu, C.; Chen, T. Conception of “signal sharing” in integrated radar and jammer system and the integrated signal design. In Proceedings of the IEEE 2002 International Conference on Communications, Circuits and Systems and West Sino Expositions, Chengdu, China, 29 June–1 July 2002; IEEE: New York, NY, USA, 2002; Volume 1, pp. 502–505. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, T. Noise-linear frequency modulation shared waveform for integrated radar and jammer system. In Proceedings of the 2007 International Conference on Communications, Circuits and Systems, Kokura, Japan, 11–13 July 2007; IEEE: New York, NY, USA, 2007; pp. 644–648. [Google Scholar] [CrossRef]
- Han, G.; He, J.; Qi, J. An Optimization Design Method of Integrated Radar and Jammer Signal Modulated by Bi-phase Sequences of Chaos. In Proceedings of the 2012 Eighth International Conference on Computational Intelligence and Security, Guangzhou, China, 17–18 November 2012; IEEE: New York, NY, USA, 2012; pp. 44–47. [Google Scholar] [CrossRef]
- Shi, Q.; Wu, S.; Huang, J.; Wang, C.; Yuan, N. A novel jamming method against LFM radar using pseudo-random code phase modulation. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China, 22–25 October 2017; IEEE: New York, NY, USA, 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Li, C.; Wu, G. A Shared Waveform Design and Processing Method for Integrated Radar Detection and Coherent Jamming Signal. In Proceedings of the 2022 IEEE 10th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 17–19 June 2022; IEEE: New York, NY, USA, 2022; Volume 10, pp. 373–380. [Google Scholar] [CrossRef]
- Li, C.; Wu, G.; Li, G. A Shared Waveform Design for Integrated Detection and Jamming Signal Based on LFM-Costas Intra-pulse Frequency Stepping. In Proceedings of the 2022 7th International Conference on Communication, Image and Signal Processing (CCISP), Chengdu, China, 18–20 November 2022; IEEE: New York, NY, USA, 2022; pp. 347–354. [Google Scholar] [CrossRef]
- Zhang, S.; Lu, X.; Yu, J.; Dai, Z.; Su, W.; Gu, H. Clutter Suppression for Radar via Deep Joint Sparse Recovery Network. IEEE Geosci. Remote Sens. Lett. 2024, 21, 3332035. [Google Scholar] [CrossRef]
- Ackroyd, M.H.; Ghani, F. Optimum mismatched filters for sidelobe suppression. IEEE Trans. Aerosp. Electron. Syst. 1973, AES-9, 214–218. [Google Scholar] [CrossRef]
- Griep, K.R.; Ritcey, J.A.; Burlingame, J.J. Poly-phase codes and optimal filters for multiple user ranging. IEEE Trans. Aerosp. Electron. Syst. 1995, 31, 752–767. [Google Scholar] [CrossRef]
- Levanon, N.; Scharf, A. Range sidelobes blanking using contrasting mismatched filters. In Proceedings of the 2009 16th International Conference on Digital Signal Processing, Santorini, Greece, 5–7 July 2009; IEEE: New York, NY, USA, 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Kajenski, P.J. Mismatch filter design via convex optimization. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1587–1591. [Google Scholar] [CrossRef]
- Fridman, L.; Ershov, G.; Myasnikov, S.; Sinitsin, E. Compression of phase-shift keyed signals by means of the mismatched sidelobe-free filter with application to coherent pulse radar. In Proceedings of the 2017 18th International Radar Symposium (IRS), Prague, Czech Republic, 28–30 June 2017; IEEE: New York, NY, USA, 2017; pp. 1–10. [Google Scholar] [CrossRef]
- Kempf, J.; Jackson, J.A. A modified least-squares mismatched filter for use in radar applications with additive noise. In Proceedings of the 2020 IEEE International Radar Conference (RADAR), Washington, DC, USA, 28–30 April 2020; IEEE: New York, NY, USA, 2020; pp. 804–809. [Google Scholar] [CrossRef]
- Golay, M. Complementary series. IRE Trans. Inf. Theory 1961, 7, 82–87. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Xu, H.; Wang, B.; Liu, L.; Chen, X. A high signal–noise ratio UWB radar for buried pipe location using golay complementary sequences. Appl. Sci. 2019, 9, 5090. [Google Scholar] [CrossRef]
- Chen, H.; Yuan, K.; Yao, M.; Xiong, J. A Novel Composite Coding Method for Incoherent Scatter Radar. Atmosphere 2021, 12, 1518. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Y.; Xie, J.; Yang, Y.; Tian, B.; Xu, S. Ultra-low sidelobe waveforms design for LPI radar based on joint complementary phase-coding and optimized discrete frequency-coding. Remote Sens. 2022, 14, 2592. [Google Scholar] [CrossRef]
- Wu, Z.J.; Wang, C.X.; Jiang, P.H.; Zhou, Z.Q. Range-Doppler sidelobe suppression for pulsed radar based on Golay complementary codes. IEEE Signal Process. Lett. 2020, 27, 1205–1209. [Google Scholar] [CrossRef]
- Lan, L.; Xu, J.; Liao, G.; Zhang, Y.; Fioranelli, F.; So, H.C. Suppression of mainbeam deceptive jammer with FDA-MIMO radar. IEEE Trans. Veh. Technol. 2020, 69, 11584–11598. [Google Scholar] [CrossRef]
- Zhang, S.; Lu, X.; Yang, J.; Su, W.; Gu, H. Enhanced Signal Processing Method for Integrated Detection and Jamming System Considering the Complex Environment. In Proceedings of the 2021 CIE International Conference on Radar (Radar), Haikou, China, 15–19 December 2021; IEEE: New York, NY, USA, 2021; pp. 2233–2237. [Google Scholar] [CrossRef]
- Lang, P.; Fu, X.; Dong, J.; Yang, J. An efficient radon Fourier transform-based coherent integration method for target detection. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Azouz, A.; Abosekeen, A.; Nassar, S.; Hanafy, M. Design and implementation of an enhanced matched filter for sidelobe reduction of pulsed linear frequency modulation radar. Sensors 2021, 21, 3835. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Yang, Y.; Sun, Z.; Cui, G.; Yeo, T.S. Multi-frame integration method for radar detection of weak moving target. IEEE Trans. Veh. Technol. 2021, 70, 3609–3624. [Google Scholar] [CrossRef]
- Zhang, X.; Su, D.; Zhou, M. The analysis and simulation research of distance resolution and ambiguity property of LFM signal. In Proceedings of the 2007 International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications, Hangzhou, China, 14–17 August 2007; IEEE: New York, NY, USA, 2007; pp. 1191–1194. [Google Scholar] [CrossRef]
- Levanon, N.; Mozeson, E. Coherent Train of LFM Pulses. In Radar Signals; Wiley: Hoboken, NJ, USA, 2004; pp. 168–190. [Google Scholar] [CrossRef]
- Lan, L.; Marino, A.; Aubry, A.; De Maio, A.; Liao, G.; Xu, J.; Zhang, Y. GLRT-based adaptive target detection in FDA-MIMO radar. IEEE Trans. Aerosp. Electron. Syst. 2020, 57, 597–613. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Wang, X.; Dong, Q.; Lyu, X. An Improved Multi-Frame Coherent Integration Algorithm for Heterogeneous Radar. Remote Sens. 2023, 15, 4026. [Google Scholar] [CrossRef]
- Gao, Y.; Hua, Y.; Li, S.; Yang, C. Acquisition method of Loran-C signal based on matched filter. In Proceedings of the 2015 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Ningbo, China, 19–22 September 2015; IEEE: New York, NY, USA, 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, H.; Hu, T.; Li, T.; Wu, D.; Xu, Z.; Xu, X.; Tian, Z. Intelligent Interference Waveform Design for Radar Detection based on Cross-Correlation Value Function. IEEE Trans. Aerosp. Electron. Syst. 2023, 60, 2061–2070. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Phase-coded sequence code length | 10 |
| Pulse width | 10 s |
| PRI | 20 s |
| CPI | 20 ms |
| Bandwidth | 20 MHz |
| Carrier frequency | 5 GHz |
| Sampling frequency | 40 MHz |
| Target velocity | 10 m/s |
| Target range | 1000 m |
| Parameter | Value |
|---|---|
| Phase-coded sequence code length | 10 |
| Phase angle | |
| Pulse width | 10 s |
| PRI | 20 s |
| CPI | 100 ms |
| Bandwidth | 20 MHz |
| Carrier frequency | 5 GHz |
| Sampling frequency | 40 MHz |
| Target velocity | 1–5 m/s |
| Target range | 1–30 m |
| Signal Type | SCNR |
|---|---|
| LFM signal | 67.18 dB |
| Traditional integrated signal based on smart modulation | 34.31 dB |
| Traditional NFM integrated signal | 28.76 dB |
| Integrated radar and jamming signal based on smart modulation and complementary coding | 61.14 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, H.; Zhang, S.; Lu, X.; Yang, J.; Duan, L.; Tan, K.; Gu, H. A Waveform Design for Integrated Radar and Jamming Based on Smart Modulation and Complementary Coding. Remote Sens. 2024, 16, 2725. https://doi.org/10.3390/rs16152725
Yan H, Zhang S, Lu X, Yang J, Duan L, Tan K, Gu H. A Waveform Design for Integrated Radar and Jamming Based on Smart Modulation and Complementary Coding. Remote Sensing. 2024; 16(15):2725. https://doi.org/10.3390/rs16152725
Chicago/Turabian StyleYan, Huabin, Shiyuan Zhang, Xingyu Lu, Jianchao Yang, Lunhao Duan, Ke Tan, and Hong Gu. 2024. "A Waveform Design for Integrated Radar and Jamming Based on Smart Modulation and Complementary Coding" Remote Sensing 16, no. 15: 2725. https://doi.org/10.3390/rs16152725
APA StyleYan, H., Zhang, S., Lu, X., Yang, J., Duan, L., Tan, K., & Gu, H. (2024). A Waveform Design for Integrated Radar and Jamming Based on Smart Modulation and Complementary Coding. Remote Sensing, 16(15), 2725. https://doi.org/10.3390/rs16152725







