Detection of Individual Corn Crop and Canopy Delineation from Unmanned Aerial Vehicle Imagery
Abstract
1. Introduction
2. Materials and Methods
2.1. UAV Data Collection
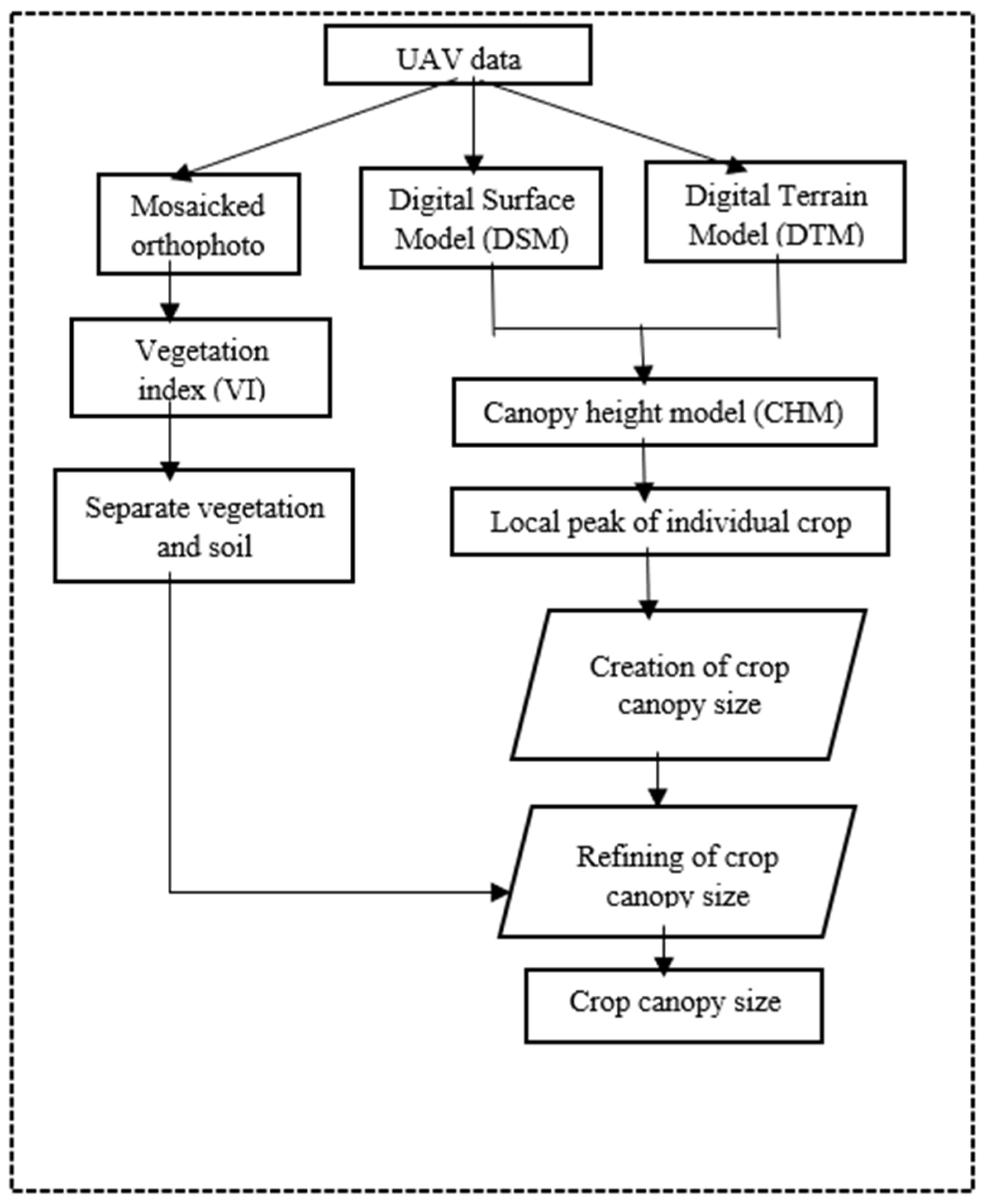
2.2. Canopy Height Model (CHM) Generation and Individual Plant Identification
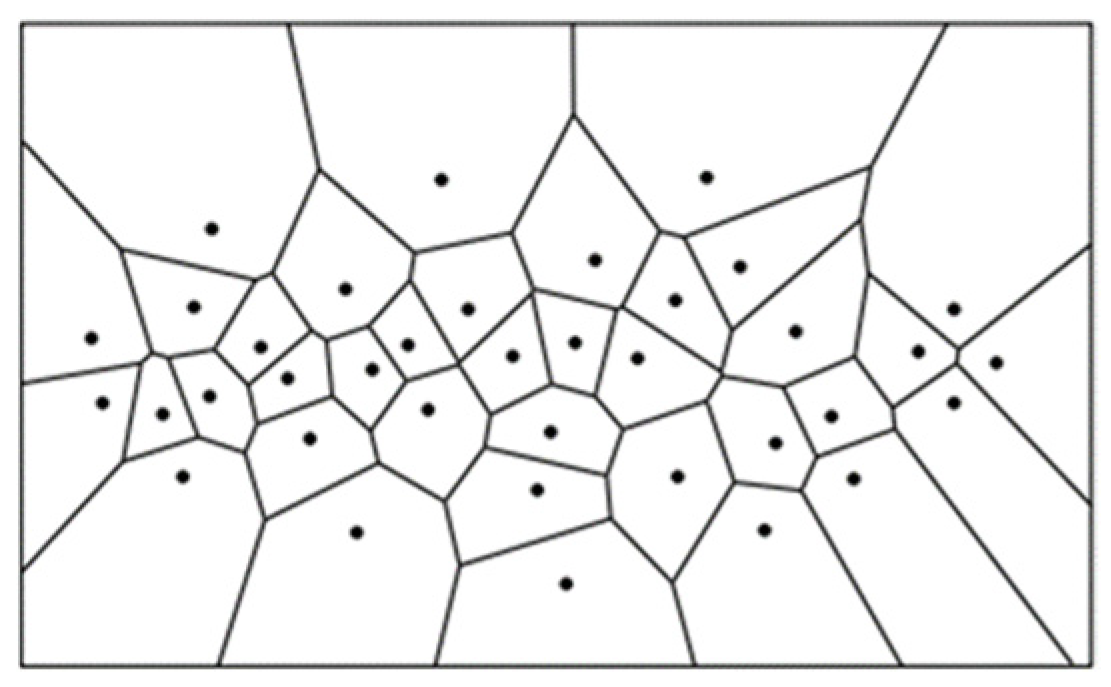
2.3. Canopy Size Delineation and Refinement
2.4. Machine Learning Integration
2.5. Evaluation Metrics
3. Implementations and Results
3.1. Study Area and Data Collection
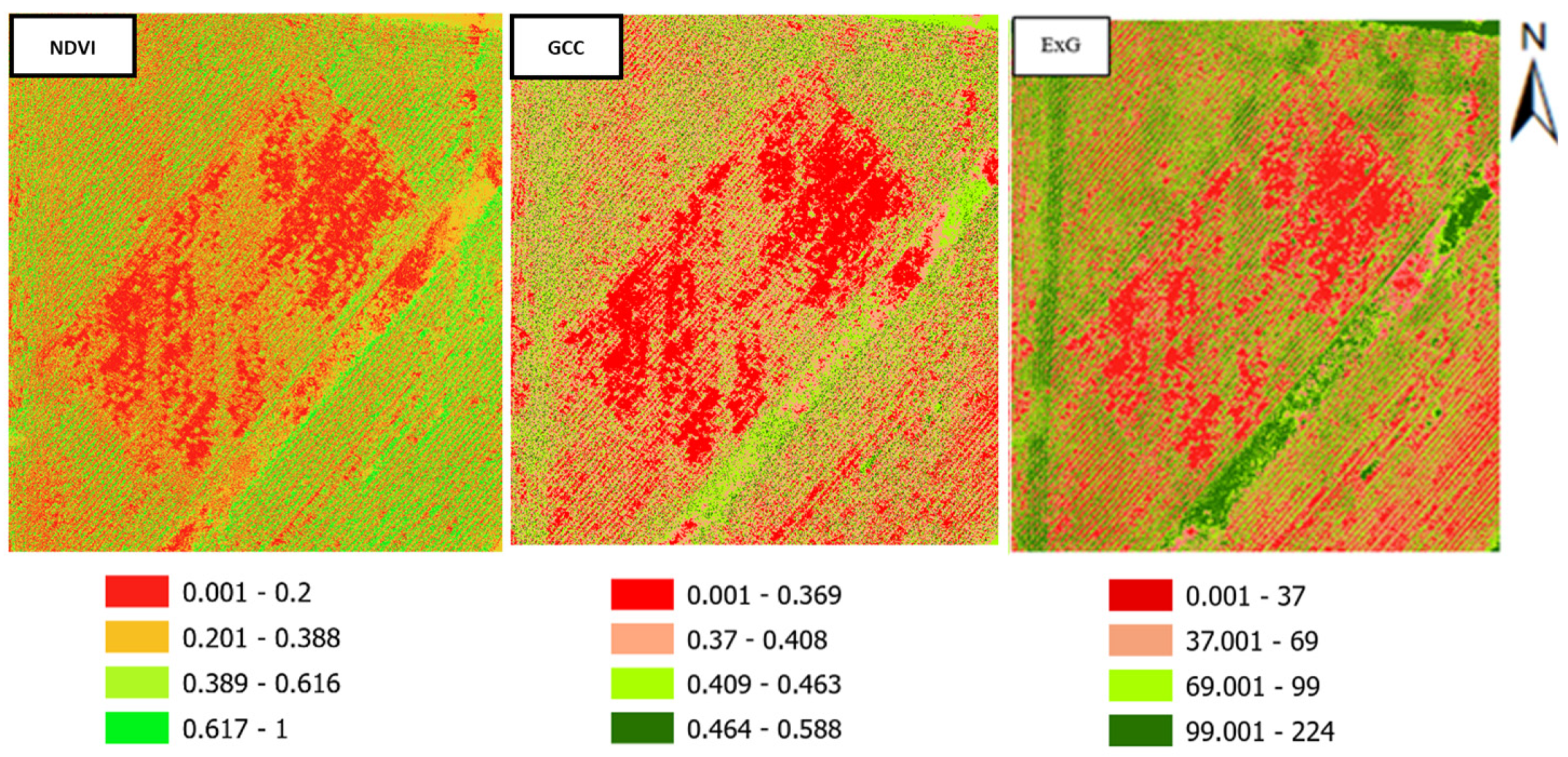
3.2. CHM Development and Crop Detection
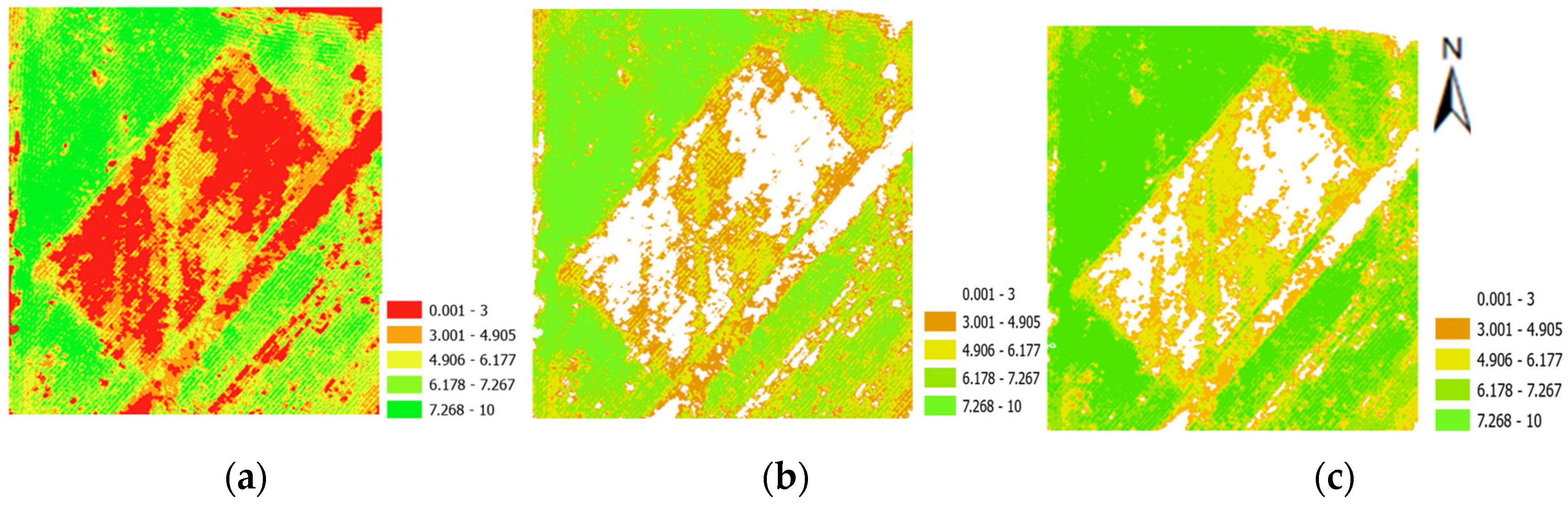
3.3. Canopy Size Estimation and Refinement
3.4. Statistical Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McConnell, M.D. Bridging the gap between conservation delivery and economics with precision agriculture. Wildl. Soc. Bull. 2019, 43, 391–397. [Google Scholar] [CrossRef]
- Higgins, V.; Bryant, M.; Howell, A.; Battersby, J. Ordering adoption: Materiality, knowledge and farmer engagement with precision agriculture technologies. J. Rural Stud. 2017, 55, 193–202. [Google Scholar] [CrossRef]
- Cisternas, I.; Velásquez, I.; Caro, A.; Rodríguez, A. Systematic literature review of implementations of precision agriculture. Comput. Electron. Agric. 2020, 176, 105626. [Google Scholar] [CrossRef]
- Beland, M.; Parker, G.; Sparrow, B.; Harding, D.; Chasmer, L.; Phinn, S.; Antonarakis, A.; Strahler, A. On promoting the use of lidar systems in forest ecosystem research. For. Ecol. Manag. 2019, 450, 117484. [Google Scholar] [CrossRef]
- Elikem, D.F.; Leila, H.-B.; Ali, K.; Abolghasem, S. UAV Remote Sensing Assessment of Crop Growth. Photogramm. Eng. Remote Sens. 2021, 87, 891–899. [Google Scholar]
- Sun, Q.; Sun, L.; Shu, M.; Gu, X.; Yang, G.; Zhou, L. Monitoring maize lodging grades via unmanned aerial vehicle multispectral image. Plant Phenomics 2019, 2019, 5704154. [Google Scholar] [CrossRef] [PubMed]
- Yurtseven, H.; Akgul, M.; Coban, S.; Gulci, S. Determination and accuracy analysis of individual tree crown parameters using UAV based imagery and OBIA techniques. Measurement 2019, 145, 651–664. [Google Scholar] [CrossRef]
- Wan Mohd Jaafar, W.S.; Woodhouse, I.H.; Silva, C.A.; Omar, H.; Abdul Maulud, K.N.; Hudak, A.T.; Klauberg, C.; Cardil, A.; Mohan, M. Improving individual tree crown delineation and attributes estimation of tropical forests using airborne LiDAR data. Forests 2018, 9, 759. [Google Scholar] [CrossRef]
- Mohan, M.; Mendonça, B.; Silva, C.; Klauberg, C.; de Saboya Ribeiro, A.S.; Araújo, E.; Monte, M.A.; Cardil, A. Optimizing individual tree detection accuracy and measuring forest uniformity in coconut (Cocos nucifera L.) plantations using airborne laser scanning. Ecol. Model. 2019, 409, 108736. [Google Scholar]
- Dorbu, F.E.; Beni, L.H. Geospatial Intelligence for Individual Crop Detection and Anomaly Monitoring. In Proceedings of the IGARSS 2023—2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; pp. 1051–1054. [Google Scholar]
- Wilke, N.; Siegmann, B.; Klingbeil, L.; Burkart, A.; Kraska, T.; Muller, O.; van Doorn, A.; Heinemann, S.; Rascher, U. Quantifying lodging percentage and lodging severity using a UAV-based canopy height model combined with an objective threshold approach. Remote Sens. 2019, 11, 515. [Google Scholar] [CrossRef]
- Wang, Z.; Nie, C.; Wang, H.; Ao, Y.; Jin, X.; Yu, X.; Bai, Y.; Liu, Y.; Shao, M.; Cheng, M.; et al. Detection and analysis of degree of maize lodging using UAV-RGB image multi-feature factors and various classification methods. ISPRS Int. J. Geo-Inf. 2021, 10, 309. [Google Scholar] [CrossRef]
- Malachy, N.; Zadak, I.; Rozenstein, O. Comparing methods to extract crop height and estimate crop coefficient from UAV imagery using structure from motion. Remote Sens. 2022, 14, 810. [Google Scholar] [CrossRef]
- Liu, X.; Bo, Y. Object-based crop species classification based on the combination of airborne hyperspectral images and LiDAR data. Remote Sens. 2015, 7, 922–950. [Google Scholar] [CrossRef]
- Dobosz, B.; Gozdowski, D.; Koronczok, J.; Žukovskis, J.; Wójcik-Gront, E. Evaluation of Maize Crop Damage Using UAV-Based RGB and Multispectral Imagery. Agriculture 2023, 13, 1627. [Google Scholar] [CrossRef]
- Aeberli, A.; Johansen, K.; Robson, A.; Lamb, D.W.; Phinn, S. Detection of banana plants using multi-temporal multispectral UAV imagery. Remote Sens. 2021, 13, 2123. [Google Scholar] [CrossRef]
- Jing, L.; Hu, B.; Noland, T.; Li, J. An individual tree crown delineation method based on multi-scale segmentation of imagery. ISPRS J. Photogramm. Remote Sens. 2012, 70, 88–98. [Google Scholar] [CrossRef]
- Marasigan, R.; Festijo, E.; Juanico, D.E. Mangrove crown diameter measurement from airborne lidar data using marker-controlled watershed algorithm: Exploring performance. In Proceedings of the 2019 IEEE 6th International Conference on Engineering Technologies and Applied Sciences (ICETAS), Kuala Lumpur, Malaysia, 20–21 December 2019. [Google Scholar]
- Huang, H.; Li, X.; Chen, C. Individual tree crown detection and delineation from very-high-resolution UAV images based on bias field and marker-controlled watershed segmentation algorithms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2253–2262. [Google Scholar] [CrossRef]
- Jensen, J.L.; Mathews, A.J. Assessment of image-based point cloud products to generate a bare earth surface and estimate canopy heights in a woodland ecosystem. Remote Sens. 2016, 8, 50. [Google Scholar] [CrossRef]
- Gao, M.; Yang, F.; Wei, H.; Liu, X. Individual maize location and height estimation in field from UAV-Borne lidar and rgb images. Remote Sens. 2022, 14, 2292. [Google Scholar] [CrossRef]
- Varela, S.; Dhodda, P.R.; Hsu, W.H.; Prasad, P.V.V.; Assefa, Y.; Peralta, N.R.; Griffin, T.; Sharda, A.; Ferguson, A.; Ciampitti, I.A. Early-season stand count determination in corn via integration of imagery from unmanned aerial systems (UAS) and supervised learning techniques. Remote Sens. 2018, 10, 343. [Google Scholar] [CrossRef]
- Fujimoto, A.; Haga, C.; Matsui, T.; Machimura, T.; Hayashi, K.; Sugita, S.; Takagi, H. An end to end process development for UAV-SfM based forest monitoring: Individual tree detection, species classification and carbon dynamics simulation. Forests 2019, 10, 680. [Google Scholar] [CrossRef]
- Miraki, M.; Sohrabi, H.; Fatehi, P. Detection of mistletoe infected trees using UAV high spatial resolution images. J. Plant Dis. Prot. 2021, 128, 1679–1689. [Google Scholar] [CrossRef]
- Abd-Elrahman, A.; Guan, Z.; Dalid, C.; Whitaker, V.; Britt, K.; Wilkinson, B.; Gonzalez, A. Automated canopy delineation and size metrics extraction for strawberry dry weight modeling using raster analysis of high-resolution imagery. Remote Sens. 2020, 12, 3632. [Google Scholar] [CrossRef]
- Valluvan, A.B.; Raj, R.; Pingale, R.; Jagarlapudi, A. Canopy height estimation using drone-based RGB images. Smart Agric. Technol. 2023, 4, 100145. [Google Scholar] [CrossRef]
- Alface, A.B.; Pereira, S.B.; Filgueiras, R.; Cunha, F.F. Sugarcane spatial-temporal monitoring and crop coefficient estimation through NDVI. Rev. Bras. Eng. Agrícola E Ambient. 2019, 23, 330–335. [Google Scholar] [CrossRef]
- Hashemi-Beni, L.; Kurkalova, L.A.; Mulrooney, T.J.; Azubike, C.S. Combining Multiple Geospatial Data for Estimating Aboveground Biomass in North Carolina Forests. Remote Sens. 2021, 13, 2731. [Google Scholar] [CrossRef]
- Hashemi-Beni, L.; Gebrehiwot, A.; Karimoddini, A.; Shahbazi, A.; Dorbu, F. Deep convolutional neural networks for weeds and crops discrimination from UAS imagery. Front. Remote Sens. 2022, 3, 755939. [Google Scholar] [CrossRef]
- Aeberli, A.; Phinn, S.; Johansen, K.; Robson, A.; Lamb, D.W. Characterisation of Banana Plant Growth Using High-Spatiotemporal-Resolution Multispectral UAV Imagery. Remote Sens. 2023, 15, 679. [Google Scholar] [CrossRef]
- Mostafavi, M.A.; Beni, L.H.; Mallet, K.H. Geosimulation of geographic dynamics based on voronoi diagram. In Transactions on Computational Science IX; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Beni, L.H. Development of a 3D Kinetic Data Structure Adapted for a 3D Spatial Dynamic Field Simulation. Ph.D. Thesis, Laval University, Quebec City, QC, Canada, 2009. [Google Scholar]
- Hashim, H.; Latif, Z.A.; Adnan, N.A. Urban vegetation classification with NDVI threshold value method with very high resolution (VHR) Pleiades imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 237–240. [Google Scholar] [CrossRef]
- St. Peter, J.; Hogland, J.; Hebblewhite, M.; Hurley, M.A.; Hupp, N.; Proffitt, K. Linking phenological indices from digital cameras in idaho and montana to MODIS NDVI. Remote Sens. 2018, 10, 1612. [Google Scholar] [CrossRef]
- Reid, A.M.; Chapman, W.K.; Kranabetter, J.M.; Prescott, C.E. Response of lodgepole pine health to soil disturbance treatments in British Columbia, Canada. Can. J. For. Res. 2015, 45, 1045–1055. [Google Scholar] [CrossRef]
- Yang, J.; Xing, M.; Tan, Q.; Shang, J.; Song, Y.; Ni, X.; Wang, J.; Xu, M. Estimating effective leaf area index of winter wheat based on uav point cloud data. Drones 2023, 7, 299. [Google Scholar] [CrossRef]
- Chauhan, S.; Darvishzadeh, R.; Boschetti, M.; Nelson, A. Estimation of crop angle of inclination for lodged wheat using multi-sensor SAR data. Remote Sens. Environ. 2020, 236, 111488. [Google Scholar] [CrossRef]
- Chauhan, S.; Darvishzadeh, R.; Boschetti, M.; Pepe, M.; Nelson, A. Remote sensing-based crop lodging assessment: Current status and perspectives. ISPRS J. Photogramm. Remote Sens. 2019, 151, 124–140. [Google Scholar] [CrossRef]






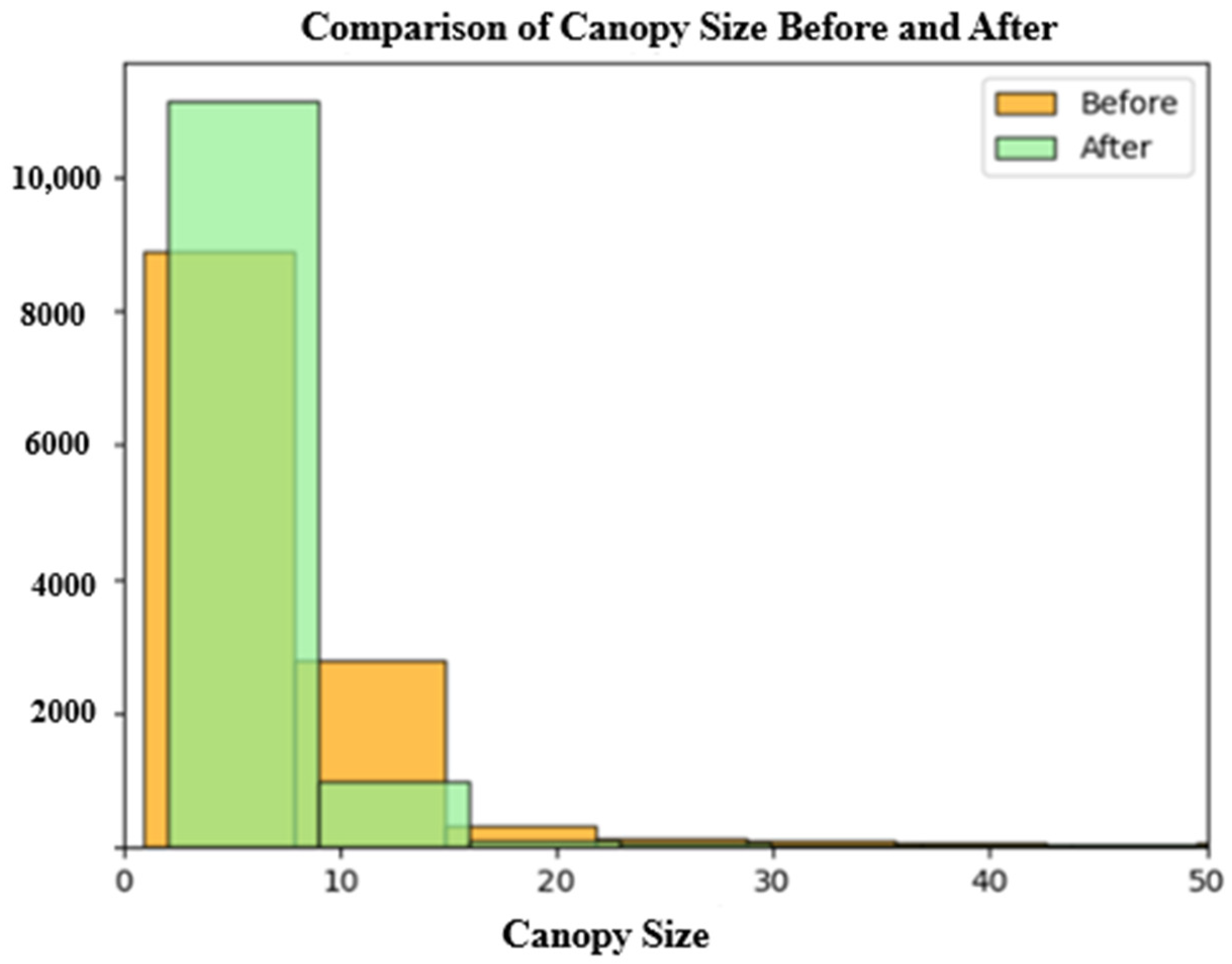
| Initial Canopy Size (ft) | Refined Canopy Size (ft) | |
|---|---|---|
| Count | 13,000 | 13,000 |
| Mean | 8.927187 | 5.781796 |
| Standard deviation | 13.858262 | 12.339383 |
| Minimum value | 0.901887 | 0.004016 |
| Maximum value | 348.572489 | 348.021710 |
| 25% | 4.666112 | 2.715247 |
| 50% | 6.177899 | 3.914694 |
| 75% | 8.341895 | 5.359943 |
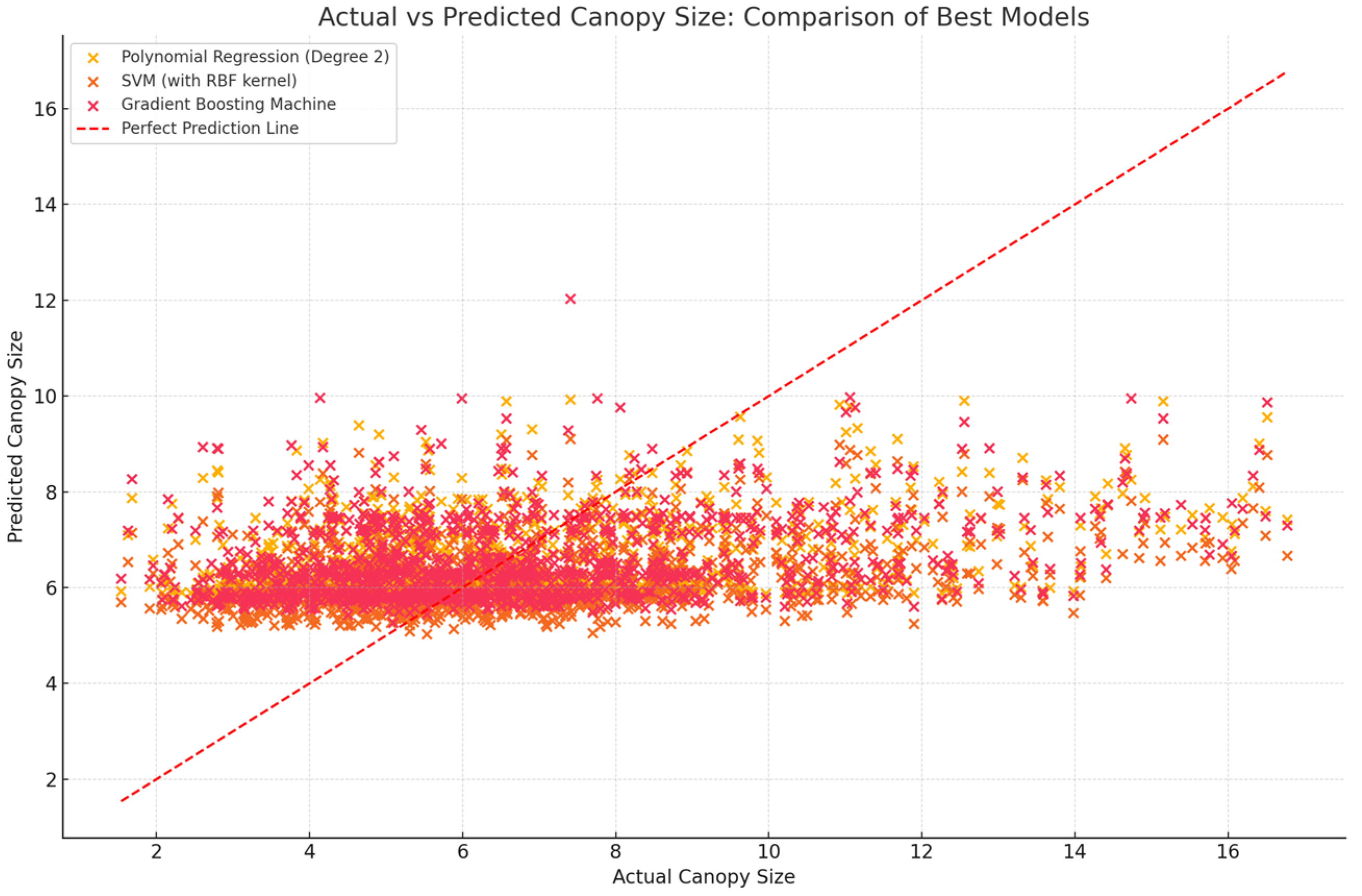
| Model | R-Squared (%) | Mean Absolute Error (MAE) |
|---|---|---|
| Polynomial Regression (Degree 2) | 11 | 2.036 |
| SVM (with RBF kernel) | 7 | 2.033 |
| Gradient Boosting Machine | 10 | 2.044 |
| Ridge | 9.6 | 2.058 |
| Linear Regression | 9.6 | 2.058 |
| OLS | 7.5 | 2.058 |
| Lasso | 0.7 | 2.133 |
| K-Nearest Neighbors | −4.0 | 2.197 |
| Random Forest | −9.0 | 2.232 |
| Decision tree | −78 | 2.940 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dorbu, F.; Hashemi-Beni, L. Detection of Individual Corn Crop and Canopy Delineation from Unmanned Aerial Vehicle Imagery. Remote Sens. 2024, 16, 2679. https://doi.org/10.3390/rs16142679
Dorbu F, Hashemi-Beni L. Detection of Individual Corn Crop and Canopy Delineation from Unmanned Aerial Vehicle Imagery. Remote Sensing. 2024; 16(14):2679. https://doi.org/10.3390/rs16142679
Chicago/Turabian StyleDorbu, Freda, and Leila Hashemi-Beni. 2024. "Detection of Individual Corn Crop and Canopy Delineation from Unmanned Aerial Vehicle Imagery" Remote Sensing 16, no. 14: 2679. https://doi.org/10.3390/rs16142679
APA StyleDorbu, F., & Hashemi-Beni, L. (2024). Detection of Individual Corn Crop and Canopy Delineation from Unmanned Aerial Vehicle Imagery. Remote Sensing, 16(14), 2679. https://doi.org/10.3390/rs16142679










