Potential Legacy of SWOT Mission for the Estimation of Flow–Duration Curves
Abstract
1. Introduction
2. Materials and Methods
2.1. GRDC River Flow Data Processing
- Selected GRDC river gauge stations must belong to river reaches wider than 100 m.
- The number of consecutive daily river flow records must be equal or larger than 10 years. In the case of small random gaps along the river flow series, up to three consecutive days, we filled in missing values through linear interpolation. In all other cases, when the series showed longer gaps, the river gauge station was discarded from the analysis.
- A GRDC river gauge station was considered to belong to the river network when the nearest river reach intersected a circular buffer area with 1 km radius area, centered on the station spatial coordinates.
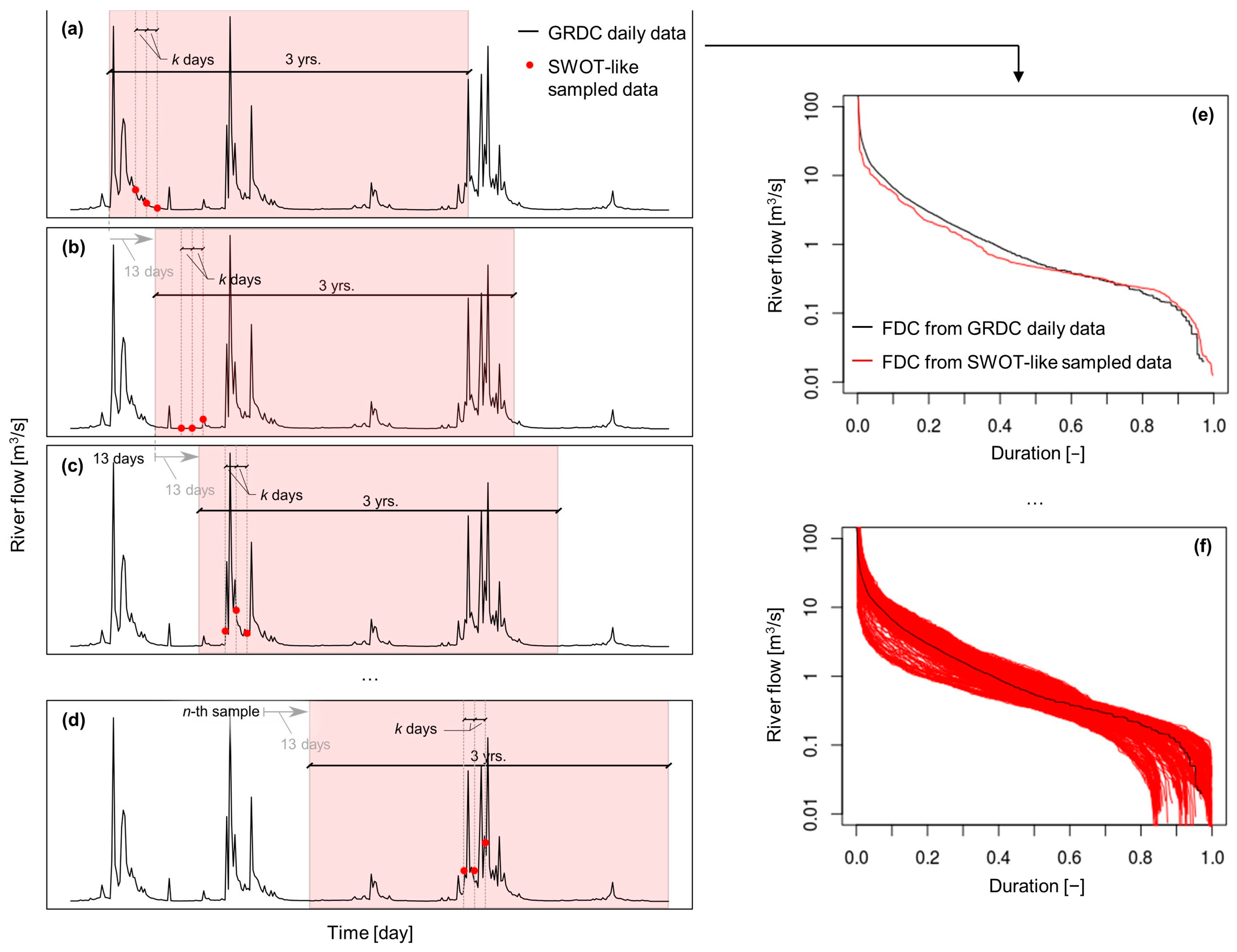
2.2. SWOT-like River Flow Data Generation
2.3. Estimation of Flow–Duration Curves from SWOT-like River Flow Data
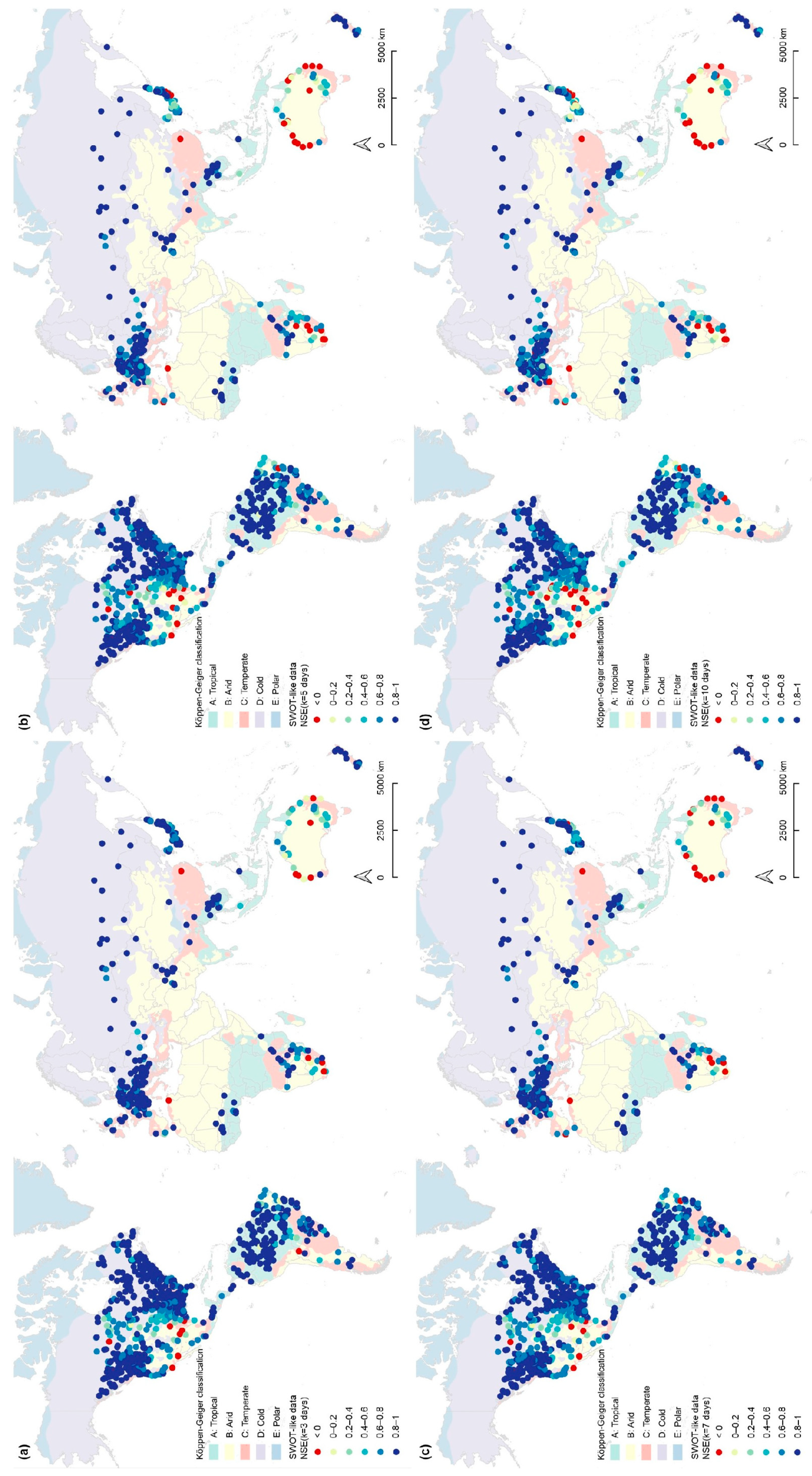
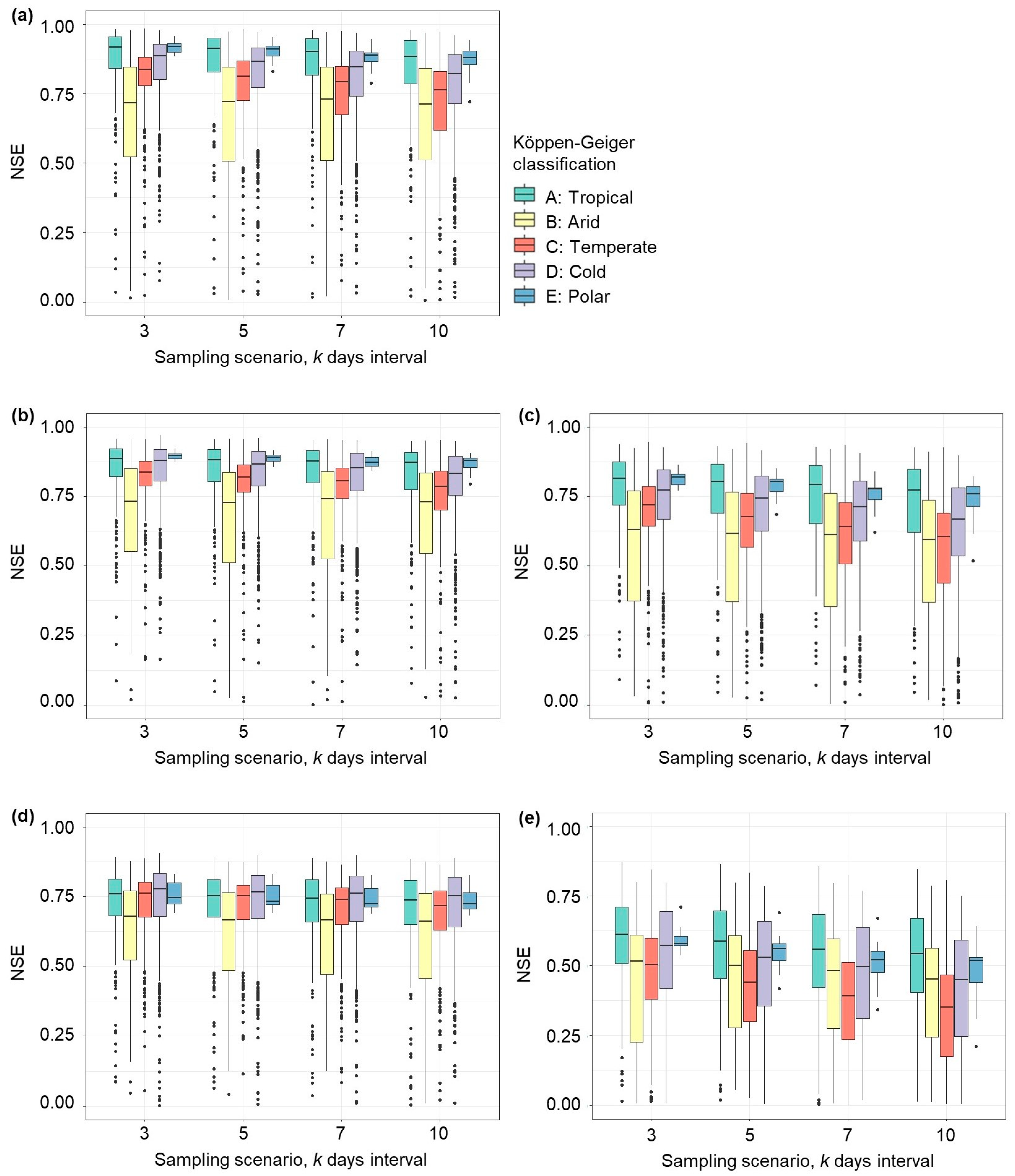
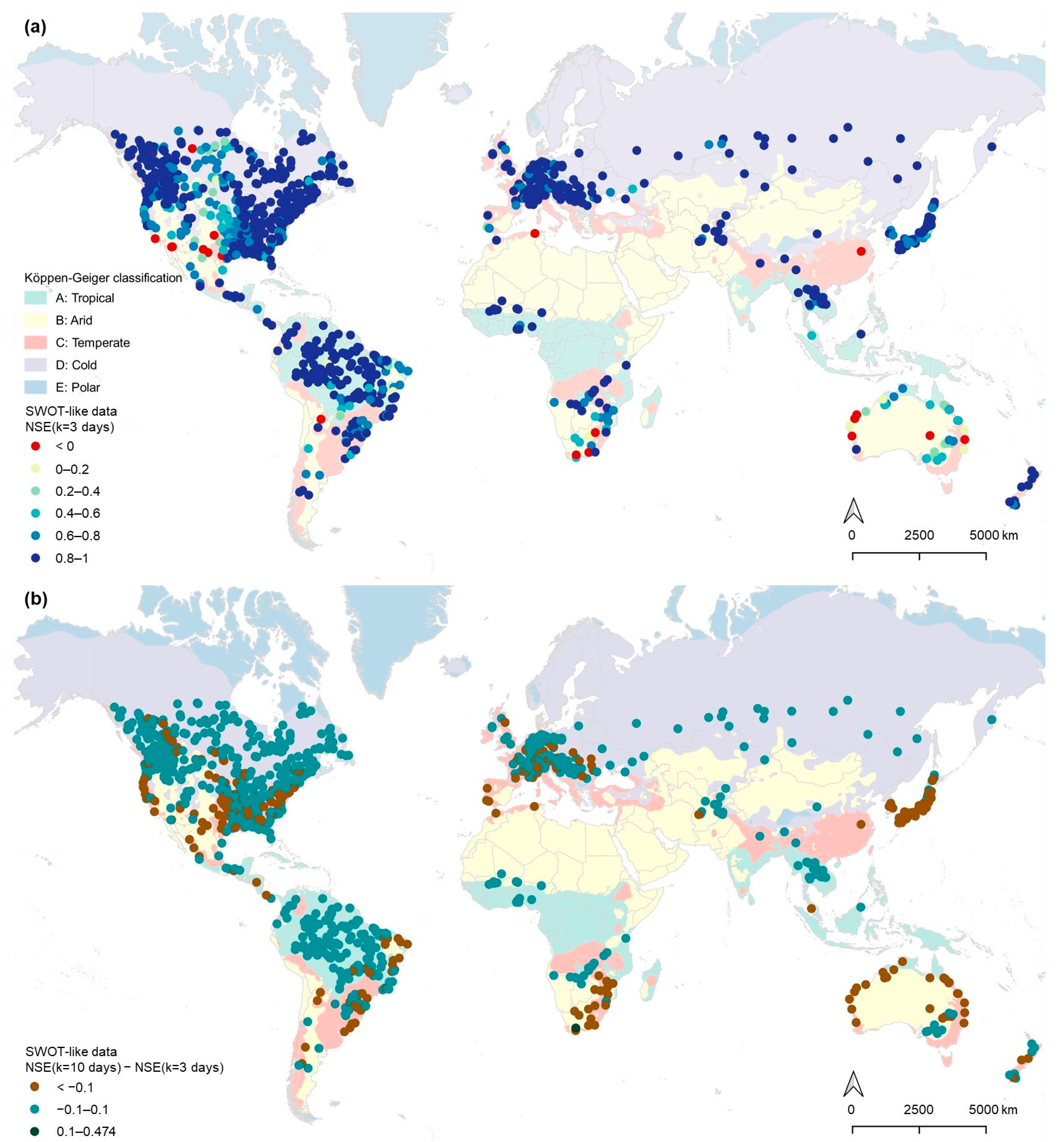
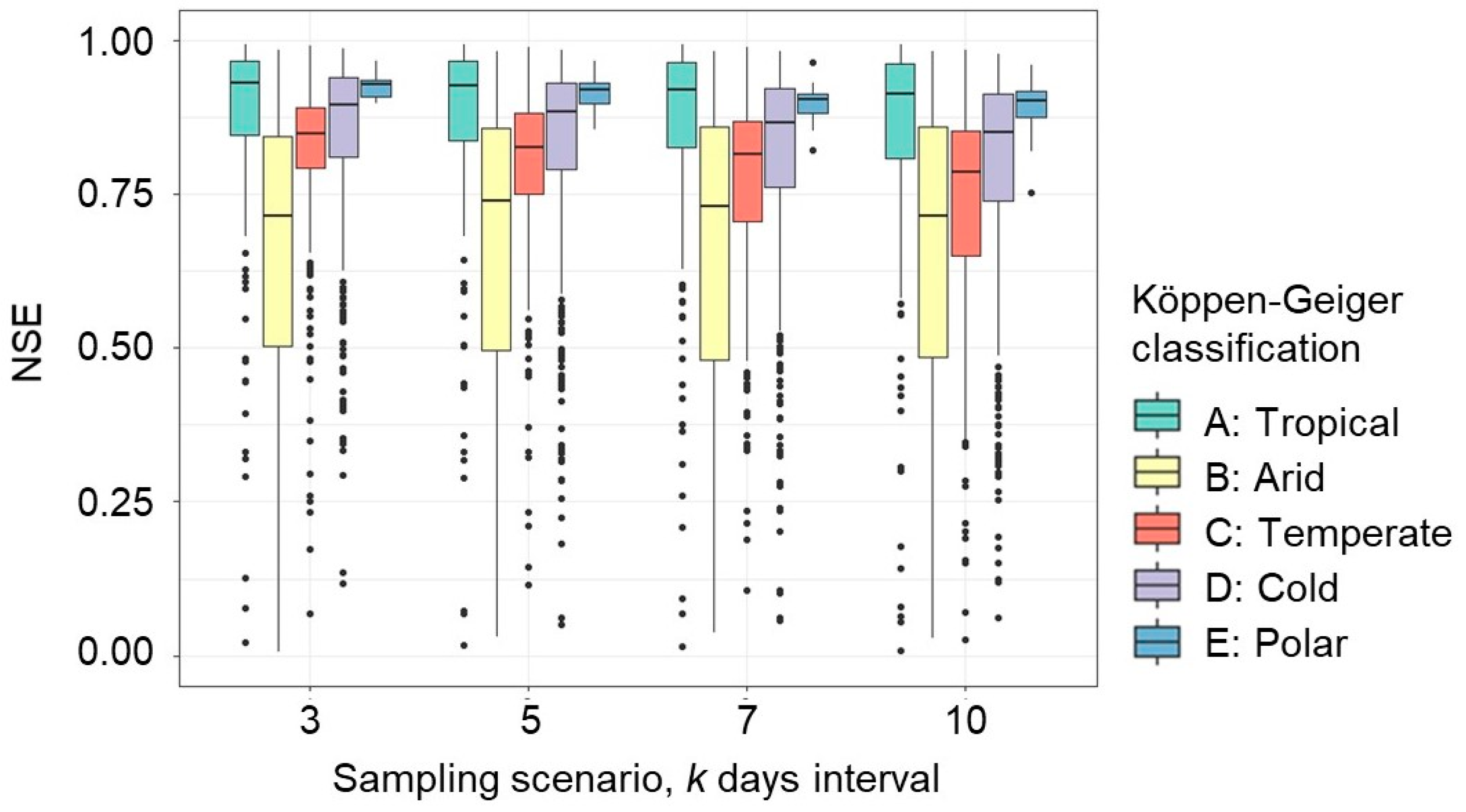
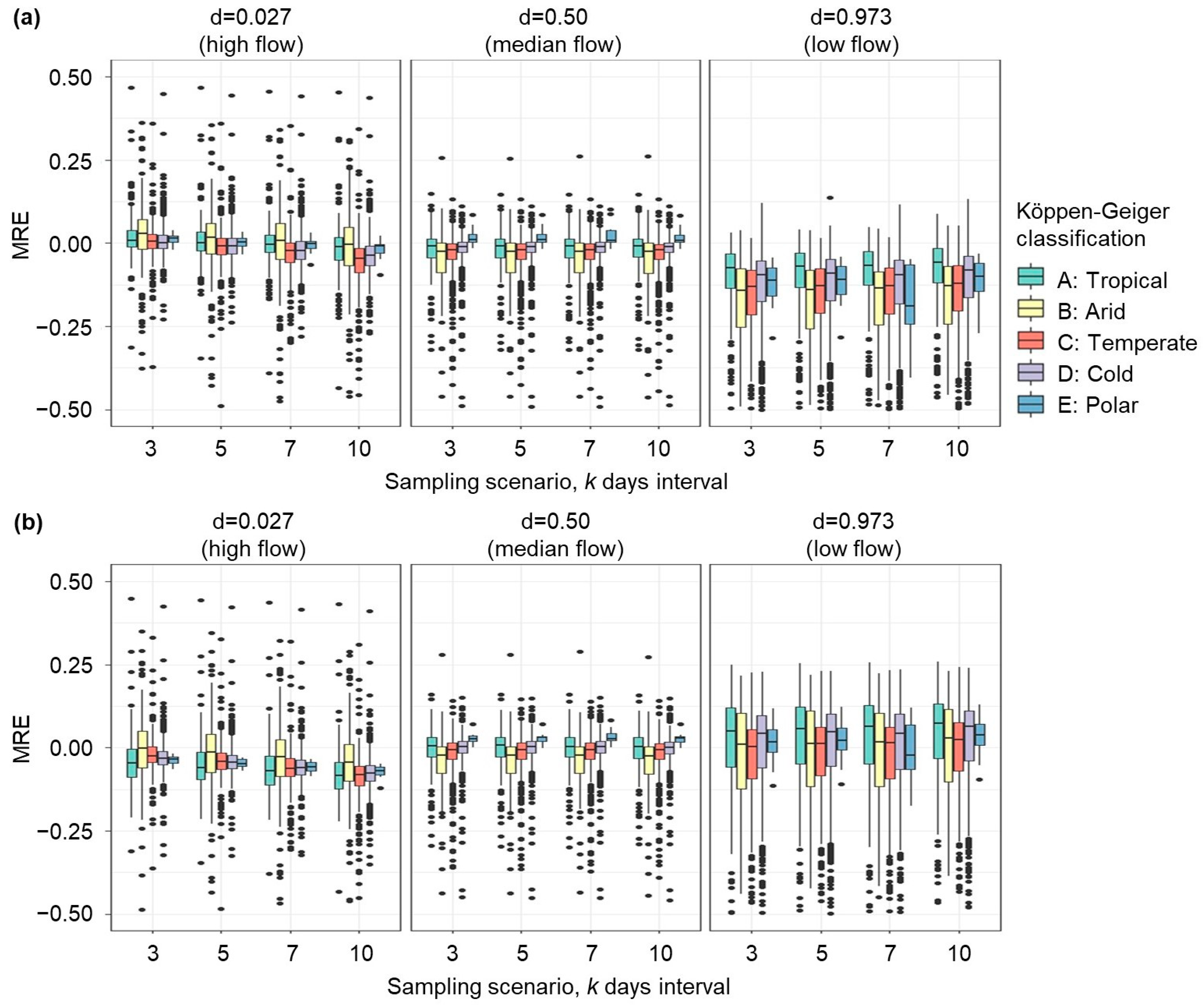
3. Results and Discussion
3.1. GRDC-Based FDCs Compliant with SWOT Mission Features
3.2. Creation of SWOT-like FDCs and Performance Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A



References
- Krabbenhoft, C.A.; Allen, G.H.; Lin, P.; Godsey, S.E.; Allen, D.C.; Ryan, M.; Delvecchia, A.G.; Fritz, K.M.; Shanafield, M.; Burgin, A.J.; et al. Assessing Placement Bias of the Global River Gauge Network. Nat. Sustain. 2022, 5, 586–592. [Google Scholar] [CrossRef]
- Hall, J.; Arheimer, B.; Borga, M.; Brazdil, R.; Claps, P.; Kiss, A.; Kjeldsen, T.R.; Kriauciuniene, J.; Kundzewicz, Z.W.; Lang, M.; et al. Understanding Flood Regime Changes in Europe: A State-of-the-Art Assessment. Hydrol. Earth Syst. Sci. 2014, 18, 2735–2772. [Google Scholar] [CrossRef]
- Tourian, M.J.; Schwatke, C.; Sneeuw, N. River Discharge Estimation at Daily Resolution from Satellite Altimetry over an Entire River Basin. J. Hydrol. 2017, 546, 230–247. [Google Scholar] [CrossRef]
- Tourian, M.J.; Sneeuw, N.; Bárdossy, a. A Quantile Function Approach to Discharge Estimation from Satellite Altimetry (ENVISAT). Water Resour. Res. 2013, 49, 4174–4186. [Google Scholar] [CrossRef]
- Blöschl, G.; Bierkens, M.F.P.; Chambel, A.; Cudennec, C.; Destouni, G.; Fiori, A.; Kirchner, J.W.; Mcdonnell, J.J.; Savenije, H.G.; Sivapalan, M.; et al. Twenty-Three Unsolved Problems in Hydrology (UPH)—A Community Perspective. Hydrol. Sci. J. 2019, 64, 1141–1158. [Google Scholar] [CrossRef]
- Vogel, R.M.; Fennessey, N.M. Flow-Duration Curves. I: New Interpretation and Confidence Intervals. J. Water Resour. Plan. Manag. 1994, 120, 485–504. [Google Scholar] [CrossRef]
- Castellarin, A.; Galeati, G.; Brandimarte, L.; Montanari, A.; Brath, A. Regional Flow-Duration Curves: Reliability for Ungauged Basins. Adv. Water Resour. 2004, 27, 953–965. [Google Scholar] [CrossRef]
- Hughes, D.A.; Smakhtin, V. Daily Flow Time Series Patching or Extension: A Spatial Interpolation Approach Based on Flow Duration Curves. Hydrol. Sci. J. 1996, 41, 851–871. [Google Scholar] [CrossRef]
- Pugliese, A.; Persiano, S.; Bagli, S.; Mazzoli, P.; Parajka, J.; Arheimer, B.; Capell, R.; Montanari, A.; Blöschl, G.; Castellarin, A. A Geostatistical Data-Assimilation Technique for Enhancing Macro-Scale Rainfall—Runoff Simulations. Hydrol. Earth Syst. Sci. 2018, 22, 4633–4648. [Google Scholar] [CrossRef]
- Ceola, S.; Pugliese, A.; Ventura, M.; Galeati, G.; Montanari, A.; Castellarin, A. Hydro-Power Production and Fish Habitat Suitability: Assessing Impact and Effectiveness of Ecological Flows at Regional Scale. Adv. Water Resour. 2018, 116, 29–39. [Google Scholar] [CrossRef]
- Yaeger, M.; Coopersmith, E.; Ye, S.; Cheng, L.; Viglione, A.; Sivapalan, M. Exploring the Physical Controls of Regional Patterns of Flow Duration Curves—Part 4: A Synthesis of Empirical Analysis, Process Modeling and Catchment Classification. Hydrol. Earth Syst. Sci. 2012, 16, 4483–4498. [Google Scholar] [CrossRef]
- Kroll, C.N.; Croteau, K.E.; Vogel, R.M. Hypothesis Tests for Hydrologic Alteration. J. Hydrol. 2015, 530, 117–126. [Google Scholar] [CrossRef]
- Vogel, R.M.; Fennessey, N.M. Flow Duration Curves II: A Review of Applications in Water Resources Planning. JAWRA J. Am. Water Resour. Assoc. 1995, 31, 1029–1039. [Google Scholar] [CrossRef]
- Castellarin, A. Regional Prediction of Flow-Duration Curves Using a Three-Dimensional Kriging. J. Hydrol. 2014, 513, 179–191. [Google Scholar] [CrossRef]
- Persiano, S.; Pugliese, A.; Aloe, A.; Skøien, J.O.; Castellarin, A.; Pistocchi, A. Streamflow Data Availability in Europe: A Detailed Dataset of Interpolated Flow-Duration Curves. Earth Syst. Sci. Data 2022, 14, 4435–4443. [Google Scholar] [CrossRef]
- Castellarin, A.; Vogel, R.M.; Brath, A. A Stochastic Index Flow Model of Flow Duration Curves. Water Resour. Res. 2004, 40, 1–10. [Google Scholar] [CrossRef]
- Castellarin, A. Probabilistic Envelope Curves for Design Flood Estimation at Ungauged Sites. Water Resour. Res. 2007, 43, 1–12. [Google Scholar] [CrossRef]
- Ganora, D.; Claps, P.; Laio, F.; Viglione, A. An Approach to Estimate Nonparametric Flow Duration Curves in Ungauged Basins. Water Resour. Res. 2009, 45, 1–10. [Google Scholar] [CrossRef]
- Pugliese, a.; Castellarin, a.; Brath, a. Geostatistical Prediction of Flow–Duration Curves in an Index-Flow Framework. Hydrol. Earth Syst. Sci. 2014, 18, 3801–3816. [Google Scholar] [CrossRef]
- Gleason, C.J.; Durand, M.T. Remote Sensing of River Discharge: A Review and a Framing for the Discipline. Remote Sens. 2020, 12, 1107. [Google Scholar] [CrossRef]
- Rodriguez, E. Surface Water and Ocean Topography Mission (SWOT) Project Science Requirements Document; JPL D-61923; California Institute of Technology: Pasadena, CA, USA, 2015. [Google Scholar]
- Durand, M.; Gleason, C.J.; Pavelsky, T.M.; Prata, R.; Frasson, D.M.; Turmon, M.; David, C.H.; Altenau, E.H.; Tebaldi, N.; Larnier, K.; et al. A Framework for Estimating Global River Discharge From the Surface Water and Ocean Topography Satellite Mission Water Resources Research. Water Resour. Res. 2023, 59, e2021WR031614. [Google Scholar] [CrossRef]
- Fu, L.L.; Pavelsky, T.; Cretaux, J.F.; Morrow, R.; Farrar, J.T.; Vaze, P.; Sengenes, P.; Shiffer, N.V.; Baron, A.S.; Picot, N.; et al. Special Section: The Surface Water and Ocean Topography Mission: A Breakthrough in Radar Remote Sensing of the Ocean and Land Surface Water. Geophys. Res. Lett. 2024, 51, e2023GL107652. [Google Scholar] [CrossRef]
- Durand, M.; Gleason, C.J.; Garambois, P.A.; Bjerklie, D.; Smith, L.C.; Roux, H.; Rodriguez, E.; Bates, P.D.; Pavelsky, T.M.; Monnier, J.; et al. An Intercomparison of Remote Sensing River Discharge Estimation Algorithms From Measurements of River Height, Width, and Slope. Water Resour. Res. 2016, 52, 4527–4549. [Google Scholar] [CrossRef]
- Prata, R.; Frasson, D.M.; Durand, M.T.; Larnier, K. Exploring the Factors Controlling the Error Characteristics of the Surface Water and Ocean Topography Mission Discharge Estimates. Water Resour. Res. 2021, 57, e2020WR028519. [Google Scholar] [CrossRef]
- Frasson, R.P.D.M.; Turmon, M.J.; Durand, M.T.; Cédric, D.H. Estimating the Relative Impact of Measurement, Parameter, and Flow Law Errors on Discharge from the Surface Water and Ocean Topography Mission. J. Hydrometeorol. 2023, 24, 425–443. [Google Scholar] [CrossRef]
- Domeneghetti, A.; Tarpanelli, A.; Grimaldi, L.; Brath, A. Flow Duration Curve from Satellite: Potential of a Lifetime SWOT Mission. Remote Sens. 2018, 10, 1107. [Google Scholar] [CrossRef]
- Biancamaria, S.; Lettenmaier, D.P.; Pavelsky, T.M. The SWOT Mission and Its Capabilities for Land Hydrology. Surv. Geophys. 2016, 37, 307–337. [Google Scholar] [CrossRef]
- Andreadis, K.M.; Schumann, G.J.P.; Pavelsky, T. A Simple Global River Bankfull Width and Depth Database. Water Resour. Res. 2013, 49, 7164–7168. [Google Scholar] [CrossRef]
- Leopold, L.B. A View of the River; Harvard University Press, Ed.; Harvard University Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Beck, H.E.; Zimmermann, N.E.; Mcvicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and Future Köppen-Geiger Climate Classification Maps at 1 -Km Resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef]
| SWOT-like River Flow Reconstruction | Bias | Random Error | Sampling Recurrence, k [Days] | |
|---|---|---|---|---|
| No perturbation | QSWOT,0,0,3 | − | − | 3 |
| QSWOT,0,0,5 | − | − | 5 | |
| QSWOT,0,0,7 | − | − | 7 | |
| QSWOT,0,0,10 | − | − | 10 | |
| No perturbation and random error | QSWOT,0,20,3 | − | 20% | 3 |
| QSWOT,0,20,5 | − | 20% | 5 | |
| QSWOT,0,20,7 | − | 20% | 7 | |
| QSWOT,0,20,10 | − | 20% | 10 | |
| Minor underestimation and random error | QSWOT,−15,20,3 | −15% | 20% | 3 |
| QSWOT,−15,20,5 | −15% | 20% | 5 | |
| QSWOT,−15,20,7 | −15% | 20% | 7 | |
| QSWOT,−15,20,10 | −15% | 20% | 10 | |
| Minor overestimation and random error | QSWOT,15,20,3 | +15% | 20% | 3 |
| QSWOT,15,20,5 | +15% | 20% | 5 | |
| QSWOT,15,20,7 | +15% | 20% | 7 | |
| QSWOT,15,20,10 | +15% | 20% | 10 | |
| Major underestimation and random error | QSWOT,−30,20,3 | −30% | 20% | 3 |
| QSWOT,−30,20,5 | −30% | 20% | 5 | |
| QSWOT,−30,20,7 | −30% | 20% | 7 | |
| QSWOT,30,20,10 | −30% | 20% | 10 | |
| Major overestimation and random error | QSWOT,30,20,3 | +30% | 20% | 3 |
| QSWOT,30,20,5 | +30% | 20% | 5 | |
| QSWOT,30,20,7 | +30% | 20% | 7 | |
| QSWOT,30,20,10 | +30% | 20% | 10 | |
| Climatic Classification | Number of River Gauge Stations | Series Length 1 (Years) | Median River Flow 1 (m3/s) | Mean Annual River 1 Flow (m3/s) |
|---|---|---|---|---|
| Tropical (A) | 211 | 35.59 | 3654.97 | 4124.62 |
| Arid (B) | 109 | 63.28 | 160.05 | 251.02 |
| Temperate (C) | 336 | 66.12 | 405.44 | 554.11 |
| Cold (D) | 533 | 68.61 | 361.93 | 437.65 |
| Polar (E) | 11 | 81 | 63.32 | 85.09 |
| SWOT-like River Flow Reconstruction | NSE | |||||
|---|---|---|---|---|---|---|
| Tropical (A) | Arid (B) | Temperate (C) | Cold (D) | Polar (E) | ||
| No perturbation | QSWOT,0,0,3 | 0.93 | 0.67 | 0.85 | 0.90 | 0.93 |
| QSWOT,0,0,5 | 0.93 | 0.65 | 0.82 | 0.89 | 0.92 | |
| QSWOT,0,0,7 | 0.92 | 0.61 | 0.80 | 0.87 | 0.91 | |
| QSWOT,0,0,10 | 0.91 | 0.56 | 0.78 | 0.85 | 0.90 | |
| No perturbation and random error | QSWOT,0,20,3 | 0.92 | 0.67 | 0.84 | 0.89 | 0.92 |
| QSWOT,0,20,5 | 0.91 | 0.64 | 0.80 | 0.87 | 0.91 | |
| QSWOT,0,20,7 | 0.90 | 0.59 | 0.78 | 0.85 | 0.89 | |
| QSWOT,0,20,10 | 0.88 | 0.57 | 0.75 | 0.82 | 0.88 | |
| Minor estimation and random error | QSWOT,−15,20,3 | 0.89 | 0.70 | 0.84 | 0.88 | 0.90 |
| QSWOT,−15,20,5 | 0.88 | 0.68 | 0.82 | 0.87 | 0.89 | |
| QSWOT,−15,20,7 | 0.88 | 0.67 | 0.80 | 0.85 | 0.87 | |
| QSWOT,−15,20,10 | 0.87 | 0.64 | 0.78 | 0.83 | 0.88 | |
| Minor overestimation and random error | QSWOT,15,20,3 | 0.81 | 0.52 | 0.71 | 0.77 | 0.82 |
| QSWOT,15,20,5 | 0.80 | 0.47 | 0.67 | 0.73 | 0.80 | |
| QSWOT,15,20,7 | 0.79 | 0.44 | 0.62 | 0.70 | 0.78 | |
| QSWOT,15,20,10 | 0.76 | 0.38 | 0.58 | 0.66 | 0.76 | |
| Major underestimation and random error | QSWOT,−30,20,3 | 0.75 | 0.66 | 0.76 | 0.78 | 0.75 |
| QSWOT,−30,20,5 | 0.75 | 0.66 | 0.75 | 0.77 | 0.73 | |
| QSWOT,−30,20,7 | 0.74 | 0.63 | 0.73 | 0.76 | 0.73 | |
| QSWOT,−30,20,10 | 0.73 | 0.63 | 0.71 | 0.75 | 0.72 | |
| Major overestimation and random error | QSWOT,30,20,3 | 0.59 | 0.23 | 0.49 | 0.55 | 0.58 |
| QSWOT,30,20,5 | 0.56 | 0.17 | 0.41 | 0.50 | 0.56 | |
| QSWOT,30,20,7 | 0.53 | 0.13 | 0.33 | 0.45 | 0.52 | |
| QSWOT,30,20,10 | 0.50 | 0.06 | 0.22 | 0.37 | 0.52 | |
| SWOT-like River Flow Reconstruction | MRE (d = 0.50; Median Flow) | |||||
|---|---|---|---|---|---|---|
| Tropical (A) | Arid (B) | Temperate (C) | Cold (D) | Polar (E) | ||
| No perturbation | QSWOT,0,0,3 | −0.01 | −0.03 | −0.02 | −0.01 | 0.01 |
| QSWOT,0,0,5 | −0.01 | −0.03 | −0.02 | −0.01 | 0.01 | |
| QSWOT,0,0,7 | −0.01 | −0.03 | −0.02 | −0.01 | 0.01 | |
| QSWOT,0,0,10 | −0.01 | −0.03 | −0.02 | −0.01 | 0.01 | |
| No perturbation and random error | QSWOT,0,20,3 | 0.01 | −0.03 | −0.01 | 0.00 | 0.03 |
| QSWOT,0,20,5 | 0.01 | −0.04 | −0.01 | 0.00 | 0.03 | |
| QSWOT,0,20,7 | 0.00 | −0.03 | −0.01 | 0.00 | 0.03 | |
| QSWOT,0,20,10 | 0.00 | −0.03 | −0.01 | 0.00 | 0.03 | |
| Minor underestimation and random error | QSWOT,−15,20,3 | 0.16 | 0.12 | 0.15 | 0.16 | 0.18 |
| QSWOT,−15,20,5 | 0.16 | 0.12 | 0.15 | 0.16 | 0.18 | |
| QSWOT,−15,20,7 | 0.16 | 0.12 | 0.15 | 0.16 | 0.18 | |
| QSWOT,−15,20,10 | 0.16 | 0.12 | 0.15 | 0.16 | 0.18 | |
| Minor overestimation and random error | QSWOT,15,20,3 | −0.15 | −0.19 | −0.16 | −0.15 | −0.12 |
| QSWOT,15,20,5 | −0.15 | −0.19 | −0.16 | −0.15 | −0.12 | |
| QSWOT,15,20,7 | −0.15 | −0.19 | −0.16 | −0.15 | −0.12 | |
| QSWOT,15,20,10 | −0.15 | −0.19 | −0.16 | −0.15 | −0.12 | |
| Major underestimation and random error | QSWOT,−30,20,3 | 0.31 | 0.28 | 0.30 | 0.31 | 0.33 |
| QSWOT,−30,20,5 | 0.31 | 0.28 | 0.30 | 0.31 | 0.33 | |
| QSWOT,−30,20,7 | 0.31 | 0.28 | 0.30 | 0.31 | 0.33 | |
| QSWOT,−30,20,10 | 0.31 | 0.28 | 0.30 | 0.31 | 0.33 | |
| Major overestimation and random error | QSWOT,30,20,3 | −0.30 | −0.34 | −0.32 | −0.30 | −0.27 |
| QSWOT,30,20,5 | −0.30 | −0.34 | −0.32 | −0.30 | −0.28 | |
| QSWOT,30,20,7 | −0.30 | −0.34 | −0.32 | −0.30 | −0.27 | |
| QSWOT,30,20,10 | −0.30 | −0.34 | −0.32 | −0.31 | −0.28 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domeneghetti, A.; Ceola, S.; Pugliese, A.; Persiano, S.; Palazzoli, I.; Castellarin, A.; Marinelli, A.; Brath, A. Potential Legacy of SWOT Mission for the Estimation of Flow–Duration Curves. Remote Sens. 2024, 16, 2607. https://doi.org/10.3390/rs16142607
Domeneghetti A, Ceola S, Pugliese A, Persiano S, Palazzoli I, Castellarin A, Marinelli A, Brath A. Potential Legacy of SWOT Mission for the Estimation of Flow–Duration Curves. Remote Sensing. 2024; 16(14):2607. https://doi.org/10.3390/rs16142607
Chicago/Turabian StyleDomeneghetti, Alessio, Serena Ceola, Alessio Pugliese, Simone Persiano, Irene Palazzoli, Attilio Castellarin, Alberto Marinelli, and Armando Brath. 2024. "Potential Legacy of SWOT Mission for the Estimation of Flow–Duration Curves" Remote Sensing 16, no. 14: 2607. https://doi.org/10.3390/rs16142607
APA StyleDomeneghetti, A., Ceola, S., Pugliese, A., Persiano, S., Palazzoli, I., Castellarin, A., Marinelli, A., & Brath, A. (2024). Potential Legacy of SWOT Mission for the Estimation of Flow–Duration Curves. Remote Sensing, 16(14), 2607. https://doi.org/10.3390/rs16142607









