A Priori Estimation of Radar Satellite Interferometry’s Sensitivity for Landslide Monitoring in the Italian Emilia-Romagna Region
Abstract
1. Introduction
2. Materials and Methods
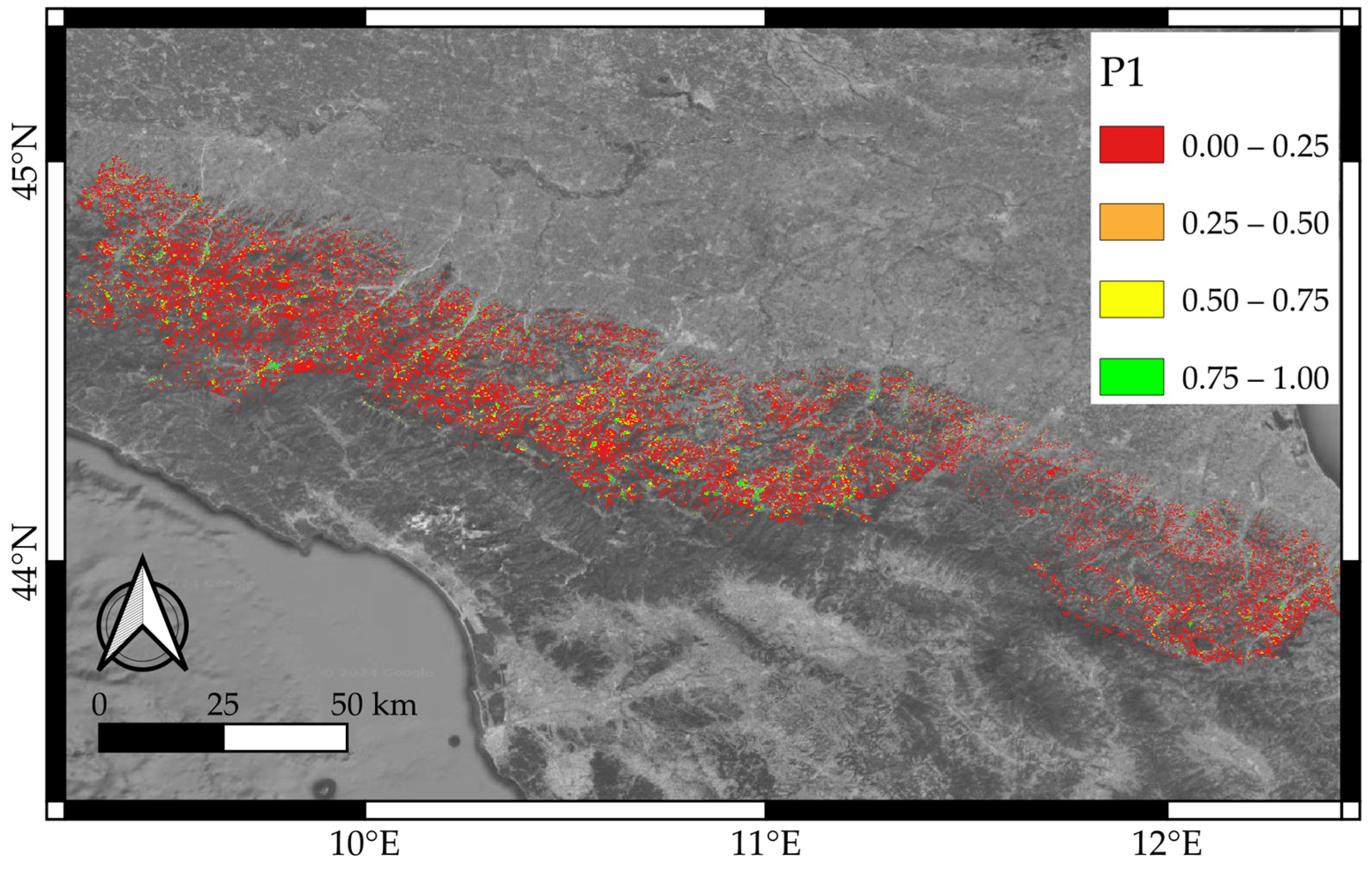
2.1. P1—SAR Land Cover Sensitivity
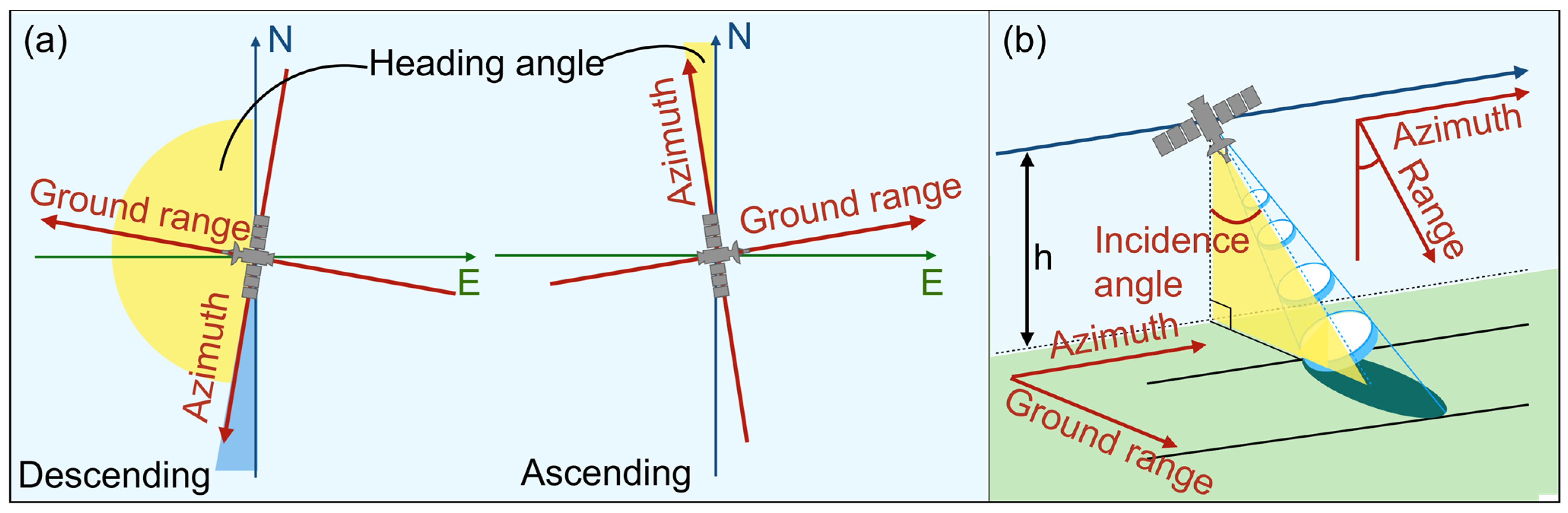
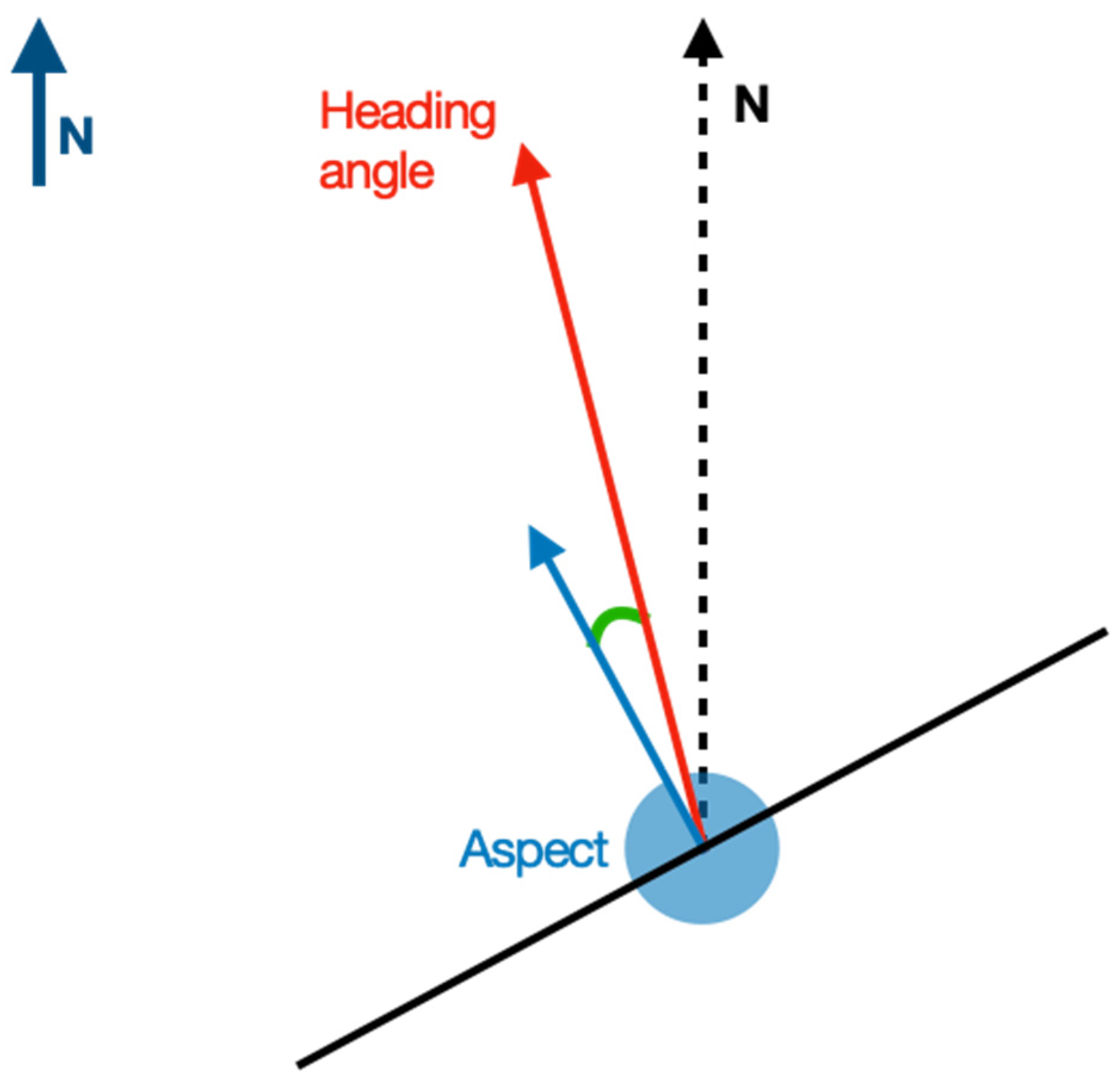
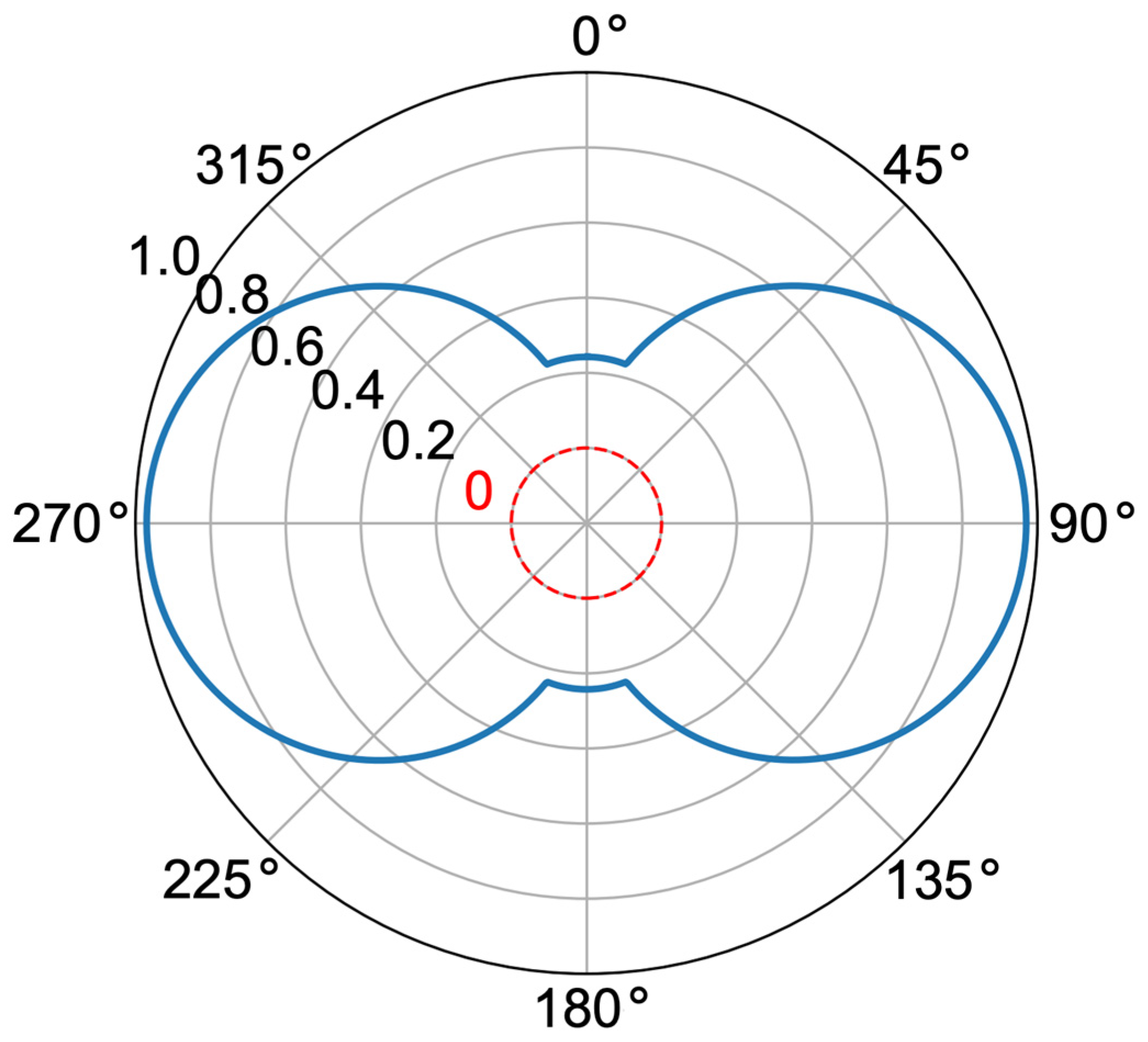
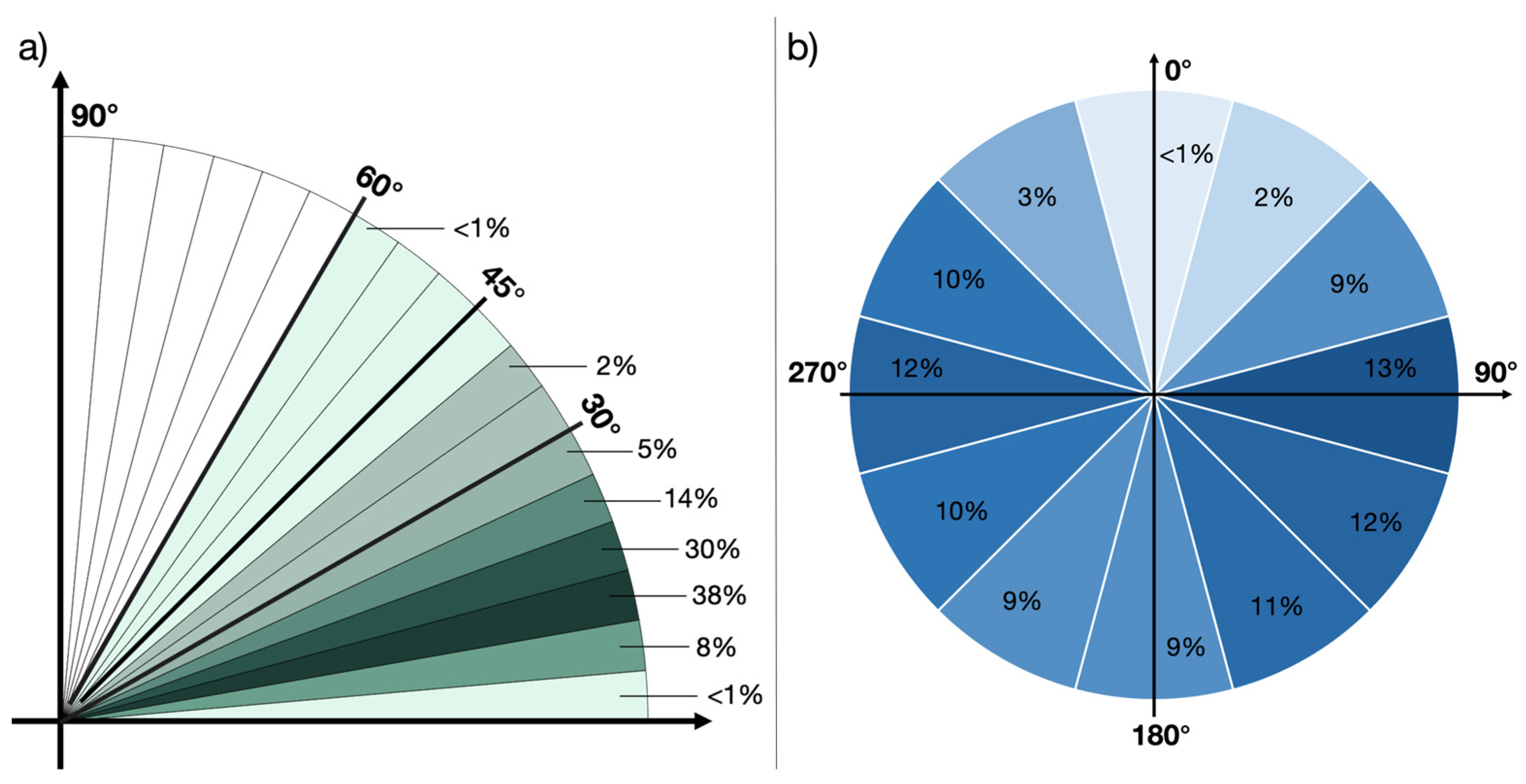
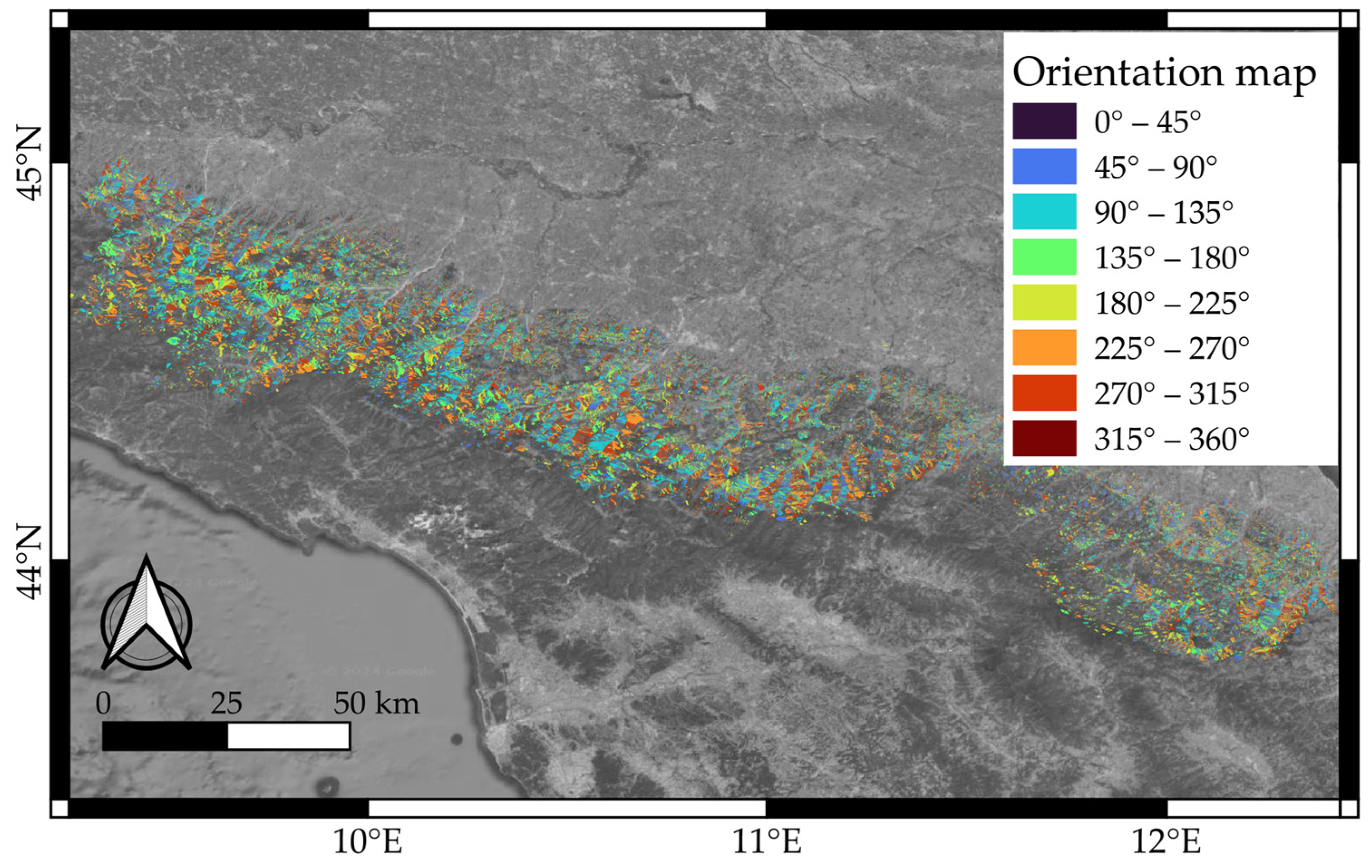
2.2. P2—A Dip Orientation Parameter
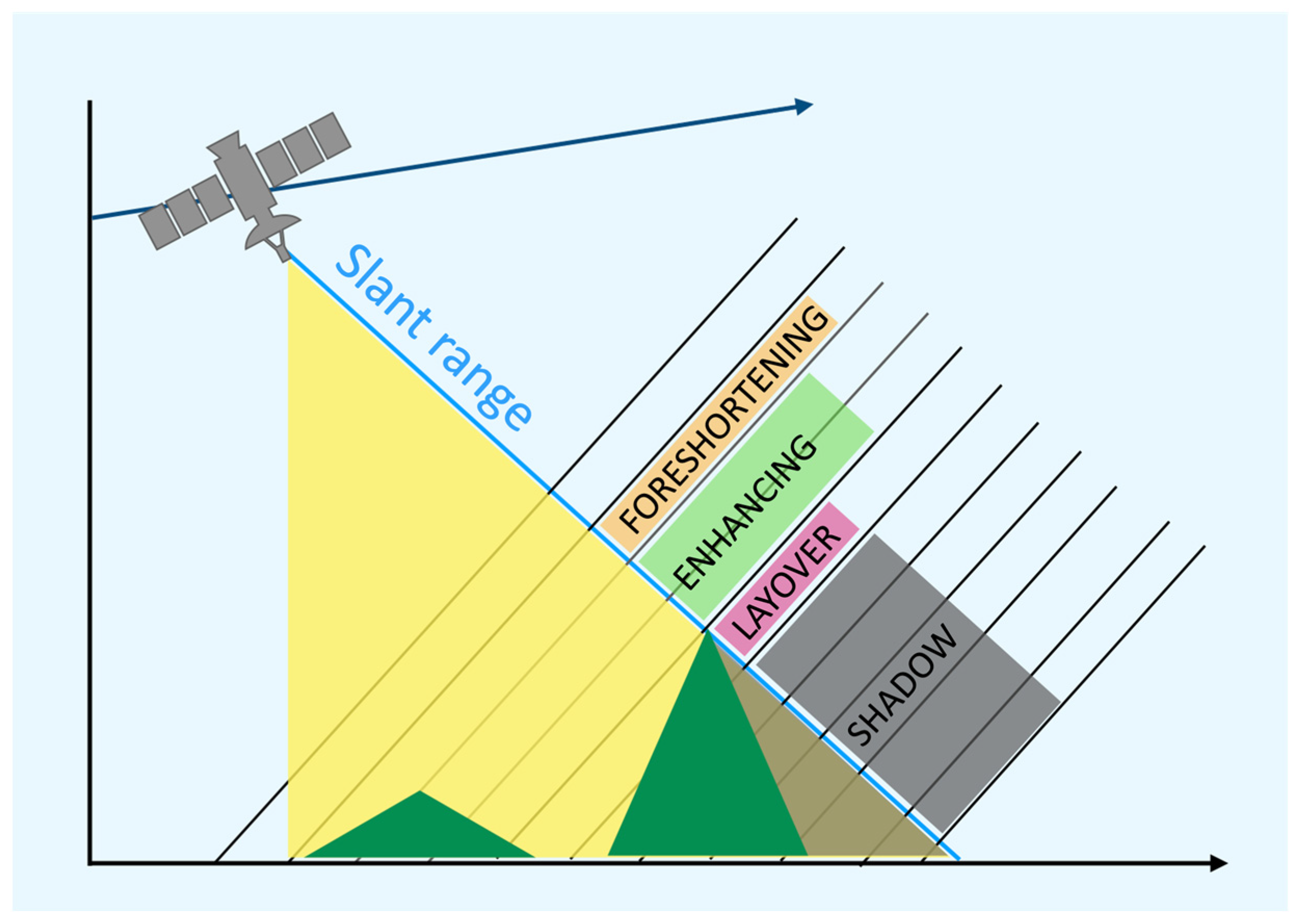
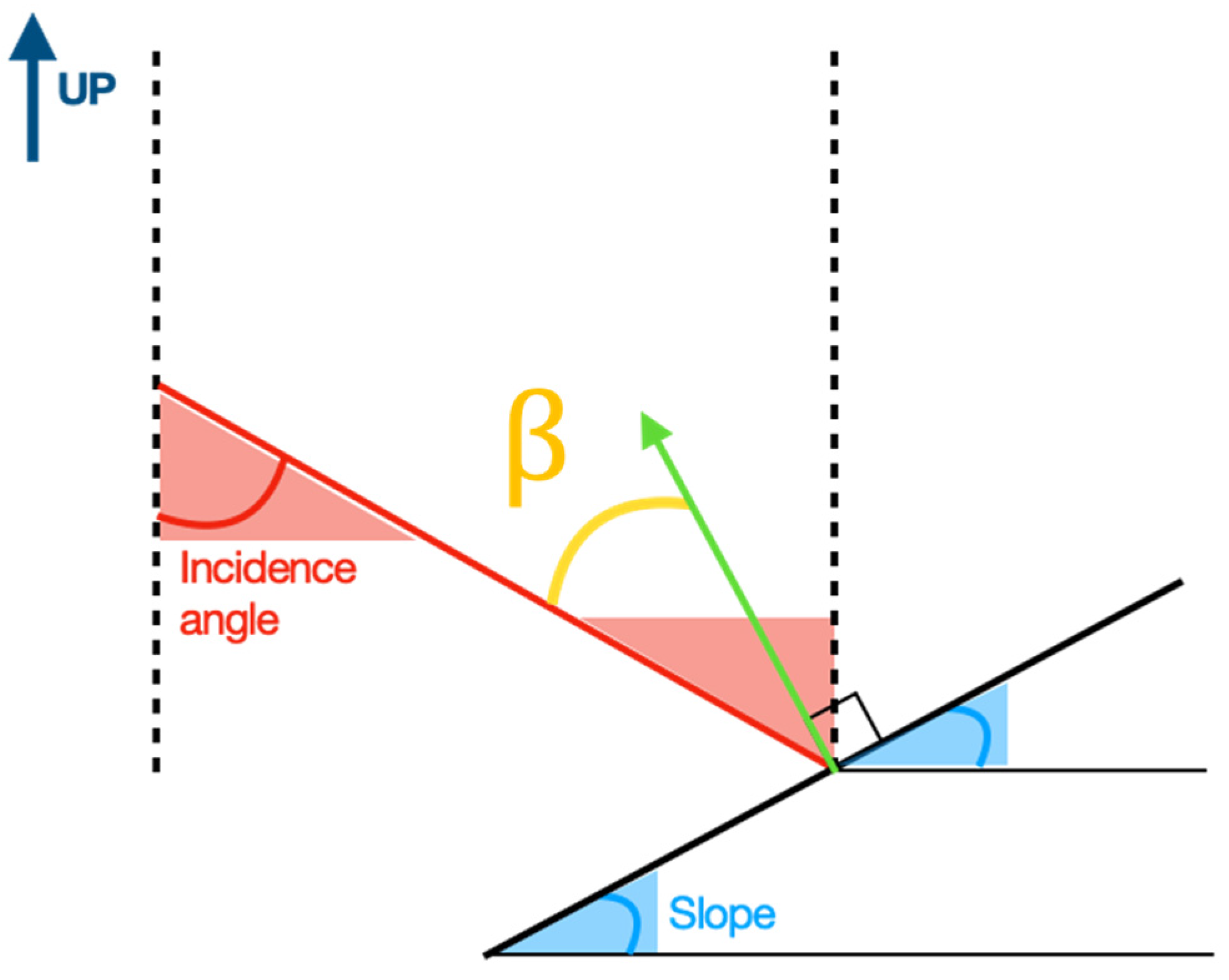
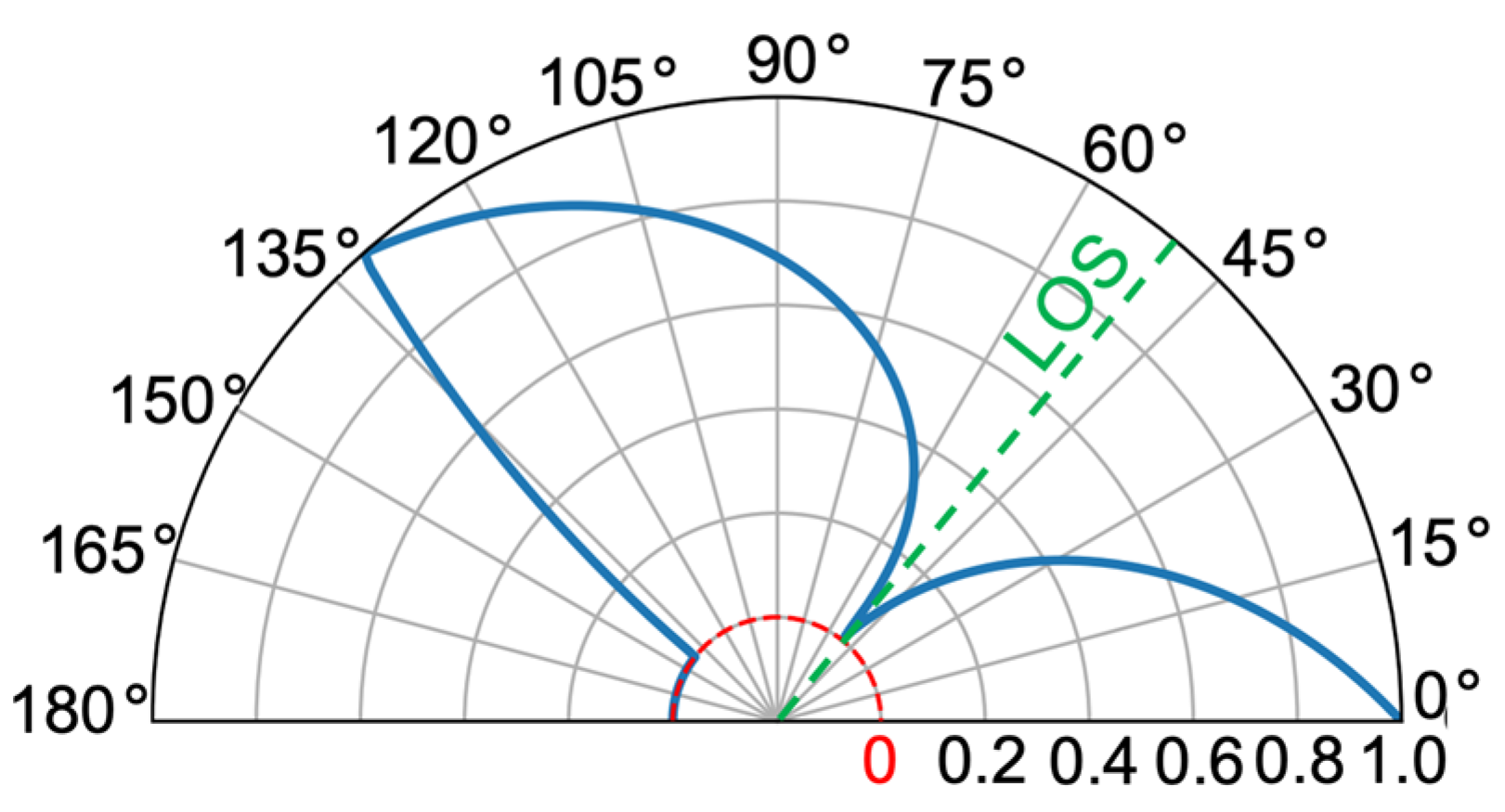
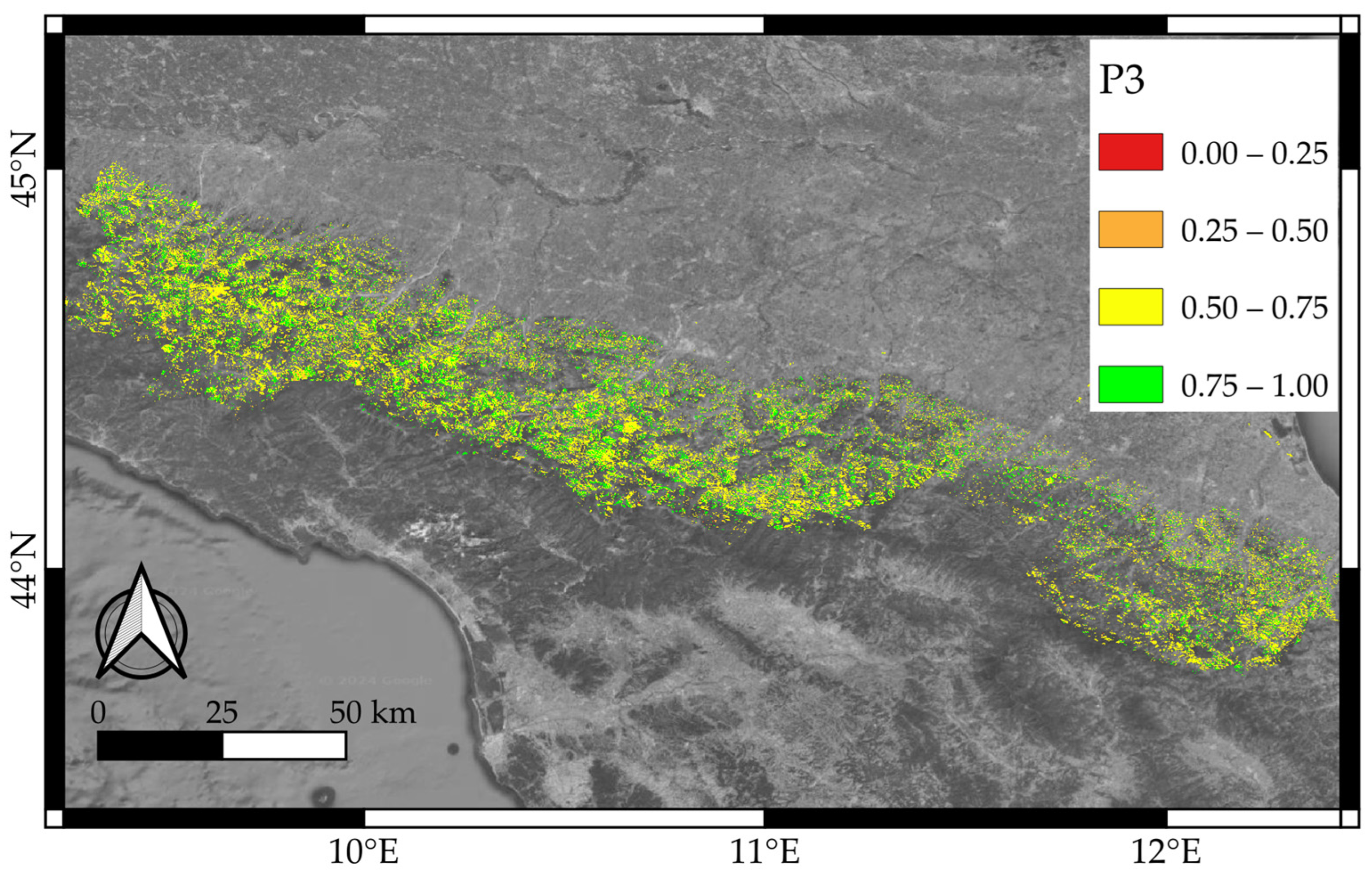
2.3. P3—A Slope Immersion Parameter
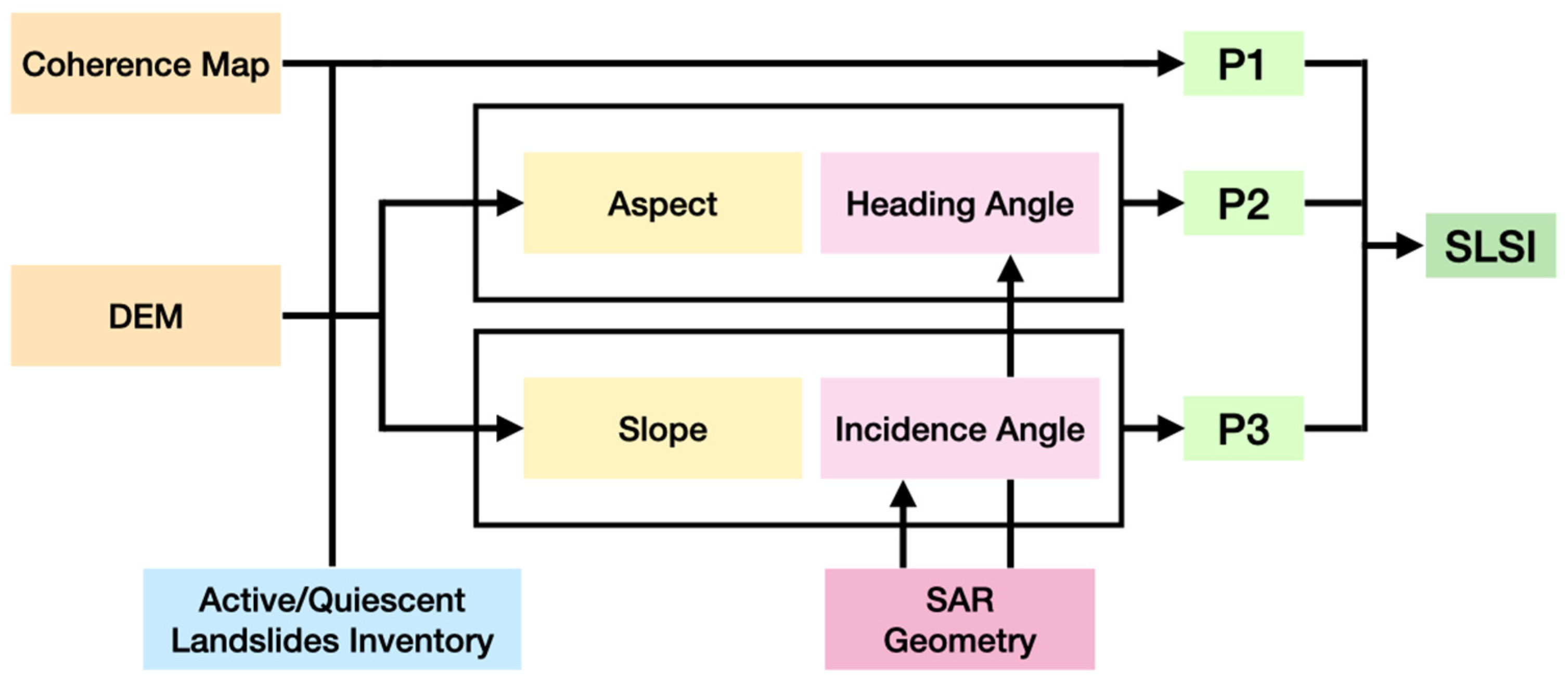
2.4. Parameter Integration and Final Index (SLSI)
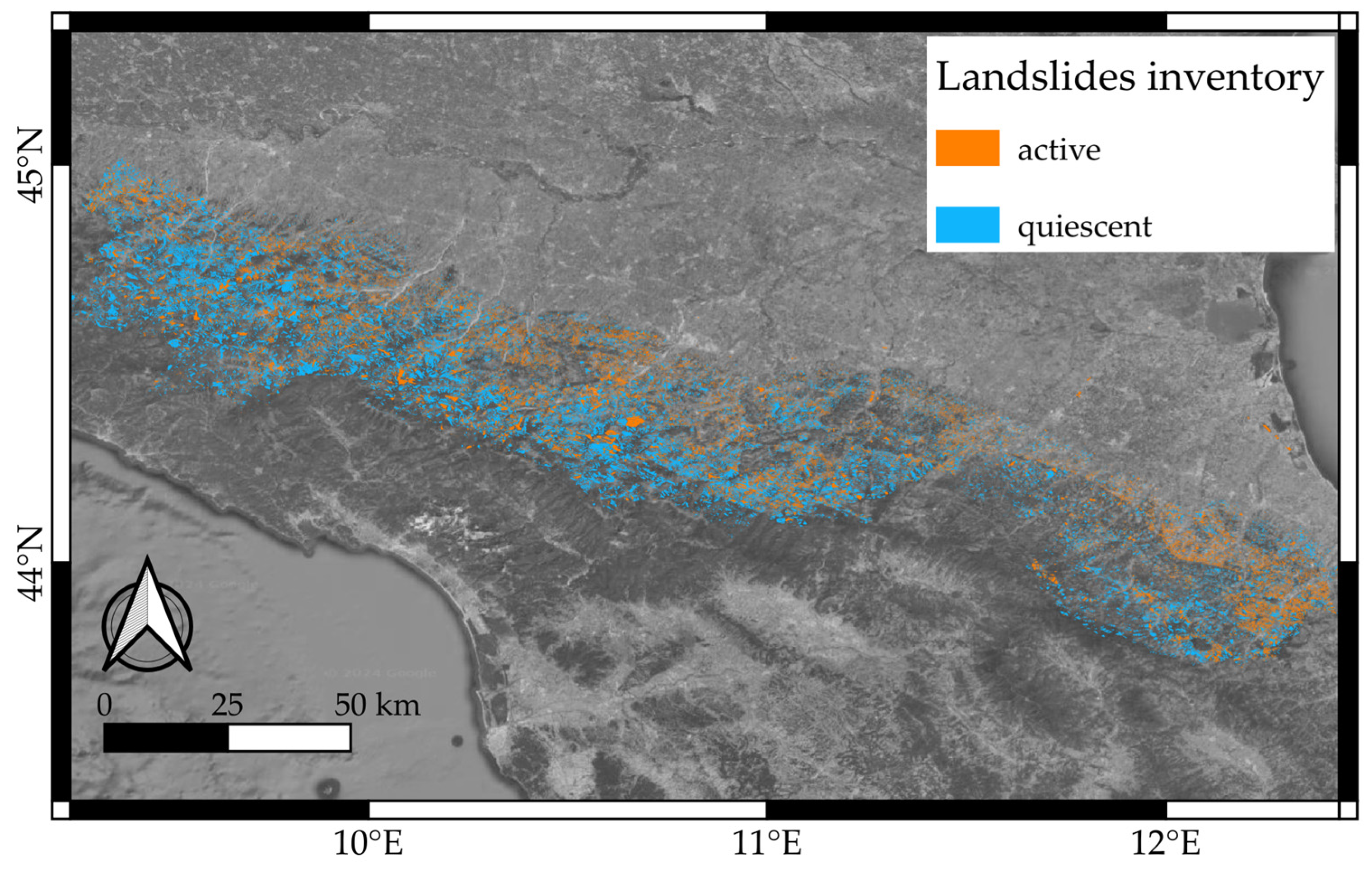
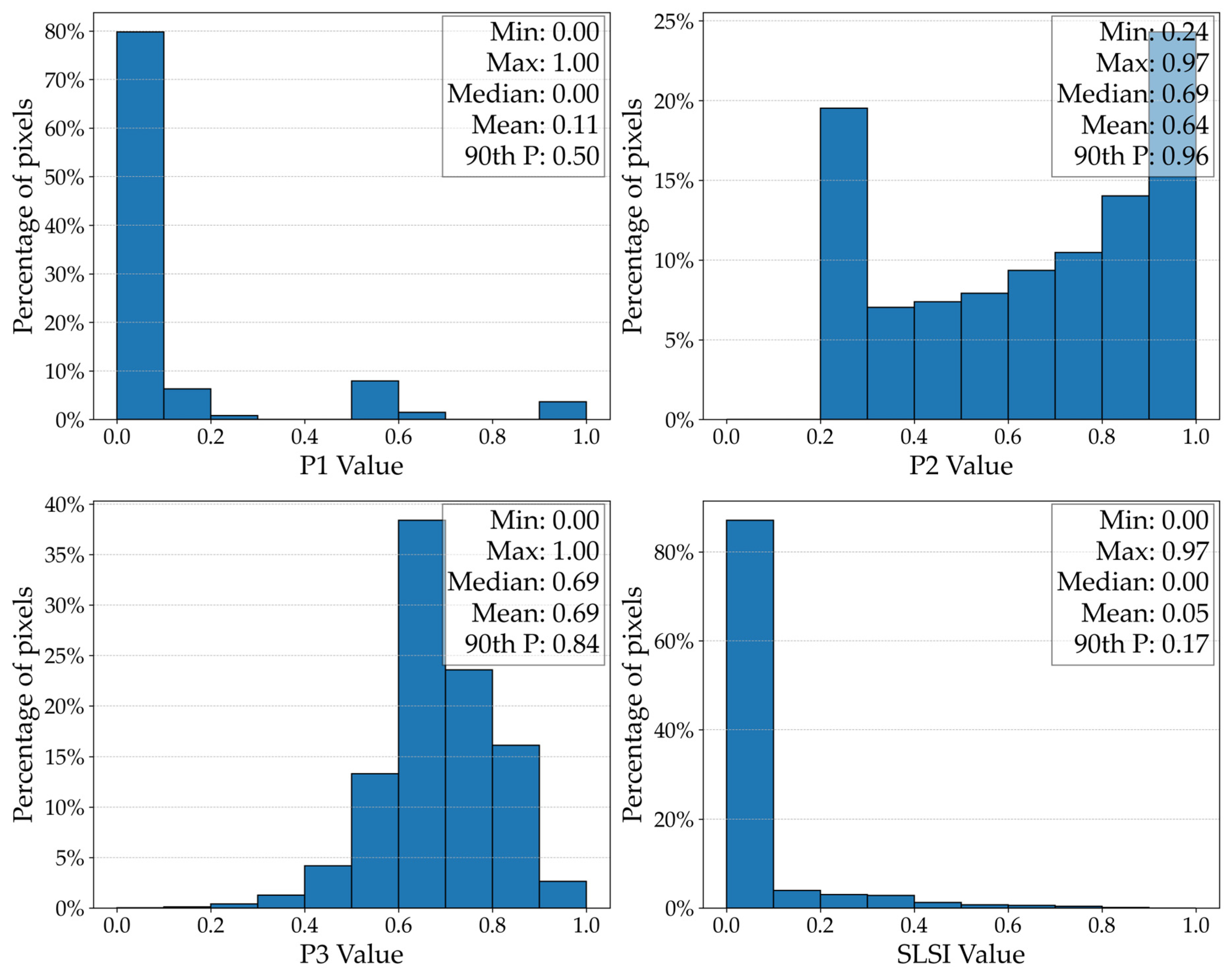
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guzzetti, F.; Carrara, A.; Cardinali, M.; Reichenbach, P. Landslide hazard evaluation: A review of current techniques and their application in a multi-scale study, Central Italy. Geomorphology 1997, 31, 181–216. [Google Scholar] [CrossRef]
- EuroGeoSurveys. Available online: http://m.eurogeosurveys.org (accessed on 1 September 2023).
- Gozza, G.; Pizziolo, M. 13. Analisi del Dissesto da Frana in Emilia-Romagna. 2006. Available online: http://isprambiente.gov.it (accessed on 1 December 2023).
- Aslan, G.; Foumelis, M.; Raucoules, D.; De Michele, M.; Bernardie, S.; Cakir, Z. Landslide mapping and monitoring using persistent scatterer interferometry (PSI) technique in the French Alps. Remote Sens. 2020, 12, 1305. [Google Scholar] [CrossRef]
- Kalia, A.C. Classification of landslide activity on a regional scale using persistent scatterer interferometry at the Moselle valley (Germany). Remote Sens. 2018, 10, 1880. [Google Scholar] [CrossRef]
- Ambiente Regione Emilia-Romagna. Available online: https://ambiente.regione.emilia-romagna.it (accessed on 1 September 2023).
- Servizio Geologico Sismico e dei Suoli (SGSS). Le Frane. 2016. Available online: https://ambiente.regione.emilia-romagna.it/it/geologia/pubblicazioni/opuscoli/le-frane-2016 (accessed on 31 May 2016).
- Kuang, J.; Ng, A.H.-M.; Ge, L. Displacement characterization and spatial-temporal evolution of the 2020 Aniangzhai landslide in Danba county using time-series InSAR and multi-temporal optical dataset. Remote Sens. 2021, 14, 68. [Google Scholar] [CrossRef]
- Hussain, S.; Pan, B.; Afzal, Z.; Ali, M.; Zhang, X.; Shi, X. Landslide detection and inventory updating using the time-series InSAR approach along the Karakoram Highway, Northern Pakistan. Sci. Rep. 2023, 13, 7485. [Google Scholar] [CrossRef] [PubMed]
- Gussoni, M.; Turconi, L. Frane, il GIS a supporto della conoscenza. Ecoscienza 2015, 3, 23–24. [Google Scholar]
- Carlà, T.; Intrieri, E.; Raspini, F.; Bardi, F.; Farina, P.; Ferretti, A.; Colombo, D.; Novali, F.; Casagli, N. Perspectives on the prediction of catastrophic slope failures from satellite InSAR. Sci. Rep. 2019, 9, 14137. [Google Scholar] [CrossRef]
- Sun, Q.; Hu, J.; Zhang, L.; Ding, X. Towards slow-moving landslide monitoring by integrating multi-sensor InSAR time series datasets: The Zhouqu case study, China. Remote Sens. 2016, 8, 908. [Google Scholar] [CrossRef]
- Kiseleva, I.; Mikhailov, V.; Smolyaninova, E.; Dmitriev, P.; Golubev, V.; Timoshkin, E.; Hooper, A.; Samiei-Esfahany, S.; Hanssen, R. PS-InSAR monitoring of landslide activity in the Black Sea coast of the Caucasus. Procedia Technol. 2014, 16, 404–413. [Google Scholar] [CrossRef]
- Béjar-Pizarro, M.; Notti, D.; Mateos, R.M.; Ezquerro, P.; Centolanza, G.; Herrera, G.; Bru, G.; Sanabria, M.; Solari, L.; Duro, J.; et al. Mapping vulnerable urban areas affected by slow-moving landslides using Sentinel-1 InSAR data. Remote Sens. 2017, 9, 876. [Google Scholar] [CrossRef]
- Dong, J.; Zhang, L.; Tang, M.; Liao, M.; Xu, Q.; Gong, J.; Ao, M. Mapping landslide surface displacements with time series SAR interferometry by combining persistent and distributed scatterers: A case study of Jiaju landslide in Danba, China. Remote Sens. Environ. 2018, 205, 180–198. [Google Scholar] [CrossRef]
- Li, Y.; Jiao, Q.; Hu, X.; Li, Z.; Li, B.; Zhang, J.; Jiang, W.; Luo, Y.; Li, Q.; Ba, R. Detecting the slope movement after the 2018 baige landslides based on ground-based and space-borne radar observations. Int. J. Appl. Earth Obs. Geoinf. 2020, 84, 101949. [Google Scholar] [CrossRef]
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent Scatterers in SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Di Traglia, F.; De Luca, C.; Manzo, M.; Nolesini, T.; Casagli, N.; Lanari, R.; Casu, F. Joint exploitation of space-borne and ground-based multitemporal InSAR measurements for volcano monitoring: The Stromboli volcano case study. Remote Sens. Environ. 2021, 260, 112441. [Google Scholar] [CrossRef]
- Chen, X.; Sun, Q.; Hu, J. Generation of complete SAR geometric distortion maps based on DEM and neighbor gradient algorithm. Appl. Sci. 2018, 8, 2206. [Google Scholar] [CrossRef]
- Fuhrmann, T.; Garthwaite, M.C. Resolving three-dimensional surface motion with InSAR: Constraints from multi-geometry data fusion. Remote Sens. 2019, 11, 241. [Google Scholar] [CrossRef]
- Dai, K.; Deng, J.; Xu, Q.; Li, Z.; Shi, X.; Hancock, C.; Wen, N.; Zhang, L.; Zhuo, G. Interpretation and sensitivity analysis of the InSAR line of sight displacements in landslide measurements. GISci. Remote Sens. 2022, 59, 1226–1242. [Google Scholar] [CrossRef]
- He, L.; Pei, P.; Zhang, X.; Qi, J.; Cai, J.; Cao, W.; Ding, R.; Mao, Y. Sensitivity Evaluation of Time Series InSAR Monitoring Results for Landslide Detection. Remote Sens. 2023, 15, 3906. [Google Scholar] [CrossRef]
- Deng, J.; Dai, K.; Liang, R.; Chen, L.; Wen, N.; Zheng, G.; Xu, H. Interferometric Synthetic Aperture Radar Applicability Analysis for Potential Landslide Identification in Steep Mountainous Areas with C/L Band Data. Remote Sens. 2023, 15, 4538. [Google Scholar] [CrossRef]
- Zhang, R.; Zhao, X.; Dong, X.; Dai, K.; Deng, J.; Zhuo, G.; Yu, B.; Wu, T.; Xiang, J. Potential Landslide Identification in Baihetan Reservoir Area Based on C-/L-Band Synthetic Aperture Radar Data and Applicability Analysis. Remote Sens. 2024, 16, 1591. [Google Scholar] [CrossRef]
- Van Natijne, A.L.; Bogaard, T.A.; van Leijen, F.J.; Hanssen, R.F.; Lindenbergh, R.C. World-wide InSAR sensitivity index for landslide deformation tracking. Int. J. Appl. Earth Obs. Geoinf. 2022, 111, 102829. Available online: https://avannatijne.users.earthengine.app/view/landslide-insar (accessed on 1 May 2024). [CrossRef]
- Chang, L.; Dollevoet, R.P.B.J.; Hanssen, R.F. Monitoring Line-Infrastructure with Multisensor SAR Interferometry: Products and Performance Assessment Metrics. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2018, 11, 1593–1605. [Google Scholar] [CrossRef]
- Cascini, L.; Fornaro, G.; Peduto, D. Analysis at medium scale of low-resolution DInSAR data in slow-moving landslide-affected areas. ISPRS J. Photogramm. Remote Sens. 2009, 64, 598–611. [Google Scholar] [CrossRef]
- Cascini, L.; Fornaro, G.; Peduto, D. Advanced low-and full-resolution DInSAR map generation for slow-moving landslide analysis at different scales. Eng. Geol. 2010, 112, 29–42. [Google Scholar] [CrossRef]
- Notti, D.; Davalillo, J.C.; Herrera, G.; Mora, O. Assessment of the performance of X-band satellite radar data for landslide mapping and monitoring: Upper Tena Valley case study. Nat. Hazards Earth Syst. Sci. 2010, 10, 1865–1875. [Google Scholar] [CrossRef]
- Notti, D.; Herrera, G.; Bianchini, S.; Meisina, C.; García-Davalillo, J.C.; Zucca, F. A methodology for improving landslide PSI data analysis. Int. J. Remote Sens. 2014, 35, 2186–2214. [Google Scholar] [CrossRef]
- Notti, D.; Meisina, C.; Zucca, F.; Colombo, A. Models to predict Persistent Scatterers data distribution and their capacity to register movement along the slope. In Proceedings of the Fringe 2011 Workshop, Frascati, Italy, 19–23 September 2011; pp. 19–23. [Google Scholar]
- Plank, S.; Singer, J.; Thuro, K.; Minet, C. The suitability of the differential radar interferometry method for deformation monitoring of landslides—A new GIS based evaluation tool. In Proceedings of the 11th IAEG Congress Geologically Active, Auckland, New Zealand, 5–10 September 2010; pp. 5–10. [Google Scholar]
- Cigna, F.; Bateson, L.B.; Jordan, C.J.; Dashwood, C. Simulating SAR geometric distortions and predicting Persistent Scatterer densities for ERS-1/2 and ENVISAT C-band SAR and InSAR applications: Nationwide feasibility assessment to monitor the landmass of Great Britain with SAR imagery. Remote Sens. Environ. 2014, 152, 441–466. [Google Scholar] [CrossRef]
- Colombo, A.; Mallen, L.; Pispico, R.; Giannico, C.; Bianchi, M.; Savio, G. Mappatura regionale delle aree monitorabili mediante l’uso della tecnica PS. In Proceedings of the 10 National Conference ASITA, Bolzano, Italy, 14–17 November 2006; pp. 14–17. [Google Scholar]
- Lazecký, M.; Spaans, K.; González, P.J.; Maghsoudi, Y.; Morishita, Y.; Albino, F.; Elliott, J.; Greenall, N.; Hatton, E.; Hooper, A.; et al. LiCSAR: An Automatic InSAR Tool for Measuring and Monitoring Tectonic and Volcanic Activity. Remote Sens. 2020, 12, 2430. [Google Scholar] [CrossRef]
- Morishita, Y. Nationwide urban ground deformation monitoring in Japan using Sentinel-1 LiCSAR products and LiCSBAS. Prog. Earth Planet. Sci. 2021, 8, 6. [Google Scholar] [CrossRef]
- Sentinel Online. Available online: https://sentinels.copernicus.eu/ (accessed on 1 September 2023).
- Geoportale Emilia-Romagna. Available online: https://geoportale.regione.emilia-romagna.it (accessed on 1 December 2023).
- APAT. Rapporto Sulle Frane in Italia. Il Progetto IFFI–Metodologia, Risultati e Rapporti Regionali; APAT Report; APAT: Roma. 78/2007. Available online: http://www.isprambiente.gov.it/it/pubblicazioni/rapporti/Rapporto-sulle-frane-in-Italia (accessed on 1 December 2023).
- Qgis Documentation. Available online: https://docs.qgis.org/2.8/en/ (accessed on 1 September 2023).
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31, L23611. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Lanari, R.; Casu, F.; Manzo, M.; Zeni, G.; Berardino, P.; Manunta, M.; Pepe, A. An overview of the small baseline subset algorithm: A DInSAR technique for surface deformation analysis. Deform. Gravity Chang Indic. Isostasy Tecton. Volcanism Clim. Change 2007, 164, 637–661. [Google Scholar]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Morishita, Y.; Lazecky, M.; Wright, T.J.; Weiss, J.R.; Elliott, J.R.; Hooper, A. LiCSBAS: An Open-Source InSAR Time Series Analysis Package Integrated with the LiCSAR Automated Sentinel-1 InSAR Processor. Remote Sens. 2020, 12, 424. [Google Scholar] [CrossRef]
- Kropatsch, W.G.; Strobl, D. The generation of SAR layover and shadow maps from digital elevation models. IEEE Trans. Geosci. Remote Sens. 1990, 28, 98–107. [Google Scholar] [CrossRef]
- Colesanti, C.; Wasowski, J. Investigating landslides with space-borne Synthetic Aperture Radar (SAR) interferometry. Eng. Geol. 2006, 88, 173–199. [Google Scholar] [CrossRef]

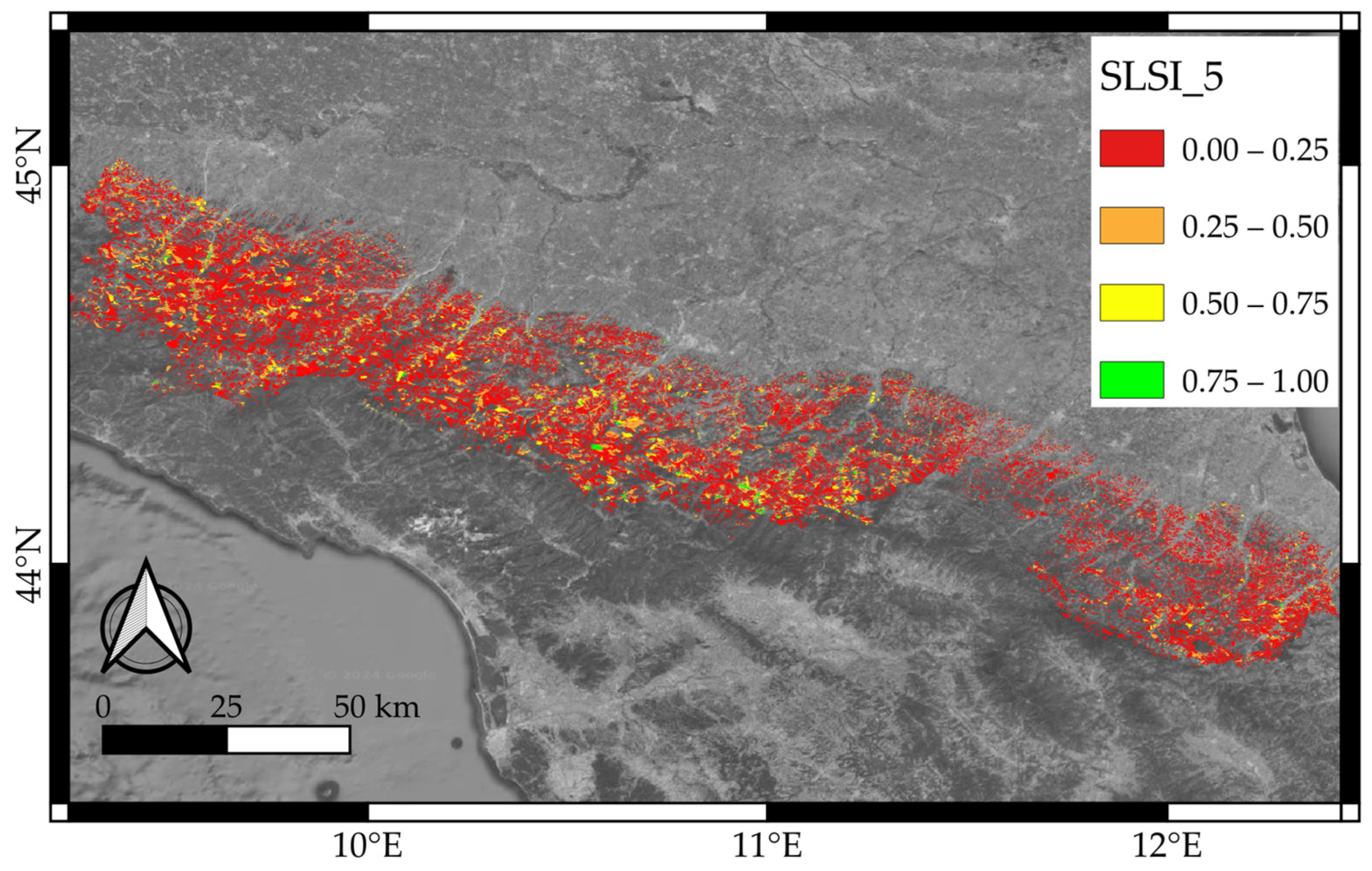
| SLSI5 Intervals | LS N | Area% |
|---|---|---|
| 0.00–0.25 | 67,741 | 74.5 |
| 0.25–0.50 | 9660 | 18.0 |
| 0.50–0.75 | 2751 | 6.5 |
| 0.75–1.00 | 680 | 1.0 |
| Parameter Value | P2 * P3 | S | ||
|---|---|---|---|---|
| Ls N | Area% | Ls N | Area% | |
| 0.00–0.25 | 9442 | 3.7 | 4394 | 3.1 |
| 0.25–0.50 | 43,777 | 66.7 | 26,431 | 38.7 |
| 0.50–0.75 | 24,996 | 28.9 | 46,287 | 56.9 |
| 0.75–1.00 | 2587 | 0.6 | 3696 | 1.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vecchi, E.; Tavasci, L.; Giorgini, E.; Gandolfi, S. A Priori Estimation of Radar Satellite Interferometry’s Sensitivity for Landslide Monitoring in the Italian Emilia-Romagna Region. Remote Sens. 2024, 16, 2562. https://doi.org/10.3390/rs16142562
Vecchi E, Tavasci L, Giorgini E, Gandolfi S. A Priori Estimation of Radar Satellite Interferometry’s Sensitivity for Landslide Monitoring in the Italian Emilia-Romagna Region. Remote Sensing. 2024; 16(14):2562. https://doi.org/10.3390/rs16142562
Chicago/Turabian StyleVecchi, Enrica, Luca Tavasci, Eugenia Giorgini, and Stefano Gandolfi. 2024. "A Priori Estimation of Radar Satellite Interferometry’s Sensitivity for Landslide Monitoring in the Italian Emilia-Romagna Region" Remote Sensing 16, no. 14: 2562. https://doi.org/10.3390/rs16142562
APA StyleVecchi, E., Tavasci, L., Giorgini, E., & Gandolfi, S. (2024). A Priori Estimation of Radar Satellite Interferometry’s Sensitivity for Landslide Monitoring in the Italian Emilia-Romagna Region. Remote Sensing, 16(14), 2562. https://doi.org/10.3390/rs16142562








