Abstract
Underwater terrain-aided navigation (TAN) can obtain high-precision positioning independently and autonomously under the conditions of a communication rejection space, which is an important breakthrough for the autonomous and refined operation of deep-sea autonomous underwater vehicles near the seabed. Although TAN originated in the aviation field, the particularity of the underwater physical environment has led to the formation of a different theoretical and technical system. In this article, the application background, operating principles, and most important technical aspects of underwater TAN are introduced. Then, the relevant algorithms involved in the two main modules (the terrain-aided positioning module and the iterative filtering estimation module) of the underwater TAN are reviewed. Finally, other cutting-edge issues in the field of underwater TAN are summarized. The purpose of this article is to provide researchers with a comprehensive understanding of the current research status and possible future developments in the TAN field.
1. Introduction
With the advancement of ocean exploration and development into deep-sea spaces, underwater vehicles face increasing challenges in terms of communication-limited and communication-denied operational environments [1,2]. This often results in the inability of human intervention to provide timely and accurate information to guide their mission progress. Therefore, underwater vehicles tasked with deep-sea operations must possess autonomy and intelligent operational capabilities to meet the long-term and precision requirements of future deep-sea operations. High-precision navigation technology serves as the foundation for the safe navigation and autonomous intelligent operation of underwater vehicles, and its theoretical and technical levels are directly related to the level of underwater vehicle intelligence.
Owing to the inability of satellite signals to penetrate seawater and reach the deep sea, the scope of acoustic navigation systems for underwater vehicles is limited. Inertial navigation error accumulates infinitely over time. Traditional navigation methods can no longer support underwater vehicles in performing long-term and fine operation tasks in deep-sea spaces [3,4]. Therefore, the research and development of high-precision, long-term autonomous navigation technology that is adaptable to deep-sea environments has become an urgent need in deep-sea exploration and development.
Deep-sea terrain-aided navigation (TAN) utilizes underwater terrain features as positioning references. It achieves the real-time positioning of underwater vehicles in a priori terrain maps by actively detecting and tracking characteristic terrains with positioning errors bounded in the time and spatial domains [5]. Therefore, the TAN is a significant breakthrough in achieving the long-term, high-precision positioning of underwater vehicles in the deep sea. As the demand for deep-sea and polar seabed exploration and development increases globally, TAN technology has garnered widespread attention in the field of deep-sea exploration and development, including such applications as abyssal lander guidance and control [3,6], the spatiotemporal modeling of oceanic dynamic processes [7,8], polar exploration [9,10], in situ observation and sampling of the seabed [11], deep-sea synchronous positioning, map generation [12], and underwater archaeological surveying [13,14,15]. The application of TAN in the field of ocean exploration is shown in Table 1.

Table 1.
Application of TAN in the field of ocean exploration.
2. Introduction to Underwater TAN
Underwater TAN, gravity-field-matching navigation [39], and geomagnetic-field-matching navigation [40] are all components of geophysical-information-matching navigation. They were initially used for spacecraft navigation in communication-constrained and -denied spaces. One of the most famous applications is the Terrain Contour Matching (TERCOM) system, which was installed on U.S. prisoner-of-war cruise missiles. TAN is also of great importance in the aerospace field [41,42], such as in the landing process of Mars probes [43,44,45]. Deep-sea spaces are typical communication-constrained environments, and high-precision navigation has always been a technological bottleneck that must be overcome for the long-duration, long-range, and fine-grained operations of underwater vehicles. In the 1980s, the Norwegian Defence Research Establishment (FFI, Forsvarets forskningsinstitut) introduced TAN technology into the field of underwater navigation. It successfully developed the underwater TAN system “TerrNav” and the experimental platform “TerrLab” [46,47]. During the past four decades, the development of underwater TAN technology has led to the formation of a relatively complete theoretical and technical system (Figure 1). The theoretical and technical system of underwater TAN mainly includes three parts: terrain measurement and restructuring [48], TAP [48,49], and the path planning of underwater TAN [50]. Among them, terrain measurement and reconstruction include measuring and reconstructing the global a priori DEM and the real-time measured terrain map, on which the relevant research is already very comprehensive. TAN/TAP and TAN path planning are the current research hotspots of TAN. TAP research mainly involves single-point TAP estimation [49], continuous recursive positioning estimation [51,52], and positioning in terrain-unknown environments [53]. TAN path planning mainly involves Terrain Adaptability Analysis [54], path search, and optimization methods [55].
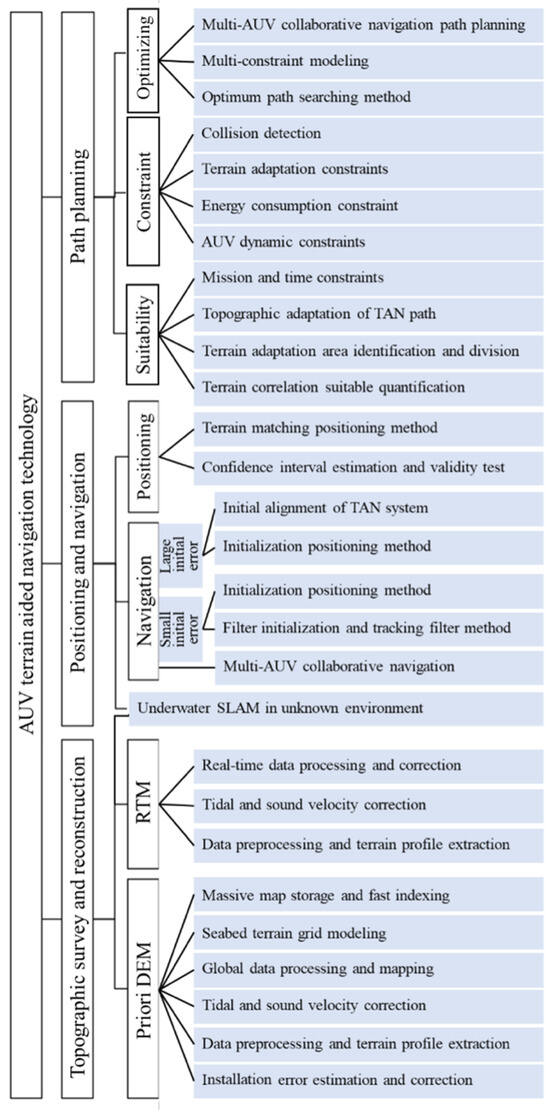
Figure 1.
Underwater TAN theory and technical system.
3. Principle of Underwater TAN
3.1. Composition of Two TAN Systems
The underwater TAN system mainly consists of three components: the main navigation system, the terrain-aided positioning (TAP) module (including the terrain measurement module), and the localization information fusion module. The main navigation system provides the basic position reference information for the underwater TAN system. The primary navigation localization module is generally based on the dead reckoning (DR) or inertial navigation systems (INSs), in which the navigation positions have recursive relationships and strong correlations. However, the positioning errors of the main navigation system accumulate over time without bounds. The TAP module is used to calculate the position probability distribution of the real-time measured map (RTM) matched to the a priori terrain map in the spatial domain. Because the RTM corresponds to the autonomous underwater vehicle (AUV) position, the position probability distribution of the RTM can also describe the positioning probability distribution of the AUV in the a priori digital elevation model (DEM). The TAP module includes the terrain measurement module, which is primarily used to obtain real-time terrain information beneath the AUV. Various sensors can be used for this purpose, such as single-beam echo sounders [46,56,57], multibeam echo sounders [3,4], the Doppler velocity log (DVL) [35,58], and structured light [59,60,61]. The TAN filter estimation module serves as the data fusion center for the entire system. It is responsible for receiving position information from both the main navigation module and the TAP module and then obtaining new positioning information through fusion estimation and iterative computation. The main modules and information flow of the TAN system are shown in Figure 2.
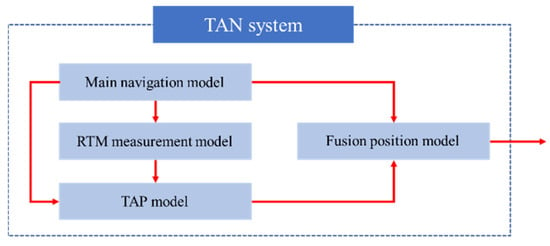
Figure 2.
Main functional modules of TAN.
3.2. Mathematical Model of the TAN System
The operation of an underwater TAN system can be described using a set of state transition equations. However, the specific forms of the state transition equations vary depending on the structure of the TAN system. The main structural modes of the TAN system include tightly and loosely coupled filtering modes [35]. The loosely coupled filtering mode, as shown in Figure 3, is the most commonly used. In this structure, the main navigation system outputs the positioning information only to the TAN system. The filter receives the positioning information from the main navigation system and the TAP information, performs fusion estimation for positioning integration, and outputs the fused positioning information. The main navigation system no longer provides independent positioning results. The state transition equations for this structure are as follows. Equation (1) describes the state transition of the main navigation system, and the second equation represents the state observation equation based on terrain matching.
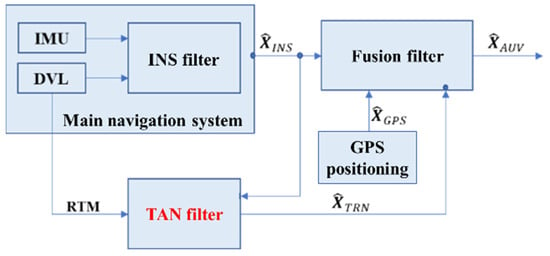
Figure 3.
Loosely coupled navigation filter.
Here, represents the positioning output of the TAN system at time , represents the input of the TAN system at time , represents the positioning output of the main navigation system at time after receiving the input , represents the system input error, represents the sequence of real-time sonar measurements of the terrain height obtained at time , represents the sequence of the interpolated terrain height at the positioning point , and represents the terrain measurement error.
Another structural mode of the TAN system is the tightly coupled mode, as shown in Figure 4. In this structure, the main navigation system outputs attitude information, velocity information, and other parameters to the TAN system. The TAN filter utilizes velocity information, attitude information, and terrain measurement information to perform positioning estimation. Furthermore, the main navigation system independently performs positioning estimation and outputs the positioning information separately, without interfering with the TAN positioning information. The state transition equations for this structure are shown in Equation (2), where the first equation describes the state transition of the main navigation system, and the second equation represents the state observation equation based on terrain matching.
where and represent the system state vectors obtained at times and , respectively. In addition, , where represents the coordinates of the AUV main navigation system, and represents the AUV attitude angles. Moreover, represents the sequence of the coordinates of the intersection points where the terrain is measured, represents the north coordinate in the map coordinate system, represents the east coordinate in the map coordinate system, represents the elevation difference between the measured terrain and the prior terrain map, denote the angular velocities of the AUV around the y-axis and z-axis, respectively, represents the rotation matrix formed by the AUV attitude matrix at time , represents the velocity matrix in the body coordinate system, and represent the changes in the roll and pitch angles measured by the attitude sensors, respectively, and represent the angular velocities, represents the unit vector in the sonar beam direction, represents the distance measured by the beam at time , and represents the measurement error of the sensor.
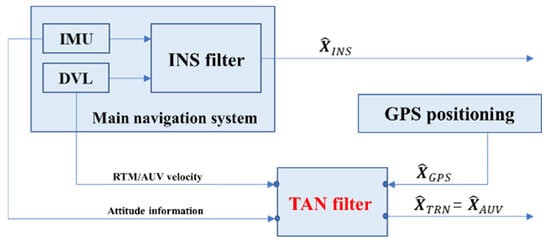
Figure 4.
Tight coupled navigation filter.
The tightly coupled navigation filtering mode is generally used for TAN estimation with low-cost sensor systems. For AUVs equipped with high-precision main navigation systems, the loosely coupled navigation filtering mode is typically employed.
3.3. TAP in Underwater TAN Systems
Underwater TAN systems utilize terrain feature matching and tracking for position estimation. Prior to providing accurate positioning information, the navigation coordinate system must be aligned with the spatial coordinate system of the terrain map. Subsequently, the TAN system performs continuous position estimation and outputs stable results by matching and tracking the underwater terrain features. In a previous study [5], the operation of underwater TAN systems was divided into two stages: initial positioning and tracking navigation. The primary objective of the initial positioning stage is to correct the accumulated time error of the main navigation system using high-precision TAP methods. This ensures the rapid convergence and stable output of the system within a short period and distance. However, the tracking positioning stage involves fusing the positioning information from the main navigation system with the TAP information, enabling continuous recursive estimation of the position and the provision of reliable positioning information. With the increasing diving depth and range of AUVs, larger initial positioning deviations can lead to challenges, such as slow convergence or even the divergence of the filtering process during the initial stage [3,4,48]. Therefore, the issue of convergence during the initial stage of underwater TAN systems has attracted significant attention. Comparative studies [3,4] have investigated the effects of different initial positioning and filtering initialization methods on navigation accuracy. These studies have shown that convergence errors and speeds during the initial stage affect the final positioning accuracy. Moreover, filter convergence serves as the foundation for reliable system operation and the generation of valid positioning information. Thus, considering system reliability, the operational stages of underwater TAN systems should encompass the initial positioning and filter initialization, the navigation filter convergence stage, and the tracking navigation filter stage, as depicted in Figure 5. The Primary algorithms utilized in the three operational phases of TAN is shown in Table 2.

Figure 5.
Operation stages of the TAN system.

Table 2.
Primary algorithms utilized in the three operational phases of a TAN.
4. Main Algorithms Involved in TAP
Underwater TAN systems exhibit strong nonlinearity and non-Gaussian input error characteristics. The state equation of the system contains insolvable terms, making it challenging to apply existing state estimation methods to underwater TAN systems. Over the years, researchers have attempted to develop high-precision and reliable technologies for underwater TAN systems, focusing on such areas as initial positioning and system tracking filtering. The research achievements can be categorized into underwater TAP techniques, underwater TAN filtering techniques, and other cutting-edge issues in underwater TAN systems. In this section, the development of underwater TAN technologies is reviewed and explored based on these aspects.
4.1. TAP Estimation
Underwater TAP estimation involves approximating the probability distribution of an AUV at a search point based on the likelihood estimation of the RTM terrain and the prior terrain. This estimation can be considered the position points of the AUV and their probability distribution in the terrain space, serving as a primary source of positioning information for underwater TAN systems. During the initial stage of system operation, TAP estimation can be used to obtain the initial position points and probability distribution estimation of the system. In the tracking filtering stage, the filter combines information from TAP with the main navigation system to output TAN positioning information. Commonly used underwater TAP methods include point-cloud-based- and image-based matching methods.
4.1.1. Terrain Point-Cloud-Based Matching
TERCOM is the most commonly used batch-processing TAP method based on terrain elevation (Figure 6). This method quantifies the likelihood measure using the elevation difference between two terrain profiles and normalizes it into a probability distribution function using an exponential function [5].
where Z represents the elevation sequence of the measured terrain, represents the error sequence of the measured terrain, H() represents the interpolation function for the terrain surface elevation, which can provide the elevation information at a given point based on its horizontal coordinates, and represents the coordinates of the search point within the search interval, where represents its index sequence number.
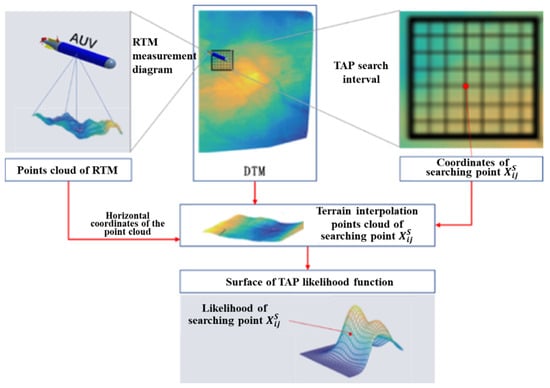
Figure 6.
Search and matching process of TERCOM.
The TERCOM algorithm can calculate the likelihood of each search point corresponding to the prior terrain map using RTM data [49]. By computing the maximum value of Equation (4), the position of the RTM in the DEM can be estimated.
Here, m and n represent the row and column indices of the measurement footprint sequence of the RTM, respectively, M and N represent the numbers of rows and columns in the measurement footprint sequence of the RTM, respectively, represents the measured elevation of the footprint with index , represents the terrain surface function, which describes the relationship between the horizontal coordinates and the elevation at each grid point on the terrain surface, represents the horizontal coordinates corresponding to the index point within the search interval , and represents the measurement error of the terrain elevation.
The mapping relationship between the RTM measurement points and the AUV position is unique. As shown in Figure 7, the RTM measurement point obtained in the bathymetric sonar coordinate system can be transformed to the vehicle coordinate system through geometric relationships and then transformed to the AUV navigation coordinate system through the navigation system, which is represented by Equation (5). Therefore, describes the probability distribution estimation of the AUV positioning points in the prior terrain map space.
where represents the coordinate sequence of the RTM measurement footprints in the navigation coordinate system, represents the coordinate vector of the RTM measurement footprints in the sonar coordinate system, represents the rotation matrix for transforming the RTM footprints from the sonar coordinate system to the vehicle coordinate system, represents the coordinate vector of the sonar installation position in the vehicle coordinate system, represents the attitude rotation matrix for transforming from the vehicle coordinate system to the navigation coordinate system, and represents the navigation output positioning at the measurement time.
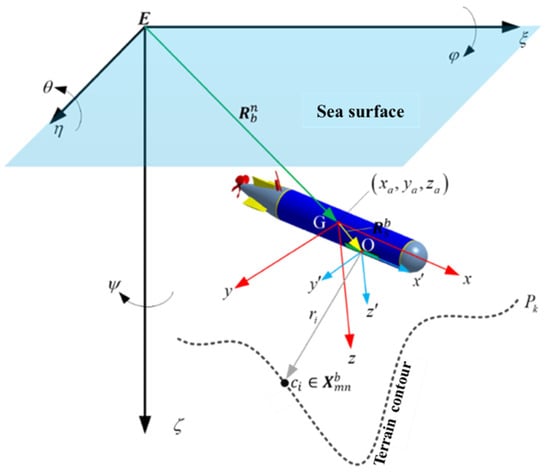
Figure 7.
Multibeam sounding data solution coordinate system.
In one study [5], the characteristics of the TERCOM algorithm were investigated extensively. It was found that the likelihood function obtained from terrain-matching positioning using the TERCOM algorithm exhibits asymptotic Gaussian distribution properties. However, the TERCOM algorithm has been found to have issues with poor stability and reliability, which has led many researchers to investigate improvements to the algorithm. Li et al. addressed these issues by introducing geometric features as descriptors to construct a multivariate feature vector for terrain representation. This approach increased the amount of terrain-matching information, leading to improved positioning accuracy and stability [49]. In addition to the TERCOM algorithm, the iterative closest point (ICP) algorithm and its variants, such as the improved convergence-constraint point (ICCP) algorithm, are commonly used for TAP based on point cloud data [62,63,85]. Because terrain elevation data can be treated as point cloud data, many researchers have applied the ICP algorithm to estimate the TAP. The principle of the ICP algorithm is illustrated in Equation (6), where the point set represents the reference point set, and represents the point set to be aligned. Here, N represents the number of elements in the point set [86]. Point set can be aligned with point set through rotation matrix and translation matrix .
where represents the rotation matrix, represents the translation matrix, represents the error vector, and represents the sum of the squared distance residuals between point sets and after rotation and translation. The optimal rotation and translation matrices are obtained when is minimized.
The ICP algorithm is widely used in outdoor mobile robot navigation for point cloud data matching and localization based on point cloud information [87,88,89]. Therefore, the ICP algorithm and its improved versions have been widely applied in underwater TAP. A previously proposed ICCP algorithm [64] provides an improved method for matching and positioning accuracy in scenarios with significant initial errors. This method models the terrain distribution feature as a two-dimensional Gaussian distribution to reduce the interference of the heading error, and a terrain feature descriptor with rotation invariance is established. Other researchers [90,91] addressed the problem of filter divergence that inertial navigation systems face when encountering large track deviations. They improved the trajectory accuracy in ICCP using the difference between the matching result and the output of the inertial navigation system as the measurement value of the Kalman filter (KF). In another work [62], a multipath parallel ICCP algorithm was proposed, which considers the error differences in the measurement frames of the multibeam sonar, thus enhancing the stability of the ICCP algorithm. However, the ICP/ICCP algorithm is sensitive to initial deviations, may converge slowly, and is prone to local minima when dealing with large initial deviations, leading to mismatches.
TERCOM localization remains the most commonly used matching and localization method for terrain-matching navigation systems. The TERCOM algorithm is less sensitive than the ICP and ICCP methods to errors and exhibits higher robustness. In addition, TERCOM describes the similarity between terrains using Euclidean distance and an exponential function, and the likelihood function obtained by TERCOM exhibits asymptotic Gaussian distribution characteristics [5]. These advantages provide significant convenience for the fusion of terrain-matching localization data and primary navigation localization data.
4.1.2. Image Matching Positioning
In addition to such methods as TERCOM, ICP, and ICCP, which utilize point cloud information for matching and positioning, underwater terrain matching and positioning algorithms based on image-matching techniques have been studied, including side-scan sonar images and optical camera images. In previous studies [92,93], matching and positioning algorithms based on side-scan images were investigated. They utilized log-polar transformation to solve the problem of estimating the rotation angle between real-time maps and reference images, thereby improving the matching accuracy and stability when there is an angular deviation in the measurement images.
In another work [94], a detailed comparison was made between the speeded-up robust features (SURF), oriented FAST and rotated BRIEF (ORB), binary robust invariant scalable keypoints (BRISK), and SURF–Harris algorithms, which were originally developed for optical image analysis. It was concluded that the further development of current feature description methodologies might be required for underwater acoustic image analysis. Other researchers [95] used an image attribute transfer algorithm and an advanced local feature descriptor to solve the problem of underwater acousto-optic image matching. The technique made it possible to preprocess multimodal images to obtain accurate matching results.
In one study [96], an underwater acoustic image simulation system was designed specifically for underwater acoustic image navigation. Building upon this system, research has been conducted on navigation systems based on forward-looking sonar images [97]. The system utilizes deep-learning methods for image processing and registration, as well as for the estimation of the attitude of the AUV [98], demonstrating the advantages of deep-learning methods in underwater acoustic image matching, positioning, and navigation. In other research [99], a novel 3D preprocessing filter, additions to line and line segment detection methods, a system description using concepts from the theory of multilevel hierarchical systems, and extensive evaluation tests using synthetic and real data were proposed.
Although the statistical moment information of the images enhances the noise resistance of the system to a certain extent, it reduces the dimensionality of the terrain elevation information, thereby weakening the amount of matching information. In the context of matching and positioning based on optical images, researchers [100,101,102] have investigated techniques for the simultaneous matching, stitching, and localization of images. These techniques make it possible to expand and map terrains in unknown underwater environments. The research conducted in these studies is important for achieving fine-grained measurements of unknown underwater topography and the high-precision positioning of AUVs. These technologies are commonly employed for precise measurements in such fields as underwater archaeology, underwater geological surveys, and underwater ecosystem assessments, as well as for the high-precision positioning of underwater robots [103,104,105]. In addition, image feature-based terrain matching and positioning techniques are widely applied in planetary rover landing positioning and navigation [106,107,108,109].
4.2. Iterative Filtering Methods for TAN
The filter serves as the data fusion center in TAN systems, where it combines information from the TAP and primary navigation positioning at the time step of the navigation solution. The TAP error is bounded in the spatial and temporal domains, whereas the propagated navigation error accumulates indefinitely. However, there is a strong correlation between the navigation points. Underwater TAN filtering algorithms integrate the boundedness of the TAP error and the strong correlation of the propagated navigation positioning, thereby harnessing the advantages of both positioning information types and obtaining more stable and accurate positioning information. Filtering methods for TAN systems have become an important research direction for underwater TAN technology. With the development of underwater mapping technology, computer hardware technology, and nonlinear estimation theory, filtering algorithms for TAN systems have gone through three major stages: Kalman, nonparametric, and robust filtering. Particle filtering has become the primary filtering method for underwater terrain-matching navigation.
4.2.1. Kalman Filter and Its Improvements
The initial iterative filtering estimation method is Kalman filtering [110]. However, the KF is a linearized filter that requires linearization of the terrain during the filtering process—specifically, linearizing the term in the state observation equation of the underwater TAN system and estimating the terrain slope [111]. Owing to the strong nonlinearity of the terrain, significant linearization errors are introduced, leading to filter divergence. Some researchers [73,112] have studied a TAN method based on the innovation transformation Kalman filtering technique, which mitigated the adverse effects of linearization errors to some extent. Comparative experiments with a particle filter (PF) and point mass filter showed that the PMF achieved the highest positioning accuracy when the measurement information was limited. As the measurement information increased, the PF approached the accuracy of the PMF, but both outperformed the KF and unscented KF in terms of positioning accuracy. Owing to the strong nonlinearity of the terrain and the non-Gaussian nature of the measurement errors, the Kalman filtering algorithm struggles to adapt to TAN systems with strong nonlinearity and non-Gaussian characteristics. PF and PMF methods, based on posterior Bayesian estimation theory and their direct numerical solution techniques, offer higher robustness and adaptability, making them particularly suitable for addressing the positioning estimation problem in TAN systems. Consequently, they have gradually replaced Kalman filtering methods as the most commonly used methods for state estimation in TAN systems.
4.2.2. Posterior Bayesian Estimation and Its Numerical Solution
The posterior Bayesian estimation equation for the underwater TAN states, as shown in Equation (7), consists of the state transition equation of the primary navigation system as the first term and the posterior Bayesian estimation equation of the system state as the second term. Solving the equation requires an evaluation of the integral term . However, does not have an analytical form, mainly because the mapping relationship between the AUV positioning and the terrain surface cannot be represented analytically. Although under the assumption of linearization and Gaussian error distribution, the Kalman filtering equations can be derived through derivation [5], the instability of the system caused by terrain linearization errors and non-Gaussian errors has become an insurmountable bottleneck. PF and PMF methods based on numerical solution techniques have been proposed to solve the state estimation problem of nonlinear dynamic systems [68,69,74,113]. The PMF and PF approximate the probability distribution function of the TAN positioning using finite grids and particle sets, making possible a direct numerical solution of the posterior Bayesian estimation of the TAN system positioning probability distribution in Equation (2) and significantly reducing the influence of terrain nonlinearity. Numerical solution methods based on Bayesian theory, such as PMF and PF, significantly improve filtering accuracy and stability [114], thereby advancing the development and application of underwater TAN technology.
where represents the predicted positioning probability distribution of the underwater TAN system at time , represents the posterior corrected probability of TAP in the underwater system, is the normalization parameter related to the terrain measurement error, represents the probability distribution of the propagated navigation system estimated position (where is the system state input information from time to ), is the system state at time , represents the integration range for solving the probability distribution of underwater TAN positioning, and represents the conditional distribution probability of observation value obtained by at time . Equations (7) and (8) make it possible to estimate the TAP points.
Similarly, the estimation of the underwater TAP error can be obtained using Equation (9):
- (1)
- Particle Filter
The FFI was one of the earliest research institutions to apply TAN technology to underwater navigation [46,47,115,116]. In the 1980s, FFI researchers introduced nonparametric filtering methods for state iteration estimation in TAN systems. The FFI also developed the TERLAB simulation platform specifically for the research on and application of underwater TAN technology [116]. Subsequently, an increasing number of researchers have studied underwater TAN technology based on PF methods. PFs approximate probability distributions with randomly distributed particles that convert an integral operation into a summation operation (Figure 8). Therefore, it can be very convenient to solve non-Gaussian problems and integral operations without analytic representations.
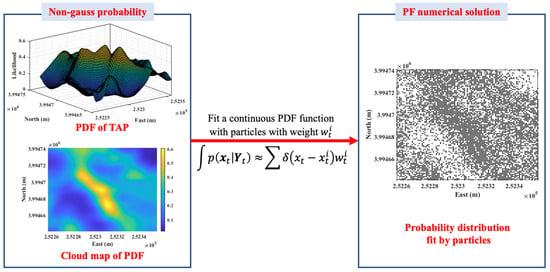
Figure 8.
PF solution for nonanalytical and non-Gaussian posterior Bayesian estimation.
The operation of a PF typically involves three steps: prediction, updating, and resampling. During the prediction step, the particle set is moved to the next navigation point based on the primary navigation information. In the updating step, the particle weights are adjusted based on the probability distribution function of TAP. The resampling step involves adjusting the distribution and weights of particles based on their weights to prevent particle degeneration. Strong nonlinearity and non-Gaussian input errors in TAN systems often lead to significant discrepancies between the true and proposed particle distributions. Furthermore, the problem of pseudopeaks in the probability distribution functions caused by terrain self-similarity further affects the stability and accuracy of the PF. Several studies [75,117,118] have addressed the issues of non-Gaussian and multimodal distributions in particle filtering owing to terrain self-similarity by proposing PF algorithms based on regularized representations and clustering analysis. To address the problem of intractable state prediction in TAN systems caused by observation equations, a Gaussian process PF method based on historical observation data and Gaussian models was proposed [119] for terrain prediction in underwater vehicle motion. A data-driven particle-filtering framework [75] was also proposed to avoid the explicit modeling of system disturbances. Another approach [76] addressed the non-Gaussian nature of the particle distribution by approximating the Bayesian function using multiple Gaussian components. To mitigate the computational burden caused by an increasing number of particles, an edge PF based on a more computationally efficient marginalized particle filter (MPF) was applied to state estimation in TAN systems [70]. A combined MPF that integrates a KF and a PF was proposed [81] to reduce the computational load of the PF process. An improved PF method based on the Huber function for modifying the particle weights was presented [77]. Furthermore, to address the problem of an explosive increase in particle quantity during the initial stage, an adaptive PF TAN filtering method utilizing the Kullback–Leibler distance measure was introduced [78]. A three-dimensional marginalized PF was proposed to enhance the filtering robustness and reduce the computational load in underwater TAN under uncertain conditions of tidal depth deviation [66,77]. An initialization sampling method for a PF based on constraints from TAP intervals was proposed [5] to reduce the particle spread range and quantity and improve the computational efficiency and convergence speed. A PF-based TAN method [120] that incorporates a nonrigid terrain transformation model that can correct nonrigid terrain transformation errors caused by the absence of a sound velocity profile and eliminate its impact on TAN was proposed. Because of its advantages in handling nonlinear and non-Gaussian noise in dynamic system state estimation problems, the PF algorithm has become the primary estimation method in TAN.
- (2)
- Marginalized Particle Filter
Similar to the PF algorithm, the MPF is a numerical method for solving posterior Bayesian estimation. It employs a finite grid approximation of the probability distribution function and is well suited for nonlinear and non-Gaussian state estimation in dynamic systems. In recent years, it has been widely applied to TAN. The MPF algorithm was initially proposed by Bucy and first applied to underwater TAN by Bergman [114,121]. As shown in Figure 9, the MPF algorithm divides the integral continuous probability function surface into volumes by using rectangular prisms with a base length of and a height equal to the probability value at that point. This transforms the integration of the continuous probability function surface into a volume summation problem. A comparative study of the MPF and PF methods in TAN state estimation was conducted [51,122], demonstrating that the MPF has a higher computational accuracy, but the computational complexity of the algorithm increases rapidly with the dimensionality of the state. However, although the PF has a lower accuracy than the MPF, it exhibits a higher computational efficiency when dealing with high-dimensional problems.
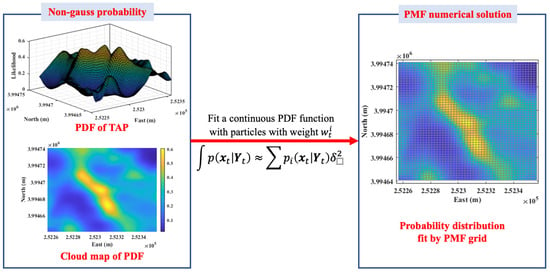
Figure 9.
MPF for nonanalytical and non-Gaussian posterior Bayesian estimation.
Because a standard grid is used in the implementation of the PMF algorithm, the grid quality can affect the estimation accuracy. The adaptive grid PMF algorithm was proposed [123,124] to achieve higher accuracy with a lower computational load. In another study [66], the application performance of the PMF algorithm under complex conditions was investigated, and it was found that the algorithm is significantly affected by measurement depth errors and initial position deviations. In other work [66], a marginalized PMF in three dimensions was developed to concurrently estimate and compensate for tidal depth bias. In this method, the tidal depth bias is extended as a state variable and estimated using a KF, whereas the horizontal position state is estimated using the original two-dimensional point mass filter. Using multibeam sonar, simulation experiments in a real DEM demonstrated that the method can accurately estimate the tidal depth bias and obtain a robust navigation solution in suitable terrain.
Although the PF- and PF-based filters have significant advantages in the state estimation of TAN systems, strong nonlinearity and non-Gaussian input errors still lead to filter instability. Currently, the techniques for measuring and reconstructing underwater terrain maps primarily include gravity field inversion, acoustic measurement, and optical measurement.
5. Other Relevant Technological Advancements
The practical application of underwater TAN technology requires high-precision prior terrain maps, which makes the practical application of underwater TAN difficult. However, the greatest bottleneck affecting the practical application of underwater TAN technology is the insufficient reliability of underwater TAN systems. The main application prospects of the underwater TAN technology lie in long-term, long-distance detection and development in deep-sea and remote areas. Because of the high investment, difficulty, and risk associated with deep-sea exploration and development, the autonomous equipment used for deep-sea exploration must possess high reliability to ensure the safety and smoothness of the detection equipment and processes. This requires underwater navigation systems with sufficiently high reliability. However, underwater terrain-aided navigation systems face several challenges and unresolved difficulties.
5.1. Prior Digital Elevation Model
Obtaining high-precision prior DEMs is crucial for effective and reliable positioning information of underwater TAN systems. However, the acquisition of underwater terrain, particularly large-scale high-precision bathymetric maps in deep and remote ocean areas, remains a global challenge. Currently, the techniques used for bathymetric map measurement and reconstruction primarily include gravity field inversion, acoustic ranging, and optical imaging.
Researchers [71,125,126] have proposed methods for obtaining bathymetric maps based on gravity field inversion, which can achieve global bathymetric inversion. However, the accuracy and resolution of the inversion results based on the gravity field are low, making them unsuitable for underwater TAN systems. High-precision bathymetric detection mainly relies on acoustic sounding techniques, such as single-beam or multibeam echo sounding. Based on the carrier of the acoustic sensor, these techniques can be categorized as shipborne, towed, or underwater-robot sounding systems. Currently, most global bathymetric data are derived from shipborne sounding systems. However, less than 20% of the seafloor has been adequately surveyed.
In 2017, the Japan Society for the Promotion of Science and the General Bathymetric Chart of the Oceans jointly discussed how marine mapping can support the United Nations’ sustainable development goals and proposed the Seabed 2030 project, which aims to achieve 100% global seafloor coverage by 2030. As of 2023, 24.9% of the global bathymetric mapping was completed [127]. However, high-precision and high-efficiency deep-sea bathymetric mapping remains a bottleneck that must be overcome.
With the rapid development of underwater robotics technology, an increasing number of research institutions have focused on developing deep-sea terrain mapping techniques based on underwater robotic platforms. These techniques show promise for improving the accuracy and efficiency of deep-sea terrain mapping. In one study [128], a technique for underwater terrain mapping based on an AUV platform was devised. This technique utilizes a multibeam sonar system mounted on an AUV to measure seabed profiles. The obtained profile information is then integrated with the AUV navigation system to compute the terrain profiles in the geodetic coordinate system, making autonomous underwater terrain mapping possible by using an AUV. However, because of the accumulation of errors in the navigation coordinate system of an AUV over time, it is challenging to achieve long-term and large-scale terrain mapping. In another study [129], a methodology was proposed for processing 3D multibeam sonar big data based on the stepwise processing of a dataset with 3D models and isoline map generation that makes fast processing possible, and the obtained DEMs were of good quality.
To address the issue of cumulative errors in AUV navigation systems over time, researchers worldwide have focused on underwater simultaneous localization and mapping (SLAM) technology. This technology aims to enable AUVs to construct global terrain maps autonomously and perform navigation and localization in unknown underwater environments without external assistance [130,131,132]. This includes bathymetric SLAM (BSLAM) based on multibeam bathymetry information [12,16,17,133,134,135], sensor-based acoustic and optical image SLAM utilizing acoustic and optical image data [136,137,138,139,140], and SLAM techniques based on structured light point cloud matching [133,141]. In BSLAM, multibeam bathymetry systems are commonly used to acquire three-dimensional point cloud information of the underwater terrain for matching and mapping. Image-based SLAM techniques utilize the image information obtained from underwater optical or acoustic devices for matching and mapping. Point cloud SLAM techniques employ stereo cameras or line-structured light sensors for data acquisition. Figure 10 shows the seabed terrain data obtained using multibeam sonar, an optical camera, and structured light.
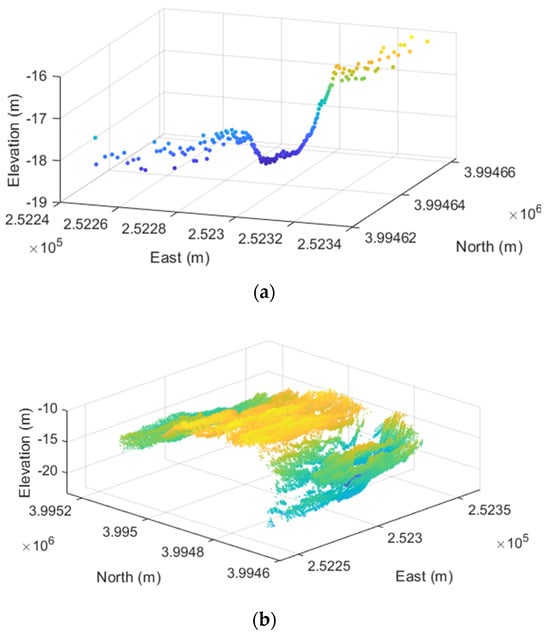
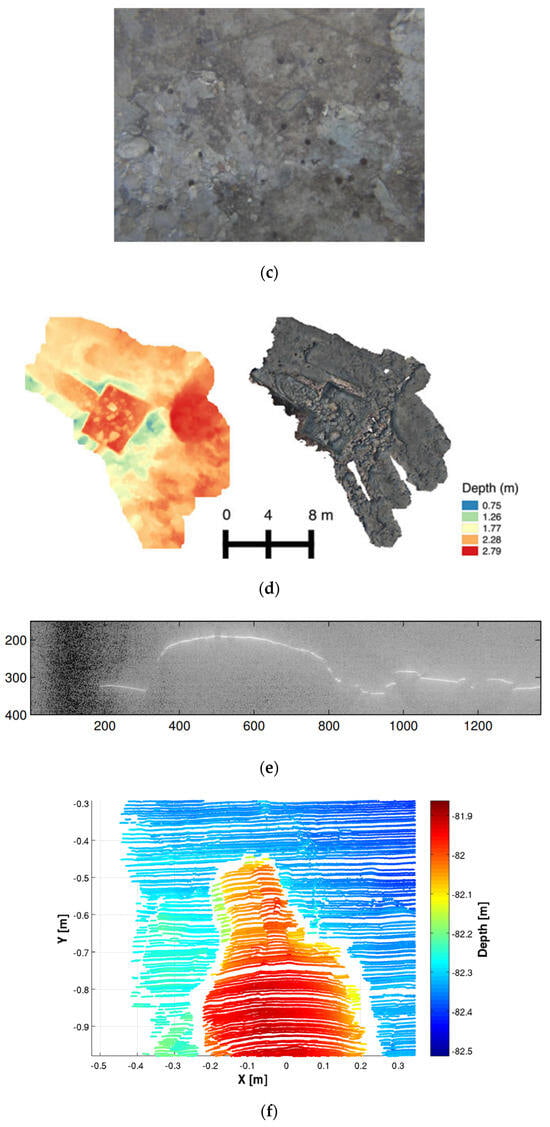
Figure 10.
Visualization of data from different sensors. (a) Multibeam Single-Measurement-Frame Footprints. (b) Multibeam Multiple-Measurement-Frame Point Cloud. (c) Camera Image Data [15]. (d) Stereo Camera Point Cloud [15]. (e) Line-Structured Light Patterns [142]. (f) Line-Structured Light Point Cloud from Multiple Frames [142].
The comparison in Figure 10 reveals that only the camera and multiline structured light [143] can provide information about a planar region in a single measurement, whereas the multibeam sonar and single-line structured light can only capture a single-line measurement. Because multibeam bathymetry can only obtain a strip-shaped terrain in a single measurement, it cannot construct continuous matching and correlation information. Therefore, submap partitioning is commonly used for map segmentation and feature matching [12,131]. Figure 11 illustrates the typical workflow for multibeam bathymetric SLAM. In contrast to single-frame multibeam bathymetry, a single-frame optical image can cover a limited planar region, making it possible to construct matching correlations between adjacent measurement frames. Therefore, there are significant differences in the algorithm design between bathymetric SLAM and image-based SLAM. However, regardless of the mapping approach, SLAM techniques rely on matching the correlations of environmental features to establish equations for AUV pose estimation. These equations serve as constraints related to AUV pose and feature matching, and they form the optimization equations for global mapping and AUV pose estimation.
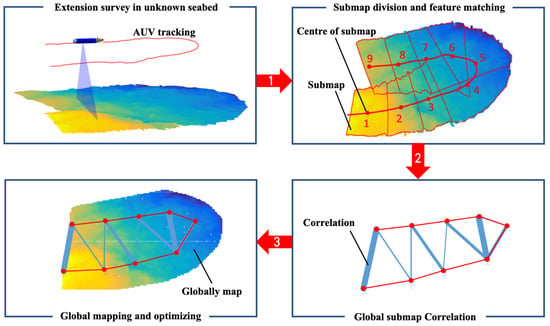
Figure 11.
Principle of multibeam bathymetric SLAM.
In the equations, represents the state transition equation with an input covariance matrix . In addition, represents the measurement equation with a measurement error of , where represents the indices of two different measurement frames that form a loop closure. Moreover, represents the set of indices of all measurement frames that form loop closures, represents the actual terrain elevation measurement sequence, represents the position information of the AUV, represents the optimized trajectory of the AUV, and represents the length of the AUV state sequence.
Due to the large measurement range and relatively low measurement accuracy of acoustic sensors, the SLAM technology is mainly used in the initial stage of seabed surveys, for large-scale seabed topography and geomorphology surveys, to obtain information on the large-scale changes in the seabed elevation and seabed substrate. Although SLAM technology solves the problem of unknown underwater terrain detection, the process of measuring the large-scale underwater terrain still faces the challenges of a low efficiency and high cost, owing to the low speed and limited range of AUVs. To address the efficiency issue, underwater terrain measurement techniques based on multi-robot collaboration have been rapidly developed [143,144,145,146]. In one study [147], large-scale seabed mapping using multiple AUVs was developed based on a graph-based cooperative bathymetric SLAM system that can compress many bathymetric measurements into small-scale acoustic packets and yield accurate navigation results with a 10% loss in acoustic packets caused by unreliable acoustic communication. In another work [148], the problem of multi-AUV collaborative online target detection was studied, and the simulation results showed that the algorithm can improve the detection efficiency by at least 40% compared with a single AUV. In another study [149], a path-planning method for a multi-AUV TAN was investigated by considering constraints, such as collision avoidance, arrival times, energy minimization, and acoustic communication between AUVs. A multi-AUV collaborative TAN technology [150] was studied, and it was verified through simulations that the proposed collaborative localization technique could extend the AUV operating time. Underwater SLAM technology was investigated [151] based on multi-robot collaboration, improving the terrain measurement efficiency and mapping accuracy. In other research [152], a multi-robot collaborative measurement method suitable for larger-scale underwater terrain measurements was developed. As shown in Figure 12, Robots A and B are both equipped with acoustic positioning devices. During the measurement process, Robot A is first submerged in a predetermined area and remains stationary as an acoustic positioning reference. Robot B, with Robot A as the positioning reference, performs terrain measurements in a certain seabed area. Once the measurement area is covered, Robot B submerges to the predetermined area and remains stationary as the new positioning reference, and Robot A, with Robot B as the positioning reference, performs terrain measurement in another seabed area. This cycle is repeated, theoretically allowing for the measurement of the entire underwater terrain.
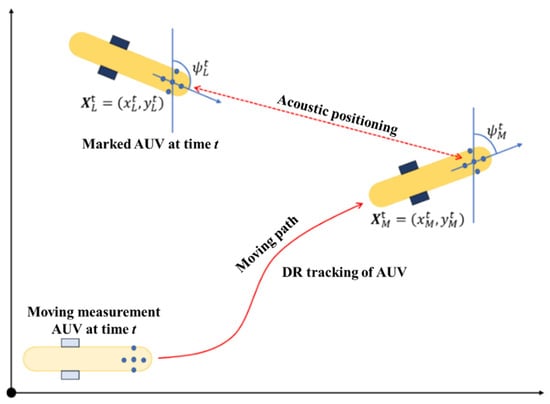
Figure 12.
Seabed terrain measurement scheme with multi-AUV collaboration.
Compared to SLAM technology based on acoustic measurement sensors, SLAM technology based on optical information is more mature and has been widely applied in autonomous vehicles, drones, and outdoor mobile robots [153]. While structured light and stereo vision measurements have a limited measurement range, they can perform close-range observation with high accuracy, making them suitable for small-scale and high-precision measurement tasks. They have been widely adopted in underwater archaeology for observation [154,155], the detection of underwater sediments or structures [156,157], and other underwater tasks. Reference [156] uses 3D visual reconstruction methods to study the sea floor hydrothermal systems and identify the habitats of Shinkaia crosnieri squat lobsters and their population density. Reference [36] presents an extensive review of the sensors and the methodologies used in archaeological underwater 3D recording and mapping, together with relevant highlights of well-renowned projects in 3D recording underwater. Furthermore, the literature [158,159,160] has investigated the common issue of light refraction correction in underwater optical measurement and SLAM. In reference [101,161], visual SLAM with a focus on a stereo camera system is presented to estimate the motion of autonomous underwater vehicles (AUVs) and build the feature map of the surrounding environment in real time. Reference [105] details the operations, discusses the results of the ancient shipwreck survey, and identifies the specific challenges of adapting AUV technology for deep water archaeology.
5.2. Terrain Adaptability Analysis and Path Planning
Underwater TAN technology can provide AUVs with positional information that has bounded errors. In theory, as long as the terrain adaptability meets the accuracy requirements of matching navigation, it can provide sufficiently accurate position information for AUVs over a long period of time. However, flat regions are likely to exist in underwater terrain maps, which have low adaptability and result in poor matching localization accuracy. This is particularly true for long-range AUV TAN, where large flat areas may exist in the extensive prior terrain map. Once the AUV enters such an area, there is a risk of filter divergence. Furthermore, AUVs have limited onboard energy; therefore, it is necessary to select the optimal path considering such factors as the mission, energy, and navigation accuracy, while ensuring that the energy reserves are sufficient to meet the consumption during the planned path tracking. Therefore, navigation path planning is a crucial research area in underwater TAN systems. Research on path planning for underwater TAN has mainly focused on terrain adaptability analysis, adaptability quantification, and path-planning algorithms. Adaptability analysis involves analyzing and parameterizing terrain features while identifying the most important terrain feature parameters that affect the matching accuracy. In one study [54], directional feature factors that affect the matching accuracy based on error analysis were derived, showing that the positioning accuracy of a point in the terrain map varies in different directions. Other research [162] addressed the selection of terrain feature parameters in adaptability analysis by constructing a binary logistic regression classifier based on factor analysis results, confirming the rationality of the factor interpretation and the effectiveness of the analysis results.
Adaptability quantification aims to evaluate the adaptability of the terrain quantitatively based on the terrain feature parameters and to divide the terrain map optimally into highly and poorly adaptable regions. In a previous study [54], an optimal partitioning method for terrain adaptability based on a terrain spatial standard grid was investigated. This method divides the terrain space using standard grids and obtains the optimal grid-based terrain map by maximizing the allocation of highly and poorly adaptable regions to different grids [54]. Figure 13 shows the grid-based results of the prior terrain map obtained using the method proposed [54]. The grid is determined based on the principle of optimal segmentation according to adaptability, in which highly and poorly adaptable regions in the terrain map are optimally allocated to different grids. Figure 14 shows the quantified values of terrain adaptability in each grid under the optimal grid partitioning.
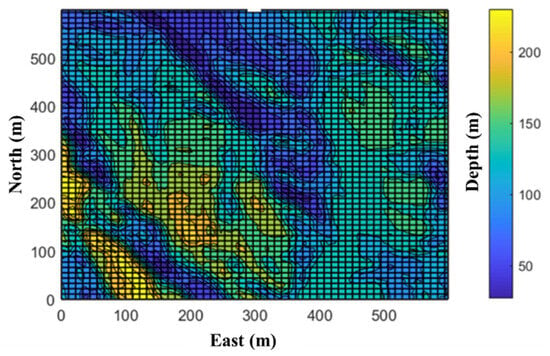
Figure 13.
Grid-based DEM.
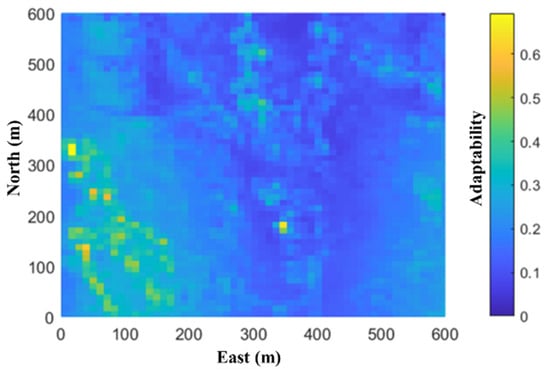
Figure 14.
Adaptability quantification map.
Path-planning algorithms primarily focus on finding optimal navigation paths considering multiple constraints, such as terrain adaptability, distance, and energy consumption. In one study [9], the navigation path-planning problem of guiding AUVs through the Arctic ice cover using underwater terrain-matching navigation was investigated. Building upon this, researchers [28] further considered such constraints as Arctic Ocean current models, high-latitude navigation estimation errors, and terrain depth measurement errors. They employed the optimized rapidly exploring random tree algorithm to obtain the optimal navigation path and conducted simulations using the Autosub Long-Range 1500 (ALR1500) AUV platform.
Currently, underwater TAN path planning only considers constraints in the horizontal plane and does not consider the vertical motion of the AUV and constraints related to vertical terrain variations. In practice, it is necessary to consider the vertical height of the AUV during underwater TAN path planning. The vertical height of the AUV from the seabed affects the range and accuracy of terrain detection, which directly impacts the matching localization accuracy. Moreover, the AUV must adjust its navigation depth based on terrain variations, which affects energy consumption. Moreover, the AUV itself has constraints on the navigation depth. Therefore, underwater TAN path planning must consider not only adaptability constraints in the horizontal plane but also depth constraints for path points and even differential constraints for the path.
5.3. Initial Positioning and Accuracy Evaluation
Previous studies have mostly focused on cases with small initial localization errors, where the use of TERCOM for initial localization can provide high-precision initial positions and PF initialization results. However, as AUV missions extend to deep-sea and long-range submerged navigation, navigation systems experience significant error accumulation because deep diving and extended travel distances are necessary. In such cases, the pseudo-peaks caused by the initial localization errors can lead to severe filter initialization errors and affect the stability and convergence of the filter.
To address the high-precision initial localization requirement in underwater TAN systems, a method [65] was proposed called the “terrain point diversity consistency test” (TPDCT) based on multiple TERCOM localization points to determine the effectiveness of TAP points. In other work [163], this method was applied to geomagnetic matching navigation, and practical experiments were conducted. However, underwater terrain acquisition is challenging, and the region suitable for matching positioning is limited. As a passive filtering method, TPDCT requires a considerable number of TAP points. In addition, the errors in the TAP points are related to the terrain features, and the probability distribution of different TAP points varies, resulting in low data utilization and poor applicability in underwater environments. Therefore, a multiple transmission–reception point fusion positioning (MTFP) positioning method [3] was studied based on data fusion estimation and trajectory validity determination. The MTFP and TPDCT methods use multiple TERCOM points for positioning estimation. Unlike the TPDCT method, the MTFP method actively uses data to obtain positioning estimates for trajectory segments. Based on this, the estimation cost of each trajectory segment is calculated, and the optimal trajectory is selected based on the lowest cost condition, thereby transforming the positioning estimation problem into a local trajectory segment estimation problem [48]. Furthermore, to address the problem of excessive pseudo-peaks in TAP causing a high computational load, researchers [39,164] proposed a PF initialization method based on confidence interval constraints. By estimating the confidence interval of the initial localization probability distribution function and using it as the distribution boundary for initializing the particle set, the number and range of initial particles are reduced, improving the convergence speed.
Regarding the accuracy evaluation of underwater TAP, most studies have used the Fisher information matrix as the lower bound for the error distribution of TAP [5,35,58]. However, the error distribution of the TAP estimates differs fundamentally from that of the recursive positioning estimates. The confidence interval is not elliptical. In one study [49], it was demonstrated that TAP points have distinct directional distribution characteristics, particularly in areas with significant terrain directionality. A stochastic jump model was proposed for the confidence interval estimation of TAP points (Figure 15), and a new equation was derived for the confidence interval estimation of TAP points, significantly improving the accuracy of the confidence interval estimation for TAP points:
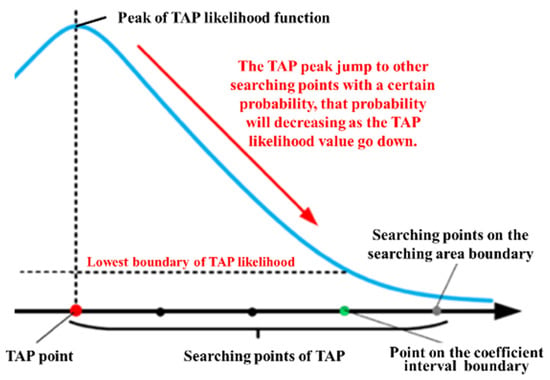
Figure 15.
TAP jump model.
Here, represents the sum of squared residuals of the TAP positions, denotes the variance in terrain measurement errors, and represents the confidence level, typically in the range of . The TAP points are randomly fluctuating points associated with terrain features in the spatial domain, and their probability distribution does not have a unique central peak but multiple pseudo-peaks, as shown in Figure 16. Therefore, the confidence intervals for TAP points cannot be estimated using the traditional elliptical confidence interval theory. Other position confidence interval estimation methods of TAN in different application scenarios list in Table 3.
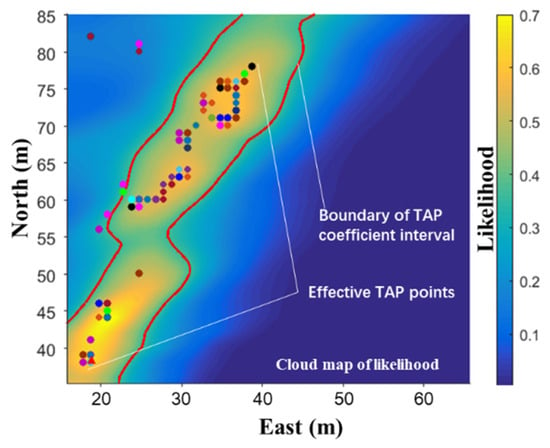
Figure 16.
TAP confidence interval.

Table 3.
Primary method for representing confidence intervals in statistics.
5.4. Simulation of an Underwater TAN System
Underwater TAN technology is primarily used for long-duration, long-distance navigation and positioning in the deep sea and remote underwater spaces. The deep-sea environment is a communication-denied space, where it is difficult for human intervention to occur quickly and effectively during operational processes. Therefore, underwater TAN systems must be sufficiently stable and reliable. Field trials and simulation experiments are important means of testing system performance. However, conducting field trials in deep-sea environments is challenging and risky. Therefore, shallow-water tests are often used as substitutes. This leads to significant differences between the experimental environment and the actual operating conditions, and the terrain features may also be limited, resulting in limited practical reference values for actual experiments. Simulation experiments offer such advantages as a low risk, high efficiency, and safety control, and they have been widely adopted in research on underwater autonomous systems. In recent years, they have been extensively used in underwater TAN research.
Obtaining system input information with high fidelity is essential to simulating underwater TAN systems, particularly when simulating input errors, which must have probabilistic completeness. This means that the input errors must encompass all possible error input patterns with a certain level of confidence. In previous research [166], a surface vessel was employed as a simulation platform to conduct sea trials using underwater TAN and SLAM techniques. FFI developed the NavLab integrated navigation simulation system and the TerrLab terrain-matching navigation simulation system [47,167]. These systems can be used for the algorithm verification and data postprocessing of underwater TAN systems, making them the earliest underwater TAN simulation platforms. The University of Southampton, UK, conducted research on the feasibility of using TAN technology to support AUVs in performing ultralong-range missions using the 6000AUV as the carrier. They also conducted a simulation verification using underwater TAN technology to assist AUVs in crossing the Arctic ice cover [9,28,168]. Currently, almost all the research institutions engaged in underwater TAN technology have developed their own simulation systems. However, most simulation studies have been limited to algorithm verification platforms based on data playback. In general, an underwater TAN simulation system should include a basic terrain measurement simulation, an AUV dynamics simulation, a TAN algorithm simulation, and other components (Figure 17). In particular, it should possess probabilistic completeness simulation capabilities for different terrain conditions and measurement systems, making it possible to simulate almost all possible operating conditions in a limited number of simulation experiments. These tasks cannot be accomplished through actual sea trials and are the core content of underwater TAN simulation systems. Some progress has been made in related research. For example, in terms of bathymetric system error analysis, researchers [169,170,171,172] have studied the error composition of multibeam bathymetric measurement systems with multiple sensors. They analyzed the distribution characteristics of depth measurement errors with respect to the wave speed and incident angle in a single measurement frame. Figure 18 shows the estimated measurement errors of multibeam bathymetric measurements at different beam angle positions as output by this simulation system. These results provide a theoretical basis for simulating bathymetric measurement errors using multibeam systems.
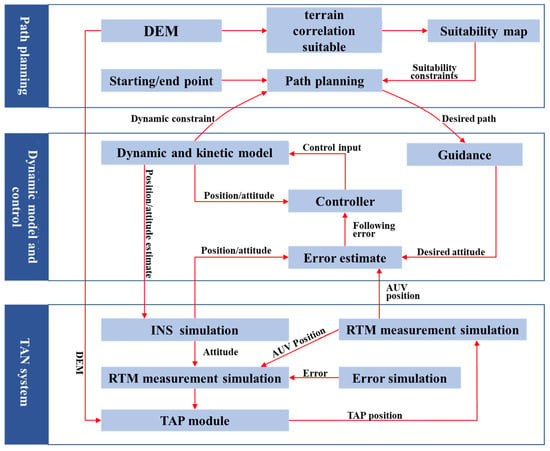
Figure 17.
Diagram of a TAP simulation system.
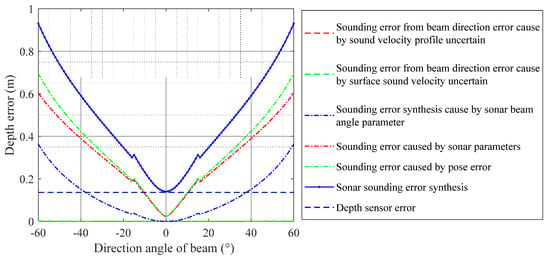
Figure 18.
Composite error of multibeam bathymetric measurements.
Currently, accurately simulating input errors for TAP systems is difficult. This is primarily because of the highly nonlinear characteristics of terrain measurement systems, where measurement errors are the result of coupling among various sensors in the measurement system. Figure 19 shows the residual sequence of the matching points in TAP. The signal in Figure 19b exhibits high autocorrelation and does not follow a Gaussian distribution, mainly because the prior terrain map was obtained through low-resolution map interpolation. Although it has been proved [5] that the residuals of terrain-matching positioning systems exhibit asymptotic Gaussian characteristics, the residual sequence of individual measurement beams still demonstrates a strong autocorrelation. Furthermore, matching residuals are closely related to terrain features, prior terrain maps, underwater acoustic environments, seabed geological conditions, and other factors. Therefore, the primary challenges are simulating non-Gaussian signals that match the measurement system, terrain features, acoustic environment characteristics, etc. and ensuring that the limited number of simulated residual signals satisfies the statistical completeness requirements of error signals. This is essential for conducting effective and reliable simulations of terrain-matching positioning and is a problem that must be addressed urgently.
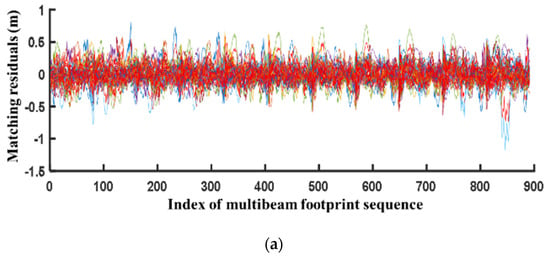
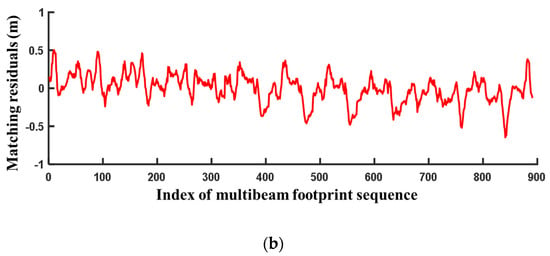
Figure 19.
TRP residual signals of a multibeam measurement system. (a) Overlapping of multiple terrain-matching residual signals. (b) Individual terrain-matching residual signal.
6. Conclusions and Outlook
Underwater TAN performs tracking and positioning navigation with non-Gaussian inputs, strong nonlinearity, and analytically intractable system state transition equations. Compared with other navigation methods, such as dead reckoning and acoustic positioning, TAN not only shares common issues related to position information fusion and estimation but also faces specific system characteristic problems owing to the uniqueness of the system input information (terrain information, terrain measurement errors, etc.). These issues result in non-Gaussian positioning errors, weak correlations between TAP points, initial instability during system operation, and the poor generalization performance of the algorithms. In addition, underwater TAN faces technical challenges, such as insufficient prior terrain maps and their accuracy, inadequate adaptability to terrain features, the accuracy and effectiveness evaluation of positioning, and high-precision system simulation. This article summarized the status of these issues, and the technical challenges that are currently faced were discussed.
Although underwater TAN technology has undergone more than 40 years of development, it has not yet been widely applied, and several important technical challenges must be overcome. Specifically, the following aspects should be addressed.
- (1)
- The stability and reliability of filters remain significant challenges, particularly for state estimation in non-Gaussian and nonlinear dynamic systems. Therefore, there is an urgent need to develop robust and reliable filtering algorithms and filters. In addition, filters should possess self-awareness and self-correction capabilities to enhance the generalization performance of the algorithms. For example, the work [97,98] has introduced machine learning into image matching, the work [173] has incorporated intelligent algorithms into Particle Filters (PFs), and the work [75] has proposed data-driven methods that can learn approximate proposal distributions from previous data. These are all good attempts.
- (2)
- With the diversification and refinement of AUV sensing information, there are differences in the granularity, data structures, and physical characteristics of the matching information. This involves matching and assimilating different resolutions, granularities, and data structure information.
- (3)
- The integration of TAN technology with underwater robot planning and control is crucial. The incorporation of TAN information into intelligent decision-making and control systems for AUVs should be explored.
- (4)
- The availability of large-scale, high-precision prior terrain maps remains a major bottleneck in the development of underwater TAN technology. Promising breakthroughs can be achieved through multi-AUV cooperative underwater positioning and terrain mapping techniques, which have the potential to improve the measurement accuracy and efficiency for unknown seafloor terrain. For instance, the work [174] and the work [152] proposed two different strategies for collaborative SLAM techniques involving multiple Autonomous Underwater Vehicles (AUVs).
Author Contributions
Methodology, R.W.; Formal analysis, Y.L., T.M. and X.Z.; Investigation, J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China 52101353.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wynn, R.B.; Huvenne, V.A.; Le Bas, T.P.; Murton, B.J.; Connelly, D.P.; Bett, B.J.; Ruhl, H.A.; Morris, K.J.; Peakall, J.; Parsons, D.R.; et al. Autonomous Underwater Vehicles (AUVs): Their past, present and future contributions to the advancement of marine geoscience. Mar. Geol. 2014, 352, 451–468. [Google Scholar] [CrossRef]
- Wakita, N.; Hirokawa, K.; Ichikawa, T.; Yamauchi, Y. Development of autonomous underwater vehicle (AUV) for exploring deep sea marine mineral resources. Mitsubishi Heavy Ind. Tech. Rev. 2010, 47, 73–80. [Google Scholar]
- Rupeng, W.; Yunsai, C.; Ye, L.; Pengfei, X.; Peng, S. High-precision initialization and acceleration of particle filter convergence to improve the accuracy and stability of terrain aided navigation. ISA Trans. 2021, 110, 172–197. [Google Scholar] [CrossRef] [PubMed]
- Rupeng, W.; Ye, L.; Teng, M.; Zheng, C.; Yusen, G.; Pengfei, X. Improvements to terrain aided navigation accuracy in deep-sea space by high precision particle filter initialization. IEEE Access 2020, 8, 13029–13042. [Google Scholar] [CrossRef]
- Nygren, I. Terrain Navigation for Underwater Vehicles. Ph.D. Thesis, KTH Electrical Engineering, Stockholm, Sweden, 2005. [Google Scholar]
- Wang, J.; Tang, Y.G.; Chen, C.X.; Li, J.X.; Chen, C.; Zhang, A.Q.; Li, Y.P.; Li, S. Terrain matching localization for hybrid underwater vehicle in the Challenger Deep of the Mariana Trench. Front. Inf. Technol. Electron. Eng. 2020, 21, 749–759. [Google Scholar] [CrossRef]
- Mileyko, Y.; Reis, G.; Chyba, M.; Smith, R.N. Energy-efficient control strategies for updating an augmented terrain-based navigation map for autonomous underwater navigation. In Proceedings of the 2017 IEEE Conference on Control Technology and Applications (CCTA), Maui, HI, USA, 27–30 August 2017; pp. 1–9. [Google Scholar]
- Reis, G.M.; Fitzpatrick, M.; Anderson, J.; Kelly, J.; Bobadilla, L.; Smith, R.N. Increasing persistent navigation capabilities for underwater vehicles with augmented terrain-based navigation. Oceans 2017, 6, 1–12. [Google Scholar]
- Salavasidis, G.; Munafò, A.; Harris, C.A.; McPhail, S.D.; Rogers, E.; Phillips, A.B. Towards arctic AUV navigation. In Proceedings of the 11th IFAC Conference on Control Applications in Marine Systems, Robotics, and Vehicles CAMS 2018, Opatija, Croatia, 9–12 September 2018; pp. 287–292. [Google Scholar]
- Claus, B.; Bachmayer, R. Terrain-aided navigation for an underwater glider. J. Field Robot. 2015, 32, 935–951. [Google Scholar] [CrossRef]
- Nakatani, T.; Ura, T.; Sakamaki, T.; Kojima, J. Terrain based localization for pinpoint observation of deep seafloors. In Proceedings of the Oceans 2009 Europe, Bremen, Germany, 11–14 May 2009; pp. 1–6. [Google Scholar]
- Ma, T.; Li, Y.; Gong, Y.; Wang, R.; Sheng, M.; Zhang, Q. AUV bathymetric simultaneous localization and mapping using graph method. J. Navig. 2019, 72, 1602–1622. [Google Scholar] [CrossRef]
- Liarokapis, F.; Kouřil, P.; Agrafiotis, P.; Demesticha, S.; Chmelik, J.; Skarlatos, D. 3D modelling and mapping for virtual exploration of underwater archaeology assets. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 425–431. [Google Scholar] [CrossRef]
- Mindell, D.A. Precision Navigation and Remotes Sensing for Underwaters Archaeology. In Remote Sensing in Archaeology; Springer: Berlin/Heidelberg, Germany, 2007; pp. 499–511. [Google Scholar]
- Henderson, J.; Pizarro, O.; Johnson-Roberson, M.; Mahon, I. Mapping submerged archaeological sites using stereo-vision photogrammetry. Int. J. Naut. Archaeol. 2013, 42, 243–256. [Google Scholar] [CrossRef]
- Ma, T.; Li, Y.; Wang, R.; Cong, Z.; Gong, Y. AUV robust bathymetric simultaneous localization and mapping. Ocean Eng. 2018, 166, 336–349. [Google Scholar] [CrossRef]
- Palomer, A.; Ridao, P.; Ribas, D.; Mallios, A.; Gracias, N.; Vallicrosa, G. Bathymetry-based SLAM with difference of normals point-cloud subsampling and probabilistic ICP registration. In Proceedings of the 2013 MTS/IEEE OCEANS, Bergen, Germany, 10–13 June 2013; pp. 1–8. [Google Scholar]
- Palomer, A.V. Probabilistic ICP for Bathymetry-based SLAM. Master’s Thesis, Universitat de Girona, Girona, Spain, 2013. [Google Scholar]
- Cheng, C.; Wang, C.; Yang, D.; Liu, W.; Zhang, F. Underwater localization and mapping based on multi-beam forward looking sonar. Front. Neurorobotics 2022, 15, 801956. [Google Scholar] [CrossRef] [PubMed]
- Énonsen, K.B.; Hagen, O.K. Recent developments in the HUGIN AUV terrain navigation system. In Proceedings of the OCEANS’11 MTS/IEEE, Kona, HI, USA, 19–22 September 2011; pp. 1–7. [Google Scholar]
- Hagen, O.K.; Ånonsen, K.B.; Skaugen, A. Robust surface vessel navigation using terrain navigation. In Proceedings of the 2013 MTS/IEEE OCEANS, Bergen, Germany, 10–13 June 2013; pp. 1–7. [Google Scholar]
- Hagen, O.K.; Ånonsen, K.B. Using Terrain Navigation to Improve MarineVessel Navigation Systems. Mar. Technol. Soc. J. 2014, 48, 45–58. [Google Scholar] [CrossRef]
- Di Massa, D.E. Terrain-Relative Navigationfor Autonomous Underwater Vehicles. Doctoral Dissertation, Massachusetts Institute of Technology Woods Hole Oceanographic Institution, Woods Hole, MA, USA, June 1997. [Google Scholar]
- Reis, G.M.; Fitzpatrick, M.; Anderson, J.; Bobadilla, L.; Smith, R.N. Augmented terrain-based navigation to enable persistent autonomy for underwater vehicles. In Proceedings of the 2017 First IEEE International Conference on Robotic Computing (IRC), Taichung, Taiwan, 10–12 April 2017; pp. 292–298. [Google Scholar]
- Fitzpatrick, M.; Reis, G.M.; Anderson, J.; Bobadilla, L.; Al Sabban, W.; Smith, R.N. Development of environmental niche models for use in underwater vehicle navigation. IET Cyber-Syst. Robot. 2020, 2, 67–77. [Google Scholar] [CrossRef]
- Stuntz, A.; Liebel, D.; Smith, R.N. Enabling persistent autonomy for underwater gliders through terrain based navigation. In Proceedings of the OCEANS 2015, Genova, Italy, 18–21 May 2015; pp. 1–10. [Google Scholar]
- Liu, Y.; Zhang, G.; Che, C. Underwater Terrain-Aided Navigation Relocation Method in the Arctic. Math. Probl. Eng. 2020, 2020, 6654368. [Google Scholar] [CrossRef]
- Salavasidis, G.; Munafò, A.; McPhail, S.D.; Harris, C.A.; Fenucci, D.; Pebody, M.; Rogers, E.; Phillips, A.B. Terrain-aided navigation with coarse maps—Toward an arctic crossing with an AUV. IEEE J. Ocean Eng. 2021, 46, 1192–1212. [Google Scholar] [CrossRef]
- Salavasidis, G.; Munafò, A.; Fenucci, D.; Harris, C.A.; Prampart, T.; Templeton, R.; Smart, M.; Roper, D.T.; Pebody, M.; Povl Abrahamsen, E.; et al. Terrain-aided navigation for long-range AUVs in dynamic under-mapped environments. J. Field Robot. 2021, 38, 402–428. [Google Scholar] [CrossRef]
- Salavasidis, G.; Munafo, A.; Harris, C.A.; Prampart, T.; Templeton, R.; Smart, M.; Roper, D.T.; Pebody, M.; McPhail, S.D.; Rogers, E.; et al. Terrain-aided navigation for long-endurance and deep-rated autonomous underwater vehicles. J. Field Robot. 2018, 36, 447–474. [Google Scholar] [CrossRef]
- Claus, B.; Bachmayer, R. Towards online terrain aided navigation of underwater gliders. In Proceedings of the 2014 IEEE/OES Autonomous Underwater Vehicles (AUV), Oxford, MS, USA, 6–9 October 2014; pp. 1–5. [Google Scholar]
- Li, Z.; Zheng, W.; Wu, F. Geodesic-based method for improving matching efficiency of underwater terrain matching navigation. Sensors 2019, 19, 2709. [Google Scholar] [CrossRef] [PubMed]
- Bandara, D.; Leong, Z.; Nguyen, H.; Jayasinghe, S.; Forrest, A.L. Technologies for under-ice AUV navigation. In Proceedings of the 2016 IEEE/OES Autonomous Underwater Vehicles (AUV), Tokyo, Japan, 6–9 November 2016; pp. 108–114. [Google Scholar]
- Gao, X.; Ding, K.; Ren, Y.G.; Fu, W.T.; Ding, Z.J.; Zhao, S.Y.; Liu, B.H. Target deployment and retrieval using JIAOLONG manned submersible in the depth of 6600 m in Mariana trench. China Ocean Eng. 2017, 31, 618–623. [Google Scholar] [CrossRef]
- Meduna, D.K. Terrain Relative Navigation for Sensor-Limited Systems with Application to Underwater Vehicles. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2011. [Google Scholar]
- Menna, F.; Agrafiotis, P.; Georgopoulos, A. State of the art and applications in archaeological underwater 3D recording and mapping. J. Cult. Herit. 2018, 33, 231–248. [Google Scholar] [CrossRef]
- Violante, C. Acoustic remote sensing for seabed archaeology. In Proceedings of the IMEKO TC4 International Conference on Metrology for Archaeology and Cultural Heritage, Trento, Italy, 22–24 October 2020. [Google Scholar]
- Johnson-Roberson, M.; Bryson, M.; Friedman, A.; Pizarro, O.; Troni, G.; Ozog, P.; Henderson, J.C. High-resolution underwater robotic vision-based mapping and three-dimensional reconstruction for archaeology. J. Field Robot. 2017, 34, 625–643. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, W.; Wu, F. Improving the reliability of underwater gravity matching navigation based on a priori recursive iterative least squares mismatching correction method. IEEE Access 2020, 8, 8648–8657. [Google Scholar] [CrossRef]
- Teixeira, F.C. Novel Approaches to Geophysical Navigation of Autonomous Underwater Vehicles. In Proceedings of the International Conference on Computer Aided Systems Theory, Las Palmas de Gran Canaria, Spain, 10–15 February 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 349–356. [Google Scholar]
- Lorenz, R.D. Planetary landings with terrain sensing and hazard avoidance: A review. Adv. Space Res. 2023, 71, 1–15. [Google Scholar] [CrossRef]
- Song, J.; Rondao, D.; Aouf, N. Deep learning-based spacecraft relative navigation methods: A survey. Acta Astronaut. 2022, 191, 22–40. [Google Scholar] [CrossRef]
- Qin, J.; Li, M.; Li, D.; Zhong, J.; Yang, K. A survey on visual navigation and positioning for autonomous UUVs. Remote Sens. 2022, 14, 3794. [Google Scholar] [CrossRef]
- Johnson, A.E.; Cheng, Y.; Trawny, N.; Montgomery, J.F.; Schroeder, S.; Chang, J.; Clouse, D.; Aaron, S.; Mohan, S. Implementation of a Map Relative Localization System for Planetary Landing. J. Guid. Control Dyn. 2023, 46, 618–637. [Google Scholar] [CrossRef]
- Johnson, A.; Aaron, S.; Chang, J.; Cheng, Y.; Montgomery, J.; Mohan, S.; Schroeder, S.; Tweddle, B.; Trawny, N.; Zheng, J.; et al. The lander vision system for mars 2020 entry descent and landing. Guid. Navig. Control 2017, 2017, 159. [Google Scholar]
- Hagen, O.K.; Hagen, P.E.; Bovio, E.; Tyce, R.; Schmidt, H. Terrain referenced integrated navigation system for underwater vehicles. In SACLANTCEN Conference Proceedings; NATO SACLANT Undersea Research Centre: La Spezia, Italy, 2000; pp. 171–180. [Google Scholar]
- Hagen, O.K. TerrLab—A generic simulation and post-processing tool for terrain referenced navigation. In Proceedings of the OCEANS 2006, Boston, MA, USA, 18–21 September 2006; pp. 1–7. [Google Scholar]
- Chen, P.; Li, Y.; Su, Y.; Chen, X. The improved Kriging interpolation algorithm for local underwater terrain based on fractal compensation. Math. Probl. Eng. 2014, 2014, 289521. [Google Scholar] [CrossRef]
- Li, Y.; Wang, R.; Chen, P.; Shen, P.; Jiang, Y. Terrain matching positioning method based on node multi-information fusion. J. Navig. 2017, 70, 82–100. [Google Scholar] [CrossRef]
- Li, Y.; Ma, T.; Chen, P.; Jiang, Y.; Wang, R.; Zhang, Q. Autonomous underwater vehicle optimal path planning method for seabed terrain matching navigation. Ocean Eng. 2017, 133, 107–115. [Google Scholar] [CrossRef]
- Anonsen, K.B.; Hallingstad, O. Terrain aided underwater navigation using point mass and particle filters. In Proceedings of the IEEE/ION PLANS 2006, San Diego, CA, USA, 25–27 April 2006; pp. 1027–1035. [Google Scholar]
- Teixeira, F.C.; Quintas, J.; Maurya, P.; Pascoal, A. Robust particle filter formulations with application to terrain-aided navigation. Int. J. Adapt. Control Signal Process. 2017, 31, 608–651. [Google Scholar] [CrossRef]
- Teng, M.; Ye, L.; Yuxin, Z.; Yanqing, J.; Qianyi, Z.; Pascoal, A.M. Efficient bathymetric SLAM with invalid loop closure identification. IEEE/ASME Trans. Mechatron. 2020, 26, 2570–2580. [Google Scholar] [CrossRef]
- Wang, R.; Li, Y.; Teng, M.; Zheng, C.; Gong, Y. Underwater digital elevation map gridding method based on optimal partition of suitable matching area. Int. J. Adv. Robot. Syst. 2019, 16, 268–283. [Google Scholar]
- Chen, P.; Shen, P.; Zhang, P.; Li, Y.; Ma, T.; Han, Y. Path planning of underwater terrain-aided navigation based on improved artificial potential field method. Mar. Technol. Soc. J. 2019, 53, 65–74. [Google Scholar] [CrossRef]
- Ma, D.; Ma, T.; Li, Y.; Ling, Y.; Ben, Y. A contour-based path planning method for terrain-aided navigation systems with a single beam echo sounder. Measurement 2024, 226, 114089. [Google Scholar] [CrossRef]
- Ma, D.; Ma, T.; Li, Y.; Ling, Y.; Ben, Y. A robust fusion terrain-aided navigation method with a single Beam Echo Sounder. Ocean Eng. 2023, 286, 115610. [Google Scholar] [CrossRef]
- Meduna, D.K.; Rock, S.M.; Mcewen, R.S. Closed-loop terrain relative navigation for AUVs with non-inertial grade navigation sensors. In Proceedings of the IEEE/OES Autonomous Underwater Vehicles, Monterey, CA, USA, 1–3 September 2011; pp. 1–10. [Google Scholar]
- Izadi, S.; Kim, D.; Hilliges, O.; Molyneaux, D.; Newcombe, R.; Kohli, P.; Shotton, J.; Hodges, S.; Freeman, D. Kinectfusion: Real-time 3d reconstruction and interaction using a moving depth camera. In Proceedings of the 24th Annual ACM symposium on User Interface Software and Technology, Santa Barbara, CA, USA, 16–19 October 2011; pp. 559–568. [Google Scholar]
- Bruno, F.; Bianco, G.; Muzzupappa, M.; Barone, S.; Razionale, A.V. Experimentation of structured light and stereo vision for underwater 3D reconstruction. ISPRS J. Photogramm. Remote Sens. 2011, 66, 508–518. [Google Scholar] [CrossRef]
- Chantler, M.J.; Clark, J.; Umasuthan, M. Calibration and operation of an underwater laser triangulation sensor: The varying baseline problem. Opt. Eng. 1997, 36, 2604–2611. [Google Scholar] [CrossRef]
- Wang, H.; Xu, X.; Zhang, T. Multipath parallel ICCP underwater terrain matching algorithm based on multibeam bathymetric data. IEEE Access 2018, 8, 48708–48715. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, L.; Li, M. Improved ICCP algorithm considering scale error for underwater geomagnetic aided inertial navigation. Math. Probl. Eng. 2019, 2019, 1527940. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, T.; Zhang, C.; Yao, Y. An improved ICCP-based underwater terrain matching algorithm for large initial position error. IEEE Sens. J. 2022, 22, 16381–16391. [Google Scholar] [CrossRef]
- Zhao, L.; Gao, N.; Huang, B.; Wang, Q.; Zhou, J. A novel terrain-aided navigation algorithm combined with the TERCOM algorithm and particle filter. IEEE Sens. J. 2015, 15, 1124–1131. [Google Scholar] [CrossRef]
- Peng, D.; Zhou, T.; Xu, C.; Zhang, W.; Shen, J. Marginalized point mass filter with estimating tidal depth bias for underwater terrain-aided navigation. J. Sens. 2019, 2019, 7340130. [Google Scholar] [CrossRef]
- Park, Y.G.; Park, C.G. Grid support adaptation for point mass filter based terrain referenced navigation using mutual information. IEEE Sens. J. 2018, 18, 7603–7610. [Google Scholar] [CrossRef]
- Duník, J.; Matoušek, J.; Straka, O. Design of Efficient Point-Mass Filter for Linear and Nonlinear Dynamic Models. IEEE Control Syst. Lett. 2023, 7, 2005–2010. [Google Scholar] [CrossRef]
- Matoušek, J.; Duník, J.; Brandner, M. Design of Efficient Point-Mass Filter with Application in Terrain Aided Navigation. arXiv 2023, arXiv:2303.05100. [Google Scholar]
- Duník, J.; Soták, M.; Veselý, M. Design of Rao–Blackwellized point-mass filter with application in terrain aided navigation. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1–10. [Google Scholar] [CrossRef]
- Wan, X.; Wang, H.; Jia, Y.; Ma, W. Performance of Haiyang-2 Derived Gravity Field Products in Bathymetry Inversion. Remote Sens. 2022, 15, 32. [Google Scholar] [CrossRef]
- Hostetler, L.; Andreas, R. Nonlinear Kalman filtering techniques for terrain-aided navigation. IEEE Trans. Autom. Control 1983, 28, 315–323. [Google Scholar] [CrossRef]
- Anonsen, K.B.; Hallingstad, O. Sigma point Kalman filter for underwater terrain-based navigation. IFAC Proc. Vol. 2007, 40, 106–110. [Google Scholar] [CrossRef]
- Elfring, J.; Torta, E.; van de Molengraft, R. Particle filters: A hands-on tutorial. Sensors 2021, 21, 438. [Google Scholar] [CrossRef] [PubMed]
- Melo, J.; Matos, A. A data-driven particle filter for terrain based navigation of sensor-limited autonomous underwater vehicles. Asian J. Control 2019, 7, 1659–1670. [Google Scholar] [CrossRef]
- Chen, P.; Chang, J.; Han, Y.; Yuan, M. Underwater terrain-aided navigation method based on improved Gaussian sum particle filtering. Int. J. Adv. Robot. Syst. 2019, 16, 1–7. [Google Scholar] [CrossRef]
- Peng, D.; Zhou, T.; Folkesson, J.; Xu, C. Robust particle filter based on Huber function for underwater terrain-aided navigation. IET Radar Sonar Navig. 2019, 13, 1867–1875. [Google Scholar] [CrossRef]
- Zhou, T.; Peng, D.; Xu, C.; Zhang, W.; Shen, J. Adaptive particle filter based on Kullback–Leibler distance for underwater terrain aided navigation with multi-beam sonar. IET Radar Sonar Navig. 2018, 12, 433–441. [Google Scholar] [CrossRef]
- Karlsson, R.; Gustafsson, F. Particle filter for underwater terrain navigation. In Proceedings of the IEEE Workshop on Statistical Signal Processing, St. Louis, MO, USA, 28 September–1 October 2003; pp. 526–529. [Google Scholar]
- Melo, J.; Matos, A. On the use of particle filters for terrain based navigation of sensor-limited AUVs. In Proceedings of the 2013 MTS/IEEE OCEANS, Bergen, Germany, 10–13 June 2013; pp. 1–8. [Google Scholar]
- Kim, T.; Kim, J.; Byun, S.W. A comparison of nonlinear filter algorithms for terrain-referenced underwater navigation. Int. J. Control Autom. Syst. 2018, 16, 2977–2989. [Google Scholar] [CrossRef]
- Casagrande, D.; Krasnosky, K.; Roman, C. Localization of a drifting underwater vehicle using a terrain-based particle filter. In Proceedings of the OCEANS 2019 MTS/IEEE, Seattle, WA, USA, 27–31 October 2019; pp. 1–8. [Google Scholar]
- Palmier, C.; Dahia, K.; Merlinge, N.; Del Moral, P.; Laneuville, D.; Musso, C. Adaptive approximate bayesian computational particle filters for underwater terrain aided navigation. In Proceedings of the 22nd International Conference on Information Fusion (FUSION), Ottawa, ON, Canada, 2–5 July 2019; pp. 1–8. [Google Scholar]
- Zhou, T.; Wang, T.; Gao, J.; Guo, Q.; Yan, Z. Particle filter underwater terrain-aided navigation based on gradient fitting. Meas. Sci. Technol. 2022, 33, 105009. [Google Scholar] [CrossRef]
- Wang, K.; Zhu, T.; Qin, Y.; Jiang, R.; Li, Y. Matching error of the iterative closest contour point algorithm for terrain-aided navigation. Aerosp. Sci. Technol. 2018, 73, 210–222. [Google Scholar] [CrossRef]
- Arun, K.S.; Huang, T.S.; Blostein, S.D. Least-squares fitting of two 3-D point sets. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 9, 698–700. [Google Scholar] [CrossRef]
- Wenberg, D. Method for Kalman Filtering Pose Estimates from Lidar Scans During the Landing Phase. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, September 2021. [Google Scholar]
- Clotet, E.; Palacín, J. SLAMICP Library: Accelerating Obstacle Detection in Mobile Robot Navigation via Outlier Monitoring following ICP Localization. Sensors 2023, 23, 6841. [Google Scholar] [CrossRef]
- Charalampous, K.; Kostavelis, I.; Chrysostomou, D.; Amanatiadis, A.; Gasteratos, A. 3D maps registration and path planning for autonomous robot navigation. arXiv 2013, arXiv:1312.2822. [Google Scholar]
- Wu, Z.; Wang, Y.; Pei, Z.; Wang, P.; He, B.; Zhu, L. An improved matching algorithm for the underwater navigation. In Proceedings of the International Conference on Control, Decision and Information Technologies, Thessaloniki, Grece, 10–13 April 2018; pp. 230–245. [Google Scholar]
- Li, P.; Sheng, G.; Zhang, X.; Wu, J.; Xu, B.; Liu, X.; Zhang, Y. Underwater terrain-aided navigation system based on combination matching algorithm. ISA Trans. 2018, 7, 80–87. [Google Scholar] [CrossRef] [PubMed]
- Song, Z.; Bian, H.; Zielinski, A. Underwater terrain-aided navigation based on multibeam bathymetric sonar images. J. Mar. Sci. Appl. 2015, 14, 425–433. [Google Scholar] [CrossRef]
- Song, Z.; Bian, H.; Zielinski, A. Application of acoustic image processing in underwater terrain aided navigation. Ocean Eng. 2016, 121, 279–290. [Google Scholar] [CrossRef]
- Oliveira, A.J.; Ferreira, B.M.; Cruz, N.A. A performance analysis of feature extraction algorithms for acoustic image-based underwater navigation. J. Mar. Sci. Eng. 2021, 9, 361. [Google Scholar] [CrossRef]
- Zhou, X.; Yu, C.; Yuan, X.; Luo, C. A matching algorithm for underwater acoustic and optical images based on image attribute transfer and local features. Sensors 2021, 21, 7043. [Google Scholar] [CrossRef]
- Almanza-Medina, J.E.; Henson, B.T.; Zakharov, Y.V. Imaging sonar simulator for assessment of image registration techniques. In Proceedings of the OCEANS 2019 MTS/IEEE, Seattle, WA, USA, 27–31 October 2019; pp. 1–7. [Google Scholar]
- Almanza-Medina, J.E. Underwater Motion Estimation Based on Acoustic Images and Deep Learning. Ph.D. Thesis, University of York, Heslington, UK, April 2022. [Google Scholar]
- Almanza-Medina, J.E.; Henson, B.; Zakharov, Y.V. Deep learning architectures for navigation using forward looking sonar images. IEEE Access 2021, 9, 33880–33896. [Google Scholar] [CrossRef]
- Patel, R.C. Three-Dimensional Underwater Acoustic Image Interpretation for ROV Navigation. Ph.D. Thesis, University College London, London, UK, 2003. [Google Scholar]
- Carrasco, P.L.N.; Bonin-Font, F.; Campos, M.M.; Codina, G.O. Stereo-vision graph-SLAM for robust navigation of the AUV SPARUS II. IFAC-PapersOnLine 2015, 48, 200–205. [Google Scholar] [CrossRef]
- Pi, S.; He, B.; Zhang, S.; Nian, R.; Shen, Y.; Yan, T. Stereo visual SLAM system in underwater environment. In Proceedings of the OCEANS 2014, Taipei, Taiwan, 7–10 April 2014; pp. 1–5. [Google Scholar]
- Bayat, M.; Aguiar, A.P. SLAM for an AUV using vision and an acoustic beacon. IFAC Proc. Vol. 2010, 43, 503–508. [Google Scholar] [CrossRef]
- Roman, C.; Mather, R. Autonomous underwater vehicles as tools for deep-submergence archaeology. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2010, 224, 327–340. [Google Scholar] [CrossRef]
- Yoerger, D.R.; Jakuba, M.; Bradley, A.M.; Bingham, B. Techniques for deep sea near bottom survey using an autonomous underwater vehicle. In Robotics Research: Results of the 12th International Symposium ISRR; Springer: Berlin/Heidelberg, Germany, 2007; pp. 416–429. [Google Scholar]
- Bingham, B.; Foley, B.; Singh, H.; Camilli, R.; Delaporta, K.; Eustice, R.; Mallios, A.; Mindell, D.; Roman, C.; Sakellariou, D. Robotic tools for deep water archaeology: Surveying an ancient shipwreck with an autonomous underwater vehicle. J. Field Robot. 2010, 27, 702–717. [Google Scholar] [CrossRef]
- Olson, C.F.; Matthies, L.H.; Wright, J.R.; Li, R.; Di, K. Visual terrain mapping for Mars exploration. Comput. Vis. Image Underst. 2007, 105, 73–85. [Google Scholar] [CrossRef]
- Helmick, D.M.; Angelova, A.; Livianu, M.; Matthies, L.H. Terrain adaptive navigation for Mars rovers. In Proceedings of the 2007 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2007; pp. 1–11. [Google Scholar]
- Cheng, Y.; Johnson, A.; Matthies, L. MER-DIMES: A planetary landing application of computer vision. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–26 June 2005; pp. 806–813. [Google Scholar]
- Wang, A.; Wang, L.; Zhang, Y.; Hua, B.; Li, T.; Liu, Y.; Lin, D. Landing site positioning and descent trajectory reconstruction of Tianwen-1 on Mars. Astrodynamics 2022, 6, 69–79. [Google Scholar] [CrossRef]
- Bergem, O. Bathymetric Navigation of Autonomous Underwater Vehicles Using a Multibeam Sonar and a Kalman Filter with Relative Measurement Covariance Matrices. Ph.D. Thesis, University of Trondheim, Trondheim, Norway, December 1993. [Google Scholar]
- Mok, S.H.; Bang, H. Terrain slope estimation methods using the least squares approach for terrain referenced navigation. Int. J. Aeronaut. Space Sci. 2013, 14, 85–90. [Google Scholar] [CrossRef]
- Lang, A. Estimation Methods for Terrain Navigation. Master’s Thesis, Royal Institute of Technology, Stockholm, Sweden, 2006. [Google Scholar]
- Královec, J.; Šimandl, M. Filtering, prediction and smoothing with point-mass approach. IFAC Proc. Vol. 2004, 37, 375–380. [Google Scholar] [CrossRef]
- Bergman, N. Recursive Bayesian Estimation Navigation and Tracking Applications. Doctoral Dissertation, Linkoping University, Linkoping, Sweden, 1999. [Google Scholar]
- Ånonsen, K.; Hagen, O.K. An analysis of real-time terrain aided navigation results from a HUGIN AUV. In Proceedings of the IEEE/ION Oceans 2010 Conference, Seattle, WA, USA, 20–23 September 2010; pp. 1–7. [Google Scholar]
- Jalving, B.; Gade, K.; Hagen, O.K.; Vestgard, K. A toolbox of aiding techniques for the HUGIN AUV integrated inertial navigation system. In Proceedings of the OCEANS 2003. Celebrating the Past…Teaming Toward the Future (IEEE Cat. No. 03CH37492), San Diego, CA, USA, 22–26 September 2003; pp. 1146–1153. [Google Scholar]
- Hong, K.; Kim, Y.; Bang, H. Comparison of solutions for measurement ambiguity in terrain referenced navigation. In Proceedings of the Navigation Conference, Lausanne, Switzerland, 9–12 May 2017; pp. 1–11. [Google Scholar]
- Melo, J.; Matos, A. Survey on advances on terrain based navigation for autonomous underwater vehicles. Ocean Eng. 2017, 139, 250–264. [Google Scholar] [CrossRef]
- Abhilash, C. Terrain Aided Navigation for Autonomous Underwater Vehicles with Local Gaussian Processes. Master’s Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2017. [Google Scholar]
- Ge, J.; Cheng, J.; Qi, B. A Non-Rigid Terrain Transformation Particle Filter Suitable for Terrain-Aided Navigation without Sound Velocity Profile. Ocean Eng. 2024, 294, 116858. [Google Scholar] [CrossRef]
- Bucy, R.S.; Senne, K.D. Digital synthesis of non-linear filters. Automatica 1971, 7, 287–298. [Google Scholar] [CrossRef]
- Ånonsen, K.B.; Hallingstad, O.; Hagen, O.; Mandt, M. Terrain aided AUV navigation—A comparison of the point mass filter and terrain contour matching algorithms. In Proceedings of the UDT Europe, Amsterdam, The Netherlands, 21–23 June 2005. [Google Scholar]
- Zhou, L.; Cheng, X.; Zhu, Y.; Dai, C.; Fu, J. An effective terrain aided navigation for low-cost autonomous underwater vehicles. Sensors 2017, 17, 680. [Google Scholar] [CrossRef]
- Sung, C.K.; Lee, S.J. Moment matched gaussian kernel and region representative likelihood for performance improvement of PMF-based TRN. Int. J. Control Autom. Syst. 2020, 18, 239–251. [Google Scholar] [CrossRef]
- Wan, X.; Ran, J.; Jin, S. Sensitivity analysis of gravity anomalies and vertical gravity gradient data for bathymetry inversion. Mar. Geophys. Res. 2019, 40, 87–96. [Google Scholar] [CrossRef]
- Wan, X.; Liu, B.; Sui, X.; Annan, R.F.; Hao, R.; Min, Y. Bathymetry inversion using the deflection of the vertical: A case study in South China Sea. Geod. Geodyn. 2022, 13, 492–502. [Google Scholar] [CrossRef]
- Mayer, L.; Jakobsson, M.; Allen, G.; Dorschel, B.; Falconer, R.; Ferrini, V.; Lamarche, G.; Snaith, H.; Weatherall, P. The Nippon Foundation—GEBCO Seabed 2030 Project: The Quest to See the World’s Oceans Completely Mapped by 2030. Geosciences 2018, 8, 63. [Google Scholar] [CrossRef]
- Caress, D.W.; Thomas, H.; Kirkwood, W.J.; McEwen, R.; Henthorn, R.; Clague, D.A.; Paull, C.K.; Paduan, J.; Maier, K.L.; Reynolds, J.R.; et al. High-resolution multibeam, sidescan, and subbottom surveys using the MBARI AUV D. Allan B. In Marine Habitat Mapping Technology for Alaska; Alaska Sea Grant: Fairbanks, AK, USA, 2008; pp. 47–69. [Google Scholar]
- Stateczny, A.; Błaszczak-Bąk, W.; Sobieraj-Żłobińska, A.; Motyl, W.; Wisniewska, M. Methodology for processing of 3D multibeam sonar big data for comparative navigation. Remote Sens. 2019, 11, 2245. [Google Scholar] [CrossRef]
- Xu, S.; Ma, T.; Li, Y.; Ding, S.; Gao, J.; Xia, J.; Qi, H.; Gu, H. An effective stereo SLAM with high-level primitives in underwater environment. Meas. Sci. Technol. 2023, 34, 105405. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Y.; Ma, T.; Cong, Z.; Zhang, W. Bathymetric particle filter SLAM with graph-based trajectory update method. IEEE Access 2021, 9, 85464–85475. [Google Scholar] [CrossRef]
- Ling, Y.; Li, Y.; Ma, T.; Cong, Z.; Xu, S.; Li, Z. Active Bathymetric SLAM for autonomous underwater exploration. Appl. Ocean. Res. 2023, 130, 103439. [Google Scholar] [CrossRef]
- Palomer, A.; Ridao, P.; Ribas, D. Multibeam 3D underwater SLAM with probabilistic registration. Sensors 2016, 16, 560. [Google Scholar] [CrossRef]
- Norgren, P.; Skjetne, R. A multibeam-based SLAM algorithm for iceberg mapping using AUVs. IEEE Access 2018, 6, 26318–26337. [Google Scholar] [CrossRef]
- Kim, T.; Kim, J. Panel-based bathymetric SLAM with a multibeam echosounder. In Proceedings of the 2017 IEEE Underwater Technology (UT), Busan, Republic of Korea, 21–24 February 2017; pp. 1–5. [Google Scholar]
- Zandara, S.; Ridao, P.; Ribas, D.; Mallios, A.; Palomer, A. Probabilistic surface matching for bathymetry based SLAM. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 40–45. [Google Scholar]
- Haraldstad, V. A Side-Scan Sonar Based Simultaneous Localization and Mapping Pipeline for Underwater Vehicles. Master’s Thesis, NTNU, Trondheim, Norway, 2023. [Google Scholar]
- Ozog, P. Advances in Simultaneous Localization and Mapping in Confined Underwater Environments Using Sonar and Optical Imaging. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2016. [Google Scholar]
- Larsen, M.K. Terrain-Based Navigation for Unmanned Underwater Vehicles Using Visual Simultaneous Localization and Mapping. Master’s Thesis, NTNU, Trondheim, Norway, 2021. [Google Scholar]
- Guth, F.; Silveira, L.; Botelho, S.; Drews, P.; Ballester, P. Underwater SLAM: Challenges, state of the art, algorithms and a new biologically-inspired approach. In Proceedings of the 5th IEEE RAS/EMBS International Conference on Biomedical Robotics and Biomechatronics, Sao Paolo, Brazil, 12–15 August 2014; pp. 981–986. [Google Scholar]
- Palomer, A.; Ridao, P.; Forest, J.; Ribas, D. Underwater Laser Scanner: Ray-Based Model and Calibration. IEEE/ASME Trans. Mechatron. 2019, 24, 1986–1997. [Google Scholar] [CrossRef]
- Roman, C.; Inglis, G.; Rutter, J. Application of structured light imaging for high resolution mapping of underwater archaeological sites. In Proceedings of the OCEANS’10 IEEE, Sydney, Australia, 24–27 May 2010; pp. 1–9. [Google Scholar]
- Yang, Y.; Zheng, B.; Kan, L.Y.; Yu, J.; Wang, J.C. 3D color reconstruction based on underwater RGB laser line scanning system. Optik 2014, 125, 6074–6077. [Google Scholar] [CrossRef]
- Han, G.; Gong, A.; Wang, H.; Martínez-García, M.; Peng, Y. Multi-AUV collaborative data collection algorithm based on Q-learning in underwater acoustic sensor networks. IEEE Trans. Veh. Technol. 2021, 70, 9294–9305. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Q.; Shen, Y.; Wang, T.; Dai, N.; He, B. Multi-AUV cooperative search method based on dynamic optimal coverage. Ocean Eng. 2023, 288, 116168. [Google Scholar] [CrossRef]
- Ma, X.; Yanli, C.; Bai, G.; Liu, J. Multi-AUV collaborative operation based on time-varying navigation map and dynamic grid model. IEEE Access 2020, 8, 159424–159439. [Google Scholar] [CrossRef]
- Ma, T.; Zhang, W.; Li, Y.; Zhao, Y.; Zhang, Q.; Mei, X.; Fan, J. Communication-constrained cooperative bathymetric simultaneous localisation and mapping with efficient bathymetric data transmission method. J. Navig. 2022, 75, 1000–1016. [Google Scholar] [CrossRef]
- Wang, Q.; He, B.; Zhang, Y.; Yu, F.; Huang, X.; Yang, R. An autonomous cooperative system of multi-AUV for underwater targets detection and localization. Eng. Appl. Artif. Intell. 2023, 121, 105907. [Google Scholar] [CrossRef]
- Häusler, A.J.; Saccon, A.; Pascoal, A.M.; Hauser, J.; Aguiar, A.P. Cooperative AUV motion planning using terrain information. In Proceedings of the 2013 MTS/IEEE OCEANS, Bergen, Germany, 10–13 June 2013; pp. 1–10. [Google Scholar]
- Tan, Y.T.; Chitre, M.; Hover, F.S. Cooperative bathymetry-based localization using low-cost autonomous underwater vehicles. Auton. Robot. 2016, 40, 1187–1205. [Google Scholar] [CrossRef]
- Paull, L.; Huang, G.; Seto, M.; Leonard, J.J. Communication-constrained multi-AUV cooperative SLAM. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 509–516. [Google Scholar]
- Matsuda, T.; Maki, T.; Sato, Y.; Sakamaki, T.; Ura, T. Alternating landmark navigation of multiple AUVs for wide seafloor survey: Field experiment and performance verification. J. Field Robot. 2018, 35, 359–395. [Google Scholar] [CrossRef]
- Al-Tawil, B.; Hempel, T.; Abdelrahman, A.; Al-Hamadi, A. A review of visual SLAM for robotics: Evolution, properties, and future applications. Front. Robot. AI 2024, 11, 1347985. [Google Scholar] [CrossRef]
- McAllister, M. The Problem with ‘Digital Realism’ in underwater archaeology: Photogrammetric digital 3D visualization and interpretation. J. Marit. Archaeol. 2021, 16, 253–275. [Google Scholar] [CrossRef]
- Bräuer-Burchardt, C.; Munkelt, C.; Bleier, M.; Heinze, M.; Gebhart, I.; Kühmstedt, P.; Notni, G. Underwater 3D scanning system for cultural heritage documentation. Remote Sens. 2023, 15, 1864. [Google Scholar] [CrossRef]
- Bodenmann, A.; Thornton, B.; Nakajima, R.; Ura, T. Methods for quantitative studies of seafloor hydrothermal systems using 3D visual reconstructions. Robomech. J. 2017, 4, 1–9. [Google Scholar] [CrossRef]
- Kotaro, Y.; Torres, R.; Castro, F. Multi-image photogrammetry to record and reconstruct underwater shipwreck sites. J. Archaeol. Method Theory 2017, 24, 703–725. [Google Scholar]
- Gu, L.; Chen, W.; Hu, X.; Tong, Z.; Shao, X. Refraction correction for deep-water three-dimensional visual measurement based on multi-objective optimization. Opt. Express 2023, 31, 31383–31396. [Google Scholar] [CrossRef]
- Jin, S.; Wang, H.; Zhu, X. A fast underwater calibration method based on vanishing point optimization of two orthogonal parallel lines. Measurement 2021, 178, 109305. [Google Scholar]
- James, S.; Smart, M.; Waslander, S.L. Underwater stereo SLAM with refraction correction. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013. [Google Scholar]
- Bonin-Font, F.; Cosic, A.; Negre, P.L.; Solbach, M.; Oliver, G. Stereo SLAM for robust dense 3D reconstruction of underwater environments. In Proceedings of the OCEANS 2015, Genova, Italy, 18–21 May 2015. [Google Scholar]
- Wang, K.; Zhu, T.; Wang, J. Impact of terrain factors on the matching performance of terrain-aided navigation. Navigation 2019, 66, 451–462. [Google Scholar] [CrossRef]
- Teixeira, F.C.; Quintas, J.; Pascoal, A. Robust methods of magnetic navigation of marine robotic vehicles. IFAC-PapersOnLine 2017, 50, 3470–3475. [Google Scholar]
- Wang, R.; Li, Y.; Teng, M.; Zheng, C.; Gong, Y.; Jiang, Y.; Qiang, Z. A new model and method of terrain-aided positioning confidence interval estimation. J. Mar. Sci. Technol. 2021, 27, 1–13. [Google Scholar]
- Xie, Y. Terrain Aided Navigation. Master’s Thesis, Royal Institute of Technology (KTH), Stockholm, Sweden, 5 May 2005. [Google Scholar]
- Choi, J.; Park, J.; Jung, J.; Lee, Y.; Choi, H.T. Development of an autonomous surface vehicle and performance evaluation of autonomous navigation technologies. Int. J. Control Autom. Syst. 2020, 18, 535–545. [Google Scholar] [CrossRef]
- Gade, K. NavLab, a Generic Simulation and Post-processing Tool for Navigation. Eur. J. Navig. 2004, 2, 51–59. [Google Scholar] [CrossRef]
- Salavasidis, G.; Harris, C.; McPhail, S.; Phillips, A.B.; Rogers, E. Terrain Aided Navigation for Long Range AUV operations at arctic latitudes. In Proceedings of the 2016 IEEE/OES Autonomous Underwater Vehicles (AUV), Tokyo, Japan, 6–9 November 2016; pp. 115–123. [Google Scholar]
- Hare, R. Depth and Position Error Budgets for Mulitbeam Echosounding. Int. Hydrogr. Rev. 1995, 72. Available online: https://journals.lib.unb.ca/index.php/ihr/article/view/23178 (accessed on 27 May 2024).
- Wang, Y.; Shao, S.; Wang, S.; Wu, Z.; Zhang, H.; Hu, X. Measurement error analysis of multibeam echosounder system mounted on the deep-sea autonomous underwater vehicle. Ocean Eng. 2014, 91, 111–121. [Google Scholar] [CrossRef]
- Mohammadloo, H.T.; Snellen, M.G.; Simons, D. Assessing the performance of the multi-beam echo-sounder bathymetric uncertainty prediction model. Appl. Sci. 2020, 10, 4671. [Google Scholar] [CrossRef]
- Wibowo, W.A.; Wisayantono, D.; Windupranata, W. Analysis of Contributing Components to Depth Error for Multibeam Echosounding. ITB Indones. J. Geospat. 2018, 5, 11–24. [Google Scholar]
- Kang, S.; Yu, M.-J. Ant-mutated immune particle filter design for terrain referenced navigation with interferometric radar altimeter. Remote Sens. 2021, 13, 2189. [Google Scholar] [CrossRef]
- Cong, Z.; Ma, T.; Li, Y.; Yuan, M.; Ling, Y.; Du, H.; Qi, C.; Li, Z.; Xu, S.; Zhang, Q. A Storage-Saving Quadtree-Based Multibeam Bathymetry Map Representation Method. J. Mar. Sci. Eng. 2023, 11, 709. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).