On Connecting Hydrosocial Parameters to Vegetation Greenness Differences in an Evolving Groundwater-Dependent Ecosystem
Abstract
1. Introduction
2. Materials and Methods
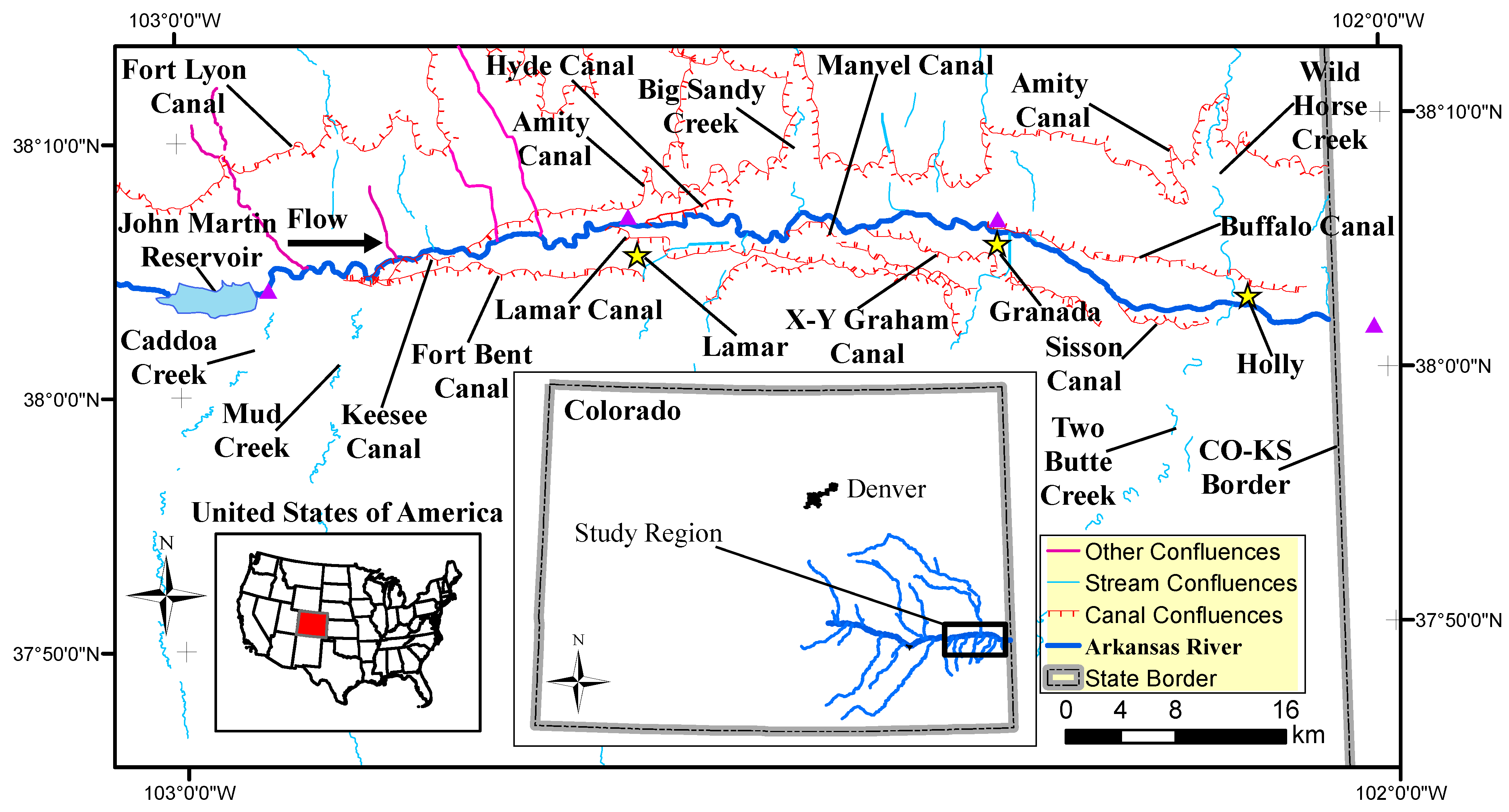
2.1. Study Area
2.2. The Landsat Data and Strategic Spatial Partitioning
2.2.1. Temporal Representation of NDVI
2.2.2. Spatial Representation of NDVI
2.3. Temporal Covariates
2.4. Spatial Covariates
2.5. The Linear Models
2.5.1. The Priors
2.5.2. Convergence, Model Checking, and Model Comparison
2.6. Prediction Testing
2.6.1. Hypothesis 1: Identifiable Temporal Trend at Catchment Scale
2.6.2. Hypothesis 2: Precipitation Will Have a Shorter Lag Effect
2.6.3. Hypothesis 3: Confluences with Perennial Streams Increase Cumulative Vegetation Density
3. Results
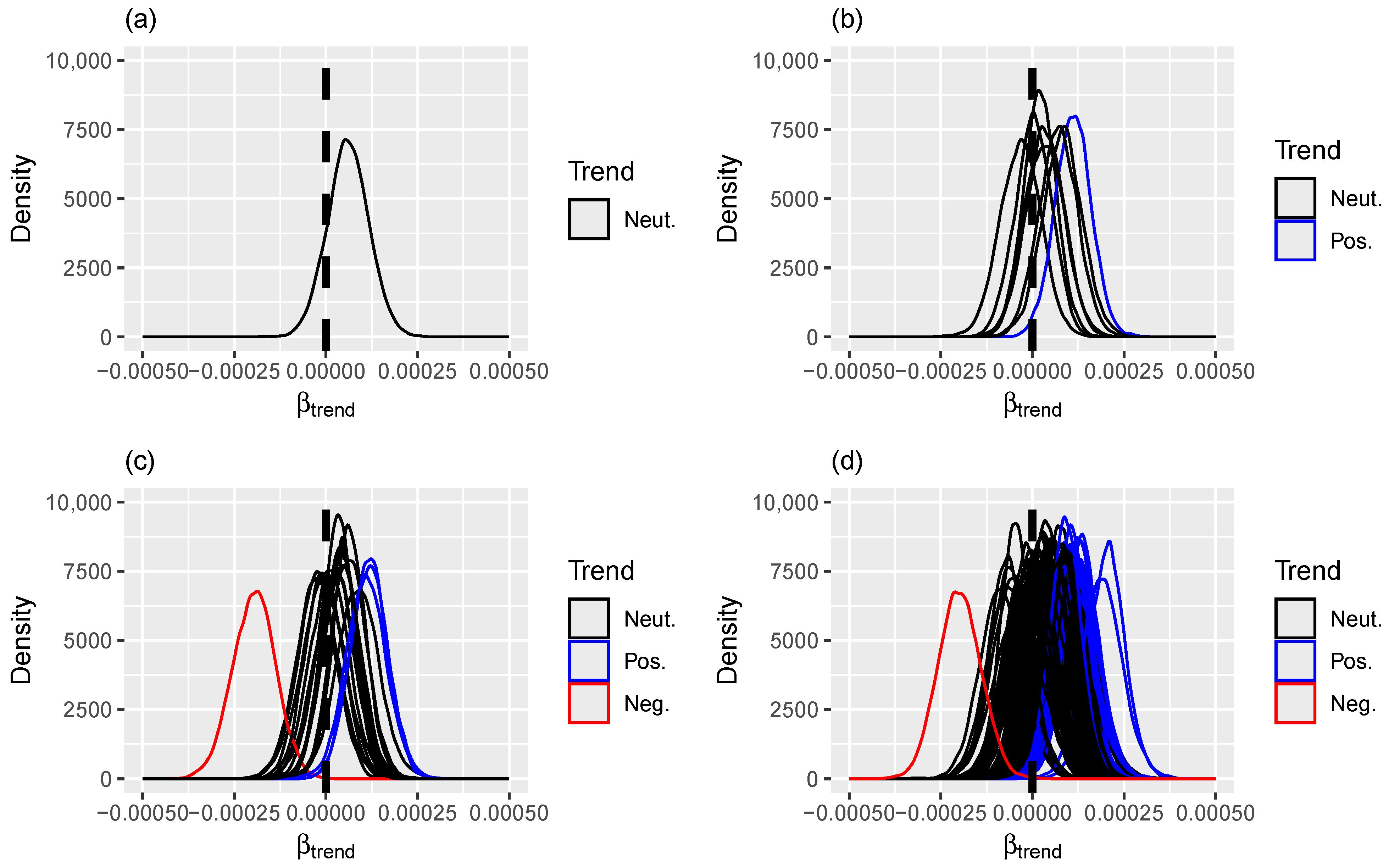
3.1. Hypothesis 1: Identifiable Temporal Trend at Catchment Scale
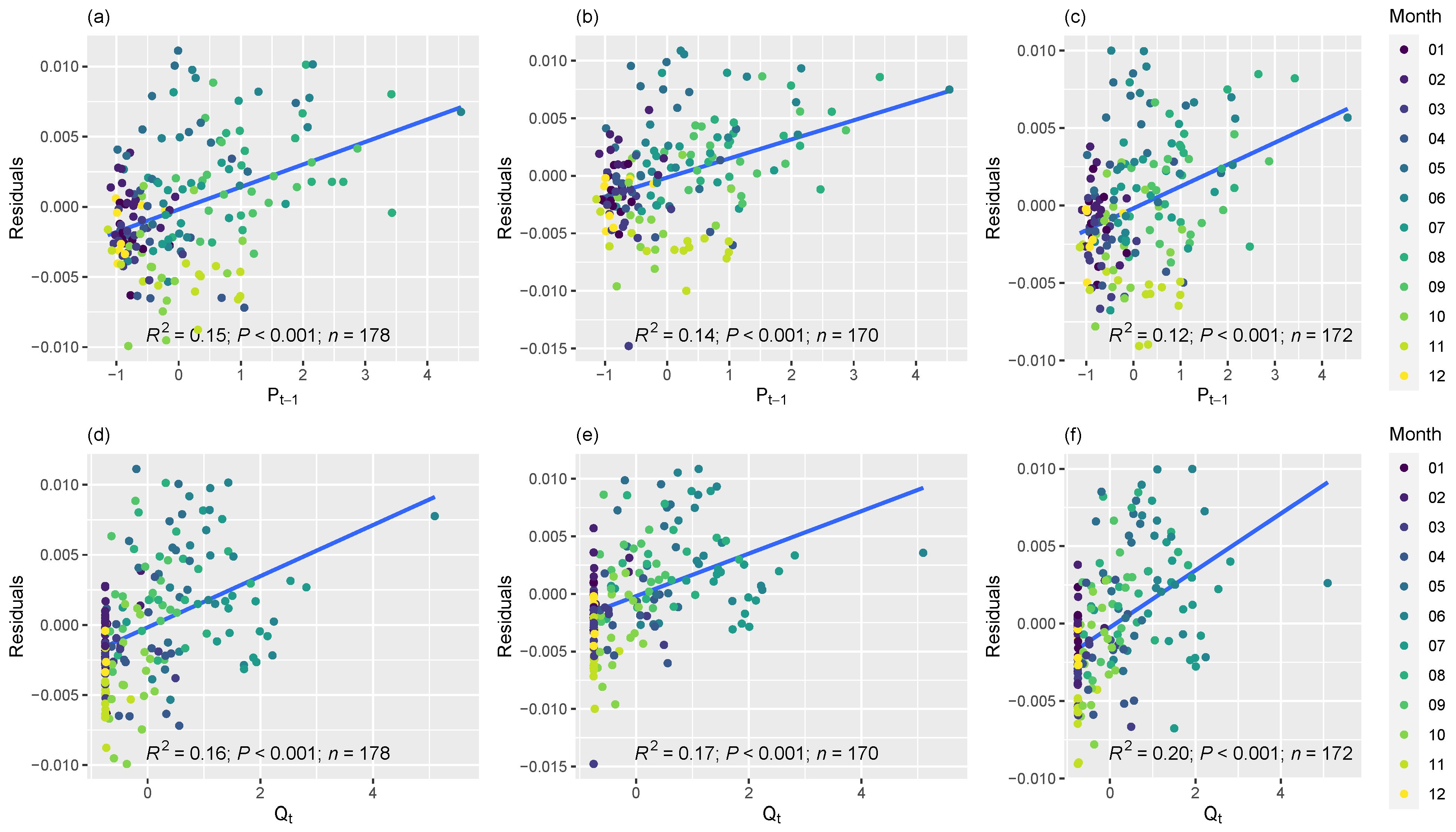
3.2. Hypothesis 2: Precipitation Will Have a Shorter Lag Effect
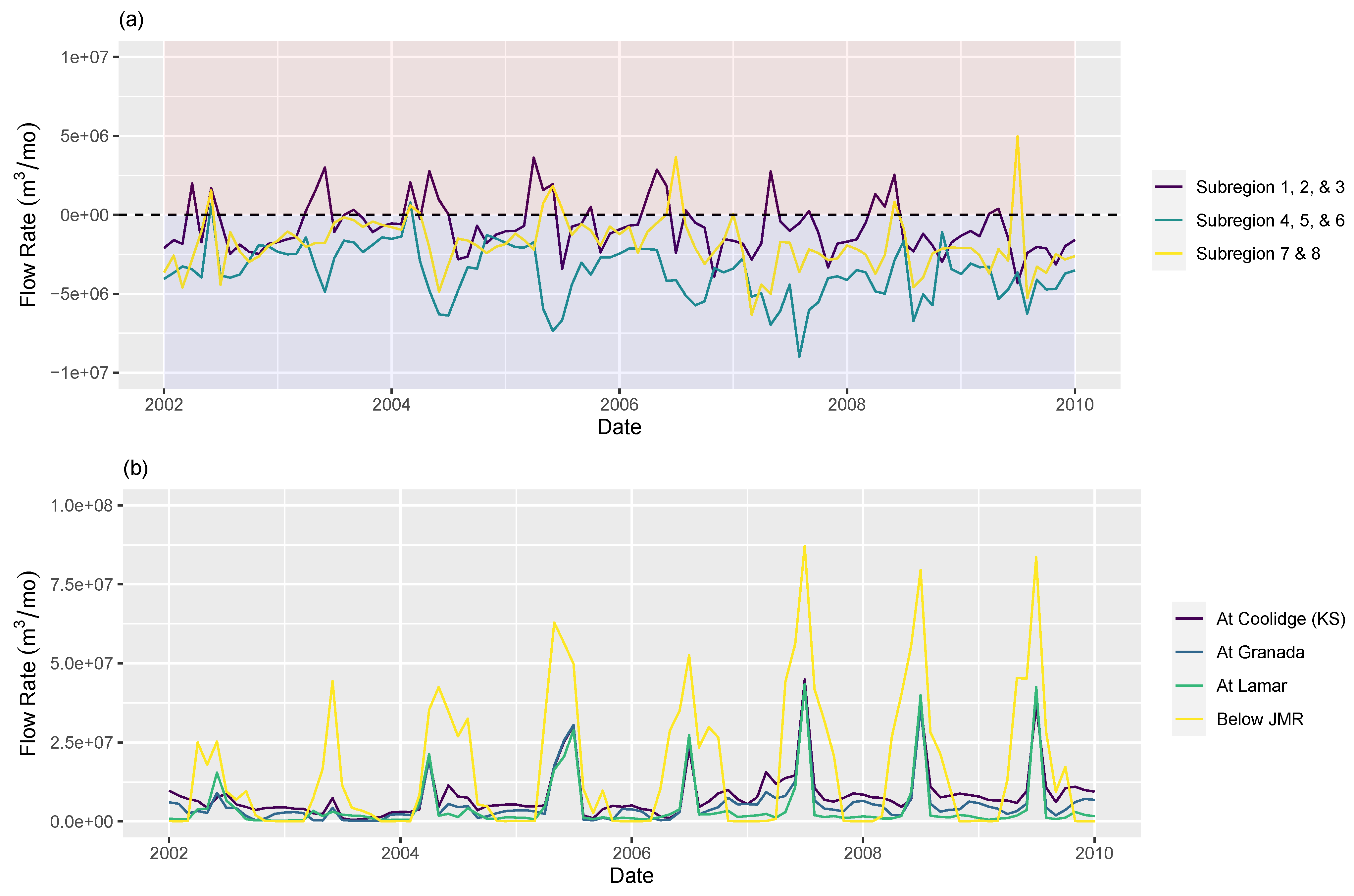
3.3. Hypothesis 3: Confluences with Perennial Streams Increase Vegetation Density
4. Discussion
4.1. Hypothesis 1: Identifiable Temporal Trend at Catchment Scale
4.2. Hypothesis 2: Precipitation Will Have a Shorter Lag Effect
4.3. Hypothesis 3: Confluences with Perennial Streams Increase Vegetation Density
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1
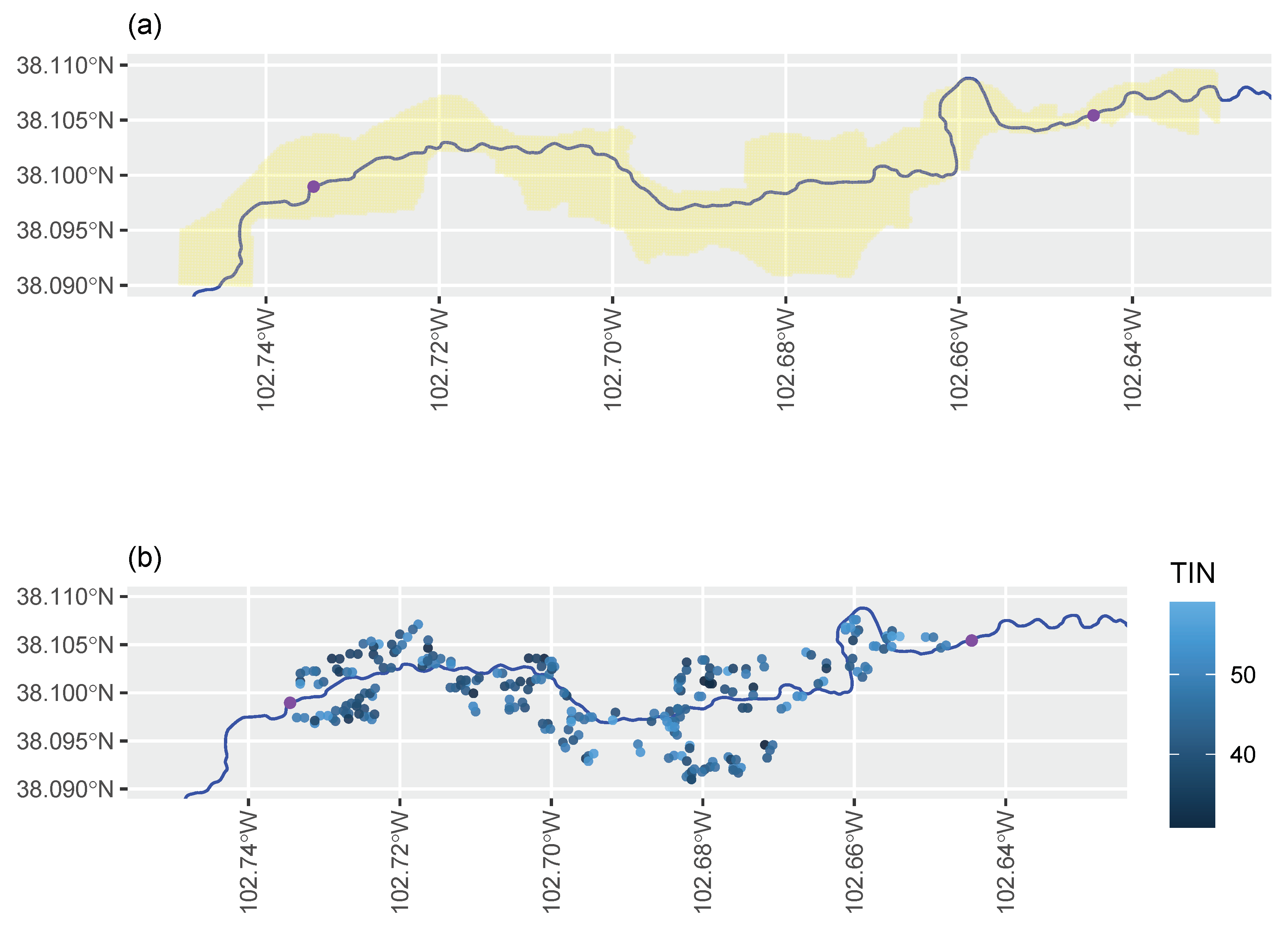
Appendix A.2

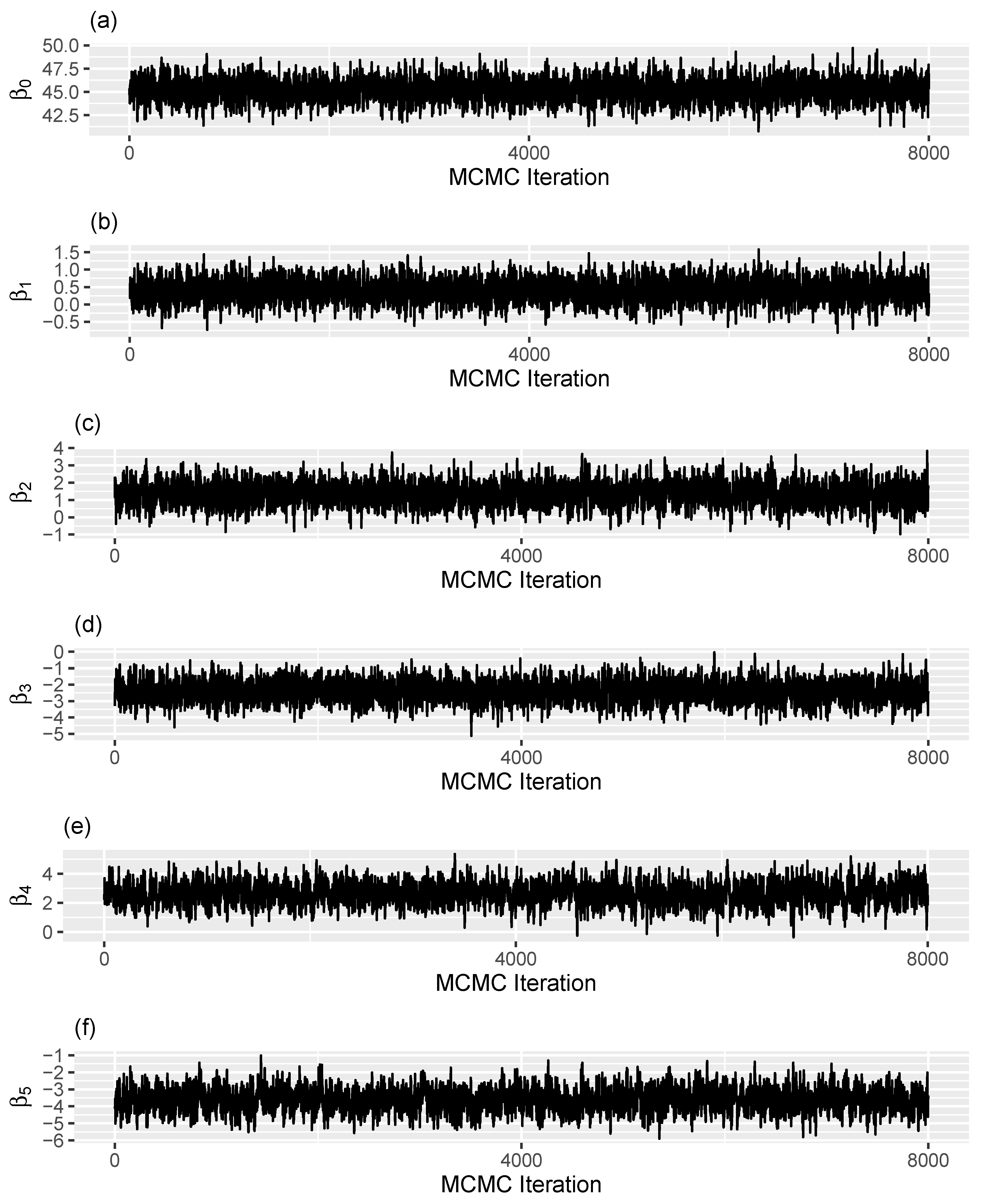
References
- Saccò, M.; Mammola, S.; Altermatt, F.; Alther, R.; Bolpagni, R.; Brancelj, A.; Brankovits, D.; Fišer, C.; Gerovasileiou, V.; Griebler, C.; et al. Groundwater is a hidden global keystone ecosystem. Glob. Change Biol. 2023, 30, e17066. [Google Scholar] [CrossRef] [PubMed]
- Pace, G.; Gutiérrez-Cánovas, C.; Henriques, R.; Carvalho-Santos, C.; Cássio, F.; Pascoal, C. Remote sensing indicators to assess riparian vegetation and river ecosystem health. Ecol. Indic. 2022, 144, 109519. [Google Scholar] [CrossRef]
- Orellana, F.; Verma, P.; Loheide, S.P.; Daly, E. Monitoring and modeling water-vegetation interactions in groundwater-dependent ecosystems. Rev. Geophys. 2012, 3, 501–512. [Google Scholar] [CrossRef]
- Eamus, D.; Hatton, T.; Cook, P.; Colvin, C. Ecohydrology: Vegetation Function, Water and Resource Management; CSIRO Publishing: Clayton, VIC, Australia, 2006. [Google Scholar] [CrossRef]
- Kendy, E.; Bredehoeft, J.D. Transient effects of groundwater pumping and surface-water-irrigation returns on streamflow. Water Resour. Res. 2006, 8. [Google Scholar] [CrossRef]
- Ronayne, M.; Roudebush, J.; Stednick, J. Analysis of managed aquifer recharge for retiming streamflow in an alluvial river. J. Hydrol. 2017, 544, 373–382. [Google Scholar] [CrossRef]
- Bailey, R.T.; Wible, T.C.; Arabi, M.; Records, R.M.; Ditty, J. Assessing regional-scale spatio-temporal patterns of groundwater–surface water interactions using a coupled SWAT-MODFLOW model. Hydrol. Process. 2016, 23, 4420–4433. [Google Scholar] [CrossRef]
- Maddock, T.; Baird, K.; Hanson, R.; Schmid, W.; Ajami, H. RIP-ET: A riparian evapotranspiration package for MODFLOW-2005. U.S. Geol. Surv. Tech. Methods 2012, 6, A39. [Google Scholar]
- Loheide, S.P.; Gorelick, S. Riparian hydroecology: A coupled model of the observed interactions between groundwater flow and meadow vegetation patterning. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Tamea, S.; Laio, F.; Ridolfi, L.; D’Odorico, P.; Rodriguez-Iturbe, I. Ecohydrology of groundwater-dependent ecosystems: 2. Stochastic soil moisture dynamics. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Laio, F.; Tamea, S.; Ridolfi, L.; D’Odorico, P.; Rodriguez-Iturbe, I. Ecohydrology of groundwater-dependent ecosystems: 1. Stochastic water table dynamics. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Albano, C.; Mcgwire, K.; Hausner, M.; Mcevoy, D.; Morton, C.; Huntington, J. Drought Sensitivity and Trends of Riparian Vegetation Vigor in Nevada, USA (1985–2018). Remote Sens. 2020, 12, 1362. [Google Scholar] [CrossRef]
- Vanderhoof, M.; Christensen, J.; Alexander, L. Influence of multi-decadal land use, irrigation practices and climate on riparian corridors across the Upper Missouri River Headwaters Basin, Montana. Hydrol. Earth Syst. Sci. 2019, 23, 4269–4292. [Google Scholar] [CrossRef]
- Huntington, J.; McGwire, K.; Morton, C.; Snyder, K.; Peterson, S.; Erickson, T.; Niswonger, R.; Carroll, R.; Smith, G.; Allen, R. Assessing the role of climate and resource management on groundwater dependent ecosystem changes in arid environments with the Landsat archive. Remote Sens. Environ. 2016, 185, 186–197. [Google Scholar] [CrossRef]
- Groeneveld, D. Remotely-sensed groundwater evapotranspiration from alkali scrub affected by declining water table. J. Hydrol. 2008, 358, 294–303. [Google Scholar] [CrossRef]
- Tuinstra, J.; van Wensem, J. Ecosystem services in sustainable groundwater management. Sci. Total Environ. 2014, 485–486, 798–803. [Google Scholar] [CrossRef] [PubMed]
- Lurtz, M. Multiscale Connections between a Groundwater Dependent Ecosystem and Socio-Hydrology: Insight Gained from Numerical Modeling, Geospatial Informatics, and Bayesian Statistics. Ph.D. Thesis, Department of Civil and Environmental Engineering, Colorado State University, Fort Collins, CO, USA, 2023. [Google Scholar]
- Morway, E.D.; Gates, T.K.; Niswonger, R.G. Appraising options to reduce shallow groundwater tables and enhance flow conditions over regional scales in an irrigated alluvial aquifer system. J. Hydrol. 2013, 495, 216–237. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Healy, R.W.; Cook, P.G. Choosing appropriate techniques for quantifying groundwater recharge. Hydrogeol. J. 2002, 10, 18–39. [Google Scholar] [CrossRef]
- Berghuijs, W.; Luijendijk, E.; Moeck, C.; van der Velde, Y.; Allen, S. Global Recharge Data Set Indicates Strengthened Groundwater Connection to Surface Fluxes. Geophys. Res. Lett. 2022, 49, e2022GL099010. [Google Scholar] [CrossRef]
- Gates, T.K.; Garcia, L.A.; Hemphill, R.A.; Morway, E.D.; Elhaddad, A. Irrigation Practices, Water Consumption, and Return Flows in Colorado’s Lower Arkansas River Basin: Field and Model Investigations; CWI Completion Report No. 221; CAES Report No. TR12-10; Colorado Water Institute: Fort Collins, CO, USA, 2012. [Google Scholar]
- Gates, T.K.; Steed, G.H.; Niemann, J.D.; Labadie, J.W. Data for Improved Water Management in Colorado’s Arkansas River Basin: Hydrological and Water Quality Studies; Colorado Water Institute Special Report No. 24; Colorado Agricultural Experiment Station No. TR-16-03; Colorado Water Institute: Fort Collins, CO, USA, 2016. [Google Scholar]
- Kittel, G.; Vanwie, E.; Damm, M.; Rondeau, R.; Kettler, S.; Mcmullen, A.; Sanderson, J. A Classification of Riparian Wetland Plant Associations of Colorado: User Guide to the Classification Project; Technical Report; Colorado Natural Heritage Program, Colorado State University: Fort Collins, CO, USA, 1999. [Google Scholar]
- Osborn, B. Lower Arkansas River Watershed Plan: John Martin Reservoir to Stateline; Technical Report; Colorado Water Institute—Colorado State University: Fort Collins, CO, USA, 2019. [Google Scholar]
- González-Sargas, E.; Shafroth, P.; Baró, F. Integrating social-ecological outcomes into invasive species management: The Tamarix case. NeoBiota 2024, 92, 173–192. [Google Scholar] [CrossRef]
- Hultine, K.R.; Froend, R.; Blasini, D.; Bush, S.E.; Karlinski, M.; Koepke, D.F. Hydraulic traits that buffer deep-rooted plants from changes in hydrology and climate. Hydrol. Process. 2020, 34, 209–222. [Google Scholar] [CrossRef]
- Yao, J.; Liu, H.; Huang, J.; Gao, Z.; Wang, G.; Li, D.; Yu, H.; Chen, X. Accelerated dryland expansion regulates future variability in dryland gross primary production. Nat. Commun. 2020, 20, 1665. [Google Scholar] [CrossRef] [PubMed]
- Nagler, P.; Morino, K.; Didan, K.; Erker, J.; Osterberg, J.; Hultine, K.; Glenn, E. Wide-area estimates of saltcedar (Tamarix spp.) evapotranspiration on the lower Colorado River measured by heat balance and remote sensing methods. Ecohydrology 2009, 2, 18–33. [Google Scholar] [CrossRef]
- Glenn, E.P.; Nagler, P.L.; Morino, K.; Hultine, K.R. Phreatophytes under stress: Transpiration and stomatal conductance of saltcedar (Tamarix spp.) in a high-salinity environment. Plant Soil 2013, 1–2, 655–672. [Google Scholar] [CrossRef]
- Yuana, G.; Zhang, P.; Shaoa, M.; Luoa, Y.; Zhu, X. Energy and water exchanges over a riparian Tamarix spp. stand in the lower Tarim River basin under a hyper-arid climate. Agric. For. Meteorol. 2014, 194, 144–154. [Google Scholar] [CrossRef]
- Brunke, M.; Gonser, T. The ecological significance of exchange processes between rivers and groundwater. Freshw. Biol. 1997, 37, 1–33. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Hooten, M.B.; Hefley, T.J. Bringing Bayesian Models to Life; Chapman and Hall/CRC: Boca Raton, FL, USA, 2019. [Google Scholar]
- Rumyantseva, O.; Sarantsev, A.; Strigul, N. Autoregressive Modeling of Forest Dynamics. Forests 2019, 10, 1074. [Google Scholar] [CrossRef]
- Jiang, B.; Liang, S.; Wang, J.; Xiao, Z. Modeling MODIS LAI time series using three statistical methods. Remote Sens. Environ. 2010, 14, 1432–1444. [Google Scholar] [CrossRef]
- Montanari, A.; Rosso, R.; Taqqu, M. Fractionally differenced ARIMA models applied to hydrologic time series: Identification, estimation, and simulation. Water Resour. Res. 1997, 33, 1035–1044. [Google Scholar] [CrossRef]
- Bras, R.L.; Rodriguez-Iturbe, I. Random Functions and Hydrology; Addison-Wesley Publ. Co.: Reading, MA, USA, 1985; ISBN 0-486-67626-9. [Google Scholar]
- Salas, J.D.; Tabios, G.Q., III; Bartolini, P. Approaches to multivariate modeling of water resources time series. J. Am. Water Resour. Assoc. 1985, 21, 683–708. [Google Scholar] [CrossRef]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications—With R Examples, 4th ed.; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Fernandes, M.R.; Aguiar, F.C.; Ferreira, M.T. Assessing riparian vegetation structure and the influence of land use using landscape metrics and geostatistical tools. Landsc. Urban Plan. 2008, 99, 166–177. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Pelgrum, H.; Wang, J.; Ma, Y.; Moreno, J.F.; Roerink, G.J.; van der Wal, T. A remote sensing surface energy balance algorithm for land (SEBAL), Part 1: Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Elhaddad, A.; Garcia, L.A. Surface Energy Balance-Based Model for Estimating Evapotranspiration Taking into Account Spatial Variability in Weather. J. Irrig. Drain. Eng. 2008, 6, 681–689. [Google Scholar] [CrossRef]
- Senay, G.B.; Budde, M.; Verdin, J.P.; Melesse, A.M. A coupled remote sensing and simplified surface energy balance approach to estimate actual evapotranspiration from irrigated fields. Sensors 2007, 6, 979–1000. [Google Scholar] [CrossRef]
- Hobbs, N.T.; Hooten, M.B. Bayesian Models: A Statistical Primer for Ecologists; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Anderson, K.; Fawcett, D.; Cugulliere, A.; Benford, S.; Jones, D.; Leng, R. Vegetation expansion in the subnival Hindu Kush Himalaya. Glob. Change Biol. 2019, 26, 1608–1625. [Google Scholar] [CrossRef]
- Nguyen, U.; Glenn, E.; Nagler, P.; Scott, R. Long-term decrease in satellite vegetation indices in response to environmental variables in an iconic desert riparian ecosystem: The Upper San Pedro, Arizona, United States. Ecohydrology 2015, 8, 610–625. [Google Scholar] [CrossRef]
- de Jong, R.; de Bruin, S.; de Wit, A.; Schaepman, M.E.; Dent, D.L. Analysis of monotonic greening and browning trends from global NDVI time-series. Remote Sens. Environ. 2010, 115, 692–702. [Google Scholar] [CrossRef]
- Lin, Y.; Xin, X.; Zhang, H.; Wang, X. The implications of serial correlation and time-lag effects for the impact study of climate change on vegetation dynamics—A case study with Hulunber meadow steppe, Inner Mongolia. Int. J. Remote Sens. 2015, 36, 5031–5044. [Google Scholar] [CrossRef]
- Hefley, T.; Broms, K.; Brost, B.; Buderman, F.; Kay, S.; Scharf, H.; Tipton, J.; Williams, P.; Hooten, M. The basis function approach for modeling autocorrelation in ecological data. Ecol. Concepts Synth. 2016, 98, 632–646. [Google Scholar] [CrossRef]
- Heaton, M.; Datta, A.; Finley, A.; Furrer, R.; Guinness, J.; Guhaniyogi, R.; Gerber, F.; Gramacy, R.; Hammerling, D.; Katzfuss, M.; et al. A Case Study Competition Among Methods for Analyzing Large Spatial Data. J. Agric. Biol. Environ. Stat. 2019, 24, 398–425. [Google Scholar] [CrossRef]
- Environmental Systems Research Institute. ArcGIS Desktop, v10.0+; Environmental Systems Research Institute: Redlands, CA, USA, 2011. [Google Scholar]
- U.S. Geological Survey. National Water Information System Data Available on the World Wide Web (USGS Water Data for the Nation). 2016. Available online: https://waterdata.usgs.gov/nwis (accessed on 1 January 2023).
- Senay, G.B.; Schauer, M.; Friedrichs, M.; Velpuri, N.M.; Singh, R.K. Satellite-based water use dynamics using historical Landsat data (1984–2014) in the southwestern United States. Remote Sens. Environ. 2017, 202, 98–112. [Google Scholar] [CrossRef]
- Hausner, M.; Huntington, J.; Nash, C.; Morton, C.; McEvoy, D.; Pilliod, D.; Hegewisch, K.; Daudert, B.; Abatzoglou, J.; Grant, G. Assessing the effectiveness of riparian restoration projects using Landsat and precipitation data from the cloud-computing application ClimateEngine.org. Ecol. Eng. 2018, 120, 432–440. [Google Scholar] [CrossRef]
- Eamus, D.; Zolfaghar, S.; Villalobos-Vega, R.; Cleverly, J.; Huete, A. Groundwater-dependent ecosystems: Recent insights from satellite and field-based studies. Hydrol. Earth Syst. Sci. 2015, 10, 4229–4256. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Dewitz, J.; U.S. Geological Survey. National Land Cover Database (NLCD) 2019 Products; Earth Resources Observation and Science (EROS) Center: Sioux Falls, SD, USA, 2021.
- US Supreme Court Case 514, C. In AMENDED APPENDIX C.1, Hydrologic—Institutional Model: Model Documentation, Amended September 2011; Colorado Department of Water Resources: Denver, CO, USA, 2011.
- Ryan, J.A.; Ulrich, J.M.; Bennett, R.; Joy, C. xts: EXtensible Time Series. 2020. Available online: https://cran.r-project.org/web/packages/xts/index.html (accessed on 1 January 2023).
- Pettorelli, N.; Vik, J.; Mysterud, A.; Gaillard, J.; Tucker, C.; Stenseth, N. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Reed, B.C.; Loveland, T.R.; Tiezen, L.L. An approach to using AVHRR data to monitor U.S. great plains grasslands. Geocarto Int. 1996, 11, 13–22. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; McEvoy, D.J.; Redmond, K.T. The West Wide Drought Tracker: Drought Monitoring at Fine Spatial Scales. Bull. Am. Meteorol. Soc. 2017, 98, 1815–1820. [Google Scholar] [CrossRef]
- Colorado Department of Natural Resources. Division of Water Resources. 2022. Available online: https://dwr.colorado.gov/ (accessed on 1 January 2023).
- Blöschl, G.; Sivapalan, M. Scale Issues In Hydrological Modelling: A Review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Scott, R.; Cable, W.; Huxman, T.; Nagler, P.; Hernandez, M.; Goodrich, D. Multiyear riparian evapotranspiration and groundwater use for a semiarid watershed. J. Arid Environ. 2008, 72, 1232–1246. [Google Scholar] [CrossRef]
- Nagler, P.; Glenn, E.; Kim, H.; Emmerich, W.; Scott, R.; Huxman, T.; Huete, A. Relationship between evapotranspiration and precipitation pulses in a semiarid rangeland estimated by moisture flux towers and MODIS vegetation indices. J. Arid Environ. 2007, 70, 443–462. [Google Scholar] [CrossRef]
- Bartolini, P.; Salas, J.; Obeysekera, J. Multivariate Periodic ARMA(1, 1) Processes. Water Resour. Res. 1988, 24, 1237–1246. [Google Scholar] [CrossRef]
- Parsons, M.; Thoms, M.C. Patterns of vegetation greenness during flood, rain and dry resource states in a large, unconfined floodplain landscape. J. Arid Environ. 2013, 88, 24–38. [Google Scholar] [CrossRef]
- Mayes, M.; Caylor, K.; Singer, M.; Stella, J.; Roberts, D.; Nagler, P. Climate sensitivity of water use by riparian woodlands at landscape scales. Hydrol. Process. 2020, 34, 4884–4903. [Google Scholar] [CrossRef]
- Nagler, P.; Doody, T.; Glenn, E.; Jarchow, C.; Barreto-Muñoz, A.; Didan, K. Wide-area estimates of evapotranspiration by red gum (Eucalyptus camaldulensis) and associated vegetation in the Murray-Darling River Basin, Australia. Hydrol. Process. 2016, 30, 1376–1387. [Google Scholar] [CrossRef]
- Velpuri, N.M.; Senay, G.B.; Schauer, M.C.; Garcia, A.; Singh, R.K.; Friedrichs, M.; Kagone, S.; Haynes, J.; Conlon, T. Evaluation of hydrologic impact of an irrigation curtailment program using Landsat satellite data. Hydrol. Process. 2020, 34, 1697–1713. [Google Scholar] [CrossRef]
- Lv, J.; Wang, X.; Zhou, Y.; Qian, K.; Wan, L.; Eamus, D.; Tao, Z. Groundwater-dependent distribution of vegetation in Hailiutu River catchment, a semi-arid region in China. Ecohydrology 2012, 1, 142–149. [Google Scholar] [CrossRef]
- Sims, N.; Colloff, M. Remote sensing of vegetation responses to flooding of a semi-arid floodplain: Implications for monitoring ecological effects of environmental flows. Ecol. Indic. 2012, 18, 387–391. [Google Scholar] [CrossRef]
- Overmars, K.P.; de Koning, G.H.J.; Veldkamp, A. Spatial autocorrelation in multi-scale land use models. Ecol. Model. 2003, 164, 257–270. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.; Gao, X.; Ferreira, L. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- McCabe, M.; Aragon, B.; Houborg, R.; Mascaro, J. CubeSats in Hydrology: Ultrahigh-Resolution Insights Into Vegetation Dynamics and Terrestrial Evaporation. Water Resour. Res. 2017, 53, 10017–10024. [Google Scholar] [CrossRef]
- Hooten, M.B.; Wikle, C.K. Shifts in the spatio-temporal growth dynamics of shortleaf pine. Environ. Ecol. Stat. 2007, 14, 207–227. [Google Scholar] [CrossRef]
- Comber, A.; Wulder, M. Considering spatiotemporal processes in big data analysis: Insights from remote sensing of land cover and land use. Trans. GIS 2019, 23, 879–891. [Google Scholar] [CrossRef]

| No. | Name | Location (Long.°) | Dist. (km) |
|---|---|---|---|
| 1 | Below JMR to Below Fort Bent Canal | (begin, −102.8°] | 10.03 |
| 2 | Below Fort Bent Canal to Below Amity Canal | (−102.8°, −102.7°] | 11.38 |
| 3 | Below Amity Canal to Lamar Gage | (−102.7°, −102.6°] | 10.48 |
| 4 | Lamar Gage to Below Manvel Canal | (−102.6°, −102.5°] | 17.39 |
| 5 | Below Manvel Canal to Below X-Y Graham Canal | (−102.5°, −102.4°] | 8.78 |
| 6 | Below X-Y Graham Canal to Granada Gage | (−102.4°, −102.3°] | 11.28 |
| 7 | Granada Gage to Below Sisson-Stubbs Canal | (−102.3°, −102.2°] | 14.43 |
| 8 | Below Sisson-Stubbs Canal to CO-KS Border | (−102.2°, end] | 12.80 |
| - | Group 1 | Group 2 | Group 3 | Group 4 | Group 5 |
|---|---|---|---|---|---|
| Subregion | No. of Confluences | Canal Augmentation | Development | Perennial Tributary | Land Dry-Up |
| 1 | 4 | 0 | 0 | 0 | 0 |
| 2 | 3 | 1 | 0 | 1 | 1 |
| 3 | 2 | 1 | 1 | 0 | 0 |
| 4 | 2 | 0 | 1 | 0 | 0 |
| 5 | 1 | 1 | 0 | 1 | 1 |
| 6 | 2 | 1 | 0 | 0 | 0 |
| 7 | 2 | 0 | 0 | 0 | 1 |
| 8 | 3 | 1 | 0 | 1 | 0 |
| Model 1 (General) | Model 2 (Time) | Model 3 (Space) |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lurtz, M.R.; Morrison, R.R.; Nagler, P.L. On Connecting Hydrosocial Parameters to Vegetation Greenness Differences in an Evolving Groundwater-Dependent Ecosystem. Remote Sens. 2024, 16, 2536. https://doi.org/10.3390/rs16142536
Lurtz MR, Morrison RR, Nagler PL. On Connecting Hydrosocial Parameters to Vegetation Greenness Differences in an Evolving Groundwater-Dependent Ecosystem. Remote Sensing. 2024; 16(14):2536. https://doi.org/10.3390/rs16142536
Chicago/Turabian StyleLurtz, Matthew R., Ryan R. Morrison, and Pamela L. Nagler. 2024. "On Connecting Hydrosocial Parameters to Vegetation Greenness Differences in an Evolving Groundwater-Dependent Ecosystem" Remote Sensing 16, no. 14: 2536. https://doi.org/10.3390/rs16142536
APA StyleLurtz, M. R., Morrison, R. R., & Nagler, P. L. (2024). On Connecting Hydrosocial Parameters to Vegetation Greenness Differences in an Evolving Groundwater-Dependent Ecosystem. Remote Sensing, 16(14), 2536. https://doi.org/10.3390/rs16142536








