Abstract
Identifying template watermarks under severe geometric distortions is a significant scientific problem in the current watermarking research for remote sensing images. We propose a novel watermarking algorithm that integrates the ring-shaped template watermark with the multiscale local contrast measure (LCM) method. In the embedding stage, the ring-shaped template watermark is embedded into the discrete Fourier transform (DFT) magnitude coefficients, converting the watermark into small targets in the DFT domain. During the detection stage, the multiscale LCM, a classic infrared small target detection method, enhances these small targets and generates a contrast map. Peak detection is then performed on the contrast map to determine the radius of the template watermark. Finally, circular edge local binarization is applied to extract the watermark information. The proposed method enables synchronization recovery of watermarks under blind conditions. The experimental results demonstrate that the method possesses strong robustness against various geometric attacks such as rotation, scaling, translation, and cropping. It outperforms comparative algorithms in terms of robustness and also exhibits good imperceptibility.
1. Introduction
Remote sensing images are a fundamental and strategic resource with broad applications in military, mapping, engineering planning, and disaster monitoring [1,2]. They possess distinctive features, such as spatial resolution, spectral resolution, temporal resolution, radiometric resolution, geometric accuracy, and extensive coverage, which make them highly valuable for detailed analysis and observation. Consequently, ensuring the security of remote sensing images is of paramount importance.
Digital watermarking, an essential technique in data security, establishes a strong relationship between digital data and watermarks. It can be categorized into various types, including robust watermarking [3,4], fragile watermarking [5,6], and reversible watermarking [7,8], among others. Robust watermarking can ensure that the embedded watermark remains unaffected by attacks, a characteristic known as robustness. Thus, it offers an effective solution for copyright protection of remote sensing images, wherein robustness is a crucial metric in assessing digital watermarking algorithms. Present research efforts to improve robustness primarily focus on minor geometric attacks. However, geometric correction, one of the basic processing methods for remote sensing images, usually causes severe geometric deformations to the data. This makes it difficult to maintain the watermark in Level 0 and Level 1 remote sensing image products after geometric correction. Thus, it presents a significant challenge in watermark synchronization under severe geometric distortions [9,10,11].
As a subset of image watermarking, remote sensing image watermarking algorithms have significantly benefited from advancements in general image watermarking research [12,13,14]. The template watermark is key to resisting geometric attacks [15,16,17]. Algorithms based on template watermarks employ regular watermark patterns. After an attack, the template watermark can be extracted and corrected to reestablish watermark synchronization. These algorithms can be divided into two categories.
The first category is the method based on spatial domain template watermarks [18,19]. This method generally involves periodically tiling template watermarks within the spatial domain. During watermark extraction, the template watermark is identified through correlation functions and other methods, which act as references for rectifying geometric transformations. For instance, the literature [20] proposes a watermarking scheme based on symmetry. In this method, watermark information is encoded through random patterns, which serve as units of the template watermark and are subsequently embedded within the spatial domain. Watermark synchronization is then achieved by employing the auto-correlation function to detect the symmetrical template watermark. This type of method couples the template watermark with the data in the spatial domain, effectively ensuring watermark synchronization when data deformation is not severe. However, due to the significant coupling between the template watermark and the data in the spatial domain, severe data deformation will also deform the template watermark, thereby affecting the extraction of the watermark.
The second category is the method based on transform domain template watermarks, typically constructed using discrete wavelet transformation (DWT) [21], discrete cosine transform (DCT), or discrete Fourier transform (DFT). Among these, template watermarks based on DFT are the most extensively studied. Additionally, Chen [22] found that DFT features exhibit greater robustness against screen-cam attacks involving geometric distortions compared to DCT and DWT. These DFT-based watermarking algorithms involve arranging watermark sequences into fixed patterns and replacing coefficients in the DFT domain. A study [23] embedded watermarks in the annular area of the DFT magnitude. Another study [24] used circular DFT template watermarks. This type of method embeds the template watermark in the transform domain, significantly reducing the spatial coupling problem in the spatial domain. However, decoupling between the template watermark and the attacked data is incomplete. For example, under cropping attacks, the proportion of the template watermark in the data will encounter irreversible reduction. Therefore, precisely identifying template watermarks in the transform domain remains challenging.
In summary, template watermarks are crucial for resisting geometric attacks in watermarking algorithms for remote sensing images. The method based on spatial domain template watermarks achieves watermark synchronization under some geometric attacks but struggles with the spatial coupling issue. The method based on transform domain template watermarks partially solves the former problem but still requires enhanced identification of template watermarks. Consequently, how to identify the template watermark efficiently remains a scientific problem.
To address the above problem, this paper proposes a watermarking algorithm for remote sensing images. In this method, we design a ring-shaped template watermark, innovatively converting the watermark into small targets in the DFT domain. This is followed by applying an infrared small target detection method, specifically the multiscale local contrast measure (LCM) [25], to facilitate watermark synchronization. The main contributions of this paper are as follows:
- Design of a ring-shaped template watermark.
- Conversion of the watermark into small targets.
- Enhancement of the watermark using multiscale LCM.
- Peak detection based on remapping and column-wise summation.
- Watermark extraction based on the circular edge local binarization method.
- Robustness against geometric attacks.
2. Methodology
This paper proposes a watermarking algorithm for remote sensing images based on a ring-shaped template watermark and the multiscale LCM method. Typically, template-based watermarking algorithms divide the watermark into the template watermark and the message watermark [15]. The template watermark is used for attack correction, while the message watermark stores copyright information. In contrast, our algorithm treats the template and message watermarks as one. The main idea of the proposed algorithm is illustrated in Figure 1.
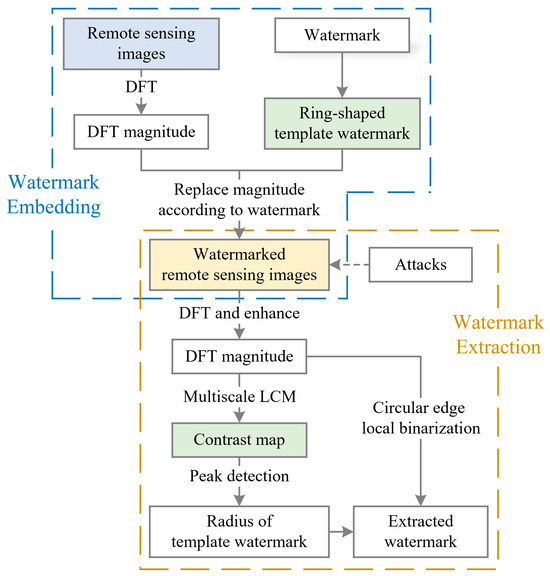
Figure 1.
The framework of the proposed method.
The core components include two main parts. (1) In the embedding stage, the ring-shaped template watermark is utilized. This stage involves converting the watermark into small targets in the DFT domain and embedding the watermark into the magnitude coefficients of the DFT. These coefficients are the features of the remote sensing image used by the proposed watermarking algorithm and serve as the watermark carrier. (2) In the detection stage, multiscale LCM is employed to enhance the small target watermark and obtain a contrast map. Peak detection is then performed on the contrast map to determine the radius of the template watermark. Subsequently, circular edge local binarization is applied to binarize the values at the corresponding radius, thereby extracting the watermark. The specific details of the proposed algorithm are provided below.
2.1. Ring-Shaped Template Watermark
The watermark to be embedded consists of a binary sequence of 0s and 1s, with a length denoted as . The watermark is represented as . A ring-shaped template watermark is constructed using the magnitude coefficients in the DFT domain. Figure 2 shows a schematic diagram of the template watermark, where black represents a DFT magnitude of 0, and white points represent non-zero magnitudes, indicating watermark bits of 1. The watermark information is evenly distributed within the ring. Due to the central symmetry of the magnitude spectrum, the calculation formula for the interval denoted as between two watermark bits is as follows:

Figure 2.
The ring-shaped template watermark.
Let the rows and columns of image be denoted as and , respectively. The center of the image is taken as the center of the template watermark. The formulas are:
where the function represents the modulo operation. The center is also the position of the image’s direct current (DC) component after DFT. Around the center, similar to a band-pass filter, a ring-shaped template watermark is constructed with a radius range of . Here, is the radius of the concentric circle at the center of the ring-shaped template watermark, referred to as the radius of the template watermark. This radius divides the ring into two equal radial segments. The parameter controls the shape of the template. A recommended value for is 2.
Figure 3 shows the magnitude spectrum of the image after embedding the template watermark, where = 40, and the watermark is a periodic repetition of the combination of 01 bits. To better display the effect, the embedding strength of the watermark has been appropriately enhanced. As shown in Figure 3a, the ring-shaped template watermark is distinctly visible, with 40 bright spots in the ring. In Figure 3b, the corresponding bright spots appear as 40 pillars forming a ring centered around the DC component.
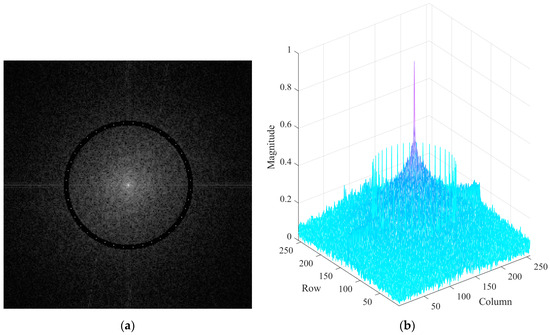
Figure 3.
Magnitude spectrum of the watermarked image: (a) 2D grayscale; (b) 3D surface.
2.1.1. Radius of Template Watermark
Determining the radius of the template watermark is a critical issue. A smaller radius means more low-frequency data will be replaced, resulting in a lower peak signal-to-noise ratio (PSNR) value between the original and watermarked data. Conversely, a larger radius results in a higher PSNR and better watermark imperceptibility but weaker robustness. The choice of radius is critical when dealing with scaling attacks. After the entire data are scaled up or down, the radius of the template watermark remains the same, that is, .
For the image , has a maximum value, denoted as , which is calculated as:
Let the image scaling factor be denoted as . To resist scaling, it must also satisfy:
This algorithm recommends . When and are equal to 256, . Thus, . In this case, the algorithm can theoretically resist all scaling attacks greater than 0.5. To resist scaling attacks with a smaller scaling factor, the value of must be correspondingly reduced.
2.1.2. Embedding of Template Watermark
Watermark embedding is achieved by replacing the magnitude values. First, the region of the ring-shaped template watermark is preprocessed by setting the magnitude values to 0. The positions need to be determined before embedding the watermark information. With as the radius and as the interval, the positions are embedded with the corresponding watermark bit. Let the DFT coefficients of the image be denoted as and the embedding positions as . When is between 0 and degrees, the positions are calculated as follows:
where the and functions first convert the input angle from degrees to radians and then compute the cosine and sine, respectively. When is between 180 and degrees, the symmetric positions are obtained by:
The replacement rule for the watermark is shown in the following equation:
where represents the phase angle of input in the interval , and is a fixed magnitude value that controls the watermark strength. A recommended value for is 40. For the symmetric position, the rule is:
where computes the complex conjugate.
2.2. Multiscale LCM
Multiscale LCM was proposed in the literature [26]. LCM, local contrast measure, is an effective contrast measurement method inspired by biological vision mechanisms, capable of enhancing targets while suppressing the background, thus effectively extracting small objects. A 3 × 3 window of an image, where each grid in the window may represent more than one pixel, is shown in Figure 4, with each grid numbered 0–8. For this window, first, calculate the maximum pixel value in area 0. Then, calculate the average grayscale value for each area in the window. The local contrast is calculated as shown in the following equation:
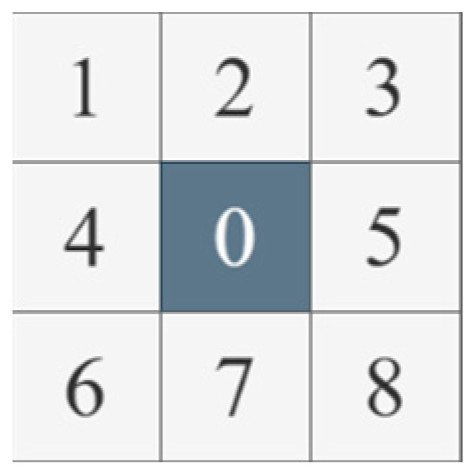
Figure 4.
The window for LCM.
Contrast is used to quantitatively describe the grayscale difference between the target and the background. Based on Equation (10), the contrast between areas 1–8 and area 0 can be calculated. When area 0 contains the target, the contrast obtained for area 0 is significantly lower than the surrounding areas. A contrast map of the image can be obtained by sliding a 3 × 3 window across the entire image and calculating the local contrast. The local contrast is enhanced according to the equation below.
When the detection result in the contrast map exceeds the threshold , the area is considered to contain the target to be detected. The definition of threshold is as shown in the following equation:
where is the average grayscale value of the contrast map, is the standard deviation of the contrast map, and is an empirical value. The final detection result can be obtained after binarizing with the threshold .
Since the target size is usually unknown and the size of the bright spots that contain watermarks can change due to attacks, it is necessary to introduce a multiscale LCM algorithm. Let the maximum size of the target be denoted as in the unit of pixels, with a recommended value of 10 in the proposed method. The LCM is performed sequentially from 1 to , producing a series of contrast maps. A maximum pooling operation is finally applied to this series of contrast maps. Figure 5 shows the results after employing the multiscale LCM to Figure 3a, with set to 3 and set to 4. As seen in Figure 5a, the watermark information is significantly enhanced, and in Figure 5b, the watermark information is precisely extracted as small targets.

Figure 5.
Results of multiscale LCM: (a) contrast map; (b) targets.
Before applying multiscale LCM, the magnitude coefficients in the DFT domain are enhanced to facilitate watermark identification. Let the magnitude coefficients be denoted as and the enhanced results be denoted as , with the enhancement formula as follows:
where the function represents min-max normalization to the interval [0, 1]. In addition, we found that normalizing the original data before applying multiscale LCM also yields better results.
2.3. Peak Detection
In the process of watermark extraction, the radius of the template watermark is extracted based on the contrast map of multiscale LCM. The main idea is to remap the contrast map to polar coordinate space. The destination image size is , and the transformation center is . The radius of the bounding circle to transform is . The interpolation method used is bicubic interpolation. The result of the transformation of Figure 5a is shown in Figure 6. From Figure 6, it is evident that the ring-shaped template watermark is converted into a vertical stripe. It is important to note that if an attack does not deform the ring-shaped template watermark, the stripe will remain vertical. However, if an attack, such as affine transformations or projection transformations, deforms the ring-shaped template watermark, the resulting stripe will also be distorted.

Figure 6.
The remapping result of the contrast map.
The warped contrast map is summed column-wise to obtain a one-dimensional sequence. The pixel position of the maximum prominence in this sequence can be found. The vertical stripe from the previous step is crucial for this process. In the remapping result, the position of the center of the template watermark is 1. Subtracting one from the position of the maximum prominence gives the radius of the template watermark, denoted as . As shown in Figure 7, the maximum prominence occurs at position 65, so equals 64, which matches the radius value used during embedding.
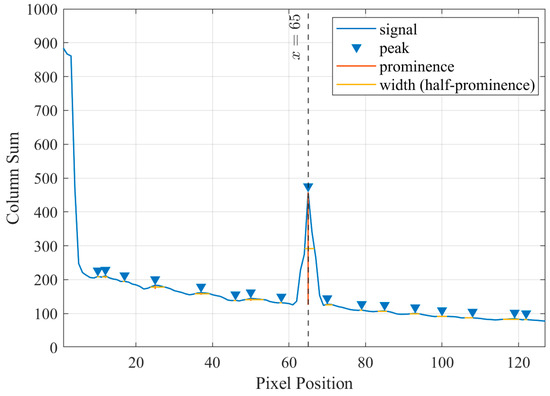
Figure 7.
The prominence of the remapping result.
2.4. Watermark Detection
The circular edge local binarization method is primarily used in the watermark extraction stage. Specifically, based on the obtained radius of the template watermark, a ring with radius is extracted from the enhanced magnitude results, denoted as . The average value of this ring is then calculated. If the value of the position is greater than the average, it is considered a watermark bit 1; otherwise, it is considered a watermark bit 0.
To resist rotation attacks, an offset degree from 0 to 180 with an interval is applied when computing extracting positions and . The interval cannot be infinitely small to ensure each position corresponds to a unique pixel. The minimum interval must be larger than degrees. When is 64, this interval is approximately 0.9 degrees. In the proposed method, we use an interval of 1 degree.
3. Experiments
3.1. Datasets
To verify the effectiveness of the proposed algorithm, a Landsat 5 TM L0 image is selected for the experiment, as shown in Figure 8. This image covers various geographical features such as farmland, oceans, buildings, and mountains. The experimental data can be downloaded from the Geospatial Data Cloud, https://www.gscloud.cn (accessed on 21 March 2024). The B1 band of image LT51480472011318KHC00, as shown in Figure 8a, has a size of 7991 × 7051 pixels. Figure 8b shows a 256 × 256 pixel image of the central block. Since the algorithm proposed in this paper is a block-based embedding algorithm, we selected a block for the experiment. Given the translation invariance of the DFT, if the algorithm can be applied to a single block, it can certainly be applied to the entire original remote sensing image.

Figure 8.
The experimental data: (a) whole data; (b) center block.
3.2. Evaluation
3.2.1. Imperceptibility
The imperceptibility of the watermarking method is measured by the PSNR, which assesses the similarity between the watermarked image and the original image. A higher similarity indicates greater imperceptibility of the watermark before and after embedding. The PSNR is calculated by measuring the ratio between the maximum value of the image signal and the background noise, reflecting the quality of the processed image, as shown in the equation below.
where MAX is the maximum value for the image color depth; for an 8-bit color depth image, the maximum value is 255. MSE is the mean-square error between the original image and the watermarked image. A higher PSNR value indicates less distortion between the processed and original images, meaning better image quality. When PSNR ≥ 40 dB, the image quality is considered excellent. A PSNR between 30 and 40 dB typically indicates good image quality.
3.2.2. Robustness
The normalized correlation (NC) is used to measure the accuracy of the extracted watermark [24]. A higher NC between the extracted watermark and the original watermark indicates higher accuracy in watermark extraction. The NC is defined as shown in the following equation.
The threshold for NC is an empirical value. In this paper, a threshold of 0.75 is set. If the NC exceeds or equals this threshold, the watermark detection is considered successful; otherwise, it is regarded as a failure.
3.3. Experiment Design and Implementation
3.3.1. Comparative Methods and Parameter Settings
Two representative algorithms based on the transform domain are selected for comparison, which are referred to as Method Sun [24] and Method Heidari [11]. Method Sun is based on DFT, while Method Heidari is based on DWT. All three algorithms use the PSNR and NC as evaluation metrics in this experiment. For the watermark information, the proposed algorithm and Method Sun use the same watermark with a length of 40, as described in Section 2.1. Method Heidari uses a binary image as the watermark, as shown in Figure 9, with a size of 32 32 pixels.

Figure 9.
The watermark used in Method Heidari.
Regarding parameter settings, for Method Sun, the constant added to the magnitude of the DFT coefficient is set to 45, and the parameter that controls the overall intensity is set to 0.15. The predefined limit for thresholding Wiener filtered values is 0.8 of the maximum. The width for removing horizontal and vertical lines is 5 pixels, and the radius for setting low frequencies to zero is set to 0.3 L. Additionally, when the data to be detected require padding, the padding value is set to 0 by default, and the padding direction is bottom-right. If cropping is needed, it starts from the top-left part and then crops the bottom-right part to ensure that the detected data and the original data are the same size, as required by Method Heidari. Both the proposed algorithm and Method Sun require the detected data to be square-shaped. That is, it should be padded to become square before watermark detection.
3.3.2. Geometric Attacks
To verify the robustness of the algorithm, this experiment designs four types of geometric attacks: rotation, scaling, translation, and cropping. Each type of attack is applied with different intensities.
- (1)
- Rotation attacks
As shown in Figure 10, the rotation attack in this experiment involves rotating the image counterclockwise around its center by a certain degree, denoted as . The value of ranges from 15 to 180 degrees in intervals of 15 degrees. The size of the data also changes accordingly. For example, when , the size becomes 314 × 314 pixels.

Figure 10.
The data after rotation attacks.
- (2)
- Scaling attacks
Scaling attacks are common in image processing and involve interpolation and resampling. In this experiment, the scaling factor is set to be equal in both the horizontal and vertical directions. The value of ranges from 0.5 to 1 in intervals of 0.1 and then from 2 to 10 in intervals of 1. Table 1 shows the dimensions of the images after applying scaling attacks with various scaling factors.

Table 1.
The dimensions of images after scaling attacks.
- (3)
- Translation attacks
As shown in Figure 11, the translation attack involves simultaneously translating the image by the same number of pixels in both the horizontal and vertical directions. The value of ranges from 10 to 120 with a gap of 10. The translation starts from the top-left corner of the data, and the space created by the translation is filled with 0s. The size of the data remains unchanged.

Figure 11.
The data after translation attacks.
- (4)
- Cropping attacks
As shown in Figure 12, the cropping attack in this experiment involves sequentially cropping the edges of the image. The cropping ratio is the ratio of the cropped area to the original image area. The value of ranges from 5% to 70% in intervals of 5%. It is evident that the size of the data continuously decreases. When the cropping ratio , the data size becomes 77 × 77 pixels.

Figure 12.
The data after cropping attacks.
4. Results and Analyses
4.1. The Results of Imperceptibility
Table 2 presents the PSNR values for the three methods. The proposed method achieves a PSNR of 45.13 dB, Method Sun achieves a PSNR of 41.30 dB, and Method Heidari achieves a PSNR of 38.24 dB. The results indicate that the proposed method significantly outperforms the other two methods in terms of imperceptibility.

Table 2.
The PSNRs of the three methods.
4.2. The Results of Rotation Attacks
Figure 13 shows the results of rotation attacks. The NC values are used to evaluate the performance of the proposed method, Method Sun, and Method Heidari under various rotation angles. The rotation angle ranges from 15° to 180°, in intervals of 15°.
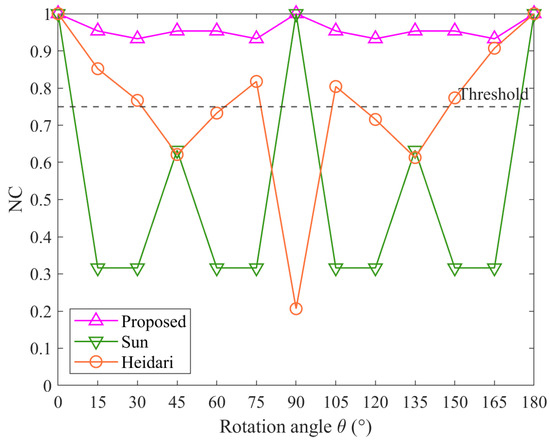
Figure 13.
The results of rotation attacks.
The NC values of the proposed algorithm remain consistently high across all rotation angles, demonstrating strong robustness against rotation attacks. The NC value stays around 1.00, indicating an almost perfect correlation between the extracted and original watermarks, regardless of the rotation angle. Specifically, the proposed method maintains NC values above 0.93 for all tested angles.
In contrast, Method Sun and Method Heidari exhibit significant fluctuations in the NC values as the rotation angle varies. For Method Sun, the NC values drop significantly at certain angles, reaching as low as approximately 0.32 at 15°, 30°, 60°, and 75°, as well as their symmetrical counterparts around 90°. This indicates that Method Sun is highly susceptible to rotation attacks. Method Heidari also shows considerable variation, with NC values dropping to around 0.21 at 90°, although it performs slightly better than Method Sun at certain angles.
Overall, the proposed method outperforms the other two methods, maintaining high NC values and demonstrating superior robustness against rotation attacks.
4.3. The Results of Scaling Attacks
Figure 14 shows the results of scaling attacks. The NC values are used to evaluate the performance of the proposed method, Method Sun, and Method Heidari under various scaling factors . The scaling factors range from 0.5 to 1 in increments of 0.1 and from 2 to 10 in increments of 1.
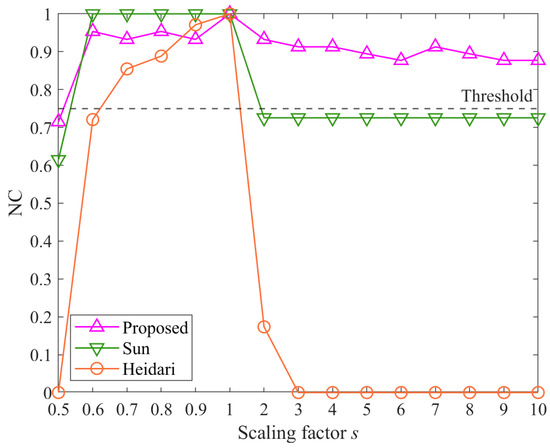
Figure 14.
The results of scaling attacks.
The NC values of the proposed algorithm remain consistently high across most scaling factors, demonstrating strong robustness against scaling attacks. The NC value stays above 0.87 for all tested scaling factors except when , indicating a high level of correlation between the extracted watermark and the original watermark. When , the NC value of the proposed method drops below the threshold of 0.75. However, it is consistent with the theoretical analysis in Section 2.1.1.
In contrast, Method Sun and Method Heidari exhibit significant fluctuations in NC values as the scaling factor varies. The NC values of Method Sun drop below the threshold of 0.75 at certain scaling factors, particularly at and higher, indicating that Method Sun is less robust to more significant scaling factors. Method Heidari shows even more pronounced variation, with NC values dropping to 0 at scaling factors greater than 1. This demonstrates that Method Heidari is highly susceptible to scaling attacks, particularly at larger scaling factors. The NC values for Method Heidari fluctuate between 0 and 1.00, showing vulnerability to scaling attacks.
Overall, the proposed method demonstrates better performance than the other two methods, consistently achieving high NC values and showing greater robustness against scaling attacks.
4.4. The Results of Translation Attacks
Figure 15 shows the results of translation attacks. The NC values are used to evaluate the performance of the proposed method, Method Sun, and Method Heidari under various translation distances . The translation distances range from 10 to 120 pixels in increments of 10 pixels.
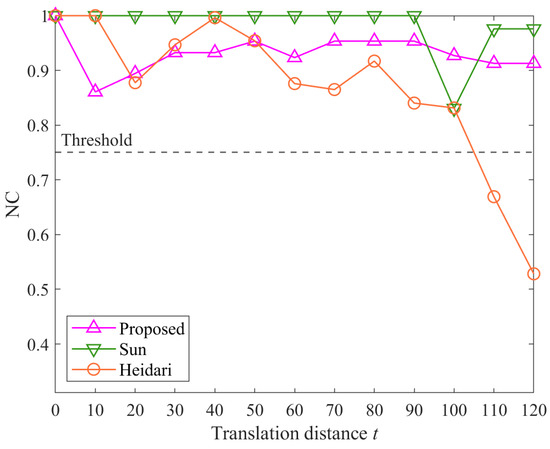
Figure 15.
The results of translation attacks.
The proposed algorithm maintains relatively high NC values across most translation distances, with values above 0.86 for all tested distances. This indicates a good level of correlation between the extracted watermark and the original watermark for the proposed method.
However, the proposed method’s performance is slightly lower than that of Method Sun. Method Sun demonstrates superior robustness against translation attacks, maintaining NC values of 1.0 for most translation distances, with a slight drop to around 0.83 at 100 pixels. This indicates that Method Sun is highly resilient to translation attacks. In contrast, Method Heidari shows considerable variation, with NC values dropping below the threshold at several distances. The NC values for Method Heidari fluctuate between 0.53 and 1.00, demonstrating higher susceptibility to translation attacks compared to both the proposed method and Method Sun.
Overall, while Method Sun generally achieves higher NC values across all tested distances, the proposed method performs well against translation attacks, consistently achieving NC values above the threshold. Method Heidari performs adequately but shows more variability in its NC values than the other methods.
4.5. The Results of Cropping Attacks
Figure 16 shows the results of cropping attacks. The NC values are used to evaluate the performance of the proposed method, Method Sun, and Method Heidari under various cropping ratios . The cropping ratios range from 5% to 70% in increments of 5%.
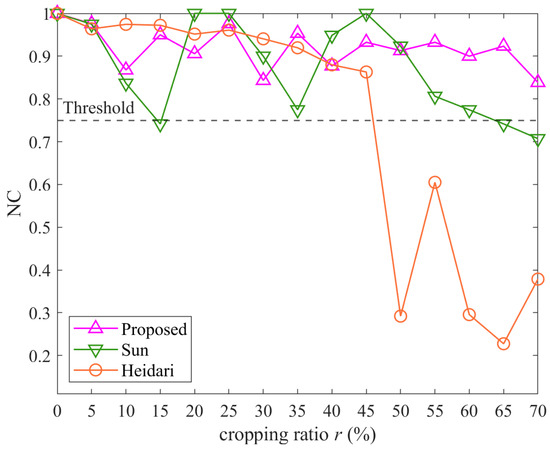
Figure 16.
The results of cropping attacks.
The proposed algorithm maintains relatively high NC values across most cropping ratios, with values above 0.84 for all tested ratios. This indicates a good level of correlation between the extracted watermark and the original watermark, even as significant portions of the image are cropped.
Method Sun generally demonstrates strong robustness against cropping attacks, maintaining NC values above the threshold of 0.75 for most cropping ratios. However, the NC values fluctuate more compared to the proposed method, with significant drops at specific points, such as 15% and 35%. Method Heidari shows the most significant variation, with NC values gradually declining and then dropping below the threshold at cropping ratios above 45%, indicating higher susceptibility to cropping attacks compared to both the proposed method and Method Sun.
Overall, the proposed method maintains high NC values and demonstrates good robustness against cropping attacks compared with the other two methods.
5. Discussion
The above experimental results show that the proposed method excels in both imperceptibility and robustness, making it a more reliable and effective choice for watermarking than Method Sun and Method Heidari. More discussions are provided to illustrate the characteristics of the proposed algorithm.
5.1. Scaling Factor of 0.5
As shown in Figure 14, when the scaling factor is 0.5, the NC value of the proposed method drops below the threshold of 0.75. The underlying reason is that the watermark, being at the edge in the DFT domain, is partially cropped during scaling. As discussed in Section 2.1.1, when and is set to 64, a scaling factor of 0.5 becomes a critical value.
Figure 17 shows the results after a 0.5 scaling attack, where the watermark is already at the edge, leading to loss of watermark information, as is evident in both the pre-enhanced and post-enhanced images in Figure 17a,b. The extracted watermark does not show a peak at position 65, indicating a failure in watermark extraction. This is further illustrated in Figure 18, which displays the prominence after a 0.5 scaling attack. The absence of a peak at the expected position confirms the loss of watermark data due to the scaling process.

Figure 17.
Results after 0.5 scaling attack: (a) magnitude spectrum; (b) contrast map.
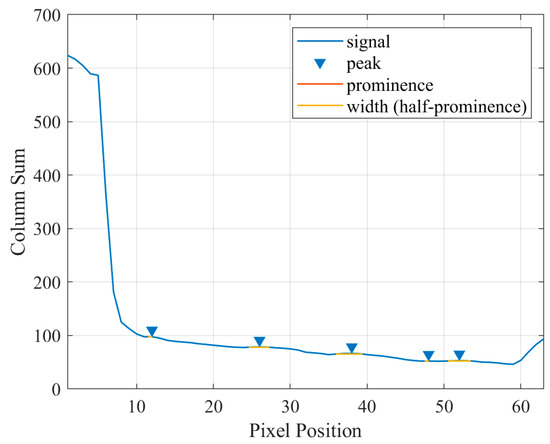
Figure 18.
The prominence after 0.5 scaling attack.
5.2. Watermark Capacity
The watermark capacity is a crucial metric for evaluating a watermarking algorithm; it is typically measured in bits per pixel (BPP) [27] and is especially important in multiple watermarking scenarios [28,29]. The proposed method does not belong to multiple watermarking. It embeds one or more identical watermarks into the data. In this method, a 40-bit watermark is embedded into a 256 × 256 dataset. For a 1024 × 1024 dataset, the watermark is embedded in blocks, each containing the same watermark. Therefore, the theoretical watermark capacity of our algorithm is calculated as 40/(256 × 256) = 0.0006 BPP.
However, issues may arise during peak detection if the watermark contains too many 0s and too few 1s. For example, when the watermark contains only ten 1s, as shown in Figure 19, the watermark detection succeeds. However, the peak value at x = 65 is significantly lower than that shown in Figure 7.
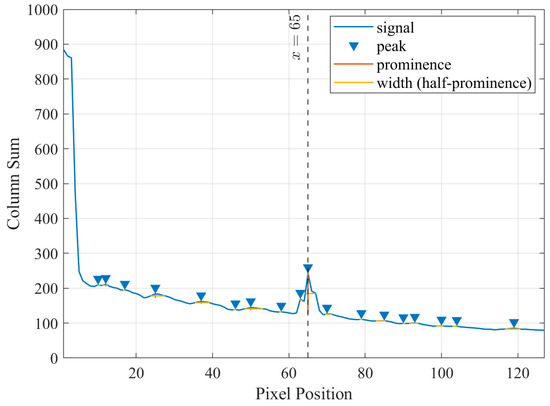
Figure 19.
The prominence with ten 1s in the watermark.
Therefore, the number of watermark bits set to 1 must maintain a certain proportion. We recommend a ratio of at least 1/2, meaning at least 20 bits should be 1s to achieve the robustness demonstrated in our experiments. Consequently, while maintaining good robustness against geometric attacks, the watermark capacity of the proposed method remains unchanged, but the number of qualified usable watermarks is reduced.
6. Conclusions and Outlooks
In this paper, we proposed a watermarking algorithm for remote sensing images based on a ring-shaped DFT template watermark and multiscale LCM. The method addresses the significant challenge of accurately identifying and synchronizing template watermarks under severe geometric distortions, which is crucial in watermarking research for remote sensing images. The experimental results demonstrate the proposed method’s strong robustness against various geometric attacks, including rotation, scaling, translation, and cropping. It consistently outperforms comparative algorithms, such as Method Sun and Method Heidari, in terms of robustness while exhibiting superior imperceptibility. These findings indicate that the proposed method excels in maintaining the integrity and synchronization of the watermark under challenging conditions, making it a more reliable and practical choice for watermarking remote sensing images. Future work will focus on further enhancing the algorithm’s robustness against a wider variety of attack scenarios, such as affine transformations and projection transformations.
Author Contributions
Conceptualization, X.P., H.S. and N.R.; methodology, Q.Z. and X.P.; software, H.S. and X.Z.; validation, Q.Z. and C.A.; formal analysis, H.S. and X.P.; resources, C.A.; writing—original draft preparation, Q.Z. and X.P.; writing—review and editing, N.R. and C.Z.; visualization, X.Z.; supervision, C.Z. and N.R.; funding acquisition, Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grant 42301482 and the Open Topic of Hunan Engineering Research Center of Geographic Information Security and Application under Grant HNGISA2023002.
Data Availability Statement
The data supporting the findings of this study are available from the Geospatial Data Cloud, https://www.gscloud.cn (accessed on 21 March 2024). The specific dataset used in this study is the B1 band of image LT51480472011318KHC00.
Acknowledgments
The authors thank Weitong Chen from the School of Information Engineering, Yangzhou University, for his patient support and explanations whenever we encountered questions related to watermarking algorithms. We also appreciate the constructive comments and suggestions from the journal editors and the reviewers, which have greatly improved this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hussain, K.; Mehmood, K.; Yujun, S.; Badshah, T.; Anees, S.A.; Shahzad, F.; Nooruddin; Ali, J.; Bilal, M. Analysing LULC Transformations Using Remote Sensing Data: Insights from a Multilayer Perceptron Neural Network Approach. Ann. GIS 2024, 1–28. [Google Scholar] [CrossRef]
- Ding, K.; Chen, S.; Wang, Y.; Liu, Y.; Zeng, Y.; Tian, J. AAU-Net: Attention-Based Asymmetric U-Net for Subject-Sensitive Hashing of Remote Sensing Images. Remote Sens. 2021, 13, 5109. [Google Scholar] [CrossRef]
- Ebrahimnejad, J.; Naghsh, A.; Pourghasem, H. A Robust Watermarking Approach against High-density Salt and Pepper Noise (RWSPN) to Enhance Medical Image Security. IET Image Process. 2024, 18, 116–128. [Google Scholar] [CrossRef]
- Chen, Y.; Jia, Z.; Peng, Y.; Peng, Y. Efficient Robust Watermarking Based on Structure-Preserving Quaternion Singular Value Decomposition. IEEE Trans. Image Process. 2023, 32, 3964–3979. [Google Scholar] [CrossRef]
- Xia, X.; Zhang, S.; Wang, K.; Gao, T. A Novel Color Image Tampering Detection and Self-Recovery Based on Fragile Watermarking. J. Inf. Secur. Appl. 2023, 78, 103619. [Google Scholar] [CrossRef]
- Huang, Y.; Zheng, H.; Xiao, D. Convolutional Neural Networks Tamper Detection and Location Based on Fragile Watermarking. Appl. Intell. 2023, 53, 24056–24067. [Google Scholar] [CrossRef]
- Qiu, Y.; Sun, J.; Zheng, J. A Self-Error-Correction-Based Reversible Watermarking Scheme for Vector Maps. ISPRS Int. J. Geo-Inf. 2023, 12, 84. [Google Scholar] [CrossRef]
- Li, D.; Dai, X.; Gui, J.; Liu, J.; Jin, X. A Reversible Watermarking for Image Content Authentication Based on Wavelet Transform. Signal, Image Video Process. 2024, 18, 2799–2809. [Google Scholar] [CrossRef]
- Favorskaya, M.; Savchina, E.; Gusev, K. Feature-Based Synchronization Correction for Multilevel Watermarking of Medical Images. Procedia Comput. Sci. 2019, 159, 1267–1276. [Google Scholar] [CrossRef]
- Ren, N.; Pang, X.; Zhu, C.; Guo, S.; Xiong, Y. Blind and Robust Watermarking Algorithm for Remote Sensing Images Resistant to Geometric Attacks. Photogramm. Eng. Remote Sens. 2023, 89, 321–332. [Google Scholar] [CrossRef]
- Heidari, M.; Karimi, S. A Novel Robust and More Secure Blind Image Watermarking for Optical Remote Sensing Using DWT-SVD and Chaotic Maps. Opt. Quantum Electron. 2023, 55, 535. [Google Scholar] [CrossRef]
- Malik, R.; Khamparia, A.; Garg, S.; Gupta, D.; Choi, B.J.; Hossain, M.S. Reversible Data Hiding and Smart Multimedia Computing Using Big Data in Remote Sensing Systems. IEEE Access 2020, 8, 153546–153560. [Google Scholar] [CrossRef]
- Yuan, G.; Hao, Q. Digital Watermarking Secure Scheme for Remote Sensing Image Protection. China Commun. 2020, 17, 88–98. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, K.; Wang, X.; Hu, J. Zero-Watermarking Algorithm for Remote Sensing Image via BEMD and DFT. Jisuanji Fuzhu Sheji Yu Tuxingxue Xuebao/J. Comput. Des. Comput. Graph. 2022, 34, 1731–1741. [Google Scholar] [CrossRef]
- Pramila, A.; Keskinarkaus, A.; Seppänen, T. Multiple Domain Watermarking for Print-Scan and JPEG Resilient Data Hiding. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2008; Volume 5041, LNCS, pp. 279–293. ISBN 3540922377. [Google Scholar]
- Chen, W.; Ren, N.; Zhu, C.; Keskinarkaus, A.; Seppänen, T.; Zhou, Q. Joint Image Encryption and Screen-Cam Robust Two Watermarking Scheme. Sensors 2021, 21, 701. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Ren, N.; Zhu, C.; Zhou, Q.; Seppänen, T.; Keskinarkaus, A. Screen-Cam Robust Image Watermarking with Feature-Based Synchronization. Appl. Sci. 2020, 10, 7494. [Google Scholar] [CrossRef]
- Li, M.; Zhang, J.; Wen, W. Cryptanalysis and Improvement of a Binary Watermark-Based Copyright Protection Scheme for Remote Sensing Images. Optik 2014, 125, 7231–7234. [Google Scholar] [CrossRef]
- Zhu, P.; Jia, F.; Zhang, J. A Copyright Protection Watermarking Algorithm for Remote Sensing Image Based on Binary Image Watermark. Optik 2013, 124, 4177–4181. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, W.; Fang, H.; Dong, X.; Geng, L.; Yu, N. Local Geometric Distortions Resilient Watermarking Scheme Based on Symmetry. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 4826–4839. [Google Scholar] [CrossRef]
- Hua, Y.; Xi, X.; Qu, C.; Du, J.; Weng, M.; Ye, B. An Adaptive Watermarking for Remote Sensing Images Based on Maximum Entropy and Discrete Wavelet Transformation. KSII Trans. Internet Inf. Syst. 2024, 18, 192–210. [Google Scholar] [CrossRef]
- Chen, W. Research on Screen-Cam Robust Watermarking Model and Algorithm for Remote Sensing Images. Ph.D. Thesis, Nanjing Normal University, Nanjing, China, 2021. (In Chinese). [Google Scholar] [CrossRef]
- Cedillo-Hernandez, M.; Cedillo-Hernandez, A.; Garcia-Ugalde, F.J. Improving DFT-Based Image Watermarking Using Particle Swarm Optimization Algorithm. Mathematics 2021, 9, 1795. [Google Scholar] [CrossRef]
- Sun, X.; Lu, Z.; Wang, Z.; Liu, Y. A Geometrically Robust Multi-Bit Video Watermarking Algorithm Based on 2-D DFT. Multimed. Tools Appl. 2021, 80, 13491–13511. [Google Scholar] [CrossRef]
- Han, J.; Liang, K.; Zhou, B.; Zhu, X.; Zhao, J.; Zhao, L. Infrared Small Target Detection Utilizing the Multiscale Relative Local Contrast Measure. IEEE Geosci. Remote Sens. Lett. 2018, 15, 612–616. [Google Scholar] [CrossRef]
- Chen, C.L.P.; Li, H.; Wei, Y.; Xia, T.; Tang, Y.Y. A Local Contrast Method for Small Infrared Target Detection. IEEE Trans. Geosci. Remote Sens. 2014, 52, 574–581. [Google Scholar] [CrossRef]
- Shih, F.Y. Digital Watermarking and Steganography: Fundamentals and Techniques, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Qiu, Y.; Duan, H. A Novel Multi-Stage Watermarking Scheme of Vector Maps. Multimed. Tools Appl. 2021, 80, 877–897. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, C.; Ding, K. Multiple Watermarking Algorithms for Vector Geographic Data Based on Multiple Quantization Index Modulation. Appl. Sci. 2023, 13, 12390. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).