Research on Inter-Satellite Laser Ranging Scale Factor Estimation Methods for Next-Generation Gravity Satellites
Abstract
1. Introduction
2. Current Methods
2.1. Cross-Calibration by JPL
2.2. Cross-Calibration by the AEI
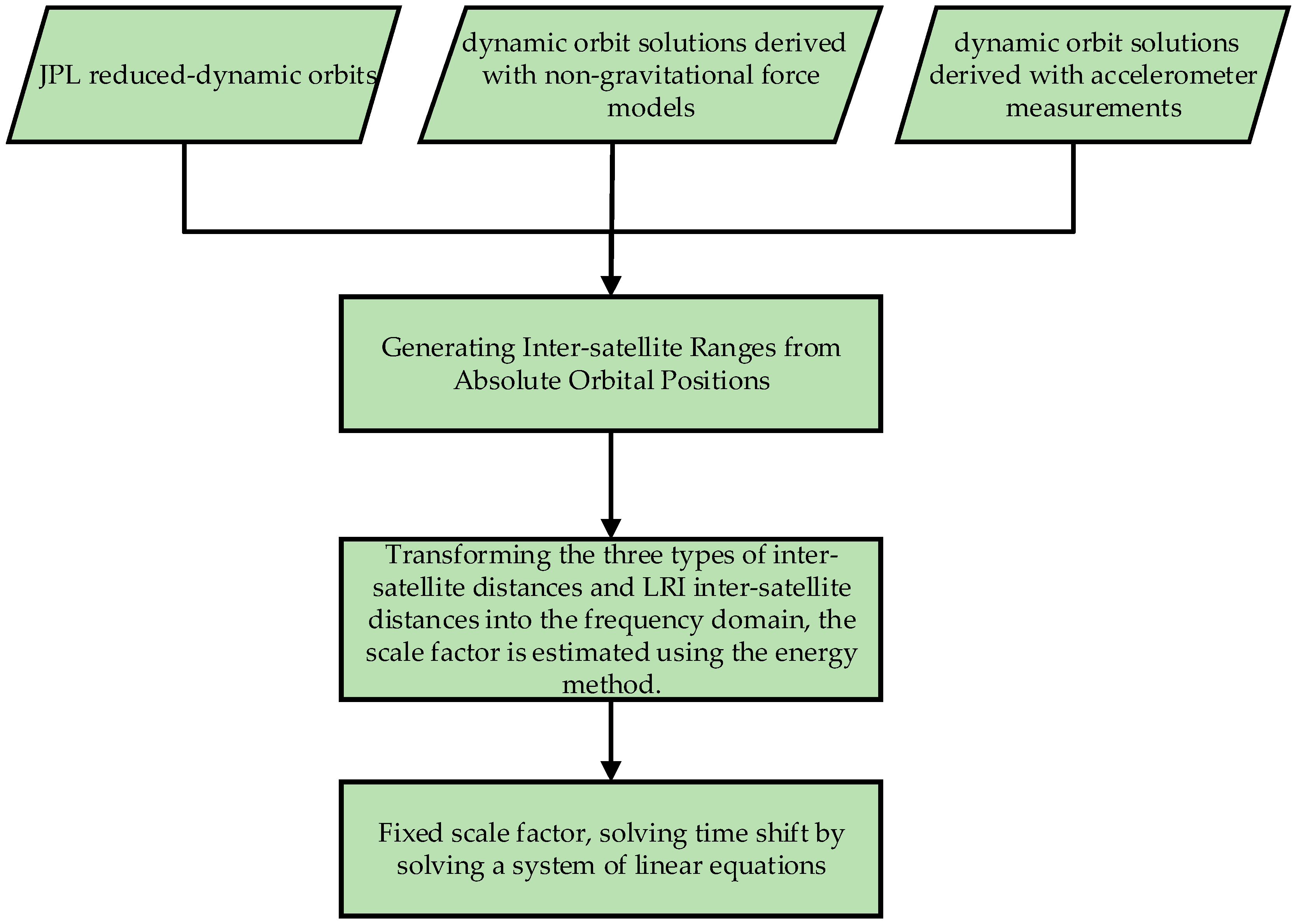
3. An Energy-Based Scale Factor Estimation Method Using POD and PBD Solutions
3.1. Precise Orbit and Baseline Determination
3.2. Generating Inter-Satellite Ranges from Absolute Orbital Positions
3.3. The Energy-Based Scale Factor Estimation Method
3.4. Time Shift Estimation
4. Discussion
4.1. Analysis of Inter-Satellite Ranges Using Precise Orbit and Baseline Determination
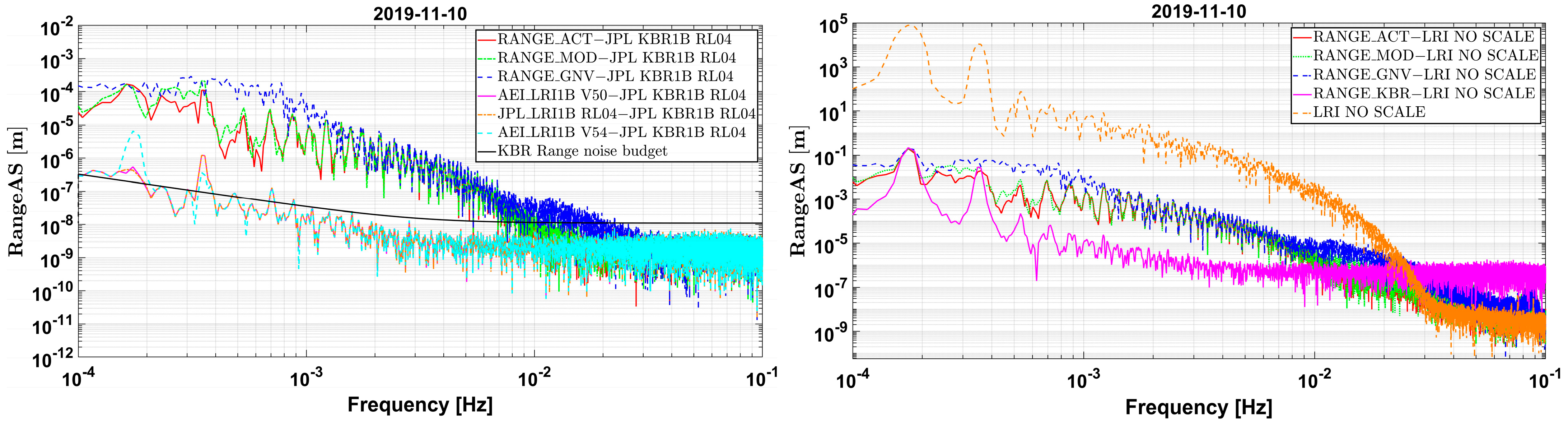
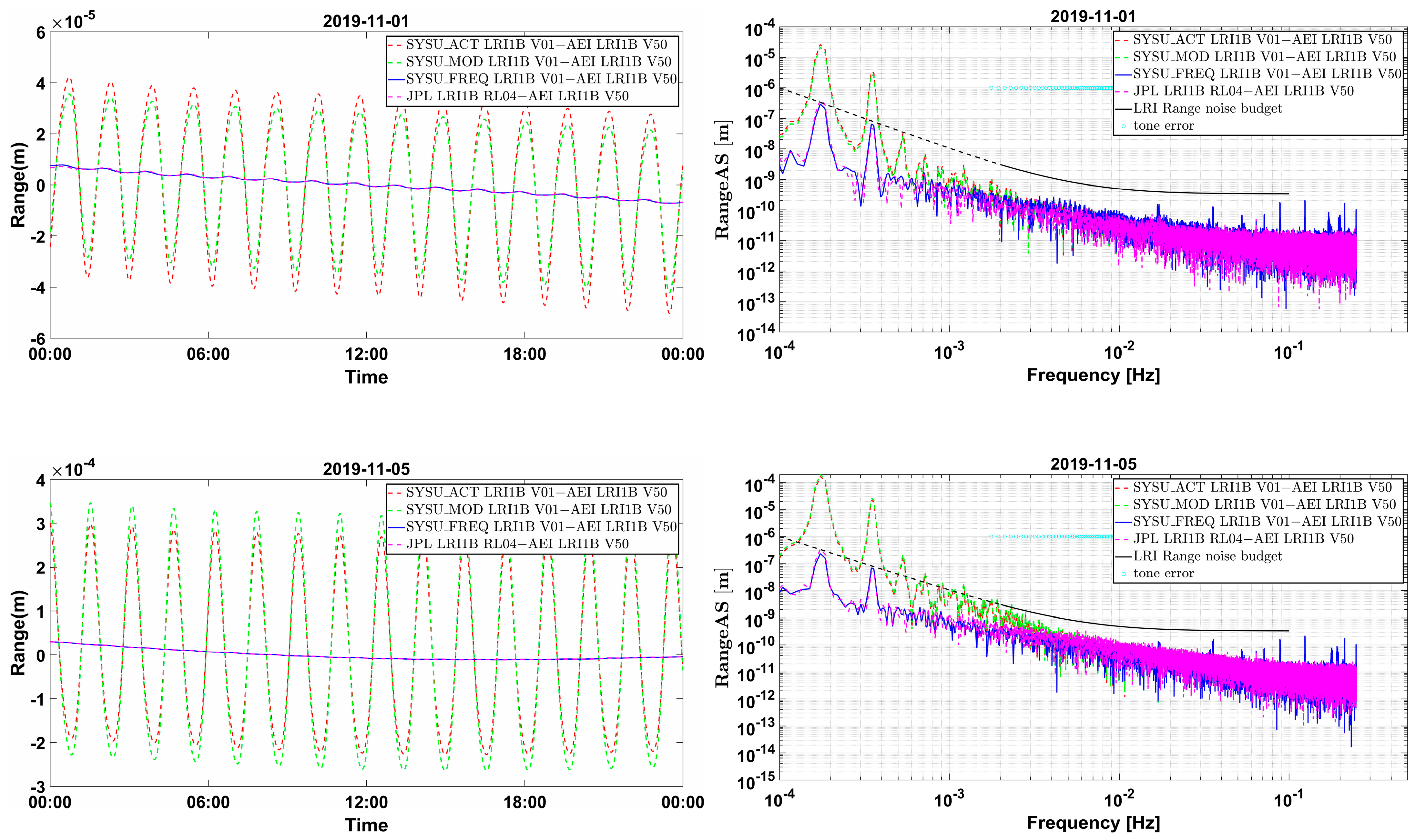
4.1.1. Comparison Analysis of Inter-Satellite Ranges Using Precise Orbit and Baseline Determination in the Time Domain
4.1.2. Comparison Analysis of Inter-Satellite Ranges Using Precise Orbit and Baseline Determination in the Frequency Domain
4.2. Analysis of the Energy-Based Scale Factor Estimation Method
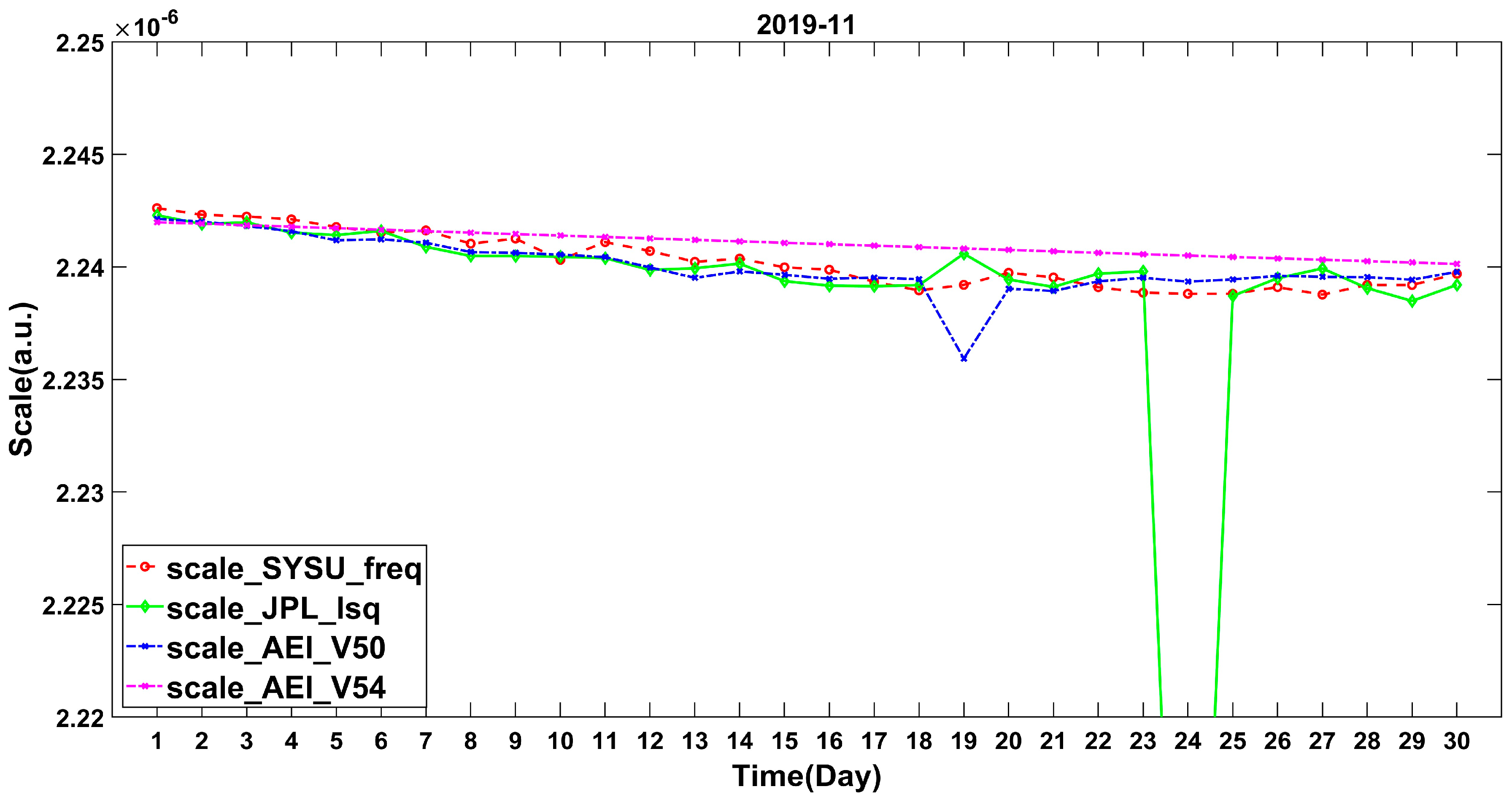
4.2.1. Comparison Analysis of the Scale Factor
4.2.2. Comparison Analysis of the Time Shift
4.3. Comparison Analysis of the Proposed Method
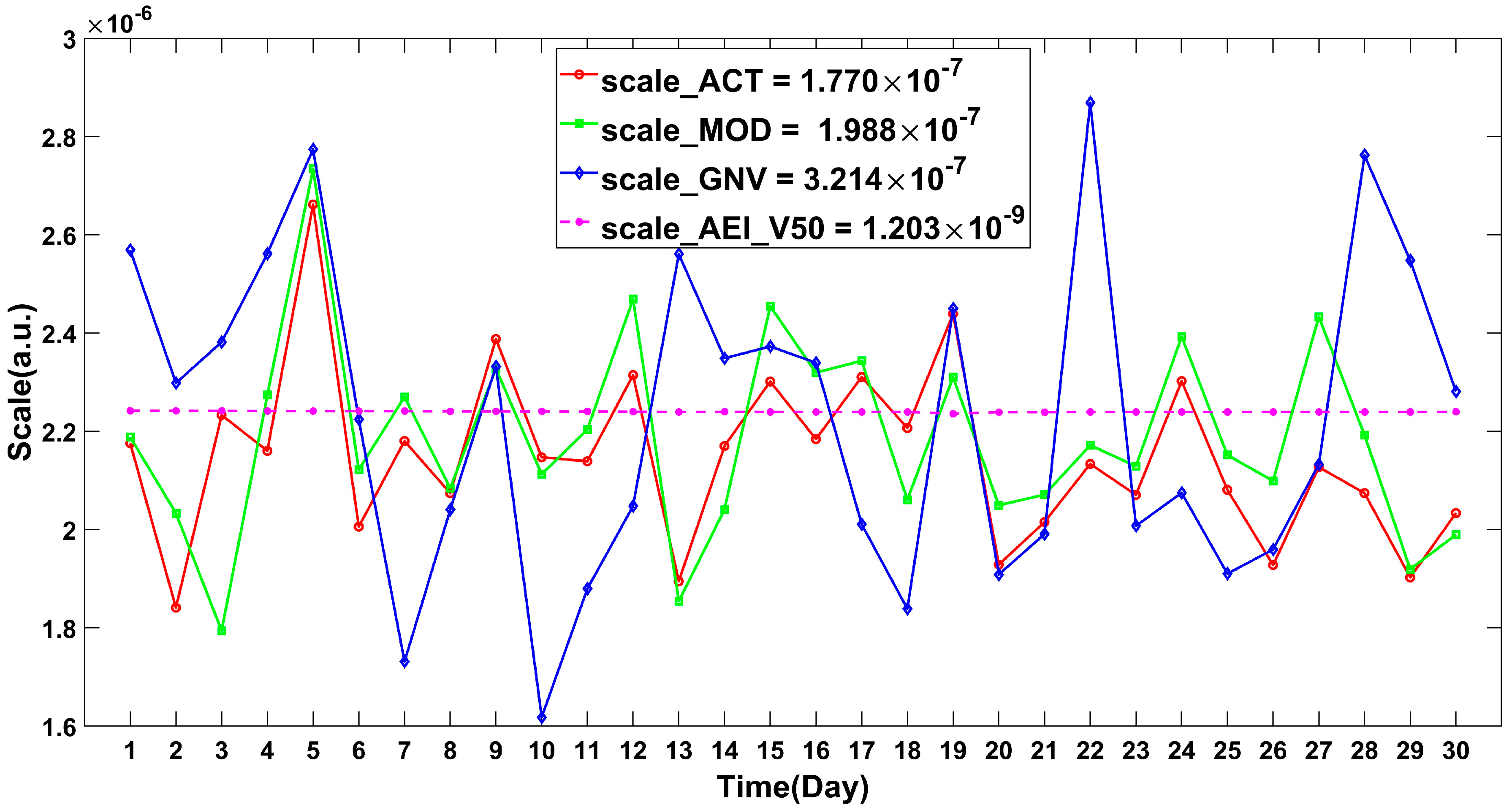
4.3.1. Comparison Analysis of the Scale Factor
4.3.2. Comparison Analysis of Instantaneous Ranges with AEI LRI1B
4.3.3. Comparison Analysis of Instantaneous Ranges with JPL KBR1B
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AEI | Albert Einstein Institute |
| ASD | Amplitude Spectral Density |
| AS | Amplitude Spectral |
| CPR | Cycles per Revolution |
| CRN | N Convolutions of a Rectangle |
| DOWR | Dual One-Way Ranging |
| ENBW | Equivalent Noise Bandwidth |
| FFT | Fast Fourier transform |
| GPS | Global Positioning System |
| GRACE | Gravity Recovery And Climate Experiment |
| GRACE-FO | GRACE Follow-On |
| IPU | MWI Instrument Processing Unit |
| JPL | Jet Propulsion Laboratory |
| KBR | Ka-Band Ranging |
| LRI | Laser Ranging Interferometer |
| LTC | Light time correction |
| LOS | Line of sight |
| MWI | Microwave instrument |
| NGGM | Next-Generation Gravity Mission |
| PBD | Precise baseline determination |
| POD | Precise orbit determination |
| RMSE | Root Mean Square Error |
| SFU | Scale Factor Unit |
| STD | Standard Deviation |
| ULE | Ultra-Low Expansion |
| USO | Ultra-Stable Oscillator |
References
- Kornfeld, R.P.; Arnold, B.W.; Gross, M.A.; Dahya, N.T.; Klipstein, W.M.; Gath, P.F.; Bettadpur, S. GRACE-FO: The Gravity Recovery and Climate Experiment Follow-On Mission. J. Spacecr. Rocket. 2019, 56, 931–951. [Google Scholar] [CrossRef]
- Sheard, B.S.; Heinzel, G.; Danzmann, K.; Shaddock, D.A.; Klipstein, W.M.; Folkner, W.M. Intersatellite laser ranging instrument for the GRACE follow-on mission. J. Geod. 2012, 86, 1083–1095. [Google Scholar] [CrossRef]
- Flechtner, F.; Neumayer, K.-H.; Dahle, C.; Dobslaw, H.; Fagiolini, E.; Raimondo, J.-C.; Güntner, A. What Can be Expected from the GRACE-FO Laser Ranging Interferometer for Earth Science Applications? Surv. Geophys. 2016, 37, 453–470. [Google Scholar] [CrossRef]
- Massotti, L.; Di Cara, D.; del Amo, J.; Haagmans, R.; Jost, M.; Siemes, C.; Silvestrin, P. The ESA Earth Observation Programmes Activities for the Preparation of the Next Generation Gravity Mission. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Guidance, Navigation, and Control and Co-located Conferences, Boston, MA, USA, 19–22 August 2013; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2013. [Google Scholar] [CrossRef]
- Gong, Y.; Luo, J.; Wang, B. Concepts and status of Chinese space gravitational wave detection projects. Nat. Astron. 2021, 5, 881–889. [Google Scholar] [CrossRef]
- Dionisio, S.; Anselmi, A.; Bonino, L.; Cesare, S.; Massotti, L.; Silvestrin, P. The “Next Generation Gravity Mission”: Challenges and consolidation of the system concepts and technological innovations. In Proceedings of the 2018 SpaceOps Conference, Marseille, France, 28 May–1 June 2018. [Google Scholar] [CrossRef]
- Yan, Y.; Müller, V.; Heinzel, G.; Zhong, M. Revisiting the light time correction in gravimetric missions like GRACE and GRACE follow-on. J. Geod. 2021, 95, 48. [Google Scholar] [CrossRef]
- Wen, H.Y.; Kruizinga, G.; Paik, M.; Landerer, F.; Bertiger, W.; Sakumura, C.; Bandikova, T.; Mccullough, C. Gravity Recovery and Climate Experiment (GRACE) Follow-On (GRACE-FO) Level-1 Data Product User Handbook; JPL: Pasadena, CA, USA, 2019; Volume D-56935. [Google Scholar]
- Misfeldt, M.; Müller, V.; Heinzel, G.; Danzmann, K. Alternative Level 1A to 1B Processing of GRACE Follow-On LRI data. In Proceedings of the Copernicus Meetings, Online, 3–8 May 2020; p. 15569. [Google Scholar]
- Misfeldt, M. Data Processing and Investigations for the GRACE Follow-On Laser Ranging Interferometer. Master’s Thesis, Leibniz University Hannover, Hanover, Germany, 2019. [Google Scholar]
- Müller, L. Generation of Level 1 Data Products and Validating the Correctness of Currently Available Release 04 Data for the GRACE Follow-on Laser Ranging Interferometer. Master’s Thesis, Leibniz Universität Hannover, Hannover, Germany, 2021. [Google Scholar]
- Misfeldt, M.; Müller, V.; Müller, L.; Wegener, H.; Heinzel, G. Scale Factor Determination for the GRACE Follow-On Laser Ranging Interferometer Including Thermal Coupling. Remote Sens. 2023, 15, 570. [Google Scholar] [CrossRef]
- Rees, E.R.; Wade, A.R.; Sutton, A.J.; Spero, R.E.; Shaddock, D.A.; McKenzie, K. Absolute frequency readout derived from ULE cavity for next generation geodesy missions. Opt. Express 2021, 29, 26014–26027. [Google Scholar] [CrossRef] [PubMed]
- Klinger, B.; Mayer-Gürr, T.A.A.A.B. The role of accelerometer data calibration within GRACE gravity field recovery: Results from ITSG-Grace2016. Adv. Space Res. 2016, 58, 1597–1609. [Google Scholar] [CrossRef]
- Malte Misfeldt, L.M.; Müller, V. AEI LRI1B and RTC1B Release Notes; Max-Planck Institute for Gravitational Physics (Albert Einstein Institute): Hanover, Germany, 2022. [Google Scholar]
- Wei, C.; Shao, K.; Gu, D.; Zhang, Z.; Zhu, J.; An, Z.; Wang, J. Enhanced orbit and baseline determination for formation-flying LEO satellites with spaceborne accelerometer measurements. J. Geod. 2023, 97, 64. [Google Scholar] [CrossRef]
- Mayer-Guerr, T.; Behzadpour, S.; Eicker, A.; Ellmer, M.; Koch, B.; Krauss, S.; Pock, C.; Rieser, D.; Strasser, S.; Suesser-Rechberger, B.; et al. GROOPS: A software toolkit for gravity field recovery and GNSS processing. Comput. Geosci. 2021, 155, 104864. [Google Scholar] [CrossRef]
- Proakis, J.G.; Manolakis, D.G. Digital Signal Processing Principles, Algorithms and Applications; Pearson Education: New Delhi, India, 2003. [Google Scholar]
- Sun, Y.; Ditmar, P.; Riva, R. Observed changes in the Earth’s dynamic oblateness from GRACE data and geophysical models. J. Geod. 2016, 90, 81–89. [Google Scholar] [CrossRef] [PubMed]
- Peidou, A.; Landerer, F.; Wiese, D.; Ellmer, M.; Fahnestock, E.; McCullough, C.; Spero, R.; Yuan, D.N. Spatiotemporal Characterization of Geophysical Signal Detection Capabilities of GRACE-FO. Geophys. Res. Lett. 2021, 49, e2021GL095157. [Google Scholar] [CrossRef]
- Heinzel, G.; Rüdiger, A.; Schilling, R. Spectrum and Spectral Density Estimation by the Discrete Fourier Transform (DFT), Including a Comprehensive List of Window Functions and Some New Flat-Top Windows; Max Planck Institutes: Hannover, Germany, 2002; Volume 12. [Google Scholar]
- Müller, V.; Hauk, M.; Misfeldt, M.; Müller, L.; Wegener, H.; Yan, Y.; Heinzel, G. Comparing GRACE-FO KBR and LRI Ranging Data with Focus on Carrier Frequency Variations. Remote Sens. 2022, 14, 4335. [Google Scholar] [CrossRef]
- Zhou, H.; Luo, Z.; Zhou, Z.; Li, Q.; Zhong, B.; Lu, B.; Hsu, H. Impact of Different Kinematic Empirical Parameters Processing Strategies on Temporal Gravity Field Model Determination. J. Geophys. Res. Solid Earth 2018, 123, 10252–10276. [Google Scholar] [CrossRef]



| Month | Mean_SYSU_FREQ | Mean_AEI_V50 | STD_SYSU | STD_AEI_V50 |
|---|---|---|---|---|
| 2020-10 | 2.235 × 10−6 | 2.235 × 10−6 | 4.983 × 10−9 | 3.153 × 10−9 |
| 2021-09 | 2.226 × 10−6 | 2.226 × 10−6 | 3.922 × 10−9 | 3.551 × 10−9 |
| 2022-06 | 2.588 × 10−6 | 2.590 × 10−6 | 9.759 × 10−9 | 8.747 × 10−9 |
| Date | Scale_ACT | Scale_MOD | RMS_ACT (mm) | RMS_MOD (mm) |
|---|---|---|---|---|
| 1 November 2019 | 2.175 × 10−6 | 2.185 × 10−6 | 0.4 | 0.6 |
| 5 November 2019 | 2.661 × 10−6 | 2.734 × 10−6 | 0.8/1.3 | 1.6/0.8 |
| 7 November 2019 | 2.180 × 10−6 | 2.270 × 10−6 | 0.5 | 0.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Gu, D.; Yin, H.; Yang, X.; Wei, C.; An, Z. Research on Inter-Satellite Laser Ranging Scale Factor Estimation Methods for Next-Generation Gravity Satellites. Remote Sens. 2024, 16, 2523. https://doi.org/10.3390/rs16142523
Wang J, Gu D, Yin H, Yang X, Wei C, An Z. Research on Inter-Satellite Laser Ranging Scale Factor Estimation Methods for Next-Generation Gravity Satellites. Remote Sensing. 2024; 16(14):2523. https://doi.org/10.3390/rs16142523
Chicago/Turabian StyleWang, Jian, Defeng Gu, Heng Yin, Xuerong Yang, Chunbo Wei, and Zicong An. 2024. "Research on Inter-Satellite Laser Ranging Scale Factor Estimation Methods for Next-Generation Gravity Satellites" Remote Sensing 16, no. 14: 2523. https://doi.org/10.3390/rs16142523
APA StyleWang, J., Gu, D., Yin, H., Yang, X., Wei, C., & An, Z. (2024). Research on Inter-Satellite Laser Ranging Scale Factor Estimation Methods for Next-Generation Gravity Satellites. Remote Sensing, 16(14), 2523. https://doi.org/10.3390/rs16142523





