Graph Neural Networks in Point Clouds: A Survey
Abstract
1. Introduction
- Unstructured data processing: GNNs and GCNs are naturally suited to handle unstructured data. The unstructured nature of point cloud data, where data points lack a fixed spatial arrangement, aligns with the free connection pattern of nodes in graph data. GNNs and GCNs can effectively learn feature representations of nodes in this unordered environment.
- Capturing local geometric structures: GNNs and GCNs capture local structural information through convolution operations defined on graphs. By transforming point clouds into a graph form—where points serve as nodes and spatial relationships between points define the edges—these networks effectively learn the local geometric characteristics of each point based on its relations with neighboring points.
- Permutation invariance: A fundamental characteristic of point cloud data is their permutation invariance, which stipulates that the 3D representation of a shape is unaffected by variations in the ordering of the data points. This attribute is critical for ensuring consistent interpretation and processing of point cloud data. GNNs and GCNs intrinsically support this permutation invariance, as the representation of a graph is independent of the ordering of its nodes. This inherent characteristic allows these networks to extract feature representations agnostic to point arrangement.
- Scalability and flexibility: GNNs and GCNs offer scalability in handling point clouds, allowing adaptation to various application needs through different graph construction strategies, such as k-nearest neighbors (KNN) or random walk. Moreover, these networks can flexibly adjust the weight on local and global information by tweaking parameters used for graph construction, such as the number of neighbors and different methods of constructing the graph.
2. Theoretical Background and Datasets
2.1. Related Theoretical Foundations
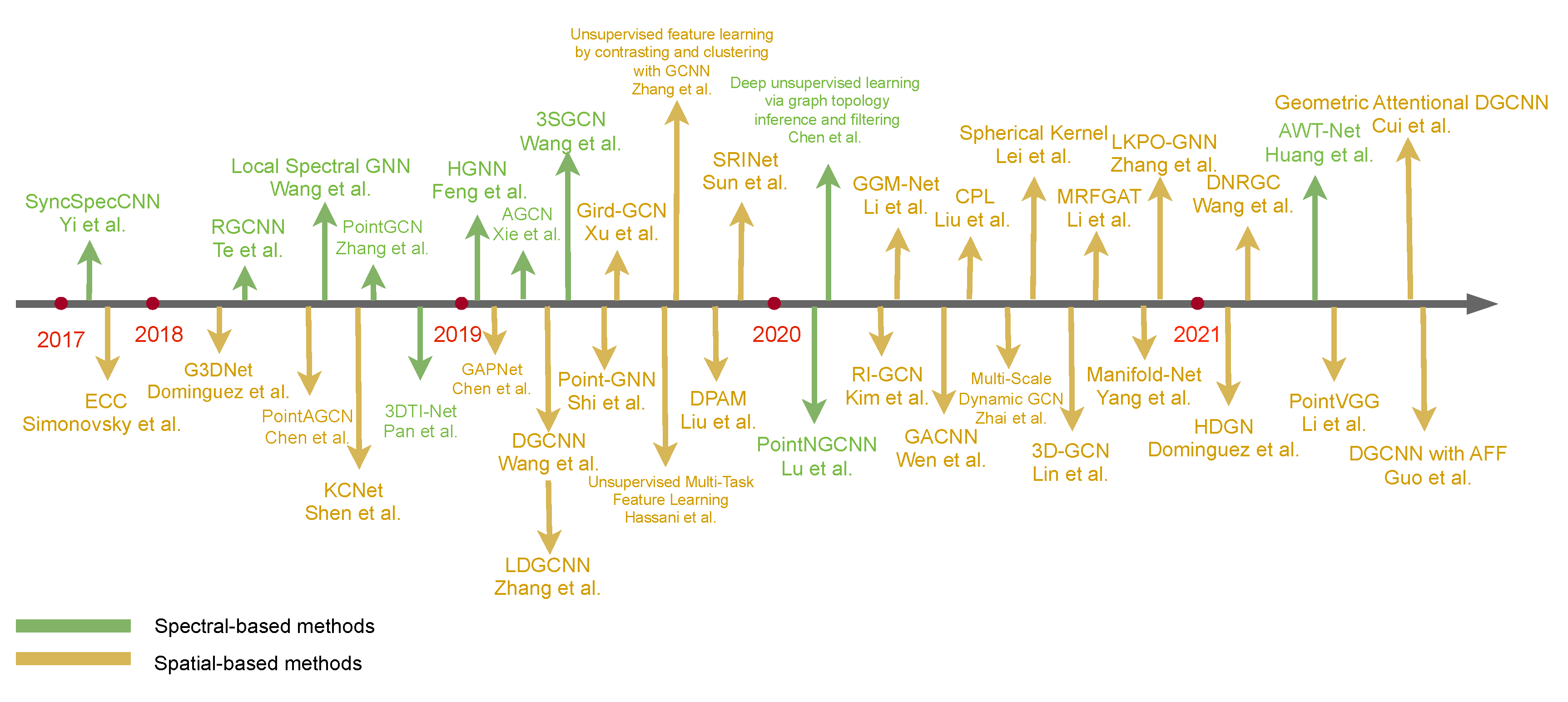
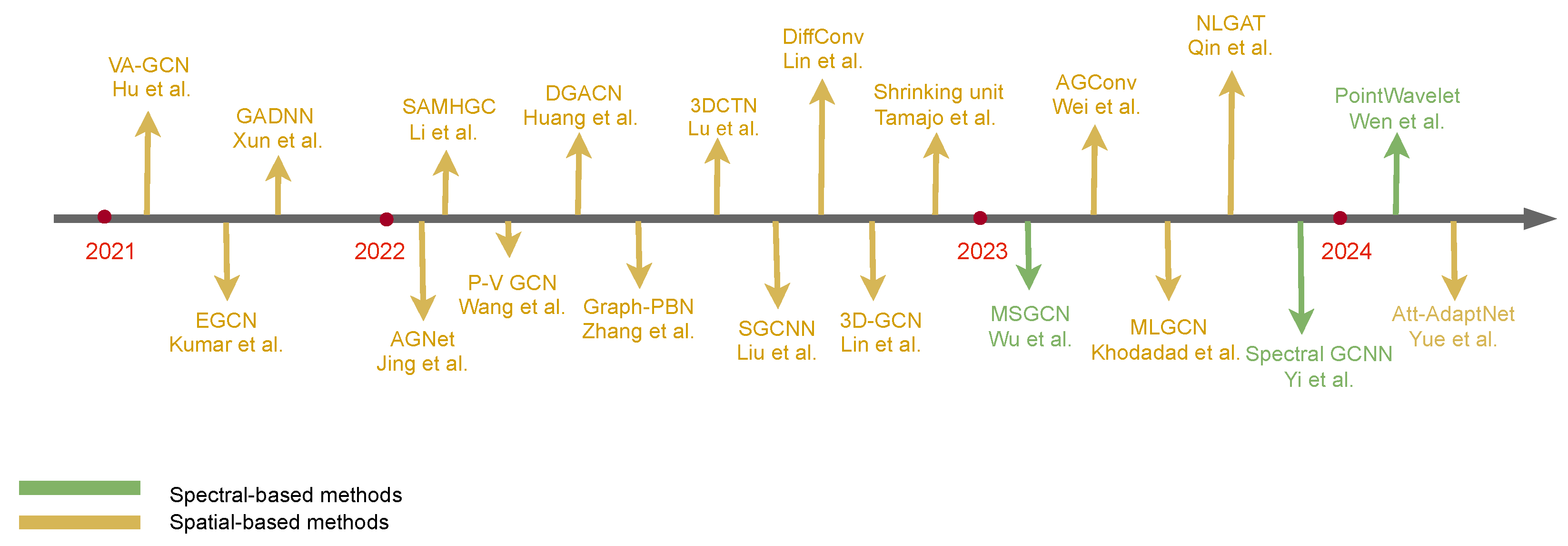
2.1.1. Spectral-Based GCN
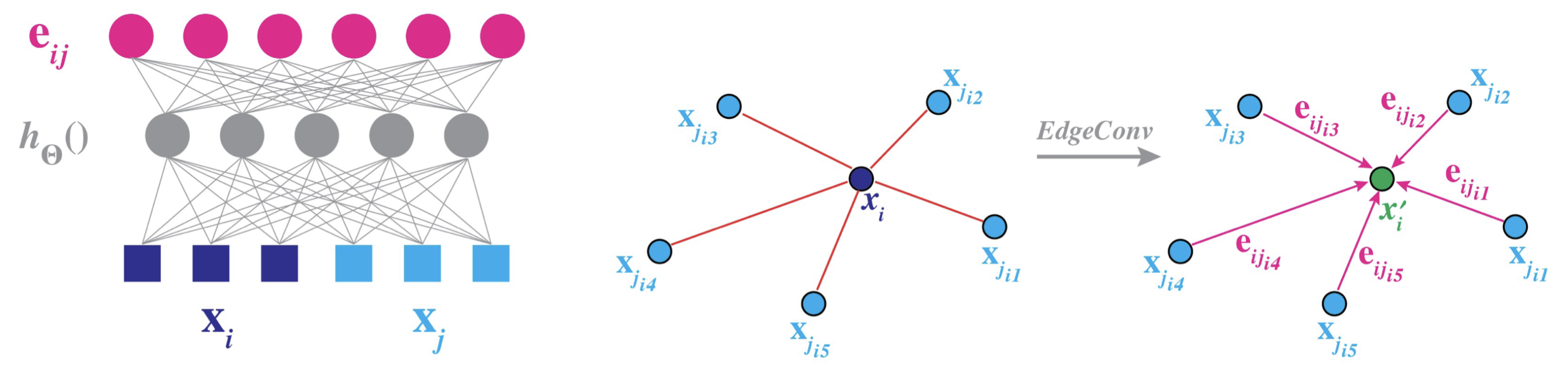
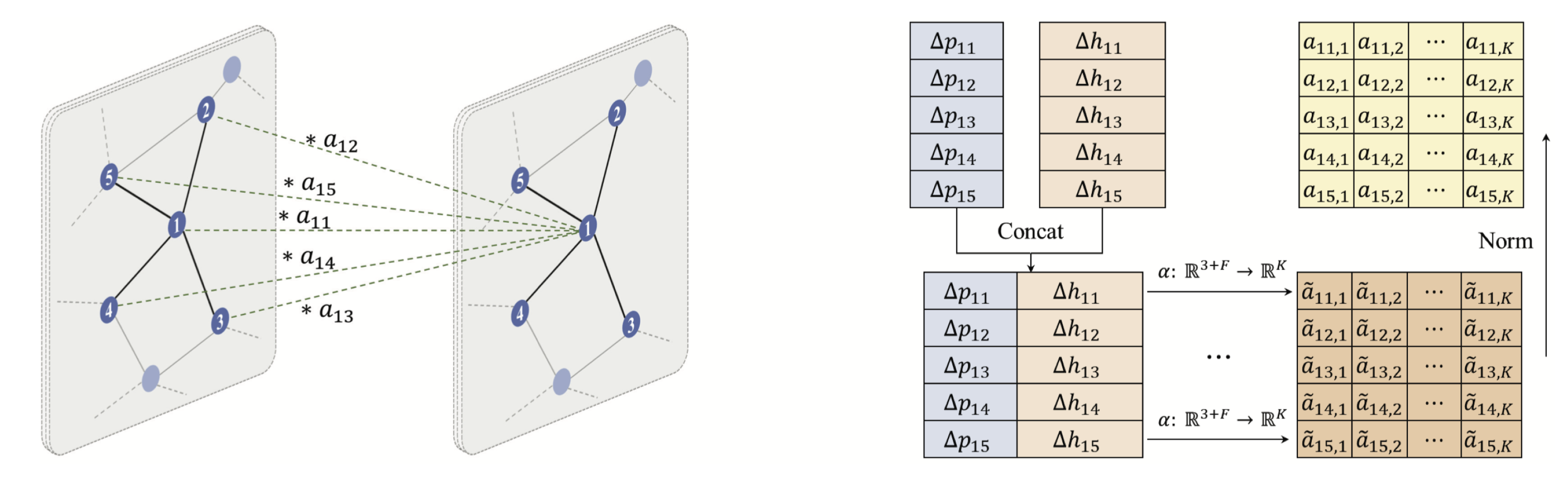
2.1.2. Spatial-Based GCN
2.1.3. Graph Attention Networks
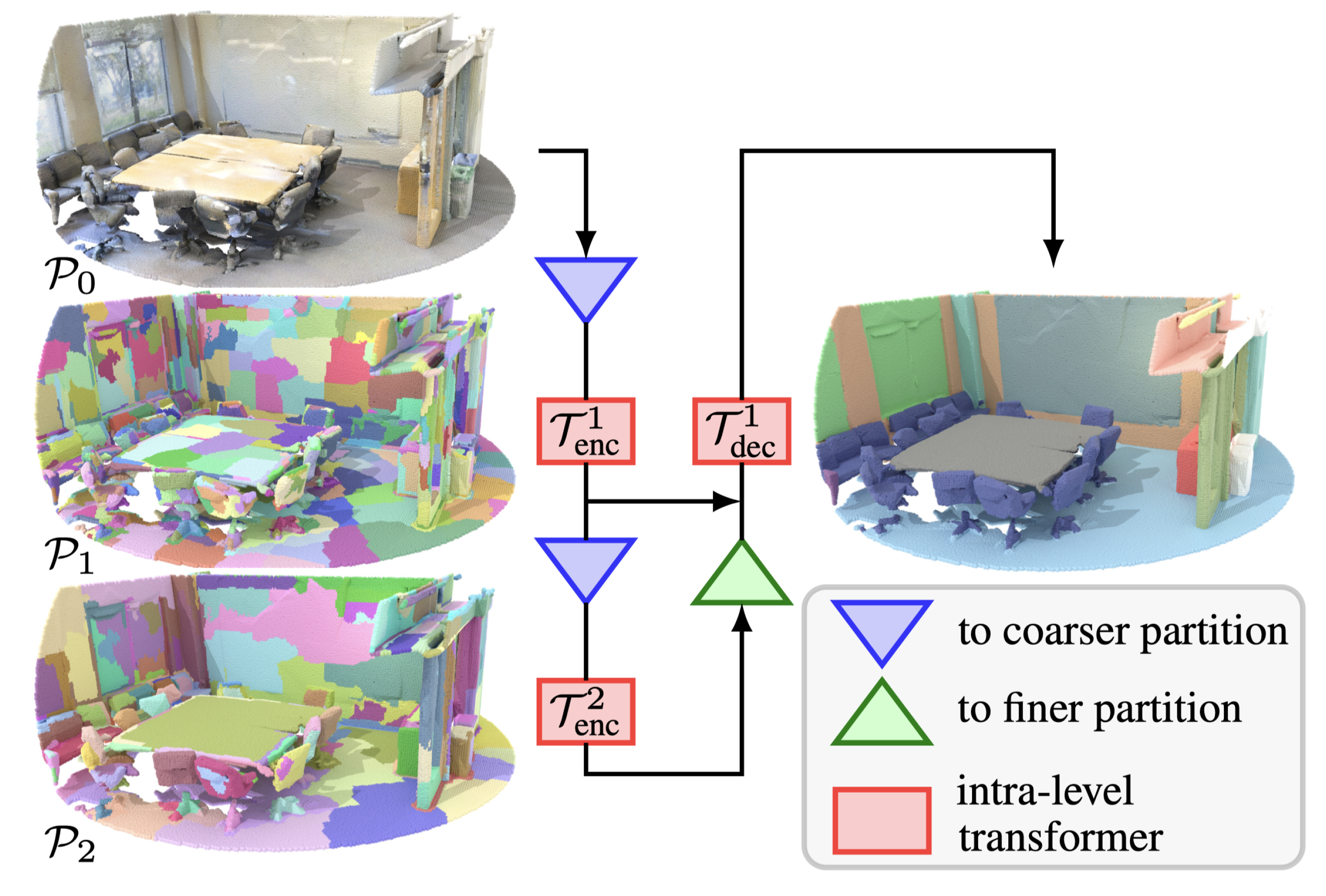
2.1.4. Graph Transformers for Point Cloud
2.2. Datasets and Evaluation Metrics
2.2.1. Datasets
2.2.2. Evaluation Metrics
| Datasets Mainly Used in 3D Shape Classification | |||||||
|---|---|---|---|---|---|---|---|
| Name and Reference | Year | Training | Test | Sample | Classes | Type | Tasks |
| McGill Benchmark [25] | 2008 | 304 | 152 | 456 | 19 | Synthetic | Cls |
| Sydney Urban Objects [26] | 2013 | - | - | 588 | 14 | Real world | Cls |
| ModelNet10 [15] | 2015 | 3991 | 605 | 4899 | 10 | Synthetic | Cls |
| ModelNet40 [15] | 2015 | 9843 | 2468 | 12,311 | 40 | Synthetic | Cls |
| ShapeNet [17] | 2015 | - | - | 51,190 | 55 | Synthetic | Cls/SemSeg/PartSeg |
| ScanNet [19] | 2017 | 9677 | 2606 | 12,283 | 17 | Real world | SemSeg |
| ScanObjectNN [16] | 2019 | 2321 | 581 | 2902 | 15 | Real world | Cls |
| Datasets Mainly Used in Point Cloud Semantic Segmentation | |||||||
| Name and Reference | Year | Points | Classes | Scans | Spatial Size | Sensors | Tasks |
| ISPRS [27] | 2012 | 1.6 M | 5(44) | 17 | - | ALS | Cls/SemSeg |
| Paris-rue-Madame [28] | 2014 | 20 M | 17 | 2 | - | MLS | Cls/SemSeg/Det |
| IQmulus [29] | 2015 | 300 M | 8(22) | 10 | - | MLS | Cls/SemSeg |
| ScanNet [19] | 2017 | - | 20(20) | 1513 | 8 × 4 × 4 | RGB-D | Cls/SemSeg/InsSeg/Det |
| S3DIS [18] | 2017 | 273 M | 13(13) | 272 | 10 × 5 × 5 | Matterport | SemSeg/InsSeg/Det |
| Semantic3D [20] | 2017 | 4000 M | 8(9) | 15/15 | 250 × 260 × 80 | TLS | SemSeg |
| Paris-Lille-3D [24] | 2018 | 143 M | 9(50) | 3 | 200 × 280 × 30 | MLS | SemSeg |
| SemanticKITTI [22] | 2019 | 4549 M | 25(28) | 23,201/20,351 | 150 × 100 × 10 | MLS | SemSeg/Compl |
| Toronto-3D [23] | 2020 | 78.3 M | 8(9) | 4 | 260 × 350 × 40 | MLS | SemSeg |
| DALES [30] | 2020 | 505 M | 8(9) | 40 | 500 × 500 × 65 | ALS | SemSeg/PanSeg |
| SemanticPOSS [31] | 2020 | 216 M | 14 | - | - | MLS | SemSeg/PanSeg |
| OpenGF [31] | 2021 | 542.1 M | - | - | - | ALS | SemSeg |
| STPLS3D [32] | 2022 | 216 M | 18/14 | - | - | ALS | SemSeg/PanSeg |
| HRHD-HK [33] | 2023 | 273 M | 7 | - | - | ALS | SemSeg |
| ARCH2S [34] | 2024 | 5 M × 5 | 14 | - | - | - | SemSeg/Gen/Recon |
| FRACTAL [35] | 2024 | 9621 M | 7 | - | - | ALS | SemSeg |
| Datasets Mainly Used in 3D Object Detection and Place Recognition | |||||||
| Name and Reference | Year | Scenes | Classes | Frames | 3D Boxes | Scene Type | Tasks |
| KITTI [21] | 2012 | 22 | 8 | 15 K | 200 K | Urban (driving) | Det |
| SUN RGB-D [36] | 2015 | 47 | 37 | 5 K | 65 K | Indoor | SemSeg/Det |
| ScanNetV2 [19] | 2018 | 1.5 K | 18 | - | - | Indoor | Cls/SemSeg/InsSeg/Det |
| H3D [37] | 2019 | 160 | 8 | 27 K | 1.1 M | Urban (driving) | Det |
| Argoverse [38] | 2019 | 113 | 15 | 44 K | 993 K | Urban (driving) | Det/Tracking |
| A *3D [39] | 2019 | - | 7 | 39K | 230 K | Urban (driving) | Det |
| Waymo Open [40] | 2020 | 1 K | 4 | 200 K | 12 M | Urban (driving) | Det/Tracking |
| nuScenes [41] | 2020 | 1 K | 23 | 40 K | 1.4 M | Urban (driving) | SemSeg/Det/Tracking |
| RadarScence [42] | 2021 | - | - | 832 K | 1.4 M | Urban (driving) | Det/Tracking |
| Name and Reference | Year | Scenes | Classes | Frames | 3D Boxes | Scene Type | Tasks |
| aiMotive [43] | 2023 | 176 | 14 | 26,583 | - | Urban (driving) | Det |
| UT Campus Object [44] | 2023 | 1 K | 53 | 5 K | 130 M | Urban | SemSeg/Det |
| Dual Radar [45] | 2023 | - | - | 10 K | - | Urban (driving) | Det/Tracking |
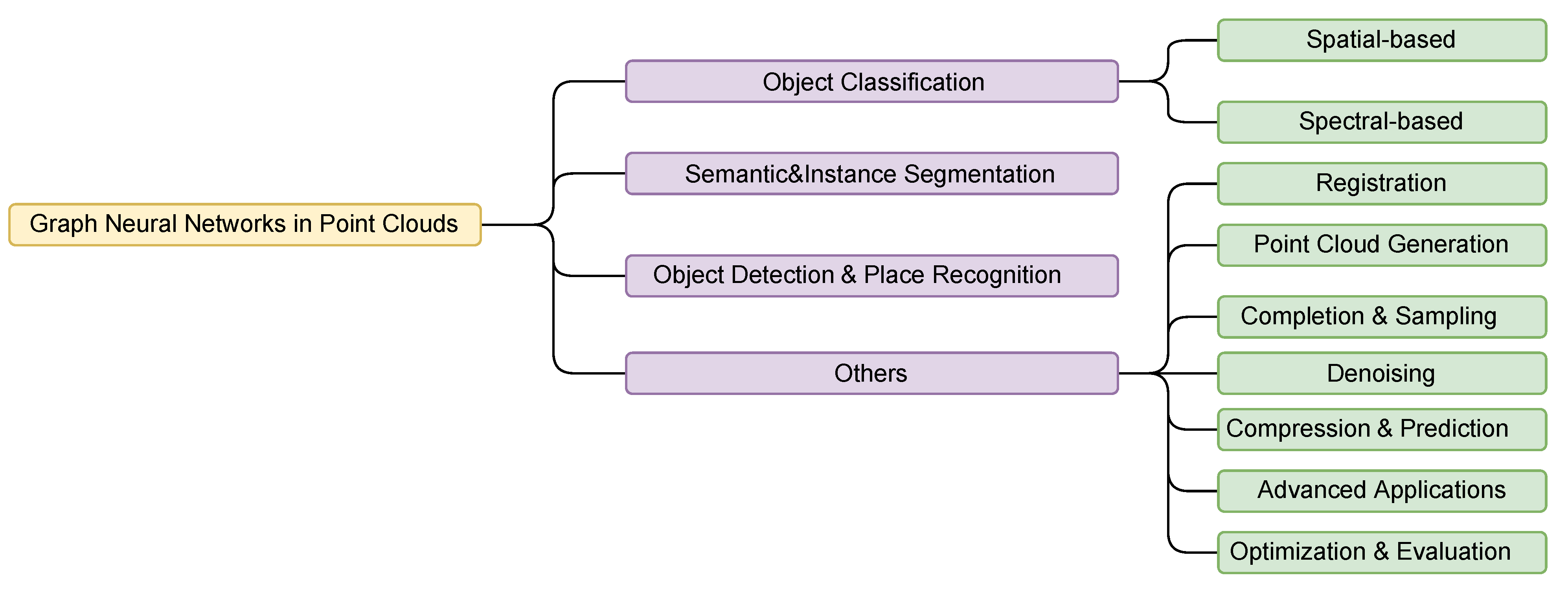
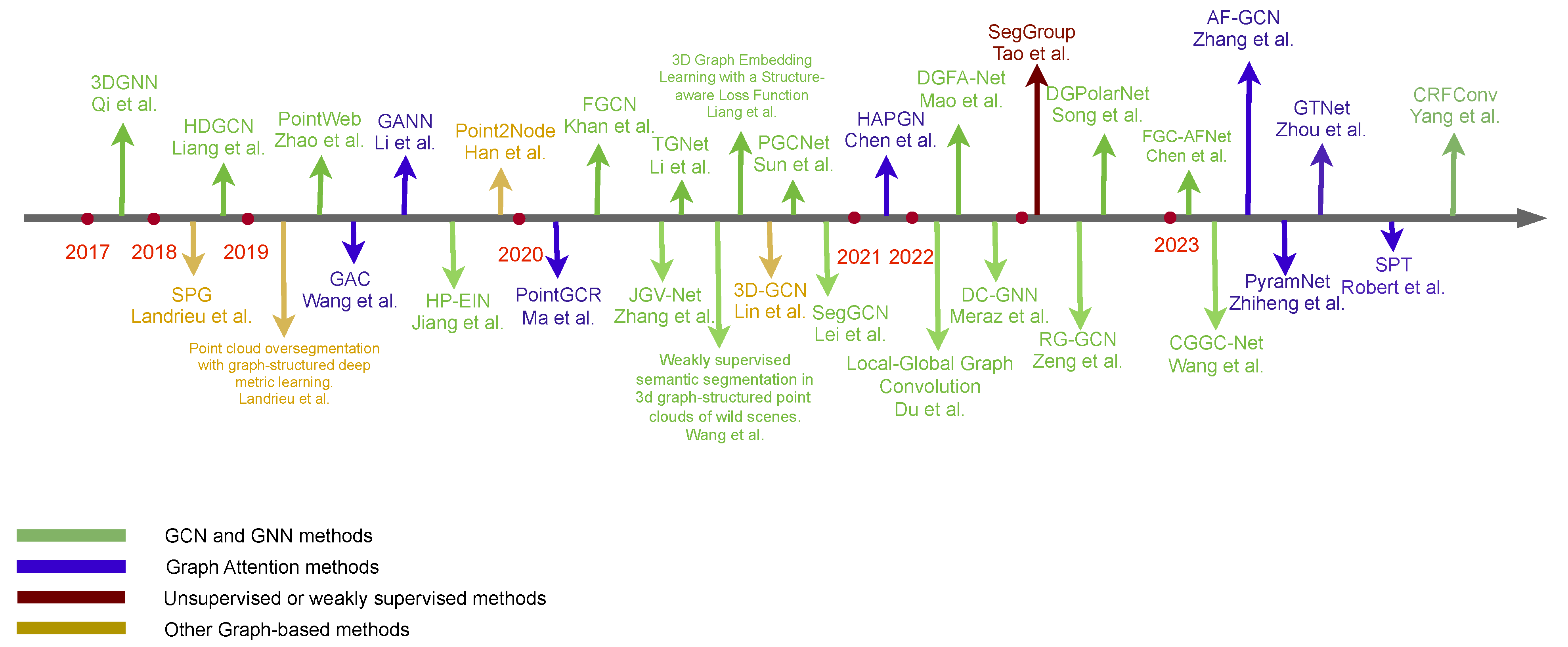
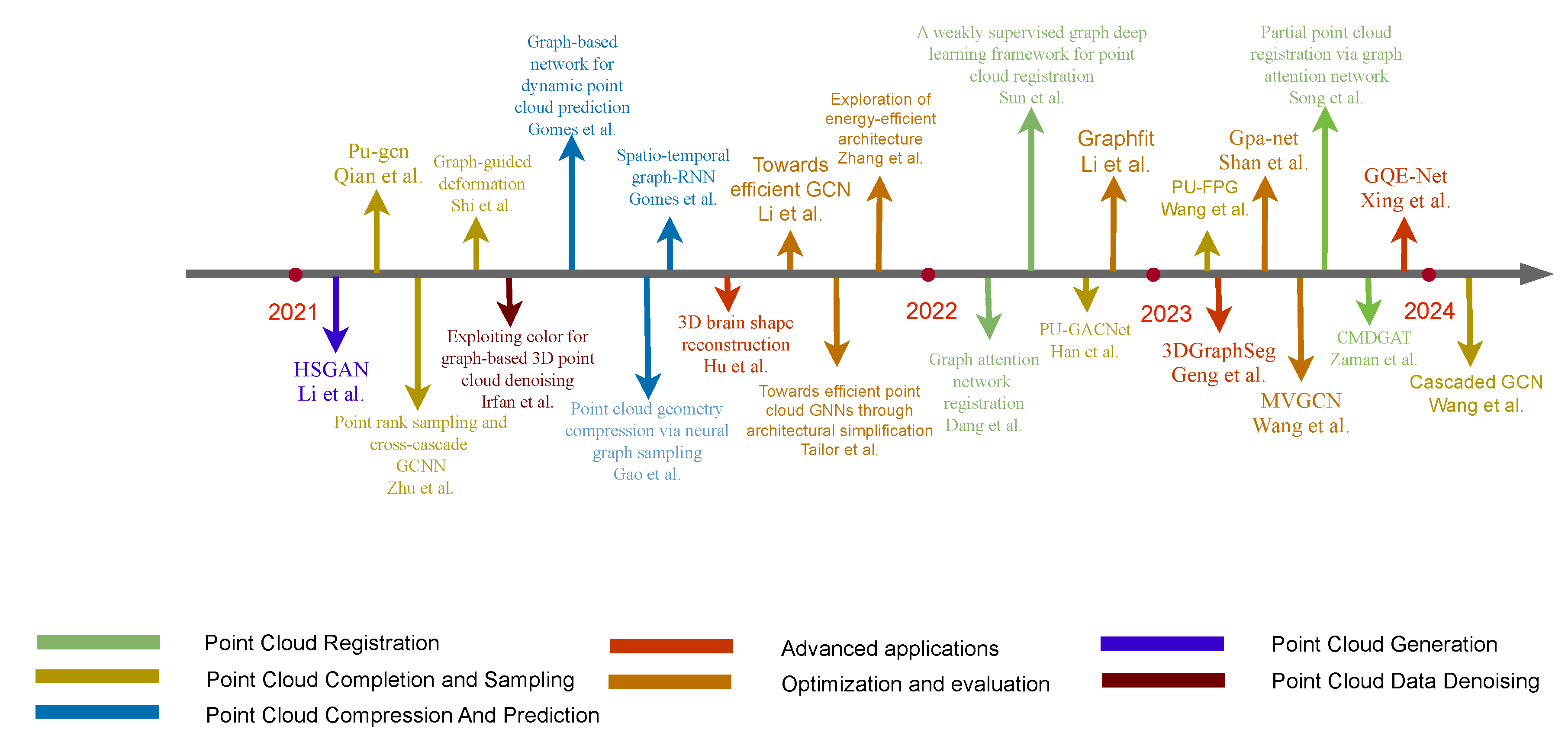
3. Graph Methods in Point Cloud Tasks
3.1. Classification
3.1.1. Spectral-Based Methods
3.1.2. Spatial-Based Methods
3.1.3. Discussion
3.2. Segmentation
3.2.1. Semantic Segmentation and Instance Segmentation
3.2.2. Discussion
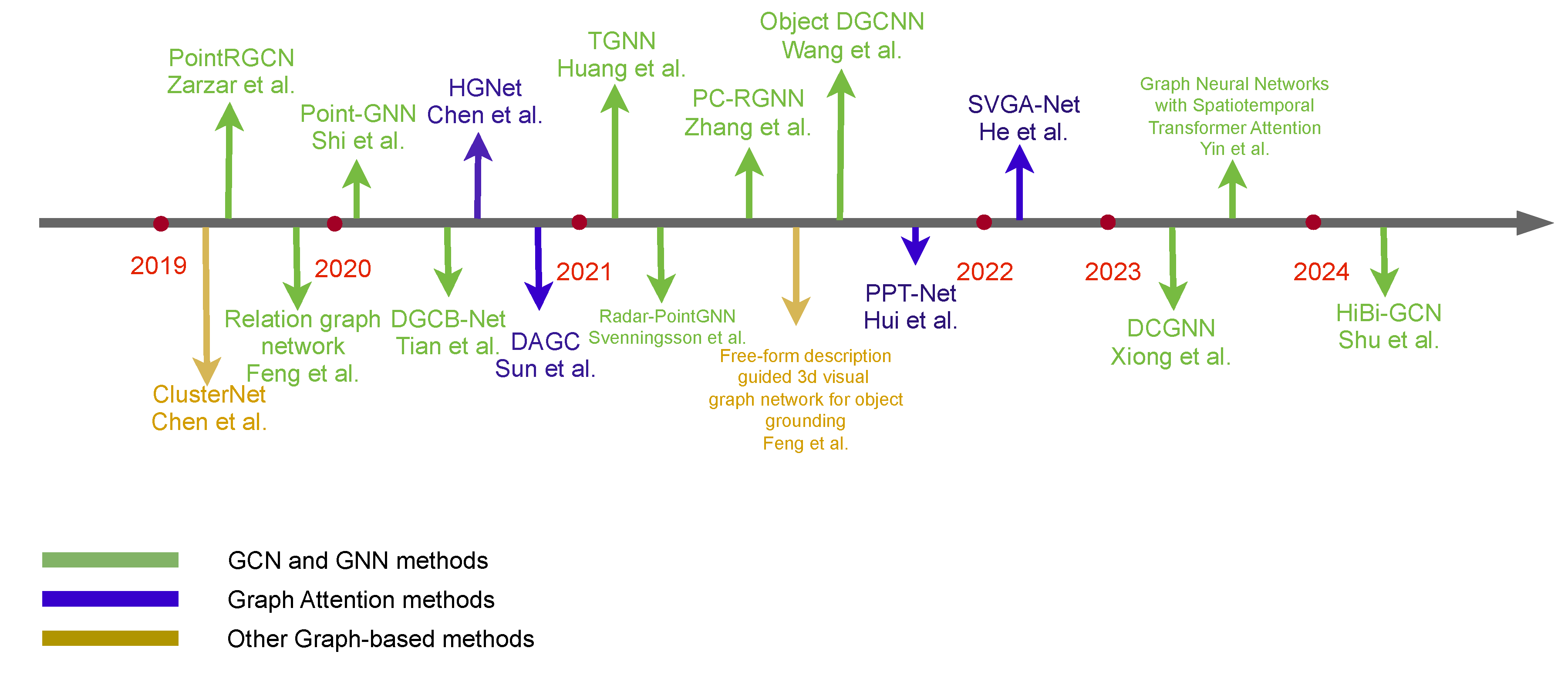
3.3. Object Detection
3.3.1. Three-Dimensional Object Detection and Place Recognition
3.3.2. Discussion
3.4. Others
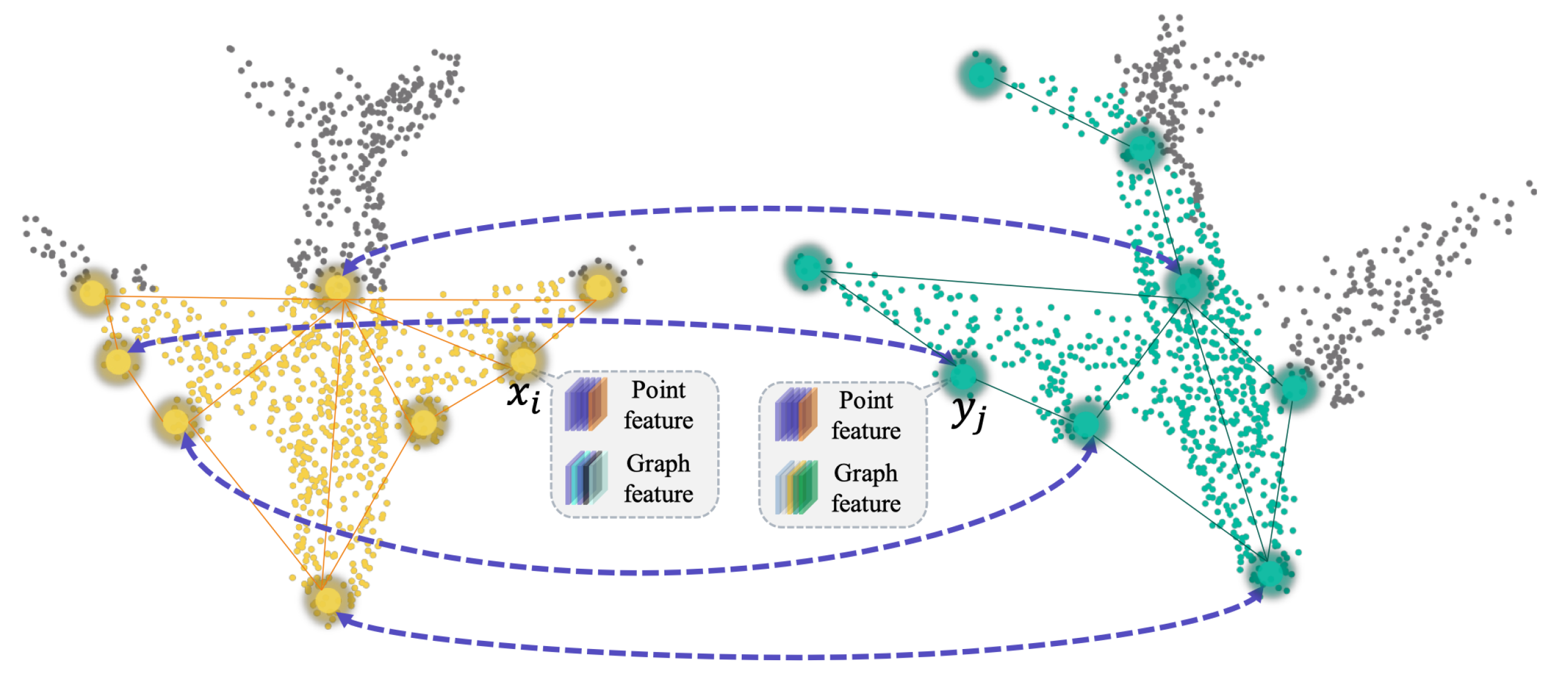
3.4.1. Point Cloud Registration
3.4.2. Discussion
3.4.3. Point Cloud Generation
3.4.4. Discussion
3.4.5. Point Cloud Completion and Sampling
3.4.6. Discussion
3.4.7. Point Cloud Denoising
3.4.8. Discussion
3.4.9. Compression and Prediction
3.4.10. Discussion
3.4.11. Advanced Applications
3.4.12. Optimization and Evaluation
4. Trends and Challenges
4.1. Observed Trends
- Hybrid graph models: The integration of both spectral and spatial graph approaches, exemplified by models such as 3SGCN [52], indicates a trend towards leveraging the strengths of each method to enhance classification accuracy and mitigate noise. This hybrid strategy provides robust handling of the complex data structures inherent in point clouds.
- Deep learning integration: The use of deep learning techniques, including autoencoders and advanced convolutional structures in models like DGCNN [151], underscores a growing convergence between deep learning and graph-based methods. This integration enables more effective extraction of complex, high-level features.
- Attention mechanisms and contextual understanding: The adoption of attention mechanisms, as seen in GAPNet [65] and HAPGN [126], is becoming widespread, underscoring an increasing focus on improving the precision of feature weighting and enhancing the contextual understanding of point cloud data. These mechanisms allow models to focus on the most pertinent parts of the data, enhancing learning efficiency and accuracy.
4.2. Challenges and Future Trends
- Scalability: With the increase in size and complexity of point cloud datasets, scalability is a paramount challenge. Existing methods, particularly those involving dynamic graph updates or spectral transformations, are computationally intensive.
- Robustness to variations: Variability in point cloud data quality, density, and coverage necessitates the development of methods that are robust to these fluctuations, as exemplified by models like 3DTI-Net [51].
- Real-time processing: For applications such as autonomous driving or augmented reality, real-time processing of point clouds is crucial. Current graph-based methods generally lack optimization for real-time performance due to their computational demands.
- Handling of high-dimensional data: Efficiently managing and processing high-dimensional data without losing essential information remains a technical challenge. Techniques that reduce dimensionality while retaining critical details, such as manifold learning, are of interest.
- Integration of global and local features: There is an ongoing need to effectively integrate global and local features to enhance model descriptive power. Future developments may focus on more sophisticated architectures that seamlessly combine these feature levels.
- Advancements in graph convolutional techniques: Future research is likely to concentrate on developing more sophisticated graph convolutional techniques that can better capture the complex structures and relationships within point clouds.
- Enhanced learning paradigms: Moving beyond supervised learning paradigms, there is a potential trend towards more adaptive, continual learning frameworks that can evolve and improve as they are exposed to new data without the need for retraining from scratch.
- Quantitative evaluation of graph-based processing: Many applications require precise and accurate processing of point clouds. Determining how to construct graph structures on point clouds to ensure their accurate and precise representation, and how to quantitatively evaluate graph-based methods, is crucial for ensuring the interpretability and effectiveness of these methods.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In Advances in Neural Information Processing Systems; MIT: Cambridge, MA, USA, 2017; Volume 30, pp. 5099–5108. [Google Scholar]
- Chen, C.; Wu, Y.; Dai, Q.; Zhou, H.Y.; Xu, M.; Yang, S.; Han, X.; Yu, Y. A survey on graph neural networks and graph transformers in computer vision: A task-oriented perspective. arXiv 2022, arXiv:2209.13232. [Google Scholar]
- Guo, Y.; Wang, H.; Hu, Q.; Liu, H.; Liu, L.; Bennamoun, M. Deep learning for 3d point clouds: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 4338–4364. [Google Scholar] [CrossRef]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. In Advances in Neural Information Processing Systems; MIT: Cambridge, MA, USA, 2016; Volume 29, pp. 3844–3852. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. In Advances in Neural Information Processing Systems; MIT: Cambridge, MA, USA, 2017; Volume 30, p. 4755450. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.H.; Koltun, V. Point transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 16259–16268. [Google Scholar]
- Guo, M.H.; Cai, J.X.; Liu, Z.N.; Mu, T.J.; Martin, R.R.; Hu, S.M. Pct: Point cloud transformer. Comput. Vis. Media 2021, 7, 187–199. [Google Scholar] [CrossRef]
- Park, C.; Jeong, Y.; Cho, M.; Park, J. Fast point transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 16949–16958. [Google Scholar]
- Lai, X.; Liu, J.; Jiang, L.; Wang, L.; Zhao, H.; Liu, S.; Qi, X.; Jia, J. Stratified transformer for 3d point cloud segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8500–8509. [Google Scholar]
- Wu, X.; Lao, Y.; Jiang, L.; Liu, X.; Zhao, H. Point transformer v2: Grouped vector attention and partition-based pooling. In Advances in Neural Information Processing Systems; MIT: Cambridge, MA, USA, 2022; Volume 35, pp. 33330–33342. [Google Scholar]
- Wu, X.; Jiang, L.; Wang, P.S.; Liu, Z.; Liu, X.; Qiao, Y.; Ouyang, W.; He, T.; Zhao, H. Point Transformer V3: Simpler Faster Stronger. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–21 June 2024; pp. 4840–4851. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Uy, M.A.; Pham, Q.H.; Hua, B.S.; Nguyen, T.; Yeung, S.K. Revisiting point cloud classification: A new benchmark dataset and classification model on real-world data. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, South Korea, 27 October–2 November 2019; pp. 1588–1597. [Google Scholar]
- Chang, A.X.; Funkhouser, T.; Guibas, L.; Hanrahan, P.; Huang, Q.; Li, Z.; Savarese, S.; Savva, M.; Song, S.; Su, H.; et al. Shapenet: An information-rich 3d model repository. arXiv 2015, arXiv:1512.03012. [Google Scholar]
- Armeni, I.; Sener, O.; Zamir, A.R.; Jiang, H.; Brilakis, I.; Fischer, M.; Savarese, S. 3d semantic parsing of large-scale indoor spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1534–1543. [Google Scholar]
- Dai, A.; Chang, A.X.; Savva, M.; Halber, M.; Funkhouser, T.; Nießner, M. Scannet: Richly-annotated 3d reconstructions of indoor scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5828–5839. [Google Scholar]
- Hackel, T.; Savinov, N.; Ladicky, L.; Wegner, J.D.; Schindler, K.; Pollefeys, M. Semantic3d. net: A new large-scale point cloud classification benchmark. arXiv 2017, arXiv:1704.03847. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The kitti vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Behley, J.; Garbade, M.; Milioto, A.; Quenzel, J.; Behnke, S.; Stachniss, C.; Gall, J. Semantickitti: A dataset for semantic scene understanding of lidar sequences. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9297–9307. [Google Scholar]
- Tan, W.; Qin, N.; Ma, L.; Li, Y.; Du, J.; Cai, G.; Yang, K.; Li, J. Toronto-3D: A large-scale mobile LiDAR dataset for semantic segmentation of urban roadways. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 202–203. [Google Scholar]
- Roynard, X.; Deschaud, J.E.; Goulette, F. Paris-Lille-3D: A large and high-quality ground-truth urban point cloud dataset for automatic segmentation and classification. Int. J. Robot. Res. 2018, 37, 545–557. [Google Scholar] [CrossRef]
- Siddiqi, K.; Zhang, J.; Macrini, D.; Shokoufandeh, A.; Bouix, S.; Dickinson, S. Retrieving articulated 3-D models using medial surfaces. Mach. Vis. Appl. 2008, 19, 261–275. [Google Scholar] [CrossRef]
- De Deuge, M.; Quadros, A.; Hung, C.; Douillard, B. Unsupervised feature learning for classification of outdoor 3d scans. In Proceedings of the Australasian Conference on Robitics and Automation, University of New South Wales Kensington, Sydney, NSW, Australia, 2–4 December 2013; Volume 2. [Google Scholar]
- Rottensteiner, F.; Sohn, G.; Jung, J.; Gerke, M.; Baillard, C.; Benitez, S.; Breitkopf, U. The ISPRS benchmark on urban object classification and 3D building reconstruction. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. I-3 2012, 1, 293–298. [Google Scholar] [CrossRef]
- Serna, A.; Marcotegui, B.; Goulette, F.; Deschaud, J.E. Paris-rue-Madame database: A 3D mobile laser scanner dataset for benchmarking urban detection, segmentation and classification methods. In Proceedings of the 4th International Conference on Pattern Recognition, Applications and Methods ICPRAM 2014, Loire Valley, France, 6–8 March 2014. [Google Scholar]
- Vallet, B.; Brédif, M.; Serna, A.; Marcotegui, B.; Paparoditis, N. TerraMobilita/iQmulus urban point cloud analysis benchmark. Comput. Graph. 2015, 49, 126–133. [Google Scholar] [CrossRef]
- Varney, N.; Asari, V.K.; Graehling, Q. DALES: A large-scale aerial LiDAR data set for semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 186–187. [Google Scholar]
- Pan, Y.; Gao, B.; Mei, J.; Geng, S.; Li, C.; Zhao, H. Semanticposs: A point cloud dataset with large quantity of dynamic instances. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2020; pp. 687–693. [Google Scholar]
- Chen, M.; Hu, Q.; Yu, Z.; Thomas, H.; Feng, A.; Hou, Y.; McCullough, K.; Ren, F.; Soibelman, L. Stpls3d: A large-scale synthetic and real aerial photogrammetry 3d point cloud dataset. arXiv 2022, arXiv:2203.09065. [Google Scholar]
- Li, M.; Wu, Y.; Yeh, A.G.; Xue, F. HRHD-HK: A benchmark dataset of high-rise and high-density urban scenes for 3D semantic segmentation of photogrammetric point clouds. arXiv 2023, arXiv:2307.07976. [Google Scholar]
- Cheung, K.L.; Lee, C.C. ARCH2S: Dataset, Benchmark and Challenges for Learning Exterior Architectural Structures from Point Clouds. arXiv 2024, arXiv:2406.01337. [Google Scholar]
- Gaydon, C.; Daab, M.; Roche, F. FRACTAL: An Ultra-Large-Scale Aerial Lidar Dataset for 3D Semantic Segmentation of Diverse Landscapes. arXiv 2024, arXiv:2405.04634. [Google Scholar]
- Song, S.; Lichtenberg, S.P.; Xiao, J. Sun rgb-d: A rgb-d scene understanding benchmark suite. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 567–576. [Google Scholar]
- Patil, A.; Malla, S.; Gang, H.; Chen, Y.T. The h3d dataset for full-surround 3d multi-object detection and tracking in crowded urban scenes. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 9552–9557. [Google Scholar]
- Chang, M.F.; Lambert, J.; Sangkloy, P.; Singh, J.; Bak, S.; Hartnett, A.; Wang, D.; Carr, P.; Lucey, S.; Ramanan, D.; et al. Argoverse: 3d tracking and forecasting with rich maps. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8748–8757. [Google Scholar]
- Pham, Q.H.; Sevestre, P.; Pahwa, R.S.; Zhan, H.; Pang, C.H.; Chen, Y.; Mustafa, A.; Chandrasekhar, V.; Lin, J. A* 3d dataset: Towards autonomous driving in challenging environments. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 2267–2273. [Google Scholar]
- Sun, P.; Kretzschmar, H.; Dotiwalla, X.; Chouard, A.; Patnaik, V.; Tsui, P.; Guo, J.; Zhou, Y.; Chai, Y.; Caine, B.; et al. Scalability in perception for autonomous driving: Waymo open dataset. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2446–2454. [Google Scholar]
- Caesar, H.; Bankiti, V.; Lang, A.H.; Vora, S.; Liong, V.E.; Xu, Q.; Krishnan, A.; Pan, Y.; Baldan, G.; Beijbom, O. nuscenes: A multimodal dataset for autonomous driving. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11621–11631. [Google Scholar]
- Schumann, O.; Hahn, M.; Scheiner, N.; Weishaupt, F.; Tilly, J.F.; Dickmann, J.; Wöhler, C. Radarscenes: A real-world radar point cloud data set for automotive applications. In Proceedings of the 2021 IEEE 24th International Conference on Information Fusion (FUSION), Rustenburg, South Africa, 1–4 November 2021; pp. 1–8. [Google Scholar]
- Matuszka, T.; Barton, I.; Butykai, Á.; Hajas, P.; Kiss, D.; Kovács, D.; Kunsági-Máté, S.; Lengyel, P.; Németh, G.; Pető, L.; et al. aimotive dataset: A multimodal dataset for robust autonomous driving with long-range perception. arXiv 2022, arXiv:2211.09445. [Google Scholar]
- Zhang, A.; Eranki, C.; Zhang, C.; Park, J.H.; Hong, R.; Kalyani, P.; Kalyanaraman, L.; Gamare, A.; Bagad, A.; Esteva, M.; et al. Towards robust robot 3d perception in urban environments: The ut campus object dataset. In IEEE Transactions on Robotics; IEEE: New York City, NY, USA, 2024. [Google Scholar]
- Zhang, X.; Wang, L.; Chen, J.; Fang, C.; Yang, L.; Song, Z.; Yang, G.; Wang, Y.; Zhang, X.; Li, J. Dual radar: A multi-modal dataset with dual 4d radar for autononous driving. arXiv 2023, arXiv:2310.07602. [Google Scholar]
- Te, G.; Hu, W.; Zheng, A.; Guo, Z. Rgcnn: Regularized graph cnn for point cloud segmentation. In Proceedings of the 26th ACM International Conference on Multimedia, Seoul, Republic of Korea, 22–26 October 2018; pp. 746–754. [Google Scholar]
- Xie, Z.; Chen, J.; Peng, B. Point clouds learning with attention-based graph convolution networks. Neurocomputing 2020, 402, 245–255. [Google Scholar] [CrossRef]
- Feng, Y.; You, H.; Zhang, Z.; Ji, R.; Gao, Y. Hypergraph neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 3558–3565. [Google Scholar]
- Wang, C.; Samari, B.; Siddiqi, K. Local spectral graph convolution for point set feature learning. In Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 52–66. [Google Scholar]
- Zhang, Y.; Rabbat, M. A graph-cnn for 3d point cloud classification. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 6279–6283. [Google Scholar]
- Pan, G.; Wang, J.; Ying, R.; Liu, P. 3dti-net: Learn inner transform invariant 3d geometry features using dynamic gcn. arXiv 2018, arXiv:1812.06254. [Google Scholar]
- Wang, Q.; Zhang, X.; Gu, Y. Spatial-Spectral Smooth Graph Convolutional Network for Multispectral Point Cloud Classification. In Proceedings of the IGARSS 2020-2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 1062–1065. [Google Scholar]
- Yi, L.; Su, H.; Guo, X.; Guibas, L.J. Syncspeccnn: Synchronized spectral cnn for 3d shape segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2282–2290. [Google Scholar]
- Lu, Q.; Chen, C.; Xie, W.; Luo, Y. PointNGCNN: Deep convolutional networks on 3D point clouds with neighborhood graph filters. Comput. Graph. 2020, 86, 42–51. [Google Scholar] [CrossRef]
- Chen, S.; Duan, C.; Yang, Y.; Li, D.; Feng, C.; Tian, D. Deep unsupervised learning of 3D point clouds via graph topology inference and filtering. IEEE Trans. Image Process. 2019, 29, 3183–3198. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Fang, Y. Adaptive wavelet transformer network for 3d shape representation learning. In Proceedings of the International Conference on Learning Representations, Vienna, Austria, 3–7 May 2021. [Google Scholar]
- Wen, C.; Long, J.; Yu, B.; Tao, D. PointWavelet: Learning in Spectral Domain for 3-D Point Cloud Analysis. In IEEE Transactions on Neural Networks and Learning Systems; IEEE: New York City, NY, USA, 2024. [Google Scholar]
- Yi, Y.; Lu, X.; Gao, S.; Robles-Kelly, A.; Zhang, Y. Graph classification via discriminative edge feature learning. Pattern Recognit. 2023, 143, 109799. [Google Scholar] [CrossRef]
- Wu, B.; Lang, B. MSGCN: A multiscale spatio graph convolution network for 3D point clouds. Multimed. Tools Appl. 2023, 82, 35949–35968. [Google Scholar] [CrossRef]
- Chen, L.; Wei, G.; Wang, Z. PointAGCN: Adaptive Spectral Graph CNN for Point Cloud Feature Learning. In Proceedings of the 2018 International Conference on Security, Pattern Analysis, and Cybernetics (SPAC), Jinan, China, 14–17 December 2018; pp. 401–406. [Google Scholar]
- Simonovsky, M.; Komodakis, N. Dynamic edge-conditioned filters in convolutional neural networks on graphs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3693–3702. [Google Scholar]
- Xu, Y.; Fan, T.; Xu, M.; Zeng, L.; Qiao, Y. Spidercnn: Deep learning on point sets with parameterized convolutional filters. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 87–102. [Google Scholar]
- Dominguez, M.; Dhamdhere, R.; Petkar, A.; Jain, S.; Sah, S.; Ptucha, R. General-purpose deep point cloud feature extractor. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Munich, Germany, 8–14 September 2018; pp. 1972–1981. [Google Scholar]
- Shen, Y.; Feng, C.; Yang, Y.; Tian, D. Mining point cloud local structures by kernel correlation and graph pooling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4548–4557. [Google Scholar]
- Chen, C.; Fragonara, L.Z.; Tsourdos, A. GAPointNet: Graph attention based point neural network for exploiting local feature of point cloud. Neurocomputing 2021, 438, 122–132. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph cnn for learning on point clouds. ACM Trans. Graph. 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Zhang, K.; Hao, M.; Wang, J.; de Silva, C.W.; Fu, C. Linked dynamic graph cnn: Learning on point cloud via linking hierarchical features. arXiv 2019, arXiv:1904.10014. [Google Scholar]
- Guo, R.; Zhou, Y.; Zhao, J.; Man, Y.; Liu, M.; Yao, R.; Liu, B. Point cloud classification by dynamic graph CNN with adaptive feature fusion. IET Comput. Vis. 2021, 15, 235–244. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, X.; Liu, H.; Zhang, J.; Zare, A.; Fan, B. Geometric attentional dynamic graph convolutional neural networks for point cloud analysis. Neurocomputing 2021, 432, 300–310. [Google Scholar] [CrossRef]
- Hassani, K.; Haley, M. Unsupervised multi-task feature learning on point clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 8160–8171. [Google Scholar]
- Zhang, L.; Zhu, Z. Unsupervised feature learning for point cloud by contrasting and clustering with graph convolutional neural network. arXiv 2019, arXiv:1904.12359. [Google Scholar]
- Liu, J.; Ni, B.; Li, C.; Yang, J.; Tian, Q. Dynamic points agglomeration for hierarchical point sets learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 7546–7555. [Google Scholar]
- Sun, X.; Lian, Z.; Xiao, J. Srinet: Learning strictly rotation-invariant representations for point cloud classification and segmentation. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; pp. 980–988. [Google Scholar]
- Bazazian, D.; Nahata, D. DCG-net: Dynamic capsule graph convolutional network for point clouds. IEEE Access 2020, 8, 188056–188067. [Google Scholar] [CrossRef]
- Kim, S.; Park, J.; Han, B. Rotation-invariant local-to-global representation learning for 3d point cloud. Adv. Neural Inf. Process. Syst. 2020, 33, 8174–8185. [Google Scholar]
- Wen, C.; Li, X.; Yao, X.; Peng, L.; Chi, T. Airborne LiDAR point cloud classification with global-local graph attention convolution neural network. ISPRS J. Photogramm. Remote Sens. 2021, 173, 181–194. [Google Scholar] [CrossRef]
- Li, D.; Shen, X.; Yu, Y.; Guan, H.; Wang, H.; Li, D. GGM-net: Graph geometric moments convolution neural network for point cloud shape classification. IEEE Access 2020, 8, 124989–124998. [Google Scholar] [CrossRef]
- Nezhadarya, E.; Taghavi, E.; Razani, R.; Liu, B.; Luo, J. Adaptive hierarchical down-sampling for point cloud classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 12956–12964. [Google Scholar]
- Zhai, Z.; Zhang, X.; Yao, L. Multi-scale dynamic graph convolution network for point clouds classification. IEEE Access 2020, 8, 65591–65598. [Google Scholar] [CrossRef]
- Lei, H.; Akhtar, N.; Mian, A. Spherical kernel for efficient graph convolution on 3d point clouds. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 3664–3680. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.H.; Huang, S.Y.; Wang, Y.C.F. Convolution in the cloud: Learning deformable kernels in 3d graph convolution networks for point cloud analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1800–1809. [Google Scholar]
- Li, X.A.; Wang, L.Y.; Lu, J. Multiscale receptive fields graph attention network for point cloud classification. Complexity 2021, 2021, 1–9. [Google Scholar] [CrossRef]
- Yang, D.; Gao, W. Pointmanifold: Using manifold learning for point cloud classification. arXiv 2020, arXiv:2010.07215. [Google Scholar]
- Wang, H.; Zhang, Y.; Liu, W.; Gu, X.; Jing, X.; Liu, Z. A novel GCN-based point cloud classification model robust to pose variances. Pattern Recognit. 2022, 121, 108251. [Google Scholar] [CrossRef]
- Zhang, W.; Su, S.; Wang, B.; Hong, Q.; Sun, L. Local k-nns pattern in omni-direction graph convolution neural network for 3d point clouds. Neurocomputing 2020, 413, 487–498. [Google Scholar] [CrossRef]
- Dominguez, M.; Ptucha, R. Directional graph networks with hard weight assignments. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 7439–7446. [Google Scholar]
- Wang, W.; You, Y.; Liu, W.; Lu, C. Point cloud classification with deep normalized Reeb graph convolution. Image Vis. Comput. 2021, 106, 104092. [Google Scholar] [CrossRef]
- Li, R.; Zhang, Y.; Niu, D.; Yang, G.; Zafar, N.; Zhang, C.; Zhao, X. PointVGG: Graph convolutional network with progressive aggregating features on point clouds. Neurocomputing 2021, 429, 187–198. [Google Scholar] [CrossRef]
- Srivastava, S.; Sharma, G. Exploiting local geometry for feature and graph construction for better 3d point cloud processing with graph neural networks. In Proceedings of the 2021 IEEE INternational Conference on Robotics and Automation (ICRA), Xian, China, 30 May–5 June 2021; pp. 12903–12909. [Google Scholar]
- Zhao, P.; Guan, H.; Li, D.; Yu, Y.; Wang, H.; Gao, K.; Junior, J.M.; Li, J. Airborne multispectral LiDAR point cloud classification with a feature Reasoning-based graph convolution network. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102634. [Google Scholar] [CrossRef]
- Xu, Q.; Sun, X.; Wu, C.Y.; Wang, P.; Neumann, U. Grid-gcn for fast and scalable point cloud learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 5661–5670. [Google Scholar]
- Hu, H.; Wang, F.; Le, H. Va-gcn: A vector attention graph convolution network for learning on point clouds. arXiv 2021, arXiv:2106.00227. [Google Scholar]
- Kumar, S.; Katragadda, S.R.; Abdul, A.; Reddy, V.D. Extended Graph Convolutional Networks for 3D Object Classification in Point Clouds. Int. J. Adv. Comput. Sci. Appl. 2021, 12. [Google Scholar] [CrossRef]
- Xun, L.; Feng, X.; Chen, C.; Yuan, X.; Lu, Q. Graph attention-based deep neural network for 3d point cloud processing. In Proceedings of the 2021 IEEE International Conference on Multimedia and Expo (ICME), Shenzhen, China, 5–9 July 2021; pp. 1–6. [Google Scholar]
- Huang, C.Q.; Jiang, F.; Huang, Q.H.; Wang, X.Z.; Han, Z.M.; Huang, W.Y. Dual-graph attention convolution network for 3-D point cloud classification. In IEEE Transactions on Neural Networks and Learning Systems; IEEE: New York City, NY, USA, 2022. [Google Scholar]
- Yue, Y.; Li, X.; Peng, Y. A 3D Point Cloud Classification Method Based on Adaptive Graph Convolution and Global Attention. Sensors 2024, 24, 617. [Google Scholar] [CrossRef]
- Jing, W.; Zhang, W.; Li, L.; Di, D.; Chen, G.; Wang, J. AGNet: An attention-based graph network for point cloud classification and segmentation. Remote Sens. 2022, 14, 1036. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, H.; Wan, H.; Yang, P.; Wu, Z. Graph-pbn: Graph-based parallel branch network for efficient point cloud learning. Graph. Model. 2022, 119, 101120. [Google Scholar] [CrossRef]
- Lu, D.; Xie, Q.; Gao, K.; Xu, L.; Li, J. 3DCTN: 3D convolution-transformer network for point cloud classification. IEEE Trans. Intell. Transp. Syst. 2022, 23, 24854–24865. [Google Scholar] [CrossRef]
- Liu, S.; Liu, D.; Chen, C.; Xu, C. SGCNN for 3D point cloud classification. In Proceedings of the 2022 14th International Conference on Machine Learning and Computing, Guangzhou, China, 18–21 February 2022; pp. 419–423. [Google Scholar]
- Lin, M.; Feragen, A. DiffConv: Analyzing irregular point clouds with an irregular view. In Proceedings of the European Conference on Computer Vision. Springer, Tel Aviv, Israel, 23–27 October 2022; pp. 380–397. [Google Scholar]
- Lin, Z.H.; Huang, S.Y.; Wang, Y.C.F. Learning of 3d graph convolution networks for point cloud analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 4212–4224. [Google Scholar] [CrossRef]
- Tamajo, A.; Plaß, B.; Klauer, T. Shrinking unit: A Graph Convolution-Based Unit for CNN-like 3D Point Cloud Feature Extractors. arXiv 2022, arXiv:2209.12770. [Google Scholar]
- Li, Y.; Tanaka, Y. Structure-Aware Multi-Hop Graph Convolution for Graph Neural Networks. IEEE Access 2022, 10, 16624–16633. [Google Scholar] [CrossRef]
- Wei, M.; Wei, Z.; Zhou, H.; Hu, F.; Si, H.; Chen, Z.; Zhu, Z.; Qiu, J.; Yan, X.; Guo, Y.; et al. AGConv: Adaptive graph convolution on 3D point clouds. In IEEE Transactions on Pattern Analysis and Machine Intelligence; IEEE: New York City, NY, USA, 2023. [Google Scholar]
- Khodadad, M.; Rezanejad, M.; Kasmaee, A.S.; Siddiqi, K.; Walther, D.; Mahyar, H. MLGCN: An Ultra Efficient Graph Convolution Neural Model For 3D Point Cloud Analysis. arXiv 2023, arXiv:2303.17748. [Google Scholar]
- Qin, S.; Li, Z.; Liu, L. Robust 3D shape classification via non-local graph attention network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 5374–5383. [Google Scholar]
- Qi, X.; Liao, R.; Jia, J.; Fidler, S.; Urtasun, R. 3d graph neural networks for rgbd semantic segmentation. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5199–5208. [Google Scholar]
- Landrieu, L.; Simonovsky, M. Large-scale point cloud semantic segmentation with superpoint graphs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4558–4567. [Google Scholar]
- Liang, Z.; Yang, M.; Deng, L.; Wang, C.; Wang, B. Hierarchical depthwise graph convolutional neural network for 3D semantic segmentation of point clouds. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, BC, Canada, 20–24 May 2019; pp. 8152–8158. [Google Scholar]
- Landrieu, L.; Boussaha, M. Point cloud oversegmentation with graph-structured deep metric learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 7440–7449. [Google Scholar]
- Wang, L.; Huang, Y.; Hou, Y.; Zhang, S.; Shan, J. Graph attention convolution for point cloud semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 10296–10305. [Google Scholar]
- Li, Z.; Zhang, J.; Li, G.; Liu, Y.; Li, S. Graph attention neural networks for point cloud recognition. In Proceedings of the 2019 IEEE International Conference on Multimedia and Expo (ICME), Shanghai, China, 8–12 July 2019; pp. 387–392. [Google Scholar]
- Zhao, H.; Jiang, L.; Fu, C.W.; Jia, J. Pointweb: Enhancing local neighborhood features for point cloud processing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5565–5573. [Google Scholar]
- Jiang, L.; Zhao, H.; Liu, S.; Shen, X.; Fu, C.W.; Jia, J. Hierarchical point-edge interaction network for point cloud semantic segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 10433–10441. [Google Scholar]
- Han, W.; Wen, C.; Wang, C.; Li, X.; Li, Q. Point2node: Correlation learning of dynamic-node for point cloud feature modeling. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 10925–10932. [Google Scholar]
- Lei, H.; Akhtar, N.; Mian, A. Seggcn: Efficient 3d point cloud segmentation with fuzzy spherical kernel. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11611–11620. [Google Scholar]
- Song, W.; Liu, Z.; Guo, Y.; Sun, S.; Zu, G.; Li, M. DGPolarNet: Dynamic graph convolution network for LiDAR point cloud semantic segmentation on polar BEV. Remote Sens. 2022, 14, 3825. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, X.; Dai, H. A graph-voxel joint convolution neural network for ALS point cloud segmentation. IEEE Access 2020, 8, 139781–139791. [Google Scholar] [CrossRef]
- Ma, Y.; Guo, Y.; Liu, H.; Lei, Y.; Wen, G. Global context reasoning for semantic segmentation of 3D point clouds. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Seattle, WA, USA, 13–19 June 2020; pp. 2931–2940. [Google Scholar]
- Khan, S.A.; Shi, Y.; Shahzad, M.; Zhu, X.X. FGCN: Deep feature-based graph convolutional network for semantic segmentation of urban 3D point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 13–19 June 2020; pp. 198–199. [Google Scholar]
- Li, Y.; Ma, L.; Zhong, Z.; Cao, D.; Li, J. TGNet: Geometric graph CNN on 3-D point cloud segmentation. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3588–3600. [Google Scholar] [CrossRef]
- Wang, H.; Rong, X.; Yang, L.; Feng, J.; Xiao, J.; Tian, Y. Weakly supervised semantic segmentation in 3d graph-structured point clouds of wild scenes. arXiv 2020, arXiv:2004.12498. [Google Scholar]
- Liang, Z.; Yang, M.; Wang, C. 3D Graph Embedding Learning with a Structure-aware Loss Function for Point Cloud Semantic Instance Segmentation. arXiv 2019, arXiv:1902.05247. [Google Scholar]
- Sun, Y.; Miao, Y.; Chen, J.; Pajarola, R. PGCNet: Patch graph convolutional network for point cloud segmentation of indoor scenes. Vis. Comput. 2020, 36, 2407–2418. [Google Scholar] [CrossRef]
- Chen, C.; Qian, S.; Fang, Q.; Xu, C. HAPGN: Hierarchical attentive pooling graph network for point cloud segmentation. IEEE Trans. Multimed. 2020, 23, 2335–2346. [Google Scholar] [CrossRef]
- Du, Z.; Ye, H.; Cao, F. A novel local-global graph convolutional method for point cloud semantic segmentation. In IEEE Transactions on Neural Networks and Learning Systems; IEEE: New York City, NY, USA, 2022. [Google Scholar]
- Mao, Y.; Sun, X.; Chen, K.; Diao, W.; Guo, Z.; Lu, X.; Fu, K. Semantic segmentation for point cloud scenes via dilated graph feature aggregation and pyramid decoders. arXiv 2022, arXiv:2204.04944. [Google Scholar]
- Meraz, M.; Ansari, M.A.; Javed, M.; Chakraborty, P. DC-GNN: Drop channel graph neural network for object classification and part segmentation in the point cloud. Int. J. Multimed. Inf. Retr. 2022, 11, 123–133. [Google Scholar] [CrossRef]
- Tao, A.; Duan, Y.; Wei, Y.; Lu, J.; Zhou, J. Seggroup: Seg-level supervision for 3d instance and semantic segmentation. IEEE Trans. Image Process. 2022, 31, 4952–4965. [Google Scholar] [CrossRef]
- Zeng, Z.; Xu, Y.; Xie, Z.; Wan, J.; Wu, W.; Dai, W. Rg-gcn: A random graph based on graph convolution network for point cloud semantic segmentation. Remote Sens. 2022, 14, 4055. [Google Scholar] [CrossRef]
- Chen, J.; Chen, Y.; Wang, C. Feature graph convolution network with attentive fusion for large-scale point clouds semantic segmentation. In IEEE Geoscience and Remote Sensing Letters; IEEE: New York City, NY, USA, 2023. [Google Scholar]
- Wang, X.; Yang, J.; Kang, Z.; Du, J.; Tao, Z.; Qiao, D. A category-contrastive guided-graph convolutional network approach for the semantic segmentation of point clouds. InIEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing; IEEE: New York City, NY, USA, 2023. [Google Scholar]
- Zhang, N.; Pan, Z.; Li, T.H.; Gao, W.; Li, G. Improving graph representation for point cloud segmentation via attentive filtering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 1244–1254. [Google Scholar]
- Zhiheng, K.; Ning, L. PyramNet: Point cloud pyramid attention network and graph embedding module for classification and segmentation. arXiv 2019, arXiv:1906.03299. [Google Scholar]
- Zhou, W.; Wang, Q.; Jin, W.; Shi, X.; Wang, D.; Hao, X.; Yu, Y. GTNet: Graph transformer network for 3D point cloud classification and semantic segmentation. arXiv 2023, arXiv:2305.15213. [Google Scholar]
- Yang, F.; Davoine, F.; Wang, H.; Jin, Z. Continuous conditional random field convolution for point cloud segmentation. Pattern Recognit. 2022, 122, 108357. [Google Scholar] [CrossRef]
- Robert, D.; Raguet, H.; Landrieu, L. Efficient 3d semantic segmentation with superpoint transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 17195–17204. [Google Scholar]
- Xu, M.; Ding, R.; Zhao, H.; Qi, X. Paconv: Position adaptive convolution with dynamic kernel assembling on point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 3173–3182. [Google Scholar]
- Chen, C.; Li, G.; Xu, R.; Chen, T.; Wang, M.; Lin, L. Clusternet: Deep hierarchical cluster network with rigorously rotation-invariant representation for point cloud analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4994–5002. [Google Scholar]
- Zarzar, J.; Giancola, S.; Ghanem, B. PointRGCN: Graph convolution networks for 3D vehicles detection refinement. arXiv 2019, arXiv:1911.12236. [Google Scholar]
- Feng, M.; Gilani, S.Z.; Wang, Y.; Zhang, L.; Mian, A. Relation graph network for 3D object detection in point clouds. IEEE Trans. Image Process. 2020, 30, 92–107. [Google Scholar] [CrossRef] [PubMed]
- Shi, W.; Rajkumar, R. Point-gnn: Graph neural network for 3d object detection in a point cloud. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–17 June 2020; pp. 1711–1719. [Google Scholar]
- Liang, M.; Yang, B.; Wang, S.; Urtasun, R. Deep continuous fusion for multi-sensor 3d object detection. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 641–656. [Google Scholar]
- Huang, P.H.; Lee, H.H.; Chen, H.T.; Liu, T.L. Text-guided graph neural networks for referring 3d instance segmentation. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 1610–1618. [Google Scholar]
- Tian, Y.; Chen, L.; Song, W.; Sung, Y.; Woo, S. Dgcb-net: Dynamic graph convolutional broad network for 3d object recognition in point cloud. Remote Sens. 2020, 13, 66. [Google Scholar] [CrossRef]
- Chen, J.; Lei, B.; Song, Q.; Ying, H.; Chen, D.Z.; Wu, J. A hierarchical graph network for 3d object detection on point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 392–401. [Google Scholar]
- Svenningsson, P.; Fioranelli, F.; Yarovoy, A. Radar-pointgnn: Graph based object recognition for unstructured radar point-cloud data. In Proceedings of the 2021 IEEE Radar Conference (RadarConf21), Atlanta, GA, USA, 7–14 May 2021; pp. 1–6. [Google Scholar]
- Zhang, Y.; Huang, D.; Wang, Y. PC-RGNN: Point cloud completion and graph neural network for 3D object detection. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 3430–3437. [Google Scholar]
- Feng, M.; Li, Z.; Li, Q.; Zhang, L.; Zhang, X.; Zhu, G.; Zhang, H.; Wang, Y.; Mian, A. Free-form description guided 3d visual graph network for object grounding in point cloud. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 3722–3731. [Google Scholar]
- Wang, Y.; Solomon, J.M. Object dgcnn: 3d object detection using dynamic graphs. Adv. Neural Inf. Process. Syst. 2021, 34, 20745–20758. [Google Scholar]
- He, Q.; Wang, Z.; Zeng, H.; Zeng, Y.; Liu, Y. Svga-net: Sparse voxel-graph attention network for 3d object detection from point clouds. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 22 February–1 March 2022; Volume 36, pp. 870–878. [Google Scholar]
- Xiong, S.; Li, B.; Zhu, S. DCGNN: A single-stage 3D object detection network based on density clustering and graph neural network. Complex Intell. Syst. 2022, 9, 251776670. [Google Scholar] [CrossRef]
- Yin, J.; Shen, J.; Gao, X.; Crandall, D.J.; Yang, R. Graph neural network and spatiotemporal transformer attention for 3D video object detection from point clouds. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 45, 9822–9835. [Google Scholar] [CrossRef] [PubMed]
- Shu, D.W.; Kwon, J. Hierarchical bidirected graph convolutions for large-scale 3-D point cloud place recognition. In IEEE Transactions on Neural Networks and Learning Systems; IEEE: New York City, NY, USA, 2023. [Google Scholar]
- Sun, Q.; Liu, H.; He, J.; Fan, Z.; Du, X. Dagc: Employing dual attention and graph convolution for point cloud based place recognition. In Proceedings of the 2020 International Conference on Multimedia Retrieval, Dublin, Ireland, 8–11 June 2020; pp. 224–232. [Google Scholar]
- Hui, L.; Yang, H.; Cheng, M.; Xie, J.; Yang, J. Pyramid point cloud transformer for large-scale place recognition. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 6098–6107. [Google Scholar]
- Zhou, Y.; Tuzel, O. Voxelnet: End-to-end learning for point cloud based 3d object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4490–4499. [Google Scholar]
- Shi, S.; Guo, C.; Jiang, L.; Wang, Z.; Shi, J.; Wang, X.; Li, H. Pv-rcnn: Point-voxel feature set abstraction for 3d object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 10529–10538. [Google Scholar]
- Xie, Q.; Lai, Y.K.; Wu, J.; Wang, Z.; Zhang, Y.; Xu, K.; Wang, J. Mlcvnet: Multi-level context votenet for 3d object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 10447–10456. [Google Scholar]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. Randla-net: Efficient semantic segmentation of large-scale point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11108–11117. [Google Scholar]
- Fu, K.; Liu, S.; Luo, X.; Wang, M. Robust point cloud registration framework based on deep graph matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 8893–8902. [Google Scholar]
- Chang, S.; Ahn, C.; Lee, M.; Oh, S. Graph-matching-based correspondence search for nonrigid point cloud registration. Comput. Vis. Image Underst. 2020, 192, 102899. [Google Scholar] [CrossRef]
- Li, J.; Zhao, P.; Hu, Q.; Ai, M. Robust point cloud registration based on topological graph and cauchy weighted lq-norm. ISPRS J. Photogramm. Remote Sens. 2020, 160, 244–259. [Google Scholar] [CrossRef]
- Li, J.; Hu, Q.; Ai, M. GESAC: Robust graph enhanced sample consensus for point cloud registration. ISPRS J. Photogramm. Remote Sens. 2020, 167, 363–374. [Google Scholar] [CrossRef]
- Saleh, M.; Dehghani, S.; Busam, B.; Navab, N.; Tombari, F. Graphite: Graph-induced feature extraction for point cloud registration. In Proceedings of the 2020 International Conference on 3D Vision (3DV), Fukuoka, Japan, 20–28 November 2020; pp. 241–251. [Google Scholar]
- Shi, C.; Chen, X.; Huang, K.; Xiao, J.; Lu, H.; Stachniss, C. Keypoint matching for point cloud registration using multiplex dynamic graph attention networks. IEEE Robot. Autom. Lett. 2021, 6, 8221–8228. [Google Scholar] [CrossRef]
- Lai-Dang, Q.V.; Nengroo, S.H.; Jin, H. Learning dense features for point cloud registration using a graph attention network. Appl. Sci. 2022, 12, 7023. [Google Scholar] [CrossRef]
- Song, Y.; Shen, W.; Peng, K. A novel partial point cloud registration method based on graph attention network. Vis. Comput. 2023, 39, 1109–1120. [Google Scholar] [CrossRef]
- Zaman, A.; Yangyu, F.; Ayub, M.S.; Irfan, M.; Guoyun, L.; Shiya, L. CMDGAT: Knowledge extraction and retention based continual graph attention network for point cloud registration. Expert Syst. Appl. 2023, 214, 119098. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, Z.; Zhong, R.; Chen, D.; Zhang, L.; Zhu, L.; Wang, Q.; Wang, G.; Zou, J.; Wang, Y. A weakly supervised graph deep learning framework for point cloud registration. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Proceedings of the Sensor fusion IV: Control Paradigms and Data Structures; Spie: Bellingham, WA, USA, 1992; Volume 1611, pp. 586–606. [Google Scholar]
- Aoki, Y.; Goforth, H.; Srivatsan, R.A.; Lucey, S. Pointnetlk: Robust & efficient point cloud registration using pointnet. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7163–7172. [Google Scholar]
- Wang, Y.; Solomon, J.M. Deep closest point: Learning representations for point cloud registration. In Proceedings of the Proceedings of the IEEE/CVF International Conference on Computer Vision, Long Beach, CA, USA, 15–20 June 2019; pp. 3523–3532.
- Pais, G.D.; Ramalingam, S.; Govindu, V.M.; Nascimento, J.C.; Chellappa, R.; Miraldo, P. 3dregnet: A deep neural network for 3d point registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 7193–7203. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Valsesia, D.; Fracastoro, G.; Magli, E. Learning localized generative models for 3d point clouds via graph convolution. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Shu, D.W.; Park, S.W.; Kwon, J. 3d point cloud generative adversarial network based on tree structured graph convolutions. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3859–3868. [Google Scholar]
- Mo, K.; Guerrero, P.; Yi, L.; Su, H.; Wonka, P.; Mitra, N.; Guibas, L.J. Structurenet: Hierarchical graph networks for 3d shape generation. arXiv 2019, arXiv:1908.00575. [Google Scholar] [CrossRef]
- Li, Y.; Baciu, G. HSGAN: Hierarchical graph learning for point cloud generation. IEEE Trans. Image Process. 2021, 30, 4540–4554. [Google Scholar] [CrossRef] [PubMed]
- Xiaomao, Z.; Wei, W.; Bing, D. PSG-GAN: Progressive Person Image Generation with Self-Guided Local Focuses. In Proceedings of the 2021 IEEE 33rd International Conference on Tools with Artificial Intelligence (ICTAI), Washington, DC, USA, 1–3 November 2021; pp. 763–769. [Google Scholar]
- Liu, X.; Kong, X.; Liu, L.; Chiang, K. TreeGAN: Syntax-aware sequence generation with generative adversarial networks. In Proceedings of the 2018 IEEE International Conference on Data Mining (ICDM), Singapore, 17–20 November 2018; pp. 1140–1145. [Google Scholar]
- Yang, G.; Huang, X.; Hao, Z.; Liu, M.Y.; Belongie, S.; Hariharan, B. Pointflow: 3d point cloud generation with continuous normalizing flows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 4541–4550. [Google Scholar]
- Chen, S.; Tian, D.; Feng, C.; Vetro, A.; Kovačević, J. Fast resampling of three-dimensional point clouds via graphs. IEEE Trans. Signal Process. 2017, 66, 666–681. [Google Scholar] [CrossRef]
- Hu, W.; Fu, Z.; Guo, Z. Local frequency interpretation and non-local self-similarity on graph for point cloud inpainting. IEEE Trans. Image Process. 2019, 28, 4087–4100. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, J.; Huang, K. Point cloud super resolution with adversarial residual graph networks. arXiv 2019, arXiv:1908.02111. [Google Scholar]
- Pan, L. ECG: Edge-aware point cloud completion with graph convolution. IEEE Robot. Autom. Lett. 2020, 5, 4392–4398. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, B.; Tian, G.; Wang, W.; Li, C. Towards point cloud completion: Point rank sampling and cross-cascade graph cnn. Neurocomputing 2021, 461, 1–16. [Google Scholar] [CrossRef]
- Shi, J.; Xu, L.; Heng, L.; Shen, S. Graph-guided deformation for point cloud completion. IEEE Robot. Autom. Lett. 2021, 6, 7081–7088. [Google Scholar] [CrossRef]
- Wang, L.; Li, J.; Guo, S.; Han, S. A cascaded graph convolutional network for point cloud completion. In The Visual Computer; Springer: Berlin/Heidelberg, Germany, 2024; pp. 1–16. [Google Scholar]
- Qian, G.; Abualshour, A.; Li, G.; Thabet, A.; Ghanem, B. Pu-gcn: Point cloud upsampling using graph convolutional networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 11683–11692. [Google Scholar]
- Han, B.; Zhang, X.; Ren, S. PU-GACNet: Graph attention convolution network for point cloud upsampling. Image Vis. Comput. 2022, 118, 104371. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, C.; Chen, S.; Wang, H.; He, Q.; Mu, H. PU-FPG: Point cloud upsampling via form preserving graph convolutional networks. J. Intell. Fuzzy Syst. 2023, 45, 8595–8612. [Google Scholar] [CrossRef]
- Yuan, W.; Khot, T.; Held, D.; Mertz, C.; Hebert, M. Pcn: Point completion network. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 728–737. [Google Scholar]
- Yu, L.; Li, X.; Fu, C.W.; Cohen-Or, D.; Heng, P.A. Pu-net: Point cloud upsampling network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2790–2799. [Google Scholar]
- Tchapmi, L.P.; Kosaraju, V.; Rezatofighi, H.; Reid, I.; Savarese, S. Topnet: Structural point cloud decoder. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 383–392. [Google Scholar]
- Qian, Y.; Hou, J.; Kwong, S.; He, Y. PUGeo-Net: A geometry-centric network for 3D point cloud upsampling. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 752–769. [Google Scholar]
- Huang, Z.; Yu, Y.; Xu, J.; Ni, F.; Le, X. Pf-net: Point fractal network for 3d point cloud completion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 7662–7670. [Google Scholar]
- Zhang, S.; Cui, S.; Ding, Z. Hypergraph spectral analysis and processing in 3D point cloud. IEEE Trans. Image Process. 2020, 30, 1193–1206. [Google Scholar] [CrossRef] [PubMed]
- Schoenenberger, Y.; Paratte, J.; Vandergheynst, P. Graph-based denoising for time-varying point clouds. In Proceedings of the 2015 3DTV-Conference: The True Vision-Capture, Transmission and Display of 3D Video (3DTV-CON), Lisbon, Portugal, 8–10 July 2015; pp. 1–4. [Google Scholar]
- Dinesh, C.; Cheung, G.; Bajic, I.V.; Yang, C. Fast 3D point cloud denoising via bipartite graph approximation & total variation. arXiv 2018, arXiv:1804.10831. [Google Scholar]
- Hu, W.; Gao, X.; Cheung, G.; Guo, Z. Feature graph learning for 3D point cloud denoising. IEEE Trans. Signal Process. 2020, 68, 2841–2856. [Google Scholar] [CrossRef]
- Pistilli, F.; Fracastoro, G.; Valsesia, D.; Magli, E. Learning graph-convolutional representations for point cloud denoising. In Proceedings of the European Conference on Computer Vision. Springer, Glasgow, UK, 23–28 August 2020; pp. 103–118. [Google Scholar]
- Luo, S.; Hu, W. Differentiable manifold reconstruction for point cloud denoising. In Proceedings of the 28th ACM International Conference on Multimedia, Seattle WA USA, 12–16 October 2020; pp. 1330–1338. [Google Scholar]
- Irfan, M.A.; Magli, E. Exploiting color for graph-based 3D point cloud denoising. J. Vis. Commun. Image Represent. 2021, 75, 103027. [Google Scholar] [CrossRef]
- Dinesh, C.; Cheung, G.; Bajić, I.V. Point cloud denoising via feature graph laplacian regularization. IEEE Trans. Image Process. 2020, 29, 4143–4158. [Google Scholar] [CrossRef] [PubMed]
- Roveri, R.; Öztireli, A.C.; Pandele, I.; Gross, M. Pointpronets: Consolidation of point clouds with convolutional neural networks. In Proceedings of the Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2018; Volume 37, pp. 87–99. [Google Scholar]
- Hermosilla, P.; Ritschel, T.; Ropinski, T. Total denoising: Unsupervised learning of 3D point cloud cleaning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 52–60. [Google Scholar]
- Zhang, C.; Florencio, D.; Loop, C. Point cloud attribute compression with graph transform. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 2066–2070. [Google Scholar]
- Thanou, D.; Chou, P.A.; Frossard, P. Graph-based motion estimation and compensation for dynamic 3D point cloud compression. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 3235–3239. [Google Scholar]
- Cohen, R.A.; Tian, D.; Vetro, A. Attribute compression for sparse point clouds using graph transforms. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 1374–1378. [Google Scholar]
- Shao, Y.; Zhang, Z.; Li, Z.; Fan, K.; Li, G. Attribute compression of 3D point clouds using Laplacian sparsity optimized graph transform. In Proceedings of the 2017 IEEE Visual Communications and Image Processing (VCIP), St. Petersburg, FL, USA, 10–13 December 2017; pp. 1–4. [Google Scholar]
- Gu, S.; Hou, J.; Zeng, H.; Yuan, H. 3D point cloud attribute compression via graph prediction. IEEE Signal Process. Lett. 2020, 27, 176–180. [Google Scholar] [CrossRef]
- Gomes, P. Graph-based network for dynamic point cloud prediction. In Proceedings of the 12th ACM Multimedia Systems Conference, Istanbul, Turkey, 28 September–1 October 2021; pp. 393–397. [Google Scholar]
- Gomes, P.; Rossi, S.; Toni, L. Spatio-temporal graph-RNN for point cloud prediction. In Proceedings of the 2021 IEEE International Conference on Image Processing (ICIP), Anchorage, AL, USA, 19–22 September 2021; pp. 3428–3432. [Google Scholar]
- Gao, L.; Fan, T.; Wan, J.; Xu, Y.; Sun, J.; Ma, Z. Point cloud geometry compression via neural graph sampling. In Proceedings of the 2021 IEEE International Conference on Image Processing (ICIP), Anchorage, AL, USA, 19–22 September 2021; pp. 3373–3377. [Google Scholar]
- Nguyen, D.T.; Quach, M.; Valenzise, G.; Duhamel, P. Lossless coding of point cloud geometry using a deep generative model. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 4617–4629. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Quach, M.; Valenzise, G.; Duhamel, P. Multiscale deep context modeling for lossless point cloud geometry compression. In Proceedings of the 2021 IEEE International Conference on Multimedia & Expo Workshops (ICMEW), Shenzhen, China, 5–9 July 2021; pp. 1–6. [Google Scholar]
- Chen, S.; Niu, S.; Lan, T.; Liu, B. PCT: Large-scale 3D point cloud representations via graph inception networks with applications to autonomous driving. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 4395–4399. [Google Scholar]
- Geng, Y.; Wang, Z.; Jia, L.; Qin, Y.; Chai, Y.; Liu, K.; Tong, L. 3DGraphSeg: A unified graph representation-based point cloud segmentation framework for full-range highspeed railway environments. IEEE Trans. Ind. Informatics 2023, 19, 11430–11443. [Google Scholar] [CrossRef]
- Hu, B.; Lei, B.; Shen, Y.; Liu, Y.; Wang, S. A point cloud generative model via tree-structured graph convolutions for 3D brain shape reconstruction. In Proceedings of the Pattern Recognition and Computer Vision: 4th Chinese Conference, PRCV 2021, Beijing, China, 29 October–1 November 2021; Proceedings, Part II 4; Springer: Berlin/Heidelberg, Germany, 2021; pp. 263–274. [Google Scholar]
- Xing, J.; Yuan, H.; Hamzaoui, R.; Liu, H.; Hou, J. GQE-Net: A graph-based quality enhancement network for point cloud color attribute. IEEE Trans. Image Process. 2023, 32, 6303–6317. [Google Scholar] [CrossRef]
- Feng, H.; Li, W.; Luo, Z.; Chen, Y.; Fatholahi, S.N.; Cheng, M.; Wang, C.; Junior, J.M.; Li, J. GCN-based pavement crack detection using mobile LiDAR point clouds. IEEE Trans. Intell. Transp. Syst. 2021, 23, 11052–11061. [Google Scholar] [CrossRef]
- Li, Y.; Chen, H.; Cui, Z.; Timofte, R.; Pollefeys, M.; Chirikjian, G.S.; Van Gool, L. Towards efficient graph convolutional networks for point cloud handling. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 3752–3762. [Google Scholar]
- Tailor, S.A.; De Jong, R.; Azevedo, T.; Mattina, M.; Maji, P. Towards efficient point cloud graph neural networks through architectural simplification. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 2095–2104. [Google Scholar]
- Zhang, J.F.; Zhang, Z. Exploration of energy-efficient architecture for graph-based point-cloud deep learning. In Proceedings of the 2021 IEEE Workshop on Signal Processing Systems (SiPS), Coimbra, Portugal, 19–21 October 2021; pp. 260–264. [Google Scholar]
- Li, K.; Zhao, M.; Wu, H.; Yan, D.M.; Shen, Z.; Wang, F.Y.; Xiong, G. Graphfit: Learning multi-scale graph-convolutional representation for point cloud normal estimation. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 651–667. [Google Scholar]
- Yang, Q.; Ma, Z.; Xu, Y.; Li, Z.; Sun, J. Inferring point cloud quality via graph similarity. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 3015–3029. [Google Scholar] [CrossRef] [PubMed]
- Shan, Z.; Yang, Q.; Ye, R.; Zhang, Y.; Xu, Y.; Xu, X.; Liu, S. Gpa-net: No-reference point cloud quality assessment with multi-task graph convolutional network. In IEEE Transactions on Visualization and Computer Graphics; IEEE: New York City, NY, USA, 2023. [Google Scholar]
- Wang, Y.; Sun, W.; Jin, J.; Kong, Z.; Yue, X. MVGCN: Multi-view graph convolutional neural network for surface defect identification using three-dimensional point cloud. J. Manuf. Sci. Eng. 2023, 145, 031004. [Google Scholar] [CrossRef]


| Method | Classification Results | Segmentation Results | |||||
|---|---|---|---|---|---|---|---|
| Datasets | mA | OA | Datasets | Cat mIoU | Ins mIou | OA | |
| RGCNN [46] | ModelNet40 | 87.3 | 90.5 | ShapeNet | 84.3 | - | - |
| AGCN [47] | ModelNet40 | 90.7 | 92.6 | ShapeNetPart | 82.6 | 85.4 | - |
| S3DIS(6-fold) | 56.63 | - | 84.13 | ||||
| HGNN [48] | ModelNet40 | 96.7 | - | - | - | - | - |
| LSConv [49] | ModelNet40 | - | 91.5 | ShapeNet | 85.4 | - | - |
| ScanNet | 85.4 | - | 84.8 | ||||
| PointGCN [50] | ModelNet40 | 86.19 | 89.27 | - | - | - | - |
| 3DTI-Net [51] | ModelNet40 | 86. | 91.7 | ShapeNet | 84.9 | - | - |
| SyncSpecCNN [53] | - | - | - | ShapeNet | 84.74 | - | - |
| PointNGCNN [54] | ModelNet40 | - | 92.8 | ShapeNetPart | 82.4 | 85.6 | - |
| S3DIS | - | - | 87.3 | ||||
| ScanNet | - | - | 84.9 | ||||
| GTIF [55] | ModelNet40 | - | 89.55 | - | - | - | - |
| AWT-Net [56] | ModelNet40 | - | 93.9 | - | - | - | - |
| ScanObjectNN | - | 88.5 | - | - | - | - | |
| PointWavelet [57] | ModelNet40 | 91.1 | 94.3 | ShapeNetPart | 85.2 | 87.0 | - |
| ScanObjectNN | 85.8 | 87.7 | S3DIS(Area5) | 71.3 | - | - | |
| MSGCN [59] | ModelNet40 | - | 92.5 | - | - | - | - |
| ShapeNetCore | - | 86.6 | - | - | - | - | |
| nuScenes | - | 74.1 | - | - | - | - | |
| PointAGCN [60] | ModelNet40 | - | 91.4 | ShapeNet | 85.6 | - | - |
| S3DIS | 52.3 | - | - | ||||
| Method | Classification Results | Segmentation Results | |||||
|---|---|---|---|---|---|---|---|
| Datasets | mA | OA | Datasets | Cat mIoU | Ins mIou | OA | |
| ECC [61] | ModelNet40 | - | 83.2 | - | - | - | - |
| SpiderCNN [62] | ModelNet40 | 90.7 | 92.4 | ShapeNet | 85.3 | - | - |
| SHREC15 | - | 95.8 | |||||
| G3DNet [63] | ModelNet40 | - | 91.7 | - | - | - | - |
| Sydney Urban Objects | - | 72.7 | - | - | - | - | |
| KCNet [64] | ModelNet40 | - | 91.0 | ShapeNet | 84.7 | - | - |
| GAPNet [65] | ModelNet40 | 89.7 | 92.4 | ShapeNet | 84.7 | - | - |
| DGCNN [66] | ModelNet40 | 90.7 | 93.5 | ShapeNet | 85.2 | - | - |
| S3DIS | 56.1 | - | 84.1 | ||||
| LDGCNN [67] | ModelNet40 | 90.3 | 92.9 | ShapeNet | 85.1 | - | - |
| DGCNN with AFF [68] | ModelNet40 | 90.6 | 93.6 | ShapeNetPart | 85.6 | - | - |
| Geometric attentional DGCNN [69] | ModelNet40 | 91.5 | 94.0 | ShapeNet | 84.6 | 86.3 | - |
| DPAM [72] | ModelNet40 | - | 91.9 | ShapeNetPart | 86.1 | - | - |
| SRINet [73] | ModelNet40 | - | 87.01 | ShapeNetPart | 89.24 | - | - |
| DCG-Net [74] | ModelNet40 | - | 93.4 | ShapeNetPart | 82.3 | 85.4 | - |
| RI-GCN [75] | ModelNet40 | - | 91.0 | - | - | - | - |
| GGM-Net [77] | ModelNet40 | 89.0 | 92.6 | - | - | - | - |
| CPL [78] | ModelNet40 | 90.53 | 92.41 | - | - | - | - |
| MSDynamic GCN [79] | ModelNet40 | - | 91.79 | ShapeNetPart | 85.47 | - | - |
| Spherical kernel [80] | ModelNet40 | - | 92.1 | ShapeNetPart | 84.9 | 86.8 | - |
| RueMonge2014 | 66.3 | - | 84.4 | ||||
| ScanNet | 61.0 | - | - | ||||
| S3DIS(Area5) | 68.9 | - | 88.6 | ||||
| 3D-GCN [81] | ModelNet40 | - | 92.1 | ShapeNetPart | 82.1 | 85.1 | - |
| MRFGAT [82] | ModelNet40 | 90.1 | 92.5 | - | - | - | - |
| Manifold-Net [83] | ModelNet40 | 90.1 | 93.0 | S3DIS | 72.6 | - | 89.9 |
| LKPO-GNN [85] | ModelNet40 | - | 91.4 | ShapeNetPart | 85.6 | - | - |
| ScanNet | 58.4 | - | 85.3 | ||||
| S3DIS | 64.6 | - | 85.8 | ||||
| HDGN [86] | ModelNet40 | - | 93.9 | ShapeNet | 85.4 | - | - |
| Method | Classification Results | Segmentation Results | |||||
|---|---|---|---|---|---|---|---|
| Datasets | mA | OA | Datasets | Cat mIoU | Ins mIou | OA | |
| DNRGC [87] | ModelNet40 | 87.12 | 89.91 | S3DIS | 41.9 | - | - |
| PointVGG [88] | ModelNet40 | - | 93.6 | ShapeNet | - | 86.1 | - |
| LGFGC [89] | ModelNet40 | 94.1 | 96.9 | ShapeNet | 72.4 | - | - |
| ScanNetV2 | 72.4 | - | - | ||||
| S3DIS(Area5) | 69.4 | - | 89.4 | ||||
| PL3D | 78.5 | - | 98.0 | ||||
| Grid-GCN [91] | ModelNet40 | 91.3 | 93.1 | ScanNet | - | - | 85.4 |
| S3DIS | 57.75 | - | 86.94 | ||||
| VA-GCN [92] | ModelNet40 | 91.4 | 94.3 | S3DIS(Area5) | 56.9 | - | - |
| ShapeNet | 82.6 | 85.5 | - | ||||
| EGCN [93] | ModelNet40 | - | 90.59 | - | - | - | - |
| Oakland | - | 89.71 | - | - | - | - | |
| GADNN [94] | ModelNet40 | - | 92.9 | ShapeNet | 85.8 | - | - |
| S3DIS | 87.5 | - | - | ||||
| DGACN [95] | ModelNet40 | 91.2 | 94.1 | - | - | - | - |
| ScanObjectNN | 77.9 | 82.1 | - | - | - | - | |
| Att-AdaptNet [96] | ModelNet40 | - | 93.8 | - | - | - | - |
| AGNet [97] | ModelNet40 | 90.9 | 93.6 | ShapeNetPart | 85.4 | - | - |
| S3DIS | 59.6 | - | 85.9 | ||||
| Graph-PBN [98] | ModelNet40 | 90.8 | 93.4 | ShapeNet | 85.5 | ||
| S3DIS | 59.2 | - | 84.9 | ||||
| 3DCTN [99] | ModelNet40 | 91.2 | 93.3 | - | - | - | - |
| SGCNN [100] | ModelNet40 | 90.4 | 93.4 | - | - | - | - |
| ScanObjectNN | - | 86.5 | - | - | - | - | |
| diffConv [101] | ModelNet40 | 90.6 | 93.6 | Toronto3D | 76.73 | - | - |
| ShapeNetPart | 85.7 | - | - | ||||
| 3D-GCN [102] | ModelNet40 | - | 92.1 | ShapeNetPart | 82.7 | 85.6 | - |
| S3DIS(Area5) | 51.9 | - | 84.6 | ||||
| Shrinking unit [103] | ModelNet10 | - | 90.6 | - | - | - | - |
| SAMHGC [104] | ModelNet40 | 91.4 | 93.6 | - | - | - | - |
| AGConv [105] | ModelNet40 | 90.7 | 93.4 | ShapeNetPart | 83.4 | 86.4 | - |
| S3DIS | 67.9 | - | 90.0 | ||||
| Paris-Lille 3D | 76.9 | - | - | ||||
| MLGCN [106] | ModelNet40 | - | 90.7 | ShapeNetPart | 83.2 | 84.6 | - |
| NLGAT [107] | ModelNet40 | - | 94.0 | - | - | - | - |
| Method | Classification Results | Segmentation Results | |||||
|---|---|---|---|---|---|---|---|
| Datasets | mA | OA | Datasets | Cat mIoU | Ins mIou | OA | |
| SPG [109] | - | - | - | Semantic3D | 76.2 | - | 92.9 |
| - | - | - | S3DIS | 62.1 | - | 85.5 | |
| HDGCN [110] | - | - | - | S3DIS(Area5) | 59.33 | - | - |
| - | - | - | Paris-Lille 3D | 68.30 | - | - | |
| GSDML [111] | - | - | - | S3DIS(6-fold) | 68.4 | - | 87.9 |
| - | - | - | vKITTI | 52.0 | - | 84.3 | |
| GAC [112] | - | - | - | S3DIS(Area5) | 62.85 | - | 87.79 |
| - | - | - | Semantic3D | 70.8 | - | 91.9 | |
| GANN [113] | ModelNet40 | - | 91.4 | S3DIS(Area5) | 57.42 | - | 85.31 |
| ShapeNetPart | 86.3 | - | - | ||||
| PointWeb [114] | ModelNet40 | 89.4 | 92.3 | S3DIS(Area5) | 60.28 | - | 86.97 |
| Point2Node [116] | ModelNet40 | - | 93.0 | S3DIS(Area5) | 62.96 | - | 88.81 |
| ScanNet | - | - | 86.3 | ||||
| SegGCN [117] | - | - | - | S3DIS(Area5) | 63.6 | - | 88.2 |
| - | - | - | ScanNet | 58.9 | - | - | |
| JGV-Net [119] | - | - | - | ISPRS | 85.0 | - | - |
| - | - | - | DFC2019 | 0.990 | - | - | |
| PointConv-GCR [120] | - | - | - | ScanNet | 60.8 | - | - |
| - | - | - | S3DIS | 52.42 | - | - | |
| - | - | - | Semantic3D | 69.5 | - | 92.1 | |
| FGCN [121] | - | - | - | S3DIS | 52.17 | - | - |
| - | - | - | Semantic3D | 62.40 | - | - | |
| - | - | - | ShapeNetPart | - | - | 83.1 | |
| Method | Classification Results | Segmentation Results | |||||
|---|---|---|---|---|---|---|---|
| Datasets | mA | OA | Datasets | Cat mIoU | Ins mIou | OA | |
| TGNet [122] | - | - | - | ScanNet | 62.2 | - | - |
| - | - | - | S3DIS(Area5) | 57.8 | - | 88.5 | |
| - | - | - | Paris-Lille-3D | 68.17 | - | 96.97 | |
| 3DGELS [124] | - | - | - | ScanNet v2 | 45.9 | - | - |
| - | - | - | NYUv2 | 43.0 | - | - | |
| PGCNet [125] | - | - | - | S3DIS(Area5) | 53.60 | - | 86.24 |
| - | - | - | ScanNet | 83.9 | - | - | |
| HAPGN [126] | ModelNet40 | 89.4 | 91.7 | ShapeNet | 89.3 | - | - |
| S3DIS | - | - | 85.8 | ||||
| LGGCM [127] | - | - | - | S3DIS | 63.28 | - | 88.77 |
| - | - | - | ScanNetV1 | 42.2 | - | 87.3 | |
| - | - | - | ScanNetV2 | 64.4 | - | 88.6 | |
| - | - | - | ShapeNetPart | 86.6 | - | - | |
| DGFA-Net [128] | - | - | - | S3DIS(Area5) | 65.8 | - | 88.2 |
| - | - | - | ShapeNetPart | 83.8 | 85.5 | - | |
| - | - | - | Toronto3D | 64.25 | - | 94.78 | |
| DC-GNN [129] | ModelNet40 | - | 93.64 | ShapeNetPart | 84.55 | - | - |
| SegGroup [130] | - | - | - | ScanNet | 62.7 | - | - |
| RG-GCN [131] | - | - | - | S3DIS(6-fold) | 63.7 | - | 88.1 |
| - | - | - | Toronto3D | 74.5 | - | 96.5 | |
| FGC-AFNet [132] | - | - | - | S3DIS | 71.2 | - | 88.6 |
| - | - | - | Toronto3D | 81.92 | - | 96.58 | |
| CGGC-Net [133] | - | - | - | SemanticKITTI | 58.4 | - | - |
| - | - | - | S3DIS | 70.2 | - | 88.0 | |
| AF-GCN [134] | - | - | - | ShapeNetPart | 85.3 | 87.0 | - |
| - | - | - | S3DIS | 73.3 | - | 91.5 | |
| PyramNet [135] | ModelNet40 | 88.3 | 91.5 | ShapeNet | 83.9 | - | - |
| S3DIS | 55.6 | - | 85.6 | ||||
| GTNet [136] | ModelNet40 | 92.6 | 93.2 | ShapeNetPart | 85.1 | - | - |
| S3DIS | 64.3 | - | 86.6 | ||||
| CRFConv [137] | - | - | - | ShapeNet Part | 83.5 | 85.5 | - |
| - | - | - | S3DIS(Area5) | 66.2 | - | 89.2 | |
| - | - | - | Semantic3D | 74.9 | - | 94.2 | |
| SPT [138] | - | - | - | S3DIS(6-Fold) | 76.0 | - | - |
| - | - | - | S3DIS(Area5) | 68.9 | - | - | |
| - | - | - | KITTI-360 Val | 63.5 | - | - | |
| - | - | - | DALES | 79.6 | - | - | |
| PAConv [139] | ModelNet40 | - | 93.9 | ShapeNetPart | 84.6 | 86.1 | - |
| S3DIS | 66.58 | - | - | ||||
| Method | Modality | Cars | Pedestrians | Cyclists | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| E | M | H | E | M | H | E | M | H | ||
| PointRGCN [141] | L | 85.97 | 75.73 | 70.60 | - | - | - | - | - | - |
| Point-GNN [143] | L | 88.33 | 79.47 | 72.29 | 51.92 | 43.77 | 40.14 | 78.60 | 63.48 | 57.08 |
| ContFuse [144] | L&I | 82.54 | 66.22 | 64.04 | - | - | - | - | - | - |
| Radar-PointGNN [148] | L | - | - | - | - | - | - | - | - | - |
| PC-RGNN [149] | L | 89.13 | 79.90 | 75.54 | - | - | - | - | - | - |
| SVGA-Net [152] | L | 87.33 | 80.47 | 75.91 | 48.48 | 40.39 | 37.92 | 78.58 | 62.28 | 54.88 |
| DCGNN [153] | L | 89.65 | 79.80 | 74.52 | - | - | - | - | - | - |
| Methods | Datasets | ||||||
|---|---|---|---|---|---|---|---|
| RGN-3DOD [142] | SunRGB-D | mAP@0.25 | |||||
| 59.2 | |||||||
| ScanNet | mAP@0.25 | mAP@0.5 | |||||
| 48.5 | 26.0 | ||||||
| TGNN [145] | ScanRefer | Unique | Multiple | Overall | |||
| Acc@0.25 | Acc@0.5 | Acc@0.25 | Acc@0.5 | Acc@0.25 | Acc@0.5 | ||
| Validation | 68.61 | 56.80 | 29.84 | 23.18 | 37.37 | 29.70 | |
| Test | 68.30 | 58.90 | 33.10 | 25.30 | 41.00 | 32.80 | |
| HGNet [147] | SunRGB-D | mAP@0.25 | cvAP | ||||
| 61.6 | 0.31 | ||||||
| Radar-PointGNN [148] | nuScenes | AP | ATE | ASE | AOE | AVE | |
| Car | 10.1 | 0.69 | 0.20 | 0.38 | 0.95 | ||
| FDG3D-VGN [150] | ScanRefer | Acc@0.5(Unique) | Acc@0.5(Multiple) | Acc@0.5(Overall) | |||
| 75.40 | 30.20 | 43.16 | |||||
| GSTA-3DVOD-PC [154] | nuScenes | NDS | mAP | ||||
| 71.8 | 67.4 | ||||||
| DAGC [156] | ScanNetV2 | mAP@0.25 | mAP@0.50 | cvAP@0.25 | cvAP@0.5 | ||
| 61.3 | 34.4 | 0.38 | 0.82 | ||||
| PPT-Net [157] | Oxford | U.S. | R.A. | B.D. | |||
| 98.4 | 99.7 | 99.5 | 95.3 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Lu, C.; Chen, Z.; Guan, J.; Zhao, J.; Du, J. Graph Neural Networks in Point Clouds: A Survey. Remote Sens. 2024, 16, 2518. https://doi.org/10.3390/rs16142518
Li D, Lu C, Chen Z, Guan J, Zhao J, Du J. Graph Neural Networks in Point Clouds: A Survey. Remote Sensing. 2024; 16(14):2518. https://doi.org/10.3390/rs16142518
Chicago/Turabian StyleLi, Dilong, Chenghui Lu, Ziyi Chen, Jianlong Guan, Jing Zhao, and Jixiang Du. 2024. "Graph Neural Networks in Point Clouds: A Survey" Remote Sensing 16, no. 14: 2518. https://doi.org/10.3390/rs16142518
APA StyleLi, D., Lu, C., Chen, Z., Guan, J., Zhao, J., & Du, J. (2024). Graph Neural Networks in Point Clouds: A Survey. Remote Sensing, 16(14), 2518. https://doi.org/10.3390/rs16142518






