Analysis of Vegetation Canopy Spectral Features and Species Discrimination in Reclamation Mining Area Using In Situ Hyperspectral Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
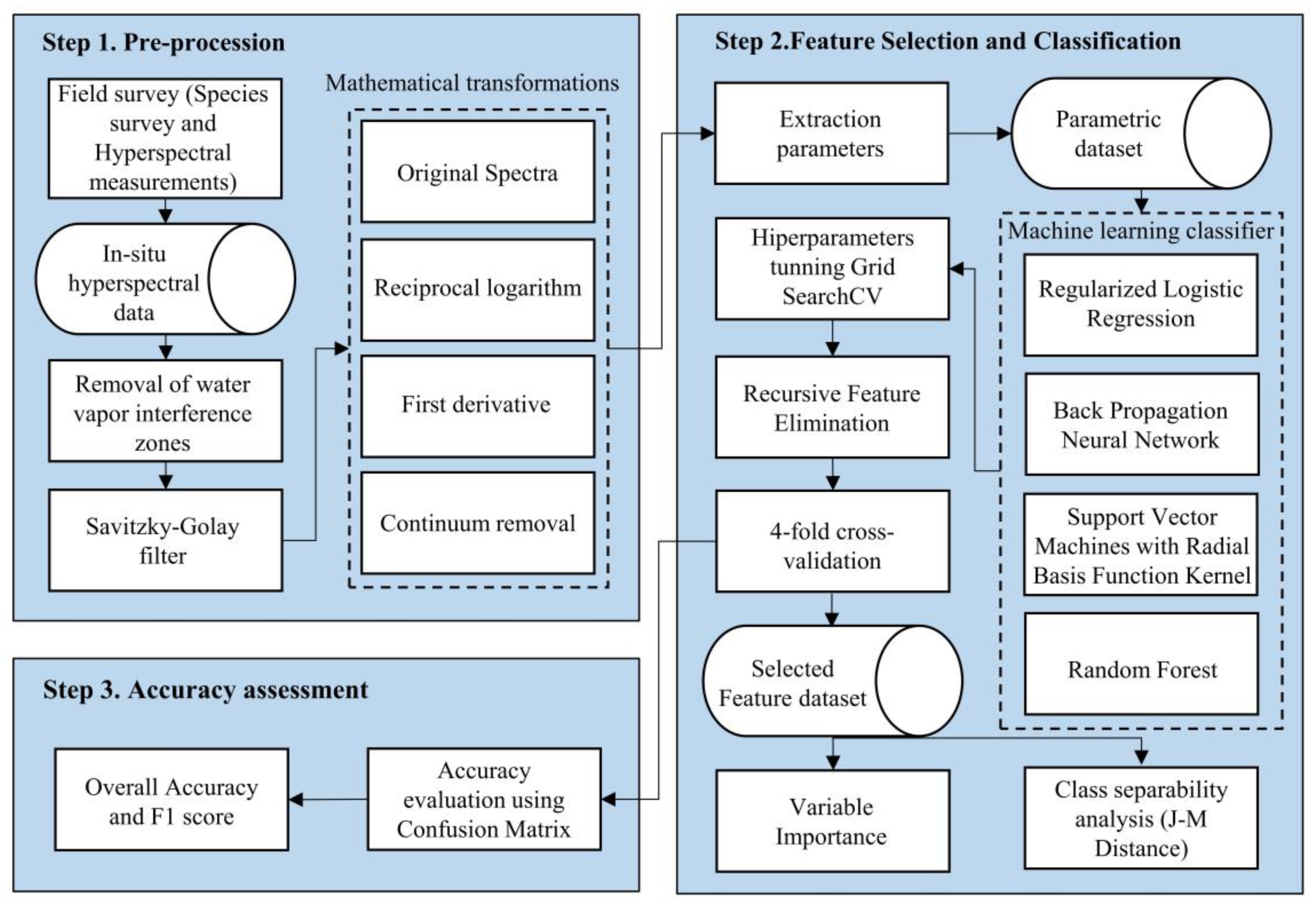
2.2. In Situ Hyperspectral Measurements and Pre-Processing
2.3. Calculation of Hyperspectral Indicators
2.4. Classification Models
2.4.1. Regularized Logistic Regression
2.4.2. Back Propagation Neural Network
2.4.3. Support Vector Machines with Radial Basis Function Kernel
2.4.4. Random Forest
2.5. Vegetation Identification Model Construction and Validation
2.6. Spectral Separability
3. Results
3.1. Spectral Characterization
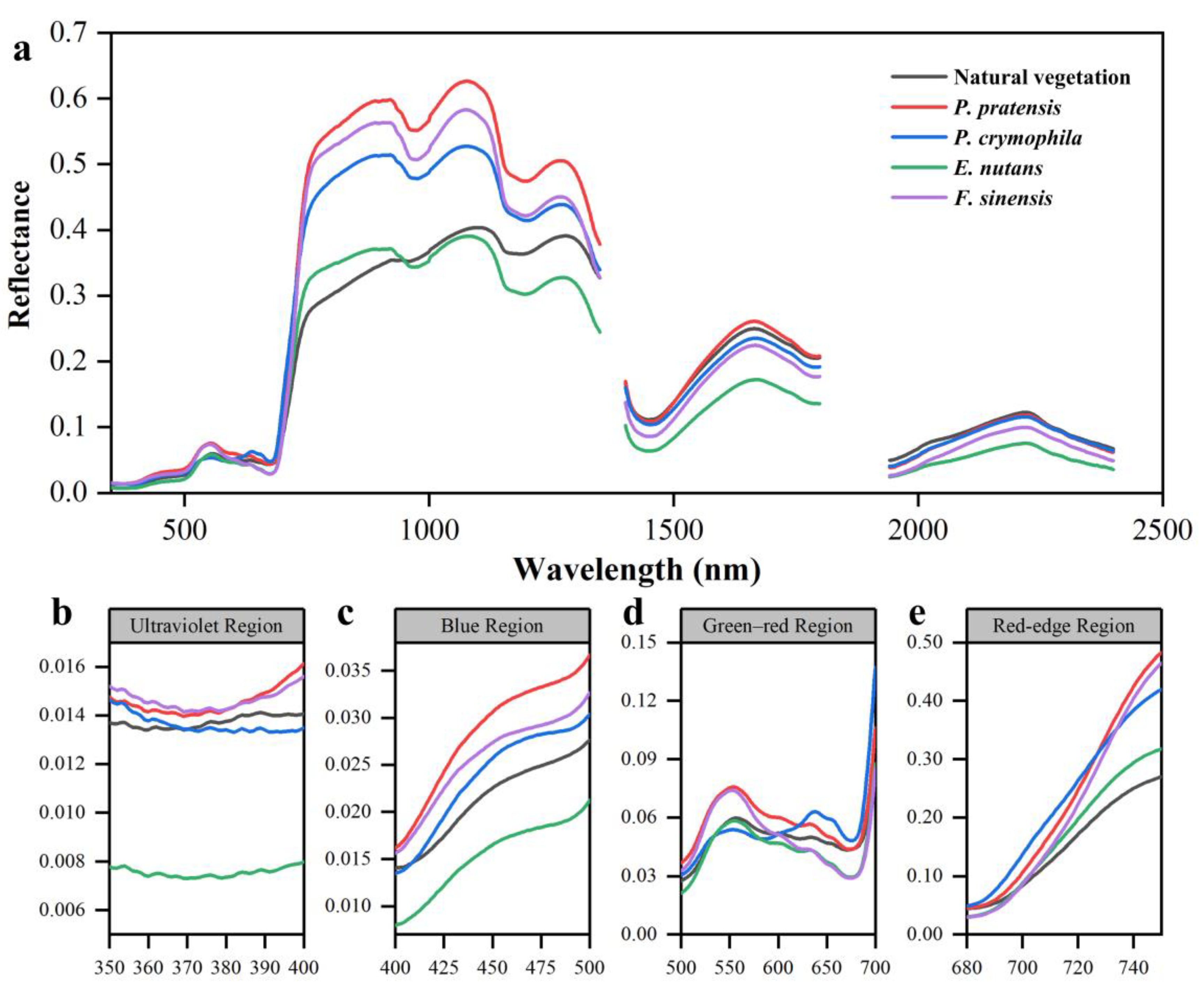
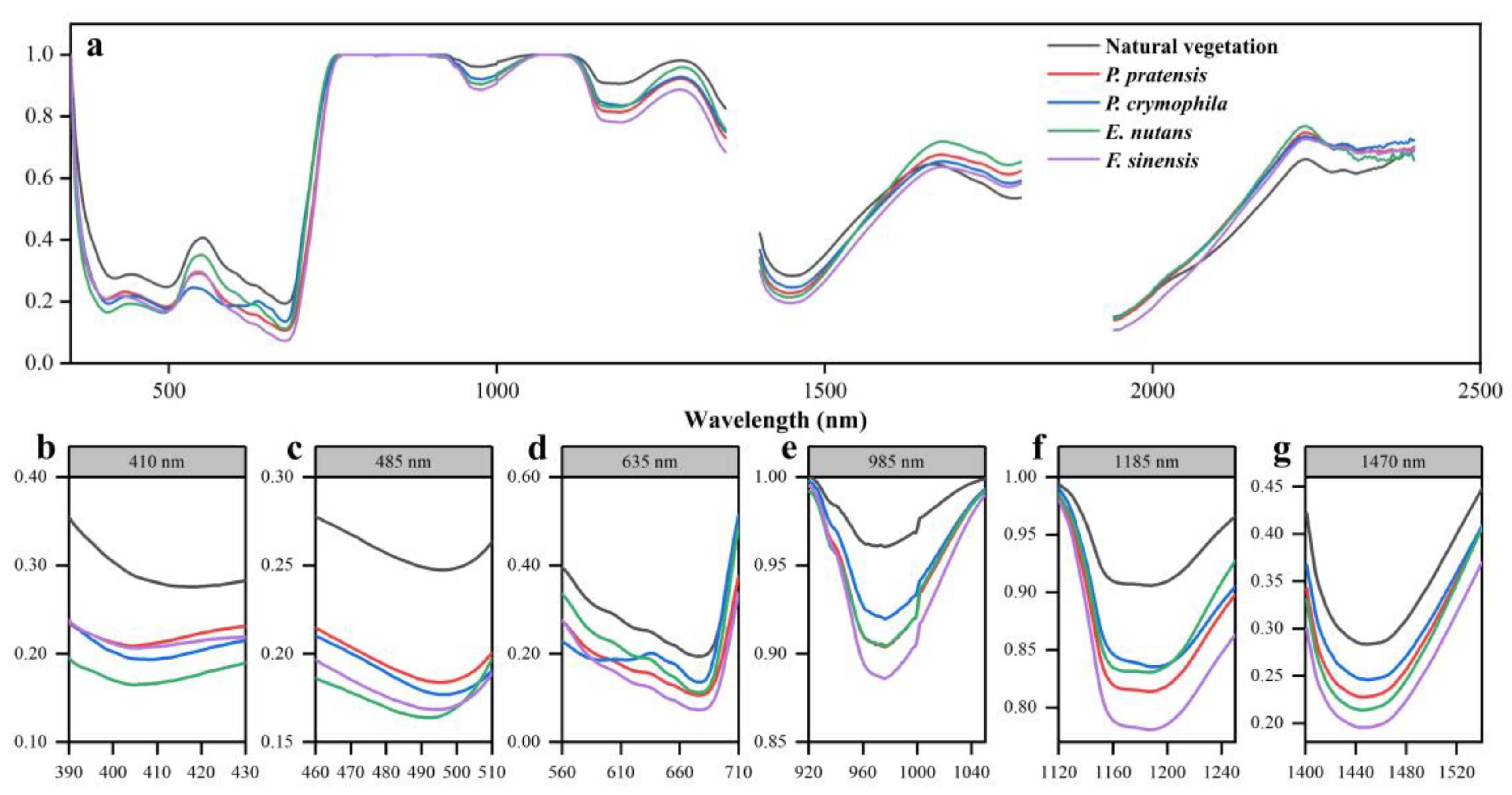
3.1.1. Original Spectral Analysis
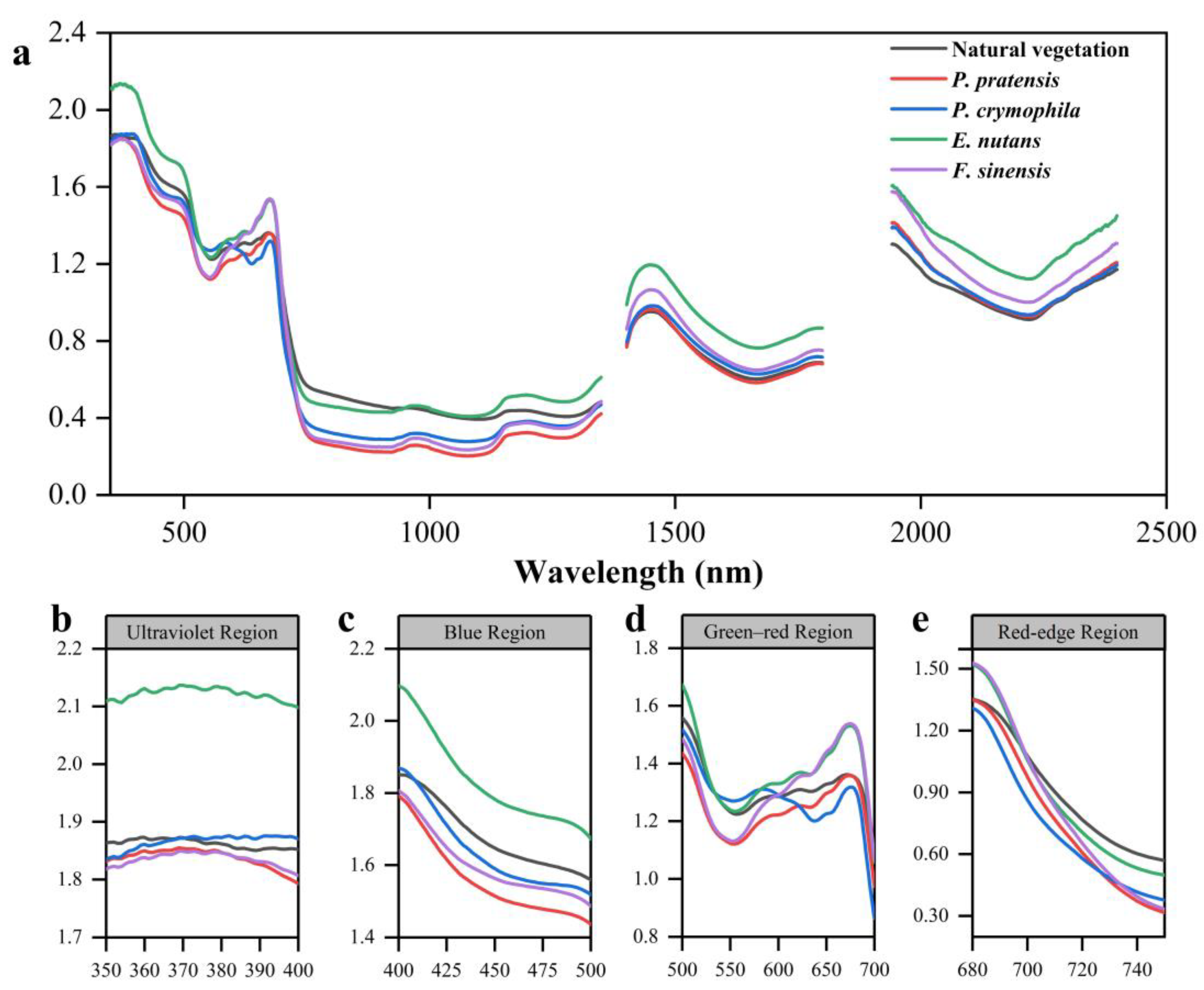
3.1.2. Reciprocal Logarithm Spectral Analysis
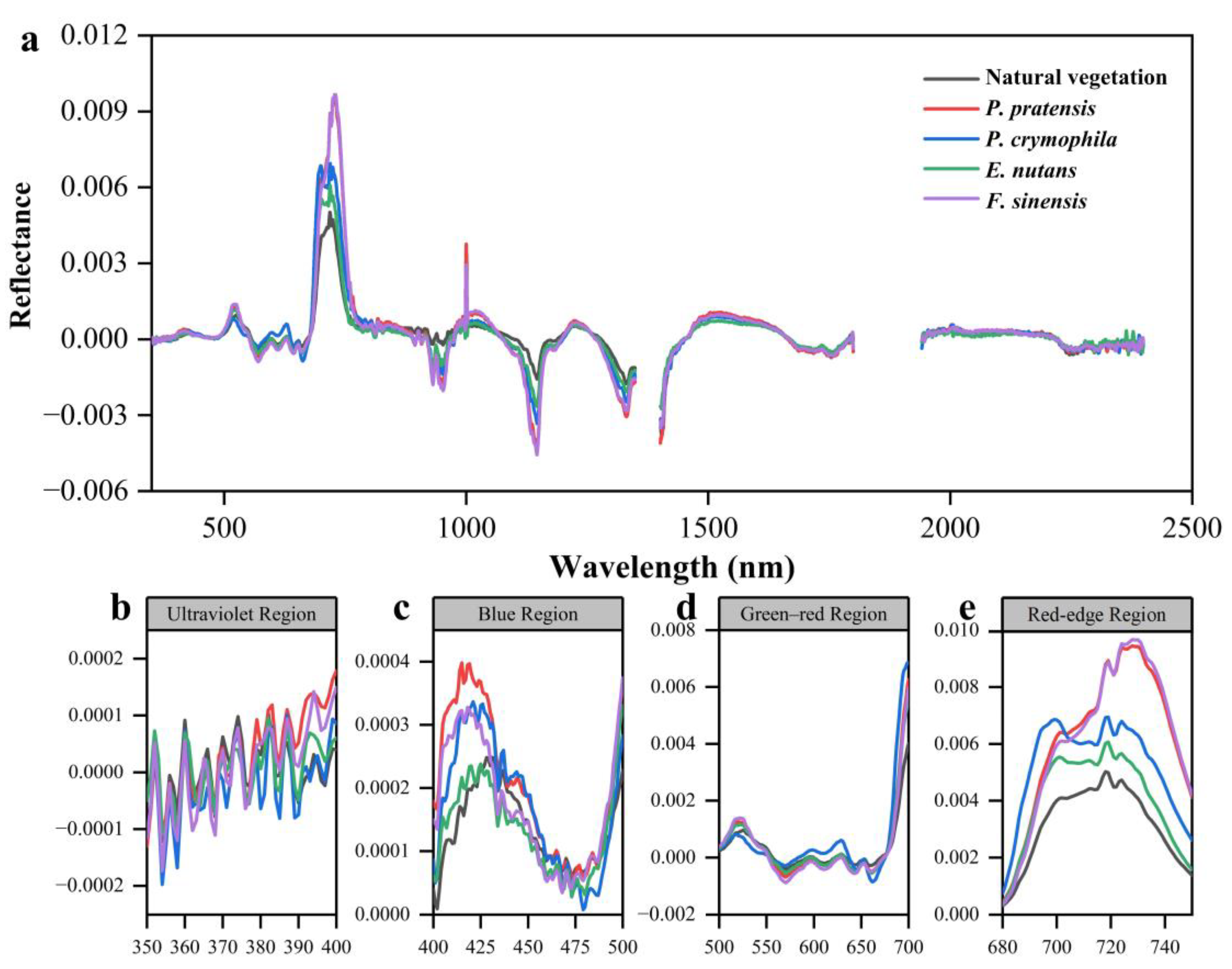
3.1.3. First Derivative Spectral Analysis
3.1.4. Continuum Removal Transform Spectral Analysis
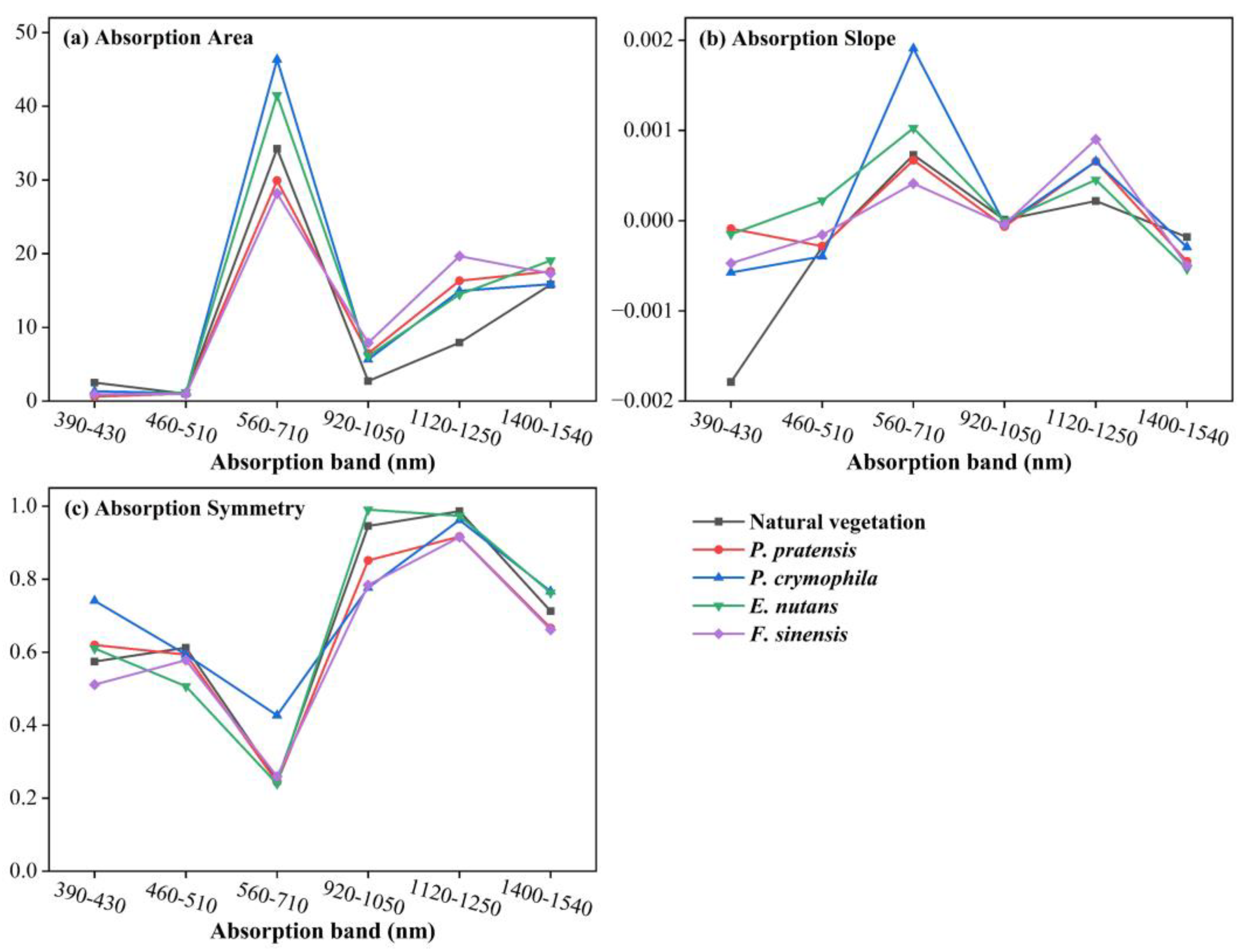
3.2. Selection of Characteristic Parameters
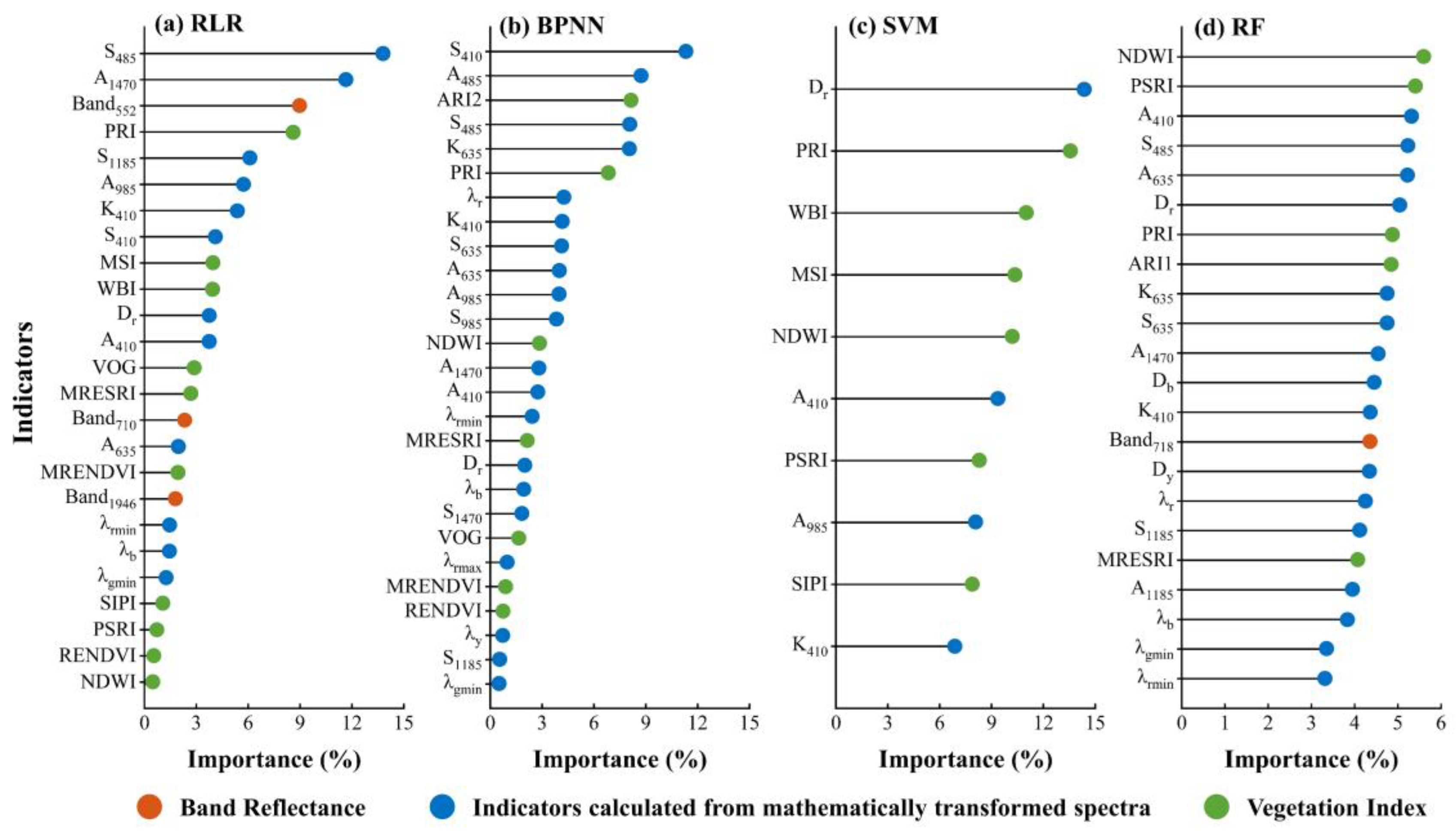
3.3. Importance of the Feature Indicators
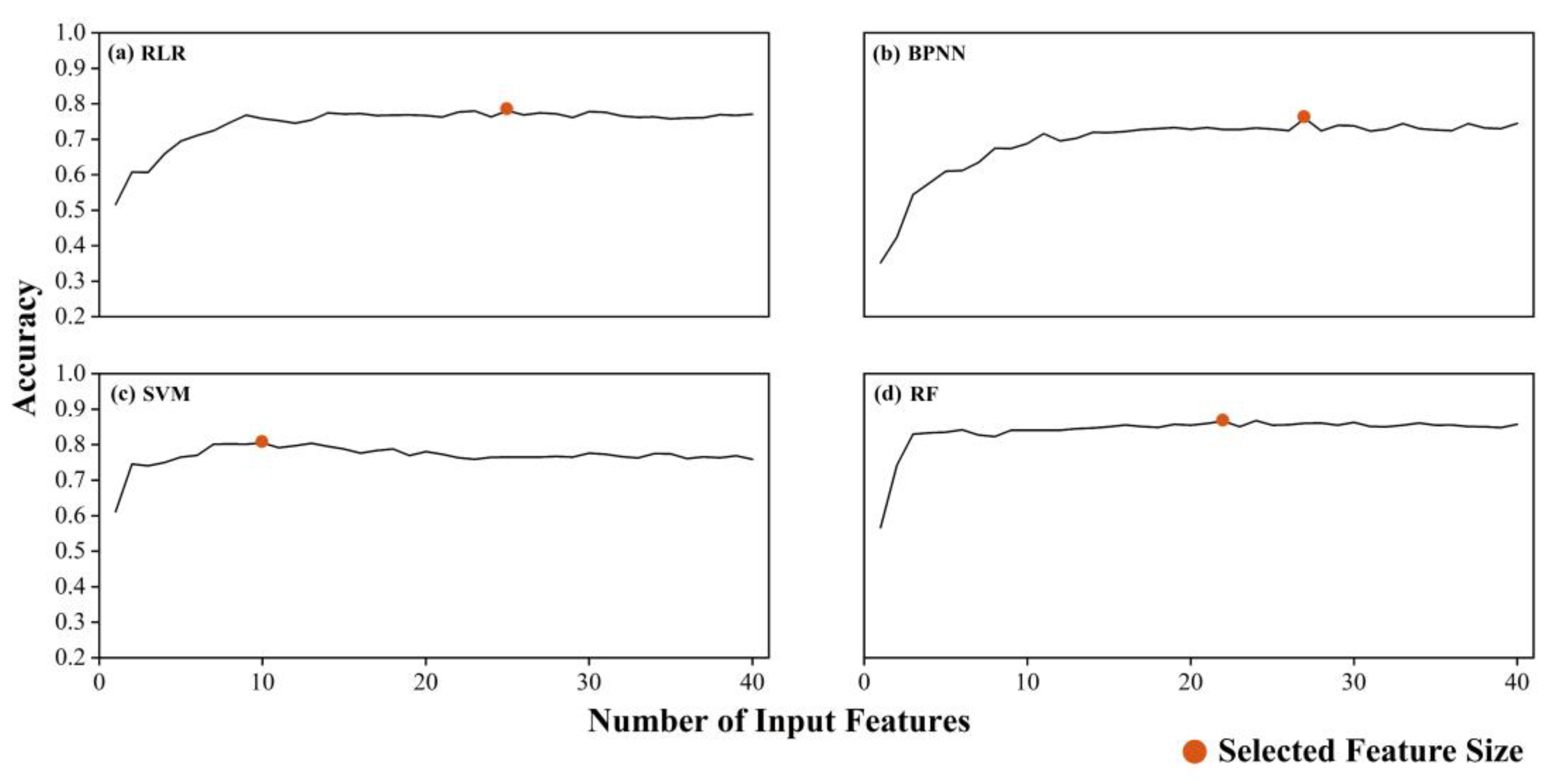
3.4. Model Validation and Comparison
3.5. Spectral Separability Analysis
4. Discussion
4.1. Differences in Vegetation Canopy Spectra
4.2. Classification Accuracy
4.3. Significant Spectral Predictors
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Feng, H.; Zhou, J.; Zhou, A.; Bai, G.; Li, Z.; Chen, H.; Su, D.; Han, X. Grassland ecological restoration based on the relationship between vegetation and its below-ground habitat analysis in steppe coal mine area. Sci. Total Environ. 2021, 778, 146221. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Liang, T.; Wang, L.; Yang, Z. Contamination and health risk assessment of heavy metals in road dust in Bayan Obo Mining Region in Inner Mongolia, North China. J. Geogr. Sci. 2015, 25, 1439–1451. [Google Scholar] [CrossRef]
- Shrestha, R.K.; Lal, R. Changes in physical and chemical properties of soil after surface mining and reclamation. Geoderma 2011, 161, 168–176. [Google Scholar] [CrossRef]
- Swab, R.M.; Lorenz, N.; Byrd, S.; Dick, R. Native vegetation in reclamation: Improving habitat and ecosystem function through using prairie species in mine land reclamation. Ecol. Eng. 2017, 108, 525–536. [Google Scholar] [CrossRef]
- Xu, H.; Xu, F.; Lin, T.; Xu, Q.; Yu, P.; Wang, C.; Aili, A.; Zhao, X.; Zhao, W.; Zhang, P.; et al. A systematic review and comprehensive analysis on ecological restoration of mining areas in the arid region of China: Challenge, capability and reconsideration. Ecol. Indic. 2023, 154, 110630. [Google Scholar] [CrossRef]
- Zhou, B.; Li, H.; Xu, F. Analysis and discrimination of hyperspectral characteristics of typical vegetation leaves in a rare earth reclamation mining area. Ecol. Eng. 2022, 174, 106465. [Google Scholar] [CrossRef]
- Ustin, S.L.; Roberts, D.A.; Gamon, J.A.; Asner, G.P.; Green, R.O. Using Imaging Spectroscopy to Study Ecosystem Processes and Properties. BioScience 2004, 54, 523–534. [Google Scholar] [CrossRef]
- Nidamanuri, R.R. Hyperspectral discrimination of tea plant varieties using machine learning, and spectral matching methods. Remote Sens. Appl. 2020, 19, 100350. [Google Scholar] [CrossRef]
- Karan, S.K.; Samadder, S.R.; Maiti, S.K. Assessment of the capability of remote sensing and GIS techniques for monitoring reclamation success in coal mine degraded lands. J. Environ. Manag. 2016, 182, 272–283. [Google Scholar] [CrossRef]
- Sun, H.; Li, M.; Li, D. The vegetation classification in coal mine overburden dump using canopy spectral reflectance. Comput. Electron. Agric. 2011, 75, 176–180. [Google Scholar] [CrossRef]
- Sun, Y.; Yao, X.; Li, C.; Xie, Y. Physiological adaptability of three gramineae plants under various vegetation restoration models in mining area of Qinghai-Tibet Plateau. J. Plant Physiol. 2022, 276, 153760. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Wang, C.; Chen, J.; Shen, M.; Shen, B.; Yan, R.; Li, Z.; Karnieli, A.; Chen, J.; Yan, Y.; et al. The superiority of the normalized difference phenology index (NDPI) for estimating grassland aboveground fresh biomass. Remote Sens. Environ. 2021, 264, 112578. [Google Scholar] [CrossRef]
- Waititu, J.M.; Mundia, C.N.; Sichangi, A.W. Spectral discrimination of invasive Lantana camara L. From co-occurring species. Int. J. Remote Sens. 2023, 119, 103307. [Google Scholar] [CrossRef]
- Cho, M.A.; Skidmore, A.K.; Atzberger, C. Towards red-edge positions less sensitive to canopy biophysical parameters for leaf chlorophyll estimation using properties optique spectrales des feuilles (PROSPECT) and scattering by arbitrarily inclined leaves (SAILH) simulated data. Int. J. Remote Sens. 2008, 29, 2241–2255. [Google Scholar] [CrossRef]
- Fourty, T.; Baret, F. On spectral estimates of fresh leaf biochemistry. Int. J. Remote Sens. 1998, 19, 1283–1297. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Hyperspectral band depth analysis for a better estimation of grass biomass (Cenchrus ciliaris) measured under controlled laboratory conditions. Int. J. Appl. Earth Obs. Geoinf. 2004, 5, 87–96. [Google Scholar] [CrossRef]
- Algamal, Z.Y.; Lee, M.H. Regularized logistic regression with adjusted adaptive elastic net for gene selection in high dimensional cancer classification. Comput. Biol. Med. 2015, 67, 136–145. [Google Scholar] [CrossRef]
- Thessler, S.; Sesnie, S.; Ramos Bendaña, Z.S.; Ruokolainen, K.; Tomppo, E.; Finegan, B. Using k-nn and discriminant analyses to classify rain forest types in a Landsat TM image over northern Costa Rica. Remote Sens. Environ. 2008, 112, 2485–2494. [Google Scholar] [CrossRef]
- Volpi, M.; Petropoulos, G.P.; Kanevski, M. Flooding extent cartography with Landsat TM imagery and regularized kernel Fisher’s discriminant analysis. Comput. Geosci. 2013, 57, 24–31. [Google Scholar] [CrossRef]
- Lottering, R.T.; Govender, M.; Peerbhay, K.; Lottering, S. Comparing partial least squares (PLS) discriminant analysis and sparse PLS discriminant analysis in detecting and mapping Solanum mauritianum in commercial forest plantations using image texture. ISPRS J. Photogramm. Remote Sens. 2020, 159, 271–280. [Google Scholar] [CrossRef]
- Cao, Z.; Zhang, S.; Liu, Y.; Smith, C.J.; Sherman, A.M.; Hwang, Y.; Simpson, G.J. Spectral classification by generative adversarial linear discriminant analysis. Anal. Chim. Acta 2023, 1261, 341129. [Google Scholar] [CrossRef] [PubMed]
- Souza, J.d.C.; Soares, S.F.C.; de Paula, L.C.M.; Coelho, C.J.; de Araújo, M.C.U.; Silva, E.C.d. Bat algorithm for variable selection in multivariate classification modeling using linear discriminant analysis. Microchem. J. 2023, 187, 108382. [Google Scholar] [CrossRef]
- Li, L.; Liu, Z.-P. Biomarker discovery for predicting spontaneous preterm birth from gene expression data by regularized logistic regression. Comput. Struct. Biotechnol. J. 2020, 18, 3434–3446. [Google Scholar] [CrossRef] [PubMed]
- Cantorna, D.; Dafonte, C.; Iglesias, A.; Arcay, B. Oil spill segmentation in SAR images using convolutional neural networks. A comparative analysis with clustering and logistic regression algorithms. Appl. Soft Comput. 2019, 84, 105716. [Google Scholar] [CrossRef]
- Chunhui, Z.; Bing, G.; Lejun, Z.; Xiaoqing, W. Classification of Hyperspectral Imagery based on spectral gradient, SVM and spatial random forest. Infrared Phys. Technol. 2018, 95, 61–69. [Google Scholar] [CrossRef]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Bajcsy, P.; Groves, P. Methodology for Hyperspectral Band Selection. Photogramm. Eng. Remote Sens. 2004, 70, 793–802. [Google Scholar] [CrossRef]
- Almeida, C.T.d.; Galvão, L.S.; Aragão, L.E.d.O.C.e.; Ometto, J.P.H.B.; Jacon, A.D.; Pereira, F.R.d.S.; Sato, L.Y.; Lopes, A.P.; Graça, P.M.L.d.A.; Silva, C.V.d.J.; et al. Combining LiDAR and hyperspectral data for aboveground biomass modeling in the Brazilian Amazon using different regression algorithms. Remote Sens. Environ. 2019, 232, 111323. [Google Scholar] [CrossRef]
- Shao, Q.; Cao, W.; Fan, J.; Huang, L.; Xu, X. Effects of an ecological conservation and restoration project in the Three-River Source Region, China. J. Geog. Sci. 2017, 27, 183–204. [Google Scholar] [CrossRef]
- Zhang, H.; Li, X.; Li, L.; Zhang, J. Effects of Species Combination on Community Diversity and Productivity of Alpine Artificial Grassland. Acta Agrestia Sin. 2020, 28, 1436–1443. [Google Scholar] [CrossRef]
- Tsai, F.; Philpot, W. Derivative Analysis of Hyperspectral Data. Remote Sens. Environ. 1998, 66, 41–51. [Google Scholar] [CrossRef]
- Bielza, C.; Robles, V.; Larrañaga, P. Regularized logistic regression without a penalty term: An application to cancer classification with microarray data. Expert Syst. Appl. 2011, 38, 5110–5118. [Google Scholar] [CrossRef]
- Zhang, X.; Akber, M.Z.; Zheng, W. Predicting the slump of industrially produced concrete using machine learning: A multiclass classification approach. J. Build. Eng. 2022, 58, 104997. [Google Scholar] [CrossRef]
- Park, M.Y.; Hastie, T. L1-Regularization Path Algorithm for Generalized Linear Models. J. R. Stat. Soc. B 2007, 69, 659–677. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Kisi, O.; Kerem Cigizoglu, H. Comparison of different ANN techniques in river flow prediction. Civ. Eng. Environ. Syst. 2007, 24, 211–231. [Google Scholar] [CrossRef]
- Hammerstrom, D. Working with neural networks. IEEE Spectr. 1993, 30, 46–53. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, B.; Yao, Y.; Tan, C.; Feng, J. A spectroscopic method based on support vector machine and artificial neural network for fiber laser welding defects detection and classification. NDT E Int. 2019, 108, 102176. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Zhong, Z.; Carr, T.R. Application of mixed kernels function (MKF) based support vector regression model (SVR) for CO2—Reservoir oil minimum miscibility pressure prediction. Fuel 2016, 184, 590–603. [Google Scholar] [CrossRef]
- Caraka, R.E.; Bakar, S.A.; Tahmid, M. Rainfall forecasting multi kernel support vector regression seasonal autoregressive integrated moving average (MKSVR-SARIMA). AIP Conf. Proc. 2019, 2111, 020014. [Google Scholar] [CrossRef]
- Cheng, K.; Lu, Z.; Wei, Y.; Shi, Y.; Zhou, Y. Mixed kernel function support vector regression for global sensitivity analysis. Mech. Syst. Signal Process. 2017, 96, 201–214. [Google Scholar] [CrossRef]
- Zhu, B.; Ye, S.; Wang, P.; Chevallier, J.; Wei, Y.-M. Forecasting carbon price using a multi-objective least squares support vector machine with mixture kernels. J. Forecast. 2022, 41, 100–117. [Google Scholar] [CrossRef]
- Monnet, J.M.; Chanussot, J.; Berger, F. Support Vector Regression for the Estimation of Forest Stand Parameters Using Airborne Laser Scanning. IEEE Geosci. Remote Sens. Lett. 2011, 8, 580–584. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cheng, S.; Yang, X.; Yang, G.; Chen, B.; Chen, D.; Wang, J.; Ren, K.; Sun, W. Using ZY1-02D satellite hyperspectral remote sensing to monitor landscape diversity and its spatial scaling change in the Yellow River Estuary. Int. J. Appl. Earth Obs. Geoinf. 2024, 128, 103716. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef]
- Bergmeir, C.; Hyndman, R.J.; Koo, B. A note on the validity of cross-validation for evaluating autoregressive time series prediction. Comput. Stat. Data Anal. 2018, 120, 70–83. [Google Scholar] [CrossRef]
- Schmidt, K.S.; Skidmore, A.K. Spectral discrimination of vegetation types in a coastal wetland. Remote Sens. Environ. 2003, 85, 92–108. [Google Scholar] [CrossRef]
- Adam, E.; Mutanga, O. Spectral discrimination of papyrus vegetation (Cyperus papyrus L.) in swamp wetlands using field spectrometry. ISPRS J. Photogramm. Remote Sens. 2009, 64, 612–620. [Google Scholar] [CrossRef]
- Cho, M.A.; Debba, P.; Mutanga, O.; Dudeni-Tlhone, N.; Magadla, T.; Khuluse, S.A. Potential utility of the spectral red-edge region of SumbandilaSat imagery for assessing indigenous forest structure and health. Int. J. Appl. Earth Obs. Geoinf. 2012, 16, 85–93. [Google Scholar] [CrossRef]
- Zipper, C.E.; Burger, J.A.; Skousen, J.G.; Angel, P.N.; Barton, C.D.; Davis, V.; Franklin, J.A. Restoring Forests and Associated Ecosystem Services on Appalachian Coal Surface Mines. Environ. Manag. 2011, 47, 751–765. [Google Scholar] [CrossRef]
- Bao, N.-s.; Wu, L.-x.; Liu, S.-j.; Li, N. Scale parameter optimization through high-resolution imagery to support mine rehabilitated vegetation classification. Ecol. Eng. 2016, 97, 130–137. [Google Scholar] [CrossRef]
- Asner, G.P. Biophysical and Biochemical Sources of Variability in Canopy Reflectance. Remote Sens. Environ. 1998, 64, 234–253. [Google Scholar] [CrossRef]
- Ollinger, S. Sources of variability in canopy reflectance and the convergent properties of plants. New Phytol. 2010, 189, 375–394. [Google Scholar] [CrossRef]
- Niu, Y.; Yang, S.; Wang, G.; Liu, L.; Hua, L. Effects of grazing disturbance on plant diversity, community structure and direction of succession in an alpine meadow on Tibet Plateau, China. Acta Ecol. Sin. 2018, 38, 179–185. [Google Scholar] [CrossRef]
- Vloon, C.; Evju, M.; Klanderud, K.; Hagen, D. Alpine restoration: Planting and seeding of native species facilitate vegetation recovery. Restor. Ecol. 2021, 30, e13479. [Google Scholar] [CrossRef]
- Fernandes, M.R.; Aguiar, F.C.; Silva, J.M.N.; Ferreira, M.T.; Pereira, J.M.C. Spectral discrimination of giant reed (Arundo donax L.): A seasonal study in riparian areas. ISPRS J. Photogramm. Remote Sens. 2013, 80, 80–90. [Google Scholar] [CrossRef]
- Jin, L.; Li, X.; Sun, H.; Zhang, J.; Zhou, W. Characteristics of vegetations and soils under different aspects of slag mountain in alpine mining area. Soil 2020, 52, 831–839. [Google Scholar] [CrossRef]
- Wang, J.; Wang, H.; Cao, Y.; Bai, Z.; Qin, Q. Effects of soil and topographic factors on vegetation restoration in opencast coal mine dumps located in a loess area. Sci. Rep 2016, 6, 22058. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Bai, Z.; Cao, Y.; Zhou, W.; Wang, J. Influence of soil physical properties and vegetation coverage at different slope aspects in a reclaimed dump. Environ. Sci. Pollut. Control Ser. 2017, 24, 23953–23965. [Google Scholar] [CrossRef] [PubMed]
- Peñuelas, J.; Gamon, J.A.; Fredeen, A.L.; Merino, J.; Field, C.B. Reflectance indices associated with physiological changes in nitrogen- and water-limited sunflower leaves. Remote Sens. Environ. 1994, 48, 135–146. [Google Scholar] [CrossRef]
- Dao, P.D.; He, Y.; Proctor, C. Plant drought impact detection using ultra-high spatial resolution hyperspectral images and machine learning. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102364. [Google Scholar] [CrossRef]
- Erudel, T.; Fabre, S.; Houet, T.; Mazier, F.; Briottet, X. Criteria Comparison for Classifying Peatland Vegetation Types Using In Situ Hyperspectral Measurements. Remote Sens. 2017, 9, 748. [Google Scholar] [CrossRef]
- Harrison, D.; Rivard, B.; Sánchez-Azofeifa, A. Classification of tree species based on longwave hyperspectral data from leaves, a case study for a tropical dry forest. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 93–105. [Google Scholar] [CrossRef]
- Guzmán, Q.J.A.; Laakso, K.; López-Rodríguez, J.C.; Rivard, B.; Sánchez-Azofeifa, G.A. Using visible-near-infrared spectroscopy to classify lichens at a Neotropical Dry Forest. Ecol. Indic. 2020, 111, 105999. [Google Scholar] [CrossRef]
- Asner, G.P.; Jones, M.O.; Martin, R.E.; Knapp, D.E.; Hughes, R.F. Remote sensing of native and invasive species in Hawaiian forests. Remote Sens. Environ. 2008, 112, 1912–1926. [Google Scholar] [CrossRef]
- Bradter, U.; O’Connell, J.; Kunin, W.E.; Boffey, C.W.H.; Ellis, R.J.; Benton, T.G. Classifying grass-dominated habitats from remotely sensed data: The influence of spectral resolution, acquisition time and the vegetation classification system on accuracy and thematic resolution. Sci. Total Environ. 2020, 711, 134584. [Google Scholar] [CrossRef]
- van den Berg, A.; Perkins, T. Nondestructive Estimation of Anthocyanin Content in Autumn Sugar Maple Leaves. HortScience 2005, 40, 685–686. [Google Scholar] [CrossRef]
- Zhang, X.; Li, M.; Yang, H.; Li, X.; Cui, Z. Physiological responses of Suaeda glauca and Arabidopsis thaliana in phytoremediation of heavy metals. J. Environ. Manag. 2018, 223, 132–139. [Google Scholar] [CrossRef] [PubMed]
- Dutta, S.; Narayan, K.S. Spectroscopic studies of photoinduced transport in polymer field effect transistors. Synth. Met. 2005, 155, 328–331. [Google Scholar] [CrossRef]
- Li, R.; Yan, C.; Zhao, Y.; Wang, P.; Qiu, G.Y. Discriminating growth stages of an endangered Mediterranean relict plant (Ammopiptanthus mongolicus) in the arid Northwest China using hyperspectral measurements. Sci. Total Environ. 2019, 657, 270–278. [Google Scholar] [CrossRef] [PubMed]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Vogelmann, J.; Rock, B.; Moss, D.M. Red edge spectral measurements from sugar maple leaves. Int. J. Remote Sens. 1993, 14, 1563–1575. [Google Scholar] [CrossRef]
- Gamon, J.A.; Peñuelas, J.; Field, C.B. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
- Penuelas, J.; Filella, I.; Lloret, P.; Munoz, F.; Vilajeliu, M. Reflectance Assessment of Mite Effects on Apple-Trees. Int. J. Remote Sens. 1995, 16, 2727–2733. [Google Scholar] [CrossRef]
- Hunt, E.R.; Rock, B.N. Detection of changes in leaf water content using Near- and Middle-Infrared reflectances. Remote Sens. Environ. 1989, 30, 43–54. [Google Scholar] [CrossRef]
- Gitelson, A.; Keydan, G.; Merzlyak, M.; Gitelson, C. Three-Band Model for Noninvasive Estimation of Chlorophyll Carotenoids and Anthocyanin Contents in Higher Plant Leaves. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Penuelas, J.; Pinol, J.; Ogaya, R.; Filella, I. Estimation of plant water concentration by the reflectance Water Index WI (R900/R970). Int. J. Remote Sens. 1997, 18, 2869–2875. [Google Scholar] [CrossRef]
- Gao, B.-c. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Li, X.; Wei, Z.; Peng, F.; Liu, J.; Han, G. Estimating the distribution of chlorophyll content in CYVCV infected lemon leaf using hyperspectral imaging. Comput. Electron. Agric. 2022, 198, 107036. [Google Scholar] [CrossRef]
- Kokaly, R.F.; Asner, G.P.; Ollinger, S.V.; Martin, M.E.; Wessman, C.A. Characterizing canopy biochemistry from imaging spectroscopy and its application to ecosystem studies. Remote Sens. Environ. 2009, 113, S78–S91. [Google Scholar] [CrossRef]


| Type | Abbr. | Model | Parameters | Feature Rank Criteria | R Package |
|---|---|---|---|---|---|
| Parametric Model | RLR | Regularized Logistic Regression | cost = 1 loss = L1, L2_dual, L2_primal epsilon = 0.001, 0.00325, 0.0055, 0.00775, 0.01 | Decrease in accuracy value by permuting a variable * | LiblineaR |
| Non-parametric Model | BPNN | Back Propagation Neural Network | 17, 18, 19, 20 decay = 0, 0.1 | combinations of the absolute values of the weights | nnet |
| SVM | Support Vector Machines with Radial Basis Function Kernel | 0, 1, 2, 3) singma = 0.1, 0.2, 0.3, ⋯1 | Decrease in accuracy value by permuting a variable * | kernlab | |
| RF | Random Forest | n.tree = 300, 500, 700, 900, 1000, 1500 (k is the number of indicators entered) | Decrease in accuracy value by permuting a variable | randomForest |
| Vegetation Type | ||||||
|---|---|---|---|---|---|---|
| Natural Vegetation | 0.000954 | 525 | 0.000113 | 629 | 0.005023 | 718 |
| P. pratensis | 0.001055 | 522 | 0.000199 | 629 | 0.008661 | 730 |
| P. crymophila | 0.000799 | 518 | 0.000547 | 629 | 0.006918 | 716 |
| Elymus nutans | 0.001285 | 522 | 0.000133 | 629 | 0.006486 | 719 |
| F. sinensis | 0.001421 | 521 | 0.000019 | 629 | 0.009942 | 728 |
| Model | F1 Score | Accuracy | ||||
|---|---|---|---|---|---|---|
| Natural Vegetation | P. pratensis | P. crymophila | E. nutans | F. sinensis | ||
| RLR | 1.000 | 0.768 | 0.808 | 0.751 | 0.755 | 0.821 |
| BPNN | 1.000 | 0.766 | 0.726 | 0.766 | 0.823 | 0.817 |
| SVM | 0.917 | 0.813 | 0.810 | 0.771 | 0.810 | 0.824 |
| RF | 1.000 | 0.838 | 0.827 | 0.824 | 0.859 | 0.871 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Xu, H.; Zhou, J.; Fang, X.; Shuai, S.; Yang, X. Analysis of Vegetation Canopy Spectral Features and Species Discrimination in Reclamation Mining Area Using In Situ Hyperspectral Data. Remote Sens. 2024, 16, 2372. https://doi.org/10.3390/rs16132372
Wang X, Xu H, Zhou J, Fang X, Shuai S, Yang X. Analysis of Vegetation Canopy Spectral Features and Species Discrimination in Reclamation Mining Area Using In Situ Hyperspectral Data. Remote Sensing. 2024; 16(13):2372. https://doi.org/10.3390/rs16132372
Chicago/Turabian StyleWang, Xu, Hang Xu, Jianwei Zhou, Xiaonan Fang, Shuang Shuai, and Xianhua Yang. 2024. "Analysis of Vegetation Canopy Spectral Features and Species Discrimination in Reclamation Mining Area Using In Situ Hyperspectral Data" Remote Sensing 16, no. 13: 2372. https://doi.org/10.3390/rs16132372
APA StyleWang, X., Xu, H., Zhou, J., Fang, X., Shuai, S., & Yang, X. (2024). Analysis of Vegetation Canopy Spectral Features and Species Discrimination in Reclamation Mining Area Using In Situ Hyperspectral Data. Remote Sensing, 16(13), 2372. https://doi.org/10.3390/rs16132372







