Next Article in Journal
Evaluation of GPM IMERG Satellite Precipitation Products in Event-Based Flood Modeling over the Sunshui River Basin in Southwestern China
Next Article in Special Issue
SimNFND: A Forward-Looking Sonar Denoising Model Trained on Simulated Noise-Free and Noisy Data
Previous Article in Journal
Lightweight Pedestrian Detection Network for UAV Remote Sensing Images Based on Strideless Pooling
Previous Article in Special Issue
Enhancing Machine Learning Performance in Estimating CDOM Absorption Coefficient via Data Resampling
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 16
Issue 13
10.3390/rs16132332
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Automated Flood Prediction along Railway Tracks Using Remotely Sensed Data and Traditional Flood Models

by
Abdul-Rashid Zakaria
1,
Thomas Oommen
2,* and
Pasi Lautala
3
1
Department of Computer and Information Science, The University of Mississippi, 201 Weir Hall, University, Oxford, MS 38677, USA
2
Department of Geological and Geological Engineering, The University of Mississippi, 120 A Carrier Hall, University, Oxford, MS 38677, USA
3
Civil, Environmental and Geospatial Engineering, Michigan Technological University, 1400 Townsend Drive, Houghton, MI 49931, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2024, 16(13), 2332; https://doi.org/10.3390/rs16132332
Submission received: 3 May 2024 / Revised: 14 June 2024 / Accepted: 24 June 2024 / Published: 26 June 2024
(This article belongs to the Special Issue Advanced Application of Artificial Intelligence and Machine Vision in Remote Sensing (Third Edition))
Browse Figures
Versions Notes

Abstract

:
Ground hazards are a significant problem in the global economy, costing millions of dollars in damage each year. Railroad tracks are vulnerable to ground hazards like flooding since they traverse multiple terrains with complex environmental factors and diverse human developments. Traditionally, flood-hazard assessments are generated using models like the Hydrological Engineering Center–River Analysis System (HEC-RAS). However, these maps are typically created for design flood events (10, 50, 100, 500 years) and are not available for any specific storm event, as they are not designed for individual flood predictions. Remotely sensed methods, on the other hand, offer precise flood extents only during the flooding, which means the actual flood extents cannot be determined beforehand. Railroad agencies need daily flood extent maps before rainfall events to manage and plan for the parts of the railroad network that will be impacted during each rainfall event. A new approach would involve using traditional flood-modeling layers and remotely sensed flood model outputs such as flood maps created using the Google Earth Engine. These new approaches will use machine-learning tools in flood prediction and extent mapping. This new approach will allow for determining the extent of flood for each rainfall event on a daily basis using rainfall forecast; therefore, flooding extents will be modeled before the actual flood, allowing railroad managers to plan for flood events pre-emptively. Two approaches were used: support vector machines and deep neural networks. Both methods were fine-tuned using grid-search cross-validation; the deep neural network model was chosen as the best model since it was computationally less expensive in training the model and had fewer type II errors or false negatives, which were the priorities for the flood modeling and would be suitable for developing the automated system for the entire railway corridor. The best deep neural network was then deployed and used to assess the extent of flooding for two floods in 2020 and 2022. The results indicate that the model accurately approximates the actual flooding extent and can predict flooding on a daily temporal basis using rainfall forecasts.

1. Introduction

Floods are common geological hazards worldwide and significantly affect the quality of life and infrastructure [1]. Railroads are susceptible to floods and washouts due to water accumulation along railway tracks. Unlike other geohazards, floods are predictable using rainfall, river discharge, river gauge, and other environmental factors. Flood-generating mechanisms vary from climate-inducing factors to drainage patterns within an area of interest (AOI).
Historically, flood mitigation and risk mapping for different study areas have been carried out using a combination of traditional flood models such as Hydrological Engineering Center–River Analysis System (HEC-RAS) models produced by the United States Army Corps of Engineers (USACE) [2], flood models that integrate geographic information systems and remotely sensed data such HYDROTEL, and soil and water assessment tool (SWAT) [3,4,5,6]. Traditional flood-assessment methods are highly effective in mapping floods using river discharge and drainage patterns. These assessments can map floods for different return periods, such as the 100-year flood [7,8], which is the limit of the flood plain for flood insurance purposes in the United States as specified by the Flood Disaster and Protection Act of 1973 [9].
Flood mapping using traditional methods is intrinsically limited to various return periods that cannot be dynamically used for different rainfall and environmental conditions prevalent in a particular location. Railway infrastructures are prone to flooding at different locations with varying degrees of flooding susceptibility, exposing the limitations of using flood maps produced from traditional methods for railway infrastructure management. When using remotely sensed maps for flood extent mapping, data may not be readily available in real time as satellites do not have constant coverage for the areas of interest. In addition, satellite data providers may not have readily available real-time satellite data considering cost and priority. Real-time flood analysis using satellite image analysis also requires high computational resources that can be costly, considering railroads traverse large swaths of terrain. Therefore, we propose real-time flood mapping for infrastructure such as railroads using a combination of traditional and satellite-based approaches for which daily flood susceptibility maps can be done.
Statistical approaches have also been used in flood studies. Kazakis et al. [10] proposed an index-based methodology for assessing flood-hazard areas. Their methodology analyzed seven features to determine flood risks for their AOI. Lee et al. [11] suggested a flood frequency ratio framework in which an aerial ratio of flood occurrence and non-occurrence for each environmental factor was estimated. All environmental factors were summated to calculate the flooded area susceptibility index (FSI). Their model achieved a 91.5% area under the curve (AUC) and can be easily deployed to regions without comprehensive maps. However, statistical methods require rigid data distribution assumptions, and prior knowledge of the data and problem at large [5,6,9,10,11,12].
Machine-learning algorithms have also been developed for flood modeling and other geohazards with support vector machines and neural networks [13,14,15]. Tehrany et al. [13] built an ensemble model that integrated support vector machine and frequency ratio. Their model achieved an 88.71% success rate and 85.21% prediction rate. The authors concluded that the ensemble model provided better accuracy on validation data than a decision tree model. Moreover, their ensemble model produced rapid and reasonable flood susceptibility maps. Their data preparation involved binning the condition factors into classes that summarize the features; however, information loss is inherent in their model. Kia et al. [16] mapped floods in Southern Malaysia using an artificial multilayer perceptron program on MATLAB on causative flood factors such as geology and land use. They further applied their models to simulate peak flows as well as base flows. Hence, flood mapping has been successfully done using a combination of statistical methods and machine-learning algorithms.
Remotely sensed data and geographic information systems offer a potential solution to the limitations of traditional flood models. Remotely sensed data have been used to monitor flood events and assess urban infrastructure [17,18,19]. In Patro et al. [20], the authors used MIKE flood, a flood-modeling tool built by the Danish Hydraulic Institute, and the river cross-sections extracted from the shuttle radar topography mission digital elevation model. Other authors, including [21,22,23], used satellite remote-sensing data to create and calibrate hydrologic models for spatial flood extent mapping.
Kourgialas and Karatzas [24] used geographic information system (GIS) data in modeling flood-hazard areas based on flow accumulation, geology, elevation, land use, slope, and rainfall intensity. These features were used to estimate the spatial distribution of areas of high to low flooding zones and further creation of a flooding hazard map. Liu et al. [25] proposed GIS-based flood modeling using a grid cell mesh and first passage time response function to calculate the rainfall-runoff response for a catchment area. Other authors, [26,27,28] also proposed methodologies, including 3D geometry modeling and graphical processing unit multithread processing for flood modeling using a combination of GIS and remote-sensing data.
Ighile et al. [29] utilized machine-learning models, specifically logistic regression and artificial neural networks, to predict flood susceptible areas, including railroads and roads, and other civil infrastructure in Nigeria, using 15 condition factors. Their study revealed that the key influencing factors were curvature, curve number, land used, and stream power index. Their artificial neural network model outperforms the logistic regression model with a 76.4% accuracy prediction rate relative to 62.5% for the former. In [30], the authors used hourly weather measurements of humidity, precipitation, wind speed and wind direction, temperature, and geographic information system techniques coupled with machine-learning models to create a flood risk index for areas prone to flooding under critical weather conditions.
Sresakoolchai et al. [31] proposed using automated machine learning recognition to determine flood resilience of railway switches and crossings. They used nonlinear finite element models validated by field measurements to mimic the dynamic characteristics of turnout supports under flooding scenarios. Their proposed method addresses the impact of extreme weather conditions like floods on railway switches and turnout supports. Elkhrachy [32] used Sentinel-1 synthetic aperture radar data, land-use data, rainfall, and digital surface maps with different regression methods for estimating flood water depth during flood events. In their study, the authors proved that machine-learning algorithms can accurately determine flood depths that can be applied to linear infrastructure such as railroads and roads.
This paper aims to deliver a robust flood prediction and extent model. To achieve that, machine learning is coupled with traditional flood models and remotely sensed data to improve flood prediction and create the premises for automated flood modeling. Therefore, we propose an automated daily flood extent prediction by combining traditional flood mapping layers (HEC-RAS 1D), flood maps created from remotely sensed data using the Google Earth Engine, and geospatial environmental data, including daily rainfall measurements obtained from the global precipitation measurements, to predict the daily flood extent along railroad tracks.

2. Materials and Methods

2.1. Study Area

The AOI is Big Horn, Montana, where railway tracks are along the Yellowstone River. The Yellowstone River is the Missouri River’s largest tributary, accounting for 55% of the combined flow. The Yellowstone River watershed consists of an 181,299.168-square-kilometer basin across three states with major tributaries in the basin, including the Big Horn River. Vegetative cover includes woodland, grassland, irrigated and dry cropland. The Yellowstone River watershed supports numerous communities, agricultural uses, industrial establishments, commercial and recreational centers, and a wide variety of biological life [33,34].

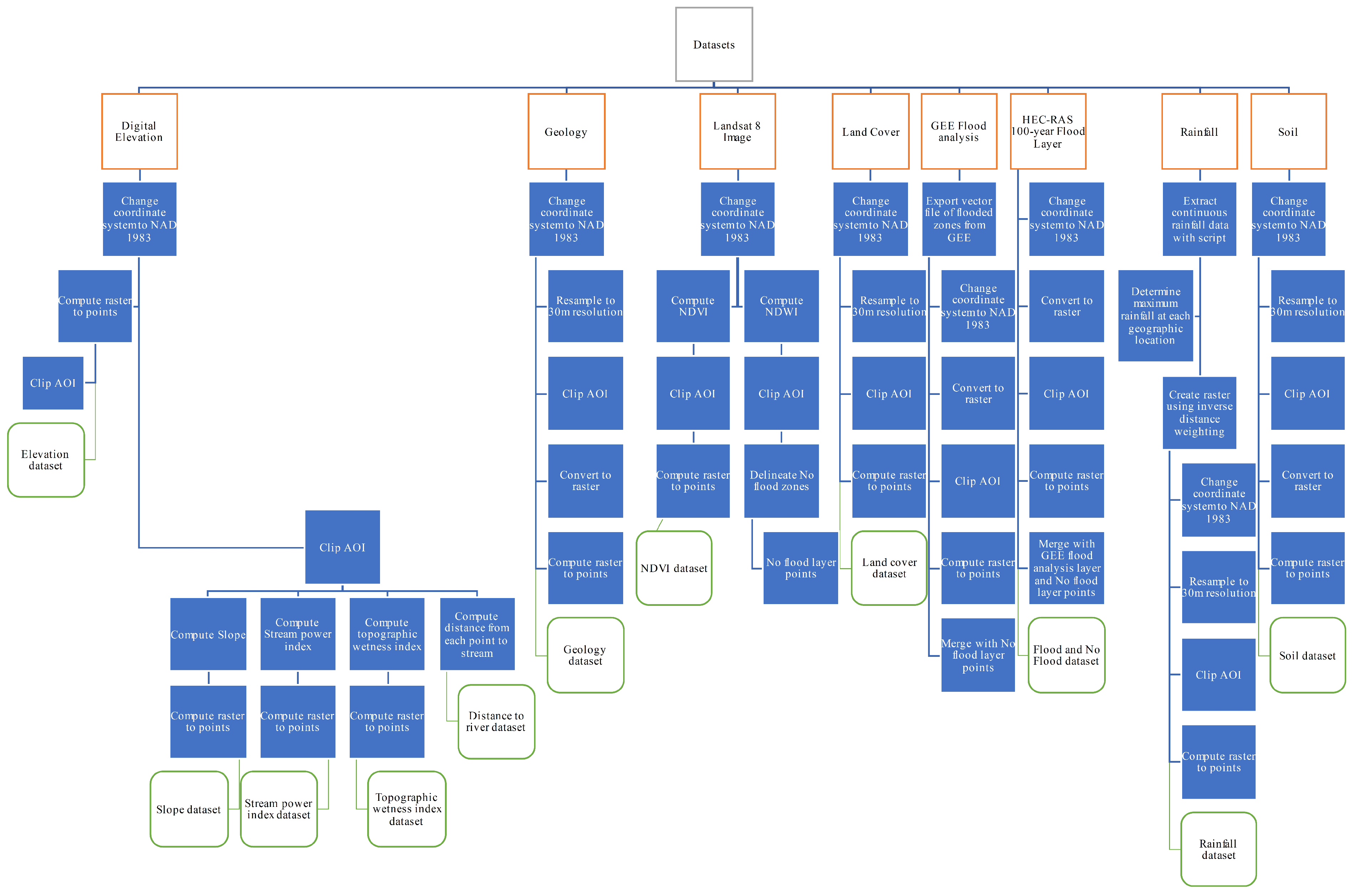
2.2. Flood Environmental Factors

Environmental factors that affect flooding are used in building the models. These features (Table 1) were obtained as raster and vector files and, in some instances, were created from other data analyses (Figure 1). Flood layers were obtained from Google Earth Engine (GEE) flood analysis for specific flood events using a change detection algorithm on Sentinel-1 synthetic aperture radar (SAR) data and HEC-RAS flood models for the 100-year return period. This spatial representation of flood assumes that floods will occur in the future under similar conditions. Hence, the environmental factors prevalent in the AOI influence the models’ quality. Ten features are generated from the environmental condition factors (Figure 1), namely elevation, geology, land-cover classification, normalized difference vegetation index (NDVI), slope, soil, stream power index (SPI), topographic power index (TWI), the distance of each point from the river, and rainfall.
The digital elevation model (DEM) was downloaded from the USGS website and converted into points at 30 m spatial resolution. The DEM provides the location’s height above the mean sea level. In addition, the DEM is used to derive slope, TWI, and SPI [29,30,31]. The slope is calculated for each raster cell at 30 m spatial resolution [32]. Flat areas or low slopes are more likely to be flooded than high slopes. Therefore, high slopes have a negative correlation with floods. The SPI (1) provides an estimate of the erosive power of the streams for each raster cell [33]. Therefore, it can be used to describe erosion downstream based on increasing slope and catchment area. Higher erosion risk is associated with a higher SPI [35,36]. SPI does not have a linear correlation with flooding. However, it affects the TWI at each location.
S P I = A s t a n β
where A s —Stream catchment area and β —cell slope in radians.
The TWI, (2) quantifies topographic control on hydrological processes such as runoff volumes and accumulation zones. This index is useful in estimating areas of potential runoff, ponding, and potential increase in soil moisture for vegetation zones [37,38,39]. TWI is not strongly linearly related to the occurrence of floods since the wetness of a particular location, in some cases, does not control the tendency of flooding at that location.
T W I = ln α tan β
α —upslope area, β —cell slope in radians.
The lithology of the study area was obtained from USGS maps and resampled at 30 m resolution. Different rock units are related to the geomorphological processes that influence flooding. The erodibility of rocks depends on the rock types, as the structural features are unique to these rock units [40,41]. The NDVI was calculated to provide information on vegetation density; high NDVI indicates locations of vegetation and vice versa (values range from +1 to −1) [42]. GEE was used for the NDVI calculations with Landsat 8 Collection 2 tier 1 calibrated top-of-atmosphere (TOA) reflectance [43].
Furthermore, land-cover and land-use changes impact the extent of flooding. Fourteen classes were obtained for this study. The occurrence of floods is negatively correlated with vegetation density; that is, areas with urban development have higher runoff volume than rural areas with vegetation. Distance from each point (elevation points) to the normalized difference water index (NDWI) was used to delimit the river. The shortest distance from each point to the vector file of the river was calculated and used as a feature of the model. Locations closer to the Yellowstone River have a higher chance of flooding than locations farther from the river ceteris paribus. The rainfall dataset, the global precipitation measurement (GPM) Level 3 Integrated Multi-satellite Retrievals for GPM (IMERG) Late Daily 10 × 10 km (daily accumulated values in mm) from 1 June 2000 to 12 October 2022, was used as the rainfall data [44]. Pivoting the data using the longitude and latitude as indices, 464 locations were obtained. Using the National Weather Service advanced hydrologic prediction service, upstream gauge and downstream gauge historical data, the dates (Table 2) for which the river crests were beyond the flood stage both upstream and downstream of the AOI and within the bounding box used in creating the rainfall data. These data were used to filter the rainfall data. After filtering, rainfall for only the filtered dates for each location was used to obtain the maximum rainfall at each longitude and latitude. Maximum rainfall was used since it was the best statistical value that accounted for most flooding along the Yellowstone River Corridor.
A 30 m resolution raster of the maximum precipitation was created from all 484 locations using the inverse distance weighting (IDW) interpolation. The AOI was then clipped from the raster. The clipped raster was reprojected to the coordinate reference system NAD 1983. The raster dataset was finally converted into points and used as a feature in the flood models.

2.3. Flood Zones and Correlations

Flood zones were created by combining the 100-year profile vector files from HEC-RAS and flood vector files created using the GEE. The former inundation vector file products are generated from a previous USACE study, which created a HEC-RAS 1D model mapping the inundation conditions along the Yellowstone River in Treasure County, Montana. The total channel flow used in the USACE HEC-RAS flood model was 2803.4 cubic meters per second for the 100-year profile [2]. The latter flood extents are based on a change detection algorithm using Sentinel-1 synthetic aperture radar (SAR) data for flooding in 2017, 2018, and 2019 for the AOI. The algorithm requires start and end dates of a period before the flood during which the Sentinel-1 image was acquired; similar dates are required for the after-the-flood image (Table 3).
Another SAR parameter that is used in the algorithm is polarization: vertical–horizontal (VH) mode means vertical waves are transmitted, and horizontal waves are received by Sentinel-1 to create the SAR image. VH mode was preferred for flood mapping since it is more sensitive to surface textures such as flooded ground. Also, the pass direction was set in ascending mode since it provided the largest collection of images available for the AOI. The algorithm uses a difference threshold between the SAR images to determine the extent of flooding. This threshold can be set manually to help improve flooding extent accuracy [19,45]. The best estimate for each flood period is provided, and it greatly affects the quality of the flood map. A final flood zone feature was created by combining the three temporal flood maps with the HEC-RAS 100-year flood map using ArcGIS Pro. These zones are delineated as ‘1’. Using the vector file representing the AOI and the NDWI, the no-flood feature map delineated as ‘0’ is created and merged with the flood zone map. The combined map is rasterized with a 30 m cell size using the ‘Polygon to Raster’ geoprocessing tool in ArCPro. Finally, the ‘Raster to Point’ tool is used to create a point for each cell of the raster layer. Similar steps are used for each feature (Figure 1).
A total of 516,260 points were obtained after using the “Raster to point” tool for each feature, which was used as the final dataset. The correlation between features (Figure 2) was calculated, as well as the distribution of each feature using histogram plots. An unbalanced data set was identified during the exploratory data analysis (EDA); hence, stratified data splitting was used to maintain the proportions of the classes in the training and testing datasets.
Figure 2 shows the correlation between the features of the model. The highest correlation, 0.75, is between the distance of each point from the river and the elevation at that location, while the target feature, the flood, and not flooded points have the highest negative correlation, 0.39, with the distance from each location to the river feature. High positive correlations mean a linear relationship between features that may result in redundant information not useful in model building, and such pairwise features often adversely affect models [46].

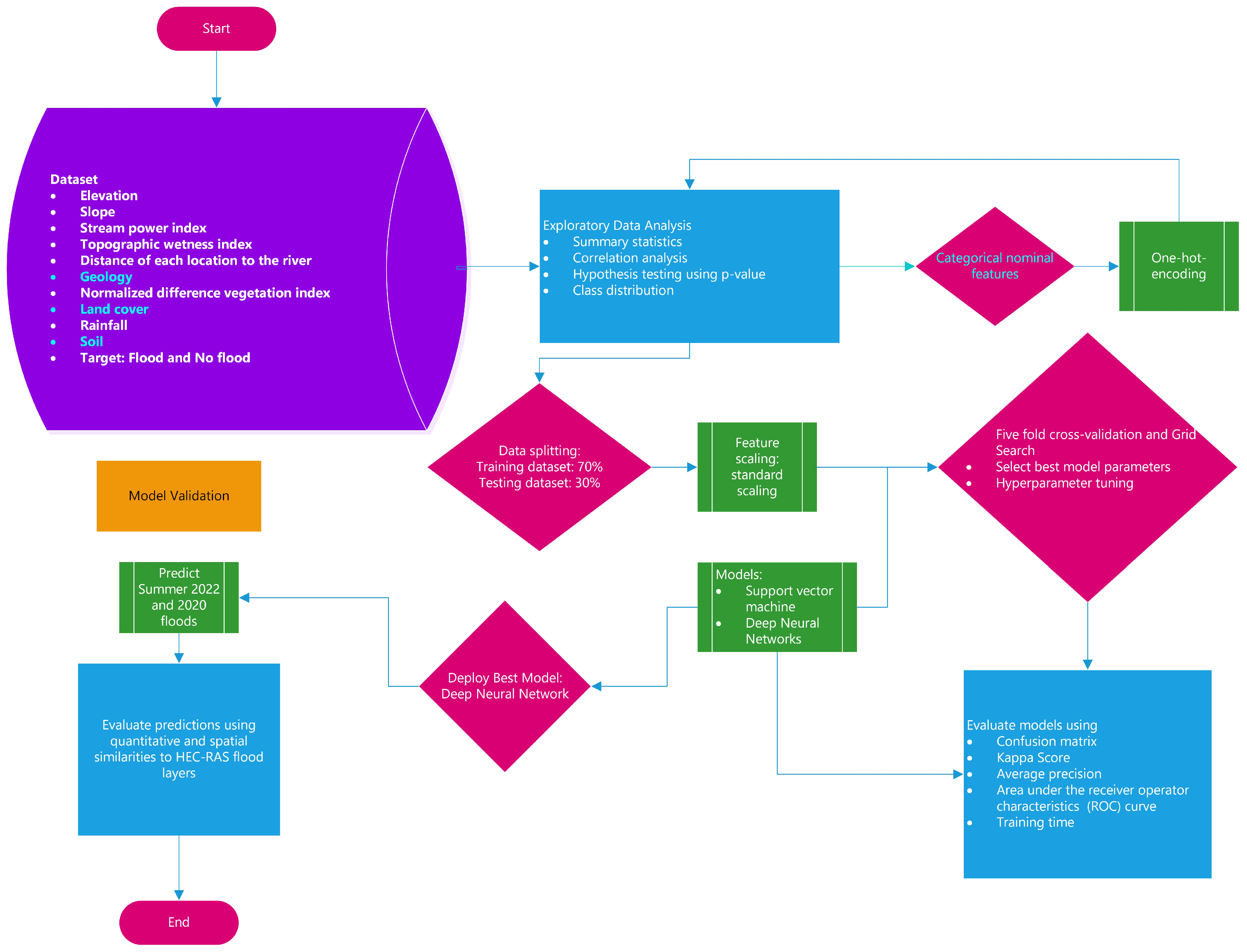
2.4. Machine Learning

The machine-learning model is integral to the predictive modeling process [46]. Zhou [47] stated that machine learning is the technique that improves system performance by learning from examples and experiences through computational methods. Some of these computational methods are classical, such as support vector machines and deep neural networks, which fall under computational intelligence, a sub-branch of artificial intelligence.

2.4.1. Support Vector Machine

Vapnik [48] defined a support vector machine as a powerful modeling technique that implements the idea of mapping input vectors. For our study, the features are mapped in a high-dimensional feature space through pre-selected nonlinear mapping. In this feature space, an optimal separating hyperplane (maximal margin hyperplane) is constructed [49]. Support vector machines have been applied to linear and nonlinear problems [48,49,50]. Kernel functions such as the radial basis function are used to encompass nonlinear functions of the features, as they are highly effective in most classification problems [46]. This study used the radial basis function kernel in model training.
The support vector machine was developed in the 1990s and is a generalization of the maximal margin classifier. Data that a hyperplane can perfectly separate implies that an infinite number of hyperplanes can be used. Hence, the best hyperplane is the optimal separating hyperplane that results in each training observation having the maximum distance to the hyperplane, where the margin refers to the perpendicular distance between a hyperplane and the training data observation. In practice, the largest maximal margin hyperplane is extremely sensitive to a change in any single data point, making overfitting a challenge during the model’s training. Therefore, it is acceptable to misclassify some training observations if a robust model can be obtained.
A robust model performs equally well on test data, but it should be less sensitive to individual training observations and generally achieve better classification of most of the training observations. A soft margin classifier or support vector classifier is desired to achieve these desirable traits, as it allows the misclassification of a small subset of the training observations. The soft margin classifier is also a solution to the optimization problem using a non-negative tuning parameter generally referred to as the cost. A cost of value zero is analogous to the maximal margin hyperplane, which exists if the two classes are always separable. Increasing the cost parameter means our model is amenable to violations to the margin; inversely, a decreasing cost means the model is resistant to misclassifications, hence a narrow margin and higher confidence in the classification.
During training, the cost is generally chosen through cross-validation. The cost parameter also controls the bias-variance trade-off of the model, i.e., when the cost is large, the margin is wider, creating less confidence and less restraint towards misclassification. Therefore, the classifier is likely biased with a lower variance. Conversely, when the cost is small, narrow margins are obtained, which means that the highly restrained model greatly fits the training data, resulting in a low-bias model with high variance [49,50].

2.4.2. Artificial Neural Network

Artificial Neural Networks (ANNs) are nonlinear regression techniques inspired by the biological network of neurons. Neural networks typically comprise an input layer, hidden layers, and an output layer. Each layer is connected to consecutive layers through links with weights that denote the strength of the outgoing signal. The input layer has the same number of nodes as the number of features used in the model. Learning of the features is carried out within the hidden units.
Haykin [51] defined the neuron as the information processing unit of a neural network. The activation function defines the output of a neuron using the induced local field and is important in solving nonlinear properties. Also, a nonlinear activation function inherently builds the model to learn nonlinear features. The backpropagation algorithm is a landmark in the development of neural network [52,53], as it provided a computationally effective process for training multilayer perceptrons.
Different types of neural networks (NN) have been developed, such as the Elman and Jordan recurrent networks and time-delay neural networks that are temporal NNs. Multilayer feedforward NN, such as the fully connected layers of a convolutional neural network (CNN) and the Hopfield network, which is a single-layer NN [54,55]. There is a wide range of other ANNs borne from NNs whose applications include (but are not limited to) pattern recognition [56], image segmentation [57], change detection [58], image processing [59], robot automation [60], speech recognition [61], and diagnosis of diseases [62].
In this study, we built deep neural network models from scratch using scikit-learn. The initial set of deep neural networks experimented with were feedforward, multilayer neural networks. In addition, custom recurrent neural network models were also created to handle cases where input features varied depending on the location along the track. These two architectures were combined in some experiments. However, there was no significant improvement in performance from the experiments. The final deep neural network model chosen was a custom feedforward model that provided the most robust and accurate results regardless of the location along the railroad track being monitored.

2.5. Machine-Learning Life Cycle

The machine-learning life cycle, Figure 3, provides the steps of this project, from obtaining the datasets to the model’s deployment. The data-collection process involved gathering remotely sensed data from external sources, creating flood maps using GEE, and further analysis and data creation and cleaning using ArCPro. Extensive EDA was carried out for each feature using Python. Scatter plots and histograms were key in identifying the distributions of each feature. Preprocessing also involved one-hot encoding categorical nominal features and stratified splitting due to the class imbalance in the target data. A total of 70% of the data were used for training, and 30% was used for testing. After data splitting, standard scaling was applied to the features to make the algorithms less sensitive to outliers. Grid search with cross-validation (5-fold) was used for hyperparameters tuning. The optimal hyperparameters were obtained, and the best machine-learning algorithm was also selected based on performance metrics obtained during the 5-fold cross-validation and performance of each algorithm on the test dataset. The final model was trained using the optimal hyperparameters, and validation was performed by predicting two flood events in 2020 and 2022. The flood extent from the model is statistically compared with HEC-RAS flood maps of the same equivalent return period.

2.6. Cross-Validation

A total of 358,484 point locations were used in training for the machine-learning models. After cross-validation, 153,636 locations were used as the test data to estimate each model’s performance on unseen data. Five-fold cross-validation was performed to obtain the baseline models, to select the best model hyperparameters, and to determine the average model training time. Cross-validation is a data-driven method for hyperparameter optimization and the production of the train-test splits required for an unbiased estimation of model performance. In the 5-fold cross-validation, the training data are split into 5 folds; 4 folds are used for training, while the remaining fold is used for testing. Evaluation of the models is one fold, resulting in a 5-fold estimation of the models’ performance. In this study, cross-validation was also used to estimate the computational time for different machine-learning methods and to select the best hyperparameters for the final training of the model. The best model was then selected based on the performance metrics obtained from the test data.

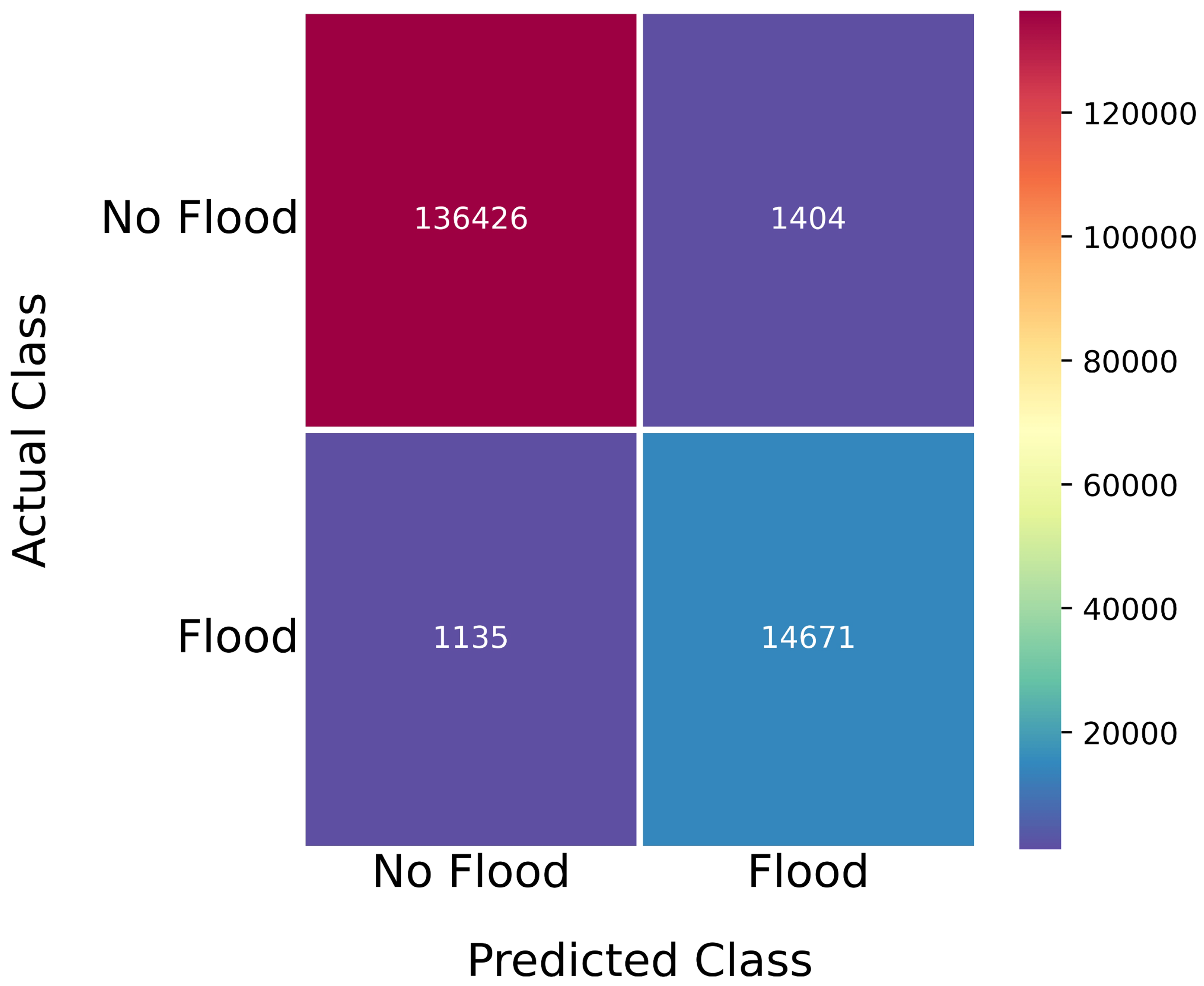
2.7. Models Assessment

The models were assessed using predictions on the test data set. The confusion matrix, true positive rate (TPR), false positive rate (FPR), area under the receiver operator characteristics (ROC-AUC) curve, Cohen’s kappa coefficient, precision-recall curves, average precision (AP), and the mean model training time during 5-fold cross-validation were used to choose the best model (Figure 3).
The ROC curve shows the variation of the error rates for all the range of defined thresholds, i.e., a plot of the FPR (3) on the X-axis against the true positive rate TPR on the y-axis for different threshold values between 0 and 1. Plotting the ROC curve helps choose a threshold that gives a desirable balance between the false positives and the false negatives [63,64]. A flooded location is positive, and a non-flooded location is negative.
The FPR is expressed as Equation (3)
F P R = F a l s e P o s i t i v e s F a l s e P o s i t i v e s + T r u e N e g a t i v e s
FPR is also known as inverted specificity. The TPR (4) provides the model’s ability to predict the positive class when the actual outcome is positive.
T P R = T r u e P o s i t i v e s T r u e P o s i t i v e s + F a l s e N e g a t i v e s
The AUC is a powerful metric for measuring the model’s overall performance. A value of 0.5 for a poor model (random) and 1.0 for a perfect model; hence, the better the classifier, the closer the model is to the top left corner of the AUC plot [65]. Cohen’s kappa expresses the level of agreement between two raters on a binary classification [66]. Kappa values above 0.80 are considered good agreement, while zero or lower ratings indicate no agreement. The kappa values range from 1 to −1. The precision-recall curves are recommended for highly imbalanced data. These curves show the trade-off in both precision and recall at different thresholds. Hence, a higher area under the curve indicates high precision and high recall, which means a low false positive rate and a low false negative rate, respectively. An ideal model should return highly accurate results with high precision and high recall that can produce all labels correctly [67,68,69]. In information retrieval, average precision is a plug-in estimate of the area under the precision-recall curve (AUCPR). In summary, average precision is a robust nonparametric estimator for binary classification [69,70,71].
This study uses ArcGIS Pro 3.1.0 software for geographic data preprocessing, remote-sensing flood models were created using GEE. Cross-validation, model training, and accuracy assessment were carried out in Python using scikit-learn.

3. Results

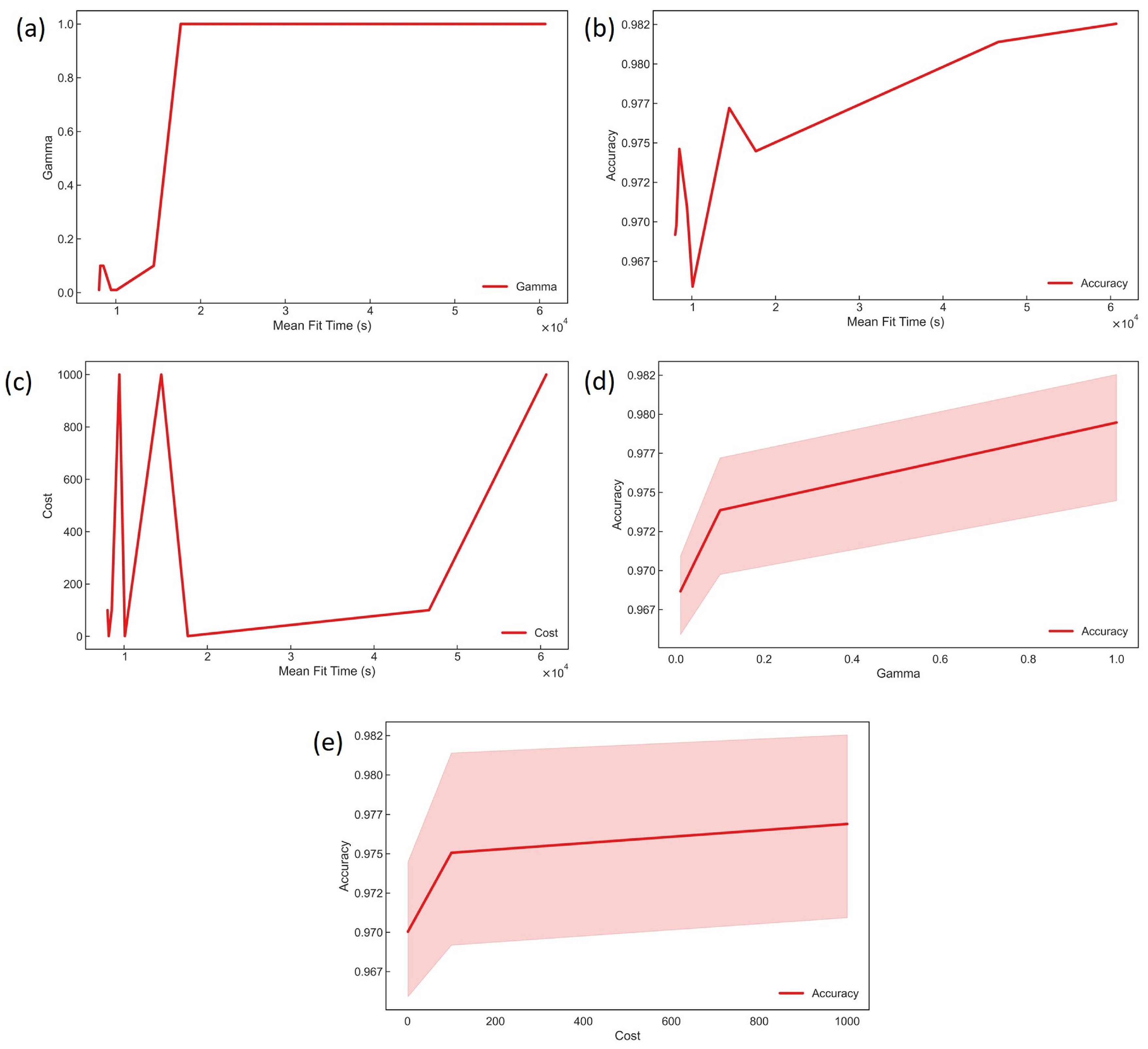
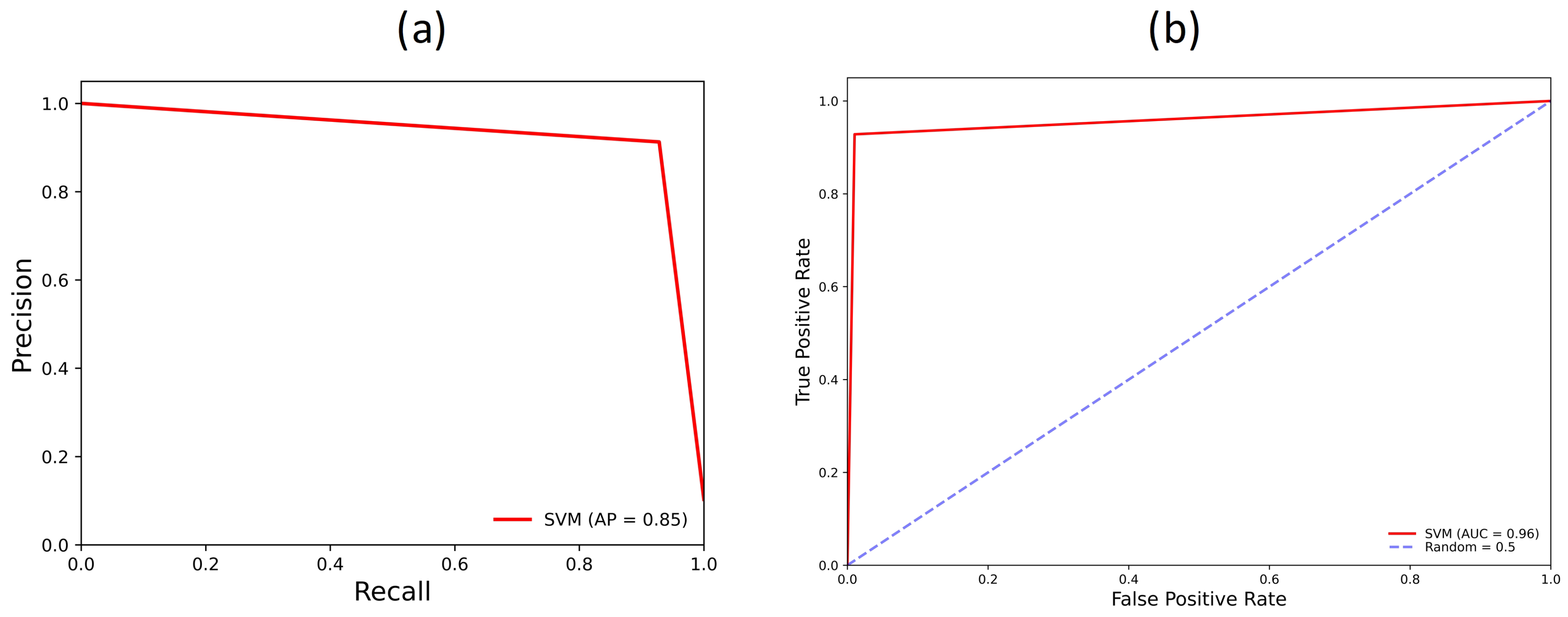
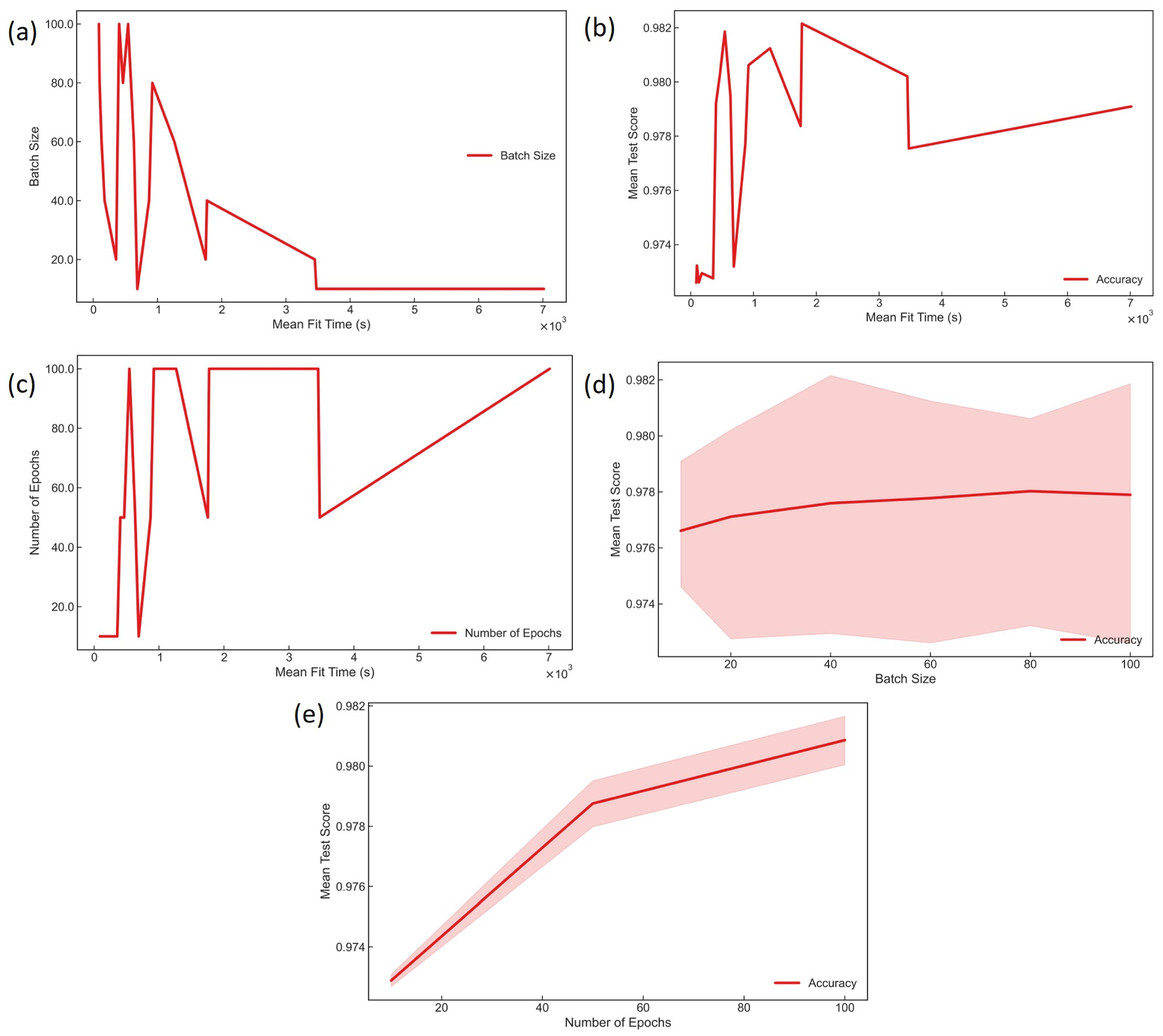
3.1. Support Vector Machine Models

Grid-search cross-validation with scikit-learn GridSearchCV summary results is shown in Figure 4. For the gamma hyperparameter, the mean fit time increased linearly for gamma values of 0.1; however, the mean fit time increased more than 10-fold for models with gamma values of one. Generally, increasing model fit time results in better accuracy, as the gamma value increases with the accuracy. This observation increases accuracy with higher gamma values, which means the model increases in non-linearity and complexity. The cost hyperparameter controls the complexity of the model such that for large values, our models become highly flexible and easily overfit the training data. From Figure 4, an increase of the cost hyperparameter results in improving accuracy. However, a nonlinear relationship is observed in the mean model fitting time, indicating that the gamma parameter affects the cost tuning. Hence, in some cases, grid search with a fixed gamma parameter is appropriate, depending on the computational resources available. Also, increasing the cost does not substantially improve the model further; hence, the requisite computational resource for higher accuracy becomes less effective. The best hyperparameters based on the 5-fold cross-validation for the SVM were a cost value of 1000 and a gamma value of 1.
The confusion matrix is a performance evaluation metric for classification problems. The model’s performance on the test data set for different metrics is illustrated in Figure 5 and Figure 6. The number of true negatives is 136,426 locations, and true positives is 14,671. Therefore, the total number of correctly classified locations is 151,097. The number of false positives (or type I errors) is 1404 locations and false negatives (type II) 1135 locations. For a flood-modeling problem, we prioritize accurately predicting all flood locations; hence, false positives are not the priority. Also, the kappa score, average precision, and area under the ROC of the support vector machine are 91.11%, 85%, and 96%, respectively. From the performance measurements on the training data, average precision is the most robust measure for this highly imbalanced dataset [72]. The average precision estimates the model generalization capability better than other performance metrics [73].
Therefore, the support vector machine model has the best performance metrics scores. However, the model training time requirements mean a larger scale model will be very computationally expensive. Hence, a deep neural network was designed and trained to reduce model training time and provide high-performance metrics on the test dataset.

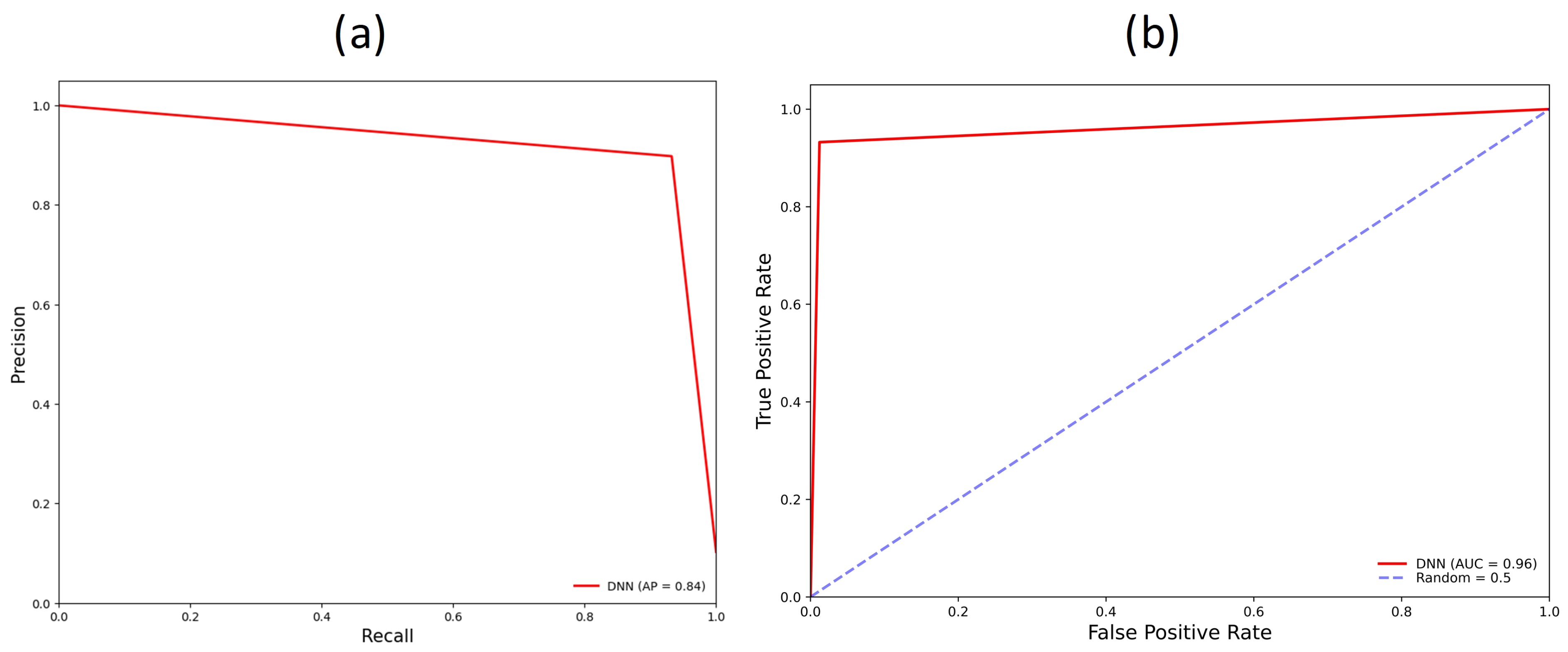
3.2. Deep Neural Network Models

The hyperparameter tuning involved 5-fold cross-validation using GridSearchCV in scikit-learn. Figure 7 illustrates all the models’ training time and optimization of the hyperparameters, number of epochs, and batch size. Batch size refers to the number of training samples fed through the neural network at once. It is an important hyperparameter that determines the computational cost and the model’s generalization ability. Large batch sizes require larger memory locations and, in some instances, longer computational time, depending on the available computing resources for that task.
Inversely, Hartman and Kopič [74] noted that bigger training batches could efficiently compute costs. In TensorFlow, increasing batch size resulted in less overhead computing than small batches, which halved their computational costs. This observation is seen in Figure 7; however, efficiently using computational resources may produce less robust models. Indeed, the batch size of training samples plays a role in gradient descent [75]. Gradient descent measures the value of the descent to find the direction of a slope that is zero, up, or down [76].
The number of epochs during training refers to the number of cycles or complete passes through the training data. Hence, it relates to the cost function and the accuracy of the model in that the cost function measures the error over the entire dataset. Each cycle of training allows the model to fit better or reduce its cost function [77]. Generally, the higher the number of epochs, the greater the model’s accuracy, as seen in the learning curve of Figure 7e. The best hyperparameters obtained during training were the batch size of 100 samples and 100 epochs. The fit times of the support vector machine models are about ten times that of the deep neural network (DNN) training time without much improvement in accuracy from the cross-validation results. Hence, the DNN is favored for the large-scale model that will be developed for the entire rail corridor.
Figure 8 is the confusion matrix of the performance of the DNN model on the test data set. The model correctly classified 150,891 locations, 136,154, and 14,737 for true negatives and true positives, respectively. Type I errors are 1676, and type II errors are 1069 locations. The total number of misclassified locations is 2745 locations. The kappa value, average precision, and area under the ROC (Figure 9) of the DNN model are 90.48%, 84%, and 96%, respectively. Comparatively, the SVM shows better performance in average precision and kappa value. In addition, the type I errors are less in the SVM than in the DNN. However, for type II errors and the number of true positives, the DNN model performs better than the SVM. Considering the priority of detecting flood locations while efficiently using computational resources, the DNN model is selected as the best model.

4. Discussion

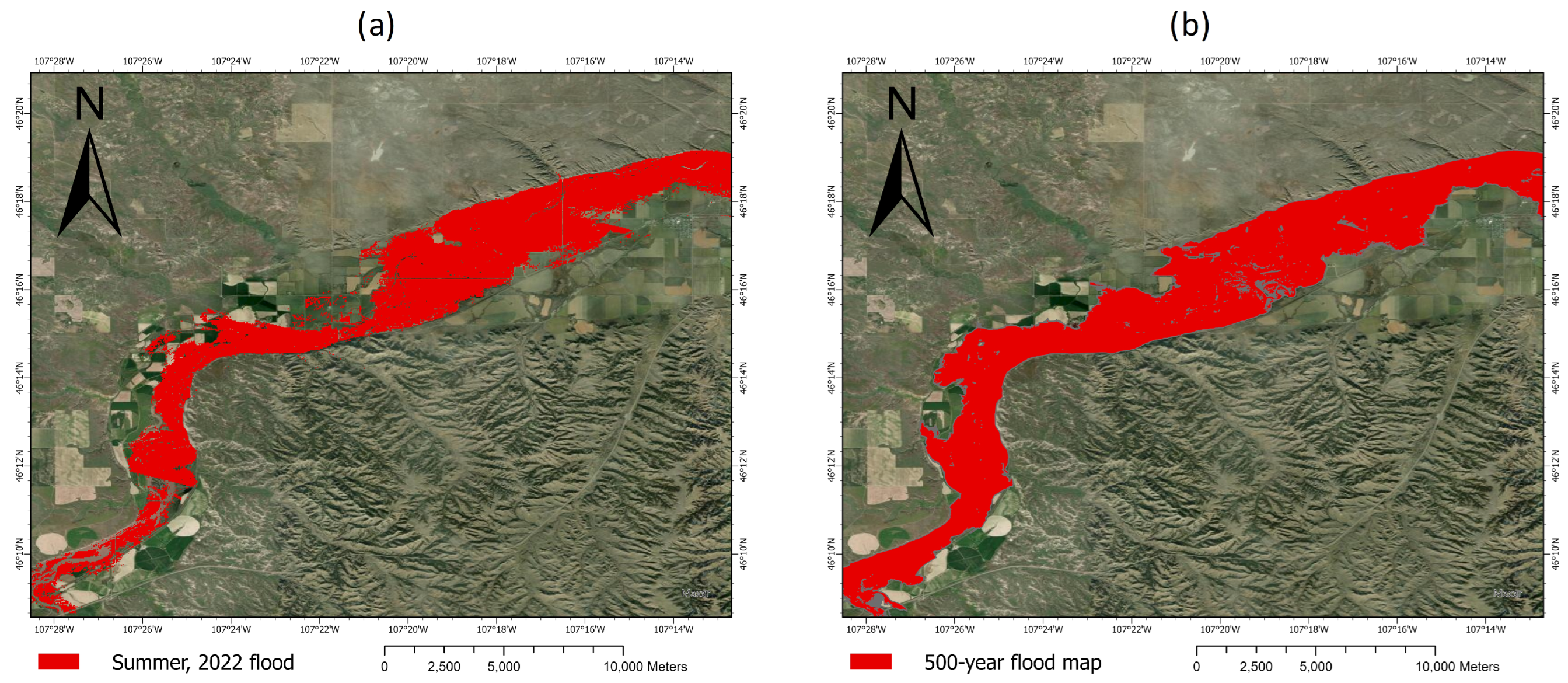
4.1. Model Validation

The DNN model was validated by predicting two flood events in 2022 and 2020. The summer flood in 2022 was for a 500-year return period, while the 2020 flood was on a smaller scale with rainfall depths equivalent to 50-year return period. Since there are no actual flood maps for these two events, the 500-year and 50-year return period maps help distinguish the model’s ability to predict floods beyond the GEE flood maps used in training. Hence, the model can predict floods for different rainfall depths [78] and changes in the other environmental datasets, as seen in the spatial comparison of the model predictions and the equivalent flood maps (Figure 10 and Figure 11) obtained for the corresponding flood return period. The potential limitation of using two flood events is the confidence in the model’s accuracy in predicting floods beyond the two storm events. Moreover, without a larger number of storm events, it is highly difficult to determine the model’s sensitivity to actual highly irregular storm events.

4.2. Statistical Methods

In addition, statistical tests were carried out to determine whether the differences are statistically significant [79] between the model predictions and the equivalent return periods flood maps generated using HEC-RAS. A statistical hypothesis is an assumption about the distribution of a random variable. In our study, the target, which is a flood or no-flood zone, is a random and ordinal variable. The prediction at each pixel or location are values from 0 to 1, with values closer to 1 indicating a high probability of flooding and values closer to 0 indicating lower chances of flooding; hence, a continuous distribution of predictions is obtained. Therefore, nonparametric statistical tests are done since the underlying distribution of the target is not normal.
The computed nonparametric tests are the Mann–Whitney U test, Spearman’s rank correlation, and Wilcoxon signed-rank test. Each test’s test statistic is determined, and the corresponding p-value was compared to the alpha value of 0.01 for a 99% confidence level. The Mann–Whitney tests a null hypothesis that the distribution of a randomly chosen observation from the HEC-RAS flood map is the same as the probability distribution for a randomly chosen observation from the DNN flood extent map against the alternative hypothesis that their probability distributions are different. The Spearman’s rank correlation coefficient, Rho, ρ measures the strength and nature between two variables [80]. The p-value for Spearman’s rank correlation tests the null hypothesis that the DNN flood extent map is linearly uncorrelated with the HEC-RAS flood extent map [81]. The Wilcoxon signed-rank test is used to test the null hypothesis that two related and matched pairs are from the same distribution [80,81,82].
From Table 4, the null hypothesis is rejected for all the tests since the p-values are lower than the significance level. Hence, for the Mann–Whitney U test, the difference between the predicted flood of 2022 and the 500-year flood map is highly significant. A similar observation is noted for the model’s prediction of the summer 2020 flood and the equivalent HEC-RAS flood map. For Spearman’s rank test, since the p-value for both validation maps is less than the significance level, each predicted flood extent map correlates with the corresponding HEC-RAS flood map. Moreover, in the case of the Wilcoxon signed-rank test, the null hypothesis is rejected. This signifies that comparing each flood extent map produced by the model with the HEC-RAS flood map, the distributions are not the same. Therefore, the nonparametric test statistics results indicate the model’s ability to predict different flood events extent using the environmental features including the rainfall forecast.

5. Conclusions

This paper discusses daily flood prediction mapping using DNN and SVM models. The study validates and practically demonstrates the feasibility of developing flood models for a particular infrastructure, such as railroads, in a given area of interest. In addition, highly accurate models can be created using remotely sensed data and traditional flood models. The paper also discusses the validation of the model by predicting two flood events in 2022 and 2020. Flood extent maps created from HEC-RAS for the 100-year return period and flood maps generated for different flood events using GEE are used as the target feature in each model. Environmental condition factors, including the daily rainfall accumulation, were used as features. Support vector machine models and deep neural networks were used in the initial training of the models. The DNN model was chosen and used as the final model for deployment because it has a relatively short training time without a massive loss in the model’s ability to predict floods and non-flooded areas accurately. Also, it produced fewer type II errors or false negatives, which is a priority for a flood prediction model. The model was subsequently used to predict two flood events in 2020 and 2022 to validate the model’s capacity to predict future events. The model can predict flood events accurately. Therefore, it will be deployed as part of a decision support system for railroad managers.
This model is limited to only the AOI since all the data used in its training were only for the AOI. In addition, the method’s accuracy depends on the quality of flood models used as the target feature. In conclusion, flood susceptibility can be mapped by combining remotely sensed data and traditional flood model layers. This model can provide daily flood predictions using daily rainfall accumulation estimates obtained from multi-satellite radar data. This study thus provides a method of using traditional flood models and remotely sensed flood susceptibility models in predicting daily flood extents.
Future research directions include aligning machine-learning flood models with traditional models using physics-based simulations. Moreover, further research must be done about the models’ robustness in a continuously changing climate and developing models for larger areas of interest, such as the entire railroad infrastructure in the United States.

Author Contributions

Conceptualization, T.O. and A.-R.Z.; methodology, A.-R.Z.; software, A.-R.Z.; validation, T.O. and P.L.; formal analysis, A.-R.Z.; investigation, P.L.; resources, T.O.; data curation, A.-R.Z.; writing—original draft preparation, A.-R.Z.; writing—review and editing, T.O. and P.L.; visualization, A.-R.Z.; supervision, P.L. and T.O.; project administration, T.O.; funding acquisition, T.O. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Federal Railroad Administration under contract No. 693JJ6-21-C-000004.

Data Availability Statement

The datasets presented in this article are not readily available because the data includes location information and sensitive data of our railroad partners. Requests to access the datasets should be directed to the corresponding author.

Acknowledgments

The authors would like to thank the Federal Railroad Administration (FRA), Michigan Tech Research Institute (MTRI), Loram Technologies, Inc., and BNSF for their assistance in this project.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Bell, L.; Bell, F.G. Geological Hazards: Their Assessment, Avoidance and Mitigation; CRC Press LLC: London, UK, 1999. [Google Scholar]
  2. USACE. Yellowstone River Corridor Study Hydraulic Analysis Modeling and Mapping Report; US Army Corps of Engineers, Omaha District: Omaha, NE, USA, 2016; p. 34.
  3. Fortin, J.P.; Turcotte, R.; Massicotte, S.; Moussa, R.; Fitzback, J.; Villeneuve, J.P. Distributed watershed model compatible with remote sensing and GIS data. I: Description of model. J. Hydrol. Eng. 2001, 6, 91–99. [Google Scholar] [CrossRef]
  4. Jayakrishnan, R.; Srinivasan, R.; Santhi, C.; Arnold, J.G. Advances in the application of the SWAT model for water resources management. Hydrol. Process. 2005, 19, 749–762. [Google Scholar] [CrossRef]
  5. Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Spatial prediction of flood susceptible areas using rule based decision tree (DT) and a novel ensemble bivariate and multivariate statistical models in GIS. J. Hydrol. 2013, 504, 69–79. [Google Scholar] [CrossRef]
  6. Tien Bui, D.; Pradhan, B.; Nampak, H.; Bui, Q.T.; Tran, Q.A.; Nguyen, Q.P. Hybrid artificial intelligence approach based on neural fuzzy inference model and metaheuristic optimization for flood susceptibilitgy modeling in a high-frequency tropical cyclone area using GIS. J. Hydrol. 2016, 540, 317–330. [Google Scholar] [CrossRef]
  7. Jodar-Abellan, A.; Valdes-Abellan, J.; Pla, C.; Gomariz-Castillo, F. Impact of land use changes on flash flood prediction using a sub-daily SWAT model in five Mediterranean ungauged watersheds (SE Spain). Sci. Total Environ. 2019, 657, 1578–1591. [Google Scholar] [CrossRef] [PubMed]
  8. Kastridis, A.; Stathis, D. Evaluation of hydrological and hydraulic models applied in typical Mediterranean Ungauged watersheds using post-flash-flood measurements. Hydrology 2020, 7, 12. [Google Scholar] [CrossRef]
  9. Lee Myers, B. The Flood Disaster Protection Act of 1973. Am. Bus. Law J. 1976, 13, 315–334. [Google Scholar] [CrossRef]
  10. Kazakis, N.; Kougias, I.; Patsialis, T. Assessment of flood hazard areas at a regional scale using an index-based approach and Analytical Hierarchy Process: Application in Rhodope–Evros region, Greece. Sci. Total Environ. 2015, 538, 555–563. [Google Scholar] [CrossRef]
  11. Lee, M.J.; Kang, J.E.; Jeon, S. Application of frequency ratio model and validation for predictive flooded area susceptibility mapping using GIS. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 895–898. [Google Scholar] [CrossRef]
  12. Benediktsson, J.A.; Swain, P.H.; Ersoy, O.K. Neural Network Approaches Versus Statistical Methods in Classification of Multisource Remote Sensing Data. IEEE Trans. Geosci. Remote Sens. 1990, 28, 540–552. [Google Scholar] [CrossRef]
  13. Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Flood susceptibility analysis and its verification using a novel ensemble support vector machine and frequency ratio method. Stoch. Environ. Res. Risk Assess. 2015, 29, 1149–1165. [Google Scholar] [CrossRef]
  14. Tehrany, M.S.; Pradhan, B.; Mansor, S.; Ahmad, N. Flood susceptibility assessment using GIS-based support vector machine model with different kernel types. CATENA 2015, 125, 91–101. [Google Scholar] [CrossRef]
  15. Bui, D.T.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Application of support vector machines in landslide susceptibility assessment for the Hoa Binh province (Vietnam) with kernel functions analysis. In Proceedings of the iEMSs 2012-Managing Resources of a Limited Planet, 6th Biennial Meeting of the International Environmental Modelling and Software Society, Leipzig, Germany, 1–5 July 2012; pp. 382–389. [Google Scholar]
  16. Kia, M.B.; Pirasteh, S.; Pradhan, B.; Mahmud, A.R.; Sulaiman, W.N.A.; Moradi, A. An artificial neural network model for flood simulation using GIS: Johor River Basin, Malaysia. Environ. Earth Sci. 2012, 67, 251–264. [Google Scholar] [CrossRef]
  17. Konadu, D.; Fosu, C. Digital elevation models and GIS for watershed modelling and flood prediction–a case study of Accra Ghana. In Appropriate Technologies for Environmental Protection in the Developing World; Springer: Dordrecht, The Netherlands, 2009; pp. 325–332. [Google Scholar] [CrossRef]
  18. DeVries, B.; Huang, C.; Armston, J.; Huang, W.; Jones, J.W.; Lang, M.W. Rapid and robust monitoring of flood events using Sentinel-1 and Landsat data on the Google Earth Engine. Remote Sens. Environ. 2020, 240, 111664. [Google Scholar] [CrossRef]
  19. Vishnu, C.; Sajinkumar, K.; Oommen, T.; Coffman, R.; Thrivikramji, K.; Rani, V.; Keerthy, S. Satellite-based assessment of the August 2018 flood in parts of Kerala, India. Geomat. Nat. Hazards Risk 2019, 10, 758–767. [Google Scholar] [CrossRef]
  20. Patro, S.; Chatterjee, C.; Mohanty, S.; Singh, R.; Raghuwanshi, N.S. Flood inundation modeling using MIKE FLOOD and remote sensing data. J. Indian Soc. Remote Sens. 2009, 37, 107–118. [Google Scholar] [CrossRef]
  21. Ouaba, M.; Saidi, M.E.; Alam, M.J.B. Flood modeling through remote sensing datasets such as LPRM soil moisture and GPM-IMERG precipitation: A case study of ungauged basins across Morocco. Earth Sci. Inform. 2023, 16, 653–674. [Google Scholar] [CrossRef]
  22. El Alfy, M. Assessing the impact of arid area urbanization on flash floods using GIS, remote sensing, and HEC-HMS rainfall-runoff modeling. Hydrol. Res. 2016, 47, 1142–1160. [Google Scholar] [CrossRef]
  23. Khan, S.I.; Yang, H.; Wang, J.; Yilmaz, K.K.; Gourley, J.J.; Adler, R.F.; Brakenridge, G.R.; Policelli, F.; Habib, S.; Irwin, D. Satellite Remote Sensing and Hydrologic Modeling for Flood Inundation Mapping in Lake Victoria Basin: Implications for Hydrologic Prediction in Ungauged Basins. IEEE Trans. Geosci. Remote Sens. 2011, 49, 85–95. [Google Scholar] [CrossRef]
  24. Kourgialas, N.N.; Karatzas, G.P. Flood management and a GIS modelling method to assess flood-hazard areas—A case study. Hydrol. Sci. J. 2011, 56, 212–225. [Google Scholar] [CrossRef]
  25. Liu, Y.B.; Gebremeskel, S.; De Smedt, F.; Hoffmann, L.; Pfister, L. A diffusive transport approach for flow routing in GIS-based flood modeling. J. Hydrol. 2003, 283, 91–106. [Google Scholar] [CrossRef]
  26. Mason, L.A. GIS Modeling of Riparian Zones Utilizing Digital Elevation Models and Flood Height Data. Master’s Thesis, Michigan Technological University, Houghton, MI, USA, 2007. [Google Scholar]
  27. Schanze, J.; Zeman, E.; Marsalek, J. Flood Risk Management: Hazards, Vulnerability and Mitigation Measures, 1st. ed.; Nato Science Series: IV; Earth and Environmental Sciences, 67; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar] [CrossRef]
  28. Tymkow, P.; Karpina, M.; Borkowski, A. 3D GIS for flood modelling in river valleys. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B8, 175–178. [Google Scholar] [CrossRef]
  29. Ighile, E.H.; Shirakawa, H.; Tanikawa, H. Application of GIS and Machine Learning to Predict Flood Areas in Nigeria. Sustainability 2022, 14, 5039. [Google Scholar] [CrossRef]
  30. Motta, M.; de Castro Neto, M.; Sarmento, P. A mixed approach for urban flood prediction using Machine Learning and GIS. Int. J. Disaster Risk Reduct. 2021, 56, 102154. [Google Scholar] [CrossRef]
  31. Sresakoolchai, J.; Hamarat, M.; Kaewunruen, S. Automated machine learning recognition to diagnose flood resilience of railway switches and crossings. Sci. Rep. 2023, 13, 2106. [Google Scholar] [CrossRef] [PubMed]
  32. Elkhrachy, I. Flash Flood Water Depth Estimation Using SAR Images, Digital Elevation Models, and Machine Learning Algorithms. Remote Sens. 2022, 14, 440. [Google Scholar] [CrossRef]
  33. Zelt, R.B. Environmental Setting of the Yellowstone River Basin, Montana, North Dakota, and Wyoming; US Department of the Interior, US Geological Survey: Denver, CO, USA, 1999; Volume 98.
  34. Chase, K.J. Streamflow Statistics for Unregulated and Regulated Conditions for Selected Locations on the Yellowstone, Tongue, and Powder Rivers, Montana, 1928–2002; US Geological Survey: Reston, VA, USA, 2014.
  35. Papangelakis, E.; MacVicar, B.; Ashmore, P.; Gingerich, D.; Bright, C. Testing a Watershed-Scale Stream Power Index Tool for Erosion Risk Assessment in an Urban River. J. Sustain. Water Built Environ. 2022, 8, 04022008. [Google Scholar] [CrossRef]
  36. Micu, D.; Urdea, P. Vulnerable areas, the stream power index and the soil characteristics on the southern slope of the lipovei hills. Carpathian J. Earth Environ. Sci. 2022, 17, 207–218. [Google Scholar] [CrossRef]
  37. Cobin, P.F. Probablistic Modeling of Rainfall Induced landslide Hazard Assessment in San Juan La Laguna, Sololá, Guatemala. Master’s Thesis, Michigan Technological University, Houghton, MI, USA, 2013. [Google Scholar]
  38. Hong, H.; Chen, W.; Xu, C.; Youssef, A.M.; Pradhan, B.; Tien Bui, D. Rainfall-induced landslide susceptibility assessment at the Chongren area (China) using frequency ratio, certainty factor, and index of entropy. Geocarto Int. 2017, 32, 139–154. [Google Scholar] [CrossRef]
  39. Sorensen, R.; Zinko, U.; Seibert, J. On the calculation of the topographic wetness index: Evaluation of different methods based on field observations. Hydrol. Earth Syst. Sci. 2006, 10, 101–112. [Google Scholar] [CrossRef]
  40. Andrews, D.A.; Lambert, G.S.; Stose, G.W. Geologic Map of Montana; Report 25; U.S. Geological Survey: Denver, CO, USA, 1944. [CrossRef]
  41. Jain, V.; Sinha, R. Geomorphological Manifestations of the Flood Hazard: A Remote Sensing Based Approach. Geocarto Int. 2003, 18, 51–60. [Google Scholar] [CrossRef]
  42. Pettorelli, N.; Ryan, S.; Mueller, T.; Bunnefeld, N.; Jędrzejewska, B.; Lima, M.; Kausrud, K. The Normalized Difference Vegetation Index (NDVI): Unforeseen successes in animal ecology. Clim. Res. 2011, 46, 15–27. [Google Scholar] [CrossRef]
  43. Chander, G.; Markham, B.L.; Helder, D.L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Environ. 2009, 113, 893–903. [Google Scholar] [CrossRef]
  44. Huffman, G.; Stocker, E.; Bolvin, D.; Nelkin, E.; Tan, J. GPM IMERG Late Precipitaion L3 1 Day 0.1 Degree x 0.1 Degree V06; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2019.
  45. UN-SPIDER. In Detail: Recommended Practice: Flood Mapping and Damage Assessment Using Sentinel-1 SAR Data in Google Earth Engine. Available online: https://un-spider.org/advisory-support/recommended-practices/recommended-practice-google-earth-engine-flood-mapping/in-detail (accessed on 13 October 2022).
  46. Kuhn, M.; Johnson, K. Applied Predictive Modeling, 1st ed.; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
  47. Zhou, Z.H. Machine Learning; Springer: Gateway East, Singapore, 2021. [Google Scholar]
  48. Vapnik, V.N. Statistical Learning Theory; Adaptive and Learning Systems for Signal Processing, Communications, and Control; Wiley: New York, NY, USA, 1998. [Google Scholar]
  49. James, G. An Introduction to Statistical Learning: With Applications in R, 2nd ed.; Springer Texts in Statistics; Springer: New York, NY, USA, 2021. [Google Scholar]
  50. Lam, H.K.; Nguyen, H.T.; Ling, S.S.H. Computational Intelligence and Its Applications Evolutionary Computation, Fuzzy Logic, Neural Network and Support Vector Machine Techniques; Imperial College Press: London, UK, 2012. [Google Scholar]
  51. Haykin, S.S. Neural Networks: A Comprehensive Foundation, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
  52. Werbos, P. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Ph.D. Thesis, Committee on Applied Mathematics, Harvard University, Cambridge, MA, USA, 1974. [Google Scholar]
  53. Werbos, P.J. The Roots of Backpropagation: From Ordered Derivatives to Neural Networks and Political Forecasting; John Wiley & Sons: New York, NY, USA, 1994; Volume 1. [Google Scholar]
  54. Engelbrecht, A.P. Computational Intelligence: An Introduction, 2nd ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2007. [Google Scholar] [CrossRef]
  55. Keller, J.M.; Liu, D.; Fogel, D.B. Fundamentals of Computational Intelligence: Neural Networks, Fuzzy Systems, and Evolutionary Computation, 1st ed.; IEEE Press Series on Computational Intelligence; Wiley: Newark, NY, USA, 2016. [Google Scholar] [CrossRef]
  56. Bhamare, D.; Suryawanshi, P. Review on reliable pattern recognition with machine learning techniques. Fuzzy Inf. Eng. 2018, 10, 362–377. [Google Scholar] [CrossRef]
  57. Liu, X.; Deng, Z.; Yang, Y. Recent progress in semantic image segmentation. Artif. Intell. Rev. 2019, 52, 1089–1106. [Google Scholar] [CrossRef]
  58. Jiang, H.; Peng, M.; Zhong, Y.; Xie, H.; Hao, Z.; Lin, J.; Ma, X.; Hu, X. A survey on deep learning-based change detection from high-resolution remote sensing images. Remote Sens. 2022, 14, 1552. [Google Scholar] [CrossRef]
  59. Qiu, M.; Qiu, H. Review on image processing based adversarial example defenses in computer vision. In Proceedings of the 2020 IEEE 6th Intl Conference on Big Data Security on Cloud (BigDataSecurity), IEEE Intl Conference on High Performance and Smart Computing, (HPSC) and IEEE Intl Conference on Intelligent Data and Security (IDS), Baltimore, MD, USA, 25–27 May 2020; IEEE: Piscatway, NJ, USA, 2020; pp. 94–99. [Google Scholar]
  60. Pierson, H.A.; Gashler, M.S. Deep learning in robotics: A review of recent research. Adv. Robot. 2017, 31, 821–835. [Google Scholar] [CrossRef]
  61. Wang, D.; Wang, X.; Lv, S. An overview of end-to-end automatic speech recognition. Symmetry 2019, 11, 1018. [Google Scholar] [CrossRef]
  62. Göçeri, E. Impact of deep learning and smartphone technologies in dermatology: Automated diagnosis. In Proceedings of the 2020 Tenth International Conference on Image Processing Theory, Tools and Applications (IPTA), Paris, France, 9–12 November 2020; IEEE: Piscatway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
  63. Oommen, T.; Baise, L.G.; Vogel, R. Validation and application of empirical liquefaction models. J. Geotech. Geoenviron. Eng. 2010, 136, 1618–1633. [Google Scholar] [CrossRef]
  64. Rajaneesh, A.; Vishnu, C.; Oommen, T.; Rajesh, V.; Sajinkumar, K. Machine learning as a tool to classify extra-terrestrial landslides: A dossier from Valles Marineris, Mars. Icarus 2022, 376, 114886. [Google Scholar] [CrossRef]
  65. Krzanowski, W.J.; Hand, D.J. ROC Curves for Continuous Data, 1st ed.; Monographs on Statistics and Applied Probability; 111; Chapman & Hall/CRC: Boca Raton, FL, USA, 2009. [Google Scholar] [CrossRef]
  66. Cohen, J. A Coefficient of Agreement for Nominal Scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
  67. Ozenne, B.; Subtil, F.; Maucort-Boulch, D. The precision–recall curve overcame the optimism of the receiver operating characteristic curve in rare diseases. J. Clin. Epidemiol. 2015, 68, 855–859. [Google Scholar] [CrossRef] [PubMed]
  68. Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
  69. Boyd, K.; Eng, K.H.; Page, C.D. Area under the Precision-Recall Curve: Point Estimates and Confidence Intervals; Springer, Machine Learning and Knowledge Discovery in Databases: Berlin/Heidelberg, Germany, 2013; pp. 451–466. [Google Scholar]
  70. Bamber, D. The area above the ordinal dominance graph and the area below the receiver operating characteristic graph. J. Math. Psychol. 1975, 12, 387–415. [Google Scholar] [CrossRef]
  71. Schütze, H.; Manning, C.D.; Raghavan, P. Introduction to Information Retrieval; Cambridge University Press Cambridge: Cambridge, UK, 2008; Volume 39. [Google Scholar]
  72. Tharwat, A. Classification assessment methods. Appl. Comput. Inform. 2021, 17, 168–192. [Google Scholar] [CrossRef]
  73. Berrar, D. On the noise resilience of ranking measures. In Proceedings of the Neural Information Processing: 23rd International Conference, ICONIP 2016, Kyoto, Japan, 16–21 October 2016; Proceedings, Part II 23; Springer: Berlin/Heidelberg, Germany, 2016; pp. 47–55. [Google Scholar]
  74. Hartman, J.; Kopič, D. Scaling TensorFlow to 300 million predictions per second. In Proceedings of the 15th ACM Conference on Recommender Systems, Amsterdam, The Netherlands, 27 September–1 October 2021; pp. 595–597. [Google Scholar]
  75. Dokuz, Y.; Tufekci, Z. Mini-batch sample selection strategies for deep learning based speech recognition. Appl. Acoust. 2021, 171, 107573. [Google Scholar] [CrossRef]
  76. Denis, R. Artificial Intelligence by Example: Acquire Advanced AI, Machine Learning, and Deep Learning Design Skills, 2nd ed.; Packt Publishing: Birmingham, UK, 2020. [Google Scholar]
  77. Hu, J.; Feng, X.; Zheng, Y. Number of Epochs of Each Model and Hyperband’s Classification Performance. In Proceedings of the 2021 2nd International Seminar on Artificial Intelligence, Networking and Information Technology (AINIT), Shanghai, China, 15–17 October 2021; IEEE: Piscatway, NJ, USA, 2021; pp. 500–503. [Google Scholar]
  78. Huffman, G.; Stocker, E.; Bolvin, D.; Nelkin, E.; Tan, J. GPM IMERG Early Precipitation L3 1 Day 0.1 Degree x 0.1 Degree V06; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2019.
  79. Kreyszig, E.; Kreyszig, H.; Norminton, E.J. Advanced Engineering Mathematics, 10th ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
  80. Beatty, W. Decision Support Using Nonparametric Statistics, 1st ed.; SpringerBriefs in Statistics; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
  81. Kokoska, S.; Zwillinger, D. CRC Standard Probability and Statistics Tables and Formulae; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
  82. Conover, W.J. Practical Nonparametric Statistics; John Wiley & Sons: New York, NY, USA, 1971; pp. 97–104. [Google Scholar]
Remotesensing 16 02332 g001
Figure 1. Data preparation and preprocessing flow diagram used in producing feature datasets and target.
Figure 1. Data preparation and preprocessing flow diagram used in producing feature datasets and target.
Remotesensing 16 02332 g001
Remotesensing 16 02332 g002
Figure 2. Correlation between model features.
Figure 2. Correlation between model features.
Remotesensing 16 02332 g002
Remotesensing 16 02332 g003
Figure 3. Workflow of machine learning used in this study.
Figure 3. Workflow of machine learning used in this study.
Remotesensing 16 02332 g003
Remotesensing 16 02332 g004
Figure 4. Hyperparameter tuning and model training times for SVM models using grid search with 5-fold cross-validation. (a) Gamma variation with training time, (b) The average testing data accuracy against the model training time (c) Variation of cost with the time required for training the model (d) Ranges of average accuracy on test data changing with gamma used during training and (e) Ranges of mean accuracy increasing with cost using in training.
Figure 4. Hyperparameter tuning and model training times for SVM models using grid search with 5-fold cross-validation. (a) Gamma variation with training time, (b) The average testing data accuracy against the model training time (c) Variation of cost with the time required for training the model (d) Ranges of average accuracy on test data changing with gamma used during training and (e) Ranges of mean accuracy increasing with cost using in training.
Remotesensing 16 02332 g004
Remotesensing 16 02332 g005
Figure 5. Confusion matrix for support vector machine model.
Figure 5. Confusion matrix for support vector machine model.
Remotesensing 16 02332 g005
Remotesensing 16 02332 g006
Figure 6. (a) Precision-recall curve metric used in determining the average precision of the best support vector machine model, (b) receiver operator characteristics (ROC) curve plot and the area under the curve (AUC) obtained after evaluation of the SVM model.
Figure 6. (a) Precision-recall curve metric used in determining the average precision of the best support vector machine model, (b) receiver operator characteristics (ROC) curve plot and the area under the curve (AUC) obtained after evaluation of the SVM model.
Remotesensing 16 02332 g006
Remotesensing 16 02332 g007
Figure 7. Hyperparameter tuning and model training times for DNN models using 5-fold cross-validation with grid search. (a) Training data batch size variation with training time, (b) The average testing data accuracy against the model training time (c) Variation of the number of epochs with the time required for training the model (d) Ranges of average accuracy on test data changing with the batch size used during training and (e) Ranges of mean accuracy increase with the number of cycles used in training.
Figure 7. Hyperparameter tuning and model training times for DNN models using 5-fold cross-validation with grid search. (a) Training data batch size variation with training time, (b) The average testing data accuracy against the model training time (c) Variation of the number of epochs with the time required for training the model (d) Ranges of average accuracy on test data changing with the batch size used during training and (e) Ranges of mean accuracy increase with the number of cycles used in training.
Remotesensing 16 02332 g007
Remotesensing 16 02332 g008
Figure 8. Confusion matrix for deep neural network model.
Figure 8. Confusion matrix for deep neural network model.
Remotesensing 16 02332 g008
Remotesensing 16 02332 g009
Figure 9. (a) Precision-recall curve obtained from test dataset (b) Receiver operator characteristics (ROC) curve plot and the area under the curve (AUC) obtained after evaluation of the DNN model.
Figure 9. (a) Precision-recall curve obtained from test dataset (b) Receiver operator characteristics (ROC) curve plot and the area under the curve (AUC) obtained after evaluation of the DNN model.
Remotesensing 16 02332 g009
Remotesensing 16 02332 g010
Figure 10. (a) DNN model prediction of Summer 2022 floods using daily accumulated early precipitation rainfall forecast (b) HEC-RAS flood extent map for the 500-year return period of the study area.
Figure 10. (a) DNN model prediction of Summer 2022 floods using daily accumulated early precipitation rainfall forecast (b) HEC-RAS flood extent map for the 500-year return period of the study area.
Remotesensing 16 02332 g010
Remotesensing 16 02332 g011
Figure 11. (a) Flood prediction for Summer 2020 flood using the rainfall forecasts of the day of the flood (b) HEC-RAS flood map for the 50-year event.
Figure 11. (a) Flood prediction for Summer 2020 flood using the rainfall forecasts of the day of the flood (b) HEC-RAS flood map for the 50-year event.
Remotesensing 16 02332 g011
Table 1. Environmental factors used in producing model features.
Table 1. Environmental factors used in producing model features.
DatasetSourceData TypeResolution (m)
ElevationUSGSRaster30
GeologyUSGSVectorVariable
Normalized Difference Vegetation IndexComputed using GEE with Landsat 8 imageRaster30
Normalized Difference Water IndexComputed using ArcGIS Pro using Landsat 8 imageRaster30
SlopeComputed using ArcGIS Pro using digital elevation modelRaster30
Stream power indexComputed using ArcGIS Pro using digital elevation modelRaster30
Topographic wetness indexComputed using ArcGIS Pro using digital elevation modelRaster30
Land coverMulti-Resolution Land Characteristics ConsortiumRaster30
Flood zonesHEC-RAS and GEE flood analysisVector30
RainfallMulti-satellite precipitation data downloaded from Earthdata NASAHDF510,000
Table 2. Flood dates along the Yellowstone River Corridor.
Table 2. Flood dates along the Yellowstone River Corridor.
Flood Dates
3/16/20035/23/20117/2/20113/10/20146/7/20176/8/2017
3/23/20185/28/20185/29/20185/30/20186/8/20196/9/2019
6/10/20196/2/20206/3/20206/4/20206/15/2022
Table 3. SAR images dates and the thresholds used in creating flood maps in GEE.
Table 3. SAR images dates and the thresholds used in creating flood maps in GEE.
Before Flood SAR ImageAfter Flood Image SAR ImageDifference Threshold
Start DateEnd DateStart DateEnd Date
06/02/201706/06/201706/07/201706/09/20171.15
05/24/201805/26/201805/29/201806/01/02181.00
06/05/201906/07/201906/08/201906/11/20191.05
Table 4. Nonparametric test statistics of model predictions with two equivalent return period flood maps obtained using HEC-RAS.
Table 4. Nonparametric test statistics of model predictions with two equivalent return period flood maps obtained using HEC-RAS.
Test Statistic
Validation Map PairResultsMann–Whitney U TestSpearman’s RankWilcoxon Signed-Rank TestConclusion
Summer 2022 flood & 500-year flood mapsp-value000Reject H 0
statistics 1.20 × 10 11 0.8 2.30 × 10 7
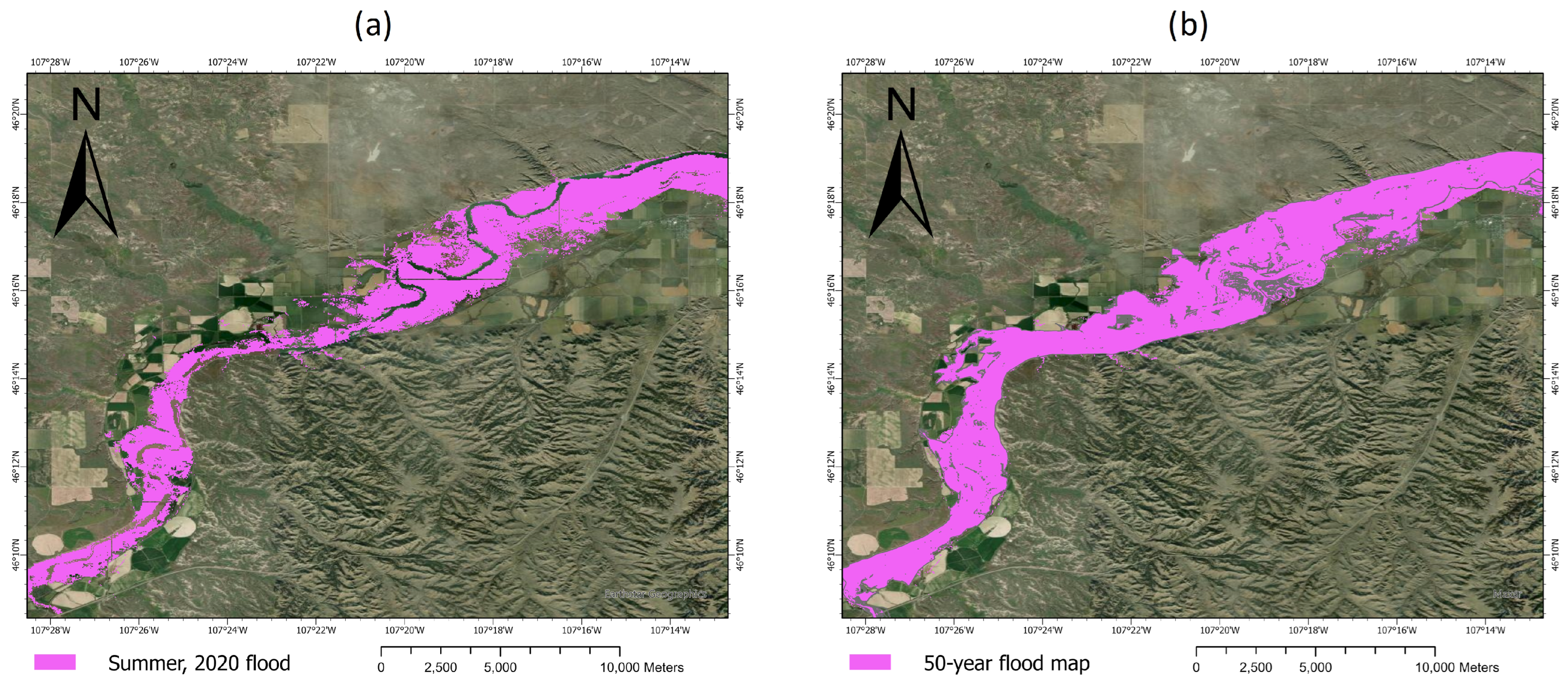
Summer 2020 flood & 50-year flood mapsp-value000Reject H 0
statistics 9.15 × 10 10 0.69 8.00 × 10 7
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zakaria, A.-R.; Oommen, T.; Lautala, P. Automated Flood Prediction along Railway Tracks Using Remotely Sensed Data and Traditional Flood Models. Remote Sens. 2024, 16, 2332. https://doi.org/10.3390/rs16132332

AMA Style

Zakaria A-R, Oommen T, Lautala P. Automated Flood Prediction along Railway Tracks Using Remotely Sensed Data and Traditional Flood Models. Remote Sensing. 2024; 16(13):2332. https://doi.org/10.3390/rs16132332

Chicago/Turabian Style

Zakaria, Abdul-Rashid, Thomas Oommen, and Pasi Lautala. 2024. "Automated Flood Prediction along Railway Tracks Using Remotely Sensed Data and Traditional Flood Models" Remote Sensing 16, no. 13: 2332. https://doi.org/10.3390/rs16132332

APA Style

Zakaria, A. -R., Oommen, T., & Lautala, P. (2024). Automated Flood Prediction along Railway Tracks Using Remotely Sensed Data and Traditional Flood Models. Remote Sensing, 16(13), 2332. https://doi.org/10.3390/rs16132332

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop