Abstract
The Pacific Decadal Oscillation (PDO), the dominant pattern of sea surface temperature anomalies in the North Pacific basin, is an important low-frequency climate phenomenon. Leveraging data spanning from 1871 to 2010, we employed machine learning models to predict the PDO based on variations in several climatic indices: the Niño3.4, North Pacific index (NPI), sea surface height (SSH), and thermocline depth over the Kuroshio–Oyashio Extension (KOE) region (SSH_KOE and Ther_KOE), as well as the Arctic Oscillation (AO) and Atlantic Multi-decadal Oscillation (AMO). A comparative analysis of the temporal and spatial performance of six machine learning models was conducted, revealing that the Gated Recurrent Unit model demonstrated superior predictive capabilities compared to its counterparts, through the temporal and spatial analysis. To better understand the inner workings of the machine learning models, SHapley Additive exPlanations (SHAP) was adopted to present the drivers behind the model’s predictions and dynamics for modeling the PDO. Our findings indicated that the Niño3.4, North Pacific index, and SSH_KOE were the three most pivotal features in predicting the PDO. Furthermore, our analysis also revealed that the Niño3.4, AMO, and Ther_KOE indices were positively associated with the PDO, whereas the NPI, SSH_KOE, and AO indices exhibited negative correlations.
1. Introduction
The Pacific Decadal Oscillation (PDO) is a global atmosphere–ocean climate phenomenon with decadal periodicity centered over the mid-latitude Pacific basin. In the past few centuries, the amplitude of the PDO has shown irregular changes on interannual and interdecadal scales [1,2]. The PDO has positive (or warm) and negative (or cool) phases. During the positive phase, the west Pacific becomes cooler and parts of the eastern ocean warm, while the opposite pattern occurs during the negative phase. The PDO index is the leading principal component (PC1) of sea surface temperature (SST) anomalies in the North Pacific (poleward of 20°N) [1]. Many studies have examined the potential climate impacts of the PDO [3,4,5]. Understanding the driving mechanism of the PDO has been a very active research topic [6].
A set of retrospective predictions (or hindcasts) from the climate models have been applied to the seasonal-to-decadal prediction of the PDO. For example, Wen et al. [7] assessed the seasonal prediction skill of the PDO in the National Centers for Environmental Prediction (NCEP) Climate Forecast System. Choi and Son [8] utilized the CMIP5 and CMIP phase 6 (CMIP6) retrospective decadal predictions to revisit the PDO predictions. However, over the North Pacific Ocean, a low prediction skill for SST performance has been observed across multiple models [9,10]. The limited forecasting skill could potentially be attributed to the fact that the PDO is not a solitary physical mode, but rather a composite of multiple mechanisms [2].
In addition to climate models, numerous statistical models that solely rely on the data themselves have also been employed for PDO prediction. Schneider and Cornuelle [11] employed various forcings, including the Aleutian Low, El Niño–Southern Oscillation (ENSO), and anomalies in oceanic zonal advection within the Kuroshio–Oyashio Extension, to reconstruct the PDO using the first-order autoregressive (AR1) model. Park et al. [12] applied the relevant work to multiple models of CMIP3. Alexander et al. [13] utilized the Linear Inverse Model method to predict the PDO time series, achieving better predictive performance than the AR1 model. Huang and Wang [14] used an incremental approach to predict the PDO based on SST, sea surface height (SSH), sea level pressure, and sea ice concentration. However, the PDO indices used in these studies are yearly data with limited time spans.
In the last few years, machine learning (ML) has proven to be one of the most popular methods for analyzing oceanographic data [15,16,17,18]. Yu et al. [19] predicted the PDO index using Long Short-Term Memory (LSTM) method based on the same parameters as mentioned in Huang and Wang [14]. Qin et al. [20] used multiple ML methods to derive monthly forecasts of the PDO based on the monthly PDO index at multiple time scales. Qin et al. [21] proposed a deep spatio-temporal embedding network to improve the PDO prediction. It indicated that the machine learning is capable of extracting nonlinear features from vast amounts of data, enabling more accurate predictions.
These successful applications of machine learning cases would help us to gain a deeper understanding of PDO and its influencing factors using machine learning methods. We aim to analyze the impact of six important factors on PDO prediction based on ML models, including Artificial Neural Networks (ANNs), Support Vector Regression (SVR), eXtreme Gradient Boosting (XGBoost), convolutional neural networks (CNNs), Long Short-Term Memory (LSTM), and Gated Recurrent Unit (GRU) models. Four factors, Niño3.4, NPI, SSH_KOE, and Thermocline_KOE, were also used in Schneider and Cornuelle [11] and Park et al. [12]. The AO and AMO are the remaining two factors that have a significant impact on PDO [22,23]. In addition, a SHapley Additive exPlanations (SHAP) visualization tool was applied to interpret the ML model’s behavior, specifically highlighting the relative importance of each dependent variable in predicting PDO. As an approach of eXplainable AI (XAI), SHAP has the potential to reveal novel insights and can serve as a valuable complement to physical models.
2. Materials and Methodology
2.1. Data Description
The following data were used to obtain the climate indices: (1) sea surface temperature (SST) from the Extend Reconstructed Sea Surface Temperature (ERSST) v5 [24] for 1871–2010 on a 2° × 2° grid; (2) sea level pressure (SLP) from the National Oceanic and Atmospheric Administration–Cooperative Institute for Research in Environmental Sciences (NOAA–CIRES) [25] for 1871–2010 on a 1° × 1° grid; and (3) ocean temperature and sea surface height (SSH) from the Simple Ocean Data Assimilation (SODA) dataset [26] for 1871–2010 on a 0.5° × 0.5° grid. To remove the linear trend from the data, a linear model was fitted to all the data and then subtracted from the original data.
2.2. Feature Selection
The following seven indices were used for PDO prediction: PDO, Niño3.4, AO, AMO, AL, SSH_KOE, and Ther_KOE. The PDO was considered to be the dependent variable, while the other six indices were considered independent variables. All the data from 1871 to 2010 (140 years) were ultimately included. The summary of the datasets and definition of all the features are shown in Table 1.

Table 1.
Summary of the datasets and definition of the indices.
The temporal evolution of these indices from 1871 to 2010 is presented in Figure 1. To capture interannual to decadal trends, all indices were identified as deviations from the annual cycle and underwent detrending across the 140-year record. Additionally, a 6-month running mean was chosen for these indices, as the PDO’s transformation is believed to be influenced by ENSO-related interannual variability due to the intricate interplay between PDO transformation and climate systems [27].
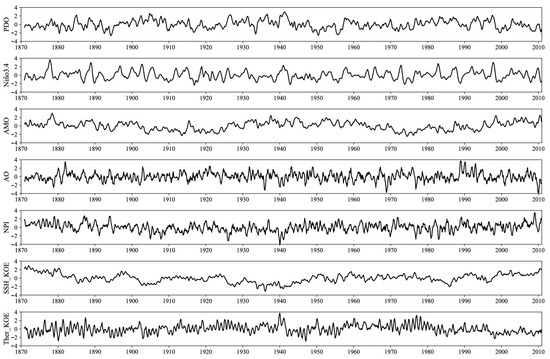
Figure 1.
Time series of monthly values of the PDO, Niño3.4, AMO, AO, NPI, SSH_KOE, and Ther_KOE indices from 1871 to 2010. All indices were smoothed by calculating the 6-month running mean and normalized by their standard deviation.
2.3. Model Algorithms
This study employed six distinct machine learning model algorithms: ANN, SVR, XGBoost, CNN, LSTM, and GRU.
An ANN is a mathematical or computational model that mimics the structure and function of biological neural networks [28]. It is composed of a large number of artificial neurons connected for computation. In most cases, artificial neural networks can change the internal structure based on external information and are adaptive systems.
SVR is among the most commonly used ML models associated with regression analysis [29]. It was developed upon the support vector machine for regression problems. As the name suggests, its algorithm supports both linear and nonlinear regressions. One of the advantages of SVR is that it consumes less computation time compared to other regression models.
XGBoost has been used for the effective implementation of the gradient boosting library for regression and classification in recent years [30]. Its algorithm is supported under the Gradient Boosting framework.
A CNN is an extended version of an ANN, which is specifically designed to process data with a similar grid structure [31]. It consists of four layers: input layer, convolutional layer, pooling layer, and fully connected layer.
The LSTM is a long short-term memory network, a special type of recurrent neural network (RNN) [32,33]. Compared to traditional RNNs, the LSTM is more suitable for processing and predicting important events with long intervals in time series.
The GRU is like the LSTM but lacks an output gate [33,34]. The GRU was proposed to simplify the LSTM. As such, it has only two gates, i.e., update and reset gates, instead of the three gates used in the LSTM. GRUs can alleviate vanishing (exploding) gradient problems through a gate mechanism, which are often found in traditional neural networks.
The calculation formulas for the GRU model are as follows:
where is the reset gate; is the update gate; is candidate activation; is activation; is the logistic sigmoid function; is element-wise multiplication; and are weight matrices; is the input sequence; and is the bias parameter.
The update gate determines whether the hidden state is to be updated with a new hidden state, namely the candidate activation. The value of ranges from 0 to 1. Assuming the value of is 0, the hidden state from the previous moment is forgotten. On the other hand, when the value of value is 1, all the previous information is taken in for updating. The reset gate decides whether the previous hidden state is ignored. The value of ranges from 0 to 1. Assuming the value of is 0, this means that it does not consider the past state and only focuses on the current state. The reset gate is not utilized in this case. Conversely, when the value of is 1, this indicates that the past state is not updated, and the current state remains the same as the past state. Therefore, the new output, namely the activation , is an interpolation between the previous activation multiplied by the reset gate and the candidate activation multiplied by the update gate.
Hyperparameter tuning is an important part of achieving good performance from an ML model, although it is very time-consuming. There is no fixed rule for hyperparameter tuning to ensure optimal performance with a given dataset. However, without correct hyperparameter tuning, the model will only obtain suboptimal results. We chose the grid search because it is one of the most basic, direct, and correct optimization methods. It generates all possible hyperparameter combinations through iteration to find the best combination that can obtain the best performance (such as minimizing the generalization error), but the calculation cost is relatively large.
2.4. Assessment Metrics
There is a multicollinearity problem in regression analysis that needs to be noted. Multicollinearity refers to a high linear correlation between the input independent variables. Multicollinearity is generally represented by variance inflation factor () and tolerance [35]. The for each independent variable is:
where is the R2 value obtained by regressing the independent variable on the remaining independent variables. The larger the value of the , the more obvious the collinearity problem. When , there is no multicollinearity; when , there is moderate multicollinearity; and when , there is high multicollinearity.
To evaluate the performance of the models, several statistical metrics were employed: correlation coefficient (R), mean absolute error (MAE), and root mean square error (RMSE).
Taylor diagrams are commonly used to graphically represent the two metrics (R and RMSE) with different ML models [36]. A Taylor diagram simultaneously presents the RMSE, the R, and the standard deviation in a visual manner. The higher the R and the lower the RMSE, the better the fit of the ML models to the reference data.
2.5. Shapley Additive Explanation (SHAP)
SHAP is an ideal XAI tool to interpret a complex ML model and make it more explainable by visualizing its output [37]. It visually shows the importance of each feature and how it impacts the predictions. Inspired by coalitional game theory [38], SHAP constructs an additive explanatory model where all features are considered as contributors. For each predicted sample, the model generates a predicted value, and the SHAP value is the numerical value assigned to each feature in the sample. This helps us understand the contribution of each feature to the model’s prediction. When all feature values are present, the simplified formula for the SHAP interpretation is:
where is an interpretable model that is a linear function of the binary variables, is the number of input variables, is the feature attribution for a feature (i.e., the SHAP value), and is a constant that is actually the predicted mean of all training samples (i.e., the base value).
2.6. Model Workflow
The workflow for the ML model’s prediction and explanation steps is illustrated in Figure 2. The implementation details of the workflow are as follows:
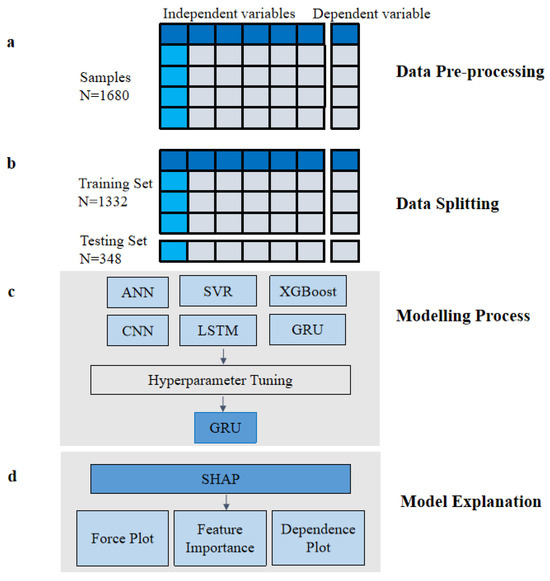
Figure 2.
Flow diagram of machine learning for the model prediction. (a) Data Pre-processing: Preparing the raw data for analysis by cleaning, transforming, and selecting relevant features; (b) Data Splitting: Splitting the dataset into training, and testing sets to ensure unbiased evaluation of the model; (c) Modelling Process: Applying the machine learning model to the data to build a predictive model; (d) Model Explanation: Providing insights into how and why the model makes its predictions using the SHAP analysis.
The first step was data pre-processing. All the independent and dependent variables were normalized using min-max standardization. In this study, the data used were a 140-year set of samples, ranging from January 1871 to December 2010, with a total of 1680 samples.
The second step was data splitting. The samples were split into two sections: the training and testing sets. The training set was from January 1871 to December 1981 (1332 samples). The test set was from January 1982 to December 2010 (348 samples). The ratio of the training and testing sets was approximately 79:21.
The third step was the modeling process. Six different ML algorithms were employed for model comparison. To achieve good performance, hyperparameter tuning was used in all the six models. Since the GRU model had the best performance, it was selected for the next process.
The fourth step was model explanation. SHAP was used for model explanation in three aspects: force plot, feature importance, and dependence plot.
In the ML, we used the following software: Python 3.9.12, Spyder 5.1.5, Notebook 6.4.11, Numpy 1.21.5, Scipy 1.7.3, Keras 2.8.0, Tensorflow 2.5.0, and SHAP 0.40.0. In addition, we used Matplotlib 3.4.3 and Seaborn 0.11.2 to plot the figures.
3. Results and Discussion
3.1. The Correlation and Multicollinearity Analysis of the Relevant Features
Building an optimal model requires training with relevant features. A correlation matrix is typically used to visualize the relationship strength between different variables [39]. A triangle correlation matrix of all input variables and output variables is presented in Figure 3a. The numerical values in the cells indicate the strength of the relationship between the variables on the horizontal and vertical axes, which is also represented by the color of the cell. For example, among the independent variables, the most significant correlation (0.35) was between the SSH_KOE index and the NPI. The relationships between the independent variables and dependent variable can also be seen in Figure 3a. Almost all regression coefficients yielded statistically significant results at a 95% confidence level, except for the correlations between PDO and AMO, SSH_KOE and Nino3.4, and AO and Ther_KOE, which exhibited p-values of 0.45, 0.90, and 0.59, respectively. As depicted in Figure 3a, the NPI has the highest correlation coefficient with the PDO (−0.54), followed by the Niño3.4, SSH_KOE, AO, Ther_KOE, and AMO indices.
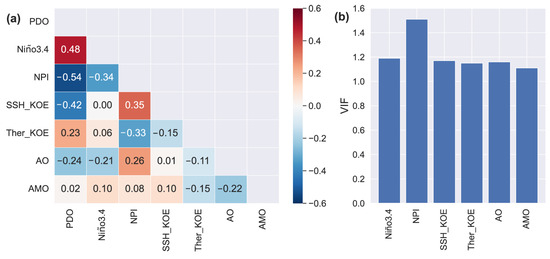
Figure 3.
(a) Correlation matrix among the indices, and (b) the values of dependent variables.
The multicollinearity problem can greatly reduce the stability and accuracy of the regression model, and excessive irrelevant dimension calculations can also be a waste of time. The results of the multicollinearity are shown in Figure 3b. The highest value is 1.51 for the NPI variable, and the values of the remaining dependent variables are almost around 1.15. The test reveals that all values are close to 1 and significantly below 5, indicating that the selected features exhibit good independence and are suitable for training the model to achieve accurate predictions.
3.2. Model Performance Comparison
3.2.1. PDO Time Series Analysis
From the training set, we tuned the hyperparameters of the ML model to minimize the difference between the testing set and actual data. The comparisons between the observed and predicted PDO indices from January 1982 to December 2010 are shown in Figure 4. In each panel, the observed and predicted time series are shown in the upper left, the errors (predicted values—observed values) series between them are presented in the lower left, and their scatter plots are also shown on the right. The black dashed line indicates the 1:1 reference line, and the red solid line indicates the linear interpolation of the predicted values. Upon comparing the peak and valley predictions, it is evident that the GRU model (Figure 4f) provides the most accurate predictions. Additionally, the GRU model exhibits lower errors compared to other models. The comparative results (i.e., R, MAE, and RMSE) for all models indicate that the GRU model tends to estimate the PDO index more accurately than other models, since it has the highest R (0.781) and lowest MAE (0.515) and RMSE (0.634).
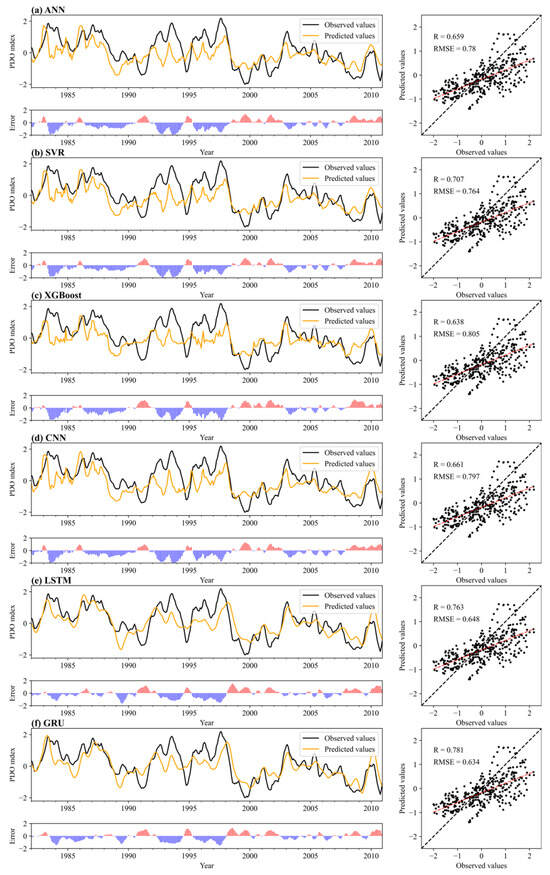
Figure 4.
The observed and predicted PDO indices in six ML models: (a) ANN, (b) SVR, (c) XGBoost, (d) CNN, (e) LSTM, and (f) GRU from January 1982 to December 2010. The error is represented as the difference between predicted values and observed values. Pink indicates positive errors, while purple represents negative errors.
The Taylor diagram is a reliable and useful evaluation tool for the simulation of skill [35]. It provides a graphical framework of the Pearson coefficient correlation, centered RMSE, and standard deviation. Before calculating these statistics, the simulated PDO index was normalized with respect to the corresponding standard deviation of the observation data, which was plotted at polar coordinates (1.0, 0.0). In the Taylor diagram of the six ML models (Figure 5), the ratio of the standard deviation between ML models and the observation is represented by the radial distance from the zero point, as shown by the dashed circles. Therefore, the distance between any point and a circle with a radius of 1 is the difference in the standard deviation between the model and the observation data. The angular axis implicates the coefficient correlation between the ML models and observation data, measured by the interceptions at the solid circle of the lines connecting the origin point (0,0) and each colored point. The ratio of the centered RMSE to the observed standard deviation is denoted by the corresponding distance from the reference (REF), as shown by the solid circles. The closer the colored point to the REF, the better the ML model performance.
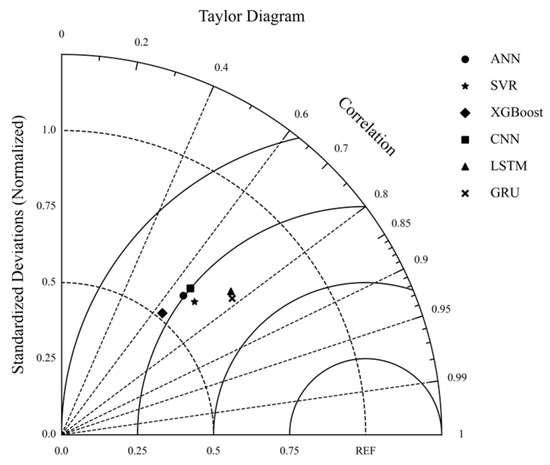
Figure 5.
Taylor diagram for the PDO index amplitude, the centered RMSE, and coefficient correlation between the model and observations. The REF point represents zero RMSE compared to the observations. The model standard deviations were normalized to the scale of the observation data. Different legend shapes represent the six different ML models.
As can be seen in Figure 5, the GRU model (cross point) is closest to the REF, which indicates that the GRU model outperformed other models. However, the standard deviations from these ML models were all less than those of the observations. The ratios between the standard deviations of the ANN, SVR, XGBoost, CNN, LSTM, and GRU models and the observations were 0.61, 0.62, 0.52, 0.64, 0.73, and 0.72, respectively. This underestimation of peak values is universal in other ML studies [40,41,42]. The characteristics and distribution of the ML training set should be taken into consideration. It is challenging to make accurate predictions beyond the range of the training set [43]. This can perhaps be attributed to the model architecture. The GRU model has an irreversible memorize–forget mechanism that determines whether to retain or discard the previous temporal memory [44]. Therefore, the peak values are probably underestimated if they are forgotten by the temporal memory. It can be seen that the GRU model point is the closest to the REF point.
3.2.2. Spatio-Temporal Analysis
Besides the time series analysis, the spatio-temporal structure for the SST anomaly (SSTA) prediction by the ML algorithms over the North Pacific (120°E–105°W, 20°N–60°N) is further examined. The predictors, training and test set splits, ML models, and hyperparameters employed in the previous PDO time series analysis have been consistently applied in this section. However, the predictand has been replaced with the SSTA of each grid point within this area, encompassing a total of 1156 pixels with non-missing (non-NaN) values. The correlation coefficient and RMSE between the observed and predicted the SSTA in six ML models from January 1982 to December 2010 are shown in Figure 6.
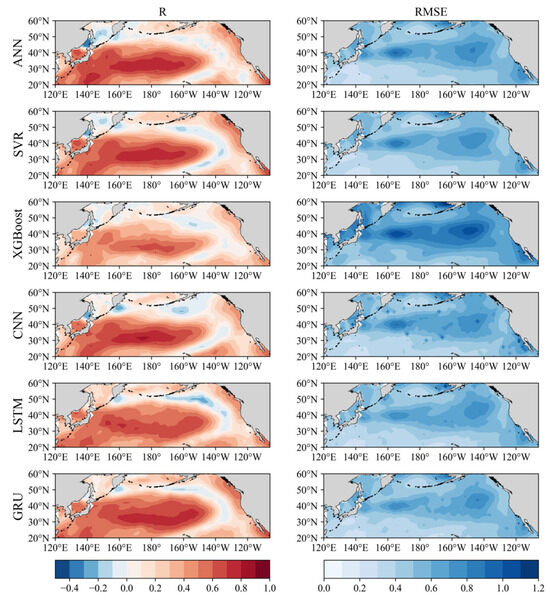
Figure 6.
The (left) correlation coefficient and (right) RMSE between the observed and predicted SSTAs in six ML models from January 1982 to December 2010.
The correlation coefficients of all ML models are almost the same, characterized by their horseshoe-shaped patterns (Figure 6, left). The positive values range from 20°N to 50°N and from 120°E to 140°W, forming a narrow band with low values (both positive and negative) surrounding it, while the remaining area comprises positive values. The high-value areas of the correlation coefficient are mainly concentrated at the latitudes 30°N to 40°N. This narrow band is located along the zero line within the PDO pattern. The regions characterized by smaller EOF values typically indicate a lesser contribution to the primary pattern, namely the PDO pattern. In such regions, predicting the SSTA may pose greater challenges, as minor changes can significantly amplify relative errors, leading to a weak or negative correlation between the predicted and observed values.
It can be seen that the range of positive high values reaches a maximum in the GRU model, and a minimum in the XGBoost model. There is a relatively large negative area in the northern part of the Sea of Japan in the ANN, SVR, XGBoost, and CNN models. The horseshoe pattern of the correlation coefficient was similarly observed in a study by Schneider and Cornuelle [11]. However, our GRU model outperforms their reported SSTA reconstruction skill in the central and eastern North Pacific, achieving values ranging from 0.6 to 0.9, whereas Schneider and Cornuelle [11] reported values within the range of 0.6 to 0.65. Indeed, when compared to the linear model AR1, the machine learning model exhibited superior capabilities in capturing the nonlinear signals of the PDO.
The corresponding RMSEs are also presented in the right part of Figure 6. The lower the RMSE, the better a ML model is able to fit the SSTA. It seems that the RMSE in the GRU model is the smallest among all six models. It is interesting that there is a broad band of large RMSE values surrounding the 40°N area. This is mainly due to the significant SSTA variability dominating in the central North Pacific, which is correspond to the leading EOF mode of the SSTA in the North Pacific (i.e., the PDO pattern).
It is easier to see the performance ability through the spatial mean of the absolute values of R and RMSE over the North Pacific for all ML models (Table 2). From the comparison results, the GRU model prefers to estimate the SSTA more accurately than other models, because it has the highest R (0.391) and lowest RMSE (0.499).

Table 2.
Summary of the spatial mean of R and RMSE over the North Pacific for all models.
Finally, the results of the temporal and spatial analysis revealed that the GRU model demonstrated superior accuracy compared to other models. PDO time series data and SSTAs in the North Pacific exhibit an inherent sequential nature, implying that the values at a particular time are contingent on previous values. In contrast to other models, LSTM and GRU, as variations of RNNs, are specifically designed to capture such sequential dependencies. They possess the ability to model long-term dependencies within the data. In comparison to LSTM, the GRU model has a simpler structure with a reduced number of parameters. This often leads to faster training and fewer challenges related to overfitting, making it a beneficial choice for PDO time series predictions. Given its superior performance, the GRU model was selected for further analysis.
3.3. Sequential Forward Selection
It is challenging to estimate in advance which combination of indicators will lead to favorable outcomes. However, the sequential forward selection analysis provides an important technique for feature selection [45]. It starts with an empty candidate set. At each step, it will select the optimal feature (i.e., the feature that contributes best to the model accuracy) out of all the features. Next, each of the remaining features is combined with the selected feature, and the best pair is selected. This process is repeated iteratively until all the features are selected. In this study, a total of six features were used for input into the ML algorithm. The sequential forward selection procession was repeated five times. The real challenge is to use the right combination of features that enables the model to achieve good performance.
The sequential forward selection analysis for the GRU model in terms of the correlation coefficient and RMSE are shown in Figure 7. In this plot, Niño3.4 was chosen as the initial feature, representing the single dependent variable that optimizes model accuracy. The best result with the fourth but very close to the first highest correlation and lowest RMSE was achieved when the Niño3.4, NPI, and SSH_KOE indices were combined. When adding the SSH_KOE, the model resulted in a correlation of 0.755 and an RMSE of 0.721. The addition of Ther_KOE, AO, and AMO to the previous subset leads to an increase in the correlation coefficient while also causing an increase in RMSE. Specifically, upon adding the AO index, the correlation reached its highest value (0.794), but the RMSE was the largest (0.774). When adding the AMO, the model yielded a correlation of 0.783 and an RMSE of 0.754.
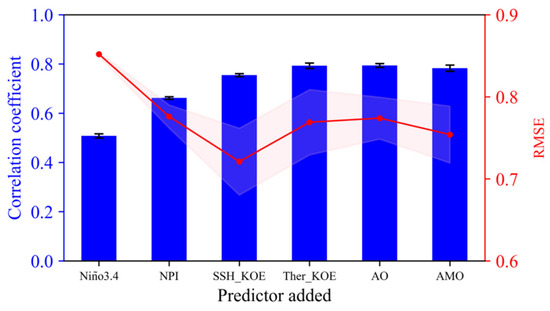
Figure 7.
Performing sequential forward selection analysis for the GRU model in terms of the correlation coefficient and RMSE as each predictor is added. Histograms and lines represent the correlation coefficient and RMSE, respectively. The error bars and pink shading indicate the standard deviation from the mean of 10 ensemble runs.
It is not a straightforward decision to determine whether to consider only the first three indices or the entire set six indices as predictors. The addition of predictors may enable the model to more precisely capture the relationship between the dependent variable and independent variables, leading to an increase in correlation. However, if there are interactions between the independent variables, and if this relationship is not accurately captured by the model, the inclusion of such predictors may result in an increase in RMSE. To comprehensively reflect the influence and relative importance of all six indices on PDO prediction, we have decided to adopt all six indices as predictors. This decision is in line with our reasoning for incorporating all six indices in the previous section’s model performance comparison, and it will further enable a more profound interpretability analysis in the subsequent section.
3.4. Interpretability Analysis
Based on the model performance evaluation, the GRU model achieved the best fitting effect. However, ML algorithms can cause the “black box” problem, which means we do not know exactly how they work [46]. It is necessary and interesting to study the inner workings of the model. For this purpose, we resorted to SHAP, a type of XAI technique that can be applied to address this challenge. In this section, we conducted a SHAP analysis to unlock the inner workings of the GRU model and gain a deeper understanding of its decision-making process. Based on the trained GRU model, SHAP values were calculated to explain the model’s prediction. They assigned an “effect” to each feature value, indicating how much it contributed to the model’s final output. The XAI capability in different formats includes local and global interpretability.
3.4.1. Local Interpretability Analysis
Local interpretability analysis provides the details of predictions, focusing on explaining how a single prediction is generated [47]. This analysis can help decision-makers trust the model and explain how various features affect the model’s single decision. The SHAP force plot serves as a powerful tool for visualizing and enhancing the interpretability of model predictions. Figure 8 shows the local interpretability results for the PDO predictions of specific samples, centering on the boreal winter season (December–January–February) in the years 1976/1977 and 1998/1999, as these periods signify a crucial turning point for both the ENSO and PDO. The PDO underwent a cool phase spanning from 1960 to 1976, subsequently transitioning into a warm phase. The warm PDO phase prevailed from 1977 to 1998, but it then shifted to a cool phase towards the end of 1998, lasting only four years. Concurrently, there was a La Niña event that occurred from 1975 to 1976, succeeded by a El Niño event in 1977–1978. Furthermore, 1997–1998 witnessed a powerful El Niño event, followed by a La Niña event in 1998–2000. In the plot, the prediction begins from a base value (), which is the mean of all predictions. Each SHAP value is visualized as an arrow, where red arrows signify positive values that elevate the prediction, and blue arrows indicate negative values that lower the prediction. The ultimate prediction is the sum of the base value and the SHAP values, denoted as f(x) in the graph.
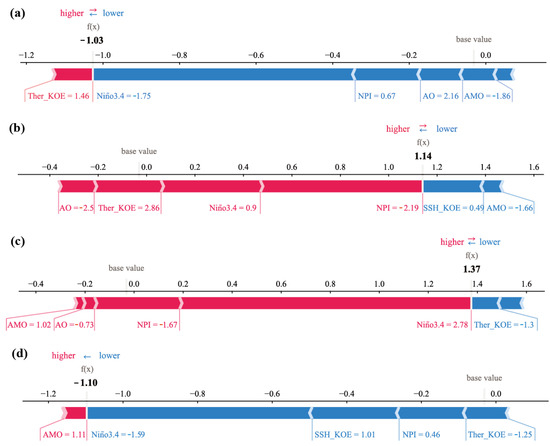
Figure 8.
SHAP force plot results for PDO prediction of samples for 1976/1977 and 1998/1999 regime shifts: (a) Winter, 1975; (b) Winter, 1976; (c) Winter, 1997; and (d) Winter, 1998.
Figure 8a,b display the SHAP force plot results for PDO prediction during the 1976/1977 regime shift. In the winter of 1975, the predicted value is −1.03, aligning closely with the observed value of −1.14. Notably, the Niño3.4 index contributes the most significantly in a negative manner, followed by the NPI and AO (Figure 8a). In the winter of 1976, the predicted value is 1.14, approximating the observed value of 1.36. The three most significant factors are NPI, Niño3.4, and SSH_KOE (with negative value) (Figure 8b). Figure 8c,d present the SHAP force plot results for PDO prediction during the 1997/1998 regime shift. In the winter of 1997, the predicted value of 1.37 closely matches the observed value of 1.54. The Niño3.4 index makes the most significant positive contribution to the predicted outcome, followed by the NPI and Ther_KOE (with a negative impact) (Figure 8c). Figure 8d depicts the same plot for the winter of 1998, revealing a predicted value of −1.1, almost identical to the observed value of −1.01. The three most significant factors are Niño3.4, SSH_KOE, and NPI, all exerting negative effects.
The results indicate that the Niño3.4 index had the greatest influence prior to the PDO regime shifts, emphasizing the pivotal role of ocean–atmosphere interactions and teleconnections in shaping the PDO. This suggests that the PDO is likely a consequence of, or closely related to, the ENSO phenomenon [48]. An El Niño (La Niña) event may trigger a shift of the PDO towards a positive (negative) phase once the vertically integrated ocean heat content down to the depth of a 20 °C isotherm attains a specific threshold. However, not all the ENSO events trigger a PDO transition. Other El Niño or La Niña events failed to induce a PDO transition due to the requisite time for heat content to build up in the off-equatorial western Pacific [49].
While the local interpretability analysis may not provide a direct physical mechanism explanation of the PDO regime shift, it offers valuable insights into the relative importance of various predictors. These insights can then be utilized to compare and validate the results obtained from models based on physical formulas.
3.4.2. Global Interpretability Analysis
The primary aim of global interpretability is to foster a comprehensive understanding of a model’s overall behavior. It comprises two components: SHAP feature importance and dependence plot.
- (1)
- SHAP feature importance
SHAP feature importance is a robust technique that presents which features are the most important to the prediction. Its concept is simple: features with large absolute Shapley values are important. The Shapely values represent the average marginal contribution of each feature in an ML model [47]. Features with high (low) Shapely values contribute more (less) to the target. The feature importance can be explained by two types of plots: a SHAP feature importance plot (Figure 9a) and a SHAP summary plot (Figure 9b). In a SHAP feature importance plot, the absolute Shapley values per feature across the data are averaged (), and the features are sorted by decreasing importance and plotted in a bar chart. A SHAP summary plot combines feature importance with feature effects. The SHAP summary plot is shown in the form of a set of beeswarm plots, including the feature importance and SHAP values distribution at the same time. Each row in the figure represents a feature, and the x-axis is the SHAP value. These features are also sorted from most important to less important. On the summary plot, each point represents a SHAP value () for a feature, while the color corresponds to the raw values of the features for each point. A dot represents a sample. The red color indicates features that were pushing the prediction higher, and the blue color indicates the opposite.
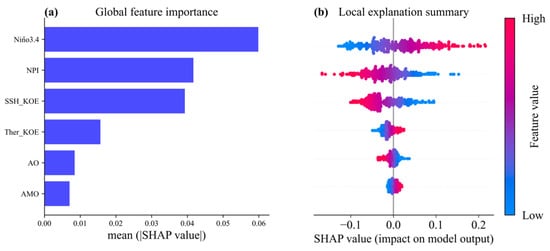
Figure 9.
(a) SHAP feature importance plot and (b) SHAP summary plot for each dependent variable.
The effect of each input variable on the output is visualized by the SHAP feature importance plot and summary plot in Figure 9. The results indicate that the Niño3.4 index emerged as the most crucial feature, whereas the AMO index played the least important role. The SHAP feature importance plot is depicted in Figure 9a. The results show that the main features, in decreasing order of importance, were Niño3.4, NPI, SSH_KOE, Ther_KOE, AO, and AMO. The results from the SHAP summary plot (Figure 9b) are the same as those of the feature importance plot. The findings reveal that high values of the Niño3.4 index positively affect the PDO forecast, while the AMO demonstrates a proportional relationship with the PDO too. Conversely, the NPI, SSH_KOE, and AO indices demonstrate an inverse proportionality to the PDO. Notably, the Ther_KOE index exhibits a complex pattern, lacking a straightforward proportional or inverse relationship with the PDO. It should be noted that the first three important features, Niño3.4, NPI, and SSH_KOE, were much greater than the last three features.
Schneider and Cornuelle [11] analyzed the hindcasting skill of individual components using the AR1 model. The results showed that the Niño3.4, NPI, and SSH_KOE indices accounted for significant fractions of the North Pacific SST anomaly variability. The Ther_KOE index tended to have little impact. Park et al. [12] found that the spatial correlation between the original PDO pattern and the regression pattern for the NPI, SSH_KOE, Niño3.4, and Ther_KOE indices was 0.85, 0.63, 0.62, and 0.34, respectively. These results are slightly different from the results of our study. However, there are also similarities such as that the Niño3.4, NPI, and SSH_KOE indices were much greater than the last three features, and the Ther_KOE index was less important. These differences might be due to two reasons: the data processing method and the length of the period. We used 6-month running mean data in this study, whereas the annual mean data were used in the studies of Schneider and Cornuelle [11] and Park et al. [12]. This may be because the Niño3.4 accounts more for the PDO prediction in terms of seasonal variability. Furthermore, our study used data from a much longer period than other studies. The data in our study covered approximately 140 years, while Schneider and Cornuelle [11] and Park et al. [12] used data that covered periods of 54 years and 42 years, respectively. The explainable model demonstrated that the Niño3.4, NPI, and SSH_KOE indices strongly pushed the output prediction value, which matches with our observations and the results of previous studies.
- (2)
- SHAP dependence plot
The SHAP dependence plot shows the marginal effects of one or two features on the prediction results of the ML model [47]. It indicates whether the relationship between the target and the feature is linear, monotonous, or more complex. The dependence plot is a global method that considers all instances and gives a global relationship between features and prediction results. It includes a single dependence plot and an interaction plot.
The SHAP dependence plot for each dependent variable is shown in Figure 10. The x-axis shows the real values of the dependent variable, whereas the y-axis values represent the corresponding SHAP values. Interestingly, the Niño3.4, AMO, and Ther_KOE indices showed a clear positive relationship with the PDO (Figure 10a,c,f), while the AO, NPI, and SSH_KOE indices showed a negative relationship (Figure 10b,d,e). For example, in Figure 10a, the range of SHAP values for Niño3.4, spanning from −0.1 to 0.2, suggests that Niño3.4 exhibits both positive and negative influences on the PDO prediction. Moreover, these contributions are notably significant in comparison to other features, as the SHAP values of other features are smaller. Positive NPI values indicate that the AL was weaker than normal, with warmer temperatures in the central North Pacific creating negative PDO anomalies. The ENSO affects the PDO primarily via changes in the AL. Warmer conditions in the eastern equatorial Pacific are associated with a warm eastern North Pacific and a cool central North Pacific, which means a positive relationship between the ENSO and PDO. The increased zonal advection (i.e., SSH_KOE index) leads to warm conditions in the western North Pacific and negative values of the PDO. This relationship between input variables and output variables is consistent with that in the study of Schneider and Cornuelle [11].
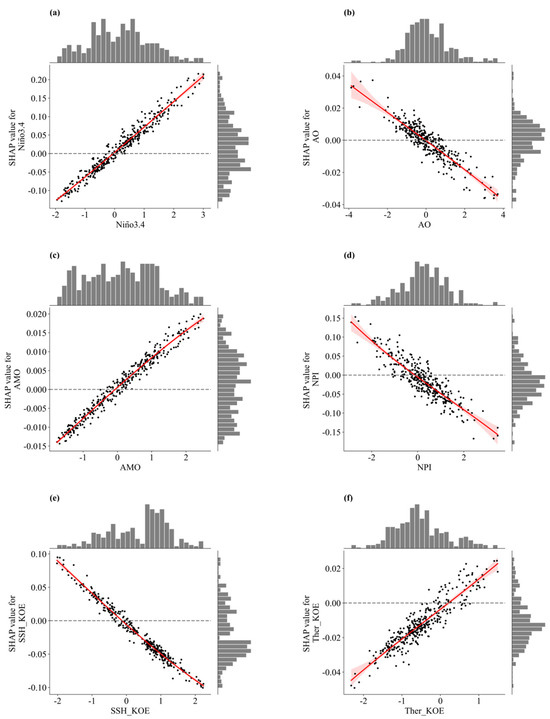
Figure 10.
SHAP dependence plot for each dependent variable: (a) Niño3.4 (°C), (b) AO (hPa), (c) AMO (°C), (d) NPI (hPa), (e) SSH_KOE (m), and (f) Ther_KOE (m). The black circles represent the SHAP values associated with different features. Red lines represent the polynomial regression of scatter points. The shaded area around each line indicates the range of a 95% confidence interval. Dashed lines represent the SHAP values equal to zero. The histograms on the top and right of each subplot indicate the distribution of feature and SHAP values.
SHAP values above the line are associated with higher PDO prediction, whereas those below it lead to lower PDO prediction. The x-axis value of the intersection of the y = 0 line and the fitted red line is approximately zero in the dependent plot for almost all the features except the Ther_KOE index. It is plausible that positive (negative) values of Niño3.4, AO, AMO, NPI, and SSH_KOE cause higher (lower) PDO predictions. From the results of the histograms for each feature, the Niño3.4, AO, and NPI are approximately normally distributed, the SSH_KOE and Ther_KOE are skewed distributed, and the AMO is uniformly distributed. More samples result in the SHAP values of SSH_KOE and Ther_KOE being less than zero.
As indicated previously, three dependent variables had the greatest impact on the PDO prediction: Niño3.4, NPI, and SSH_KOE. It is important to understand the interactions between these variables through a three-dimensional space regarding SHAP values. The SHAP interaction plot is shown for the Niño3.4 and SSH_KOE indices in Figure 11a, where the x- and y-axes indicate the features’ values while the z-axis and the colors represent the SHAP values. It appears that the impacts on the PDO prediction became more important as the magnitudes of Niño3.4 and SSH_KOE increased and decreased, respectively. This is easy to understand since the Niño3.4 (SSH_KOE) index had a positive (negative) relationship with the PDO. The interactions between the Niño3.4 index and NPI are presented in Figure 11b. When they were combined, the Niño3.4 index pushed the PDO, while the NPI had the opposite effect. The interactions between the SSH_KOE index and NPI are shown in Figure 11c. Their impact on the PDO prediction became less important as the magnitudes of NPI and SSH_KOE increased, since the SSH_KOE index and NPI had a negative relationship with the PDO.
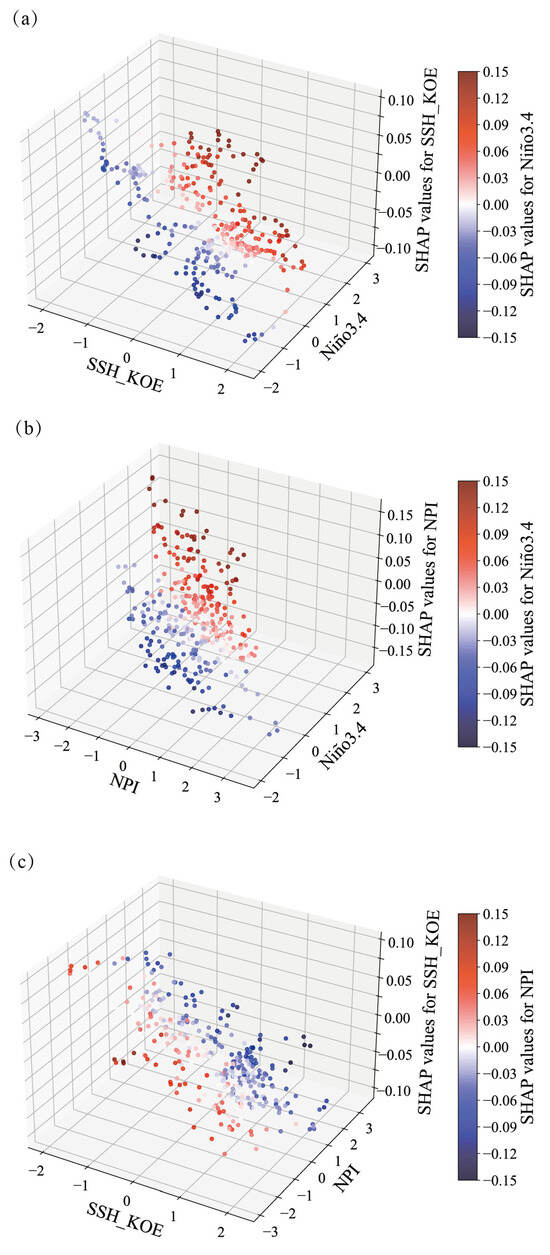
Figure 11.
SHAP interaction plot for the GRU model with respect to (a) the Niño3.4 and SSH_KOE indices, (b) the Niño3.4 index and the NPI, and (c) the SSH_KOE index and the NPI. Each point represents an example of the testing set.
4. Summary
This study investigated the temporal and spatial analysis of PDO prediction, utilizing six ML models: ANN, SVR, XGBoost, CNN, LSTM, and GRU. The SHAP analysis was employed for model interpretation, revealing the factors influencing the model’s decisions within the GRU model. Based on the results, several conclusions were drawn:
- (1)
- Among the models considered, the GRU model tends to offer more precise predictions.
- (2)
- The Niño3.4, NPI, and SSH_KOE indices are the three most important features for PDO prediction.
- (3)
- The PDO exhibits a positive correlation with the Niño3.4, AMO, and Ther_KOE indices, whereas it displays a negative correlation with the SSH_KOE, NPI, and AO indices.
Despite conducting hyperparameter tuning in this study, there is still potential to further refine the model’s performance. With the application of more intricate hyperparameter tuning techniques and the exploration of novel ML algorithms, the accuracy of PDO prediction might be further improved. While this study employed several widely used ML methods, there are numerous other approaches that have emerged. To this end, future research should focus on conducting additional model experiments and exploring new ML algorithms to enhance the performance of PDO prediction models.
Author Contributions
Conceptualization, Z.Y. (Zhixiong Yao), D.X., J.W. and J.R.; methodology, Z.Y. (Zhixiong Yao); software, Z.Y. (Zhixiong Yao) and Z.Y. (Zhenlong Yu); validation, Z.Y. (Zhixiong Yao), D.X., C.Y. and M.X.; formal analysis, Z.Y. (Zhixiong Yao) and D.X.; investigation, Z.Y. (Zhixiong Yao); resources, D.X.; data curation, H.W. and X.T.; writing—original draft preparation, Z.Y. (Zhixiong Yao); writing—review and editing, Z.Y. (Zhixiong Yao) and D.X.; visualization, Z.Y. (Zhixiong Yao); supervision, D.X.; project administration, D.X.; funding acquisition, D.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key R&D Program of China (Grant No. 2022YFC2803901), the Research Fund of Zhejiang Province (Grant No. 330000210130313013006), and the National Natural Science Foundation of China (Grant Nos. 41806032 and 42176005).
Data Availability Statement
Publicly available datasets were analyzed in this study. The observational datasets used in this work are from Asia-Pacific Data Research Center (http://apdrc.soest.hawaii.edu/data/data.php, accessed on 15 October 2021).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mantua, N.J.; Hare, S.R.; Zhang, Y.; Wallace, J.M.; Francis, R.C. A Pacific interdecadal climate oscillation with impacts on salmon production. Bull. Amer. Meteor. Soc. 1997, 78, 1069–1080. [Google Scholar]
- Newman, M.; Alexander, M.A.; Ault, T.R.; Cobb, K.M.; Deser, C.; Di Lorenzo, E.; Mantua, N.J.; Miller, A.J.; Minobe, S.; Nakamura, H.; et al. The Pacific decadal oscillation, revisited. J. Clim. 2016, 29, 4399–4427. [Google Scholar] [CrossRef]
- Mantua, N.J.; Hare, S.R. The Pacific decadal oscillation. J. Oceanogr. 2002, 58, 35–44. [Google Scholar] [CrossRef]
- Hamlington, B.D.; Leben, R.R.; Strassburg, M.W.; Nerem, R.S.; Kim, K.Y. Contribution of the Pacific Decadal Oscillation to global mean sea level trends. Geophys. Res. Lett. 2013, 40, 5171–5175. [Google Scholar] [CrossRef]
- Wei, W.; Yan, Z.; Li, Z. Influence of Pacific Decadal Oscillation on global precipitation extremes. Environ. Res. Lett. 2021, 16, 044031. [Google Scholar] [CrossRef]
- Di Lorenzo, E.; Xu, T.; Zhao, Y.; Newman, M.; Capotondi, A.; Stevenson, S.; Amaya, D.; Anderson, B.; Ding, R.; Furtado, J.; et al. Modes and Mechanisms of Pacific Decadal-Scale Variability. Annu. Rev. Mar. Sci. 2023, 15, 249–275. [Google Scholar] [CrossRef] [PubMed]
- Wen, C.; Xue, Y.; Kumar, A. Seasonal prediction of North Pacific SSTs and PDO in the NCEP CFS hindcasts. J. Clim. 2012, 25, 5689–5710. [Google Scholar] [CrossRef]
- Choi, J.; Son, S.W. Seasonal-to-decadal prediction of El Niño-southern oscillation and pacific decadal oscillation. Npi Clim. Atmos. Sci. 2022, 5, 29. [Google Scholar] [CrossRef]
- Guemas, V.; Doblas-Reyes, F.J.; Lienert, F.; Soufflet, Y.; Du, H. Identifying the causes of the poor decadal climate prediction skill over the North Pacific. J. Geophys. Res.-Atmos. 2012, 117, 1–17. [Google Scholar] [CrossRef]
- Liu, Z.; Di Lorenzo, E. Mechanisms and predictability of Pacific decadal variability. Curr. Clim. Change Rep. 2018, 4, 128–144. [Google Scholar] [CrossRef]
- Schneider, N.; Cornuelle, B.D. The forcing of the Pacific decadal oscillation. J. Clim. 2005, 18, 4355–4373. [Google Scholar] [CrossRef]
- Park, J.H.; An, S.I.; Yeh, S.W.; Schneider, N. Quantitative assessment of the climate components driving the pacific decadal oscillation in climate models. Theor. Appl. Climatol. 2013, 112, 431–445. [Google Scholar] [CrossRef]
- Alexander, M.A.; Matrosova, L.; Penland, C.; Scott, J.D.; Chang, P. Forecasting Pacific SSTs: Linear inverse model predictions of the PDO. J. Clim. 2008, 21, 385–402. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, H. A possible approach for decadal prediction of the PDO. J. Meteorol. Res. 2020, 34, 63–72. [Google Scholar] [CrossRef]
- Ahmad, H. Machine learning applications in oceanography. Aquat. Res. 2019, 2, 161–169. [Google Scholar] [CrossRef]
- Ham, Y.G.; Kim, J.H.; Luo, J.J. Deep learning for multi-year ENSO forecasts. Nature 2019, 573, 568–572. [Google Scholar] [CrossRef] [PubMed]
- Dasgupta, P.; Metya, A.; Naidu, C.V.; Singh, M.; Roxy, M.K. Exploring the long-term changes in the Madden Julian Oscillation using machine learning. Sci. Rep. 2020, 10, 18567. [Google Scholar] [CrossRef]
- Li, C.; Feng, Y.; Sun, T.; Zhang, X. Long Term Indian Ocean Dipole (IOD) Index Prediction Used Deep Learning by convLSTM. Remote Sens. 2022, 14, 523. [Google Scholar] [CrossRef]
- Yu, Z.; Xu, D.; Yao, Z.; Yang, C.; Liu, S. Research on PDO index prediction based on multivariate LSTM neural network model (in Chinese with English abstract). Acta Oceanic. Sin. 2022, 6, 58–67. [Google Scholar]
- Qin, M.; Du, Z.; Hu, L.; Cao, W.; Fu, Z.; Qin, L.; Wu, S.; Zhang, F. Deep Learning for Multi-Timescales Pacific Decadal Oscillation Forecasting. Geophys. Res. Lett. 2022, 49, e2021GL096479. [Google Scholar] [CrossRef]
- Qin, M.; Hu, L.; Qin, Z.; Wan, L.; Qin, L.; Cao, W.; Wu, S.; Du, Z. Pacific decadal oscillation forecasting with spatiotemporal embedding network. Geophys. Res. Lett. 2023, 50, e2023GL103170. [Google Scholar] [CrossRef]
- Johnson, Z.F.; Chikamoto, Y.; Wang, S.Y.S.; McPhaden, M.J.; Mochizuki, T. Pacific decadal oscillation remotely forced by the equatorial Pacific and the Atlantic Oceans. Clim. Dynam. 2020, 55, 789–811. [Google Scholar] [CrossRef]
- Zhang, R.; Delworth, T.L. Impact of the Atlantic multidecadal oscillation on North Pacific climate variability. Geophys. Res. Lett. 2007, 34, L23708. [Google Scholar] [CrossRef]
- Huang, B.; Thorne, P.W.; Banzon, V.F.; Boyer, T.; Chepurin, G.; Lawrimore, J.H.; Menne, M.J.; Smith, T.M.; Vose, R.S.; Zhang, H.-M. NOAA extended reconstructed sea surface temperature (ERSST), version 5. NOAA Natl. Cent. Environ. Inf. 2017, 30, 8179–8205. [Google Scholar] [CrossRef]
- Slivinski, L.C.; Compo, G.P.; Whitaker, J.S.; Sardeshmukh, P.D.; Giese, B.S.; McColl, C.; Allan, R.; Yin, X.; Vose, R.; Titchner, H.; et al. Towards a more reliable historical reanalysis: Improvements for version 3 of the Twentieth Century Reanalysis system. Q. J. R. Meteor. Soc. 2019, 145, 2876–2908. [Google Scholar] [CrossRef]
- Carton, J.A.; Giese, B.S. A reanalysis of ocean climate using Simple Ocean Data Assimilation (SODA). Mon. Weather Rev. 2008, 136, 2999–3017. [Google Scholar] [CrossRef]
- Meehl, G.A.; Hu, A.; Teng, H. Initialized decadal prediction for transition to positive phase of the Interdecadal Pacific Oscillation. Nat. Commun. 2016, 7, 11718. [Google Scholar] [CrossRef] [PubMed]
- Livingstone, D.J. Artificial Neural Networks: Methods and Applications; Humana Press: Totowa, NJ, USA, 2008. [Google Scholar]
- Vapnik, V.N.; Vapnik, V. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; van Merrienboer, B.; Gülçehre, Ç.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing, Doha, Qatar, 25–29 October 2014; Association for Computational Linguistics: Stroudsburg, PA, USA. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar] [CrossRef]
- Daoud, J.I. Multicollinearity and regression analysis. J. Phys. Conf. Ser. 2017, 949, 012009. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res.-Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4765–4774. [Google Scholar]
- Shapley, L. A Value for n-Person Games. Contributions to Theory Games. In Classics in Game Theory; Harold, W.K., Ed.; Princeton University Press: Princeton, NJ, USA, 1997; Volume II, pp. 307–318. [Google Scholar]
- Kleinbaum, D.G.; Kupper, L.L.; Muller, K.E. Applied Regression Analysis and Other Multivariate Methods; PES-KENT Publishing Company: Boston, MA, USA, 1988. [Google Scholar]
- Hashemi, M.R.; Spulding, M.L.; Shaw, A.; Farhadi, H.; Lewis, M. An efficient artificial intelligence model for prediction of tropical storm surge. Nat. Hazards 2016, 82, 471–491. [Google Scholar] [CrossRef]
- Luo, C.; Li, X.; Wen, Y.; Ye, Y.; Zhang, X. A novel LSTM model with interaction dual attention for radar echo extrapolation. Remote Sens. 2021, 13, 164. [Google Scholar] [CrossRef]
- Ramos-Valle, A.N.; Curchitser, E.N.; Bruyère, C.L.; McOwen, S. Implementation of an Artificial Neural Network for Storm Surge Forecasting. J. Geophys. Res.-Atmos. 2021, 126, e2020JD033266. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar]
- Jozefowicz, R.; Zaremba, W.; Sutskever, I. An empirical exploration of recurrent network architectures. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; Association for Computational Linguistics: Lille, France, 2015. [Google Scholar]
- Marcano-Cedeño, A.; Quintanilla-Domínguez, J.; Cortina-Januchs, M.G.; Andina, D. Feature selection using sequential forward selection and classification applying artificial metaplasticity neural network. In Proceedings of the IECON 2010-36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010. [Google Scholar]
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.; Compo, G.P.; Alexander, M.A. ENSO-forced variability of the Pacific decadal oscillation. J. Clim. 2003, 16, 3853–3857. [Google Scholar] [CrossRef]
- Lu, Z.; Yuan, N.; Yang, Q.; Ma, Z.; Kurths, J. Early warning of the Pacific Decadal Oscillation phase transition using complex network analysis. Geophys. Res. Lett. 2021, 48, e2020GL091674. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).