Two-Dimensional Autofocus for Ultra-High-Resolution Squint Spotlight Airborne SAR Based on Improved Spectrum Modification
Abstract
1. Introduction
2. Materials and Methods
2.1. Signal Model and Problems Discussion
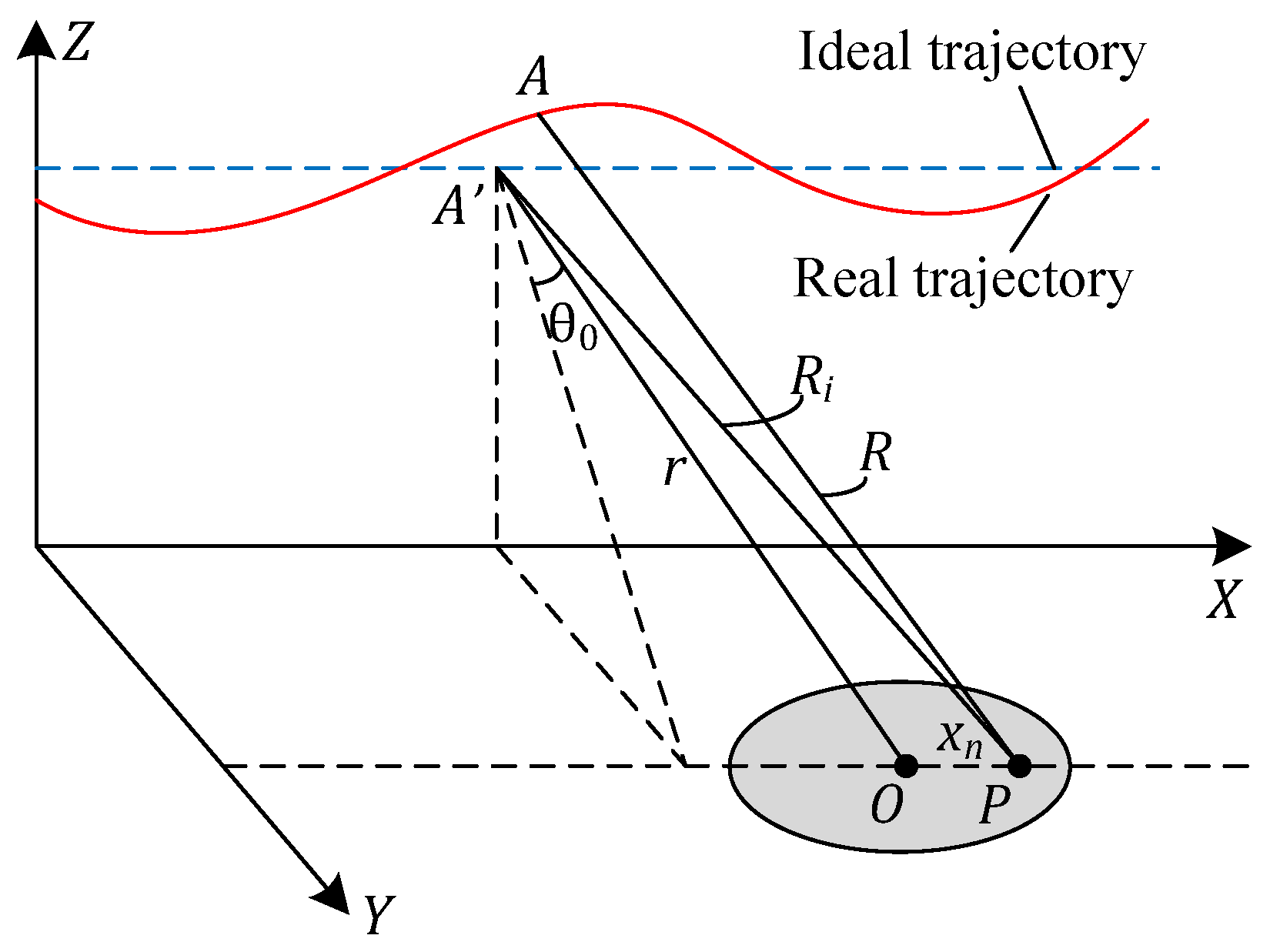
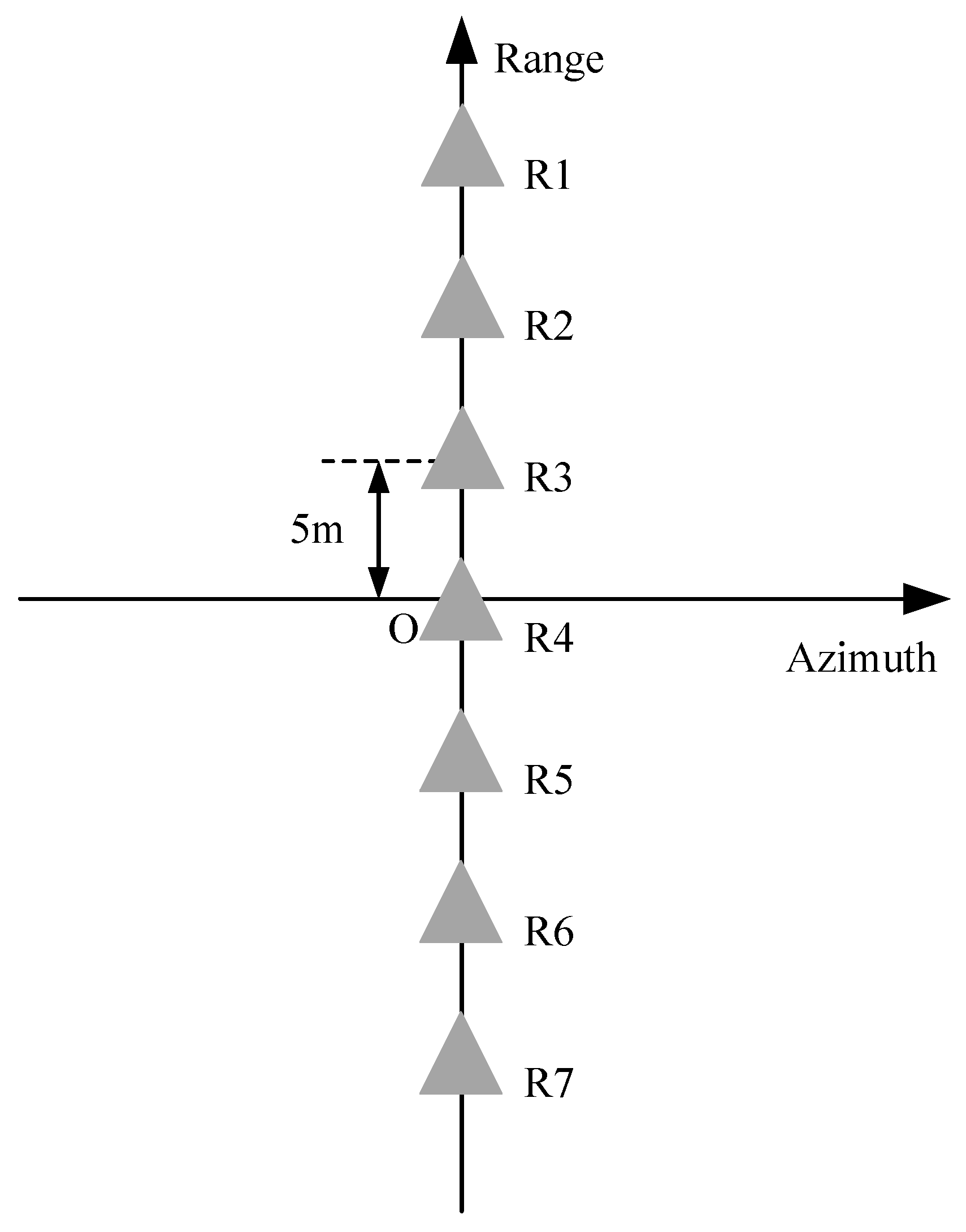
2.1.1. Signal Model
2.1.2. Negative Effects of Squint Angle
2.1.3. Accurate Structure of the 2D Phase Error
2.2. 2D Autofocus for UHR Squint Spotlight SAR
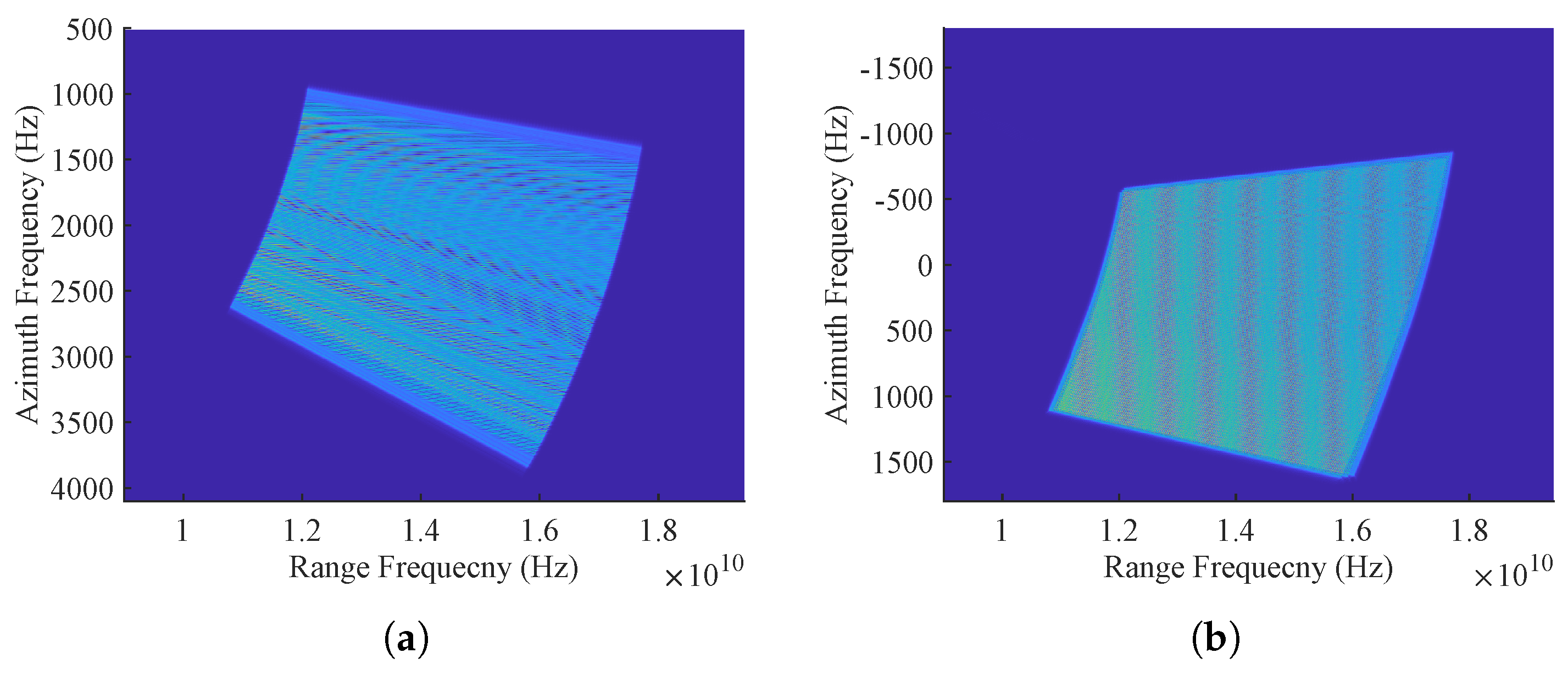
2.2.1. Support Region Analysis
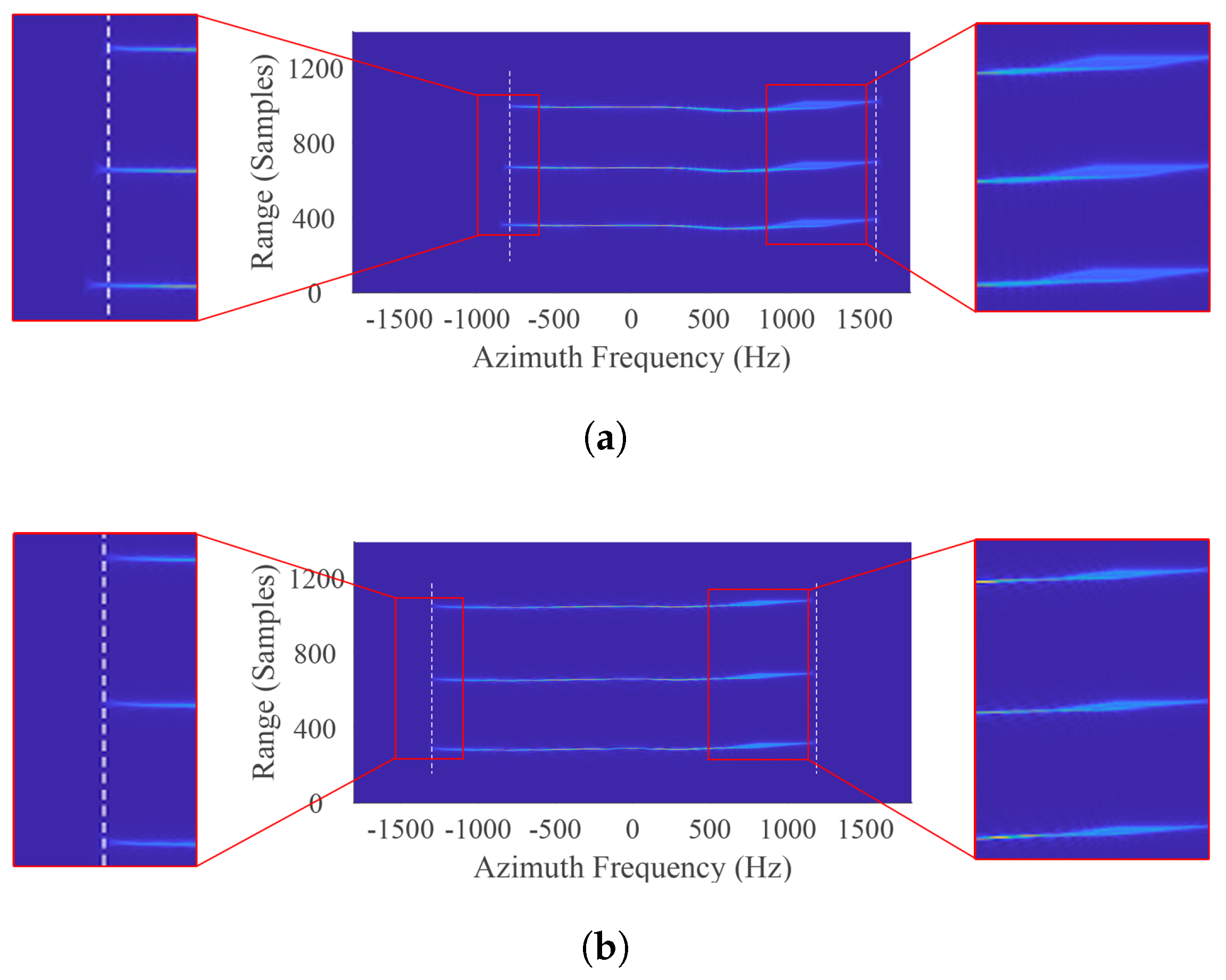
2.2.2. Azimuth Spectrum Shifting
2.2.3. Range Spectrum Shifting
2.2.4. 2D Phase-Error Mapping
2.2.5. 2D Autofocus Processing
- Spectrum modification. Perform azimuth spectrum shifting with (24) in the domain and then range spectrum shifting with (29) in the domain. After that, the squint spectrum transforms into a quasi-side-looking one. The range defocus and RESE can be greatly alleviated, and the support regions of targets at different locations are aligned in the wavenumber domain.
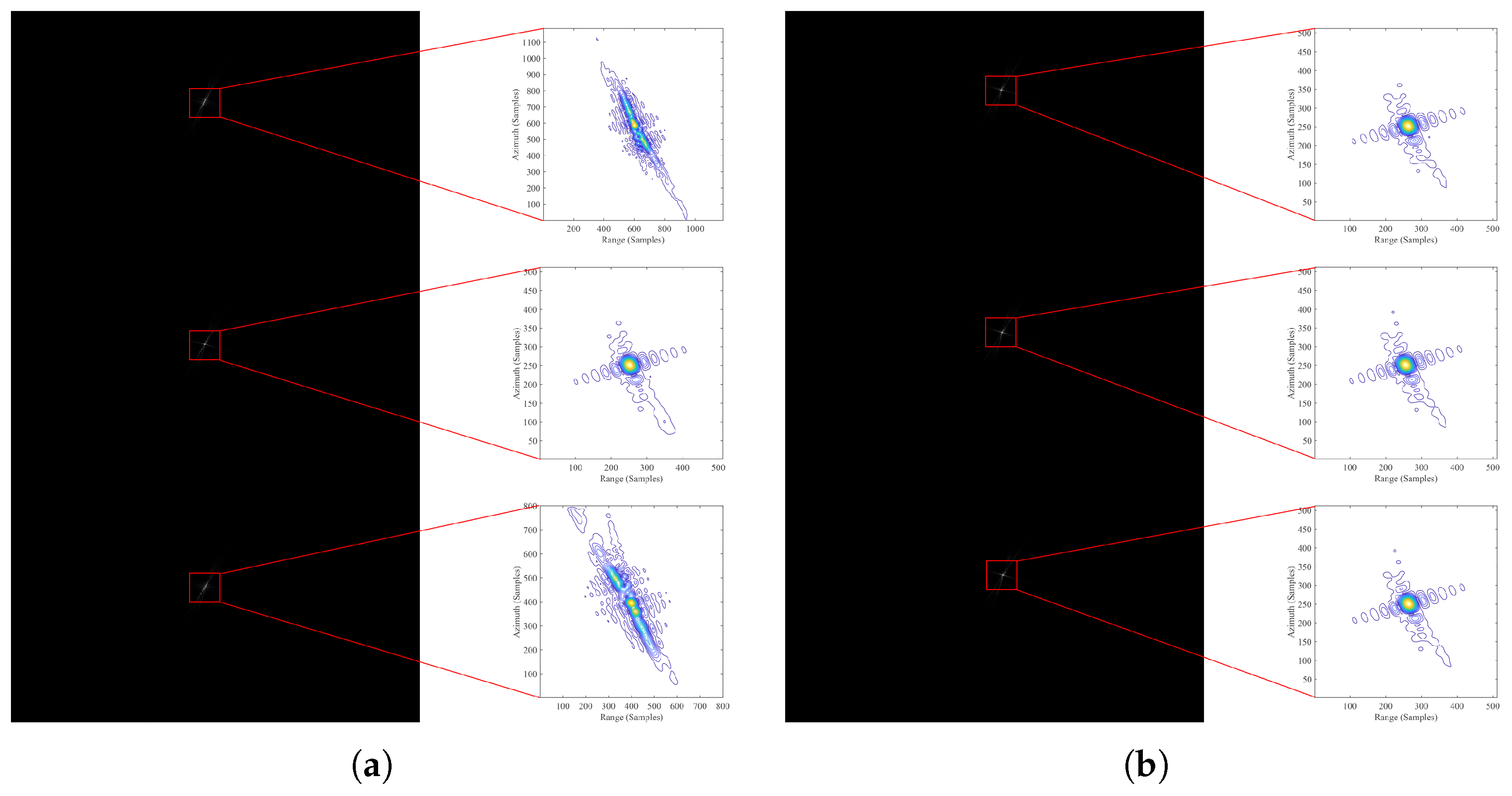
- Phase error estimation and correction. In order to obtain an accurate estimation of APE, we need first to eliminate the effect of the RESE, which can be completed by the downsampling method [27] or minimum entropy method [39]. The former enlarges the range cell by downsampling so that the RESE will be smaller than one range cell. The latter estimates the RESE by entropy minimization of the average range profile. After that, the APE can be estimated with conventional autofocus methods such as PGA [22] in the aligned range-Doppler domain. Then, with the estimated APE, perform 2D mapping using (33) and compensate for it in the 2D wavenumber domain.
3. Results
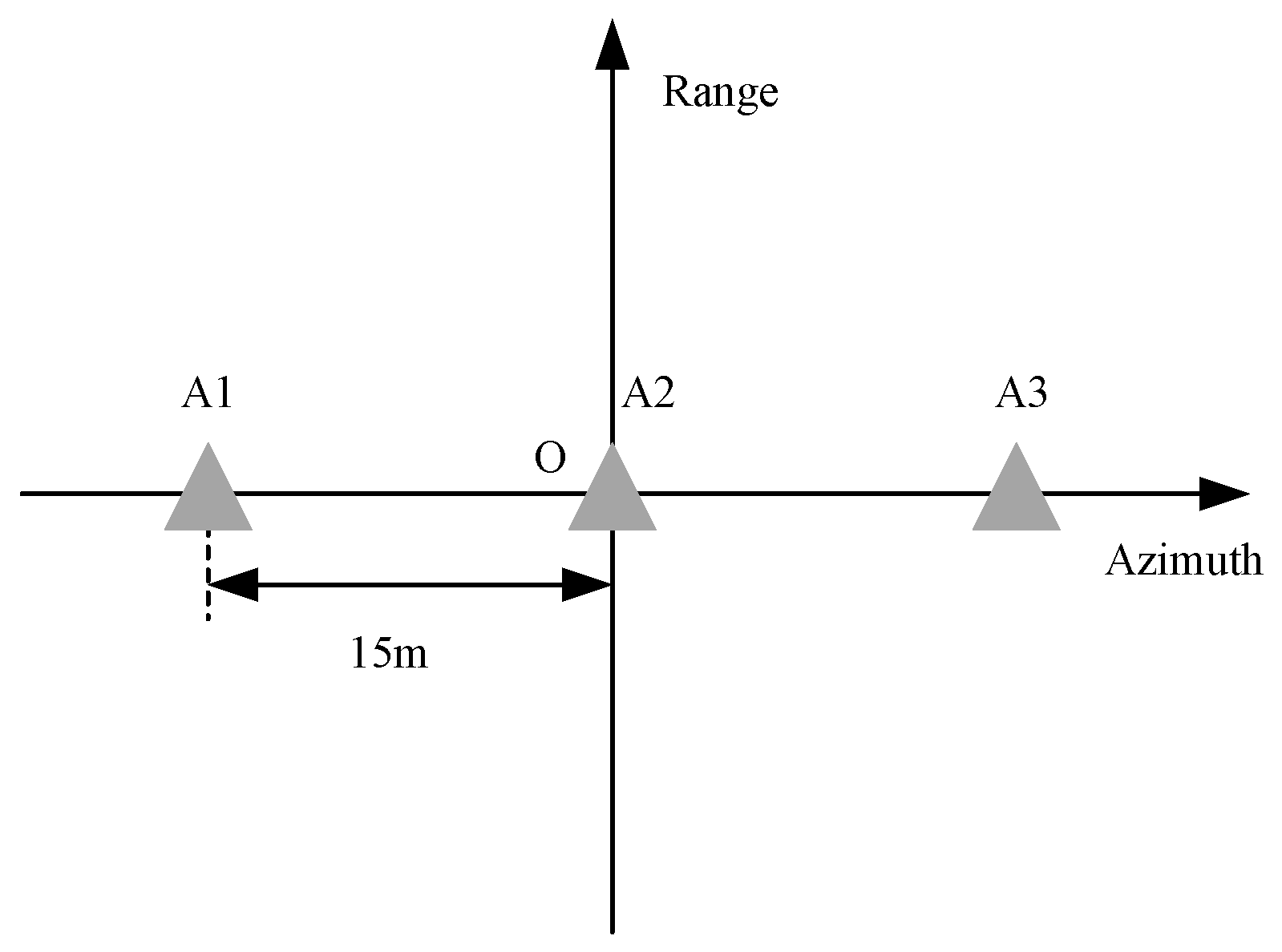
3.1. Phase Error Analysis and Performance Comparison
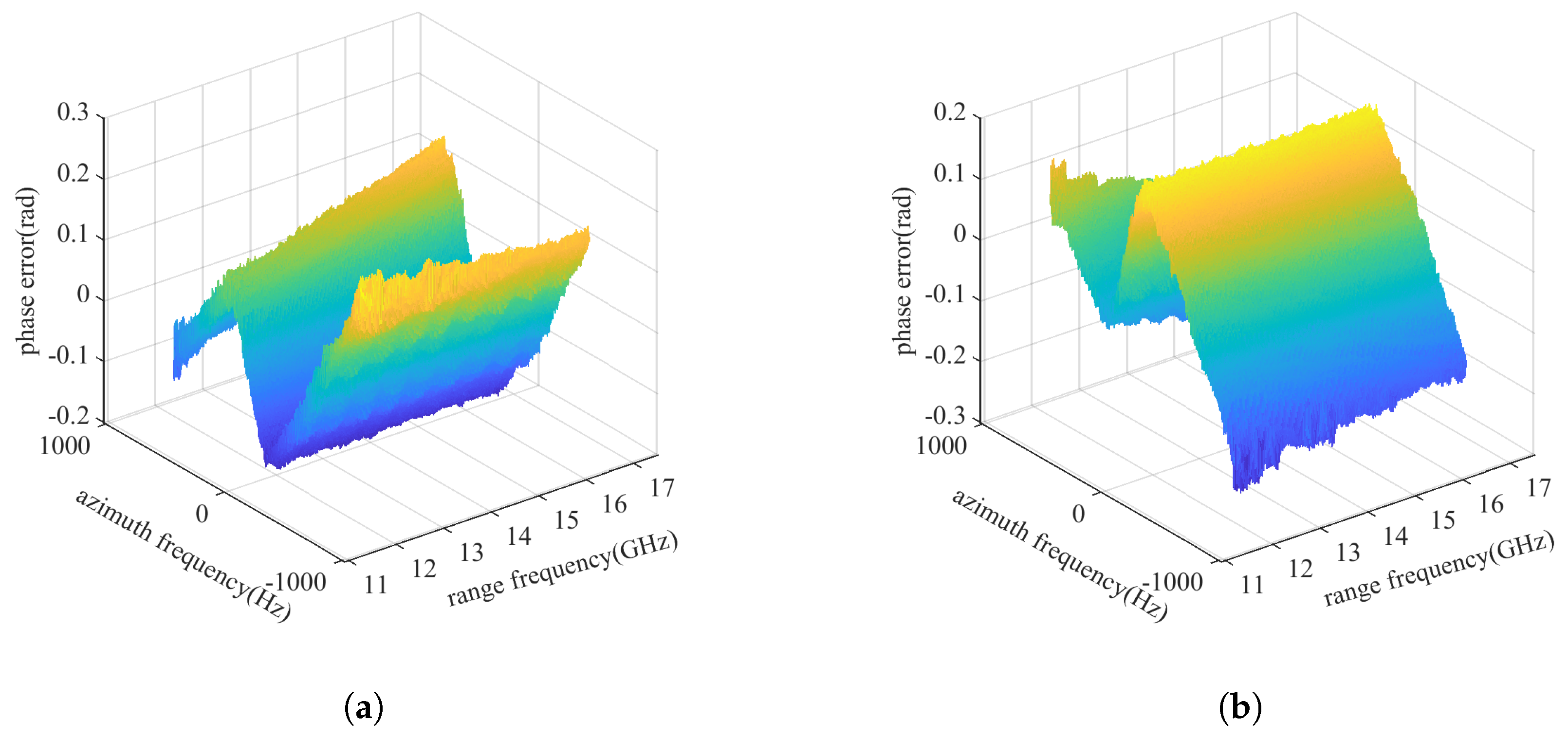
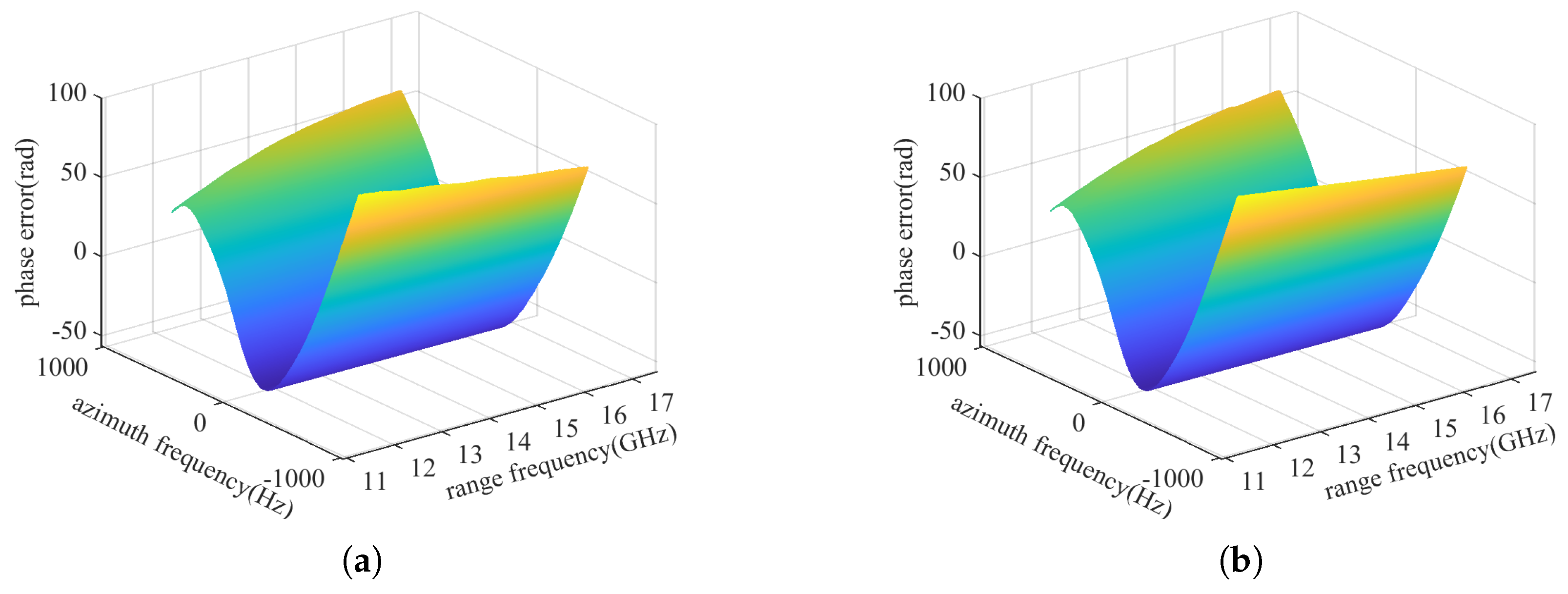
3.1.1. 2D Phase Error Analysis
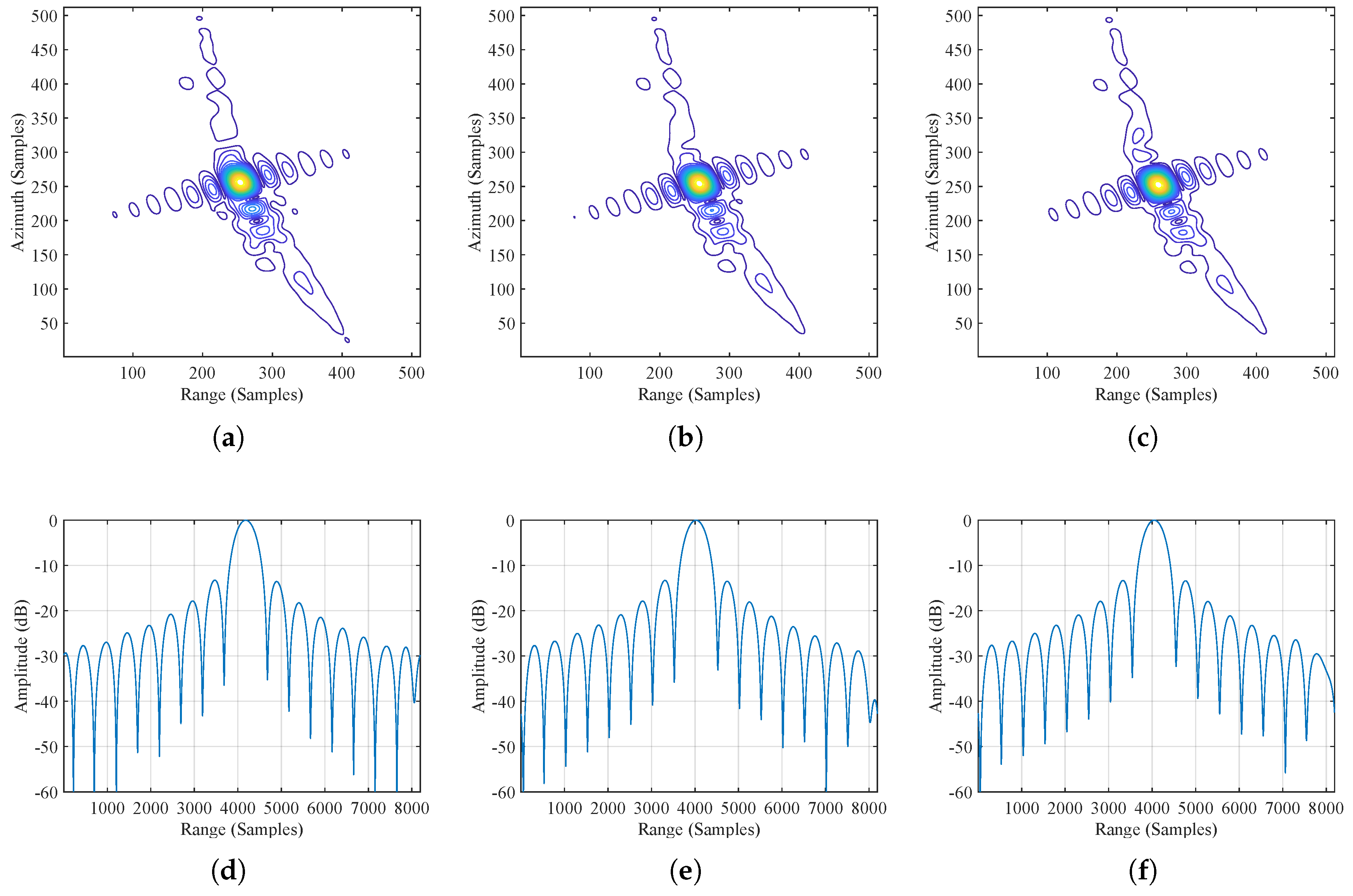
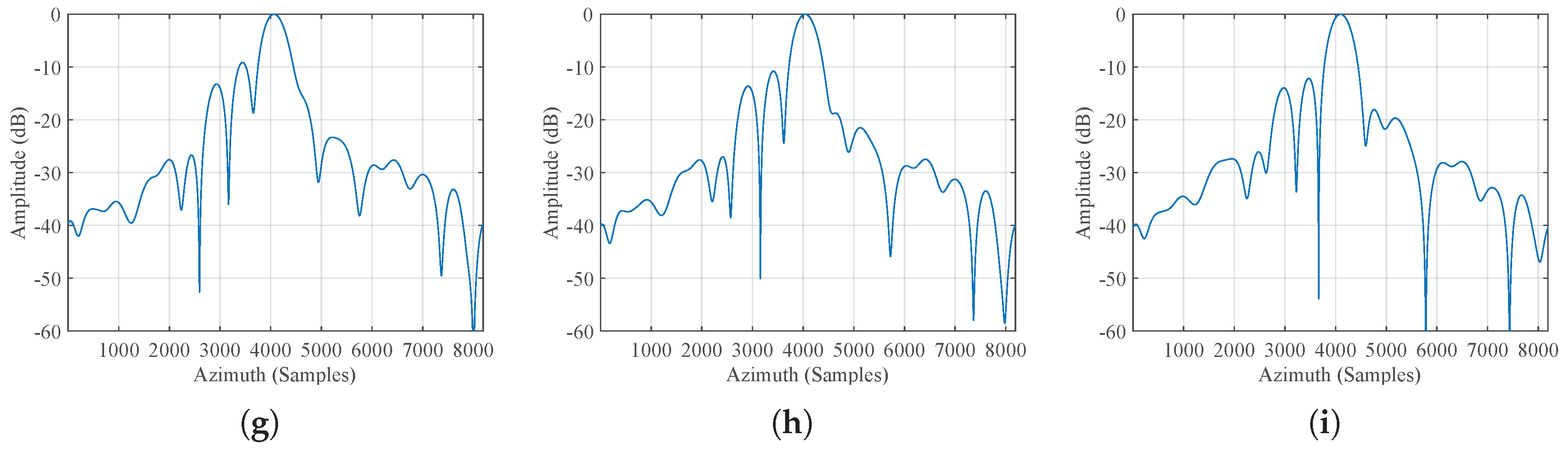
3.1.2. Performance Comparison
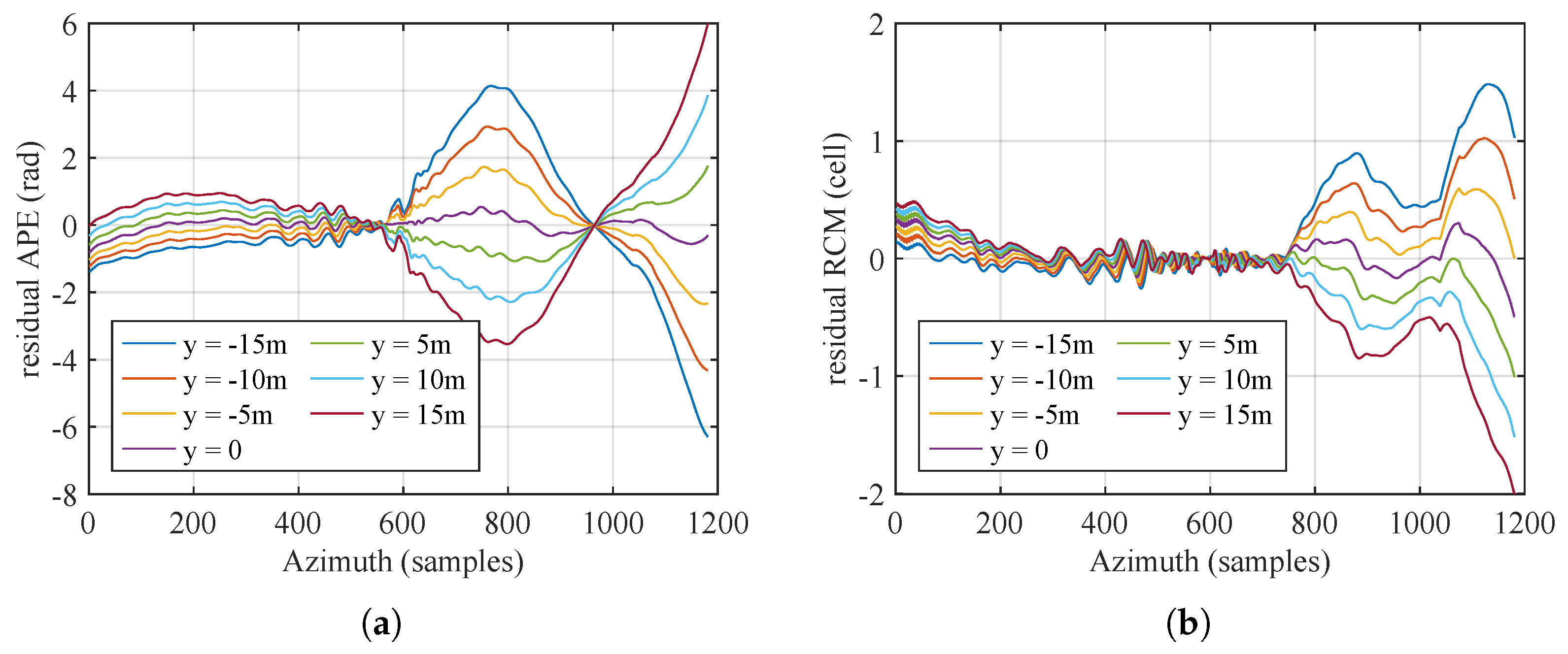
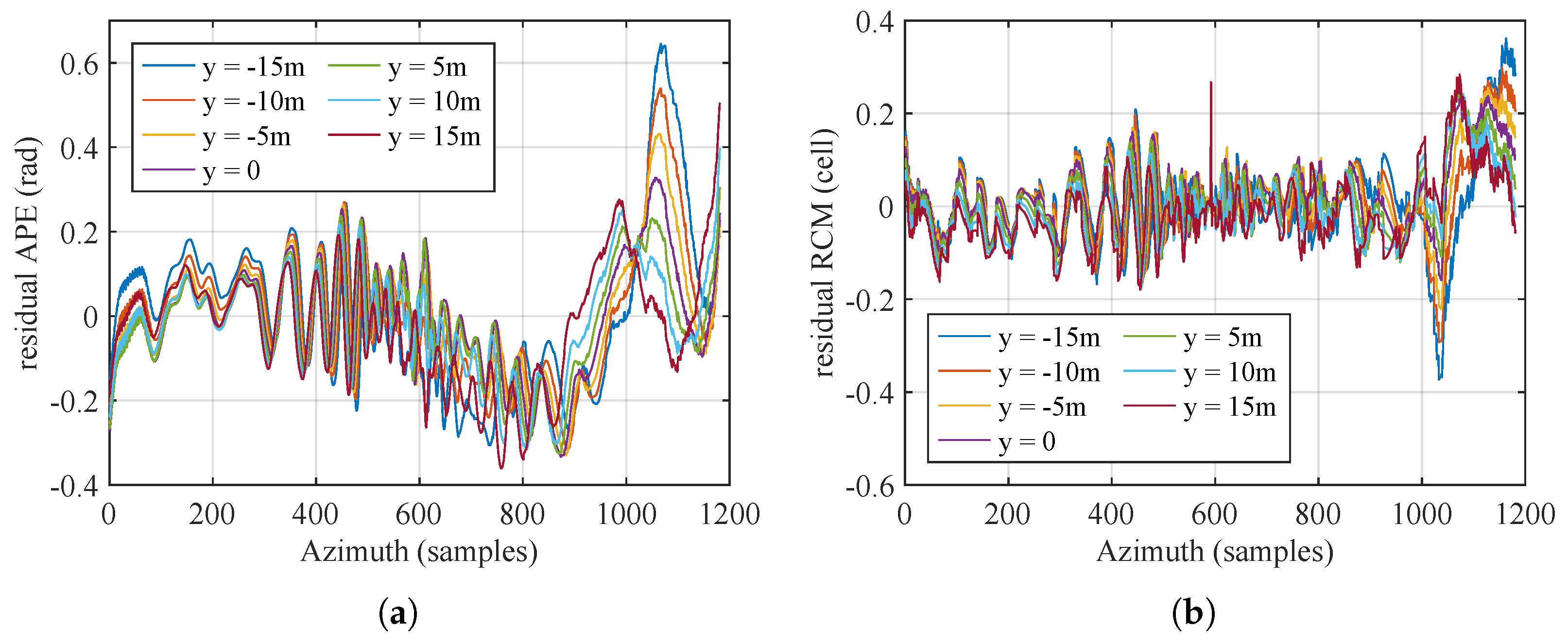
3.2. Range-Variant Compensation
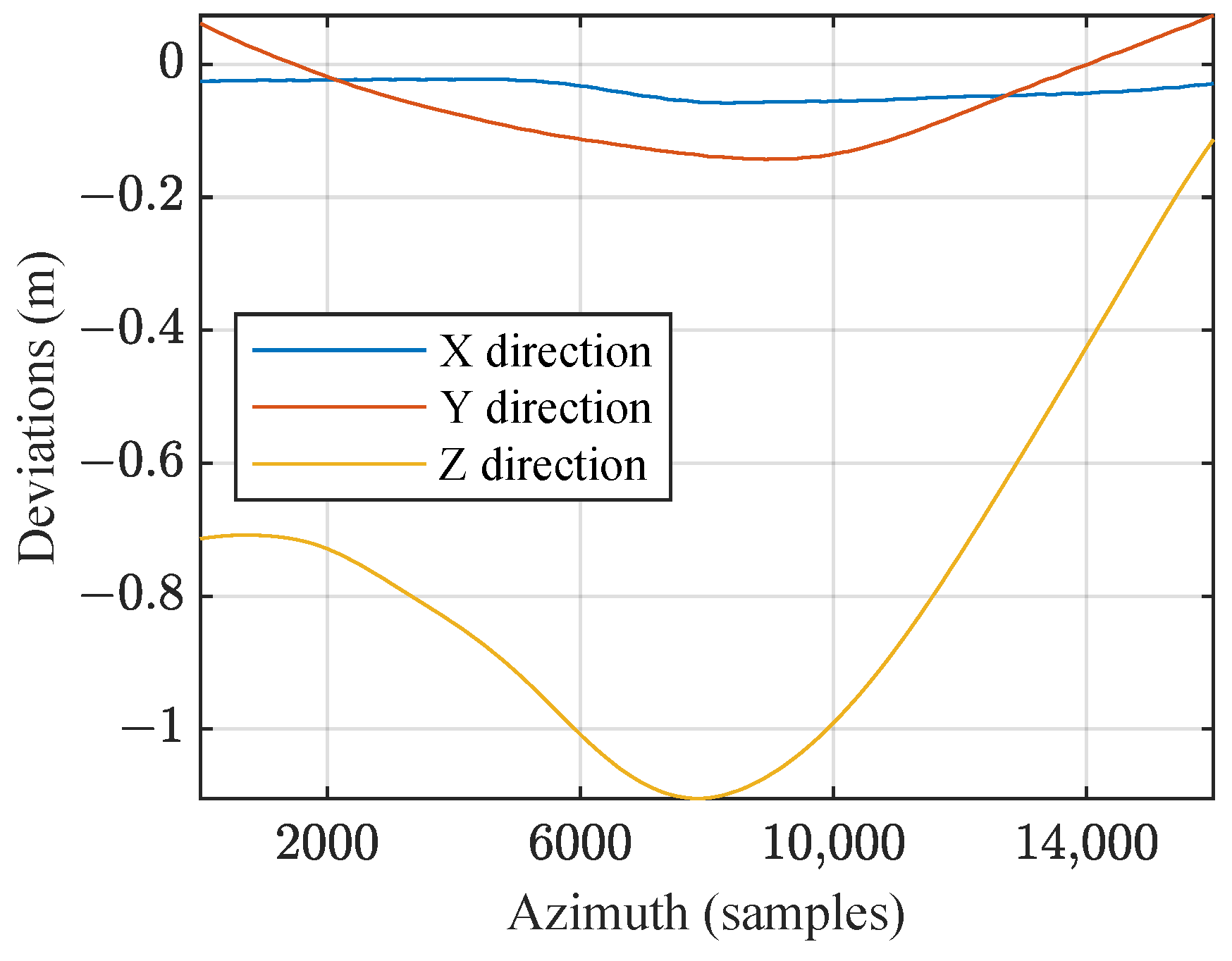
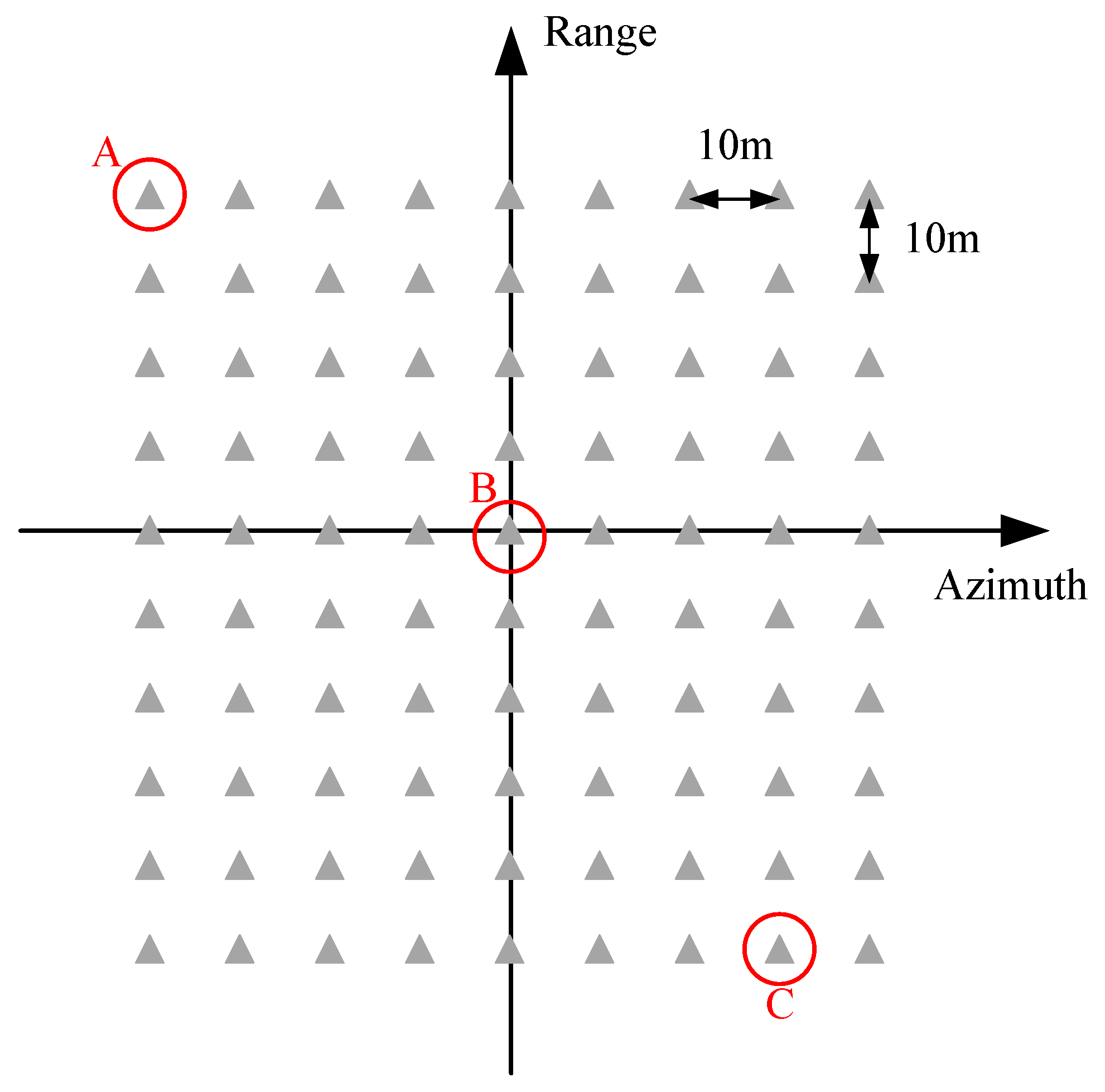
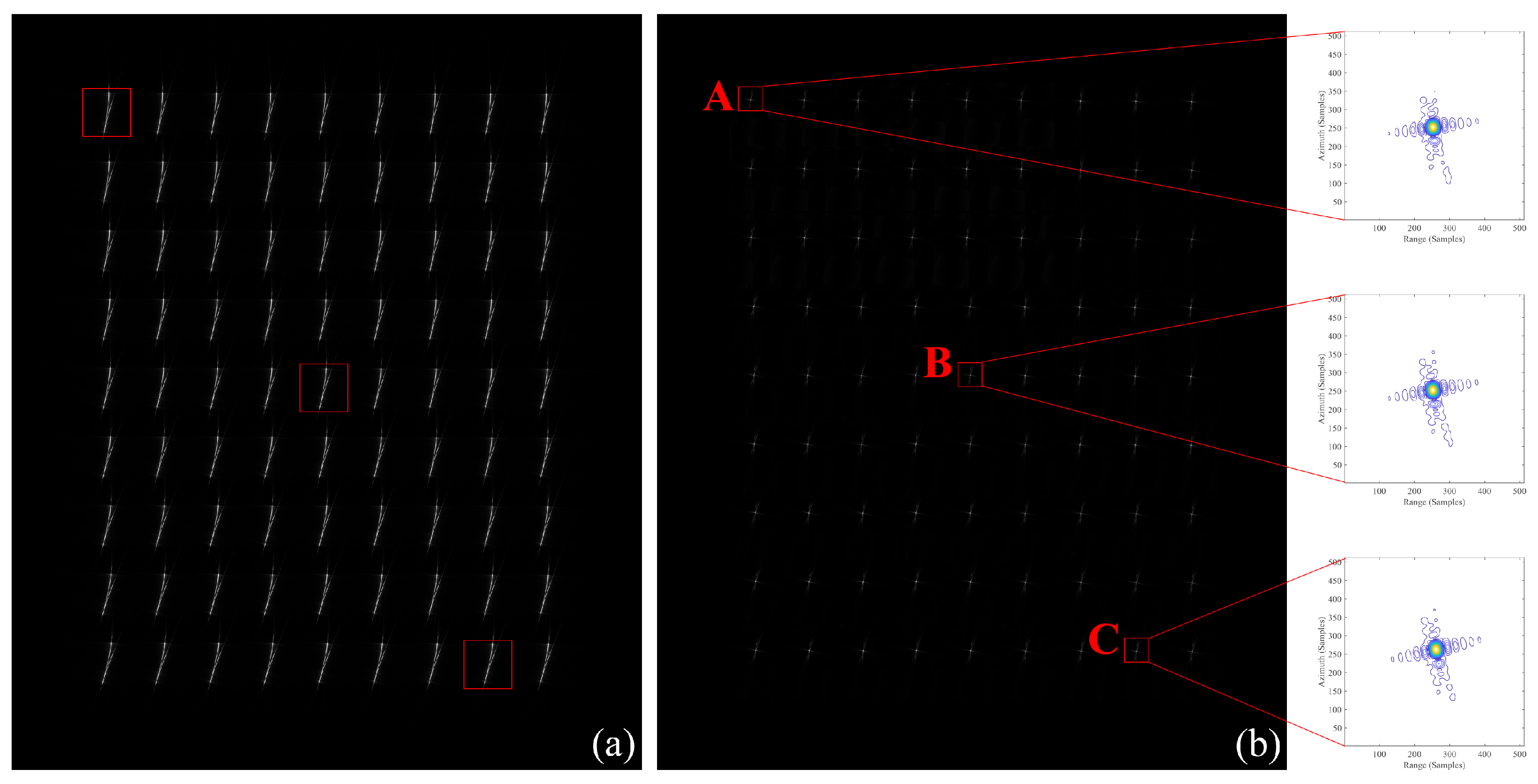
3.3. Large Scenario Verification
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Carrara, W.G.; Goodman, R.S.; Majewski, R.M. Spotlight Synthetic Aperture Radar: Signal Processing Algorithms; Artech House: Norwood, MA, USA, 1995. [Google Scholar]
- Cumming, I.G.; Wong, F.H. Digital Signal Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Norwood, MA, USA, 2004. [Google Scholar]
- Li, R.; Li, W.; Dong, Y.; Wen, Z.; Zhang, H.; Sun, W.; Yang, J.; Zeng, H.; Deng, Y.; Luan, Y.; et al. PFDIR—A Wideband Photonic-Assisted SAR System. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4333–4346. [Google Scholar] [CrossRef]
- Deng, Y.; Xing, M.; Sun, G.C.; Liu, W.; Li, R.; Wang, Y. A Processing Framework for Airborne Microwave Photonic SAR With Resolution Up To 0.03 m: Motion Estimation and Compensation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Chen, M.; Qiu, X.; Li, R.; Li, W.; Fu, K. Analysis and Compensation for Systematical Errors in Airborne Microwave Photonic SAR Imaging by 2D Autofocus. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2023, 16, 2221–2236. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, P.; Zhou, X.; He, T.; Chen, J. A Decoupled Chirp Scaling Algorithm for High-Squint SAR Data Imaging. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–17. [Google Scholar] [CrossRef]
- Chen, X.; Hou, Z.; Dong, Z.; He, Z. Performance Analysis of Wavenumber Domain Algorithms for Highly Squinted SAR. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2023, 16, 1563–1575. [Google Scholar] [CrossRef]
- Chen, J.; Xing, M.; Yu, H.; Liang, B.; Peng, J.; Sun, G.C. Motion Compensation/Autofocus in Airborne Synthetic Aperture Radar: A Review. IEEE Geosci. Remote Sens. Mag. 2022, 10, 185–206. [Google Scholar] [CrossRef]
- Jin, M.Y.; Wu, C. A SAR correlation algorithm which accommodates large-range migration. IEEE Trans. Geosci. Remote Sens. 1984, GE-22, 592–597. [Google Scholar] [CrossRef]
- Raney, R.K.; Runge, H.; Bamler, R.; Cumming, I.G.; Wong, F.H. Precision SAR processing using chirp scaling. IEEE Trans. Geosci. Remote Sens. 1994, 32, 786–799. [Google Scholar] [CrossRef]
- Wong, F.H.; Cumming, I.G. Error Sensitivities of a Secondary Range Compression Algorithm for Processing Squinted Satellite Sar Data. In Proceedings of the IGARSS, Vancouver, BC, Canada, 10–14 July 1989; Volume 4, pp. 2584–2587. [Google Scholar] [CrossRef]
- Moreira, A.; Huang, Y. Airborne SAR processing of highly squinted data using a chirp scaling approach with integrated motion compensation. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1029–1040. [Google Scholar] [CrossRef]
- Davidson, G.W.; Cumming, I.G.; Ito, M.R. A chirp scaling approach for processing squint mode SAR data. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 121–133. [Google Scholar] [CrossRef]
- An, D.; Huang, X.; Jin, T.; Zhou, Z. Extended Nonlinear Chirp Scaling Algorithm for High-Resolution Highly Squint SAR Data Focusing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3595–3609. [Google Scholar] [CrossRef]
- Sun, G.; Xing, M.; Liu, Y.; Sun, L.; Bao, Z.; Wu, Y. Extended NCS Based on Method of Series Reversion for Imaging of Highly Squinted SAR. IEEE Geosci. Remote Sens. Lett. 2011, 8, 446–450. [Google Scholar] [CrossRef]
- Munson, D.; O’Brien, J.; Jenkins, W. A tomographic formulation of spotlight-mode synthetic aperture radar. Proc. IEEE 1983, 71, 917–925. [Google Scholar] [CrossRef]
- Cafforio, C.; Prati, C.; Rocca, F. SAR data focusing using seismic migration techniques. IEEE Trans. Aerosp. Electron. Syst. 1991, 27, 194–207. [Google Scholar] [CrossRef]
- Samczynski, P.; Kulpa, K.S. Coherent MapDrift Technique. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1505–1517. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, M.; Wang, G.; Wang, H. Range-Dependent Map-Drift Algorithm for Focusing UAV SAR Imagery. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1158–1162. [Google Scholar] [CrossRef]
- Wang, J.; Liu, X. SAR Minimum-Entropy Autofocus Using an Adaptive-Order Polynomial Model. IEEE Geosci. Remote Sens. Lett. 2006, 3, 512–516. [Google Scholar] [CrossRef]
- Gao, Y.; Yu, W.; Liu, Y.; Wang, R.; Shi, C. Sharpness-Based Autofocusing for Stripmap SAR Using an Adaptive-Order Polynomial Model. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1086–1090. [Google Scholar] [CrossRef]
- Wahl, D.E.; Eichel, P.H.; Ghiglia, D.C.; Jakowatz, C.V. Phase gradient autofocus-a robust tool for high resolution SAR phase correction. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 827–835. [Google Scholar] [CrossRef]
- Van Rossum, W.L.; Otten, M.P.G.; Van Bree, R.J.P. Extended PGA for range migration algorithms. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 478–488. [Google Scholar] [CrossRef]
- Zhu, D.; Jiang, R.; Mao, X.; Zhu, Z. Multi-Subaperture PGA for SAR Autofocusing. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 468–488. [Google Scholar] [CrossRef]
- Zeng, T.; Wang, R.; Li, F. SAR Image Autofocus Utilizing Minimum-Entropy Criterion. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1552–1556. [Google Scholar] [CrossRef]
- Morrison, R.L.; Do, M.N.; Munson, D.C. SAR Image Autofocus By Sharpness Optimization: A Theoretical Study. IEEE Trans. Image Process. 2007, 16, 2309–2321. [Google Scholar] [CrossRef]
- Doerry, A.W. Autofocus Correction of Excessive Migration in Synthetic Aperture Radar Images; Technical Report; Sandia National Laboratories (SNL): Albuquerque, NM, USA; Livermore, CA, USA, 2004.
- Mao, X.; He, X.; Li, D. Knowledge-Aided 2D Autofocus for Spotlight SAR Range Migration Algorithm Imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5458–5470. [Google Scholar] [CrossRef]
- Mao, X.; Zhu, D. Two-dimensional Autofocus for Spotlight SAR Polar Format Imagery. IEEE Trans. Comput. Imag. 2016, 2, 524–539. [Google Scholar] [CrossRef]
- Mao, X.; Ding, L.; Zhang, Y.; Zhan, R.; Li, S. Knowledge-Aided 2-D Autofocus for Spotlight SAR Filtered Backprojection Imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9041–9058. [Google Scholar] [CrossRef]
- Zhang, L.; Sheng, J.; Xing, M.; Qiao, Z.; Xiong, T.; Bao, Z. Wavenumber-Domain Autofocusing for Highly Squinted UAV SAR Imagery. IEEE Sens. J. 2012, 12, 1574–1588. [Google Scholar] [CrossRef]
- Xu, G.; Xing, M.; Zhang, L.; Bao, Z. Robust Autofocusing Approach for Highly Squinted SAR Imagery Using the Extended Wavenumber Algorithm. IEEE Trans. Geosci. Remote Sens. 2013, 51, 5031–5046. [Google Scholar] [CrossRef]
- Ran, L.; Liu, Z.; Li, T.; Xie, R.; Zhang, L. Extension of Map-Drift Algorithm for Highly Squinted SAR Autofocus. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2017, 10, 4032–4044. [Google Scholar] [CrossRef]
- Lin, H.; Chen, J.; Xing, M.; Chen, X.; You, D.; Sun, G. 2-D Frequency Autofocus for Squint Spotlight SAR Imaging With Extended Omega-K. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, G.; Qiao, Z.; Wang, H.; Sun, L. Two-Stage Focusing Algorithm for Highly Squinted Synthetic Aperture Radar Imaging. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5547–5562. [Google Scholar] [CrossRef]
- Chen, J.; Liang, B.; Zhang, J.; Yang, D.G.; Deng, Y.; Xing, M. Efficiency and Robustness Improvement of Airborne SAR Motion Compensation With High Resolution and Wide Swath. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Chen, J.; Liang, B.; Yang, D.G.; Zhao, D.J.; Xing, M.; Sun, G.C. Two-Step Accuracy Improvement of Motion Compensation for Airborne SAR With Ultrahigh Resolution and Wide Swath. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7148–7160. [Google Scholar] [CrossRef]
- Chen, J.; Xing, M.; Sun, G.C.; Li, Z. A 2-D Space-Variant Motion Estimation and Compensation Method for Ultrahigh-Resolution Airborne Stepped-Frequency SAR With Long Integration Time. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6390–6401. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, L.; Yu, Y.; Tao, Q.; Zhu, Z. Robust ISAR Range Alignment via Minimizing the Entropy of the Average Range Profile. IEEE Geosci. Remote Sens. Lett. 2009, 6, 204–208. [Google Scholar] [CrossRef]
- Chan, H.L.; Yeo, T.S. Noniterative quality phase-gradient autofocus (QPGA) algorithm for spotlight SAR imagery. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1531–1539. [Google Scholar] [CrossRef]
- de Macedo, K.A.C.; Scheiber, R.; Moreira, A. An Autofocus Approach for Residual Motion Errors With Application to Airborne Repeat-Pass SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3151–3162. [Google Scholar] [CrossRef]
- Panda, S.S.S.; Panigrahi, T.; Parne, S.R.; Sabat, S.L.; Cenkeramaddi, L.R. Recent Advances and Future Directions of Microwave Photonic Radars: A Review. IEEE Sens. J. 2021, 21, 21144–21158. [Google Scholar] [CrossRef]
- Li, R.; Li, W.; Dong, Y.; Wang, B.; Wen, Z.; Luan, Y.; Yang, Z.; Yang, X.; Yang, J.; Sun, W.; et al. An Ultrahigh-Resolution Continuous Wave Synthetic Aperture Radar with Photonic-Assisted Signal Generation and Dechirp Processing. In Proceedings of the 2020 17th European Radar Conference (EuRAD), Utrecht, The Netherlands, 10–15 January 2021; pp. 13–16. [Google Scholar] [CrossRef]





| Time-Domain Methods [31,32,33] | Frequency-Domain Methods [34] | |
|---|---|---|
| Characteristics |
|
|
| Limitations |
|
|
| Parameters | Values |
|---|---|
| Carrier frequency | 15.14 GHz |
| Bandwidth | 5.72 GHz |
| Time width | 10 us |
| Sampling frequency | 2500 MHz |
| Synthetic aperture length | 296.34 m |
| Pulse repetition frequency | 3600 Hz |
| Center slant range | 885 m |
| Velocity | 67 m/s |
| Referenced Method | Proposed Method | |
|---|---|---|
| Entropy | 5.9719 | 4.4266 |
| Contrast | 13.3200 | 17.5166 |
| Range | Azimuth | |||||
|---|---|---|---|---|---|---|
| Point | IRW (m) | PSLR (dB) | ISLR (dB) | IRW (m) | PSLR (dB) | ISLR (dB) |
| A | 0.0236 | −13.116 | −10.442 | 0.0260 | −12.535 | −12.823 |
| B | 0.0238 | −13.053 | −10.298 | 0.0268 | −12.420 | −12.612 |
| C | 0.0239 | −13.076 | −10.281 | 0.0278 | −12.358 | −12.529 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.; Qiu, X.; Cheng, Y.; Shang, M.; Li, R.; Li, W. Two-Dimensional Autofocus for Ultra-High-Resolution Squint Spotlight Airborne SAR Based on Improved Spectrum Modification. Remote Sens. 2024, 16, 2158. https://doi.org/10.3390/rs16122158
Chen M, Qiu X, Cheng Y, Shang M, Li R, Li W. Two-Dimensional Autofocus for Ultra-High-Resolution Squint Spotlight Airborne SAR Based on Improved Spectrum Modification. Remote Sensing. 2024; 16(12):2158. https://doi.org/10.3390/rs16122158
Chicago/Turabian StyleChen, Min, Xiaolan Qiu, Yao Cheng, Mingyang Shang, Ruoming Li, and Wangzhe Li. 2024. "Two-Dimensional Autofocus for Ultra-High-Resolution Squint Spotlight Airborne SAR Based on Improved Spectrum Modification" Remote Sensing 16, no. 12: 2158. https://doi.org/10.3390/rs16122158
APA StyleChen, M., Qiu, X., Cheng, Y., Shang, M., Li, R., & Li, W. (2024). Two-Dimensional Autofocus for Ultra-High-Resolution Squint Spotlight Airborne SAR Based on Improved Spectrum Modification. Remote Sensing, 16(12), 2158. https://doi.org/10.3390/rs16122158





