Abstract
A doppler radar holds promising prospects in the field of indoor target localization. However, traditional Doppler radar systems suffer from high power consumption, large size, and noticeable radio frequency interference issues when transmitting carriers of different frequencies. Therefore, an ISABO-based (improved subtraction-average-based optimizer) target localization algorithm for a single-frequency Doppler radar is proposed in this paper. Firstly, a mathematical model for target localization is established according to the spatial geometric relationships during the target movement and the Doppler frequency-shift information in the single-frequency echo signal. Then, the optimization function is constructed with the target motion error as the optimization goal. Finally, an improved subtraction-average-based optimizer algorithm is proposed to solve the optimal parameters and realize the target positioning. The experimental results show that the proposed method can achieve centimeter-level localization accuracy with a cost-effective system structure.
1. Introduction
The accurate tracking and localization of human targets are essential in a wide range of civil and military applications [1,2,3,4]. Due to the outstanding advantages of penetrating ability, high measuring precision, and being scarcely influenced by light and weather conditions, Doppler radars play an increasingly important role in human target localization, such as in anti-terrorism detection [5,6], post-disaster rescue [7], military operations [8], indoor guidance [9], non-contact home monitoring [10], and so on. However, with the advancement of technology, there is an increasing demand for portable, cost-effective, and high-precision detection equipment for emergency applications. Therefore, designing a compact and low-cost Doppler radar system for accurate short-range target localization has become a critical research direction that needs to be explored.
Currently, most research in target detection focuses on dual-frequency Doppler radar (DF-DR) systems. In [11], the echo phase difference between the receivers was used to estimate the target motion range of a DF-DR, which is one of the most classic methods, but it is not very noise resistant. To solve this problem, an improved tracking algorithm was proposed in Refs. [12,13], which uses the Doppler frequency integration form of the target instead of the direct phase difference estimation, successfully obtaining more stable target estimation results. Ref. [14] proposes a compact DR-FR system consisting of one transmitter and two receivers, which can better optimize the antenna configuration of the system. However, the experimental results show that the estimation of an echo phase is highly sensitive to noise interference. In [13], a DR-FR localization method using velocity difference compensation was proposed, effectively improving the accuracy of target positioning. In [15,16], a combination of array processing technology and the method of a time–frequency analysis was used to extract target information from the range-Doppler space to achieve the positioning of the trajectory of human motions, which provides a better idea for improving positioning accuracy. Furthermore, many time–frequency enhancement algorithms have been proposed for obtaining more accurate Doppler frequency and localization results [17]. However, the large amount of computation required for this method makes its real-time performance decrease. A target tracking algorithm based on data fusion is proposed in Ref. [18], but, compared with the most compact DF-DR radar structure, the proposed system needs to add an additional receiving unit. To optimize system costs, this paper chooses to improve the dual-frequency Doppler radar and mainly concentrates on a single-frequency Doppler radar (SF-DR).
A traditional SF-DR with a single transmitter and single receiver has the simplest structure and the lowest power consumption, enabling high-precision measurements of Doppler frequency information. However, it lacks the ability to estimate distance. For example, in [19], an SF-DR was used in gas gun experiments to detect particle velocities after small explosions. To achieve target positioning, many methods propose to increase the number of receivers to obtain multiple sets of direction of arrival information (DOA) for SF-DR moving-target positioning [20,21]. Nonetheless, the positioning accuracy and noise immunity of this method are not ideal. To better estimate target information, the literature [22] proposes to increase the number of transmitter units, employing array processing technology to estimate target motions. However, this array configuration requires a large-sized antenna group, significantly increasing the size and power consumption of the radar system. In [23], a scheme for the minimum receiver configuration of an SF-DR system is deduced for linear arrays, and a linear state estimation framework is preliminarily explored to address information loss due to the reduced number of sensors. In [24], a method of positioning with a combination of single and dual frequencies was proposed. However, the requirement for numerous repetitive experiments limits its practicality.
Different from existing methods, this article mainly focuses on a compact SF-DR system consisting of one transmitter and two receivers. And a target localization method for an SF-DR system based on the SABO (improved subtraction-average-based optimization) algorithm is proposed, which provides a more cost-effective solution for the portability of radar positioning systems. Compared with the traditional method, the main innovations of the proposed method are as follows:
- (1)
- An SF-DR target localization model is proposed. In this paper, the structure of the single-frequency radar system is simplified. Based on the compact structure of one transmitter and two receivers, the target positioning model is constructed by using the spatial geometric relationship and the Doppler frequency-shift information in the single-frequency echo signal. In this way, the system size and operating power consumption are optimized, and the problem of RF interference is reduced.
- (2)
- Different from the traditional method, which regards each time point as an independent detection unit, the proposed method considers the continuity of the target motion and divides the solution process into two stages: initial information estimation and trajectory information update. According to the inertia of human movements, the early motion parameters are used as a reference, and the later motion parameters are used as feedback to improve the accuracy of complex trajectory estimation.
- (3)
- Following the principle of least squares, this work proposes a corresponding SF-DR target positioning optimization function with the error of target motion information as the optimization goal and the changing trend of Doppler frequency as the constraint. The calculation process is simplified by converting and solving the unique solution of the superdefinite equations into finding the minimization of the fitness function.
- (4)
- An ISABO method is proposed and introduced into the process of solving target motion parameters. By merging the leader learning strategy, the learning information of the optimal solution vector is quickly provided for the overall movement of the individual populations. At the same time, the individuals that exceed the threshold are reset, and their corresponding calculation weights are removed to reduce the impact of invalid individuals on the solution. This approach can achieve decimeter-level positioning accuracy.
The remainder of this article is organized as follows. Section 2 presents the system model of a traditional DF-DR and the principle of the SABO algorithm. Section 3 presents the SF-DR target localization algorithm based on the ISABO method. Section 4 presents the experimental results. Section 5 discusses the experimental results of the proposed method. Section 6 concludes this article. Symbolic definitions are shown in the Appendix A.
2. System Model and Principles
2.1. Traditional Dual-Frequency Doppler Radar Positioning Model
Currently, in the field of human target detection, the most commonly used method is the DF-DR system. The most compact DF-FR system consists of a transmitter () and two receivers ( and ) [25]. Taking the receiver as the origin, a two-dimensional coordinate system is established, as shown in Figure 1.
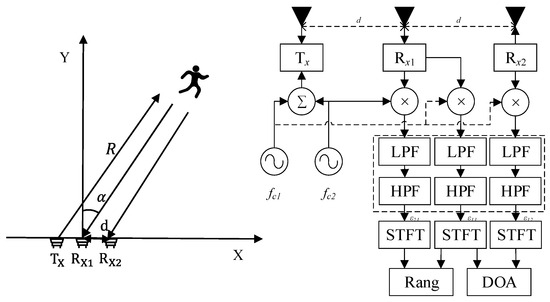
Figure 1.
The traditional double-frequency Doppler radar (DF-CW) positioning approach.
The transmitted signal T(t) be expressed as follows:
where A, , , , and are the carrier component amplitude, frequencies, and initial phases, respectively.
The echo signal is received by the receiver , and the echo signal is obtained after hardware filtering and demodulation, which can be represented as follows:
where is the number of targets, and is the m-th target scattering coefficient. is the distance between the transmitter and the n-th target. is the distance between the receiver and the n-th targets. C is the light velocity.
Then, the distance and the direction of arrival between the human target and the receiver can be expressed as follows:
where is the target Doppler frequency corresponding to the carrier frequency at the receiver . represents the initial phase for range and DOA estimation, respectively. is the wavelength of the first carrier component. d is the distance between antennas. C is the light velocity.
Therefore, the two-dimensional space coordinates of the mth target can be expressed as follows:
2.2. Subtraction-Average-Based Optimizer
The subtractive-average-based optimization (SABO) algorithm is a new evolutionary-based approach used to find the best solution to an optimization problem [25]. The key point of the algorithm is to update the position of group members in the search space by subtracting the average of the population individuals, since each individual population corresponds to a solution to the optimization problem. From a mathematical point of view, the population X can be expressed as an N × m matrix, where N is the number of individuals in the population and m is the search space dimension. The random initialization position of the population individuals in the search space is shown in Equation (6):
where represents the value of the i-th population in the search space in the d-dimension; is the random number between [0, 1]; and and are the lower and upper thresholds of the decision variables, respectively.
Then, according to Equation (7), move the individuals in the solution space and obtain a new position:
where is the position of the individual population after moving, and is a vector of the dimension D, in which components have a normal distribution with the values from the interval [0, 1]. is a special computational concept proposed by the SABO algorithm to deal with the arithmetic mean of the population individuals, as shown in Equation (8):
where and are the values of the objective function of the search individuals A and B, respectively. The sign is the signum function. is a D-dimensional vector, whose component is a random number distribution between [1, 2].
Finally, the moving population individuals were substituted into the objective function. According to the criterion of Equation (9), it is decided whether to update the position of the individuals in the population in that round.
where and are the objective function values corresponding to individual and , respectively. When all population individuals are updated, the first iteration of the algorithm is completed. After each iteration, the best individuals to date will be updated and retained until the last iteration of the algorithm. In the end, the best individual to be retained is the best solution to the optimization problem sought.
The initialization steps of the SABO algorithm for dealing with an optimization problem with m decision variables have a complexity that is equal to O(), where N is the number of search agents. Furthermore, the process of updating these search agents has a complexity that is equal to O(), where T is the total number of iterations of the algorithm. Therefore, the computational complexity of the SABO algorithm is equal to O().
3. SF-DR Target Localization Algorithm Based on the ISABO Method
3.1. Single-Frequency Doppler Radar Localization Model
In order to simplify the structure of the radar system and reduce the operating power consumption of the radar system, a positioning model and algorithm for SF-DR are proposed. The structure of the model refers to the structure of a compact DF-DR system. The SF-DR system structure consists of a transmitter () and two receivers ( and ), and its two-dimensional plane structure is shown in Figure 2. The human target moves in the direction of the dotted line with a speed of and an acceleration of .
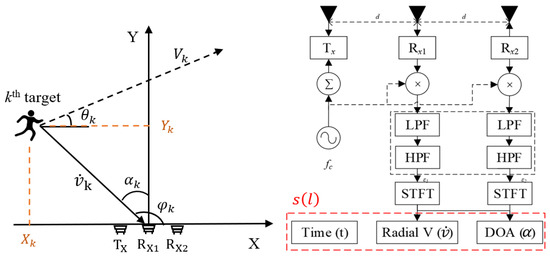
Figure 2.
The single-frequency Doppler radar (SF-DR) positioning approach.
Since the echo signal of a Doppler radar is a typical non-stationary signal, it is complicated to analyze and extract the corresponding Doppler features directly. In this paper, the most classical short-time Fourier transform (STFT) method is used for a time–frequency analysis to obtain the instantaneous frequency of the target. According to the obtained Doppler frequency estimation results, the corresponding mathematical model is constructed based on the spatial relationship between the receiver and the target, so as to derive the motion information of the target.
Specifically, in the proposed localization model, we take the time (), DOA and radial velocity of the target as inputs and the position () and motion information () of the target as outputs. Based on the kinematic theory, we establish a set of nonlinear superdefinite equations reflecting the change trend within the selected time window.
As shown in Figure 3, the data are selected along the sampling timeline in the form of a sliding time window with a length of L and an interval of ∆T, where ∆T = 1/2∙L. The available data in the window are denoted as , which contains the time , DOA , and radial velocity in the processed echo signal. Each corresponds to a nonlinear equation. By solving L equations, the target motion state corresponding to the first time point l = 1 in the time window j can be obtained. To ensure the accuracy and efficiency of the target positioning results, the calculation process was divided into two parts, viz., the initial-information-estimation and information-updating steps.
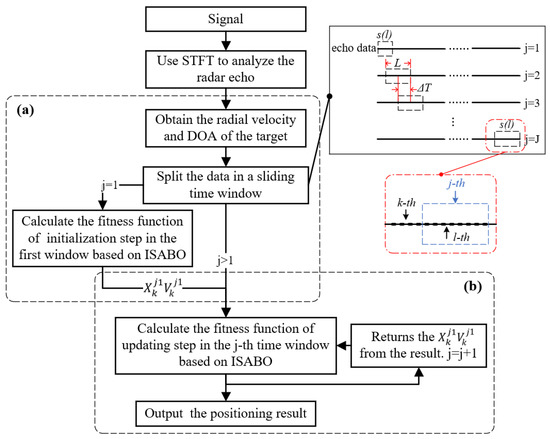
Figure 3.
Flowchart of the ISABO-based SF-DR human target localization algorithm.
- (a)
- Initial information estimation
In this step, the processing data involves the echo only in the first time window, and the time-window length is set to be short enough to make the target velocity variation negligible, viz., the target is assumed to move with a constant velocity. By simplifying the motion state to reduce the influence parameters, a more accurate initial position and state of the target motion can be obtained. Then, according to the geometric relationship in Figure 2, the position coordinates of the lth target in the jth time window (j = 1) are expressed as follows:
where are the target x-coordinate, velocity, moving direction angle, position angle, and direction of arrival, respectively, as Figure 2 shows.
Meanwhile, the connection between k, l, and j is based on the following numerical relationship:
can be expressed as follows:
Therefore, the nonlinear superdefinite system of equations used to solve can be expressed as follows:
- (b)
- Information updating
In this step, the processing data involves the echo in the subsequent windows, and the initial information obtained in the previous step will be used as reference information. To improve computational efficiency, the time-window length is extended. Moreover, the influence of acceleration on the target trajectory will be taken into account to improve the accuracy of the trajectory estimation results and the adaptability to complex trajectories. Then, the coordinates of the lth target in the jth time window can be expressed as follows:
where is the acceleration.
Furthermore, the system of equations used to solve can be expressed as follows:
3.2. Optimization Function for Targeting
It is difficult and inefficient to solve complex nonlinear superdefinite equations using traditional analytical methods. In order to solve this problem, we propose to build an optimization model for the localization problem. The error of the target motion information is taken as the optimization goal, and the motion law and mathematical law of the target in the given sliding window are taken as the constraints. Thus, the problem of solving a system of superdefinite equations is transformed into a problem of finding the minimum value of the optimization function.
Specifically, each optimization problem has a solution space, and the dimension of the space is equal to the number of decision variables for a given problem. The matrix K is used to represent the overall solution vector of the algorithm, as shown in Equation (18).
where N is the number of components, and D is the spatial dimension. is a set of components of a solution vector that contains information about a set of decision variables. In the initial-information-estimation stage, , and in the trajectory update phase, .
The optimization goal of the algorithm is the error of motion information. In this paper, it is expressed as the absolute value of the difference between the ideal value () and the estimated value (): . Therefore, in the initial-information-estimation step, the fitness equation for solving the target information at point k-th is as follows:
In the trajectory-update step, the fitness equation for solving the target information at the k-th point can be expressed as follows:
At the same time, the objective optimization function is defined as the mean square error value of all fitness equations within a set of time windows. Then, Equation (15), for the initial-information-estimation step in Part 3.1, can be transformed into the following:
Similarly, the objective optimization function in the trajectory-update step can be expressed as follows:
3.3. Improved Subtractive-Average-Optimization Algorithm
In this paper, an improved subtractive-average-optimization (ISABO) algorithm is proposed to solve the SF-DR target positioning optimization function.
The main principle of the SABO algorithm is to update the position of individuals in the population by using the arithmetic averaging of all individuals in the population. In this way, the ability of the algorithm to jump out of the local optimal is enhanced, and the accuracy of the optimization results is improved, which provides a new approach to solving optimization problems. However, the undifferentiated population-update steps in the traditional SABO algorithm will lead to a waste of computing resources, which will reduce the computational efficiency of the overall algorithm.
Therefore, to enhance the search ability of the algorithm, this paper improves the population position update mechanism (Equation (7)) of the SABO algorithm in combination with the leader learning strategy:
where the is the best individual in the current iteration round, and is a vector of the dimension D, in which components have a random distribution with the values from the interval [2,3].
Therefore, the traditional starting point of individual population positions is replaced by , and the information of the best individuals is used to improve the global search ability. At the same time, on this basis, the weight of the random factor is increased to ensure the development ability of individuals in the exploration stage and avoid falling into local optimum.
In addition, the traditional SABO algorithm does not deal with individuals that exceed the threshold range, which affects the accuracy and efficiency of the calculation results when dealing with complex optimization functions. Therefore, the extra individual reset step is added after the position update step (Equation (8)), as follows:
3.4. Localization Algorithm Flow
As shown in Figure 3, the specific process of an SF-DR target localization algorithm based on the ISABO method is as follows.
Initialize the ISABO parameters: the population size N; maximum number of iterations ; population dimension D; population individual position (decision variable); and the upper and lower bound and lower bound of the decision variable.
According to Equation (22), calculate the fitness function value corresponding to each population individual, where the individual with the smallest fitness function value is the best individual of the current round.
Calculate the position of the individuals in the population after displacement according to Equation (24).
Update the population individuals according to Equation (9) and reset the individuals that are out of the threshold range. And the best individual and the corresponding function value are retained.
Determine whether to terminate the cycle. When the number of iterations reaches the maximum value or the objective function result reaches the preset accuracy, the ISABO calculation process of the round is terminated, and the optimal individual and the corresponding function value are output. Otherwise, go back to step 2.
According to the output results obtained in the j(j = 1) round, input the solved and as reference quantities into the j + 1 round of ISABO calculation (the trajectory-information-update step). j = j + 1. Update the ISABO parameter settings: the population size , maximum number of iterations , and population dimension . And set the thresholds ( and ) of population individuals to the near range of the results from the previous round.
Change the fitness function in step 2 from Equation (22) to Equation (23). Repeat steps 2 to 5 until the global optimal individual and corresponding function value are obtained.
Record the output result. Repeat steps 6 to 7 until all available data have been calculated. Finally, the trajectory result of the target motion is obtained.
4. Experimental Results
In order to verify the performance of the proposed method, we set up an experimental scenario of 8 m × 8 m in the laboratory, as shown in Figure 4a. The Doppler radar device used is shown in Figure 4b, and the radar parameter settings are shown in Table 1.

Figure 4.
(a) Detection scene; (b) Doppler radar prototype.

Table 1.
Radar system parameters.
The radar system used is an improved version of the traditional compact DF-DR system. It is based on the original single-transmitter, dual-receiver system but with one less transmission carrier frequency. The radar system collects echo signals every 0.005 s and sends the signals to a computer for processing. In the process of experimental measurements, we first use the labels on the ground to draw the human target’s movement path. Then, we statistic to obtain the speed of the target, find each step length, and mark on the path, as shown in Figure 5. In our experiments, the human targets were in accordance with a constant stepping frequency of 2 Hz along the path of motion.
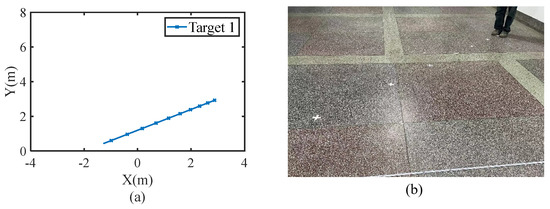
Figure 5.
Motion trajectory with information on each step point. (a) Target movement trajectory; (b) Trajectory markers in the experimental scene.
The reference coordinate system, as shown in Figure 2, is established with the receiver as the coordinate origin (0, 0). At the same time, the traditional short-time Fourier transform (STFT) method based on the DF-DR system, the Bezier-based Hough transforms (Bezier–Hough) method [26] based on the DF-DR system, and the SABO method based on the SF-DR system were used as comparison algorithms, and the performance differences between them and the proposed algorithm were compared and analyzed.
4.1. Single-Target Localization
In the first experiment, the human target moved from coordinates (3, 1.5) to coordinates (0.87, 7) with a velocity of 0.4 m/s and an acceleration of 0.3 m/s2, and its reference trajectory is shown in Figure 5a. In the initial-information-estimation step of the proposed method, the time-window length was set to 6, and Table 2 shows the parameters of ISABO and SABO in this stage. In the trajectory-information-update step, set the window length to 10, and the parameters of ISABO and SABO are updated to those shown in Table 3.

Table 2.
Initial parameter settings for the ISABO algorithm.

Table 3.
Parameter update settings of ISABO algorithm.
Figure 6b–e shows the trajectory localization results of the four algorithms. The red line is the estimation result of each algorithm, and the black dotted line is the real trajectory. As can be seen from Figure 6b, due to the limitation of Heisenberg’s principle and the high dynamic characteristics of the target echo, the positioning results of the STFT algorithm present a large deviation from the actual trajectory. Compared with the STFT algorithm, the Bezier–Hough method improves the frequency estimation accuracy and thus optimizes the localization results, as shown in Figure 6c. However, a small range of errors still exists especially around the endpoints of each time window. Figure 6d shows the single-frequency positioning results based on the SABO method, and it can be seen that although the method can realize the positioning of single-frequency target trajectories, the positioning results are highly fluctuating and present large deviations in some areas. In contrast, the trajectory localization results of the proposed method based on the ISABO algorithm in Figure 6e are the best during the whole detection period. Figure 6f gives the coordinate estimation error for each of the four methods in absolute form. It can also be seen from this figure that the estimation results of the ISABO algorithm are more stable and accurate. Table 4 lists the root mean square (RMS) errors of the four methods for the complete trajectory positioning results. From the tabular data, it can be seen that, compared with the STFT method, the Bezier–Hough method and the SABO method, the estimation accuracy of the proposed algorithm is improved by 42%, 6%, and 51.0%, respectively.
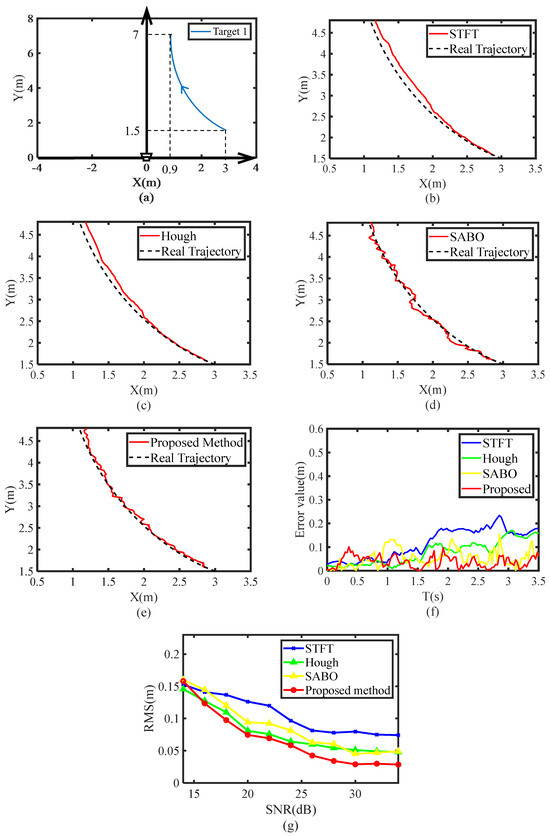
Figure 6.
(a) Trajectory of the target; (b) trajectory estimation results of STFT; (c) trajectory estimation results of Bezier–Hough; (d) trajectory estimation results of SABO; (e) trajectory estimation results of the proposed method; (f) comparison of trajectory estimation errors; (g) the RMS errors with different SNRs.

Table 4.
RMS errors for single-target localization results.
Moreover, the original echo SNR is about 35 dB. To test the robustness of the algorithms, additional Gaussian white noise (WGN) was added to the original echo to adjust the signal-to-noise ratio (SNR) from 15 dB to 35 dB. Comparative experiments are carried out every 2 dB interval to obtain the estimation results of the above algorithms in different SNR conditions, and the specific RMS error is shown in Figure 6g. From the figure, it can be seen that the robustness of the proposed algorithm is the best when the SNR is greater than 17 dB. This is mainly because the randomness of the ISABO algorithm and the redundancy of the computing data can effectively enhance the noise immunity of the proposed tracking algorithm. When the SNR is 22 dB, the estimation errors of the STFT method, the Bezier–Hough method, the SABO method and the proposed algorithm can be increased by 0.0254 m, 0.0224 m, and 0.0298 m, respectively. When the SNR was 17 dB, it increased by 0.785 m, 1.057 m, and 1.297 m, respectively. In this process, the positioning error estimated by the STFT method is the largest, but the estimation results of the Bezier–Hough method, the SABO method, and the algorithm proposed in this paper are more sensitive to noise changes. This is mainly because the estimation error of the Bezier–Hough method has a strong correlation with the accuracy of the model endpoint selection, which results in poor noise immunity. The algorithm proposed in this paper is based on solving nonlinear superdefinite equations, and even if there is a close calibration of the ISABO algorithm, the accuracy of the calculation results will be affected when the accuracy of the input data is greatly affected by noise.
To verify the performance of the improved subtractive-average-optimization algorithm, four high-latitude multimodal functions (F8–F11) in the CEC2017 test set were selected as test functions. Particle swarm optimization (PSO) and the gray wolf algorithm (GWO) were added as comparison algorithms for simulation experiments. The experimental results are shown in Figure 7, Figure 8, Figure 9 and Figure 10. The blue star line represents the convergence curve of the PSO algorithm, the purple triangle line represents the convergence curve of the GWO algorithm, the green circle line represents the convergence curve of the SABO algorithm, and the red pentagon line represents the convergence curve of the ISABO algorithm.
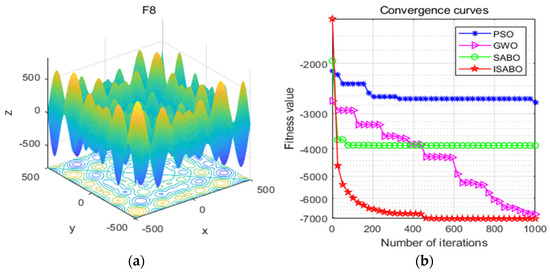
Figure 7.
(a) Three-dimensional diagram of the F8 function; (b) comparison of the fitness function convergence curves.
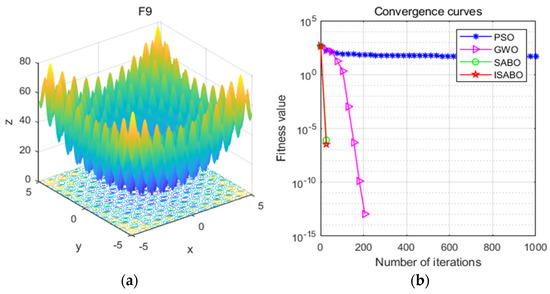
Figure 8.
(a) Three-dimensional diagram of the F9 function; (b) comparison of the fitness function convergence curves.
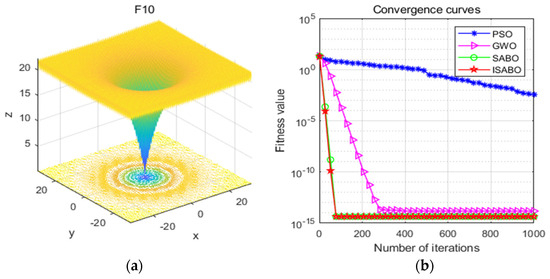
Figure 9.
(a) Three-dimensional diagram of the F10 function; (b) comparison of the fitness function convergence curves.
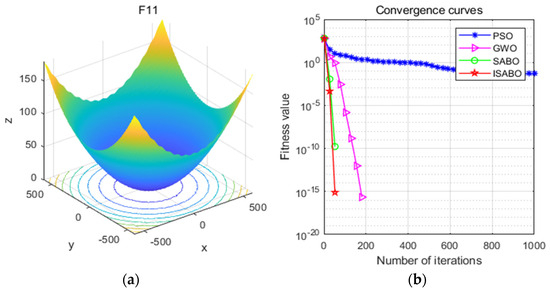
Figure 10.
(a) Three-dimensional diagram of the F11 function; (b) comparison of the fitness function convergence curves.
Figure 7a, Figure 8a, Figure 9a and Figure 10a are three-dimensional schematic diagrams of the function. It can be seen that the high-latitude multimodal has a large number of local optimal solutions, which can test the algorithm’s exploration ability and jump out of the local optimal ability. Figure 7b, Figure 8b, Figure 9b and Figure 10b show the convergence process of the fitness function value of the ISABO algorithm with other comparison algorithms. As can be seen from these figures, the fitness value curve corresponding to the improved SABO algorithm decreases faster and finally converges to a smaller value. This means that when solving the proposed algorithm, there will be fewer iterations required to reach the optimal solution, and at the same time, the accuracy will be higher.
Figure 11 shows the convergence of the fitness function value corresponding to the initial-information-estimation stage in the proposed positioning algorithm. As can be seen from this figure, the ISABO algorithm also performs best when solving the proposed problem.
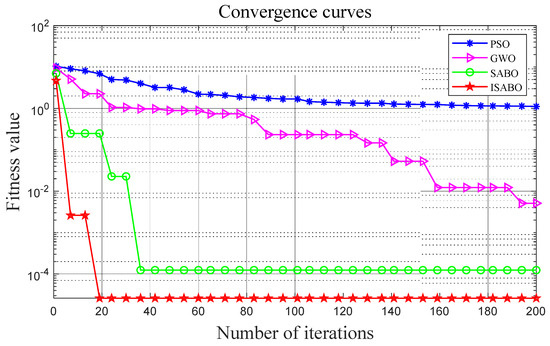
Figure 11.
The convergence comparison of the proposed fitness functions.
4.2. Multi-Target Localization
To further evaluate the algorithm’s performance in a multi-target tracking scenario, two moving targets were arranged to move in the detection area. As shown in Figure 12a, target 1 moved from coordinates (−2, 2.5) to coordinates (1.63, 5.77) with an initial velocity of 0.7 m/s and an acceleration of 0.1 m/s2, while target 2 moved from coordinates (−2.5) to coordinates (3.22, 2.76) with an initial velocity of 0.6 m/s and an acceleration of 0.2 m/s2. The estimation results of the above three methods are shown in Figure 12b–d, where the black dotted line is the real trajectory. As can be seen from Figure 12b, there is a large deviation in the estimation results of the STFT method, which is mainly due to the insufficient frequency resolution caused by the uncertainty principle, and in turn causes the frequency estimation error. The Bezier–Hough method solves this problem by curve fitting, but it is still affected by the accuracy of data endpoint selection at the beginning of target 1’s movements, resulting in a small range of deviations, as shown in Figure 12c. In contrast, the algorithm proposed in this paper performs best in the trajectory estimation of both targets. The RMS errors of the above three methods for the overall trajectory estimation results of the two targets are recorded in Table 5. As can be seen from this table, the positioning accuracy of the proposed algorithm is improved by 30.5% and 15.2% and 23.6% and 4.5%, respectively, compared with the STFT method and the Bezier–Hough method.
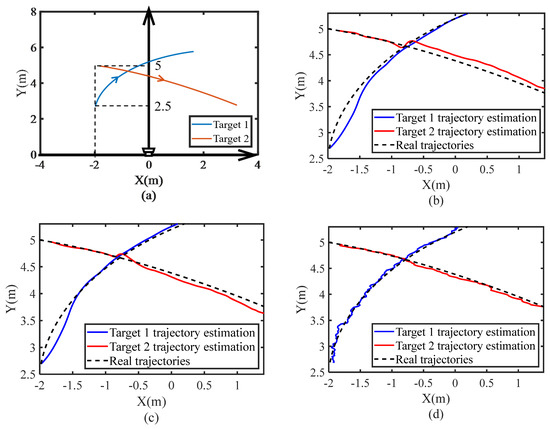
Figure 12.
(a) Trajectory of the target; (b) trajectory estimation results of STFT; (c) trajectory estimation results of Bezier–Hough; (d) trajectory estimation results of the proposed method.

Table 5.
RMS errors for multiple-target localization results.
5. Discussion
The optimization results of the aforementioned F8-F11 test functions indicate that the ISABO algorithm successfully provided the global optimal solution for all four test functions, demonstrating a high exploration capability. Analysis of the results also reveals that, compared to the other three competing algorithms, the ISABO algorithm shows superior performance in solving high-dimensional multimodal function problems, converging to lower optimal fitness values with fewer iterations. Additionally, when handling the proposed optimization function, the ISABO algorithm demonstrates a faster convergence rate and lower convergence values compared to the traditional SABO algorithm. This effectively enables accurate estimation of indoor target motion trajectories using single-frequency continuous wave radar.
Applying the proposed ISABO algorithm to the SF-DR target localization method, experimental results indicate that, compared to the traditional DF-DR localization method based on STFT and the DF-DR localization method based on the Bezier-Hough approach, this algorithm can achieve more accurate localization results at a lower cost, effectively enabling decimeter-level precision tracking of targets.
However, the proposed algorithm’s noise resistance needs to be enhanced. The study simulated the algorithm’s performance under different SNRs by adding WGN to the echo signals. However, environmental noise in real-world applications is much more complex and variable. Therefore, future research should consider a wider range of environmental conditions to further investigate and improve the algorithm’s noise resistance.
6. Conclusions
In this paper, a single-frequency Doppler radar human target localization algorithm based on an improved SABO algorithm is proposed. To solve the defects of a complex antenna array structure and poor positioning accuracy of traditional SF-DRs, this paper improves the traditional SF-DR antenna array to form a single-transmitter, dual-receiver system structure. By analyzing the variation trends of Doppler frequency information across different receiving units, a mathematical optimization model for target localization is proposed. Unlike traditional methods that treat each time point as an independent detection unit, this approach divides the solution process into two stages: initial information estimation and trajectory information update. This effectively enhances target localization accuracy and system operational efficiency while reducing transmission power consumption and avoiding RF interference issues. To optimize the efficiency of solving the SF-DR target localization function, an improved SABO method is introduced. This method incorporates a leader learning strategy to rapidly provide optimal solution vectors for the overall displacement of the individuals. At the same time, it resets individuals exceeding the threshold and removes their computational weights to reduce the impact of ineffective individuals on the solution. The experimental results indicate that the proposed ISABO-based SF-DR target localization algorithm achieves centimeter-level localization accuracy while optimizing computational costs.
However, the proposed method has some limitations. First, although it achieves good localization accuracy, the overall computation time is still subject to the parameter settings of the optimization algorithm and requires further optimization. Second, the noise resistance of the algorithm needs improvement. This study simulated the algorithm’s performance under various SNRs by adding Gaussian white noise to the echo signal, but real-world environmental noise is more complex and variable. Future research should incorporate a wider range of environmental conditions. Lastly, the proposed method’s ultimate application scenario is through-wall radar detection. Future work should integrate wall-interference algorithms to address more indoor detection scenarios.
Author Contributions
Conceptualization, Y.J. and Y.D.; methodology, Y.J.; software, Y.J.; validation, Y.J. and Y.D.; formal analysis, Y.J.; investigation, Y.J.; resources, Y.D.; data curation, Y.J.; writing—original draft preparation, Y.J.; writing—review and editing, Y.J. and Y.D.; visualization, Y.J.; supervision, Y.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Special Foundation for Hunan Innovation Province Construction under Grant 2020RC3004 and the Foundation Research Funds for the Natural Science Foundation of Hunan Province under Grant 2022JJ30749.
Data Availability Statement
The original contributions presented in this study are included in the article, and further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| SABO | Subtraction-average-based optimizer |
| ISABO | Improved subtraction-average-based optimization |
| SF-DR | Single-frequency Doppler radar |
| MF-DR | Multi-frequency Doppler radar |
| FM-DR | Frequency-modulated Doppler radar |
| LPF | Low-pass filter |
| HPF | High-pass filter |
| DOA | Direction of arrival |
| STFT | Short-time Fourier transform |
| Bezier–Hough | Bezier-based Hough transforms |
| RMS | Root mean square |
| PSO | Particle swarm optimization |
| GWO | Gray wolf algorithm |
Appendix A

Table A1.
Nomenclature.
Table A1.
Nomenclature.
| Notation | Implication |
|---|---|
| Frequency | |
| Initial phase for range | |
| Initial phase for DOA | |
| Wavelength | |
| C | Light velocity |
| N | Number of individuals |
| m | Search space dimension |
| Value of i-th population in d-dimension search space | |
| Random number between [0, 1] | |
| Lower thresholds of the decision variables | |
| Upper thresholds of the decision variables | |
| Normal distribution from the interval [0, 1] | |
| Subtractive-averaging operator | |
| Speed of the target | |
| Acceleration of the target | |
| L | Time-window length |
| Direction of arrival | |
| t | Time |
| Radial velocity of the target | |
| Moving direction angle of the target | |
| Position angle of the target | |
| x-coordinate of the target | |
| y-coordinate of the target | |
| Improved Subtractive-averaging operator |
References
- Li, C.; Zhen, J.; Chang, K.; Xu, A.; Zhu, H.; Wu, J. An Indoor Positioning and Tracking Algorithm Based on Angle-of-Arrival Using a Dual-Channel Array Antenna. Remote Sens. 2021, 13, 4301. [Google Scholar] [CrossRef]
- Kim, D.; Farhad, A.; Pyun, J. UWB positioning system based on LSTM classification with mitigated NLOS effects. IEEE Internet Things J. 2020, 10, 1822–1835. [Google Scholar] [CrossRef]
- Zhang, R.; Cheng, L.; Wang, S.; Lou, Y.; Gao, Y.; Wu, W.; Ng, D. Integrated Sensing and Communication with Massive MIMO: A Unified Tensor Approach for Channel and Target Parameter Estimation. IEEE Trans. Wirel. Commun. 2024, 1, 1276–1536. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Ding, Z. Multi-Target Position and Velocity Estimation Using OFDM Communication Signals. IEEE Trans. Commun. 2020, 68, 1160–1174. [Google Scholar] [CrossRef]
- Lin, A.; Hao, H. Doppler and direction-of-arrival (DDOA) radar for multiple-mover sensing. IEEE Trans. Aerosp. Electron. Syst. 2009, 43, 1496–1509. [Google Scholar] [CrossRef]
- Ding, Y.; Lin, X.; Sun, Y. Modified linear predictive coding approach for moving target tracking by Doppler radar. J. Appl. Remote Sens. 2016, 10, 035020. [Google Scholar] [CrossRef]
- Gu, C.; Peng, Z.; Li, C. High-Precision Motion Detection Using Low-Complexity Doppler Radar with Digital Post-Distortion Technique. IEEE Trans. Microw. Theory Tech. 2016, 64, 961–971. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Q.; Fathy, A. CW and Pulse–Doppler Radar Processing Based on FPGA for Human Sensing Applications. IEEE Trans. Geosci. Remote Sens. 2012, 51, 3097–3107. [Google Scholar] [CrossRef]
- Leigsnering, M.; Ahmad, F.; Amin, M.; Zoubir, A. Compressive Sensing-Based Multipath Exploitation for Stationary and Moving Indoor Target Localization. IEEE J. Sel. Top. Signal Process. 2015, 9, 1469–1483. [Google Scholar] [CrossRef]
- Grajal, J.; Yeste-Ojeda, A.; Rubio-Cidre, G.; Badolato, A.; Mencia-Oliva, B. Multiple purpose hardware for sensors at 100 GHz. In Proceedings of the IET International Conference on Radar Systems (Radar 2012), Glasgow, UK, 22–25 October 2012; p. 23. [Google Scholar]
- Herath, S.C.K.; Nagahawatte, C.V.D.; Pathirana, P.N. Tracking multiple mobile agents with single frequency Continuous Wave radar. In Proceedings of the 2009 International Conference on Intelligent Sensors, Sensor Networks and Information Processing (ISSNIP), Melbourne, Australia, 7–10 December 2009; pp. 163–167. [Google Scholar]
- Li, F.; Xia, Y.; Ma, X.; Zhao, B. Indoor Human Localization Method of Dual Frequency Continuous Wave Radar with Velocity Deviation Compensation. J. Electron. Inf. Technol. 2017, 39, 1432–1438. [Google Scholar]
- Shobao, S.R.; Hao, L. Through-wall tracking of human movers using joint Doppler and array processing. IEEE Geosci. Remote Sens. Lett. 2008, 5, 537–541. [Google Scholar]
- Amin, M.; Zemany, P.; Setlur, P.; Ahmad, F. Moving Target Localization for Indoor Imaging using Dual Frequency CW Radars. In Proceedings of the Fourth IEEE Workshop on Sensor Array and Multichannel Processing, Waltham, MA, USA, 12–14 July 2006; pp. 367–371. [Google Scholar]
- Pathirana, P.N.; Herath, S.C.; Savkin, A.V. Multitarget Tracking via Space Transformations Using a Single Frequency Continuous Wave Radar. IEEE Trans. Signal Process. 2012, 60, 5217–5229. [Google Scholar] [CrossRef]
- Zhou, C.; Griffin, J.D. Accurate phase-based ranging measurements for backscatter RFID tags. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 152–155. [Google Scholar] [CrossRef]
- Peng, Y.; Ding, Y.; Zhang, J.; Jin, B.; Chen, Y. Target trajectory estimation algorithm based on time–frequency enhancement. IEEE Trans. Instrum. Meas. 2023, 72, 8500807. [Google Scholar] [CrossRef]
- Zhu, A.; Qi, X.; Fan, T. Indoor localization for passive moving objects based on a redundant SIMO radar sensor. IEEE J. Emerg. Sel. Top. Circuits Syst. 2018, 8, 271–279. [Google Scholar] [CrossRef]
- Gu, Z.; Wang, J.; Shen, F. Blind Separation of Doppler Human Gesture Signals Based on Continuous-Wave Radar Sensors. IEEE Trans. Instrum. Meas. 2019, 69, 2659–2661. [Google Scholar] [CrossRef]
- Kim, Y.; Sekhon, S.S. Detection of moving target and localization of clutter using Doppler radar on mobile platform. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1156–1160. [Google Scholar]
- Jin, T.; Song, Y. Review on human target detection using through-wall radar. Chin. J. Radio Sci. 2020, 35, 486–495. [Google Scholar]
- Zhang, J.A.; Liu, F.; Masouros, C. An overview of signal processing techniques for joint communication and radar sensing. IEEE J. Sel. Top. Signal Process. 2021, 15, 1295–1315. [Google Scholar] [CrossRef]
- James, W.B. Atmospheric laser Doppler velocimetry—An overview. Opt. Eng. 1980, 19, 533–542. [Google Scholar]
- Volkan, C.; James, H.M. General direction-of-arrival tracking with acoustic nodes. IEEE Trans. Signal Process. 2005, 53, 1–12. [Google Scholar]
- Pavel, T.; Mohammad, D. Subtraction-Average-Based Optimizer: A New Swarm-Inspired Metaheuristic Algorithm for Solving Optimization Problems. Biomimetics 2023, 8, 149. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Sun, Y.; Yu, X. Bezier-Based Hough Transforms for Doppler Localization of Human Targets. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 173–177. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).